Abstract
Copy number variants (CNVs), ranging from about one kilobase to several megabases, are alterations of DNA of a genome that results in the cell having a less or more than two copies of segments of the DNA. Such CNVs have been shown to be associated with many complex phenotypes, ranging from diseases to gene expressions. Novel methods have been developed for identifying CNVs both at individual and at population levels. However, methods for testing CNV association are limited. Most available methods employ a two-step approach, where CNVs carried by the samples are identified first and then tested for association. However, the results of such tests depend on the threshold used for CNV identification and also the number of CNVs to be tested. We develop a method, CNVtest, to directly identify the trait-associated CNVs without the need of identifying sample-specific CNVs. We show that CNVtest asymptotically controls the type I error and identifies true trait-associated CNVs with a high probability. We demonstrate the methods using simulations and an application to identify the CNVs that are associated with population differentiation.
Keywords: Generalized linear model, Population differentiation, Scan statistics, Score Statistic
1. INTRODUCTION
Structural variants in the human genome (Sebat et al., 2004; Feuk et al., 2006), including copy number variants (CNVs) and balanced rearrangements such as inversions and translocations, play an important role in the genetics of complex disease. CNVs, ranging from about one kilobase to several megabases, are alterations of DNA of a genome that results in the cell having less or more than two copies of segments of the DNA. Analysis of CNVs in developmental and neuropsychiatric disorders (Feuk et al., 2006; Walsh et al., 2008; Stefansson et al., 2008; Stone et al., 2008) and in cancer (Diskin et al., 2009) has led to the identification of novel disease-causing mutations, thus contributing important new insights into the genetics of these complex diseases. Identifying the CNVs that are associated with complex traits is an important problem in human genetic research.
Many novel and powerful statistical methods have been developed recently for identifying the CNVs in a given sample based on array data, SNP chip intensity data and next generation sequencing data. Important examples include the optimal likelihood ratio selection method (Jeng et al., 2010), the hidden Markov model-based method (Wang et al., 2007) and change-point based methods (Olshen et al., 2004). To identify the recurrent copy number variants that appear in multiple samples, Zhang et al. (2010) introduced a method for detecting simultaneous change-points in multiple sequences that is only effective for detecting the common variants. Siegmund et al. (2010) extended their method by introducing a prior variant frequency that needs to be specified. Jeng et al. (2013) proposed a proportion adaptive sparse segment identification procedure that is adaptive to the unknown CNV frequencies.
Despite these novel methods for CNV detection and identification, methods for testing the CNV association are very limited. Current methods for CNV testing fall into two categories. One is to assume that a set of CNVs are known and to test association of these CNVs with complex phenotypes. Barnes et al. (2008) developed an approach for testing CNV association using a latent variable and mixture modeling framework. However, the current database of all CNVs are still very incomplete and testing only the known CNVs can miss the new CNVs that are associated with the phenotype of interest. Another common approach for CNV testing is a two-step approach, where CNVs are first identified for each sample and the CNVs that appear in multiple samples are then tested using chi-square or Fisher’s exact test. One limitation of such approaches is that the uncertainty associated with the inferred CNVs are not accounted for in the testing and the CNVs identified depend on the threshold used. In addition, it is not clear how one should control for the genome-wide error rate since the number of CNVs to be tested is not known before performing the single sample CNV analysis. Shi et al. (2014) developed a variable threshold exact test (VTET) for testing disease associations of CNVs randomly distributed in the genome using intensity data from SNP arrays. The test was developed for the scenario that cases are more frequently disrupted by CNVs than controls in a given genomic region while CNVs are randomly distributed in the region with various boundaries.
In this paper, we propose a new statistical method for identifying trait-associated CNVs. Instead of assuming a known set of CNVs or first identifying the CNVs carried by the samples, the proposed method directly identifies the CNVs that are associated with the trait of interest. Different from VTET that partitions autosomal chromosomes into segments with a pre-defined length (e.g., 50 SNPs), the proposed procedure scans the genome with intervals of variable lengths and identifies the trait-associated CNVs based on examining the score statistics. Specifically, for a given candidate interval, we first evaluate whether there are any samples that may contain CNVs overlaping with this interval. We consider all candidate intervals of variable lengths and identify the set of interval that overlap with the CNVs of at least one sample. We then test for phenotype association only for the intervals in the selected set. The procedure is computationally faster than the two-step approaches since it only requires to scan the genome once. In addition, since the association test is performed for each interval in the identified set, we overcome the problem of post-processing the intervals of possible variable lengths identified in single-sample CNV identification. We show that the procedure can control the genome-wide error rate and also has a high probability of identifying the trait-associated CNVs.
The paper is organized as follows. We present the statistical model and score test for a candidate genomic segment or interval in Section 2. In Section 3, we present a scanning procedure for identifying trait-associated CNVs and give the theoretical properties. We evaluate the performance of our test using simulations in Section 4. In Section 5, we demonstrate our method in identifying the CNVs that are associated with population differentiation. Finally, we give a brief discussion in Section 6.
2. Statistical Model and CNV Association Test
Suppose that we have data on n independent individuals. Let Yi be the phenotype value for the ith individual, Xij be the observed marker intensity (e.g., the log R Ratio from the SNP chip data) for the ith individual and jth marker, for i = 1, ···, n and j = 1, ···, m. Here Yi can be a binary variable as in case-control studies or continuous variable, e.g., in eQTL studies where Yi can be the expression level of a gene. For the SNP chip data, the observed marker intensity data is log R-Ratio, Xij = log2(Robs=Rref ), where Robs represents the total intensity of two alleles at the jth SNP for the ith sample and Rref the corresponding quantity for a reference sample. When there is no copy number change in a genomic region for individual i, we expect that Xijs in that region are realizations of a baseline distribution. In the following, for each sample, we normalize the intensity data to have variance of 1 by dividing the median absolute deviation. Suppose there is a total of q = qm,n CNVs in all n individuals with q possibly increasing with m and n and is unknown. Let
 = {I1, …, Iq} be the collection of the corresponding CNV segments/intervals. The value Xij in a CNV region deviates from 0 to the negative or positive side depending on whether the region is deleted or duplicated.
= {I1, …, Iq} be the collection of the corresponding CNV segments/intervals. The value Xij in a CNV region deviates from 0 to the negative or positive side depending on whether the region is deleted or duplicated.
Since only a certain proportion of the samples carry a given CNV, we denote the carriers proportion for CNV at Ik as πk, 1 ≤ k ≤ q. We assume
| (1) |
where μk ≠ 0 represents the mean value of the jump sizes in the k-th CNV region and σk may or may not equal to 1 to reflect the fact that different variation may be introduced by the CNV carriers. Here πk, μk and σk are unknown for each Ik ∈
 .
.
For a given candidate interval τ and individual i, we summarize the marker intensity data in this interval by the length-standardized sum
| (2) |
Further, define
| (3) |
for some ν > 0 to indicate whether or not the ith individual carry some copy number changes in interval τ. The threshold ν will be specified in next section. To link carrier status at interval τ to the phenotype, we assume the following generalized linear model (GLM) for the phenotype Yi with the likelihood function given by,
| (4) |
where ψ= g(α+ βτ Ziτ) is the link function for Ziτ and Yi and γ is the dispersion parameter. In this model, α is the intercept and βτ is the regression coefficients that associates the possible CNV τ to the mean value of the phenotype. Our goal is to identify the elements in
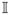 that have non-zero β coefficient. The identified elements indicate the locations of the trait-associated CNVs.
that have non-zero β coefficient. The identified elements indicate the locations of the trait-associated CNVs.
3. A Procedure for Identifying the Trait-associated CNVs and Its Theoretical Properties
In this section, we present a scanning procedure for identifying the trait-associated CNVs followed by the theoretical analysis of its type I error controls and power.
3.1 A scanning procedure for identifying the trait-associated CNVs
Since most of CNVs are short, we only consider short intervals with length ≤ L in the sequences of the observed genome-wide data. The L is chosen to satisfy the following condition:
| (5) |
where s̄ = max1≤k≤q |Ik| and d = min1≤k≤q−1{distance between Ik and Ik+1}. This condition guarantees that all the CNV segments can be covered by some intervals considered in the algorithm and, at the same time, none of the intervals is long enough to reach more than one CNV segment. Since most CNVs are very short and sparse, condition (5) is easy to be satisfied. In practice, we tend to choose L based on some prior knowledge about the data generating platforms. For 600K SNP arrays, the typical size of CNVs is fewer than 20 SNPs. We usually choose L = 20. Ideally, we should choose L a little larger than the maximum length of the CNVs. Large L increases the computational time since Lm intervals have to be scanned. In contrast, small L tends to divide long CNVs into two small contiguous ones. However, post-processing of the results can easily combine the contiguous CNVs into one CNV. Let
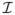 be the collection of all mL intervals of length ≤ L. The threshold in (3) is set at
be the collection of all mL intervals of length ≤ L. The threshold in (3) is set at
| (6) |
This is the same threshold used in Jeng et al. (2010) for detecting CNVs in a long sequence of m genome-wide observations for one individual. Threshold at this level optimally controls false positive CNV identification for each individual asymptotically under the assumption of additive Gaussian noises with equal variances. It can separate the CNVs from the noise as long as the signal segments are in the identifiable region (Jeng et al., 2010). This greatly reduces the number of intervals that need to be considered for association test.
We first select the intervals in
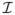 that have Ziτ = 1 for at least one individual and denote the collection of such intervals as
that have Ziτ = 1 for at least one individual and denote the collection of such intervals as
| (7) |
Let r̂ = |
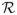 | be the total number of such intervals. Note that the collection
| be the total number of such intervals. Note that the collection
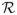 is much smaller than
is much smaller than
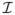 and only includes intervals where copy number changes are observed in the samples.
and only includes intervals where copy number changes are observed in the samples.
As a second step, based on the GLM model (4), we test
for any τ ∈
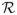 using the score statistic
using the score statistic
| (8) |
where SZτ and SY are the sample standard deviations of Zτ and Y. The score statistic Sn,τ has an asymptotic standard normal distribution under Hτ0 for τ ∈
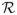 . Therefore, we reject Hτ0 if |Sn,τ| > λ, where λ is a threshold determined by the limiting distribution of Sn,τ under Hτ0 and the number of the score tests performed. We set
. Therefore, we reject Hτ0 if |Sn,τ| > λ, where λ is a threshold determined by the limiting distribution of Sn,τ under Hτ0 and the number of the score tests performed. We set
| (9) |
in order to control the genome-wide error. This threshold is chosen based on extreme value theory of standard normal random variable. We have
with probability tending to 1 under the null hypothesis of no phenotype-associated CNVs.
Our scanning procedure, called CNVtest, identifies the elements in
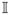 that are significantly associated with the trait value Y by selecting the intervals in
that are significantly associated with the trait value Y by selecting the intervals in
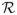 with their absolute score statistics above λ and achieving local maximums. Specifically, CNVtest involves the following steps:
with their absolute score statistics above λ and achieving local maximums. Specifically, CNVtest involves the following steps:
Pick an L. Select
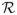 as in (7).
as in (7).Calculate Sn,τ as in (8) for all τ ∈
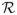 .
.Let
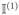 = {τ ∈
= {τ ∈
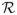 : |Sn,τ| > λ}, where λ is defined in (9). Let l = 1.
: |Sn,τ| > λ}, where λ is defined in (9). Let l = 1.Let Îl =
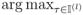 |Sn,τ|, and update
|Sn,τ|, and update
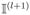 =
=
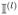 \{τ ∈
\{τ ∈
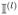 : τ ∩ Îl ≠ ∅}.
: τ ∩ Îl ≠ ∅}.Repeat Step 4–5 with l = l + 1 until
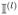 is empty.
is empty.
Finally, we denote the trait-associated CNVs by
 = {Î1, Î2, …}. If this set is empty, then we conclude that there is no trait-associated CNV.
= {Î1, Î2, …}. If this set is empty, then we conclude that there is no trait-associated CNV.
3.2 Theoretical results on error control and power analysis
Recall that q = qm,n is the total of number of true CNVs in n individuals. We assume
| (10) |
which implies that the CNVs are sparse. Further, for each CNV, we assume
| (11) |
for some ε > 0. Condition 11 is required since Jeng et al. (2010) shows that this is the detection boundary for any statistical procedure to identify the CNVs. This condition assumes that our combined CNV set
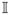 only include the statistically detectable CNVs.
only include the statistically detectable CNVs.
The following theorem states that with a large probability, CNVtest controls the genome-wide error rate. In other words, the CNVtest does not select the null intervals in
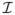 .
.
Theorem 1
Assume (1), (4), (10), (11), and (5). Let
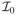 = {τ ∈
= {τ ∈
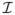 : τ ∩ Ik = ∅ for all Ik ∈
: τ ∩ Ik = ∅ for all Ik ∈
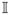 } be the set of intervals that do not overlap with any of the CNVs in the true CNV set
} be the set of intervals that do not overlap with any of the CNVs in the true CNV set
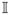 . Then
. Then
This theorem implies that the probability of CNVtest identifying wrong trait-associated CNVs goes to zero when the sample size is large enough. Our proof of Theorem 1 in Appendix implies that P(∃τ ∈ I0 : τ ∈ Î) is asymptotically bounded by , which goes to zero given conditions (5) and (10). Therefore, the convergence rate is asymptotically faster than , where q is the number of CNVs, m the dimensionality/total number of markers, and L the length of the longest scanning interval.
We next study the power of CNVtest in identifying the trait-associated CNVs. A key quantity that is related to the power is
| (12) |
where g() and α are defined in the GLM model (4).
Theorem 2
Assume the same conditions as in Theorem 1. Suppose there exists an element Ik ∈
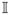 such that
such that
| (13) |
for some η > 0. Then, HIk0 is rejected by the CNVtest with probability going to 1 as n → ∞ Further, suppose πk < 1/2 and βIk ≥ βτ for all τ ∩ Ik ≠ ∅. Then, P(Sn,Ik > Sn,τ) → 1 as n → ∞ for all τ ∩ Ik ≠ ∅ and τ ≠ Ik.
The proof of this theorem is given in Appendix. The first part of Theorem 2 shows that with a large probability, Ik is selected to enter the candidate set
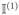 in the algorithm. The second part shows that with a large probability, the score statistic of the true segment Ik dominates the score statistics of other intervals overlapping with Ik, so that the true segment Ik can be identified by the algorithm. The additional conditions in the second part of the theorem imply the monotonicity of the mean value of Sn,τ with respect to how much τ overlapping with Ik.
in the algorithm. The second part shows that with a large probability, the score statistic of the true segment Ik dominates the score statistics of other intervals overlapping with Ik, so that the true segment Ik can be identified by the algorithm. The additional conditions in the second part of the theorem imply the monotonicity of the mean value of Sn,τ with respect to how much τ overlapping with Ik.
4. Simulation Studies
We present Monte Carlo simulations to evaluate the performance of CNVtest. We simulate data sets with n = 1000 individuals, of whom 500 are cases and 500 are controls. For each individual, we generate the log-R intensity values at m = 5000 markers. We simulate two CNVs, one null CNV with the same frequency of 0.15 in both cases and control, another disease-associated CNV has a frequency of 0.10 in controls and a frequency of p = 0.15, 0.20, 0.25 and 0.30 in the case group. The length of both CNV segments is set to s = 10. The first model (Disease (I)) assumes that the disease-associated CNV has the same genomic locations in all samples. For the second model (Disease (II)), instead of assuming that all carriers of the disease-associated CNVs have the segments at exactly the same genomic locations, we consider the case when the locations of the CNVs vary within an interval of length 15, where CNV segments with length s = 10 are randomly selected within a fixed interval of length 15. Therefore, the CNV carriers have overlapping but not exactly the same CNV segments. We consider the shifted mean of the CNVs of μ = 1.5, 1.75, 2, 2.25 and 2.5. Each observation Xij, i = 1, …, n, j = 1, …, m is generated from N(Aij, 1). If marker j is located in a CNV segment and the ith individual is a carrier of the variant, Aij = μ; otherwise, Aij = 0. The phenotype Yi, i = 1, …, n takes value of 1 and 0 for case and control individual, respectively.
We apply CNVtest with L = 15 and to select the disease-associated CNVs. The simulations are repeated 50 times. To evaluate the performance of CNVtest, we consider three summary statistics, SS, EP, and EO, where SS is the score statistic calculated in (8) for an interval, EP is the empirical power, which equals to the proportion of times that disease associated segment is selected in 50 replications. EO is the empirical over-selection, which equals to the proportion of simulations that an interval that does not overlap with the disease-associated CNV is selected. The estimated standard errors of the means of these statistics are derived by calculating the standard deviation of 500 bootstrap means of 50 results from 50 replications.
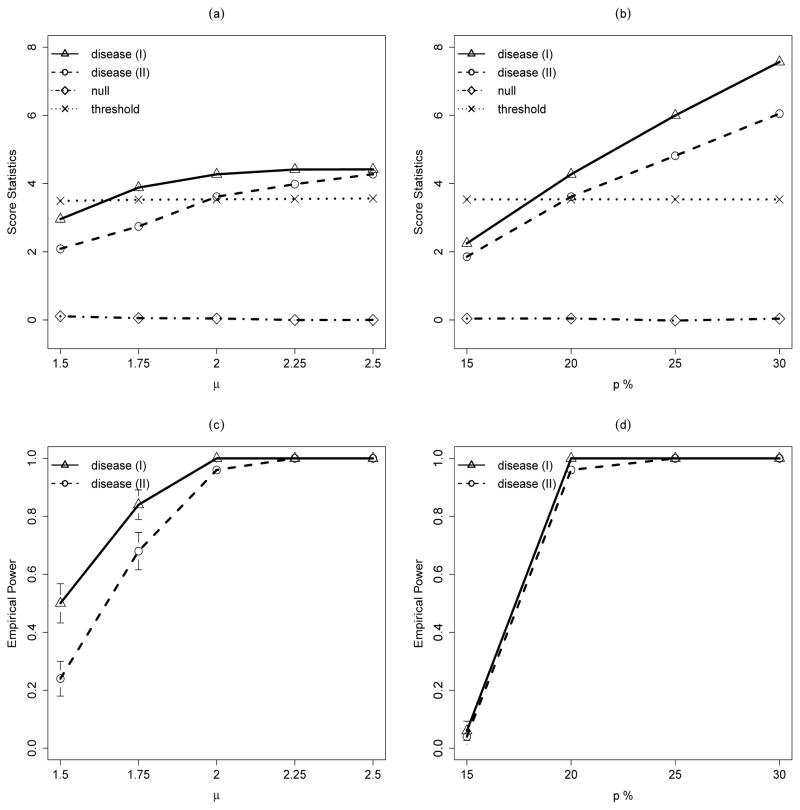
We first examine the effects of CNV jump size μ on the CNVtest performances where we fix the CNV carries frequency at 20% in cases and 10% in controls. Figure 1(a) shows the score statistics calculated for the true CNV intervals for the null CNV and also the disease-associated CNVs as we change the jump size of the CNVs from 1.5 to 2.5, together with the threshold level determined by (9). We observe that the score statistics for the null CNV is constant and is always much smaller than the threshold. On the other hand, the score statistics for the disease associated CNVs increases as μ increases. In addition, shifts in exact CNV boundaries lead to smaller score statistics, especially when μ is small. Figure 1(c) shows the empirical power of CNVtest for identifying the disease-associated CNVs. As expected, larger μ leads to a high power of identifying the true CNVs. Again, shifts in exact CNV boundaries lead to a slight loss of power, especially when μ is small. We observed that the empirical over-selections are always zero for all data sets simulated, and they are not affected by the values of μ.
Figure 1.
Simulation results for disease-associated CNV models. Disease (I) assumes that the disease-associated CNVs have the same genomic locations and Disease (II) assumes that the disease-associated CNVs have the variable genomic locations in different samples. (a) and (c): Effect of the CNV jump size μ from 1.5 to 2.25 on (a) score statistics for CNVs with carrier probability of 20% in case and 10% in control and (b) power of detecting the associated CNV. (b) and (d): Effect of the CNV frequency in case p from 15% to 30% on (c) score statistics for CNVs with carrier probability of 20% in case and 10% in control and (d) power of detecting the associated CNV. Each line represents the average of the corresponding statistic over 50 runs. For plots (a) and (b), dotted lines represent the average of the thresholds determined by equation (9) for Disease (I).
We then fix μ = 2.0 and examine how the carrier proportion in cases affect the power of identifying the disease-associated CNVs (Figure 1(d)). Figure 1(b) shows the score statistics evaluated at the true CNV intervals for the null CNV and also the disease-associated CNVs as we change the case CNV carrier proportion from 15% to 30%, together with the threshold level determined by (9). We observe that the score statistics for the null CNV is constant and is always much smaller than the threshold. On the other hand, the score statistics for the disease associated CNVs increases as the carrier proportion in the cases increases. Again, for all simulations, we did not observed any false identification.
5. Application to Population Differentiation CNV study
Redon et al. (2006) presented the first genome-wide global variation analysis of DNA copy number in the human genome where DNA EBV-transformed lymphoblastoid cell lines of the 270 HapMap samples was screened for CNVs using clone-based comparative genomic hybridization (Whole Genome TilePath, WGTP) array consisting of 27000 large-insert clones. To demonstrate our method, we consider data from two populations: 89 of European descent from Utah (CEU), 45 unrelated Japanese from Tokyo (JPT) and 45 unrelated Han Chinese from Beijing (CHB). Our goal is to identify the genomic regions that show difference in copy number between CEU and Asian populations (JPT+CHB). Such population differentiation in CNV can provide important insights into genetic diversity and evolution.
For each individual, we first standardize the clone intensity data by mean and variance for calculated for this individual. Since one clone covers a longer region than the SNP data, we choose L = 10 in our CNVtest so that the largest CNV covers at most 10 clones. Here we consider both duplication and deletion copy number variants and modify (3) by
for duplication and
for deletion, where
. The resulting r̂dup(= |
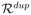 |) = 26496 and r̂del(= |
|) = 26496 and r̂del(= |
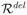 |) = 13585. Note that both r̂dup and r̂del are much smaller than the number of possible intervals in the whole genome, which is at the order of m2. Consequently, the threshold
and
, respectively.
|) = 13585. Note that both r̂dup and r̂del are much smaller than the number of possible intervals in the whole genome, which is at the order of m2. Consequently, the threshold
and
, respectively.
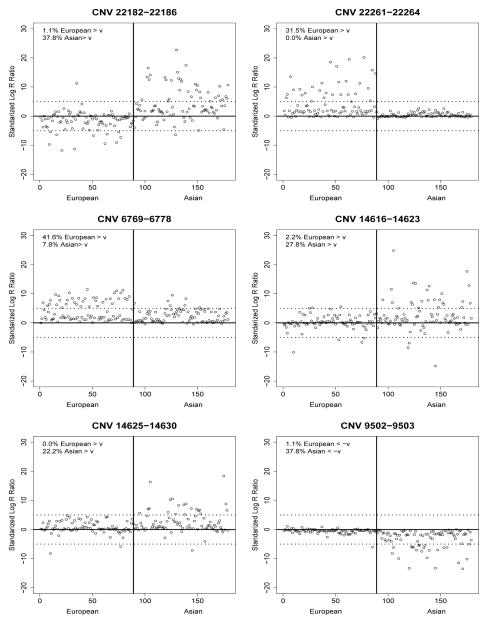
CNVtest identified five duplication CNVs and one deletion CNV that showed different frequencies between the European and Asian populations. Table 1 shows their clone locations, size, overlapping genes and their score statistics defined in (8). Figure 2 shows the scatter-plots of the length-adjusted sum of clone intensity statistics defined in (2) for each of the samples for each of the six identified CNV regions, clearing indicating the differences of the carrier frequencies. To shows that the clones in the identified CNV regions indeed have different intensities for samples in these two different populations, we show in Figure 3 the observed clone intensities for the clone within the identified CNV regions and those are outside for each of the samples. Again, the identified CNV regions indeed show some differences in clone intensities from their neighboring clones. Note that the two CNVs on chromosome 9 are very close to each other and have similar intensity patterns in the samples. It is likely they form a large CNV. This is due to the fact that we chose L = 10 in CNVtest. However, as in any CNV analysis, a post-processing step may simply combine these two CNVs into one.
Table 1.
The CNVs identified by CNVtest that show different frequencies of copy number between Europe and Asian populations. Clone locations, chromosome, CNV size, overlapping genes (based on NCBI36, March 2006) and the corresponding score statistics are shown.
| Clone | Start–End | Chrom | Size | Genes | Score Statistics |
|---|---|---|---|---|---|
| Duplication CNV | |||||
| 22182-22186 | 31,239,836–31,981,395 | 17 | 741 Kb | RDM1,CCL1/L2/L3/L4, TBC1D3G/C, PRC17, AK125932,LYZL6, ZNHIT3,MY019,etc | −6.15 |
| 22261-22264 | 41,439,751–41,722,491 | 17 | 282 Kb | MAPT, KANSL1, LOC284058 | 5.76 |
| 6769-6778 | 68,858,466–70,272,807 | 4 | 1414 Kb | UGT2B, YTHDC1, TMPRSS11E | 5.22 |
| 14616-14623 | 44,819,176–45,798,788 | 9 | 979 Kb | LOC100132167, CR615666 | −4.75 |
| 14625-14630 | 64,368,148–65,433,585 | 9 | 1065 Kb | LOC401507, AL953854.2-002 | −4.69 |
| Deletion CNV | |||||
| 9502-9503 | 150,080,197–150,265,935 | 5 | 186 Kb | DCTN4, MST150, ZNF300 | −4.77 |
Figure 2.
Length-standardized sum of the clone intensities the European (CEU) and Asian samples (JPT+CHB) for the 6 CNVs identified by CNVtest. The estimated CNV carrier proportions in European and Asian are also shown. The dotted lines represent the threshold ±ν = ±5.00 for duplication or deletion and the vertical solid line separates the samples into European and Asian.
Figure 3.
The clone intensities around the 6 CNVs identified by CNVtest (marked by dashed vertical lines) for each of the European (CEU) and Asian samples (JPT+CHB).
Redon et al. (2006) reported two CNVs that exhibit the highest population differentiation between CEU and JPT+CHB, one of which, the duplication CNV on chromosomes 17 that includes gene MAPT, is also identified by CNVtest. CNVtest did not identify the CNV on chromosome 3 reported by Redon et al. (2006). However, this CNV only includes one clone and does not have any known genes in it. The deletion CNV identified by CNVtest, which includes gene DCTN4, was shown to show the highest population differentiation between CEU and Yoruban samples. The intensity plot in Figure 3 for this region shows clear a difference between the CEU and JPT+CHB samples.
Besides samples from CEU and JPT+CHB, Redon et al. (2006) also obtained the clone data for 90 Yoruban (YRI) samples. When compared CEU and YRI, CNVtest identified 4 deletion CNVs and 11 duplication CNVs that showed very different frequencies. These CNVs includes all 6 CNVs that were reported in Redon et al. (2006) to have the highest population differentiation. When compared YRI and JPT+CHB, CNVtest identified 2 deletion CNVs and 12 duplication CNVs, including 2 CNVs that were reported in Redon et al. (2006) to have the highest population differentiation.
6. Conclusion and Discussion
We have developed a new statistical method, CNVtest, for genome-wide CNV association studies. Compared with the commonly used two-step approaches, CNVtest is computationally much faster because since the genome is only scanned once. The computational complexity of this method is the same as the likelihood ratio selector of Jeng et al. (2010) and the multiple sample CNV analysis procedure of Jeng et al. (2013), all in the order of O(mL). In addition, it avoids the often trouble-some task of determining which CNV regions one should test for association and how to adjust for multiple comparisons. The method is particularly effective when the CNV regions from the different carriers do not exactly cover the same intervals. CNVtest is also flexible and can be applied for identifying CNV association of different phenotypes through the use of the generalized linear models. One can also easily extend CNVtest to account for dosage effect by simply replacing the Ziτ in equation (3) by Ziτ = 1(|X̃iτ > ν) × X̃iτ.
CNVtest can also be applied to identify the CNV association using the read depth data from the next generation sequencing. One can use the local median transformation procedure proposed in Cai et al. (2012) to transform the read-depth data to approximately normally distributed data and directly apply the CNVtest to the transformed data. We expect to have similar power and genome-wide error control as the intensity-based data.
Acknowledgments
This research is supported by NIH grants CA127334 and GM097505.
Appendix
Proof of Theorem 1
According to the construction of Sn,τ in the algorithm, we only need to show
Based on the standard result for the score statistic, Sn,τ →L N(0, 1) for τ ∈
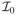 ∩
∩
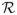 . Then it is enough to show
. Then it is enough to show
| (14) |
The r̂ is a random variable determined by the number of intervals included in
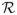 . It can be shown that
. It can be shown that
| (15) |
for some C > 0. The first inequality is by the definition of
 and the condition s̄ ≤ L < d in (5); the third inequality is by the choice of ν and condition (11); the forth inequality is by Mills’ ratio and the condition log L = o(log m) in (5); and the last step is by log q = o(log m) in (10). Next, we have
and the condition s̄ ≤ L < d in (5); the third inequality is by the choice of ν and condition (11); the forth inequality is by Mills’ ratio and the condition log L = o(log m) in (5); and the last step is by log q = o(log m) in (10). Next, we have
Then (14) follows by (15) and the condition q → ∞ as n → ∞ in (10).
Proof of Theorem 2
By the asymptotic results for score statistic, Sn,Ik is asymptotically normally distributed with mean and variance 1. Then is approximately equal to
for some C > 0, where the second inequality is by (13), and the last step is by η = O(1) and Mill’s Ratio. Therefore, HIk0 is rejected with probability going to 1.
Now consider the rest of Theorem 2. By the asymptotic results of score statistics, P(Sn,Ik > Sn,τ) is approximately equal to
| (16) |
where the last step is by βIk ≥ βτ for all τ ∩ Ik ≠ ∅. Then it is left to show that
| (17) |
Since
then by the monotonicity of function f(x) = x(1−x) with x < 1/2, (17) is implied by
| (18) |
and
| (19) |
Note that by (1) and (2), we have
Since (1− πk)P{|N(0, 1)| > ν} = o(1) given ν ≫ 1, and given πk < 1/2, (18) follows. It is also easy to show that
then (19) follows given the fact that for all τ ∩ Ik ≠ θ and τ ≠ Ik.
References
- Barnes C, Plagnol V, Fitzgerald T, Redon R, Marchini J, Clayton D, Hurles M. A robust statistical method for case-control association testing with copy number variation. Nature Genetics. 2008;40:1245–1252. doi: 10.1038/ng.206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai i, Jeng J, Li H. Robust detection and identification of sparse segments in ultra-high dimensional data analysis. Journal of Royal Statistical Society, Series B. 2012;74:773–797. doi: 10.1111/j.1467-9868.2012.01028.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diskin S, Hou C, Glessner J, Attiyeh E, Laudenslager M, Bosse1 K, et al. Copy number variation at 1q21.1 associated with neuroblastoma. Nature. 2009;459:987–991. doi: 10.1038/nature08035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feuk L, Carson A, Scherer S. Structural variation in the human genome. Nature Review Genetics. 2006;7:85–97. doi: 10.1038/nrg1767. [DOI] [PubMed] [Google Scholar]
- Jeng J, Cai T, Li H. Simultaneous discovery of rare and common segment variants. Biometrika. 2013 doi: 10.1093/biomet/ass059. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeng JJ, Cai TT, Li H. Optimal sparse segment identification with application in copy number variation analysis. J Am Statist Ass. 2010;105:1156–1166. doi: 10.1198/jasa.2010.tm10083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olshen AB, Venkatraman ES, Lucito R, Wigler M. Circular binary segmentation for the analysis of array-based dna copy number data. Biostatistics. 2004;5 (4):557–572. doi: 10.1093/biostatistics/kxh008. [DOI] [PubMed] [Google Scholar]
- Redon R, Ishikawa S, Fitch K, Feuk L, Perry G, Andrews T, Fiegler H, et al. Global variation in copy number in the human genome. Nature. 2006;444:444–454. doi: 10.1038/nature05329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sebat J, Lakshmi B, Troge J, Alexander J, Young J, Lundin P, et al. Large-scale copy number polymorphism in the human genome. Science. 2004;305:525–528–97. doi: 10.1126/science.1098918. [DOI] [PubMed] [Google Scholar]
- Shi J, Yang X, Caporaso N, Landi M, Li P. Vtet: a variable threshold exact test for identifying disease-associated copy number variations enriched in short genomic regions. Fontiers in Genetics. 2014;40:53. doi: 10.3389/fgene.2014.00053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegmund DO, Yakir B, Zhang NR. Detecting simultaneous variant intervals in aligned sequences. Annals of Applied Statistics. 2010;5:645–668. [Google Scholar]
- Stefansson H, Rujescu D, Cichon S, Pietilainen O, Ingason A, Steinberg A, et al. Large recurrent microdeletions associated with schizophrenia. Nature. 2008;455:178–179. doi: 10.1038/nature07229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stone J, O’Donovan M, Gurling H, Kirov G, Blackwood D, Corvin A, et al. Rare chromosomal deletions and duplications increase risk of schizophrenia. Nature. 2008;455:237–241. doi: 10.1038/nature07239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walsh T, McClellan J, McCarthy S, Addington A, Pierce S, Cooper G, et al. Rare structural variants disrupt multiple genes in neurodevelopmental pathways in schizophrenia. Science. 2008;320:539–543. doi: 10.1126/science.1155174. [DOI] [PubMed] [Google Scholar]
- Wang K, Li M, Hadley D, Liu R, Glessner J, Grant S, Hakonarson H, Bucan M. Penncnv: an integrated hidden markov model designed for high-resolution copy number variation detection in whole-genome snp genotyping data. Genome Research. 2007;17:1665–1674. doi: 10.1101/gr.6861907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang NR, Siegmund DO, Ji H, Li J. Detecting simultaneous change-points in multiple sequences. Biometrika. 2010;97:631–645. doi: 10.1093/biomet/asq025. [DOI] [PMC free article] [PubMed] [Google Scholar]