Multiscale Model of Mycobacterium tuberculosis Infection Maps Metabolite and Gene Perturbations to Granuloma Sterilization Predictions

Abstract

Granulomas are a hallmark of tuberculosis. Inside granulomas, the pathogen Mycobacterium tuberculosis may enter a metabolically inactive state that is less susceptible to antibiotics. Understanding M. tuberculosis metabolism within granulomas could contribute to reducing the lengthy treatment required for tuberculosis and provide additional targets for new drugs. Two key adaptations of M. tuberculosis are a nonreplicating phenotype and accumulation of lipid inclusions in response to hypoxic conditions. To explore how these adaptations influence granuloma-scale outcomes in vivo, we present a multiscale in silico model of granuloma formation in tuberculosis. The model comprises host immunity, M. tuberculosis metabolism, M. tuberculosis growth adaptation to hypoxia, and nutrient diffusion. We calibrated our model to in vivo data from nonhuman primates and rabbits and apply the model to predict M. tuberculosis population dynamics and heterogeneity within granulomas. We found that bacterial populations are highly dynamic throughout infection in response to changing oxygen levels and host immunity pressures. Our results indicate that a nonreplicating phenotype, but not lipid inclusion formation, is important for long-term M. tuberculosis survival in granulomas. We used virtual M. tuberculosis knockouts to predict the impact of both metabolic enzyme inhibitors and metabolic pathways exploited to overcome inhibition. Results indicate that knockouts whose growth rates are below ∼66% of the wild-type growth rate in a culture medium featuring lipid as the only carbon source are unable to sustain infections in granulomas. By mapping metabolite- and gene-scale perturbations to granuloma-scale outcomes and predicting mechanisms of sterilization, our method provides a powerful tool for hypothesis testing and guiding experimental searches for novel antituberculosis interventions.

INTRODUCTION

Tuberculosis (TB), caused by inhalation of the pathogen Mycobacterium tuberculosis, is a leading cause of death worldwide (1, 2). The main sites of infection during TB are lung granulomas, dense collections of immune cells and bacteria that develop following infection (3). Understanding M. tuberculosis dynamics within granulomas could aid in development of new antibiotic therapies, since M. tuberculosis growth rates, heterogeneity, and dynamics can affect antibiotic efficacy (3–7).

Two in vitro-observed adaptations of M. tuberculosis, suspected to be important in the ability of M. tuberculosis to persist in the host lung, are (i) the adoption of a nonreplicating phenotype and (ii) the accumulation of lipid inclusions, aggregates of neutral lipids inside bacteria (8–13). Hypoxia is known to be a trigger for the transition to a nonreplicating phenotype and the formation of lipid inclusions (9, 12, 14, 15).

The in vivo role of the nonreplicating phenotype remains controversial. It has been suggested that M. tuberculosis acquires the nonreplicating phenotype in response to stresses present in the host (such as hypoxia) and that this phenotype allows M. tuberculosis to persist in the presence of antibiotics (3, 4, 16). Supporting this view, granulomas in a number of animal models of TB are hypoxic (17) and likely contain significant levels of nitric oxide, both of which represent conditions that induce the nonreplicating phenotype (9, 12, 14, 15, 18). Slow-growing and nonreplicating bacteria have been observed in vivo (19–21), and transcriptional profiles of bacteria in patient sputum samples and of nonreplicating bacteria in vitro are similar (22). Nevertheless, direct evidence of nonreplicating bacterial subpopulations within granulomas has been challenging to obtain. Furthermore, the chemical makeup of the granuloma microenvironment is heterogeneous (23), as is M. tuberculosis gene expression within a single granuloma (24, 25) or over time (25). These results suggest that multiple in vitro stress conditions reflecting distinct granuloma microenvironments may be required to mimic the behavior of bacteria in vivo in different regions or during different stages of infection.

Lipid inclusions are hypothesized to be a carbon source for M. tuberculosis while it is in its nonreplicating state or upon reactivation (14, 26). Inclusions may also be sinks for nutrients, leading to lower bacterial replication rates (6). M. tuberculosis lipid inclusions are observed during growth arrest in mouse lung (13) and under in vitro stress conditions (6, 10, 12, 14, 15, 27–29). Bacteria form lipid inclusions by rerouting metabolic carbon fluxes from biomass generation pathways to storage pathways (13). While direct evidence for lipid inclusions in bacteria harbored within granulomas has not been reported, M. tuberculosis bacilli in sputum from TB patients do contain lipid inclusions (22). The impact of inhibiting the utilization of lipid inclusions, via a broad-spectrum lipase inhibitor, has been investigated in vitro (26). Though the inhibitor was shown to prevent regrowth of a hypoxic culture with substantial lipid inclusions, the lipase inhibitor also inhibited bacteria without lipid inclusion during log-phase growth. Thus, the effect of specifically targeting lipid inclusion formation and utilization as a therapy for TB remains unclear (30).

M. tuberculosis remains challenging to study in vivo. Experimental difficulties include the time required for animal models to develop features of TB (e.g., 40 days for necrosis in C3HeB/FeJ mice [31]), complications encountered in isolating sufficient bacterial material for high-throughput studies (32), and bacterial genetic redundancy (33) that buffers genetic effects. Additionally, results of investigations of the role of particular M. tuberculosis phenotypes (such as the nonreplicating phenotype) can be difficult to interpret without a well-defined genetic model. Thus, it is challenging to map in vitro observations and predictions into the in vivo granuloma environment experimentally. Efforts to identify M. tuberculosis gene essentiality through in vitro screening of genetic knockout (KO) mutants could result in false predictions, if the in vitro conditions are unable to accurately capture intragranuloma microenvironments and dynamics. For example, knockout mutants can be identified as attenuated in vitro but can exhibit no attenuation when tested in vivo (representing what might be termed a “false-positive” attenuation prediction; see, e.g., KO3 in Fig. 1). Similarly, mutants could be dismissed as nonattenuated in vitro but could show attenuation in vivo (representing a “false-negative” attenuation prediction; see, e.g., KO2 in Fig. 1). We aim to identify and minimize such false attenuation predictions by mapping in vitro outcomes to in vivo outcomes using a computational model of M. tuberculosis infection in granulomas.

FIG 1.

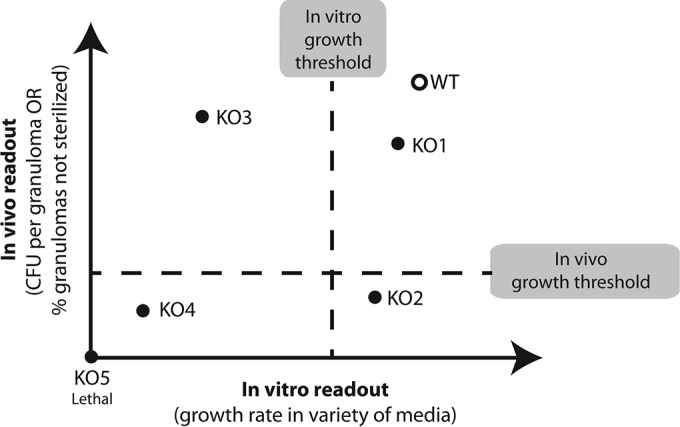
Paradigm for predicting in vivo attenuations from in vitro experiments. In screening for M. tuberculosis drug targets, the correct method for mapping in vitro phenotypes of knockout (KO) mutants (bacterial scale) to in vivo outcomes (host tissue scale) is not obvious. Defining attenuated mutants relative to wild-type (WT) growth in vitro can result in incorrect identification of drug targets. For example, KO mutants can be identified as attenuated in vitro but can result in no attenuation when tested in vivo (i.e., false-positive attenuation prediction associated with, e.g., KO3). Or mutants could be dismissed as nonattenuated in vitro but could show attenuation in vivo (i.e., false-negative attenuation prediction associated with, e.g., KO2). Our model system is capable of bridging in vitro and in vivo outcomes. Results can be used to identify such misclassifications, to guide in vivo screening, and to suggest in vitro screening conditions that are more predictive of in vivo infection outcomes.

Computational methods can complement experimental systems, especially in the complex granuloma environment. We have established computational models of granuloma formation (34–37) to map host immune mechanisms from the molecular scale to the granuloma scale (34, 35, 38) and to explore new antibiotic treatment strategies (39–41). Other models have predicted hypoxic granuloma regions based on granuloma size (42) or have used oxygen and nitric oxide concentrations to determine M. tuberculosis growth and to predict M. tuberculosis dynamics (43). More-sophisticated models can incorporate additional features, such as the asymmetrical cell division observed in M. tuberculosis (5).

Direct links between bacterial genetics and metabolism are provided by metabolic reconstructions, which specify the metabolic reactions that are possible given the enzymes encoded by a genome. Flux balance analysis (FBA) uses such reconstructions together with a steady-state assumption for internal metabolite pools to define a feasible space for metabolic fluxes; an optimal flux is typically selected to maximize the flux through a reaction defining the biomass required to create a new cell. Using the FBA approach, constraint-based models (CBMs) predict bacterial growth in specific environments. The parameters of these CBMs are generally selected to reproduce bacterial growth rates and known metabolic fluxes (44). CBMs of M. tuberculosis include GSMN-TB (45, 46), iNJ661 (47), and, more recently, sMtb (48), which aimed to merge previous models.

There are numerous published CBMs that have extended the FBA approach in different ways. Dynamic CBMs describe bacterial growth in changing environments by relaxing the steady-state assumption of CBMs and instead assuming pseudo-steady states over short time periods (49–52). CBMs have been coupled with gene expression data to probe metabolic changes in M. tuberculosis in response to hypoxia (53) or with spatial models of competing bacterial species to determine bacterial ecosystem dynamics (54). These types of models provide a mechanism to include detailed bacterial dynamics within the context of a larger simulation representing the host tissue and immune response.

In this work, we present a novel multiscale computational model (GranSim-CBM) combining for the first time a model of host immunity with a model capturing nonreplicating M. tuberculosis phenotypes, M. tuberculosis metabolism, lipid inclusion formation, hypoxia, and nutrient limitation in a granuloma. GranSim-CBM is a hybrid model, integrating an agent-based model (ABM) of granuloma formation (GranSim), which we have developed and calibrated to nonhuman primate (NHP) data (34–37), and a dynamic CBM describing M. tuberculosis metabolism and growth. GranSim-CBM is a multiscale model spanning metabolic, cellular, and tissue scales. We use GranSim-CBM to correlate bacterial growth rates predicted by the CBM alone in specific defined media (“in vitro” outcomes) to growth of M. tuberculosis predicted within a granuloma (“in vivo” outcomes). This in vitro to in vivo mapping of M. tuberculosis growth characteristics could inform screening strategies for new antibiotics and antibiotic targets (Fig. 1). We apply this tool to address the following four questions. Which bacterial phenotypes emerge over time in granulomas? What roles (if any) might the nonreplicating M. tuberculosis phenotype and lipid inclusions play during infection? What effects manifest at the granuloma scale when inhibiting specific metabolic pathways in M. tuberculosis? Can we predict the potential of in vitro screening (using different media and different oxygen levels) to identify useful bacterial metabolic targets for treatment of TB? Answers to these questions may help to guide future experimental studies and drug screening assays.

MATERIALS AND METHODS

The methods of GranSim-CBM build on an established framework for tissue-scale simulation with coarse-grained bacterial populations. We discuss the methods required to couple this model to a detailed metabolic model for each bacterial cell and to introduce metabolic switches to permit nonreplicating bacterial phenotypes and lipid reserve accumulation and usage in response to hypoxia. We calibrate our model to experimental NHP and rabbit data and perform sensitivity analysis (SA) to determine the parameters most important to simulated infection outcomes. We group bacteria based on their local nutrient conditions to connect bacterial growth to granuloma characteristics and use virtual knockouts of bacterial metabolic genes to predict in vivo phenotypes and identify metabolic bypasses for bacterial reactions. A summary of methods used in this work is presented in Table 1.

TABLE 1.

Summary of modeling methods and their application in our multiscale computational approach

Method	Description (reference[s])	Application (reference[s])
Agent-based model (ABM)	Stochastic model that describes the behavior of a population of individuals. ABMs consist of an environment, individuals (agents), and rules. Each agent is tracked individually in the environment, and their behavior is determined based on predefined rules and probabilities. Emergent behavior of the system is observed and analyzed (55–57).	GranSim describes the behavior of a population of host cells and bacteria in the lung environment based on biological rules. Granuloma formation and function is an emergent behavior of this population of cells. http://malthus.micro.med.umich.edu/GranSim/GranSim-CBM/ (34–37).
Constraint-based model (CBM)	Model that determines the possible set of behaviors, or the optimal behavior according to a predefined criterion, of a system within certain constraints, and assuming a steady state. CBMs use flux balance analysis to determine the possible set of fluxes through a metabolic network given constraints on enzymatic reactions and nutrient availability (45–48).	Our CBM determines the optimal flux of metabolites through the M. tuberculosis metabolic network, to maximize production of a combination of biomass and lipid inclusions.
Dynamic CBM	CBM that replaces the steady-state assumption with a pseudo-steady-state assumption to capture changes in the system or the environment over time (49–52).	Our CBM assumes a pseudo-steady state to capture changes in nutrient microenvironments within the granuloma over time.
Multiscale model	Model that captures and integrates real-world dynamics at multiple spatial or temporal scales (55, 56, 58).	GranSim-CBM is a multiscale model that captures dynamics from the metabolic, cellular and tissue scales on time scales spanning minutes to years.
Latin hypercube sampling (LHS)	Sampling method that stratifies the sampling space to achieve the same accuracy as random sampling with fewer samples (59).	LHS is used as part of uncertainty and sensitivity analysis to sample the large parameter space for GranSim-CBM.
Partial rank correlation coefficient (PRCC)	Method that determines the correlation between an input factor(s) and an output, by removing the influence of other simultaneously varying input factors (59).	PRCC is used during sensitivity analysis to determine the most influential model parameters in determining granuloma level outputs.
Hierarchical clustering	Method that calculates the difference between individual observations based on a predefined distance metric. Individual observations are then grouped/clustered such that similar observations are collected in a single cluster (60).	We cluster individual bacteria (observations) based on their growth rate and local nutritional environment.

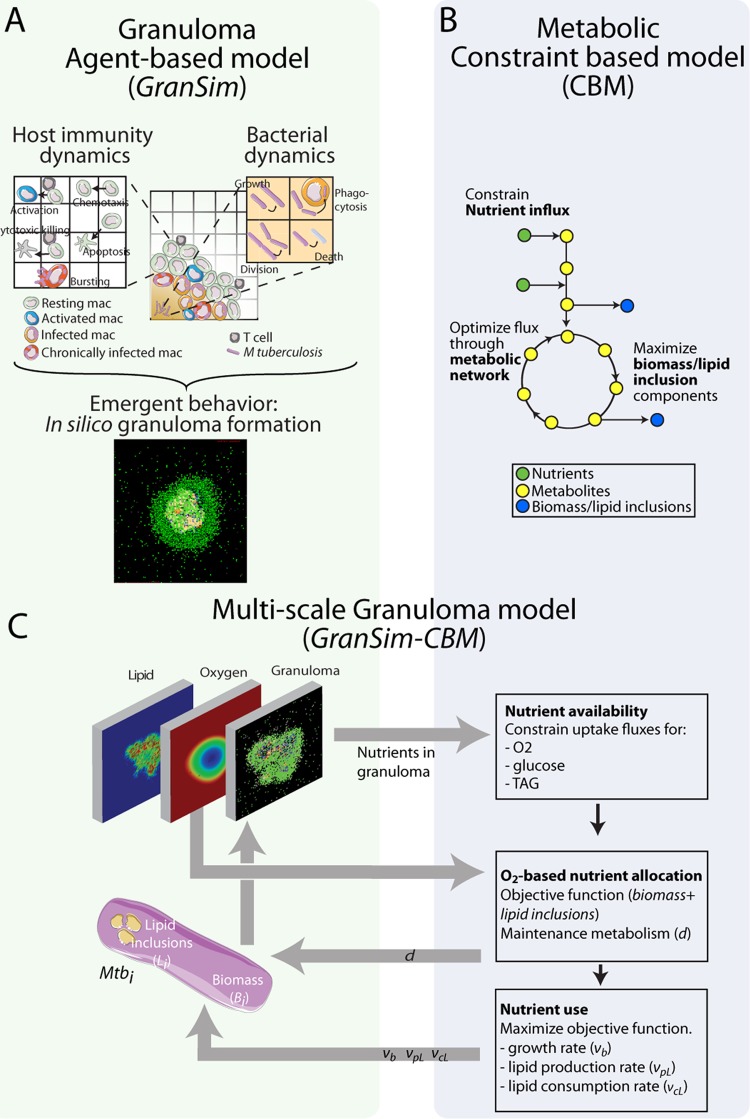
(i) Agent-based granuloma model (GranSim).

Briefly, GranSim captures molecule-, cell-, and tissue-scale events. At the tissue scale, we include cellular movement based on the chemokine environment on a two-dimensional (2D) simulation grid, with granuloma formation as an emergent behavior of the system (Fig. 2A). At the cellular scale, we model individual macrophages and their states (resting, activated, infected, or chronically infected), as well as individual T cells and their types (cytotoxic T cells, regulatory T cells, or gamma interferon [IFN-γ]-producing T cells) and interactions. At the molecular level, the model accounts for secretion, diffusion, binding, and degradation of cytokines and chemokines. The model has been extensively calibrated to NHP data and successfully predicts granuloma outcomes for tumor necrosis factor alpha (TNF-α), interleukin-10 (IL-10), and IFN-γ knockouts (34–41, 61).

FIG 2.

Multiscale model system bridging metabolic scale to tissue scale. (A) GranSim, our agent-based model of granuloma formation and function, incorporates host immune functions (see references 34–36, and 37 for details) as well as bacterial dynamics for the first time on an individual-bacterium level. In silico granulomas are an emergent behavior of the system. mac, macrophages. (B) The constraint-based model (CBM) uses a stoichiometric matrix representing the metabolic network of M. tuberculosis (45) to predict growth rates based on the bacterial objective function (growth versus lipid inclusion production) (13). (C) The combination model GranSim-CBM tracks granuloma formation and environmental nutrient conditions (oxygen, TAG, and glucose) (left) and uses the CBM to predict growth rates and lipid inclusion formation for each bacterial agent based on its local environment and internal lipid inclusion stores (right). Mtb_i, ith bacterial agent.

In previous versions of GranSim, we separated bacteria into three subpopulations on the basis of location (intracellular, replicating extracellular, and nonreplicating extracellular in caseum). Each subpopulation was represented by continuous values in each grid compartment or macrophage. This continuous representation has the benefit of simplicity and computational ease for capturing the overall interaction between host and pathogen when probing immunological questions. However, to better address mycobacterial questions in granulomas with heterogeneous M. tuberculosis populations (5, 62), we implement here a discrete representation of individual M. tuberculosis bacilli.

In our discrete M. tuberculosis model, each bacillus is modeled as an individual “agent,” with state variables for biomass (B_i), lipid inclusions (L_i), and location (X_i) (intracellular or extracellular) tracked for each bacterium i. Growth rates, generation times, sizes, and lipid inclusion levels are tracked for each bacillus over time. Table 2 describes GranSim rules regarding M. tuberculosis growth, division, death, phagocytosis, and macrophage bursting for continuous versus discrete M. tuberculosis representations, with variable and parameter definitions given in Tables 3 and 4, respectively. Host parameters are given in Table S1 in the supplemental material. Changing the representation of M. tuberculosis in GranSim from continuous variables to individual agents does not affect predicted average CFU trajectories in simulated granulomas (Fig. 3A).

TABLE 2.

GranSim rules for M. tuberculosis modeled as continuous variables or individual agents^a

Bacterial event	Rule for continuous M. tuberculosis variables	Rule for individual M. tuberculosis agents
Growth (intracellular or extracellular)	νb = growth rate	νb = growth rate
	Mtb(t + 1) = (1 + νb)Mtb(t)	Shuffle MtbList
		For i = 1 to Mtb(t)
		Bi(t + 1) = (1 + νb)Bi(t)
		If Bi > τdiv
		Make new Mtb agent
		Divide Bi and Li into fractions f and (1 − f) between two daughter agents
		Else if Bi < τdeath
		Mtb agent dies
Death (from host-mediated killing or lack of nutrients)	nrKill = nr of Mtb to kill	nrKill = nr of Mtb to kill
	Mtb(t + 1) = Mtb(t)-nrKill	Shuffle MtbList
		Delete 1st “nrKill” Mtb agents on MtbList
Dispersion of a fraction of intracellular M. tuberculosis to Moore neighborhood (when a chronically infected macrophage bursts)	fd = fraction to disperse	fd = fraction to disperse
	dispMtb = fdMtb(t)	dispMtb = fdMtb(t)
	dMtb = dispMtb/NM	dMtbBase = dispMtb/NM
	for m = 1 to NM	dMtbExtra = mod(dispMtb,NM)
	Mtbm(t + 1) = Mtbm(t) + dMtb	Shuffle MtbList
		For m = 1 to dMtbExtra
		Move 1st “dMtbBase + 1” agents in MtbList to compartment m
		For m = dMtbExtra + 1 to NM
		Move 1st dMtbBase agents in MtbList to compartment m
		Delete the rest of MtbList
Phagocytosis (move extracellular M. tuberculosis to intracellular location)	count = nr of Mtb to phagocytose	count = nr of Mtb to phagocytose
	MtbE(t + 1) = MtbE(t) − count	Shuffle MtbEList
	MtbI(t + 1) = MtbI(t) + count	Move 1st “count” Mtb agents from MtbEList to MtbIList

^aSee Tables 3 and 4 for variable and parameter definitions, respectively. nr, number; Mtb, M. tuberculosis.

TABLE 3.

Variables used in GranSim-CBM^a

Variable	Unit	Description
νb	h−1	Growth rate
νL	h−1	Net lipid inclusion generation rate
νpL	h−1	Lipid inclusion production rate predicted by CBM
νcL	h−1	Lipid inclusion consumption rate predicted by CBM
d	timestep−1	Biomass degradation rate
η		Switching parameter to calculate objective function and biomass degradation rate
MtbXList		List of M. tuberculosis agents in location X (E, extracellular; I, intracellular)
Mtb(t)		No. of bacteria as continuous variables or individual agents in MtbList at timestep t
Bi(t)	BU	Biomass of M. tuberculosis agent i at timestep t
Li(t)	fmol	Lipid inclusions of M. tuberculosis agent i at timestep t
Xi(t)		Location of M. tuberculosis agent i at timestep t (E, extracellular; I, intracellular)
NM		No. of grid compartments in Moore neighborhood (adjacent grid compartments in a 2-dimensional grid)
vilow	fmol/h · BU	Lower limit on import flux for nutrient i (set to zero)
viup	fmol/h · BU	Upper limit on import flux for nutrient i (dependent on Vmax,i and Ki)
Z		Objective function to be optimized by the CBM (a linear combination of νb and νL)

^aConversion factor, 10 min/timestep. 1 BU = 196 fg dry weight.

TABLE 4.

Parameters used in GranSim-CBM^a

Parameter	Description	Unit	Range for uncertainty analysis	Range for sensitivity analysis	Baseline parameter set
τdiv	Biomass division threshold	BU		1.7 to 2.5	2
τdeath	Biomass death threshold	BU		0.2 to 0.6	0.5
f	Division fraction		0.25 to 0.5	0.25 to 0.5	0.47
D	Diffusivity of oxygen	cm2/s	1 × 10−6 to 1 × 10−4	7 × 10−7 to 7 × 10−5	7.3 × 10−6
O2,plasma	Plasma oxygen concn	M	8 × 10−4 to 1 ×10−2	9 ×10−5 to 9 ×10−3	1 × 10−3
p	Vascular permeability of oxygen	cm/s	1 ×10−6 to 1 ×10−4	1 ×10−6 to 1 ×10−4	1.1 ×10−5
Vmax-host	Maximum host cell oxygen consumption rate	moles/cell/s	6 ×10−18 to 6e−16	1 ×10−18 to 1 ×10−16	1.26 ×10−17
khost	Michaelis-Menten constant for host cell oxygen consumption	mM	2 ×10−4 to 2 ×10−2	8 ×10−4 to 8 ×10−2	8 × 10−3
GlcE	Initially available glucose per grid compartment	fmol	0.2 to 200	0.05 to 5	0.5
TAGI	Initially available TAG per host cell	fmol	6.4 to 640	2 to 200	23
s	Oxygen depletion sensitivity parameter	M−1	2 to 500	4 to 400	42
h	Half-saturation point of oxygen for switching from biomass to lipid inclusion production	M	1 ×10−5 to 1 ×10−4	1 ×10−6 to 1 ×10−4	1.3 ×10−5
Vmax,glc	Maximum glucose uptake flux	fmol/h · BU	0.15 to 1	0.05 to 5	0.6
Vmax,TAG	Maximum TAG uptake flux (external TAG)	fmol/h · BU	0.01 to 0.1	7 × 10−3 to 7 × 10−1	0.08
Vmax,O2	Maximum oxygen reduction	fmol/h · BU	0.3 to 0.5	0.3 to 0.5	0.4
Vmax,L	Maximum lipid inclusion utilization flux	fmol/h · BU	1 ×10−3 to 1 × 10−1	4 ×10−4 to 4 ×10−2	0.005
Kglc	Michaelis constant for glucose uptake	μM	1 ×10−5 to 1 ×10−3	9 ×10−5 to 9 ×10−3	0.0009
KTAG	Michaelis constant for TAG uptake	M	1 ×10−8 to 1 ×10−5	2 ×10−7 to 2 ×10−5	2 ×10−6
KO2	Michaelis constant for oxygen reduction	M	1 ×10−9 to 5 ×10−5 (and <hO2)	1 ×10−6 to 1 ×10−4	1 × 10−5
KL	Michaelis constant for lipid inclusion utilization	fmol/BU	1 ×10−9 to 5 ×10−3	8 ×10−8 to 8 ×10−6	8 ×10−7
dmin	Biomass degradation rate for nonreplicating bacteria	Timestep−1	1 ×10−9 to 1 ×10−5	1 ×10−7 to 1 ×10−5	1 ×10−6
dmax	Biomass degradation rate for actively replicating bacteria	Timestep−1	1 ×10−5 to 2 × 10−2	2 ×10−4 to 2 ×10−2	2 × 10−3
Lmax	Maximum allowed lipid inclusions per bacterium	fmol	0.1 to 10	0.04 to 4	0.370273174
VR	At half-saturation, the “value” of 1 unit of lipid inclusion	BU/fmol	0.038 to 380		183

^aConversion factor, 10 min/timestep.

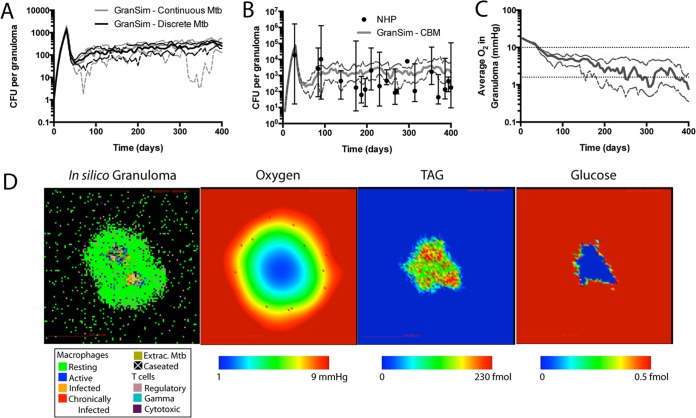
FIG 3.

GranSim-CBM model calibration to experimental data. (A) Discretization of M. tuberculosis in GranSim does not affect bacterial loads in granulomas (CFU) compared to previous model versions with continuous M. tuberculosis representation (35–38, 40, 41). (B) GranSim-CBM is calibrated to experimental data from animal models of TB. GranSim-CBM predictions of CFU per granuloma are calibrated to measurements from the NHP model of TB (21, 77–79). (C) The predicted oxygen concentration in granulomas is calibrated to direct measurements in rabbit granulomas (lower dotted line), and the threshold for pimonidazole (PIMO) hypoxia stain is shown for reference (upper dotted line). For panels A to C, solid lines show medians and dashed lines show 95% confidence intervals. n = 15. (D) Snapshot of a representative in silico granuloma at 300 dpi, with predicted oxygen, TAG, and glucose levels within the granuloma. Extrac., extracellular.

(ii) Capturing nutrient dynamics in GranSim-CBM.

We track on the simulation grid the distribution and bacterial utilization of three nutrients: glucose, triacylglycerol (TAG) (representing fatty acid carbon sources), and oxygen. The metabolic requirements of M. tuberculosis have been extensively studied. Intracellular M. tuberculosis likely utilizes a range of host-derived carbon sources and amino acids as nutrient sources, including cholesterol and TAG (63, 64). Additionally, glycolysis under hypoxic conditions leads to the accumulation of toxic byproducts (65). Therefore, fatty acids are considered to be a major carbon source of M. tuberculosis in vivo.

Lipids are a carbon source for M. tuberculosis in vivo in mice (19, 64), inside macrophages (63, 66), and in caseum (67) and are an internal nutrient reserve stored by M. tuberculosis under conditions of hypoxic stress (12, 14, 26). We use TAG to represent fatty acid carbon sources in each of these locations (in cells, in caseum, and in lipid inclusions). The lipid content of caseum is believed to be the result of the accumulation of host cell debris (67). Therefore, in the model, each dying macrophage deposits its TAG onto the grid compartment where it died, making the TAG available to extracellular bacteria. Activated macrophages in GranSim have the ability to heal caseation in the 8 adjacent grid spaces on the 2D grid. When caseation is healed, the TAG levels are reduced to reflect the return of the simulation grid compartment to a “normal lung tissue” state.

We model oxygen levels in the granuloma by assuming constant oxygen concentrations in the blood (O_2,plasma), tracking oxygen permeation onto the grid at rate p via vascular source grid compartments, diffusion on the grid with diffusivity D, and consumption by host cells using Michaelis-Menten kinetic parameters V_max-host and k_host. We use reaction-diffusion methods described previously (55).

Within granulomas, less is known about glucose levels than about oxygen levels. Glucose is not believed to be a major carbon source for intracellular M. tuberculosis (63), either because glucose is not made available to bacteria in phagosomes or because it is not the preferred carbon source for M. tuberculosis in the intracellular environment. Therefore, we fix glucose levels available to intracellular M. tuberculosis at zero. While a C3 carbon source is likely available to intracellular bacteria (63), the identity of this source is currently unknown and we therefore exclude it from the current model. Extracellular glucose is set to an initial amount at each grid cell (Glc_E) and is gradually consumed by M. tuberculosis without replenishment.

(iii) Constraint-based model of M. tuberculosis metabolism.

CBMs describe the relationship between nutrient uptake (e.g., glucose and oxygen), waste export (e.g., CO₂), and the production rate of biomaterials for new cells, under the assumption of a steady state for internal metabolite pools (68). A CBM makes predictions about cellular metabolism utilizing the metabolites present, the reactions and corresponding enzymes responsible for metabolic transformations, and the constraints on ν_i (the flux through reaction i): ν_i^low < ν_i < ν_i^up (Fig. 2B). Mathematically, the steady-state assumption is formulated as S · ν = 0. Rows of the stoichiometry matrix S correspond to metabolites, and columns of S correspond to enzyme-catalyzed reactions, active and passive transport, and other uncatalyzed reactions. The row-column entry is the number of metabolite molecules that are reactants (negative sign) or products (positive sign) for the reaction. For metabolic reactions, the flux constraints depend on maximum reaction rates for enzymes. For import of metabolites into the bacterial cell, the rates depend on the properties of transporters and on the extracellular metabolite concentration. As described below, the CBM uses Michaelis-Menten kinetics to model the import fluxes.

Biomass flux (ν_b) is defined as the flux of the reaction Σ_iw_im_i → 1b, where m_i is metabolite i, w_i is the number of molecules of metabolite i required to build one new cell, and b is the total biomass composition of a new cell. By definition, the growth rate of the cell is ν_b.

In conventional CBMs, a standard assumption is that bacteria have evolved to maximize growth rates. Therefore, to compute the growth rate, the maximum value of ν_b is identified within the feasible space of flux vectors defined by bounds on the fluxes and the steady-state assumption. Because the objective function and the constraints are linear, an optimal solution may be found efficiently using a linear programming solver. However, M. tuberculosis grows more slowly than most bacteria and adjusts its growth rate in response to environmental cues (9, 12, 14, 15, 18). We therefore adjust the assumption of maximized growth rate by modifying the objective function as described below.

In this work, we developed a dynamic CBM based on an existing CBM describing M. tuberculosis metabolism (45, 46), using the “static-optimization approach” (50). The original model of M. tuberculosis metabolism is an updated version of GSMN-TB (45, 46) kindly provided by the authors (Johnjoe McFadden, personal communication). These updates to the published model include corrections of a few reaction imbalances, changes in the ATP penalties for the biomass function, and inclusion and exclusion of additional reactions based on new data. We chose GSMN-TB over other available metabolic models of M. tuberculosis due to its relative simplicity, validated predictions for essential genes in vitro, and inclusion of metabolic reactions that we wished to study. Inclusion of the host metabolism in a metabolic model, as in iAB-AMØ-1410-Mt-661 (112), introduces significant complexity to modeling infection, as additional parameters for host nutrient uptake and transport to the phagosome must be specified. GSMN-TB is more accurate for in vitro predictions of gene essentiality than iNJ661 (45, 47). Additionally, both iNJ661 and its descendant iAB-AMØ-1410-Mt-661 did not include the reactions for synthesizing and catabolizing triacylglycerol (TAG) within the bacterium. Inclusion of these reactions is critical for studying the role of TAG as a storage compound and energy source during infection. Another alternative would be the sMtb model (48), which is a unification of GSMB-TB with iNJ661. A qualitative comparison between GSMN-TB and sMtb (see Table S2 in the supplemental material) suggests that they will give similar results in our granuloma simulations.

We make additional modifications to the existing CBM to enable integration with GranSim. In particular, GSMN-TB includes glycerol as a carbon source, but experiments suggest that M. tuberculosis does not utilize glycerol in vivo (69). We therefore exclude the glycerol import reaction from our model. The GSMN-TB model also includes cholesterol metabolism reactions. Cholesterol is metabolized via the methylcitrate cycle and the tricarboxylic acid (TCA) cycle, generating pyruvate, acetyl coenzyme A (acetyl-CoA), and propanoyl-CoA (70). Pyruvate can then be converted to acetyl-CoA by the pyruvate dehydrogenase complex (71). TAG, a primary component of lipid inclusions (12), is metabolized into odd-length fatty acids and a glycerol molecule. The fatty acids are in turn also metabolized to propanoyl-CoA and acetyl-CoA via beta-oxidation, while the glycerol can be metabolized by conversion to pyruvate (71 [see pages 429 and 605]). Given these similarities in metabolism, we simplify the model by grouping cholesterol and TAG together as a single effective TAG metabolite; similarly, GranSim represents the local concentration of cholesterol and TAG as a single effective TAG metabolite.

We rescale the published GSMN-TB biomass function to provide a quantitative match with the biomass of a newly divided cell rather than with that of an average cell during log-phase growth. Experimental measurements of an actively growing mycobacterial population found that individual bacilli had a dry weight of 274.5 fg, including cells with partially or fully replicated genomes (72). It was also estimated that each cell contained 1.4 genome copies rather than a single genome copy (72). We therefore define one biomass unit (BU) as equal to 196 fg (274.5 fg/1.4) of dry weight. With this definition, a cell with a biomass of 1 BU corresponds to a nascent daughter cell from a symmetric cell division, and a cell with a biomass of 2 BU is on the cusp of division. We also rescale the GSMN-TB flux uptake units for metabolites from millimoles per hour per gram dry weight to femtomoles per hour per BU.

(iv) Switching between M. tuberculosis biomass growth and lipid inclusion accumulation in response to hypoxic stress.

We further modify GSMN-TB to include the accumulation of lipid inclusions in nonreplicating M. tuberculosis and a mechanism for hypoxic stress to trigger the transition to a nonreplicating bacterial phenotype that accumulates lipid inclusions. Here we refer to bacteria maintained under low-oxygen conditions as nonreplicating and use the term to encompass both nonreplicating and slowly replicating bacteria (growth rates < 0.0015 h⁻¹). Lipid inclusions contain many different lipid species, including triacylglycerols (TAGs) (12). We therefore introduce to each bacterial agent in GranSim a new intracellular compartment, the “lipid inclusion” compartment, which accumulates TAG. We add two new transport reactions to shuttle TAG between the lipid inclusions and the cytoplasm. In order to prevent an internal cycle (73), in which both directions are active with no net TAG transport, a small ATP penalty (0.1 ATP) is added for TAG transport into the lipid inclusions. The two new transport reactions are, specifically, transfer of TAG into the lipid inclusions (1 TAG[c] → 1 TAG[inclusion], with flux ν_pL) and transfer of TAG from the lipid inclusions back to cytoplasm (1 TAG[inclusion] + 0.1 ATP → 1 TAG[c] + 0.1 ADP + 0.1 P [inorganic phosphate], with flux ν_cL). The net flux of TAG into the lipid inclusions is defined as ν_L = ν_pL − ν_cL. Each molecule of TAG, when fully metabolized, yields between 364.6 and 489.2 molecules of ATP depending on the oxygen level, a large yield compared to the 0.1 molecule penalty.

As in previous work (13), we consider two CBM objective functions, one under conditions of high oxygen that maximizes the biomass growth rate, ν_b, and the other under conditions of hypoxia that maximizes the lipid inclusion accumulation rate, ν_L (Fig. 2B). We introduce a continuous oxygen-sensitive switching function η that weighs the two objective functions. The combined objective function Z is as follows:

$$Z=\text{η}{v}_b+(1-\text{η})V_R{v}_L$$ (1)

where parameter V_R provides a convenient scaling between the two objectives. This parameter is necessary, as the relative levels of importance of 1 unit of biomass and 1 unit of lipid inclusions may not be equivalent and would generally be dependent on the particular units chosen. The switching function is as follows:

$$\text{η}=\text{1/}(\hspace{0.17em}1\hspace{0.17em}+\hspace{0.17em}\text{exp}[-s(\left[{\text{O}}_2\right]-h)/h])$$ (2)

where [O₂] is the oxygen concentration, s determines the sensitivity of the switching (steepness of the sigmoid), and h is the half-saturation concentration of the switch. Oxygen-dependent metabolic maintenance costs are calculated using the active/nonreplicating switch parameter η (equation 2) and implemented as biomass degradation rate d as follows:

$$d=d_{\min \hspace{0.17em}}+\text{η}(d_{\max \hspace{0.17em}}-d_{\min \hspace{0.17em}})$$ (3)

where d_max is the biomass degradation rate in fully aerated replicating M. tuberculosis and d_min is the biomass degradation rate in nonreplicating M. tuberculosis. Thus, we lower the biomass degradation rate (i.e., maintenance metabolism) in response to lower oxygen availability, allowing us to capture the reduced metabolic requirements for survival in the absence of replication. The original GSMN-TB model instead used a lower bound on ATP hydrolysis to incorporate biomass maintenance costs (45, 46). Our form reflects the decreased maintenance cost in decreasing oxygen concentrations. It also ensures a feasible CBM solution when low levels of nutrients constrain the ATP hydrolysis rate. However, GSMN-TB does not capture metabolism in the absence of oxygen (via anaerobic respiration [74, 75]). This is a limitation of our model, though we do not expect it to significantly impact our results, as the metabolism of M. tuberculosis is very slow during hypoxia. We expect this very slow bacterial metabolic state to be well approximated by our model, which predicts the total absence of metabolism under anoxic conditions.

(v) Coupling CBM to local nutrient resources in GranSim to create a dynamic CBM.

To capture the variable nutrient conditions available to M. tuberculosis during infection, the upper bounds (ν_i^up) for the rates of nutrient uptake (oxygen, glucose, and TAG) are determined by the local nutrient availability provided by GranSim (Fig. 2A and B). Four uptake fluxes are constrained: oxygen, glucose, and TAG from the external environment and reimport of TAG back from the lipid inclusion to the cytoplasm. In each case, constraints are modeled using a Michaelis-Menten functional form with Hill coefficient 1 and two parameters corresponding to the maximum flux, V_max,i, and the metabolite concentration K_i at half of the maximum as follows:

$${v_i}^{\text{up}}=V_{\max ,i}\left[N\right]/(K_i+[N\left]\right)$$ (4)

for i corresponding to each of the four constrained import fluxes. For import from the extracellular environment, [N] refers to the local concentration provided by GranSim. For import of TAG from the lipid inclusion, the concentration is computed as L_i/B_i. For all four import fluxes, ν_i^low is set to zero. The 8 parameters (V_max,glc, V_max,TAG, V_max,O2, V_max,L, K_glc, K_TAG, K_O2, and K_L) for the 4 import flux upper bounds are selected by fitting to experimental data as described below.

(vi) Multiscale dynamics with GranSim-CBM.

The multiscale model (Fig. 2C) tracks concentrations of three nutrients (oxygen, glucose, and TAG) in the granuloma environment as well as internal bacterial lipid inclusions. Available nutrients on the simulation grid are used to determine the upper bounds for CBM transport fluxes (equation 4), to switch the CBM objective function between biomass production and lipid inclusion production (equation 2), and to calculate the biomass degradation rate (equation 3). The optimal fluxes from the CBM are used in GranSim to update bacterial state variables (biomass [B_i] and lipid inclusions [L_i]) as well as the environmental nutrient pools in the granuloma (see Fig. S1 in the supplemental material for more detail).

Using the growth rate (ν_b) and the net lipid inclusion production rate (ν_L) calculated by the CBM, GranSim updates the state variables for biomass (B_i) and lipid inclusion (L_i) for the i^th bacterium with time increment Δt as follows:

$$B_i(t\hspace{0.17em}+\text{\hspace{0.17em}Δ}t)=(v_b-d)B_i\left(t\right)\text{Δ}t+B_i\left(t\right)$$ (5)

$$L_i(t\hspace{0.17em}+\text{\hspace{0.17em}Δ}t)=\left(v_L\right)B_i\left(t\right)\text{Δ}t+L_i\left(t\right)$$ (6)

Biomass degradation rate d represents metabolic maintenance and is scaled by hypoxia switching function η (equation 2).

The biomass of each bacterium is kept between a death threshold (τ_death) and a division threshold (τ_div). If the biomass reaches τ_div, the bacterium divides into two asymmetric daughter bacilli with biomass (1 − f) and (1 + f) BU (f is the asymmetric division fraction), and lipid inclusions split proportionally. If the biomass falls below τ_death, the bacterium dies and is removed from the simulation. Bacterial survival and replication therefore depend on a balance between the growth rate and the biomass degradation rate. In our model, the growth rate is determined by oxygen, glucose, TAG, and lipid inclusion availability, while the biomass degradation rate is determined by oxygen availability via the growth switch parameter (equation 2). Therefore, a shortage in any of these nutrients, (resulting in ν_b < d), causes a net loss of biomass, leading to death from starvation (or “suffocation” in the case of lack of oxygen) when biomass falls below τ_death.

Lipid inclusions per bacterium are constrained to be below a realistic maximum value (L_max). If L_i(t + Δt) > L_max then we instead set L_i(t + Δt) = L_max and convert the excess TAG to extracellular TAG to prevent loss of mass. Note that if glucose is being used to produce lipids when lipid inclusion levels reach the maximum then some mass will be lost. We have monitored the amount of lipids lost during a 400-day simulation and found that a negligible amount (∼0.01%) of the total TAG molecules present on the grid is lost as a result.

(vii) Uncertainty and sensitivity analysis.

Uncertainty analysis (UA) identifies the variation in model outputs caused by uncertainty in model parameters. We previously identified the bacterial growth rate as a major contributor to uncertainty in GranSim outputs (36, 76) and therefore investigate the contribution of individual CBM and bacterial GranSim parameters (Table 4), drivers of the bacterial growth rate, to granuloma-level outputs in GranSim-CBM.

We use Latin hypercube sampling (LHS) (59) to uniformly and simultaneously sample multiple parameters within the multidimensional parameter space (Table 4). We generate 1,500 parameter sets. Agent-based models contain both aleatory uncertainty from stochastic variation and epistemic uncertainty from parameter variation. In order to sample aleatory uncertainty, we perform 5 independent replicate simulations for each parameter set. Candidate parameter sets are selected using the following criteria based on single-granuloma CFU data from NHP (Fig. 3B) (21, 77–79) and oxygen measurements in rabbit granulomas (Fig. 3C) (17).

• 5,000 < day 30 total CFU < 100,000 for 4 or 5 of 5 replicates.

• Day 80 total CFU of <10,000 for any of the replicates.

• Day 200 total CFU of <2,500 for 4 or 5 of 5 replicates.

• (Day 200 total CFU)/(day 100 total CFU) < 2 for any of the replicates.

• Only 1 or 2 of 5 replicates clearing infection before day 200.

• 1 mg/liter < day 30 oxygen in the granuloma < 200 mg/liter for any of the replicates.

The final parameter set (Table 4) is selected by visual inspection from 5 candidate sets identified by the criteria listed above. A representative granuloma generated with this parameter set is shown in Fig. 3D, along with the predicted oxygen, TAG, and glucose levels within the granuloma. This parameter set captures tissue-scale outcomes of TNF-α, IL-10, and IFN-γ knockouts in mice and NHPs (80–86) (see Fig. S2 in the supplemental material).

Sensitivity analysis (SA) quantifies the strength of correlation between model parameters and outputs of interest and therefore can identify the main driving mechanisms in the model for specific outputs. SA is performed by calculating partial ranked correlation coefficients (PRCCs) between model parameters and model outputs (59). We again use LHS to simultaneously vary multiple parameters. While a number of other sensitivity analysis methods are available (87–94), our chosen approach allows global sensitivity analysis, i.e., identification of the contribution of a set of parameters to model outcomes in the context of other parameter variations, instead of local sensitivity analysis, i.e., variation of single parameters against baseline values for other parameters. The method also allows the evaluation of parameter contributions to a large number of model outputs at multiple time points. Using LHS to perform parameter sampling and performing multiple replications of the stochastic model for each parameter set alleviates the significant computational limitations of large parameter sweeps in conventional sensitivity analyses. Parameter ranges used for the SA (Table 4) are constructed around the final parameter set from the uncertainty analysis described above. We sample the parameter space 1,500 times and perform 5 replicates for each parameter set to estimate contributions from both aleatory uncertainty and epistemic uncertainty. Parameters are ranked in terms of strength of correlation with model outputs using the z-test. Significant PRCC and z-test results are defined as having P values of <0.01.

(viii) GranSim-CBM validation.

For model validation, we compare killing of bacteria in our model with in vivo measurements (19, 21). Bacterial killing can be assessed as CFU/CEQ, where CEQ (representing chromosomal equivalents) is a measure of all bacteria that have been in the granuloma during the entire infection. A low CFU/CEQ fraction value indicates effective killing of bacteria by the host (21). We measure this ratio in GranSim-CBM by tracking the cumulative number of bacteria in the simulation, including dead bacteria (38). The median value of CFU/CEQ at 75 days postinfection (dpi) is 9 × 10⁻³, with a 95% confidence interval of 7 × 10⁻³ to 1 × 10⁻². In comparison, experimental CFU/CEQ ratios from nonhuman primates (NHP) at 77 dpi (21) (rhesus macaque) are on average 2 × 10⁻³, with a range of 1 × 10⁻⁵ to 2 × 10⁻¹.

(ix) Hierarchical clustering of bacteria.

In order to explore heterogeneity in the bacterial populations in our simulations, we group bacteria according to their growth rates and locally available nutrients. Growth rates depend on local nutrients (using the CBM) as well as host adaptive immunity (using GranSim). For grouping, we use hierarchical clustering based on Euclidean distances (Matlab Release 2014b; The MathWorks, Inc., Natick, MA, USA), standardizing by growth rate and available nutrient levels (oxygen, glucose, TAG, lipid inclusions). Each resulting cluster of bacteria represents a group of bacteria with similar growth rates and nutrient environments. Clustering is performed on a collection of bacteria pooled from multiple time points in a single granuloma, to identify patterns that continued throughout the simulation (temporally) as well as patterns that developed at specific times (spatially). Furthermore, clusters are visualized as a heat map augmented to display model variables not used for clustering (time, CBM fluxes, maintenance metabolism, and intracellular/extracellular location).

(x) Simulations of lipid inclusion defects and virtual M. tuberculosis knockouts.

Since the nonreplicating growth phenotype and lipid inclusion formation appear to be important adaptations of M. tuberculosis, these adaptations could be attractive antibiotic targets. To explore the potential effects of inhibiting these two adaptations, we perform additional simulations in which bacteria are unable to enter the nonreplicating state or to accumulate lipid inclusions. To allow bacteria to slow their growth but not accumulate lipid inclusions, the hypoxia switch is retained but the maximum lipid inclusion parameter (L_max) is set to zero. To prevent bacteria from slowing their growth, the half-saturation parameter (h) is set to 1 × 10^–100.

Gene deletion mutants (virtual knockouts) are simulated in the CBM by removing the set of reactions requiring the corresponding gene product. Removing reactions shrinks the feasible space. Our approach is appropriate to capture the long-term effect of a deletion; other approaches may be more appropriate for capturing immediate short-term effects (95) or partial inhibition by drugs or other small molecules.

Of the 759 enzymes in the M. tuberculosis metabolic model, 291 block the biomass reaction when removed and are essential within the CBM. Of the remaining 468 enzymes, 277 do not change the CBM when removed because other enzymes catalyze the same reaction and, in the context of GranSim-CBM, are identical to those of the wild type (WT). The remaining 191 virtual knockouts cause changes in the metabolic network, potentially causing growth defects under certain nutrient conditions. These “attenuated” but not essential mutants are suited for further analysis using GranSim-CBM. We simulate these 191 mutants in the multiscale model by running GranSim-CBM with the virtual knockout CBMs for 10 replications per mutant. We then test the hypothesis that the 10-simulation mean CFU count at 400 dpi (μ_KO,i) is identical to the corresponding mean for WT strains. An empirical mean distribution (μ_WT) for the WT is constructed by performing 100 WT simulations and then generating N_b = 4,000 bootstrap samples of 10 simulations selected uniformly with replacement from the 100. The empirical one-sided P value p for each deletion mutant is then calculated as the percentile of the observed mean CFU for the knockout strain using the bootstrapped WT distribution as follows:

$$p=r/(N_b+1)$$ (7)

where r is the rank of μ_KO,i when included in the 4,000 WT bootstrap replicates. We corrected for multiple testing of the 191 attenuated mutants using the Benjamini-Hochberg method (96) with a false-discovery rate (FDR) constrained to 0.05 or less. Increasing N_b to 10,000 did not affect the list of attenuated mutants. The TubercuList database was used to map the gene names (Rv) present in GSMN-TB to their common names (97).

When enzymes are removed from the M. tuberculosis metabolic model, the remaining reactions may have different ranges of permitted fluxes. We use flux variability analysis (FVA) (98) to identify “bypass reactions” for each mutant, defined as those reactions not required for maximum growth in WT but required for maximum growth in the mutant considered. Practically, this is done by considering the range of each flux that could result in maximum growth as calculated by the CBM. Those fluxes with ranges that do not contain 0 in the mutant but contain 0 in the WT are labeled as bypasses for the removed reaction(s).

(xi) Efficient implementation of GranSim-CBM.

Because most of the CBM reactions are effectively unconstrained, the dynamic CBM optimum depends only on a small number of external variables. For computational ease in the multiscale model, we exploit this observation and replace linear programming with lookup tables generated using linear programming outside GranSim-CBM. The values in the lookup tables are used to calculate the optimal flux state for each bacillus. Lookup tables are indexed by five input variables: the growth switch parameter (η), the oxygen import flux upper bound (ν_O2^up), the extracellular glucose import flux upper bound (ν_glc^up), the extracellular TAG import flux upper bound (ν_TAG^up), and the lipid inclusion TAG import flux upper bound (ν_L^up). Note that although η depends on oxygen concentration (and therefore on ν_O2^up), the relationship varies with the parameters s and h (equation 2) as well as V_max-host and k_host. Therefore, indexing by both η and oxygen import fluxes allows the use of a single lookup table with multiple values of these parameters. Since inputs and table entries are normalized to correspond to a bacillus with a biomass of 1 BU, outputs are then scaled linearly by the actual biomass for each bacterium in GranSim-CBM. Six output variables from the CBM are used to update local variables in GranSim-CBM: the biomass growth rate (ν_b), the oxygen import flux, the glucose import flux, the extracellular TAG import flux, the lipid inclusion production (ν_pL), and lipid inclusion usage rate (ν_cL). As a tradeoff between lookup table size and accuracy, the lookup table uses 16 points in each input dimension spaced at equal intervals between a minimum and maximum value, with each of the 16⁵ entries then storing the 6 output variables. Multidimensional linear interpolation is used to calculate outputs between the table entries. The lookup table entries are calculated using the Cobra Toolbox for MATLAB (99), custom MATLAB scripts, and CPLEX (IBM Corp., Armonk, NY) for the linear programming optimization. Computational time to generate one lookup table was approximately 28 h on Intel E5 8-core (Sandy Bridge) processors.

GranSim and GranSim-CBM are implemented in C++ with Boost libraries (distributed under the Boost software license and available at www.boost.org). The graphical user interface (GUI), which allows us to visualize, track, and plot different facets of our simulated granulomas in real time, uses the Qt framework (open source; distributed under GPL). The model can be used with or without GUI visualization and is cross-platform (Mac, Linux, Windows). Average run time for GranSim is approximately 10 h per simulation for 1,000 days on Dell 8-core processors. Further details and a model executable and parameter file for GranSim-CBM are available online at http://malthus.micro.med.umich.edu/GranSim/GranSim-CBM/.

RESULTS

Our goal is to predict M. tuberculosis metabolic influences on bacterial loads within granulomas using our multiscale computational model, GranSim-CBM (Fig. 2), which is calibrated to nonhuman primate and rabbit data (Fig. 3). The model captures interactions between M. tuberculosis, host immunity, and the nutrient environment within granulomas, including the ability of M. tuberculosis to slow its growth and accumulate lipid inclusions in response to hypoxia. This approach enables the mapping of in vitro M. tuberculosis growth onto in vivo M. tuberculosis survival in granulomas (Fig. 1).

(i) Infection outcome correlates more strongly with bacterial properties than with environmental properties.

We identify the key molecule- and metabolism-scale mechanisms that drive granuloma outcomes using sensitivity analysis. We simultaneously vary multiple GranSim-CBM parameters and test their contributions to variations in granuloma outcomes of interest (e.g., bacterial load and oxygen concentration). We quantify these contributions by calculating the partial rank correlation coefficient (PRCC) between each model parameter and granuloma outcome. Sensitivity analysis reveals (Table 5) that two bacterial parameters, biomass degradation rate (d_max, representing maintenance metabolism of a replicating bacterium) and maximum oxygen reduction (V_max,O2, the maximum rate at which oxygen is reduced by the bacterium), are the main drivers of most granuloma outcomes. Lower-ranked parameters with significant correlations are related to granuloma environment, primarily plasma oxygen concentration (O2_,plasma), vascular permeability of oxygen (p), and available TAG per macrophage (TAG_I). Overall, these correlations are similar whether calculated at early time points (<40 dpi) or late time points (>200 dpi) in the simulation. Parameters that increased total bacterial load tend to decrease the proportion of intracellular bacteria. These results indicate that oxygen-related bacterial properties and, to a lesser extent, environmental properties are the main molecular/metabolic contributors to granuloma outcomes.

TABLE 5.

Results of sensitivity analysis summarized for key granuloma outputs and significantly correlated parameters^a

Parameter	Granuloma outcome
	Total CFU		Intracellular CFU		Extracellular CFU		Proportion intracellular		Caseation		Mean O2 in granuloma		TNF:IL-10
	Early	Late	Early	Late	Early	Late	Early	Late	Early	Late	Early	Late	Early	Late
Bacterial
Biomass degradation rate (dmax)	− − − −	− − − −	− − − −	− − − −	− − − −	− − − −	+ + + +	+ + + +	− − − −	− − − −	+	+	− − − −	− − − −
Maximum O2 flux (Vmax,O2)	+ + +	+ + +	+ + +	+ + +	+ + +	+ + +	− − −		+ + +	+ + +			+ + +	+ + +
Environmental
TAG per macrophage (TAGI)	+ +	+ + +			+ +	+ + +	− − −	− − −
Plasma O2 (O2,plasma)	+ +	+ + +	+ +	+ +	+ +	+ + +	− −	− − −	+ +	+ +	+ + + +	+ + + +
O2 vascular permeability (p)			+ +	+ +						+ +	+ + +	+ + +
Macrophage O2 consumption (Vmax−host)											− −	− −

^aKey granuloma outputs are indicated in the table columns and significantly correlated parameters in the table rows. PRCC results are reported as a sign(s) (positive [+] or negative [−]) as well as rank (from strongest correlation [+ + + + or −−−−] to weakest correlation [+ or −]) as determined by z-test results. Significance in PRCC and z-test calculations, alpha = 0.01. Early, <40 dpi; late, >200 dpi.

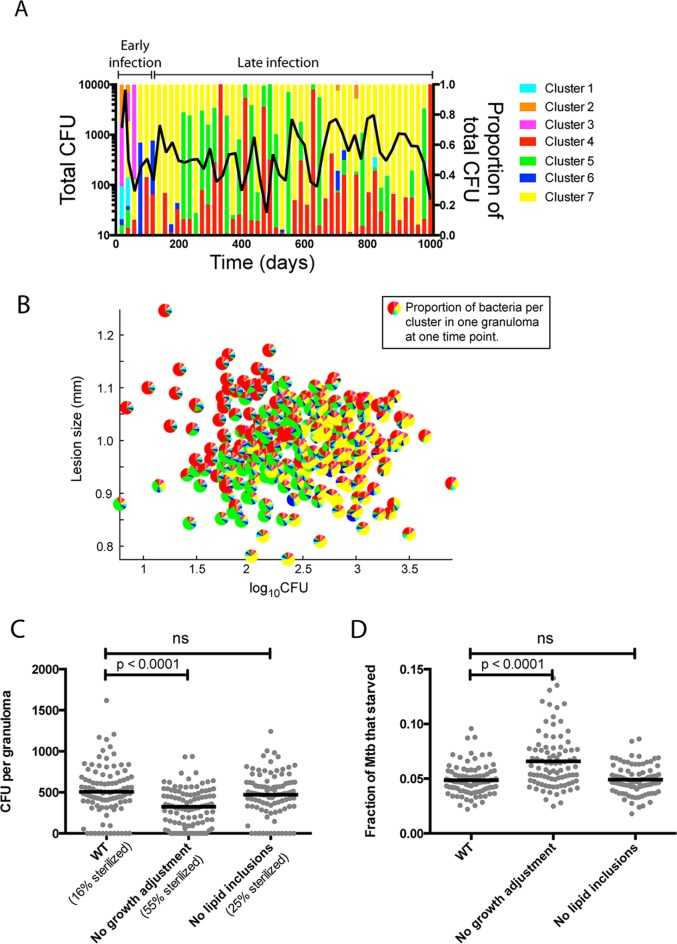
(ii) Bacterial growth phenotypes in granulomas are dynamic and heterogeneous.

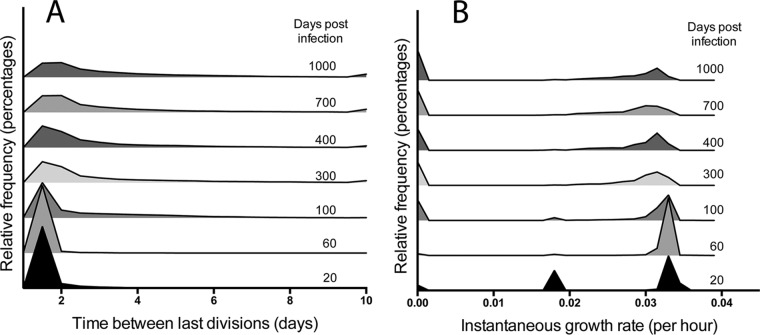
We characterize M. tuberculosis growth phenotypes existing within granulomas for wild-type (WT) strains. Since the model is stochastic, we can capture variability in granuloma outcomes by conducting 100 replicate simulations with the baseline parameter set in Table 4. We examine whether bacteria within a granuloma exist in a nonreplicating state. Infection is initialized by placing a single infected macrophage, containing a single bacterium, on the simulation grid. The growth status of each bacillus is investigated using two measures: generation time (time between previous divisions) and instantaneous growth rate (instantaneous flux through the biomass reaction). There is a trend toward increased generation times over the course of infection (Fig. 4A), though the trend is statistically insignificant after 200 dpi (see Fig. S3A in the supplemental material), with a maximum generation time of up to 94 days for a few bacteria at 1,000 dpi. Most bacteria have shorter generation times, however, and the median generation time of 1.5 days at 20 dpi increases to only 3.7 days at 1,000 dpi. The distribution of instantaneous growth rates is bimodal (Fig. 4B), reflecting distinct populations of replicating bacteria with growth rates of ∼0.033 h⁻¹ and of nonreplicating bacteria with growth rates of <0.0015 h⁻¹. This bimodal distribution is a reflection of the growth adaptation mechanism, i.e., the sigmoidal switching function (equation 2), as well as the pseudo-steady-state assumption in the dynamic CBM. This version of the model does not yet capture the time for gene regulation and for expression changes that the bacterium might require to reorganize its metabolic network. The majority of bacteria remain in the replicating population throughout infection (see Fig. S3B in the supplemental material). These results suggest that bacterial growth rates remain dynamic throughout infection.

FIG 4.

Distributions of bacterial growth over time. (A) Histogram showing the distribution of populations of bacteria by generation time. Bacteria with generation times longer than 10 days are included in the histogram at the 10-day time point. (B) Histogram showing distribution of bacteria by instantaneous growth rate. Results are averages of 100 replicate simulations performed with the baseline parameter set in Table 4.

(iii) Local nutrient conditions drive bacterial heterogeneity.

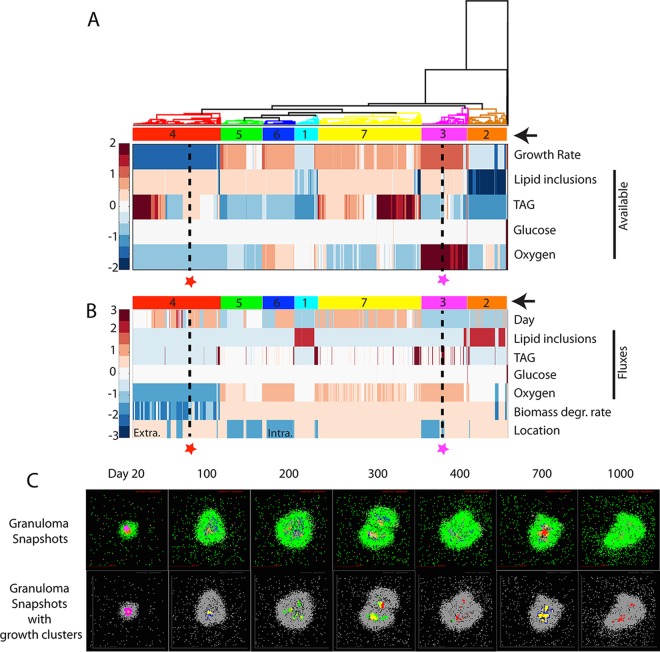
To probe the environmental factors driving changes in growth rates over time, we pool bacteria from a single representative granuloma at multiple time points (20, 100, 200, 300, 400, 700, and 1,000 dpi) representing the different phases of granuloma formation. We perform hierarchical clustering of these bacteria based on instantaneous growth rate, local concentrations of oxygen, glucose, and external TAG, and availability of TAG in lipid inclusions (Fig. 5A). In this analysis, bacteria with similar growth rates and nutrient environments are clustered. The nutrient conditions that drive M. tuberculosis growth rates in Fig. 4 can be represented by 7 unique growth clusters, as described in Table 6. For example, a bacterium in growth cluster 4 (red star and dashed line in Fig. 5A) is clustered with other bacteria that encounter medium-to-high-level carbon sources and low oxygen levels, causing them to switch to slow growth due to lack of oxygen. Similarly, a bacterium in cluster 3 (magenta star and dashed line in Fig. 5A) is clustered with other bacteria that encounter medium-level carbon sources and high oxygen levels, resulting in relatively rapid growth. The clustered bacteria are then further characterized (Fig. 5B) based on time point (dpi), nutrient utilization fluxes (lipid inclusions, TAG, glucose, and oxygen), biomass degradation rates, and location (intracellular/extracellular). The example bacterium in cluster 4 (red star and dashed line in Fig. 5B) is revealed to be from a later time point, using very little carbon and oxygen; its slowed metabolism is reflected in a low biomass degradation rate, and it is extracellular. The example bacterium in cluster 3 (magenta star and dashed line in Fig. 5B) is shown to be from an earlier time point, with high TAG and oxygen consumption levels and a high biomass degradation rate, and it is intracellular.

FIG 5.

Hierarchical clustering of bacteria by nutrient conditions and spatial location. (A) Bacteria (columns) from multiple time points from a representative granuloma are hierarchically clustered based on growth rate and level of lipid inclusions, TAG, glucose, and oxygen available in each bacterium's immediate environment (rows). Data for each nutrient are standardized to the row average. Clusters are numbered and highlighted with color codes indicated by arrows on the right. Two bacteria are highlighted (red and magenta stars with black dashed lines) as examples discussed in the text. These two bacteria are also used as examples in the discussion of panels B and C. (B) Bacterial clusters from panel A are further characterized by plotting their time points (day), fluxes from the CBM (i.e., optimal uptake fluxes for each nutrient calculated by the CBM based on the available nutrients), biomass degradation rate, and cellular location. Values for each output are standardized by row values. Extra., extracellular; Intra., intracellular. (C) Bacteria and their growth clusters are localized within granulomas. Granuloma simulation snapshots are shown in the top row with agent colors corresponding to those in Fig. 3D. The example bacteria from panels A and B are located in these granuloma snapshots with stars in the panels for 20 dpi and 700 dpi. Bacterial growth clusters are shown in the granulomas (bottom row) using color codes of clusters from panels A and B.

TABLE 6.

Summary of growth clusters identified in Fig. 5

Cluster	Description
1	Early lesions; low-level carbon sources; low-medium oxygen level; utilization of lipid inclusions; slow growth due to lack of carbon sources; high biomass degradation rate
2	Early lesions; low-level carbon sources; low-medium oxygen level; lipid inclusions very low; slow growth due to lack of carbon sources; high biomass degradation rate
3	Early lesions; medium-level carbon sources; high oxygen level; no significant utilization of lipid inclusions; fastest growers; high biomass degradation rate
4	Late, large lesions; low CFU; medium-to-high-level carbon sources; low oxygen level; no significant utilization of lipid inclusions; slow growth with low biomass degradation rate due to lack of oxygen
5	Late, medium-size lesions; medium CFU; medium-level carbon sources; low-medium oxygen level; no significant utilization of lipid inclusions; fast growth with high-maintenance metabolism
6	Early lesions following onset of adaptive immunity; medium-level carbon sources; high oxygen level; no significant utilization of lipid inclusions; fast growth with high-maintenance metabolism
7	Late, small lesions; high CFU; high-level carbon sources; low-medium oxygen level; no significant utilization of lipid inclusions; fast growth with high-maintenance metabolism

Bacteria from early time points group in clusters 1 to 3. Although most bacteria at 20 dpi have high available oxygen levels, bacteria in clusters 1 and 2 at 20 dpi have low growth rates (Fig. 5A and B) compared to those in cluster 3. Thus, while different clusters are representative of bacteria during different stages of infection, heterogeneity exists even early on. Clusters 4 to 7 are enriched for bacteria from later time points (Fig. 5A and B). Cluster 4 represents bacteria that have slowed their growth in response to low-oxygen conditions (as reflected in lower biomass degradation rate).

We can also locate each bacterium within the granuloma at each time point (Fig. 5C). For example, the bacterium from cluster 4 (red stars and dashed lines in Fig. 5A and B) is from 700 dpi in a small group of bacteria in the top right of the granuloma (red star in Fig. 5C; 700 dpi). The bacterium in cluster 3 (magenta stars and dashed lines in Fig. 5A and B) is located along with most other bacteria in cluster 3, in the outer rim of the bacterial population at 20 dpi (magenta star in Fig. 5C; 20 dpi). Examining the spatial distribution of bacteria from all seven growth clusters within the granuloma over time reveals that clusters 1 and 2, which are limited in available TAG, are located in the innermost part of the granuloma (Fig. 5C). This suggests that the rapid expansion of bacteria at this early time point is generating a carbon-limited subpopulation of bacteria, leading these bacteria to utilize their lipid inclusions (Fig. 5B). Furthermore, the major heterogeneity occurs over time rather than space. Bacterial populations shift from one growth cluster to another, e.g., from mostly clusters 5 and 7 at 300 dpi to mostly cluster 4 at 400 dpi. These results indicate that fluctuations occur within granulomas, with M. tuberculosis bacteria continually responding to the dynamic granuloma microenvironments by changing their growth rates.

(iv) Growth phenotype changes reflect granuloma size and bacterial loads.

To explore how the fluctuations in bacterial growth phenotypes connect to granuloma environmental properties, we examine the total number of bacteria and relative fraction of bacteria within each growth cluster at 20-day intervals for a representative granuloma (Fig. 6A). Note again the differences in predominant growth clusters between the early (<100 dpi, clusters 1 to 3) and late (>100 dpi, clusters 4 to 7) time points. After 100 dpi, when CFU levels are high, the majority of bacteria are in cluster 7, with sufficient carbon sources and low but not limiting oxygen levels. When CFU levels in the granulomas are low, the majority of bacteria are in cluster 4, with ample carbon sources but with growth slowed by hypoxia. These nonreplicating bacteria can reenter the replicating state when hypoxia is relieved, as a granuloma shrinks. Reducing hypoxia in granulomas has been suggested as a strategy to resensitize bacteria to antibiotics (100). The dynamics between bacterial load, granuloma size, and bacterial growth clusters are also evident if we examine multiple granulomas at multiple time points between 200 and 1,000 dpi (Fig. 6B; see also Fig. S4 in the supplemental material). Smaller granulomas with high bacterial loads have bacteria mostly in growth cluster 7, while larger granulomas have lower bacterial loads, with the majority of bacteria in cluster 4. Bacteria in cluster 5 mostly occupy granulomas that are intermediate in size and bacterial load. We explore the role of different growth clusters with respect to long-term bacterial survival in granulomas by removing the factors of slow growth and lipid accumulation independently. Removing M. tuberculosis's ability to slow its growth, i.e., its ability to enter growth cluster 4 (but not its ability to accumulate lipid inclusions), leads to lower bacterial loads and higher sterilization rates (Fig. 6C). These differences can be linked to increased bacterial death from starvation (Fig. 6D). Specifically, since growth cluster 4 normally adjusts to lack of oxygen by lowering its maintenance metabolism (Table 6), the increased bacterial death shown in Fig. 6D is due to oxygen levels insufficient to sustain maintenance metabolism. This suffocation is in contrast to bacterial death due to a lack of carbon sources (such as the conditions encountered by growth clusters 1 and 2 early during infection (Fig. 5C and Table 6). Collectively, these results connect bacterial growth phenotypes to granuloma properties and show the importance of growth adaptation for long-term survival of M. tuberculosis in granulomas.

FIG 6.

Importance of growth adaptation for long-term survival of M. tuberculosis in granulomas. (A) Proportions of bacteria in each growth cluster (the 7 clusters identified in Fig. 5) were quantified every 20 days over the course of infection (right y axis) and plotted with total CFU (left y axis). (B) Each pie symbol represents 1 granuloma (data represent 300 granulomas randomly selected from a collection of 100 granulomas sampled at different time points after 200 dpi). Slices represent proportions of bacterial populations within each growth cluster. (C and D) Comparisons of WT simulations to simulations in which growth adaptation or the ability to accumulate lipid inclusions was removed. (C) Time-averaged CFU between 200 and 1,000 dpi. (D) Fraction of bacteria that died from starvation by 1,000 dpi (i.e., biomass < τ_death) for individual granulomas (n = 100). P values indicate results from the Kruskall-Wallis test with Dunn's correction for multiple comparisons. Lines show means. ns, not significant.

(v) The timing of metabolic enzyme inhibition, early versus late in infection, influences attenuation.

To explore the potential of metabolic enzymes as antibiotic targets, we predict the effect of removal of each enzyme on both growth rate in vitro (using the CBM) and bacterial load in granulomas (using GranSim-CBM). We generate virtual metabolic enzyme knockout mutants (KOs) by systematically removing one enzyme at a time from the metabolic network in the CBM. For in vitro predictions, we consider different culture media as well.

Of 191 KOs tested, we identified 41 as significantly attenuated (FDR, 0.05) relative to the WT based on bacterial load within granulomas at 400 dpi (see Fig. S5A and B and Table S3 in the supplemental material). These 41 enzymes catalyze 22 distinct reactions, primarily within the electron transport chain: 10 different genes encoding components of the cytochrome c oxidase complex and 13 genes encoding components of NADH-ubiquinone oxidoreductase. The attenuation predicted for these KOs suggests that they could be potential antibiotic targets. Note that our predictions overestimate the amount of attenuation possible with antibiotics because antibiotics typically result in only partial inhibition of target enzymes and because antibiotic treatment of TB typically starts well after infection, when the patient seeks medical care.

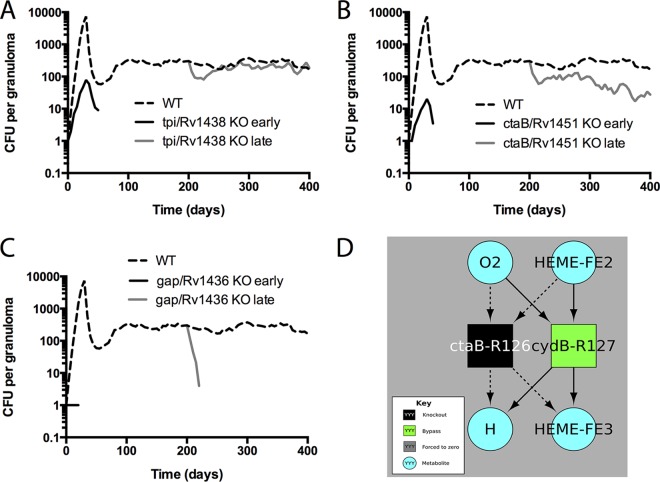
We therefore tested the effect of a knockout occurring mid-infection (at 200 dpi) (Fig. 7) for the 41 KOs identified in the previous analysis. Mid-infection KOs fall broadly into three categories: (i) no attenuation for mid-infection knockouts (Fig. 7A) (category 1), (ii) less attenuation for mid-infection knockouts than for preinfection knockouts (category 2) (Fig. 7B), and (iii) similar levels of attenuation in pre- and mid-infection knockouts (category 3) (Fig. 7C). KOs that fall into category 2 or category 3 (but not category 1) could potentially be good antibiotic targets because they are attenuated if knocked out mid-infection. These results suggest that methods that screen for new antibiotic targets should account for differences between bacterial requirements for survival early versus late in infection.

FIG 7.

Bacterial loads over time for different virtual KO mutants. Data represent predicted total CFU (median) over time for the WT (dashed line), knockouts from the start of infection (black line), or mid-infection knockouts from 200 dpi (gray line). Data from three representative gene products are shown. (A) tpi/Rv1438, a triosephosphate isomerase which has a role in glycolysis. (B) ctaB/Rv1451, a cytochrome c oxidase assembly factor. (C) gap/Rv1436, a probable GAPDH (glyceraldehyde 3-phosphate dehydrogenase) involved in the second phase of glycolysis. n = 20 for the knockouts; n = 100 for the WT. (D) Bypass reactions identified by flux variability analysis (FVA). Squares represent chemical reactions corresponding to the enzyme label. Metabolites used or produced by any of the depicted reactions are included (teal circles). This diagram shows the reactions eliminated by a gene knockout (black square) and reactions that became “required” (defined as leading to attenuation if removed) in the knockout but that were not required in the WT (green square). Dashed arrows correspond to metabolite usage or production no longer present in the knockout (as the reaction has been removed); solid arrows correspond to reactants of the bypass (green) reactions. To summarize what can be gleaned from this figure, the protein encoded by ctaB is required for cytochrome bc1 oxidase activity. Thus, a knockout mutant in ctaB makes use of a bypass flux through cydB, which is part of the less efficient cytochrome bd complex. Under conditions in which cydB was also knocked out (or severely inhibited by drugs), the model predicts that M. tuberculosis would be further attenuated in growth (though not necessarily incapable of growth). Identical results were obtained for knockouts in any of the following genes annotated as required for cytochrome c oxidase activity: ctaB, ctaC, ctaD, ctaE, fixA, fixB, qcrA, qcrB, qcrC, and Rv1456c.

(vi) Metabolic bypass pathways mitigate growth defects in attenuated mutants and may represent auxiliary drug targets.

What drives the differential levels of attenuation in early versus late KO mutants? We use the CBM to identify metabolic mechanisms that allow some KO mutants to sustain infection in granulomas. We use flux variability analysis (FVA) to identify bypass reactions activated in response to enzyme knockouts. Of the 41 attenuated mutants identified with GranSim-CBM, 28 were observed to have a nonzero growth rate in lipid-only media, and these were mapped to a unique subset of 7 reactions (Table 7). Growth rates of the corresponding mutants range from 30% to 75% of the wild-type growth rate in an in vitro environment with high lipid levels and high oxygen levels. At the maximum growth rate, the mutants all reduce oxygen at the same rate as the wild-type genotype, indicating that oxygen reduction is the limiting reaction for both the wild-type strain and these mutants. Several mutants require greater TAG import, suggesting less-efficient stoichiometry in the conversion of TAG to biomass. Mutants with reduced TAG import relative to wild-type levels utilize oxygen less efficiently and consequently display significant attenuation.

TABLE 7.

The defect for each of the attenuated but nonlethal mutants can be explained by a change of the permitted stoichiometry between oxygen, TAG, and biomass for in vitro growth in lipid-only media in high levels of oxygen^a

Gene removed from the reaction set in each KO mutant	Enzymatic activityb	Reaction catalyzed	Optimal rate of biomass production (1/h)	Import rates during optimal growth (fmol/h-BU)
				TAG	Oxygen
WT	NA	NA	0.034	0.003	0.272
tpi/Rv1438	Triose-phosphate isomerase	DHAP ⇔ G3P	0.023	0.005	0.272
pgk/Rv1437	Phosphoglycerate kinase	ADP + 13PDG ⇔ ATP + 3PG	0.013	0.007	0.272
nuoA/Rv3145, nuoB/Rv3146, nuoD/Rv3148, nuoE/Rv3149, nuoF/Rv3150, nuoG/Rv3151, nuoH/Rv3152, nuoI/Rv3153, nuoJ/Rv3154, nuoK/Rv3155, nuoL/Rv3156, nuoM/Rv3157, nuoN/Rv3158	Type I NADH dehydrogenase, NuoA-N	MK + NADH → MKH2 + NAD + 4 H	0.025	0.003	0.272
glcB/Rv1837c	Malate synthase	ACCOA + GLX → COA + MAL	0.010	0.007	0.272
gap/Rv1436	Glyceraldehyde-3-phosphate dehydrogenase	NAD + PI + G3P ⇔ NADH + 13PDG	0.013	0.007	0.272
eno/Rv1023	Phosphopyruvate hydratase	2PG ⇔ PEP	0.010	0.007	0.272
ctaB/Rv1451, Rv1456c, ctaE/Rv2193, qcrC/Rv2194, qcrA/Rv2195, qcrB/Rv2196, ctaC/Rv2200c, fixB/Rv3028c, fixA/Rv3029c, ctaD/Rv3043c	aa3-type cytochrome c oxidase, ctaCDE AND cytochrome bc1	0.5 O2 + 2 HEME-FE2 → 6 H + 2 HEME-FE3	0.019	0.002	0.272

^aAttenuated mutants were identified by hypothesis testing using GranSim-CBM data. The nonlethality of the mutants was determined by CBM in lipid-only media. NA, not applicable.

^bAnnotation is provided in reference 45.

To identify the reactions used by the KO mutants to bypass knocked-out enzymes, we can visualize metabolic subnetworks involving knockouts, bypass reactions, and metabolite reactants and products used by these KO mutants to compensate for loss of an enzyme (Fig. 7D; see also Fig. S6 to S13 in the supplemental material). An electron transfer system example is provided by the knockout of ctaB, which eliminated the activity of the cytochrome bc1 protein complex within the cytochrome c system. This function is bypassed by the less efficient cytochrome bd complex, which is not used by the wild-type organism under the same conditions (Fig. 7D). This bypass allows the ctaB knockout to persist in granulomas at nearly WT levels (Fig. 7B). These computational results are consistent with recent experimental results obtained using small molecules to poison cytochrome bc1 activity, resulting in upregulation of cytochrome bd (101). Similarly, knockout of eno requires a bypass reaction for generation of 3-phosphoglycerate (see Fig. S6). Inhibitors of enolases have been reported, including phosphonoacetohydroxamate (102) and ENOblock (103). Our computational results suggest that these inhibitors could be made more effective at inhibiting the growth of M. tuberculosis by cotreatment with inhibitors of bypass enzymes encoded by genes such as gap (glyceraldehyde 3-phosphate dehydrogenase) or tpi (triosephosphate isomerase). These results illustrate how CBMs can be used to broadly characterize the metabolic defects caused by individual drugs and, potentially, to identify secondary targets required for bypassing chemically or genetically inactivated reactions.

(vii) Multiscale analysis reveals in vitro culture medium and growth thresholds predictive of M. tuberculosis survival in granulomas.

M. tuberculosis mutants that grow well in rich media (high glucose, high TAG, and high oxygen levels) may have growth restrictions in the depleted environment of an in vivo granuloma. With the aim of identifying in vitro conditions that may predict in vivo readouts (Fig. 1), we investigate which in vitro nutrient conditions yield M. tuberculosis growth rates that correlate with predicted in silico granuloma outcomes such as bacterial load.

Growth rates calculated for knockouts in rich media (r = 0.67; P value < 0.001) and lipid-only media (r = 0.73; P value < 0.0001) are correlated with predicted CFU per granuloma (Fig. 8A and B). Thirteen of the 191 mutants are not predicted to be attenuated in rich media but are attenuated in simulated granulomas (Fig. 8A; similar to KO2 in Fig. 1). Such false-negative attenuation predictions are not present using growth rates predicted on lipid-only media (Fig. 8B). Knockouts conducted at 200 dpi rather than preinfection also show a correlation (r = 0.81; P value < 0.001) between the lipid-only growth rate for the knockout and the bacterial load in granulomas (Fig. 8C). These correlations are not unexpected as a reflection of the model constraint that intracellular bacteria use only TAG and not glucose. However, it is unclear which threshold in growth rates should be used to define attenuation relative to the WT growth rate. If the same in vitro growth rate threshold (∼85% of the WT growth rate) is used to define attenuation in the early (Fig. 8B) and late (Fig. 8C) knockouts, two late knockout mutants appear to be attenuated on the basis of lipid medium growth rates but are not attenuated in simulated granulomas (Fig. 8C; similar to KO3 in Fig. 1). A lower threshold (∼66% of the WT growth rate) is necessary to predict which mutants would be unable to sustain long-term infections (Fig. 8C). In other words, KOs with predicted growth rates between ∼66% and 85% of the WT growth rate are able to sustain but not establish infections within granulomas.

FIG 8.

Predicting in vivo attenuations from in vitro M. tuberculosis growth rates. We implemented the paradigm described in Fig. 1 by correlating CBM-predicted growth rates and average GranSim-CBM-predicted CFU per granuloma. We plotted CBM-predicted growth rates for single gene knockouts in rich media (A) or lipid-only media (B and C) versus average GranSim-CBM predicted CFU per granuloma when knocked out from the start of infection (A and B) or knocked out mid-infection at 200 dpi (C). Scatter plot of means ± standard errors of the means (SEM) (n = 20) for each knockout and wild type. Note that the high-CFU-burden knockouts can be cleanly separated from the low-CFU-burden knockouts on the basis of the CBM growth rate in lipid-only media but that the timing of the knockout moves the in vitro threshold to the left (arrow in panel C).

These data identify ∼66% of the WT growth rate in lipid media as a threshold for predicting in vivo attenuation.

DISCUSSION

A better understanding of the microbiology of TB granulomas could help to identify new antibiotic targets or host-directed therapies (104, 105) that could limit long-term M. tuberculosis survival in vivo. We present a multiscale computational model that maps genetic and metabolic detail at the bacterial scale to in vivo granuloma outcomes such as bacterial load. This model recapitulates tissue-level outcomes observed in vivo (21, 77–79), affording us a first-time tool to track dynamics occurring on the bacterial and granuloma scales.

The view of long-term M. tuberculosis survival in a nonreplicating state within granulomas suggests a static equilibrium between host and pathogen. However, evidence points to a more dynamic host-pathogen balance (77), with nonsterilized granulomas in latently infected individuals indistinguishable from granulomas in individuals with active TB disease (21, 23) based on CFU and on CFU/CEQ, where CEQ (representing chromosomal equivalents) is a measure of all bacteria that have been in the granuloma during the entire infection. Our model supports a dynamic persistence mechanism in which M. tuberculosis surviving in long-term granulomas can be actively dividing and continually responding to changing granuloma environments. This would imply that TB is not only a highly heterogeneous infection (106) but, on the granuloma level, also a highly dynamic one. Specifically, our model suggests that the slowly replicating or nonreplicating phenotypes of M. tuberculosis preserve the bacterial population in vivo by continuously adapting to dynamic granuloma microenvironments, and we show that removing the ability of bacteria to slow their growth mid-infection impairs their ability to sustain a long-term infection. Inhibitors of the nonreplicating phenotype could potentially improve treatment outcomes, similarly to the “shock-and-kill” approach currently being investigated in HIV therapy (107). The role of the nonreplicating phenotype in dynamic adaptation could, to some extent, be tested in vitro using dynamic nutrient condition manipulation in chemostats or other culture methods (26, 28) combined with knockouts in genes suspected to be connected to the phenotype (e.g., relA, dosR).

Our predicted nutrient conditions encountered by M. tuberculosis in granulomas could help guide the environmental conditions used for in vitro drug screens. In vitro drug or drug target screening assays with slowly replicating or nonreplicating M. tuberculosis (including starvation, low-oxygen, and nitric oxide assays) are typically used to represent in vivo bacterial phenotypes, and there is significant research effort put into recreating granuloma-like stress conditions in vitro (3). Even in the absence of a hoped-for granuloma-in-a-dish experimental system, our results suggest the most relevant in vitro experimental systems for predicting granuloma outcomes. Mutant phenotypes in simulated granulomas (“in vivo”) are in greatest concordance with growth rates in simulated lipid-only media (“in vitro”). These results could support new directions for in vitro drug or drug target screening (63). Our results further identify an attenuation threshold, showing that drugs should result in lipid-only growth rates below 66% of the WT rate to be able to effectively inhibit bacterial survival in granulomas. Note that this threshold provides an upper limit of growth under conditions of inhibition, since our granuloma results are based on complete knockout of the genes whereas novel antibiotics are unlikely to continuously and completely eliminate the enzymatic activity of the target. This granuloma-dependent threshold for mutant attenuation suggests a novel strategy for translating in vitro discoveries into potential new therapies.

Our model also identifies bypass pathways that are not essential in WT M. tuberculosis but which are essential for optimal growth of a knockout mutant in the granuloma environment. Bypass pathways could be used to identify secondary targets for combination therapy or potential failure modes for inhibition of metabolic enzymes. Bypass reactions may also suggest novel combinations of drugs with synergistic anti-M. tuberculosis activity.

Computational methods have been successfully applied in the drug discovery pipeline against a number of pathogens (108–110). Genes (and combinations of genes) that we identify to be important for in vivo survival can now be tested as potential new drug targets using existing drugs or KO strains in animal models. Combining GranSim-CBM with our existing model of antibiotic distribution and activity in the granuloma (40, 41) could also help elucidate the contributions of bacterial heterogeneity, asymmetric division and growth, and lipid inclusion levels to treatment outcomes (5, 111). Such insight can in turn inform new regimens and strategic drug design.

Funding Statement

Computational support was provided by the National Energy Research Scientific Computing Center, which is supported by the Office of Science of the U.S. Department of Energy under contract no. DE-AC02-05CH11231, and the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1053575.