Binding Energy Distribution Analysis Method (BEDAM): Hamiltonian replica exchange with torsional flattening for binding mode prediction and binding free energy estimation

Abstract

Molecular dynamics modeling of complex biological systems is limited by finite simulation time. The simulations are often trapped close to local energy minima separated by high energy barriers. Here, we introduce Hamiltonian replica exchange (H-REMD) with torsional flattening in the Binding Energy Distribution Analysis Method (BEDAM), to reduce energy barriers along torsional degrees of freedom and accelerate sampling of intra-molecular degrees of freedom relevant to protein-ligand binding. The method is tested on a standard benchmark (T4 Lysozyme/L99A/p-xylene complex) and on a library of HIV-1 integrase complexes derived from the SAMPL4 blind challenge. We applied the torsional flattening strategy to 26 of the 53 known binders to the HIV Integrase LEDGF site found to have a binding energy landscape funneled towards the crystal structure. We show that our approach samples the conformational space more efficiently than the original method without flattening when starting from a poorly docked pose with incorrect ligand dihedral angle conformations. In these unfavorable cases convergence to a binding pose within 2-3 angstroms from the crystallographic pose is obtained within a few nanoseconds of the Hamiltonian replica exchange simulation. We found that torsional flattening is insufficient in cases where trapping is due to factors other than torsional energy, such as the formation of incorrect intra-molecular hydrogen bonds and stacking. Work is in progress to generalize the approach to handle these cases and thereby make it more widely applicable.

Introduction

Accurate prediction of the binding free energy for a protein-ligand complex is important to biophysical chemistry and rational drug design.^1–6 Estimation of binding free energies depends mainly on two critical factors; an accurate energy function and sufficient conformational sampling.⁴ In the present study, we focus on improving the conformational sampling of slow degrees of freedom. In prospective binding free energy calculations, initial structures of receptor-ligand complexes typically come from docking, which is known to have limited accuracy.⁷ Currently, accurate binding free energy calculations still rely on having the correct initial structure of the complex,^8,9 because free energy simulations will usually be trapped in the neighborhood of the starting conformational basin.⁴ The problem arises mainly from high energy barriers that separate different free energy basins.^{1–3,10–14} This has limited the applications of binding free energy methods in drug discovery. Several advanced sampling methods^15–28 have been developed to overcome this problem. Two of the recent enhanced sampling methods are the two-dimensional replica exchange method²⁹ and replica exchange with solute tempering method (REST2).^10–12 They have been shown to improve the efficiency of conformational sampling and lead to faster convergence in some protein-ligand systems. The two dimensional (2D)-replica exchange method implements Replica Exchange in the alchemical λ space and applies a biasing potential to side chains of the protein residues forming the binding pocket to accelerate the sampling of the binding induced ligand-receptor reorganization. ^17,29 The REST2 method uses fewer parallel replicas to accelerate sampling by scaling the interaction potentials in the localized region surrounding the binding pocket of the receptor (the “hot region”).^10–12 The REST2 method has been successfully used for relative binding free energy calculations in explicit solvent with the free energy perturbation (FEP) method on a number of ligand-protein systems.^{10–12,30,31}

The Binding Energy Distribution Analysis method (BEDAM)^13,32–34 has been developed in our group to compute the absolute binding free energy using implicit solvent models of a ligand to a protein. BEDAM occupies a niche between docking methods on one hand and high resolution FEP methods in explicit solvent on the other. In the SAMPL4 challenge BEDAM came in first among the purely computational methods for predicting enrichment for a focused library of inhibitors designed to bind to the LEDGF allosteric site of HIV Integrase.^8,35,36 In this method, alchemical free energy simulations at different lambda values that span from fully coupled (λ = 1) to decoupled (λ = 0) states are performed and Hamiltonian replica exchange (H-REMD) is employed along the alchemical space to help enhance the conformational mixing (λ-hopping). While the rotational and translational coordinates of a ligand with respect to a receptor are sampled in the decoupled states, no measure is taken to accelerate the sampling of the internal degrees of freedom in either the receptor or ligand (e.g. the protein side chains and ligand torsions).⁴ In order to improve conformational sampling, here we have modified the effective potential function in the BEDAM method. The idea of expressing a biasing potential as a parametric function of λ is similar in spirit to the REST2 approach developed by Berne and Friesner et al.^10–12,30 to enhance the conformational sampling in FEP calculations for relative binding free energy calculations. In our method, the potential function is modified to reduce torsional energy barriers and accelerate the sampling along the slow degrees of freedom relevant to binding processes at intermediate λ values; the bias function is switched off at the physical λ = 0 and λ = 1 states. This allows us to substantially improve the prediction of the true binding mode, and also the convergence of the corresponding binding free energy estimates. Compared with FEP/REST2, our method includes thermodynamic states in which the ligand and receptor are fully decoupled, which allows the conformational space to be more fully explored through unhindered sampling of the external coordinates of the ligand in the coordinate frame of the receptor. In addition, the use of implicit solvent also accelerates sampling. In the current study, we have applied the method to ligand binding to two receptors; T4 Lysozyme (T4L)/L99A/p-xylene and HIV-1 Integrase.^8,35,36 In the case of the T4L/L99A/p-xylene complex, the binding induced structural reorganization occurs in the protein non-polar binding pocket upon binding of the p-xylene ligand. For HIV Integrase/ligand systems, the main focus is on ligand intramolecular degrees of freedom because ligand rotameric states play a critical role in the ligand binding for some ligand classes. Our results show that the BEDAM simulations with torsional flattening starting from an initial docked structure that deviates from the experimental structure by ≥ 5 Å is capable of recapitulating the crystallographic binding mode. While the method is able to predict ligand binding poses significantly closer to the crystallographic pose for many ligands that were docked with incorrect rotamer states, for others, we found that non-native ligand intramolecular interactions (e. g. non-native hydrogen bonds and stacking interactions) prevent them from sampling the crystallographic binding pose and additional biasing functions will need to be constructed in order to address this issue. We have also shown that the method is able to improve the computed binding free energy estimates in addition to exploring conformational space more efficiently than standard parallel replica exchange simulations.

Methods

This section begins with a brief description of the BEDAM binding free energy method, its effective potential energy function, and the torsional flattening implementation, and then it follows with a description of the system preparation and computational details.

BEDAM binding free energy protocol

The BEDAM method¹³ is a method with a clear statistical mechanics framework to compute the absolute binding free energy $\Delta G_b^0$ between a receptor A and a ligand B. It employs a λ_b-dependent effective potential energy function with implicit solvation of the form

$$V_{{\lambda }_b}\left(r\right)=V_0\left(r\right)+{\lambda }_{b}u\left(r\right)$$ (1)

where r = (r_A, r_B) denotes the atomic coordinates of the complex, with r_A and r_B denoting those of the receptor and ligand, respectively,

$$V_0\left(r\right)=V\left(r_A\right)+V\left(r_B\right)$$ (2)

is the potential energy of the complex at the unbound state, and

$$u\left(r\right)=u(r_A,r_B)=V(r_A,r_B)-V\left(r_A\right)-V\left(r_B\right)$$ (3)

is the binding energy function defined for each conformation r = (r_B , r_A) of the complex, which equals the difference between the effective potential energies V(r) with implicit solvation³⁷ of the bound and unbound conformations of the complex without internal conformational rearrangements.

As seen from Eq. (1),Eq. (2) and Eq. (3), V_λb=1 corresponds to the effective potential energy of the fully coupled complex and V_λb=0 corresponds to the state in which the receptor and ligand are uncoupled. Intermediate λ_b values trace an alchemical thermodynamic path connecting these two states. The difference in free energy between these two states is the binding free energy △G_b. The standard free energy of binding is related to this by the relation¹

$$\Delta G_b^0=-k_{B}Tln{C}^0{V}_{site}+\Delta G_b$$ (4)

where k_B is the Boltzmann constant; T is temperature; C⁰ is the standard concentration of ligand molecules (C⁰ = 1 M, or equivalently 1,668 Å⁻³) and V_site is the volume of the binding site.¹³

A modified “soft-core” binding energy function is used to improve convergence of the free energy near λ_b = 0 (as given in Eq. (5)).

$$u^{\prime }\left(r\right)=\{\begin{array}{cc}{u}_{max}tanh[u\left(r\right)∕u_{max}]\hfill & \text{if}u\left(r\right)>0\hfill \\ u\left(r\right)\hfill & u\left(r\right)\le 0\hfill \end{array}\phantom{\}}$$ (5)

where u_max is some large positive value (it is 1,000 kcal/mol in this work). This modified binding energy function, which is the actual binding energy function used ( Eq. (3)) caps the maximum unfavorable value of the binding energy while leaving unchanged the value of favorable binding energies.³⁸

BEDAM with torsional flattening

The new functional form of the effective energy with torsional flattening in BEDAM is given in Eq. (6) and the relation between scaling parameter of the torsional flattening term (λ_D) and binding parameter (λ_b) is shown schematically in Fig. S1 of supplementary information (S.I.). To accelerate conformational sampling of receptor side chain and/or ligand torsions, torsional flattening is applied to the sum of dihedral torsions and 1-4 non-bonded interactions of associated torsions given as V_Dihe ( Eq. (8)).

$$V_{{\lambda }_b}\left(r\right)=V_0\left(r\right)+{\lambda }_{b}u\left(r\right)-{\lambda }_D{V}_{Dihe}\left(r\right)$$ (6)

where

$${\lambda }_D=\{\begin{array}{cc}2{\lambda }_b\hfill & \text{if}{\lambda }_b\le 0.5\hfill \\ 2-2{\lambda }_b\hfill & {\lambda }_b>0.5\hfill \end{array}\phantom{\}}$$ (7)

and

$$V_{Dihe}\left(r\right)=\sum _{selecteddihedrals}\left(\frac{V_n}{2}[1+cos\left(n\varphi \right)]+\sum _{i<j}{\left[\frac{A_{ij}}{r_{ij}^{12}}-\frac{B_{ij}}{r_{ij}^6}\right]}_{1-4}+\sum _{i<j}{\left[\frac{q_i{q}_j}{ϵr_{ij}}\right]}_{1-4}\right)$$ (8)

In Eq. (8), V_n is the barrier height (dihedral coefficient); n is the periodicity of the potential; φ is dihedral angle.

Throughout the alchemical transformation from initial λ_b to final λ_b, λ_D is linearly increased from 0 for initial λ_b = 0 to 1 for the λ_b = 0.5 and then is linearly decreased back to 0 for the final λ_b = 1 (S. I. Fig. S1) so that the effective energies of the initial and final states correspond to physical states and the binding free energy △G_b between a receptor A and a ligand B can be computed. At λ_b = 0.5, the scaled V_λb(r) potential cancels the corresponding torsional terms in V₀(r) and the selected torsions are fully flattened. In this way, conformational sampling is achieved through the effective potential with flattened torsional barriers for selected dihedrals at intermediate λ_b states.

The BEDAM method employs a Hamiltonian replica exchange (H-REM) λ_b-hopping strategy whereby replicas periodically attempt to exchange λ_b values through Monte Carlo (MC) λ-swapping moves rather than simulating each λ_b state independently. λ_b-exchanges are accepted with the Metropolis probability min[1, exp(−β △λ_b△u)].¹³ In this study, the Metropolis acceptance probability with torsional flattening energy is given with min[1, exp(−β(△λ_b△u − △λ_D△V_Dihe))] where △λ_b is the difference in λ_b’s being exchanged and △u is the difference in binding energies; △λ_D is the difference in λ_D’s being exchanged (dependent on λ_b) and △V_Dihe is the difference in flattened dihedral energies between the replicas exchanging them. As shown in previous studies^{10–12,15,17,18,20–24,29–31} for efficient conformational sampling of complex biological systems to study their structural and dynamic properties, replica exchange strategies of this kind yield superior conformational sampling and more rapid convergence rates by allowing conformational transitions to occur at the value of λ_b at which they are most likely to occur and to be then propagated to other states.¹⁴

In order to compute the binding free energy △G_b from a set of binding energies, u, sampled from molecular dynamics simulations at a series of λ_b values, the multistate-Bennett acceptance ratio estimator (MBAR)^38,39 is used in this study. △G_b = kT(f₁ − f₀) is computed directly from dimensionless free energies f_λb = −lnZ_λb where Z_λb is λ_b dependent biased partition functions and dimensionless free energies f_λb are estimated self-consistently in MBAR.³⁹

System preparation and Computational details

BEDAM employs an effective potential in which the effect of the solvent is represented implicitly by means of the AGBNP2 implicit solvent model^40,41 together with the OPLS-AA^42,43 force field for bonded and non-bonded atomic interactions.

T4L/L99A/p-xylene

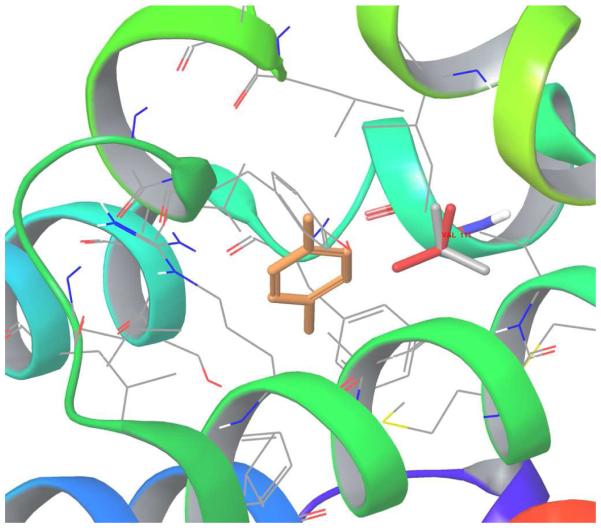
The structure of p-xylene (orange stick) bound to T4 Lysozyme is shown in Figure 1; the Val111 side-chain rotameric state shown in gray (gauche state) and another Val111 side-chain rotameric state shown in red (trans state). Initial structures for the complex of p-xylene with the L99A mutant of T4 lysozyme were prepared based on the corresponding crystal structure (PDB access code 187L). The Val111 key residue of T4 Lysozyme is in trans conformation in the protein structure with no bound p-xylene ligand; in the binding complex of ligand p-xylene, the Val111 changes its rotameric state from the trans conformation (χ≈−180) to the gauche (χ≈−60) conformation.

Figure 1.

The structure of p-xylene (orange stick) bound to T4 Lysozyme: the Val111 side-chain gauche state shown in gray and Val111 side-chain trans state shown in red.

The binding site volume was defined as any conformation in which the center of mass of the aromatic ring of p-xylene ligand is within 6 Å from the center of mass of the Cα atoms of residues 88, 102, 111 of the T4L/L99A receptor. The ligand was confined in this binding site volume by means of a flat-bottom harmonic potential. Based on the definition of the volume of the binding site, V_site, is calculated as 469 ų corresponding to the value of −kT ln C⁰ V_site = 0.75 kcal/mol. The Cα atoms of the residues of the receptor were restrained by means of spherical harmonic restraints with force constant k_f =0.6 kcal mol/ Ų, which allows for approximately 4 Å range of motion at the simulation temperature, T = 300 K. The backbone atoms and side chains of the binding site residues were allowed to move freely. Bond lengths with hydrogen atoms were constrained using SHAKE. A 12 Å residue based cutoff was imposed on both direct and generalized Born pair interactions. Each complex was energy minimized and thermalized at 300 K. λ_b-biased replica exchange molecular dynamics simulations were conducted for ≈ 2 ns (≈ 32 ns total for each complex) with a 2 fs MD time step at 300 K with 16 replicas at λ_b = 0, 0.002, 0.005, 0.008, 0.01, 0.04, 0.1, 0.2, 0.35, 0.5, 0.6, 1.7 , 0.8, 0.9, 0.95 and 1. The λ_b values were selected according to an exponential distribution and based on our previous work (the original BEDAM paper and other BEDAM papers in the references^13,14,34) to ensure overlaps between neighboring binding energy distributions and frequent accepted λ exchanges (acceptance ratio of at least 50 %), but minimize the number of required replicas. We have checked that these are sufficient energy overlaps between each lambda value and also sufficient exchanges between different lambda states over the simulation time (see Figures S9 and S10 in S.I.). Binding energies were sampled with a frequency of 1 ps for a total of 16 × 2000 = 32,000 binding energy samples per complex approximately. The IMPACT program⁴⁴ was used to perform all simulations.

HIV-1 Integrase/ Ligands from SAMPL4 study

Previously, as part of the HIV-1 integrase virtual screening SAMPL4 challenge,^35,36 over 300 ligands were studied to screen likely binders to the LEDGF site of integrase⁴⁵ by applying the BEDAM binding free energy model.⁸ Docked structures for all ligands were obtained by using AutoDock Vina³⁵ for the SAMPL4 challenge.³⁵ We have selected a total of 53 SAMPL4 ligands for which the crystal structures were made available (they are known as the set of true binders from experiments) to apply H-REMD with torsional flattening in order to test its effectiveness. In the SAMPL4 study,⁸ from binding free energy analysis, 25 of them (false negatives) were predicted incorrectly by us as non-binders mainly due to bad initial docked structures compared to their crystal structures with larger than 2 Å RMSD, while 28 (true positives) are predicted correctly as binders in our BEDAM simulations. We have computed RMSD values of the ligand with respect to its crystal structure throughout the BEDAM trajectories and in-place-RMSD (no superposition of the ligand) of the ligand was computed using heavy atoms. Here, we examine the complexes of these 53 ligands by running REMD simulations starting both from the docked and crystal structures before performing BEDAM calculations with torsional flattening. Structural analysis and binding free energy estimates for all ligands are summarized in S.I. Tables S1, S2 and S3.

From structural analysis with the original version of BEDAM without torsional flattening, we report that nineteen out of 25 for false negatives and 16 out of 28 true positives have initial docked structures with RMSD of larger than 2 Å. Based on binding free energy calculations, for false negatives, 22 out of 25 (88 %) binding free energy estimates starting from crystal structures have more favorable binding free energy (△ G) value than the corresponding results starting from docked structures. For true positives, 21 out of 28 (75 %) △ G’s starting from crystal structures have a more favorable binding free energy (△ G) values than the corresponding results obtained when starting from docked structures. In total, 43 out of 53 (81 %) of the free energy estimates based on choosing crystal structure as the initial pose are more favorable than the free energy estimates starting from docked structures. From this analysis, we conclude that it is possible to improve binding free energy estimations if either initial docked structures are close to the corresponding crystal structures with a RMSD value less than 2 Å or (as described below) if the sampling is sufficient in the BEDAM calculations to find poses near the crystal structure starting from an initial docked pose that is not near crystal structure pose.

We note that these numbers (28 binders and 25 misclassified as non-binders) do not reflect the enrichment factor which is a different statistic that depends on the fraction of true positives found within a selected scoring cutoff. There are two possible causes for the false negatives; errors in the energy function and/or inadequate conformational sampling. To separate these two factors, we have computed the binding energy landscape (as a diagnostic metric) to examine how well our effective energy function OPLS-AA/AGBNP2 can energetically distinguish crystallographic poses from a myriad of docked poses. This helps us to better differentiate between problems arising from the potential energy function and insufficient conformational sampling. To investigate the cause of failures, we calculated the binding energy landscapes of all ligands in the bound state from simulations at λ_b = 1 ( Table 1). We find that the BEDAM calculations starting with a native crystallographic pose had favorable binding free energy estimates over those beginning from docked poses ≈ 90 % of the time. Improved binding free energy estimates for binders, as shown in Figure 2 starting from a native crystallographic pose, hints at the fact that enhanced sampling of the conformational space of the ligand and the protein can reduce the number of false negatives using BEDAM. By considering binding energies from simulations starting from the docked and crystal structures together ( Table 1), 26 ligands (16 false negatives and 10 true positives) have a funneled energy landscape favoring the crystallographic binding mode (funneled towards the x-ray structure); the binding energy landscape is funneled towards the docked structure for 10 ligands (3 false negatives and 7 true positives) and it is flat for 17 of them (6 false negatives and 11 true positives). There are 10 ligands which are “fragments" for which a funneled energy landscape is not expected. Twenty-six ligands have been selected in this work to apply our H-REMD with torsional flattening for binding mode prediction and binding free energy estimation, because their binding energy landscape favors the crystallographic binding pose and suggests that for these ligands, the AGBNP2/OPLS-AA energy function gives a clear description of their binding to the LEDGF site of the HIV-1 integrase. The binding energy landscapes for these 26 ligands are shown in S. I. Figures S2 and S3. Two ligands (AVX38783-1-1 and AVX40811-0) which have an average binding energy difference between the crystal and docked structures greater than 8 kcal/mol and 3 kcal/mol, respectively were selected as examples to explain our findings throughout the result section.

Table 1.

Summary of the binding energy landscapes of all ligands from the SAMPL4 challenge which bind to the LEDGF binding site of HIV-1 Integrase

	False Negatives (25)	True Positives (28)	Total (53)
Funneled towards x-ray structure	16	10	26
Funneled towards docked structure	3 (1 small)	7 (2 small)	10 (3 small)
Flat	6 (3 small)	11 (4 small)	17 (7 small)

When small ligands and ligands with flat binding energy were dropped, 26/33 (78.8 %) have a funnel energy landscape towards the x-ray structure. Note that the binding energy landscape can not distinguish the binding pose for small ligands (fragments) with number of heavy atoms less than 30.

Figure 2.

The distribution of △G and binding energy (BE) values from BEDAM simulations for binders vs non-binders starting from the crystallographic pose and the docked pose.

The protein-ligand complexes were prepared as described previously in the SAMPL4 study.⁸ The dimer of the catalytic core domain (CCD) of HIV-1 integrase was prepared from the known crystal structure with PDB ID 3NF8. All other molecules including ligands, water molecules and crystallization ions were removed from the crystal structure during the protein preparation process. In Figure 3 and Figure 4, as an example, the structures of the ligands AVX38783-1-1 and AVX40811-0 (a- the crystal and b- the docked structures of ligand in green) are shown in the receptor binding site. The binding site volume was defined as any conformation in which the center of mass of the ligand was within 6 Å of the center of mass of the binding site defined in terms of the Cα atoms of residues 168-174 and 178 of chain A and residues 95, 96, 98, 99, 102, 125, 128, 129, and 132 of chain B (residue and chain designations according to the 3NF8 crystal structure). Based on this definition the volume of the binding site, V_site, is calculated as 904 ų corresponding to −kT ln C⁰ V_site = 0.69 kcal/mol. Parallel molecular dynamics simulations were conducted with the IMPACT program. ⁴⁴ The simulation temperature was set to 300 K and the complex was energy minimized and thermalized at this temperature. We employed 18 intermediate steps at λ_b = 0, 0.001, 0.002, 0.004, 0.006, 0.008, 0.01, 0.04, 0.07, 0.13, 0.25, 0.37, 0.5, 0.6, 0.7, 1.8 , 0.9, and 1 for HIV-1 Integrase/ligand systems.⁸ The λ_b values were selected with similar strategy as mentioned in previous section. BEDAM calculations for HIV-1 Integrase/ Ligand systems were performed for 2 ns of MD per replica ( 36 ns total for each complex) starting from the crystal and docked ligand poses. Binding energies were sampled with a frequency of 1 ps for a total of 18 × 2000 = 36,000 binding energy samples per complex. The data shown with ‘flat’ or ‘flattening’ explicitly are all from BEDAM simulations with torsional flattening. Otherwise, they are from the original version BEDAM without torsional flattening.

Figure 3.

The crystal (a) and the docked (b) structures of ligand AVX38783-1-1 in the binding site; ligand in green, receptor residues within 5 Å from the ligand and hydrogen bonds between receptor-ligand shown with dashed red line. On the top, rotatable torsions of the ligand used for torsional flattening are listed.

Figure 4.

The crystal (a) and the docked (b) structures of ligand AVX40811-0 in the binding site; ligand in green, receptor residues within 5 Å from the ligand and hydrogen bonds between receptor-ligand shown with dashed red line. On the top, rotatable torsions of the ligand used for torsional flattening are listed.

Results and Discussion

Test on model system-T4Lysozyme/L99A/p-xylene

It is known that the ligand (p-xylene)-binding induces structural reorganization of the Val111 side chain in the binding pocket of T4 Lysozyme/L99A. ^10,26,29 This model system was used as a test case for different enhanced sampling methods^10,26,29 designed to overcome insufficient sampling of the side chain orientations in the binding pocket. The Val111 side chain is in the trans conformation in the apo-protein structure and in the complex with ligand p-xylene, the Val111 changes its rotameric state from the trans conformation (χ≈−180) to the gauche (χ≈−60) conformation. ^10,26,29 We have performed BEDAM calculations with and without torsional flattening both starting with gauche and trans initial conformations of Val111 in the T4L/L99A/p-xylene complex.

In Figure 5, we show the Val111 side chain dihedral angle χ as a function of simulation time for λ = 1 the Hamiltonian state where the ligand and receptor are fully coupled. The two figures on the top are for simulations with no flattening applied on the side chain torsion starting with gauche (a) and trans (b) initial conformations. The two figures on the bottom are for simulations with flattening applied on the side chain torsion starting with gauche (c) and trans (d) conformations. Our results from BEDAM calculations with no torsional flattening in Figure 5 (a and b) showed that Val111 side chain was trapped in the initial starting conformation, in either the trans or gauche conformation, throughout the ≈ 2 ns simulation time. In the BEDAM calculations with torsional flattening by canceling only the VAL111 side-chain torsion terms in the effective potential, we observe that the VAL111 side-chain transits between trans and gauche conformations many times with the gauche conformation dominating, in good agreement with previous results.^10,26,29

Figure 5.

Val111 side chain dihedral angle as a function of simulation time for the final lambda values. Two figures on the top are for simulations with no flattening of side chain torsions: Initial starting conformation is gauche (a), Initial starting conformation is trans (b). Two figures on the bottom are for simulations with flattening of side chain torsions: Initial starting conformation is gauche (c), Initial starting conformation is trans (d).

In Table 2, the estimated binding free energy of T4L/L99A/p-xylene starting from trans and gauche conformations from REMD simulations with and without torsional flattening of VAL111 side chain torsion is given. From ≈ 2 ns BEDAM simulations without torsional flattening, the estimated binding free energy of T4L/L99A/p-xylene depends on the starting conformations. The binding free energy from the trans conformation is more positive than the binding free energy value from the gauche conformation (−2.55 ± 0.21 vs −3.02 ± 0.22 kcal/mol). The calculated binding free energy starting from either the trans or gauche conformation is improved by BEDAM simulations with torsional flattening and the results (−3.07 ± 0.17 and −3.21 ± 0.29 kcal/mol, respectively) are close to the reported values in the study of Mobley et. al.²⁶ which used a “confine and release” protocol to sample ligand binding-induced reorganization (−3.31 ± 0.20 and −3.54 ± 0.17 kcal/mol starting from trans and gauche conformations, respectively).

Table 2.

Binding free energy of T4L/L99A/p-xylene starting from trans and gauche conformations from BEDAM-REMD simulations with and without flattening of VAL111 side chain torsion

Starting Conformation	Method	$\Delta G_{Binding}^{\ast }$
Trans	REMDno–flattening	−2.55 ± 0.21
	REMDflattening	−3.07 ± 0.17
Gauche	REMDno–flattening	−3.02 ± 0.22
	REMDflattening	−3.21 ± 0.29

^*in kcal/mol and experimental binding affinity data (−4.67 kcal/mol) for the T4L system from Mobley’s paper (ref.²⁶) (also reported by Jiang et. al in ref.²⁹).

HIV-1 Integrase/Ligands

Having tested our new sampling approach on the model system T4 Lysozyme, we then applied it on a realistic drug target HIV-1 Integrase. A total of 26 candidate ligands from the SAMPL4 study⁸ which have “funneled” binding energy landscapes favoring the crystal structure have been used in our calculations for structural prediction and binding free energy estimation. These ligands allow us to test whether the correct crystal structure pose will be “discovered” starting from an incorrectly docked pose, using the combination of biasing along the receptor-ligand interaction λ coordinate plus torsional flattening. Figure 6 and Figure 7 show two representative examples to explain our findings described in the present study. We first discuss the binding mode predictions for these ligands. In Figure 6, we show the trajectory of the RMSD from the crystal structures of ligand AVX38783-1-1 (a) and AVX40811-0 (b) at λ_b=1 from BEDAM simulations with (blue) and without (green) torsional flattening starting from docked structure conformations. In both cases, the initial RMSDs are ≈ 5 Å or more from the crystal structure. Without flattening, the ligands remained trapped close to the initial docked structure shown in green in Figure 6. However, poses with RMSD of <3 Å or less are sampled when the torsional barriers of the rotatable bonds are flattened.

Figure 6.

All heavy atom RMSD of ligand AVX38783-1-1 (a) and AVX40811-0 (b) at λ_b=1 from BEDAM simulations with (blue) and without (green) torsional flattening (starting conformation is docked structure).

Figure 7.

Binding energy of the ligand AVX38783-1-1 (a) and AVX40811-0 (b) with ligand RMSD at λ_b=1 from three different BEDAM simulations; green: starting conformation is docked structure without torsional flattening, red: starting conformation is crystal structure without torsional flattening, blue: starting conformation is docked structure with torsional flattening. Additionally, the RMSD between predicted pose (gray) and the validation (crystallographic) pose (green) for each ligand are given.

In Figure 7, we have plotted the binding energy of the ligand AVX38783-1-1 and AVX40811-0 as a function of RMSD to the crystal at λ_b=1 obtained using BEDAM simulations with flattening and without flattening. The binding energy as a function of ligand RMSD from the crystal structures of AVX38783-1-1 ( Figure 7-a) and AVX40811-0 (Figure 7-b) at λ_b=1 from two different simulations starting from docked and crystal structures are given in green and red, respectively. As shown in Figure 7, the complexes have two distinct regions of ‘binding energy vs RMSD’ depending on the starting conformations. We see that it is possible to sample the transitions between these two distinct regions using the BEDAM method with torsional flattening. Successful transitions for other ligands starting from docked structure to crystal structure are shown in the S. I. Figure S4. The initial docked structures have larger RMSD mainly due to improper structural orientation of substituent groups while the core group for each ligand has close overlap with the crystal structure. Our structural predictions for 10 out of 26 ligands lead to binding poses significantly closer to the crystallographic poses. For this set of ligands, torsional flattening enables sufficient sampling to find poses close to the crystal structure. For the majority of remaining cases where torsional flattening did not lead to improvement in ligand pose prediction, intramolecular non-native hydrogen bonding and stacking interactions between the ligand core and functional groups prevented the ligand from sampling the crystal structure pose. This is discussed later on in this section.

In addition to improving binding pose prediction, the torsional flattening method also leads to improved binding free energy estimates. In Table 3a, the estimated binding free energies of the 10 ligands which sample close to the crystal pose when torsional flattening is applied are listed. From the simulations preformed without torsional flattening, the estimated binding free energies differ depending on the starting conformations. For example, for ligand AVX38783-1-1, the binding free energy from the BEDAM simulations without torsional flattening is substantially more positive than that from the BEDAM simulations with torsional flattening (1.76 ± 0.11 kcal/mol vs −2.67 ± 0.16 kcal/mol) and the binding free energy value obtained from BEDAM simulations starting from the crystal structure is −3.53 ± 0.14 kcal/mol. For ligand AVX40811-0, the predicted binding free energies from the BEDAM simulations without torsional flattening and with torsional flattening starting from the docked conformation are more positive than the value starting from the crystal structure of the ligand (−2.18 ± 0.24 and −6.86 ± 0.21 kcal/mol, respectively vs −7.87 ± 0.13 kcal/mol). For both representative ligands, binding free energy estimations from the calculations with or without torsional flattening are more positive than free energy estimations starting from the crystal structures. However, the estimated binding free energy results for all ligands which have enhanced conformational sampling show still more promising results (with average △ G (docked) = −3.53 ± 0.18 kcal/mol, Table 3a) and give better estimation of binding free energies by flattening the torsions of interest than the ones from BEDAM simulations with no torsional flattening because better conformational sampling generally leads to improved binding free energy estimates, as shown in Table 3a. In Table 3b, we have also showed the predicted binding free energies for 16 ligands where torsional flattening was not successful in helping to find the ligand crystal pose. However, it is evident that binding free energy estimates starting the BEDAM simulations from the crystal structures are still more favorable than their corresponding initial docked structures.

Table 3a.

Binding free energy of 10 ligands with the correct binding pose prediction in the LEDGF binding site of HIV-1 Integrase

Ligand	$\Delta G_{No-Flat\left(docked\right)}^{\ast }$	$\Delta G_{Flat\left(docked\right)}^{\ast }$	$\Delta G_{crystal}^{\ast }$
AVX38747-0	−2.59 ± 0.20	−5.43 ± 0.25	−4.27 ± 0.14
AVX38749-0	−4.14 ± 0.22	−4.07 ± 0.21	−6.04 ± 0.18
AVX38782-1	−0.74 ± 0.12	−0.59 ± 0.18	−4.54 ± 0.11
AVX38783-1-1	1.76 ± 0.11	−2.67 ± 0.16	−3.53 ± 0.14
AVX38787-1	3.18 ± 0.13	0.37 ± 0.17	−3.49 ± 0.13
AVX38788-1	3.33 ± 0.13	1.35 ± 0.20	−3.59 ± 0.18
AVX40811-0	−2.18 ± 0.24	−6.86 ± 0.21	−7.87 ± 0.13
AVX40812-0	−0.93 ± 0.18	−5.97 ± 0.16	−7.19 ± 0.12
GL5243102-0-2	−6.28 ± 0.13	−5.84 ± 0.15	−6.79 ± 0.10
GL5243106-0	−1.41 ± 0.08	−5.64 ± 0.13	−5.14 ± 0.11
AVERAGE	−1.08 ± 0.15	−3.53 ± 0.18	−5.24 ± 0.13

* in kcal/mol

Table 3b.

Binding free energy of 16 ligands which remained trapped close to the initial docked structure

Ligand	$\Delta G_{No-Flat\left(docked\right)}^{\ast }$	$\Delta G_{Flat\left(docked\right)}^{\ast }$	$\Delta G_{crystal}^{\ast }$
AVX38789-1	0.65 ± 0.10	0.81± 0.21	−4.96 ± 0.19
AVX38673-1	−3.80 ± 0.12	−4.03 ± 0.31	−7.54 ± 0.13
AVX38784-5	1.94 ± 0.15	1.91 ± 0.18	−4.03 ± 0.10
AVX38780-0	0.36 ± 0.13	−1.83 ± 0.15	−4.10 ± 0.09
AVX38785-1-1	−1.15 ± 0.11	−0.79 ± 0.15	−7.11 ± 0.10
AVX38779-0-1	−1.86 ± 0.08	−0.46 ± 0.28	−4.66 ± 0.14
AVX101118-0	−0.4 ± 0.12	−0.12 ± 0.18	−5.20 ± 0.11
AVX38786-1-1	−2.49 ± 0.13	−2.01 ± 0.16	−4.72 ± 0.16
AVX17587-2	−5.30 ± 0.21	−5.98 ± 0.20	−6.23 ± 0.16
AVX38672-0	−4.32 ± 0.18	−4.49 ± 0.26	−10.02 ± 0.21
AVX17684-0-1	−4.84 ± 0.18	−4.21 ± 0.18	−8.16 ± 0.14
GL5243100-0	−4.18 ± 0.09	−4.52 ± 0.14	−6.34 ± 0.11
AVX38781-1-1	−4.88 ± 0.17	−4.06 ± 0.16	−6.73 ± 0.12
AVX17556-3	−8.23 ± 0.16	−8.55 ± 0.18	−9.31 ± 0.21
GL5243104-0	−5.70 ± 0.14	−5.56 ± 0.18	−8.23 ± 0.16
AVX101124-1	−7.64 ± 0.18	−7.81 ± 0.21	−10.62 ± 0.19
AVERAGE	−3.24 ± 0.14	−3.23 ± 0.19	−6.74 ± 0.16

* in kcal/mol

Evidence of enhanced sampling of internal motions

The BEDAM method for estimating the binding affinity of a ligand to a protein samples very efficiently the external degrees of freedom (i.e. the rotational and translational coordinates) of the ligand with respect to the receptor in the binding site. In the supplementary information Figure S7 and S8, the efficient sampling of these external degrees of freedom (rotational and translational) of the AVX38783-1-1 with respect to the receptor from different BEDAM simulations are given since at λ = 0 there is no restriction on these variables other than the external flat bottom potential which restraints the ligand within V_site. We have augmented BEDAM’s power for sampling the translational and rotational degrees of freedom of the ligand with torsional flattening of intramolecular degrees of freedom of the ligand and receptor to increase the rate of conformational sampling. In this study, these degrees of freedom are torsional coordinates, e.g. the VAL111 side-chain of T4L/L99A and the rotameric states of the ligand e.g. rotatable torsions of the ligands in the binding site of HIV-1 Integrase (see Figure 3 and Figure 4).

Results from BEDAM simulations with torsional flattening show that it improves the sampling of structures in the binding pocket of the receptor. In Figure 8, as an example, we show the distributions of the first four rotatable torsions of the ligand AVX38783-1-1 from simulations at λ_b = 1 with and without torsional flattening starting from the crystal and docked structures are compared. The figure illustrates the differences between the standard BEDAM calculations and the BEDAM with torsional flattening of key rotatable torsions of the ligand. It is clear that sampling of ligand rotatable torsions using BEDAM with torsional flattening algorithm explores more conformational space than the standard BEDAM simulations starting from the docked structure. Our results for binding mode prediction also show that sampling the crystallographic binding mode starting from the docked poses appears to be important for the correct prediction of the binding affinity and also, using torsional flattening with BEDAM gives a better rank ordering for the ligands compared to using the standard BEDAM method.

Figure 8.

Distributions of the first four torsions (a, b, c, d for X₁, X₂, X₃, X₄ , respectively and also see the Figure 3 for the definition of the flattened torsions) of the ligand AVX38783-1-1 from simulations at λ_b = 1 with and without torsional flattening starting from the crystal and docked structures. In the standard BEDAM (with no flattening), each torsion angle shows one or two peak(s) at different locations depending on the initial ligand poses. In the BEDAM with torsional flattening calculations (in blue), simulations started with the docked ligand structure were able to sample correct ligand poses given in the crystal structures, thus it shows different peaks where we get from the standard BEDAM calculations starting with the docked and crystal structures.

In Table 3a, the results show that there is a significant improvement in the binding free energies in addition to better predicted structures for ligands in the binding site of HIV-1 Integrase using torsional flattening. Four ligands which were predicted as non-binders (false negatives, in bold) previously from standard BEDAM calculations are predicted to be true positives with the BEDAM method augmented by torsional flattening, since the different possible ligand poses were taken into consideration. The results of Table Table 3a shows that while the binding free energies obtained using enhanced sampling △G_Flat(docked) are more negative than those obtained without using torsional flattening △G_{No−Flat(docked)}, △G_Flat(docked) are still not as negative as those obtained from simulations starting from the crystal structures △G_crystal. This reflects that while the results △G_Flat(docked) obtained using torsional flattening have a significant improvement over the regular BEDAM results △G_{No−Flat(docked)}, the simulations have not fully converged. In fully converged simulations, both native and non-native poses are sampled according to their Boltzmann weights at all alchemical lambda states, and the inclusion of non-native poses will always make the overall binding free energy lower than the intrinsic binding free energy for any of the individual poses, including that associated with the dominant native pose.⁴⁶ In the simulations of Table 3a, although the enhanced sampling in computing △G_Flat(docked) have sampled both crystallographic and non-native poses and therefore have captured to some degree the contributions from different poses, the relative populations of the native pose at different lambdas is likely to be underestimated(see Figure 8), which resulted in the less negative values of △G_Flat(docked) compared with △G_crystal. (Since no confinement constraints are used in simulations for △G_Flat(docked) or △G_crystal, in a truly converged simulation △G_Flat(docked) or △G_crystal should give the same answer.)

Importance of non-bonded intramolecular interactions

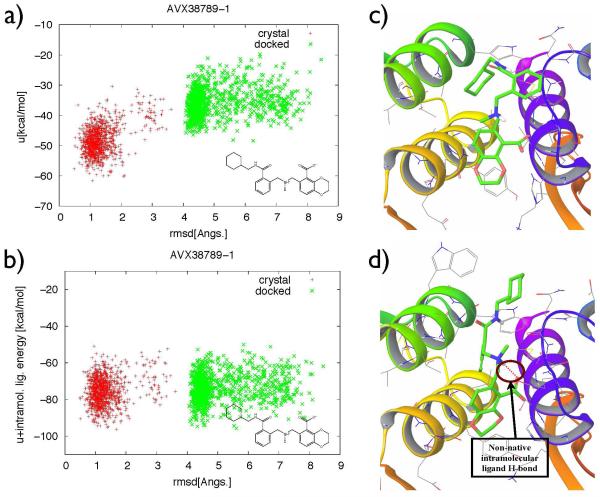
For ligands where torsional flattening did not lead to improvement in ligand pose prediction, the non-native binding modes sampled by the BEDAM with flattening at λ_b = 1 were stabilized by non-native ligand intramolecular interactions, which correspond to non-native H-bonds (an example of non-native intramolecular ligand H-bonds shown in Figure 9-d, which is not seen in its initial crystal structure in Figure 9-c), or non-native aromatic-aromatic ring stacking. Such ligand intramolecular interactions are not affected by torsional flattening. However, they can significantly modify the energy landscape for ligand-receptor coupling. Figure 9 shows such an example, a) is the binding energy landscape (intermolecular + changes in solvation energy), b) shows the corresponding landscape with binding energy + ligand intramolecular energy. It shows that when the latter is included, there is no driving force for the ligand to undergo the expected transitions in binding mode. Energy barriers due to non-native intramolecular non-bonded interactions can be reduced by scaling the corresponding energy terms in addition to torsional terms in the potential function for further improvement of efficient sampling of ligand structure in the binding side of receptor. Work is under way to implement this biasing scheme in BEDAM in order to further enhance sampling for protein-ligand binding free energy estimates.

Figure 9.

a) Binding energy of AVX38789-1 and b) Binding energy + intramolecular ligand energy of AVX38789-1 with ligand RMSD at λ_b=l from two different BEDAM simulations; green: starting conformation is docked structure, red: starting conformation is crystal structure. c) No intramolecular ligand hydrogen bond (H-bond) formed in the initial crystal structure, d) A non-native intramolecular ligand hydrogen bond (H-bond) formed between polar hydrogen and carboxylate oxygen in the initial docked structure.

Conclusions

In this work, we introduce H-REMD with torsional flattening in the BEDAM method to accelerate slow degrees of freedom relevant to the binding process. Compared with the two widely used methods docking and FEP, BEDAM provides unique advantages for in silico ligand discovery: in comparison with the fast docking methods, BEDAM can provide better accuracy at a moderate computational cost; compared with high resolution FEP methods, BEDAM provides more extensive conformational sampling necessary for treating chemically distinct ligands. Furthermore, we can also use this sampling method for binding mode prediction. We have applied the method to two different examples; the standard test case VAL111 side-chain of T4L/L99A receptor, and the rotatable torsions of 26 ligands with funneled type energy landscapes favoring the crystallographic binding mode (funneled towards the x-ray structure) in the binding site of HIV-1 Integrase, to illustrate applications to the torsional coordinates of the protein and rotameric states of the ligand, respectively. BEDAM simulations with torsional flattening explore more conformational space than standard BEDAM simulations. We have also shown that the method is capable of recapitulating crystallographic binding poses of ligands starting from a poorly docked pose with incorrect ligand torsions by adjusting the torsions and external coordinates. However, additional biasing (or rescaling) of non-bonded ligand intramolecular interactions is necessary to further improve sampling when the initial ligand pose includes non-native hydrogen bonds and/or stacking interactions.