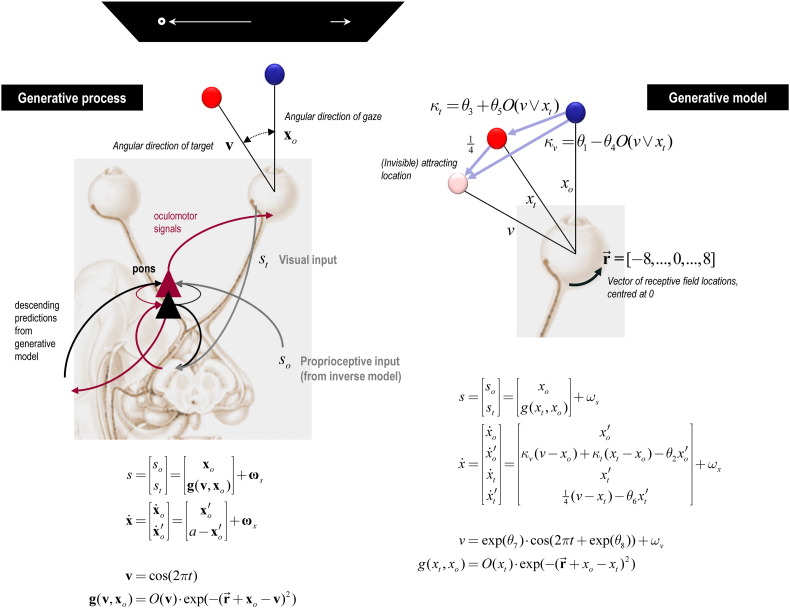
Fig. 1.

Generative process and generative model used to simulate oculomotor pursuit.

This schematic illustrates the process (left panel) and generative model of that process (right panel) used to simulate Bayes-optimal pursuit of a target moving sinusoidally along a horizontal path, part of which is occluded (top left). The graphics on the left show part of a putative predictive coding scheme (with superficial pyramidal cells in red and deep pyramidal cells in black in the pontine nuclei) processing proprioceptive information during smooth pursuit. These cells receive proprioceptive information from an inverse model in the subcortical oculomotor system and respond reflexively to minimise proprioceptive prediction error through action. This prediction error rests on descending predictions from the generative model on the right. The actual movement of the target is determined by a hidden cause (target location), which determines the visual input for any given direction of gaze (equations on the left). O is an occluder function whose output is 0 when the target location v is occluded and 1 otherwise. The generative model entails beliefs about how the target and eyes move (equations on the right). The agent believes both the target and centre of gaze are drawn to a (fictive) attracting location v that is a sinusoidal function of time with parameters controlling its amplitude and phase (θ₇, θ₈). This location attracts the target with a viscosity θ₆. Changes in eye velocity ẋ_o′ are determined by a weighted combination of the distance between the eye and the invisible location and target κ_v(v − x_o) + κ_t(x_t − x_o). Each weight (κ_v, κ_t) has a fixed component and an occluder-dependent component (c.f. Bogadhi et al., 2013) that depends on the remaining kinetic parameters (θ₁, θ₃, θ₄, θ₅), where the viscosity of eye movements is encoded by θ₂. Real states that are hidden from observation in the real world are in bold, whereas the hidden states assumed by the generative model are in italics. Please see Adams et al. (2015) – from which this figure is adapted – for a full description of the variables and equations.