Development and testing of hyperpolarized ¹³C MR calibrationless parallel imaging

Abstract

A calibrationless parallel imaging technique developed previously for ¹H MRI was modified and tested for hyperpolarized ¹³C MRI for applications requiring large FOV and high spatial resolution. The technique was demonstrated with both retrospective and prospective under-sampled data acquired in phantom and in vivo rat studies. A 2-fold acceleration was achieved using a 2D symmetric EPI readout equipped with random blips on the phase encode dimension. Reconstructed images showed excellent qualitative agreement with fully sampled data. Further acceleration can be achieved using acquisition schemes that incorporate multi-dimensional under-sampling.

1. Introduction

Hyperpolarized (HP) ¹³C techniques [1] increase spin magnetization for ¹³C nuclei by several orders of magnitude compared to polarization achieved at thermal equilibrium. This dramatic signal enhancement has enabled in vivo magnetic resonance imaging (MRI) and spectroscopy (MRS) of ¹³C labeled biomolecules with high contrast and temporal resolution [2–5]. Nevertheless, the short time window due to T₁ relaxation and metabolism presents a significant challenge to these techniques [3,4,6–12]. Fast data acquisition is imperative to mitigate signal loss due to relaxation and to measure rapid in vivo substrate uptake and metabolic conversion rates. Current methods have worked adequately in preclinical animal studies with fields-of-view (FOVs) less than 10 cm and coarse resolution, but much larger FOV’s with high spatial resolution is needed for future clinical studies.

Parallel imaging schemes with multi-channel coils offer the potential for improved spatial coverage and high acceleration while maintaining high SNR. However, the transient nature of HP ¹³C signal presents a new obstacle to parallel imaging. Traditional SENSE [13] or SMASH [14]-based reconstruction techniques use a priori knowledge of coil sensitivity, which is typically acquired in a calibration scan obtained prior to the actual scan. However, there is insufficient endogenous ¹³C signal for coil sensitivity calibration prior to injection of HP substrate, at which time a separate calibration scan is impractical due to the limited HP magnetization time and the desire to acquire dynamic metabolic data throughout the time following injection. Alternatively, an external ¹³C phantom can be used [15], but this approach is complicated by the low sensitivity of ¹³C nuclei and variations in coil shape and/or position between the calibration and actual scans, which are especially problematic with the use of flexible coils that are highly desirable for clinical studies. Auto-calibrated reconstruction techniques such as GRAPPA and SPIRiT [16–19] incorporate fully-sampled auto-calibration scan (ACS) regions into the acquired data and effectively overcome the need for a separate reference. Yet, the amount of required ACS data is substantial given the low matrix sizes in ¹³C studies, greatly limiting the efficiency and effective SNR for HP ¹³C imaging.

Recently, a new class of parallel imaging techniques has been reported that does not require explicit calibration of coil sensitivity. Shin et al. [20] proposed the Simultaneous Auto-calibrating and K-space Estimation (SAKE) method, which provides implicit calibration by recasting k-space data into a structured low-rank matrix. Trzasko et al. [21] described another method named Calibration-free Locally low-rank Encouraging Reconstruction (CLEAR), which explores the local low-rankness of k-space data. Both methods overcome the need for a separate calibration step.

The goal of this study was to validate the efficacy of the SAKE calibrationless parallel imaging acceleration strategy for hyperpolarized ¹³C imaging, as acquiring large clinical sized FOVs with fine spatial resolution will be critical for clinical translation to patient studies. For this proof-of-concept study, we designed an acquisition scheme with a single-shot 2D symmetric EPI readout to achieve a 2-fold acceleration on the phase encode dimension and tested this approach with its requisite reconstruction method in both phantoms and in vivo animal studies. We demonstrate that the scheme can be applied both for hyperpolarized metabolic agents (pyruvate) as well as perfusion agents such as t-butanol, which is more diffusible especially in brain tissue compared with pyruvate and urea [22,23].

2. Materials and methods

2.1. Hardware setup

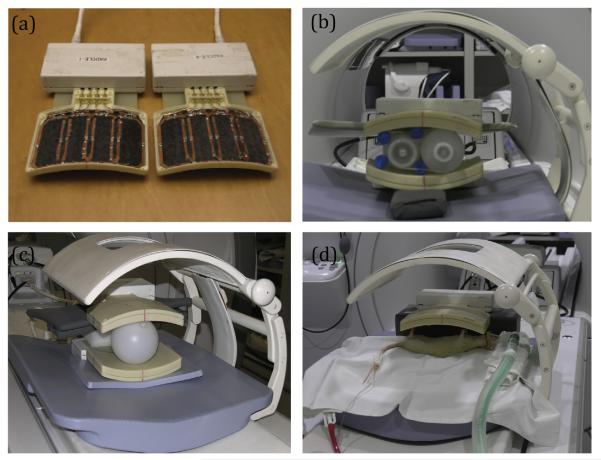
All scans were acquired using a 3T scanner (MR750, GE Healthcare) equipped with multi-nuclear capability. Proton MR anatomical images were acquired with the built-in body coil. For ¹³C RF excitation, a custom-designed ¹³C transmitter was used [15]. This transmitter coil consists of a Helmholtz resonant pair in which two loops are arranged in a clamshell manner mounted on a dedicated patient cradle for volumetric transmission. The transmitter coil was dynamically detuned at the time of reception. For ¹³C receive, an 8-channel array coil was used with 2 sets of four coil elements in a linear arrangement as shown in Fig. 1(a) [24,25]. Each rectangular element was approximately 5 × 10 cm and adjacent elements were overlapped to minimize mutual inductance. The total length of each panel was around 18 cm [24].

Fig. 1.

(a) Eight-channel ¹³C receive coil with a linear arrangement of four coil elements in each housing. (b) Ethylene glycol phantom study set-up. (c) HP ¹³C-pyruvate phantom set-up. (d) In vivo rat study set-up.

2.2. Hyperpolarization

For the phantom study, 1.47 g [1-¹³C] pyruvate mixed with 15 mM OX063 radical (GE Healthcare) was hyperpolarized in a 5 T SpinLab DNP polarizer (GE Healthcare) for 2 h and then dissolved into a 40 ml aqueous solution of 250 mM hyperpolarized [1-¹³C] pyruvate. The solution was immediately injected (within 5 s) into a plastic sphere (~10 cm diameter) containing 400 ml water (Fig. 1(c)). The final phantom solution contained about 440 ml of 23 mM hyperpolarized [1-¹³C]pyruvate.

For the in vivo study, 110 mg of mixed ¹³C-t-butanol, glycerol (t-butanol and glycerol are 1:1 by volume) and 15 mM ‘Finland’ trityl radical (Oxford Instruments) were polarized in a HyperSense DNP polarizer (Oxford instruments) for 1.5 h and then dissolved with 5 ml phosphate-buffered saline. The final solution containing 100 mM ¹³C-t-butanol was then carried to the scanner and ~3.0 ml of this solution was injected into the rat through a tailvein catheter over a period of 12 s. The polarization level for both [1-¹³C]pyruvate and ¹³C-t-butanol was approximately 20%.

2.3. Symmetric, ramp-sampled EPI

In this study, we applied a symmetric, ramp-sampled EPI sequence [26] to acquire fast MR molecular imaging of HP ¹³C substrates. To correct for the timing inconsistencies between odd and even echoes, a reference scan without phase encoding from the hyperpolarized substrate was acquired immediately after the image acquisition.

2.4. Thermally polarized phantom study

The phantom used consisted of two bottles and four small tubes filled with thermally polarized ethylene glycol as shown in Fig. 1 (b). Due to the low sensitivity of natural abundance ¹³C in ethylene glycol, a 12 cm axial slab was excited using a 45° spectral-spatial pulse and signal was averaged over 13 min. The spectral-spatial pulse was designed for hyperpolarized imaging of [1-¹³C]pyruvate and metabolites at 3T, with a passband full-width at half-maximum of 120 Hz and a stopband of 600 Hz. This passband was sufficiently narrow to excite only the central ¹³C resonance of ethylene glycol. The typical linewidth of ¹³C spectra at the 3T scanner is around 10 Hz (~0.3 ppm). A FOV of 16 × 16 cm² was acquired using the aforementioned ¹³C-EPI sequence with a 64 × 64 (fully sampled) matrix. The effective TE was 40 ms with an echo spacing of 1.3 ms, with a readout bandwidth of 166 kHz. A reference scan for the EPI reconstruction was acquired at the end of the scan with the same excitation pulse.

2.5. Hyperpolarized ¹³C-pyruvate phantom study

Acquisition started 30 s after the injection of HP ¹³C-pyruvate to minimize turbulence and ensure sufficient mixing with the solvent. A 15 mm axial slice across the spherical phantom containing 440 mL aqueous solution of 23 mM HP [1-¹³C]pyruvate was excited using a 45° spectral-spatial pulse. A FOV of 16 × 16 cm² was acquired with a 64 × 32 (2-fold under-sampling in the phase encode direction as described in the image reconstruction session below) matrix using the same EPI readout as that used in the thermal phantom study, with an effective TE of 20 ms. And the data was subsequently reconstructed to a 64 × 64 matrix (2.5 × 2.5 mm² resolution). The reference scan was acquired immediately after the under-sampled scan with the same excitation pulse.

2.6. In vivo hyperpolarized ¹³C-t-butanol study

All animal studies were carried out under protocols approved by the UCSF Institutional Animal Care and Use Committee. A normal Sprague–Dawley rat was placed on a heating pad atop one of the paddle receiver and anesthetized with 1.5% of isoflurane delivered via nose cone (flow rate 1 L/min). The rat was positioned supine with its head and tail positioned to the right and left respectively looking into the magnet bore (Fig. 1(d)). The proton anatomical images were acquired using a T₂-weighted 2D Fast Spin Echo (FSE) sequence. For the HP ¹³C experiment, a coronal slice with 2 cm thickness was excited with a 20 × 20 cm² FOV and 3.1 × 3.1 mm² in-plane resolution (Fig. 6(b)). Imaging was initiated 20 s after the start of injection with a 12.8 ms 60° sinc pulse to excite a 15 mm coronal slice, followed by a symmetric, ramp-sampled EPI readout that covered a FOV of 20 × 20 cm² with a 64 × 32 matrix size (2-fold undersampling in the phase encode direction) with an effective TE of 26 ms, an echo spacing of 1.1 ms and a readout bandwidth of 200 kHz. The total TR was 200 ms. As in the phantom study, a reference scan was acquired for the symmetric EPI. Lastly, a separate scan using partial Fourier acquisition (TE = 26 ms) with 25% over-sampling in the phase-encode direction was acquired to compare with SAKE reconstruction.

Fig. 6.

In vivo rat experiment with HP ¹³C-t-butanol, (a), (b) and (c) are ¹³C images of a coronal slice of 2 mm thickness. (a) Zero-filled image after 2-fold under-sampling on the phase encode (top to bottom) direction (b) SAKE reconstructed image based on the under-sampled image in (a). (c) Partial Fourier reconstruction with 25% over sampling. (d) ¹H T₂ FSE reference image of the 15 mm coronal slice. (e) SAKE reconstruction overlaid on the ¹H FSE image, two ROIs are drawn to cover one kidney and the brain. The ¹³C signal intensity ratio between the kidney and the brain is 0.93. (f) Partial Fourier reconstruction overlaid on ¹H FSE, similar ROIs are drawn and ¹³C signal intensity ratio between the kidney and brain is 1.08.

2.7. Image reconstruction

Ramp-sampled EPI data were interpolated to a Cartesian k-space grid and corrected for timing delays using the Orchestra reconstruction toolbox (GE Healthcare, WI, USA). Partial Fourier k-space data was reconstructed with homodyne processing using the Orchestra toolbox while the under-sampled k-space data were first zero-filled to a 64 × 64 matrix and subsequently reconstructed with SAKE or GRAPPA algorithm using MATLAB before 2D Fourier transform.

For the thermal phantom study, different undersampling patterns were applied retrospectively to the acquired data. The 2-fold undersampling pattern for SAKE (Fig. 3(d)) was derived from a central line across a 2D variable density Poisson-disc undersampling pattern [27], which is known to provide a high degree of incoherence and has been generally applied to compressed sensing[28,29]. We also generated a 3-fold undersampling pattern for SAKE (Fig. 3(e)) by skipping more lines in the peripheral region of the 2-fold pattern. For GRAPPA reconstruction, we generated 2 undersampling patterns with fully sampled ACS areas. The first one had 16 calibration lines and the outer k-space was 3-fold under sampled for a 2-fold overall acceleration (Fig. 3(b)) and the second had 12 calibration lines and the outer k-space was 4-fold under sampled for a 2.6-fold overall acceleration (Fig. 3(c)). Reconstruction coefficients were estimated with these ACS lines using a 4-by-3 kernel (4 phase encoding and 3 frequency encoding neighbor data points). For the hyperpolarized studies, only the 2-fold SAKE variable-density pattern (Fig. 3(d)) was used for prospective data undersampling.

Fig. 3.

Comparison between fully sampled and under sampled ethylene glycol phantom images. (a–e) are individually scaled against their maximum signal intensities. (a) fully-sampled image (b and c) each panel has the reconstructed image (left), 5 times the error between the reconstruction and the fully sampled image (right) and the undersampling patterns (center top). (b) GRAPPA reconstruction with 2-fold under sampled data. The central ACS has 16 lines and the outer k-space is 3-fold under sampled. The mean square error (MSE) compared to (a) is 2.70 × 10⁻⁴. (c) GRAPPA reconstruction with 2.6-fold under sampled data. ACS has 12 lines and the outer k-space is 4-fold under sampled. MSE is 2.70 × 10⁻³. (d) SAKE reconstruction based on a 2-fold under sampled data. MSE is 2.67 × 10⁻⁴. (e) SAKE reconstruction based on a 3-fold under sampled data, MSE is 4.38 × 10⁻⁴.

A prior publication [20] detailed a formal treatment of SAKE reconstruction theory and its application to ¹H MRI. The reconstruction algorithm reduces ultimately to the following optimization problem:

$$\begin{array}{cc}\hfill & \min {\Vert \mathit{Dx}-y\Vert }^2\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\mathit{rank}\left(A\right)=k,\hfill \\ \hfill & x=H^{+}\left(A\right)\hfill \end{array}$$ (1)

where the least squares objective function enforces data consistency between the reconstructed k-space data x and acquired data y, which are related by the sampling operator D. A is the structured low-rank matrix generated by sliding a multi-channel window across the k-space data x. Such operation, represented by operator H gives rise to stacked, block-wise Hankel structure in A and H⁺ denotes the inverse projection from A to x. The Block Hankel matrix is known [30] to possess well defined subspaces and the first equality constraint ensures its low rank property. As coil sensitivities vary smoothly in the image domain, we can assume that the bandwidths in k-space of all the coils are bound by some small number s. Then, it was shown in the previous study [20] that we can choose a large enough window size w to make the block Hankel matrix A to be a low rank matrix with its rank k bound by (w + s − 1)². Therefore, the window-size normalized rank is bound by (w + s − 1)²/w². Accordingly, as the window size w increases, the normalized rank shrinks towards one, leading to a more compact signal subspace. In addition, the rank value is affected by the object size with smaller object size giving rise to lower rank value. In the current study, based on the object size and coil set-up, a 6 × 6 (w²) window was used to slide across the acquired k-space data. This window size (6 × 6) was chosen to guarantee a compact signal space while keeping the reconstruction time short, as larger window size (e.g., 8 × 8) significantly increases computation time. The k-space data matrix has a size of N_x × N_y N_c (64 × 64 × 8) where N_x and N_y are the readout and phase encode dimensions and N_c is the number of elements. The generated A matrix has size w²N_c × (N_x − w +1) (N_y + w + 1), resulting in 288 × 3481 for the current study.

This optimization was implemented using the Cadzow [31] algorithm, which is an alternating projection method. The iteration begins with projecting the zero-filled multi-channel k-space data matrix x onto data matrix A. Then with assumed rank value as discussed below, a hard thresholding on singular values was applied to A to enforce the low rankness projection. Lastly, an inverse transform converts the Hankel matrix back to k-space and consistency between reconstructed (x) and acquired data (y) was imposed. The reconstruction terminates either when the change between two consecutive iterations falls below a certain threshold or upon the request from user after a certain number of iterations. As a priori knowledge of the rank value is required for the retrospectively under-sampled data (Section 3.1), it was estimated (1.1 normalized against window size, w²) based on SVD of fully sampled data. As shown in Fig. 4, it was chosen at the turning point of the SVD plot such that all dominant singular values are considered as in the signal space. Without fully sampled data, the rank for the prospectively under-sampled data (Sections 3.2 and 3.3) cannot be estimated the same way. However, we assume the same value is valid due to the very comparable size of all studied objects within the chosen FOV. An effective method to de-noise image without sacrificing small signal is to impose sparsity in some transformed domain (e.g., wave-lets). Due to the relatively low SNR in the in vivo study, a joint-sparsity model (Ref. [27]) was adopted and a generalized l₁-norm regularization was incorporated into the general SAKE reconstruction. The regularized optimization problem is:

$$\begin{array}{cc}\hfill & \min {\Vert D\left(x\right)-y\Vert }^2+\lambda \sum _r\sqrt{\sum _c\Psi {\mid \left\{\mathit{IFFT}\left(x\right)\right\}\mid }^2}\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\mathit{rank}\left(A\right)=k\hfill \\ \hfill & x=H^{+}\left(A\right)\hfill \end{array}$$ (2)

Here Ψ denotes the transform from image domain to wavelets domain and r and c are indices for the spatial and coil element dimensions, respectively. λ controls the compromise between the a priori knowledge of sparsity and the data consistency constraint.

Fig. 4.

Singular values of the block Hankel data matrix A from the (a) fully sampled and (b) zero-filled under-sampled k-space data. The green dashed line indicates the threshold that divides the signal space from the discarded noise space. This threshold is determined in (a) as the point of maximum curvature. The corresponding rank of the A matrix (normalized by window size (6 × 6)) is 1.1 for the fully sampled phantom data (Fig. 3(a)). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

3. Results

3.1. SAKE reconstruction on retrospectively under-sampled phantom data

Fully sampled images from individual coils are shown in Fig. 2. Comparison between the square root of the sum of squares (ssos) image from the fully sampled data and the images from SAKE and GRAPPA reconstruction are shown in Fig. 3. The undersampling patterns are inserted into panels (b)–(e) of Fig. 3. Notably, as opposed to GRAPPA (Fig. 3(b) and (c)), no fully sampled ACS was required for SAKE (Fig. 3(d) and (e)). Accordingly, with the same overall acceleration rate, undersampling patterns for SAKE are more flexible and can better cover the peripheral region of k-space. As shown in Fig. 3, performance of SAKE and GRAPPA against 2-fold under-sampled data are comparable (Fig. 3(b) and (d)) with mean square errors (MSE) of 2.70 × 10⁻⁴ and 2.67 × 10⁻⁴, respectively, compared to the ssos image. However, with an ACS of 12 lines, GRAPPA failed (Fig. 3(c), MSE = 2.70 × 10⁻³) at an overall acceleration rate of 2.6 due to aggressive under-sampling of the outer k-space (4-fold). Even with 3-fold acceleration, SAKE still largely suppressed aliasing artifact across the phase encode direction (Fig. 3(e), MSE = 4.38 × 10⁻⁴).

Fig. 2.

Individual coil images (a–h) of the fully sampled ethylene glycol phantom. Two paddle-shaped coil compartments are set up as shown in Fig. 1(b).

For SAKE reconstruction, a 6 × 6 window size was chosen empirically to generate a low-rank block Hankel data matrix A (Eq. (2)). The window-size normalized rank was chosen to be 1.1. As shown in Fig. 4(a), this rank value was chosen at the “elbow point” in the singular value distribution curve of the fully sampled data matrix to separate the signal space and the noise space. This rank value however, cannot be directly estimated from the under-sampled data in general, since undersampling has obscured the transition between dominant and non-dominant singular values [20,32] (Fig. 4(b)). The iterative reconstruction of SAKE converged within 25 s on a MacBook Pro equipped with 2.2 GHz quad-core Intel Core i7 processor.

3.2. SAKE reconstruction on prospectively under-sampled phantom data

Due to variations between dissolutions, specifically sample transfer time and polarization levels between hyperpolarized studies, no fully sampled image was acquired to benchmark reconstruction on the prospectively under-sampled data. The zero-filled and SAKE reconstructed images of HP ¹³C-pyruvate phantom (Fig. 1(c)) are shown in Fig. 5. The sampling pattern is the same as that shown in Fig. 3(d). The image was acquired with a single scan using the same FOV and matrix size as the ethylene glycol study. SAKE reconstruction assumed the same parameters, but converged slowly (~150 s), which is not unexpected due to the slightly larger object size compared to the thermal ethylene glycol phantom. The SAKE reconstruction shows no aliasing artifacts in the phase encode direction that would indicate a failure in the reconstruction, and the sharp edge of the phantom is clearly delineated. The dark line near the top left corner is likely due to B₀ inhomogeneity or turbulence in the phantom that resulted in imperfect excitation given by the aforementioned spectral-spatial pulse.

Fig. 5.

HP ¹³C-pyruvate phantom images (a) zero-filled after 2-fold under sampling on the phase encode direction (b) SAKE reconstruction.

3.3. SAKE reconstruction of in vivo HP ¹³C-t-butanol data

¹³C-t-butanol is considered freely diffusible and has been previously used for hyperpolarized in vivo perfusion studies[22,23]. As opposed to most other hyperpolarized ¹³C molecules, such as ¹³C-urea, ¹³C-t-butanol quickly crosses the blood brain barrier and therefore generates strong signal in brain as well as in other organs (e.g., kidney). Moreover, since t-butanol is not metabolized in vivo, it suffers no signal loss due to metabolism as metabolic agents do (e.g., pyruvate to lactate). As shown in Fig. 6 (e) and (f), high signal intensity was observed in the rat kidneys and brain. The co-registration of ¹³C signal is reasonable considering the different slice thickness for the proton FSE (2 mm) and ¹³C EPI images (15 mm). The two kidneys were not symmetrical in the image due to the non-planar orientation of the rat and the thin slice for proton image. Evident aliasing due to under sampling can be seen in the zero-filled image (Fig. 6(a)) but is suppressed in SAKE reconstructed image (Fig. 6(b)). Notably, the SAKE reconstruction, which converges within 30 s, shows better differentiation between the renal cortex and inner medulla compared to the data acquired with partial Fourier coverage (compare the kidney in the lower right position in Fig. 6(e) and (f)). The effective echo time (TE) of the SAKE scan is comparable to that of the partial Fourier acquisition (75% partial Fourier fraction). However, a quantitative comparison is difficult due to the enhanced SNR of SAKE reconstruction due to SVD thresholding as well as the enforced sparsity by wavelet transform. Here the regularization parameter λ in Eq. (2) was empirically chosen to be 0.32. The signal intensity ratio of kidney versus brain is comparable in SAKE (0.93) and the partial Fourier acquisition (1.08), which was calculated using the two ROIs in Fig. 6(e) and (f).

4. Discussion

A major challenge facing clinical studies using hyperpolarized ¹³C MR molecular imaging is the need to acquire the prepolarized, high SNR signals with adequate spatial coverage while maintaining high temporal and spatial resolution. Fast acquisition techniques such as EPI and parallel imaging with multichannel coils have the potential to address these challenges. A previous ¹H MRI study [20] demonstrated the SAKE reconstruction for 2D accelerated, proton image acquisition with both Cartesian and non-Cartesian k-space coverage (e.g., spiral). The goal of this study was to apply this calibration-less parallel imaging approach to HP ¹³C studies. HP ¹³C studies have a critical demand of acquisition speed given the short T₁ lifetime and low gyromagnetic ratio of ¹³C spins; the former limits the time window for signal acquisition and the latter puts a constraint on the achievable speed to traverse k-space due to limited gradient strength on clinical scanners. Therefore, a sub-Nyquist sampling strategy is beneficial, especially when a large FOV with fine spatial resolution is desirable such as in clinical human studies. As an initial, proof-of-concept demonstration, we applied SAKE reconstruction to a 2D symmetric EPI readout with a 2-fold under sampling on the phase encode direction. As shown above, this reconstruction strategy does not require explicit calibration and is robust against aliasing due to under sampling. This gives SAKE a unique advantage over conventional parallel imaging schemes that require separate calibration scans. As shown in this study, to keep up with the same acceleration factor, GRAPPA with a typical ACS of 10–20 lines needs to aggressively under-sample the peripheral region of k-space, leading to loss of fine structure and unrecovered aliasing artifacts.

This calibration-less parallel imaging approach can also be applied to HP ¹³C MRI data acquired with multi-dimensional acceleration, especially as higher channel count coils are developed. While higher 1D acceleration rates (e.g., 2.5 or 3-fold, as demonstrated in this study) for SAKE are achievable with the current coil setup, sequences such as a 3D multi-shot EPI offer the potential of even greater acceleration since incoherent undersampling can be performed on both phase-encode dimensions. With multi-shot excitation, one can also expect improved SNR when this undersampling strategy is combined with a tailored variable flip angle (VFA) schedule to efficiently allocate full HP magnetization to fewer excitations.

5. Conclusion

In this study, we investigated a calibrationless parallel imaging method (SAKE) for hyperpolarized ¹³C imaging. We implemented and tested this technique using a symmetric EPI readout with 2-fold random undersampling in the phase encoding direction. Future work will focus on applying this technique to 3D acquisitions with 2D under-sampling, which is expected to result in further acceleration and improved SNR.