Accurately achieving target busulfan exposure in children and adolescents with very limited sampling and the BestDose software

Abstract

Background

Busulfan dose adjustment is routinely guided by plasma concentration monitoring using 4–9 blood samples per dose adjustment, but a pharmacometric Bayesian approach could reduce this sample burden.

Methods

The authors developed a non-parametric population model with Pmetrics. They used it to simulate optimal initial busulfan dosages, and in a blinded fashion, they compared dosage adjustments using the model in the BestDose^™ software to dosage adjustments calculated by non-compartmental estimation of AUC at a national reference laboratory in a cohort of patients not included in model building.

Results

Mean (range) age of the 53 model-building subjects was 7.8 (0.2 – 19.0) years and weight was 26.5 (5.6 – 78.0) kg, similar to nearly 120 validation subjects. There were 16.7 (6 – 26) samples per subject to build the model. The BestDose cohort was also diverse: 10.2 (0.25 – 18) years and 46.4 (5.2 – 110.9) kg. Mean bias and imprecision of the one-compartment model-predicted busulfan concentrations were 0.42% and 9.2%, and were similar in the validation cohorts. Initial dosages to achieve average concentrations of 600–900 ng/mL were 1.1 mg/kg (≤12kg, 67% in the target range and 1.0 mg/kg (>12 kg, 76% in the target range). Using all 9 concentrations after dose 1 in the Bayesian estimation of dose requirements, the mean (95% CI) bias of BestDose calculations for the third dose was 0.2% (−2.4% to 2.9%, P=0.85), compared with the standard non-compartmental method based on 9 concentrations. With one optimally timed concentration 15 minutes after the infusion (calculated with the authors’ novel MMopt algorithm) bias was −9.2% (−16.7% to −1.5%, P=0.02). With two concentrations at 15 minutes and 4 hours bias was only 1.9% (−0.3% to 4.2%, P=0.08).

Conclusions

BestDose accurately calculates busulfan intravenous dosage requirements to achieve target plasma exposures in children up to 18 years of age and 110 kg using only two blood samples per adjustment compared to 6 – 9 samples for standard non-compartmental dose calculations.

Introduction

Busulfan is an alkylating agent used in conditioning regimens prior to hematopoietic stem cell transplantation (HSCT). Dosing by intravenous administration is now the preferred route in many centers. Despite intravenous dosing, numerous studies have documented highly variable pharmacokinetics (PK) and plasma exposures between patients.^1–4 Moreover, there is a considerable body of evidence that the target exposure for busulfan is quite narrow, such that there is a small difference between higher plasma concentrations associated with increased risk of toxicity^5,6 and lower concentrations associated with increased risk of graft failure due to residual host immune cells.^7–9

Busulfan therapeutic drug monitoring (TDM) and management is routinely recommended and practiced at pediatric transplantation centers because of the unpredictability of concentrations for a given dose and the need to maximize chances of successful therapy within a narrow exposure range. In the United States, initial busulfan dosing, according to the FDA-approved package insert, is 0.8 mg/kg IV every 6 hours for patients >12 kg, and 1.1 mg/kg for those ≤12 kg. However, as reported in the insert, based on population modeling and simulated probability of target attainment, this dosing is expected to achieve the proper exposure in only 60% of patients. European Medicine Agency (EMA) guidelines, based on a continuous log-linear function between busulfan clearance and body weight,³ are also associated with suboptimal target attainment.¹⁰

To adjust dosing, most centers appear to use several measured busulfan concentrations obtained after the first dose, typically 4–9 samples.¹¹ From these, they estimate the AUC_0-∞ or steady-state AUC_0-t, where t is the dosing interval, by non-compartmental methods, including trapezoidal approximation. From this estimate, dosing is adjusted by simple proportionality according to the equation Dose_new = Dose_given • AUC_desired/AUC_measured. For example, this method is used by the Seattle Cancer Care Alliance Pharmacokinetics Laboratory (SCCAPL, Seattle, WA),¹² which serves as a reference center for busulfan measurement, interpretation, and dosing adjustments in the United States. According to their report, SCCAPL fit all concentrations for a patient using a single- compartment, first-order elimination model in WinNonlin (Pharsight Corporation, Mountain View, CA, USA) to estimate AUC.

A major problem with calculation of AUC from the first dose will arise if accumulation of drug until steady state is neglected, which would cause an underestimation of total AUC, and overestimation of required dosages. ¹³ Another problem with this approach is the large number of blood samples that must be obtained during a single dosing interval to estimate AUC. The package insert recommends a minimum of three, and preferably four (or more). Our own hospital (Children’s Hospital Los Angeles) uses 9 samples to precisely calculate AUC within a 6-hour window. This is very burdensome to nurses, phlebotomists, laboratory personnel, and the patients, who must be dedicated to obtaining the required results in a timely enough fashion to permit any necessary dose adjustments. For this reason, centers are beginning to turn towards population modeling (a.k.a. pharmacometrics) as a means to tailor initial dosing more finely than available in the package US and European inserts and to adjust subsequent dosing to achieve the target exposure with fewer blood samples.

Several population models of busulfan pharmacokinetics have been published in the last three years,^14–20 and alternative methods for calculating the initial dose of busulfan have been proposed, based on these models. ^10,21 Recently, the group from the University of San Francisco has begun to develop a tool to use a model for dose optimization.¹⁴ They rightly point out that the vast majority of population models are complex and not conducive to use in the average clinical setting, which we feel is an important area for great improvement with the field of pharmacometrics. However, their tool is an Excel spreadsheet that currently is only designed to choose the initial dose based on the mean population parameter values and the patient’s age and weight.

Despite the abundant literature describing the pharmacokinetics of busulfan, a simple and accurate tool is still needed to rapidly adjust busulfan dosage early in the course of therapy, to use the fewest samples possible, and to achieve the target exposure most accurately and precisely. Therefore, we reviewed our own busulfan dosing and monitoring practice at the Children’s Hospital Los Angeles, with the goal of developing a non-parametric population model of busulfan pharmacokinetics, and including this model within the BestDose software for individual patient therapeutic drug dose management (www.lapk.org).

Materials and Methods

Study Design

This was a quality improvement (QI) project at the Children’s Hospital Los Angeles (CHLA). The project was to review busulfan dosing and sampling practice with a goal of reducing the number of blood samples obtained from each patient by using a population modeling approach. The CHLA Institutional Review Board approved publication of the results and a waiver of informed consent, as we only used existing clinical data, which we de-identified for this project.

Subjects

Any patient receiving busulfan as part of their standard care at CHLA, a large tertiary-care facility, was eligible for inclusion. At the time of model building in early 2013, we generated a convenience sample of 53 patients with available records who had been admitted in the years 2010, 2011 and the first part of 2013. Records from 2012 were not assembled at the time. After developing the model, we used an additional 11 patients admitted in the latter part of 2013, who were not included in the model-building cohort, to form an external validation group.

As another validation cohort, we also used the busulfan dosing history and measured concentrations from 105 pediatric patients managed at the University Hospitals of Lyon (Hospices Civils de Lyon), France from June 2006 to September 2012.

Finally, to validate the application of the model in our BestDose software for multiple-model, Bayesian adaptive control of therapeutic drug dosing,^22–25 we used an additional 20 patients admitted to CHLA from the end of 2013 through 2014, who were not part of any other cohort.

Busulfan dosing and target concentrations

Patients at CHLA are administered intravenous busulfan with a starting dose of 1 mg/kg, infused over 2 hours. Doses are administered every 6 hours, for a total of 16 doses over 4 days. The target exposure may be expressed in various ways (see Table 1). We use the average concentration (C_ave), which is obtained by dividing the area under the time-concentration curve (AUC) by its corresponding interval, e.g. AUC_0-96/96. C_ave is expressed in ng/mL (see Table 1). Clinicians at CHLA target a busulfan C_ave of 700–900 ng/mL from 0 to 96 hours.

Table 1.

Different PK targets used in the clinical TDM of busulfan in children. AUC, area under the time-concentration curve; C_ave, average concentration.

Target type (Units)	Time Span (hours)	Target Range
AUC (μM*min)
AUC0–6	0 – 6	877 – 1315
AUC24	0 – 24	3508 – 5260
AUC96	0 – 96	14032 – 21048
AUC (mg*h/L)
AUC0–6	0 – 6	3.6 – 5.4
AUC24	0 – 24	14.4 – 21.6
AUC96	0 – 96	57.6 – 86.1
Cave (ng/mL)	0 – 96	600 – 900

Sample collection

The standard protocol at CHLA is to collect 9 blood samples for measurement of plasma busulfan with the first dose and every dose that is different from the previous dose. The samples are collected just prior, and 0, 0.25, 0.5, 1, 1.5, 2.5, 3.5, and 4 hours after the end of a 2-hour infusion.

In the Lyon cohort, two blood samples were drawn 0.5 and 2 hours after the end of the first busulfan infusion in each patient. Afterwards, individual PK parameter values of a one-compartment model²⁶ were estimated using the maximum a posteriori (MAP) Bayesian modeling program included in the USC*PACK software.²⁷ Individually estimated (Bayesian posterior) PK parameters were used to perform calculation of the AUC after the initial dose, subsequent estimation of busulfan plasma concentrations, and adjustment of the future doses necessary to achieve the target range for the rest of the regimen. According to the results, additional blood samples could be drawn for confirmation of the subsequent dosage regimen to achieve the target concentrations.

Sample analysis

All samples from CHLA are assayed for busulfan in the Special Chemistry Laboratory, a CLIA-certified laboratory, using a validated HPLC assay. ²⁸ Busulfan plasma concentrations from Lyon were measured by HPLC with UV detection for data before 2010,²⁹ and by an updated, cross-validated liquid chromatography – tandem mass spectrometry method after 2010.³⁰ All the assays used were linear from 20 to 2000 ng/mL with an interday imprecision of <10%.

Population Modeling

We constructed a non-parametric population model of busulfan pharmacokinetics using the Non-Parametric Adaptive Grid^31,32 algorithm in the Pmetrics package for R³³ and the individual patient busulfan dosing history, concentrations, and covariates.

We tested one-compartment models consisting of an infusion into a central compartment with volume V and elimination Ke, with differing initial ranges for both parameters. We also tested models with an additional peripheral compartment and transfer of drug to the peripheral compartment from the central (KCP) and the reverse (KPC). To construct a unified pediatric and adult model, and based on superior predictions early in the modeling process, we scaled V and Ke for body size allometrically in all subsequent models by using fixed exponents on body weight of −0.25 for Ke and of 1 for V.³⁴ Subsequent to inclusion of allometrically scaled weight, we tested the effect of age on model likelihood and predictions. Age and weight, actual body weight (ABW) or ideal bodyweight (IBW) calculated using the Traub and Johnson formula,³⁵ were the only covariates that we included in the model-building process. Busulfan is not eliminated in the urine, so we did not include a renal function descriptor. Although some data have suggested that genetic polymorphisms of busulfan metabolizing enzyme may influence the drug PK, this was not investigated, as we did not have any pharmacogenomic patient data available to us.³⁶

For the fitting procedure, to weight the concentrations with the Fisher information of 1/SD², where SD is the standard deviation of the measured concentration, we used an error polynomial of the form SD =0.0019+0.021* [conc] − 0.017* [conc]², where conc is the busulfan concentration. We estimated the coefficient values based on the reported intra-assay standard concentrations and standard deviations of six replicates of the assay used at CHLA,²⁸ fitted to zero- to third-degree polynomials with the makeErrorPoly function in Pmetrics. For the Lyon cohort, the polynomial was SD =0.0007 + 0.056* [conc] − 0.019* [conc]², based on their assays.³⁰ Both second-degree polynomials fitted their respective assay validation data with an R² of >0.99.

Additionally, during the modeling process, we allowed Pmetrics to fit a fixed but unknown additive lambda term, such that concentrations were weighted by ((SD + λ)²)⁻¹, where lambda is representative of additional noise such as errors in sample timing or model misspecification. The final cycle value of lambda was 0.058, about half of the lowest measured concentration (0.11 mg/L), indicating very low error beyond measurement noise and very low model misspecification.

We chose the final model primarily to minimize the bias and imprecision of the predictions vs. observations, but we also evaluated the Akaike Information Criterion (AIC),³⁷ which is a function of the log-likelihood penalized for over-parameterization, residual plots, and visual and numerical predictive checks (VPC/NPC). Bias was the mean error of the difference between predictions (pred_i) and observations (obs), i.e. $\mathit{Bias}=\frac{1}{N}{\sum }_{i=1}^N({\mathit{pred}}_i-{\mathit{obs}}_i)$, where N is the total number of observations. Imprecision was the square root of variance of prediction error, i.e. bias-adjusted root mean squared error calculated by $\sqrt{\left[\frac{1}{N}{\sum }_{i=1}^N{({\mathit{pred}}_i-{\mathit{obs}}_i)}^2\right]-{\mathit{Bias}}^2}$. The VPC was based on 1000 simulated profiles for each subject, using his/her own weight, busulfan dosing history over 4 days, sampling schedule, and the final population model parameter value means and covariances as the prior from which each simulated set of parameter values was randomly sampled. All simulated profiles were combined and concentration times were binned in 12-minute intervals to adjust for minor differences in sampling times across the patient population and to smooth the 2.5^th, median, and 97.5^th quantiles of the simulated concentrations. Finally, observed concentrations were plotted over the simulated quantiles. We visually checked that their distribution was similar to the simulated quantiles, and we also numerically checked with a binomial test to determine the probability that the proportion of observed concentrations below each quantile differed from the expected by chance.

As we did for our voriconazole model,²² we summarized parameter values in the final model as weighted medians for central tendencies of a non-parametric distribution with a 95% confidence interval (95% CI) around the median, and the median absolute weighted deviation (MAWD) from the median as a measure of the variance of a non-parametric distribution, with its 95% CI. These estimates correspond to weighted mean, 95% CI of the mean, variance, and 95% CI of the variance, respectively, for a sample from a normal distribution.

Validation against external cohorts

Using the final model, we calculated the non-parametric Bayesian posterior parameter value distributions for each of the 105 French patients and the 11 additional CHLA patients using their own busulfan dosing, concentrations and weights. We calculated bias, imprecision and linear regression descriptors for the observations vs. predictions, with predictions for each subject based on the median of his/her Bayesian posterior parameter value distribution.

Calculation of optimal sampling times

Our Multiple Model optimal (MMopt) sampling algorithm chooses the sample times which minimize the risk of misrepresenting the patient as the wrong set of support points in the model, i.e. estimating the wrong set of PK parameters for the patient.³⁸ For this analysis, we used the latest version of our algorithm, which is a weighted MMopt (wMMopt), tuned in this case to specifically ensure that we could estimate the patient’s busulfan AUC most reliably.³⁹ We tested n = 1 or 2 for the number of optimal samples, restricted to the available sample times after dose 1. However, we excluded the immediate post-infusion sample at time 2 hours, as our experience clinically has been that this concentration is the most likely to be falsely elevated due to contamination in the line from residual busulfan and inadequate flushing prior to sampling.

Optimal initial dosage

From the final model, we simulated 1000 time-concentration profiles for several dosage amounts of busulfan administered every 6 hours for 96 hours. To generate a realistic simulated population, we included weight and age as described in the Pmetrics User Manual (www.lapk.org). Since weight and age were not parameters in the original model, we could not take advantage of Pmetrics’ ability to simulate from the discrete nonparametric prior,⁴⁰ but rather used the option for a unimodal, multivariate prior with the parameter means and covariances from the population model augmented with the means and covariances for weight and age derived from the model-building population. For each dosage amount, we determined the proportion of simulated 96-hour C_ave that were between 600 ng/mL and 900 ng/mL, selecting the dosage with the highest proportion as a reasonable initial dose. We then used CDC growth tables (http://www.cdc.gov/growthcharts/1977charts.htm) to calculate the starting dose in mg/kg for a range of ages and weights.

Busulfan software dosing controller construction and validation

We incorporated the final model into our busulfan multiple-model Bayesian adaptive dosing controller,^23,24,41 which we call a software “cartridge” in our BestDose computer program for individual patient therapeutic drug dose optimization. The busulfan cartridge included the structural model equations relating input (busulfan dosing and patient’s covariates) to output (busulfan plasma concentrations), and the discrete joint probability distribution of the values of the equation pharmacokinetic parameters in the population, consisting of support points in the final model. BestDose uses the cartridge and each patient’s covariates (e.g. weight and age) and busulfan dosing and concentration data to find the least biased and most precise dosage regimen relative to a target patient drug exposure (i.e. busulfan AUC) as previously described for voriconazole.⁴² We found during the development process that when patients were below their IBW, ABW provided a better fit.

To validate the busulfan dosing strategy (BestDose cartridge), for the 20 patients who were not part of any other cohort, the CHLA laboratory provided all busulfan concentrations and the patients’ ideal/actual body weights. All 20 patients had a pre-specified C_ave target, either 700 (N=4) or 800 (N=16) ng/mL. We were also provided the doses each patient had actually received. All patients except for two had 3 sets of 9 samples; the remaining two patients had only 2 sets. Our task was to use BestDose to make three dose recommendations to achieve the overall target C_ave: 1) for doses 3–16 based on sampling after dose 1 and the first 2 doses given; 2) for doses 7–16 based on sampling after doses 1 and 5 and the first 6 doses given; 3) for doses 11–16 based on sampling after doses 1, 5, and 9 and the first 10 doses given. We first used all available concentrations for a given patient to generate the Bayesian posterior from which we used BestDose to calculate the doses that achieved the target C_ave. In BestDose it is possible to directly target an AUC, so in each case we used AUC_0-96 as the target and divided it by 96 to get C_ave. We then repeated this process using only the samples at the one or two wMMopt times in each sampling period to generate the Bayesian posteriors for dose calculations.

The exact same data and targets were sent to the Seattle Cancer Care Alliance Pharmacokinetics Laboratory (SCCAPL). We were blinded to their dose recommendations when generating BestDose recommendations from either the full set of measured concentrations for each patient (18 – 27 samples), or the reduced MMopt set (4 – 6 samples). After generating all the BestDose recommendations, we computed percentage bias (%bias) and imprecision, analogous to those used in the modeling process described above, compared to the SCCAPL dose recommendations. We defined %bias as (BestDose − SCCAPL)/SCCAPL, and mean percent bias as $\mathit{MPB}=\frac{1}{D}{\sum }_{i=1}^D\%{\mathit{bias}}_i$, where D is the total number of dose recommendations. This means that a positive %bias indicates BestDose recommendations were higher than SCCAPL recommendations. Imprecision was the square root of variance in %bias (root mean bias-adjusted percent squared error), i.e. $\sqrt{\left(\frac{1}{D}{\sum }_{i=1}^D\%{\mathit{bias}}_i^2\right)-{\mathit{MPB}}^2}$.

Results

Population characteristics

The characteristics of the various populations used in this project are shown in Table 2. The model building and validation populations were similar in age and weight, but the French cohort had far fewer busulfan blood samples per patient by design (see Methods). The BestDose cohort was heavier than the others, because the pharmacy and laboratory deliberately selected patients with a wide range of weights for the validation.

Table 2.

Characteristics of the patient cohorts. Data are presented as mean (range). CHLA, Children’s Hospital Los Angeles; C_ave, average concentration over 96 hours.

Cohort	Model Building	Validation 1	Validation 2	BestDose
Source	CHLA	Lyon	CHLA	CHLA
Number	53	105	11	20
Age (years)	7.8 (0.2 – 19.0)	5.6 (0.1 – 21)	5.8 (0.5 – 14.2)	10.2 (0.25 – 18)
Weight (kg)	26.5 (5.6 – 78.0)	20.3 (3.4 – 59.6)	22.7 (5.2 – 53.4)	46.4 (5.2 – 110.9)
All Doses (mg/kg)	1.1 (0.7 – 1.8)	1.2 (0.6 – 5.2)	1.2 (0.9 – 1.5)	0.83 (0.5 – 1.3)
Samples/patient	16.7 (6 – 26)	3.3 (1 – 13)	15.9 (8 – 26)	25.2 (17 – 26)
Cave(ng/mL)	750 (390 – 1190)	750 (390 – 1860)	780 (550 – 950)	714 (564 – 914)

Busulfan population pharmacokinetic model

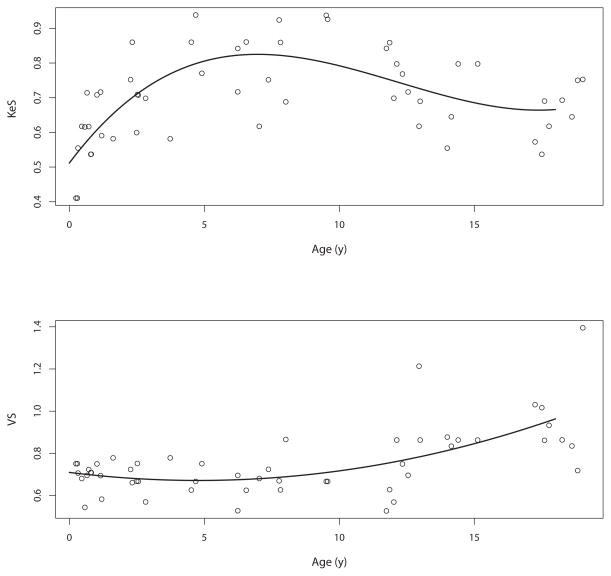
We tested one- and two-compartment models with and without allometric scaling for body size, using the lesser of ideal body weight and actual body weight. In addition to body size, we also found a relationship between age and both busulfan elimination and volume of distribution, as shown in Figure 1. Based on the shape of trend curve, we used Pmetrics to fit zero to third order polynomials to the median posterior values of elimination and volume, adjusted for size, for each patient and their age. The plots of these polynomials are included in Figure 1.

Figure 1.

Relationship between (top) KeS (elimination adjusted allometrically for body size) and (bottom) VS (volume adjusted allometrically for body size) and age. Equations for the polynomials are shown in the legend for Table 4.

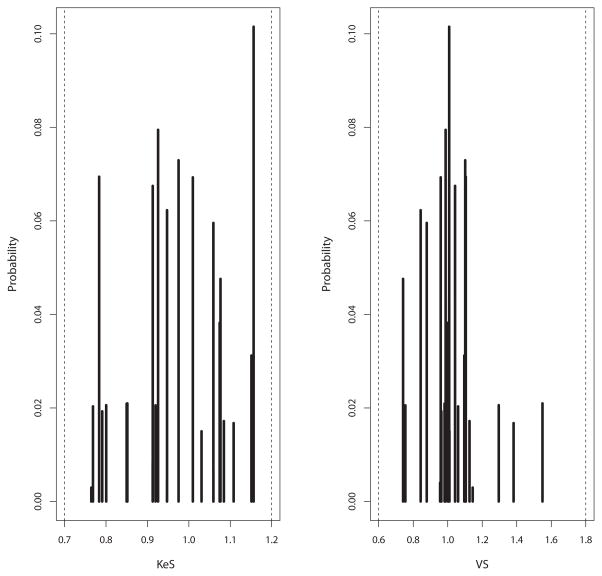
Model comparisons are shown in Table 3. Considering all six candidate models divided into three pairs of one- and two-compartment models without covariates, with size scaling, and with size plus age scaling, respectively, within each model pair, the two-compartment model had the best (lowest) likelihood and AIC. Overall, the pair of one- or two-compartment allometric + age models were the most likely. Within this pair, the two-compartment model was more likely. However, based on lower prediction bias and parsimony, we chose the one-compartment, allometrically and age-scaled model (#5 in Table 3) as the final structural model, with equations and population parameter values shown in Table 4. The marginal probability densities of the 29 support points are shown in Figure 2.

Table 3.

Comparison of candidate models, all after 100 cycles. Comp, number of compartments; Ke, elimination from central compartment, V, volume of central compartment; KCP, transfer rate from central to peripheral compartment; KPC, transfer rate from peripheral to central compartment; LL, log-likelihood; AIC, Akaike Information Criterion. Bias and Imprecision are calculated as reported in the text, based on the median population parameter values for each model. Models are reported in order of complexity, with allometric indicating allometric scaling of model parameter values for body size, and age indicating the addition of an age polynomial to allometrically scaled models, as described in the text. Based on the discussion in the text, we chose model #5 to develop further.

Model #	Comp	Parameters	−2*LL	AIC	Bias	Imprecision
1	1	Ke, V	−1944	−1938	0.003	0.076
2	2	Ke, V, KCP, KPC	−2172	−2162	0.000	0.072
3	1	#1 + allometric	−1982	−1976	−0.001	0.069
4	2	#2 + allometric	−2370	−2360	−0.012	0.058
5	1	#3 + age	−2012	−2006	−0.003	0.070
6	2	#4 + age	−2436	−2426	−0.008	0.056

Table 4.

Population parameter value summaries in the final model. MAWD is the median absolute weighted deviation, analogous to variance for a normal distribution (see text). In the model, Ke = KeS * ibw^−0.25 (C₀ + C₁ * [age] + C₂ * [age]² + C₃ * [age]³) and V = VS * ibw * (C₀ + C₁ * [age] +C₂ * [age]²), where Ke is the elimination rate constant from the central compartment in h⁻¹, KeS is the scaled Ke; ibw is ideal bodyweight in kg, calculated using the Traub and Johnson formula; ³⁵ V is the volume of the central compartment in L; and VS is the scaled volume. C₀, …, C₃ are the coefficients describing the age dependence of Ke and V, which were fixed in the final model. For Ke, C₀=0.51, C₁=0.10, C₂=−0.010, C₃=0.00029. For V, C₀=0.71, C₁=−0.016, C₂=0.0017.

Parameter	Median (95% CI)	MAWD (95% CI)	Range
KeS	1.01 (0.93 – 1.07)	0.084 (0.050 – 0.13)	0.76 – 1.16
VS	1.01 (0.98 – 1.04)	0.052 (0.021 – 0.11)	0.74 – 1.55

Figure 2.

Marginal plots of population parameter value distributions for busulfan KeS (elimination adjusted allometrically for body size and age) and VS (volume adjusted allometrically for body size and age).

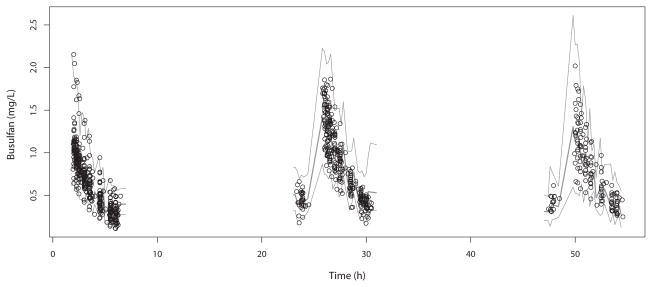
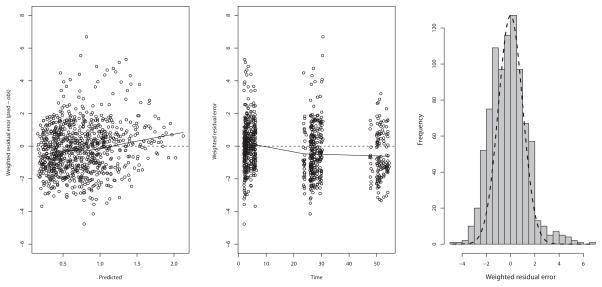
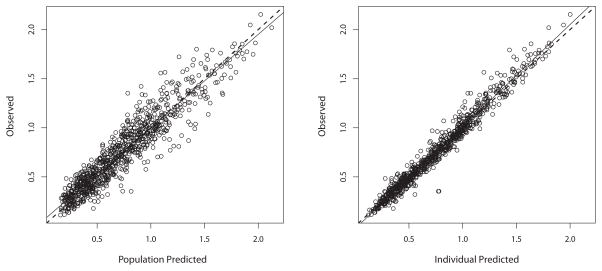
The visual predictive check is shown in Figure 3. Numerically, 2.9% of the observed concentrations were below the 2.5^th percentile of simulated concentrations (P=0.51, Binomial test), 43.8% were below the median (P=0.0003), and 98.3% were below the 97.5^th percentile (P=0.16). This numerical check indicates that the model central tendency of predictions is slightly below the observations but that the variability in the model represents the variability in the population well. This conclusion is also supported by the residual plot of population predictions in Figure 4, which are largely clustered within 2 standard deviations of 0, but show a slight underprediction at later time points. This is likely due to a small decline in clearance over time in some patients, ⁴³ such that measured busulfan concentrations can be slightly higher than predicted. However, this interoccasion change in clearance is typically on the order of 10% and not explained by any covariate, ^15,17,19 and thus we did not feel that inclusion in our model was necessary for accurate dose calculations. Indeed, predicted busulfan concentrations, based either on population or Bayesian posterior medians, were well matched to their corresponding measured concentrations, as shown in Figure 5. The Bayesian posterior bias (mean prediction error) was −3.2 ng/mL with an imprecision (root mean bias-adjusted squared error) of 70 ng/mL. To put these in context, the mean observed concentration was 758 ng/mL; therefore the mean bias is only 0.42% of this, with an imprecision of 9.2%.

Figure 3.

Visual predictive check for the final model. Circles are measured concentrations, the lower and upper lines are the 2.5^th and 97.5^th percentiles of simulated concentrations, and the central line is the median of the simulated concentrations.

Figure 4.

Residual plot for the model predictions, based on the median population parameter values. In the residual plot, there is a tendency to slightly underpredict later concentrations as seen in the middle panel. In the right panel is shown a histogram of the residuals with an ideal normal distribution as a dashed line.

Figure 5.

Observed vs. predicted plots for busulfan. Predictions were based on the median population parameter values (left) or the medians of the individual Bayesian posterior parameter values (right).

Validation against external cohorts

Using the model as the prior and the 0-cycle option in Pmetrics, we calculated Bayesian posterior parameter value distributions for both the French and CHLA validation cohorts to determine how well the model could predict concentrations in patients who did not contribute to the model. From each subject’s median Bayesian posterior parameter values, we calculated the predicted busulfan concentrations and compared them to the measured values. For the French cohort (n=105), the bias was −4.6 ng/mL and imprecision was 124 ng/mL. The intercept of the regression line for observations vs. predictions was 21.4 (95% CI −9.3 to 52.1) and the slope was 0.98 (95% CI 0.94 to 1.01), indicating than neither were significantly different from their ideal values of 0 and 1, respectively. The regression coefficient of determination (R²) was 0.89. For the CHLA validation cohort (n=11), prediction bias was 16.4 ng/mL and imprecision was 119 ng/mL. The intercept of the regression line for observations vs. predictions was −6.9 (95% CI −46.0 to 32.2) and the slope was 1.03 (95% CI 0.99 to 1.08). R² was 0.92.

wMMopt limited sample times

For a 1-sample design, the wMMopt time was 2.25 hours after starting a 2-hour infusion, or 15 minutes after the end of the infusion. For the 2-sample design, the wMMopt times were 2.25 and 6 hours after the start of the infusion, or 15 minutes and 4 hours after the end of the infusion, i.e. a peak and trough.

Probability of Target Attainment and Initial Dosing Matrix

Simulations of doses of 4, 4.5, 5, 5.5 and 6 mg per age-adjusted, allometrically scaled kg resulted in target attainment rates of 68%, 77%, 64%, 46%, and 27%, respectively. Using 4.5 as the best dose, we calculated the dose in mg/kg for all combinations of weights from 0 to 100 kg in 2.5 kg increments, and ages from 0 to 18 years in one-year increments. We excluded weight-for-age combinations <5^th percentile and >95^th percentile by CDC criteria. The range of doses was 0.88 mg/kg to 1.24 mg/kg, with the highest doses in the lightest 5–6 year olds, and the lowest doses in the heaviest teenagers. The mean in those ≤12 kg was 1.1 mg/kg and in those >12 kg was 1.0 mg/kg, with 67% and 76% predicted to achieve a 96-hour C_ave of 600 to 900 ng/mL, respectively. These doses can be considered as reasonable starting doses in the absence of a tool like BestDose, which we describe in the next section.

BestDose busulfan dosing strategy validation

Table 5 shows the summaries of dose recommendations from SCCAPL compared to the BestDose recommendations using the full set of concentrations or the wMMopt subsets to generate the Bayesian posteriors, as well as the bias and imprecision. Using all available data to generate the Bayesian posterior resulted in dose calculations by BestDose that had negligible overall bias across all dose recommendations of 0.1%, relative to the calculations by SCCAPL, and a very low imprecision of 9.0%. The one-sample wMMopt schedule tended towards low dose recommendations, with an average bias of −10.3%, and with greater imprecision of 18.1%. The two-sample wMMopt dose recommendations also had very low bias of only 1.7% and an imprecision of 8.8%.

Table 5.

Bias and imprecision of dose calculations made with BestDose, multiple-model adaptive control, and the final population model, compared to recommendations made by the Seattle Cancer Care Alliance Pharmacokinetics Laboratory (SCCAPL) using non-compartmental estimation of busulfan area under the time concentration curve (AUC). A negative bias indicates that the BestDose calculation was less than the SCCAPL dose. Full, all data points were used to generate the individual patient’s Bayesian posterior parameter value distribution from the population model; MMopt1, only the concentrations 15 minutes after the end of the infusion were used to generate the Bayesian posterior; MMopt2, only concentrations 15 minutes and 4 hours after the end of the infusion (i.e. a peak and trough) were used to generate the Bayesian posterior.

Dose 3
	SSCAPL	Full	MMopt1	MMopt2
Mean (range) dose mg	35.7 (6.0 – 60.0)	35.7 (6.1 – 63.0)	32.3 (6.1 – 58.0)	36.5 (6.1 – 68)
Mean (95% CI) bias	-	0.2% (−2.4 to 2.9, P=0.85)	−9.2% (−16.7 to − 1.5, P=0.02)	1.9% (−0.3 to 4.2, P=0.08)
Imprecision	-	5.5%	15.7%	4.6%
Dose 7
	SSCAPL	Full	MMopt1	MMopt2
Mean (range) dose mg	32.1 (4.8 – 57.0)	31.9 (4.5 – 61.0)	29.1 (3.9 – 57.5)	32.1 (4.6 – 61.5)
Mean (95% CI) bias	-	−1.3% (−6.1 to 3.5, P=0.57)	−10.8% (−18.6 to − 3.0, P=0.01)	−0.7% (−5.5 to 4.0, P=0.75)
Imprecision	-	9.9%	16.4%	9.9%
Dose 11
	SSCAPL	Full	MMopt1	MMopt2
Mean (range) dose mg	31.3 (4.8 – 66.0)	32.4 (4.6 – 82.0)	28.7 (3.6 – 73.6)	32.7 (4.8 – 81.6)
Mean (95% CI) bias	-	1.6% (−4.0 to 7.3, P=0.55)	−11.1% (−21.8 to − 0.6, P=0.04)	4.0% (−1.8 to 9.9, P=0.16)
Imprecision	-	11.6%	22.1%	12.1%

Discussion

For this project to examine our busulfan monitoring practice with the goal of reducing the number of samples per patient, we first developed a non-parametric population pharmacokinetic model of intravenous busulfan in 53 children of diverse ages and weights. We specifically chose a non-parametric model because we intended to use it in the multiple-model Bayesian control algorithm in BestDose. A one-compartment model with age and weight dependence adequately described the data in the model-building population. For the average age in the population of 8 years and an ideal body weight of 26.7 kg, Ke is 0.36 h⁻¹, V is 0.69 L/kg, and clearance is 4.14 ml/min/kg, which agree well with clearance and volume in the package insert of 0.64 L/kg and 3.37 ml/min/kg, respectively as well as in other reports. ^17,43,44

Our model includes weight and age as significant covariates that are independently associated with busulfan pharmacokinetics across the entire pediatric age range. Other models have included an age function only in the youngest children,^10,16 while the model of Long-Boyle et al also included age effects across the entire pediatric age range, defined by an increasing rate of allometrically scaled clearance up to a fixed age of 12 years, after which clearance declined.¹⁴ We did not fix our age function in any way, preferring to simply fit a continuous age-related polynomial to avoid a uniform maturation breakpoint applied to all patients. Investigating age-related changes resulting from maturation of physiological processes is one of the biggest challenges in pediatric PK modeling, and weight and maturation are of course highly correlated.⁴⁵ By first scaling weight allometrically, we were able to discern the additional age relationship to busulfan elimination and volume of distribution, but despite the quality of the model fit, it is an empiric fit, and mechanistic interpretation of the polynomial relationship between age and PK parameters is limited. Without further data in adults, this model should only be used for the pediatric population up to age 18 years.

We have verified the ability of the model to closely predict busulfan concentrations in nearly 120 additional children who were not included in the model-building dataset. Most importantly, we then incorporated that model as a software cartridge in the BestDose computer program for optimizing target-oriented doses of busulfan using our multiple-model, Bayesian adaptive control algorithm. In a blinded comparison, we have shown that with only two optimally timed samples using our MMopt algorithm, this model can very closely match busulfan dose recommendations based on non-compartmental analysis that requires 6–9 concentrations. This is only the second study describing a limited sampling strategy for IV busulfan in pediatrics. Dupuis et al. recommended a three-sample strategy to calculate AUC with an acceptable level of precision and a lack of bias. ⁴⁶ However, their strategy was based on multiple linear regression after the first dose only, and its applicability after that is unknown. Our wMMopt times (15 minutes and 4 hours after the end of any infusion, i.e. a peak and trough) are easy to remember, fit well into common drug monitoring paradigms, and could reduce problems related to the timing of the blood samples. Even one sample, should the other be lost or contaminated, is sufficient to make a reasonable estimate of AUC. Furthermore, Bayesian approaches are generally more accurate than nomograms, ^47,48 and they are robust enough to provide interpretable results when sample times deviate from a schedule, which is not true for nomograms. The implementation of the tools and limited sampling strategies presented in this work in clinical practice can greatly reduce the burden and cost of the traditional approach of busulfan monitoring in many centers treating stem-cell transplant children, while preserving accurate estimation of drug exposure and dose requirements.

We have also provided initial busulfan dose recommendations based on weight ≤12 kg or >12 kg. With 1.1 mg/kg IV every 6 hours for 16 doses, 67% of the lighter patients are expected to be within a C_ave of 600–900 ng/mL. For the heavier patients, 76% will be in this range with 1.0 mg/kg IV every 6 hours for 16 doses. Our dose recommendations are very similar but somewhat simpler than those of Long-Boyle et al,¹⁴ and we also found that older, heavier individuals need a slightly higher dose on average than in the package insert. Zao et al. found that of 111 pediatric patients, 66% of the patients achieved a C_ave within the prespecified target range after the first dose.⁴⁹ They also noted that existing algorithms may be less applicable in very overweight or very young populations, both of which were represented in our cohorts (Table 2).

However, we must emphasize that targeted exposures may need to be more tailored than this broad range, and it is impossible to know beforehand whether a patient lies within the 24–33% who will be outside the therapeutic range. For this drug, TDM clearly remains mandatory.

The major limitation of our project is the general availability of BestDose. We are looking at ways to possibly make the software commercially available as a web-based clinical service supported by expert review. However, at this time, we are happy to discuss use of BestDose on an individual basis. As for other limitations, one can always criticize the sample size of a pharmacokinetic study. Because traditional sample size calculations are based on comparisons between groups, proposed sample size calculations for Phase I studies are based on estimation of parameter values with a tolerable imprecision, e.g. 95% confidence interval of the mean within ±20%.⁵⁰ The parameters in our model are estimated with <10% imprecision. Furthermore, we have validated sufficient diversity of the study population by testing the model in as many ways possible: internally by simulation methods, externally on additional cohorts, and in a blinded fashion to calculate dosages.

Conclusion

We developed a population PK model for busulfan in pediatrics with an original methodology-based limited sampling strategy using only two points (peak and trough). We have validated its ability to predict concentrations in independent cohorts of patients, as well as to accurately and precisely calculate busulfan dosages to achieve desired concentrations when used in the BestDose software.