The application of a mathematical model linking structural and functional connectomes in severe brain injury

Abstract

Following severe injuries that result in disorders of consciousness, recovery can occur over many months or years post-injury. While post-injury synaptogenesis, axonal sprouting and functional reorganization are known to occur, the network-level processes underlying recovery are poorly understood. Here, we test a network-level functional rerouting hypothesis in recovery of patients with disorders of consciousness following severe brain injury. This hypothesis states that the brain recovers from injury by restoring normal functional connections via alternate structural pathways that circumvent impaired white matter connections. The so-called network diffusion model, which relates an individual's structural and functional connectomes by assuming that functional activation diffuses along structural pathways, is used here to capture this functional rerouting. We jointly examined functional and structural connectomes extracted from MRIs of 12 healthy and 16 brain-injured subjects. Connectome properties were quantified via graph theoretic measures and network diffusion model parameters. While a few graph metrics showed groupwise differences, they did not correlate with patients' level of consciousness as measured by the Coma Recovery Scale — Revised. There was, however, a strong and significant partial Pearson's correlation (accounting for age and years post-injury) between level of consciousness and network diffusion model propagation time (r = 0.76, p < 0.05, corrected), i.e. the time functional activation spends traversing the structural network. We concluded that functional rerouting via alternate (and less efficient) pathways leads to increases in network diffusion model propagation time. Simulations of injury and recovery in healthy connectomes confirmed these results. This work establishes the feasibility for using the network diffusion model to capture network-level mechanisms in recovery of consciousness after severe brain injury.

Highlights

• •A “functional rerouting” hypothesis in recovery from brain injury is tested.
• •The connectome-based network diffusion model measures functional rerouting.
• •Recovery in severe brain injury correlates with a network diffusion model parameter.
• •Simulation in healthy connectomes independently validates the results in patients.

1. Introduction

Subjects with severe brain injury suffer widespread connectivity loss between brain regions, at times resulting in disorders of consciousness (DOC). Recovery from DOC can occur over many months or years post-injury (Lammi et al., 2005, Sidaros et al., 2008, Voss et al., 2006) in a variety of etiologies (Estraneo et al., 2010, Luauté et al., 2010, Nakase-Richardson et al., 2012), but the process and mechanisms of this process are poorly understood. It is, however, increasingly becoming clear that recovery is largely dependent on recruitable cerebral reserve (Schiff, 2010). One interpretation of cerebral reserve could be in the reorganization of neuronal connections via synaptogenesis and axonal sprouting (Bütefisch, 2006, Frost et al., 2003, Nudo, 2006, Wang et al., 2010) that is known to occur in post-injury recovery. One interpretation of cerebral reserve is the concept of cerebral reorganization or plasticity, i.e. changes in the brain's functional connections/activation patterns in response to changes in the environment or damage/disease, which has been proposed in various forms by previous work (Moretti et al., 2012, Nithianantharajah and Hannan, 2009, Schoonheim et al., 2015). However, details of how the brain performs network-level reorganization in recovery from injury remain unknown. Here, we consider the implications of functional reorganization in the context of structural and functional connectomes, or whole-brain networks. Neuroimaging methods offer the ability to measure the brain's structural and functional connectivity networks, i.e. connectomes, which in turn allows insight into network-level changes underlying disorders of and recovery of consciousness.

Studies using diffusion (dMRI) and/or functional (fMRI) imaging modalities (Cabral et al., 2013, Damoiseaux and Greicius, 2009, Fox and Raichle, 2007) have allowed investigation of the brain's structural connectivity (SC) and functional connectivity (FC) networks (Bullmore and Sporns, 2009, Sporns et al., 2004) and their sensitivity to clinical state, disease and behavioral variability (Calhoun et al., 2011, Cocchi et al., 2014, Griffa et al., 2013, Lo et al., 2010). In patients with DOC, numerous studies have used fMRI to provide evidence of language and cognitive abilities and establish functional network reserve (Laureys and Schiff, 2012). Resting state fMRI analyses in DOC patients have shown functional disconnections within the default mode network that appear to correlate with clinical severity (Boly et al., 2012, Soddu et al., 2011). Many times DOCs result from traumatic brain injury (TBI), which has been studied extensively using network approaches; see Sharp et al. (2014) for a review. Using a graph theory approach, TBI has been shown to impair small-world topology (Pandit et al., 2013) normally associated with healthy brain networks (Bassett and Bullmore, 2006, Watts and Strogatz, 1998). Differences between SC and FC graph network metrics between TBI and controls and correlations between network metrics with cognitive abilities have been shown (Caeyenberghs et al., 2013, Caeyenberghs et al., 2012, Castellanos et al., 2011). In addition, the location of injury in TBI with respect to influence on the SC network metrics has been related to cognitive impairment (Kuceyeski et al., 2011), while recovery from TBI has been shown to correlate with a gradual return to normal FC network metrics (Nakamura et al., 2009).

One important question that is only beginning to be addressed is whether and how the structural and functional networks are related in both health and pathology. Recent work has focused on predicting FC networks from SC networks and vice-versa in normal subjects in order to better understand their relationship (Cabral et al., 2011, Das et al., 2014, Deco et al., 2012, Fernández Galán, 2008, Honey et al., 2009, Messé et al., 2014, Woolrich and Stephan, 2013). One of the most recent developments in this area (Abdelnour et al., 2014) presented a connectome-based mathematical model that assumes functional activation spreads along structural connections like a diffusive agent, similar to the model presented in Fernández Galán (2008). The main difference between the two is that the former uses the Laplacian of the structural connectivity network, while the latter uses the structural connectivity network directly. Abdelnour et al. (2014) showed that this simple linear model resulted in predictions of FC from the SC networks that were comparable to or better than predictions from both the model in Fernández Galán (2008) and more complicated non-linear models. The model detailed in Abdelnour et al. (2014)) enables novel quantification of the relationship between structural and functional connectomes, which may relate more to an individual's behavior than individual analysis of either connectome.

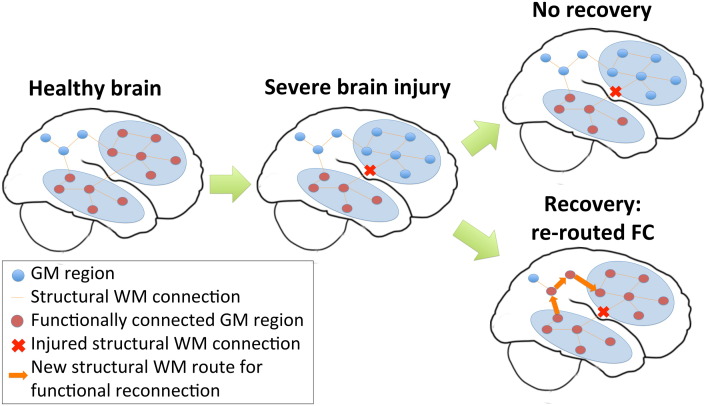
In this work, we conjecture that recovery from brain injury could entail re-establishment of normal FC without requiring a concurrent change in the SC network. A few reports of positive changes in SC related to recovery from brain injury exist (Fernández-Espejo et al., 2011, Sidaros et al., 2008, Voss et al., 2006), however one recent study showed long-term impairment of WM structures 5 years after severe brain injury even in the presence of recovery (Dinkel et al., 2014). FC network improvements are more widely reported in the context of recovery after brain injury (Demertzi et al., 2014, Laureys and Schiff, 2012, Sharp et al., 2011, Soddu et al., 2011, Vanhaudenhuyse et al., 2010). In a study of chronic TBI patients, Palacios and co-authors found increases in FC in frontal areas compared to healthy controls that was positively associated with better cognitive outcomes and negatively associated with a measure of SC (Palacios et al., 2013). They concluded that altered SC between brain regions could be in part compensated for by increases of FC. Along this line of reasoning, we further speculate that this return to normal/above-normal levels of FC, made possible by the plasticity of the brain's functional connections, may be performed within the confines of a possibly further degenerating post-injury SC network. Specifically, we propose a network-level “functional rerouting” hypothesis that states recovery from injury depends on the brain's ability to reestablish FC by circumventing impaired SC via alternate intact white matter pathways (see Fig. 1). It is important to note that functional rerouting via alternate white matter pathways only requires synaptic switching at the local circuit level; no physical changes to extant white matter projections are required. Furthermore, we hypothesized that the connectome-based network diffusion model in Abdelnour et al. (2014)) could be used to capture and quantify this network-level functional rerouting mechanism. While the network diffusion model was used in a previous study to predict FC from SC, we instead apply it here to obtain a measure of the relationship between the FC and SC. This measure, which we refer to as model propagation time, represents the amount of SC that is used to recapitulate the observed FC, i.e. “network depth”. We expected that our proposed functional rerouting mechanism that utilizes alternate, and presumably less efficient, structural pathways would increase propagation time. Higher propagation time in this context means the existence of intact SC routes whose recruitment by the brain would result in more accurate recapitulation of the observed FC. It follows that longer propagation times should be positively correlated with better recovery measures.

Fig. 1.

Functional rerouting hypothesis. A schematic of the hypothesized mechanism of injury and recovery in severe brain injury.

To test this hypothesis, we applied the network diffusion model to both severe brain injury patient connectomes and simulated injury and recovery networks derived from healthy connectomes. We compared the strength of the relationships between the network diffusion model's propagation time with those of standard graph theoretical measures of the FC and SC networks. Next we investigated the functional rerouting hypothesis at a region-pair level, i.e. at the level of connectivity between pairs of regions. If region-pair functional rerouting were true, more normal FC between pairs of regions with impaired SC should correspond to better recovery. Therefore, we identified region-pairs with significantly impaired SC in our severe brain injury cohort and tested for correlations between measures of recovery and the amount of FC, compared to control FC, between these regions.

2. Materials and methods

2.1. Data

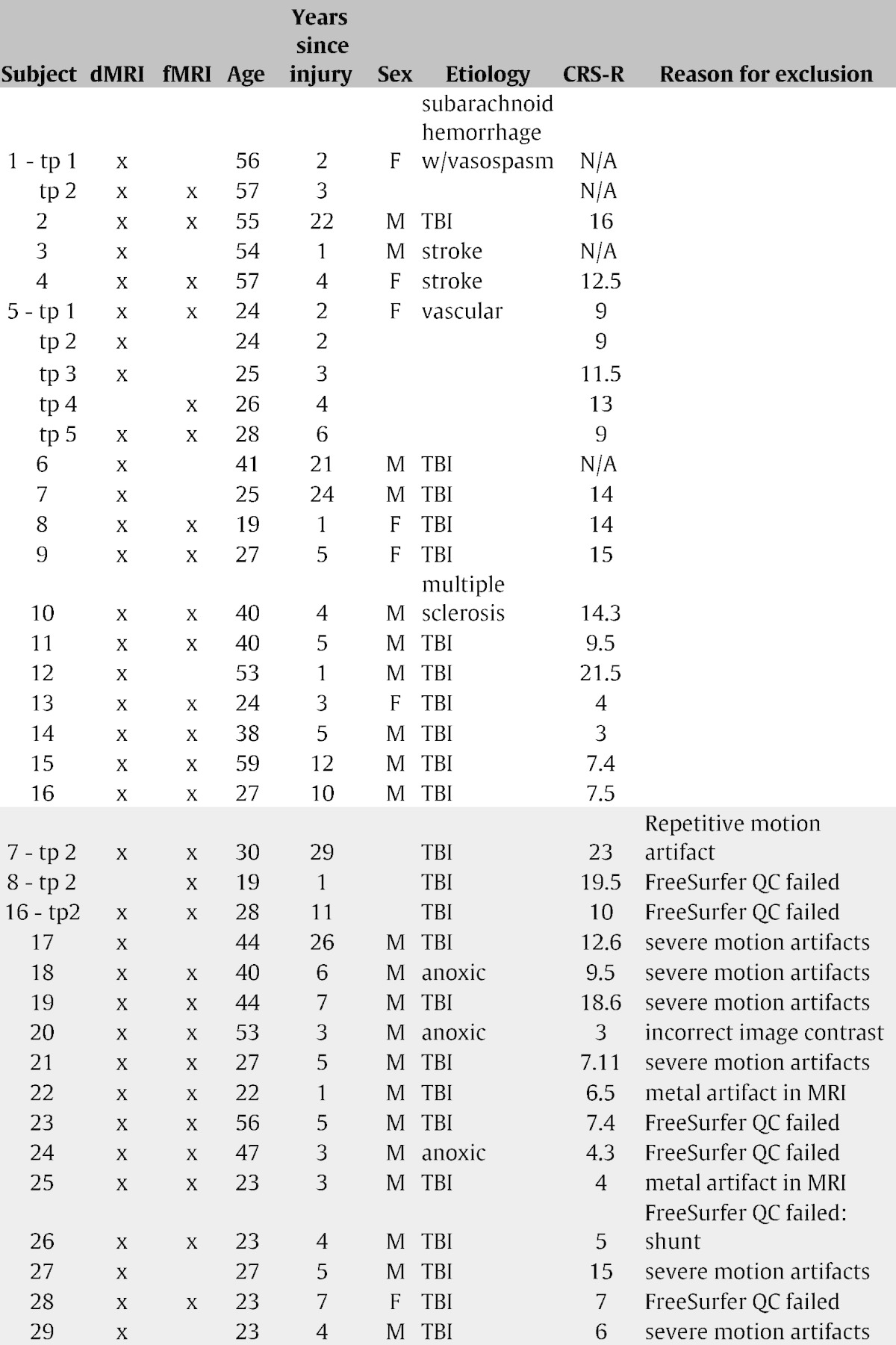
The Institutional Review Board of Weill Cornell Medical College approved all experiments (IRB # 0309006330A028 and IRB # 0903010274). Written informed consent was obtained from the healthy control volunteers and the legally authorized representatives of the subjects with severe brain injury. Data was collected from 12 normal controls (9 male, 34.8 ± 11.6 years) and 29 subjects (22 male, 37.6 ± 13.5 years). Some patients had data collected at multiple time points; in total there were 37 sets of data. Some patients were excluded on the basis of imaging artifacts or failures in post-processing; 21 sets of scans from 16 subjects were used in the final analysis (10 males, age: 39.9 ± 14.1 years, time since injury: 7.8 ± 8.1 years), see Table 1 for details. Consciousness level was assessed with the Coma Recovery Scale — Revised test that measures operationally-defined behavioral responses, including auditory, visual, motor, oromotor, communication and arousal (Giacino et al., 2004). No subjects that had CRS-R scores were known to have locked-in syndrome, which can result in an underestimation of level of consciousness due to an inability to respond to motor commands. Resting-state fMRI, dMRI and anatomical MRI scans were collected at the same time as the CRS-R test was administered.

Table 1.

Demographics and image information for the patient population. Excluded scans are indicated with a gray background. Abbreviations: TBI (traumatic brain injury), QC (quality control), tp (time point).

2.1.1. General Electric MRI acquisition

All but one of the scans were acquired on a 3.0 Tesla General Electric Signa Excite HDx (Waukesha, WI) clinical MRI system with an eight-channel head receive-only coil. FMRI pulse sequences consisted of an echo-planar gradient-echo sequence with repetition time TR = 2 s, echo time TE = 30 ms, flip angle = 70°, axial field of view 24 cm, slice thickness = 5 mm, matrix size = 64 × 64 × 28, 180 time samples. DMRI scans were obtained using a spin-echo diffusion tensor pulse sequence with one T2-weighted image, 55 diffusion-weighted images evenly distributed on a sphere with b = 1000 s/mm², minimum TE, TR = 13.5 s, field of view = 23 cm, slice thickness = 1.8 mm, matrix size = 128 × 128 × 72 (yielding isotropic resolution), reconstructed with zero filling to 256 × 256 × 72, covering the whole brain. Anatomical imaging was performed with an axial 3D-IRFSPGR sequence (BRAVO) with inversion time = 400 ms, TR = 8.864 ms, TE = 3.524 ms, flip angle = 13°, axial field of view = 24 cm, slice thickness = 1.2 mm, matrix size = 256 × 256 × 120, parallel imaging acceleration factor = 2.

2.1.2. Seimens MRI acquisition

One set of scans were acquired on a 3.0 Tesla Seimens TIM Trio (Erlangen, Germany) clinical MRI system with a 12-channel head coil. FMRI pulse sequences consisted of an echo-planar gradient-echo sequence with repetition time TR = 2 s, echo time TE = 30 ms, flip angle = 90 degrees, axial field of view 24 cm, slice thickness = 4 mm, matrix size = 64 × 64 × 32, 180 time samples. DMRI scans were obtained using a spin-echo diffusion tensor pulse sequence with one T2-weighted image (2 averages), 30 diffusion-weighted images evenly distributed on a sphere with b = 1000 s/mm² (2 averages), TE = 91 ms, TR = 9.5 s, field of view = 24 cm, slice thickness = 2.5 mm, matrix size = 96 × 96 × 68 (yielding isotropic resolution), covering the whole brain. Anatomical imaging was performed with a sagittal 3D-MPRAGE sequence with inversion time = 900 ms, TR = 1900 ms, TE = 2.43 ms, flip angle = 9°, sagittal field of view = 25 × 31 cm, slice thickness = 1.2 mm, matrix size = 208 × 256 × 144, yielding an isotropic resolution of 1.2 mm.

Ten out of the 12 healthy controls had both fMRI and dMRI. Out of the 21 sets of scans that were used, 13 had both dMRI and fMRI, 7 had dMRI only and one had fMRI only. Out of the 13 sets of scans with both dMRI and fMRI, 12 had associated CRS-R scores.

2.2. Network construction

Gray matter and white matter tissues were classified and the gray matter further parcellated into 86 anatomical regions of interest using the semi-automated FreeSurfer software (Fischl and Dale, 2000). Manual control points that assist the software in tissue segmentation were used when necessary. Cortical and subcortical parcellations were then used in the construction of the SC and FC networks.

2.2.1. Functional connectivity networks

The fMRI data was preprocessed using the CONN toolbox (http://www.nitrc.org/projects/conn) (Whitfield-Gabrieli and Nieto-Castanon, 2012) within Statistical Parametric Mapping 8 (SPM8) in Matlab. Spatial processing of the data (SPM8) included slice-timing correction, realignment, coregistration and/or normalization, and spatial smoothing before segmentation of gray matter, white matter and cerebrospinal fluid. The toolbox implemented the CompCor method for removal of cardiac and respiratory artifacts (Behzadi et al., 2007). The toolbox also performs a rigorous regression of head motion artifacts that does not regress out global signal, allowing for interpretation of anti-correlations (Chai et al., 2012). Band-pass filtering (0.008–0.09 Hz) of the residual blood oxygen level-dependent (BOLD) contrast signal was also conducted. The preprocessing steps were implemented using the ‘Simult’ option in the toolbox to simultaneously regress and band-pass filter, a process which has been shown to reduce nuisance-related variability (Hallquist et al., 2013). The preprocessed data was then co-registered from rsfMRI space to FreeSurfer's cortical and subcortical parcellations using SPM8's normalization algorithm and the spatial signal average within each region of interest was computed for each time point. The pairwise FC between two regions was defined as the Pearson correlation coefficient between these time-dependent regional signal averages.

2.2.2. Structural connectivity networks

Eddy current and motion correction was performed on the dMRI images within FSL. Orientation distribution function construction and probabilistic fiber tracking was performed as previously described (Kuceyeski et al., 2013, Kuceyeski et al., 2011, Raj et al., 2012). In short, orientation distribution functions were constructed using the approach introduced in Raj et al. (2011) that uses spatial information to regularize the estimation. The probabilistic fiber tracking algorithm introduced in Iturria-Medina et al. (2005) was used. This algorithm considers tissue probability maps as well as diffusion orientation functions in a Bayesian manner to trace likely white matter fibers. Fiber tracing stopped when the track entered a voxel that was not in the white matter mask (from FreeSurfer) or when the angle between steps exceeded pi/3. The matrix defining the pairwise SC strengths had entries that were simply the count of fibers starting in one gray matter region and ending in another.

2.3. Global network metrics

Before computing global network metrics, non-significant (p > 0.05) entries in the FC matrices were replaced with zero. Correction for multiple comparisons over all entries in the FC matrices for each individual was performed using the linear step-up procedure for false discovery rate (FDR) correction of p-values introduced in Benjamini and Hochberg (1995), see Appendix A.1 for details. The FC matrices were then converted to absolute values and divided by the mean value for inter-subject normalization. The SC matrices were divided by the sum of the surface area of the two regions, as in the Anatomical Connection Density (ACD) metric proposed in Iturria-Medina et al. (2008). Normalization by the sum of region-pair surface area allows correction for different sized regions that would have proportionally more/less number of seeds in the tractography algorithm. It also adjusts the patient SC to account for any damage-related atrophy in the gray matter regions, allowing for better comparison of graph theoretical measures, since the normalized connection strength is a measure of amount of connectivity proportional to the amount of gray matter that remains. Global metrics of characteristic path length, efficiency, clustering coefficient and modularity were calculated for the weighted SC and FC networks using the Brain Connectivity Toolbox (Rubinov and Sporns, 2010). Small-world index s was calculated using the following equation:

$$s=\frac{c/{\bar{c}}_{\mathit{rand}}}{p/{\bar{p}}_{\mathit{rand}}}$$

where c and p are the clustering coefficient and characteristic path length of the individual's network. The variables ${\bar{c}}_{\mathit{rand}}$ and ${\bar{p}}_{\mathit{rand}}$ are the mean of the clustering coefficient and characteristic path length values obtained by randomly permuting the original connectivity network's edges 100 times. Small-world networks are defined as those that have s > 1.

Group-wise differences in global SC and FC network measures were assessed with permutation testing; correlations with CRS-R scores were performed using partial Pearson's correlation accounting for age and time since injury. Due to the small sample size, robustness of the correlation results was assessed via calculation of the 95% bias corrected and accelerated confidence intervals using bootstrapping (resampling with replacement) (DiCiccio and Efron, 1996). Our hypotheses were that patient SC and FC networks would have longer characteristic path length, lower efficiency, higher clustering coefficient and modularity and lower small world index than normal controls as a result of fewer or weaker pairwise connections that arise from pathology. In line with our proposed network-level functional re-routing mechanism, we hypothesized that 1) correlations exist between FC network metrics and a patient's level of consciousness as measured with the CRS-R score, specifically, the closer a patient's FC network metrics were to healthy ranges, the more normal their CRS-R and 2) no correlations exist between CRS-R and SC network measures.

2.4. Network diffusion model: Measuring the relationship between FC and SC

The model for relating FC and SC is based on the assumption that FC can be described as the diffusion of neuronal activity within the SC network (Abdelnour et al., 2014). The model assumes that the diffusing quantity representing functional activation undergoes a random walk on a graph representing the strength of structural connections. Thus, the rate of change of activation at any node i, denoted x_i, is related to the difference between the level of activation at that node and its connected neighbors, relative to the sum of outgoing connections of each node (node degree). That is,

$$\frac{d{x}_i\left(t\right)}{\mathit{dt}}=\frac{\beta }{\sqrt{{\delta }_i}}{\displaystyle {\sum }_{j}j{c}_{\mathit{ij}}\frac{1}{\sqrt{{\delta }_j}}{x}_j\left(t\right)-x_i\left(t\right)}$$ (1)

where the coefficients c_ij are the elements of the SC matrix C, ${\delta }_i={\displaystyle {\sum }_j{c}_{\mathit{ij}}}$ is the degree of node i and β is the rate constant of the exponential decay (see the original paper for construction details). This relationship can be easily extended to the entire brain network x(t)

$$\frac{d\mathit{x}\left(t\right)}{\mathit{dt}}=-\beta \mathcal{L}\mathit{x}\left(t\right)$$ (2)

where $\mathcal{L}$ is the well-known network Laplacian. The network Laplacian can take different forms depending on the user's choice of normalization factors. Our choice of normalization by node degree as in Eq. (1) results in the Laplacian $\mathcal{L}$ = I − Δ^− 1/2CΔ^− 1/2, where ∆ is the diagonal matrix with entries δ_i, as in Abdelnour et al. (2014). We chose to normalize by node degree in order to control for different sized regions in the gray matter parcellation. Therefore, the matrix C in the calculation of the Laplacian is the SC matrix based on streamline count. Eq. (2) has the explicit solution for a given initial configuration, or activation pattern, x₀:

$$\mathit{x}\left(t\right)=exp\left(-\beta \mathcal{L}t\right){\mathit{x}}_0$$ (3)

Let A be the measured FC matrix and $\widehat{\mathrm{A}}$ be the predicted FC matrix. It was assumed that the estimated FC of region i with all other regions at time t is the evolution on the graph of an initial configuration involving only region i, i.e. ${\widehat{a}}_i\left(t\right)=exp\left(-\beta \mathcal{L}t\right){\mathrm{e}}_i$ where e_i is the unit vector in the ith direction. If we collect all regions/unit vectors together, we obtain $〈{\widehat{a}}_1\left(t\right)|\cdots |{\widehat{a}}_1\left(t\right)〉=exp\left(-\beta \mathcal{L}t\right)〈{\mathrm{e}}_1|\cdots |{\mathrm{e}}_N〉$, or

$$\widehat{\mathrm{A}}\left(t\right)=exp\left(-\beta \mathcal{L}t\right)$$ (4)

which gives the prediction for the measured FC matrix A. The accuracy of this prediction depends on the time t at which the model is evaluated. We do not have an empirical value for β, so we absorb it into the estimation (by setting it to 1) and allowing t to vary. For example, $\widehat{A}\left(0\right)=\mathit{I}$ and $\widehat{A}\left(\infty \right)=D$, where D = u₀u₀^T is the steady state solution, i.e. the outer product of the eigenvector of $\mathcal{L}$ that corresponds to the eigenvalue of 0. Between those extremes, a range of functional networks exists. Therefore, the value of t that gives the maximal correlation between the subject's measured FC and the model's predicted FC (which is based on the same subject's SC) must be calculated. We called this optimal t the model propagation time, denoted t_m. More formally, model propagation time is the t that maximizes

$$\mathrm{c}\left(t\right)=\frac{\mathit{cov}\left(A,\widehat{A}\left(t\right)\right)}{{\sigma }_A{\sigma }_{\widehat{A}\left(t\right)}}$$ (5)

Note that in Eq. (5), A and $\widehat{\mathrm{A}}$ are vectorized versions of the original matrices that 1) include only those regions with non-zero measured FC and 2) exclude the values on the diagonal. The diagonal was removed because this is a somewhat artificial value in the observed FC network (always 1). The other network diffusion model parameter, called model correspondence, is the maximal correlation between the model's predicted FC and measured FC, i.e. c(t_m). To summarize, the process above uses the network diffusion model to estimate an individual's FC from their SC and then finds the t that gives the best agreement of the model's estimated FC with the individual's observed FC (model propagation time). The way in which we interpret propagation time here is as a measure of how much of the SC is used to recapitulate the observed FC. Note: the network diffusion model does not explicitly consider axonal conduction delays or the effect of fiber lengths. However, in the frequencies governed by fMRI (0.01–0.2 Hz), axonal conduction delays cannot be detected and therefore do not materially affect the observed relationship between FC and SC. The most plausible delay parameters (e.g. 10 m/s conduction velocity, 10 m/s membrane capacitance) are too fast to show any effect in this very low frequency range, whose characteristic time constant will be around 5–100 s. It must also be noted that model propagation time does not represent physical conduction speeds through axons, but rather the ability of information transference via rewired routes in the brain's connectome. This time is unit-less, and should not be confused with actual time.

Differences between normal and patient groups in the two model parameters, model correspondence and model propagation time, were assessed with permutation testing. Partial Pearson's correlations, accounting for age and time since injury, were calculated between the two model parameters and the CRS-R score. Again, robustness of the correlation results was assessed via calculation of the 95% bias corrected and accelerated confidence intervals using bootstrapping (resampling with replacement) (DiCiccio and Efron, 1996). We hypothesized that model propagation time would be positively correlated with CRS-R scores (larger propagation time = better recovery) and that model correspondence would be positively correlated with CRS-R scores (larger correspondence = better recovery).

2.5. Investigating FC between region-pairs with impaired SC

We began by investigating which structural connections were more susceptible to injury in patients. We calculated the average fiber length of the connecting white matter streamlines for each region-pair that had a non-zero SC (N = 963). We defined non-zero SC as those region-pairs that had a non-zero median over the normal groups' structural connectivity matrices, thus reducing noise associated with inconsistent/spurious connections. A Wilcoxon rank-sum test was performed on each pairwise non-zero entry in the SC network based on streamline count (see reasoning below) to quantify group-wise SC impairment. The resulting rank sum was correlated with average fiber length using Spearman's rho, due to non-normality of the quantities. Next, we defined impaired SC as those non-zero pairwise connections that had significantly lower SC in the patient group versus the normal group (p < 0.05, corrected) as identified using the Wilcoxon rank-sum test described above. P-values were FDR-corrected for 963 multiple comparisons using the linear step-up procedure introduced in Benjamini and Hochberg (1995), see Appendix A.1 for details. We created a histogram of total SCs and impaired SCs, divided by type (cortico-cortical, cortical-subcortical, and cerebellar/subcortical-subcortical). For each patient, we then calculated their mean z-score of FC (compared to the normal controls) between the impaired SCs and the unimpaired SCs. This mean z-score captures the extent of each patient's amount of FC, compared to normal levels, between impaired and unimpaired SC. We then calculated the correlation between the two measures of amount of FC compared to normal (impaired and unimpaired) and CRS-R scores using partial Pearson's correlation. If our functional rerouting hypothesis is true, there should be a positive correlation between the measures, particularly for the impaired SCs. Since the impaired SCs were identified at a group-wise level, an individual's strength of SC between impaired connections may also influence their FC. Therefore, we accounted for an individual's amount of SC in the impaired connections by controlling for sum of SC in the partial correlation (as well as age and time since injury). Robustness of the correlation results was assessed via calculation of the 95% bias corrected and accelerated confidence intervals using bootstrapping (resampling with replacement) (DiCiccio and Efron, 1996).

For this particular analysis, we chose to use the streamline count matrices (not normalized by sum of region-pair surface area) for the following reason. If a patient had an impaired white matter connection and therefore a lower number of streamlines between two given gray matter regions (smaller numerator in the surface area normalized SC matrix), they should have significantly impaired SC when compared to normal controls. However, if the gray matter regions this white matter tract connected were also atrophied, it would mean a smaller denominator in the surface area normalized SC matrix. Decreases in both the numerator and denominator of the surface area normalized SC matrix could cancel each other out and possibly result in structural connection strength that was not different from healthy controls. Therefore, we chose to compare directly the streamline count matrices for the between group comparison described in this section.

2.6. Correction for multiple comparisons and bootstrapping technique

We carefully controlled for all of the comparisons performed in this study. In total, 31 statistical tests based on FC and SC networks were performed, i.e. groupwise differences of 7 FC and 7 SC network metrics, correlations with CRS-R scores and 8 FC and 8 SC network metrics, and one correlation of SC impairment and fiber length. All 31 p-values were grouped together and FDR-adjusted for multiple comparisons using the linear step-up procedure introduced in Benjamini and Hochberg (1995), see details in Appendix A.1.

We used bootstrapping (DiCiccio and Efron, 1996) to create empirical distributions for the correlations between the network metrics and recovery measures as follows. We resampled with replacement the data from the disorders of consciousness patients. That is, we produced a random sample of the indices k = 1, 2, …N, where N is the number of patients, and repeating indices was allowed. We then took the network metrics/model parameters and corresponding CRS-R scores from the subjects with that random sample's indices and recalculated their correlation. We repeated this resampling process 5000 times. The result is an empirical bootstrapped distribution that approximates the true underlying distribution of the actual correlation. From the empirical distribution, we can calculate summary statistics (median) and confidence intervals. If the confidence interval does not include 0, then we can be even more confident that the correlation was significantly non-zero. If the original correlation is similar to the mean of the bootstrapped sample, then we can be more confident that the original correlation's value is not as dependent on the original population makeup.

2.7. Simulating injury and recovery

We constructed a simulation to test the network diffusion model behavior under controlled conditions. “Injury” was simulated with normal subjects' connectomes by removing selected pairwise SC and decreasing the corresponding FC by a percent of the original value (100%, 75%, 50%, 25%). “Recovery” was simulated with normal subjects' connectomes by removing pairwise SC but leaving corresponding FC unchanged. In this simulated recovery, the brain has been structurally injured but, via some (un-modeled) mechanism, was able to fully restore normal FC. We performed random removal of SC, ranging from 0 to 80% of all pairwise connections with at least one non-zero connection in the group of healthy controls. Once we modified the networks, model correspondence and model propagation time parameters were recalculated. Results were recorded for each of the 10 normal controls over the varying levels of injury and recovery.

3. Results

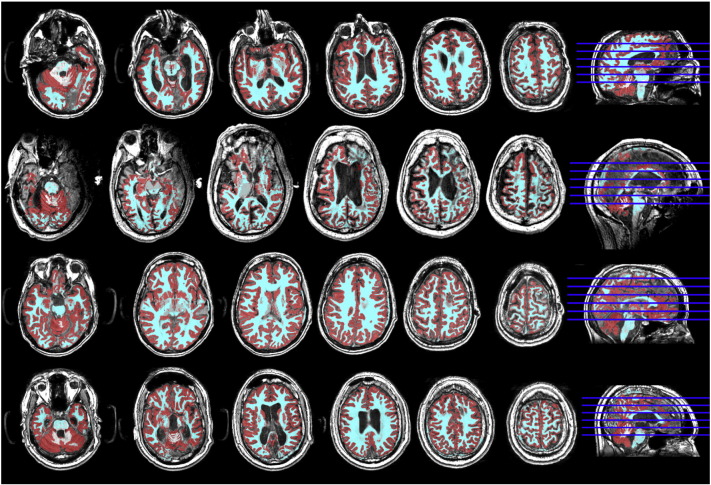
Segmentation and parcellation was checked carefully due to the high level of anatomical abnormalities in the data. Fourteen sets of scans were discarded due to segmentation errors in FreeSurfer or severe image artifacts (see Table 1). Fig. S1 gives representative examples of the segmentation results for four patients that were included in the analysis.

Fig. S1.

Image processing results: Examples of the tissue segmentation for the T1 scans of four severe brain injury subjects (red = gray matter and cyan = white matter).

3.1. Global network metrics

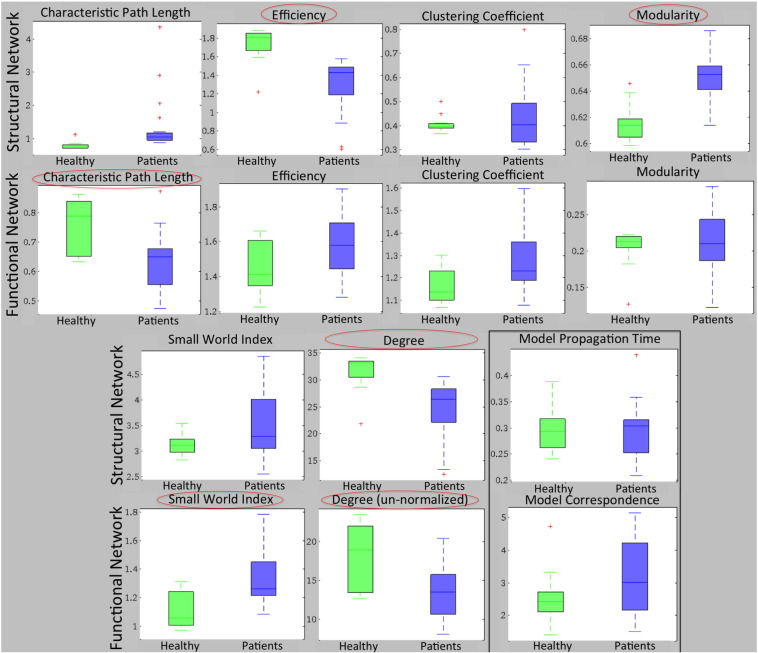
Boxplots of each of the six global network metrics are given for the SC (top rows) and FC (bottom rows) in Fig. 2, with the results of the statistical tests in Table 2. Metrics with significant differences after correction are circled. SC network modularity was higher in patients than in normal controls and efficiency and degree lower. FC network characteristic path length and un-normalized degree was smaller and small world index higher in patients than in normal controls. No network metrics had significant correlations with CRS-R scores; accordingly, all 95% bias corrected and accelerated CIs of the bootstrapped correlations included 0 (see Table 2).

Fig. 2.

Groupwise comparison of global network measures. Global network metrics for the SC and FC networks for normal controls (green) and patients (blue). Metrics with significant differences between groups (Benjamini-Hochberg FDR corrected) are circled. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Table 2.

List of measurements used and the results from the group-wise permutation test and correlations with a measure of consciousness response (CRS-R). All p-values, shown in parenthesis, have been False Discovery Rate adjusted for 31 multiple comparisons (30 tests in this table and one test for correlation between SC impairment and fiber length, shown in Fig. 5A) using the linear step-up procedure, see Appendix A.1 for details. The final column contains the 95% bias corrected and accelerated confidence interval (CI) for the correlations in the fourth column, calculated via bootstrapping (resampling with replacement).

List of measurements used and the results from the group-wise permutation test and correlations with a measure of consciousness response (CRS-R). All p-values, shown in parenthesis, have been False Discovery Rate adjusted for 31 multiple comparisons (30 tests in this table and one test for correlation between SC impairment and fiber length, shown in Fig. 5A) using the linear step-up procedure, see Appendix A.1 for details. The final column contains the 95% bias corrected and accelerated confidence interval (CI) for the correlations in the fourth column, calculated via bootstrapping (resampling with replacement).

Measurement Type	Metric	Group-wise test: patients-healthy	Correlations with CRS-R	95% CI of correlations with CRS-R
Structural network	Characteristic path length	2.23 (0.10)	0.095 (0.87)	[− 0.67. 1.00]
Efficiency	− 6.83 (2.5 × 10− 6)a	0.40 (0.34)	[− 0.71. 0.81]
Clustering coefficient	0.14 (0.93)	− 0.26 (0.58)	[− 0.79. 0.51]
Modularity	5.72 (3.5 × 10− 5)a	− 0.58 (0.16)	[− 0.88. 0.13]
Small world index	1.78 (0.16)	− 0.045 (0.93)	[− 0.77. 0.79]
Degree	− 5.57 (4.0 × 10− 5)a	0.22 (0.64)	[− 0.67. 0.79]
Functional network	Characteristic path length	− 2.80 (0.043)a	0.44 (0.31)	[− 0.28. 0.97]
Efficiency	1.95 (0.16)	− 0.42 (0.32)	[− 0.93. 0.36]
Clustering coefficient	2.40 (0.083)	− 0.59 (0.16)	[− 0.95. 0.22]
Modularity	0.68 (0.61)	− 0.19 (0.66)	[− 0.95. 0.48]
Small world index	3.06 (0.032)a	− 0.57 (0.16)	[− 0.96. 0.15]
Un-normalized degree	− 2.68 (0.050)a	0.48 (0.28)	[− 0.23. 0.95]
Model parameters	Model propagation time	1.36 (0.31)	0.76 (0.043)a	[0.40. 0.95]b
Model correspondence	0.0090 (0.99)	0.42 (0.32)	[− 0.67. 0.86]
z-Score of FC between region-pairs	Region-pairs w/intact SC	NA	0.30 (0.58)	[− 0.97. 0.91]
Region-pairs w/impaired SC	NA	0.67 (0.13)	[− 0.96. 0.91]

^aSignificant at level α = 0.05.

^bBootstrapped 95% bias corrected and accelerated confidence interval does not include zero.

3.2. Network diffusion model: Measuring the relationship between FC and SC

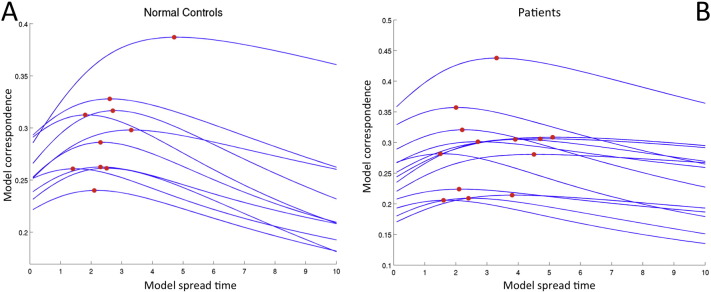
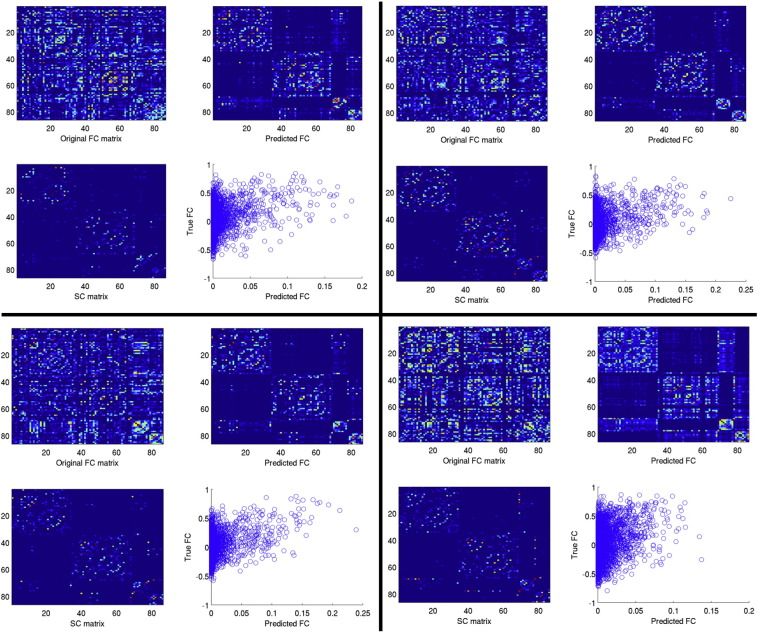
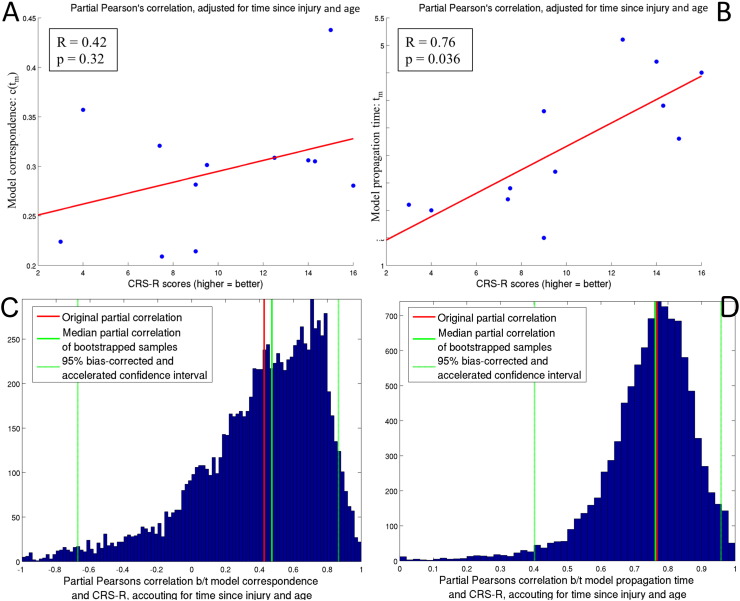
Curves representing measured versus predicted FC are displayed in Fig. S2, with panel A showing the normal controls and panel B showing the patients. The red dots are plotted at the point of model propagation time and model correspondence, i.e.(t_m, c(t_m)). Fig. S3, Fig. S4 illustrate the network diffusion model results for four normal controls and four patients, respectively, by displaying the observed FC, predicted FC at t_m, a scatter plot of the two and the SC network. Video S1 also shows a time progression of the predicted FC. As we can see from comparing the model correspondence values (Fig. S2 and Appendix A.2), the amount of observed FC captured by the model was similar to what was found in Abdelnour et al. (2014). For further examination of the quality of the network diffusion model's prediction, see Appendix A.2 and Fig. S5. The level of agreement varied across individuals, but was not very different between normal controls and patients. In fact, model correspondence was essentially the same between normal controls and patients (t = − 0.0090, p = 0.99). Model propagation time was higher in patients than in normal controls, but, again, the effect was not significant (t = 1.36, p = 0.31). Model correspondence was not correlated with CRS-R scores (r = 0.42, p = 0.32) while model propagation time was strongly and significantly correlated with CRS-R scores (r = 0.76, p = 0.043). Scatter plots with the line of best fit are given in Fig. 3 (panels A and B). Panels C and D show the original correlation value along with a histogram, median and 95% bias-corrected and accelerated CI of the bootstrapped samples. The median of the bootstrapped samples' correlation between CRS-R and model correspondence (0.76) was almost equal to the original value (0.76) and its 95% CI did not include 0.

Fig. S2.

Curves indicating the correlation, c(t), of the predicted FC versus true FC. One curve is plotted per subject for normal controls (Panel A) and patients (Panel B).

Fig. S3.

Examples of the network diffusion model's prediction for four different normal controls. The upper left panel is the true FC, upper right is the predicted FC, lower left is the SC and lower right is the correlation of predicted FC versus true FC.

Fig. S4.

Examples of the network diffusion model's prediction for four different patients. The upper left panel is the true FC, upper right is the predicted FC, lower left is the SC and lower right is the correlation of predicted FC versus true FC.

Fig. S5.

Histograms of the residuals for the network diffusion model's prediction of FC for the 10 normal controls (Panel A) and for the patients (Panel B).

Fig 3.

Network diffusion model parameters and consciousness. Panels A and B show the scatter plots of the CRS-R scores versus the diffusion model parameters for each individual. Partial Pearson's correlation, adjusting for time since injury and age, is given in the legend, along with the FDR-corrected p-value. Panels C and D give the bootstrapping (resampling) results for the correlations in Panels A and B, along with the original value (solid red line), bootstrapped median (solid green line) and 95% bias corrected and accelerated confidence interval (dashed green line). The results for model correspondence, c(t_m), are given in Panels A and C while the results for model propagation time t_m are given in Panels B and D. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

3.3. Investigating FC between impaired SC

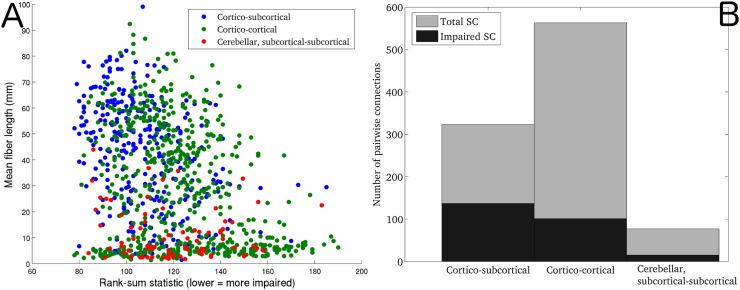
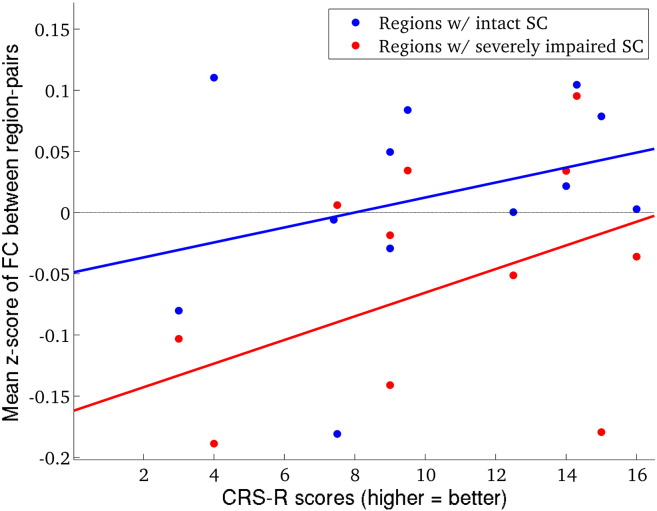
Unsurprisingly, a significant negative correlation was observed between pairwise average fiber length in normal controls and the rank sum statistic of pairwise SC in the patient versus normal group (r = − 0.32, p ≈ 0), see Fig. 4A. In this figure, the type of SC is indicated by color: blue indicates cortical-subcortical, green indicates cortico-cortical and red indicates subcortical-subcortical/cerebellar. This result indicates that the longer a white matter connection was, the more likely it was to be impaired in patients with severe brain injury. Fig. 4B shows a stacked barplot of the breakdown of the total and impaired SC by type. Fig. 5 shows the CRS-R scores plotted against the mean of the z-scores of FC between impaired SCs (red) and intact SCs (blue). A trend for positive correlation was found for region-pairs with impaired SC (r = 0.67, p = 0.13) but not for region-pairs with intact SC (r = 0.30, p = 0.58). This indicated that more normal FC between regions with impaired SCs tended to be associated with more normal consciousness response as measured with the CRS-R. CIs for both correlations included zero, indicating that these measures may not be very robust to population resampling. Unsurprisingly, the mean z-score of FC was closer to normal ranges in intact versus impaired SC.

Fig 4.

Fiber length and type vs. impairedness. (Panel A) Scatter plots of mean fiber length versus impaired-ness of each region-pair with significantly non-zero median in 10 normal controls (963 pairwise connections), color-coded by connection type (blue = cortico-subcortical, green = cortico-cortical and red = cerebellar, subcortical-subcortical). Correlations between mean fiber length and impairedness were calculated using Spearman's rho. (Panel B) Stacked bar-plots of SC divided by type. The total SC for each type is denoted with the gray bar, while the impaired SC are denoted with the black bar. (For interpretation of the references to color in this figure, the reader is referred to the web version of this article.)

Fig 5.

Amount of FC, compared to normal levels of FC, in impaired and intact SC. CRS-R scores versus mean z-score of FC between impaired SC, divided into intact SC (plotted in blue) and impaired SC (plotted in red). Correlations were calculated using partial Pearson's correlation, adjusting for time since injury and age. (For interpretation of the references to color in this figure, the reader is referred to the web version of this article.)

3.4. Simulated injury and recovery

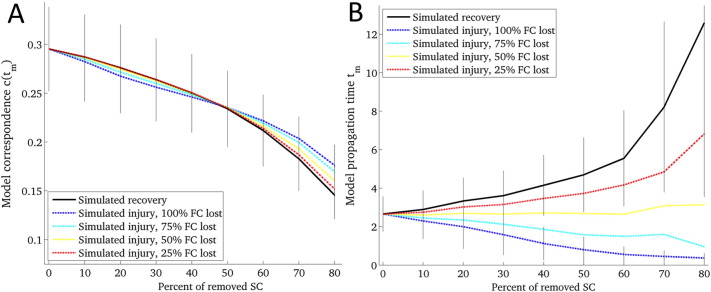
The results of the simulated injury and recovery are given in Fig 6. The x-axis shows the percent of removed connections, starting with the intact network and increasing until 80% of non-zero connections were removed. Panel A shows the model correspondence parameter while Panel B shows the model propagation time parameter. The parameters for injured brains are illustrated with the dashed lines that vary the percent of lost FC while the recovered brains are illustrated with the solid line. The solid vertical lines visualize the standard deviations over the 10 normal control subjects for the recovered and the fully injured case (100% FC lost).

Fig 6.

Simulated injury and recovery using the diffusion model. The behavior of model correspondence c(t_m) (Panel A) and model propagation time t_m (Panel B) under simulated recovery (solid line) and injury (dashed lines) in normal subjects (N = 10). The amount of lost FC in the injured case varied from 100% to 25%. The amount of injured SC varied from 0% (baseline) to 80% of all non-zero pairwise connections.

4. Discussion

We proposed and provided evidence for a network-level functional rerouting hypothesis in recovery from severe brain injury. This hypothesis stated that recovery from severe brain injury depends on re-routing of FC between regions with impaired SC, without requiring any underlying changes to the SC. Results from graph theory, applied to the SC and FC networks separately, suggested trends for recovery-related plasticity in the FC networks that was not present in the SC networks. Furthermore, we performed a novel joint analysis of the SC-FC relationship using a recently developed network diffusion model. The network diffusion model's propagation time showed a strong positive relationship with recovery that exhibited robustness over data resampling. Finally, we validated our results from patient data by analyzing simulated injured and recovered networks. Below we describe each result in detail, first covering global graph metrics, then the joint analysis of SC and FC using the network diffusion model, and finally the simulated injury and recovery.

4.1. Graph theoretical measures

While positive changes in SC in the context of recovery from brain injury have been shown in a few papers (Fernández-Espejo et al., 2011, Sidaros et al., 2008, Voss et al., 2006), FC network improvements related to recovery are more often reported (Demertzi et al., 2014, Laureys and Schiff, 2012, Sharp et al., 2011, Vanhaudenhuyse et al., 2010). In a study of subjects most similar to ours, Crone and colleagues (Crone et al., 2014) observed lower global FC modularity in patients versus controls while characteristic path length and efficiency were not significantly different between the two groups. In addition, they showed that CRS-R scores were moderately correlated with the AUC values of clustering coefficient in right middle frontal gyrus and the frontal pole (r = 0.40 and 0.29, respectively). Pandit et al. (Pandit et al., 2013) found reduced overall FC, longer characteristic path lengths and reduced efficiency in patients versus normal controls, however these patients had only mild to moderate brain injury and did not have DOC. In a study where subjects were administered propofol, which disrupts long-range FC and induces loss of consciousness, FC networks had increases in average path length, clustering coefficient and modularity (Lee et al., 2013). They concluded that the topology of the network, rather than the strength of connections, was more closely related to states of consciousness. This finding was echoed in (Achard et al., 2012), where it was shown that while global FC network metrics did not differ between normal controls and comatose subjects, their hubs were radically reorganized in the acute phase after injury. These varying and at times divergent findings in the existing literature are most likely a result of the heterogeneity of the populations studied, noise in the imaging data and complexity of the relationship between the brain's networks and consciousness.

We hypothesized that the group-wise differences observed in the SC network measures are a partial result of the damage to or loss of long-range connections typically affected in brain injury, e.g. thalamo-cortical (Adams et al., 2000, Crone et al., 2014) or callosal connections (Gentry et al., 1988, Rutgers et al., 2008), an observation that was reflected in our data (see Fig 4). This impairment of long-range connections that typically connect disparate clusters of highly connected nodes leads to an increase in segregation of the SC network and a decrease in efficiency. We hypothesize that the seemingly inconsistent results of the FC networks are due to an increase of FC within highly connected sub-networks of short-range connections that may occur in both injury and under our hypothesized network-level mechanism of recovery in the patient group, leading to significant group differences. None of the structural or functional graph network metrics were significantly correlated with CRS-R. The FC network metrics had higher magnitude correlations with CRS-R scores than the SC network metrics. The directions of the correlations indicate the closer a patient's FC network measures were to the normal group, the higher that patient scored on the CRS-R. This finding reflects the gradual return to normal in the FC network observed previously (Nakamura et al., 2009). These findings are also in line with our hypothesis that recovery depends on re-routing of FC between regions with impaired SC, without any underlying improvements in the SC. In fact, a recent study showed losses of white matter integrity in the two years after severe traumatic brain injury, which were still present at 5 years after injury, even in those patients that may have improved functionally (Dinkel et al., 2014). If this were the case, then SC network measures would not be as related to a person's longitudinal outcomes as would their FC network measures; this was exactly in line with our results. These observations highlight the critical role of FC network plasticity in recovery from brain injury.

We did not investigate the relationship of regional FC or SC measures with CRS-R scores for many reasons. First, regional measures are much more sensitive to the noise introduced at each step in the acquisition and post-processing pipeline (see Limitations) than global measures. Second, while there may be regions that are more important to consciousness than others, we believe that there may be a more robust relationship with global measures of connectivity, as consciousness requires the proper functioning of distributed networks. In fact, in two post hoc analyses we investigated the relationship between CRS-R and FC/SC network degree at two non-global levels: 1) individual regions and 2) 8 functionally-defined resting-state subnetworks defined in (Yeo et al., 2011). First, we calculated Pearson's partial correlation, accounting for time since injury and age, between CRS-R scores and node degree of FC and SC networks based on streamline count (see Section 2.5 for reasoning on using the streamline count versus the streamline count normalized by region surface area). We observe that out of all 86 × 2 = 172 correlations, none were significant after using Benjamini-Hochberg FDR correction for multiple comparisons, detailed in Appendix A.1. There were three partial correlations between CRS-R and structural network node degree that had 95% bias corrected and accelerated CIs that did not include zero - left pars opercularis, left insula and left thalamus. However, the first two of these correlations were negative (lower SC = better recovery) and thus are difficult to interpret. The last correlation in the list is interesting due to the role that the thalamus has been known to play in consciousness(Crone et al., 2014, Schiff, 2008). However, the original correlation was not significant after multiple comparisons correction (p = 0.34) and the left boundary of the 95% CI is quite close to zero [0.07.0.96], indicating that it could be spurious and may not extrapolate to larger datasets. While potentially interesting, this result warrants further investigation with larger datasets. Next, we assigned each of the 86-regions in our network to one of the 8 resting-state subnetworks defined previously (Yeo et al., 2011), i.e. visual, somatomotor, dorsal attention, ventral attention, limbic, fronto-parietal, default mode and cerebellar/subcortical. We calculated the mean FC/SC degree of the regions in each subnetwork and then calculated the Pearson's partial correlation, accounting for age and time since injury, of these 8 × 2 = 16 values with CRS-R scores. No correlations survived Benjamini-Hochberg correction for multiple comparisons and all 95% CIs included zero. These results emphasize the importance of a global measure of recovery, at least in this population of severe brain injury subjects who have widespread brain injury. We believe that recovery of specific functions (attention, memory, motor skills, language) is probably more related to connectivity of individual regions or subnetworks. However, here we are analyzing a general measure of consciousness response in patients that have all had a global and severe brain injury. It is not surprising then that we only detect significant and robust relationships between recovery and global network measures, not individual regions or subnetworks. In other neurological disorders that have more focal or subtler injury, i.e. stroke or multiple sclerosis, it may indeed be better to investigate the connectivity of individual regions or subnetworks.

4.2. Joint analysis of FC and SC networks

Despite the fact that function and structure are invariably linked, previous studies of FC and SC networks together in this patient population are sparse. Most studies focus on specific regions of interest within the default mode network instead of the brain network as a whole. One joint dMRI and fMRI study showed that TBI patients with more abnormal metrics of white matter integrity had less FC within the default mode network (Sharp et al., 2011). They also showed that higher resting-state FC in the posterior cingulate cortex was correlated with more efficient response speeds. Another set of joint analyses of SC and task-based FC networks in moderate TBI showed that there were 1) no correlations between FC and SC network metrics in patients and 2) no differences in the SC network metrics and significant increases in FC strength in patients versus healthy controls (Caeyenberghs et al., 2013). The FC network results are in agreement and the SC network results are in disagreement with our current findings. However, they conjecture that the lack of differences in SC could have been the choice of their gray matter parcellation atlas, as an earlier study by the same group did indeed find worse SC network measures in mTBI versus healthy controls (Caeyenberghs et al., 2012). Finally, a study of chronic TBI patients found increases in FC in frontal areas compared to healthy controls that was positively associated with better cognitive outcomes and negatively associated with a measure of SC (Palacios et al., 2013). They concluded that altered SC between brain regions could be in part compensated for by increases of FC. This last conjecture is in alignment with the current study's findings.

In our joint analysis of FC and SC connectomes using the network diffusion model, larger values of model propagation time, which corresponded to higher levels of consciousness response, indicate that these brains require a longer time for putative functional activation to propagate on the SC network in order to recapitulate their observed FC. A parsimonious explanation of this finding is that a patient's consciousness as inferred from behavioral measurements may be related to the ability of the brain to reestablish FCs using synaptic remodeling of alternate white matter pathways (see Fig 1). We further supported this conjecture by showing that subjects with higher CRS-R sores have more normal FC between region pairs with impaired SC. However, these region-pair FC correlations were not as strong as the correlations with the global metric of model propagation time, which may be attributed to the fact that the latter takes into account the individual's entire network connectivity while the former does not.

4.3. Simulated injury and recovery

Previous studies have simulated connectome disruption by the removal of nodes or edges to investigate network effects of injury (Achard et al., 2006, Honey and Sporns, 2008, Kaiser et al., 2007). Because our patient data contains noise from many different sources (see Limitations), we decided to validate the patient results using simulated connectomes representing injury and recovery. The network diffusion model parameters calculated from these simulated brain networks reflect all of the relationships that were observed in the patient group. These results support the use of the network diffusion model in capturing network-level functional rerouting. We observed that with increasing injury severity, simulated injury showed a decrease in model propagation time while simulated recovery showed an increase in model propagation time. This relationship held even while varying the percent of lost FC, with the curve shifting toward the recovered case for lower percent of lost FC. This was not the case in the model correspondence parameter, which decreased over increasing injury levels and varied percent of lost FC for both groups. The rather large gap between model propagation time in injured versus recovered brains, even in the case of only 25% FC lost, indicated that this metric is a good biomarker for recovery. This is exactly what we found in the patient data in that we had a strong, significant correlation between propagation time and CRS-R scores.

4.4. Limitations

There are several limitations in the current work, first and foremost is the relatively small size and heterogeneity of the sample. To assess the robustness of the correlation results to the particular population makeup, we implemented a bootstrapping technique (resampling with replacement). The resampled results reflected the original observations (see Table 2), lending confidence that our results and conclusions are not overly biased due to our particular (small) sample. Furthermore, we would like to point out that the small sample size is a consequence of the difficulties involved acquiring datasets of this type, given the population characteristics and the threshold for high quality data placed by the authors. The 29 subjects reported in Table 1 were collected over a period of 9 years (2005 to 2014) and represented those subjects out of 40 total collected in the Laboratory of Cognitive Neuromodulation that had either dMRI or fMRI. The 11 subjects that did not have MRIs could not be scanned due a variety of reasons, e.g. MR compatibility, excessive patient movements, patient non-cooperation. Of the 29 subjects (37 scans) with either DTI or rsfMRI, only 16 subjects (21 scans) met the high threshold for image quality imposed in this paper, i.e. minimal movements, minimal anatomical damage allowing for adequate automatic segmentation. From the 21 sets of scans, only 12 scans had all three criteria needed for the global network/CRS-R analysis (rsfMRI, dMRI and CRS-R scores). These difficulties are reflected in the sample sizes of publications that have utilized the same and similar populations (Bardin et al., 2012, Bardin et al., 2011, Goldfine et al., 2011, Liu et al., 2011).

In addition, image processing methods that require segmentation and parcellation of brain regions are notoriously difficult in populations with severe anatomical abnormalities. We did mitigate these adverse affects by carefully checking the segmentation and parcellation images for errors, using control points in FreeSurfer and rejecting those that did not have high enough quality. Noise is also introduced at many levels in the construction of the SC and FC networks, i.e. image acquisition, post-processing, parcellation choice, tractography, network construction and threshold imposition.

We did consider performing analysis using regional functional rerouting metrics, and decided against it for several of reasons. First and foremost is that we believe that the global measure of functional rerouting would be more robust in this cohort of relatively heterogeneous patients. These subjects in general have rather large areas of damage/injury (see Supplemental Fig. 1) and subsequent spread of structural damage to other brain regions distal to the primary injury/damage, so we anticipated that a global measure would indeed be more sensitive to changes occurring in the brain. This fact, coupled with the relatively small sample size, indicates that the chances are low that any particular regions are going to be consistently affected across the population. Therefore, it would be difficult to detect such an effect in this heterogeneous population-based study of cross sectional design and limited number of subjects. We do agree that investigating functional rerouting on a regional basis would be an excellent area of research, and we plan to do this with longitudinal data from a different population of larger size.

The CONN toolbox (Whitfield-Gabrieli and Nieto-Castanon, 2012) used in this work has been extensively tested on healthy control data to extract FC networks and its results seem to plausibly reflect the anatomy of neuronal connectivity for several subsystems of the brain (Fransson et al., 2014, Gabitov et al., 2015, Haag et al., 2015, Horowitz-Kraus et al., 2015, Keller et al., 2014). However, two factors need to be kept in mind for a correct interpretation of our results. One, recent work has shown that “functional networks” as defined here are based on the blood oxygen level dependent (BOLD) signal as a proxy and might include non-neuronal, i.e. vascular, components (44). Two, in the minimally conscious state, due to reduced cerebral metabolism, we cannot take for granted that the BOLD response reflects neuronal activity in the same way as in healthy subjects but might be diminished or disturbed. For example, in fMRI experiments of subjects who are minimally conscious, dissociations between behavioral and fMRI-based evaluations of cognitive function have been reported and their cause has yet to be understood (Bardin et al., 2011).

The dMRI processing and probabilistic tractography used in this work are able to handle complex fiber populations within a given voxel, i.e. crossing and kissing fibers. However a drawback is that long-range connections may be more susceptible to errors in tractography. In order to assess for general robustness of tractography, we calculated the correlations between the entries in the streamline count SC matrices for pairs of individuals. The mean Pearson correlation between the elements in the SC matrices for each pair of normal controls is 0.91 ± 0.04, indicating SC network consistency across normal individuals. Unsurprisingly, the patient set is less consistent since the damage is heterogeneous and pairwise connections will be differently affected. Even so, the average correlation of the pairs of patients is 0.75 ± 0.064. We believe this inter-subject consistency, even in the patients, provides a measure of confidence in the dMRI processing and tractography methods.

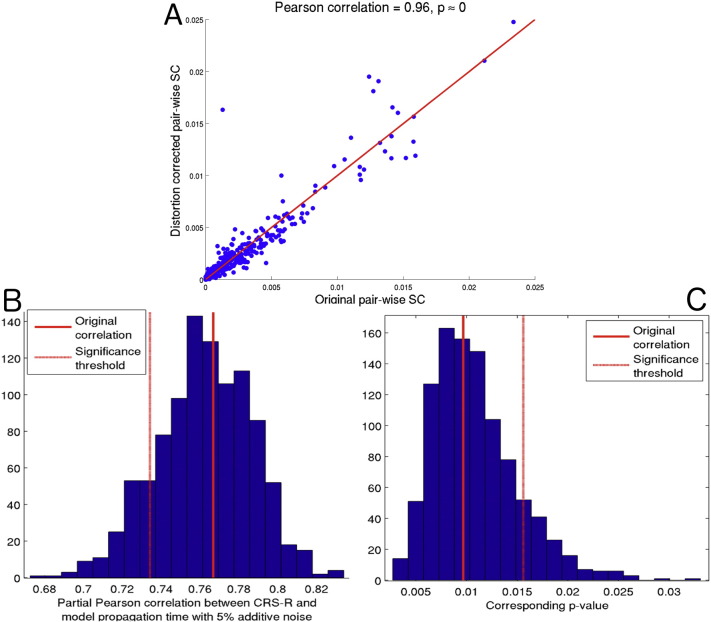
Due to the MRI acquisition used, we were not able to fully correct for b0 field inhomogeneities that can be problematic for EPI acquisitions. We performed eddy current and motion correction on the dMRI, and the tractography is seeded from voxels derived from anatomical imaging that is not subject to such distortions. Even so, there may be some influence of this distortion on the dMRI and subsequent tractography results. This fact, as well as the presence of other noise and pathology, is why we focus here on global, whole-brain measures which are more robust to such errors, rather than focusing on the connectivity of any one region. Therefore, bias in a few particular regions will be less influential to the overall analysis. We did have one patient whose scan allowed for distortion correction (the one Seimen's MRI had two EPI scans with opposite phase encoding). We assessed the influence of the distortion correction on that patient's global measures (see Appendix A.3 for details). In short, the entries in the pre-distortion and post-distortion SC matrices were highly correlated (r = 0.96, see Fig. S6, Panel A), the network diffusion's model correspondence parameter did not change and the model propagation time decreased by only 5%. To investigate how 5% error would affect the main correlation result of model propagation time with CRS-R, we added 5% Gaussian noise ($\mathcal{N}\left(0,0.05t_m\right)$) to each of the patients' model propagation times and recalculated the correlation. Only around 13% of the samples fall above the current FDR corrected significance threshold (Fig. S6, panels B and C). We conclude that the main results involving the network diffusion model are not greatly affected by EPI-related distortion.

Fig. S6.

(Panel A) Scatter plot of the original SC matrix entries versus the SC entries for the distortion corrected SC matrix entries for the one subject with Seimen's MRI scan. (Panel B) Histogram of partial Pearson's correlation between CRS-R scores and model propagation time with randomly sampled 5% Gaussian noise. (Panel C) Histogram of the corresponding p-values of the correlations in Panel B. In both Panels B and C, the solid line is the original value and the dashed line is the FDR corrected significance threshold.

To control for all the sources of noise and further test our hypotheses, we simulated injury and recovery using normal brain networks and observed the behavior of the model parameters. These were, of course, a simple approximation of what we assume actually happens in severe brain injury. Here, we assumed that injury was a loss of SC and FC between region-pairs, while recovery was a loss of SC but maintained FC between region-pairs. Of course, reality is much more complex and is not well known. Injured brains most likely have more regions with disrupted FC than just those region pairs with a lost SC. Recovered brains probably have increased FC in intermediate regions between the region pairs with lost SC. However, the simulation results allow us a controlled look at the behavior of the various parameters and measures under imposed conditions closely resembling injury and recovery.

4.5. Conclusions and future work

Taken together, these results shed new light on a possible network-level mechanism of, and a mathematical model for, recovery of consciousness in severe brain injury. We proposed and validated a network-level functional rerouting hypothesis that states recovery after injury is based on the brain's ability to reestablish lost or impaired functional connections via alternate structural pathways. We showed that measures of FC between region-pairs with impaired SC tended to relate to recovery of consciousness in severe brain injury. Furthermore, we provided evidence that the network diffusion model was able to capture global functional rerouting while standard network metrics of FC and SC were not. Specifically, we showed that increases in the network diffusion model's propagation time were significantly associated with better recovery of consciousness in brain injury subjects. Analysis of simulated injury and recovery networks further supported these findings.

These results raise important questions about how alternate structural pathways are used to reestablish functional links between regions with impaired structural connections due to injury. Longitudinal data acquired as individuals recover from severe brain injury would be required to examine specific region-pair functional rerouting hypotheses. Transcranial magnetic or direct current stimulation could be investigated as a tool to help reshape these compensatory pathways in order to encourage restoration of functional connections and possibly recovery of consciousness.

The following are the supplementary data related to this article.

Appendix A.1

The Benjamini-Hochberg multiple comparisons procedure.

Appendix A.2

Analysis of the Network Diffusion Model Fit.

Appendix A.3

Analysis of the impact of distortion correction.

Video S1

A time lapsed video of the network diffusion model's prediction in a particular normal controls. The upper left panel is the true FC, upper right is the SC, lower left is the predicted FC over time, lower middle is the scatter plot of predicted FC versus true FC over time and the lower right plot is time versus the correlation of predicted and true FC.