Biomolecular Force Field Parameterization via Atoms-in-Molecule Electron Density Partitioning

Abstract

Molecular mechanics force fields, which are commonly used in biomolecular modeling and computer-aided drug design, typically treat nonbonded interactions using a limited library of empirical parameters that are developed for small molecules. This approach does not account for polarization in larger molecules or proteins, and the parametrization process is labor-intensive. Using linear-scaling density functional theory and atoms-in-molecule electron density partitioning, environment-specific charges and Lennard-Jones parameters are derived directly from quantum mechanical calculations for use in biomolecular modeling of organic and biomolecular systems. The proposed methods significantly reduce the number of empirical parameters needed to construct molecular mechanics force fields, naturally include polarization effects in charge and Lennard-Jones parameters, and scale well to systems comprised of thousands of atoms, including proteins. The feasibility and benefits of this approach are demonstrated by computing free energies of hydration, properties of pure liquids, and the relative binding free energies of indole and benzofuran to the L99A mutant of T4 lysozyme.

1. Introduction

Molecular mechanics (MM) force fields for biomolecular simulations are undergoing increased scrutiny as access to improved algorithms and hardware allow for validation of, for example, protein dynamics,¹ protein–ligand binding free energies,² and liquid properties³ on an unprecedented scale. Overall, force fields describe biomolecular interactions well. Their success likely stems from a functional form that is based on physical laws, and very meticulous parametrization by many research groups on increasingly large databases of ab initio and experimental data.⁴⁻⁷ Force fields that model the nonbonded component of the total energy by Coulomb interactions between fixed atom-centered point charges and Lennard-Jones (LJ) interactions are, by far, the most widely used functional form today, and form the basis of the OPLS, AMBER, CHARMM, GROMOS, and many other force fields.

An underlying feature of these force fields is their transferability. The force field parameters have undergone extensive fitting against ab initio binding energies of complexes and properties such as free energies of hydration and liquid densities and heats of vaporization for small molecules.⁸⁻¹³ Furthermore, it has been shown that, when small molecules are assembled into macromolecules such as proteins, the same parameters perform reasonably well in the prediction of, for example, temperature-dependent structural changes¹ and protein–ligand interactions.² With the wealth of validation tests available in the literature, a user can be confident that dynamical simulations of simple proteins with a state-of-the-art transferable force field will provide an ensemble of structures that is representative of the experimental reality.

Given the widespread use of transferable force fields, it is important to consider the long-term routes to their improvement. As computational chemistry advances, one can continue to fit parameters to more-accurate quantum mechanical electrostatic potentials and energy surfaces within the confines of a fixed functional form. One can even consider amending the functional form, and important steps in this direction are being taken in the development of polarizable force fields. However, each advance comes at a cost. Each time that the method for the derivation of point charges is updated, for example, the library of parameters that describe the LJ interactions must be refit to experimental data. For a typical force field, this library may consist of many hundreds of parameters, although automated parameter optimization programs, such as ForceBalance,¹⁴ promise to bring down the cost of these fitting efforts in the future.

Yet, even if force field functional forms and parameters are found that perfectly reproduce the empirical and ab initio properties of small molecules, the question of transferability remains. It is well-established that adding electron-withdrawing or electron-donating functional groups to a molecule can significantly alter its chemistry through polarization effects. For example, trends in hydrogen bond strength between a para-substituted phenol and a water molecule were investigated using two force fields: one nonpolarizable (OPLS-AA) and one in which the charge distribution of the phenyl ring responds to the presence of the substituents (OPLS/CM1A).¹⁵ The OPLS/CM1A variant reproduced ab initio binding energies more accurately than the nonpolarizable version of the force field, which was attributed to the ability of the charge derivation scheme to respond to the chemical environment. In this regard, it is common in small-molecule force field parametrization for the user to assign atom-centered charges based on quantum mechanical calculations. Care must be taken that the obtained charges are compatible with both the LJ parameters and the force field used to describe the surrounding environment, which could contain water, protein, lipids, and so forth. Finally, the effects of environmental polarization are not limited only to the force field charges. It has been shown that the dispersion (or van der Waals (vdW)) coefficients also are sensitively dependent on both the local environment of the atom¹⁶ and long-ranged electrodynamic screening.^17,18 Hence, the accuracy of the force field may also be improved if the LJ parameters, as well as the charges, were able to respond to the chemical environment.

Interestingly, a fundamentally different approach to force field parametrization was used recently by Grimme in the development of the quantum mechanically derived force field (QMDFF).¹⁹ Here, instead of relying on a small number of research groups to fit parameters and package them into a force field with the implicit assumption that the parameters are transferable and consistent with small molecule force fields, the user derives all of the nonbonded parameters that are specific to their system in an automated fashion from quantum mechanical calculations.^20,21 Such a scheme might be termed an environment-specific, rather than transferable, force field.

More generally, we envisage future environment-specific force fields being derived in the same manner as today’s small molecule force fields, except that it would be possible to also (i) derive LJ parameters and (ii) derive parameters for both small molecules and macromolecules such as proteins. Environment-specific force fields have the potential to be more accurate than their transferable counterparts, since they would be derived explicitly for the system under study. However, of course, it would be necessary to extensively benchmark their accuracy against a wide range of biomolecular data, such as nuclear magnetic resonance (NMR) structural data,^1,7,22 protein–ligand binding free energies,² and so forth. A second advantage is that there would be no need for the user to mix force fields. Protein and small-molecule force fields would be computed by the user simultaneously, thus ensuring their consistency. Furthermore, charges and LJ parameters would be computed from the same quantum mechanical data and so the parameters would be inherently consistent. If the user wishes to use a more advanced quantum chemistry method to perform the quantum mechanics (QM) calculation, then both the charges and vdW parameters would respond to the change in QM electron density by construction. Thus, the user would be able to experiment with more advanced chemistry or with alternative functional forms of the force field without relying on another research group to fit the library of force field parameters to experimental data. A disadvantage of such a scheme is that the user would require sufficient computational resources to perform a QM calculation on their system of interest. However, with ongoing advances in large-scale density functional theory (LS-DFT) software²³ and increasing access to improvements in hardware, QM calculations in excess of 1000 atoms are becoming routine.²⁴⁻²⁶ As an example, Ufimtsev et al. have computed the electronic structure of a 2634-atom protein–water complex at the B3LYP/6-31G level using the TeraChem software and a single desktop workstation with eight GPUs within <3 h.²⁷

In recent years, we have started to develop the techniques necessary to derive environment-specific force fields for large systems. The force field is based on the concept of atoms-in-molecule (AIM) electron density partitioning, whereby the total QM electron density of the system under study is computed and then partitioned into approximately spherical atomic basins. Although there is no unique way to perform this partitioning, it has been shown, by careful choice of the weighting functions, that AIM densities can be optimized to simultaneously produce chemically meaningful partial atomic charges, yield an efficiently converging multipole expansion of the electrostatic potential, and be insensitive to small conformational changes or to buried atoms.²⁸⁻³⁰ Furthermore, by combining AIM partitioning with LS-DFT calculations, atomic partial charges may be computed for systems that are comprised of many thousands of atoms, including proteins.^30,31

Using this combination of AIM electron density partitioning and LS-DFT, we have previously derived partial charges for many small proteins and shown that they reproduce very well the electrostatics of the underlying DFT calculation, as well as experimental NMR order parameters when used in MM molecular dynamics simulations.³¹ However, a more sensitive test of intermolecular interactions is to compare hydration free energies and liquid properties of small organic molecules with the experiment. These properties are commonly used to validate new force fields^8,12,13,32 since there exists a wealth of experimental data, which is directly comparable with simulation. Furthermore, any difference between the experiment and the theory may be unambiguously attributed to errors in the force field, rather than finite sampling errors and so forth, which may affect more-complex validation datasets. Initial tests revealed that the AIM charges are not as accurate as we would like when coupled with the LJ parameters of commonly used force fields. For example, the combination of AIM charges with OPLS LJ parameters gave a computed free energy of hydration of −12.8 kcal/mol for acetamide, which may be compared with the experimental result of −9.7 kcal/mol.

One solution might be to reparameterize libraries of LJ parameters for compatibility with AIM charges in the knowledge that this procedure would need to be repeated periodically whenever an adjustment to the charge model is made. Instead, we show here that the LJ parameters may be obtained, in conjunction with the atomic partial charges, directly from AIM electron densities. The LJ parameters are thereby specific to the system under study and respond automatically to the chemical environment of the atom. Similar to that observed with the charges, they may be derived for both small and large molecules, including proteins. The LJ parameters are computed from the same QM electron density as the partial charges and, hence, the entire parameter set is consistent and there is no additional computational cost to the user. Perhaps most importantly, there are a very small number of fitting parameters in the model. As we will describe, our nonbonded force field contains only seven fitting parameters, which is sufficient to describe the chemistry of a wide range of small organic molecules and proteins. In contrast, typical transferable force fields require many tens or hundreds of fitting parameters to model nonbonded interactions in the same systems.

In what follows, the method for the derivation of charge and LJ parameters is described. The possible applications of biomolecular force fields are extremely wide and varied, ranging from protein–ligand binding free energies for drug discovery, to pK_a prediction, to dynamics for studying protein function, to hybrid QM/MM simulations for enzymology. As such, it is not possible to validate a new force field approach in all of these contexts in a single study. Instead, following the example of many other development efforts,^8,12,13,32 we begin by validating our proposed nonbonded force field against experimental free energies of hydration, liquid densities, and heats of vaporization of small organic molecules. As we will show, AIM techniques are extremely competitive with existing transferable force fields for this dataset, which will motivate future validation tests beyond those presented in this study. Furthermore, since our goal is to eventually derive force fields for large systems, such as protein–ligand complexes, we present here a proof-of-principle derivation of a force field for an ∼1600 atom model of the L99A mutant of T4 lysozyme. We compare and contrast the derived nonbonded parameters with a standard transferable force field and compute the relative binding free energy of indole and benzofuran to the protein.

2. Methods

2.1. Theory

The quantum mechanical interaction energy is typically decomposed into four components: (i) electrostatics, (ii) induction, (iii) dispersion, and (iv) exchange-repulsion.^33,34 Here, we shall discuss how each of these terms, in turn, is incorporated into an effective force field, which, for two atoms i and j separated by a distance r_ij, is typically written in the form of eq 1:

1

2.1.1. Electrostatics

The first term of the nonbonded expression describes the classical electrostatic interactions between the charge distributions of the two atoms. It is usually described by fixed atom-centered point charges (q_i), although off-site charges to model, for example, lone-pairs^35,36 and σ-holes³⁷ are relatively common. Typically, the charges are fit to reproduce ab initio electrostatic properties of small molecules, either by fitting to the electrostatic potential or by distributed multipole analysis.³⁸ However, neither of these methods has been applied to very large systems, such as proteins, due to the difficulties of fitting charges to buried atoms or the expense of the QM calculation. Here, we instead use an AIM approach whereby the total QM electron density (n(r)) is partitioned into overlapping atomic densities (n_i(r)):

2

The atomic partial charges are then computed by integrating the atomic electron densities over all space:

3

where N_i is the number of electrons assigned to atom i and z_i is its effective nuclear charge. Similarly, higher-order atomic multipoles may be computed as first-order, second-order, ... moments of the atomic electron densities. Various definitions of the weighting factors w_i(r) exist. For example, in Hirshfeld partitioning, they are set equal to neutral gas-phase atomic densities,³⁹ although these weights are known to result in atomic populations that are too close to zero.⁴⁰ Instead, we employ density-derived electrostatic and chemical (DDEC) electron density partitioning.^28,29 The form of the DDEC weighting function is described in detail elsewhere,^29,30 but in brief the atomic weights are simultaneously optimized to resemble the spherical average of n_i(r) and the density of a reference ion of the same element with the same atomic population N_i. In this way, the assigned atomic densities yield a rapidly converging multipole expansion of the QM electrostatic potential and the computed populations are chemically reasonable.

2.1.2. Induction

The induction term results from the distortion of a molecule’s electron density in response to its environment. For example, moving a molecule from the gas phase into water enhances the molecule’s dipole moment. In fixed-charge MM force fields for condensed-phase simulations, which are the focus of this paper, induction is treated in an effective manner by polarizing the atomic charges. This is generally achieved either by using an empirical bond-order correction,⁴¹ a scaling factor,^13,42,43 or by computing the charges using an artificially polarized quantum chemistry method or an implicit solvent model.¹¹ Here, the latter approach is used whereby the QM electron density is computed via direct solution of the inhomogeneous Poisson equation in a medium with a dielectric constant ε.^44,45 To determine which value of ε should be used, let us consider the case of the transfer of a molecule from the gas phase to water. Use of ε = 1 would neglect the attractive inductive interactions between the polarized charge distribution of the molecule and water and lead to computed free energies of hydration that are too positive. On the other hand, the use of ε = 80 (to model the dielectric constant of water) neglects the energetic cost of distorting the electronic wave function, which has been shown to amount to several kcal/mol,⁴⁶ and would lead to computed free energies of hydration that are too negative. In fact, the magnitudes of both of these energetic contributions may be estimated using the implicit solvent model,⁴⁶ and it can be shown that they approximately counterbalance each other for a wide range of molecules if the electron density is computed in a dielectric medium of ε = 4 (Section S2 in the Supporting Information). This is also the dielectric constant that is frequently used to model protein interiors,⁴⁷ and, as we will show, produces a net polarization effect that is consistent with that recommended by Karamertzanis et al.⁴⁸ and the developers of the latest generation of AMBER force fields.^49,50 Therefore, a background dielectric constant value of ε = 4 is used to compute all condensed-phase QM electron densities in this study.

2.1.3. Dispersion

Dispersion (or vdW) interactions are typically modeled in MM force fields by the attractive B_ijr_ij^–6 term in eq 1. The B_ij parameters are atom-dependent but are almost always determined empirically and are assigned to new molecules from outside the fitting set, using a library of atom types. Despite their empirical treatment in MM force fields, dispersion interactions are inherently a quantum mechanical phenomenon, which arise even in nonpolar molecules, because of interactions between spontaneous electron density fluctuations. Standard DFT exchange-correlation functionals fail to capture the correct long-ranged behavior of the dispersion interaction, but much progress has been made in recent years in computing the strength of the dipole–dipole pairwise dispersion interactions (that is, the B_ij parameters) from the ground-state electron density of a molecule.^51,52 In this paper, the Tkatchenko–Scheffler (TS) scheme is employed to compute B_ij coefficients by rescaling accurate free atom reference data by the effective volume of the atom in the molecule.¹⁶ Specifically, the ratio of the AIM volume to the volume of the atom in free space is computed using the DDEC atomic densities from eq 2:

4

where r is the distance from the nucleus of atom i, and n_i^free(r) is the electron density of the free atom i in vacuum. V_i was computed for each of the seven elements used in the current study, using the MP4(SDQ)/aug-cc-pVQZ method in Gaussian 09,⁵³ and the chargemol code⁵⁴ and the data are provided in Table S1 in the Supporting Information. The environment-specific atomic dispersion coefficient is then computed by¹⁶

5

The B_i^free parameters are obtained from time-dependent density functional theory (TDDFT) calculations from the literature⁵⁵ and are tabulated in Table S1. The TS method traditionally uses atomic volumes computed using Hirshfeld electron density partioning. However, it has been shown that computed dispersion coefficients of ionic systems are substantially improved by allowing the weights in eq 2 to update self-consistently with the AIM densities.^56,57 Hence, in what follows, we use DDEC electron density partitioning to compute both the atomic charges and volumes. Finally, in the OPLS force field, heteronuclear B_ij parameters are computed via a geometric combining rule, and the same approach is adopted here:

6

Figure 1 demonstrates the potential utility of this approach for classical force field design. For benzene, the DDEC AIM population and dispersion coefficient are essentially identical to those used in the OPLS/CM5 force field, which has been extensively parametrized to reproduce the liquid properties of the molecule.^8,13 For a druglike molecule, with more-complex bonding environments, greater differences exist between OPLS/CM5 and the AIM approach. Both methods agree that the N atom in the pyridine ring (blue) has a high electron population, and therefore is expected to be more polarizable and is assigned a high dispersion coefficient. In contrast, the N atom highlighted in red on the triazole ring has a lower electron population. The AIM approach responds to the local environment of the N atom and correspondingly reduces the dispersion coefficient to account for electron depletion. OPLS, like most force fields, assigns identical dispersion parameters to N atoms in pyridine and triazole rings and is thus expected to overestimate the dispersion coefficient in the latter case. Fundamentally, there should be coupling between the electron density on an atom and its capacity for dispersion interactions.

Figure 1.

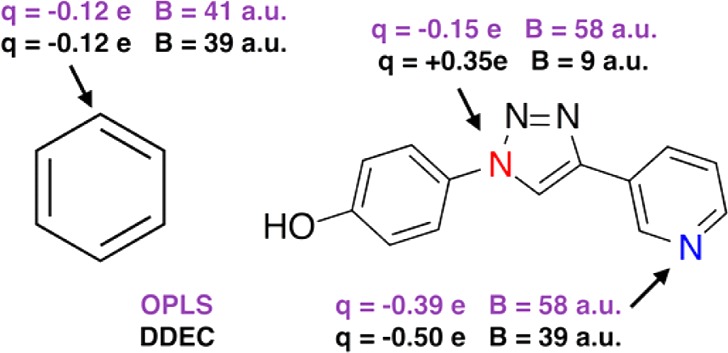
Comparison between the DDEC AIM parametrization approach used in this work and the OPLS/CM5 force field for (left) benzene and (right) a larger druglike aryl-1,2,3-triazole molecule.⁵⁸

2.1.4. Exchange-Repulsion

Exchange-repulsion is primarily intended to account for repulsion between overlapping electron clouds due to the Pauli exclusion principle, but it also effectively describes other terms that are dependent on electron density overlap, such as electrostatic penetration energies.^20,33 It is typically modeled in MM force fields by a repulsive LJ term of the form A_ijr_ij^–12. This term is problematic because there is no clear method to parametrize the atomic A_i values directly from QM calculations.³⁴ Here, one approach to derive the strength of the LJ repulsion is hypothesized and justified a posteriori by comparison between computed and empirical condensed-phase properties of small molecules. In the OPLS force field, in order to ensure that the LJ potential has a minimum that is coincident with the van der Waals (vdW) radii of the atoms (R_i^AIM), the repulsive parameters of the Lennard-Jones expression are related to the dispersion coefficients via⁵⁹

7

Here, the scaling relationship suggested by Tkatchenko and Scheffler¹⁶ is used to estimate the vdW radius of the atom in the molecule from the radius of the free atom in a vacuum:

8

Thus, by substituting eq 8 into eq 7, environment-specific A_i terms are estimated from free atom reference data and the AIM-partitioned volume of the atom in the molecule (eq 4). Heteronuclear A_ij parameters are derived via the geometric combining rule:

9

The atomic radius of an atom in a vacuum cannot be measured directly, and so the R_i^free are treated as variable fitting parameters. Since computed liquid densities are very sensitive to the A_i coefficients used in MM force fields, we have fit the R_i parameters by hand to reproduce empirical liquid densities. The parameters for H, C, N, O, S, F, and Cl are provided in Table S1. These seven radii are the only fitting parameters used in the construction of our nonbonded force field. This may be contrasted with typical transferable force fields which require many tens, or even hundreds, of fitting parameters to describe charge and LJ interactions in biomolecular systems.

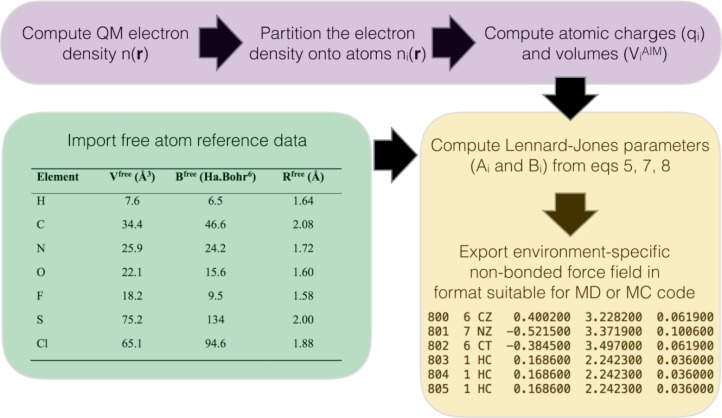
To summarize, Figure 2 shows the suggested workflow for derivation of nonbonded force field parameters from QM calculations. We use the ONETEP linear-scaling DFT code to perform the ground-state electronic structure calculations,⁶⁰ and the DDEC atomic population analysis and atomic volume calculations have been implemented here as post-processing routines.^30,31 Apart from the QM calculation, the only input data required is summarized in the green box in the figure (and Table S1). These are the atomic volumes and dispersion coefficients of free atoms in vacuo, and they have been computed using QM calculations as described earlier. The free atom radii (R_i^free) have been fit to reproduce experimental liquid densities. These parameters are optimized for the QM method described below and they do not need to be refit by the force field user. A simple script is used to rescale the free-atom parameters according to eqs 5, 7, and 8 to provide environment-specific force field parameters that are unique to each atom in the system.

Figure 2.

Workflow for environment-specific force field derivation. The operations in the purple box are performed using QM software. The force field input parameters are tabulated in the green box (and Table S1 in the Supporting Information). In the yellow box, a script computes the LJ parameters and exports them into a suitable format. The acetonitrile example shown is designed for BOSS input, in the standard OPLS format q (e), σ (Å), ε (kcal/mol).

2.2. Computational Methods

For the testing on liquid-state properties, 41 small molecules (listed in Table S4 in the Supporting Information) were optimized under vacuum at the MP2/cc-pVTZ level using the Gaussian 09 package.⁵³ The ground-state electron density was computed using the ONETEP linear-scaling DFT code⁶⁰ with the PBE exchange-correlation functional.⁶¹ ONETEP combines computational efficiency with accuracy equivalent to traditional plane-wave DFT codes by optimizing a minimal set of spatially truncated nonorthogonal generalized Wannier functions (NGWFs) on each atom.⁶² One NGWF was used for hydrogen and four for all other elements used in the current study. The NGWFs were expanded in a periodic sinc (psinc) basis with an equivalent plane-wave cutoff energy of 1020 eV, and were localized in real space with 10 Bohr radii. PBE OPIUM⁶³ norm-conserving pseudopotentials were used for all DFT calculations. Figure S3 in the Supporting Information shows good agreement between the gas-phase dipole moments of the set of small molecules computed with ONETEP as described here and those computed at the MP2/cc-pVTZ level in Gaussian 09,⁵³ although the DFT approach overestimates the dipole moment of more polar molecules by up to 0.4 D in some cases.

To account for induction in an effective manner, DFT calculations were performed using a smeared ion representation under open-boundary conditions with a relative dielectric constant of ε = 4.^44,45 The dielectric cavity is defined by an isosurface of the electronic density under vacuum, with parameters controlling the smoothness and density threshold taken from the literature.^44,64 Partitioning of the polarized ground-state electron density was performed using the DDEC scheme in ONETEP as described in detail elsewhere,^30,31 with the mixing parameter (γ) set to 0.02, which appeared in preliminary tests to give reasonable agreement between DDEC and OPLS force field charges for a wide range of functional groups. LJ parameters were computed as described in Figure 2.

To avoid nonphysical asymmetries in force field simulations, the DDEC charges and LJ parameters were symmetrized for identical atoms.⁴² LJ parameters for polar H atoms (that is, H atoms bonded to O, N, or S) were set to zero. However, this neglects important dispersive interactions in the current format, and so the B_i coefficient of the neighboring heavy atom is correspondingly increased according to eq 10,

10

where B_X and B_X^′ are the old and new dispersion parameters for atom X (= O, N, or S), n_H is the number of neighboring H atoms, and B_H represents their dispersion coefficients. Bonded interactions were represented by the OPLS-AA force field and, for simulations involving water, the rigid TIP4P model was used.⁶⁵

The environment-specific force field for a 1646-atom cluster extracted from the L99A mutant of T4 lysozyme (PDB: 185L)⁶⁶ was also derived in an identical manner from a single point QM calculation, which is a routine computation using LS-DFT.²⁴⁻²⁶ The cluster included the 105 amino acid residues nearest to the ligand. For computational feasibility, the cluster did not undergo prior structural optimization and the nonbonded parameters were not symmetrized. Setup of the protein complexes, liquid simulations, and free-energy calculations were performed using standard procedures⁶⁷ with the BOSS and MCPRO codes,⁶⁸ as detailed in the Supporting Information (Section S1).

3. Results

3.1. Electrostatics

Figure 3a compares the computed QM dipole moments in implicit solvent (ε = 4) with the same quantity under vacuum (ε = 1) for the 41 neutral organic molecules. As expected, the dielectric medium increases the polarity of the molecules. Interestingly, the dipole moment is increased by an approximately constant factor of 1.19, independent of the chemical nature of the molecule. This finding helps to justify the common use of scaled gas-phase charges in condensed-phase modeling to account for polarization effects.^42,43 In fact, the scaling relationship between the gas-phase and condensed-phase dipole moments found here is very similar to the CM5 scaling factor (1.20), which was optimized to reproduce a range of experimental data.¹³ We have also plotted the line of best fit through the dipole moments of the molecules computed with a dielectric constant of ε = 80 to model water (dashed line in Figure 3a). The polarity of the molecules is now increased further, by a factor of 1.41, relative to that under vacuum. It has been argued that charges for condensed-phase simulation should be polarized halfway between those charges computed under vacuum and those computed in a condensed-phase reaction field potential in order to account for induction in an effective manner.⁴⁸⁻⁵⁰Figure 3a reveals that AIM charges computed in a dielectric medium (ε = 4) should be fully consistent with this charge-fitting philosophy.

Figure 3.

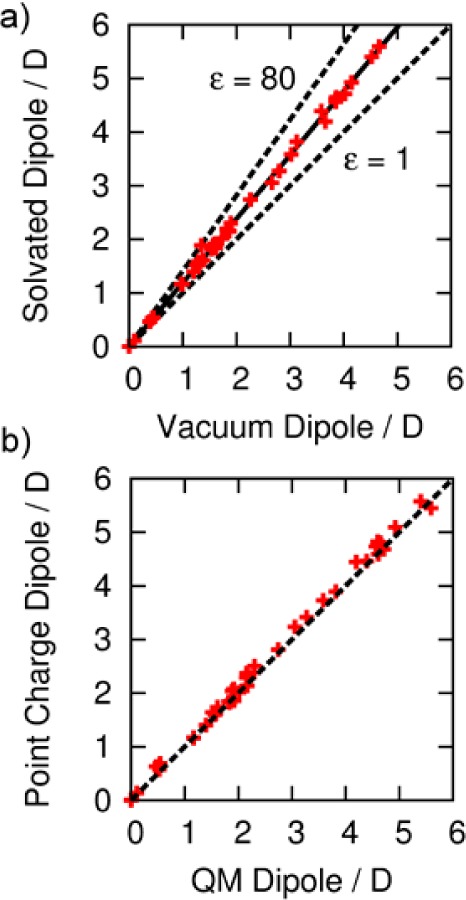
(a) Comparison between condensed phase (ε = 4) and vacuum dipole moments of 41 small molecules (red crosses). Dashed lines indicate the dipole moments of molecules computed using the implicit solvent model with ε = 80 and ε = 1. (b) Comparison between point-charge and QM dipole moments of the same database, after the addition of extra point sites to 12 molecules.

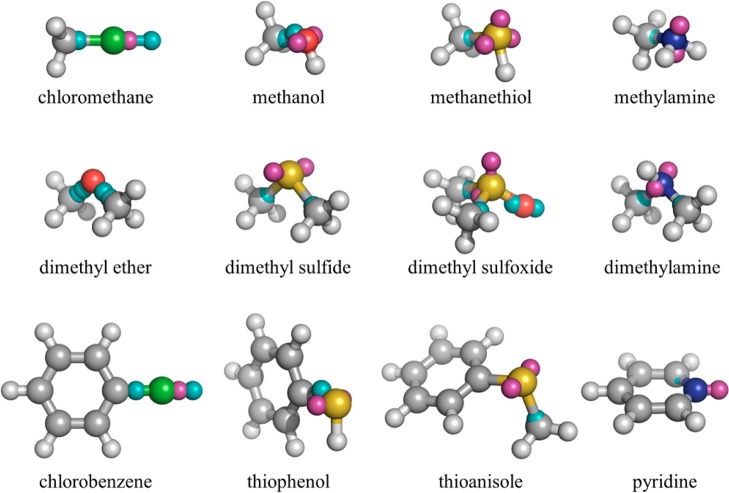
An important measure of the likely success of AIM charges in condensed-phase modeling is the ability of the point-charge model to reproduce the electrostatic properties of the underlying QM calculation. The DDEC atomic densities are optimized to be close to spherically symmetric, and hence the atomic multipole moments should be small and the electrostatic potential surrounding the molecule well-approximated using an atom-centered point charge model. However, there are certain well-documented cases, such as atoms that possess lone pairs or σ-holes, in which the atomic electron density is anisotropic and the AIM atom-centered charges are expected to produce a poor approximation to the QM electrostatic potential.⁶⁹ In Section S3 in the Supporting Information, the anisotropy in the atomic electron densities is analyzed up to quadrupole order for every atom in the 41 molecule test set. Fifteen (15) molecules were identified as containing at least one atom with significant anisotropy. All amines (6) and molecules containing sulfur (5) or chlorine (2) were identified by this analysis. The remaining two molecules were dimethyl ether and methanol, although these were borderline cases.

A common approach in the design of MM force fields is to move charge from the atoms to off-center sites to model anisotropic electron density,³⁵⁻³⁷ where the positions and magnitudes of the charges are parameters that are fit to empirical data. In keeping with our intentions in this work of minimizing the number of fitting parameters, the positions and charges of the extra sites are automatically optimized to reproduce the dipole and quadrupole moments of the AIM atomic electron densities. The optimization procedure is described in Section S3 in the Supporting Information, and the errors in the atomic dipole and quadrupole moments before and after the addition of extra sites are given in Table S3 in the Supporting Information. Figure 3b compares the dipole moments of all 41 molecules, using the AIM point charge model with the QM dipole moments, after the addition of extra sites on 12 molecules. The mean unsigned error (MUE) across the entire set (excluding two molecules whose dipole moment is zero by symmetry) is 0.10 D, compared to that without the extra sites (MUE = 0.17 D).

The positions and signs of the derived charges are for the most part chemically intuitive (Figure 4). Chlorine carries an off-site positive charge in the position of the σ-hole, which has been shown to be important for the accurate description of halogen bonding in MM force fields.³⁷ The majority of the other molecules carry off-site negative charges on lone-pair sites. It is striking that the number of extra point sites required to reproduce the QM multipole moments is larger than that typically used in MM force fields. This is perhaps best exemplified by chloromethane to which the optimization procedure has assigned three extra sites, rather than one extra site. The dipole moment of chloromethane in the AIM atom-centered point charge model is 2.55 D, which is larger than the QM dipole moment in implicit solvent (2.17 D). The σ-hole extra point site has a charge of +0.20 e at 1.40 Å from the Cl atom, which may be compared with the extra site used in the OPLS-AAx force field of +0.075 e at 1.60 Å.³⁷ However, with this single extra site, the dipole moment of chloromethane decreases to 1.19 D. By allowing a second site on the Cl atom and one site on the neighboring C atom, the dipole and quadrupole moments of the QM atomic electron densities are reproduced by the extra sites, as is the net dipole moment of the molecule (2.14 D). It should be emphasized that the fitting procedure is automated and parameter-free, thus all of the chemistry of the intermolecular interaction is derived directly from the electron density, rather than relying on chemical intuition.

Figure 4.

Positions of extra point charge sites on 12 molecules from the benchmark set. Negative charges are displayed in magenta, positive in cyan.

3.2. Condensed-Phase Properties

It has been shown in the previous section that, to a good approximation, AIM charges are capable of reproducing the QM electrostatics of small molecules, especially when off-center charges are used to model anisotropy in the electron density. Our long-term goal is to investigate the accuracy of AIM nonbonded interactions in condensed-phase modeling, particularly in the context of protein–ligand binding free energies where the ligand is transferred from bulk solvent to the binding site. Pure liquid and hydration properties are commonly used as a surrogate for this process; liquid densities, heats of vaporization, and free energies of hydration can be precisely measured experimentally and the sampling requirements are low, so any discrepancies between simulation and experiment can be directly attributed to the force field. As such, these properties are widely used as a starting point for the validation of new force fields. To investigate the accuracy of AIM charges for pure liquid simulations and free-energy calculations, they were combined with the AIM LJ parameters described in section 2.1 and OPLS-AA bonded parameters⁹ to form a complete MM force field (eq 1). The extra charge sites do not have LJ parameters in the current model. The full list of nonbonded parameters for the 41 molecules studied here are provided in the Supporting Information.

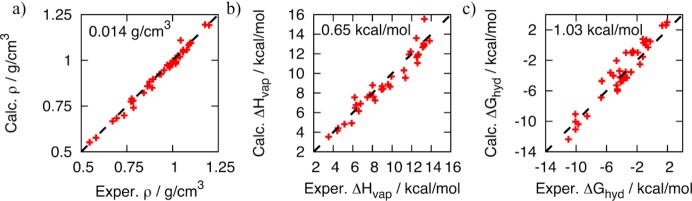
Figure 5 shows the liquid densities and heats of vaporization, as well as the free energies of hydration, for the 41 organic molecules computed using the derived force field for the cases where experimental data are available. The complete results are listed in Tables S4 and S5 in the Supporting Information. The MUE values, compared with those of the experiment, were, respectively, 0.014 g/cm³, 0.65, and 1.03 kcal/mol. Liquid densities are particularly well-reproduced using the current method, which supports the derivation of the A_ij parameters from the AIM vdW radii (eq 7). A modest outlier is acetic acid, which is predicted to have a higher density (1.11 g/cm³) than observed experimentally (1.04 g/cm³). A notable feature of the computed energetics is that nonpolar molecules, particularly those containing benzene rings, have a tendency to be more weakly bound (lower heat of vaporization and less exoergic free energy of hydration) than suggested by the experiment. Possible reasons for this discrepancy include the neglect of higher-order dispersion terms beyond the dipole–dipole interaction,⁷⁰ under-estimation of C–H···O hydrogen bonding interactions,⁷¹ and a lack of explicit treatment of polarization, which has been shown to induce the long-ranged hydrophobic effect.⁷²

Figure 5.

Properties of organic molecules: (a) liquid densities, (b) heats of vaporization, and (c) free energies of hydration. Mean unsigned error (MUE) values, relative to the experiment, are also shown. The raw data and experimental references are provided in Tables S4 and S5 in the Supporting Information.

Nevertheless, the accuracy of the AIM force field is extremely competitive with existing force fields. For example, the MUE values for a similar dataset computed using the OPLS/CM5 force field are, respectively, 0.024 g/cm³, 1.06, and 0.94 kcal/mol.¹³ The MUE values for free energies of hydration for a large database of 239 small molecules was reported to be 1.93 kcal/mol (CHARMM), 1.17 kcal/mol (GAFF), and 0.73 kcal/mol (OPLS2.1).² The reported root-mean-square deviations for the densities and heats of vaporization are 0.083 g/cm³ and 2.53 kcal/mol for GAFF, and 0.026 g/cm³ and 1.12 kcal/mol for CGENFF, which were computed for databases consisting of more than 100 molecules.³ It should be emphasized that the number of empirical fitting parameters in the current study (seven in total) is substantially lower than in the generation of these other force fields. All of the nonbonded parameters in the present case arise directly from the DFT calculations.

3.3. Protein–Ligand Binding Free Energies

A notable feature of our AIM-based nonbonded force field is that, in principle, the methods scale to arbitrarily large system sizes, potentially allowing the derivation of virtually parameter-free environment-specific force fields for systems comprised of many thousands of atoms. While our ultimate goal is to benchmark the accuracy of this force field for the study of protein–ligand binding free energies, this is beyond the scope of the current study. Instead, here, we demonstrate the feasibility and potential benefits of using the AIM approach in computer-aided drug design efforts and compare the derived parameters with a standard transferable force field.

For our proof-of-principle example, we have chosen to study the binding of two small molecules, indole and benzofuran, to the L99A mutant of T4 lysozyme. This target is an engineered hydrophobic binding pocket for which extensive binding data and X-ray crystal structures are available.^66,73 Importantly, there are no water molecules in the binding pocket, the protein adopts an almost-identical conformation in the two crystal structures, and the ligands are small, relatively rigid, and isosteric. Thus, the transformation can be studied via a simple one-step free-energy calculation, sampling requirements are low, and any discrepancy between experiment and theory may be attributed directly to force field error. Intriguingly, despite the structural similarities between the two bound crystal structures, free-energy methods are unable to reproduce the experimental binding free energy of benzofuran, relative to indole (−0.57 kcal/mol),⁷³ with estimates of −2.3 kcal/mol (AM1-BCC charges)⁷⁴ and −1.9 kcal/mol (RESP charges).⁷⁵

First, an AIM force field was derived for the two small molecules, as in the previous section. It was found that no off-center extra point sites were required. The relative free energy of hydration of the two molecules was computed and is shown in Table 1. No experimental data are available, to the best of our knowledge, but the observation that indole has a much lower free energy of hydration than benzofuran is consistent with calculations performed using the OPLS/CM1A force field, the QM dipole moments of the two molecules (2.19 D vs 0.67 D under vacuum), and their observed octanol/water partition coefficients (2.14 and 2.67).⁷⁶ Thus, it is not surprising that benzofuran should be more strongly bound, inside the hydrophobic lysozyme pocket, than the more polar, isosteric indole.

Table 1. Free Energies of Hydration and Binding to the L99A Mutant of T4 Lysozyme of Benzofuran (Relative to Indole)^a.

	free energy of hydration, ΔΔGhyd (kcal/mol)	free energy of binding, ΔΔGbind (kcal/mol)
AM1-BCCb		–2.3
RESPc		–1.9
OPLS/CM1A	+5.11 ± 0.03	–2.35 ± 0.08
this work
no X-sites	+4.48 ± 0.04	–1.20 ± 0.22
with X-sitesd		–0.37 ± 0.12
experimente		–0.57

^aAll simulations have been run in triplicate, and the standard error in the mean is shown.

^bData taken from ref (74).

^cData taken from ref (75).

^dX-sites denotes the use of extra off-center point charges on residue Met102.

^eData taken from ref (73).

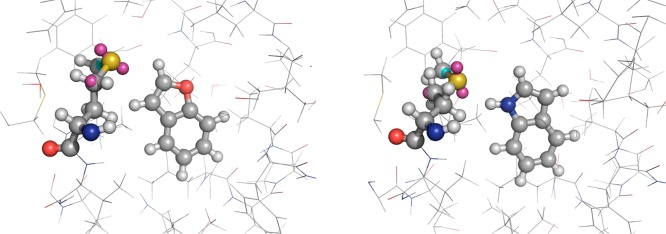
To investigate whether the inclusion of native state polarization in the force field derivation procedure affects the description of protein–ligand binding, a protein-specific force field was built for a significant portion of the T4 lysozyme protein (1646 atoms). The entire AIM nonbonded parameter set is provided in the Supporting Information. Figure 6a shows the correlation between the atom-centered point charges derived using the AIM approach, and OPLS-AA force field charges for lysozyme. Generally, there is good correlation, although, as expected, the AIM charges have a wider spread, because they can respond to the macromolecular environment. The contrast in the computed dispersion parameters is much more pronounced (Figure 6b). Similar to all common force fields, OPLS uses a library of atom types, while the AIM dispersion coefficients are derived from the atomic electron densities via eq 5. As an example, both OPLS and AIM assign charges of −0.50 e and −0.14 e to the backbone N atoms of residues Leu84 and Pro86, respectively. However, OPLS assigns the same B parameter to the two atoms (58 a.u.), while the AIM force field gives 51 a.u. on Leu84 and 19 a.u. on Pro86. The cluster of atoms highlighted by an arrow in Figure 6b are carbonyl carbon atoms, which are electron-deficient and thus intuitively expected to interact weakly through dispersive effects. Interestingly, of the 1646 atoms in the protein cluster, only five atoms required off-center point sites to model anisotropy. Four sites occurred on S atoms of Met residues, and one on a neutral Lys residue, which is used by MCPRO to neutralize the system. This unexpectedly low number may, in part, be a selection effect, since halogens and neutral amines are not found in the structure (there are no His residues in the modeled cluster). However, Table S3 in the Supporting Information shows that the anisotropy for Met102 is much lower than on, for example, dimethyl sulfide. In what follows, extra point sites were added to Met102, since it is the only anisotropic site in contact with the ligands (Figure 7).

Figure 6.

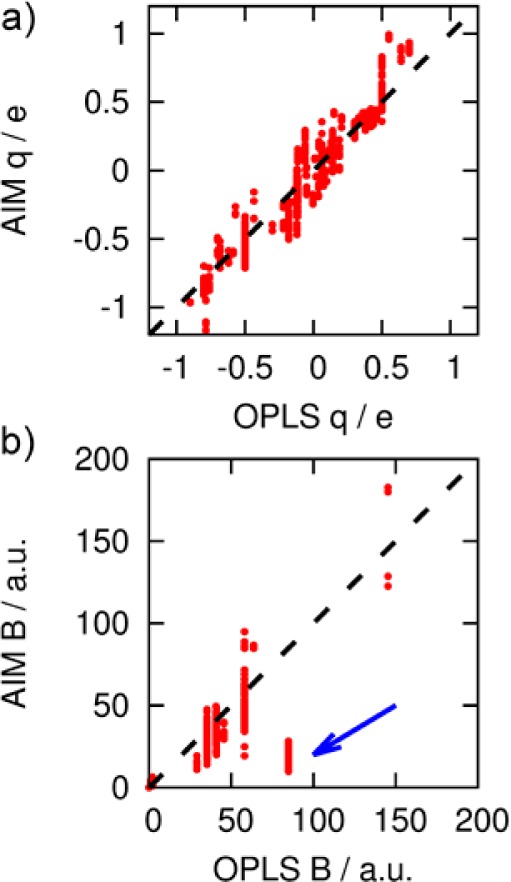
Comparison between AIM and OPLS (a) charge and (b) dispersion parameters for the L99A mutant of T4 lysozyme. The blue arrow indicates a significant discrepancy for carbonyl C atoms.

Figure 7.

Final snapshots of (left) benzofuran and (right) indole bound to the hydrophobic pocket of the L99A mutant of T4 lysozyme from Monte Carlo free-energy calculations. Extra point sites on Met102 are also shown. Negative charges are displayed in magenta; positive charges are displayed in cyan.

The relative free energy of binding of benzofuran and indole to the L99A mutant of T4 lysozyme was computed with free-energy perturbation theory, using the MCPRO software⁶⁸ (see Table 1). The standard OPLS-AA force field, with scaled CM1A charges for the ligands, overestimates the binding free energy of benzofuran, relative to indole, by ∼2 kcal/mol, in agreement with previous force field studies.^74,75 Replacing the nonbonded parameters by AIM-derived charge and LJ coefficients reduces the relative binding free energy by ∼1 kcal/mol, which may be attributed to the lower ΔΔG_hyd in Table 1, as well as the altered protein–ligand nonbonded interactions. Finally, adding the extra point sites to Met102 (Figure 7) results in a relative binding free energy of −0.37 kcal/mol, which is in excellent agreement with the experiment (−0.57 kcal/mol). Thus, it appears that the accurate treatment of the electrostatic potential around the NH group of indole is an important determinant of binding. In this regard, note that several experimental and theoretical studies have highlighted the importance of N–H···S hydrogen bonds in protein biochemistry.⁷⁷⁻⁷⁹ While the studied substitution demonstrates the feasibility and benefits of the developed methods, clearly many more comparisons with benchmark data must be performed to ascertain the accuracy for drug discovery applications.

4. Conclusions

In this paper, the feasibility of deriving the nonbonded parameters of molecular mechanics (MM) force fields from large-scale density functional theory (DFT) calculations has been demonstrated. Atomic charges and LJ coefficients are all computed directly from partitioned atoms-in-molecule electron densities, thus incorporating local and long-ranged polarization that is specific to the environment under study, while requiring only a minimal number of fitting parameters. This latter feature is a key part of the new force field. In the current study, all of the nonbonded interactions of 41 organic molecules and the lysozyme protein were described using just seven fitting parameters (the van der Waals (vdW) radii of the free atoms in a vacuum (R^free), presented in Table S1 in the Supporting Information). Users of the force field will be able to derive parameters for their own environment-specific force fields using these simple input parameters and the procedure outlined in Figure 2.

In contrast, typical transferable force fields require a large number of fitting parameters to describe the wide ranging chemistry of intermolecular interactions in organic molecules. In these standard MM force fields, if one wishes to investigate the effect of computing atomic charges with a method different from that was used to parametrize the Lennard-Jones (LJ) interactions (for example, using a larger quantum mechanics (QM) basis set), then, for the sake of consistency, the entire library of LJ parameters should be refit, which is a formidable undertaking and one that discourages advances in force field accuracy. In our proposed atoms-in-molecule (AIM) force field, both charge and LJ parameters update consistently with changes in the QM atomic electron densities. Since liquid densities are extremely sensitive to the atomic size, the R^free parameters are straightforward to fit to the experiment and, thus, a new force field could be developed within less than a week. This simplicity of design will allow the straightforward investigation of new QM methods and potentially even new functional forms of the force field. In this regard, a goal of this investigation has been to investigate the accuracy of AIM force field parameters within the fixed functional form of eq 1, such that the methods are consistent with the majority of widely used MM codes. Future studies will investigate alternative functional forms of the repulsive vdW potential, such as an exponential Born-Mayer form,³³ and the inclusion of explicit atomic polarizability. In this regard, combinations of density-derived electrostatic and chemical (DDEC) electron density partitioning with standard Tkatchenko–Scheffler (TS) methods^16,17 and also with a new self-consistent screening method to compute atomic polarizabilities and dispersion coefficients are currently under development.⁸⁰

Note that only the nonbonded parameters of the force field have been derived in this study, while the bonded parameters have been taken directly from the OPLS-AA force field. We have not tested these nonbonded parameters with other force fields. The compatibility of the AIM nonbonded parameters with the bonded parameters of standard force fields—in particular, the torsional parameters—will need to undergo substantial benchmarking against experimental properties such as nuclear magnetic resonance (NMR) measurements^7,22 and temperature-dependent structural propensities,¹ which is beyond the scope of the current study. The accuracy of our results for the small molecule benchmark set implies that the use of OPLS-bonded parameters is a reasonable approximation, although these molecules are relatively rigid. Possible long-term strategies for improving the compatibility between bonded and nonbonded parameters involve on-the-fly parametrization of torsional parameters for an AIM protein and small molecule force field using existing⁷ and automatically generated^2,19 QM torsional scans, or machine learning of bonded force fields.⁸¹

The data presented in Figure 5 reveal that the free energies of hydration appear to be difficult to predict computationally. Part of the reason for this may be that we have used the standard TIP4P water model for these calculations. While this model has been extensively validated against experimental data, other combinations of nonbonded parameters also accurately describe many physical properties of water.³² In future research, it would be interesting to develop a water model based on our AIM force field parametrization strategy to investigate whether it improves the correlation between computed free energies of hydration and the experiment.

One of the advantages of the proposed methods, namely, the specificity of the parameters to their environment, is also one of the potential disadvantages. The derived force field is not expected to be transferable between different systems, and, hence, a new QM calculation is required to parametrize each new molecule under investigation. However, this is not expected to add a substantial time cost to the investigation. To draw an example from our own interests in computer-aided drug design, it is already commonplace to perform a series of inexpensive QM calculations to parametrize a set of small molecule drug candidates, while the only additional cost in the new scheme would be a single large-scale DFT calculation to parametrize the target protein.

In this investigation, we have used DDEC electron density partitioning as implemented in the ONETEP linear-scaling DFT code to compute the atomic electron densities, and a variant of the Tkatchenko–Scheffler method to compute vdW coefficients. DDEC partitioning has been shown to yield an efficiently converging multipole expansion of the electrostatic potential,²⁸⁻³¹ which is important for minimizing anisotropies in the atomic densities. Here, it has been shown that residual anisotropy may be accurately represented by a small number of off-center charges. A further advantage of DDEC partitioning for flexible force field design is that the computed atomic electron densities are relatively insensitive to small changes in conformation,^29,31 thus dynamical simulations of a protein fluctuating about its native state are expected to be accurate, while the applicability of the derived force fields to protein folding may be questionable and will require extensive validation. The use of the TS method for the computation of environment-specific dispersion coefficients is, to the authors’ knowledge, its first use in MM force field design, although Grimme has recently used the D3 dispersion scheme as part of a quantum mechanically derived force field (QMDFF) with extremely encouraging results.¹⁹ The agreement between computed and experimental liquid properties and free energies of hydration in the current study further supports the use of nonempirical vdW parameters in force field design. In future work, it will be interesting to investigate the effects of long-ranged electrodynamic screening effects that are thought to dampen dispersion interactions in the condensed phase.^17,18

In this paper, we have benchmarked the accuracy of AIM nonbonded parameters in the description of ∼120 experimental liquid densities, heats of vaporization, and free energies of hydration. The obtained results are extremely competitive with existing transferable force fields that have been specifically parametrized against similar datasets. Furthermore, all of the methods described here scale linearly with system size and are accurate even for buried atoms,²⁸⁻³¹ thus allowing the derivation of environment-specific force fields for systems of unprecedented size. Recent advances in LS-DFT algorithms and access to GPU computing will allow rapid and routine electronic structure analysis of systems comprising tens of thousands of atoms in the future.^27,82,83 The largest molecule studied in this paper is a substantial portion of the L99A mutant of T4 lysozyme, consisting of 1646 atoms. The computed relative free energies of binding of indole and benzofuran to the protein are encouraging and demonstrate the importance of accurately modeling anisotropic electron density. While we would encourage users to experiment with deriving their own environment-specific force fields by following the scheme suggested in Figure 2, we emphasize that further validation is required before their widespread adoption. Our own priorities are (i) to test the compatibility between AIM nonbonded parameters and standard bonded force fields, and to develop alternative bonded force fields if necessary, and (ii) to run hundreds of free-energy calculations across multiple protein targets to extensively compare the accuracy of environment-specific force fields with state-of-the-art transferable force fields in the description of protein–ligand binding.^2,84

Supporting Information Available

This material is available free of charge via the Internet at http://pubs.acs.org/. The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.6b00027.

• Supporting methods, optimal dielectric constant for computing atomic charges, free atom reference data, comparison between DFT and MP2 dipole moments, extra point charge site derivation, raw data, and experimental references for Figure 5 (PDF)

• DDEC nonbonded parameters for the 41-molecule test set and lysozyme (XLSX)

The authors declare no competing financial interest.