Monte Carlo Simulation of the Treatment of Eye Tumors with ¹⁰⁶Ru Plaques: A Study on Maximum Tumor Height and Eccentric Placement

Abstract

Background/Aims

Ruthenium plaques are used for the treatment of ocular tumors. There is, however, a controversy regarding the maximum treatable tumor height. Some advocate eccentric plaque placement, without a posterior safety margin, to avoid collateral damage to the fovea and optic disc, but this has raised concerns about marginal tumor recurrence. There is a need for quantitative information on the spatial absorbed dose distribution in the tumor and adjacent tissues. We have overcome this obstacle using an approach based on Monte Carlo simulation of radiation transport.

Methods

CCA and CCB ¹⁰⁶Ru plaques were modeled and their geometry embedded in a computerized tomography scan of the eye of a patient. Different tumor sizes and locations were simulated with the general-purpose Monte Carlo code PENELOPE.

Results

Cumulative dose-volume histograms were obtained for the tumors and the tissues at risk considered. Plots of isodose lines for both plaques were obtained in a computerized tomography study.

Conclusions

Ruthenium eye plaques are an adequate treatment option for tumors up to around 5 mm in height. According to our results, assuming a correct placement of the plaque, a tumor of 6.5 mm apical height is about the maximum size that can be treated safely with the large CCB plaque.

Introduction

Uveal melanoma is a common intraocular tumor in adults. Brachytherapy with ¹⁰⁶Ru plaques is one of the treatments intended to preserve the eye and to maintain visual acuity to some extent [1]. The surgical technique for placing an eye plaque consists of a full or partial peritomy for exposing the sclera in the tumor area. Then any eye muscle in the base of the melanoma must be disinserted. Some surgeons opt to disinsert muscles even if they are not in the tumor base in order to facilitate the placement of the plaque, particularly in posterior tumor locations [2]. It is common practice to place the plaque centrically over the tumor, overlapping its base by at least 2 mm in all directions [3]. However, some surgeons choose an eccentric location of the plaque either when anatomical structures around the eye do not facilitate a centric placement or in situations in which a centric location could result in a large dose to structures at risk such as the papilla, the optic nerve, the fovea, the macula or the eye lens [3].

The tumor control rates, number of patients with preserved useful vision, risk of local recurrence, number of metastases, number of enucleations and survival rates after brachytherapy with ¹⁰⁶Ru plaques vary from one research group to another [3,4,5,6,7,8]. Some groups have concluded that ¹⁰⁶Ru plaques are of limited use [5,9], while another group considers these plaques adequate even when used in eccentric placements or for large tumors whose height exceeds 5 mm [10]. There are many reasons why the rate of treatment failure shows large variation, from 5 up to 40%, depending on the study considered. Some of these reasons are: (1) each research group uses different criteria for selecting patients to be treated with ¹⁰⁶Ru plaques based on tumor size and location [8,11]; (2) different surgical techniques for plaque placement are employed, with some groups routinely disinserting any extraocular muscle affecting the position of the plaque; (3) some groups confirm the plaque position after surgery, while others do not [12], and (4) different dose prescriptions for the tumor are given, with minimum apical doses ranging from 60 to 130 Gy. These discrepancies reflect that, in general, there is no full consensus on critical aspects of the treatment such as patient eligibility, maximum tumor size and location, surgical techniques, plaque placement, delivered dose and adjuvant therapies [13,14].

A vast literature is available on the adequacy of ¹⁰⁶Ru plaques for the treatment of uveal melanomas (see Pe'er [2] and the references therein). However, most published works base their conclusions on retrospective clinical studies. There is a lack of knowledge about the spatial absorbed dose distribution in the structures at risk and in the tumor volume [15]. Quantitative knowledge about the spatial dose distribution in the tumor and in the structures at risk is necessary, although not sufficient, for determining the reasons for the success or failure of the therapy in a given patient, and it is also desirable for improving the technique of placement of the plaque.

For almost three decades, the Monte Carlo simulation of radiation transport has been used to estimate the absorbed dose in radiotherapy patients [16]. The Monte Carlo estimation of dose absorption is regarded as one of the most accurate dose computation methods. In particular, the results obtained with Monte Carlo simulations for small radiation fields, like the ones required for eye irradiation, are more accurate than those computed with analytical or semi-analytical algorithms [17,18]. However, until recently, to the best of our knowledge, only six published studies had mainly focused on the use of Monte Carlo simulations to estimate the dose delivered by ¹⁰⁶Ru plaques [19,20,21,22,23,24]. All six works estimated the dose in a spherical homogeneous water phantom, disregarding the anatomical structure of the eye and the orbit.

We present results from a Monte Carlo algorithm of radiation transport that incorporates a realistic model of a plaque embedded in a computerized tomography scan of the eye while simulating the continuous beta decay spectrum. The scope of this study was to simulate a generalized case from which general conclusions about the treatment with ruthenium plaques can be derived. In particular, we aimed at giving guidance on the largest tumor height value that can be treated with a ¹⁰⁶Ru plaque based on dosimetric results obtained from the simulations, taking into account the centric or eccentric placement of the plaque. Our simulations computed the spatial absorbed dose distribution in the computerized tomography scan of a patient, allowing obtaining isodose maps and dose-volume histograms for the target volume and structures at risk. These maps and histograms provide quantitative information on the treatment that up until now has not been available.

Materials and Methods

Simulation Codes

The radioactive isotope ¹⁰⁶Ru decays into ¹⁰⁶Rh, producing a beta spectrum with a maximum energy of 39 keV and a half-life of 368 days. ¹⁰⁶Rh then decays into stable ¹⁰⁶Pd, producing a beta spectrum with a maximum energy of 3.540 MeV and a half-life of 29.8 s. This latter disintegration is used for therapeutic purposes. Simulations were run with the Monte Carlo general-purpose radiation transport code PENELOPE [25,26] using penEasy [27] as the main steering program. penEasy is not prepared for simulating a spectrum resulting from a beta decay; therefore, the original code was modified to simulate the decay of ¹⁰⁶Rh into ¹⁰⁶Pd through the five disintegrations with the highest yields, i.e. 3.540 MeV (78.6%), 3.050 MeV (8.1%), 2.410 MeV (10.0%), 2.000 MeV (1.77%) and 1.539 MeV (0.46%) [28]. For each primary particle sampled, an endpoint energy was chosen at random according to the probabilities given by the yields. The initial electron energies were then sampled at random from the corresponding beta decay spectrum. The beta decay spectra were generated with an adapted version of the code EFFY [29] incorporated in the modified penEasy code. EFFY calculates beta spectra from the Fermi theory of beta decay, taking shape factors into account.

Geometry of the Plaques

The eye plaques we used for this study were models CCA and CCB produced by the manufacturer BEBIG (Eckert & Ziegler BEBIG, Berlin, Germany). These plaques are shaped like truncated spherical shells. The inner radius of the shells, along the symmetry axis, is 12.0 mm. The outer diameters of the shells, across the rim, are 15.5 and 20.2 mm for the CCA and the CCB plaques, respectively. Both shells are 1.0 mm in thickness and are divided into 3 layers. The thicknesses of these layers from the inner to the outer surface of the shell are 0.1, 0.2 and 0.7 mm. All layers are made of silver, with the middle layer containing the emitter substance. However, the emitter substance does not cover the whole shell, falling short of the shell rim by 0.7 mm. With the exception of the diameter across the shell, all other dimensions are equal for the CCA and the CCB plaques. The geometries of the plaques were modeled using the constructive quadric geometry package provided by PENELOPE, which defines bodies by grouping quadric surfaces (spheres, planes, etc.). The distribution of the emitter substance was assumed to be homogeneous. The accuracy of our simulation system for eye plaques was previously validated by comparison of our simulated data in a water phantom with experimental results [30].

Voxelized Geometry

A computerized tomography scan of the eye of an anonymized adult patient was used as a voxelized human phantom. The size of an emmetropic eyeball does not show large variation from one individual to another [31]. It is, therefore, justified to employ a phantom based on only one individual for the investigation we are presenting, whose scope is to allow general conclusions on the dose distribution obtained using a generalized model. The axial length of the eye employed in this study was 22.8 mm. Earlier versions of this phantom were already used in previous works [32,33]. The computerized tomography scan had 256 × 256 × 59 voxels of 0.03125 × 0.03125 × 0.1 cm size. Hounsfield units of the original computerized tomography were converted into mass density values via the calibration curve of the computerized tomography scanner. For material assignment, three media were considered: water, air and bone. Provided the mass density of each voxel is correctly assigned through the calibration curve of the scanner, the approximation of different soft tissues to water produces compatible doses within the standard statistical uncertainty (2%) reached in the simulation results. A distinctive feature of penEasy is the possibility of simulating quadric geometries superimposed on voxelized geometries. This feature allows the simulation of the geometry of the eye plaque, defined as a spherical shell, positioned inside the voxelized human phantom.

Tumors, Plaque Locations and Organs at Risk

The basal extent of a tumor determines the size of the eye plaque to be used, with larger plaques used for tumors with larger basal extension. The apical height of a tumor determines the applicability of ¹⁰⁶Ru eye plaques, which in its turn is dictated by the penetration depth of the electrons derived from the beta decay process. Following this reasoning, we decided to study the treatment using idealized tumor volumes, the apical height of which we varied while keeping their basal diameter constant. The idealized tumor volumes were segmented in the computerized tomography scan with a paraboloid truncated by a sphere representing the inner scleral surface. The sclera was defined by means of a spherical shell of a thickness of 1.7 mm. The height of the tumor did not include the thickness of the sclera.

Although spheres and paraboloids were used as boundary surfaces in the segmentation process of the sclera and the tumor volumes, these structures (i.e. sclera and tumors) were actually defined in the computerized tomography study; this means that a voxel divided by a boundary surface was either assigned to the corresponding structure or to the ‘outside’. The immediate consequence of this voxelized definition of the structures is that the thickness of the sclera is not constant, ranging from approximately 1.2 mm to approximately 2.1 mm depending on the number of voxels that are included between the two boundary spherical surfaces used for defining the sclera at any location. The chosen scleral thickness, although larger than that normally seen in patients, gives a safety margin of about 0.5 mm. Additionally, the chosen thickness is in agreement with the default value of 1.5 mm employed in the code EYEPLAN [34,35].

The same situation as described for the definition of the sclera arises when defining the tumor volumes. Owing to the voxelized nature of the segmented tumor volumes, all reported tumor apical heights lie within ±0.5 mm of the quoted value. In contraposition, it must be stressed that the geometry of the eye plaques was actually modeled as a spherical shell and embedded in the computerized tomography scan; thus, the thickness of the eye plaques is constant. Other segmented structures of the eye for this study were the cornea, the lens and the optic disc. The structures in the orbit that were segmented in this model were the optic nerve and the lacrimal gland.

All tumor models were done nasally from the optic nerve. The symmetry axes of the tumors were made coplanar with the computerized tomography axial plane where the eyeball showed its largest diameter. Tumors were placed in 3 nasal (i.e. medial) locations: equatorial, anterior (i.e. pre-equatorial) and posterior (i.e. postequatorial). Equatorial tumors have their symmetry axis along the eyeball equator, which was determined to be 15° above an imaginary horizontal axis (with respect to the computerized tomography) passing through the center of the eyeball. The anterior location was set at 15° above the equator, i.e. 30° above the horizontal axis. The posterior location was set 45° below the equator, i.e. 30° below the horizontal axis. All tumors had a basal diameter of 10 mm. Five tumor heights were considered for the equatorial location, namely 3, 5, 6.5, 7 and 7.5 mm. The apical height of the anterior and posterior tumors was set at 3 mm in both cases.

Eye plaques were placed according to tumor position. With the pre-equatorial and equatorial tumors, the CCA plaque was placed centrically with respect to the tumor. With the postequatorial tumor, the CCA plaque was placed eccentrically with respect to the tumor, with its symmetry axis 15° below the horizontal axis instead of 30°. The CCB plaque was only placed in the equatorial position (centric to the equatorial tumors). Figure 1 shows the positions of the plaques and the tumors.

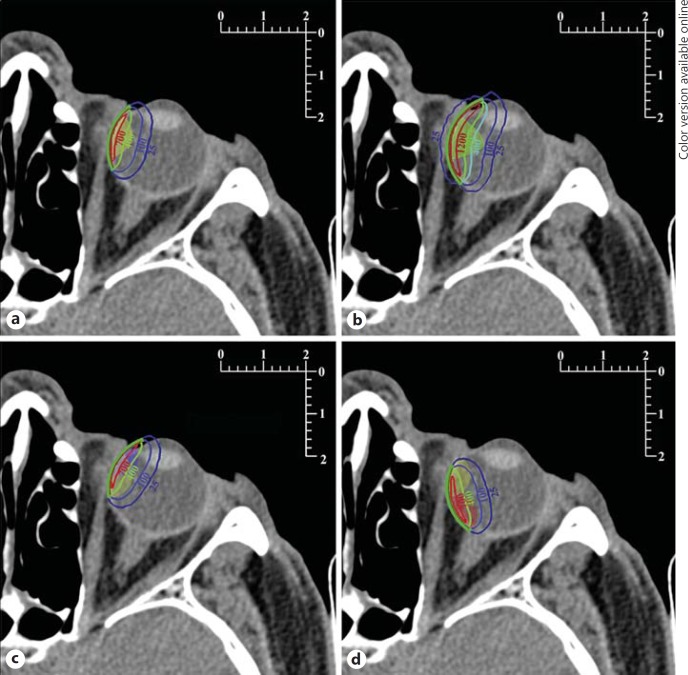
Fig. 1.

Isodose lines plotted on the slice coplanar with the plaques' symmetry axes. Metric scales are in centimeters. The cross-sections of the plaques are drawn in green (colors in online version only) with the emitter layers in red. The labels of the isodose lines are given in gray (Gy). Tumors are shown as translucent areas. Other tumor sizes can be inferred by the reader using the accompanying metric scales. a Equatorial 3-mm tumor treated centrically with the CCA plaque. b Equatorial 6.5-mm tumor treated centrically with the CCB plaque. c Equatorial 3-mm tumor treated eccentrically from the anterior position with the CCA plaque; the anterior tumor is also shown. d Equatorial 3-mm tumor treated eccentrically from the posterior position with the CCA plaque; the posterior tumor is also shown.

Dose Prescription

The simulations run with PENELOPE estimated the absorbed dose at each voxel of the computerized tomography scan. The computed dose is expressed in units of electron volt per gram per primary particle. These units can be converted to milligrays per megabecquerel-hours. The dose in gray can then be obtained by knowing the activity of the plaque in megabecquerel and the irradiation time in hours. The activities of the CCA and CCB BEBIG plaques, as quoted by the manufacturer, are 13.7 and 25.9 MBq, respectively.

To determine the irradiation time, we used the following dose prescription method. The time required for achieving a dose of 700 Gy to the sclera is calculated. If the tumor apex receives a dose greater than 100 Gy, the treatment is performed using that time. If not, then the irradiation time is increased until the apical dose is 100 Gy. If, however, the new time results in a scleral dose exceeding 1,500 Gy, then the ¹⁰⁶Ru plaque is rejected and other plaque models or alternative treatments are considered. The apical minimum dose chosen for the present study (100 Gy) was a compromise between the apical dose commonly used in many hospitals, i.e. between 80 and 100 Gy, and that prescribed at the Universitätsklinikum Essen, which is 130 Gy. Usage of the prescription of 700 Gy to the sclera gives a reasonable allowance for uncertainties associated with the measurement of the apical height of the tumor or with the process of plaque placement.

The apical and scleral doses reported from Monte Carlo simulations in this work are absorbed doses at a voxel. In the case of the apical dose, the voxel belonging to the tumor volume located at the greatest distance from the eye plaque is used. For the scleral dose, the voxel belonging to the segmented sclera closest to the eye plaque and located along the symmetry axis of the plaque is used. The described dose prescription method was employed to calculate the apical tumor and scleral doses for each tumor if treated with the CCA and the CCB plaques by means of the spatial dose distributions obtained with the PENELOPE simulations (table 1).

Table 1.

Dose prescription for the different tumor locations, tumor apical heights and plaque models

Location	Height, mm	Plaque	Sclera, Gy	Apex, Gy	Time, h
Anterior	3	CCA	700	128	96
Posterior	3	CCA	700	100	109
Equatorial	3	CCA	700	153	116
Equatorial	3	CCB	700	161	107
Equatorial	5	CCA	1,361	100	227
Equatorial	5	CCB	892	100	171
Equatorial	6.5	CCA	3,083	100	514
Equatorial	6.5	CCB	1,787	100	343
Equatorial	7	CCA	6,249	100	1,041
Equatorial	7	CCB	3,032	100	581
Equatorial	7.5	CCA	6,856	100	1,142
Equatorial	7.5	CCB	3,058	100	586

Doses to the sclera exceeding the 1,500-Gy limit are typeset in italics.

Assessment of the various treatments was done using isodose curves and cumulative dose-volume histograms. In order to calculate the latter, the aforementioned segmentation of the tumor volumes and the structures at risk was used in conjunction with the spatial dose distributions estimated with the PENELOPE simulations. Cumulative dose-volume histograms plotted the percentage of the volume of the segmented structure that receives a dose equal to or greater than the value in the abscissa. In the cases of eccentric plaque placement, the irradiation time used was that of the corresponding centric irradiation, with the exception of the posterior tumor irradiation for which all placements are eccentric.

Results and Discussion

Study of Tumor Size

Small Tumors (3 and 5 mm Apical Height)

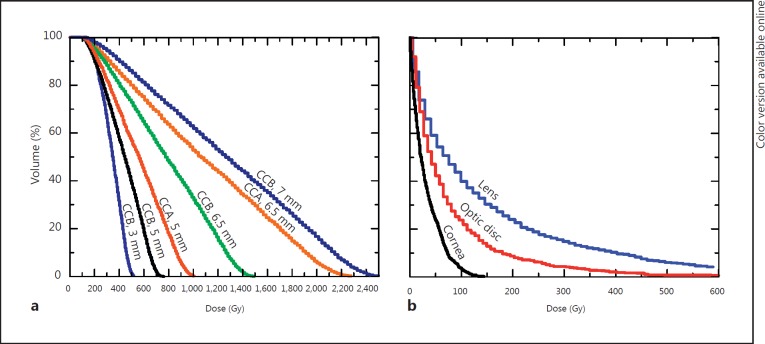
The dependency of cumulative dose-volume histograms on tumor height is reproduced in figure 2a, which shows plots corresponding to equatorial tumors treated centrically. Only the 3-mm (fig. 1a) and the 5-mm tumors are adequately treated. For the 3-mm tumor and CCA plaque, 100% of the tumor volume receives a dose of at least 140 Gy. Our modeled 5-mm-thick tumor can be treated with either the CCA or the CCB plaque, both of which deliver a dose of at least 100 Gy to 100% of the tumor volume, which is the prescribed minimum dose (fig. 2a). The dose coverage is slightly better with the CCB plaque. The risk of collateral damage to the optic disc, however, is smaller with the CCA plaque. Treating a 5-mm-thick equatorial tumor would deliver 50-200 Gy to 20% of the optic disc volume if a CCB plaque were used (fig. 3a, histogram ‘CCB equator, 5 mm’), as compared with a maximum of only 30 Gy being delivered to the whole optic disc with a CCA plaque (fig. 3a, histogram ‘CCA equator, 5 mm’).

Fig. 2.

a Cumulative dose-volume histograms for equatorial tumors of different sizes, all irradiated centrically with equatorial plaque placement. Each histogram label indicates the plaque used and the height of the treated tumor. ‘CCB plaque, 7.5 mm’ is not shown, since it is similar to the 7-mm case. b Cumulative dose-volume histograms for structures and organs at risk if a 7-mm equatorial tumor is irradiated centrically with a CCB plaque.

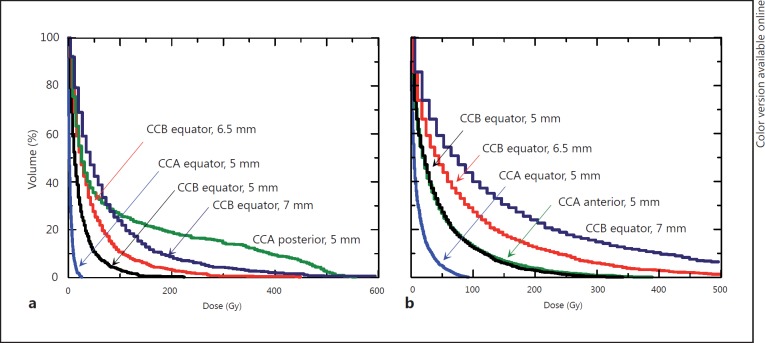
Fig. 3.

Cumulative dose-volume histograms obtained for ocular structures at risk. Each histogram label indicates the plaque used, its placement and the tumor height. a Dose-volume histograms for the optic disc. b Dose-volume histograms for the lens.

The treatment of a 6.5-mm-thick equatorial intraocular tumor is shown in figures 1b and 2a. Of the two plaques studied, neither can be used for the treatment of this tumor without exceeding the 1,500-Gy limit to the sclera (table 1). Cumulative dose-volume histograms of the tumor are plotted for each plaque in figure 2a (histograms ‘CCA, 6.5 mm’ and ‘CCB, 6.5 mm’). If treatment of the 6.5-mm tumor with the CCB plaque were accepted with a dose to the sclera of 1,787 Gy, the entire tumor volume would receive the minimum prescribed dose of 100 Gy, but 40% of the tumor volume would absorb doses ranging from 1,000 to 1,500 Gy, with sight-threatening doses being delivered to the lens, optic disc and cornea (fig. 1b) [36,37,38,39]. The optic nerve would also receive a dose similar to that to the optic disc, whereas the lacrimal gland would receive a tolerable dose of only 3 Gy. Figure 3 shows how the dose-volume histograms for the optic disc and the lens, respectively, increase with the size of the plaque and the proximity of placement to the structure at risk.

Large Tumors (7 and 7.5 mm Apical Height)

The irradiation of tumors larger than 6.5 mm in apical height either with the CCB or the CCA plaque would require a dose greater than 2,000 Gy to the sclera (table 1), which is not acceptable according to the dose prescription method used at Essen. The cumulative dose-volume histograms of the lens, optic disc and cornea (fig. 2b) for a tumor 7 mm in apical height also reveal excessive doses to these structures at risk [35,36,37,38].

Eccentric Treatment

Anterior Tumor

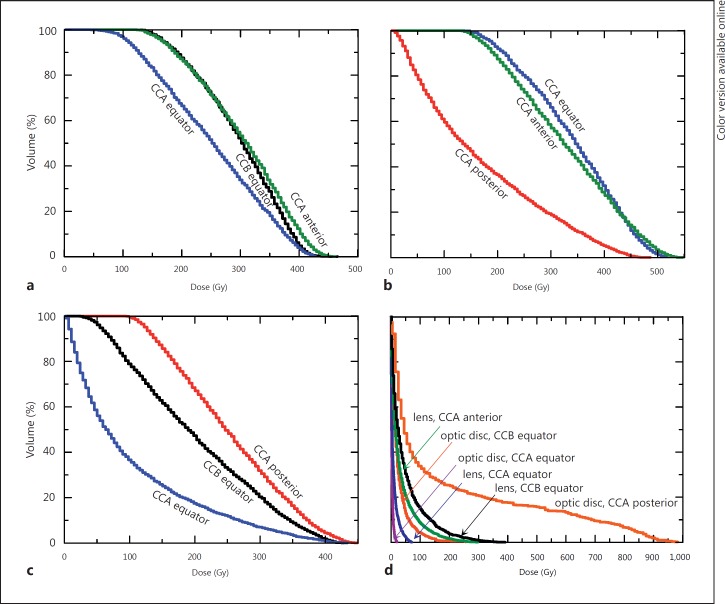
Figure 4a (histogram ‘CCA anterior’) shows that if a 3-mm-thick tumor is treated with a centrically placed CCA plaque, 100% of the tumor volume receives a dose of at least 130 Gy. However, with the same tumor treated with an eccentrically placed CCA plaque (i.e. equatorial plaque with pre-equatorial tumor), the dose delivered to the lens is reduced by 80% (fig. 4d, histograms ‘lens, CCA anterior’ and ‘lens, CCA equator’; fig. 1a), albeit at the cost of reducing the dose to the tumor to 50 Gy (fig. 4a, histogram ‘CCA equator’). If a 3-mm-thick pre-equatorial tumor is treated with an eccentrically placed CCB plaque, the tumor receives the same dose that it would absorb with a centrically placed CCA plaque (fig. 4a, histograms ‘CCB equator’ and ‘CCA anterior’), but the lens absorbs slightly more of the dose, i.e. up to an additional 10% (fig. 4d, histograms ‘lens, CCB equator’ and ‘lens, CCA anterior’).

Fig. 4.

Cumulative dose-volume histograms obtained for the 3-mm tumors and structures at risk. Each histogram label indicates the plaque used and its placement. a Anterior tumor. b Equatorial tumor. c Posterior tumor. d Structures at risk obtained with irradiation of the 3-mm melanomas.

Equatorial Tumor

Following our dose prescription method, a 3-mm equatorial tumor receives a minimum dose of 135 Gy if treated with a CCA plaque, whether this plaque is positioned equatorially or pre-equatorially (fig. 4b, histograms ‘CCA equator’ and ‘CCA anterior’; fig. 1c, a). For tumors with an apical height of 3 mm or less, it follows that eccentric placement with the edge of the plaque aligned with the lateral tumor margins is acceptable and is equivalent in terms of dose coverage to the tumor to centric treatment in which the plaque overlaps the tumor by at least 2 mm in all directions. It must be remembered that the emitter in the eye plaque does not cover its full surface but falls short of the rim of the plaque by 0.7 mm. Therefore, a plaque aligned with the tumor edge leaves an area uncovered by the emitter substance. It is reassuring that, despite this uncovered area of the tumor base, the dose coverage to a tumor obtained with eccentric treatment does not differ from that reached with centric treatment for tumors of apical heights of less than 3 mm.

Posterior Tumor

Figure 4c shows the cumulative dose-volume histograms obtained for the 3-mm posterior tumor if irradiated eccentrically from a posterior placement with a CCA plaque (histogram ‘CCA posterior’) and with a larger eccentricity from an equatorial placement with a CCB (histogram ‘CCB equator’) or a CCA (histogram ‘CCA equator’) plaque. If the eccentric placement implies that the plaque does not cover 2 mm or more of the tumor base, there are parts of the tumor that do not receive the minimum dose prescribed (fig. 1d). This holds true even for treatments done with a plaque larger than necessary, as is the case in this eccentric treatment of a tumor of 3 mm apical height with a CCB plaque. An eccentric irradiation of the posterior tumor from a posterior CCA plaque delivers a maximum dose of about 550 Gy to the optic disc (fig. 4d, histogram ‘optic disc, CCA posterior’), with the tumor absorbing a dose of at least 100 Gy (fig. 4c, histogram ‘CCA posterior’; fig. 1b). A small posterior melanoma is particularly problematic. An eccentric treatment from a posterior placement provides the minimum prescribed dose to the whole tumor volume at the expense of a large dose to the optic disc and the optic nerve.

Conclusions

With respect to the currently available treatment planning system, the advantage of the presented method of computing the dose distribution from a ¹⁰⁶Ru plaque on an eye is the possibility of obtaining dose-volume histograms for the planned target volume and structures at risk. This information allows the oncologist to better assess the adequacy of the treatment. An additional benefit of our method derives from the more accurate dose distribution achieved, since for its computation the real geometry as found in a patient as well as its inhomogeneous mass density distribution can be taken into account.

If the method is applied to a generalized phantom, as was done in our study, some general conclusions can be drawn. These conclusions must of course be put into perspective considering the abovementioned assumptions of the model and the dose prescription method followed at the Universitätsklinikum Essen. Our study suggests a large therapeutic window for the safe use of ¹⁰⁶Ru plaques for tumors with apical heights of less than 3 mm. The choice of plaque size will depend on the tumor dimensions and adjacent ocular structures at risk. Tumors with apical heights of 3 mm or less are adequately treated with CCA plaques if the tumor base is completely covered by the plaque. For tumors with apical heights between 3 and 5 mm, the ¹⁰⁶Ru plaque should overlap the tumor base by 2 mm. Tumors between 5 and 6.5 mm in thickness are, in principle, treatable with ¹⁰⁶Ru plaques, provided there exists an accurate knowledge of the tumor dimensions including subclinical lateral extensions. Furthermore, tumors of this size require accurate positioning of the plaque. Both conditions are difficult to meet, and thus the treatment of tumors more than 5 mm thick may increase the probability of local recurrence.

Regarding the controversy as to whether tumors of apical heights around 6.5 mm can be treated with ¹⁰⁶Ru plaques, our study shows that a centrically placed CCB plaque cannot deliver an apical dose of 100 Gy without exceeding the 1,500-Gy scleral dose limit enforced at Essen. With tumors exceeding 6.5 mm in thickness, our simulations show that high doses to the sclera, and hence to other structures of the eye, are required, thus increasing the risk of collateral damage. We cannot quantitatively evaluate the increased risk of damage and rely only on the clinical experience accumulated at Essen. In part, this limitation arises from the fact that most published radiation tolerances for the eye and the adnexa are obtained for fractionated external beam radiotherapy and, to a lesser extent, for eye brachytherapy with photon emitters, but not for brachytherapy with ¹⁰⁶Ru plaques [35,36,37,38].