Characterizing magnetic resonance signal decay due to Gaussian diffusion: the path integral approach and a convenient computational method

Abstract

The influence of Gaussian diffusion on the magnetic resonance signal is determined by the apparent diffusion coefficient (ADC) and tensor (ADT) of the diffusing fluid as well as the gradient waveform applied to sensitize the signal to diffusion. Estimations of ADC and ADT from diffusion-weighted acquisitions necessitate computations of, respectively, the b-value and b-matrix associated with the employed pulse sequence. We establish the relationship between these quantities and the gradient waveform by expressing the problem as a path integral and explicitly evaluating it. Further, we show that these important quantities can be conveniently computed for any gradient waveform using a simple algorithm that requires a few lines of code. With this representation, our technique complements the multiple correlation function (MCF) method commonly used to compute the effects of restricted diffusion, and provides a consistent and convenient framework for studies that aim to infer the microstructural features of the specimen.

1 Introduction

Diffusion-induced attenuation of the MR signal leads to unique image contrasts, which have been of great value in both clinical and basic science applications of MR. Such contrast emerges from variations in the diffusion decay rate, referred to as apparent diffusion coefficient (ADC) [1] when diffusion is measured along one orientation, and apparent diffusion tensor (ADT) [2] for the case of anisotropic diffusion. The amount of signal attenuation is controlled by the b-value [3] and b-matrix [4], respectively. Accurate estimations of ADC and ADT are possible only when all parameters of the pulse sequence (gradient waveform) are taken into account in b-factor estimations [5]. The dependence of the b-matrix on the gradient waveform can be exploited to devise novel diffusion sensitization schemes that lead to b-matrices with desired characteristics [6].

The b-factors enable one to fully characterize the effect of Gaussian diffusion on the MR signal. To address the same problem for restricted diffusion, the multiple correlation function (MCF) framework [7] has been developed in recent years following a number of important theoretical developments [8, 9, 10, 11]. Since its inception that featured the solutions for simple geometries of slabs, cylinders, and spheres, the MCF method has been formulated for layered structures [12, 13], capped cylinders [14], and triangular pores [15]. Other advances include the incorporation of surface relaxation [16], structure-specific susceptibility gradients [17], and most relevant for this work is the technique’s generalization to account for variations in the direction of the gradients [18] akin to the transition from b-value to b-matrix in the case of Gaussian diffusion.

Diffusion-weighted acquisitions have been employed widely to infer microstructural descriptors of the specimen under examination. In thin and long geometries like long cylindrical fibers, diffusion perpendicular to the long axis of the pore is restricted while diffusion is Gaussian along the axis. When the gradients are neither parallel nor perpendicular to the long axis, the solutions for restricted and free diffusion should be employed simultaneously. Within the brain, the presence of a Gaussian diffusion component and the benefits of eliminating it from the signal profile have been recognized [19, 20]. Moreover, multi-compartment descriptions of tissue microstructure have been proposed [21, 22] wherein diffusion within the cells is modeled as restricted and diffusion in the interstitial space is assumed to be Gaussian. In recent years, this approach has been employed to model the signal obtained using relatively complicated pulse sequences [23, 24, 25]. Common to all these problems and applications is the need for modeling Gaussian diffusion simultaneously with restricted diffusion. Therefore, a method that yields the free diffusion response using the stepwise gradient scheme employed by the MCF technique would yield a consistent framework that could be used to address these important problems.

In this work, we provide alternative approaches for characterizing signal decay due to Gaussian diffusion. After introducing the most essential concepts and relationships in the next section, we provide a detailed proof of the analytical expression for the b-factors in Section 3. In our proof, we employ a path integral approach, which provides a more intuitive description compared to earlier derivations. In Section 4, we demonstrate that the b-values and b-matrices necessary to quantify the attenuation due to Gaussian diffusion can be computed very conveniently and efficiently for all pulse sequences using a few lines of a computer program without the need to employ analytical derivations specific to a given pulse sequence [26, 27] or a symbolic mathematics software package [28] such as Maple or Mathematica. Both of these alternatives could be tedious and impractical for complicated waveforms like those employed in rapid imaging sequences. The input structure of our method is consistent with the MCF framework, thus making the technique suitable to be employed in studies where solutions for free and restricted diffusion are needed.

2 Basic concepts

The signal attenuation for Gaussian diffusion in one-dimension can be expressed as

$$E(b)=exp(-b{D}_0),$$ (1)

where D₀ is the diffusion coefficient and b is the b-value. Karlicek and Lowe [29] showed that for a general gradient waveform characterized by the function G(t), the b-value is given by

$$b={\gamma }^2{\int }_0^T{\left({\int }_0^{t}G(t^{\prime })\mathrm{d}{t}^{\prime }\right)}^2\mathrm{d}t,$$ (2)

where γ denotes the gyromagnetic ratio of the diffusing nuclei and T is the duration of the pulse sequence. Here, G(t) is assumed to be the “effective” waveform with appropriate sign reversals necessary to incorporate the effects of the 180° radiofrequency (RF) pulses.

For the more general case of three-dimensional diffusion characterized by the diffusion tensor D₀, these equations are [4]

$$E(\mathbf{b})=exp\left(-\sum _{i=x,y,z}\sum _{j=x,y,z}{b}^{ij}{D}_0^{ij}\right),$$ (3)

$$b^{ij}={\gamma }^2{\int }_0^T\left({\int }_0^t{G}^i(t^{\prime })\mathrm{d}{t}^{\prime }\right)\left({\int }_0^t{G}^j(t^{″})\mathrm{d}{t}^{″}\right)\mathrm{d}t.$$ (4)

Note that Eqs. 1–2 can be obtained from Eqs. 3–4 through the simple substitutions

$$D_0^{ij}=D_0{\delta }^{ij},$$ (5)

$$b=b^{xx}+b^{yy}+b^{zz},$$ (6)

where δ^ij is the Kronecker delta, which is unity when i = j and vanishes otherwise. Consequently, we henceforth focus on the three-dimensional problem, and employ the above substitutions in the end to obtain the solution for the one-dimensional problem.

3 The path integral approach for general gradient waveforms

In this section we shall introduce a new derivation of Eqs. 2 and 4. In earlier derivations [29, 30], the authors solved the Bloch-Torrey equation [31], which is a differential equation that describes the evolution of local magnetization. We instead employ only probabilistic concepts, express the signal as a path integral and subsequently evaluate it. The reader is referred to Ref. [32] for a recent discussion on the relations between the Bloch-Torrey equation and probabilistic concepts.

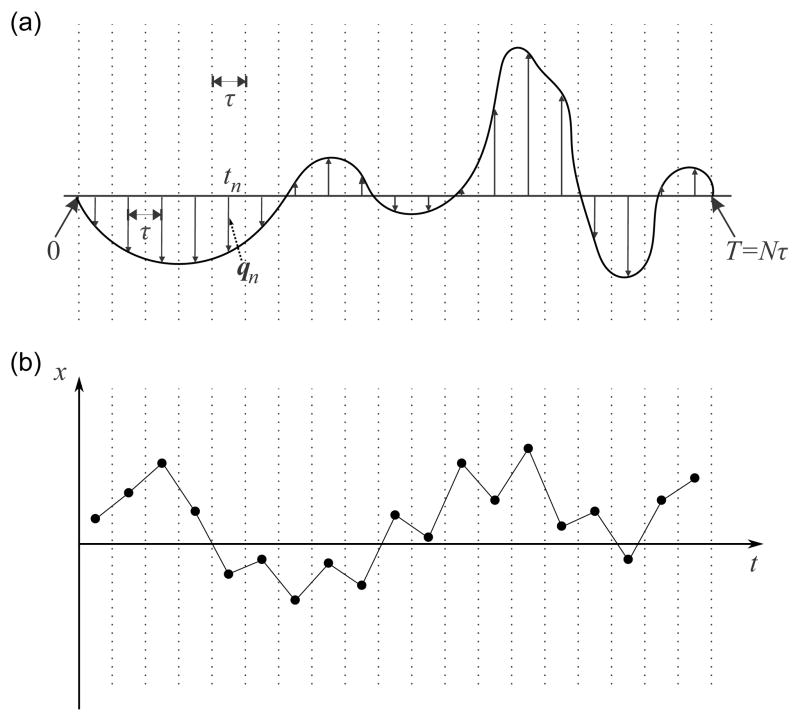
In Figure 1a, we illustrate a general gradient waveform G(t). This waveform is represented by a train of impulses indicated by vertical arrrows. This discretization or “time slicing” is performed by dividing the waveform into N equal intervals, each of duration τ [33]. The duration of the entire waveform is thus T = Nτ. The nth interval is centered at $t_n=(n-\frac{1}{2})\tau$. At this point in time, an impulse is assumed to be applied in lieu of the G(t) within the interval. The strength of the impulse is determined by the following useful quantity having dimension of inverse length:

$${\mathbf{q}}_n=\frac{\gamma }{2\pi }{\int }_{t_n-\frac{\tau }{2}}^{t_n+\frac{\tau }{2}}\mathbf{G}(t)\mathrm{d}t.$$ (7)

Figure 1.

(a) An arbitrary gradient waveform and its representation via a series of impulses. (b) The particle undergoes a random walk during the course of the waveform.

Note that in order for maximum detectable signal to form, the integral of G(t) during the course of the waveform should vanish, which results in the condition:

$$\sum _{n=1}^N{\mathbf{q}}_n=0.$$ (8)

Next, we shall consider the movement of a single spin. As shown in Figure 1b, the particle resides at a different location at each of the time points t_n. Depending on the position of the particle, it acquires a phase shift given by ϕ_n = 2πq_n · r_n. Thus, the phase of the particle at time T is $\varphi ={\sum }_{n=1}^N{\varphi }_n$. The MR signal is given by the sum of magnetic moments of each spin in the specimen, i.e.,

$$E=\underset{\tau \to 0}{lim}\int \mathrm{d}{\mathbf{r}}_1\int \mathrm{d}{\mathbf{r}}_2\dots \int \mathrm{d}{\mathbf{r}}_{N}P({\mathbf{r}}_1,{\mathbf{r}}_2,\dots ,{\mathbf{r}}_N;t_1,t_2,\dots ,t_N)exp\left(-i2\pi \sum _{n=1}^N{\mathbf{q}}_n·{\mathbf{r}}_n\right).$$ (9)

Here, t₁ < t₂ <…< t_N and P(r₁, r₂, …, r_N; t₁, t₂, …, t_N) denotes the probability density for the particle to be located at r₁, r₂, …, r_N at times t₁, t₂, …, t_N, respectively. The sequence of positions r₁, r₂, …, r_N defines a particular trajectory in the limit τ → 0, i.e., N → ∞ while Nτ = T. Thus, P(r₁, r₂, …, r_N; t₁, t₂, …, t_N) indicates the likelihood for a particular trajectory during the experiment. Expressions such as the one above are commonly referred to as “path integrals” as the integration is performed over the space of all possible paths. In summary, Eq. 9 symbolizes the fact that the particle collects different phases at different time points depending on its trajectory. Its resulting phase at t = T is determined by the gradient waveform G(t) as well as the path the particle travels r(t). The signal is just the sum of magnetic moment vectors (represented by the exponential factor) resulting from all possible trajectories.

We are now in a position to evaluate the path integral for Gaussian diffusion. To this end, we first exploit the fact that Gaussian diffusion is Markovian, i.e., the particle’s motion is not influenced by its motional history. For such processes, the following relationship holds:

$$P({\mathbf{r}}_1,{\mathbf{r}}_2,\dots ,{\mathbf{r}}_N;t_1,t_2,\dots ,t_N)=P({\mathbf{r}}_1,t_1)P({\mathbf{r}}_2,t_2\mid {\mathbf{r}}_1,t_1)P({\mathbf{r}}_3,t_3\mid {\mathbf{r}}_2,t_2)\dots P({\mathbf{r}}_N,t_N\mid {\mathbf{r}}_{N-1},t_{N-1}),$$ (10)

where P(r₁, t₁) is the density of particles at t₁, and P (r_n, t_n|r_n−1, t_n−1) denotes the conditional probability for a particle to move from r_n−1 to r_n during the time interval [t_n−1, t_n]. The latter is called the propagator. For Gaussian diffusion, it is given by^*

$$P({\mathbf{r}}_n,t_{n-1}+\tau \mid {\mathbf{r}}_{n-1},t_{n-1})=\frac{1}{{(4\pi \tau )}^{3/2}{\mid {\mathbf{D}}_0\mid }^{1/2}}{e}^{-{({\mathbf{r}}_n-{\mathbf{r}}_{n-1})}^{\top }{\mathbf{D}}_0^{-1}({\mathbf{r}}_n-{\mathbf{r}}_{n-1})/(4\tau )},$$ (11)

where |D₀| denotes the determinant of the diffusion tensor.

We would like to employ the last two equations in evaluating the path integral in Eq. 9. Let’s introduce a family of functions through the expression:

$$f({\mathbf{R}}_2,\mathbf{k},\{{\mathbf{K}}_1,{\mathbf{K}}_2,\dots ,{\mathbf{K}}_M\})=e^{-i2\pi \mathbf{k}·{\mathbf{R}}_2}exp\left(-4{\pi }^2\tau \sum _{n=1}^M{\mathbf{K}}_n^{\top }{\mathbf{D}}_0{\mathbf{K}}_n\right).$$ (12)

Here, {K₁, K₂, …, K_M } denotes any sequence of M vectors, where M can take any nonnegative integer value. For M = 0, the definition is simply f(R₂, k, {}) = e^{−i2πk·R₂}.

Next, we define an operator that we shall denote as ℒ_R2 (R₁, q). Here, the subscript is to indicate that the operator will act on functions of variable R₂. When applied on the family of functions introduced above, it yields

$${\mathcal{L}}_{{\mathbf{R}}_2}({\mathbf{R}}_1,\mathbf{q})f({\mathbf{R}}_2,\mathbf{k},\{{\mathbf{K}}_1,{\mathbf{K}}_2,\dots ,{\mathbf{K}}_M\})=\int \mathrm{d}{\mathbf{R}}_{2}P({\mathbf{R}}_2,\tau \mid {\mathbf{R}}_1,0)e^{-i2\pi \mathbf{q}·{\mathbf{R}}_2}f({\mathbf{R}}_2,\mathbf{k},\{{\mathbf{K}}_1,{\mathbf{K}}_2,\dots ,{\mathbf{K}}_M\}).$$ (13)

The integral above can be evaluated analytically. To this end, the integral is expressed in a frame of reference in which D₀ is diagonal. Noting that dot products, quadratic forms, and determinant of a matrix are invariant under rotations, the integral is decomposed into the product of three independent integrals, each of which being along one dimension in the new reference frame. The details of this scheme are provided in the Appendix. Following this approach, one obtains the result

$${\mathcal{L}}_{{\mathbf{R}}_2}({\mathbf{R}}_1,\mathbf{q})f({\mathbf{R}}_2,\mathbf{k},\{{\mathbf{K}}_1,{\mathbf{K}}_2,\dots ,{\mathbf{K}}_M\})=f({\mathbf{R}}_1,\mathbf{q}+\mathbf{k},\{{\mathbf{K}}_1,{\mathbf{K}}_2,\dots ,{\mathbf{K}}_M,\mathbf{q}+\mathbf{k}\}).$$ (14)

The utility of this finding becomes clear when one realizes that the path integral in Eq. 9 can be written in terms of the operator ℒ and the function f:

$$E=\underset{\tau \to 0}{lim}\int \mathrm{d}{\mathbf{r}}_{1}P({\mathbf{r}}_1,t_1)e^{-i2\pi {\mathbf{q}}_1·{\mathbf{r}}_1}{\mathcal{L}}_{{\mathbf{r}}_2}({\mathbf{r}}_1,{\mathbf{q}}_2){\mathcal{L}}_{{\mathbf{r}}_3}({\mathbf{r}}_2,{\mathbf{q}}_3)\dots {\mathcal{L}}_{{\mathbf{r}}_N}({\mathbf{r}}_{N-1},{\mathbf{q}}_N)f({\mathbf{r}}_N,0,\{\}).$$ (15)

Now we can employ Eq. 14 iteratively, and obtain

$${\mathcal{L}}_{{\mathbf{r}}_N}({\mathbf{r}}_{N-1},{\mathbf{q}}_N)f({\mathbf{r}}_N,0,\{\})=f({\mathbf{r}}_{N-1},{\mathbf{q}}_N,\{{\mathbf{q}}_N\})$$ (16)

$$\begin{array}{ll}\hfill {\mathcal{L}}_{{\mathbf{r}}_{N-1}}({\mathbf{r}}_{N-2},{\mathbf{q}}_{N-1}){\mathcal{L}}_{{\mathbf{r}}_N}({\mathbf{r}}_{N-1},{\mathbf{q}}_N)f({\mathbf{r}}_N,0,\{\})& =f({\mathbf{r}}_{N-2},{\mathbf{q}}_{N-1}+{\mathbf{q}}_N,\{{\mathbf{q}}_N,{\mathbf{q}}_{N-1}+{\mathbf{q}}_N\})\hfill \\ \hfill \dots & =\dots \hfill \end{array}$$ (17)

$${\mathcal{L}}_{{\mathbf{r}}_2}({\mathbf{r}}_1,{\mathbf{q}}_2){\mathcal{L}}_{{\mathbf{r}}_3}({\mathbf{r}}_2,{\mathbf{q}}_3)\dots {\mathcal{L}}_{{\mathbf{r}}_N}({\mathbf{r}}_{N-1},{\mathbf{q}}_N)f({\mathbf{r}}_N,0,\{\})=f({\mathbf{r}}_1,-{\mathbf{q}}_1,\{{\mathbf{q}}_N,{\mathbf{q}}_{N-1}+{\mathbf{q}}_N,\dots ,{\mathbf{q}}_2+{\mathbf{q}}_3+\dots +{\mathbf{q}}_N\}),$$ (18)

where we employed Eq. 8 in the second argument of f in the last expression. With this result, Eq. 15 reads

$$\begin{array}{l}E=\underset{\tau \to 0}{lim}\int \mathrm{d}{\mathbf{r}}_{1}P({\mathbf{r}}_1,t_1)e^{-i2\pi {\mathbf{q}}_1·{\mathbf{r}}_1}{e}^{i2\pi {\mathbf{q}}_1·{\mathbf{r}}_1}\\ \times exp\{-4{\pi }^2\tau [{\mathbf{q}}_N^{\top }{\mathbf{D}}_0{\mathbf{q}}_N+{({\mathbf{q}}_{N-1}+{\mathbf{q}}_N)}^{\top }{\mathbf{D}}_0({\mathbf{q}}_{N-1}+{\mathbf{q}}_N)+\dots \\ {({\mathbf{q}}_2+{\mathbf{q}}_3+\dots +{\mathbf{q}}_N)}^{\top }{\mathbf{D}}_0({\mathbf{q}}_2+{\mathbf{q}}_3+\dots +{\mathbf{q}}_N)]\}.\end{array}$$ (19)

Here, the first two exponentials cancel out, and the remaining exponential factor is independent of r₁, so it comes out of the integral. The remaining integral is just unity due to the normalization of the probability density.

Now we shall define a function F as the integral of the gradient waveform, i.e.,

$$\mathbf{F}(t)={\int }_0^t\mathbf{G}(t^{\prime })\mathrm{d}{t}^{\prime }.$$ (20)

Note that the following expression holds:

$${\mathbf{q}}_1+{\mathbf{q}}_2+{\mathbf{q}}_3+\dots +{\mathbf{q}}_n=\frac{\gamma }{2\pi }\mathbf{F}(n\tau ).$$ (21)

Eq. 19 becomes

$$E=\underset{\tau \to 0}{lim}exp\{-{\gamma }^2\tau [\mathbf{F}{(\tau )}^{\top }{\mathbf{D}}_0\mathbf{F}(\tau )+\mathbf{F}{(2\tau )}^{\top }{\mathbf{D}}_0\mathbf{F}(2\tau )+\dots +\mathbf{F}{(N\tau )}^{\top }{\mathbf{D}}_0\mathbf{F}(N\tau )]\}.$$ (22)

Using the definition of the Riemann integral, we obtain

$$E=exp\left[-{\gamma }^2{\int }_0^T\mathbf{F}{(t)}^{\top }{\mathbf{D}}_0\mathbf{F}(t)\mathrm{d}t\right],$$ (23)

which is just a restatement of Eqs. 3 and 4, thus concluding our derivation.

4 A convenient computational scheme

In this section we shall introduce a numerical scheme for computing the b-factors to characterize the effect of Gaussian diffusion. As pointed out in Introduction, our goal is to come up with a convenient scheme, which complements the solutions for restricted diffusion obtained through the MCF framework. As such, our approach differs from that described above. Instead, as in the case of MCF, we consider a piecewise function as the gradient waveform, and note that an arbitrary waveform can be approximated accurately by a piecewise constant function, making the technique applicable to all diffusion encoding schemes.

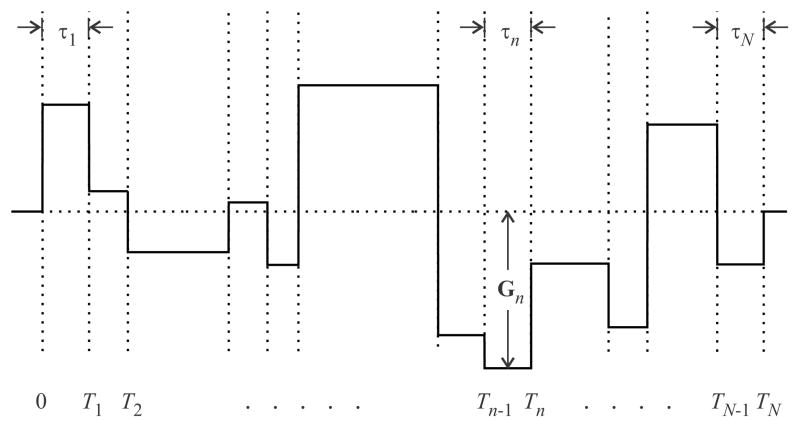
The construction of the piecewise function is the same as in Ref. [18], and illustrated in Figure 2. According to this scheme, the gradient waveform is represented as a series of N intervals of duration τ_n, where (n = 1, 2, 3, …, N). The time-independent gradient vector G_n is applied during the nth interval, which is between the time points T_n−1 and T_n. Thus, τ_n = T_n−T_n−1. The gradient waveform starts at the time point T₀ = 0, and ends at T_N = T.

Figure 2.

A piecewise-constant gradient waveform. When the gradient waveform is piecewise-constant, our computational scheme yields exact estimates for the b-factors.

We write the ith component of the gradient waveform as

$$G^i(t)=\sum _{n=1}^N{g}_n^i(t),$$ (24)

with

$$g_n^i(t)=\{\begin{array}{ll}\hfill G_n^i& \text{if}{T}_{n-1}\le t<T_n,\hfill \\ \hfill 0& \text{otherwise}.\hfill \end{array}$$ (25)

The time integral of Gⁱ(t) can be evaluated as

$$\begin{array}{l}{F}^i(t)={\int }_0^t{G}^i(t^{\prime })\mathrm{d}{t}^{\prime }\\ =\sum _{n=1}^N{f}_n^i(t),\end{array}$$ (26)

where

$$f_n^i(t)=\{\begin{array}{ll}\hfill 0& \text{if}t<T_{n-1}\hfill \\ \hfill G_n^i(t-T_{n-1})& \text{if}{T}_{n-1}\le t<T_n\hfill \\ \hfill G_n^i{\tau }_n& \text{if}{T}_n\le t.\hfill \end{array}$$ (27)

With these definitions, the components of the b-matrix can be written as

$$\begin{array}{l}{b}^{ij}={\gamma }^2{\int }_0^T{F}^i(t)F^j(t)\mathrm{d}t\\ ={\gamma }^2\sum _{m=1}^N\sum _{n=1}^N{I}_{mn}^{ij},\end{array}$$ (28)

where

$$I_{mn}^{ij}={\int }_0^T{f}_m^i(t)f_n^j(t)\mathrm{d}t.$$ (29)

After some algebra, these functions are obtained to be

$$I_{mn}^{ij}=\{\begin{array}{ll}\hfill G_n^i{G}_n^j{\tau }_n^2(T-T_{n-1}-\frac{2}{3}{\tau }_n)& \text{if}m=n\hfill \\ \hfill G_m^i{G}_n^j{\tau }_m{\tau }_n(T-T_{n-1}-\frac{1}{2}{\tau }_n)& \text{if}m<n\hfill \\ \hfill G_m^i{G}_n^j{\tau }_m{\tau }_n(T-T_{m-1}-\frac{1}{2}{\tau }_m)& \text{if}m>n.\hfill \end{array}$$ (30)

Plugging Eq. 30 into Eq. 28 provides us with an expression that relates the b-matrix to arrays of G_n and τ_n values^†. These arrays are also employed by the MCF technique for quantifying the effect of restricted diffusion. Hence, the above formulation can be regarded as a consistent extension of the MCF framework complementing it for the case of Gaussian diffusion. Moreoever, these results enable the computation of the b-factors, hence the effect of Gaussian diffusion, using a few lines of a computer program.

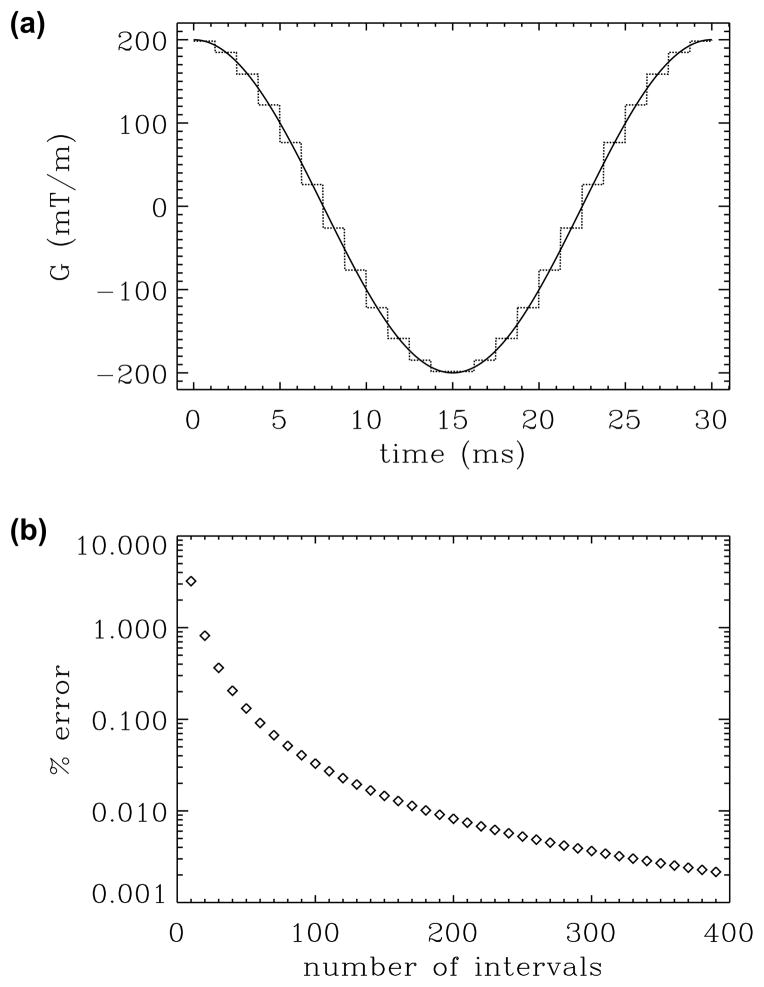
To establish the correctness of the computational scheme and assess its accuracy, we computed the b-value for a cosine-modulated waveform shown in Figure 3a. In Figure 3b, we plot the percent deviation in our b-value estimates from its theoretical value [35] against the number of distinct time intervals (in steps of 10) when all intervals were taken to have the same duration. As expected, the errors in the estimates decay rapidly to negligible levels as the number of intervals is increased. It should be noted that the instrument’s gradient waveform generator typically receives a piecewise constant function as the input. Therefore, the b-factors computed using our approach, with the appropriate choice of number of intervals, may be more accurate than its theoretical value, which assumes perfectly continuous waveforms.

Figure 3.

Assessment of the error in discretizing continuous waveforms. (a) Continuous gradient waveform (continuous line) is approximated by a piecewise constant function (dotted line). (b) Percent error in the b-value estimates plotted against the number of intervals.

5 Discussion

In the preceding sections, we revisited the problem of how Gaussian diffusion influences the magnetic resonance signal when arbitrary gradient waveforms are applied. We approached the problem from theoretical as well as computational points of view, and presented two loosely connected frameworks. Unlike in earlier derivations, our analytical approach was based on path integrals, and relied solely on probabilistic concepts. The essential idea in path integrals is the time-slicing performed to represent the gradient waveform as a series of impulses. As noted in Ref. [36], such slicing, hence an inherent path integration, is performed in the multiple propagator technique [37, 38], which is introduced as a numerical tool to compute the restricted diffusion signal.

In our computational framework, we employed a slightly different scheme of time-slicing, this time representing the waveform as a piecewise constant function. The latter is consistent with the multiple correlation function (MCF) method also used to quantify the effect of restricted diffusion. As discussed in detail in Ref. [32], the multiple propagator and MCF techniques are closely-related. The MCF approach is favored from a computational point of view when the gradient waveform is already given by a piecewise constant function, which is the case in pulsed field gradient (PFG) experiments [32].

In this article, our focus has been on the manipulation of transverse magnetization by incorporating general gradient waveforms into spin-echo like sequences [39]. However, the approaches described in this work could be extended to other techniques involving the temporal evolution of magnetization. For example, by employing repetition times that are much shorter than the transverse relaxation rate, one could obtain the steady state free precession (SSFP) signal [40]. Such techniques could be advantageous over the more conventional ones, e.g., when rapid physiological processes are to be examined [41]. Characterizing the effects of diffusion in such sequences is of current interest [42, 43].

The reader is cautioned that the b-factors and the discussion in this work are relevant when the signal attenuation originates from truly Gaussian diffusion. When MR measurements are concerned, it is tempting to treat non-Gaussian diffusion as “Gaussian” at the low diffusion sensitivity (large signal intensity) regime because the identity E ≈ 1−(cγG)² ≈ e^−(cγG)2 is expected to hold in this regime. Here, c is some quantity of dimension (length) × (time); its exact form is determined by the particular mechanism that leads to non-Gaussianity. As a result of the above correspondence, the b-factors are occasionally employed to characterize such apparently Gaussian processes [44]. However, the particular dependence of the b-factors on the timing parameters of the employed sequence may not be adequately captured by the expressions for the b-factors when diffusion is non-Gaussian.

To illustrate this point, it is instructive to compare the solutions for Gaussian diffusion above with those for restricted diffusion. In Ref. [36], the authors employed a path integral representation of the diffusion process, which is based on the time-slicing idea of a gradient waveform [37, 38], to derive the expression

$$E^{\text{rest}}\approx 1-2{\gamma }^2{a}^2\sum _{n=1}^{\infty }{s}_{Dn}{\int }_0^T{e}^{{\omega }_{Dn}t}\mathbf{G}(t)·\left[{\int }_t^T\mathbf{G}(t^{\prime })e^{-{\omega }_{Dn}{t}^{\prime }}\mathrm{d}{t}^{\prime }\right]\mathrm{d}t,$$ (31)

with the definitions ${\omega }_{Dn}=a^{-2}{\alpha }_{Dn}^2{D}_0$ and $s_{Dn}={\left[{\alpha }_{Dn}^2({\alpha }_{Dn}^2-D+1)\right]}^{-1}$, where α_1n = (n−1/2)π, and α_2n and α_3n satisfy the expressions $J_1^{\prime }({\alpha }_{2n})=0$ and $j_1^{\prime }({\alpha }_{3n})=0$, respectively. Eq. 31 provides the solution valid for a general gradient waveform G(t), for geometries of parallel plates (D = 1) with separation 2a, and cylinders (D = 2) and spheres (D = 3) with radii a. Therefore, Eq. 31 can be considered analogous to Eqs. 3 and 4.

To exemplify the difference in the signal dependencies for Gaussian and restricted diffusion processes, we shall consider the special case of a traditional Stejskal-Tanner (ST) sequence [45] featuring gradients of magnitude G, duration δ, and separation Δ. For the case of restricted diffusion, the expected signal decay is given by

$$E_{\text{ST}}^{\text{rest}}\approx exp\left\{-2{(\gamma Ga)}^2\sum _{n=1}^{\infty }{s}_{Dn}\left[\frac{2\delta }{{\omega }_{Dn}}-\frac{1}{{\omega }_{Dn}^2}\left(2-2e^{-{\omega }_{Dn}\delta }+e^{-{\omega }_{Dn}(\mathrm{\Delta }-\delta )}-2e^{-{\omega }_{Dn}\mathrm{\Delta }}+e^{-{\omega }_{Dn}(\mathrm{\Delta }+\delta )}\right)\right]\right\}.$$ (32)

On the other hand, the same expression for Gaussian diffusion is [45]

$$E_{\text{ST}}^{\text{Gaussian}}=exp\left[-D_0{(\gamma \delta G)}^2\left(\mathrm{\Delta }-\frac{\delta }{3}\right)\right].$$ (33)

Eqs. 32 and 33 clearly exhibit different dependencies on δ and Δ, demonstrating that the b-factors cannot be used to model the dependence of the signal attenuation due to restricted diffusion on the experimental timing parameters even at low levels of signal attenuation.

6 Conclusion

By explicitly evaluating the relevant path integral, we presented a new derivation leading to the link between an impressed gradient waveform and the detected MR signal. The new derivation is more intuitive than the earlier ones as it is based solely on probabilistic notions rather than the Bloch-Torrey equation. We also presented a simple and convenient method for computing the b-value and b-matrix for an arbitrary gradient waveform. This solution could be employed to: (i) conveniently incorporate the effects of imaging gradients in traditional Stejskal-Tanner sequences, (ii) compute the signal attenuation for more sophisticated diffusion encoding schemes (e.g., schemes with oscillating waveforms, and multiple pairs of gradients), and (iii) complement the existing solutions for restricted diffusion in modeling studies. Finally, we pointed out that the signal for Gaussian and non-Gaussian diffusion could exhibit different dependencies on the timing parameters of the gradient waveform even at low diffusion sensitivity (high signal) regime.

Appendix

In this Appendix, we shall detail how one evaluates the integral in Eq. 13.

Let U be the orthogonal transformation that diagonalizes the apparent diffusion tensor, i.e.,

$$\mathbf{\Lambda }=\left(\begin{array}{ccc}{\mathrm{\Lambda }}_1& 0& 0\\ 0& {\mathrm{\Lambda }}_2& 0\\ 0& 0& {\mathrm{\Lambda }}_3\end{array}\right)=\mathbf{U}{\mathbf{D}}_0{\mathbf{U}}^{\top },$$ (34)

where Λ_i denotes the ith eigenvalue of D₀, whose determinant can be written as |D₀| = Λ₁Λ₂Λ₃. Since U is orthogonal, it obeys the relationship U^⊤U = UU^⊤ = I, where I is the 3×3 identity matrix. Multiplying both sides of Eq. 34 from left by U^⊤ and from right by U, one obtains

$${\mathbf{D}}_0={\mathbf{U}}^{\top }\mathbf{\Lambda }\mathbf{U}.$$ (35)

By inverting the matrices on both sides of the last two expressions, we note that the same relationships hold for the inverses of these matrices, i.e.,

$${\mathbf{\Lambda }}^{-1}=\mathbf{U}{\mathbf{D}}_0^{-1}{\mathbf{U}}^{\top }$$ (36a)

$${\mathbf{D}}_0^{-1}={\mathbf{U}}^{\top }{\mathbf{\Lambda }}^{-1}\mathbf{U}.$$ (36b)

Next, we consider the effect of the same transformation on a vector. We shall adopt the convention that the matrix U transforms an arbitrary vector v into v′. Then the following relationships hold:

$${\mathbf{v}}^{\prime }=\mathbf{Uv}$$ (37a)

$${{\mathbf{v}}^{\prime }}^{\top }={\mathbf{v}}^{\top }{\mathbf{U}}^{\top }$$ (37b)

$$\mathbf{v}={\mathbf{U}}^{\top }{\mathbf{v}}^{\prime }$$ (37c)

$${\mathbf{v}}^{\top }={{\mathbf{v}}^{\prime }}^{\top }\mathbf{U}.$$ (37d)

These expressions are instrumental in proving that the quadratic forms and dot products are invariant under orthogonal transformations. Take, for example,

$$\begin{array}{l}{\mathbf{v}}^{\top }{\mathbf{D}}_0\mathbf{v}={{\mathbf{v}}^{\prime }}^{\top }\mathbf{U}{\mathbf{U}}^{\top }\mathbf{\Lambda }\mathbf{U}{\mathbf{U}}^{\top }{\mathbf{v}}^{\prime }\\ ={{\mathbf{v}}^{\prime }}^{\top }\mathbf{\Lambda }{\mathbf{v}}^{\prime }\\ ={\mathrm{\Lambda }}_1{v}_x^{\prime 2}+{\mathrm{\Lambda }}_2{v}_y^{\prime 2}+{\mathrm{\Lambda }}_3{v}_z^{\prime 2}.\end{array}$$ (38)

Similarly,

$$\begin{array}{l}\mathbf{v}·\mathbf{w}={\mathbf{v}}^{\top }\mathbf{w}\\ ={{\mathbf{v}}^{\prime }}^{\top }\mathbf{U}{\mathbf{U}}^{\top }{\mathbf{w}}^{\prime }\\ ={\mathbf{v}}^{\prime }·{\mathbf{w}}^{\prime }\\ =v_x^{\prime }{w}_x^{\prime }+v_y^{\prime }{w}_y^{\prime }+v_z^{\prime }{w}_z^{\prime }\end{array}$$ (39)

Now, we shall write down the integral in Eq. 13 explicitly by inserting the definition of f(.) into Eq. 12. We obtain

$${\mathcal{L}}_{{\mathbf{R}}_2}({\mathbf{R}}_1,\mathbf{q})f({\mathbf{R}}_2,\mathbf{k},\{{\mathbf{K}}_1,{\mathbf{K}}_2,\dots ,{\mathbf{K}}_M\})=exp\left(-4{\pi }^2\tau \sum _{n=1}^M{\mathbf{K}}_n^{\top }{\mathbf{D}}_0{\mathbf{K}}_n\right)J({\mathbf{R}}_1,\mathbf{q},\mathbf{k}),$$ (40)

where

$$J({\mathbf{R}}_1,\mathbf{q},\mathbf{k})=\int \mathrm{d}{\mathbf{R}}_2\frac{exp[-{({\mathbf{R}}_2-{\mathbf{R}}_1)}^{\top }{\mathbf{D}}_0^{-1}({\mathbf{R}}_2-{\mathbf{R}}_1)/4\tau ]}{{(4\pi \tau )}^{3/2}{\mid {\mathbf{D}}_0\mid }^{1/2}}exp[-i2\pi (\mathbf{q}+\mathbf{k})·{\mathbf{R}}_2].$$ (41)

To evaluate the above integral, we perform a change of variables via the transformation U, i.e., ${\mathbf{R}}_2^{\prime }=\mathbf{U}{\mathbf{R}}_2$. Since the determinant of an orthogonal matrix is ±1, the Jacobian of this transformation is unity. We shall define the components of all relevant vectors as follows:

$${\mathbf{R}}_1={(X_1,Y_1,Z_1)}^{\top }$$ (42a)

$${\mathbf{R}}_1^{\prime }={(X_1^{\prime },Y_1^{\prime },Z_1^{\prime })}^{\top }$$ (42b)

$${\mathbf{R}}_2={(X_2,Y_2,Z_2)}^{\top }$$ (42c)

$${\mathbf{R}}_2^{\prime }={(X_2^{\prime },Y_2^{\prime },Z_2^{\prime })}^{\top }$$ (42d)

$$\mathbf{q}={(q_x,q_y,q_z)}^{\top }$$ (42e)

$${\mathbf{q}}^{\prime }={(q_x^{\prime },q_y^{\prime },q_z^{\prime })}^{\top }$$ (42f)

$$\mathbf{k}={(k_x,k_y,k_z)}^{\top }$$ (42g)

$${\mathbf{k}}^{\prime }={(k_x^{\prime },k_y^{\prime },k_z^{\prime })}^{\top }.$$ (42h)

Using Eq. 38 for the inverse of the diffusion tensor and with v = R₂−R₁, the exponential in the numerator becomes

$$exp[-{({\mathbf{R}}_2-{\mathbf{R}}_1)}^{\top }{\mathbf{D}}_0^{-1}({\mathbf{R}}_2-{\mathbf{R}}_1)/4\tau ]=exp\left[-\frac{{(X_2^{\prime }-X_1^{\prime })}^2}{4{\mathrm{\Lambda }}_1\tau }-\frac{{(Y_2^{\prime }-Y_1^{\prime })}^2}{4{\mathrm{\Lambda }}_2\tau }-\frac{{(Z_2^{\prime }-Z_1^{\prime })}^2}{4{\mathrm{\Lambda }}_3\tau }\right]$$ (43)

Similarly, using Eq. 39, one obtains the following expression for the second exponential in the integral (41):

$$exp[-i2\pi (\mathbf{q}+\mathbf{k})·{\mathbf{R}}_2]=exp\{-i2\pi [(q_x^{\prime }+k_x^{\prime })X_2^{\prime }+(q_y^{\prime }+k_y^{\prime })Y_2^{\prime }+(q_z^{\prime }+k_z^{\prime })Z_2^{\prime }]\}.$$ (44)

The above two exponentials can be written as the product of three exponentials, each of which contains the parameters for only one principal orientation of the diffusion tensor. Such decomposition can be utilized to write J(R₁, q, k) as

$$J({\mathbf{R}}_1,\mathbf{q},\mathbf{k})=J_x{J}_y{J}_z,$$ (45)

with

$$J_x=\frac{1}{{(4\pi {\mathrm{\Lambda }}_1\tau )}^{1/2}}{\int }_{-\infty }^{\infty }exp\left[-\frac{{(X_2^{\prime }-X_1^{\prime })}^2}{4{\mathrm{\Lambda }}_1\tau }\right]exp[-i2\pi (q_x^{\prime }+k_x^{\prime })X_2^{\prime }]\mathrm{d}{X}_2^{\prime }$$ (46a)

$$J_y=\frac{1}{{(4\pi {\mathrm{\Lambda }}_2\tau )}^{1/2}}{\int }_{-\infty }^{\infty }exp\left[-\frac{{(Y_2^{\prime }-Y_1^{\prime })}^2}{4{\mathrm{\Lambda }}_2\tau }\right]exp[-i2\pi (q_y^{\prime }+k_y^{\prime })Y_2^{\prime }]\mathrm{d}{Y}_2^{\prime }$$ (46b)

$$J_z=\frac{1}{{(4\pi {\mathrm{\Lambda }}_3\tau )}^{1/2}}{\int }_{-\infty }^{\infty }exp\left[-\frac{{(Z_2^{\prime }-Z_1^{\prime })}^2}{4{\mathrm{\Lambda }}_3\tau }\right]exp[-i2\pi (q_z^{\prime }+k_z^{\prime })Z_2^{\prime }]\mathrm{d}{Z}_2^{\prime }$$ (46c)

where we employed also the fact that the Jacobian of the coordinate transformation is unity. The above integrals conform to the following Gaussian integral

$${\int }_{-\infty }^{\infty }{e}^{-c{\xi }^2+d\xi }\mathrm{d}\xi =\sqrt{\frac{\pi }{c}}{e}^{d^2/4c}.$$ (47)

Using this expression with appropriate values for c and d, we obtain

$$J_x=exp[-i2\pi (q_x^{\prime }+k_x^{\prime })X_1^{\prime }]exp[-4{\pi }^2{(q_x^{\prime }+k_x^{\prime })}^2{\mathrm{\Lambda }}_1\tau ]$$ (48a)

$$J_y=exp[-i2\pi (q_y^{\prime }+k_y^{\prime })Y_1^{\prime }]exp[-4{\pi }^2{(q_y^{\prime }+k_y^{\prime })}^2{\mathrm{\Lambda }}_2\tau ]$$ (48b)

$$J_z=exp[-i2\pi (q_z^{\prime }+k_z^{\prime })Z_1^{\prime }]exp[-4{\pi }^2{(q_z^{\prime }+k_z^{\prime })}^2{\mathrm{\Lambda }}_3\tau ]$$ (48c)

Note that we need the product of these three expressions, which can be written as

$$\begin{array}{l}{J}_x{J}_y{J}_z=exp\{-i2\pi [(q_x^{\prime }+k_x^{\prime })X_1^{\prime }+(q_y^{\prime }+k_y^{\prime })Y_1^{\prime }+(q_z^{\prime }+k_z^{\prime })Z_1^{\prime }]\}\times exp\{-4{\pi }^2\tau [{(q_x^{\prime }+k_x^{\prime })}^2{\mathrm{\Lambda }}_1+{(q_y^{\prime }+k_y^{\prime })}^2{\mathrm{\Lambda }}_2+{(q_z^{\prime }+k_z^{\prime })}^2{\mathrm{\Lambda }}_3]\}\\ =exp\{-i2\pi [({\mathbf{q}}^{\prime }+{\mathbf{k}}^{\prime })·{\mathbf{R}}_1^{\prime }]\}\times exp\{-4{\pi }^2\tau [{({\mathbf{q}}^{\prime }+{\mathbf{k}}^{\prime })}^{\top }\mathbf{\Lambda }({\mathbf{q}}^{\prime }+{\mathbf{k}}^{\prime })]\}.\end{array}$$ (49)

Using Eqs. 38 and 39, we obtain

$$J({\mathbf{R}}_1,\mathbf{q},\mathbf{k})=exp\{-i2\pi [(\mathbf{q}+\mathbf{k})·{\mathbf{R}}_1]\}\times exp\{-4{\pi }^2\tau [{(\mathbf{q}+\mathbf{k})}^{\top }{\mathbf{D}}_0(\mathbf{q}+\mathbf{k})]\}.$$ (50)

Inserting this result into Eq. 40, we get

$${\mathcal{L}}_{{\mathbf{R}}_2}({\mathbf{R}}_1,\mathbf{q})f({\mathbf{R}}_2,\mathbf{k},\{{\mathbf{K}}_1,{\mathbf{K}}_2,\dots ,{\mathbf{K}}_M\})=exp\left\{-4{\pi }^2\tau \left[{(\mathbf{q}+\mathbf{k})}^{\top }{\mathbf{D}}_0(\mathbf{q}+\mathbf{k})+\sum _{n=1}^M{\mathbf{K}}_n^{\top }{\mathbf{D}}_0{\mathbf{K}}_n\right]\right\}\times exp\{-i2\pi [(\mathbf{q}+\mathbf{k})·{\mathbf{R}}_1]\}.$$ (51)

With the observation that the right hand side of the expression conforms to the definition of f(.) given in Eq. 12, we obtain the desired result

$${\mathcal{L}}_{{\mathbf{R}}_2}({\mathbf{R}}_1,\mathbf{q})f({\mathbf{R}}_2,\mathbf{k},\{{\mathbf{K}}_1,{\mathbf{K}}_2,\dots ,{\mathbf{K}}_M\})=f({\mathbf{R}}_1,\mathbf{q}+\mathbf{k},\{{\mathbf{K}}_1,{\mathbf{K}}_2,\dots ,{\mathbf{K}}_M,\mathbf{q}+\mathbf{k}\}).$$ (52)