Probing surface recombination velocities in semiconductors using two-photon microscopy

Abstract

The determination of minority-carrier lifetimes and surface recombination velocities is essential for the development of semiconductor technologies such as solar cells. The recent development of two-photon time-resolved microscopy allows for better measurements of bulk and subsurface interfaces properties. Here we analyze the diffusion problem related to this optical technique. Our three-dimensional treatment enables us to separate lifetime (recombination) from transport effects (diffusion) in the photoluminescence intensity. It also allows us to consider surface recombination occurring at a variety of geometries: a single plane (representing an isolated exposed or buried interface), two parallel planes (representing two inequivalent interfaces), and a spherical surface (representing the enclosing surface of a grain boundary). We provide fully analytical results and scalings directly amenable to data fitting, and apply those to experimental data collected on heteroepitaxial CdTe/ZnTe/Si.

I. INTRODUCTION

The minority-carrier lifetime may be considered the most critical parameter for photovoltaic materials. However, in polycrystalline materials like CdTe, the exact contribution of bulk, grain boundaries and other interfaces to recombination losses is still unclear. Optical techniques, such as time-resolved photoluminescence (TRPL), have been developed to probe the bulk lifetime and surface recombination velocities of direct bandgap materials. These experiments consist of optically generating electron-hole pairs and observing the time-dependence of the photons emitted from radiative recombination. The time constant of the signal decay contains information about bulk and surface recombination.

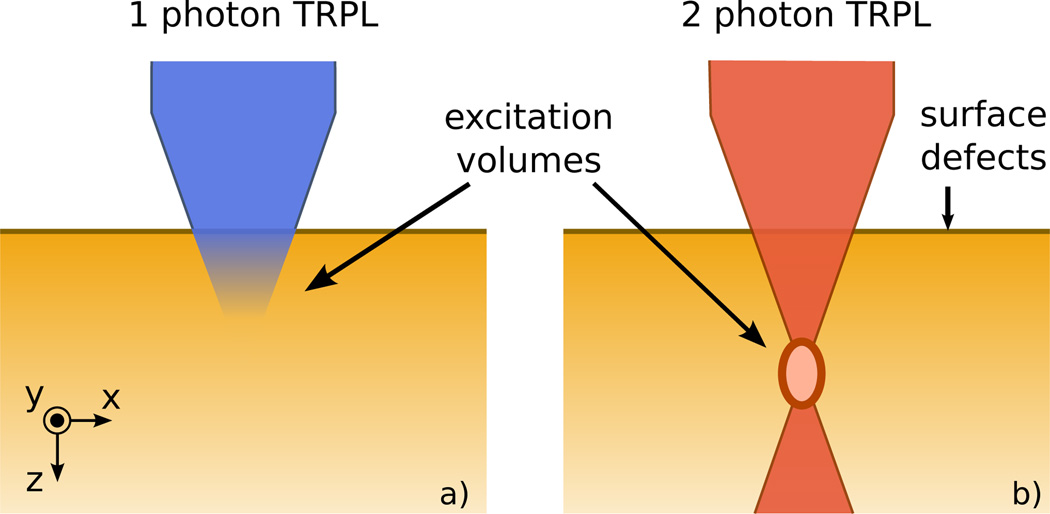
TRPL measurements are most commonly conducted using one-photon excitation. In this case the energy of the incident photons is larger than the semiconductor bandgap so that a single photon generates an electron-hole pair (or exciton). The absorption in the bulk decays exponentially away from the sample surface, as shown in Fig. 1(a). More recently, two-photon TRPL has been developed and applied to photovoltaic materials^1–3. In this case, the energy of the incident photons is smaller than the bandgap such that multiple photon absorptions are required to excite an electron-hole pair. This non-linear absorption process is obtained by focusing a laser beam under the sample surface, as shown in Fig. 1(b). The procedure allows one to generate carriers at any desired depth inside the material, so that surface and bulk contributions can be disentangled in the TRPL response. We refer to the literature^4,5 for details on the operating principle and experimental setups.

FIG. 1.

Schematics of the one- and two-photon excitation microscopy techniques. (a) The incident beam is absorbed exponentially away from the surface. (b) Charge carriers are excited at the focal point of the incident beam, under the surface of the sample.

While there exists an abundant literature on the modeling of one-photon TRPL measurements^6–8, theoretical works for two-photon TRPL are still scarce and limited to numerical studies⁹. The present work builds on the extensive body of mathematical analysis developed from earlier investigations of one-photon TRPL, which assumed an optical excitation that decays away from the sample surface into the bulk according to Beer’s law.

In this work we analyze the diffusion problem related to the two-photon TRPL microscopy technique. Because PL intensities often depend on material parameters in non-trivial ways, we use the analytical solutions of our modeling to propose scalings and experimental procedures which enable convenient extraction of these parameters. We are considering a model of excess carrier diffusion in three dimensions in the low-injection regime (i.e. with first order recombination), with recombination that is first order in carrier density. We provide general results for the minority-carrier concentration and the PL intensity for an excitation of arbitrary spatial dependence. Because the free carriers can diffuse away from the photon collection region before they radiatively recombine, the PL signal is strongly affected by the dimensions of generation and collection volumes. This makes our 3D treatment relevant to identifying the impact of the free carriers transport on the time decay of the PL intensity. The paper is organized as follows: We present our model for the transport of optically-generated minority carriers in Sec. II. The Green’s function of the diffusion problem is introduced, and we show how it relates to the minority-carrier density. Section III presents the case of a volume bounded by a single planar boundary with enhanced recombination. We provide the solution of the 3D diffusion equation for an arbitrary generation and collection volume. We then consider the special case of point-like excitation and collection, and use this result to derive expressions which can be conveniently used for data fitting. We end the section using this solution to fit the experimental data obtained on heteroepitaxial CdTe/ZnTe/Si in Ref. 5. A second planar boundary in the axial direction is added in Sec. IV. Finally, we investigate the spherical diffusion of minority carriers in Sec. V to determine the surface recombination velocity of an enclosing grain boundary surface.

II. MODEL FOR THE LASER BEAM INDUCED MINORITY-CARRIER TRANSPORT

Without loss of generality we develop our analysis for a p-type material. We model the transport of optically-induced electrons with the time-dependent diffusion equation

$$\frac{\partial n}{\partial t}(\mathbf{r},t)-D\mathrm{\Delta }n(\mathbf{r},t)+\frac{n(\mathbf{r},t)}{\tau }=g(\mathbf{r})\delta (t),$$ (1)

where n(r, t) is the electron concentration, D is their diffusion constant, τ their bulk lifetime and g(r)δ(t) is the carrier generation, assumed instantaneous. The recombination rate is taken to first order in minority-carrier density, so that Eq. (1) is valid only in the low-injection regime. For the purpose of calculating the distribution of electrons after a laser pulse, we introduce the Green’s function G(r, r′,t) that satisfies

$$\frac{\partial G}{\partial t}(\mathbf{r},\mathbf{r}\prime ,t)-D\mathrm{\Delta }G(\mathbf{r},\mathbf{r}\prime ,t)+\frac{G(\mathbf{r},\mathbf{r}\prime ,t)}{\tau }=\delta (\mathbf{r}-\mathbf{r}\prime )\delta (t).$$ (2)

Upon solving Eq. (2) with the appropriate boundary conditions, the electron density is obtained with the convolution

$$n(\mathbf{r},t)=\int \mathrm{d}\mathbf{r}\prime G(\mathbf{r},\mathbf{r}\prime ,t)g(\mathbf{r}\prime ),$$ (3)

and integrating the above density over a collection volume V yields the PL intensity

$$I(t)=\frac{1}{{\tau }_r}{\int }_V\mathrm{d}\mathbf{r}n(\mathbf{r},t),$$ (4)

where τ_r = 1/Bp₀ is the radiative lifetime (B: radiative recombination coefficient of the material, p₀: hole doping). The lateral collection area is set by the spot size, while the generation volume is contained within the spot size and is generally smaller (the generation volume is determined in part by the laser fluence¹⁰). The volumes in Eqs. (3) and (4) are therefore different. For simplicity, we take these volumes to be equal in the experimental procedures presented in Secs. III and V. The results of the successive integrations of the Green’s function (one for the carrier density and a second one for the PL intensity) become quickly very messy in the rare cases where we can compute them analytically. However, this is easily done numerically.

The model introduced here has several limitations. First, it does not include the self-absorption of radiatively emitted photons with the subsequent electron-hole pair creation, or so-called photon recycling¹¹. Photon recycling can alter the measured PL lifetime only when the radiative recombination mechanism is not negligible. For direct band gap polycrystalline semiconductors with low majority-carrier densities (10¹⁵ – 10¹⁶ cm⁻³), the Schockley-Read-Hall recombination mechanism dominates. Photon recycling can therefore be neglected in these materials. Second, the model leaves out space charge effects caused by surface-induced electric fields and differences in electron and hole mobilities. These non-linear effects have been studied numerically⁹. Finally, while refraction and diffraction are not limitations of this model per se, we will discuss how the optics influences the extraction of physical parameters from experimental data in the Section III.

We will now proceed with the resolution of Eq. (2) for various boundary conditions.

III. TWO-PHOTON TRPL IN A SEMI-INFINITE SYSTEM

We discuss the case of a volume bounded by a single planar surface with enhanced recombination. This surface can be the sample surface, as depicted in Fig. 1, or any buried subsurface or material interface. We provide the analytic solution to the 3D diffusion problem. Next we introduce the ratio of the PL signals for excitations deep in the bulk and near the surface, and show that it varies linearly with time. The slope of this linear variation can be used to determine the diffusion constant and the surface recombination velocity.

Eq. (2) is solved in the half volume z ≥ 0 with the boundary conditions determined by the surface recombination velocity S at z = 0,

$$D\frac{\partial n}{\partial z}=S_n, z=0,$$ (5)

$$n=0, z\to +\infty .$$ (6)

The solution reads

$$G(x,x\prime ,y,y\prime ,z,z\prime ,t)=\frac{e^{-t/\tau }}{2}\frac{e^{-\frac{{(x-x\prime )}^2}{4Dt}}}{2\sqrt{\pi Dt}}\frac{e^{-\frac{{(y-y\prime )}^2}{4Dt}}}{2\sqrt{\pi Dt}}[\frac{e^{-\frac{{(z-z\prime )}^2}{4Dt}}+e^{-\frac{{(z+z\prime )}^2}{4Dt}}}{\sqrt{\pi Dt}}-2\frac{S}{D}{e}^{\frac{S}{D}(z+z\prime )+\frac{S^2}{D}t}\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{c}(\frac{z+z\prime }{2\sqrt{Dt}}+S\sqrt{\frac{t}{D}}\left)\right],$$ (7)

where erfc is the complementary error function. A derivation can be found in Ref. 12 and in Appendix A. Direct numerical integration of Eq. (3) with the Green’s function Eq. (7) over the generation/collection region yields the time-dependent PL intensity for this geometry. Eq. (7) is an exact solution to the problem and, with the aforementioned numerical work, can be used for data fitting. However the expression is complicated and not especially intuitive.

To gain insight into the role of diffusion and surface recombination, we consider a limiting case of Eq. (7), for which the generation/collection regions are both point sources. These are strong approximations but they give good insights for i) the shape of the PL signal, in particular the behavior at short times, and ii) possible procedures to determine the recombination velocity S. The point source is positioned at (0, 0, z₀) with amplitude g₀

$$g(x,y,z)=g_0\delta (x)\delta (y)\delta (z-z_0).$$ (8)

Applying Eq. (3) yields the spatial distribution of electrons in the system

$$n(x,y,z,t)=G(x,0,y,0,z,z_0,t).$$ (9)

The PL intensity of photons originating from z = z₀ is given by

$$I(t)=\frac{g_0}{{\tau }_r}\frac{e^{-t/\tau }}{8\pi Dt}[\frac{1+e^{-z_0^2/(Dt)}}{\sqrt{\pi Dt}}-2\frac{S}{D}{e}^{\frac{S}{D}2z_0+\frac{S^2}{D}t}\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{c}(\frac{z_0}{\sqrt{Dt}}+S\sqrt{\frac{t}{D}}\left)\right].$$ (10)

We first consider an excitation in the bulk, far from the surface (z₀ ≥ L_d, $L_d=\sqrt{D\tau }$: diffusion length). In this case we can ignore the second term in square brackets in Eq. (10), and get

$$I_b(t)=\frac{g_0}{{\tau }_r}\frac{e^{-t/\tau }}{8{(\pi Dt)}^{3/2}}.$$ (11)

This result indicates that the diffusion of carriers mostly influences the PL intensity at short times (e^−t/τ ≈ 1), giving an algebraic form to the decay instead of an exponential one. At long times, the bulk lifetime dominates the PL signal but the PL decay is still not purely exponential. One recovers a purely exponential decay when the laser spot size is much greater than the diffusion length. Formally this amounts to integrating Eq. (7) over all spatial directions ignoring the second term in the square brackets. Next we consider an excitation near the surface (z₀ ≤ St, $z_0\le \sqrt{Dt}$), and focus on long times (t > τ). In this case, we obtain

$$I_s(t)=\frac{g_0}{{\tau }_r}\frac{{(z_0+D/S)}^2{e}^{-t/\tau }}{8{\pi }^{3/2}{(Dt)}^{5/2}}.$$ (12)

Although Eqs. (11) and (12) were derived for a point source generation/collection region, we find that for a finite generation/collection region of volume V, the same relations hold with an additional prefactor of V². This assumes a uniform carrier generation, and times long enough so that carriers have diffused outside the collection volume, that is $\sqrt{Dt}\ge V^{1/3}$. We notice that the time dependence of the signal for near-surface excitations I_s(t) has an additional factor of 1/t compared with the bulk excitation signal I_b(t). For this reason we propose that forming the ratio of these PL signals may be a convenient way of estimating material parameters. Including the generation/collection volume factors we discussed above, the ratio is given by

$$I_b(t)/I_s(t)=1+{\left(\frac{V_b}{V_s}\right)}^2\frac{Dt}{{(z_0+D/S)}^2},$$ (13)

where V_b and V_s are the generation/collection volumes in the bulk and close to the surface respectively; z₀ is now the distance of the center of the uniform generation volume from the surface.

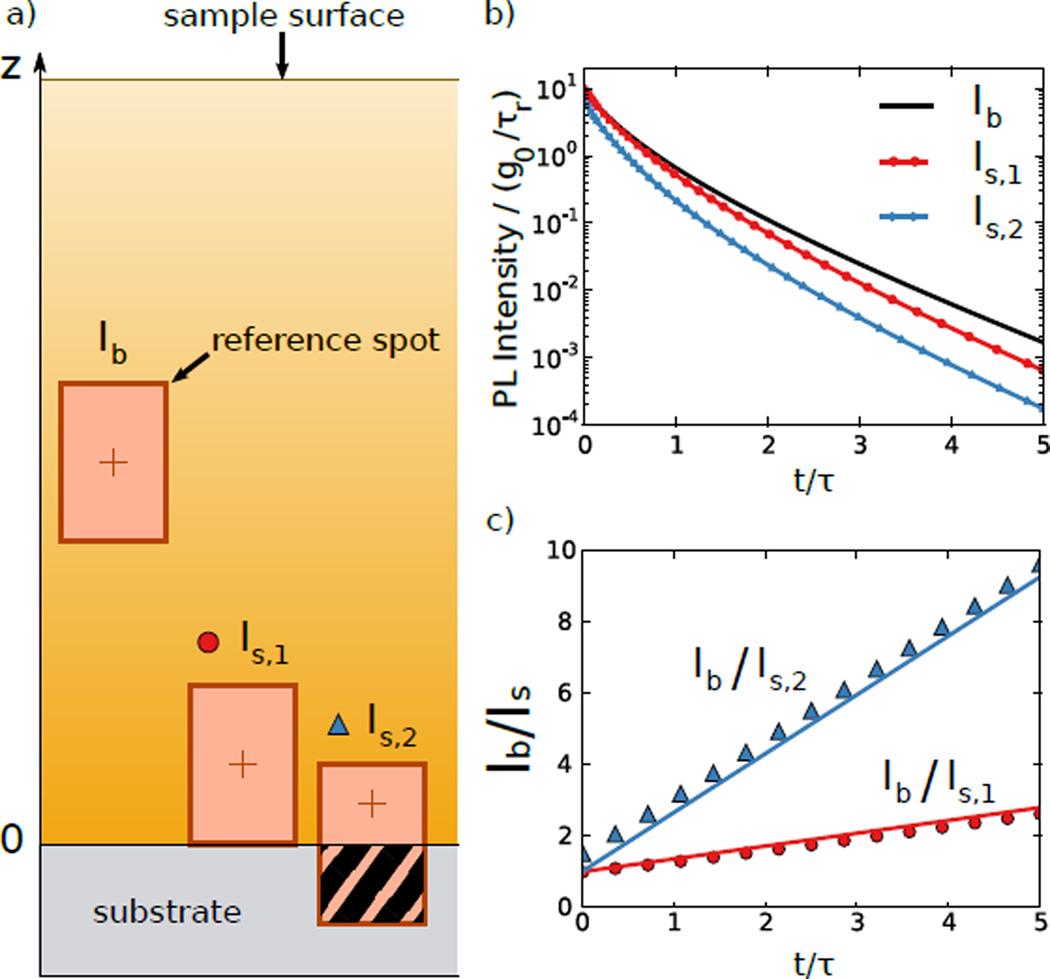
To test the accuracy and demonstrate the use of Eq. (13), we perform numerical calculations in which we compare Eq. (13) to the full numerical integration of Eqs. (3) and (7). Fig. 2(a) shows the geometry; we choose three focal points for the generation/collection region: one in the bulk, and two near a buried sample-substrate interface. Note that as the generation/collection region approaches the interface, a portion of it falls outside the sample and does not contribute to the generation or collection (hatching in the right spot of Fig. 2(a)). Fig. 2(b) shows the PL time traces obtained by direct numerical integration. As expected, the signal decreases more quickly for excitations near the sample-substrate interface (I_s,1 and I_s,2). The symbols of Fig. 2(c) show the ratios between the two subsurface excitations and the bulk excitation. The solid lines of Fig. 2(c) show Eq. (13), demonstrating good agreement with the full numerical calculations. Given a similar set of experimental data (one bulk and two near-surface excitations, or two values of z₀), one can form the ratio of the PL signals of excitations in the bulk and near the surface, and use the resulting slopes to estimate S and D.

FIG. 2.

Procedure to determine the surface recombination velocity and the diffusion constant at a sample substrate/active layer interface. (a) Schematic of the sample with three focal points for the generation/collection region respectively in the bulk and at the substrate/active layer interface. (b) PL intensities as a function of time corresponding to the three excitations obtained for uniform rectangular shaped generation/collection volumes, as shown in a). The curves are numerical integrations of Eq. (3). The reference spot in the bulk (black, I_b) has lateral size 2L_d and axial size 3L_d. The axial sizes of the spots in the active layer at the substrate/system interface are 3L_d (red with dots, I_s,1) and 2L_d (blue with triangles, I_s,2). (c) Ratio of the bulk and interface PL intensities. Symbols correspond to the ratio of the data plotted in b). The continuous lines correspond to Eq. (13) with z₀ indicated by the red cross inside each spot in a). z₀ values are L_d (blue, triangles) and 1.5L_d (red, dots). The reference spot has z₀ = 9L_d. The surface recombination velocity was chosen such that S = 6υ (υ: diffusion velocity).

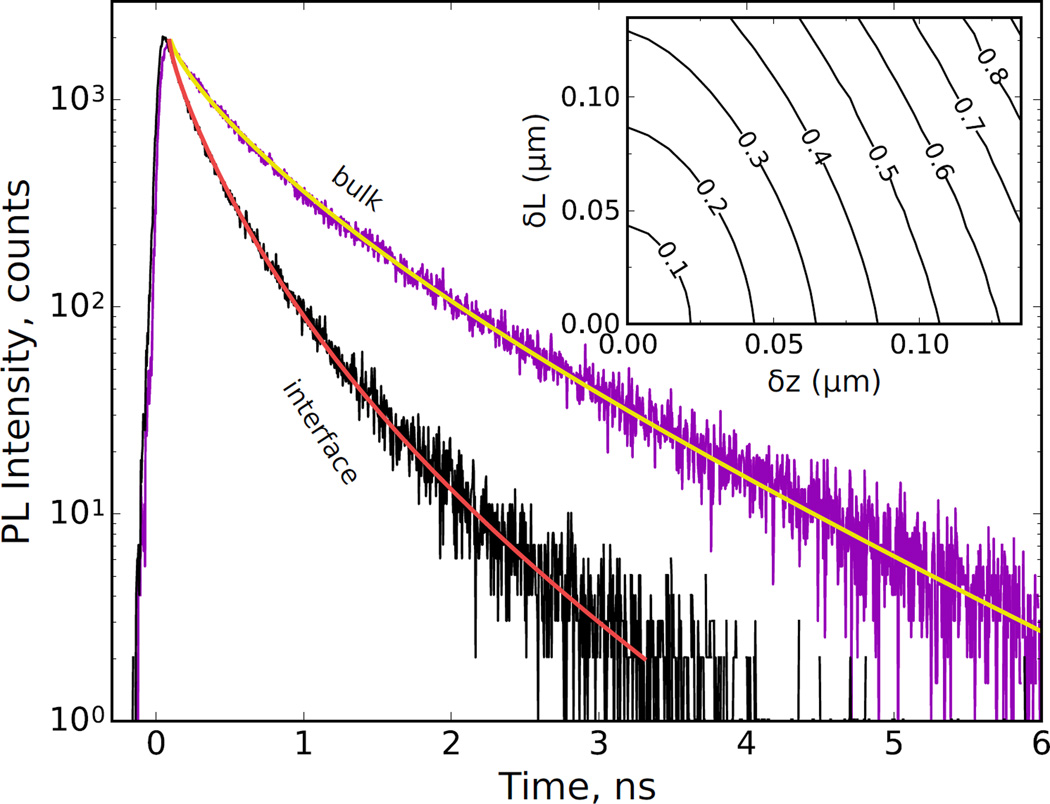
We now apply the formulas derived above to fit the experimental data taken from Ref. 5. Kuciauskas and coworkers reported on one- and two-photon TRPL studies of CdTe grown on Si(211) substrates. Here we focus on the characterization of the buried heteroepitaxial CdTe/ZnTe/Si interface presented in Fig. 6 of the article (CdTe layer thickness: 17.5 µm). In particular we consider two spot positions: in the bulk (purple) and close to the interface (black). Fig. 3 shows the experimental data with our fitting curves. Our theoretical model for the generation volume consists of a uniform generation of rectangular shape. The generation and collection volumes were kept the same with lateral length 2 µm. The axial spot size was 5.5 µm in the bulk (yellow) and 1.2 µm at the interface (red). We attribute this reduction to a large amount of the laser spot being partially focused on the silicon substrate, hence reducing significantly the number of electrons generated in the CdTe layer. The material parameters obtained after a least square fitting are S = 4.4 × 10⁵ cm s⁻¹, D = 6.5 cm² s⁻¹ and τ = 1.6 ns. This gives the diffusion length L_d = 1.0 µm. These values are to be compared with the ones found in Ref. 5: S = (6 ± 2) × 10⁵ cm s⁻¹, D = 17.0 ± 0.3 cm² s⁻¹.

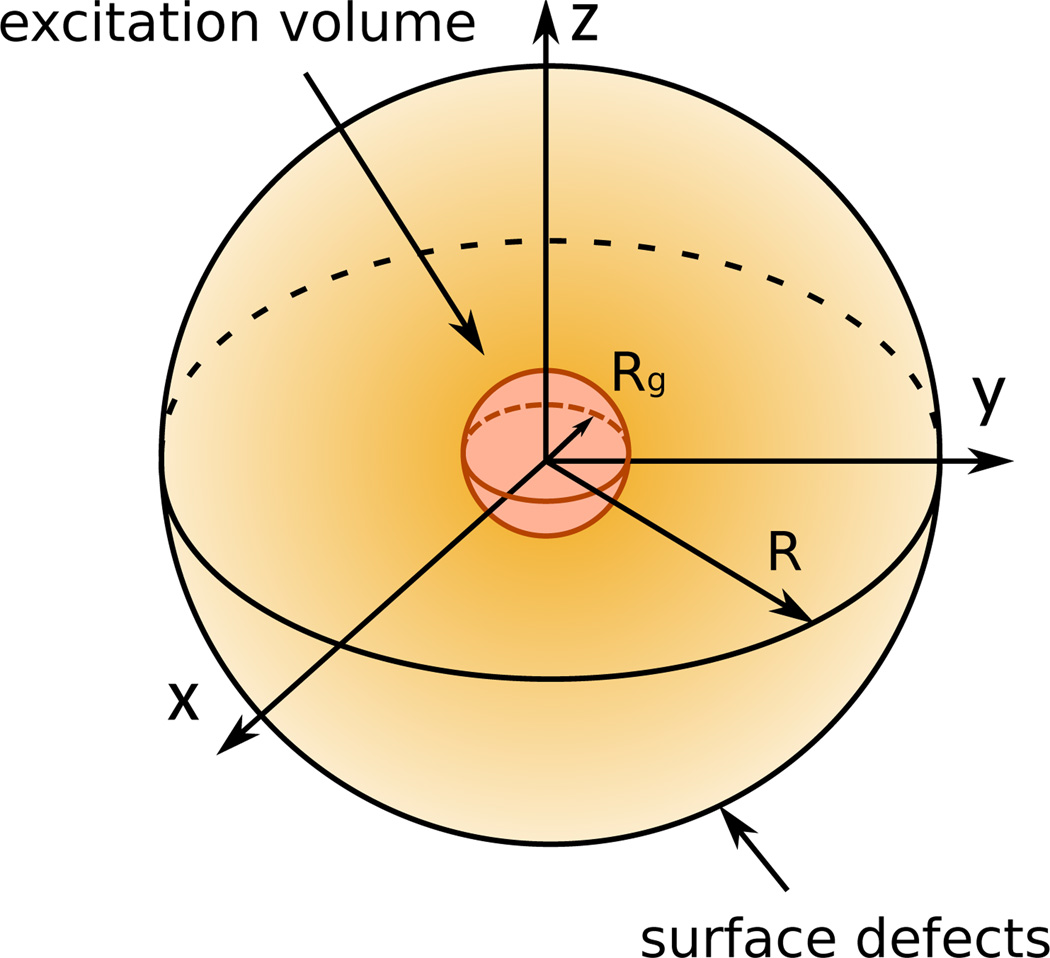
FIG. 6.

Optical beam focused at the center of a single grain of radius R of a polycrystalline material, creating a spherical generation of carriers with radius R_g. The surface defects corresponds to the grain boundary.

FIG. 3.

Fitting of the experimental data of Fig. 6 from Ref. 5. The purple and black traces are two-photon TRPL measurements taken respectively in the bulk and close to the heteroepitaxial CdTe/ZnTe/Si interface of a CdTe layer grown on Si substrate. The yellow and red curves correspond to numerical evaluations of Eq. (3) with the Green’s function Eq. (7). The generation and collection volumes are the same with lateral size (x and y) 2 µm, and axial sizes 5.5 µm (yellow) and 1.2 µm (red). The center of the spot is at 8.75 µm from the interface for the yellow curve and 0.6 µm for the red curve. Parameters obtained after least square fitting: S = 4.4 × 10⁵ cm s⁻¹, D = 6.5 cm² s⁻¹, τ = 1.6 ns. Inset: Relative uncertainty δS/S on the extracted values of S as a function of the hypothetical error on the position of the center of the spot (δz), and its axial length (δL).

There is some degree of insensitivity of the fitting parameters. For example, we find that good fitting persists for variations of the diffusion constant, the bulk lifetime and the surface recombination by 13 %, 7.5 % and 30 % respectively. Furthermore, the inset of Fig. 3 shows the uncertainty on the extracted surface recombination as the uncertainties of the center of the laser spot (δz) and its axial length (δL) vary. We chose hypothetical uncertainties which lead to reasonable uncertainties (< 100 %) in the extracted surface recombination. We find that an error on both spot location and axial length of only 0.1 µm results in a 60 % relative error on S. Uncertainties larger than 1 µm on the laser spot lead to values of S greater than the thermal velocity, so that the fitting procedure is inconclusive. This sensitivity implies that a precise knowledge of the optical generation and collection volumes is required for a precise extraction of physical parameters from experimental data.

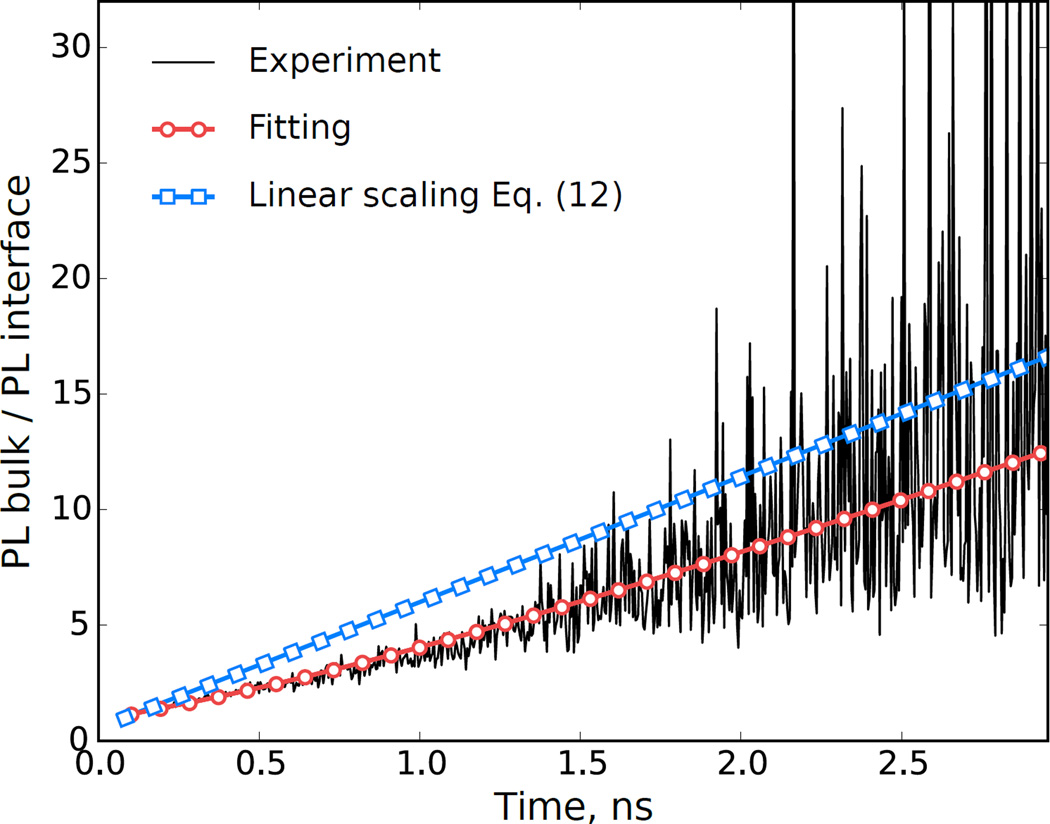
Fig. 4 compares the scaling proposed in Eq. (13) to the ratio of the PL signals taken in the bulk and at the interface. The time interval (< 3 ns) is small compared with the lifetime τ = 1.6 ns, and Eq. (13) applies for t > τ. Nevertheless, the scaling agrees with the trend of the experimental data. In addition to the aforementioned experimental challenges related to optics, another difficulty is to obtain data at the surface with little noise on a time scale at least several times the minority-carrier lifetime. This can be difficult because of the fast decay of the PL intensity caused by the enhanced recombination occurring near the surface.

FIG. 4.

Ratio of bulk and interface photoluminescence intensities as a function of time. The black (red-white dotted) continuous line corresponds to the ratio of the experimental (numerical) data presented in Fig. 3 The blue line with square symbols corresponds to Eq. (13) with the parameters used in Fig. 3.

A complicating factor in real systems is the large concentration of dislocations near interfaces that can make the carrier lifetime depth dependent^5,13. Our assumption of a spatially uniform lifetime remains valid as long as the diffusion length and spot size are smaller than the length scale over which the lifetime varies. In this case the time scale for the exponential decay of the signal is the local bulk lifetime at the excitation position. Forming the ratio of signals from bulk and surface in this instance leads to an additional exponentially decaying factor in Eq. (13) with a time constant of (1/τ_bulk − 1/τ_surf), where τ_bulk and τ_surf are the bulk decay times far from the surface and in the vicinity of the surface, respectively. The presence of such an exponential term will then indicate the existence of a depth-dependent carrier lifetime near the interface.

IV. DIFFUSION BOUNDED BY TWO PARALLEL PLANES

We now turn to a system with finite thickness d in the z-direction. This situation is especially applicable to thin films of thickness on the order of the laser spot axial dimension (typically a few µm), as depicted in Fig. 5. The PL signal is then sensitive to the sample surface as well as the sample/substrate interface. We provide the analytic solution to the 3D diffusion problem studied Section III with the additional boundary condition

$$D\frac{\partial n}{\partial z}=-S\prime n, z=d$$ (14)

The solution of Eq. (2) with the boundary conditions Eq. (5) and Eq. (14) is given by

$$G(x,x\prime ,y,y\prime ,z,z\prime ,t)=e^{-t/\tau }\frac{e^{-\frac{{(x-x\prime )}^2}{4Dt}}}{2\sqrt{\pi Dt}}\frac{e^{-\frac{{(y-y\prime )}^2}{4Dt}}}{2\sqrt{\pi Dt}}U(z,z\prime ,t)$$ (15)

with

$$U(z,z\prime ,t)=\sum _{n>0}{A}_n(z\prime )A_n(z)e^{-{\alpha }_n^{2}Dt},$$ (16)

where the coefficients α_n satisfy the transcendental relation

$$\text{tan}({\alpha }_{n}d)=\frac{{\alpha }_n(S+S\prime )D}{{\alpha }_n^2{D}^2-SS\prime }.$$ (17)

The details of the calculations as well as the expression of the coefficient A_n(z) are given in Appendix B. As with the single planar boundary, the diffusion in free space results in non-exponential terms to the PL signal given by the x and y components in Eq. (15). The transcendental equation Eq. (17) has already been found and studied in the context of excess minority-carrier excitation decay^14,15. The literature provides approximations for the characteristic time τ₁ corresponding to the first non-zero root of Eq. (17). For any values of S and S′, τ₁ can be approximated by¹⁶

$${\tau }_1=\frac{({\tau }_D+{\tau }_S+{\tau }_{S\prime })({\tau }_D+{\tau }_S)({\tau }_D+{\tau }_{S\prime })}{{({\tau }_D+({\tau }_S+{\tau }_{S\prime })/2)}^2},$$ (18)

with τ_D = d²/π²D, τ_S = d/4S and τ_S′ = d/4S′. Equation (18) encompasses approximations found in earlier works, in particular in the case where S = S′, τ₁ can be approximated by⁶

$${\tau }_1\approx \frac{d^2/D}{{\pi }^2}+\frac{d}{2S},$$ (19)

and in the case where S′ = 0 (or equivalently S = 0) it has been found that¹⁵

$${\tau }_1\approx \frac{4d^2/D}{{\pi }^2}+\frac{d}{S}.$$ (20)

For times long compared with d²/(π²D) the Fourier series Eq. (16) can be reduced to its first term so that the exponential component of the PL signal decays with the effective characteristic time

$$\frac{1}{{\tau }_{PL}}=\frac{1}{\tau }+\frac{1}{{\tau }_1}.$$ (21)

This remains valid whatever the shape of the generation volume (because the successive integrations on Eq. (15) will not affect the time-dependent term), as long as the laser pulse duration is much smaller than all other characteristic times.

FIG. 5.

Schematic of a sample with thickness d on the same order of the laser spot size.

Equation (21) together with Eq. (17) (or with the approximation Eq. (18)) require prior knowledge of the bulk lifetime and the diffusion constant in order to access S and S′. Assuming that this condition is met, one would make two devices with different thicknesses to determine both surface recombination velocities. To simplify the extraction of the parameters from experimental data, one may consider a laser beam with lateral dimensions much larger than the diffusion length. This procedure allows one to formally integrate Eq. (15) over x and y, so that the PL decay becomes purely exponential. As the thickness d increases, τ₁ asymptotes to d²/π²D, and no longer contains information about the surface; therefore d must be sufficiently small to extract S. Also, d must be chosen so that 1/τ₁ is not negligible compared with 1/τ. As an example, with S = S′ = 5 × 10⁵ cm s⁻¹, D = 10 cm s⁻¹ and τ = 1 ns, one finds that d ≤ 2.7 µm is needed to obtain τ₁ ≤ τ.

V. DETERMINATION OF THE SURFACE RECOMBINATION VELOCITY OF A GRAIN BOUNDARY

In this section we consider a case more readily applicable to the analysis of a single grain and its associated enclosing surface. The shape of the grains in a polycrystalline sample strongly depends on the material and the fabrication process¹⁷. Here we limit ourselves to the case of a grain with spherical symmetry of radius R, as depicted in Fig. 6. This grain can be identified, for instance, in the bulk of a sample after 3D mapping of the granular structure¹⁸. The geometry considered here also approximates systems for which the distance between the sample surface and the buried sample-substrate interface is roughly the same as the lateral grain size. This would apply to CdTe photovoltaics, for which both layer thickness and grain size are on the order of 1 – 3 µm. The surface recombination velocity S then represents an average over these three distinct surfaces (sample surface, buried interface surface, and grain boundary surface). As in Sections III and IV, we first solve the general diffusion equation for this geometry, and then use the solution to propose procedures for convenient data analysis.

The diffusion problem Eq. (1) is now treated in spherical coordinates with the boundary condition

$$D\frac{\partial n}{\partial r}(R,t)=-S_n(R,t).$$ (22)

The generation volume is centered in the middle of the grain such that the diffusion problem has radial symmetry. The solution of Eq. (2) with the boundary condition Eq. (22) is given by

$$G(r,r\prime ,t)=\frac{e^{-t/\tau }}{2\pi R}\sum _{n>0}{c}_n\frac{\text{sin}({\alpha }_{n}r\prime )}{r\prime }\frac{\text{sin}({\alpha }_{n}r)}{r}{e}^{-{\alpha }_n^{2}Dt},$$ (23)

with

$$c_n=\frac{{\alpha }_n^2{R}^2+{(SR/D-1)}^2}{{\alpha }_n^2{R}^2+(SR/D-1)SR/D}$$ (24)

where the coefficients α_n satisfy the transcendental relation

$$\text{tan}(\alpha R)=\frac{\alpha R}{1-SR/D}.$$ (25)

The details of the calculations are in Appendix C. The system being bounded in all directions, the time decay of the PL signal is now only given by exponential terms. An approximation of the first non-zero root of Eq. (25) was found¹⁹

$${\tau }_1\approx \frac{R}{3S}+\frac{R^2}{{\pi }^{2}D}.$$ (26)

For collection times longer than R²/π²D, the Fourier expansion in Eq. (23) is dominated by its first term so that the PL signal decays following a single exponential with an effective characteristic time given by Eq. (21).

We next propose a method for conveniently estimating S and D, assuming that the bulk lifetime is already known, by varying the generation/collection region radius. For a uniform spherical carrier generation/collection volume of radius R_g and a carrier generation per unit volume g₀. Integrating Eq. (23) twice over the sphere of radius R_g yields the PL intensity

$$I(t)=\frac{g_0}{{\tau }_r}{e}^{-t/\tau }\frac{8\pi }{R}\sum _{n>0}\frac{c_n}{{\alpha }_n^4}{A}_n(R_g)e^{-{\alpha }_n^{2}Dt},$$ (27)

with

$$A_n(R_g)={[\text{sin}({\alpha }_n{R}_g)-{\alpha }_n{R}_g\text{ cos}({\alpha }_n{R}_g)]}^2.$$ (28)

In the long time limit (t ≥ R²/π²D) Eq. (27) reads

$$I(t)=\frac{g_0}{{\tau }_r}\frac{8\pi }{R}\frac{c_1}{{\alpha }_1^4}{A}_1(R_g)e^{-(1/\tau +{\alpha }_1^{2}D)t}.$$ (29)

We notice that the time constant of the signal decay is independent of the excitation radius R_g. Indeed, R_g enters only in the prefactor A₁(Rg). For this reason, the ratio of PL signals from two different excitation radii is a time-independent constant

$$\frac{I_1(t)/g_{0,1}}{I_2(t)/g_{0,2}}=\frac{A_1(R_{g,1})}{A_1(R_{g,2})},$$ (30)

where I₁(t) and I₂(t) are two PL signals corresponding to generation/collection volumes with radii R_g,1 and R_g,2, and generations per unit volume g_0,1 and g_0,2. We next outline how Eq. (30) can be used to conveniently estimate D and S. In Fig. 7, we show the time-dependent PL intensities for two excitations with different radii. The symbols correspond to PL signals given by the exact solution of Eq. (27) with two different radii. The solid lines, corresponding to the estimate Eq. (29), show that the slopes of both signals are the same, equal to $1/\tau +{\alpha }_1^{2}D$. If the bulk lifetime is already known, these slopes can be used to determine ${\alpha }_1^{2}D$. We now need to find α₁. We take the logarithm of Eq. (30) and replace A₁ with Eq. (28) to obtain

$$\delta =2\text{ log }\left[\frac{\text{sin}({\alpha }_1{R}_{g,1})-{\alpha }_1{R}_{g,1}\text{ cos}({\alpha }_1{R}_{g,1})}{\text{sin}({\alpha }_1{R}_{g,2})-{\alpha }_1{R}_{g,2}\text{ cos}({\alpha }_1{R}_{g,2})}\right],$$ (31)

where α₁ is given by the approximation Eq. (26)

$${\alpha }_1=\frac{1}{\sqrt{D(\frac{R}{3S}+\frac{R^2}{{\pi }^{2}D})}}.$$ (32)

Measuring the distance between both PL signals after the initial rapid decay, gives δ, as shown in Fig. 7. Given δ, Eq. (31) can be used to determine α₁. Having determined ${\alpha }_1^{2}D$ and α₁, finding D is trivial and Eq. (32) yields the surface recombination

$$S=\frac{R}{3}\frac{{\alpha }_1^{2}D}{1-{(\frac{{\alpha }_{1}R}{\pi })}^2}.$$ (33)

FIG. 7.

PL intensities (normalized by the carrier generation g₀) as a function of time (in units of τ) for a uniform spherical excitation. Symbols and lines correspond to Eq. (27) computed up to n = 200 and Eq. (29) respectively, with R_g = 0.5R (dots, red), R_g = 0.8R (triangles, blue). The grain radius is R = 1 µm. We used D = 10 cm² s⁻¹, τ = 2 ns and S = 5 × 10⁵ cm s⁻¹. Inset: schematic of the increase of the spot size (red) inside a grain (orange).

This procedure generally relies on the assumption of a spatially uniform minority-carrier lifetime. However, if the surface recombination is much larger than the grain interior recombination, then the latter can be neglected and no assumptions on the minority carrier lifetime are needed for our analysis. This simplification applies for τ ≥ τ₁. As an example, with τ = 1 ns, D = 10 cm² s⁻¹, S = 10⁶ cm s⁻¹ and R = 1 µm, one finds τ₁ ≈ 0.1 ns which satisfies the aforementioned requirement by a factor 10.

VI. CONCLUSIONS

The present work investigates the diffusion problem related to the two-photon TRPL measurement technique. This non-invasive and non-destructive optical technique can spatially resolve surface and subsurface features. We have modeled the transport of excess minority-carriers in three dimensions in the low injection limit. A variety of boundary conditions were considered corresponding to different experimental and material geometries. The results obtained here suggested different routes for measuring physical parameters (diffusion constant, bulk lifetime, surface recombination velocity) by making use of the PL amplitude and time decay. Using the calculations done for a single planar boundary, we fitted experimental data collected in the bulk and at the substrate/active layer interface of heteroepitaxial CdTe/ZnTe/Si. We found that the optics (spot size and location) significantly impacts the precision of the extracted physical parameters. Finally, we have shown that PL signals are in general not purely exponential. Purely exponential decays are recovered, for instance, when the laser spot size is much greater than the diffusion length. This case consists in assuming that all radiatively emitted photons are collected.

Appendix A

DERIVATION OF EQ.(7)

We present here the steps followed to derive Eq. (7). Our starting point is Eq. (2) in Cartesian coordinates. Performing a Laplace transform with respect to the time variable t and two Fourier transforms with respect to the space variables x and y leads to

$$\frac{{\partial }^{2}G}{\partial z^2}-{\mu }^{2}G=\frac{e^{-i(k_{x}x\prime +k_{y}y\prime )}}{D}\delta (z-z\prime )$$ (34)

with $\mu =\sqrt{k_x^2+k_y^2+s/D+1/(D\tau )}$. The general solution to this equation is given by

$$\forall z<z\prime , G(k_x,x\prime ,k_y,y\prime ,z,z\prime ,s)=A{e}^{\mu z}+B{e}^{-\mu z}$$ (35)

$$\forall z>z\prime , G(k_x,x\prime ,k_y,y\prime ,z,z\prime ,s)=C{e}^{-\mu z}$$ (36)

The continuity of G at z = z′, the discontinuity of ∂_zG at z = z′ and the boundary condition Eq. (5) fix the three constants A, B, C so that we obtain

$$G(k_x,x\prime ,k_y,y\prime ,z,z\prime ,s)=\frac{e^{-i(k_{x}x\prime +k_{y}y\prime )}}{2D\mu }\times [e^{-\mu |z-z\prime |}+\frac{\mu D-S}{\mu D+S}{e}^{-\mu (z+z\prime )}].$$ (37)

We now use the shift theorem of the Laplace transform,

$$ℒ[e^{-\mathit{\text{at}}}f(t)]=F(s+a),$$ (38)

to separate the Fourier and Laplace transforms

$$G(k_x,x\prime ,k_y,y\prime ,z,z\prime ,t)=\frac{1}{2}{e}^{-(D(k_x^2+k_y^2)+1/\tau )t-i{k}_{x}x\prime -i{k}_{y}y\prime }\times {\int }_{c-i\infty }^{c+i\infty }\mathrm{d}s\frac{e^{sDt}}{\sqrt{s}}[e^{-|z-z\prime |\sqrt{s}}+\frac{D\sqrt{s}-S}{S\sqrt{s}+S}{e}^{-(z+z\prime )\sqrt{s}}]$$ (39)

where we changed the variable s/D for s. The inverse Fourier transform is now straightforward and so is the inverse Laplace transform with the two identities

$${ℒ}^{-1}\left[\frac{e^{-\sqrt{as}}}{\sqrt{s}}\right]=\frac{e^{-a/(4t)}}{\sqrt{\pi t}}$$ (40)

$${ℒ}^{-1}\left[\frac{e^{-a\sqrt{s}}}{\sqrt{s}(\sqrt{s}+\beta )}\right]=e^{a\beta +{\beta }^{2}t}\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{c}(\frac{a}{2\sqrt{t}}+\beta \sqrt{t})$$ (41)

where erfc is the complementary error function. These transformations yield Eq. (7).

Appendix B

DERIVATION OF EQ.(15)

We now turn to the derivation of the Green’s function Eq. (15). Our starting point is Eq. (2) in Cartesian coordinates. Because the diffusion remains in free space in the x- and y-direction and based on the previous calculation, we introduce the following ansatz for the Green’s function

$$G(x,x\prime ,y,y\prime ,z,z\prime ,t)=U(z,z\prime ,t)e^{-t/\tau }\frac{e^{-\frac{{(x-x\prime )}^2}{4Dt}}}{2\sqrt{\pi Dt}}\frac{e^{-\frac{{(y-y\prime )}^2}{4Dt}}}{2\sqrt{\pi Dt}}.$$ (42)

Substitution of Eq. (42) into Eq. (2) yields the standard diffusion equation for t > 0

$$D\frac{{\partial }^{2}U}{\partial z^2}=\frac{\partial U}{\partial t}$$ (43)

with the initial profile U(z, z′, 0) = δ(z − z′). The diffusion equation has been extensively studied for various boundary conditions by Carslaw and Jaeger for the heat flow problem²⁰. The following form is assumed with constants A and B determined by boundary conditions

$$U(z,z\prime ,t)=(A\text{ cos}(\alpha z)+B\text{ sin}(\alpha z))e^{-D{\alpha }^{2}t}.$$ (44)

The boundary conditions Eq. (5) and Eq. (14) yield

$$B=AS/(\alpha D)$$ (45)

$$\text{tan}(\alpha d)=\frac{\alpha (S+S\prime )D}{{\alpha }^2{D}^2-SS\prime }$$ (46)

The general solution to Eq. (43) is given by the summation over all the roots of Eq. (46)

$$U(z,z\prime ,t)=\sum _{n>0}{c}_n(z\prime )(D{\alpha }_n\text{ cos}({\alpha }_{n}z)+S\text{ sin}({\alpha }_{n}z))e^{-{\alpha }_n^{2}Dt},$$ (47)

where the coefficients c_n(z′) are given by

$$c_n(z\prime )=\frac{{\int }_0^d\mathrm{d}z\delta (z-z\prime )(D{\alpha }_n\text{ cos}({\alpha }_{n}z)+S\text{ sin}({\alpha }_{n}z))}{{\int }_0^d\mathrm{d}z{(D{\alpha }_n\text{ cos}({\alpha }_{n}z)+S\text{ sin}({\alpha }_{n}z))}^2},$$ (48)

which gives after some algebra

$$c_n(z\prime )=\frac{2(D{\alpha }_n\text{ cos}({\alpha }_{n}z\prime )+S\text{ sin}({\alpha }_{n}z\prime ))}{\frac{D^2{\alpha }_n^2+S^2}{D^2{\alpha }_n^2+{S\prime }^2}[d(D^2{\alpha }_n^2+{S\prime }^2)+DS\prime ]+DS}.$$ (49)

The coefficient A_n(z) given in Eq. (16) comes from a rewriting of Eq. (47) and reads

$$A_n(z)=\frac{\sqrt{2}(D{\alpha }_n\text{ cos}({\alpha }_{n}z)+S\text{ sin}({\alpha }_{n}z))}{\sqrt{\frac{D^2{\alpha }_n^2+S^2}{D^2{\alpha }_n^2+{S\prime }^2}[d(D^2{\alpha }_n^2+{S\prime }^2)+DS\prime ]+DS}}.$$ (50)

Appendix C

DERIVATION OF EQ. (23)

The derivation of Eq. (23) follows the same procedure used in App. B, except that our starting point is Eq. (2) in spherical coordinates

$$-\frac{\partial G}{\partial t}(r,r\prime ,t)+D\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial G}{\partial r}\right)(r,r\prime ,t)-\frac{G(r,r\prime ,t)}{\tau }=\frac{\delta (r-r\prime )}{4\pi r^2}\delta (t).$$ (51)

The Green’s function takes the form

$$G(r,r\prime ,t)=\frac{U(r,r\prime ,t)}{r}{e}^{-t/\tau },$$ (52)

where U satisfies the one-dimensional diffusion equation

$$D\frac{{\partial }^{2}U}{\partial r^2}=\frac{\partial U}{\partial t}$$ (53)

with the boundary condition

$$D\frac{\partial U}{\partial r}(R,t)=(\frac{D}{R}-S)U(R,t)$$ (54)

and the initial profile

$$U(r,r\prime ,0)=\frac{\delta (r-r\prime )}{4\pi r^2}.$$ (55)

The details of solution of Eq. (55) can be found in Carslaw and Jaerger’s work²⁰, and is given by the Fourier series

$$U(r,r\prime ,t)=\frac{1}{2\pi R}\sum _{n>0}{A}_n(r\prime )\text{ sin}({\alpha }_{n}r)e^{-{\alpha }_n^{2}Dt}$$ (56)

where

$$A_n(r\prime )=\frac{D^2{\alpha }_n^2{R}^2+{(SR-D)}^2}{D^2{\alpha }_n^2{R}^2+SR(SR-D)}\frac{\text{sin}({\alpha }_{n}r\prime )}{r\prime },$$ (57)

and the coefficients α_n are given by the transcendental relation Eq. (25).