Abstract
In winter wheat, grain development is asynchronous. The grain number and grain weight vary significantly at different spikelet and grain positions among wheat cultivars grown at different plant densities. In this study, two winter wheat (Triticum aestivum L.) cultivars, ‘Wennong6’ and ‘Jimai20’, were grown under four different plant densities for two seasons, in order to study the effect of plant density on the grain number and grain weight at different spikelet and grain positions. The results showed that the effects of spikelet and grain positions on grain weight varied with the grain number of spikelets. In both cultivars, the single-grain weight of the basal and middle two-grain spikelets was higher at the 2nd grain position than that at the 1st grain position, while the opposite occurred in the top two-grain spikelets. In the three-grain spikelets, the distribution of the single-grain weight was different between cultivars. In the four-grain spikelets of Wennong6, the single-grain weight was the highest at the 2nd grain position, followed by the 1st, 3rd, and 4th grain positions. Regardless of the spikelet and grain positions, the single-grain weight was the highest at the 1st and 2nd grain positions and the lowest at the 3rd and 4th grain positions. Overall, plant density affected the yield by controlling the seed-setting characteristics of the tiller spike. Therefore, wheat yield can be increased by decreasing the sterile basal and top spikelets and enhancing the grain weight at the 3rd and 4th grain positions, while maintaining it at the 1st and 2nd grain positions on the spikelet.
Introduction
Wheat (Triticum aestivum L.) is the second most widely produced crop in the world [1] and the demand for food is projected to be doubled by 2050 in addition to the increasing demand for high-quality food for a healthy diet [2]. Wheat production needs to be boosted mainly through improvements in yield and agronomic practices, as the cultivated area can only marginally increase [3–5]. Therefore, greater efforts need to be made to breed new wheat varieties with higher yield potential and improve crop management in order to enhance the average farm yields.
The increase in grain number per spike contributes considerably to improve wheat grain yield potential. A wheat spike is composed of spikelets which produce reproductive structures called florets. The grain number and grain weight in wheat are influenced by both genetic and environmental factors [6]. Within a spike, they are unevenly distributed and largely different due to its unbalanced development [7–9], while they depend on the spatial position of the kernel [10]. The spatial distribution of the grain number and grain weight shows parabolic changes, and as a result, the basal grains in the central spikelets are heavier than those in the near apical and near basal spikelets [11]. Within the central spikelets, the weight at the 2nd grain position is higher than that at the 1st, 3rd, and 4th grain positions, when moving from the most proximal to the most distal spikelet positions [6, 11, 12]. These differences can be attributed to the poor filling of inferior spikelets, due to carbon limitations [13–15], sink capacity limitations [16], unbalanced hormone levels [17, 18], the low gene expression and activity of enzymes involved in the sucrose-to-starch conversion [19–21], and impediments to assimilate transportation [22, 23].
Plant density is an important factor that influences the growth and yield formation in wheat [24, 25]. Previous studies have focused on identifying the optimal density for wheat cultivation, but the results vary based on the experimental conditions and tested parameters [26, 27]. In wheat, the number of spikelets per spike changes under different planting densities [28]. Qu et al. [29] reported that grain yield was improved with increasing plant density as a result of the increased spikelets number. Yoshida [30] reported that dense planting maximizes the leaf area index (LAI), ensuring that plant photosynthesis meets the high yield requirements. Nakano et al. [31] also reported that dense planting might increase the grain yield, the percentage of filled spikelets, and the 1000-grain weight in forage rice (Oryza sativa L.). However, some studies have reported that dense planting does not necessarily increase the grain yield [32–34]. Overall, there is limited information about the effect of plant density on seed-setting traits at different spikelet and grain positions between the main stem and tiller spikes.
The objective of this study was to elucidate the effect of plant density on the grain number and grain weight at different spikelet and grain positions in winter wheat. The obtained information will help to provide a theoretical basis for the development of wheat varieties with improved yield potential.
Materials and Methods
Plant material and experimental design
The field experiments were carried out for two growing seasons from October 2010 to June 2011 and from October 2011 to June 2012 at the Tai’an Experimental Station of Shandong Agricultural University, Tai’an, China (36° 09’ N, 117° 09’ E; 128 m above sea level). Maize (Zea mays L.) was the previous crop. The soil was a sandy loam, and the 0–20-cm layer contained 12.9 g kg-1 total organic matter, 120 mg kg-1 total nitrogen (N), 87.2 mg kg-1 available N, 64.2 mg kg-1 available phosphate (PO43-), and 109 mg kg-1 available potassium (K). In both seasons, fertilizer was applied before planting at a rate of 120 kg N ha-1 (46% N in urea), 100 kg P2O5 ha-1 (16% P2O5 in triple superphosphate), and 120 kg K2O ha-1 (60% K2O in muriate of potash). Additionally, topdressing N was applied at a rate of 120 kg N ha-1 during the jointing stage in the spring (GS31) [35].
The experimental arrangement was a 2 × 4 split-plot with three replicates (split plot design), in which cultivar was the primary factor and plant density was the secondary factor. We used two local winter wheat (Triticum aestivum L.) cultivars (‘Wennong6’, a large-spike cultivar with a relatively low number of tillers and ‘Jimai20’, a medium-spike cultivar with a relatively high number of tillers) and four plant densities (75 [D1], 225 [D2], 375 [D3], 525 plants m-2 [D4]). Each experimental plot consisted of 10 rows with 25 cm in-row spacing, while plant-to-plant spacing was 4.65 cm in D1, 1.50 cm D2, 0.90 cm in D3, and 0.64 cm in D4.
Seeds were sown on October 10 in 2010 and 2011 and harvested on June 16 in 2011 and June 14 in 2012. No noticeable crop damage was observed due to weeds, insects, or diseases. All agronomic practices were performed according to the precise high-yielding cultivation system as described by Yu [36].
Plant sampling
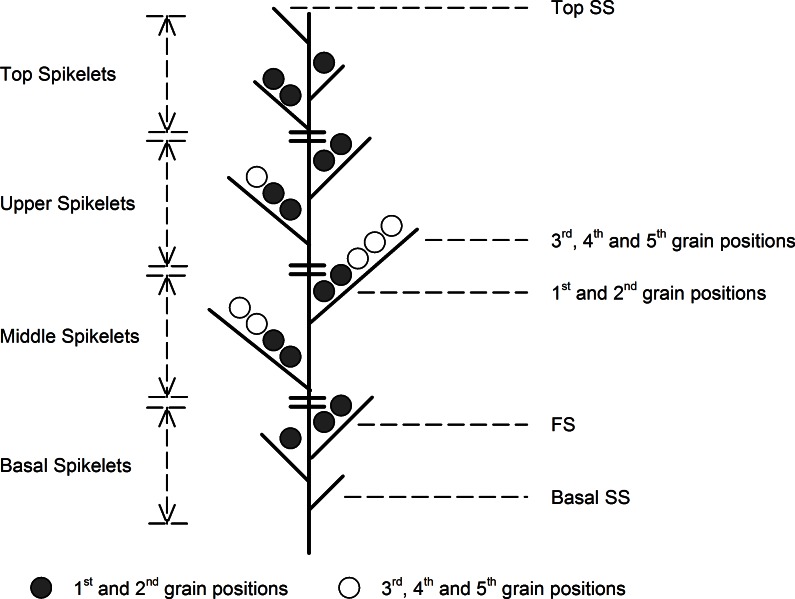
A total of 100 spikes, flowering on the same date, were labeled in two central rows of each plot, and 50 of those were removed at harvest (50 spikes × 3 replications). Each spike was divided into four parts as follows (Fig 1): the basal spikelets (basal–6th spikelet), middle spikelets (7th–15th spikelet), upper spikelets (16th–20th spikelet), and top spikelets (21st–terminal spikelet). The grains of each spike were numbered according to the grain position. Samples collected along 1 m of a separate central row were used to evaluate seed-setting traits at different spikelet and grain positions of the main stem and tiller spikes, while 1 m2 in each plot was harvested to evaluate yield.
Fig 1. Schematic diagram indicating the specific spikelet and grain positions analyzed in detail.
Fertile and sterile spikelets are classified by whether or not there are grains in the spikelets. SS, sterile spikelets (SSN, number of sterile spikelets per spike); FS, fertile spikelets (FSN, number of fertile spikelets per spike); GNS, grain number per spikelet; SGW, single-grain weight; GWS, grain weight per spikelet.
Statistical analysis
All traits were evaluated in triplicate. Analysis of variance in conjunction with Student–Newman–Keuls test was performed to identify significant differences between the treatments at P < 0.05. Statistical analysis was carried out using SPSS 18.0 (IBM Corp., Chicago, IL, USA)
Results
Differences in experimental factors
Table 1 presents the mean square significance between treatments and interactions for the number of spikes per plant (SP), the number of fertile spikelet per spike (FSN), the number of sterile spikelets per spike (SSN) at the top, the number of sterile spikelets per spike (SSN) at the bottom, the number of grains per spike (GN), 1,000-grain weight (TGW), spike number m-2 (SN), and grain yield m-2 (GY). Plant density and cultivar × density (C × D) interaction significantly affected SP, basal SSN, GN, TGW, SN, and GY, but not FSN or top SSN. All the traits, except for basal SSN, were significantly affected by cultivar (Table 1). Variations due to year (Yr) or Yr × C and Yr × D interactions were not significant (Table 1).
Table 1. Mean square significance among treatments and interactions for grain yield and its component in winter wheat.
| Source of variation | SP | FSN | Top SSN | Basal SSN | GN | TGW | SN | GY |
|---|---|---|---|---|---|---|---|---|
| Year (Yr) a | NS | NS | NS | NS | NS | NS | NS | NS |
| Cultivar (C) | ** | * | NS | * | ** | ** | * | ** |
| Plant density (D) | ** | NS | NS | * | * | * | * | * |
| Yr × C | NS | NS | NS | NS | NS | NS | NS | NS |
| D × Yr | NS | NS | NS | NS | NS | NS | NS | NS |
| C × D | * | NS | NS | * | * | * | * | * |
aExperiments were conducted at the Shandong Agricultural University Research Farm, Shandong Province, China, in the growing seasons 2010/2011 and 2011/2012.
SP, number of spikes per plant; FSN, number of fertile spikelets per spike; SSN, number of sterile spikelets per spike; GN, number of grains per spike; TGW, 1,000-grain weight; SN, number of spikes m-2; GY, grain yield m-2; Yr × C, year by cultivar interaction; D × Yr, plant density by year interaction; C × D, cultivar by plant density interaction. NS, not significantly different at P < 0.05
*, significantly different at P < 0.05
**, significantly different at P < 0.01.
Effects of plant density on seed-setting traits of the main stem and tiller spikes
The FSN, GN, and TGW of Wennong6 were higher than those of Jimai20, while the SP and SN of Wennong6 were lower than those of Jimai20 under the same plant density conditions (Table 2). The SP, GN, and TGW of both cultivars significantly reduced with the increasing plant density (Table 2). However, SN showed different patterns of change in response to plant density between cultivars. The SN of Wennong6 increased with the increasing plant density, while that of Jimai20 was the highest in D3. Plant density had little influence on FSN; however, SSN tended to increase with the increasing plant density. The yield of both cultivars was the highest in D2 and progressively reduced in D3, D4, and D1 (Table 2). These results indicated that a moderate plant density had a positive effect on GY, while a low or high plant density could negatively affect GY.
Table 2. Seed-setting traits of spike and yield components in two wheat cultivars, ‘Wennong6’ and ‘Jimai20’, grown under four different plant densities.
| Treatment | SP | FSN | SSN | SN | GN | TGW (g) | GY (g m-2) |
|---|---|---|---|---|---|---|---|
| Wennong6 | |||||||
| D1 | 4.05±0.03a | 19.60±0.28a | 3.35±0.02c | 389±5c | 56.01±0.28a | 47.56±0.16a | 896.6±5.6c |
| D2 | 2.59±0.02b | 19.37±0.25a | 3.48±0.14bc | 553±5b | 54.11±0.15b | 47.31±0.22a | 1055.8±23.1a |
| D3 | 1.46±0.01c | 19.44±0.15a | 3.67±0.07ab | 597±4a | 51.48±0.35c | 44.21±0.06b | 996.6±11.7b |
| D4 | 1.15±0.01d | 19.97±0.10a | 3.86±0.03a | 614±9a | 48.59±0.30d | 41.84±0.34c | 964.6±12.2b |
| Jimai20 | |||||||
| D1 | 4.70±0.18a | 17.15±0.11a | 3.14±0.09c | 456±14c | 39.41±0.28a | 36.71±0.29a | 719.1±7.2d |
| D2 | 3.73±0.03b | 17.04±0.42a | 3.60±0.05b | 837±13b | 35.65±0.28b | 35.03±0.20a | 948.5±5.9a |
| D3 | 2.48±0.02c | 17.21±0.07a | 3.90±0.03a | 933±6a | 31.52±0.06c | 32.45±0.33b | 906.9±5.7b |
| D4 | 1.52±0.02d | 16.63±0.17a | 3.84±0.02a | 804±11b | 31.35±0.24c | 32.11±0.37b | 787.0±5.6c |
| Comparison of densities | P < 0.01 | P > 0.05 | P > 0.05 | P < 0.05 | P < 0.05 | P < 0.05 | P < 0.05 |
| Standard error difference | 0.030 | 0.385 | 0.107 | 14.05 | 0.417 | 0.425 | 29.89 |
SP, number of spikes per plant; FSN, number of fertile spikelets per spike; SSN, number of sterile spikelets per spike; SN, number of spikes m-2; GN, number of grains per spike; TGW, 1,000-grain weight; GY, grain yield m-2; D1, 75 plants m-2; D2, 225 plants m-2; D3, 375 plants m-2; D4, 525 plants m-2. Data are means of three replicates. Standard error difference represents standard error of the difference between means. Means within each cultivar followed by a different letter are significantly different at P < 0.05.
The FSN, GN, and spike weight (SW) of Wennong6 were higher than those of Jimai20 under the same plant density conditions (Table 3). The seed-setting traits of the main stem spike were superior to those of the tiller spike in both cultivars, and basal SSN was significantly higher than top SSN. Significant decrease was observed in SW of both cultivars with the increasing plant density except SW in main stem of Jimai20. (Table 3).
Table 3. Seed-setting traits of main stem and tiller spikes in two wheat cultivars, ‘Wennong6’ and ‘Jimai20’, grown under four different plant densities.
| Treatment | Main stem spike | ||||
| FSN | Top SSN | Basal SSN | GN | SW (g) | |
| Wennong6 | |||||
| D1 | 20.81±0.25a | 0.61±0.01a | 2.17±0.14a | 61.80±1.02a | 2.53±0.01a |
| D2 | 20.61±0.11ab | 0.63±0.01a | 2.32±0.10a | 60.68±0.89a | 2.45±0.02b |
| D3 | 20.39±0.17ab | 0.53±0.01b | 2.27±0.06a | 53.83±1.14b | 2.23±0.02c |
| D4 | 20.01±0.06b | 0.39±0.01c | 2.24±0.06a | 50.14±0.11c | 2.20±0.02c |
| Jimai20 | |||||
| D1 | 18.73±0.18a | 0.47±0.05a | 2.55±0.06b | 41.05±0.46a | 1.94±0.02a |
| D2 | 18.68±0.14a | 0.54±0.02a | 2.84±0.01a | 38.02±0.66b | 1.85±0.01a |
| D3 | 18.14±0.04b | 0.53±0.02a | 2.83±0.04a | 33.01±1.05c | 1.79±0.03a |
| D4 | 16.97±0.13c | 0.37±0.01b | 2.99±0.04a | 32.41±1.00c | 1.79±0.00a |
| Comparison of densities | P < 0.05 | P < 0.05 | P > 0.05 | P < 0.05 | P < 0.05 |
| Standard error difference | 0.308 | 0.03 | 0.11 | 1.24 | 0.028 |
| Treatment | Tiller spike | ||||
| FSN | Top SSN | Basal SSN | GN | SW (g) | |
| Wennong6 | |||||
| D1 | 18.83±0.07a | 1.47±0.06b | 2.91±0.04b | 51.83±0.67a | 2.11±0.06a |
| D2 | 18.29±0.13b | 1.45±0.03b | 2.77±0.03c | 51.08±0.46ab | 2.00±0.01ab |
| D3 | 18.24±0.09b | 2.13±0.08a | 3.65±0.03a | 48.37±1.00bc | 1.93±0.02b |
| D4 | 17.69±0.16c | 2.14±0.03a | 3.62±0.02a | 47.38±1.11c | 1.93±0.07b |
| Jimai20 | |||||
| D1 | 16.26±0.07a | 0.47±0.03b | 2.82±0.06c | 39.02±0.12a | 1.65±0.02a |
| D2 | 16.38±0.21a | 0.70±0.01a | 3.20±0.03b | 36.05±0.50bc | 1.57±0.02b |
| D3 | 16.24±0.24a | 0.69±0.03a | 3.84±0.03a | 31.63±0.14c | 1.44±0.03c |
| D4 | 15.56±0.43b | 0.46±0.02a | 3.82±0.05a | 30.20±0.21d | 1.39±0.01c |
| Comparison of densities | P < 0.05 | P < 0.05 | P < 0.05 | P < 0.05 | P < 0.05 |
| Standard error difference | 0.300 | 0.058 | 0.058 | 0.905 | 0.05 |
FSN, number of fertile spikelets per spike; SSN, number of sterile spikelets per spike; GN, number of grains per spike; SW, spike weight; D1, 75 plants m-2; D2, 225 plants m-2; D3, 375 plants m-2; D4, 525 plants m-2. Data are means of three replicates. Standard error difference represents standard error of the difference between means. Means within each cultivar followed by a different letter are significantly different at P < 0.05.
Effects of plant density on the grain number per spikelet at different spikelet positions
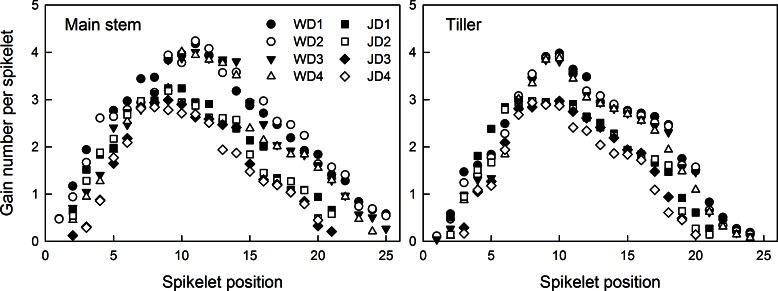
In the main stem and tiller spikes, grain number per spikelet (GNS) first increased and then decreased from the bottom to the top spikelets, showing a parabolic change. The GNS of the main stem spike was obviously higher than that of the tiller spike (Fig 2). The correlation between the grain number per spikelet and its position in the main stem and tiller spike were significant (Table 4). However, the spatial distribution of GNS was not symmetrical. The highest grain number was observed in the 7th-13th spikelets of Wennong6 and the 8th-11th spikelets of Jimai20, followed by the 3rd-6th and 3rd-7th spikelets and the 14th-20th and 12th-18th spikelets of Wennong6 and Jimai20, respectively. Therefore, the highest grain number was observed in the middle spikelets, followed by the basal, upper, and top spikelets. GNS increased from the basal to the middle spikelets, following a linear trend, and then reduced slowly from the middle to the top spikelets. The differences between the grain numbers at different spikelet positions of the basal spikelets were much higher than those of the middle spikelets.
Fig 2. Grain number per spikelet at different spikelet positions in two wheat cultivars ‘Wennong6’ (W) and ‘Jimai20’ (J), grown under four different plant densities.
D1, 75 plants m-2; D2, 225 plants m-2; D3, 375 plants m-2; D4, 525 plants m-2.
Table 4. Fitting equations of grain number per spikelet (y) at different spikelet positions (x) in two wheat cultivars, ‘Wennong6’ and ‘Jimai20’, grown under four different plant densities.
| Treatment | Main stem spike | Tiller spike | ||
|---|---|---|---|---|
| Equation | Coefficient (r) | Equation | Coefficient (r) | |
| Wennong6 | ||||
| D1 | y = -0.0217x2 + 0.5113x + 0.5542 | 0.874** | y = -0.0265x2 + 0.6257x - 0.2957 | 0.917** |
| D2 | y = -0.0220x2 + 0.5303x + 0.4251 | 0.897** | y = -0.0268x2 + 0.6354x - 0.4006 | 0.913** |
| D3 | y = -0.0245x2 + 0.5995x - 0.2195 | 0.809** | y = -0.0270x2 + 0.6500x - 0.6641 | 0.898** |
| D4 | y = -0.0264x2 + 0.6030x - 0.3884 | 0.871** | y = -0.0274x2 + 0.6570x - 0.7638 | 0.886** |
| Jimai20 | ||||
| D1 | y = -0.0271x2 + 0.5783x - 0.1306 | 0.891** | y = -0.0280x2 + 0.5958x - 0.2601 | 0.917** |
| D2 | y = -0.0272x2 + 0.5781x - 0.1494 | 0.884** | y = -0.0297x2 + 0.6384x - 0.5884 | 0.923** |
| D3 | y = -0.0306x2 + 0.6093x - 0.3324 | 0.872** | y = -0.0315x2 + 0.6874x - 1.0190 | 0.930** |
| D4 | y = -0.0279x2 + 0.6033x - 0.7403 | 0.861** | y = -0.0295x2 + 0.6354x - 0.8985 | 0.884** |
**Significant at P < 0.01.
D1, 75 plants m-2; D2, 225 plants m-2; D3, 375 plants m-2; D4, 525 plants m-2.
The GNS of both cultivars tended to decline with the increasing plant density (Fig 2). The grain number per spikelet at the basal (1st and 2nd) and top spikelet positions was lower than that at other positions. The grain number at the basal spikelet positions (except for the 1st and 2nd) reduced significantly with the increasing plant density, while that at the middle and upper spikelet positions showed no significant change. The results indicated that plant density had a stronger effect on the seed-setting traits at the basal spikelet positions than those of other spikelet positions.
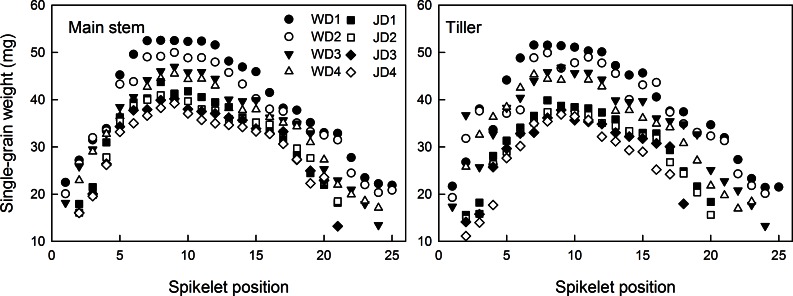
Spatial distribution of single-grain weight at different spikelet positions
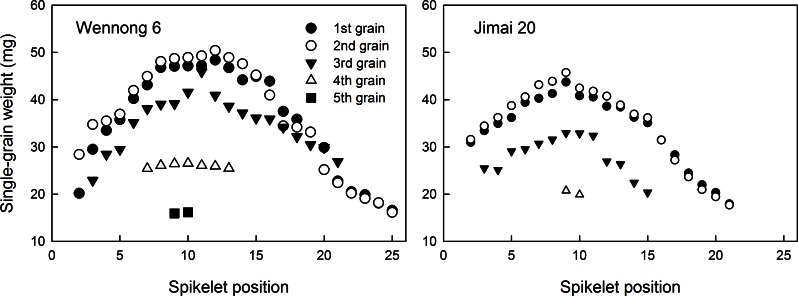
The effects of spikelet and grain positions on single-grain weight (SGW) varied with the grain number per spikelet (Fig 3). SGW was significantly positively correlated with GW and grain position and showed a parabolic change at the 1st, 2nd, and 3rd grain positions (Table 5). The SGW at the 1st grain position was similar to that at the 2nd grain position, but higher than those at the 3rd and 4th grain positions. In addition, the SGW of the basal and middle spikelets was the highest at the 2nd grain position. At the 1st and 2nd grain positions, the SGW of middle spikelets (7th–15th spikelet) of Wennong6 was heavier (p<0.01) than that of Jimai20 (Fig 3).
Fig 3. Distribution of single-grain weight at different spikelet positions in two wheat cultivars, ‘Wennong6’ (W) and ‘Jimai20’ (J), grown under four different plant densities.
D1, 75 plants m-2; D2, 225 plants m-2; D3, 375 plants m-2; D4, 525 plants m-2.
Table 5. Fitting equations of single-grain weight (y, mg) for a specific grain position at different spikelet positions (x) in two wheat cultivars, ‘Wennong6’ and ‘Jimai20’.
| Grain position | Equation | Coefficient (r) |
|---|---|---|
| Wennong6 | ||
| 1st | y = -0.2124x2 + 5.0286x + 16.530 | 0.927** |
| 2nd | y = -0.1946x2 + 4.2832x + 23.358 | 0.912** |
| 3rd | y = -0.1955x2 + 4.6533x + 13.027 | 0.863** |
| 4th | y = -0.1119x2 + 2.2167x + 15.453 | 0.924** |
| Jimai20 | ||
| 1st | y = -0.1841x2 + 3.0321x + 28.600 | 0.964** |
| 2nd | y = -0.2019x2 + 3.6623x + 25.880 | 0.961** |
| 3rd | y = -0.2845x2 + 4.8014x + 11.961 | 0.911** |
**Significant at P < 0.01.
Effects of plant density on the spatial distribution of grain weight per spikelet
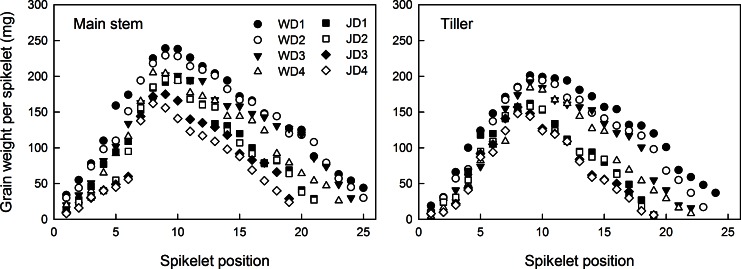
The grain weight per spikelet (GWS) of the main stem and tiller spikes showed parabolic changes, since it first increased and then decreased from the bottom to the top (Fig 4). The GWS at the middle spikelet position (8th–12th) was the highest, while the basal spikelets had higher differences in GWS that the middle or top spikelets. In addition, the GWS of the main stem spike was much higher than that of the tiller spike. The results also showed that GWS was significantly correlated with the spikelet position in the main stem and tiller spikes (Table 6).
Fig 4. Distribution of grain weight per spikelet at different spikelet positions in two wheat cultivars, ‘Wennong6’ (W) and ‘Jimai20’ (J), grown under four different plant densities.
D1, 75 plants m-2; D2, 225 plants m-2; D3, 375 plants m-2; D4, 525 plants m-2.
Table 6. Fitting equations of grain weight per spikelet (y, mg) at different spikelet positions (x) in two wheat cultivars, ‘Wennong6’ and ‘Jimai20’, grown under four different plant densities.
| Treatment | Main stem spike | Tiller spike | ||
|---|---|---|---|---|
| Equation | Coefficient (r) | Equation | Coefficient (r) | |
| Wennong6 | ||||
| D1 | y = -1.2629x2 + 30.709x + 21.963 | 0.869** | y = -1.3017x2 + 31.636x - 4.5899 | 0.931** |
| D2 | y = -1.2817x2 + 31.761x + 4.8035 | 0.903** | y = -1.4388x2 + 33.874x - 22.988 | 0.924** |
| D3 | y = -1.2645x2 + 31.577x - 14.210 | 0.928** | y = -1.5326x2 + 35.518x - 38.896 | 0.921** |
| D4 | y = -1.4182x2 + 33.439x - 23.604 | 0.866** | y = -1.4917x2 + 34.696x - 45.630 | 0.917** |
| Jimai20 | ||||
| D1 | y = -1.6372x2 + 35.936x - 30.931 | 0.873** | y = -1.7869x2 + 34.968x - 30.907 | 0.903** |
| D2 | y = -1.6657x2 + 37.386x - 48.280 | 0.822** | y = -1.7828x2 + 34.882x - 35.109 | 0.895** |
| D3 | y = -1.7275x2 + 37.109x - 55.257 | 0.813** | y = -1.7040x2 + 33.213x - 37.348 | 0.844** |
| D4 | y = -1.6053x2 + 33.587x - 47.445 | 0.811** | y = -1.6420x2 + 32.037x - 37.803 | 0.854** |
**Significant at P < 0.01.
D1, 75 plants m-2; D2, 225 plants m-2; D3, 375 plants m-2; D4, 525 plants m-2.
The GWS of the main stem and tiller spikes of Wennong6 was higher than that of Jimai20, especially under low plant density conditions (Fig 4). GWS tended to decline with the increasing plant density (Fig 4), while it was lower at the basal (1st and 2nd) and top spikelet positions compared with that at the middle spikelet positions. The GWS at the basal spikelet position (except for 1st and 2nd) significantly reduced with the increasing plant density. However, the GWS at the middle and upper spikelet positions showed no significant changes under different plant density conditions. Plant density had a stronger effect on the GWS of Wennong6 than that of Jimai20.
Effects of plant density on the distribution of single-grain weight
The SGW of the main stem and tiller spikes showed parabolic changes, since it first increased and then decreased from the bottom to the top (Fig 5). SGW was the lowest at the basal (1st and 2nd) and top spikelet positions. In Wenong6, the SGW in the middle spikelets of the main stem spike did not differ significantly from that of the tiller spike, whereas in Jimai20, the SGW in the middle spikelets of the main stem spike was higher than that of the tiller spike. SGW was significantly correlated with the grain position (Table 7). However, the spikelet position had a stronger effect on the SGW of the main stem spike than that of the tiller spike. The SGW of Wennong6, especially at the middle and upper spikelets, significantly reduced with increasing plant density and varied more greatly in the main stem spike than in the tiller spike. However, plant density had a weak effect on the SGW of Jimai20.
Fig 5. Distribution of single-grain weight at different spikelet positions in two wheat cultivars, ‘Wennong6’ (W) and ‘Jimai20’ (J), grown under four different plant densities.
D1, 75 plants m-2; D2, 225 plants m-2; D3, 375 plants m-2; D4, 525 plants m-2.
Table 7. Fitting equations of single-grain weight (y, mg) at different spikelet positions (x) in two wheat cultivars, ‘Wennong6’ and ‘Jimai20’, grown under four different plant densities.
| Treatment | Main stem spike | Tiller spike | ||
|---|---|---|---|---|
| Equation | Coefficient (r) | Equation | Coefficient (r) | |
| Wennong6 | ||||
| D1 | y = -0.2004x2 + 4.6732x + 22.668 | 0.861** | y = -0.1886x2 + 4.3293x + 24.021 | 0.858** |
| D2 | y = -0.1832x2 + 4.2374x + 22.091 | 0.865** | y = -0.2145x2 + 4.9155x + 18.987 | 0.878** |
| D3 | y = -0.2164x2 + 4.8388x + 17.671 | 0.954** | y = -0.2062x2 + 4.5155x + 19.723 | 0.919** |
| D4 | y = -0.2272x2 + 5.4229x + 11.069 | 0.815** | y = -0.2435x2 + 5.4215x + 13.183 | 0.817** |
| Jimai20 | ||||
| D1 | y = -0.2530x2 + 5.4961x + 11.732 | 0.910** | y = -0.3069x2 + 5.9571x + 10.751 | 0.924** |
| D2 | y = -0.2388x2 + 5.3670x + 10.169 | 0.876** | y = -0.2755x2 + 6.0210x + 6.7899 | 0.949** |
| D3 | y = -0.2511x2 + 5.5623x + 8.878 | 0.906** | y = -03937x2 + 8.1616x + 3.7644 | 0.868** |
| D4 | y = -0.2757x2 + 5.9607x + 6.647 | 0.854** | y = -0.4496x2 + 9.0132x - 7.9437 | 0.925** |
**Significant at P < 0.01.
D1, 75 plants m-2; D2, 225 plants m-2; D3, 375 plants m-2; D4, 525 plants m-2.
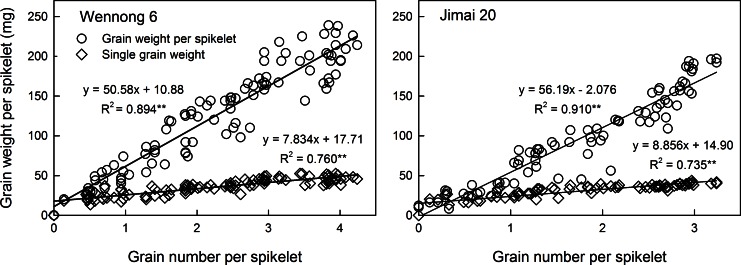
Relationship among grain weight per spikelet, grain number, and single-grain weight
GWS was significantly positively correlated with GNS (Fig 6) and the latter with SGW. In addition, GWS was significantly positively correlated with SGW, and the correlation coefficients were 0.855 and 0.671 for Wennong6 and Jimai20, respectively. Both GNS and GN had a strong positive effect on GWS.
Fig 6. Relationships between grain weight per spikelet, grain number, and single-grain weight at different spikelet positions in two wheat cultivars, ‘Wennong6’ and ‘Jimai20’.
Distribution of single-grain weight at different grain positions
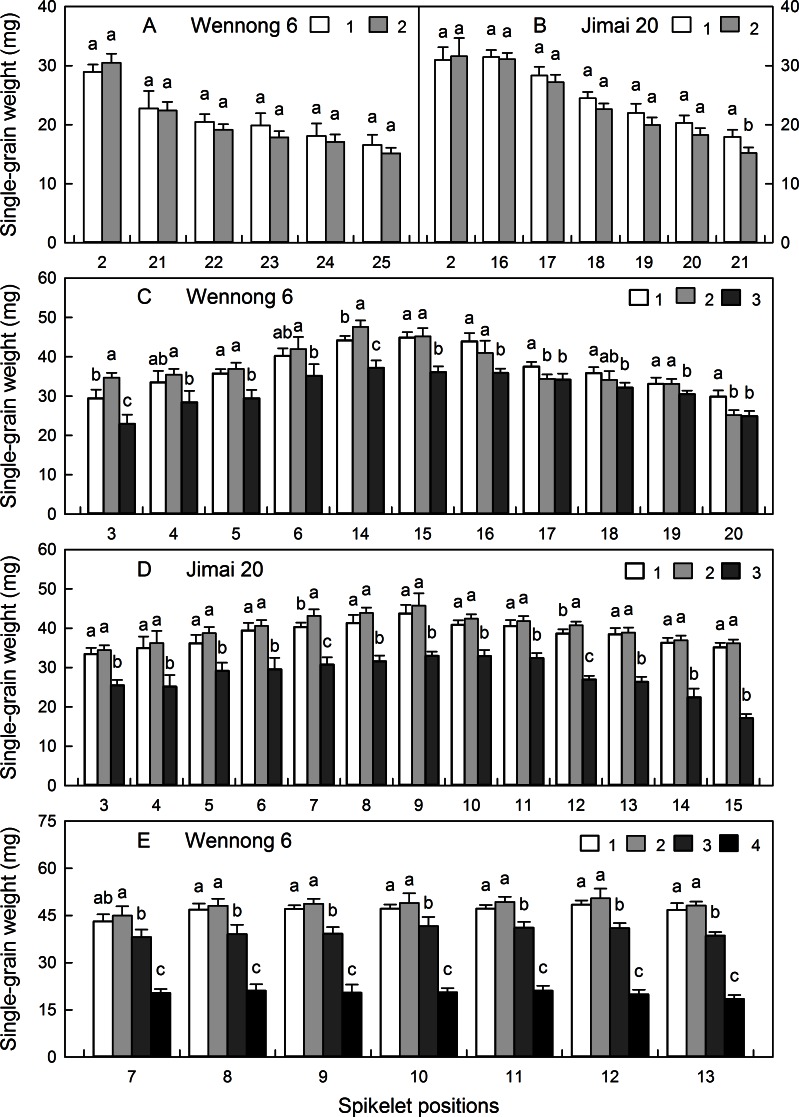
The effects of spikelet and grain positions on SGW varied with the GN of spikelets and cultivars. The two-grain spikelets were mainly distributed at the basal (2nd) and top spikelet positions. In the basal two-grain spikelets of both cultivars, the SGW at the 2nd grain position was higher than that at the 1st grain position, whereas the opposite occurred in the top two-grain spikelets (Fig 7A and 7B). In the three-grain spikelets, the distribution of SGW was different between cultivars. In the basal (3rd–6th) and middle (14th and 15th) three-grain spikelets of Wennong6, SGW was the highest at the 2nd grain position, followed by the 1st and 3rd grain positions, while in the top spikelets, SGW was the highest at the 1st grain position, followed by the 2nd and 3rd grain positions (Fig 7C). In the basal and middle three-grain spikelets of Jimai20, SGW was the highest at the 2nd grain position, followed by the 1st and 3rd grain positions (Fig 7D). In the four- and five-grain spikelets of Wennong6, SGW was the highest at the 2nd grain position, followed by the 1st, 3rd, 4th, and 5th grain positions (Fig 7E). Regardless the spikelet and grain positions, SGW was the highest at the 1st and 2nd grain positions and the lowest at the 3rd and 4th grain positions.
Fig 7.
Single-grain weight of two-grain (A and B), three-grain (C and D), and four-grain (E) spikelets at different grain positions in two wheat cultivars, ‘Wennong6’ and ‘Jimai20’.
Discussion
The variation of GN and grain weight (GW) was a major factor for determining the effects of spikelet and grain positions on the grain set and matter accumulation [9, 11, 12]. Li et al. [37] reported that GWS, GNS, and SGW at different spikelet and grain positions, and the seed-setting rate showed a partial spindle distribution and differed between the main stem and tiller spikes. Our results showed that GN, GWS, and GW at different spikelet positions from the bottom to the top showed parabolic changes, which were in agreement with previous studies [9, 11, 12]. It has been suggested that GN depended on the fecundity of basic spikelets, while GW and GY depended on matter accumulation in the grains of top spikelets and was mainly associated with the development of spikelets and florets [38].
It has been reported that the degree and rate of grain number and grain weight highly differ between spikelets based on their positions in the wheat spike [11, 12, 29]. Large differences have been observed between florets in the amount and size of vascular bundles, carbon amount, sink capacity, endogenous hormone levels, activity and/or gene expression of enzymes involved in sucrose-to-starch conversion, and assimilate transportation, resulting in an asynchronous grain development and nutriment accumulation as well as in yield differences among spikelets and grains [13–16, 18–21, 23]. Jiang et al. [39] suggested that superior grains have higher sucrose contents at the early and middle grain filling, and thus, a greater ability for starch synthesis. Ru et al. [40] found that TGW in wheat was different at different spikelet and grain positions. In this study, we found that the effects of spikelet and grain positions on SGW varied with the grain number of spikelet. The SGW at the 1st grain position was similar to that at the 2nd grain position and higher than that at the 3rd and 4th grain positions. In the basal (2nd) to top (15th) two-grain, three-grain, and four-grain spikelets, the SGW at the 2nd grain position was higher compared to that at the 1st grain position. These findings were in agreement with those reported by Qu et al. [29] and Pan et al. [11], but in disagreement with those of Zhu [41], probably due to differences in the used wheat varieties. The variation in the 2nd grain position was a major factor for determining the effects of spikelet and grain positions on grain development, the spatial distribution of grain weight, and matter accumulation under different conditions as well as a major target for improving yield [9]. The results suggested that wheat production could be boosted by enhancing the GW at the 3rd and 4th grain positions, while maintaining it at the 1st and 2nd grain positions. Wennong6 has a greater potential in improving yield than Jimai20, since the former has a higher GW at the 3rd and 4th grain positions than the latter.
Plant density is an important factor that influences the growth and yield in wheat [13, 24, 25]. In this study, GN and GW reduced with the increasing plant density. Li et al. [37] reported that under dense planting, the grain number at the 3rd and 4th grain positions and the 1st and 2nd grain positions of the basal and top spikelets decreased. In this study, we found that the seed-setting characteristics and GW of Wennong6 were superior to those of Jimai20. Meanwhile, the seed-setting traits of the main stem spike were superior to those of the tiller spike. SW showed decreasing trends with the increasing plant density, and the decrease was even greater in Wennong6. Therefore, plant density probably had a stronger effect on cultivars with higher grain numbers, suggesting that the interaction of genotype and plant density may determine the variation in the grain number and matter accumulation of the wheat spike.
Previous studies showed that the differences in SW under different plant density conditions were significant in wheat [9, 42] and rice [43]. A very high plant density increases SN, but decreases GWS in wheat [29]; therefore, extreme plant density conditions may have a negative effect on yield. The wheat cultivar Jimai20 is a medium-spike cultivar, which produces more tillers per grain than the larger spike cultivar at the same density. As the density increases, tillers produced by a single grain become less. There is considerable compensation by the crops grown at low densities, which was in agreement with Whaley et al. [44]. SN is determined by total tillers, which is equal to the product of density and tillers produced by a single grain. Thus, a targeted SN might be shaped from different density due to genotypes. The differences between genotypes are reflected in spikelet positions and form the substantive characteristics of spikes between cultivars [45]. Therefore, in wheat production, we should properly trade off the relationship between GN and GW, and then improve these two yield components along with SW in order to reach their maximum potential.
Conclusions
FSN, GN, and SGW significantly decreased with the increasing plant density. The seed-setting characteristics in the main stem spike were relatively stable, while plant density affected the yield by controlling the seed-setting characteristics in the tiller spike. To boost wheat production, we should choose the appropriate plant density based on cultivars to maintain the seed-setting characteristics of the tiller spike, increase the seed-setting rate by supplying sufficient nutrients, mainly nitrogen nutrient, to decrease the number of basal and top sterile spikelets, and enhance the grain weight at the 3rd and 4th grain positions, while maintaining it at the 1st and 2nd grain positions.
Supporting Information
Figs 2–7 were plotted based on this excel file.
(XLSX)
Tables 2–7 were created based on this excel file.
(XLSX)
Acknowledgments
The research was supported by the National Natural Science Foundation of China (NO. 31271661, 31271667, 30871477), the Shandong Modern Agriculture Technology and Industry System. A Project of Shandong Province Higher Educational Science and Technology Program (J14LF12). The National Basic Research Program of China (973 Program, NO. 2015CB150404), the Special Fund for Agro-scientific Research in the Public Interest of China (No. 201203100, 201203029) and the National Science and Technology Support Program of China (No. 2012BAD04B05).
Data Availability
Data available in Supporting Information file or Email: woooowo@126.com.
Funding Statement
This research was supported by the National Natural Science Foundation of China (no. 31271661, 31271667, 30871477), the Shandong Modern Agriculture Technology and Industry System, A Project of Shandong Province Higher Educational Science and Technology Program (J14LF12), The National Basic Research Program of China (973 Program, no. 2015CB150404), the Special Fund for Agro-scientific Research in the Public Interest of China (no. 201203100, 201203029) and the National Science and Technology Support Program of China (no. 2012BAD04B05).
References
- 1.FAO I, WFP. The state of food insecurity in the world: meeting the 2015 international hunger targets: taking stock of uneven progress FAO; Rome; 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Singh J, Kaur S, Majithia H. Emerging genetic technologies for improving the security of food crops. Emerging technologies for promoting food security: Overcoming the world food crisis. 2015; 23–41. [Google Scholar]
- 3.Long SP, Ort DR. More than taking the heat: crops and global change. Curr Opin Plant Biol. 2010; 13(3): 241–248. 10.1016/j.pbi.2010.04.008 [DOI] [PubMed] [Google Scholar]
- 4.Chand R. Challenges to ensuring food security through wheat. CAB reviews: Perspectives in agriculture, veterinary science, nutrition and natural resources. 2009; 4(65): 1–13. [Google Scholar]
- 5.Reynolds M, Foulkes MJ, Slafer GA, Berry P, Parry MA, Snape JW, et al. Raising yield potential in wheat. J Exp Bot. 2009; 60(7): 1899–1918. 10.1093/jxb/erp016 [DOI] [PubMed] [Google Scholar]
- 6.Bustos DV, Hasan AK, Reynolds MP, Calderini DF. Combining high grain number and weight through a DH-population to improve grain yield potential of wheat in high-yielding environments. Field Crops Res. 2013; 145: 106–115. [Google Scholar]
- 7.Miralles DJ, Slafer GA. Individual grain weight responses to genetic reduction in culm length in wheat as affected by source-sink manipulations. Field Crops Res. 1995; 43(2): 55–66. [Google Scholar]
- 8.Chen Y, Yuan L, Wang X, Zhang D, Chen J, Deng Q, et al. Relationship between grain yield and leaf photosynthetic rate in super hybrid rice. J Plant Physiol Mol Biol. 2007; 33(3): 235–243. [PubMed] [Google Scholar]
- 9.Ferrante A, Savin R, Slafer GA. Relationship between fruiting efficiency and grain weight in durum wheat. Field Crops Res. 2015; 177: 109–116. [Google Scholar]
- 10.Calderini DF, Reynolds MP. Changes in grain weight as a consequence of de-graining treatments at pre-and post-anthesis in synthetic hexaploid lines of wheat. Funct Plant Biol. 2000; 27(3): 183–191. [Google Scholar]
- 11.Pan J, Jiang D, Cao WX, Sun CF. Effects of spikelet and grain positions on grain number, weight and protein content of wheat spike. Acta Agron Sin. 2005; 31: 431–437. [Google Scholar]
- 12.Pei XX, Wang JA, Dang JY, Wang XB, Zhang DY. Effects of spikelet and grain position on fertile spikelet number, grain weight and quality of wheat. Sci Agric Sin. 2008; 41: 381–390. [Google Scholar]
- 13.Murty P, Murty K. Spikelet sterility in relation to nitrogen and carbohydrate contents in rice. Indian J. Plant Physiol. 1982; 25: 40–48. [Google Scholar]
- 14.Dreccer MF, van Herwaarden AF, Chapman SC. Grain number and grain weight in wheat lines contrasting for stem water soluble carbohydrate concentration. Field Crops Res. 2009; 112(1): 43–54. [Google Scholar]
- 15.Wang Y. Effectiveness of supplied nitrogen at the primordial panicle stage on rice characteristics and yields. Int Rice Res Newsl. 1981; 6: 23–24. [Google Scholar]
- 16.Kato T. Effect of spikelet removal on the grain filling of Akenohoshi, a rice cultivar with numerous spikelets in a panicle. J Agric Sci. 2004; 142(2): 177–181. [Google Scholar]
- 17.Yang J, Zhang J. Grain filling of cereals under soil drying. New phytologist. 2006; 169(2): 223–236. [DOI] [PubMed] [Google Scholar]
- 18.Zhang H, Tan G, Yang L, Yang J, Zhang J, Zhao B. Hormones in the grains and roots in relation to post-anthesis development of inferior and superior spikelets in japonica/indica hybrid rice. Plant Physiol. Bio. 2009; 47(3): 195–204. [DOI] [PubMed] [Google Scholar]
- 19.Ishimaru T, Hirose T, Matsuda T, Goto A, Takahashi K, Sasaki H, et al. Expression patterns of genes encoding carbohydrate-metabolizing enzymes and their relationship to grain filling in rice (Oryza sativa L.): comparison of caryopses located at different positions in a panicle. Plant Cell Physiol. 2005; 46(4): 620–628. [DOI] [PubMed] [Google Scholar]
- 20.Jeng T, Wang C, Chen C, Sung J. Effects of grain position on the panicle on starch biosynthetic enzyme activity in developing grains of rice cultivar Tainung 67 and its NaN 3-induced mutant. J Agric Sci. 2003; 141(3–4): 303–311. [Google Scholar]
- 21.Wang E, Wang J, Zhu X, Hao W, Wang L, Li Q, et al. Control of rice grain-filling and yield by a gene with a potential signature of domestication. Nat Genet. 2008; 40(11): 1370–1374. 10.1038/ng.220 [DOI] [PubMed] [Google Scholar]
- 22.Serrago RA, Alzueta I, Savin R, Slafer GA. Understanding grain yield responses to source–sink ratios during grain filling in wheat and barley under contrasting environments. Field Crops Res. 2013; 150: 42–51. [Google Scholar]
- 23.Yang JC, Zhang JH. Crop management techniques to enhance harvest index in rice. J Exp Bot. 2010; 61(12): 3177–3189. 10.1093/jxb/erq112 [DOI] [PubMed] [Google Scholar]
- 24.Hiltbrunner J, Streit B, Liedgens M. Are seeding densities an opportunity to increase grain yield of winter wheat in a living mulch of white clover? Field Crops Res. 2007; 102(3): 163–171. [Google Scholar]
- 25.Grassini P, Thorburn J, Burr C, Cassman KG. High-yield irrigated maize in the Western US Corn Belt: I. On-farm yield, yield potential, and impact of agronomic practices. Field Crops Res. 2011; 120(1): 142–150. [Google Scholar]
- 26.Lloveras J, Manent J, Viudas J, Lopez A, Santiveri P. Seeding rate influence on yield and yield components of irrigated winter wheat in a Mediterranean climate. Agron J 2004; 96(5): 1258–1265. [Google Scholar]
- 27.Luo LP, Yu ZW, Wang D, Zhang YL, Shi Y. Effects of Plant Density and Soil Moisture on Photosynthetic Characteristics of Flag Leaf and Accumulation and Distribution of Dry Matter in Wheat. Acta Agron Sin. 2011; 37(6): 1049–1059. [Google Scholar]
- 28.Dornbusch T, Baccar R, Watt J, Hillier J, Bertheloot J, Fournier C, et al. Plasticity of winter wheat modulated by sowing date, plant population density and nitrogen fertilisation: dimensions and size of leaf blades, sheaths and internodes in relation to their position on a stem. Field Crops Res. 2011; 121(1): 116–124. [Google Scholar]
- 29.HuiJuan Q, JinCai L, XueShan S, FengZhen W, ChengYu W, ShengJun Z. Effects of plant density and seeding date on accumulation and translocation of dry matter and nitrogen in winter wheat cultivar Lankao Aizao 8. Acta Agron Sin. 2009; 35(1): 124–131. [Google Scholar]
- 30.Yoshida S. Fundamentals of rice crop science: Int Rice Res Inst. 1981. [Google Scholar]
- 31.Nakano H, Morita S, Kitagawa H, Wada H, Takahashi M. Grain yield response to planting density in forage rice with a large number of spikelets. Crop Sci. 2012; 52(1): 345–350. [Google Scholar]
- 32.Takeda T, Hirota O. Relationship between Spacing and Grain Yield of Rice Plant. Japan J Crop Sci. 1971; 40: 381–385. [Google Scholar]
- 33.Akita K, Tanaka N. Effects of Planting Density and Planting Patterns of Young Seedlings Transplanting on the Growth and Yield of Rice Plants. Japan J Crop Sci. 1992; 61(1): 80–86. [Google Scholar]
- 34.Gendua PA, Yamamoto Y, Miyazaki A, Yoshida T, Wang Y. Responses of yielding ability, sink size and percentage of filled grains to the cultivation practices in a Chinese large-panicle-type rice cultivar, Yangdao 4. Plant Production Sci. 2009; 12(2): 243–256. [Google Scholar]
- 35.Zadoks JC, Chang TT, Konzak CF. A decimal code for the growth stages of cereals. Weed Res. 1974; 14(6): 415–421. [Google Scholar]
- 36.Yu SL. Wheat in Shandong Province. Beijing, China: China Agriculture Press; 1990. [Google Scholar]
- 37.Xu HC, Cai T, Wang ZL, He MR. Physiological basis for the differences of productive capacity among tillers in winter wheat. J Integr Agr. 2015; 14(10): 1958–1970. [Google Scholar]
- 38.Yu ZW. Crop cultivation (in northern area) Beijing, China: China Agriculture Press; 2003. [Google Scholar]
- 39.Jiang D, Cao W, Dai T, Jing Q. Activities of key enzymes for starch synthesis in relation to growth of superior and inferior grains on winter wheat (Triticum aestivum L.) spike. Plant Growth Regul. 2003; 41(3): 247–257. [Google Scholar]
- 40.Ru ZG, Li G, Hu TZ, Li LB. Analysis of grain weight and quality at different floret position of strong glutinin wheat. J Triticeae Crops. 2006; 26: 134–136. [Google Scholar]
- 41.Zhu XK, Guo WS, Wang YJ, Feng CN, Peng YX. Study of distribution rule of wheat grain weight and their relationship. Seed. 2004; 23: 67–71. [Google Scholar]
- 42.Guo T, Zha F, Ma D, Song X, Yue Y. Effects of plant density on the accumulation and transfer of dry matter and nitrogen and grain yield of two winter wheat cultivars with different spike types. Acta Agric Boreali-Sin. 2007; 22(6): 152–156. [Google Scholar]
- 43.Xu ZJ, Chen WF, Shun ZH, Zhang SL, Liu LX, Zhou SQ. Distribution of rice grains on panicle axis and its relationship with seed-setting ability in Liaoning, China. Sci Agric Sin. 2006; 5: 202–208. [Google Scholar]
- 44.Whaley J, Sparkes D, Foulkes M, Spink J, Semere T, Scott R. The physiological response of winter wheat to reductions in plant density. Ann Appl Biol. 2000; 137(2): 165–177. [Google Scholar]
- 45.Yang JC, Liu LJ, Wang ZQ, Lang YZ, Zhu QS. Effects of flowering time of spikelets on endosperm development in rice and its physiological mechanism. Sci Agric Sin. 1999; 32: 44–51. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figs 2–7 were plotted based on this excel file.
(XLSX)
Tables 2–7 were created based on this excel file.
(XLSX)
Data Availability Statement
Data available in Supporting Information file or Email: woooowo@126.com.