Advances in thermometry

Abstract

The last 25 years have seen tremendous progress in thermometry in the moderate temperature range (1 K to 1235 K). Various primary thermometers — based on different physics —have uncovered errors in the International Temperature Scale of 1990 and set the stage for the planned redefinition of the kelvin.

Thermodynamic temperature T is the physical property that two objects have in common when they are isolated from the rest of the universe and allowed to exchange energy with each other. The actual shared property is the average energy per degree of freedom. In the International System of Units (SI), the unit of energy is the joule and ‘number of degrees of freedom’ is a dimensionless number. Therefore, the property that objects in thermodynamic equilibrium share can be expressed in joule per degree of freedom. For example, if we allow the air in a comfortable room to come into equilibrium with a thermometer, the thermometer will read 4.04×10⁻²¹ J per degree of freedom. For historical reasons, temperature is expressed in kelvin and of course the aforementioned thermometer reading in kelvin is T = 293 K. The conversion factor between temperature expressed in kelvin and joule per degrees of freedom is the Boltzmann constant, k_B = 1.380 648 52×10⁻²³ J/K. It is important to keep in mind that the product k_BT is the physical quantity that characterizes the thermal equilibrium between a particular pair of objects, one of which might be a thermometer.

The (re)definition of the kelvin

Today, the kelvin, the unit of thermodynamic temperature, is “the fraction 1/273.16 of the thermodynamic temperature of the triple point of water.” (We abbreviate “the temperature of the triple point of water” as T_TPW.) As of 2014, k_B has been measured with a relative standard uncertainty of u_r(k_B) = 5.7×10⁻⁷ and, by definition, u_r(T_TPW) = 0; therefore, u_r( k_BT_TPW) = 5.7×10⁻⁷ [1]. The present SI definition of the kelvin has two disadvantages that will disappear when k_B is assigned a fixed value and the relative uncertainty of k_BT_TPW is entirely due to that of T_TPW. First, the special role of the triple point of water in defining T will be eliminated; however, the measured value of T_TPW will still be close to 273.16 K. Although this change is conceptually important, triple-point-of-water cells will continue to be essential for practical thermometry because they are inexpensive, stable, portable, and highly reproducible. Second, with the present definition of the kelvin, no matter how accurately k_BT is measured, the resulting relative uncertainty of the temperature u_r(T) must de facto be greater than or equal to the uncertainty of k_B. After the planned redefinition of the kelvin, it will be possible, in principle, for a future metrologist to accurately measure k_BT_x at a temperature T_x far from T_TPW (say, T_x = 2000 K) with an uncertainty attributed to T_x that is smaller than the uncertainty of T_TPW. (After k_B is fixed in 2018, this possibility will be realized only in the unlikely circumstance that u_r(T_x) ≤ u_r(T_TPW) ≈ 5.7×10⁻⁷.)

Thermodynamic thermometry

To accurately measure k_BT (the average energy per degree of freedom), a metrologist must use a primary thermometer, that is, any instrument that has a well-understood connection between a measureable quantity and k_BT. In the following, we briefly discuss five different measureable quantities that are used or can be used for primary thermometry: (1) the pressure of a gas in a constant volume, (2) the speed of sound in a monatomic gas, (3) the dielectric constant of a gas, (4) the power spectral density of Johnson-noise in a resistor and, (5) the radiation emitted by a black body. References and more detailed discussions can be found in the reviews by Fischer et al. [2,3].

Gas thermometry

Gas thermometry relies on the statistical-mechanical connection between the three kinetic degrees of freedom of an ideal gas and thermodynamic temperature: ½ m〈v²〉 = 3k_BT, where m is the mass of an atom and 〈v²〉 is the mean-square velocity of the atom. An immediate consequence of this connection is the ideal gas law, which relates the number density n and pressure p to temperature: k_BT = p/n. For monatomic gases, kinetic theory also predicts 〈v²〉 = 9u²/5, where u is the speed of sound in the gas. Therefore, the speed of sound is connected to the temperature through k_BT = 3mu²/5.

Prior to 1990, many of the measurements of thermodynamic temperature T conducted at national metrology institutes (NMIs) used helium-filled, constant-volume gas thermometers. These thermometers involve a fixed quantity of helium confined within a cavity — the ‘thermometer bulb’. The pressure of the helium gas was measured as the temperature was changed from the defining temperature T_TPW to an unknown temperature T_x. Because helium is not an ideal gas, the ratio of the pressures yielded an approximation to the ratio of the temperatures: p(T_x)/p(T_TPW) ≈ T_x/T_TPW, which becomes exact in the limit of zero pressure. Therefore, the pressure ratio measurements were repeated with less helium in the thermometer bulb. Finally, a series of pressure ratio data were empirically extrapolated to zero pressure. Because constant-volume gas thermometry used pressure ratios, which can be measured more accurately than individual pressures, it was expected that the temperature ratios would have uncertainties on the order of 10⁻⁵ T; in hindsight, the errors were 2 to 3 times larger.

To the best of the authors’ knowledge, no NMI has made constant-volume gas thermometry measurements since 1990. The empirical extrapolation to zero pressure is outdated: nowadays, helium pressure-ratio measurements made at moderate densities would be extrapolated to zero density using the density virial coefficients of helium calculated from quantum mechanics and statistical mechanics [4]. For helium, the calculated values of acoustic virial coefficients, thermal conductivity, viscosity, dielectric constant, and refractive index are more accurate than the best measurements. Therefore, the calculated values of these properties are used, for example, in acoustic gas thermometry and dielectric-constant gas thermometry, as discussed below. Moreover, the calculated values of helium’s properties are even used as standards for calibrating apparatuses that are used to measure these properties.

Advances in theory and computation have also reduced the uncertainties of the thermophysical properties of argon, particularly at temperatures away from ambient conditions; therefore, argon can also be used to measure the thermodynamic temperature without an empirical extrapolation to zero pressure (see the supplementary material in Ref. 5).

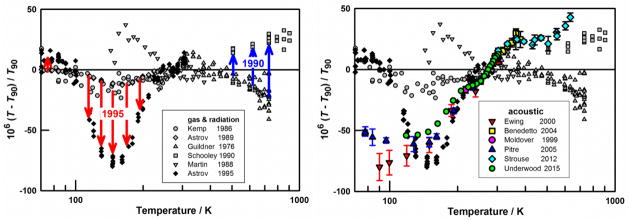
Contemporary acoustic-gas thermometers simultaneously measure the frequencies f_a of several acoustic resonances and the frequencies f_m of several microwave resonances in a metal cavity filled with helium or argon [5]. Each frequency ratio f_a/f_m is approximately proportional to u/c, the ratio of the speed of sound to the speed of light in the gas. The proportionality constants for the various acoustic and microwave modes depend upon the shape of the cavity. The frequency ratios f_a/f_m are measured at the defining temperature T_TPW and an unknown temperature T_x; the unknown temperature is determined through the relation (T_x/T_TPW)^1/2 = (f_a/f_m)_Tx/(f_a/f_m)_TTPW. Remarkably, this ratio of frequency ratio measurements is only weakly sensitive to the gas pressure and is insensitive to small changes in the shape of the cavity caused by thermal expansion. As shown in Fig. A (right panel), diverse acoustic gas thermometers made at different NMIs agree with each other within a small fraction (≈3×10⁻⁶ T) in the range 84 K < T < 550 K.

To facilitate accurate frequency measurements, the shape of the gas-filled cavity is chosen to have high-Q, non-overlapping microwave and acoustic resonances. Most often, the cavity is a quasi-sphere formed by joining two nearly-hemispherical shells (Fig. 1). Typically, this shape is well approximated by a triaxial ellipsoid with axis ratios 1:(1 + e):(1 − e), with 0.0005 < e < 0.001. The parameter e is just large enough to separate the degenerate microwave frequencies, but small enough so that shape imperfections contribute errors of order e² to calculations of the acoustic and microwave frequencies [5]. Because the assembled shell has a joint, frequencies of its mechanical vibrations may differ significantly from those of a spherical shell. The coupling of these mechanical vibrations to the acoustic vibrations is an important source of errors to measurements made at high pressures.

Figure 1.

Acoustic gas thermometers. Left: 3-liter, stainless-steel-walled, spherical cavity, courtesy of NIST (National Institute of Standards and Technology, US); Right: 1-liter, copper-walled, quasi-spherical cavity, courtesy of NPL (National Physical Laboratory, UK).

Dielectric-constant gas thermometry

In dielectric-constant gas thermometry, the thermodynamic temperature of a noble gas is determined by using the gas’ equation of state p(ρ,T) to eliminate the density ρ from the Clausius–Mossotti expansion of the gas’ dielectric constant ε(ρ,T) to obtain k_BT = p[(ε+2)/(ε−1)][1+…]/a_ε. Here, a_ε is the static dipole polarizability of a gas atom; for helium, a_ε has been calculated with sub-part-per-million uncertainty. In practice, the dielectric constant is determined using a gas-dielectric capacitor mounted inside a gas-filled thermometer ‘bulb’ at T_x. A tube leading from the bulb to ambient temperature facilitates accurate pressure measurements. As the pressure in the bulb is increased, the capacitor shrinks; this is taken into account via an elastic model and measurements of the elastic properties of the materials used in manufacturing the capacitor. Gaiser et al. [7] achieved state-of-the-art temperature measurements between 2.5 K and 36 K using a purpose-built capacitance bridge, the non-linearity and resolution of which were a few parts in 10⁹.

As temperature increases, the challenges of dielectric-constant gas thermometry also increase. Because the capacitance bridge is used at its resolution limit, the working range of the gas’ dielectric constant (and its density) must not decrease as the temperature is raised. Therefore, the working pressure must increase with temperature, along with the correction resulting from the shrinkage of the capacitor under pressure. If dielectric-constant gas thermometry is used above ambient temperature, the large influence of polar impurities, particularly water, on the small dielectric constant of the noble gas may become a problem. In principle, the concentrations of impurities generated by outgassing within the thermometer can be reduced by flowing the thermometric gas through a getter and then through the thermometer. Several recently- constructed, acoustic thermometers operate with flowing gas [5].

Black-body radiation thermometry

Objects at finite temperatures emit photons as described by the well-known Planck radiation law. The radiation emitted from a small hole in the wall of an interior cavity will closely approximate Planck’s law if the interior wall of the cavity is highly emissive (i.e., black) and maintained at a constant, uniform temperature, T. The radiation from the opening is then emitted by a ‘black body’ and its temperature can be determined by measuring either its total radiated power or the power radiated in a selected spectral region. The spectral radiance from such an opening is given by Planck’s radiation law and the spectrally integrated total energy radiated per unit surface area emitted by such an opening is σT⁴ (Stefan–Boltzmann law, with σ = 2π⁵k_B⁴/15h³c² the Stefan–Boltzmann constant). Radiation thermometers rely on the traceability of their optical power response to electrical standards and also require traceability to the meter for their wavelength and geometric-view-factor calibrations. These non-contact thermometers can be used at any temperature but are particularly useful at temperatures above 660 K, where a contact thermometer may not be stable. In a recent international comparison, nine NMIs used radiation thermometers to measure metal-carbon eutectic points, showing that thermodynamic temperatures could be measured with uncertainties lower than obtained by ITS-90 techniques [6]. (Certain material mixtures have a eutectic point; i.e. a distinct, lowest-possible, melting temperature that can be used as a fixed point in much the same way as the distinct melting point of a pure material.) Blackbody-radiation thermometry, along with acoustic gas thermometry, will be one of the widely accepted methods for the realization of thermodynamic temperature measurements based on the new definition of the kelvin.

Johnson-noise thermometry

At any temperature above absolute zero, voltage fluctuations appear across an electrical resistance R; a measurement of their power spectral density ν_T provides a fundamental measurement of thermodynamic temperature. In the low-frequency/high-temperature limit, the fluctuation–dissipation theorem reduces to the familiar frequency-independent form ν_T = 4k_BTR, as first experimentally observed by Johnson and described theoretically by Nyquist. Modern implementations of Johnson-noise thermometry utilize digital processing in the frequency domain to calculate cross-correlated power spectra. These thermal noise spectra are sampled with Nyquist frequencies of a few MHz and compared to similarly sampled spectra generated by a suitable noise-voltage reference [8]. The noise spectral density ν_Q of the reference must be calibrated or otherwise known in SI units and it is designed to match the thermal noise power such that ν_T/ν_Q ≈ 1. The most accurate noise-voltage references are synthesized using arrays of Josephson junctions such as those shown in Fig. 2. During the past 15 years, Johnson-noise thermometry has achieved uncertainties of only a few parts per million for temperatures near 273 K after several months of averaging time [9]. The method is also useful at higher temperatures, with uncertainties of ~40 μK/K demonstrated at temperatures of up to 800 K [10].

Figure 2.

Two arrays, each with 10 superconducting/normal/superconducting-metal Josephson junctions on a 1 cm² chip. The arrays are programmed to generate noise voltages that have a spectrum similar to that of Johnson noise with sub-part-per-million uncertainties [10]. Photo: courtesy of U.S. National Institute of Standards.

Dissemination of temperature via practical scales

The dissemination of T₉₀ (see ‘Box: The ITS-90 international temperature scale’) requires many fixed points in contrast with, for example, the meter, which at one time was defined and disseminated using only one artifact. Why? Length is an extensive quantity; therefore, a distance of 2 m can be realized (at least in principle) by adding, end-to-end, two distances, each 1 m long. In contrast, temperature is an intensive quantity: there is no method for realizing the temperature 546.32 K by somehow manipulating two triple-point-of-water cells, each at 273.16 K. It follows that practical thermometers must be calibrated at several temperatures; for the lowest uncertainties, this is done at NMIs by using several fixed points.

Box. The international temperature scale of 1990 (ITS-90).

Various international temperature scales have been used for practical temperature dissemination since circa 1900. These scales use various combinations of fixed-point temperatures to calibrate defined interpolation instruments. In addition to the triple point of water, these fixed points include the freezing points of various pure metals (In, Sn, Zn, Al, …) and several triple points of non-metals (H₂, Ne, O₂, Ar, … ). The ITS-90 defines temperatures between fixed points using specified instruments and specified interpolation equations. Standard platinum resistance thermometers are the interpolating instruments for the interval 13.8 K < T₉₀ < 1235 K [14] and the interpolation equations account for the slight differences that exist from one platinum sample to another. Above 1235 K, temperatures are determined by extrapolation using radiation thermometers calibrated using radiances from one of the fixed-point blackbodies (Ag, Au, or Cu) and the Planck radiance law. Over most of the platinum resistance range, the relative imprecision of T₉₀ is approximately 2×10⁻⁶, which is more than good enough for all commercial and scientific purposes known to the authors. The values assigned to the fixed-point temperatures used in pre-ITS-90 scales and in ITS-90 were based on the state-of-the-art knowledge of thermodynamic temperature at the time of inception of each scale. As shown in the Fig. A (right panel), advances in thermometry since 1990 reveal deviations between the ITS-90 temperatures and thermodynamic temperature that are more than ten times larger than the imprecision.

The proposed redefinition of the kelvin will not impact practical thermometry because it will change neither the ITS-90 nor the thermometer calibrations conducted by NMIs. Because of its small imprecisions, the ITS-90 has served as a reproducible baseline for comparing primary thermometers based on different physics and located in different places. When these comparisons yield mutually consistent results, they reinforce our confidence that the primary thermometers are well understood.

Figure A.

Evolving knowledge of T − T₉₀. Left: radiation thermometry data (Martin 1988) and constant-volume gas thermometry data up to 1990. Schooley’s 1990 data and Guildner’s 1976 data came from the same laboratory, as indicated by the blue arrows. In 1995, Astrov et al. replaced their 1989 data, as indicated by the red arrows. Right: six acoustic data sets from 1999 to 2015 (in color). They are close to Astrov et al.’s 1995 data and closer to Schooley’s 1990 data than Guildner’s 1976 data. For references, see Refs. 2, 3, 5.

Fig. A (left panel) shows many of the measurements that led to ITS-90. The baseline is ITS-90 itself and the deviations of the data from the baseline are a measure of the uncertainty of ITS-90. If we exclude the data marked by arrows and dated 1995, we would conclude that the differences between ITS-90 and the thermodynamic temperature are within ±3×10⁻⁵ T. This conclusion was contradicted by Astrov et al.’s 1995 publication, reporting that the measured thermal expansion of parts of their copper thermometer bulb differed substantially from the values that they had used in their 1989 publication. Accounting for this difference generated the red arrows labeled “1995” in Fig. A (left panel). In hindsight, a similar problem might account for the blue arrows labeled “1990”, which link two sets of data acquired using two different thermometer bulbs assembled at the NBS (National Bureau of Standards, US, now NIST). The committee that developed the ITS-90 scale did not know which of the two NBS data sets was more reliable. As Fig. A shows, the committee chose the ITS-90 scale to be approximately the average of the two data sets, within their range of overlap.

Figure B.

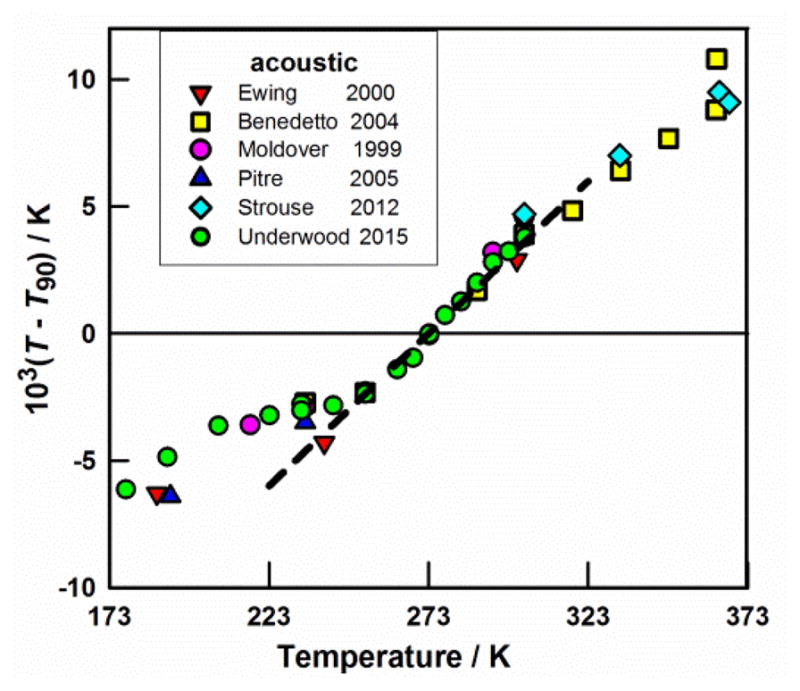
Acoustic-gas thermometry measurements of T − T₉₀ near T_TPW = 273.16 K. The dashed line through the data has the slope 0.00010, implying that (dT₉₀/dT) ≈ 1.0001 near T_TPW. For references, see Ref. 2.

The NMIs disseminate ITS-90 instead of the thermodynamic temperature T because it is simply easier (and therefore less expensive) to maintain and use a set of fixed-point cells than it would be to maintain several complex research-style apparatuses to measure T over a wide range with the small imprecisions that are obtained using ITS-90. In fact, the capability of measuring T with imprecisions as small as 3×10⁻⁶ T in the key range 84 K < T < 550 K has become possible only during the past few years [5].

Since 1990, the fixed-point cells used in artifact-based thermometry have been improved. The definition of T_TPW now accounts for the variation in the relative abundances of the isotopes among samples of pure water. This improvement reduced the variation among triple-point-of-water cells used by NMIs from 0.05 mK to 0.025 mK [11]. Furthermore, triple-point-of-water cells made of fused silica are now known to be more stable than cells made from glasses with lower-melting points. Since 1990, an entirely new class of fixed-point cells for use at temperatures above 1235 K has been developed. These cells consist of graphite envelopes filled with eutectic mixtures of carbon and a pure metal. The cells exploit the fact that the eutectic temperature of a carbon-metal eutectic does not change if some of the graphite dissolves into the mixture. For example, rhenium-carbon cells from several laboratories have reproducibilities of the order of 20 mK at the eutectic point 2747 K [8].

The future of thermometry

By definition, the difference (T − T₉₀) is zero at the temperature of the triple point of water, T_TPW. At other temperatures, the difference grows, as determined by acoustic thermometry, reaching (T − T₉₀) = +70×10⁻⁶ T at 100 K and (T − T₉₀) = −35×10⁻⁶ T at 650 K (Fig. A (right panel)). Also, as indicated by the dashed line in Fig. B, the derivative dT₉₀/dT is approximately 1.0001 near ambient temperature. One consequence of this error is that all heat capacities measured using ITS-90 have an error of approximately 0.01 %. However, these known flaws have not yet led to difficulties in either engineering or science. One exception, though, is the rapidly advancing field of optical lattice clocks. Recently, a clock achieved such low time uncertainties that radiative corrections to its optical frequency required knowledge of the thermodynamic temperature with an uncertainty of the order of 5 mK, which is close to the difference (T − T₉₀) ≈ 4 mK near 300 K [12].

At their regular meetings, temperature metrologists have considered replacing ITS-90 with a new scale that better approximates the thermodynamic temperature. To date, the experts’ consensus is that the cost of introducing a new scale far outweighs the benefits. Thus, we expect that NMIs will continue to disseminate ITS-90, even after the redefinition of the kelvin in 2018.

Current research in thermometry is directed towards more accurate measurements of the thermodynamic temperatures of the fixed points, particularly the new fixed points defined by metal–carbon eutectics. Additional work aims to improve the electronics used by radiation thermometers and Johnson-noise thermometers in order to lower their uncertainties in the middle of the platinum resistance range (13.8 K < T₉₀ < 1235 K). Several NMIs are extending acoustic gas thermometry down to the λ-point of helium (2.17 K) and up to the melting point of copper (1358 K). If successful, these efforts will reduce the uncertainty of (T − T₉₀) throughout the range that includes most temperature measurements. Dielectric-constant gas thermometry is being extended to higher temperatures. A refractive-index gas thermometer operating at cryogenic temperatures is under development. It will determine T from the pressure-dependence of the microwave resonance frequencies of a cavity filled with helium gas. This thermometer will share many of the advantages and problems of a dielectric-constant gas thermometer that determines T from measurements of the pressure-dependence of a helium-filled gas-dielectric capacitor.

Very recently, researchers determined k_B with a relative uncertainty of 24×10⁻⁶ by measuring the Doppler broadening of an optical absorption line in the spectrum of H₂¹⁸O [13]. They (and other groups [3]) are optimistic that measurements and models of optical spectra can be refined to uncertainty levels approaching those achieved by acoustic gas thermometry and Johnson-noise thermometry. Current research at NIST is directed towards finding rugged, stable alternatives to fragile platinum resistance thermometers for disseminating ITS-90, possibly using photonic technologies.

When the current research initiatives are completed, those who conducted the research will certainly advocate that ITS-90 be replaced with a more accurate, internationally recognized temperature scale. When that time comes, a new cost/benefit analysis will be carried out. By then, one or more of the primary thermometers may become a cost-effective replacement for ITS-90, at least in part of the moderate temperature range.