ESTIMATING HETEROGENEOUS GRAPHICAL MODELS FOR DISCRETE DATA WITH AN APPLICATION TO ROLL CALL VOTING

Abstract

We consider the problem of jointly estimating a collection of graphical models for discrete data, corresponding to several categories that share some common structure. An example for such a setting is voting records of legislators on different issues, such as defense, energy, and healthcare. We develop a Markov graphical model to characterize the heterogeneous dependence structures arising from such data. The model is fitted via a joint estimation method that preserves the underlying common graph structure, but also allows for differences between the networks. The method employs a group penalty that targets the common zero interaction effects across all the networks. We apply the method to describe the internal networks of the U.S. Senate on several important issues. Our analysis reveals individual structure for each issue, distinct from the underlying well-known bipartisan structure common to all categories which we are able to extract separately. We also establish consistency of the proposed method both for parameter estimation and model selection, and evaluate its numerical performance on a number of simulated examples.

1. Introduction

The analysis of roll call data of legislative bodies has attracted a lot of attention both in the political science and statistical literature. For political scientists, such data allow to study broad issues such as party cohesion as well as more specific ones such as coalition formation; see, for example, the books by Enelow and Hinich (1984), Matthews and Stimson (1975), Morton (1999), Poole and Rosenthal (1997). A popular tool in political science is the ideal point model [Clinton, Jackman and Rivers (2004)] that posits a one-dimensional latent political space along which legislators and bills they vote for are aligned. A legislator’s position corresponds to an ideal point, where bills coinciding with that position maximize his/her utility. These ideal points reveal legislators’ preferences and it is of interest to infer them from roll call data. An extension of this model that incorporates information about the text of the bills being voted upon is discussed in Gerrish (2011), while the impact of absenteeism is examined in Han (2007).

A statistical challenge is how to best model and present the roll call data in a way that makes interesting patterns apparent and facilitates subsequent analyses. A number of techniques have been employed including principal components analysis (PCA) [de Leeuw (2006)], multidimensional scaling (MDS) [Diaconis, Goel and Holmes (2008)], Bayesian spatial voting models [Clinton, Jackman and Rivers (2004)], and graphical models for binary data [Banerjee, El Ghaoui and d’Aspremont (2008)].

Dimension reduction techniques such as PCA and MDS aim at constructing a “map,” with the members of the legislative body positioned relative to their peers according to their voting pattern. A typical example of such a map of the U.S. Senate members in the 109th Congress (2005–2006) using multidimensional scaling for selected votes is shown in Figure 1; for a detailed description of the data see Section 4. A clear separation between members of the two parties is seen (Republicans to the left of the map and Democrats to the right), together with some members exhibiting a voting pattern deviating from their party, for example, Nelson (Democrat of Nebraska), and Collins and Snow (Republicans of Maine), while the independent Jeffords (shown in purple) votes like a Democrat. More interestingly, the voting patterns within both parties form distinct subclusters. While the nature of this division is impossible to infer from an MDS or a PCA representation such as the one shown in Figure 1, our subsequent analysis will show that this difference is driven by votes on defense/security and healthcare issues.

Fig. 1.

Multidimensional scaling projection of roll call data of the U.S. Senate for the period 2005–2006 (Republicans shown in red and Democrats in blue).

This finding suggests that treating all votes as homogeneous, that is, assuming that they represent the same underlying relationship between senators, may mask more subtle patterns which depend on the issues being voted upon. Therefore, treating votes as heterogeneous is more accurate and can provide further insight into the voting behavior of different groups of senators on different issues. In this paper, we focus on voting records on three types of bills: defense and national security, environment and energy, and healthcare issues. Voting on the latter category is typically more partisan than voting on defense and national security and, thus, we expect to see different connections in different categories.

The voting records of the U.S. Senate from the 109th Congress covering the period 2005–2006 were obtained directly from the Senate’s website (www.senate.gov). We chose the 109th Congress because its voting patterns have been previously analyzed in the literature [see, e.g., Banerjee, El Ghaoui and d’Aspremont (2008)], but as we have discovered, the version of the data previously analyzed was contaminated with voting records from the 1990s (when the set of senators would have been different). Thus, we collected the data ourselves, on all the 645 votes that the Senate deliberated and voted on during that period, which include bills, resolutions, motions, debates and roll call votes. To study the potential heterogeneity in the voting patterns, we focused on the three largest meaningful (i.e., excluding purely procedural votes) categories of votes extracted from bills, resolutions and motions: (1) defense and security issues; (2) environment and energy issues; (3) health and medical care issues. The categories were extracted by a combination of text analysis of bill names and manual labeling. A complete analysis of this data set will be presented in Section 4.

Our goal in this paper is to develop a statistical model for studying dependence patterns in such situations: there is some overall structure present (party affiliation, which affects everything) and there are also distinct categories with their own individual structures. Since we are dealing with voting data, we use Markov network models to capture the dependence structure of binary or categorical random variables. Similar to Gaussian graphical models, nodes in a Markov network correspond to (categorical) variables, while edges represent dependence between nodes conditional on all other variables. Graphical models are an exploratory data analysis tool used in a number of application areas to explore the dependence structure between variables, including bioinformatics [Airoldi (2007)], natural language processing [Jung et al. (1996)] and image analysis [Li (2001)]. In the case of Gaussian graphical models, which assumes the variables are jointly normally distributed, the structure of the underlying graph can be fully determined from the corresponding inverse covariance (precision) matrix, the off-diagonal elements of which are proportional to partial correlations between the variables. A number of methods have been recently proposed in the literature to fit sparse Gaussian graphical models [see, e.g., Banerjee, El Ghaoui and d’Aspremont (2008), Meinshausen and Bühlmann (2006), Peng, Zhou and Zhu (2009), Rothman et al. (2008), Yuan and Lin (2007), Ravikumar et al. (2011) and references therein]. Sparse Markov networks for binary data (Ising models) have been studied by Guo et al. (2009), Höfling and Tibshirani (2009), Ravikumar, Wainwright and Lafferty (2010), Anandkumar et al. (2012), Xue, Zou and Cai (2012). These methods do not allow for different categories within the data.

To allow for heterogeneity, we develop a framework for fitting different Markov models for each category that are nevertheless linked, sharing nodes and some common edges across all categories, while other edges are uniquely associated with a particular category. This will allow us to borrow strength across categories instead of fitting them completely separately. For the Gaussian case, this type of joint graphical model was first studied by Guo et al. (2011), who proposed a joint likelihood based estimation method that borrowed strength across categories. Several other papers have proposed alternative algorithms for the Gaussian case [Danaher, Wang and Witten (2011), Hara and Washio (2013), Yang et al. (2012)]. We note that a context-specific graphical model was proposed for count data in the form of contingency tables by Højsgaard (2004), but contingency tables are not suitable for high-dimensional data and the context-specific model is not sparse.

The advantage of using a Markov graphical model in this context is that it quantifies the degree of conditional dependence between the senators based on their voting record, and hence the obtained network, and is directly interpretable. Techniques like multidimensional scaling and principal components analysis represent relative similarities between senators’ voting records on the map and, hence, the distance between any two senators can be interpreted as a quantitative measure of similarity between their voting records. However, unlike in a Markov network, these distances are not interpretable in the context of a generative probability model.

The remainder of the paper is organized as follows. Section 2 introduces the Markov network and addresses algorithmic issues, and Section 3 briefly illustrates the performance of the joint estimation method on simulated data. A detailed analysis of the U.S. Senate’s voting record from the 109th Congress is presented in Section 4. Some concluding remarks are drawn in Section 5, and the Appendix presents results on the asymptotic properties of the method. The electronic supplementary material contains a detailed investigation of missing data imputation methods for the Senate vote data.

2. Model and estimation algorithm

In this section we present the Markov model for heterogeneous data, focusing on the special case of binary variables (also known as the Ising model). The extension to general categorical variables is briefly discussed in Section 5. We start by discussing estimation of separate models for each category and then develop a method for joint estimation.

The main technical challenge when estimating the likelihood of Markov graphical models is its computational intractability due to the normalizing constant. To overcome this difficulty, different methods employing computationally tractable approximations to the likelihood have been proposed in the literature; these include methods based on surrogate likelihood [Banerjee, El Ghaoui and d’Aspremont (2008), Kolar and Xing (2008)] and pseudo-likelihood [Guo et al. (2010), Höfling and Tibshirani (2009), Ravikumar, Wainwright and Lafferty (2010)]. Höfling and Tibshirani (2009) also proposed an iterative algorithm that successively approximates the original likelihood through a series of pseudo-likelihoods, while Ravikumar, Wainwright and Lafferty (2010) and Guo et al. (2010) established asymptotic consistency of their respective methods.

2.1. Problem setup and separate estimation

We start from setting up notation and reviewing previous work on estimating a single Ising model, which can be used to estimate the graph for each category separately. Suppose that data have been collected on p binary variables in K categories, with n_k observations in the kth category, k = 1, …, K. Let ${\mathbf{x}}_i^{(k)}=(x_{i,1}^{(k)},\dots ,x_{i,p}^{(k)})$ denote a p-dimensional row vector containing the data for the ith observation in the kth category and assume that it is drawn independently from an exponential family with the probability mass function

$${\mathrm{f}}_k(X_1,\dots ,X_p)=\frac{1}{\mathrm{Z}({\mathbf{\Theta }}^{(k)})}\text{exp}(\sum _{j=1}^p{\theta }_{j,j}^{(k)}{X}_j+\sum _{1\le j<j\prime \le p}{\theta }_{j,j\prime }^{(k)}{X}_j{X}_{j\prime }).$$ (2.1)

The partition function $\mathrm{Z}({\mathbf{\Theta }}^{(k)})={\sum }_{X_j\in \{0,1\},j}\text{exp}({\theta }_{j,j}^{(k)}{X}_j+{\sum }_{j<j\prime }{\theta }_{j,j\prime }^{(k)}{X}_j{X}_{j\prime })$ ensures that the probabilities in (2.1) add up to one. The parameters ${\theta }_{j,j}^{(k)}$, 1 ≤ j ≤ p correspond to the main effect for variable X_j in the kth category, and ${\theta }_{j,j\prime }^{(k)}$ is the interaction effect between variables X_j and X_j′, 1 ≤ j < j′ ≤ p. The underlying network associated with the kth category is determined by the symmetric matrix ${\mathbf{\Theta }}^{(k)}={({\theta }_{j,j\prime }^{(k)})}_{p\times p}$. Specifically, if ${\theta }_{j,j\prime }^{(k)}=0$, then X_j and X_j′ are conditionally independent in the kth category given all the remaining variables and, hence, their corresponding nodes are not connected. For each category, (2.1) is referred to as the Markov network in the machine learning literature and as the log-linear model in the statistics literature, where ${\theta }_{j,j\prime }^{(k)}$ is also interpreted as the conditional log odds ratio between X_j and X_j′ given the other variables. Although general Markov networks allow higher order interactions (3-way, 4-way, etc.), Ravikumar, Wainwright and Lafferty (2010) pointed out that in principle one can consider only the pairwise interaction effects without loss of generality, since higher order interactions can be converted to pairwise ones by introducing additional variables [Wainwright and Jordan (2008)]. For the rest of this paper, we only consider models with pairwise interactions of the original binary variables.

The simplest way to deal with heterogenous data is to estimate K separate Markov models, one for each category. If one further assumes sparsity for the kth category, the structure of the underlying graph can be estimated by regularizing the log-likelihood using an ℓ₁ penalty:

$$\underset{{\mathbf{\Theta }}^{(k)}}{\text{max}}\frac{1}{n_k}\sum _{i=1}^{n_k}\{\sum _{j=1}^p{\theta }_{j,j}^{(k)}{x}_{i,j}^{(k)}+\sum _{j<j\prime }{\theta }_{j,j\prime }^{(k)}{x}_{i,j}^{(k)}{x}_{i,j\prime }^{(k)}\}-\text{log }\mathrm{Z}\left({\mathrm{\Theta }}^{(k)}\right)-\lambda \sum _{j<j\prime }|{\theta }_{j,j\prime }^{(k)}|.$$ (2.2)

The ℓ₁ penalty shrinks some of the interaction effects ${\theta }_{j,j\prime }^{(k)}$ to zero and λ controls the degree of sparsity. However, estimating (2.2) directly is computationally infeasible due to the nature of the partition function. A standard approach in such a situation is to replace the likelihood with a pseudo-likelihood [Besag (1986)], which has been shown to work well in a range of situations. Here, we use a pseudo-likelihood estimation method for Ising models [Guo et al. (2010), Höfling and Tibshirani (2009)], based on

$$\underset{{\mathbf{\Theta }}^{(k)}}{\text{max}}\frac{1}{n_k}\sum _{i=1}^{n_k}\sum _{j=1}^p\left[x_{i,j}^{(k)}\right({\theta }_{j,j}^{(k)}+\sum _{j\prime \ne j}{\theta }_{j,j\prime }^{(k)}{x}_{i,j\prime }^{(k)})-\text{log}\{1+\text{exp}({\theta }_{j,j}^{(k)}+\sum _{j\prime \ne j}{\theta }_{j,j\prime }^{(k)}{x}_{i,j\prime }^{(k)})\left\}\right]-\lambda \sum _{j<j\prime }|{\theta }_{j,j\prime }^{(k)}|,$$ (2.3)

where Θ^(k) is restricted to be symmetric. Criterion (2.3) can be efficiently maximized using the modified coordinate descent algorithm of Höfling and Tibshirani (2009).

2.2. Joint estimation of heterogeneous networks

The separate estimation methods reviewed in the previous section do not take advantage of the shared nodes among the categories and potential common structure. Our goal here is to explicitly include this into the estimation procedure. We start by reparameterizing each ${\theta }_{j,j\prime }^{(k)}$ as

$${\theta }_{j,j\prime }^{(k)}={\varphi }_{j,j\prime }{\gamma }_{j,j\prime }^{(k)},\hspace{1em}\hspace{1em}1\le j\ne j\prime \le p;1\le k\le K.$$ (2.4)

To avoid sign ambiguities between ϕ_{j, j′} and ${\gamma }_{j,j\prime }^{(k)}$, we restrict ϕ_{j, j′} ≥ 0, 1 ≤ j < j′ ≤ p. To preserve the symmetry of Θ^(k), we also require ϕ_{j, j′} = ϕ_{j′, j} and ${\gamma }_{j,j\prime }^{(k)}={\gamma }_{j\prime ,j}^{(k)}$, for all 1 ≤ j < j′ ≤ p and 1 ≤ k ≤ K. Moreover, for identifiability reasons, we restrict the diagonal elements ϕ_{j, j} = 1 and ${\gamma }_{j,j}^{(k)}={\theta }_{j,j}^{(k)}$. Note that ϕ_{j, j′} is a common factor across all K categories that controls the occurrence of common links shared across categories, while ${\gamma }_{j,j\prime }^{(k)}$ is an individual factor specific to the kth category. The proposed joint estimation method maximizes the following penalized criterion:

$$\underset{{\{{\mathbf{\Phi }}^{(k)},{\mathbf{\Gamma }}^{(k)}\}}_{k=1}^K}{\text{max }}\sum _{k=1}^K\frac{1}{n_k}\sum _{i=1}^{n_k}\sum _{j=1}^p\left[x_{i,j}^{(k)}\right({\theta }_{j,j}^{(k)}+\sum _{j\prime \ne j}{\theta }_{j,j\prime }^{(k)}{x}_{i,j\prime }^{(k)})-\text{log}\{1+\text{exp}({\theta }_{j,j}^{(k)}+\sum _{j\prime \ne j}{\theta }_{j,j\prime }^{(k)}{x}_{i,j\prime }^{(k)})\left\}\right]-{\eta }_1\sum _{j<j\prime }{\varphi }_{j,j\prime }-{\eta }_2\sum _{j<j\prime }\sum _{k=1}^K|{\gamma }_{j,j\prime }^{(k)}|,$$ (2.5)

where Φ^(k) = (ϕ_{j, j′})_p×p and ${\mathbf{\Gamma }}^{(k)}={({\gamma }_{j,j\prime }^{(k)})}_{p\times p}$. The tuning parameter η₁ controls sparsity of the common structure across the K networks. Specifically, if ϕ_{j, j′} is shrunk to zero, all ${\theta }_{j,j\prime }^{(1)},\dots ,{\theta }_{j,j\prime }^{(K)}$ are also zero and, hence, there is no link between nodes j and j′ in any of the K graphs. Similarly, η₂ is a tuning parameter controlling sparsity of links in individual categories. Due to the nature of the ℓ₁ penalty, some of ${\gamma }_{j,j\prime }^{(k)}$’s will be shrunk to zero, resulting in a collection of graphs with individual differences. Note that this two-level penalty was originally proposed by Zhou and Zhu (2007) for group variable selection in linear regression.

The criterion (2.5) achieves the stated goal of estimating common structure and hence borrows strength across the K data categories, but requires the selection of two tuning parameters. However, there is an equivalent criterion presented next that only involves a single tuning parameter, thus simplifying the estimation task

$$\underset{{\{{\mathbf{\Theta }}^{(k)}\}}_{k=1}^K}{\text{max }}\sum _{k=1}^K\frac{1}{n_k}\sum _{i=1}^{n_k}\sum _{j=1}^p\left[x_{i,j}^{(k)}\right({\theta }_{j,j}^{(k)}+\sum _{j\prime \ne j}{\theta }_{j,j\prime }^{(k)}{x}_{i,j\prime }^{(k)})-\text{log}\{1+\text{exp}({\theta }_{j,j}^{(k)}+\sum _{j\prime \ne j}{\theta }_{j,j\prime }^{(k)}{x}_{i,j\prime }^{(k)})\left\}\right]-\lambda \sum _{1\le j<j\prime \le p}\sqrt{\sum _{k=1}^K|{\theta }_{j,j\prime }^{(k)}|},$$ (2.6)

where $\lambda =2\sqrt{{\eta }_1{\eta }_2}$. The optimization problems given by (2.5) and (2.6) are equivalent in the sense that for each pair of (η₁, η₂) there is a λ that gives the same solution and vice versa. Their equivalence can be formalized as follows (here A · B denotes the Schur–Hadamard element-wise product of two matrices):

Proposition 1

Let ${\{{\hat{\mathbf{\Theta }}}^{(k)}\}}_{k=1}^K$ be a local maximizer of (2.6). Then there exists a local maximizer of (2.5), $(\hat{\mathbf{\Phi }},{\{{\hat{\mathrm{\Gamma }}}^{(k)}\}}_{k=1}^K)$, such that Θ̂^(k) = Φ̂ · Γ̂^(k), for all 1 ≤ k ≤ K. On the other hand, if $(\hat{\mathbf{\Phi }},{\{{\hat{\mathbf{\Gamma }}}^{(k)}\}}_{k=1}^K)$ is a local maximizer of (2.5), then there also exists a local maximizer of (2.6), ${\{{\hat{\mathbf{\Theta }}}^{(k)}\}}_{k=1}^K$, such that Θ̂^(k) = Φ̂ · Γ̂^(k), for all 1 ≤ k ≤ K.

The proof of this proposition is similar to the proofs of Lemma 1 and Theorem 1 in Zhou and Zhu (2007) and is omitted here. Note that even though choosing a single tuning parameter λ corresponds to a particular path in the (η₁, η₂) space, this restriction affects only the individual estimates ϕ_{j, j′} and γ_{j, j′}, but not their product θ_{j, j′}.

2.3. Algorithm and model selection

Criterion (2.6) leads to an efficient estimation algorithm based on the local linear approximation. Specifically, letting ${({\theta }_{j,j\prime }^{(k)})}^{[t]}$ denote the estimates from the tth iteration, we approximate $\sqrt{{\sum }_{k=1}^K|{\theta }_{j,j\prime }^{(k)}|}\approx {\sum }_{k=1}^K|{\theta }_{j,j\prime }^{(k)}|/\sqrt{{\sum }_{k=1}^K|{({\theta }_{j,j\prime }^{(k)})}^{[t]}|}$, when ${\theta }_{j,j\prime }^{(k)}\approx {({\theta }_{j,j\prime }^{(k)})}^{[t]}$. Thus, at the (t + 1)th iteration, problem (2.6) is decomposed into K individual optimization problems:

$$\underset{{\mathbf{\Theta }}^{(k)}}{\text{max }}\frac{1}{n_k}\sum _{i=1}^{n_k}\sum _{j=1}^p\left[x_{i,j}^{(k)}\right({\theta }_{j,j}^{(k)}+\sum _{j\prime \ne j}{\theta }_{j,j\prime }^{(k)}{x}_{i,j\prime }^{(k)})-\text{log}\{1+\text{exp}({\theta }_{j,j}^{(k)}+\sum _{j\prime \ne j}{\theta }_{j,j\prime }^{(k)}{x}_{i,j\prime }^{(k)})\left\}\right]-\lambda \sum _{1\le j<j\prime \le p}{(\sum _{k=1}^K|{\left({\theta }_{j,j\prime }^{(k)}\right)}^{[t]}|)}^{-1/2}|{\theta }_{j,j\prime }^{(k)}|.$$ (2.7)

Note that criterion (2.7) is a variant of criterion (2.3) with a weighted ℓ₁ penalty and hence can be solved by the algorithm of Höfling and Tibshirani (2009). For numerical stability, we threshold $\sqrt{{\sum }_{k=1}^K|{({\theta }_{j,j\prime }^{(k)})}^{[t]}|}$ at 10⁻¹⁰. The algorithm is summarized as follows:

• Step 1. Initialize ${\hat{\theta }}_{j,j\prime }^{(k)}$’s (1 ≤ j, j′ ≤ p; 1 ≤ k ≤ K) using the estimates from the separate estimation method;

• Step 2. For each 1 ≤ k ≤ K, update ${\hat{\theta }}_{j,j\prime }^{(k)}$’s by solving (2.7) using the pseudo-likelihood algorithm Guo et al. (2010), Höfling and Tibshirani (2009).

• Step 3. Repeat step 2 until convergence.

The tuning parameter λ in (2.6) controls the sparsity of the resulting estimator and can be selected using cross-validation. Specifically, for each 1 ≤ k ≤ K, we randomly split the data in the kth category into D subsets of similar sizes and denote the index set of the observations in the dth subset as ${𝒯}_d^{(k)}$, 1 ≤ d ≤ D. Then λ is selected by maximizing

$$\frac{1}{D}\sum _{d=1}^D\sum _{k=1}^K\frac{1}{|{𝒯}_d^{(k)}|}\sum _{i\in {𝒯}_d^{(k)}}\sum _{j=1}^p{x}_{i,j}^{(k)}\{{({\hat{\theta }}_{j,j}^{(k)})}^{[-d]}(\lambda )+\sum _{j\prime \ne j}{({\hat{\theta }}_{j,j\prime }^{(k)})}^{[-d]}(\lambda )x_{i,j\prime }^{(k)}\}-\text{log}[1+\text{exp}\{{({\hat{\theta }}_{j,j}^{(k)})}^{[-d]}(\lambda )+\sum _{j\prime \ne j}{({\hat{\theta }}_{j,j\prime }^{(k)})}^{[-d]}(\lambda )x_{i,j\prime }^{(k)}\left\}\right],$$ (2.8)

where $|{𝒯}_d^{(k)}|$ is the cardinality of ${𝒯}_d^{(k)}$ and ${({\hat{\theta }}_{j,j\prime }^{(k)})}^{[-d]}(\lambda )$ is the joint estimate of ${\theta }_{j,j\prime }^{(k)}$ based on all observations except those in ${𝒯}_d^{(1)}\cup \cdots \cup {𝒯}_d^{(K)}$, as well as the tuning parameter λ.

3. Simulation study

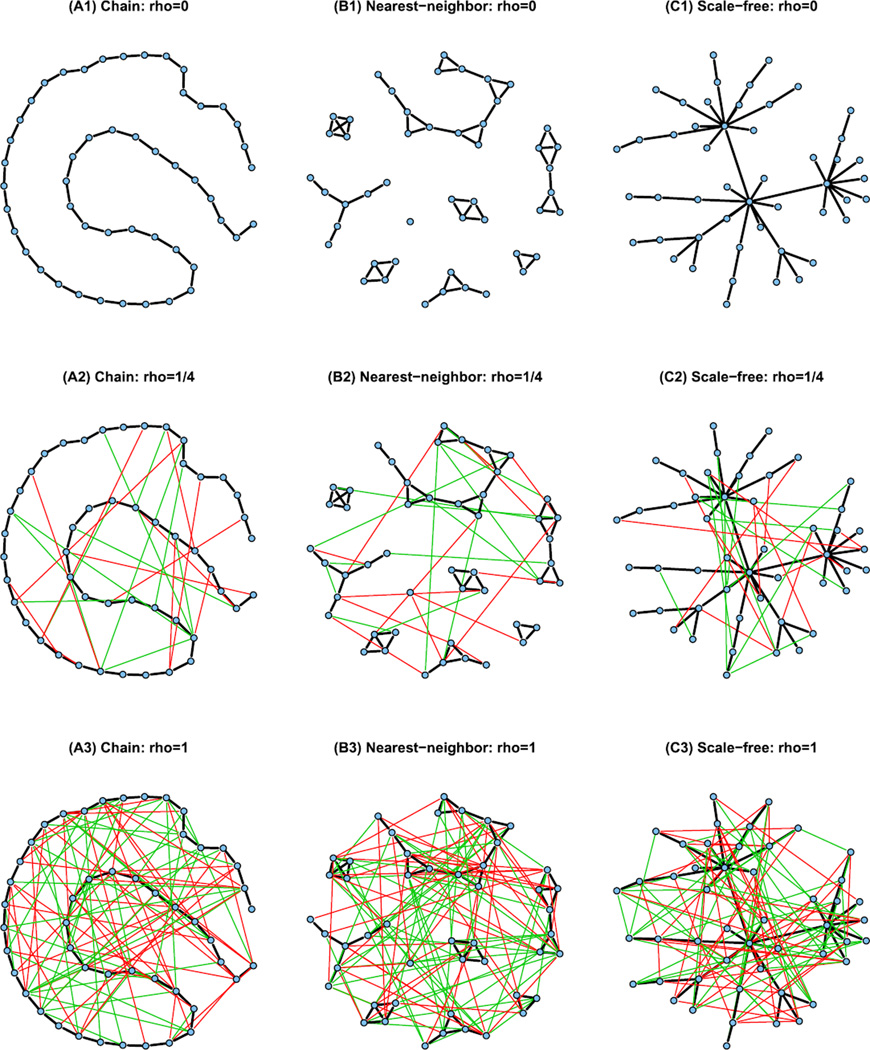
Before turning our attention to examining the U.S. Senate voting patterns, we evaluate the performance of the joint estimation method on three synthetic examples, each with p = 100 variables and K = 3 categories. The network structure in each example is composed of two parts: the common structure across all categories and the individual structure specific to a category. The common structures in these examples are a chain graph, a nearest neighbor graph and a scale-free graph. These graphs are generated as follows:

• Example 1: Chain graph. A chain graph is generated by connecting nodes 1 to p in increasing order, as shown in Figure 2(A1).

• Example 2: Nearest neighbor graph. The data generating mechanism of the nearest neighbor graph is adapted from Li and Gui (2006). Specifically, we generate p points randomly on a unit square, calculate all p(p − 1)/2 pairwise distances, and find three nearest neighbors of each point in terms of these distances. The nearest neighbor network is obtained by linking any two points that are nearest neighbors of each other. Figure 2(B1) illustrates a nearest-neighbor graph.

• Example 3: Scale-free graph. A scale-free graph has a power-law degree distribution and can be simulated by the Barabasi–Albert algorithm [Barabási and Albert (1999)]. A realization of a scale-free network is depicted in Figure 2(C1).

Fig. 2.

The networks used in three simulated examples. The black lines represent the common structure, whereas the red, blue and green lines represent the individual links in the three categories. ρ is the ratio of the number of individual links to the number of common links.

In each example, the network for the kth category (k = 1, …, K) is created by randomly adding links to the common structure. The individual links in different categories are disjoint and have the same degree of sparsity, measured by ρ, the ratio of the number of individual links to the number of common links. In particular, ρ = 0 corresponds to identical networks for all three categories. In the simulation study, we consider ρ = 0, 1/4 and 1, gradually increasing the proportion of individual links (Figure 2). Given the graphs, the symmetric parameter matrix Θ^(k) is generated as follows. Each ${\theta }_{j,j\prime }^{(k)}={\theta }_{j\prime ,j}^{(k)}$ corresponding to an edge between nodes j and j′ is uniformly drawn from [−1, −0.5] ∪ [0. 5, 1], whereas all other elements are set to zero. Then we generate the data using Gibbs sampling. Specifically, suppose the ith iteration sample has been drawn and is denoted as ${(x_1^{(k)})}^{[t]},\dots ,{(x_p^{(k)})}^{[t]}$; then, in the (t + 1)th iteration, we draw ${(x_j^{(k)})}^{[t+1]}$, 1 ≤ j ≤ p, from the Bernoulli distribution:

$${(x_j^{(k)})}^{[t+1]}~\text{Bernoulli}\left(\frac{\text{exp}({\theta }_{j,j}^{(k)}+{\sum }_{j\prime \ne j}{\theta }_{j,j\prime }^{(k)}{(x_{j\prime }^{(k)})}^{[t]})}{1+\text{exp}({\theta }_{j,j}^{(k)}+{\sum }_{j\prime \ne j}{\theta }_{j,j\prime }^{(k)}{(x_{j\prime }^{(k)})}^{[t]})}\right).$$ (3.1)

To ensure that the simulated observations are close to i.i.d. samples from the target distribution, the first 1,000,000 rounds are discarded (burn-in) and the data are collected every 100 iterations from the sampler. In the simulation study, we consider a balanced scenario and an unbalanced scenario. The former consists of n_k = 300 observations in each category, whereas the latter has three unbalanced categories with sample sizes n₁ = 200, n₂ = 300 and n₃ = 400.

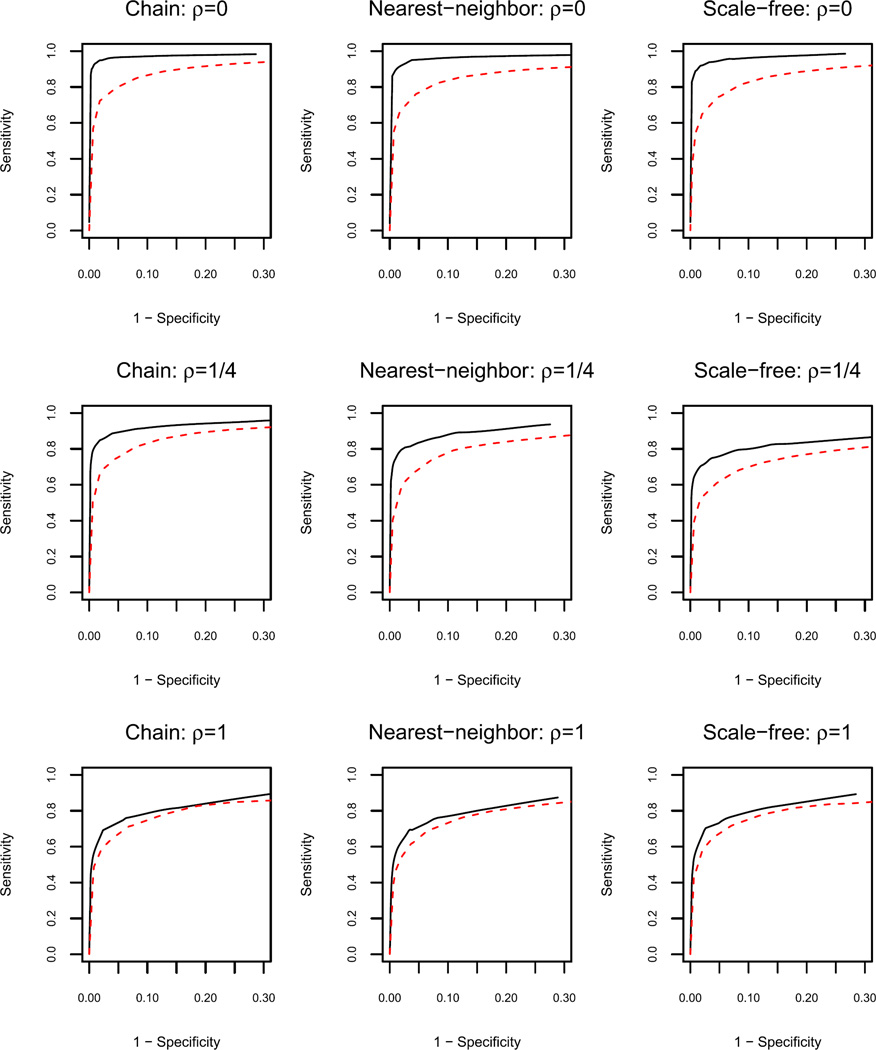
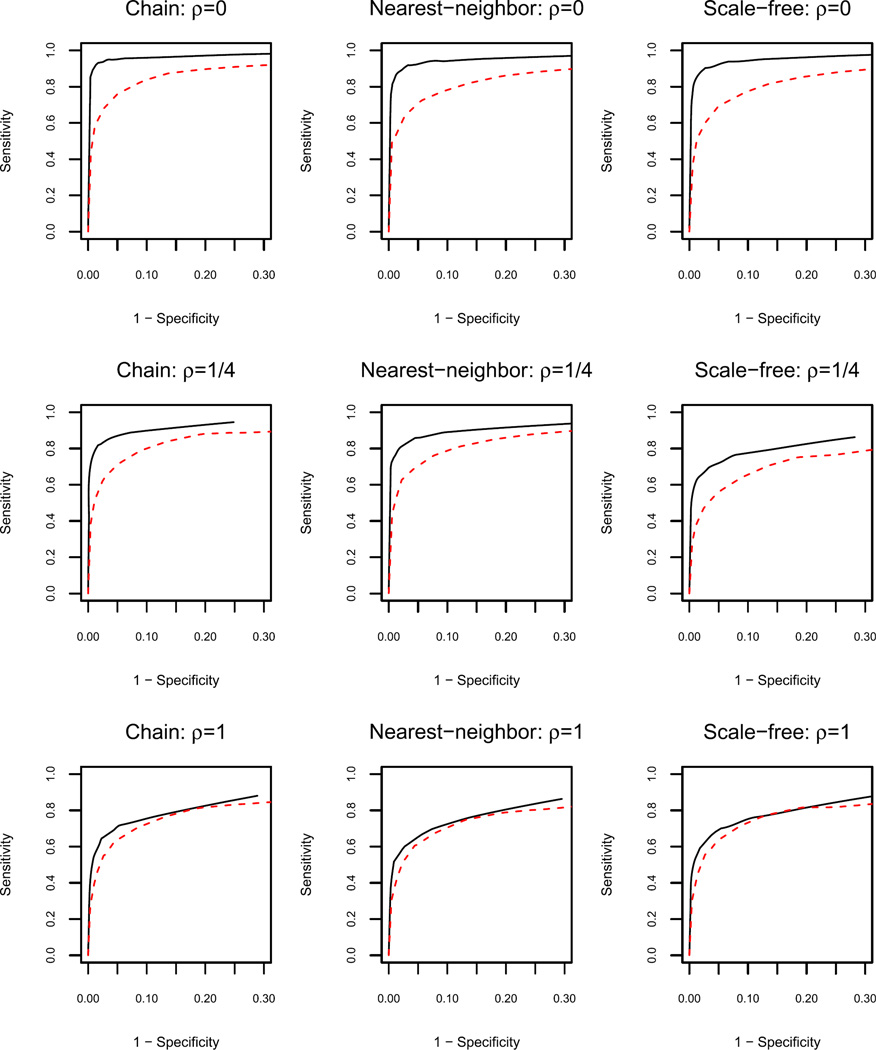
We compared the structure estimation results of the joint estimation method and the separate estimation method using ROC curves, which dynamically characterize the sensitivity (proportion of correctly identified links) and the specificity (proportion of correctly excluded links) by varying the tuning parameter λ. Figure 3 shows the ROC curves averaged over 10 replications from the three examples in the balanced scenario, where the joint estimation method dominates separate estimation when the proportion of individual links is low. As ρ increases, the structures become more different, and the joint and separate methods move closer together. This is expected, since the joint estimation method is designed to take advantage of common structure. The results in the unbalanced scenario exhibit a similar pattern (Figure 4).

Fig. 3.

Results for the balanced scenario (n₁ = n₂ = n₃ = 300) and dimension p = 100. Black solid curve: joint estimation; red dashed curve: separate estimation. The ROC curves are averaged over 10 replications. ρ is the ratio between the number of individual links and the number of common links.

Fig. 4.

Results for the unbalanced scenario (n₁ = 200, n₂ = 300, n₃ = 400) and dimension p = 100. Black solid curve: joint estimation; red dashed curve: separate estimation. The ROC curves are averaged over 10 replications. ρ is the ratio between the number of individual links and the number of common links.

4. Analysis of the U.S. Senate voting records

We applied the proposed joint estimation method to the voting records of the U.S. Senate from the 109th Congress covering the period 2005–2006. The p = 100 variables correspond to the senators. The Senate held 645 votes in that period, from which we extracted n = 222 votes in the three largest categories, namely, defense and security (141), environment and energy (34), and healthcare (47). The votes are recorded as “yes” (encoded as “1”) and “no” (encoded as “0”). The assumption of our model is that bills within a category are an i.i.d. sample from the same underlying Ising model. In reality, the voting process may be more complex, with possible temporal factors and further dependencies among bills, possibly reflecting backroom deals. Neverthless, this is an improvement on previous analyses of such data, which treated all bills in all categories as i.i.d. [Banerjee, El Ghaoui and d’Aspremont (2008)], and is a reasonable trade-off for an exploratory data analysis tool.

There were missing observations, as not all senators vote on all bills. The number of bills containing at least one missing vote was 98 out of 141 for defense and security, missing a total of 2.26% of all votes; 24 out of 34 for environment and energy, missing a total of 3.23% of votes; and 20 out of 47 for healthcare, missing 2.38% of all votes. While the number of bills that are missing at least one Senator’s vote is relatively high, the overall proportion of missing observations is quite low and, thus, we do not expect it to create a major problem in the analysis. Nevertheless, we have investigated multiple strategies for imputing the missing data in the electronic supplement; specifically, we considered replacing the missing vote by the party’s majority, by the majority vote of the five most similar Senators and, to test robustness to the imputation method, also by the opposite party’s majority and at random. We found that the main conclusions of the analysis are not very sensitive to missing data imputation methods. In the subsequent analysis, we replace a missing vote for a Senator by his/her party’s majority vote on the bill; for the Independent Senator Jeffords, we take the Democratic majority vote. After the imputation, the bills with a “yes/no” proportion greater than 90% or less than 10% were excluded from the analysis, as these typically correspond to procedural votes. This left 97, 29 and 40 bills in the three categories, respectively. Given that two of the sample sizes are fairly small (29 and 40), we added an ℓ₂ penalty with a small tuning parameter λ₂ = 0.01. This approach, known as the elastic net, has been shown to help avoid extremely sparse networks in such situations [Zou and Hastie (2005)].

The main tuning parameter for our method was selected through cross-validation. Following Li and Gui (2006), we used a bootstrap procedure for final edge selection, estimating the network for 100 bootstrap samples of the same size, and only retained edges that appeared more that α percent of the time. This procedure is similar to stability selection [Meinshausen and Bühlmann (2010)].

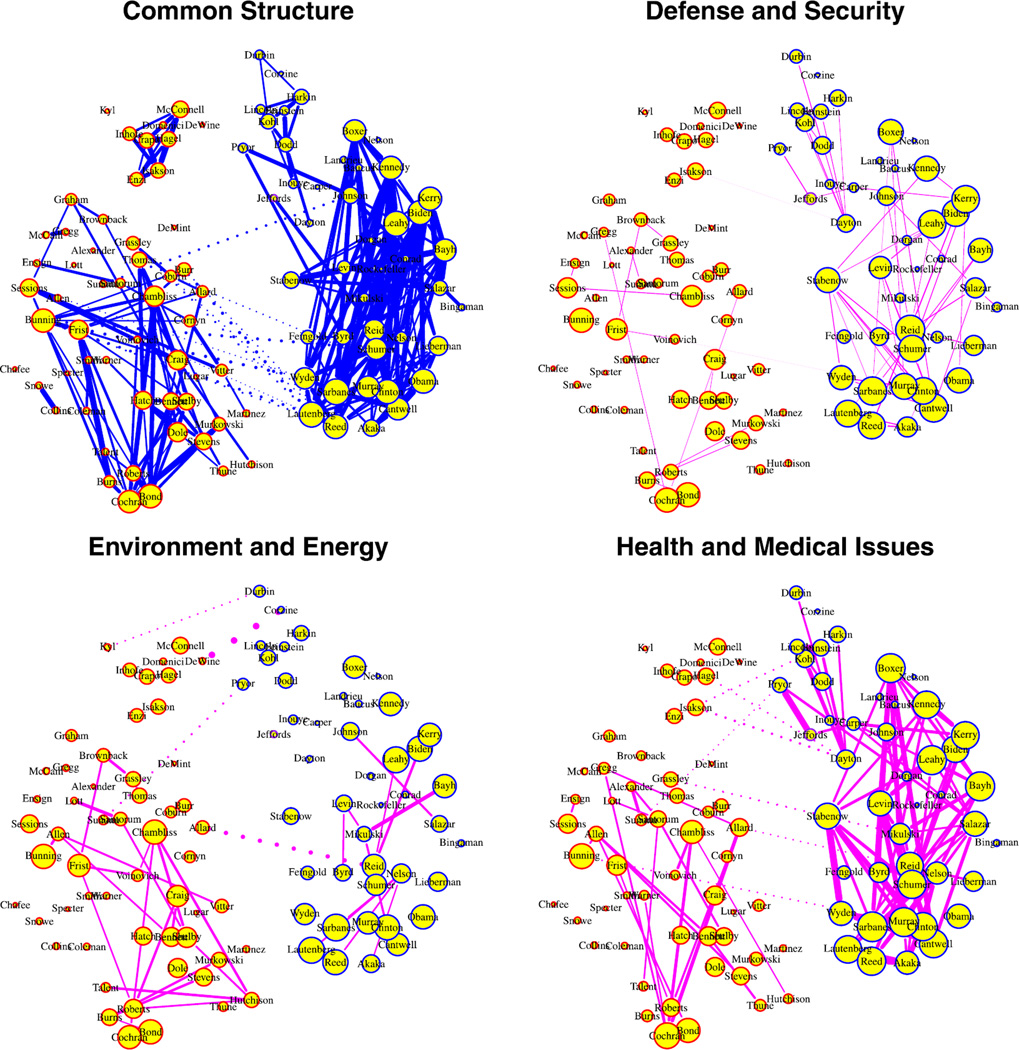
The network representation, depicting both the common and the individual structures with a cutoff value for inclusion α = 0.4 and a value of λ = 0.05, is depicted in Figure 5. Note that unlike techniques such as principal components analysis and multidimensional scaling that directly embed the senators in a two-dimensional map, the proposed method estimates the edges and constructs the adjacency matrix of the graph of Senators; subsequently, we employed a graph drawing program to visualize this graph. The common network structure estimated by the joint estimation method is shown in the top left panel of Figure 5. For the individual categories, we only plot the edges associated with the category that is not part of the common network, to enhance the readability of the graphs. As expected, members of the two political parties are clearly separated. For both tuning parameter values, there are strong positive associations between senators of the same party and selected strong negative associations between senators of opposite parties. Obviously, at the higher tuning parameter value the common dependence structure becomes sparser. Of particular interest is the finding that at both tuning values there are many more associations between Democratic senators than Republican ones and this pattern holds for both the common and individual structures. One possible explanation may be that during that period the Democrats were in the minority and thus voting more frequently as a block. Further, the Independent Senator Jeffords is associated with the Democrats, while the moderate Republicans Collins, Snowe, Chafee and Specter (who switched to the Democratic party in early 2009) are not strongly associated with their Republican colleagues, thus confirming results of previous analyses by Clinton, Jackman and Rivers (2004) and de Leeuw (2006) (albeit based on data from the 105th Congress). The conservative Democrat Nelson (Nebraska) is also not closely associated with his party, as well as the very conservative Republican de Mint (South Carolina). Also, the analysis suggests that Senator Lieberman had a solid Democratic voting record before becoming an Independent in 2008.

Fig. 5.

The estimated graphical models for the three categories in the Senate voting data with an inclusion cutoff value of 0.4 and tuning parameter value of 0.5. Edges common to all three categories are shown under the heading “common structure”; all other edges are shown on category-specific graphs. The nodes represent the 100 senators, with red, blue and purple node colors corresponding to Republican, Democrat or Independent (Senator Jeffords), respectively. A solid line corresponds to a positive interaction effect and a dashed line to a negative interaction effect. The width of a link is proportional to the magnitude of the corresponding overall interaction effect.

Other interesting patterns emerging from the analysis are that the more moderate members of the two parties are located closer to the center of their respective “clouds” (e.g., Warner, Frist, Voinovich and Smith on the Republican side, and Levin, Reid, Mikulski and Rockefeller on the Democratic side), the cluster of economic conservatives on the Republican side (McConnell, Domenici, Crapo, Inhofe), the close ties of the liberal Democrats Kennedy, Boxer and Nelson (Florida), the close voting records of senators from the same state (Schumer and Clinton from New York, Murkowski and Stevens from Alaska, Snowe and Collins from Maine, Cantwell and Murray from Washington). There is also a strong dependence between Durbin, Corzine, Lincoln, Harkin and Dodd on the Democratic side.

Examining the individual networks for the three categories shown in Figure 5, we note that additional positive associations among Democrats emerge, primarily for defense and healthcare categories, thus indicating a stronger ideological cohesion on these issues. Further, a number of stable negative associations emerge in the environment and healthcare categories, indicating a stronger ideological divide between senators.

On defense, some additional strong ties emerge between more liberal leaning Democrats (Stabenow, Biden, Leahy, Kerry, Boxer), while a strong cluster on environmental issues arises between Republican senators from energy producing states (Murkowski and Stevens from Alaska, Thune from South Dakota, Hutchison from Texas, but also Bond from Missouri, Chambliss from Georgia, Craig from Idaho and Roberts from Kansas with their unwavering support for offshore drilling). On health and medical issues, a number of additional strong positive associations emerge among Democratic senators, possibly reflecting the fact that the 109th Congress dealt with issues ranging from veterans affairs, to medical malpractice to food safety and especially on health savings accounts legislation to reduce medical insurance costs.

Different imputation strategies for missing data were also examined and the analysis results are given in Figures 1–3 in the Supplement for the same values of the cutoff α and tuning parameter λ. It can be seen that similar patterns emerge, although alternative methods of imputation may lead to the emergence of a few more associations. Nevertheless, the main findings seem to be robust to the examined choices of the imputation mechanism, although at very high levels of absenteeism this may not hold [Han (2007)].

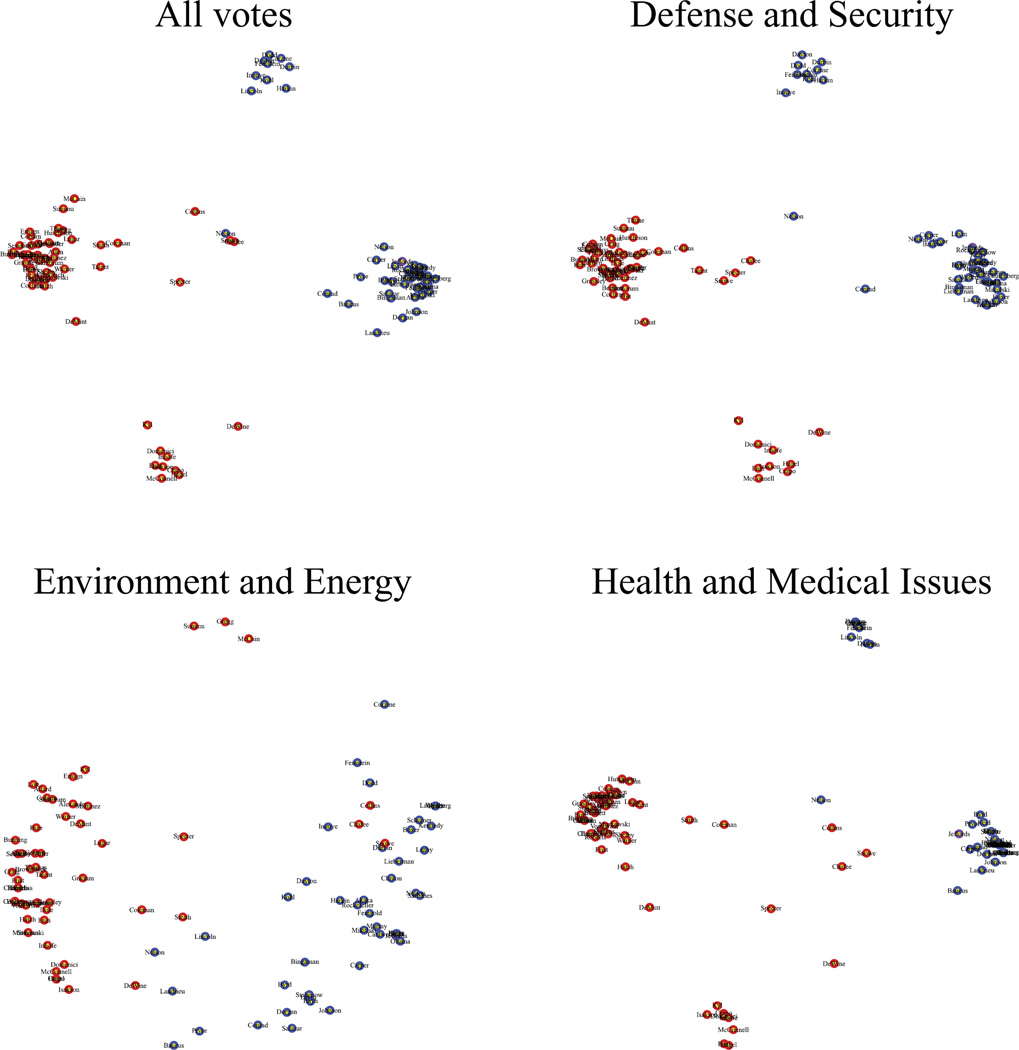
For comparison purposes, separate multidimensional scaling analyses are shown in Figure 6 for all the votes together and for the three categories separately. MDS (or PCA or factor analysis) is one of the commonly taken approaches in social sciences when graphical modeling is not considered. Figure 6 suggests that the overall vote clustering in the two parties is driven to a large extent by the corresponding clustering in the defense and health categories. On the other hand, voting on environmental issues creates a clear separation between the two parties, although the moderate Republicans Chafee, Collins and Snowe are shown to have a voting record similar to the Democrats, while the Democrats Nelson (Nebraska) and Landrieu are closer to the Republicans. At a high level, MDS-based findings are similar to ours, which is a satisfactory result, but they do not provide explicit clusters or edges, nor do they provide a way to quantify the amount of dependence between individual pairs (visualized via edge thickness in Figure 5).

Fig. 6.

Multidimensional scaling analysis for all the votes together, and the three individual categories. The nodes represent the 100 senators, with red, blue and purple node colors corresponding to Republican, Democrat or Independent (Senator Jeffords), respectively.

Another relevant comparison is to fitting a separate graphical model to each of the three categories, as could have been done with any of the previously developed methods for fitting the Ising model. The results are shown in Figure 7, in the same format as in Figure 5, with edges common to all three categories shown under “common structure,” and all other edges under their own category. We followed the same tuning procedure as we did for joint estimation, bootstrapping the data 100 times for stability selection and selecting the value of the tuning parameter on a validation data set. Even with the cutoff set at 1 (we included only the edges appearing in all the bootstrap replications), the graphs are dense and difficult to interpret. Similar to MDS, they capture party cohesion through strong positive associations between members of the same party for all three categories and some negative associations between members of opposite parties. However, different voting patterns between categories are not clear, although the results suggest a more cohesive voting record for both parties for the defense category. Note that since this is exploratory data analysis, it is hard to verify which set of results is “better.” Nevertheless, those obtained from the joint estimation method are more nuanced and interpretable and therefore provide better insights into voting strategies of members of Congress.

Fig. 7.

The estimated graphical models for the three categories in the Senate voting data fitted via separate estimation. Edges common to all three categories are shown under the heading “common structure”; all other edges are shown on category-specific graphs. The cutoff value is 1 (only edges appearing in all bootstrap replications are included). The nodes represent the 100 senators, with red, blue and purple node colors corresponding to Republican, Democrat or Independent (Senator Jeffords), respectively. A solid line corresponds to a positive interaction effect and a dashed line to a negative interaction effect. The width of a link is proportional to the magnitude of the corresponding overall interaction effect.

5. Concluding remarks

We have proposed a joint estimation method for the analysis of heterogenous Markov networks motivated by the need to jointly estimate heterogeneous networks, such as those of the Senate voting patterns. The method improves estimation of the networks’ common structure by borrowing strength across categories, and allows for individual differences. Asymptotic properties of the method have been established. In particular, we show that the convergence rate is similar to the rate for Gaussian graphical models in a similar context [Guo et al. (2010)]. The proposed method can be extended to deal with general categorical data with more than two levels using the strategy described in Ravikumar, Wainwright and Lafferty (2010) and Guo et al. (2010). The most interesting feature emerging from the analysis of the Senate voting records is the existence of more stable associations for the Democrats, both in terms of the common structure and in the healthcare and defense categories.

There are other techniques suitable for analyzing roll call data. Dimension reduction techniques create maps, where the relative positioning of the senators allows one to infer similarity in their voting patterns. They provide a useful visual tool to capture broad patterns and relationships. On the other hand, a Markov network model aims directly at estimating the associations between the senators and thus provides an alternative view of the voting patterns, which together with the thresholding technique employed gives a measure of the stability of such associations. Further, the joint estimation method allows one to separately study the overall voting patterns and those driven by specific issues. In our view, both sets of techniques are useful, with dimension reduction providing a global perspective and the Markov model revealing more nuanced patterns.

APPENDIX

ASYMPTOTIC PROPERTIES

In this section we study the asymptotic properties of the proposed joint estimation method. Since the structure of the underlying network only depends on the interaction effects, we focus on a variant of the model without main effects. Specifically, we solve

$$\underset{{\{{\mathbf{\Theta }}^{(k)}\}}_{k=1}^K}{\text{max }}\sum _{k=1}^K\frac{1}{n_k}\sum _{i=1}^{n_K}\sum _{j=1}^p\left[x_{i,j}^{(k)}\right(\sum _{j\prime \ne j}{\theta }_{j,j\prime }^{(k)}{x}_{i,j\prime }^{(k)})-\text{log}\{1+\text{exp}\left(\sum _{j\prime \ne j}{\theta }_{j,j\prime }^{(k)}{x}_{i,j\prime }^{(k)}\right)\left\}\right]-\lambda \sum _{j<j\prime }\sqrt{\sum _{k=1}^K|{\theta }_{j,j\prime }^{(k)}|}.$$ (A.1)

We will show that the estimator in criterion (A.1) is consistent in terms of both parameter estimation and model selection, when p and n go to infinity and the tuning parameter λ goes to zero at some appropriate rate. We note that our results are pointwise rather than uniform in Θ, as is standard in the literature. Some interesting implications of nonuniform bounds for sparse estimators in linear regression have recently been discussed by Leeb and Pötscher (2008), Pötscher and Leeb (2009), although their conclusions do not apply to graphical models.

Before stating the main results, we introduce necessary notation and regularity conditions. For each k = 1, …, K, denote ${\mathit{\theta }}^{(k)}=({\theta }_{1,2}^{(k)},\dots ,{\theta }_{j,j\prime }^{(k)},\dots ,{\theta }_{p-1,p}^{(k)})$ as a p(p − 1)/2-dimensional vector, recording all upper triangular elements in Θ^(k). Let θ̅^(k) be the true value of θ^(k). Let Q̅^(k) be the population Fisher information matrix of the model in criterion (A.1) (see the Appendix for a precise definition) and let ${𝒳}_{(i)}^{(k)}$ be a matrix with p rows and p(p − 1)/2 columns, whose (j, j′)th column is composed of zeros except for the j th (j′th) component being x_{i, j′} (x_{i, j}). In addition, we define ${\mathbf{Ū}}^{(k)}=E[{\mathit{𝒳}}_{(i)}^{{(k)}^{\mathtt{T}}}{𝒳}_{(i)}^{(k)}]$. To index the zero and nonzero elements, let $S_k=\{(j,j\prime ):{\theta }_{j,j\prime }^{(k)}\ne 0,1\le j<j\prime \le p\}$ and $S_k^c=\{(j,j\prime ):{\theta }_{j,j\prime }^{(k)}=0,1\le j<j\prime \le p\}$, and let $S_{\cap }={\cap }_{k=1}^K{S}_k,S_{\cup }={\cup }_{k=1}^K{S}_k$. The cardinalities of S_k and S_∪ are denoted by q_k and q, respectively. For any matrix W and subsets of row and column indices 𝒰 and 𝒱, let W_𝒰,𝒱 be the matrix consisting of rows 𝒰 and columns 𝒱 in W. Finally, let Λ_min(·) and Λ_max(·) denote the smallest and largest eigenvalue of a matrix, respectively.

The asymptotic properties of the joint estimation method rely on the following regularity conditions:

1. Nonzero elements bounds: There exist positive constants γ_min and γ_max such that:

   1. min_1≤k≤K ${\text{min}}_{(j,j\prime )\in S_k}|{\overline{\theta }}_{j,j\prime }^{(k)}|\ge {\gamma }_{\text{min}}$;
   2. max_1≤k≤K ${\text{max}}_{(j,j\prime )\in S_k\backslash S_{\cap }}|{\overline{\theta }}_{j,j\prime }^{(k)}|\le {\gamma }_{\text{max}}$.
2. Dependency: There exist positive constants τ_min and τ_max such that for any k = 1, …, K,

   $${\mathrm{\Lambda }}_{\text{min}}\left({\overline{\mathbf{Q}}}_{S_k,S_k}^{(k)}\right)\ge {\tau }_{\text{min}}\hspace{1em}\text{and}\hspace{1em}{\mathrm{\Lambda }}_{\text{max}}\left({\mathbf{Ū}}_{S_k,S_k}^{(k)}\right)\le {\tau }_{\text{max}}.$$ (A.2)
3. Incoherence: There exists a constant $\tau \in (1-\sqrt{{\gamma }_{\text{min}}/4{\gamma }_{\text{max}}},1)$ such that for any k = 1, …, K,

   $${\Vert {\overline{\mathbf{Q}}}_{S_k^c,S_k}^{(k)}{({\overline{\mathbf{Q}}}_{S_k,S_k}^{(k)})}^{-1}\Vert }_{\infty }\le 1-\tau .$$ (A.3)

Condition (A) enforces a lower bound on the magnitudes of all nonzero elements, as well as an upper bound on the magnitudes of those nonzero elements associated with individual links. Conditions (B) and (C) bound the amount of dependence and the influence that the nonneighbors can have on a given node, respectively. Conditions similar to (B) and (C) were also assumed by Meinshausen and Bühlmann (2006), Ravikumar, Wainwright and Lafferty (2010), Peng, Zhou and Zhu (2009) and Guo et al. (2010). Our conditions are most closely related to those of Guo et al. (2010), but here they are extended to the heterogenous data setting.

Theorem 1 (Parameter estimation)

Suppose all regularity conditions hold. If the tuning parameter $\lambda =C_{\lambda }\sqrt{(\text{log }p)/n}$ for some constant $C_{\lambda }>(8-4\tau )\sqrt{{\gamma }_{\text{min}}}/(1-\tau )$ and if $\text{min}\{n/q^3,n_1/q_1^3,\dots ,n_K/q_K^3\}>(4/C)\text{log }p$ for some constant $C=\text{min}\{{\tau }_{\text{min}}^2{\tau }^2/288{(1-\tau )}^2,{\tau }_{\text{min}}^2{\tau }^2/72,{\tau }_{\text{min}}\tau /48\}$, then there exists a local maximizer of the criterion (A.1), ${\{{\hat{\mathit{\theta }}}^{(k)}\}}_{k=1}^K$, such that, with probability tending to 1,

$$\sum _{k=1}^K{\Vert {\hat{\mathit{\theta }}}^{(k)}-{\overline{\mathit{\theta }}}^{(k)}\Vert }_2\le M\sqrt{\frac{q\text{ log }p}{n}},$$ (A.4)

for some constant $M>(2K{C}_{\lambda }/{\tau }_{\text{min}}\sqrt{{\gamma }_{\text{min}}})(3-2\tau )/(2-\tau )$.

Theorem 2 (Structure selection)

Under conditions of Theorem 1, with probability tending to 1, the maximizer ${\{{\hat{\mathit{\theta }}}^{(k)}\}}_{k=1}^K$ from Theorem 1 satisfies

$${\hat{\theta }}_{j,j\prime }^{(k)}\ne 0\hspace{1em}\mathit{\text{for all}}(j,j\prime )\in S_k,k=1,\dots ,K;$$

$${\hat{\theta }}_{j,j\prime }^{(k)}=0\hspace{1em}\mathit{\text{for all}}(j,j\prime )\in S_k^c,k=1,\dots ,K.$$

Theorems 1 and 2 establish the consistency in terms of parameter estimation and structure selection, respectively.

The main idea of the proofs is closely related to Guo et al. (2010), and some strategies for dealing with the joint estimation are borrowed from Guo et al. (2011). We introduce notation first. For the kth category, we define the log-likelihood as

$$l({\mathit{\theta }}^{(k)})=\frac{1}{n_k}\sum _{i=1}^{n_k}\sum _{j=1}^p\left[x_{i,j}^{(k)}\right(\sum _{j\prime \ne j}{\theta }_{j,j\prime }^{(k)}{x}_{i,j\prime }^{(k)})-\text{log}\{1+\text{exp}\left(\sum _{j\prime \ne j}{\theta }_{j,j\prime }^{(k)}{x}_{i,j\prime }^{(k)}\right)\left\}\right],$$

whose first derivative and second derivative are denoted by ∇l(θ^(k)) and ∇²l(θ^(k)), respectively. Note that ∇l(θ^(k)) is a p(p −1)/2-dimensional vector and ∇²l(θ^(k)) is a p(p − 1)/2 × p(p − 1)/2 matrix. Then, the population Fisher information matrix of the model in (A.1) at θ̅ can be defined as Q̅^(k) =−E[∇²l(θ̅^(k))], and its sample counterpart is Q̂^(k) =−∇²l(θ^(k)). We also write ${\mathbf{Û}}^{(k)}=1/n{\sum }_{i=1}^n{{\mathit{𝒳}}_{(i)}^{(k)}}^{\mathtt{T}}{\mathit{𝒳}}_{(i)}^{(k)}$ for the sample counterpart of Ū^(k). Let ${\underset{¯}{\mathit{\theta }}}^{(k)}=({\underset{¯}{\theta }}_{1,2}^{(k)},\dots ,{\underset{¯}{\theta }}_{j,j\prime }^{(k)},\dots ,{\underset{¯}{\theta }}_{p-1,p}^{(k)})$ be the same as θ^(k) except that all elements in $S_k^c$ are set to zero and write δ^(k) = θ^(k) − θ̅^(k) and δ̲^(k) = θ̲^(k) − θ̅^(k). Finally, let 𝒲 be a subset of the index set {1, 2, …, p(p − 1)/2}. For a p(p − 1)/2-dimensional vector β, we define β_𝒲 as the vector consisting of the elements of β associated with 𝒲.

Next, we introduce a variant of criterion (A.1) by restricting all true zeros in ${\{{\mathit{\theta }}^{(k)}\}}_{k=1}^K$ to be estimated as zero. Specifically, the restricted criterion is formulated as follows:

$$\underset{{\{{\underset{¯}{\mathit{\theta }}}^{(k)}\}}_{k=1}^K}{\text{max}}\sum _{k=1}^{K}l({\underset{¯}{\mathit{\theta }}}^{(k)})-\lambda \sum _{1\le j<j\prime \le p}\sqrt{\sum _{k=1}^K|{\underset{¯}{\theta }}_{j,j\prime }^{(k)}|},$$ (A.5)

and its maximizer is denoted by ${\{{\underset{¯}{\hat{\mathit{\theta }}}}^{(k)}\}}_{k=1}^K$. In addition, we consider the sample versions of regularity conditions (B) and (C):

• (B′) Sample dependency: There exist positive constants τ_min and τ_max such that for any k = 1, …, K,

  $${\mathrm{\Lambda }}_{\text{min}}({\hat{\mathbf{Q}}}_{S_k,S_k}^{(k)})\ge {\tau }_{\text{min}}\text{ and }{\mathrm{\Lambda }}_{\text{max}}({\mathbf{Û}}_{S_k,S_k}^{(k)})\le {\tau }_{\text{max}}.$$ (A.6)
• (C′) Sample incoherence: There exists a constant $\tau \in (1-\sqrt{{\gamma }_{\text{min}}/4{\gamma }_{\text{max}}},1)$ such that for any k = 1, …, K,

  $${\Vert {\hat{\mathbf{Q}}}_{S_k^c,S_k}^{(k)}{({\hat{\mathbf{Q}}}_{S_k,S_k}^{(k)})}^{-1}\Vert }_{\infty }\le 1-\tau .$$ (A.7)

For convenience of the readers, the proof of our main result is divided into two parts: Part I presents the main idea of the proof by listing the important propositions and the proofs of Theorems 1 and 2, whereas part II contains additional technical details and proofs of propositions in part I.

Part I: Propositions and proof of Theorems 1 and 2

The proof consists of the following steps. Proposition 2 shows that, under sample regularity conditions (B′) and (C′), the conclusions of Theorems 1 and 2 hold for the local maximizer of the restricted problem (A.5). Next, Proposition 3 proves that the population regularity conditions (B) and (C) give rise to their sample counterparts (B′) and (C′) with probability tending to one, hence, the conclusions of Proposition 2 also hold with the population regularity conditions. Last, we show that the local maximizer of (A.5) is also a local maximizer of the original model (A.1). This is established via Proposition 4, which sets out the Karush–Kuhn–Tucker (KKT) conditions for the local maximizer of criterion (A.1), and Proposition 5, which shows that, with probability tending to one, the local maximizer of (A.5) satisfies these KKT conditions.

Proposition 2

Suppose condition (A) and the sample conditions (B′) and (C′) hold. If the tuning parameter $\lambda =C_{\lambda }\sqrt{(\text{log }p)/n}$ for some constant $C_{\lambda }>(8-4\tau )\sqrt{{\gamma }_{\text{min}}}/(1-\tau )$ and $q\sqrt{(\text{log }p)/n}=o(1)$, then with probability tending to one, there exists a local maximizer of the restricted criterion, ${\{{\underset{¯}{\hat{\mathit{\theta }}}}^{(k)}\}}_{k=1}^K$, satisfying:

1. ${\sum }_{k=1}^K{\Vert {\underset{¯}{\hat{\mathit{\theta }}}}^{(k)}-{\overline{\mathit{\theta }}}^{(k)}\Vert }_2\le M\sqrt{q(\text{log }p)/n}$ for some constant $M>(2K{C}_{\lambda }/{\tau }_{\text{min}}\sqrt{{\gamma }_{\text{min}}})[(3-2\tau )/(2-\tau )]$;

2. For each k = 1, …, K, ${\underset{¯}{\hat{\theta }}}_{j,j\prime }^{(k)}\ne 0$ for all (j, j′) ∈ S_k and ${\underset{¯}{\hat{\theta }}}_{j,j\prime }^{(k)}=0$ for all $(j,j\prime )\in S_k^c$.

Proposition 3

Suppose the regularity conditions (B) and (C) hold, then for any ε > 0, the following inequalities hold with probability tending to one for all k = 1, …, K:

1. $\mathrm{P}\{{\mathrm{\Lambda }}_{\text{min}}({\hat{\mathbf{Q}}}_{S_k,S_k}^{(k)})\le {\tau }_{\text{min}}-\epsilon \}\le 2\text{ exp}\{-({\epsilon }^2/2)(n_k/q_k^2)+2\text{ log }{q}_k\}$;

2. $\mathrm{P}\{{\mathrm{\Lambda }}_{\text{max}}({\mathbf{Û}}_{S_k,S_k}^{(k)})\le {\tau }_{\text{max}}+\epsilon \}\le 2\text{ exp}\{-({\epsilon }^2/2)(n_k/q_k^2)+2\text{ log }{q}_k\}$;

3. $\mathrm{P}[{\Vert {\hat{\mathbf{Q}}}_{S_k^c,S_k}^{(k)}{({\hat{\mathbf{Q}}}_{S_k,S_k}^{(k)})}^{-1}\Vert }_{\infty }\ge 1-\tau /2]\le 12\text{ exp}(-C{n}_k/q_k^3+4\text{ log }p)$, for some constant $C=\text{min}\{{\tau }_{\text{min}}^2{\tau }^2/288{(1-\tau )}^2,{\tau }_{\text{min}}^2{\tau }^2/72,{\tau }_{\text{min}}\tau /48\}$.

Proposition 4

${\{\hat{\mathit{\theta }}\}}_{k=1}^K$ is a local maximizer of problem (A.1) if and only if the following conditions hold for all k = 1, …, K:

$${\nabla }_{j,j\prime }l({\hat{\mathit{\theta }}}^{(k)})=\lambda \text{ sgn}({\hat{\theta }}_{j,j\prime }^{(k)})/{(\sum _{k=1}^K|{\hat{\theta }}_{j,j\prime }^{(k)}|)}^{1/2}\hspace{1em}\mathit{\text{if}}{\hat{\theta }}_{j,j\prime }^{(k)}\ne 0;$$ (A.8)

$$|{\nabla }_{j,j\prime }l({\hat{\mathit{\theta }}}^{(k)})|<\lambda /{(\sum _{k=1}^K|{\hat{\theta }}_{j,j\prime }^{(k)}|)}^{1/2}\hspace{1em}\mathit{\text{if}}{\hat{\theta }}_{j,j\prime }^{(k)}=0.$$

Proposition 5

Under all conditions of Proposition 2, with probability tending to one, we have, for each k = 1, …, K,

$${\nabla }_{j,j\prime }l({\underset{¯}{\overset{^}{\mathit{\theta }}}}^{(k)})=\lambda \text{ sgn}\left({\underset{¯}{\overset{^}{\theta }}}_{j,j\prime }^{(k)}\right)/{(\sum _{k=1}^K|{\underset{¯}{\overset{^}{\theta }}}_{j,j\prime }^{(k)}|)}^{1/2}\hspace{1em}\mathit{\text{for all}}(j,j\prime )\in S_k;$$ (A.9)

$$|{\nabla }_{j,j\prime }l({\underset{¯}{\overset{^}{\mathit{\theta }}}}^{(k)})|<\lambda /{(\sum _{k=1}^K|{\underset{¯}{\overset{^}{\theta }}}_{j,j\prime }^{(k)}|)}^{1/2}\hspace{1em}\mathit{\text{for all}}(j,j\prime )\in S_k^c.$$

Proof of Theorems 1 and 2

The condition $\text{min}\{n/q^3,n_1/q_1^3,\dots ,n_K/q_K^3\}>(4/C)\text{ log }p$ implies that, for each k = 1, …, K, we have $-C{n}_k/q_k^3+4\text{ log }p<0$ and $-({\epsilon }^2/2)(n_k/q_k^2)+2\text{ log }{q}_k<0$ when q_k is large enough. This condition also implies $q\sqrt{(\text{log }p)/n}=o(1)$. In addition, by Proposition 3, the sample conditions (B′) and (C′) hold with probability tending to one when regularity conditions (B) and (C) hold. Therefore, by Proposition 2, with probability tending to one, the solution of the restricted problem ${\{{\underset{¯}{\hat{\mathit{\theta }}}}^{(k)}\}}_{k=1}^K$ satisfies both parameter estimation consistency and structure selection consistency. On the other hand, by Proposition 5, with probability tending to one, ${\{{\underset{¯}{\hat{\mathit{\theta }}}}^{(k)}\}}_{k=1}^K$ also satisfies the KKT conditions in Proposition 4, thus, it is a local maximizer of criterion (A.1). This proves Theorems 1 and 2.

Part II: Proofs of propositions

Before proving the propositions, we state a few lemmas which will be used in the proofs. These lemmas are variants of Lemmas 1, 2 and 5 in Guo et al. (2010), adapted to the settings of the heterogenous model and, thus, the proofs are omitted here. Likewise, the proof of Proposition 3 is very similar to the proof of Propositions 3 and 4 in Guo et al. (2010) and is omitted.

Lemma 1

For each k = 1, …, K, with probability tending to 1, we have ${\Vert \nabla l({\overline{\mathit{\theta }}}^{(k)})\Vert }_{\infty }\le C_{\nabla }\sqrt{(\text{log }p)/n}$ for some constant C_∇ > 4.

Lemma 2

If the sample dependency condition (B′) holds and $q\sqrt{(\text{log }p)/n}=o(1)$ then for any α_k ∈ [0, 1], k = 1, …, K, the following inequality holds with probability tending to 1:

$$-\sum _{k=1}^K{\mathit{\delta }}_{S_k}^{{(k)}^{\mathtt{T}}}{[{\nabla }^{2}l({\overline{\mathit{\theta }}}^{(k)}+{\alpha }_k{\underset{¯}{\mathit{\delta }}}^{(k)}\left)\right]}_{S_k,S_k}{\mathit{\delta }}_{S_k}^{(k)}\ge \frac{1}{2}{\tau }_{\text{min}}\sum _{k=1}^K{\Vert {\underset{¯}{\mathit{\delta }}}^{(k)}\Vert }_2^2.$$ (A.10)

Lemma 3

Suppose the sample dependency condition (B) holds. For any α_k ∈ [0, 1], k = 1, …, K, the following inequality holds with probability tending to one:

$${\Vert [{\nabla }^{2}l({\overline{\mathit{\theta }}}^{(k)}+{\alpha }_k{\underset{¯}{\mathit{\delta }}}^{(k)})-{\nabla }^{2}l({\overline{\mathit{\theta }}}^{(k)})]{\underset{¯}{\mathit{\delta }}}^{(k)}\Vert }_{\infty }\le {\tau }_{\text{max}}{\Vert {\underset{¯}{\mathit{\delta }}}^{(k)}\Vert }_2^2.$$ (A.11)

Proof of Proposition 2

The main idea of the proof was first introduced in this context in Rothman et al. (2008) and has since been used by many authors. Define

$$\mathrm{G}({\{{\underset{¯}{\mathit{\delta }}}^{(k)}\}}_{k=1}^K)=-\sum _{k=1}^K[l({\overline{\mathit{\theta }}}^{(k)}+{\underset{¯}{\mathit{\delta }}}^{(k)})-l({\overline{\mathit{\theta }}}^{(k)})]+\lambda \sum _{1\le j<j\prime \le p}\{{(\sum _{k=1}^K|{\overline{\theta }}_{j,j\prime }^{(k)}+{\underset{¯}{\delta }}_{j,j\prime }^{(k)}|)}^{1/2}-{(\sum _{k=1}^K|{\overline{\theta }}_{j,j\prime }^{(k)}|)}^{1/2}\}.$$ (A.12)

It can be seen from (A.5) that ${\{{\underset{¯}{\hat{\mathit{\delta }}}}^{(k)}\}}_{k=1}^K$ minimizes $\mathrm{G}{(\{{\underset{¯}{\mathit{\delta }}}^{(k)}\}}_{k=1}^K)$ and $\mathrm{G}({\{\mathbf{0}\}}_{k=1}^K)=0$. Thus, we must have $\mathrm{G}(\{{{\underset{¯}{\hat{\mathit{\delta }}}}^{(k)}\}}_{k=1}^K)\le 0$. If we take a closed set 𝒜 which contains ${\{\mathbf{0}\}}_{k=1}^K$ and show that G is strictly positive everywhere on the boundary ∂𝒜, then it implies that G has a local minimum inside 𝒜, since G is continuous and $\mathrm{G}{(\{\mathbf{0}\}}_{k=1}^K)=0$. Specifically, we define $𝒜=\{{\{{\underset{¯}{\mathit{\delta }}}^{(k)}\}}_{k=1}^K:{\sum }_{k=1}^K{\Vert {\underset{¯}{\mathit{\delta }}}^{(k)}\Vert }_2\le M{a}_n\}$, with boundary $\partial 𝒜=\{{\{{\underset{¯}{\mathit{\delta }}}^{(k)}\}}_{k=1}^K:{\sum }_{k=1}^K{\Vert {\underset{¯}{\mathit{\delta }}}^{(k)}\Vert }_2=M{a}_n\}$, for some constant $M>(2K{C}_{\lambda }/{\tau }_{\text{min}}\sqrt{{\gamma }_{\text{min}}})[(3-2\tau )/(2-\tau )]$ and $a_n=\sqrt{q(\text{log }p)/n}$. For any ${\{{\underset{¯}{\mathit{\delta }}}^{(k)}\}}_{k=1}^K\in \partial 𝒜$, the Taylor series expansion gives $\mathrm{G}({\{{\underset{¯}{\mathit{\delta }}}^{(k)}\}}_{k=1}^K)=I_1+I_2+I_3$ where

$$I_1=-\sum _{k=1}^K{[\nabla l({\overline{\mathit{\theta }}}^{(k)})]}_{S_k}^{\mathtt{T}}{\mathit{\delta }}_{S_k}^{(k)},$$

$$I_2=-\sum _{k=1}^K{\mathit{\delta }}_{S_k}^{{(k)}^{\mathtt{T}}}{[{\nabla }^{2}l({\overline{\mathit{\theta }}}^{(k)}+{\alpha }_k{\underset{¯}{\mathit{\delta }}}^{(k)})]}_{S_k,S_k}{\mathit{\delta }}_{S_k}^{(k)}\hspace{1em}\text{for some }{\alpha }_k\in [0,1],$$ (A.13)

$$I_3=\lambda \sum _{(j,j\prime )\in S_{\cup }}\{{(\sum _{k=1}^K|{\overline{\theta }}_{j,j\prime }^{(k)}+{\underset{¯}{\delta }}_{j,j\prime }^{(k)}|)}^{1/2}-{(\sum _{k=1}^K|{\overline{\theta }}_{j,j\prime }^{(k)}|)}^{1/2}\}.$$

Since $C_{\lambda }>(8-4\tau )\sqrt{{\gamma }_{\text{min}}}/(1-\tau )$, we have $[(1-\tau )/(2-\tau )]C_{\lambda }/\sqrt{{\gamma }_{\text{min}}}>4$. By Lemma 1,

$$|I_1|\le \sum _{k=1}^K{\Vert {[\nabla l({\overline{\mathit{\theta }}}^{(k)})]}_{S_k}\Vert }_{\infty }{\Vert {\mathit{\delta }}_{S_k}^{(k)}\Vert }_1\le [(1-\tau )C_{\lambda }M{\gamma }_{\text{min}}^{-1/2}/(2-\tau )](q\text{ log }p)/n.$$ (A.14)

In addition, by condition $q\sqrt{(\text{log }p)/n}=o(1)$, Lemma 2 holds and, thus,

$$I_2\ge ({\tau }_{\text{min}}/2)\sum _{k=1}^K{\Vert {\underset{¯}{\mathit{\delta }}}^{(k)}\Vert }_2^2\ge [{\tau }_{\text{min}}/(2K)]M^{2}q(\text{log }p)/n.$$ (A.15)

Finally, by the triangular inequality and regularity condition (A),

$$|I_3|\le \lambda \sum _{(j,j\prime )\in S_{\cup }}\sum _{k=1}^K\frac{||{\overline{\theta }}_{j,j\prime }^{(k)}+{\underset{¯}{\delta }}_{j,j\prime }^{(k)}|-|{\overline{\theta }}_{j,j\prime }^{(k)}||}{{({\sum }_{k=1}^K|{\overline{\theta }}_{j,j\prime }^{(k)}+{\underset{¯}{\delta }}_{j,j\prime }^{(k)}|)}^{1/2}+{({\sum }_{k=1}^K|{\overline{\theta }}_{j,j\prime }^{(k)}|)}^{1/2}}\le (\lambda {\gamma }_{\text{min}}^{-1/2})\sum _{k=1}^K\sum _{(j,j\prime )\in S_{\cup }}|{\underset{¯}{\delta }}_{j,j\prime }^{(k)}|\le (\lambda q^{1/2}{\gamma }_{\text{min}}^{-1/2})\sum _{k=1}^K{\Vert {\underset{¯}{\mathit{\delta }}}^{(k)}\Vert }_2\le (M{C}_{\lambda }{\gamma }_{\text{min}}^{-1/2})\{q(\text{log }p)/n\}.$$ (A.16)

Then we have

$$\mathrm{G}\left({\{{\underset{¯}{\mathit{\delta }}}^{(k)}\}}_{k=1}^K\right)\ge M^2\frac{q\text{ log }p}{n}(\frac{{\tau }_{\text{min}}}{2K}-\frac{(1-\tau )C_{\lambda }}{(2-\tau )M{\gamma }_{\text{min}}^{1/2}}-\frac{C_{\lambda }}{M{\gamma }_{\text{min}}^{1/2}})>0.$$ (A.17)

The last inequality uses the condition $M>(2K{C}_{\lambda }/{\tau }_{\text{min}}\sqrt{{\gamma }_{\text{min}}})[(3-2\tau )/(2-\tau )]$. Therefore, with probability tending to 1, we have ${\sum }_{k=1}^K{\Vert {\widehat{\underset{¯}{\mathit{\theta }}}}^{(k)}-{\overline{\mathit{\theta }}}^{(k)}\Vert }_2\le M\sqrt{q(\text{log }p)/n}$, and consequently claim (i) in Proposition 2 holds.

On the other hand, by the definition of ${\widehat{\underset{¯}{\mathit{\theta }}}}^{(k)}$, we have ${\widehat{\underset{¯}{\theta }}}_{j,j\prime }^{(k)}=0$ for all $(j,j\prime )\in S_k^c$. By regularity condition (A) and Proposition 2(i), for any (j, j′) ∈ S_k, k = 1, …, K, we have $|{\widehat{\underset{¯}{\theta }}}_{j,j\prime }^{(k)}|\ge |{\overline{\theta }}_{j,j\prime }^{(k)}|-|{\widehat{\underset{¯}{\theta }}}_{j,j\prime }^{(k)}-{\overline{\theta }}_{j,j\prime }^{(k)}|\ge {\gamma }_{\text{min}}/2>0$, when n is large enough.

Proof of Proposition 5

By Proposition 2, with probability tending to one, we have ${\widehat{\underset{¯}{\theta }}}_{j,j\prime }\ne 0$ for all (j, j′) ∈ S_k. Since ${\{{\widehat{\underset{¯}{\mathit{\theta }}}}^{(k)}\}}_{k=1}^K$ is a local maximizer of the restricted problem (A.5), with probability tending to one, ${\nabla }_{j,j\prime }l({\widehat{\underset{¯}{\mathit{\theta }}}}^{(k)})=\lambda \text{sgn}({\widehat{\underset{¯}{\theta }}}_{j,j\prime }^{(k)})/{({\sum }_{k=1}^K|{\widehat{\underset{¯}{\theta }}}_{j,j\prime }^{(k)}|)}^{1/2}$, for all (j, j′) ∈ S_k.

To show the second claim, we apply the mean value theorem and write $\nabla l({\underset{¯}{\hat{\mathit{\theta }}}}^{(k)})=\nabla l({\overline{\mathit{\theta }}}^{(k)})+{\mathbf{r}}^{(k)}-{\hat{\mathbf{Q}}}^{(k)}{\underset{¯}{\hat{\mathit{\delta }}}}^{(k)}$, where ${\mathbf{r}}^{(k)}=\{{\nabla }^{2}l({\overline{\mathit{\theta }}}^{(k)}+{\alpha }_k{\underset{¯}{\hat{\mathit{\delta }}}}^{(k)})-{\nabla }^{2}l({\overline{\mathit{\theta }}}^{(k)})\}{\underset{¯}{\hat{\mathit{\delta }}}}^{(k)}$. After some simplifications, we have

$${[\nabla l({\underset{¯}{\overset{^}{\mathit{\theta }}}}^{(k)})]}_{S_k^c}={[\nabla l({\overline{\mathit{\theta }}}^{(k)})]}_{S_k^c}+{\mathbf{r}}_{S_k^c}^{(k)}-[{\hat{\mathbf{Q}}}_{S_k^c,S_k}^{(k)}{({\hat{\mathbf{Q}}}_{S_k,S_k}^{(k)})}^{-1}]\{{[\nabla l({\overline{\mathit{\theta }}}^{(k)})]}_{S_k}+{\mathbf{r}}_{S_k}^{(k)}-{[\nabla l({\underset{¯}{\overset{^}{\mathit{\theta }}}}^{(k)})]}_{S_k}\}$$ (A.18)

and, thus,

$${\Vert {[\nabla l({\underset{¯}{\overset{^}{\mathit{\theta }}}}^{(k)})]}_{S_k^c}\Vert }_{\infty }\le {\Vert {[\nabla l({\overline{\mathit{\theta }}}^{(k)})]}_{S_k^c}\Vert }_{\infty }+{\Vert {\mathbf{r}}_{S_k^c}^{(k)}\Vert }_{\infty }+{\Vert {\hat{\mathbf{Q}}}_{S_k^c,S_k}^{(k)}{({\hat{\mathbf{Q}}}_{S_k,S_k}^{(k)})}^{-1}\Vert }_{\infty }\times \{{\Vert {[\nabla l({\overline{\mathit{\theta }}}^{(k)})]}_{S_k}\Vert }_{\infty }+{\Vert {\mathbf{r}}_{S_k}^{(k)}\Vert }_{\infty }+{\Vert {[\nabla l({\underset{¯}{\overset{^}{\mathit{\theta }}}}^{(k)})]}_{S_k}\Vert }_{\infty }\}\le (2-\tau ){\Vert \nabla l({\overline{\mathit{\theta }}}^{(k)})\Vert }_{\infty }+(2-\tau ){\Vert {\mathbf{r}}^{(k)}\Vert }_{\infty }+(1-\tau ){\Vert {[\nabla l({\underset{¯}{\overset{^}{\mathit{\theta }}}}^{(k)})]}_{S_k}\Vert }_{\infty }\le [(1-\tau )C_{\lambda }/\sqrt{{\gamma }_{\text{min}}}]\sqrt{(\text{log }p)/n}+(2-\tau ){\tau }_{\text{max}}{M}^{2}q(\text{log }p)/n+(1-\tau )\lambda /\underset{(j,j\prime )\in S_k}{\text{min}}{[\sum _{k=1}^K|{\underset{¯}{\overset{^}{\theta }}}_{j,j\prime }|]}^{1/2}\le [2(1-\tau )/\sqrt{{\gamma }_{\text{min}}}]\lambda +o_p(\lambda ).$$ (A.19)

On the other hand, $\lambda /{[{\sum }_{k=1}^K|{\underset{¯}{\hat{\theta }}}_{j,j\prime }^{(k)}|]}^{1/2}=+\infty$ when $(j,j\prime )\in S_{\cup }^c$. Otherwise, if (j, j′) ∈ S_∪\S_k, then

$$\lambda /{(\sum _{k=1}^K|{\underset{¯}{\overset{^}{\theta }}}_{j,j\prime }|)}^{1/2}\ge \lambda /{\{\sum _{k=1}^K|{\underset{¯}{\overset{^}{\theta }}}_{j,j\prime }-{\overline{\theta }}_{j,j\prime }|+|{\overline{\theta }}_{j,j\prime }|\}}^{1/2}\ge \lambda /\sqrt{{\gamma }_{\text{max}}}\ge (2-2\tau )\lambda /\sqrt{{\gamma }_{\text{min}}}.$$

Thus, for any $(j,j\prime )\in S_k^c(k=1,\dots ,K)$, we have

$$|{\nabla }_{j,j\prime }l({\underset{¯}{\overset{^}{\mathit{\theta }}}}^{(k)})|\le \underset{1\le k\le K}{\text{max}}\underset{(j,j\prime )\in S_k^c}{\text{max}}|{\nabla }_{j,j\prime }l({\underset{¯}{\overset{^}{\mathit{\theta }}}}^{(k)})|<\underset{1\le k\le K}{\text{min}}\underset{(j,j\prime )\in S_k^c}{\text{min}}\lambda /\sqrt{\sum _{k=1}^K|{\underset{¯}{\overset{^}{\theta }}}_{j,j\prime }^{(k)}|}\le \lambda /\sqrt{\sum _{k=1}^K|{\underset{¯}{\overset{^}{\theta }}}_{j,j\prime }^{(k)}|}.$$ (A.20)