Regression mixture models: Does modeling the covariance between independent variables and latent classes improve the results?

Abstract

Regression mixture models are increasingly used as an exploratory approach to identify heterogeneity in the effects of a predictor on an outcome. In this simulation study, we test the effects of violating an implicit assumption often made in these models – i.e., independent variables in the model are not directly related to latent classes. Results indicated that the major risk of failing to model the relationship between predictor and latent class was an increase in the probability of selecting additional latent classes and biased class proportions. Additionally, this study tests whether regression mixture models can detect a piecewise relationship between a predictor and outcome. Results suggest that these models are able to detect piecewise relations, but only when the relationship between the latent class and the predictor is included in model estimation. We illustrate the implications of making this assumption through a re-analysis of applied data examining heterogeneity in the effects of family resources on academic achievement. We compare previous results (which assumed no relation between independent variables and latent class) to the model where this assumption is lifted. Implications and analytic suggestions for conducting regression mixture based on these findings are noted.

The search for differential effects – individual differences in the relationship between a predictor and an outcome – has become of increasing salience across substantive domains in the health and behavioral sciences. This is implied in common theoretical perspectives such as multifinality, which proposes that individuals exposed to similar conditions of risk experience variability in outcomes due to heterogeneity in the processes that relate risk to health and behavioral problems (Cicchetti & Rogosch, 1996). Understanding these differential effects is important for applied researchers as it begins to move beyond the question of “does x predict y” to answer “for whom does x predict y?” In order to understand the complex ways in which psychosocial factors shape behavioral and health outcomes, explicit empirical attention to variability in effects is warranted.

Regression mixture models are an exploratory approach that search for evidence of heterogeneity in the effects of a predictor on an outcome. Unlike the use of statistical interactions (which test whether the effects of a predictor on an outcome vary as a function of a measured third variable), regression mixtures explore the data for evidence of groups of respondents who differ in the effects of the predictor on the outcome. The method first emerged in the economics literature in the form of switching regression models (Quandt, 1972; Quandt & Ramsey, 1978), and was further developed and applied in statistical and marketing fields, primarily as a means to understand market segmentation and other facets of consumer behavior (Bai, Yao, & Boyer, 2012; Bartolucci & Scaccia, 2005; Cleaver & Wedel, 2001; Desarbo, Jedidi, & Sinha, 2001; Grewal, Chandrashekaran, Johnson, & Mallapragada, 2013; Jedidi, Ramaswamy, DeSarbo, & Wedel, 1996; Sarstedt, 2008; Wedel & DeSarbo, 1994, 1995). Until relatively recently, these methods have not been used in the social and health sciences. With the growing gap between theories that postulate differential effects across subpopulations and a lack of alternative methods to test these theories, however, the use of regression mixtures in the social and behavioral sciences is increasing (Dyer, Pleck, & McBride, 2012; Nowrouzi et al., 2013; Van Horn et al., 2009). Regression mixtures have recently been used to answer research questions about heterogeneity in diverse areas: for example, factors associated with youth substance use and risky behavior (Montgomery, Vaughn, Thompson, & Howard, 2013; Schmiege, Levin, & Bryan, 2009); predictors of vehicle crashes (Zou, Zhang, & Lord, 2013); antipsychotic induced weight gain (Nowrouzi et al., 2013); the age of onset of bipolar disorder (Manchia et al., 2010); and predictors of academic achievement (Van Horn et al., 2009). These models work by empirically identifying subgroups that differentially respond to a predictor, and have been successful at finding differential effects that other methods missed (Dyer et al., 2012; Montgomery et al., 2013).

Regression mixture models utilize a finite mixture model framework to capture unobserved heterogeneity in the effects of predictors on outcomes (Wedel & DeSarbo, 1994, 1995). Differential effects can be identified regardless of the inclusion of predictors of the differential effects, or whether the reasons for the heterogeneity are measured or known at the time of the study. The method offers promise for exploring the complex ways in which contexts affect individuals. However, as a relatively new methodology in behavioral sciences, more work is needed to better understand the performance of these models under varying conditions and model specifications. Regression mixtures rely on a set of strong assumptions; in particular, regression mixtures are a large sample method that assume normality of the outcome. Simulation studies show that these models are highly sensitive to violations to distributional assumptions (George, Yang, Jaki, et al., 2013; George, Yang, Van Horn, et al., 2013; Liu & Lin, 2014; Van Horn et al., 2012) and are rather sensitive to sample size requirements (Jaki, Kim, Lamont, & Van Horn, under review), underscoring the importance of testing these models prior to wide-spread applied use to ensure trustworthy model results.

In this article, we explore the effects of violating an implicit assumption often made when estimating regression mixture models: that the mean of the predictor variable is equal across latent classes. There exists some controversy in the literature about whether a relationship between the predictor and the latent classes should be modeled. We demonstrate that failure to include this relationship results in assuming that the means of the predictor are the same across latent classes, and then examine the effects violating this assumption (that the means of the predictor are constant across latent classes when, in reality, they are not equal). This article specifically focuses on the consequences of excluding this relationship from a regression mixture model under two very different scenarios.

Regression Mixture Models: Overview and Specification

Regression mixture models belong to the broad class of statistical models known as finite mixture models whose general function is to estimate population heterogeneity through a finite set of empirically-derived latent classes. Regression mixture models specifically focus on the identification of systematic differences in the effect of a predictor on an outcome. This focus on systematic differences in the association between two variables is what differentiates the regression mixture model from other more commonly known finite mixtures, such as growth mixture models (B. O. Muthén, 2006; B. O. Muthén et al., 2002) and semi-parametric models (Nagin, 2005; Nagin, Farrington, & Moffitt, 1995). Regression mixtures model differences in effects between groups (e.g. differences in the effects of x on y), whereas other mixtures estimate differences in levels and the variance of the outcome between groups (e.g. differences in the intercept across groups) (Desarbo et al., 2001; Van Horn et al., 2009; Wedel & DeSarbo, 1994). The resultant latent classes in regression mixtures represent distinct differential effects, or subgroups of individuals for whom the effects of the predictor on the outcome may differ in magnitude and/or direction from the other latent classes.

Consider a sample of n individuals for which outcome variable, y_i, and P covariates, x=(x₁,x₂,…,x_P) are observed, with realized values x_p for subject i denoted x_ip. This formulation can also be extended to a general form of a multivariate case for a sample of n individuals with y=(y₁,y₂,…y_m) measured outcomes. The multivariate conditional probability density function of y given x is modeled as a weighted sum of the probability densities within each class. We use bolded letters to indicate vectors of covariates and outcomes in the general specification, indicating that the model can be extended to multivariate contexts.

Class membership is indicated by a latent categorical variable, C, where C = 1, 2,…,K. Most models require a priori specification of K. The contribution of each class to the overall density is estimated by π₁, π₂,…, π_K, which represent the probability of being in each class.

Using this formulation, we write the joint distribution of y|x as

$$f(\mathrm{y}\mid \mathbf{\phi },\mathbf{x})={\sum }_{\mathrm{k}=1}^{\mathrm{K}}{\mathrm{\pi }}_{\mathrm{k}}{f}_{\mathrm{k}}({\mathrm{Y}}_{\mathrm{k}}\mid {\mathbf{\Theta }}_{\mathrm{k}},\mathbf{x}),$$ (1)

where φ=(π,Θ) denotes the vector of all unknown parameters to be estimated - that is, π=( π₁,π₂,…,π_K−1) and Θ=(θ₁,θ₂,…,θ_K). A typical assumption made in these models is that errors are multivariate normal, which yields the following class-specific equations:

$$\begin{array}{l}{y}_{i\mid \mathbf{x},k}={\beta }_{0k}+\sum _{p=1}^P{\beta }_{pk}{x}_{ip}+{\epsilon }_{ik},\\ {\epsilon }_{ik}~N(0,{\sigma }_k^2),\end{array}$$ (2)

where β_0k is the vector of class specific intercepts (which simplifies to means in the case of no covariates), σ²_k is the residual variance/covariance matrix for class k, and β_pk is the vector of regression coefficients for covariates x_p in latent class k. The class-specific coefficients identify this as a regression mixture model.

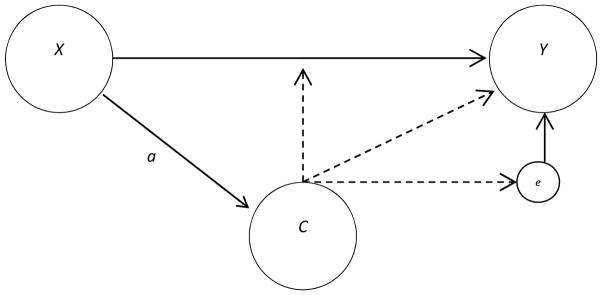
If the ‘a’ path is excluded from the model depicted in Figure 1, we have the regression mixture model described above. On inspection, we believe that this specification makes an implicit assumption that the observed exogenous variables, x, are not related to latent classes. The lack of an estimated path between the exogenous predictor, x, and the categorical latent class variable, C (the ‘a’ path in Figure 1), implies that the predictor is not related to class membership; and, by extension, assumes that the mean of x is equal in each latent class. Most of the existing research using regression mixture models does not include a relationship between x and C (Ding, 2006; Dyer et al., 2012; Fagan, Van Horn, Hawkins, & Jaki, 2012; George, Yang, Van Horn, et al., 2013; Nowrouzi et al., 2013; Van Horn et al., 2009; Van Horn et al., 2012; Yau, Lee, & Ng, 2003; Zhu & Heping, 2004). This means that the assumption of equal means is rather common among users of regression mixtures.

Figure 1.

Regression mixture model connecting the predictor with the latent class; Dotted lines indicate heterogeneity in effects captured by the latent class variable, C. X is the predictor in the model, Y is the outcome, e is the class specific-residual, a is the pathway of interest in this article.

Finite mixture models in general (Dayton & Macready, 1988) and regression mixture models in particular (B. O. Muthén & Asparouhov, 2009; Wedel, 2002) can be extended to include covariates that predict the latent classes. Using the notation above, the probability of latent class membership can be estimated using a multinomial logistic regression with the following equation:

$$Pr(c_i=k\mid {\mathbf{z}}_i)=\frac{exp({\alpha }_k+{\displaystyle \sum _{q=1}^Q}{\gamma }_{qk}{z}_{iq})}{{\displaystyle \sum _{s=1}^K}exp({\alpha }_s+{\displaystyle \sum _{q=1}^Q}{\gamma }_{qs}{z}_{iq})}$$ (3)

where α_k is the class-specific intercept and γ_k is the class-specific effect of z, the covariates. Latent class predictors, z, may either be unique from the x variables (for which differential effects on the outcome are being assessed), or x and z may overlap (B. O. Muthén & Asparouhov, 2009; Wedel, 2002), in which case z can be replaced or partially replaced by x. Others have extended the regression mixture to the multivariate case, and the issue raised in this article – i.e., the relaxation of the assumption of equal means through the estimation of a pathway between x and the C – can be easily extended to the multivariate case. Similar to the univariate model, the typical use of the regression mixture with multiple covariates excludes the pathway between C and the covariates, thereby making the assumption of equal means across classes. In the multivariate case, the assumption is made multiple times, once for each covariate for which a regression mixture is estimated. For simplicity, the simulations in this article use only one covariate x to test the implications of this assumption.

Including the exogenous x variable as a predictor of the latent classes results in the estimation of the ‘a’ path in Figure 1 (we will refer to this as the C on x path), and explicitly allows for mean differences in x across latent classes. Although we do not suggest a direct, substantive interpretation of this path, there are at least two rationales for including the regression of C on x in the regression mixture model. The first is a matter of convenience, inclusion of the C on x path is one approach that relaxes the assumption that C and x are unrelated (Ingrassia, Minotti, & Vittadini, 2012). The second is more theoretical in nature: in some cases, it may make conceptual sense that the latent classes as well as the outcome would be a function of the predictors (B. O. Muthén & Asparouhov, 2009). Take, for example, the case of the effect of family resources on student achievement, the working example introduced later in this article. In the original study, we hypothesized that family resources would differentially impact youth achievement. We did not include any relationship between family resources and the categorical latent class variable (C) for two reasons: 1) we were theoretically interested in heterogeneity in the effects of family resources as captured by the latent classes, and it made little theoretical sense to model the effect of family resources on classes, which represent the effect of family resources; and 2) it was not obvious to us initially that excluding the relationship between x and C was equivalent to assuming that the means of x were the same for each latent class. This current research was undertaken, in part, because additional work with these models and new research by Ingrassia and colleagues (Ingrassia et al., 2012) suggest the potential meaningfulness of the equal means assumption. This assumption would be violated if, for example, the students most impacted by family resources are those from families relatively lower in basic needs. We were motivated to examine the consequences of misspecifying the model by excluding the C and x relationship in this applied model predicting student achievement.

We emphasize that we see little rational for expecting or interpreting a causal relationship between the latent classes and the covariate, e.g. family resources. The inclusion of the C on x path is intended to relax the assumption that the classes have equal means on the covariate, not for substantive purposes. This pathway is simply proposed to aid in estimation.

One rationale for not including the C on x path, besides the fact that it seems to change the focus of the model, is that it adds to an already quite complex model. A very simple model (such as the one in Figure 1) with one predictor, one outcome, and two classes uses only the information contained in the bivariate distribution of x and y to estimate seven parameters without the C on x path, and eight parameters with that path. Relaxing the assumption of equal means on x makes less information available to estimate the model, and would be expected to make the model somewhat less stable. If we are not substantively interested in the relationship between C and x, then not including this path simplifies the model. The second reason for not including the regression of C on x is theoretical: If C represents differences in the relationship between x and y, then allowing x to influence C appears to create a scenario where x influences the relationship between x and y. This suggests a curvilinear relationship between x and y - another type of heterogeneous effect that is typically not estimated by a regression mixture. The type of heterogeneity estimated in a regression mixture is unobserved subgroups that differ in the relationship between x and y (versus a curvilinear relationship between x and y in a single population). In this article, we examine how regression mixtures capture these two different types of heterogeneity in the effect of x on y, and how the inclusion of exclusion of the C on x path impacts the results. We are specifically concerned that unobserved heterogeneity between x and y not be confused with a curvilinear relationship between x and y.

Study Aims

This study seeks to evaluate the effects of violating an assumption often implicitly made in regression mixture models - that independent variables in the model are not directly related to latent classes. The simplest way to relax this constraint is by including the regression of the latent class variable (C) on the covariate (x) in the model. The inclusion of the C on x path allows the means of x to differ across latent classes. For the first aim, we use simulations to examine the effects of including versus excluding the C on x path from a regression mixture model as differences between classes in the mean of x increase. We specifically aim to test bias resulting from failure to include the relationship between C and x on class enumeration and, when the correct number of classes are chosen, in parameter estimates. We hypothesize that as the mean difference between the latent classes on x increases (i.e., the violation of the assumption of equal means becomes greater), there will be an increase in parameter bias and number of classes selected. We expect that additional classes will be selected in order to account for the mean difference.

Because the inclusion of C on x in the model suggests a nonlinear relationship between x and y, our second aim is to examine whether a true non-linear relationship would be detected in a regression mixture model. We specifically focus on a piecewise relationship in this study. We emphasize that, in this aim, we are not testing the utility of regression mixtures to estimate piecewise relationships that are hypothesized a priori. Rather, we are concerned with whether it is possible to differentiate a piecewise relationship from unobserved heterogeneity in effects, and how a true piecewise effect would be detected in this case. Simulations are used in which data is generated from a piecewise relationship between x and y, and analyzed using regression mixture models with and without the C on x path included. The piecewise model was selected because it corresponds closely to the effects expected in a regression mixture if a separate piecewise slope was estimated for each class. The difference between the piecewise model and the typical regression mixture is that the piecewise model has a strict cutoff value on x that completely defines classes (in this way, it may be considered a special case of the model tested in the first aim). In both the models, there are mean differences on x. The models differ in that there is a deterministic relationship between x and the latent class in the piecewise model, which is not the case in the typical regression mixture. Because the inclusion of the C on x pathway implies a nonlinear relationship, we hypothesize that in order for a regression mixture to fit a piecewise relationship, differences in the means of x across classes must be allowed.

An applied example examining differential effects of family resources on academic achievement is used to illustrate the effects of including the C on x path in the analysis model. Previous research found evidence for heterogeneity in these effects (Van Horn et al., 2009). We replicate the findings of this past work, and compare them to the model in which C on x is jointly estimated in order to examine the effects of including the relationship between C and x in applied analyses.

Methods

A Monte Carlo simulation study was conducted to test the impact of assuming equality of the mean of x across classes. For all conditions, a regression mixture model was estimated with the C on x path both estimated and then omitted; results from these models were compared. Data were generated in R (R Core Team, 2015). Regression mixture models may be conducted in Latent Gold (Vermunt & Magidson, 2005), Mplus (L. K. Muthén & Muthén, 1998–2012), and using the FLEXMIX package in R (R Core Team, 2015). In this case, models were estimated using Mplus and called from and analyzed through R, using maximum likelihood estimation. Code for generating a single dataset in R and for estimating the model in Latent Gold and Mplus are provided in supplemental material online.

Model specification for Aim 1

Data were generated under a simple yet important condition with two populations (latent classes), each containing 50% of the sample, and a single predictor variable, x, and a single outcome variable, y. Sample size and the difference between classes in the means of x were the research factors. There are several reasons for choosing these simple conditions. First, the primary interest in this article was on the specification of the relationship between the independent variable and the latent classes. We acknowledge that changing class proportions, the number of classes, or the number of outcomes would impact power and class separation, and may change these results; however, the purpose here is to present simulations that serve to frame the issue in general so that it can be acknowledged when applied models are being fit. Second, this case focuses on a very salient type of differential effect: heterogeneity in the effects of one predictor on one outcome. In studying effect heterogeneity, we find it common for researchers to break down the results into components that resemble the simple comparison tested in this study. Third, simulations with more complex models are quite difficult to interpret and explain (for example, class sorting with regression mixtures can be quite problematic with three latent classes, unless class separation is quite strong). We therefore chose to focus on relatively parsimonious conditions that, in principal, should generalize to other regression mixtures. In these simulations, a single x was generated from a normal distribution for both classes. Classes were generated so that the means on x differed by a 0 standard deviation (mean of 0 in both classes), .5 standard deviation (mean of .25 in class 1 and −.25 in class 2), 1 standard deviation (mean of .5 in class 1, −.5 in class 2), or 2 standard deviation (mean of 1 in class 1 and −1 in class 2) difference.

The outcome, y, was generated according to the following equations:

$$\begin{array}{c}\text{Class}1:y_i=.2x_i+e_1\\ \text{Class}2:y_i=.5+.7x_i+e_2\end{array}$$

Values for the residual variances were chosen so that the total variance of y in each of the two populations (latent classes) would be equal to 1: e₁ ~ N(0, .96) e₂ ~ N(0, .51). This scales the regression weights to be correlations. These conditions were chosen to represent effect sizes typically considered as moderately small and moderately large in the behavioral sciences (Cohen, Cohen, West, & Aiken, 2003). Differences in regression weights of this size would, for many applications, be large enough to indicate a qualitatively important difference between classes. We see this as an important threshold condition such that if regression mixtures are to be useful for finding differential effects they should at a minimum be able to recover differences of this size. To facilitate interpretation of estimates across simulations and avoid the problem of label-switching, we used an identifiability constraint to sort two-class models such that the class with the greater regression weight of y on x was always class two (McLachlan & Peel, 2000; Sperrin, Jaki, & Wit, 2010).

Two samples of n=6,000 and n=2,000 observations were generated. The larger sample replicated those used in other simulation articles on regression mixture models (George, Yang, Jaki, et al., 2013; George, Yang, Van Horn, et al., 2013; Van Horn et al., 2012). The moderately sized sample, although still large, was intended to resemble a more realistic sample size in the behavioral sciences. Evidence suggests that this is close to the lower boundary for obtaining stable estimates using regression mixtures with class separation values similar to those used in this study (Jaki et al., under review). A fully crossed design with 16 conditions was implemented: sample size (n = 6000 or 2000)*C on x path (included vs. excluded)*mean differences in x (0, .5, 1, or 2 standard deviations). Five hundred replications were conducted of each model for each condition.

Model specification for Aim 2

The second aim examined how a piecewise relationship between x and y may be detected using regression mixtures. The covariate was generated as x ~ N(0,1). Because the interest of this analysis was in showing how a piecewise relationship may be evident in parameter estimates and diagnostics of regression mixture models (rather than testing bias in enumeration or parameter estimates across repetitions), analyses were conducted for a single repetition of a large sample of n=100,000 observations. To observe performance in a more realistic sample size, analyses were also conducted with a sample of n=2,000 observations.

The piecewise model was selected because it closely corresponds to a regression mixture model in that there are two groups of respondents for whom the effect of x on y differs. However, unlike in the data generated for Aim 1, these differences were completely determined by a threshold value of x, which defined the inflection point of the piecewise trend. For data generation, an arbitrary threshold of 0 was used. For the piecewise model, y was generated as follows:

$$\{\begin{array}{ll}x<0,\hfill & y_i=.2x_i+e_1\hfill \\ \mathit{otherwise},\hfill & y_i=.7x_i+e_2\hfill \end{array}$$

Values for the residual variances were chosen so that the total variance of y in each of the two populations (latent classes) would be equal to 1: e₁ ~ N(0, .96) e₂ ~ N(0,.51).

Both aims contain heterogeneity in the relationship between x and y, the major difference between them is the relationship between level of x and class membership. For Aim 1, there is a small probabilistic relationship between C and x. This is in comparison to the piecewise case in Aim 2, where there is a very strong, deterministic relationship between C on x. There is a clear decision rule in the piecewise model that determines class (and respective slope) based on level of x.

Model selection

The first step in estimating a regression mixture model is to determine the optimal number of classes supported by the data (class enumeration) by testing a series of models with a progressively increasing number of classes and assessing model fit. For the first aim, data were generated to have two classes; thus, we would expect a correctly specified model to select the two class model over a model with any other number of latent classes. We fitted one, two, and three class models under each condition with C on x both included and omitted. Although we knew that the data were generated to include only two classes, in practice, this information would not be known, and the analyst would be dependent on the results of this progressive model fitting procedure. We wanted to test the number of times each model correctly selected the two-class model, leading the analyst to the correct results. For the second aim, where data were generated as a piecewise model with two slopes, we fit a progressively larger number of classes to the data, proceeding based on fit statistics and model estimability. Model selection was guided by the Bayesian information criterion (BIC; Schwarz, 1978) and the sample size adjusted BIC (adjBIC). Smaller values in BIC and adjusted BIC indicate a better model fit. In the case of disagreement between fit statistics, analyst judgments (based on parameter estimates and class proportions) are often required, since neither fit statistic is a “gold standard” in the literature. We opted not to use the bootstrap likelihood ratio test (McLachlan & Peel, 2000) because of high-computational costs and evidence showing inadequate performance with regression mixture models (Van Horn et al., 2012).

Estimation quality

We then assessed the quality of parameter estimation for the true two-class model. Our assessment focused primarily on parameter bias, or the difference between the expected value of the estimator and the true value of the parameter. We examine bias of regression coefficients as well as the proportion of respondents estimated in each latent class.

Since bias is only one aspect of estimator quality, we also assessed the variance of the estimator; specifically, we present the standard deviation and range of estimates resulting from each condition. Additionally, we assessed the proportion of times the true value of the parameter fell between the .95 confidence interval (referred to as coverage) and calculated the Root Mean Squared Error (RMSE, defined as the second moment of the errors, which incorporates both the estimator bias and variability).

Methods: Applied Example

Data from this study came from the National Head Start Public School Transition Demonstration Study, a multi-site (n=30 sites), 5-year longitudinal intervention for disadvantaged youth (for a complete description of the intervention, see C. T. Ramey, Ramey, & Phillips, 1996; S. L. Ramey et al., 2001). These data are available for public use for research purposes. The Transition study followed two cohorts of families of former Head Start children from Kindergarten until third grade during the years 1992 through 1997. This study focuses on the cross-sectional sample of third-graders (collected in 1996 for cohort 1 and 1997 for cohort 2). In the main impact study, the intervention showed no effects on children’s academic achievement (S. L. Ramey et al., 2001); therefore, intervention status is not included in these analyses. A total of 6,205 third grade students are included in the current study. This is the same sample used a previous report using regression mixtures to find heterogeneity of effects (Van Horn et al., 2009). Children were from diverse ethnicities (33% African American; 48% White, non-Hispanic; 6% Hispanic; and 13% other) and half were female. As expected for Head Start populations, the mean income of study families was below the poverty line. Data were collected during in-person interviews, with the exception of child outcome measures, which were assessed in schools by trained assessors. For the purposes of this demonstration, clustering of students due to site is ignored.

Measures

Family resources were measured using the Family Resource Scale (FRS; Dunst & Leet, 1994; Dunst, Leet, & Trivette, 1988). The FRS measures the resources and needs of families of high-risk youth. It focuses on the following resource areas: ability to meet basic needs, adequacy of financial resources, amount of time spent together as a family, and amount of time parents have for themselves (Van Horn, Bellis, & Snyder, 2001). Coefficent alpha ranged from .72 to .84 across subscales, and validity of the subscales has been demonstrated elsewhere (e.g., via relationships with poverty level, education, work status; Van Horn et al., 2001). Consistent with previous analyses of the data, we standardized and averaged items on each subscale to derive a subscale score. Skewness ranged from −1.4 (basic needs) to −.11 (availability of financial resources); kurtosis ranged from 1.97 (time for self) to 6.50 (basic needs).

Student achievement was assessed via standardized measures in three domains: reading, mathematics, and language. Reading and mathematics achievement were measured using the broad math and reading scales on the Woodcock-Johnson achievement tests (Woodcock & Johnson, 1990). The Woodcock-Johnson is a nationally normed and standardized test of intellectual abilities. Reading scores are based on tests of Passage Comprehension and Letter-Word Identification subscales; math scores are based on Calculation and Applied Problems. Receptive language skills were measured on the Peabody Picture Vocabulary Test-Revised (PPVT; Dunn & Dunn, 1981). Although the PPVT is a good predictor of school performance among low-income children, data suggest mean differences across ethnic groups. Thus, child ethnicity will be held constant in all analyses, consistent with previous analysis of the data (Van Horn et al., 2009). Skewness of variables ranged from −.76 (reading) to −.28 (ppvt) and kurtosis ranged from 3.3 (ppvt) to 4.18 (reading).

Results

Aim 1. What are the effects of failure to model the relationship between a predictor and a latent class variable on latent class enumeration and model parameter estimates?

Class enumeration

Analyses were run for each generated dataset with one, two, and three latent classes. Because this is a simulation study, we knew that there were two true populations (classes); however, in an applied study, this information would be unknown. We test whether misspecifying the model by failing to include the C on x path results in finding too many latent classes. The proportion of repetitions that chose the two class over the one class solution, and the three class over the two class solution using both the BIC and the adjusted BIC are reported in Table 1. When the relationship between C and x was included in the model, each criteria did a satisfactory job at selecting the two-class over the one-class and three-class models. However, when this path was omitted from the model, the adjusted BIC selected the three-class over the two-class model when class separation was large. For example, the adjBIC selected the three-class solution 27% of the time when there was a one standard deviation difference between classes in x, and 83% of the time when the difference between classes in x was two standard deviations and the sample was large. The BIC was less affected by the exclusion of C on x pathway, and performed more favorably when the mean difference between classes was large. With the moderate (n=2,000) sample size (see Table 1), the effect of misspecifying the relationship between x and C on latent class enumeration appears to be limited.

Table 1.

Proportion of replications (n=500) favoring each solution over the solution with one less class in a regression mixture when the covariance between the latent class (C) and predictor (x) is included or excluded.

	2-class over 1-class		3-class over 2-class
	Bayesian Information Criterion (BIC)	Adjusted Bayesian Information Criterion (adjBIC)	Bayesian Information Criterion (BIC)	Adjusted Bayesian Information Criterion (adjBIC)
N=6,000
C on x included
sd=0	1.00	1.00	.002	.012
sd=.5	1.00	1.00	.000a	.026
sd=1	1.00	1.00	.000 b	.020b
sd=2	1.00	1.00	.000	.010
C on x omitted
sd=0	1.00	1.00	.004	.028
sd=.5	1.00	1.00	.002	.060
sd=1	1.00	1.00	.028	.270
sd=2	1.00	1.00	.356	.828
N=2,000
C on x included
sd=0	.904	.998	.000	.084
sd=.5	.998	1.00	.000	.102
sd=1	1.00	1.00	.000	.082
sd=2	1.00	1.00	.000	.124
C on x omitted
sd=0	.972	.998	.002	.098
sd=.5	.990	1.00	.002	.114
sd=1	.984	.998	.002	.138
sd=2	.958	1.00	.028	.298

^a493 replications converged in the 3-class solution;

^b497 replications converged in the 3-class solution.

Note: C indicates the latent class variable, x indicates the predictor, C on x represents the regression of the latent class variable (C) on the predictor (x), which is the pathway of interest in this article; N=sample size; sd=standard deviation difference in x between classes (class separation)

We note that as sample size (and respective power) increase, the three-class solution would be likely supported more often when the model is misspecified. When selected over the two class solution, the class proportions of the three class solution were often large enough to be considered a stable solution. For example, in the 414 (of 500; 82.8%) replications that selected the three-class solution (using the adjusted BIC in the sd=2, large sample condition), the smallest class was, on average, .107 (range=.001–.301, median=.102). In 219 (of 500; 53%) replications, the smallest class contained more than 10% of cases. This suggests that if the true values were unknown (as in a typical applied analysis) and mean differences between classes on x are quite large, the analyst may incorrectly select a model with too many classes on the basis of fit statistics, if the C on x path is not included in estimation.

Estimation quality

We then examined the quality of parameter estimates for the two-class solution. The purpose was to understand how well the model estimated true values, if the two-class solution was chosen. Estimation quality for the one- and three-class solutions did not have much utility since those classes did not exist in the population. Specifically, we explored class-specific parameter bias and variability.

First, we examined parameter bias, defined as the difference between the population value and the estimated value (mean across repetitions). As seen in Table 2, parameter estimates for the two class model were generally very close to the population values, even under conditions of model misspecification (exclusion of C on x). We observed that the intercept and residual variance in class one were downward biased as differences between classes in x increased, when the C on x path is omitted. However, these differences would not substantially affect the conclusions that would be drawn from the models. Overall, the findings suggests that the exclusion of the C on x path introduces minimal bias into the model. There is one major exception, however. Class proportions showed increasing bias as class separation on the mean of x between the latent classes increased. Bias estimates ranged from −.011 (sd=0) to .769 (sd=2). As the assumptions of equal means was increasingly violated, too many respondents were placed in class one, in this case, when the C on x path was omitted from estimation. Table 3 shows the estimated class proportions, which were generated to be 50/50. These proportions were maintained when C on x is included in the model, but become biased when C on x is omitted and class separation increased. ¹

Table 2.

Parameter estimates for the two-class solution when the C on x path is omitted from the regression mixture model.

	True value	Mean N=6,000	Std Error N=6,000	Bias N=6,000	RMSE N=6,000	Coverage N=6,000	Mean N=2,000	Std Error N=2,000	Bias N=2,000	RMSE N=2,000	Coverage N=2,000
Class separation at sd=0
Class 1
Intercept	0	−.007	.052	−0.007	.049	.964	−.030	.107	−0.030	.126	.940
Slope	.2	.196	.044	−0.004	.046	.952	.189	.082	−0.011	.083	.932
Residual	.96	.958	.039	−0.002	.077	.942	.941	.077	−0.019	.093	.948
Class 2
Intercept	.5	.500	.036	0.000	.061	.936	.505	.065	0.005	.072	.936
Slope	.7	.698	.033	−0.002	.042	.932	.696	.061	−0.004	.062	.918
Residual	.51	.509	.044	−0.001	.053	.920	.505	.080	−0.005	.082	.900
Class 1 mean	0	−.011	.252	−0.011	.260	.924	−.054	.477	−0.054	.490	.920
Class separation at sd=.5
Class 1
Intercept	0	−.047	.046	−0.047	.067	.894	−.056	.104	−0.056	.116	.932
Slope	.2	.199	.030	−0.001	.032	.942	.196	.055	−0.004	.054	.948
Residual	.96	.871	.035	−0.089	.106	.271	.864	.073	−0.096	.123	.665
Class 2
Intercept	.5	.540	.040	0.040	.067	.822	.542	.075	0.042	.091	.902
Slope	.7	.706	.039	0.006	.046	.922	.710	.079	0.010	.078	.912
Residual	.51	.476	.044	−0.034	.062	.860	.470	.083	−0.040	.094	.878
Class 1 mean	0	.323	.228	0.323	.424	.619	.343	.472	0.343	.560	.808
Class separation at sd=1
Class 1
Intercept	0	−.084	.046	−0.084	.097	.586	−.112	.090	−0.112	.159	.830
Slope	.2	.208	.024	0.008	.045	.870	.198	.044	−0.002	.045	.938
Residual	.96	.815	.032	−0.145	.206	.014	.797	.061	−0.163	.180	.236
Class 2
Intercept	.5	.563	.050	0.063	.139	.691	.561	.089	0.061	.109	.860
Slope	.7	.700	.050	0.000	.085	.823	.693	.086	−0.007	.087	.884
Residual	.51	.460	.050	−0.050	.112	.685	.464	.084	−0.046	.097	.864
Class 1 mean	0	.593	.256	0.593	.638	.403	.548	.460	0.548	.736	.631
Class separation at sd=2
Class 1
Intercept	0	−.197	.053	−0.197	.205	.019	−.217	.099	−0.217	.246	.261
Slope	.2	.231	.020	0.031	.174	.270	.223	.037	0.023	.059	.741
Residual	.96	.744	.031	−0.216	.545	.000	.738	.058	−0.222	.257	.058
Class 2
Intercept	.5	.519	.074	0.019	.438	.006	.524	.126	0.024	.194	.776
Slope	.7	.645	.063	−0.055	.275	.127	.652	.100	−0.048	.132	.733
Residual	.51	.488	.061	−0.022	.060	.907	.470	.099	−0.040	.144	.726
Class 1 mean	0	.769	.341	0.769	.501	.804	.759	.573	0.759	.979	.603

Note: Estimates for replications that selected the two-class solution using the Bayesian Information Criterion (BIC) are reported only; Class 1 mean refers to the probability of being in Class 1 over Class 2 (logit scale), a true value of 0 indicates classes were generated to be balanced. C indicates the latent class variable, x indicates the predictor, RMSE=Root Mean Squared Error, sd=standard deviation, N=sample size. Bolded values point to areas of poor performance.

Table 3.

Estimated class proportions for the two class solution (class1/class2) of the regression mixture model when the covariance between the latent class (C) and predictor (x) is included or excluded.

	N=6,000			N=2,000
	10% quantile	50% quantile	90% quantile	10% quantile	50% quantile	90% quantile
C on x included
sd=0	.42/.58	.50/.50	.57/.43	.33/.67	.49/.51	.63/.37
sd=.5	.42/.58	.51/.49	.58/.42	.18/.82	.49/.51	.65/.35
sd=1	.44/.76	.51/.49	.58/.42	.34/.66	.51/.49	.65/.35
sd=2	.43/.57	.51/.49	.59/.41	.35/.651	.52/.481	.67/.331
C on x omitted
sd=0	.42/.58	.50/.50	.57/.42	.34/.66	.49/.51	.61/.39
sd=.5	.50/.50	.59/.41	.66/.34	.45/.55	.59/.41	.71/.29
sd=1	.56/.44	.65/.35	.72/.28	.49/.51	.64/.36	.75/.25
sd=2	.55/.45	.70/.30	.78/.22	.48/.52	.70/.30	.83/.17

¹Results based on n=498 repetitions due to extreme values fixed for the latent class intercept on two replications.

C=latent class variable, x=predictor, C on x represents the pathway of interest in this article, N=sample size, sd=standard deviation (class separation).

Table 2 additionally presents estimates of coverage (defined as the proportion of times the true value fell within the .95 confidence limit of the estimated values) and Root Mean Squared Error (RMSE; a composite of bias and variability of the estimator). Consistent with bias, these statistics show that the quality of estimation decreased as class separation on the mean of x increased, when C on x was not included in the model. In particular, RMSE values suggest that there was increasing variability in estimates as the class separation increased, which can explain the poor coverage rates when class separation is large. This suggests that although parameter estimates are, on average, unbiased, failure to estimate C on x may yield variable estimates more likely to “miss” the true parameter value.

In sum, these results show that the major risks in failing to model the relationship between C and x in a regression mixture model is an increase in the probability of selecting additional latent classes, biased proportions of individuals in each class, and increased variability in estimates. This is particularly true when class separation is large and for large sample sizes. The model captured the true value a greater proportion of times with the more moderate sample size because estimation is less precise with the smaller sample.

It is also worth noting that, in this case, we saw no cost in estimating the C on x path - that is, the correct models all converged, parameter estimates were unbiased, and there was no evidence of instability. Table 1 reports some problems in estimating the three-class model with the C on x path; in our experience, when using simulated data, it is common to occasionally have problems estimating a model with more classes than exists in the population. We take occasional failure to converge as indicating support for the model with fewer classes.

Aim 2. How can a piecewise relationship between x and y be detected with a regression mixture model?

We examined how to identify a piecewise relationship using a simulation in which data were generated to have a piecewise relationship between x and y, and where the results were analyzed with regression mixture models. We tested the model under two conditions: first, the asymptotic performance was tested with a single sample of n=100,000; then, performance under more realistic conditions (n=2,000) was tested. The purpose was to evaluate a very different type of effect heterogeneity than in Aim 1. In this aim, the heterogeneity was due to a strong piecewise relationship between x and y, rather than unobserved groups that have modest differences in the relationship between x and y. Because our primary purpose was the detection of a piecewise relationship (rather than inference), we started with a single replication in a very large sample, followed by a validation with a more realistic sample to ensure that the same diagnostics worked on a more moderate sample size.

The first step in the analysis was class enumeration. When the relationship between C on x was included in model estimation, both the BIC and adjusted BIC selected a two-class solution (see Table 4); however, when the C on x path was omitted, both fit statistics selected additional classes when the sample size was large (three classes were the most tested in these simulations).

Table 4.

Fit statistics for the regression mixture model (one to three classes) when the true underlying relationship between x and y is a piecewise relationship

	N=100,000			N=2,000
	1 Class	2 Classes	3 Classes	1 Class	2 Classes	3 Classes
C on X included
BIC	255512.733	247447.549	247491.312	5150.703	5040.0771	5063.7201
adjBIC	255503.199	247422.125	247449.997	5141.172	5014.6611	5022.4191
C on X omitted
BIC	255512.733	252775.038	252128.167	5150.703	5130.501	5152.313
adjBIC	255503.199	252752.792	252093.209	5141.172	5108.261	5117.365

¹Best loglikelihood value not replicated;

C=latent class variable, x=predictor, C on x represents the pathway of interest in this article, N=sample size, BIC=Bayesian Information Criterion, adjBIC=adjusted Bayesian Information Criterion; Bolded values indicate best fitting model.

We then examined parameter estimates, given that the two-class solution was selected. Results showed that the two-class model with the C on x path omitted showed substantial bias in the estimation of the intercept for both classes and the residual of y for class one (see Table 5). The intercept of class one was also slightly overestimated, which is consistent with the inflated class proportion of class one in this model, and indicates that more respondents are being placed in one of the classes (class one, in this example). Conversely, when the C on x path was included, we did not find evidence of parameter bias. The one noteworthy estimate found in Table 5 is the regression coefficient of C on x, which in this case was very large (estimated on the boundary). This large value is explainable because C is completely determined by x, making the regression not estimable. Because the regression weight could not be estimated, the intercept for this regression is also not meaningful.

Table 5.

Parameter estimates for the two class regression mixture model (with and without the C on x path included) when the true underlying relationship between x and y is a piecewise relationship

	True values		N=100,000				N=2,000
			C on x path omitted		C on x path included		C on x path omitted		C on x path included
	Class 1	Class 2	Class 1	Class 2	Class 1	Class 2	Class 1	Class 2	Class 1	Class 2
Class Proportion	.50	.50	.57	.43	.50	.50	.58	.42	.49	.51
Y on X	.2	.7	.285 (.007)	.773 (.013)	.202 (.007)	.713 (.005)	.284 (.049)	.801 (.079)	.240 (.050)	.672 (.040)
Intercept Y	0	0	.496 (.012)	−.226 (.015)	−.002 (.007)	−.009 (.005)	.431 (.063)	−.260 (.091)	−.030 (.052)	.003 (.036)
Residual Y	.96	.51	.584 (.005)	.560 (.007)	.954 (.006)	.507 (.003)	.582 (.034)	.597 (.047)	.982 (.042)	.511 (.021)
Class Intercept/Mean	0		.279 (.068)		−89.459 (.698)		−.333 (.386)		−228.001 (27.984)
C on X	∞		na		not estimable		na		Not estimable

Explanation of terms: Class proportions refer to the proportion of cases estimated in each class; Y on x refers to the regression coefficient for each class; Intercept Y refers to the intercept for the regression of Y on x for the class; Residual Y refers to the residual associated with the regression of Y on x for the class; Class Intercept/Mean refers to the intercept from regressing C on x (logistic regression with one class as the reference group) or the class mean when C on x is excluded; C on x refers to the regression of class membership on x (logistic regression). N=sample size, na=not estimated.

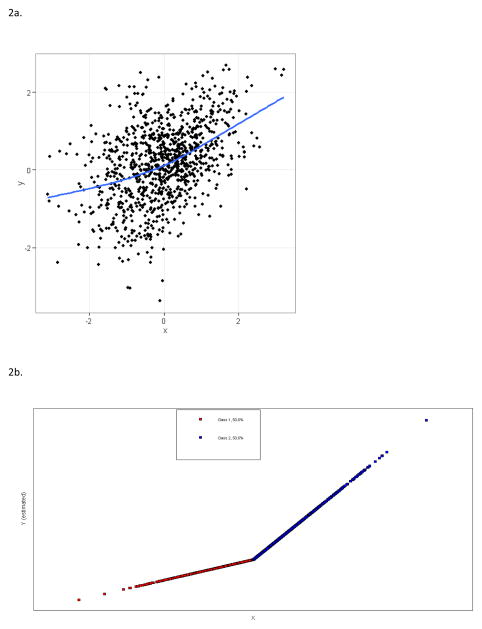
The primary intent of this research aim was to practically detect a piecewise relationship between x and y, as opposed to the type of differential effects between x and y commonly found in a regression mixture. As indicated in Figure 2a, the piecewise relationship may not be obvious by examination of the raw data alone, which may lead a researcher to search for differential effects using a regression mixture. The lowess line (Cleveland, 1979) was added to the plot to illustrate the true underlying piecewise relationship. When the C on x path was omitted from model estimation, it was very difficult to detect the piecewise relation. In practice, this may lead to incorrectly interpreting the piecewise relationship as two heterogeneous populations that differ in the relationship of x and y, missing the true piecewise component of the data and incorrectly interpreting the data. However, when the C on x path was included in the model, the presence of a piecewise relationship between x and y became very clear.

Figure 2.

Plot of raw data with lowess non-parametric fit line overlayed (panel 2a); Plot of the regression line estimated from the regression mixture model’s predicted values when the C on x path was included (panel 2b). Plot of the regression line estimated from the regression mixture model’s predicted values when the C on x path was omitted from estimation (panel 2c). The C on x path refers to the regression of the latent class variable C on the predictor x and is the pathway of interest in this article.

There are two primary ways this piecewise relation could be detected when C on x is included. The first way to detect a potential confusion of a piecewise relationship for heterogeneity in effects is through estimation problems. Because class membership is completely determined by the value of x (i.e., the slope depends on the value of x, which differs from a regression mixture in which slope depends on class and is not linearly dependent on x), estimates of the C on x path (logit scale) go to infinity and present a problem with the calculation of the second-order derivatives. This produces an error message in Mplus software (using standard code, as shown in supplemental materials online), though the problem can be prevented using alternative parameterizations (e.g., using Bayes Constants in Latent Gold software).

Perhaps the clearest way to see the piecewise relationship is through plots of the observed x values and estimated response variable, y (see Figure 2b and 2c). These plots require that individuals be classified into a particular class; in this case, this was accomplished using pseudoclass draws whereby individuals were assigned to each class using posterior probabilities.² The piecewise relationship between x and y is clearly evident in Figure 2b, which includes estimated responses from the model with the C on x path. The same graph for the model with the C on x path omitted appears in Figure 2c. Comparison of the figures demonstrates the danger of failing to test the assumption that x is constant across C. Figure 2c (C on x omitted) is what we would expect for the results of a regression mixture model where the results represent heterogeneity in the relationship between x and y. This may lead the researcher to faulty conclusions, since a piecewise model may not be hypothesized a priori, and there was no evidence for a piecewise relationship revealed through model estimation.

Applied Example. What are the effects of specifying the C on x path with applied data?

To demonstrate how modeling the relationship between C and x impacts real world results, we reanalyzed a previously published finding examining differential effects in the relationship between family resources and academic achievement. Family resources were operationalized as having sufficient resources to meet the basic needs of the family, parents having enough time to spend with family, enough time for themselves. We examined whether there was a differential impact of these resources on standard measures of reading, math, and language abilities. There is theoretical and empirical rationale for expecting differential effects of family resources on child development: some youth are resilient to the effects of disadvantage, while others are impacted by poor family context. Heterogeneity in the effects of family resources on academic achievement was previously assessed using regression mixture models. Results from a sample of 6,205 third grade student found three groups of children, defined by their response to family resources and mean values on outcomes (Van Horn et al., 2009). The largest group (42%) were strongly affected by basic needs such that the more basic needs that were met, the better the child achievement. Another group was defined primarily by low achievement on all outcomes assessed. These two classes were consistent with previous work on the effects of disadvantage on child development. Interestingly, the authors additionally revealed a third class of resilient children, who were relatively unaffected by family disadvantage. This class has particular implications for early intervention programs, since these are youth who are successful despite high levels of risk.

The regression mixture used by Van Horn and colleagues (2009) used the common specification of a regression mixture, which excluded the C on x path and thereby made the assumption that all three classes had equal means on family resources (see Figure 3). However, it may be true that those youth who are most impacted by family resources come from families with lower resources, suggesting a correlation or possibly even a causal relationship between x and C. Thus, we re-analyze the previously published data using a regression mixture with and without the C on x path to test whether relaxing the assumption of equal means on the independent variables changed model results. Fit statistics and parameter estimates (for the final model) are printed here for ease of comparison. The results printed here are from the reanalysis of the published version. The reader should note that these estimates differ very slightly from the original published version due to changes in model estimation between versions of Mplus.

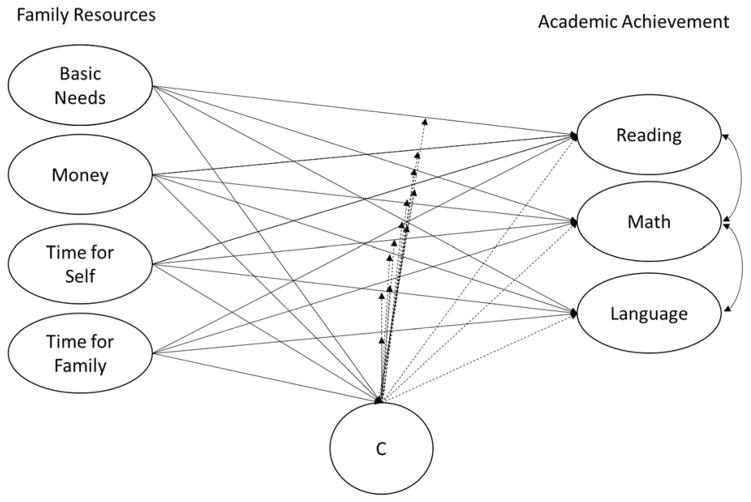
Figure 3.

Theoretical model for the applied example testing differential effects of family resources on academic achievement. Dotted lines from latent class variable, C, to outcomes represents heterogeneity in the effect of the predictor on the outcome.

Results from the applied analysis are shown in Tables 6 (class enumeration) and 7 (parameter estimates). Consistent with the original analysis (Van Horn et al, 2009), using the BIC, adjBIC, and class proportions, we found evidence that the three class model fit the data best (see Table 6). This solution includes a “low achieving” class of students that have lower means on reading and math scores; a “basic needs” class in which there was a strong positive effect of the availability of basic needs (food, shelter, clothing, and heat) and a weaker negative effect of time that the family has to be together; and finally a “resilient” class in which there was no negative impact of the lack of basic needs. Comparison of the model with and without the C on x pathway shows results consistent with the simulation results presented in Aim 1. When C on x was included, both BIC and adjBIC supported a three-class solution. When the path was excluded, the adjusted BIC supported the three-class solution, but the adjBIC provided ambiguous support for either the three-class or four-class model. Examination of the parameter estimates for the three-class model showed a major cost of including the C on x path in the model: a substantial increase in standard errors. Although the parameter estimates remain similar in direction and magnitude, numerous estimates that were greater than two standard errors from zero without the C on x path became less than two standard errors from zero with the path included. This may be due to the added complexity of the model, although in the simulations the effects of this path on standard errors were far less. There were no problems with estimation of either three-class model.

Table 6.

Fit statistics for the two, three, and four class regression mixture model testing for heterogeneity in the effects of family resources on academic achievement (reading, math, language).

	2-class	3-class	4-class
C on x path included
Loglikelihood	−70305.656	−70206.870	−70151.507
Parameters	53	76	99
BIC	141075.013	141078.672	141169.175
adjBIC	140906.593	140837.164	140854.579
Class Proportions
Class 1	.276	.224	.177
Class 2	.724	.428	.322
Class 3		.348	.140
Class 4			.360
C on x path excluded
Loglikelihood	−70319.941	−70225.916	−70172.293
Parameters	49	68	87
BIC	141068.588	141046.771	141105.758
adjBIC	140912.879	140830.685	140829.295
Class Proportions
Class 1	.271	.360	.120
Class 2	.729	.226	.375
Class 3		.414	.496
Class 4			.009

C=latent class variable, x=predictor, BIC=Bayesian Information Criterion, adjBIC=adjusted Bayesian Information Criterion; Smaller values indicate better fit; C on x refers to the regression of class membership on x (logistic regression).

Discussion

Regression mixture models are an increasingly popular method for identifying heterogeneity in the effects of a predictor on an outcome in the applied literature. Yet, previous work shows that the standard model is not robust to distributional violations (George, Yang, Jaki, et al., 2013; George, Yang, Van Horn, et al., 2013; Liu & Lin, 2014; Van Horn et al., 2012). Data show that with small samples or small deviations of non-normality, a regression mixture can produce highly inaccurate results (George, Yang, Jaki, et al., 2013; George, Yang, Van Horn, et al., 2013; Jaki et al., under review). It is important to understand the behavior of these models under varying specifications and conditions. The primary aim of the current article was to test an implicit assumption often made when estimating regression mixtures: that independent variables are not related to latent classes. To relax this assumption, we specified a relationship between the latent class variable, C, and the predictor, x. Although we were not substantively interested in the causal relation between x and C (in fact, we caution researchers not to substantively interpret this path unless theoretically meaningful), estimating C on x allows the mean of x to vary across classes and thus relaxes the assumption that the means of x are equal across classes. We tested this path with two types of non-linear effects: 1) a general regression mixture model where heterogeneity was due to unobserved groups that differ in the effects of x on y; and 2) a piecewise model where heterogeneity was due to a curvilinear relationship between x and y where C is completely determined by x. In these simulations, we examined class enumeration and the quality of parameter estimation associated with (wrongly) making the assumption of mean equality.

For the first scenario (where heterogeneity was due to unobserved groups), overall, results indicated that the biggest risk of making the assumption of equal means was a small amount of bias in certain model parameters and high variability on some parameters when there were large differences in the class-specific means of x. This was most evident in estimates of the proportion of observations in each class. The impact of violating the assumption of equal means was verified in an applied example, which showed that the inclusion of the C on x path resulted in only small changes in previously reported parameter estimates. However, including this additional path did come at a cost in the applied example where many standard errors increased dramatically.

Because the regression of latent classes on the independent variable in the model could reflect a piecewise relationship between the predictor and the outcome, rather than heterogeneity in this relationship, the second aim of this article was to show how a piecewise relationship between x and y could be detected in a regression mixture model. This is important because missing a true piecewise relationship and estimating a regression mixture could lead to faulty results – namely, results will indicate the presence of differential effects instead of piecewise relations. In the scenario reported here, the piecewise relationship was not readily evident in graphs of the raw data. It was detected in regression mixture models when the relationship between the latent class and the predictor was included. The first indicator of the piecewise relationship was a very strong relationship between the predictor x and C. Another indication of the piecewise relationship came from plots of the estimated values of y and observed values of x. When the C on x path was included, the piecewise relationship was clearly apparent. This was not the case when C on x was excluded. This result suggests that the inclusion of the C on x path in estimation, along with the examination of respective plots, is an important step in the model checking process. Failure to include the C on x path in a true piecewise model may result in the inaccurate conclusion that there are heterogeneous groups underlying the relationship between x and y.

It is important to note that we recommend a piecewise relationship between x and y be examined prior to estimating any model, including regression mixtures. Whenever a piecewise relationship is obvious in the raw data or there is a strong a priori hypothesis for a piecewise relationship, we do not typically advocate using a regression mixture. Other methods that directly test for a piecewise relationship between x and y are usually better suited for this situation. Conversely, there are other times when a piecewise relationship may not be readily apparent or theory for a piecewise relationship is lacking. Results show that the regression mixture model may have utility for detecting piecewise relationships that can be well characterized by a small number of linear slopes. In the case reported here, the regression mixture model fit the data very well and did not require that the threshold where the two lines cross be specified a priori. A comparison of multiple methods to detect piecewise processes was not the original purpose of this article, so we simply note that, in the case of hidden piecewise relationships, the regression mixture is one reasonable approach for detection; and, more importantly, including the C on x path is a way to ensure that a piecewise relationship will not be confused with heterogeneity of effects.

Put together, these results suggest that when the relationship between C on x is small and probabilistic (such as that in Aim 1), the impact of violating the assumption of equal means is relatively minor. Class proportions may be biased and the variability of estimates may be increased; but, generally speaking, substantive conclusions will not be altered. However, when the relationship between C on x is very strong and deterministic (such as in a piecewise model with a clear decision rule defining classes), the impact of violating the assumption is greater. Without the C on x path, the analyst may incorrectly conclude that there are classes of individuals when, in reality, there is a piecewise relationship.

These findings lend themselves to the following analytic suggestions. First, under conditions where the true relationship between x and y is linear, there is rarely a large risk in excluding the C on x path from the model. Although the simulations also did not show a drawback in estimating this effect when it was zero, the applied analyses did suggest a cost. Parameter estimates were generally consistent with and without the C on x path, but estimates of standard errors were substantially increased with the path in the model. We recommend that regression mixtures should generally be estimated with and without this effect. If the C on x relationship is small, then model results may be more efficient with this effect excluded. We also note that if there are strong piecewise relationships, this should be quite obvious in the strength of the relationship between x and C and through graphical examination. Failure to check for a piecewise process may lead to incorrect interpretation of model, since the assumption of no relationship between C and x makes it impossible to capture a piecewise relationship in the correct manner.

In making this recommendation, it is important to note that we are not necessarily promoting the regression mixture model unconditionally. There are many known limitations to regression mixtures (George, Yang, Jaki, et al., 2013; George, Yang, Van Horn, et al., 2013; Liu & Lin, 2014; Van Horn et al., 2012). In particular, regression mixtures should be seen as a large sample method that is highly sensitive to distributional assumptions (George, Yang, Jaki, et al., 2013; George, Yang, Van Horn, et al., 2013; Jaki et al., under review; Liu & Lin, 2014; Van Horn et al., 2012). The exclusion of the C on x path should be considered as part of a broader model fitting process in which the analyst considers other limitations of the model and takes necessary steps to ensure a proper fitting model. We note that in our applied example, we saw moderate levels of skewness and kurtosis in the outcome distributions. For the purposes of this article, we overlooked this non-normality to be consistent with the original analysis of the data, which was conducted prior to the impact of non-normality in regression mixtures was known. Substantial work has been conducted that examines the impact of non-normality in regression mixtures (George, Yang, Jaki, et al., 2013; George, Yang, Van Horn, et al., 2013; Liu & Lin, 2014) and other finite mixture models (Bauer & Curran, 2003). Multiple alternative specification strategies are now available that address non-normal error terms (George, Yang, Jaki, et al., 2013; George, Yang, Van Horn, et al., 2013). Because we did not test alternative strategies in this article, substantive conclusions based on the applied example should be taken with caution. It is possible that too many classes were derived from the data as an empirical attempt to deal with non-normal errors. Future researchers should take care should be taken to selecting the best fitting model; under conditions where regression mixtures have been shown to perform poorly, an alternative model or specification should be considered. This article focus on this one assumption; data analyst should be aware of the other limitations of this method, as well.

Placed within the larger discussion about estimating the relationship between predictors and outcomes in regression mixture models (Ingrassia et al., 2012; B. O. Muthén & Asparouhov, 2009), these suggestions represent a middle ground. Regression mixtures have typically been estimated without allowing for a relationship between predictor and latent classes. We see the regression of C on x as being a convenient way to relax the assumption that x is constant across C whether or not this path is to be interpreted substantively. This article finds that even when this assumption is violated the models still perform reasonably well unless there are very large differences between classes in the means of x. However, results also suggest that it is important to evaluate this assumption more carefully than has been typical. Finally, although the regression of C on x is one way to relax this assumption, other methods have also been proposed. For example, this could be achieved by regressing x on C (the reverse of the pathway tested in this article) in the model (Ingrassia et al., 2012; Wedel, 2002). Including this path allows for a relationship between x and C and does not imply that x causes heterogeneity in the relationship between x and y. However, this comes at the cost of additional assumptions about the shape of the distribution of x – typically that x is normally distributed after controlling for the latent classes.

This article focused on the assumption of equal means across the independent variable; a related assumption concerns the variances. Although it isn’t obvious from the model specification, preliminary work suggests that even with the inclusion of the C on x path the model still assumes that variances of x are equal across classes. One way to relax this is using the x on C path, which can be implemented using the cluster weighted model of Ingrassia et al (2012). Since heteroscedasticity was not considered in this article, we do not know the consequences of violating this assumption.

This study focused on a relatively small number of conditions in order to understand this one model assumption. We tested the effects of making the assumption that independent variables are not directly related to latent class under relatively optimal conditions: two classes with a 50/50 split in the proportion of observations in each class, a single x variable, and two sample sizes (n=6,000; n=2,000). Our aim was to focus on these rather straightforward scenarios in order to better understand model performance under ideal and realistic conditions in the health and behavioral sciences. However, as with any simulation study, we cannot know whether these results generalize to any particular situation. As the applied example showed, regression mixtures are often less stable with real data than they appear to be in simulations. This would seem to reinforce the recommendation to test the model both with and without the C on x path as part of a model building process.

Regression mixture models are being increasingly used as an approach for identifying unobserved heterogeneity in the relationship between a predictor and an outcome in the applied literature. However, as an exploratory approach, these models can be highly sensitive to distributional and model assumptions (George, Yang, Van Horn, et al., 2013; Van Horn et al., 2012), and it is important to recognize the limitations of the approach before wide-spread application. This study finds that these models are generally robust against small to moderate violations of the assumption of no relation between the independent variable and latent class but also suggests that it is wise to examine this relationship in the model building process

Table 7.

Parameter estimates for the three-class regression mixture model examining heterogeneity in the relationship between family resources and academic achievement

	Model: C on x included			Model: C on x omitted
	Class 1 (22.4%)	Class 2 (42.8%)	Class 3 (34.8%)	Class 1 (22.6%)	Class 2 (41.4%)	Class 1 (36.0%)
C on x				-	-	-
Basic	−.451 (.419)	−.383 (.470)	Ref	-	-	-
Money	−.192 (.274)	.203 (.296)	Ref	-	-	-
Time self	.099 (.277)	−.246 (.397)	Ref	-	-	-
Time family	.178 (.196)	.275 (.221)	Ref	-	-	-
C intercept	−.448 (.374)	.220 (.647)	Ref	−.608(.203)	−.141 (.307)	Ref
Reading
Intercept	465.519 (1.099	485.826 (1.195)*	489.627 (0.582)*	465.594 (1.079)*	486.121 (0.865)*	489.678 (0.545)*
Basic	0.315 (0.889)	1.735 (1.020)	3.612 (1.879)	1.729 (0.929)	−1.050 (0.997)	2.947 (0.850)*
Money	1.682 (1.456)	1.686 (2.059)	1.147 (1.202)	3.696 (1.096)*	2.313 (1.042)*	1.277 (0.795)
Time self	1.375 (1.645)	0.071 (1.876)	−0.293 (0.977)	−0.130 (1.214)	−0.082 (0.855)	−0.383 (0.681)
Time family	−1.899 (1.776)	−0.573 (1.029)	−1.862 (0.863)*	−2.008 (1.220)	−0.444 (0.781)	−1.694 (0.810)*
White	4.561 (0.334)*	4.561 (0.334)*	4.561 (0.334)*	4.562 (0.334)*	4.562 (0.334)*	4.562 (0.334)*
Black	−1.989 (0.365)*	−1.989 (0.365)*	−1.989 (0.365)*	−1.960 (0.366)*	−1.960 (0.366)*	−1.960 (0.366)*
Hispanic	−1.505 (0.626)*	−1.505 (0.626)*	−1.505 (0.626)*	−1.511 (0.622)*	−1.511 (0.622)*	−1.511 (0.622)*
Math
Intercept	472.494 (0.895)*	489.422 (2.008)*	486.482 (1.303)*	472.790 (0.799)*	489.923 (0.922)*	486.197 (0.687)*
Basic	−0.184 (0.618)	−0.467 (0.949)	2.757 (0.693)*	0.390 (0.582)	−0.671 (0.682)	2.699 (0.636)*
Money	0.527 (1.137)	0.512 (0.717)	0.612 (0.906)	2.358 (0.808)*	1.053 (0.648)	0.861 (0.736)
Time self	0.951 (0.992)	1.118 (0.633)	−0.368 (0.991)	−0.058 (0.732)	0.551 (0.558)	−0.530 (0.638)
Time family	−1.123 (1.270)	−1.091 (0.653)	−1.551 (0.953)	−1.244 (0.828)	−0.620 (0.543)	−1.428 (0.640)*
White	2.520 (0.291)*	2.520 (0.291)*	2.520 (0.291)*	2.500 (0.267)*	2.500 (0.267)*	2.500 (0.267)*
Black	−1.820 (0.286)*	−1.820 (0.286)*	−1.820 (0.286)*	−1.791 (0.284)*	−1.791 (0.284)*	−1.791 (0.284)*
Hispanic	−0.950 (0.498)	−0.950 (0.498)	−0.950 (0.498)	−0.990 (0.497)*	−0.990 (0.497)*	−0.990 (0.497)*
Language
Intercept	97.681 (0.405)*	102.501 (0.635)*	99.248 (1.335)*	97.849 (0.376)*	102.484 (0.362)*	99.623 (0.438)*
Basic	0.648 (0.408)	0.213 (0.371)	3.781 (2.948)	0.721 (0.410)	0.182 (0.256)	2.466 (0.586)*
Money	1.004 (0.516)	0.234 (0.553)	0.884 (0.950)	1.444 (0.422)*	0.251 (0.379)	1.415 (0.472)
Time self	−0.097 (0.451)	0.021 (0.397)	−0.216 (0.746)	−0.277 (0.393)	−0.084 (0.313)	−0.656 (0.382)*
Time family	−1.046 (0.550)	−0.580 (0.409)	−1.906 (1.032)	−1.168 (0.444)*	−0.288 (0.314)	−1.294 (0.514)*
White	4.622 (0.173)*	4.622 (0.173)*	4.622 (0.173)*	4.671 (0.160)*	4.671 (0.160)*	4.671 (0.160)*
Black	−2.350 (0.180)*	−2.350 (0.180)*	−2.350 (0.180)*	−2.342 (0.169)*	−2.342 (0.169)*	−2.342 (0.169)*
Hispanic	−1.221 (0.282)*	−1.221 (0.282)*	−1.221 (0.282)*	−1.243 (0.282)*	−1.243 (0.282)*	−1.243 (0.282)*

^*Denotes significance at p<.05;

Ref indicates reference class; C indicates the latent class variable, x represents the predictor