Unique Length-Dependent Biophysical Properties of Repetitive DNA

Abstract

Expansion of a trinucleotide repeat (TNR) sequence is the molecular signature of several neurological disorders. Formation of non-canonical structures by the TNR sequence is proposed to contribute to the expansion mechanism. Furthermore, it is known that the propensity for expansion increases with repeat length. In this work we use calorimetry to describe the thermodynamic parameters (ΔH, TΔS, and ΔG) of the non-canonical stem-loop hairpins formed by the TNR sequences (CAG)_n and (CTG)_n, and also the canonical (CAG)_n/(CTG)_n duplexes, for n = 6–14. Using a thermodynamic cycle, we calculated the same thermodynamic parameters describing the process of converting from non-canonical stem-loop hairpins to canonical duplex. In addition to these thermodynamic analyses, we used spectroscopic techniques to determine the rate at which the non-canonical structures convert to duplex, and the activation enthalpy ΔH^‡ describing this process. We report that the thermodynamic parameters of unfolding the stem-loop (CTG)_n and (CAG)_n hairpins, along with the thermodynamic and kinetic properties of hairpin to duplex conversion, do not proportionally corresponding to the increase of length, but rather show a unique pattern that depends on whether the sequence has an even or odd number of repeats.

Graphical Abstract

INTRODUCTION

Trinucleotide repeat (TNR) expansion has been identified as the molecular basis for numerous neurodegenerative disorders including Friedrich’s ataxia, Myotonic dystrophy, Spinocerebellar ataxias, Fragile X syndrome, Kennedy’s disease, and Huntington’s disease (HD).^1–4 For example, HD is caused by the expansion of a (CAG)_n/(CTG)_n TNR sequence in exon 1 of the huntingtin gene. Healthy individuals have fewer than 35 repeats; 36–39 repeats is a pre-mutation range which can expand further upon transmission to offspring; and the disease state is characterized by 40 or more repeats.⁵

Although the mechanism(s) of TNR expansion are still not fully understood, DNA replication- and DNA repair-dependent mechanisms have been proposed.⁴ In both instances, formation of non-canonical secondary structures, such as stem-loop hairpins, is proposed to contribute to the expansion mechanism. In a replication-dependent expansion, stem-loop hairpin formation is proposed in a polymerase-slippage model^6,7 or a replication-restart model.^8,9 In a repair-dependent event, such as repair of the oxidative DNA lesion 8-oxo-7,8-dihydroguanine (8-oxoG),^10,11 stem-loop hairpins are formed and can be ligated into DNA, which leads to the expansion.¹² In either replication- or repair-dependent expansion, the thermodynamic and kinetic stabilities of the TNR stem-loop hairpins are crucial factors. Expansion is expected when these stem-loop hairpins are stable and persist on a biologically-relevant timescale. In contrast, if the stem-loop hairpins convert to canonical duplex with the complementary DNA, expansion is not expected to occur.

Previous spectroscopic and calorimetric studies of TNR stem-loop hairpins revealed that the thermodynamic stability of these structures depends on both the TNR sequence and the number of repeats.^13–15 Notably, a common procedure in these prior studies was to examine DNA substrates in which the number of TNR repeats was incrementally increased by 5 or 10. While this methodology allows for a large range in the number of TNR repeats, these studies lack the resolution to observe differences that might occur with smaller changes in repeat number.

For this reason, we previously examined the stability of a series of (CTG)_n stem-loop hairpins in which the size of the hairpin was varied in increments of one repeat (within the range n = 6–14).¹⁶ Using spectroscopic techniques and van’t Hoff analysis, we observed a pattern whereby the enthalpic stability (ΔH) of the (CTG)_n stem-loop hairpins generally increases with repeat number; however, instead of increasing linearly with the number of repeats, an apparent stepping is observed. Indeed, ΔH is comparable for the pairs of stem-loop hairpins when n = even and n = odd (throughout this manuscript “odd” is defined as “even + 1”). Notably, a plateau in ΔH was observed with greater than 10 repeats due to the failure of the melting transition to follow a two-state model.¹⁶ Instead of melting directly from stem-loop hairpin to an unstructured form, the DNA exists as a population of structural intermediates throughout the melting transition. Indeed, a limitation of van’t Hoff analysis is the required assumption that the melting transition follows a two-state model. In addition to determining ΔH, our previous structural and biophysical studies showed that when n = odd one repeat overhangs the end of the stem.¹⁶ The presence of this overhang shortens the lifetime of the non-canonical structure and facilitates conversion to the canonical CAG/CTG duplex.

To circumvent the limitation of the model-dependent van’t Hoff analysis used in our previous study, in this work we used differential scanning calorimetry (DSC) to characterize the thermodynamic properties of (CTG)_n stem-loop hairpins (n = 6–14). In addition, we also studied the complementary (CAG)_n stem-loop hairpins (n = 6–14). DSC allows for direct measurement of the heat supplied to or released from a system during a melting transition and provides a model-independent measure of the thermodynamic properties of the stem-loop hairpins.^17,18 Furthermore, in this work we also define the thermodynamic properties of the canonical (CAG)_n/(CTG)_n duplex and the conversion from non-canonical stem-loop hairpins to canonical duplex. In addition to these thermodynamic analyses, we performed kinetic studies to determine the rates at which complementary (CAG)_n and (CTG)_n stem-loop hairpins convert to canonical (CAG)_n/(CTG)_n duplexes, as well as the activation enthalpies (ΔH^‡). We find that the rate of conversion to canonical duplex is significantly faster when n is odd due to a lower ΔH^‡. Taken together, our data provide a thermodynamic and kinetic description of the non-canonical hairpin structures involved in the proposed expansion mechanisms.

EXPERIMENTAL PROCEDURES

Oligonucleotide synthesis and purification

All oligonucleotides were synthesized using standard phosphoramidite chemistry with a BioAutomation MerMade 4 DNA/RNA synthesizer. Oligonucleotides were purified using a Dynamax Microsorb C18 reverse phase HPLC column (10 × 250 mm) according to published procedures.¹⁹ Oligonucleotide concentrations were determined at 90 °C using the molar extinction coefficient estimated for single-stranded DNA²⁰ using a Beckman Coulter DU800 UV-visible spectrophotometer equipped with a Peltier thermoelectric device. The identity of the oligonucleotides was confirmed by electrospray ionization mass spectrometry.

Differential scanning calorimetry (DSC) analysis

Calorimetric experiments were performed using a TA Instruments Nano DSC III. The (CTG)_n sequences were at concentrations of 50 μM and the (CAG)_n sequences were at concentrations of 100 μM. All oligonucleotides were suspended in 20 mM sodium phosphate, 100 mM NaCl, pH 7.0. Both the oligonucleotide samples and reference buffer sample were degassed in vacuo for 15 min at 25 °C before analysis. All data were recorded with TA Instrument Nano DSCRun software version 4.2.6. Data were obtained by continuously monitoring the excess power required to maintain both sample cell and reference cell at the same temperature. The samples were heated from 0 °C to 105 °C followed by cooling from 105 °C to 0 °C, both at 1.0 °C/min. The sample equilibrated for 10 min at 0 and 105 °C between each cooling and heating cycle, respectively. The resulting thermograms display excess heat capacity as a function of temperature. A total of 12 thermograms were obtained for each DNA sequence. A buffer reference was analyzed using the same procedure described above and the thermograms were corrected using this background. Further analyses were performed on TA NanoAnalyze software version 3.5.1 and thermodynamic parameters were obtained from the forward scans. The thermograms were normalized for concentration and a baseline correction was performed using a 5^th order polynomial baseline (Figure S1). The ΔH was obtained by integrating the area under the thermogram curve. The melting temperature was determined as the T_max of each transition. In cases where there is overlap between the lower and higher temperature transitions, the data were deconvoluted using Origin software, assuming each transition follows the two-state model of unfolding,²¹ to determine ΔH for the transition of interest (Figure S2).

A flash-cooling experiment was also performed for (CTG)₉. The sample was heated to 90 °C for 5 min and immediately place in an ice/water bath for at least 30 min before loading into the DSC sample cell, which was pre-equilibrated at 4 °C.

Native polyacrylamide gel electrophoresis

Following analysis by DSC, the samples were retrieved and 15 μL of each sample was added to 30,000 cpm of the corresponding dried radiolabeled oligonucleotide. In all cases, the amount of radiolabeled DNA is less than 5 pmol and the change in concentration is neglible. The samples were heated at 105 °C for 15 min and then the temperature was decreased at a rate of 1 °C/min to the final temperature of 10 °C. Fifteen μL of native loading dye (15 % Ficoll, 0.25 % bromophenol blue and 0.25 % xylene cyanol) were added and 3,000 cpm of each sample was resolved by 12 % native polyacrylamide gel electrophoresis (PAGE), where the gel was pre-run at 100 V at 4 °C for at least 1 h, and the gel was run at 35 V at 4 °C for 12 h and visualized by Phosphorimagery.

Kinetics of hairpin to duplex conversion

The (CTG)_n and (CAG)_n oligonucleotides (2 μM each) were separately incubated at 37 °C for 20 min followed by mixing of 162 μL of each oligonucleotide. Using a Beckman Coulter DU800 UV-visible spectrophotometer the absorbance at 260 nm was monitored as a function of time while the sample temperature was maintained at 37 °C. Data were collected until the absorbance remained constant for at least 10 min. The absorbance values were normalized such that the Y-axis represents the fraction of hairpin remaining.²² The data were fit with KaleidaGraph software to a second-order equation²³ that describes the rate of duplex formation from two equimolar complementary hairpins with a 15 s time correction²⁴ to account for the time lag between mixing the two oligonucleotides and beginning to monitor the absorbance.

$$I=I_0\frac{{\epsilon }_{\mathit{duplex}}}{{\epsilon }_{\mathit{CTG}}+{\epsilon }_{\mathit{CAG}}}+(1-\frac{{\epsilon }_{\mathit{duplex}}}{{\epsilon }_{\mathit{CTG}}+{\epsilon }_{\mathit{CAG}}})(\frac{I_0}{1+[I_0/({\epsilon }_{\mathit{CTG}}+{\epsilon }_{\mathit{CAG}}]k(t-15)})$$ (1)

where I is the absorbance at any time point, I₀ is the absorbance at the start of the reaction, ε_duplex, ε_CTG and ε_CAG are the ε₂₆₀ for the CAG/CTG duplex, CTG and CAG hairpins, respectively, k is the rate constant, and t is the reaction time in seconds. At least 5 replicate experiments were performed for each hairpin to duplex conversion and a representative graph of hairpin fraction remaining versus time is provided.

The activation enthalpy (ΔH^‡) describing hairpin to duplex conversion can be determined by performing the same experiment described above at multiple temperatures, where all of the temperatures are below the melting temperature of the hairpin. For these experiments the (CTG)_n and (CAG)_n oligonucleotides were diluted to the same concentration such that after mixing of the complementary sequences, the final UV-visible absorbance was ~0.3–0.4 (~1–2 μM). The resulting data were fit using the Eyring equation to determine ΔH^‡.25,26

$$ln\frac{k}{T}=-\frac{\mathrm{\Delta }{H}^{‡}}{R}•\frac{1}{T}+ln\frac{k_B}{h}+\frac{\mathrm{\Delta }{S}^{‡}}{R}$$ (2)

where k is the rate constant, T is the absolute temperature, R is the gas constant, k_B is the Boltzmann constant, h is Planck’s constant, and ΔH^‡ and ΔS^‡ are the activation enthalpy and activation entropy, respectively.

RESULTS AND DISCUSSION

In this work we used a series of (CAG)_n and (CTG)_n DNA oligonucleotides where n = 6–14 to provide a comprehensive calorimetric and thermodynamic analysis of: (1) the stability of non-canonical stem-loop hairpins formed by the single-stranded oligonucleotides, (2) the stability of canonical (CAG)_n/(CTG)_n duplexes, and (3) the factors affecting the conversion of the non-canonical structures to canonical duplex. In addition, we performed a spectroscopy-based kinetic analysis of the rates at which the non-canonical stem-loop hairpins convert to canonical duplexes and report ΔH^‡ for this process.

DSC Characterization of (CAG)_n and (CTG)_n Stem-Loop Hairpins

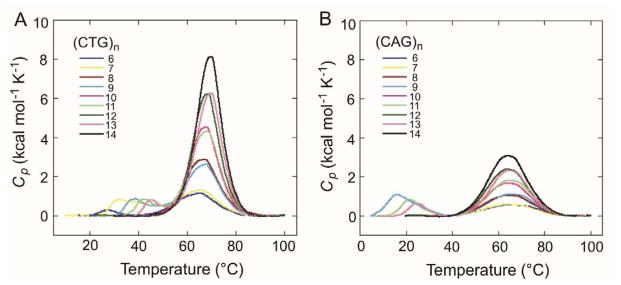
Using DSC we obtained thermograms characterizing the melting of the (CTG)_n and (CAG)_n samples under physiologically relevant salt conditions (Figure 1). In the thermograms excess heat capacity is plotted as a function of temperature. As seen for the (CTG)_n sequences (Figure 1A), when n = 6–14, a transition centered at ~65 °C is observed in each thermogram; furthermore, when n = 6, 7, 8, 9, 11, or 13, a second transition is observed and is centered at 25–45 °C. In contrast, when n = 10, 12, or 14 this lower temperature transition is not observed. Similar behavior is observed for the (CAG)_n sequence when n = 6–14 (Figure 1B). When n = 6–14, all thermograms for (CAG)_n display a transition centered at ~65 °C, and only when n = 9, 11, or 13, a lower temperature transition is observed and is centered at 15–25 °C. Although previous studies only reported single transition for (CTG)_n or (CAG)_n hairpins of similar length,¹⁵ this work did not include repeat number of n = 7 and 9, where the lower temperature transitions are most prevalent in our study.

Figure 1.

DSC thermograms for (A) (CTG)_n and (B) (CAG)_n sequences where n = 6–14. Conditions are 50 μM (CTG)_n or 100 μM (CAG)_n in 20 mM sodium phosphate, 100 mM NaCl, pH 7.0.

Electrophoretic Mobility of (CAG)_n and (CTG)_n by Native PAGE

To determine whether the two transitions observed by DSC are due to the melting of two different structures, we performed native PAGE analysis for both (CAG)_n and (CTG)_n (Figure 2). For (CTG)_n two distinct species (labeled species A and B) are observed when n is odd and the relative intensity of the two species varies depending on n (Figure 2A). While species B is prevalent when n is odd, it is much less prevalent when n is even. Similar results were reported previously for (CTG)_n when n = 2–10.²⁷ For (CAG)_n we observe only one species by native PAGE, except n = 13 when two species are observed (Figure 2B).

Figure 2.

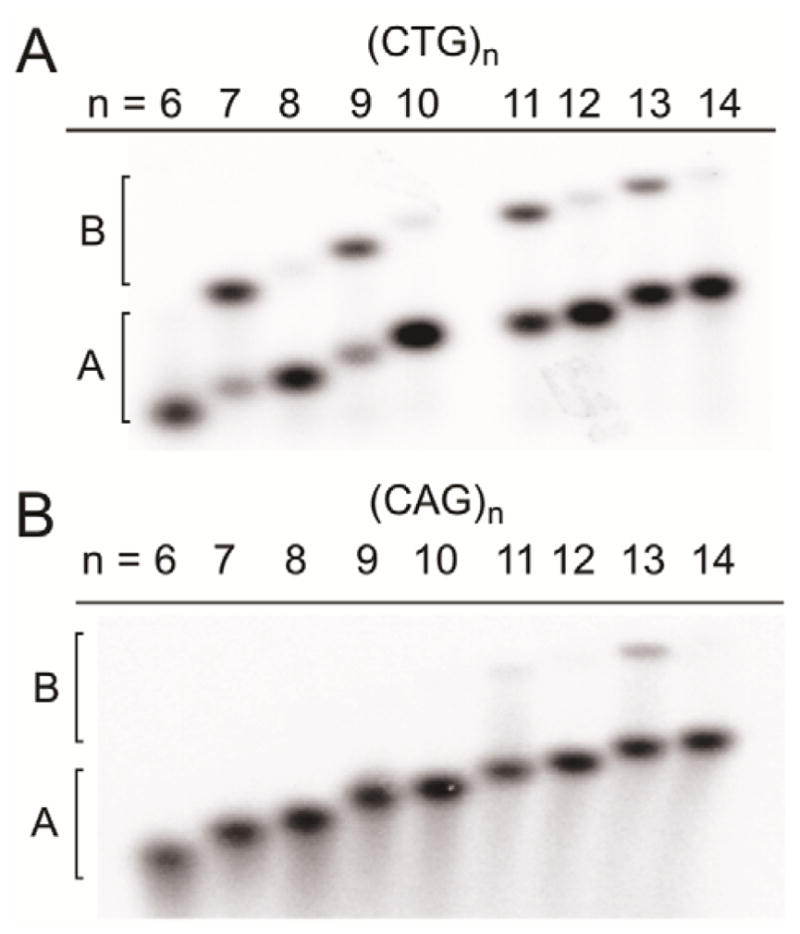
Native PAGE characterization for (A) (CTG)_n sequences (n = 6–14) at 50 μM; (B) (CAG)_n sequences (n = 6–14) at 100 μM. In all cases DNA was in 20 mM sodium phosphate, 100 mM NaCl, pH 7.0.

Using (CTG)₇ as a representative sample, the electrophoretic mobility of species A and B were compared to authentic standards. Native PAGE reveals that species A of (CTG)₇ co-migrates with a (CTG)₇ stem-loop hairpin control while species B co-migrates with a (CTG)₇/(CAG)₇ canonical heteroduplex control (Figure S3). As described previously by Lam, we assign species B as (CTG)₇/(CTG)₇ homoduplex due to its slower electrophoretic mobility relative to (CTG)₇ stem-loop hairpin.²⁷ Further analysis showed that the amount of homoduplex increases as a function of both oligonucleotide and salt concentration (Figure S3). It is noteworthy that using a flash-cooling annealing procedure prior to native PAGE or DSC, a process which is expected to trap any kinetically favored species, did not influence the amount of stem-loop hairpin or homoduplex (data not shown). Consistent with this result, previous studies using the dimerization initiation site of HIV-1 genomic RNA showed that concentration of the RNA, rather than the annealing procedure, is the major parameter dictating stem-loop hairpin formation.²⁸

Previous work from our¹⁶ and other laboratories^13,15,22 has shown that (CTG)_n and (CAG)_n stem-loop hairpins show very little change in melting temperature (T_m) as a function of length. A lack of dependence on length is also seen for the higher temperature transitions in DSC; this observation suggests that the transitions centered at ~65 °C are due to the melting of the stem-loop hairpins. Thus, the length-dependent transitions at lower temperature are ascribed to melting of homoduplexes. Shown in Table 1 are the T_m values obtained by DSC for the homoduplexes and stem-loop hairpins. For the (CTG)_n sequences the T_m values of the stem-loop hairpins vary from 62.8–69.2 °C. The T_m values for the homoduplexes increase with n over a range of ~26–45 °C. For the (CAG)_n sequences there is very little variation in the T_m of the stem-loop hairpins when n = 6–14; the average T_m is 64.3 °C. The T_m for (CAG)_n homoduplexes increase as a function of length over a range of ~16–25 °C. It is noteworthy that due to the very low melting temperature of the short (CAG)_n homoduplexes, these structures likely melt due to the heat generated during electrophoresis and explains why no homoduplex species are observed by native PAGE characterization but the species is observed by DSC.

Table 1.

DSC-Derived Melting Temperatures and Thermodynamic Parameters for (CTG)_n and (CAG)_n Stem-Loop Hairpins.¹,²

Sequence	Tm Hairpin (°C)	Tm Homoduplex (°C)	ΔH (kcal mol−1)	TΔS3 (kcal mol−1)	ΔG3 (kcal mol−1)
(CTG)6	65.4	27.8	22.4 ± 0.7	20.4 ± 0.6	1.9 ± 0.2
(CTG)7	66.1	32.0	24.9 ± 2.3	22.8 ± 2.1	2.1 ± 0.2
(CTG)8	67.3	-	48.1 ± 1.4	43.7 ± 1.2	4.3 ± 0.1
(CTG)9	67.7	38.7	45.0 ± 1.0	40.9 ± 0.9	4.1± 0.1
(CTG)10	68.2	-	67.7 ± 1.8	61.4 ± 1.6	6.2 ± 0.1
(CTG)11	68.5	42.0	64.7 ± 1.2	58.6 ± 0.9	6.0 ± 0.1
(CTG)12	68.8	-	86.4 ± 2.5	78.4 ± 2.2	8.0 ± 0.2
(CTG)13	70.1	45.1	82.1 ± 1.0	74.1 ± 0.9	7.9 ± 0.1
(CTG)14	70.0	-	108 ± 1	97.3 ± 0.6	10.4 ± 0.1
(CAG)6	64.3	-	14.2 ± 0.6	13.1 ± 0.5	1.1 ± 0.1
(CAG)7	64.1	-	15.1 ± 1.1	13.9 ± 1.0	1.2 ± 0.1
(CAG)8	63.9	-	25.6 ± 0.6	23.5 ± 0.6	2.1 ± 0.1
(CAG)9	65.2	16.4	25.0 ± 2.7	22.9 ± 2.4	2.1 ± 0.3
(CAG)10	64.1	-	37.4 ± 1.1	34.4 ± 0.9	3.0 ± 0.1
(CAG)11	64.3	21.6	38.6 ± 3.0	35.3 ± 2.8	3.2 ± 0.3
(CAG)12	64.0	-	50.1 ± 1.3	45.9 ± 1.2	4.0 ± 0.1
(CAG)13	65.0	24.5	49.8 ± 1.5	45.6 ± 1.2	4.2 ± 0.1
(CAG)14	64.1	-	62.6 ± 1.4	57.7 ± 1.2	5.1 ± 0.1

¹In 20 mM sodium phosphate, 100 mM NaCl, pH 7.0.

²Errors represent standard deviation from the analysis of three scans of a single sample preparation.

³Values at 37 °C.

For both (CTG)_n and (CAG)_n, the T_m of their homoduplex forms increases as a function of length, similar to the canonical heteroduplex. In contast, the T_m of their hairpin forms show either weak length-dependence for (CTG)_n hairpins or no length-dependence for (CAG)_n hairpins, a phenomenon which has been observed previously.^15,16 Lah and coworkers showed that incorporation of a 4-base loop into a canonical duplex, generating a hairpin with a 4-base loop, greatly enhanced thermal stability of the duplex.²⁹ We therefore propose that the 4-base loop region of our hairpins dictates the T_m of the hairpins and is why the T_m of the hairpins is independent of length.

Determining the Nature of Homoduplex Melting

Here we are particularly interested in the thermodynamic parameters describing melting of the stem-loop hairpins, which are the transitions centered at ~65 °C. While the thermodynamic parameters of the homoduplex are not our focus per se, the nature of homoduplex melting could affect our analysis of the transition centered at ~65 °C. In order to determine thermodynamic parameters from a DSC thermogram, the concentration of the species undergoing the melting transition must be known.

We envision two possible scenarios to describe homoduplex melting: (1) the homoduplex converts to a stem-loop hairpin; the stem-loop hairpins subsequently melt to unstructured single-stranded DNA at the transition centered at ~65 °C, or (2) the homoduplex melts directly to unstructured single-stranded DNA. If scenario 1 is followed, the transition at ~65 °C would correspond to melting of the entire population of DNA in the sample. In contrast, if scenario 2 is followed and the homoduplex melts directly to unstructured single-stranded DNA, the transition at ~65 °C would not involve the entire population but rather some fraction of the entire DNA population. To determine the nature of homoduplex melting, we performed DSC and native PAGE experiments as a function of concentration for (CTG)₉ (Figure S4). Native PAGE was used to obtain the percentage of stem-loop hairpin and homoduplex present at each concentration. Since both the percentages of stem-loop hairpin and homoduplex are concentration-dependent, based on the amount of stem-loop hairpin and homoduplex, we obtained values for ΔH corresponding to stem-loop hairpin melting using the DSC thermograms and assuming either scenario 1 or scenario 2 (Figure S4). It is known that ΔH for stem-loop hairpin melting would be independent of concentration,¹⁷ which is the data we obtain assuming scenario 1 is followed; thus, we conclude that scenario 1 is followed and the homoduplex converts to a stem-loop hairpin first. Therefore, the remaining DSC thermograms were analyzed assuming that the transition at ~65 °C corresponds to melting of a stem-loop hairpin for the entire population of DNA.

Analysis of DSC Thermograms for (CAG)_n and (CTG)_n Stem-Loop Hairpins

The assignment of the two thermal transitions in DSC allows us to further analyze the thermodynamic parameters for unfolding of (CAG)_n and (CTG)_n stem-loop hairpins. It is straightforward to analyze thermodynamic parameters for samples with only a single transition or with two well-separated transitions. For samples with overlapped transitions in the thermograms, it is best to deconvolute the experimental data into three transitions, assuming each of the transitions follows the two-state model of unfolding (Figure S2).²¹ Notably, ΔH for the hairpin to unstructured transition remains the same regardless of the number of transitions used during the deconvolution (Figure S2). Based on the deconvolution results, it is clear that for samples with overlapped transitions, all of the homoduplex has been converted to hairpin before the T_m of the hairpin itself, so the higher temperature transition contains the entire concentration of DNA and simplifies the analysis of thermodynamic parameters. The thermodynamic parameters describing the transition from stem-loop hairpin to unstructured single strand are summarized in Table 1. Notably, the reported values describe the process of melting from stem-loop hairpin to unstructured single strand and ΔH, TΔS, and ΔG are all positive values. We observe that when n is the same, the (CTG)_n stem-loop hairpins are enthalpically (ΔH) stabilized and entropically (TΔS) destabilized relative to the (CAG)_n stem-loop hairpins, as the values for ΔH and TΔS are greater for the (CTG)_n stem-loop hairpins. It can also be seen that (CTG)_n stem-loop hairpins with n = even have similar thermodynamic parameters, as when n = odd [i.e., (CTG)₆ and (CTG)₇ have similar thermodynamic parameters, as do (CTG)₈ and (CTG)₉, (CTG)₁₀ and (CTG)₁₁, and (CTG)₁₂ and (CTG)₁₃] (Figure 3). The same pattern is observed for the (CAG)_n stem-loop hairpins (Figure 3). These results can be explained based on our previous structural characterization of the (CTG)_n hairpins.¹⁶ For hairpins with n = even and n = odd, they both contain 4 bases in the loop and the same numbers of C•G base pairs and T•T mismatches in the stem region. The only difference is that when n = odd, a single CTG repeat overhangs at either 3′ or 5′ end of the hairpin. These 3 bases are unstructured and do not contribute to the stability of the hairpin. Finally, while n = even and n = odd hairpins have similar thermodynamic parameters, there is an overall increase in ΔH, ΔS, and ΔG as a function of repeat length across the series n = 6–14.

Figure 3.

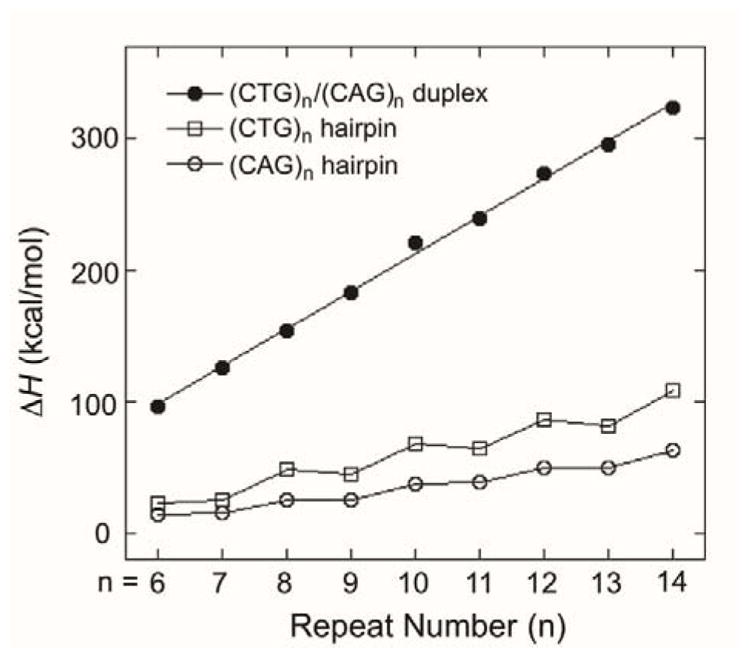
Enthalpy change (ΔH) for stem-loop hairpin (CTG)_n or (CAG)_n and duplex (CTG)_n/(CAG)_n (n = 6–14) to unstructured single-stranded DNA transition.

With this understanding of the length dependence of hairpin thermodynamics, we can return to explain why (CTG)₆ and (CTG)₈ showed a low temperature transition by DSC. Because of their small repeat number, these hairpins are not as thermodynamically stable as the hairpins with a greater number of repeats. We propose that some population of the short hairpins convert to homoduplex and melting of this homoduplex represents the low temperature transition. This analysis is also consistent with our kinetic data (vida infra) that show the conversion of short hairpins to duplex is kinetically favored relative to longer hairpins.

In order to confirm the validity of our analysis of the thermograms containing overlapping transitions, we also looked for experimental conditions where no or minimal homoduplex was observed. It is known that at low concentrations, (CAG)_n and (CTG)_n will form predominantly intramolecular stem-loop hairpins, as confirmed by the hairpin control in our native gel (Figure S3). We also found that the homoduplex population was decreased in low salt buffer conditions. Therefore, we repeated the calorimetry experiments for (CAG)_n and (CTG)_n under conditions where the homoduplex population is significantly reduced, as shown by native gel electrophoresis (20 mM potassium phosphate, pH 7.2) (Figure S5). As expected, we only observed a single transition for all samples, while the even/odd pattern remains as indicated by the almost superimposed thermograms for the even and odd number of hairpins (Figure S6, S7). Due to the reduced salt concentration, both the T_m and ΔH values derived from the stem-loop hairpin to unstructured transitions decrease compared to previous analyses (Table S1). Both sets of the calorimetry results suggest that the change in ΔH for hairpin melting is not only proportional to the number of CAG or CTG repeats, but also depends on whether the number is even or odd. Although the low salt conditions used in this experiment are less biologically relevant compared to the experiments described above, the results provide support for our analysis of thermograms with overlapping transitions.

Our results show that (CTG)_n stem-loop hairpins are enthalpically and thermodynamically more stable than the (CAG)_n stem-loop hairpins with the same number of repeats. The notable difference between these stem-loop hairpins is the presence of T•T or A•A mismatches in the stem. Mitas has shown that the T•T mismatches in (CTG)_n stem-loop hairpins are well stacked and can form two hydrogen bonds, while the A•A mismatches in (CAG)_n are less well stacked, and no hydrogen bonds are formed in the mismatch.³⁰ Furthermore, Arnold and co-workers showed by ¹H-NMR that in canonical duplex, the adenines in an A•A mismatch are tilted and pushed apart to avoid overlap of the exocyclic amino groups.³¹ In contrast, the T•T mismatch results in little distortion of the bases or sugar-phosphate backbone. Both of these observations are consistent with the increased stability of (CTG)_n stem-loop hairpins relative to the corresponding (CAG)_n hairpins.

Thermodynamics of Stem-Loop Hairpin to Duplex Conversion

In addition to the thermodynamic characterization of the (CAG)_n and (CTG)_n stem-loop hairpins, we are interested in the thermodynamic parameters describing conversion of the non-canonical stem-loop hairpins to canonical duplex when the two complementary hairpins are combined. However, the DSC experiments do not allow us to monitor the process directly; a significant amount of the stem-loop hairpins convert to duplex during the dead time of the experiment. Instead, thermodynamic parameters for the stem-loop hairpin to duplex conversion process were calculated using a thermodynamic cycle, a procedure which was validated previously by Breslauer and co-workers for Ω-DNA structures.³² In order to utilize this cycle, the thermodynamic parameters for melting of (CAG)_n/(CTG)_n duplexes are required, and these values were determined by DSC. The thermograms for (CAG)_n/(CTG)_n duplexes all show a single transition where the T_m and ΔH increase as a function of length (Figure 3) as compared to the stepwise increase of (CTG)_n and (CAG)_n hairpins. Indeed, a linear increase with repeat length is observed for all the thermodynamic parameters (ΔH, TΔS, and ΔG) as expected for duplexes of increasing length (Figure S8, Table S2).

A thermodynamic cycle was used to calculate the thermodynamic parameters describing the stem-loop hairpin to duplex conversion (Table 2, HFigure 4). It is noteworthy that the values for Δ, TΔS, and ΔG are all negative, indicating the process is enthalpically and thermodynamically favored but entropically disfavored. Importantly, both ΔH and TΔS display an oscillating pattern across the range of sequence lengths; when n = odd the values are more negative than when n = even. This observation can be rationalized by structural differences in the stem-loop hairpins. When n = odd, one repeat overhangs the end of the stem, and this overhang provides three additional base pairs and additional base stacking when duplex is formed. However, this enthalpic stabilization is not expected for stem-loop hairpins when n = even; in the latter case, the stem has a blunt end with no overhang. Nevertheless, for all values of n, the ΔH term is always more negative than TΔS. Thus, the process of stem-loop hairpin to duplex conversion is enthalpically driven. Converting the mismatches in the stem and the unpaired bases in the loop to well-matched base pairs in duplex provides the enthalpic driving force. The values for ΔG also show an oscillating pattern depending on whether n = even or n = odd, although the difference is much less pronounced than for ΔH and TΔS. Importantly, as n increases, the duplex is increasingly more thermodynamically stable than the stem-loop hairpins.

Table 2.

Thermodynamic Parameters for Conversion of (CAG)_n and (CTG)_n Stem-Loop Hairpins to (CAG)_n/(CTG)_n Duplex.¹,²

n	ΔH (kcal mol−1)	TΔS3 (kcal mol−1)	ΔG3 (kcal mol−1)
6	−59.4 ± 3.2	−51.2 ± 2.8	−8.2 ± 0.4
7	−86.0 ± 2.8	−73.6 ± 2.5	−12.4 ± 0.3
8	−80.7 ± 2.3	−66.7 ± 2.1	−13.9 ± 0.2
9	−113 ± 4	−94.5 ± 3.2	−18.7 ± 0.5
10	−116 ± 5	−94.0 ± 3.9	−21.8 ± 1.5
11	−135 ± 3	−109 ± 3	−25.9 ± 2.2
12	−138 ± 7	−109 ± 6	−28.1 ± 1.0
13	−163 ± 5	−132 ± 5	−31.3 ± 0.7
14	−154 ± 8	−121 ± 7	−32.7 ± 1.2

¹In 20 mM sodium phosphate, 100 mM NaCl, pH 7.0.

²Errors represent standard deviation from the analysis of three scans of a single sample preparation.

³Values at 37 °C.

Figure 4.

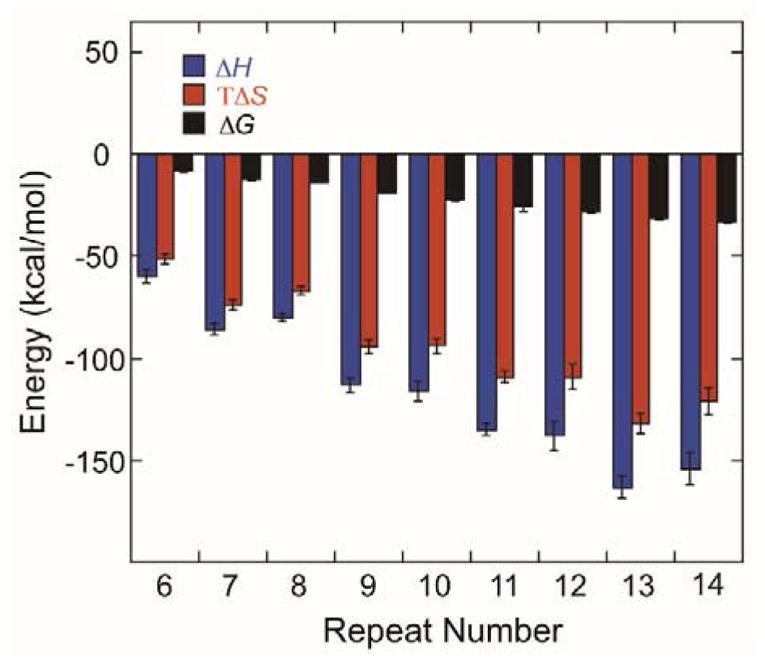
Thermodynamic parameters for conversion of stem-loop hairpins to duplex calculated via a thermodynamic cycle. Entropy (TΔS) and free energy (ΔG) were determined at 37 °C.

In light of our observation that the canonical duplex is increasingly thermodynamically favored over stem-loop hairpins as the repeat length increases, the question arises whether this conversion will proceed within a biologically-relevant time scale. Therefore, we also characterized the kinetic parameters describing the stem-loop hairpin to duplex conversion.

Kinetic Analysis of Stem-Loop Hairpin to Duplex Conversion

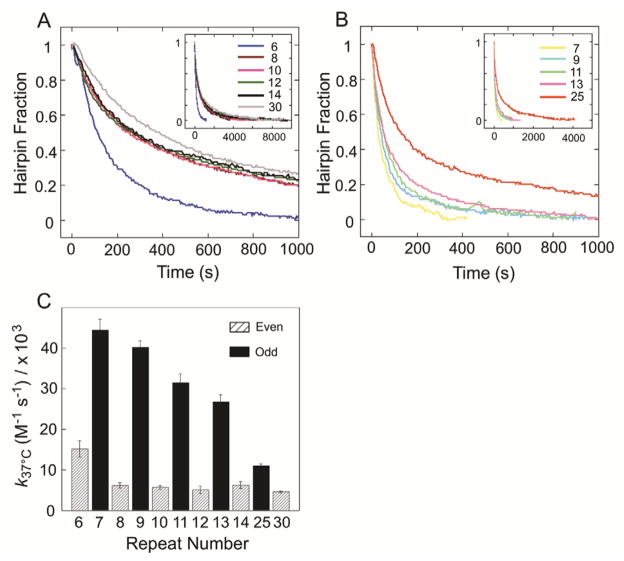
In order to determine how repeat number influences the rate at which non-canonical stem-loop hairpins convert to duplex, we performed a spectroscopy-based kinetic analysis. In these experiments, complementary (CAG)_n and (CTG)_n stem-loop hairpins were combined at 37 °C and the absorbance at 260 nm was monitored as a function of time. The data were fit to a second-order equation to obtain the rate of stem-loop hairpin to duplex conversion (Table 3).²³ Importantly, at the DNA concentrations used for these kinetic analyses, no homoduplex was observed by native PAGE, and the starting species were exclusively stem-loop hairpins (data not shown). Over the range of n = 6–14 we observe that when n is odd, the stem-loop hairpins convert to duplex faster than when n is even (Figure 5). Furthermore, when n = even there is a statistically significant decrease from n = 6 to n = 8, but with continued increase in n, the rate remains the same (Figure 5A,C). When n = odd the rate of conversion to duplex decreases with n (Figure 5B,C). To determine whether the rates of hairpin to duplex conversion reach a lower limit with increasing repeats, especially when n = even, we measured the rate at which (CAG)₂₅ and (CTG)₂₅, and also (CAG)₃₀ and (CTG)₃₀, stem-loop hairpins convert to duplexes. When n = 25, a significant decrease in rate for hairpin to duplex conversion is observed relative to n = 7, 9, 11, 13; however when n= 30, only a small decrease in rate was observed relative to when n = 8, 10, 12, or 14 (Table 3, Figure 5C).

Table 3.

Rate and Activation Enthalpy for Stem-Loop Hairpin to Duplex Conversion at 37 °C.¹

n	k37°C2 (M−1 s−1) / × 103	ΔH‡ 3 (kcal mol −1)
6	15.2 ± 2.0	29.1 ± 3.2
7	44.4 ± 2.7	6.76 ± 0.57
8	6.2 ± 0.6	-
9	40.2 ± 1.6	-
10	5.7 ± 0.4	35.8 ± 4.1
11	31.4 ± 2.3	21.4 ± 3.6
12	5.1 ± 0.9	-
13	26.8 ± 1.7	-
14	6.3 ± 0.8	41.0 ± 5.1
25	11.0 ± 0.5	-
30	4.6 ± 0.2	-

¹In 20 mM sodium phosphate, 100 mM NaCl, pH 7.0.

²Errors represent standard deviation from a minimum of three experiments.

³Errors represent the uncertainty derived from fitting the rate constants at four different temperatures to the Eyring equation.

Figure 5.

Kinetic characterization of stem-loop hairpin (CTG)_n and (CAG)_n to duplex (CTG)_n/(CAG)_n (n = 6–14, 25, 30) conversion for (A) n = even (B) n = odd at 37 °C. Insets show results in longer time scale. Reaction was monitored by UV absorbance at 260 nm. Each single strand was present at 2 μM in 20 mM sodium phosphate, 100 mM NaCl, pH 7.0. (C) Plot of rate constant k at 37 °C as a function of repeat number.

The conversion from stem-loop hairpins to duplex is proposed to involve two possible mechanisms: interaction of the complementary stem-loop hairpins by either the loop regions or the stem termini.^28,33 We previously showed that both mechanisms are utilized when (CAG)₁₀ and (CTG)₁₀ stem-loop hairpins convert to duplex.³³ We also previously reported that the rate of formation of (CAG)₁₀/(CTG)₁₁ duplex is 4-fold faster than formation of the (CAG)₁₀/(CTG)₁₀ duplex.¹⁶ We postulated that the unpaired nucleobases of the overhanging repeat of the (CTG)₁₁ stem-loop hairpin facilitated interactions at the termini of the stems and this additional triplet overhang is responsible for the faster conversion to duplex. In the current work, we show that when both stem-loop hairpins have n = odd, the rate of conversion to duplex is faster than when n = even. We propose that this faster rate of duplex formation is aided by the presence of the overhangs on the stem-loop hairpins. In detail, the three-base overhang for hairpins with odd number of repeats is able to form three base pairs to initiate the hairpin to duplex conversion, and formation of such base pairs will facilitate the breaking of the hydrogen bonds in the stem region of the hairpins. This facilitation provides a lower energy transition state for hairpin to duplex conversion. This facilitation is not present for even number repeat hairpins without the overhang.

By conducting similar kinetics experiments as a function of temperature, we determined the activation enthalpy (ΔH^‡), which is used to characterize the transition state during the process of converting from the non-canonical stem-loop hairpins to canonical duplex (Figure S9). The error associated with this experiment is large; thus, ΔH^‡ are not reported for all values of n, but rather for n = 6, 7, 10, 11 and 14 (Table 3). For both n = even and n = odd, the values of ΔH^‡ increase as a function of n. This result is consistent with the rates of stem-loop hairpin to duplex conversion obtained at 37 °C where the rates decrease as a function of n both when n = even and n = odd. Indeed, this increase in ΔH^‡ provides a potential rationale for the propensity of longer TNR sequences to expand – the non-canonical stem-loop hairpins persist rather than convert to canonical duplex. Besides, the ΔH^‡ determined for each hairpin-to-duplex conversion is less than the total enthalpy required for melting the (CTG)_n and (CAG)_n stem-loop hairpins (Table 1,3). This observation confirms our previous proposal that the conversion from stem-loop hairpins to canonical duplex does not require the stem-loop hairpins to be denatured globally;^32,34 rather, the structured stem-loop hairpins interact via the loop and/or stem regions to convert to duplex.

CONCLUSION

In summary, our results reveal differences for both (CAG)_n and (CTG)_n stem-loop hairpins depending on whether n = even or n = odd; differences in the thermodynamic stability of the non-canonical stem-loop hairpins, rate of conversion to canonical duplex, and ΔH^‡ were observed (Figure 6A). The conversion of hairpin to duplex is thermodynamically and kinetically more favorable for n = odd, as indicated by the more stabilized duplex ΔH_H→D and lower activation enthalpy ΔH^‡ when compared to n = even (Figure 6A). As a result of the even/odd pattern, changing the length of hairpins does not linearly influence the biophysical properties of either stem-loop hairpin unfolding or the hairpin-to-duplex conversion. However, within the even (n = 6, 8, 10, 12, 14) or odd (n = 7, 9, 11, 13) series, in other words, by increasing the repeat number n by 2, the hairpin-to-duplex conversion is thermodynamically more favorable but kinetically unfavorable as evidenced by the more stabilized duplex ΔH_H→D but higher ΔH^‡ (Figure 6B). Taken together, our analyses of length dependence of (CTG)_n and (CAG)_n hairpin related thermodynamic and kinetic properties may contribute to the understanding of the role of non-canonical structures in TNR expansion and should be considered when evaluating proposed mechanisms for expansion.

Figure 6.

Length dependence of ΔH for the conversion of stem-loop hairpins to canonical duplex. (A) Comparison between even and odd hairpins and (B) comparison among even or odd series.