Mapping 3D Strains with Ultrasound Speckle Tracking: Method Validation and Initial Results in Porcine Scleral Inflation

Abstract

This study aimed to develop and validate a high frequency ultrasound method for measuring distributive, 3D strains in the sclera during elevations of intraocular pressure. A 3D cross-correlation based speckle-tracking algorithm was implemented to compute the 3D displacement vector and strain tensor at each tracking point. Simulated ultrasound radiofrequency data from a sclera-like structure at unde-formed and deformed states with known strains were used to evaluate the accuracy and signal-to-noise ratio (SNR) of strain estimation. An experimental high frequency ultrasound (55 MHz) system was built to acquire 3D scans of porcine eyes inflated from 15 to 17 and then 19 mmHg. Simulations confirmed good strain estimation accuracy and SNR (e.g., the axial strains had less than 4.5% error with SNRs greater than 16.5 for strains from 0.005 to 0.05). Experimental data in porcine eyes showed increasing tensile, compressive, and shear strains in the posterior sclera during inflation, with a volume ratio close to one suggesting near-incompressibility. This study established the feasibility of using high frequency ultrasound speckle tracking for measuring 3D tissue strains and its potential to characterize physiological deformations in the posterior eye.

INTRODUCTION

Elevated intraocular pressure (IOP) is a primary risk factor for glaucoma, the second leading cause of blindness worldwide.²⁵ Although the relationship between glaucoma progression and IOP elevation is not completely understood, mechanical insults are expected to play an important role.¹ A clinical hallmark of glaucoma is the excavation of the lamina cribrosa, a connective tissue within the optic nerve head (ONH) that spans the scleral canal and supports the retinal ganglion cell axons when they turn and exit the eye on their way to the visual cortex. Previous computational studies predicted that scleral modulus could significantly impact the mechanical insults experienced by the lamina cribrosa during IOP elevations.^20,27 These predictions have motivated many recent studies that aim to characterize the complex mechanical behavior of the posterior sclera in order to better understand its roles in glaucoma etiology.

Mechanical characterization of sclera using uniaxial mechanical testing has shown that the sclera is nonlinear and viscoelastic.^5,7,21,26 Biaxial mechanical testing (loading in two orthogonal in-plane directions) has shown a significantly different response between the circumferential and meridional directions in the porcine posterior sclera,⁴ but the contrast was less obvious in the human sclera.⁶ Uniaxial and biaxial mechanical testing provide measurements of mechanical constants but have several known drawbacks including the disruption of tissue integrity during specimen excision and the introduction of artificial pre-stresses on sample surfaces that are naturally curved.

Inflation testing avoids disruption of the tissue microstructure and better mimics physiological loading. Several studies have utilized inflation mechanical testing to characterize the deformation of the posterior sclera. These studies have measured the surface^3,8,9 or 2D cross-sectional^19,30 deformation of the sclera while the ocular shell was pressurized to controlled IOP levels. These studies showed a non-linear deformation response to IOP as well as regional/quadrant differences in the deformation profiles of the peripapillary sclera.⁸ The cross-sectional measurements revealed and quantified the larger through-thickness compression of the posterior sclera in addition to the tangential stretch during inflation.^19,30

Volumetric acquisition and analysis of 3D scleral deformation in response to IOP have not been previously reported. The aim of this study was to develop and validate a 3D ultrasound speckle tracking technique for measuring the 3D deformation of the posterior sclera during IOP elevation. Our laboratory has developed a 2D technique³⁰ to measure strains within a cross-section of interest in the sclera^19,30 and cornea.²² The 2D configuration is simple and fast, but tissue deformation is 3D in nature. A 3D method obtains the full 3D characterization of tissue mechanical behavior, including principal strains and directions, maximum shear, and volumetric changes. With the 3D reconstruction, strain maps of any cross-sections of the tissue are available, not restricted to surface or scanned cross-sections. Methods for 3D strain measurements have been developed in the past using microCT¹⁶ or optical imaging¹⁴ to better define the in situ tissue mechanical demands. Three dimensional ultrasound speckle tracking has also been investigated in recent years, for measuring soft tissue such as the cornea,¹⁰ arteries,¹⁵ and cardiac muscles.¹⁸ Compared to most existing ultrasound elastography techniques, our method uses very high frequency (i.e., center frequency at 55 MHz) and very high spatial sampling rate, which predict a higher accuracy in strain estimation than previous methods. We also implemented a 3D least squares method to reduce noise in strain estimation. The present study evaluated the accuracy and signal-to-noise ratio of the 3D technique in displacement and strain estimation using simulated ultrasound radiofre-quency (RF) data with known displacements or strains. The technique was then applied to the porcine sclera to measure its 3D inflation response.

MATERIALS AND METHODS

3D Ultrasound Speckle Tracking Algorithm

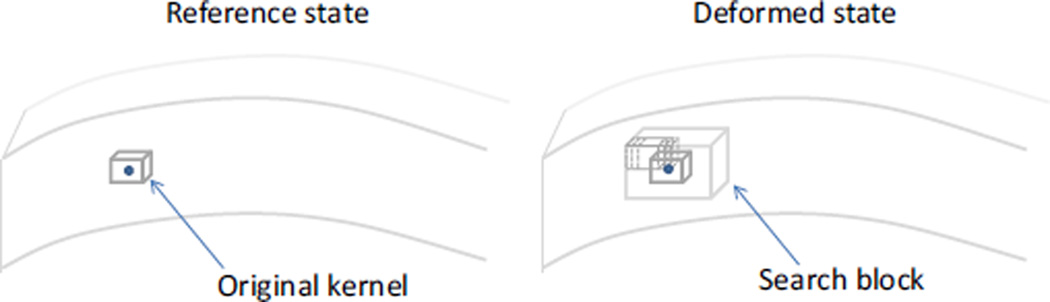
A 3D speckle tracking algorithm was developed based on normalized cross-correlations. Briefly, a mesh grid is defined in the volume of interest and a small rectangular volume centered at each grid point is defined as a kernel (Fig. 1). To find the displacement of a given grid point, the signal values within the corresponding kernel in the reference state are compared with those from a series of kernels within a search block in the deformed state using cross-correlations (Fig. 1). The search block is a sub-volume of the deformed state centered at the location of the original grid point. The correlation coefficient between the original kernel centered at the grid point (i₀, j₀, k₀) in the original signal A and the kernel centered at (i₀ + l, j₀ + m, k₀ + n) in the deformed signal B is calculated as follows:

$${\rho }_{l,m,n}(i_0,j_0,k_0)=\frac{\sum _{i=i_0-(I/2)}^{i_0+(I/2)}\sum _{j=j_0-(J/2)}^{j_0+(J/2)}\sum _{k=k_0-(K/2)}^{k_0+(K/2)}(a_{i,j,k}-\overline{a})(b_{i+l,j+m,k+n}^{*}-{\overline{b}}^{*})}{\sqrt{\sum _{i=i_0-(I/2)}^{i_0+(I/2)}\sum _{j=j_0-(J/2)}^{j_0+(J/2)}\sum _{k=k_0-(K/2)}^{k_0+(K/2)}{|a_{i,j,k}-\overline{a}|}^2\sum _{i=i_0-(I/2)}^{i_0+(I/2)}\sum _{j=j_0-(J/2)}^{j_0+(J/2)}\sum _{k=k_0-(K/2)}^{k_0+(K/2)}{|b_{i+l,j+m,k+n}-\overline{b}|}^2}}$$ (1)

where a and b are the signal values in signal A and B, the ā and b̄ are the average values of the corresponding kernels, and the size of the kernel is (I + 1) × (J + 1) × (K + 1) voxels. The correlation coefficients are calculated for all kernels in the search block by varying l, m,, and n one voxel a time (Fig. 1). A higher correlation coefficient means a higher resemblance of the signal values (i.e., speckle patterns) between the original kernel and the kernel in comparison. The kernel center with the maximum correlation coefficient is identified as the peak location. The correlation coefficients are interpolated using a 3D spline function and the new peak after interpolation is used for calculating the displacement at sub-voxel resolution. For multiple consecutive deformation states (e.g., incremental inflation pressures), the displacement vectors are added from the previous step to track the same material point over the multiple deformation steps.

FIGURE 1.

The solid circle represents a grid point in the tissue. A rectangular volume centered at the grid point is defined as a kernel. The new location of the grid point in the deformed state is determined by a search for the maximum cross-correlation coefficient (with interpolation) between the original kernel in the reference state and those within a search block in the deformed state.

3D LEAST SQUARES STRAIN ESTIMATION

The strain was calculated using a 3D least squares strain estimator (LSQSE). Previous studies have shown that piecewise linear curve fitting (i.e., local regression in the sense of least squares) using displacement data from multiple neighboring points significantly reduces noise and preserves the true strain contrast better than the moving-average smoothing of strains.¹³ In 3D LSQSE, the displacement data from a 3D matrix of neighbor grid points was used simultaneously to obtain the displacement gradients for the center grid point. Typically, displacement data of 7 × 7 × 7 grid points was used (3 on each side of the center point). The number of neighboring points used was adaptively reduced (e.g., 5 × 5 × 5 or 3 × 3 × 3) for the grid points close to tissue boundaries because fewer neighbors were available in these regions.

The 3D LSQSE fits the displacement gradients to the displacement data at the grid points as follows:

$$u=\frac{\partial u}{\partial x}x+\frac{\partial u}{\partial y}y+\frac{\partial u}{\partial z}z+C_1$$

$$v=\frac{\partial v}{\partial x}x+\frac{\partial v}{\partial y}y+\frac{\partial v}{\partial z}z+C_2$$ (2)

$$z=\frac{\partial z}{\partial x}x+\frac{\partial z}{\partial y}y+\frac{\partial z}{\partial z}z+C_3$$

where u, v, and w are the displacements computed from cross-correlation based speckle tracking; x, y, and z are the coordinates of the grid points; and C_i’s are the local fitting constants. Equation (2) is an extension of the 2D LSQSE proposed by Lopata et al., who have shown that a higher order LSQSE yields more accurate strain estimates and is less susceptible to noise in the displacement data than a lower order LSQSE.

After obtaining the displacement gradients, the infinitesimal strain tensor was calculated for each kernel as follows, assuming small strains (negligible quadratic terms):

$$\underset{\_}{\underset{\_}{\epsilon }}=\left[\begin{array}{ccc}\hfill \frac{\partial u}{\partial x}\hfill & \hfill \frac{1}{2}(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x})\hfill & \hfill \frac{1}{2}(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x})\hfill \\ \hfill \frac{1}{2}(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x})\hfill & \hfill \frac{\partial v}{\partial y}\hfill & \hfill \frac{1}{2}(\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y})\hfill \\ \hfill \frac{1}{2}(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x})\hfill & \hfill \frac{1}{2}(\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y})\hfill & \hfill \frac{\partial w}{\partial z}\hfill \end{array}\right]$$ (3)

The principal strains and principal vectors were found by computing the eigenvalues and eigenvectors of the strain tensor.

Because all components of the 3D strain tensor are made available, the maximum shear and volume ratio can be found at each grid point. The maximum shear is calculated as follows:

$${\gamma }_{\text{max}}=\frac{1}{2}({\epsilon }_{\text{max}}-{\epsilon }_{\text{min}})$$ (4)

where γ_max is the maximum shear strain, and ε_max and ε_min are the maximum and minimum principal strains. The volume ratio is calculated as:

$$V_{\mathrm{R}}=\frac{V_{\mathrm{f}}}{V_0}=(1+{\epsilon }_1)(1+{\epsilon }_2)(1+{\epsilon }_3)$$ (5)

where V₀ is the initial volume, V_f is the deformed volume, and ε₁, ε₂, and ε₃ are the principal strains. An incompressible material has a volume ratio of 1.

Analysis of Displacement and Strain Estimation Accuracy Using Simulated Radiofrequency Data

The accuracy of the 3D ultrasound speckle tracking algorithm in displacement and strain estimation was evaluated using simulated ultrasound RF data where synthetic displacements or strains were introduced in the “deformed” signals. The original RF data for a sclera-like volume were generated using the Field II Ultrasound Simulation Program^11,12, with a customized MATLAB sub-routine implemented to run in parallel at the supercomputing center of our institute (Ohio Supercomputing Center, Columbus, OH). The simulation program convolved the point spread function (PSF) of an ultrasound transducer (with the same characteristics as the one used in the experiments of this study) with a 3D cloud of randomly distributed scatterers that simulate the sclera. Random noise (−38-dB) was added to the RF data to simulate electronic noise in the ultrasound system (this level of noise was typically observed in our experiments). The transducer was scanned at 20 µm intervals in the lateral and elevational directions and the RF data were sampled at 500 MHz (equivalent to 1.5 µm interval in the axial direction). The axial direction is the direction of ultrasound propagation [y in Eqs. (2) and (3)] and has a much higher sampling density than the other directions. The lateral direction is perpendicular to the axial direction within the B-mode image plane [(x in Eqs. (2) and (3)]. The elevational direction is the direction perpendicular to the B-mode image plane [z in Eqs. (2) and (3)]. Due to the exponentially increased computational cost in 3D simulations, a small volume (3 × 2.25 × 3 mm³, lateral × axial × elevational) was simulated. The simulated volumes had 151 × 1499 × 151 voxels in the lateral, axial, and elevational directions (the voxel number in the axial direction was higher because of the higher sampling density).

To simulate rigid-body translation, a single volume was translated by a uniform amount of 0, 0.5, 1.0, and 2.0 voxels in each coordinate direction. The 0.5-voxel-translation image was generated from interpolation. The calculated displacements were compared with the intended displacements. To simulate uniform strains, each scatterer in the Field II simulation was displaced by a certain amount to introduce the same strain in each coordinate direction (no shear strains), and the “deformed” scatterer cloud was convolved again with the transducer point spread function to generate the “deformed” ultrasound RF signals using the Field II simulation program.

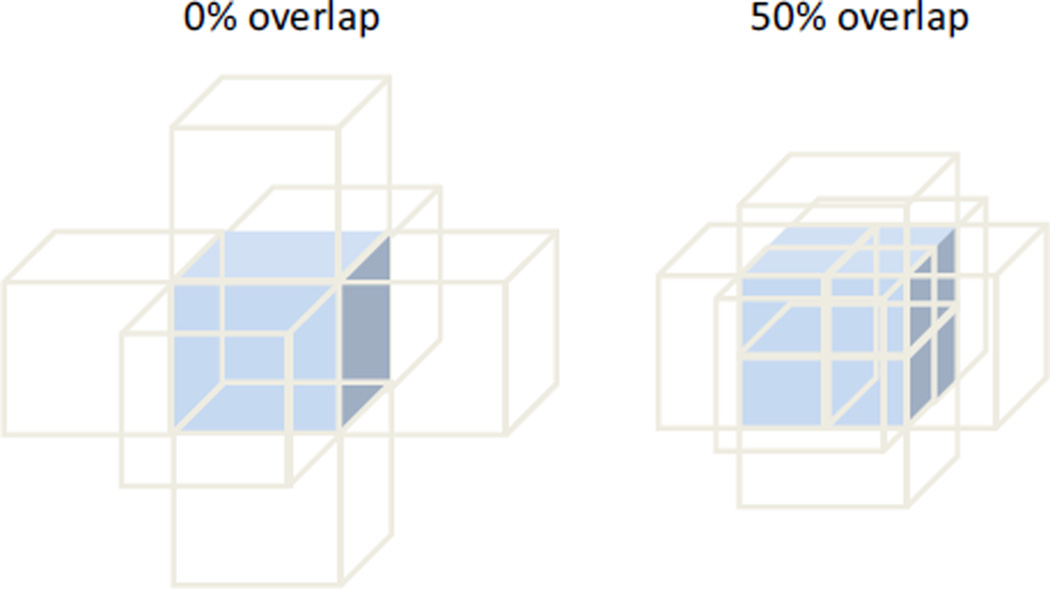
Different kernel sizes (i.e., 7 × 51 × 7 voxels, 11 × 51 × 11 voxels, 21 × 51 × 21 voxels, 31 × 51 × 31 voxels, and 41 × 51 × 41 voxels, lateral × axial × elevational) were compared to evaluate the influence of kernel size on strain estimation. The size in the axial direction was chosen to be 51 voxels to be at least twice of the axial resolution.² The size in the lateral and elevational directions was varied to identify an optimal combination of accuracy and SNR for tracking strains at 0.005. The size of the search block was proportionally adjusted with the kernel size (for the small strains expected in the simulated and experimental data from the sclera, the search block was set as twice of the kernel size in each direction). Partially overlapping kernels increase the spatial density of the grid points and thus improve the spatial resolution of the strain image, although with increased computational costs. For example, the grid density in a given direction is doubled with a 50% overlap in that direction (Fig. 2). Previous studies have shown that a 50% kernel overlap achieves the best trade-off between signal-to-noise ratio and spatial resolution of the strain image.²⁹ Therefore, a kernel overlap of 50% was used in the present study. With this overlap, the simulated volume (3 × 2.25 × 3 mm³) yielded 15 × 60 × 15 grid points.

FIGURE 2.

The grid points (i.e., kernel centers) have a higher spatial density for the same sized kernels if they overlap.

After optimizing the kernel size, the simulated RF data from the original and deformed states at different strain levels (0.001–0.05) were input to the 3D cross-correlation speckle-tracking algorithm to compute the displacements and strains. The calculated axial, lateral, and elevational strains $(\mathrm{i}.\mathrm{e}.,\frac{\partial u}{\partial x},\frac{\partial v}{\partial y},\frac{\partial w}{\partial z})$ were compared with the simulated strains to evaluate the accuracy and signal-to-noise ratio. Two variables were computed from each set of strain data: the average strains (axial, lateral, and elevation) within the simulated 3D volume and the standard deviation. Accuracy is defined as the percent error comparing the calculated to the true strain. The SNR is defined as the standard deviation divided by the average strain. The magnitudes of the shear strains $(\mathrm{i}.\mathrm{e}.,\frac{1}{2}(\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}),\frac{1}{2}(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}),\frac{1}{2}(\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y}\left)\right)$ were also compared with the known values, which were all zero for the simulated shear free condition.

Experimental Testing in Porcine Eyes

Five porcine eyes were obtained (SiouxPreme Packing Co., IA) and tested within 72 h post-mortem to avoid tissue degradation. To prepare the ocular shell for inflation testing, the cornea was removed using a 9 mm trephine and the intraocular structures were gently removed. The ocular shell was then mounted on a customized pressurization chamber.¹⁹

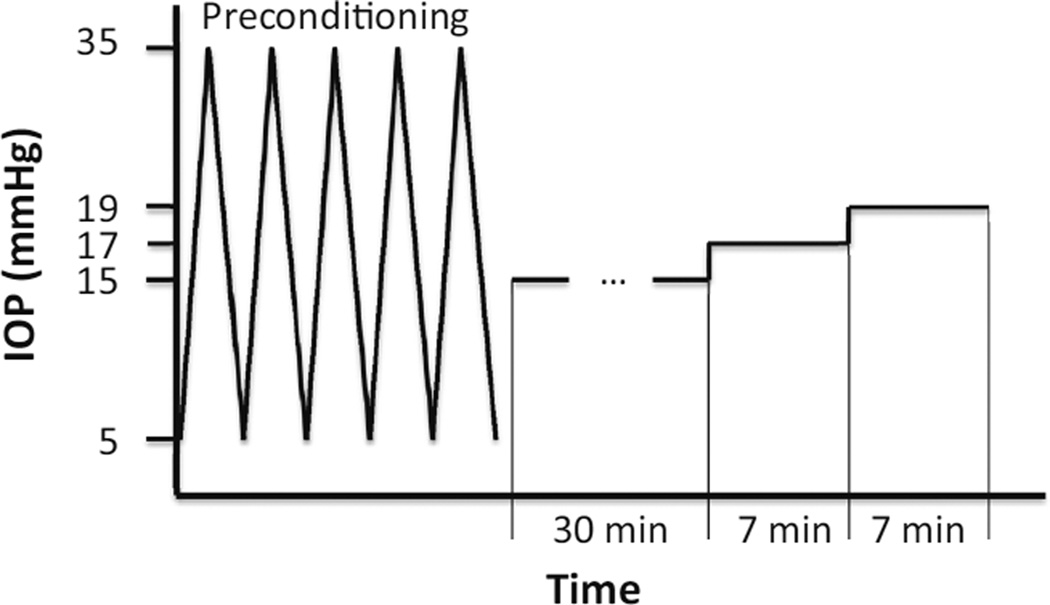
The IOP was initially set to 5 mmHg by infusing 0.9% saline. Five cycles of pressure increase from 5 to 35 mmHg were utilized to precondition the tissue and stabilize the mechanical responses.³³ After preconditioning, the IOP was set to a reference pressure of 15 mmHg and the tissue was allowed to equilibrate for 30 min. The IOP was then raised to 17 and 19 mmHg with 7 min of equilibration between the pressure steps (Fig. 3).

FIGURE 3.

The experimental loading protocol.

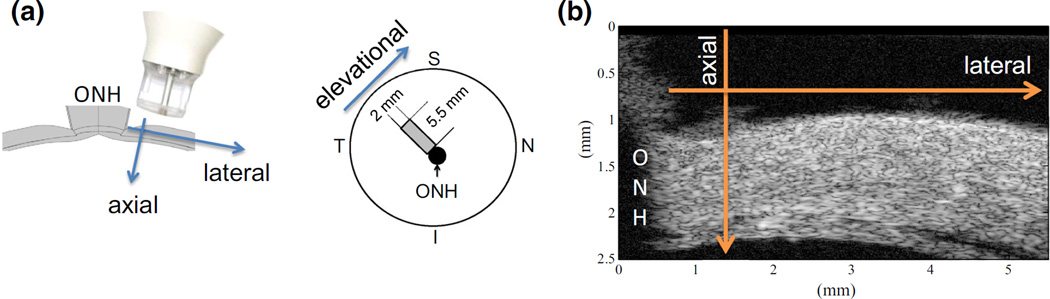
At each pressure (including the reference pressure), a total volume of 5.5 × 3 × 2 mm³ (lateral × axial × elevational) in the superotemporal region (Fig. 4a) was scanned ultrasonically, yielding 384 × 2000 × 144 voxels and 48 × 154 × 18 grid points. At a given transducer location, an A-line is acquired consisting of the echoes from the entire tissue depth at the transducer location (Fig. 4b). The transducer (55 MHz, Vevo 660, VisualSonics Inc., Toronto, CA) was moved in the lateral direction to form a 2D frame. At the completion of each lateral scanning, the transducer was moved along the elevational direction by using an automated actuator (TRA25CC, Newport, Irvine, CA) at 14 µm steps. Using the built-in B-mode of the ultrasound imaging system, the A-lines (i.e., 1D) were temporarily stored in batches of 2D frames. These 2D frames were later decomposed back to individual 1D A-lines for the volume reconstruction. The data acquisition and probe displacement were controlled by a customized LabView interface (National Instruments, Austin, TX). All radiofrequency ultrasonic data was acquired real-time using a high-speed digitizer (500 MHz, DP105; Acqiris, Monroe, NY) controlled by the same LabView interface.

FIGURE 4.

(a) Schematics of the experimental setting showing the ultrasound scanning orientations with respect to the anatomy of the posterior sclera (S superior, N nasal, I inferior, T temporal, ONH optic nerve head); (b) Cross-sectional ultrasound image showing the speckle pattern and the thickness-tapering of the peripapillary sclera.

The strain tensor was computed at each 3D grid point over the tissue volume, and the principal strains and maximum shear during mild IOP elevations (from 15 to 17 to 19 mmHg) were calculated. The volume ratios were also calculated.

RESULTS

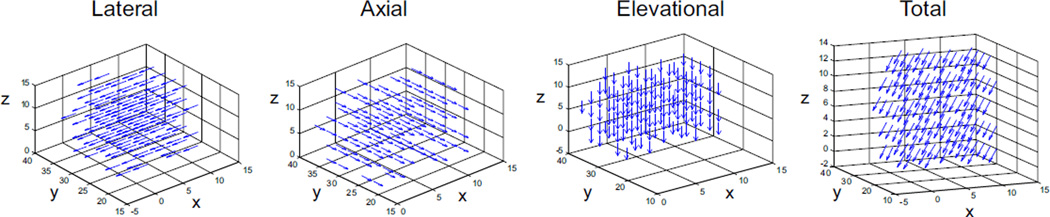
The accuracy of displacements in uniform translations is summarized in Table 1. The absolute error was less than 0.01 voxel in all coordinate directions for all simulated translations. The error in the axial direction was typically lower than those in the lateral and elevation directions, while the performance in lateral and elevational was similar. The displacement vector field plot shows homogeneous displacements throughout the volume (Fig. 5).

TABLE 1.

Displacement accuracy for uniform translations in all directions.

Intended displacement				Calculated displacement
	µm				Voxel			µm			% Error
Voxel	AX	LA	EL		AX	LA	EL	AX	LA	EL	AX	LA	EL
0	0	0	0	Mean	0.000	0.000	0.001	0.000	0.009	0.022	N/A	N/A	N/A
				SD	0.001	0.002	0.005	0.002	0.048	0.091
0.5	0.75	10	10	Mean	0.500	0.495	0.494	0.750	9.891	9.883	0.035	1.087	1.172
				SD	0.004	0.014	0.013	0.006	0.278	0.260
1	1.5	20	20	Mean	1.000	0.997	0.996	1.500	19.931	19.928	0.004	0.344	0.362
				SD	0.002	0.009	0.008	0.002	0.176	0.152
2	3	40	40	Mean	2.000	1.997	1.996	3.000	39.933	39.926	0.003	0.166	0.186
				SD	0.002	0.009	0.008	0.003	0.170	0.159

(AX axial, LA lateral, EL elevational).

FIGURE 5.

Displacement vector fields for the simulated 0.5-voxel displacement. The grid points were down-sampled for clarity. The axes show grid point indices (x lateral, y axial, z elevational).

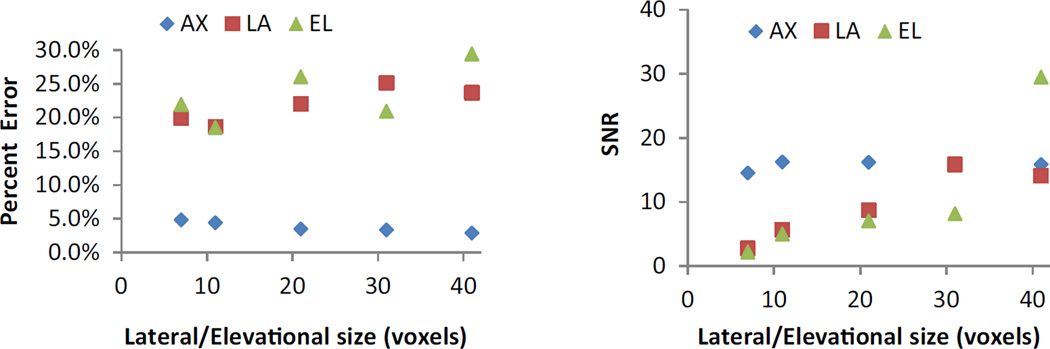
The influence of the kernel size on accuracy and SNR was evaluated by comparing the performance at 0.005 simulated strain (Fig. 6). As the lateral/elevational size increased, the lateral/elevational strain accuracy decreased but the SNR increased. The performance for axial strains remained essentially the same at different lateral/elevational sizes (axial size was kept the same). The kernel sizes of 21 × 51 × 21 and 31 × 51 × 31 voxels achieved the best combination of accuracy and SNR in all directions. For the small volume used in simulations, a kernel size of 21 × 51 × 21 voxels was used. For the larger volume in the experimental scans, a kernel size of 31 × 51 × 31 voxels was used.

FIGURE 6.

The effect of lateral/elevational kernel size on accuracy and SNR for true strain at 0.005. The axial kernel size was 51.

The accuracy and signal-to-noise ratio (SNR) of the 3D strain estimation were examined using the simulated data at 0.001–0.05 strains. The accuracy and signal-to-noise ratios corresponding to different simulated tensile strains are summarized in Table 2 (the results for compressive strains were similar and not shown). The computed shear strains were minimal (<0.00006), consistent with the simulated shear free condition.

TABLE 2.

SNR and % error in the calculated strains and volume ratios at different induced tensile strains based on simulated RF data (AX axial, LA lateral, EL elevational, Vr volume ratio).

Induced		SNR				% Error
AX, LA, EL	Vr	AX	LA	EL	Vr	AX	LA	EL	Vr
0.0010	1.003	58.3	15.1	17.7	5935.7	10.36	25.68	26.01	0.08
0.0050	1.015	16.6	10.7	10.2	1921.0	4.39	21.31	24.08	0.25
0.0101	1.031	22.3	4.6	4.8	357.7	3.78	1.86	1.47	0.06
0.0204	1.062	20.7	5.2	4.6	210.6	3.54	2.66	5.73	0.32
0.0526	1.166	19.1	71.6	65.5	346.7	3.41	0.05	0.02	0.24

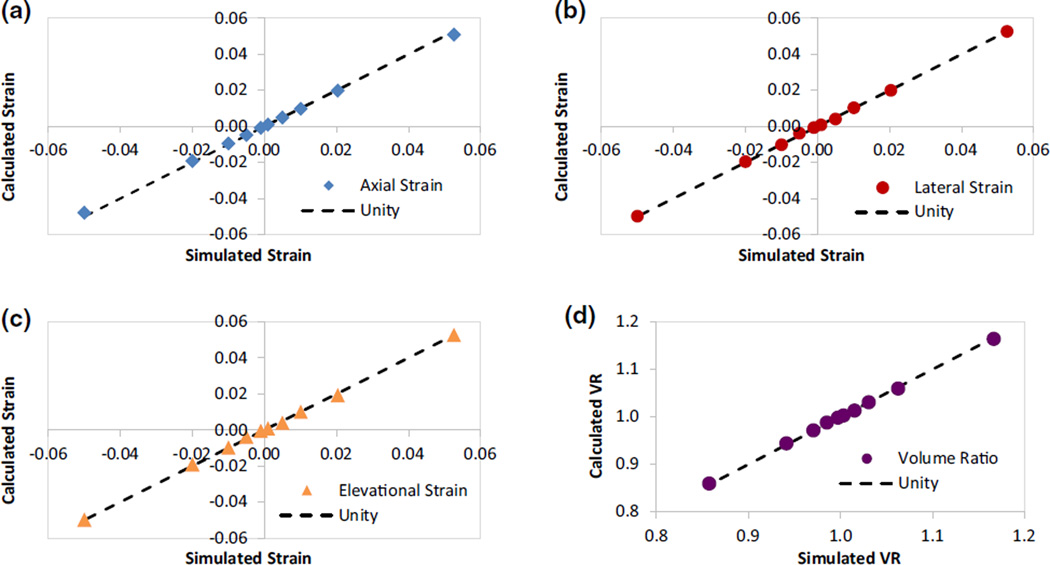
To visualize the comparison and correlation to true strains, the calculated normal strains at different simulated strains are plotted (Fig. 7). The calculated strains all fell close to the unity line (true values), demonstrating good accuracy. The axial strains had small percent errors at all strain levels. Using tensile strains as an example, the percent error was 3–4% for strains at 0.005–0.05; and about 10% for strains at 0.001. The lateral and elevational strains had similarly low percent errors for strains 0.01–0.05 (<6%). At low strains (0.001 or 0.005), the percent error for lateral and elevational strains increased to 20–30%. The SNR was generally higher for axial strains (> 16) than lateral and elevational strains, but at a strain of 0.05, all three directions had very high SNR. Accuracy and SNR results for the compressive strains were similar to those reported above. The percent error for volume ratio was very low (<0.5%) and the SNR was very high (>200) at all strain levels.

FIGURE 7.

Simulated vs. calculated normal strains and volume ratios along the three orthogonal directions: (a) axial, (b) lateral, (c) elevational, and (d) volume ratio.

Inflation testing in porcine scleral shells showed increasing magnitudes of strains during mild IOP elevation from 15 to 19 mmHg. The magnitudes of the three principal strains and the max shear increased during inflation from 17 to 19 mmHg (Table 3). Principal strain ε₁ was the largest positive (i.e., tensile) normal strain and principal strain ε₃ was the largest negative (i.e., compressive) normal strain. Principal strain ε₂ had a minimal magnitude at both pressure levels (<0.0001 on average). By definition, the max shear was about the average magnitudes of ε₁ and ε₃. The average volume ratio decreased slightly from 17 to 19 mmHg (Table 3). Although the absolute change in volume ratio was small, it decreased in every tested eye, showing a statistically significant difference between the two pressure steps (p = 0.002, paired t test).

TABLE 3.

Average principal strains (ε₁, ε₂, ε₃) and maximum shear (MS) in milli-strains, and volume ratio (VR) for the scanned volume in porcine eyes at 17 and 19 mmHg (n = 5).

IOP	ε1 (milli)	ε2 (milli)	ε3 (milli)	MS (milli)	VR
17 mmHg	6.56 ± 1.15	0.04 ± 0.87	−13.00 ± 2.70	9.77 ± 1.78	0.993 ± 0.002
19 mmHg	9.79 ± 2.46	−0.06 ± 1.42	−24.12 ± 5.32	1.68 ± 3.21	0.985 ± 0.005

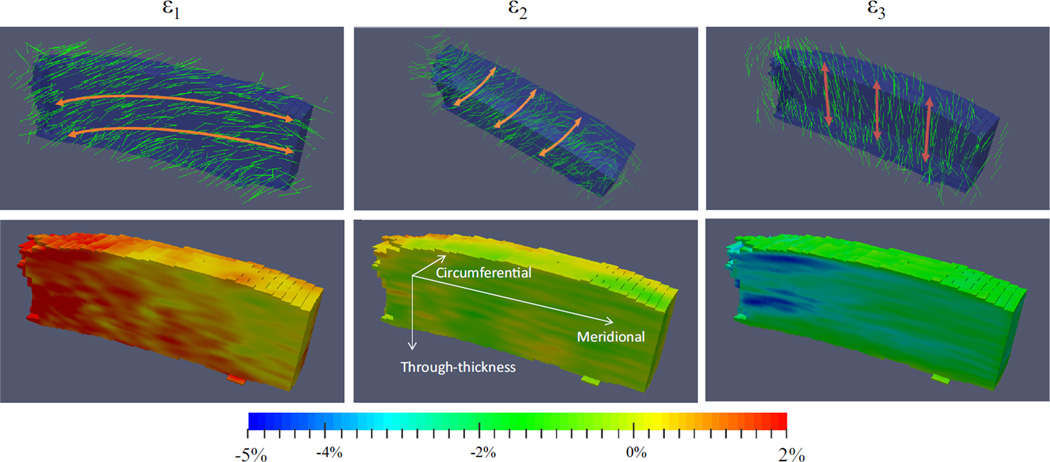
The principal strains and the corresponding principal vectors for a representative specimen at 19 mmHg were plotted (Fig. 8). Some heterogeneity in both the strain magnitudes and vector orientations was observed in the scanned volume.

FIGURE 8.

Principal strains and vectors superimposed over the scanned volume on a representative specimen at 19 mmHg. The ONH is on the left side of the volume. The maximum shear appeared to lie in the through-thickness, meridional plane (coordinates shown in ε₂ strain image).

DISCUSSION

We have developed a new experimental method based on high frequency ultrasound speckle tracking to obtain a 3D characterization of the strains in the posterior sclera during physiological elevations of intraocular pressure. The accuracy and the signal-to-noise ratio of this approach were analyzed with simulated radiofrequency data from a sclera-like structure deformed with known strains. Good agreement was found between simulated and calculated strains. Using this novel approach, we evaluated the mechanical responses of the porcine sclera to changes in IOP.

Previous studies have shown that the accuracy and signal-to-noise ratio of strain estimation are influenced by factors related to the image acquisition system (e.g., the transducer frequency and the sampling rate) and the speckle tracking algorithm parameters (e.g., kernel size).^28,31 Higher transducer frequency and higher sampling rate both improve speckle tracking performance, but in practice, the choices are limited by other factors. For example, the transducer frequency is limited by having sufficient ultrasound penetration into the tissue (i.e., high frequency sound waves attenuate fast). The frequency used in the present study, 55 MHz, is near the upper limit for penetrating a 1 mm thick sclera. The sampling rate in the lateral direction is determined by the transducer design and consideration of temporal resolution (i.e., frame rate). In our current system, the lateral sampling rate is 14 or 20 µm per voxel. The sampling rate in the elevational direction is controlled by the linear actuator, and theoretically could be any value within the resolution of the actuator. In practice, we match the sampling rate in the elevational direction to the lateral, to achieve symmetry in those two directions. The sampling density in the axial direction is mainly determined by the sampling rate of the analogue-to-digital conversion of the radiofrequency data. Our current RF sampling rate (500 MHz) is about 5 times the highest frequency in the ultrasound signals, which sufficiently preserves the signal information based on Nyquist theorem (i.e., at least twice the highest signal frequency). This corresponds to a 1.5 µm per voxel spatial sampling rate in the axial direction.

The accuracy of the 3D ultrasound speckle tracking algorithm for displacement measurements was evaluated using translations by whole or sub-voxels (Table 1). With noise added, the algorithm performed remarkably well for whole voxel translations with an error lower than 0.4%. The error for the 0.5-voxel displacement was higher (axial: 0.035%, lateral: 1.087%, and elevational: 1.172%), likely because it involved two interpolation processes: the generation of the simulated volume translated by a sub-voxel distance and the speckle tracking. Therefore, the true error associated with speckle tracking could be lower in this case than the values in Table 1.

In order to evaluate the efficacy of the ultrasound speckle tracking algorithm along with the 3D least squares for strain estimation, the calculated strains (three normal and three shear) were compared with Field II simulated strains for a volume of ultrasonic radiofrequency data with both deformed and unde-formed states. Based on the simulation experiments, the calculated normal strains matched well with the simulated strains in all three orthogonal directions (axial, lateral, and elevational, Fig. 7) with essentially no shear strains, consistent with the simulated shear free condition. The percent error at small strains (0.001 and 0.005) was larger, especially for lateral and elevational directions. We performed additional simulations at true compressive strains of 0.005 and 0.006, 0.01 and 0.011, 0.02 and 0.021, as well as 0.05 and 0.051 (each pair differed by 0.001 absolute strain). The algorithm consistently estimated these strains so that the difference between the pairs persisted in the calculated strains. Using elevational strains as an example (axial and lateral directions performed the same or better), the calculated strains for the pairs were: 0.0039 and 0.0050, 0.0099 and 0.0116, 0.0193 and 0.0202, 0.0499 and 0.0509. This suggested that the approach could reliably resolve a small difference in tissue response.

The simulations also showed a general trend that the axial direction had better accuracy and SNR than the other two directions, while the lateral and elevational directions had similar outcomes. This contrast is a well-known phenomenon in ultrasound elastography, largely due to the higher spatial resolution and denser sampling rate in the axial direction. For the ultrasound system used in the present study, the spatial resolution was 30 µm in the axial direction and 62.5 µm in the lateral and elevational directions. The high sampling rate of the radiofrequency data (500 MHz) further improved the axial voxel size to 1.5 µm, while the lateral and elevational voxel size was 20 µm in the simulations and 14 µm in the porcine eye experiments. Surface strain measurement methods, such as digital image correlation (DIC)³ or electronic speckle pattern interferometry (ESPI),⁸ have a much higher lateral resolution (i.e., a few microns) and likely have a higher accuracy in measuring lateral strains. Speckle tracking using ultrasound radiofrequency data preserves the phase information along the axial direction, and together with the dense sampling, results in a very high displacement sensitivity and high accuracy and SNR for strain estimation in the axial direction. We found a maximum percent error of 10% and a minimum SNR of 16 for the simulated axial strains from 0.001 to 0.05. At low strains, the error primarily arises from the electronic noise added to the simulated RF data to mimic the noise in actual systems. The performance in the lateral and elevational directions was similar, which is consistent with the same spatial resolution and sampling rate in these two directions. It is also noted that the performance of the 3D ultrasound speckle tracking reported in this study was similar to the 2D case reported earlier.³⁰

Using porcine globes, we applied the 3D data acquisition system and 3D strain estimation algorithm to evaluate the deformation of the posterior sclera in response to mild IOP elevations. The general pattern of the principal strains was characterized by a compressive strain with the largest magnitude among the three principals, a tensile strain slightly smaller in magnitude than the compressive strain, and another strain with minimal magnitude. Based on analyses of a simple linear, elastic, thin shell model with typical dimensions of sclera (inner radius of curvature = 12 mm, thickness = 0.8 mm), a 2-mmHg pressure increase would generate the level of principal tensile strains measured in the present study for a modulus of 0.2 MPa. This modulus is of the same order of magnitude as what we previously measured in porcine posterior sclera using biaxial testing.⁴

The principal directions showed an interesting correspondence to the tissue’s anatomic structure (Fig. 8). The third principal was compressive and largely oriented in the through-thickness direction, which is consistent with the expected through-thickness compression in an inflated thin shell. The first principal was tensile and predominantly oriented in the in-plane, meridional direction. The second principal strain (minimal in magnitude) was also largely in-plane, and along the circumferential direction. The anisotropy of the in-plane strains was likely related to the microstructural anisotropy of the peripapillary sclera, which has a collagen annulus ring circumferential to the scleral canal.²⁴ Future studies are needed to better understand this structure-function relationship.

Derived from the 3D principal strains, the maximum shear in the posterior sclera during mild IOP elevations appeared to reach 0.01–0.02. Previous surface strain measurements showed minimal shear in the posterior sclera,³ possibly a characteristic of the scleral surface but not representative of the internal stroma. Our previous biaxial testing in the more peripheral region of the sclera also did not detect significant shear during equal biaxial loading in the porcine posterior sclera;⁴ however the biaxial loading does not replicate the structural bending of the peripapillary region during inflation caused by structure and material property differences between the sclera and the ONH. By definition, the maximum shear lies in the plane of the maximum and minimum principals and is oriented in the direction of the principal vectors rotated by 45°. Based on the experimental results, the maximum shear in the peripapillary sclera appeared to be largely in the through-thickness, meridional planes (Fig. 8). Recent reports have shown significantly higher tilt and torsion of the ONH in glaucoma patients, especially those with normal tension glaucoma,²³ suggesting possible involvement of abnormal peripapillary scleral shear in the pathophysiology of glaucoma. It is noted that the cerebrospinal fluid pressure also acts on this region from the external side of the sclera,³² likely affecting the stress and strain states of this region in vivo, although this was not captured in the current experimental setup.

The 3D technique also offered an opportunity to evaluate the volumetric changes during scleral deformation. As defined in Eq. (5), a volume ratio of 1 represents no volume change. Our simulation results showed excellent accuracy and SNR for volume ratio calculations in simulated compression or tension at different strains and different true volume reduction or expansion (Table 2). The experimental results showed that the volume ratios in all tested samples were slightly less than 1, suggesting a small amount of volume loss during inflation. Sclera is a proteoglycan-rich tissue, and postmortem tissue is likely somewhat swollen after immersion in an aqueous solution during testing. It is interesting to note that the volume ratio further reduced at the second pressure increase, possibly due to fluid being pushed out during the compression of sclera. Nonetheless, the overall volume change was small (the lowest average volume ratio in the tested samples was 0.97), supporting the assumption of near-incompressibility.

This study has several limitations. First, the simulation validations were performed on a small volume of uniform strains. Generation of the 3D ultrasonic radiofrequency data is computationally costly, and larger volume simulations are practically challenging. However, our current results are informative in terms of understanding the performance of the 3D algorithm. Due to the same issue with computational costs, heterogeneous strains were not simulated. Given the similar performance for measuring uniform strains, we expect that the performance of the 3D algorithm in detecting local heterogeneities would be similar to that of the 2D algorithm, which has been reported in detail in our previous publication.³⁰ Second, only a small pressure range (from 15 to 19 mmHg) was used in the experiments. The 15 mmHg reference pressure is what is often considered a normal in vivo IOP. The successive increases to 17 and 19 mmHg represent mild IOP elevations demonstrating the trend in the biomechanical responses within the physiological range and the proof of concept of the 3D approach in characterizing scleral strains. Because of this small pressure range, infinitesimal strain tensors were used to calculate the strains ignoring the quadratic terms. Future studies at larger pressure ranges will include analyses using finite strain theories. Third, a small strip of the sclera (2 mm wide and 5.5 mm long) was used to sample a volume of the posterior sclera in this study. Future studies will include the entire posterior scleral dome and evaluate potential regional variance. In addition, only average strains were reported in the present study, while we observed some level of strain heterogeneity within each sample. Since the scanned volume was limited to the 2 mm wide meridional strip, it is difficult to determine the nature of these strain heterogeneities. Future studies will analyze the strain variations in larger scanned volumes and compare with histology or other microstructure analyses.

In summary, a 3D ultrasound speckle tracking technique for strain estimation was successfully implemented and validated for characterizing the response of sclera to IOP. The simulation experiments showed satisfactory accuracy and SNR. Initial experiments in porcine eyes showed tensile, compressive, and shear strains and near-incompressibility in the posterior sclera during mild pressure increase. This technique provides a non-invasive evaluation of the through-thickness, 3D strains in the sclera, and may be applied to the characterization of other tissues with a thickness less than 2 mm to allow for full thickness penetration of the high frequency ultrasound waves.