New Perspectives on the Charging Mechanisms of Supercapacitors

Abstract

Supercapacitors (or electric double-layer capacitors) are high-power energy storage devices that store charge at the interface between porous carbon electrodes and an electrolyte solution. These devices are already employed in heavy electric vehicles and electronic devices, and can complement batteries in a more sustainable future. Their widespread application could be facilitated by the development of devices that can store more energy, without compromising their fast charging and discharging times. In situ characterization methods and computational modeling techniques have recently been developed to study the molecular mechanisms of charge storage, with the hope that better devices can be rationally designed. In this Perspective, we bring together recent findings from a range of experimental and computational studies to give a detailed picture of the charging mechanisms of supercapacitors. Nuclear magnetic resonance experiments and molecular dynamics simulations have revealed that the electrode pores contain a considerable number of ions in the absence of an applied charging potential. Experiments and computer simulations have shown that different charging mechanisms can then operate when a potential is applied, going beyond the traditional view of charging by counter-ion adsorption. It is shown that charging almost always involves ion exchange (swapping of co-ions for counter-ions), and rarely occurs by counter-ion adsorption alone. We introduce a charging mechanism parameter that quantifies the mechanism and allows comparisons between different systems. The mechanism is found to depend strongly on the polarization of the electrode, and the choice of the electrolyte and electrode materials. In light of these advances we identify new directions for supercapacitor research. Further experimental and computational work is needed to explain the factors that control supercapacitor charging mechanisms, and to establish the links between mechanisms and performance. Increased understanding and control of charging mechanisms should lead to new strategies for developing next-generation supercapacitors with improved performances.

1. Introduction

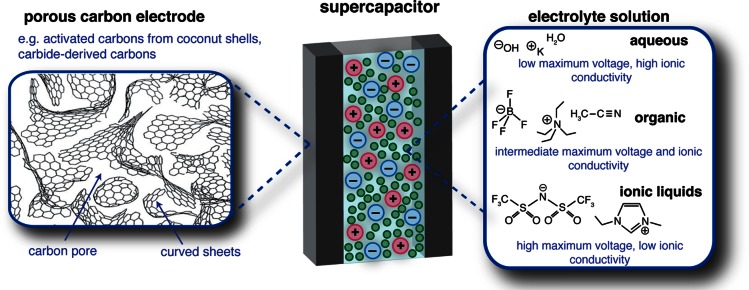
Supercapacitors (strictly, electric double-layer capacitors) store charge at the interface between porous carbon electrodes and an electrolyte solution (Figure 1). In contrast to batteries, charge storage in supercapacitors is non-faradaic and occurs by the physical adsorption and desorption of ions inside the pores of the carbon electrodes when an external voltage is applied. As electronic charge accumulates in an electrode, it is balanced at the interface by an equal and opposite ionic charge in the electrolyte. This physical mechanism of charge storage gives rise to fast charge and discharge times and long cycle lives, characteristic properties that make supercapacitors attractive devices to complement batteries (which can store and deliver more energy but with slower charge and discharge times). Today, supercapacitors are used in a range of industrial, automotive, and electric utility applications including electric buses, trains, uninterruptible power supply systems, elevators, camera flashes, cranes, and engine starters.^1,2 Their more widespread use could be facilitated by the development of new devices with improved energy densities, which retain the high power densities and long cycle lives that are characteristic of supercapacitors.

Figure 1.

Schematic view of a supercapacitor. Porous carbon materials with disordered structures are used as the electrodes, and the cell is soaked with an electrolyte that may be organic, aqueous or ionic liquid-based, with some typical electrolytes shown. Note, for simplicity the separator (which prevents short circuit), the binder that holds the electrode materials together and the current collectors are not shown. Schematic porous carbon structure adapted from ref (17) with permission from Springer.

Typical materials for supercapacitors are highlighted in Figure 1. Porous carbon electrode materials are generally prepared by the heat treatment and subsequent chemical activation of organic materials, such as coconut shells and wood,³ while a related class of materials, “carbide-derived carbons” (CDCs), are obtained from metal carbides by extracting the metal atoms.⁴ More exotic materials such as carbon nanotubes (CNTs) and graphenes are also being developed for supercapacitor application, but here we will focus our attention on disordered porous carbons (activated carbons) as they are well-studied and widely used in commercial devices due to their cheap price, facile synthesis, and sustainability. For the electrolyte, the most widely used systems are comprised of salts dissolved in organic solvents (e.g., tetraethylammonium tetrafluoroborate in acetonitrile solvent, NEt₄–BF₄/ACN). Such organic electrolytes offer a good balance of relatively large maximum operating voltages (∼2.5 V) and high ionic conductivities (∼20–60 mS·cm^–1). The stored energy, E, is given by

1

where C is the cell capacitance, and V is the operating voltage. Thus, organic electrolytes are typically preferred to aqueous electrolytes that are limited to ∼1 V before water decomposes.⁵ Aqueous-based systems are, however, being studied for applications where cost is a critical parameter (e.g., on the electricity grid).⁶⁻⁸ Room-temperature ionic liquids are also emerging as alternative electrolytes for supercapacitors, with operating voltages as high as 4 V achievable.^5,9−11 However, the increase in energy by eq 1 comes at a cost, as slower ionic transport (ionic conductivities are typically below 20 mS·cm^–1) results in poorer device power performances.

Most efforts to increase the energy density of supercapacitors have focused on the development of new carbon materials with increased capacitances, so that more energy can be stored, as shown by eq 1. However, the success of such an approach requires an understanding of the carbon structure, and how this in turn affects the charge storage mechanism and the capacitance. This is a complex problem, as porous carbon materials lack long-range order, making their characterization challenging. These materials do, however, exhibit order on a local scale (at length scales up to 10 or 20 Å). While analysis of the broad Bragg peaks in diffraction experiments offers little information, pair distribution function (PDF) analysis and nuclear magnetic resonance (NMR) experiments show that typical activated carbons and CDCs consist of predominantly sp²-hybridized carbon atoms organized in a hexagonal arrangement.¹²⁻¹⁵ Recent studies have suggested that non-hexagonal rings, such as 5-membered¹⁶ and 7-membered rings,¹⁵ are also present, giving rise to curvature in the carbon sheets (see schematic structure in Figure 1).^17,18 The curved and defective carbon sheets and fragments do not pack together well (structures are typically non-graphitizing, with graphite not formed even on heating to temperatures as high as 3000 °C),^19,20 and nanometer-sized pores exist between the various carbon surfaces (see Figure 1). This porosity is typically characterized by pore size distributions obtained from the analysis of gas sorption isotherms. State of the art methods use classical density functional theory (DFT) to obtain the pore size distribution.²¹⁻²³ The recently developed NLDFT (non-local DFT) and QSDFT (quenched solid DFT) methods both rely on the assumption that the porous material is a collection of pores with identical shapes (typically slit-shaped pores), and with different pore widths. Classical DFT is used to determine gas adsorption profiles inside the pores, and a set of partial isotherms corresponding to different pore sizes are generated. The pore size distribution is then obtained by fitting the experimental isotherm to a sum of partial isotherms. Owing to the relative ease of this technique, pore size distributions are the most frequently used metric in the characterization of carbon structure, and have been used as the primary tool in the search for relationships between carbon structure and capacitance.

Seminal studies in 2006 showed that the carbon capacitance could be increased by optimizing the pore size of the carbon electrodes.^24,25 An “anomalous” increase in capacitance was observed as the carbon pore size was decreased below 1 nm. These results showed the importance of pore size, and challenged the previous view that pores smaller than the solvated electrolyte ions do not contribute significantly to the capacitance. It was hypothesized that in small pores ion desolvation allows a closer approach of charge centers at the electrode–electrolyte interface, which increases the capacitance.^24,26 However, the capacitance increase was also observed in experimental,²⁷ and theoretical,²⁸⁻³² studies of ionic liquids, with the capacitance maximized when the pore size matched the ion size. It was even shown that the capacitance varies in an oscillatory fashion as the (slit-)pore width is varied.²⁸⁻³² These findings indicate that factors beyond simple ion desolvation arguments are responsible for the anomalous capacitance increase. Interestingly, some experimental studies have reported that there is no correlation between pore size and capacitance,^33,34 with the origin of these differences currently unclear. Needless to say, the observation of pore size effects led to a wave of interest in the mechanisms of charge storage in porous carbon electrodes.

In the past 10 years, pioneering experimental and theoretical studies have led to an improved understanding of the molecular mechanisms of charge storage in supercapacitors. This perspective seeks to bring together recent findings from a range of studies to provide a coherent and detailed view of modern theories of supercapacitor charging mechanisms. Recent studies have shown that charging is not simply driven by adsorption of counter-ions into the electrode pores, as was previously believed (note, counter-ions are defined as having opposite charge to the electrode). NMR experiments and molecular dynamics (MD) simulations show that porous carbon electrodes typically contain a large number of ions in the absence of an applied potential, such that a range of different charging mechanisms, based on different amounts of ion adsorption and desorption, are then possible when a voltage is applied. New in situ experimental techniques (NMR spectroscopy, electrochemical quartz crystal microbalance (EQCM), infrared (IR) spectroscopy, and scattering approaches) have shown that the charging mechanism is sensitive to the electrode and electrolyte materials used, as well as the polarization of the electrode. Understanding and controlling the charge storage mechanism of supercapacitors may hold the key to developing next generation devices with enhanced properties, and we identify new areas of research that can facilitate this process.

2. Characterizing the Electrode–Electrolyte Interface at 0 V

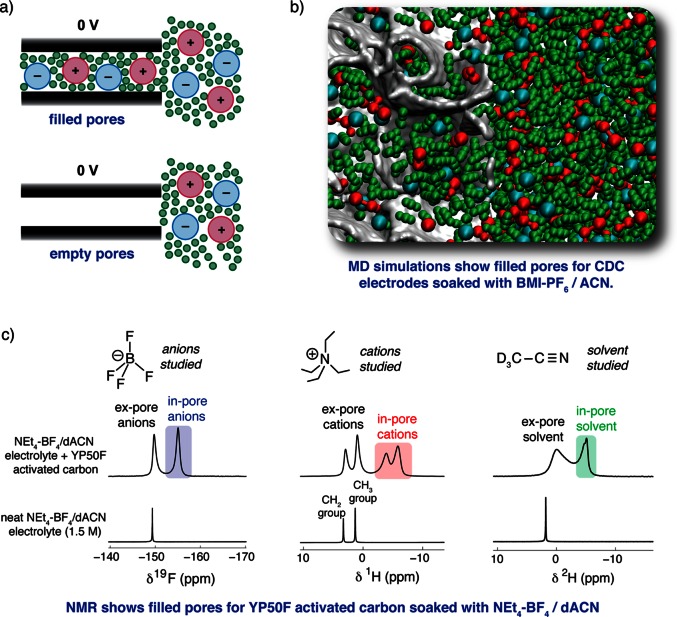
Before embarking on the study of supercapacitor charging mechanisms, it is crucial to have a detailed understanding of the structure of the electrode–electrolyte interface in the absence of an applied potential (i.e., at 0 V). As illustrated by Figure 2a, the carbon nanopores may be either filled with electrolyte ions, or they may contain no ions. These two possibilities have been described as “ionophilic” and “ionophobic” pores by Kornyshev and Kondrat (see later).³⁵⁻³⁷ Together, MD simulations and NMR spectroscopy experiments have shown that the pores of the carbon electrodes are generally filled at 0 V. Coarse-grained MD simulations of the ionic liquid butylmethylimidazolium hexafluorophosphate (BMI–PF₆) showed a large number of ions inside the carbon nanopores of realistic carbon³⁸ (CDC) structures at zero applied potential (Table 1).³⁹ With the MD approach, subtly different local adsorption environments could be identified for confined ions, sitting at sheet edges, on top of sheet planes, inside curved hollows, and inside small pockets.⁴⁰ BMI–PF₆ dissolved in ACN to 1.5 M (i.e., an organic electrolyte) has also been studied under nanoconfinement, with a considerable number of in-pore ions again observed (Figure 2b). In this case the solvent molecules replace some of the in-pore ions, leading to a lower in-pore population relative to the neat ionic liquid study, with the small solvent molecules tending to occupy the most confined pore sites. Other theoretical studies based on idealized electrode geometries, such as CNTs^41,42 and slit pores,^28,43 have also shown spontaneous pore-filling behavior.

Figure 2.

(a) Schematic illustrating the concept of filled and empty carbon pores at 0 V. The carbon (slit-)pore walls are represented by black rectangles. (b) Snapshot of an MD simulation showing the presence of in-pore ions and solvent molecules at 0 V. Red, blue, and green correspond to cations, anions, and solvent molecules, respectively, while the carbon surfaces are gray. See ref (40) for details of the MD study. (c) NMR (9.4 T) measurements of YP50F activated carbon soaked with a typical supercapacitor electrolyte, NEt₄–BF₄/dACN (1.5 M), recorded with magic angle spinning at a frequency of 5 kHz. Note, deuterated acetonitrile (dACN) was used here to allow a convenient separation of the signals from the cations and the solvent molecules. MD simulations and NMR experiments both reveal a significant number of in-pore ions in the absence of an applied potential.

Table 1. In-Pore Ionic Populations at 0 V from MD Simulations and NMR Spectroscopy^a.

method	electrolyte	carbon	pore size (average)/nm	in-pore population at 0 V/mmol g–1 carbon	ref
NMR	EMI–TFSI ionic liquid	YP50F	1.01	1.8	(53)
NMR	Pyr13–TFSI ionic liquid	YP50F	1.01	1.6	(53)
MD	BMI–PF6 ionic liquid	CDC	0.93	1.87	(39)
MD	EMI–TFSI ionic liquid	slit pore	1.10	1.74	(43)
MD	EMI–TFSI ionic liquid	slit pore	1.00	1.43	(28)
MD	EMI–Cl ionic liquid	MWCNT	1.36	1.8b	(41)
MD	EMI–BF4 ionic liquid	CNT	1.08	0.7	(42)
NMR	EMI–TFSI/ACN (1.9 M)	YP50F	1.01	1.2	(53)
NMR	Pyr13–TFSI/ACN (1.8 M)	YP50F	1.01	1.1	(53)
MD	BMI–PF6/ACN (1.5 M)	CDC	0.93	0.68	(40)
NMR	PEt4–BF4/ACN (1.5 M)	YP50F	1.01	0.86	(52)
NMR	PEt4–BF4/ACN (0.75 M)	YP50F	1.01	0.47	(52)
NMR	PEt4–BF4/ACN (0.5 M)	YP50F	1.01	0.31	(52)
NMR	NaF aq (0.8 mol kg–1)	PEEK AC	1.55	>0	(55)
NMR	NaF aq (0.8 mol kg–1)	PEEK AC	0.58	0	(55)

^aIn the NMR studies the commercially activated carbon YP50F was studied in all cases, except for in ref (55), where activated carbons derived from poly(ether-ether-ketone) (PEEK AC) were studied. In most of the MD simulations listed, idealized carbon geometries such as slit pores and multi-walled carbon nanotubes (MWCNTs) were studied, with the exception of the studies of model CDC electrodes in refs (39) and (40).

^bFor the calculation of the gravimetric in-pore population from ref (41), only the inner wall of the MWCNT was considered for the mass calculation. Note: Pyr₁₃–TFSI is 1-methyl-1-propylpyrrolidinium bis(trifluoromethanesulfonyl)imide, and EMI–TFSI is 1-ethyl-3-methylimidazolium bis(trifluoromethanesulfonyl)imide.

Experimental results from NMR spectroscopy are in excellent accord with the findings from MD simulations, also revealing the predominance of filled pores in the absence of an applied potential (see Table 1). In NMR experiments, ions and solvent molecules inside carbon pores (“in-pore”) give rise to peaks which are distinct to those from species in bulk electrolyte between the carbon particles (“ex-pore”).^14,44 By studying different NMR nuclei, the anions, cations, and solvent molecules can be studied separately. For example, for YP50F (a commercial activated carbon) soaked with the electrolyte NEt₄–BF₄ in ACN (1.5 M), clear resonances can be distinguished for in-pore anions (¹⁹F NMR), cations (¹H NMR), and solvent (²H NMR) (Figure 2c). In each case the in-pore peak appears at a negative chemical shift (relative to the ex-pore) due to the local magnetic field originating from the circulation of the carbon’s delocalized π electrons in the applied magnetic field.^14,45,46 These effects are largely independent of the choice of NMR nucleus, such that anions, cations, and solvent molecules all experience a similar change of chemical shift upon adsorption in a given carbon. Since NMR is quantitative, the number of ions inside the carbon pores can be readily determined by fitting and integration of the spectra.

NMR studies have been carried out on carbons soaked with a range of organic electrolytes.^{14,44,47−52} For PEt₄–BF₄ in ACN (1.5 M) and the carbon YP50F, there was 0.86 mmol of in-pore anions and cations per gram of carbon, with this number decreasing at lower electrolyte concentrations (Table 1).⁵² NMR studies of ionic liquids and YP50F carbon have revealed larger numbers of in-pore ions at 0 V (Table 1).⁵³ When the ionic liquid samples were diluted with ACN (to ∼1.8 M), the in-pore ion populations dropped as solvent molecules displaced some of the ions (Table 1).⁵³ This is consistent with MD simulations on model CDC electrodes with and without a solvent present (Table 1). The NMR approach has also recently been applied to study the confinement of aqueous electrolytes, highlighting the versatility of the method.^54,55 It was shown that for a carbon with a relatively small average pore width (0.58 nm) soaked with NaF (0.8 mol kg^–1 aq), the ions were unable to enter the carbon pores in the absence of an applied potential, despite the presence of in-pore water.⁵⁵ Measurements on a carbon with larger pores (average width 1.55 nm) showed there were a considerable number of in-pore ions, confirming that the absence of in-pore ions in the former carbon arose from steric factors. In the absence of any steric effects, it is currently unknown if it is possible to synthesize carbons with ionophobic pores (see later). We note that the study of the electrode–electrolyte interface in aqueous systems is highly complex, as the chemical nature of the carbon surface will depend on the (de)protonation of the various functional groups, and OH^– and H₃O⁺ ions are present alongside the main electrolyte ions.

Beyond NMR spectroscopy and MD simulations, small-angle X-ray scattering (SAXS) and small-angle neutron scattering (SANS) have also emerged as experimental methods to probe the wetting of carbon pores in the absence of an applied potential.⁵⁶⁻⁶⁰ Changes of the scattered neutron intensity after the addition of ACN to activated carbon fabric suggested that the solvent had wetted the carbon nanopores.⁵⁶ Interestingly, this approach allows wetting to be studied as a function of pore size, and it was shown that the pore wetting of activated carbon fabrics was incomplete for the smallest nanopores.⁵⁶ In contrast to NMR and MD simulations, however, these methods have not yet allowed an absolute quantification of the numbers of in-pore anions, cations, and solvent molecules.

3. Studies of Supercapacitor Charging Mechanisms

3.1. Possible Mechanisms of Charge Storage

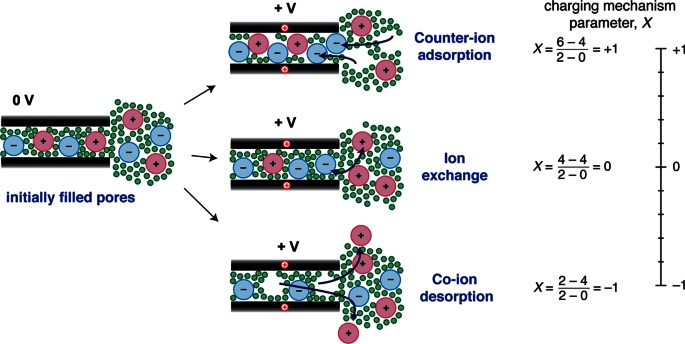
Given the large number of ions inside the carbon pores at 0 V, a range of different charging mechanisms are possible (Figure 3).⁴⁹ First, charge may be balanced by the adsorption of counter-ions. This is the traditional view of charging. A second possibility is that counter-ion adsorption is accompanied by simultaneous co-ion desorption from the pores, which we refer to as ion exchange (where co-ions are defined as having charge with the same sign as the electrode). A third possibility is that charging is driven purely by the desorption of co-ions (Figure 3). In each case the excess ionic charge inside the carbon pores is equal and opposite to the electronic charge stored in the carbon. In practice, charging may involve a combination of the different mechanisms shown in Figure 3. For example, ion-exchange and counter-ion adsorption could occur simultaneously.

Figure 3.

Different possible charging mechanisms for carbon pores that are initially filled with electrolyte: counter-ion adsorption, ion exchange, and co-ion desorption. The different charging mechanisms may be described by the charging mechanism parameter, X, as defined in eq 2. Example calculations of X (using eq 2) are shown for the three depicted charging mechanisms, with V₀ taken as 0 V. A value of X = +1 is obtained for charging solely by counter-ion adsorption, while X = 0 is obtained for ion exchange, and X = −1 for co-ion desorption. As indicated by the scale on the right, X is a continuous variable (e.g., an X value intermediate between 1 and 0 would indicate that both io-exchange and counter-ion adsorption processes occur during charging). Part of this figure is adapted from ref (49) with permission from The Royal Society of Chemistry.

It is useful to describe the charging mechanism with a single mathematical quantity. Here we introduce the charging mechanism parameter, X(V,V₀), defined as

2

where N(V) is the total number of in-pore ions at a charging voltage V, N(V₀) is the total number of in-pore ions at some initial voltage V₀ (typically 0 V), and N_counter(V) and N_co(V) are the number of in-pore counter-ions and co-ions, respectively, at a voltage V. Q_ionic(V) and Q_ionic(V₀) are then the net in-pore ionic charges at the two voltages, and e is the elementary charge. Put simply, X gives a measure of the roles of counter-ion adsorption, ion exchange, and co-ion desorption in the charging mechanism. For the classical charging mechanism of counter-ion adsorption, X = +1. For ion exchange, X = 0, while for co-ion desorption, X = −1 (see example calculations in Figure 3). Intermediate values of X are also possible; for example, X = 0.3 would indicate that both ion exchange and counter-ion adsorption occur during charging, with ion exchange dominating (as 0.3 is closer to 0 than it is to 1). We stress that this parameter refers to charging; i.e., |V| must be greater than |V₀|. It is also important to realize that X can take different values in the positive and negative electrodes, such that separate calculations must be performed for each, and that X may also depend on the studied voltage range.

We note that for pores that are initially empty, charging must at least initially proceed by counter-ion adsorption (X = 1), as there are no in-pore co-ions available for desorption. For such ionophobic pores, charging may also involve the net movement of pairs of ions into the carbon pores. In this unusual case, X can take values greater than 1. As we will see in the next section, the different charging mechanisms can be probed with computational and experimental techniques, and the mechanism depends on the electrode and electrolyte materials studied.

3.2. Computational Methods

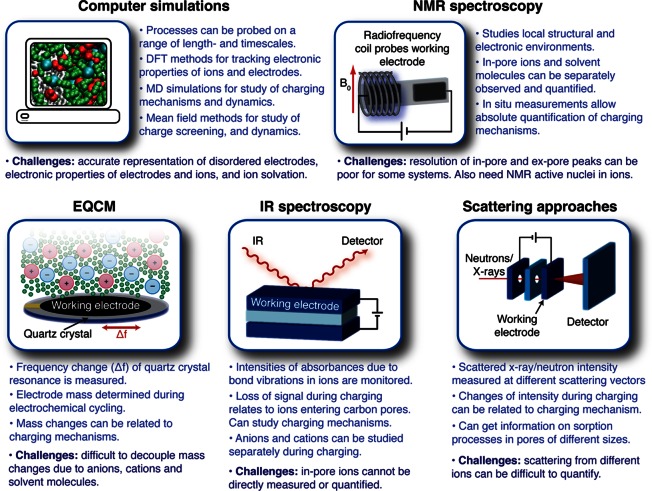
A schematic illustrating some of the main approaches that have been developed to study the charging mechanisms of supercapacitors is shown in Figure 4. Computational methods have been extremely successful in this area as they allow one to probe local length scales. The simulation of supercapacitors and their charging mechanisms presents a number of challenges which have been tackled through different approaches ranging from mean-field theories to MD simulations. One of the main difficulties is related to the complex structure of the carbon electrodes. In mean-field theories, electrodes are usually represented as single slit or cylindrical pores. In molecular simulations, it is also difficult to account for the complexity of the carbon structure as (i) an accurate description of the structure at the atomistic scale is not readily available and (ii) a realistic representation of the carbon structure requires the use of a large number of atoms in the simulations, which is time consuming. Nevertheless, MD simulations are valuable as they provide a precise description of the ion–ion correlations and packing effects that are important in the context of the concentrated electrolytes used in supercapacitors.

Figure 4.

Schematic showing the different approaches for studying the charging mechanisms of supercapacitors, and their advantages and challenges.

Another challenging aspect is the electronic conductivity of the carbon electrodes. Experiments and simulations have shown that the materials and conditions used in the carbon synthesis have a large effect on the ordering of the carbon sheets.^{12,13,15,38,61−63} This ordering, as well as the presence of functional groups, impacts the electronic conductivity of the carbons and their performances as electrode materials.^62,64,65 In molecular simulations, there are two main approaches to deal with the electrode charge: (i) constant charge and (ii) constant potential.^66,67 In the constant charge approach, charges are assigned to the carbon atoms at the beginning of the simulations and kept constant throughout. As such, this approach neglects the existence of charge redistribution on the electrode. The converse approach is to consider the electrode as metallic and include the fluctuation of carbon atom charges in the simulations.⁶⁸ While this approach is likely to be more realistic, especially for carbons with high degrees of order,⁶² it is much more computationally expensive and has been used in only a limited number of studies. Further work is needed to assess the validity of these different approaches and also to develop quantum mechanical methods to treat the carbon charge.

One way of circumventing the problem of computational cost is to explore the effects of confinement and polarization through analytical expressions. Indeed, while early theories considered ions as point charges and electrolytes as dilute, new advances in this field have allowed the inclusion of steric interactions and charge screening in the representation of the systems.^31,69 Such mean-field theories predicted the “superionic effect” which states that the packing of ions of the same charge is easier in confined spaces because of an exponential screening of the electrostatic interactions by the charged pore wall. This charge screening has recently been explored in more detail by inserting atoms in gold nanotubes and CNTs using DFT calculations.⁷⁰⁻⁷² The authors showed that the atoms were fully ionized upon insertion, turning the initially semi-conducting nanotubes into conductors. Both analytical theories and quantum chemistry simulations have provided valuable insights into the understanding of charging mechanisms by investigating the impact of charge screening. Nevertheless, the specific performances of different electrolytes, with or without solvent, can be understood only via techniques that explicitly account for ionic correlations, and the size and shape of the electrolyte molecules. Classical MD simulations are currently the method of choice here, although MD-DFT simulations will become increasingly important as computational power increases.

Ideally, MD simulations of supercapacitors would include a realistic representation of the carbon electrode structure, as well as a description of its electronic conductivity. As mentioned above, this is very challenging, as it involves using a large number of atoms for the carbon porous structure and a constant potential approach, which are both computationally expensive. To date, only a few studies have included both of these characteristics.^39,40,73,74 MD simulations have highlighted how the lack of “overscreening” effects in nanoporous electrodes contributes to the anomalous capacitance increase observed in nanometer-sized pores.³⁹ In nanoporous electrodes, only a single layer (or a few layers) of adsorbed ions is present between the pore walls.³⁹ This is in stark contrast to planar electrode surfaces, such as the graphite surface, where several layers of ions of alternating charge extend from the charged surface into the bulk.^75,76 At planar surfaces, the first layer of adsorbed counter-ions carries a greater charge than the electrode surface (“overscreening” the surface charge), and subsequent layers of co-ions and counter-ions then balance the excess charge in the first layer. The lack of overscreening in nanoporous electrodes does not, however, account for all of the anomalous capacitance, and hence a more atomistic/molecular understanding of charge storage is required. To this end, MD simulations of a pure ionic liquid (BMI–PF₆) and CDC electrodes have shown that charge storage does not occur by counter-ion adsorption alone (Table 2).³⁹ In the positive electrode, charging occurred by a combination of ion exchange and counter-ion adsorption (X = 0.34), while in the negative electrode charging was mainly by ion exchange, with a small amount of co-ion desorption (X = −0.11). Thus, it appears that the PF₆ anions are the more “active” species here, playing the dominant role in the charge storage process in both electrodes. Similar results were found for the same disordered carbon with the organic electrolyte (BMI–PF₆/ACN), showing that the solvent does not significantly affect the capacitance or charging mechanism (Table 2).^39,40 For a model supercapacitor system with slit-pore electrodes and the ionic liquid 1-ethyl-3-methylimidazolium– bis(trifluoromethanesulfonyl)imide (EMI–TFSI), charging in the positive electrode involved both ion exchange and co-ion desorption (X = −0.36), while charging in the negative electrode involved both ion exchange and counter-ion adsorption (X = 0.45); i.e., the EMI cations are more “active” in this system.⁴³ These observations for the different MD studies indicate that ion packing effects and ion–ion interaction energies influence the charging mechanism that operates. We note that, for an identical potential difference and a similar pore size, the difference between the number of anions and cations in the charged electrodes (which is proportional to the capacitance) is 4 times larger in the disordered CDC electrodes compared to the single slit pores (Table 2). This is partly because both sides of the carbon sheets are accessible to ions in the disordered electrodes while only a single surface is accessible in the slit-pore system. Accounting for this, the capacitance is still twice as large for the disordered electrodes, indicating that the curved and defective nature of the carbon sheets facilitates charge separation. It has been shown that more confined “pocket-like” ion adsorption sites allow the more effective storage of charge, than “plane” sites,⁴⁰ presumably because the curved surfaces maximize favorable Coulombic interactions between the carbon surfaces and the counter-ions (while also screening repulsive interactions between different counter-ions). These effects result in a much larger capacitance for disordered porous electrodes and highlight the importance of using complex porous carbon structures in simulations of supercapacitors.

Table 2. Details from MD Simulations at a Charging Voltage of 1 V^a.

carbon, electrolyte	Ncounter-ion – Nco-ion (at 1 V)/mmol g–1	charging mechanism parameter, X
		positive electrode	negative electrode	ref
CDC, BMI–PF6 ionic liquid	1.12	0.34	–0.11	(39)
CDC, BMI–PF6/ACN (1.5 M)	1.03	0.57	–0.02	(40)
slit pore (1.1 nm), EMI–TFSI	0.33	–0.36	0.45	(43)

^aN_counter-ion – N_co-ion is proportional to the excess ionic charge (which is in turn directly proportional to gravimetric capacitance). Charging mechanism parameters, X, are also given.

Besides providing a microscopic picture and fundamental understanding of the local processes occurring during supercapacitor charging, both mean-field theories and molecular simulations can be used to explore new ideas to improve energy storage efficiency in supercapacitors. An interesting example of these hypothetical explorations is the concept of ionophobicity and ionophilicity. Simulations can be used to investigate the effects of having initially empty (ionophobic) pores, on both the energy stored and the charging rate.³⁵⁻³⁷ Both mean-field theories and MD simulations for single slit pores have shown that ionophobic pores perform better in terms of charging rate,³⁶ and suggest that, in some cases, the quantity of energy stored is higher for ionophobic pores.³⁷ One interesting aspect is that the charging of initially filled pores usually leads to an overfilling of the porosity, corresponding to a temporary state where the density of ions is higher than the final density at the end of charging. This type of phenomena raises the issues of kinetic barriers and the difference between static and dynamic charging of supercapacitors. While the effects of ionophobicity and ionophilicity are now well studied in idealized slit-pore geometries, it would be interesting to study similar ideas in realistic three-dimensional porous geometries where it was shown that charging mechanisms are different from slit pores due to local heterogeneities in the carbon structure.^77,78

3.3. Electrochemical Quartz Crystal Microbalance (EQCM)

Experiments using an EQCM were some of the first to investigate the molecular mechanisms of supercapacitor charging. Levi et al. demonstrated that by depositing porous carbon electrodes on a quartz crystal, it was possible to measure changes of electrode mass during the operation of a supercapacitor cell.⁷⁹ In practice, variations of the resonance frequency of the quartz crystal are measured, and these are converted into mass changes using the Sauerbrey equation.⁸⁰ These experiments have mostly been performed with dynamic charging conditions, with the voltage continuously swept between the voltage limits at a constant rate (i.e., cyclic voltammetry). The extracted mass changes are then typically compared to the predicted mass changes assuming the adsorption of a single counter-ion to balance each electronic charge in the electrode (i.e., assuming X = 1). While this assumption generally does not hold, deviations from the predicted mass changes can be used to infer the presence of ion-exchange, and qualitative studies of the supercapacitor charging mechanism are possible.

Initial studies of activated carbon electrodes with an aqueous CsCl (0.5 M) electrolyte suggested that counter-ion adsorption processes dominated the charging mechanism. In contrast, further experiments on tetrabutylammonium chloride (NBu₄Cl, 0.5 M aq), with the bulky NBu₄ cation, suggested that charging was brought about predominantly by the migration of chloride anions (i.e., counter-ion adsorption in the positive electrode, and co-ion desorption in the negative electrode), with these experiments providing the first evidence that the charging mechanism depends on the electrolyte.⁷⁹ In follow-on studies on organic electrolytes, different charging mechanisms could be discerned depending on the magnitude of the charge stored in the electrode (i.e., depending on the cell voltage), see Figure 5a.⁸¹ For low charge densities (region I), the measured mass change was smaller than that expected for pure counter-ion adsorption processes, indicating the presence of ion exchange. For larger (intermediate) charge densities (region II), the measured mass changes were consistent with a counter-ion adsorption mechanism. Finally, for high charge densities (region III), the measured mass changes were larger than those predicted for pure counter-ion adsorption, and it was suggested the source of the additional mass was extra solvent molecules that entered the electrode pores. This is surprising given that the pores are already densely packed with ions and solvent molecules, and we note that MD simulations have suggested that the in-pore solvent population does not significantly change during charging.^74,82 Further studies are thus needed to investigate how the in-pore solvent population varies during charging. Interestingly, when electrolytes with different cations were studied with EQCM (Figure 5b), it was shown that the ion-exchange processes in the negative electrode became more significant for electrolytes with bulkier cations (e.g., NBu₄–BF₄), with the role of desorption of the smaller anions becoming more important.⁸¹

Figure 5.

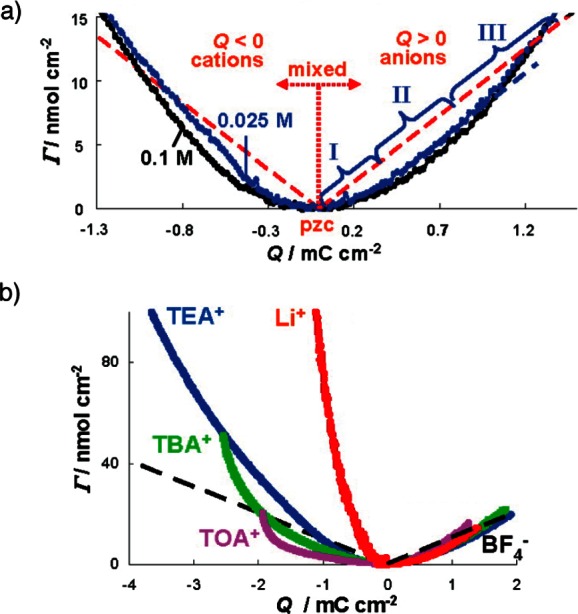
EQCM measurements of the charge storage mechanism of supercapacitors. Γ gives the moles of ions per surface area of quartz crystal, obtained from the measured electrode mass changes with the assumption of charge storage solely by counter-ion adsorption processes. Dashed lines showing theoretical Γ values for charging by pure counter-ion adsorption. (a) Measurements for YP-17 activated carbon and NEt₄–BF₄ in propylene carbonate (PC) solvent at two different concentrations. (b) Further measurements for YP-17 carbon supercapacitors with different electrolyte salts (0.1 M in PC): TEA⁺, TBA⁺, and TOA⁺ are tetraethylammonium, tetrabutylammonium, and tetraoctylammonium (NOc₄), respectively. Adapted with permission from ref (81). Copyright 2010 American Chemical Society.

More recently, EQCM methods have been applied to devices with EMI–TFSI ionic liquid and CDC electrodes.⁸³ Again, the charging mechanism was found to depend on the magnitude of the charge stored on the electrodes. In the positive electrode ion exchange was observed at low charge densities, with counter-ion adsorption processes then dominating at higher charge densities. In the negative electrode, on the other hand, counter-ion adsorption appeared to dominate over the full range of studied charge densities. Going further, the ionic liquids were diluted with ACN. Interestingly, the charging mechanism was largely unaffected by the presence of solvent, though additional mass changes were detected in the negative electrode, assigned to the solvent molecules that the EMI cations carried into the pores. Following the approach developed by Levi for aqueous electrolytes,⁸⁴ a solvation number of 3.7 could be estimated for the EMI cations by assuming a purely ion-adsorption-driven charging mechanism, and assuming that the unaccounted mass was due to ACN solvent molecules. Given the assumptions here, it would be beneficial if solvation numbers could be verified by a second method such as NMR spectroscopy (see later).

EQCM studies have advanced our understanding of supercapacitor charging mechanisms. However, a significant limitation of these studies is that a single parameter is measured (the electrode mass), which depends on the number of cations, the number of anions and the number of solvent molecules. Thus, the populations of the various in-pore species cannot be determined. This makes it difficult to fully quantify the charging mechanism and obtain X values, such that information from other experimental techniques is crucial.

3.4. Nuclear Magnetic Resonance (NMR) Spectroscopy

As discussed in section 2, NMR experiments allow the absolute quantification of ions inside the carbon nanopores, with the separate study of anions, cations, and solvent possible. Along with co-workers, we have developed the in situ NMR approach for studying supercapacitors, such that in-pore ion populations can be tracked at different charging potentials in working supercapacitor cells.^49,52,85,86 These measurements are typically performed in constant voltage mode; i.e., a fixed voltage is applied to the cell, and NMR spectra are acquired after equilibration of the system. A detailed overview of the in situ NMR methodology can be found elsewhere.⁸⁶

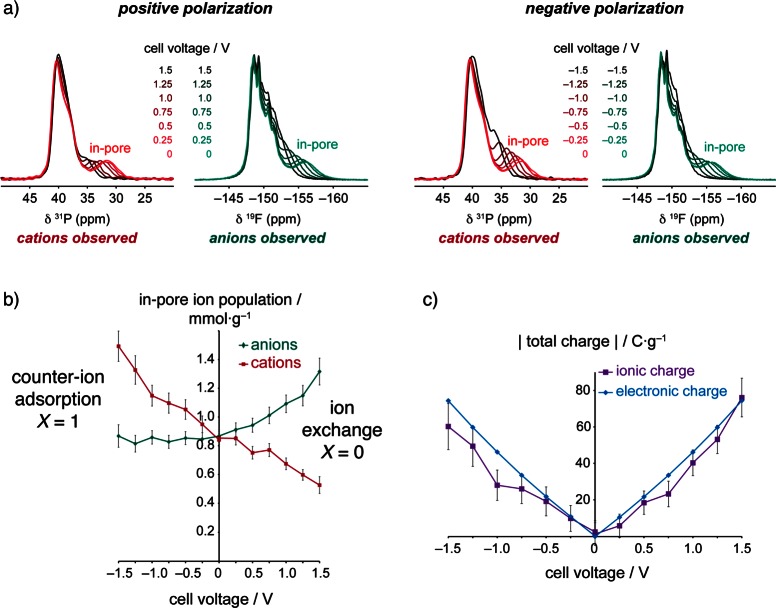
Figure 6a shows in situ NMR spectra for a supercapacitor cell with YP50F activated carbon electrodes and a PEt₄–BF₄/ACN (1.5 M electrolyte), with ³¹P and ¹⁹F NMR allowing the study of the PEt₄ cations and BF₄ anions, respectively.⁵² Changes of in-pore chemical shift during charging arise from the changes of the carbon electronic structure as electrons are added or removed from the electrodes.⁸⁶ Crucially, changes of in-pore peak intensities relate directly to changes of the in-pore ion populations. By fitting the spectra the number of in-pore cations and anions could be determined, revealing that the charge storage mechanism is inherently different depending on the polarization of the electrode (see Figure 6b).⁵² In the positive electrode, charging in this system occurs mainly by ion exchange (X = 0), with simultaneous counter-ion adsorption and co-ion desorption. In contrast, charging in the positive electrode occurs purely by counter-ion adsorption (X = 1). Despite the different charging mechanisms, the excess ionic charge in the carbon pores balances the electronic charge in both electrodes (Figure 6c). Interestingly, the charging mechanism was also found to be invariant to the concentration of the electrolyte, with the same mechanisms observed for concentrations of 1.5, 0.75, and 0.5 M. This mirrors observations on neat and diluted ionic liquids studied by EQCM⁸³ and MD simulations^39,40 above, and further confirms the idea that the solvent concentration does not necessarily dictate which charging mechanism operates, but simply modulates the absolute in-pore populations. In our study, the findings from the NMR measurements were corroborated by EQCM measurements, where a small negative mass change was observed in the positive electrode, as the slightly heavier cations were desorbed from the pores while the lighter anions were adsorbed. Meanwhile, a positive mass change was observed in the negative electrode, in agreement with the counter-ion adsorption mechanism revealed by NMR. The mass increase in this electrode was greater than that expected due to cation adsorption, and the additional mass was ascribed to solvent molecules, with an estimated cation solvation number of 5.4. ²H NMR experiments were also performed to study the deuterated acetonitrile solvent, though the large peak line widths precluded the quantification of the in-pore solvent. Future in situ NMR studies may allow quantitative measurement of in-pore ion solvation numbers, allowing comparison with the results from EQCM analysis.

Figure 6.

(a) In situ NMR measurements of a supercapacitor with YP50F electrodes and PEt₄–BF₄/ACN (1.5 M) electrolyte. (b) In-pore ion populations at different charging voltages, obtained by fitting of the spectra in (a). (c) Ionic charge stored by in-pore ions, obtained from the in-pore ion populations in (b), as well as electronic charge, obtained from electrochemistry data. Reprinted with permission from ref (52). Copyright 2015 Macmillan Publishers Ltd.

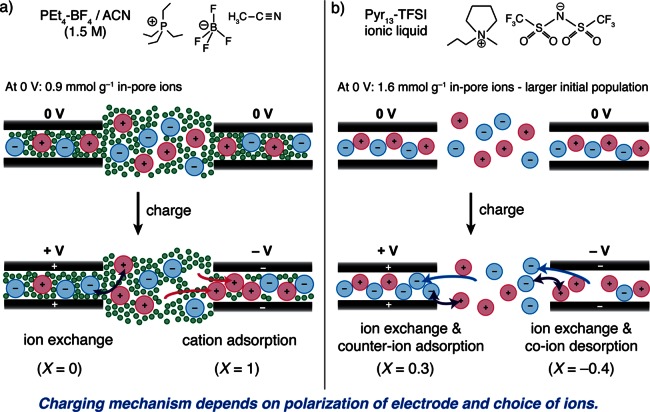
Further NMR measurements on the same activated carbon (YP50F) and a range of different electrolytes have revealed that the charging mechanism can vary significantly when different electrolyte ions are studied. Ex situ NMR studies of supercapacitors with the ionic liquid Pyr₁₃–TFSI showed that in the positive electrode charging took place by ion exchange and counter-ion adsorption (X = 0.3), while in the negative electrode ion exchange and co-ion desorption were observed (X = −0.4).⁵³ In this system the TFSI anions are more active in the charge storage than the Pyr₁₃ cations. This charging mechanism is markedly different to that observed for the PEt₄–BF₄/ACN system above, where the BF₄ anions played no significant role in charging in the negative electrode (see schematic in Figure 7). Similarly, in situ¹⁹F NMR measurements on YP50F with Li–TFSI/ACN (1.5 M) and Na–TFSI/ACN (1.5 M) electrolytes revealed significant co-ion desorption processes in the negative electrode, though the cations were not studied.⁴⁹ The exact origin of these different charging mechanisms is currently unclear, but ion packing and ion–carbon interaction energies are expected to be important. Co-ion (anion) desorption was also observed in the positive electrode of a supercapacitor with the electrolyte NBu₄–BF₄, suggesting that the large size of the NBu₄ cations impeded their adsorption into the carbon pores, necessitating desorption of anions to store charge.⁴⁹ This finding is consistent with EQCM studies on activated carbons, where the role of the anions (co-ions) in the negative electrode became more significant for electrolytes with larger cations.⁸¹ It should, however, be kept in mind that the EQCM measurements were performed in a dynamic mode, with the frequency response of the quartz crystal measured during cyclic voltammetry measurements. Such dynamic measurements with EQCM are more likely to reveal kinetic effects (e.g., effects due to the different diffusion rates of the anions and cations) than the in situ NMR measurements that were performed at equilibrium after charging to a specific voltage.

Figure 7.

Schematics showing charge storage mechanisms determined by NMR experiments. For the same activated carbon (YP50F) electrodes, the charging mechanism differs depending on the electrolyte: (a) PEt₄–BF₄/ACN (1.5 M) and (b) Pyr₁₃–TFSI ionic liquid. Calculations of X are also given based on the experimental data. Note in part (b) the X value given for the negative electrode is the experimentally measured one, whereas based on the number of ions in the schematic one obtains an X value of −0.3. This simplification maintains clarity in the schematic. See refs (52) and⁵³ for the original studies.

Other research groups have also applied NMR methods to the study of supercapacitor charging mechanisms. Ex situ NMR measurements by Deschamps et al. on NEt₄–BF₄/ACN showed that ion-exchange processes operated in both the positive and negative electrodes of two different activated carbons.⁴⁸ More recently, Luo et al. have applied the in situ NMR methodology to supercapacitors with aqueous electrolytes.^54,55 They studied an activated carbon material with small pores that were inaccessible to the ions (Na⁺ and F^–) in the absence of an applied potential.⁵⁵ However, when a potential above 0.4 V was applied, the F^– anions were able to enter the pores of the positive electrode, with charging proceeding via counter-ion adsorption. Following discharge to 0 V, some ions remained in the carbon pores, suggesting the presence of a hysteresis in the charging mechanism. Interestingly, changes of in-pore chemical shift at ∼0.8 V indicated that the solvation number of the ions decreased above this voltage.

The strength of the NMR approach arises from the ability to separately observe and quantify in-pore ions, as well as to separately detect anions and cations. This allows the absolute quantification of supercapacitor charging mechanisms (and X values can be determined). The technique, however, is limited to ions with NMR active nuclei, and if many experiments are to be performed at different voltages, ions containing sensitive nuclei such as ¹H, ¹⁹F, ³¹P, ⁷Li, ¹¹B, and ²³Na must generally be studied. Another limitation is that in some cases the in-pore resonances cannot be clearly resolved (e.g., due to broad peaks, or small ring current shifts), and methods should thus be developed to improve spectral resolution for challenging carbon and electrolyte systems. For example, we have shown how cross-polarization experiments can be used to edit the NMR spectrum to reveal peaks solely due to ions at the carbon surface (i.e., in-pore ions).⁴⁴

3.5. Infrared (IR) Spectroscopy

Beyond EQCM and NMR, IR spectroscopy has also been demonstrated as a useful probe of supercapacitor charging mechanisms.^87,88 Here, changes in intensity of the absorbances from bond vibrations in the electrolyte anions and cations are monitored during charging, allowing the behavior of the two ions to be tracked separately. The IR radiation is directed on the working electrode of a supercapacitor cell (which is clamped onto the surface of a diamond attenuated total reflectance (ATR) crystal), and the reflected signal intensity is recorded to obtain an absorbance spectrum. In these measurements the IR radiation penetrates to ∼1 μm depth in the working electrode.

In experiments on titanium carbide-derived carbon (TiC-CDC) supercapacitors with ionic liquid (EMI–TFSI) electrolyte, approximately equal losses of intensity were observed for both the anion and cation absorbances during charging, suggesting that both ions penetrated deeper into the carbon particles, beyond the depth to which the IR photons were able to penetrate.⁸⁷ This was explained by postulating that both anions and cations had entered the carbon nanopores during charging, with experiments on nonporous onion-like carbons revealing no significant changes of absorbance during charging and supporting the hypothesis. These experiments demonstrated that ions entered the carbon nanopores during charging, though the charging mechanism was not fully quantified. Further experiments with EMI–TFSI and nanoporous carbon nanofiber (CNF) electrodes revealed similar losses of intensity for anions and cations in the positive electrode,⁸⁸ though the intensity loss was more significant for the anions than the cations, explaining how an excess of ionic charge could develop inside the carbon pores. Experiments were also performed on modified CNFs, which had been activated with KOH at 800 °C and contained more oxygen-containing functional groups. In contrast to the measurements on the untreated CNFs, an increase in intensity was observed for the cation absorbances, indicating that cations were desorbed from the nanopores of the CNFs in the positive electrode. Together with the observation of the loss of intensity of the anion absorbance (as anions entered the pores of the CNFs), it was shown that an ion-exchange mechanism was operating. The measurements intriguingly showed how the charging mechanism of supercapacitors is dependent on the surface chemistry of the carbon materials.⁸⁸ IR spectroscopy experiments have revealed new insights into the charging mechanisms of supercapacitors. However, a key limitation of the IR approach is that the in-pore ions cannot be directly detected, and instead one must rely on measurements of the bulk electrolyte surrounding the carbon particles. It is therefore challenging to make fully quantitative studies of the supercapacitor charging mechanism, and X values cannot be readily determined.

3.6. Scattering Approaches

Scattering-based methods have also been applied to the study of supercapacitor charging mechanisms. In situ SANS experiments utilize the different scattering properties of the various atoms in the electrolyte and electrode. By measuring the scattered neutron intensity from a single (working) electrode at different charging potentials, qualitative changes of the in-pore ion populations can be obtained. For example, in a study of aqueous H₂SO₄ electrolytes in activated carbon fabric electrodes, changes of scattered intensity were dominated by the migration of the hydrogen-containing ions and solvent molecules.⁵⁷ On this basis it was inferred that ion-exchange processes bring about charging in activated carbon fabric electrodes, for example, with H₃O⁺ replacing HSO₄^– and SO₄^2– in the negative electrode. Similar findings were obtained for devices with the organic electrolyte NEt₄–BF₄ in dACN (1 M).⁵⁶ Here, the increase in scattered intensity in the negative electrode indicated that the strong H-containing scatterers NEt₄⁺ were adsorbed into the carbon pores, while neutron-absorbing ¹⁰BF₄^– were desorbed from the pores, i.e., an ion-exchange mechanism. Converse effects were observed in the positive electrode, again rationalized by an ion-exchange mechanism. An interesting feature of small-angle scattering measurements is that adsorption/desorption processes can be monitored as a function of the carbon pore size. Boukhalfa et al. found that the largest changes of scattered intensity were observed for the smallest pores (i.e., at large scattering wavevectors). These measurements have the potential to complement MD simulations, where the relative ion populations in pores of different geometries and sizes can be tracked.⁴⁰ However, in the SANS measurements full quantification of the in-pore ionic species at different potentials was not possible as the scattered neutron intensity (a single measured quantity) depends on the population of anions, cations, and solvent molecules.

A recent study by Prehal et al. developed in situ X-ray transmission (XRT) and SAXS methods to provide deeper insights into the charging mechanisms of supercapacitors with simple aqueous electrolytes (CsCl, KCl, and NaCl, all 1 M concentration) and the activated carbon YP-80.⁵⁸ SAXS measurements on evacuated and electrolyte-soaked carbon electrodes confirmed that the pores were filled with electrolyte at 0 V. Variations of the XRT intensity during electrochemical cycling, taken together with the electrochemical data, then allowed semi-quantitative measurements of the changes of ion concentrations at different charging potentials. The analysis relies on the different X-ray attenuation coefficients of the cations and anions, and it is assumed that changes of the amount of solvent (water) have no significant effects on the XRT signal. This analysis showed that an ion-exchange mechanism (X = 0) occurs for all three electrolytes studied, with the charging mechanism independent of the choice of cation. In situ SAXS measurements were consistent with these findings and also indicated that the counter-ions became more closely associated with the pore surfaces as the potential was increased.⁵⁸ Further work with scattering-based approaches stands to further our understanding of supercapacitor charging mechanisms.

4. Summary and Outlook

In summary, NMR spectroscopy measurements and MD simulations have shown that the pores of the carbon electrodes contain a considerable number of electrolyte ions in the absence of an applied potential. Larger in-pore populations are observed for more concentrated electrolytes, with the largest populations observed for ionic liquids. Given the large in-pore ion population in the absence of an applied potential, different charging mechanisms can operate when a potential is applied: counter-ion adsorption, co-ion desorption, and ion exchange (and combinations of these). We have introduced the charging mechanism parameter, X, to allow a convenient comparison of different charging mechanisms. In situ characterization experiments (NMR, EQCM, IR, and scattering methods) and simulations have shown that supercapacitor charging does not generally take place by counter-ion adsorption alone, as is the traditional view, and ion exchange plays an important role in the charge storage process. As shown by Table 3, in a wide range of experimental and computational studies, charging almost always involved some degree of ion exchange (X ≠ 1), and only rarely was charging driven purely by counter-ion adsorption (X = 1). Experiments have shown that the exact charging mechanism depends on the polarization of the electrode, the choice of electrolyte ions, and the choice of electrode material (Table 3). Surprisingly, the solvent concentration does not appear to significantly influence the charging mechanism that operates (Table 3), and it appears the role of the solvent is less significant than previously thought. This suggests that ion confinement effects,⁴⁰ screening of ions by the carbon surfaces,³¹ as well as the lack of overscreening³⁹ dominate the capacitance increase reported for nanoporous carbons,^24,25 rather than ion desolvation, while different in-pore ion populations at 0 V and fundamentally different charging mechanisms may also play a role. The wide range of charging mechanisms (X values) presented in Table 3 indicate that factors such as ion-packing energies and ion–carbon interaction energies dictate which charging mechanism is the thermodynamic one. Under dynamic (fast) charging conditions the charging mechanism may differ, though studies contrasting thermodynamic and kinetic charging mechanisms have not yet been carried out. When studying Table 3 it should be kept in mind that only NMR and MD simulations allow the absolute quantification of the different electrolyte species at different potentials, and that various assumptions must be made when inferring charging mechanisms from other in situ methods (e.g., with EQCM changes of in-pore anion, cation, and solvent populations have to be determined from a single measured parameter, the electrode mass).

Table 3. Selected Charging Mechanisms from in situ Characterization Methods and Computer Simulations^a.

	carbon, electrolyte		charging mechanism
method		cycling mode	positive electrode	negative electrode	ref
NMR	YP50F, PEt4–BF4/ACN (1.5 M)	static	ion exchange (X = 0)	counter-ion adsorption (X = 1)	(52)
NMR and EQCM	YP50F, PEt4–BF4/ACN (0.75 M)	static
NMR	YP50F, PEt4–BF4/ACN (0.5 M)	static
NMR	YP50F, Pyr13–TFSI ionic liquid	static	ion exchange and counter-ion adsorption (X = 0.3)	ion exchange and co-ion desorption (X = −0.4)	(53)
MD	CDC, BMI–PF6 ionic liquid	static	ion exchange and counter-ion adsorption (X = 0.34)	ion exchange and co-ion desorption (X = −0.11)	(39)
MD	CDC, BMI–PF6/ACN (1.5 M)	static	ion exchange and counter-ion adsorption (X = 0.57)	ion exchange and co-ion desorption (X = −0.02)	(40)
MD	slit pore (1.1 nm), EMI–TFSI ionic liquid	static	ion exchange and co-ion desorption (X = −0.36)	ion exchange and counter-ion adsorption (X = 0.45)	(43)
NMR	ACs, NEt4–BF4/ACN (1 M)	static	ion exchange (X = 0)	ion exchange (X = 0)	(48)
XRT	YP-80, CsCl (aq) (1 M)	dynamic	ion exchange (X = 0)	ion exchange (X = 0)	(58)
XRT	YP-80, KCl (aq) (1 M)	dynamic
XRT	YP-80, NaCl (aq) (1 M)	dynamic
EQCM	CDC, EMI–TFSI ionic liquid	dynamic	low V, ion exchange; high V, counter-ion adsorption	counter-ion adsorption	(83)
EQCM	CDC, EMI–TFSI/ACN (1.5 M)	dynamic
EQCM	YP17, NEt4–BF4 (0.1 M)	dynamic	low V, ion exchange; high V, counter-ion adsorption	low V, ion exchange; high V, counter-ion adsorption as above, except ion exchange over wider V range	(81)
EQCM	YP17, NOc4–BF4 (0.1 M)	dynamic
IR	CNFs, EMI–TFSI ionic liquid	dynamic	involves counter-ion adsorption	not studied	(88)
IR	modified CNFs, EMI–TFSI ionic liquid	dynamic	involves ion exchange	not studied

^aX values are given where possible.

Further in situ characterization of supercapacitors with a wide range of different electrolytes and carbon materials will help to fully elucidate the factors which control supercapacitor charging mechanisms. As discussed above, each in situ characterization method comes with its limitations, and these methods must be further developed such that they can be applied to a wide range of systems in a quantitative manner, and on a range of charging time scales. Beyond experiments, advanced theoretical methods that can properly take into account the electronic structure of the ions and carbon electrodes could provide new insights. If one can properly understand the factors that influence the charging mechanism, it should be possible to tailor the mechanism by choice of the correct electrolyte-electrode combination. In particular, it would be interesting to study the relative magnitudes of ion–ion and ion–carbon interaction energies within the carbon pores. Additionally, one could investigate packing effects by studying ions with different shapes and sizes within carbon pores of different geometries. It is clear that systematic studies in which the electrolyte and carbon structure are varied independently will allow the understanding to progress here.

This leads to an important question: How does the charging mechanism affect the performance of a supercapacitor? The mechanism should have a significant effect on the power that supercapacitors can offer, and tailoring the mechanism may allow us to improve the power performance of devices. Indeed, theoretical work has indicated that initially empty pores (ionophobic pores) should charge more quickly than initially filled pores (ionophilic pores),³⁶ though this effect is yet to be realized experimentally. Similarly, we expect that ion adsorption, ion exchange, and ion desorption mechanisms from initially filled pores should each result in different device power performances, and work must be done to establish which mechanism is optimal for fast charging. Purely counter-ion adsorption processes might be expected to allow fast charging in a front-like manner, with net migration of ions into the interior of the carbon nanoporosity, while ion exchange requires ionic migration in opposite directions. At the same time, these different mechanisms will bring about changes of in-pore ionic density, and therefore packing during charging, which will also affect the charging rate. For example, counter-ion adsorption mechanisms will increase the number of ions inside the carbon pores, and recent theoretical work has suggested that more densely packed pores result in slower ionic diffusion.⁸⁹ As well as ion packing effects, interactions of the different ions with charged carbon surfaces will also affect in-pore transport processes.⁷⁸ Clearly, experimental measurements and simulations of diffusion and migration processes in charged carbon nanopores represents another exciting area of research.

In principle, the charging mechanism will affect the capacitance, and therefore the energy density, that can be achieved in supercapacitors. Under thermodynamic conditions, the charge storage mechanism which operates is the one that minimizes the increase in free energy associated with charging, thus minimizing the voltage increase per unit charge (i.e., maximizing the capacitance as C = Q/V). Kondrat and Kornyshev point out that counter-ion adsorption is disfavored here, as there is an entropic penalty for an ion entering a pore, and there are also unfavorable electrostatic (enthalpic) terms associated with the packing of ions of the same charge inside the carbon pores (though this is alleviated to some extent by charge screening from the pore walls).³⁷ In principle, the ion-exchange mechanism reduces the enthalpic penalty associated with denser ion packing because the total in-pore density remains essentially constant during charging, while the entropic penalty associated with charging will also be reduced. This may help to explain the prevalence of ion exchange mechanisms revealed by in situ characterization methods detailed in this article (Table 3). Charging by co-ion desorption should minimize the enthalpic penalty due to interactions between like charges, while also increasing entropy, and should thus maximize the capacitance.³⁷ That said, charging by purely co-ion desorption (X = −1) has not yet been observed, indicating that other factors beyond these simple arguments are important. It is clear that additional work must be done to understand the interplay between supercapacitor charging mechanisms and capacitance. Under kinetic control, the charging mechanism will depend on the relative rates of in-pore motion of the anions and cations, and we again stress the need for further experimental and theoretical studies of these effects. If the diffusion rates of the different in-pore ions can be controlled, then it should be possible to control the kinetic charging mechanism and thus improve the capacitance.

Finally, we stress that the structural complexity^17,18 of porous carbon electrodes poses a significant challenge as we aim to design enhanced supercapacitors. Ideally the electrode structure would be modified in a controlled way to study its performance, though for this to happen new tools must be developed to characterize and model amorphous carbon structures.¹⁵ Beyond activated carbons, more ordered carbon materials based on nanotubes, graphenes, and templated materials may serve as model systems to probe structure–property relationships.

The authors declare no competing financial interest.

Notes

This is a review article, and therefore all data underlying this study is cited in references.