Identification and Structural Characterization of an Intermediate in the Folding of the Measles Virus X Domain

Abstract

Although most proteins fold by populating intermediates, the transient nature of such states makes it difficult to characterize their structures. In this work we identified and characterized the structure of an intermediate of the X domain of phosphoprotein (P) of measles virus. We obtained this result by a combination of equilibrium and kinetic measurements and NMR chemical shifts used as structural restraints in replica-averaged metadynamics simulations. The structure of the intermediate was then validated by rationally designing four mutational variants predicted to affect the stability of this state. These results provide a detailed view of an intermediate state and illustrate the opportunities offered by a synergistic use of experimental and computational methods to describe non-native states at atomic resolution.

Introduction

A major goal in protein folding studies lies in identifying intermediates and in characterizing their structure (1–8). This task is often challenging because, as marginally stable, folding intermediates are elusive and can be detected only transiently during the folding reaction. The combination of experimental and theoretical approaches represents a powerful strategy to address this problem, providing the possibility to unveil the molecular structure of folding intermediates and to define their role in the reaction mechanism.

The viral polymerase complex of paramyxoviruses is composed by the protein L and by the phosphoprotein P (9–11). In measles virus (a member of the Morbillivirus genus), the C-terminal region of phosphoprotein P is a globular domain of 49 amino acids, called X domain (XD),² composed of three α-helices organized as an anti-parallel bundle (12). Previous investigations on measles virus XD have suggested this domain to be structurally heterogeneous, populating at least two alternative conformations under native conditions (13). This feature is consistent with the findings of Kingston et al. (14), who suggested that the native state of XD from mumps virus (a Rubulavirus member) represents an example of folding induced by crystal packing effects. Notably, the lack of a unique stable three-dimensional structure is not a feature unique to mumps virus XD, being also shared by the corresponding domains from other rubulaviruses that were found to populate in solution a structural continuum ranging from stable α-helical bundles to largely disordered (15). Because of such heterogeneity, XD represents an ideal candidate for folding studies, as it is likely to populate partially structured states at equilibrium, displaying an overall stability comparable with that of the native conformation.

In this work we characterized the folding pathway of XD, and present the high resolution structure of an intermediate while characterizing its mechanistic role in time-resolved kinetic experiments. The occurrence of a folding intermediate is supported by the observation of bi-phasic (un)folding transitions in discharge-induced temperature-jump experiments as well as by all-atom replica-averaged metadynamics simulations with NMR chemical shift restraints. In an effort to further address the structure of the intermediate state, we designed rationally and characterized experimentally mutational variants that selectively tune the stability of this state with respect to that of the native state.

Experimental Procedures

Experiments were performed on a fluorescent pseudo-wild type XD variant Y480W, which was previously produced and characterized. All proteins were expressed and purified as described (16). All reagents were of analytical grade.

Circular Dichroism Equilibrium Experiments

Circular dichroism equilibrium denaturation experiments were carried out on a JASCO circular dichroism (CD) spectropolarimeter (Jasco, Inc., Easton, MD). CD spectra were recorded between 200 and 250 nm using a quartz cuvette with a light path of 1 cm, at different urea concentrations. For each urea concentration three spectra were averaged. Protein concentration was typically 10 μm, and the buffer used was 50 mm sodium phosphate, 300 mm NaCl at pH 7.2. The experiments were performed at 25 °C.

Fluorescence Equilibrium Experiments

Fluorescence equilibrium denaturation experiments were carried out using a Fluoromax single photon counting spectrofluorometer (Jobin-Yvon, Edison, NJ). Emission spectra were recorded between 300 and 400 nm using a quartz cuvette with a light path of 1 cm, at different urea concentrations. The excitation wavelength was 280 nm. Protein concentration was typically 5 μm, and the buffer used was 50 mm sodium phosphate, 300 mm NaCl at pH 7.2. The experiments were performed at 25 °C.

Temperature-jump Fluorescence Spectroscopy

Kinetic (un)folding experiments were performed using a Hi-Tech PTJ-64 capacitor-discharge T-jump apparatus (Hi-Tech, Salisbury, UK). Temperature was rapidly changed with a jump-size of 9 °C, from 16 °C to 25 °C. The fluorescence change of N-acetyltryptophanamide (NATA) was used in control measurements. Degassed samples were slowly pumped through the 0.5 × 2-mm quartz flow cell before data acquisition. Usually 10 individual traces were averaged. The excitation wavelength was 296 nm, and the fluorescence emission was collected using a 320-nm cut-off glass filter. Protein concentration was typically 100 μm, and the buffer used was 50 mm sodium phosphate, 300 mm NaCl at pH 7.2.

Replica-averaged Metadynamics Simulations

Replica-averaged metadynamics simulations (17, 18) were performed using GROMACS compiled with PLUMED and ALMOST (19). The system was simulated using the Amber03W force field (20) in explicit TIP4P05 water (21). Van der Waals and short-range electrostatic interactions were cut off at 0.9 nm, whereas long range electrostatic interaction was treated with the Particle Mesh Ewald method and a mesh size of 0.12 nm (22). The isothermal-isobaric ensemble was enforced using the Bussi thermostat (23) at 300 K and the Parrinello-Rahman barostat (24) at 1 bar. The starting conformation for XD was taken from the 2K9D NMR solution structure (25). The structure was solvated with 5845 water molecules and 3 chloride ions.

Replica-averaged metadynamic simulations were performed using chemical shifts as replica-averaged restraints and bias-exchange metadynamics (18). Four replicas of the system were simulated in parallel with a restraint applied on the square difference between the CamShift (26) back-calculated NMR chemical shifts for the Hα and HN hydrogens and the experimental data using a force constant of 6 and 3 kJ/(mol ppm²), respectively. Each of the four replicas is bias along one of the following four collective variables: α-helical content, radius of gyration, root mean square deviation from the crystal structure calculated over the Cα carbons, and number of contacts among the heavy atoms of the hydrophobic residues. Gaussian deposition was performed with an initial rate of 0.125 kJ/mol/ps, a bias factor of 10, and with σ values set to 0.2, 0.005, 0.1, and 0.25, respectively. Each replica was been evolved for 180 ns, with exchange trials every 50 ps.

Results and Discussion

Detection of an Intermediate in the Folding Pathway of XD

Urea-induced denaturation of XD was monitored both by far-UV CD and by Trp fluorescence emission (Fig. 1A). In each data set the apparent equilibrium transition was consistent with a two-state sigmoidal transition (27); however, a comparison between these different techniques highlighted an additional complexity. In fact, the denaturation midpoint shows a small difference, 5.4 ± 0.1 m from CD experiments and 5.0 ± 0.1 m from fluorescence, with a similar m value of ∼0.7 ± 0.1 kcal mol⁻¹ m⁻¹. These differences, which are just larger than the sensitivity of the experiments, would suggest the presence of an equilibrium folding intermediate (28) and demand additional investigation.

FIGURE 1.

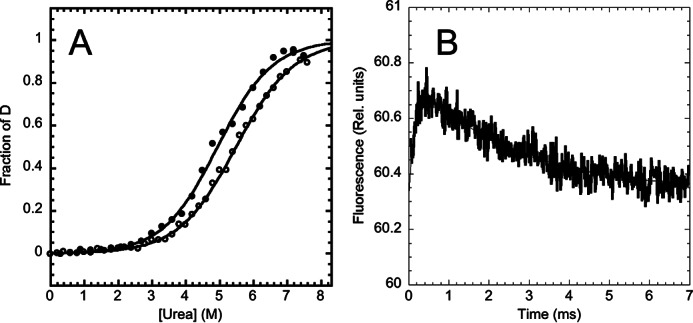
Equilibrium and time resolved unfolding of XD, the X domain of the phosphoprotein P, as follows at pH 7.2, 50 mm sodium phosphate, 300 mm NaCl, and 25 °C. Panel A, urea-induced equilibrium denaturation of XD, monitored by fluorescence (close circles) and CD (open circles). Both fluorescence and CD, recorded at multiple wavelengths, were fitted to a two-state (continuous lines). Panel B, temperature jump induced unfolding transition of XD, induced by a rapid jump of 9 °C to a final temperature of 25 °C.

The (un)folding time course of XD in the absence of denaturant, measured by T-jump, is reported in Fig. 1B. The time-resolved fluorescence conforms to a double exponential decay, the two kinetic phases displaying, in the absence of denaturant, similar relative amplitude but opposite sign. This finding confirms unequivocally that the folding of XD implies the presence of an intermediate, which is remarkably populated at equilibrium also in the absence of denaturant. Importantly, because the observed transition displays two distinct kinetic phases, it follows that the intermediate state displays a fluorescence emission, which is different from that of the denatured and native states.

The urea dependence of the two kinetic rate constants λ₁ and λ₂ is reported in Fig. 2 (chevron plot). Given the relatively low stability of the intermediate, we could not observe the fast phase λ₁ at urea concentrations higher than 3 m. A folding intermediate may represent either an on-pathway species en route to the native state or a misfolded off-pathway kinetic trap competing with productive folding, with the two different scenarios displaying characteristic signatures in the corresponding chevron plots (2, 3, 7, 29–34). In fact, although the off-pathway kinetic model implies the microscopic rate constant k_ID (i.e. the rate constant for the unfolding of the intermediate to the denatured state) as necessarily faster than the observed rate constant λ₂, the on-pathway model does not imply this constraint. To quantitatively describe the folding pathway of XD, we globally fitted the chevron plots for the two observed relaxation rate constants. As shown in Fig. 2, both the on- and off-pathway models fit fairly well with the experimental data and, therefore, remain indistinguishable at this stage. The main difference between the two models lies in the lower stability of the intermediate state predicted by the off-pathway model, corresponding to a maximal difference in stability between I and D being 0.4 ± 0.1 kcal mol⁻¹, which in turn suggests a negligible population of the intermediate state in the absence of denaturant (≪1% of the molecules). The calculated rate constants from the global analysis arising from the two curve-fitting are listed in Table 1 together with the predicted stability of the intermediate and native states for the two different scenarios. Analysis of the calculated m values, reported in Table 1, suggests that the intermediate state is relatively compact, the β_T values being 0.8 ± 0.1 and 0.6 ± 0.1, as calculated from the on-pathway and the off-pathway scenarios, respectively.

FIGURE 2.

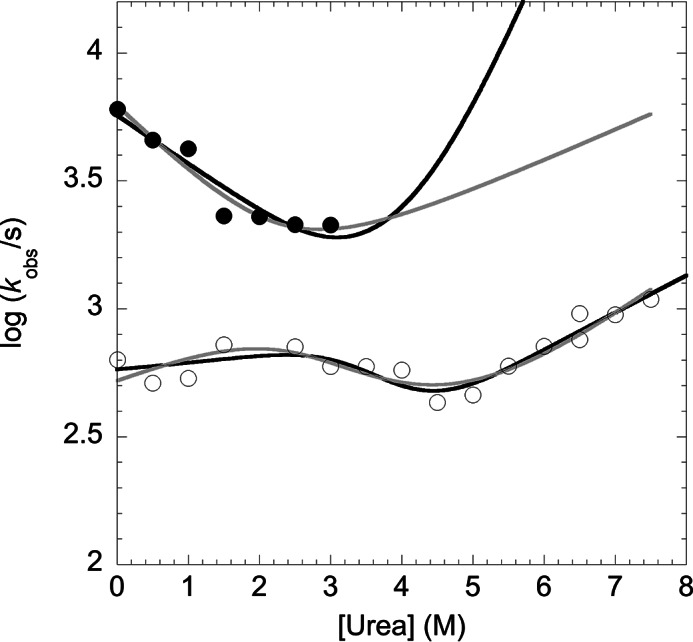
Chevron plot of XD. The urea dependence of the fast λ₁ (closed circles) and slow λ₂ (open circles) folding phases of XD is reported. The lines are the best global fit to an on-pathway (black) and off-pathway (gray) scenario. It must be noted that the off-pathway model would imply the microscopic rate constant k_ID (for the transition from the intermediate to the denatured state) to be necessarily faster than the observed rate constant λ₂, accounting for a maximal stability of I versus D of 0.4 ± 0.3 kcal mol⁻¹.

TABLE 1.

Kinetic folding parameters of XD

D, I, and N indicate denatured, intermediate and native states.

	kDIa	kIDa	kINa	kNIa	kDNa	kNDa	ΔGDI	ΔGIN
	s−1	s−1	s−1	s−1	s−1	s−1	kcal mol−1	kcal mol−1
On pathway	5700 ± 500 (0.2 ± 0.05)	2.9 ± 0.7 (0.8 ± 0.05)	480 ± 70 (0.04 ± 0.05)	94 ± 10 (0.2 ± 0.03)			4.2 ± 0.9 (1.0 ± 0.07)	0.9 ± 0.1 (0.24 ± 0.07)
Off pathway	1400 ± 300 (0.3 ± 0.05)	683 ± 60 (0.16 ± 0.05)			4700 ± 900 (0.5 ± 0.1)	39 ± 0.01 (0.25 ± 0.05)	0.4 ± 0.1 (0.46 ± 0.07)	2.3 ± 0.5 (0.30 ± 0.15)

^a The microscopic rate constants were calculated by globally fitting the two observed relaxation rate constants to the analytical solution of a three-state mechanism involving an off-pathway intermediate. The m value associated to each rate constant, expressed in kcal mol⁻¹·m⁻¹, is reported in parentheses.

Structure of the Folding Intermediate

To provide a structural characterization of the folding intermediate, we performed all-atom replica-averaged metadynamics simulations with the previously published NMR chemical shift of XD as structural restraints (17, 18, 35, 36). This approach is based on the observation that, given that the relaxation kinetics suggests that the intermediate is significantly populated even in the absence of denaturant, it may be possible to detect the structure of the intermediate in the structural ensemble of XD, obtained under native conditions.

Simulations were performed at 300 K using chemical shifts as replica-averaged structural restraints over 4 replicas and bias-exchange metadynamics to enhance the sampling, as previously described (17, 18, 35, 36). Metadynamics was applied on four collective variables, namely the α-helical content, the radius of gyration (R_g), the root mean square deviation from the crystal structure calculated over the Cα carbons, and the number of contacts among the heavy atoms of the hydrophobic residues. The conformational search was limited up to 6 Å from the crystal structure to avoid a complete unfolding of the protein. After 140 ns of simulation per replica the free energies as a function of the collective variables were converged, and the simulations were extended up to 180 ns per replicas.

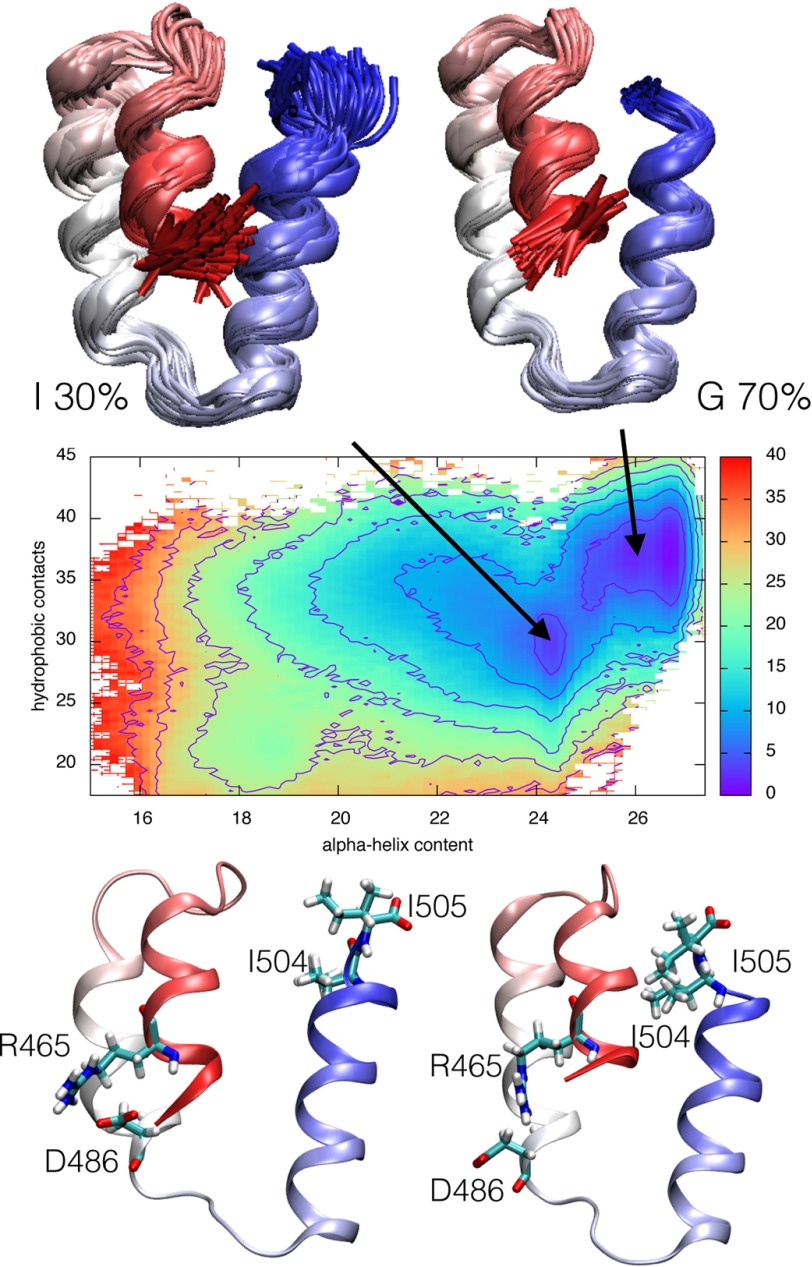
The effect of the bias on the simulations was removed using a weighted-histogram analysis technique (37), and the resulting ensemble was clustered in the four-dimensional space defined by the selected collective variables. We thus determined the presence of two major states populated at ∼70 and 30%, respectively (Fig. 3). The most relevant population of the ensemble is structurally homogeneous and superposes well onto the native state of XD, as determined by x-ray crystallography (PDB code 1OKS) (12). On the other hand, the alternative conformational ensemble of XD, although characterized by a native-like content of secondary structure, displays a different structural organization of the three-helix bundle, with a much stronger heterogeneity. This less populated state was taken to reflect the structure of the intermediate state.

FIGURE 3.

Free energy surface (in kJ/mol) of the replica-averaged metadynamic XD ensemble as a function of α-helical content and number of hydrophobic contacts. The projection highlights a 70% populated ground state and a 30% populated intermediate state. The two states are represented as an ensemble of structures (top) as well as an average structure (bottom).

To validate the structural ensembles described above, the chemical shifts for both the H_N and Hα atoms were calculated and compared with those experimentally determined by NMR and those calculated from the crystal structure (supplemental Fig. S1). It is evident that the values from the ensemble obtained by metadynamics resemble very closely those obtained by NMR and are in significantly better agreement than those calculated from the crystal structure. This finding suggests that some effects of the dynamics of the ensemble are lost in the crystallization, as previously suggested for the XD of mumps virus (14).

Validation of the Three-dimensional Structure of the Folding Intermediate by Tuning Its Stability

To further support the structural model, we adopted the strategy to rationally design site-directed mutants aimed at tuning its thermodynamic stability. A comparison between the intermediate and the native conformations highlights a reorganization of the α-helix bundle while maintaining a similar α-helical content. In particular, we observed that positions Arg-465 and Asp-486, located at the interface between helix1 and helix2, are involved in a salt bridge in the native state, whereas they are not in contact in the intermediate state; furthermore, positions I504 and I505, located at the C-terminal end of the domain, constitute a structural link between the three α-helices. Therefore, we produced the D486N, R465A, I504A, and I505A variants. Fig. 3 highlights the different environment of these four residues in the two states.

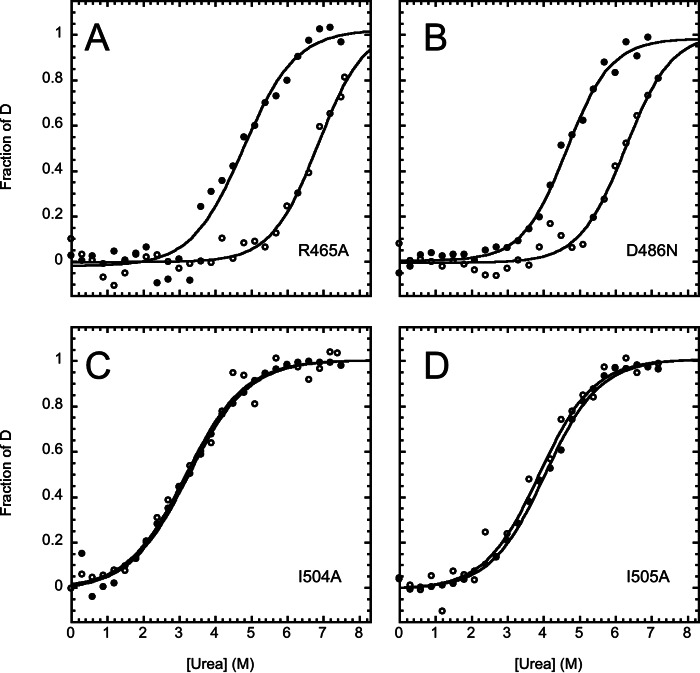
The urea-induced equilibrium (un)folding transitions followed by CD and fluorescence for the four variants are reported in Fig. 4. In all cases each individual transition conforms to an apparent two-state process similar to that reported above for the wild type protein. However, in the case of the R465A and D486N variants there was a large difference between the observed midpoints of urea denaturation as observed by fluorescence and CD and the values of [urea]_1/2, 6.8 ± 0.3 m from CD and 4.8 ± 0.1 m from fluorescence for R465A, and 6.3 ± 0.2 m from CD and 4.6 ± 0.1 m from fluorescence in the case of D486N. By contrast, in the case of the I504A and I505A variants, the overall transitions and urea midpoints followed by CD and fluorescence are superimposable within experimental error. These findings indicate that, although the intermediate state is stabilized in the D486N and R465A variants, the I504A and I505A variants conform to a two-state transition. Because Asp-486 and Arg-465 are engaged in a salt bridge in the native but not in the intermediate state, it is likely that the observed stabilization of the intermediate in the D486N and R465A variants arises from a relative destabilization of the native state relative to I.

FIGURE 4.

Urea-induced denaturation of the XD variants. Data were recorded in 50 mm sodium phosphate at pH 7.2, 300 mm NaCl, and 25 °C, monitored by fluorescence (closed circles) and CD (open circles). All the lines are the best fit to a two-state model.

In light of these experimental observations, it is of interest to compare the emission spectra of the different variants to those of wild type XD (supplemental Fig. S2). In fact, both the I504A and I505A mutants, which display a two-state folding transition, display a different λ_max compared with the other variants. This finding supports the view that in the case of wild type XD, R465A, and D486N, the intermediate state is partially populated, whereas in the case of the I504A and I505A there is a shift toward the native state only.

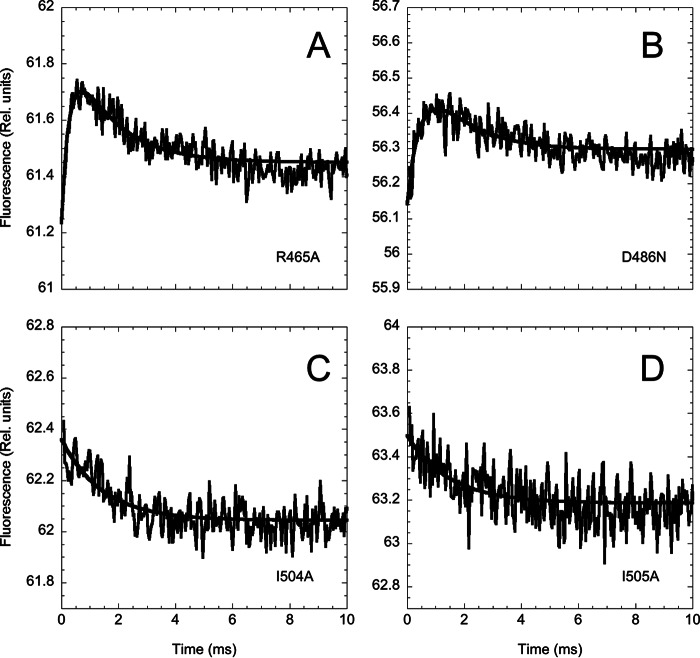
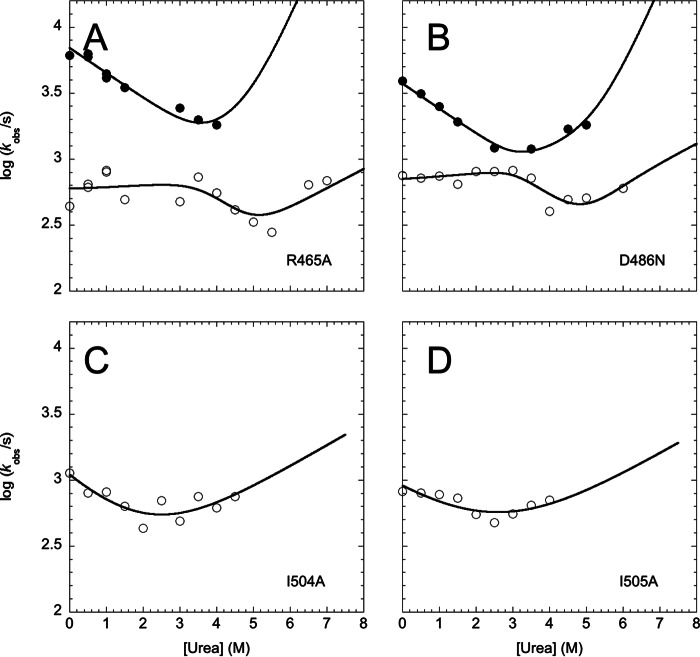
Additional evidence for the stabilization of the intermediate in the D486N and R465A variants and its destabilization in the case of the I504A and I505A mutants was then provided by assessing the (un)folding kinetics of these variants. As shown by time-resolved temperature jump transition of the four different mutants (Fig. 5), in the case of D486N and R465A, the relative amplitude of the fast versus the slow unfolding phase increases with respect to that of the native state. On the other hand, both I504A and I505A (un)fold via an apparent single-exponential time course, consistent with a two-state transition. The chevron plots for these four variants are shown in Fig. 6.

FIGURE 5.

Temperature jump induced unfolding transition of the XD variants measured in 50 mm sodium phosphate at pH 7.2, 300 mm NaCl, and at a final temperature of 25 °C. Unfolding was induced by a rapid increase of 9 °C. Although the R465A and the D486N mutants display a double exponential time course, in the case of I504A and I505A, data were consistent with a single exponential time course.

FIGURE 6.

Chevron plot of XD variants. Urea dependence of the fast λ₁ (closed circles) and slow λ₂ (open circles) unfolding phases of XD. The lines are the best global fit to an on-pathway scenario. For simplicity, data were fitted by constraining the m values to those observed in wild type XD. As described under “Results and Discussion,” in the case of the I504A and I505A variants, only the slow phase λ₂ could be observed. Accordingly, in these cases, the chevron was fitted to a two-state model.

Conclusions

We have identified and characterized an intermediate state of the X domain of phosphoprotein P, which is populated for ∼30% of the time. To obtain this result we exploited the recent development of NMR-restrained all-atom replica-averaged metadynamics simulations, which allow the structures of weakly populated states under-native conditions to be determined (18, 38).

Through a comparison with the thermodynamic parameters obtained from chevron analysis, we found that the intermediate state is an on-pathway species en route to the native state rather than an off-pathway kinetic trap. Although in the case of the former model, the intermediate is estimated to be populated in the absence of denaturant by ∼30% of the molecules, the latter model would predict the intermediate to be only weakly populated under native conditions (≪1%) due to its intrinsic constraint(s) (i.e. k_ID > λ₂). The calculated structure of the intermediate is fairly compact and displays a native-like secondary structure content. The α-helix bundle, however, is characterized by a different overall topological organization. This finding is fully consistent with equilibrium denaturation experiments, which indicate that the intermediate displays a native-like α-helical content, as probed by CD, while characterized by a different fluorescence emission. Moreover, mutations designed with the specific aim of perturbing the interfaces between the α-helices modulated the stability of the intermediate as predicted such that folding can be tuned toward a simple two-state reaction. Future work based on site-directed mutagenesis will elucidate the mechanistic details of the three-state folding transition of XD and its possible biological significance.

Author Contributions

D. B. and L. V. conducted the experimental work. C. C. determined the structure of the intermediate. D. B, C. C., L. V., S. L., M. B., M. V., and S. G, analyzed and discussed the data. S. G. conceived the idea of the project and wrote the main draft of the manuscript, which was later edited by all the authors.