Dynamic filtering improves attentional state prediction with fNIRS

Abstract

Brain activity can predict a person’s level of engagement in an attentional task. However, estimates of brain activity are often confounded by measurement artifacts and systemic physiological noise. The optimal method for filtering this noise – thereby increasing such state prediction accuracy – remains unclear. To investigate this, we asked study participants to perform an attentional task while we monitored their brain activity with functional near infrared spectroscopy (fNIRS). We observed higher state prediction accuracy when noise in the fNIRS hemoglobin [Hb] signals was filtered with a non-stationary (adaptive) model as compared to static regression (84% ± 6% versus 72% ± 15%).

1. Introduction

Previous findings from functional magnetic resonance imaging (fMRI) suggest that distinct networks of the human brain underlie attention to external and internal events. First, the “task-positive” network (TPN), which includes the dorsolateral prefrontal cortex (DLPFC), dorsal anterior cingulate cortex, superior and inferior parietal lobe, and anterior insula, is thought to enable attention to external task-relevant stimuli and responses [1, 2]. Consistent with this view, activity in this network increases when participants perform a task as compared to when they rest [1, 2]. Second, the “task-negative” network (TNN), which overlaps with the Default Mode Network and includes the anterior medial frontal gyrus (MFG), posterior cingulate cortex, and certain regions of lateral parietal cortex, is thought to enable internal attention to thoughts, emotions, and daydreams [3, 4]. In line with this view, activity in this network increases when participants rest as compared to when they perform a task [3–5].

Since the TPN and the TNN underlie distinct aspects of attention, it is not surprising that key regions of these networks interact. Functionally-connected activity in the TPN and the TNN is often negatively correlated [5–7]. It is unclear whether this anti-correlation reflects competition for limited resources [6], intrinsic competitive interactions in the brain [5], or the need to suppress one network (e.g., the TNN) when the other is active (e.g., the TPN). However, such network interactions are ubiquitous across different studies and populations [4, 8]. Further, interactions between key regions of the TPN and TNN vary with task engagement – as indexed by reaction time – in attentional tasks [9]. In sum, both (1) activity in the TPN and the TNN and (2) interactions between key regions of these networks vary with the degree to which participants are engaged in performing a task. Monitoring brain activity in key regions of the TPN and TNN may therefore allow researchers to distinguish between high and low levels of task engagement [10–13].

The ability to make this distinction in the real world is important for detecting and avoiding performance decrements during safety-critical operational tasks. As we have discussed previously [13], such tasks include commercial aviation, air traffic control, space walks, performing surgery, and driving. Since accident-causing errors can be made even by skilled professionals [14], monitoring brain activity for signs of low task engagement in real time could serve as an “early warning system” for detecting and preventing performance errors before they occur. For instance, to promote optimal human performance, intelligent flight decks of the future could monitor for changes in brain activity that typically signal low levels of task engagement. If such changes are observed when they are inappropriate given the operational context, mitigation could be attempted. In more general applications, the ability to detect such cognitive lapses, perhaps due to long duration monitoring, sleep-deprivation [11, 15], distraction [16], fatigue [17], combat [18] or divided attention [19, 20] could be useful for avoiding significant errors.

Given the considerations above, the goal of the present study was to quantify and improve the ability to use brain activity to predict a person’s level of task engagement. To this end, we asked study participants to perform an attentional task while we measured their brain activity with functional near infrared spectroscopy (fNIRS). FNIRS is an optical neuroimaging technique that measures hemodynamic activity in the brain. This technique is relatively low-cost, non-confining, non-invasive, and safe for repeated or long-duration monitoring of brain activity [21–25]. It also offers sub-second temporal resolution and acceptable spatial resolution (about 1 cm²) [26–28]. Further, measures of brain activity made with fNIRS are consistent with those made with fMRI [24, 25, 29–32] and electroencephalography (EEG) [33, 34]. Of importance for present purposes, activity in key regions of the TPN and the TNN can be measured with fNIRS because these regions reside in the cortical, or “outer”, layers of the brain.

It is also important to mention that, due to its portable nature, fNIRS allows neuroimaging in the field. Cognitive state measures based on fNIRS [13, 35–38] could therefore be used to optimize human performance during operational tasks (e.g., by informing computer software for automation or a human operator of a potentially hazardous psychological state). Other ambulatory brain measurement techniques such as EEG can quantify electrical brain activity in the field as well, but fNIRS offers a measure of localized hemodynamic response. This may produce synergistically complementary information in a multi-modal attentional monitoring system that also includes EEG sensors. Before exploring such a system, however, we first investigate the capabilities and most appropriate methods for the unimodal use of fNIRS. Along these lines, fNIRS has already been employed to measure brain activity during driving simulations [39] and to develop a robot that adapts to the cognitive state of a human operator [40]. Further developing the ability to predict a person’s level of task engagement using fNIRS would also support the development of an effective means for monitoring, or optimizing, a pilot’s level of task engagement during flight. Thus, the ability to predict a person’s level of task engagement is of particular importance to aviation safety [41, 42].

However, the best signal processing methods for accomplishing this objective have not been fully explored and are far from standardized [43]. In the present study, we moved further toward the objective of predicting task engagement using fNIRS by exploring various approaches for increasing the signal to noise ratio of fNIRS signals and thus improving the predictive power of fNIRS-based cognitive state classification systems. In particular, we quantified state prediction accuracy using various fNIRS signal processing methods to identify which method produced the highest accuracy for predicting a participant’s level of engagement in an attentional task. Building on prior work showing that fNIRS can be used in the laboratory to predict a participant’s level of engagement in an attentional task (using activity in the TPN and the TNN [13]), we monitored brain activity in two key regions of interest – the DLPFC in the TPN and the MFG in the TNN – while participants alternated between performing and not performing a complex attentional task. Processing was conducted by filtering changes in hemoglobin concentration across time in multiple ways, including static and adaptive regression to remove concurrently-measured physiological noise. Finally, we employed multivariate pattern classification techniques using the processed hemoglobin time series in the DLPFC and MFG regions to distinguish between high levels of task engagement (i.e., performing a task) and low levels of task engagement (i.e., resting) for each processing method employed. We observed higher prediction accuracy when noise from hemoglobin concentration ([Hb]) signals was filtered with adaptive as compared to static regression. This finding extends our understanding of how existing noise removal methods influence the ability to predict a person’s level of task engagement. More specifically, our findings reveal that the ability to predict attentional state from fNIRS data can be enhanced by employing adaptive regression methods.

The signal processing methods we explored included adaptive regression techniques because there may be a non-stationary relationship between (a) noise in the superficial layers and (b) the as-measured, deep signals of interest in the brain. This variation over time and space could complicate the contribution of nuisance physiological changes to deep signals of interest [44–48]. Standard regression is useful for the removal of such noise, but not allowing beta fit parameters to change in time can limit the effectiveness of this technique. Given a good model of the expected task-related activations, it should be possible to better identify dynamic noise in the signals for removal at each time instance. Adaptive estimation attempts to model these variations by allowing restricted temporal variations of the model parameters. Therefore, we explored an adaptive time-point-by-time-point general linear model (GLM) to dynamically filter out non-static physiological noise as in [44] using the short-distance channel measurements as regressors (see [49] for a recent example of a similar variable regression technique applied in a fMRI study).

Dynamic or adaptive filters have previously been implemented for processing fNIRS data. In one study, a state space model was used with a Kalman filter to estimate simulated responses added to real auxiliary physiological (noise) data that were collected during rest (using simulated responses but short separation measures) [47]. In a second study, an adaptive GLM was implemented with a Kalman filter to classify right vs. left single-trial finger tapping after removing physiological noise from measured response signals by modeling the cardiac signal, respiration and Mayer waves (using long separation measures and modeled short separation signals) [44]. In a third study, a GLM was implemented with a Kalman filter using measured short source-detector separation signals and simulated task responses. The results showed that adaptive filtering improved recovery of the hemodynamic response (using simulated long separation signals and short separation measures) [50]. Moreover, a follow-up study revealed that double short separation measures further improve filter performance (using both simulated and measured long and short separation signals during finger tapping) [51].

In yet other investigations, a tapped delay filter (with coefficients optimized on a sample-by-sample basis and [HbR] filtered separately from [HbO]) [45] was used to recover the hemodynamic response to a visual task by additively regressing out short source-detector separation channel measurements from visual response measurements). For example, Zhang, et al. [46] showed that measurements with poor signal to noise ratios do not benefit from such filtering, that such filtering can degrade the recovered signal of interest if that signal is not dominated by “global interference” or physiological contributions, and that such filtering improves contrast for [HbO] only. Finally, a channel-by-channel adaptive GLM was implemented with fNIRS data by Aqil, et al. [52] who used a recursive least squares estimation method to recover the hemodynamic response to a finger tapping task. The present study applies an adaptive Kalman filter using measured fNIRS data for both the noise and the task response to be recovered and applies adaptive filtering methods to a cognitive attention task that is more complex than the tapping and visual tasks used in prior studies.

2. Methods

2.1 Behavioral methods

Data were collected as specified in a protocol that was approved by Institutional Review Boards at the University of Michigan Medical School and NASA. Informed written consent was obtained from all participants (seven healthy adults (3 female, 4 male); age range: 21-50 years).

Brain activity was recorded with fNIRS in two regions of interest (DLPFC and MFG) with fMRI-compatible head probes during simultaneous fNIRS-fMRI scanning (fMRI results to be reported separately). During fNIRS recording, participants performed an attentional task in four 400-second-long runs. All participants were right-handed, with the exception of a single participant who was ambidextrous as determined by self-report. If vision correction was needed, participants wore either their own contact lenses or MR-compatible corrective lenses.

To facilitate our ability to distinguish between high and low levels of task engagement, we asked participants to alternate between performing a modified version of the multi-source interference task (MSIT) [53, 54] and resting (i.e., not performing a task). During rest, participants were instructed to look at a crosshair and think of nothing in particular. The MSIT is a selective attention task in which optimal performance requires participants to suppress multiple sources of interference. It reliably and robustly activates the TPN, even in individual task blocks from the same participant [53]. Given these characteristics, we reasoned that the task protocol would induce relatively high (during the MSIT) and relatively low (during rest) levels of external, goal-oriented task engagement, thereby providing a strong signal with which to monitor task engagement.

In each trial of the MSIT (duration, 2 seconds), participants viewed a horizontally-oriented array of four digits at the center of the screen (duration, 1 second). A target digit was printed in a larger font than each of three distracter digits (72 point vs. 60 point). The stimulus sizes were chosen to make the digits visible within the MRI scanner. Moreover, the large target digit was chosen to be about 20% larger than the small distracter digits to make the task sufficiently difficult, as we have described previously [13]. The task was displayed at the end of the scanner behind the participant’s head and viewed through a mirror.

Participants were instructed to identify the target digit in each trial (1, 2, 3, or 4) by pressing the key which corresponded to the spatial position (1st, 2nd, 3rd or 4th from left to right) of the target digit with one of four fingers (1 = right thumb, 2 = right index finger, 3 = right middle finger, 4 = right ring finger) as quickly as possible without making mistakes. Half of the trials were congruent, and the other half were incongruent. In congruent trials, both the spatial position of the target and the identity of the three distracter digits were mapped to the same response as the target (1111, 2222, 3333, 4444; bold font indicates the target digit, which was larger than the other digits). In incongruent trials, both the spatial position of the target and the identity of the three distracter digits were mapped to a conflicting response, such as a 2 in the 1st position or a 4 in the 3rd position (2111, 2122, 3343, 4443). To prevent stimulus and response repetitions from occurring in consecutive trials [55, 56], the stimuli were composed of the digits 1 and/or 2 in odd trials of each block but of the digits 3 and/or 4 in even trials. Responses were recorded via a MR-compatible response device (Psychology Software Tools, Inc., Sharpsburg, PA). The task was implemented using a combination of MATLAB [57] and the Psychophysics Toolbox [58].

Trials were presented in a block design wherein periods of performing the MSIT alternated with periods of rest. In each of four runs (run duration, 400 s), an initial 16 s rest block was followed by 12 alternations between the MSIT (16 s, 8 trials per block) and rest (16 s). Thus, each run contained 96 trials. All participants practiced the behavioral task with performance feedback for 1 minute at the beginning of the study.

2.2 fNIRS data acquisition methods

Data were acquired with an Imagent NIRS instrument and fiber optic cables (ISS, Inc., Champaign, IL). Light was sourced using laser diodes at 690nm and 830nm. Changes in optical intensity were detected with photomultiplier tubes. Using continuous wave analysis with the DC component of the detected signals, time traces of relative changes in the concentration of both oxygenated and deoxygenated hemoglobin species ([HbO] and [HbR], respectively) were produced for each source-detector pair (each optode). Standard calculations were made using the modified Beer-Lambert law [21, 59–61]. Differential path length factor values were 5.49 for the 690nm signals and 6.00 for the 830nm signals [62]. All analysis scripts were custom-written by the first author in MATLAB [57]. The data collection rate was 6.25 Hz.

During each task run, 2500 time points were collected. NIRS sources and detectors, herein called optodes, were placed as shown schematically in Fig. 1 with respect to the International 10-20 locations with the aid of an electroencephalography net and grease pencil markings on the participant’s head as described previously [13]. A measurement channel is defined as data collected from a particular source-detector pair. The array of probes used to interrogate the MFG contained two sources placed 3 cm from one detector between FP_z and FP₂. The array of probes used to interrogate the DLPFC contained four sources placed 3 cm from a second detector near F4. The line toward F_z was marked and the array rotated until it fell between optode channels 2 and 3.

Fig. 1.

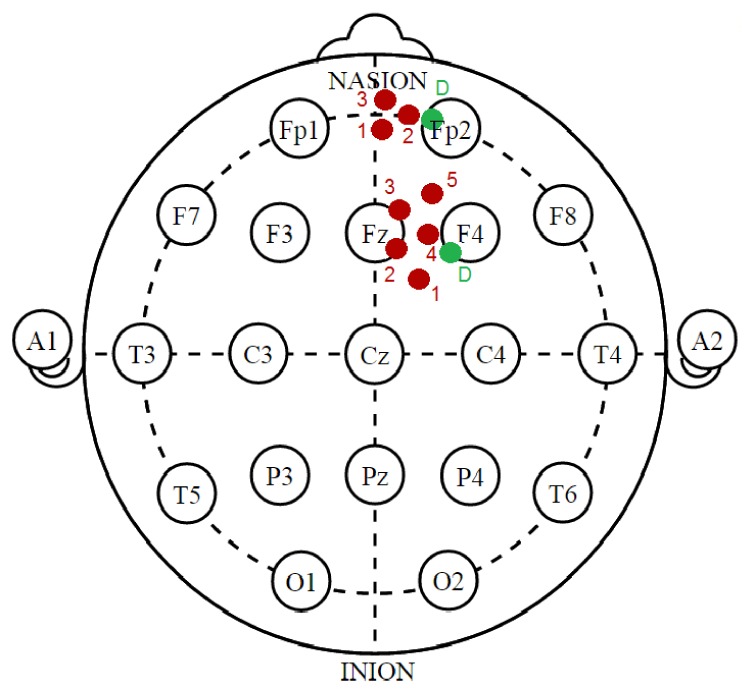
Optodes used to interrogate the DLPFC and MFG. Source optodes (red) are arranged around detector optodes (green), shown schematically with respect to the International 10-20 locations.

In NIRS, the penetration depth of a measurement channel increases with the distance between the source and detector. A common approach to separating superficial (shallow) and brain (deeper) signals uses a probe containing different channel distances. Signals with shallow sensitivity were collected using channels with a short source-detector separation distance of 1 cm (producing a shallow signal dominated by physiology in the superficial tissue [50, 63]), while the deeper measurements used a long source-detector separation distance of 3 cm (producing a deep signal that samples the brain as well as superficial tissue). Both shallow and deep tissue measurements are very sensitive to physiological effects from superficial tissue, but to differing degrees [45]. Recent modeling work [64] has indicated that the optimum short source-detector separation to reduce brain sensitivity to 5% of the signal is 8.4 mm, which is only 1.6mm less than the distance used in the current and many prior studies (including [50, 51]). Shallow signals from the DLPFC were detected on DLPFC array channel 4 near F4 while shallow signals from the MFG were detected on MFG array channel 2 near FP₂. Deep signals from the DLPFC were detected on DLPFC array channels 1, 2, 3 and 5 while deep signals from the MFG were detected on MFG array channels 1 and 3.

We built fMRI-compatible probes using a combination of detector fiber bundles from ISS, Inc. and customized source fibers [36, 37]. Results based on simultaneously-recorded fMRI data will be reported separately. The headgear (see Fig. 2) performed well and was redesigned until compatible with all aspects of the fMRI laboratory environment. Prototype probe sets were scanned and any fMRI-artifact-generating material was replaced. The source fibers were 450 micrometer core glass, and each detector was a 3 mm diameter glass fiber bundle. We employed glass right-angle prisms in periscope assemblies (see Fig. 3) to facilitate placement within the space limitations of the fMRI head receiver coil. Source fibers were held in place with a nylon set screw within the periscopes, which were machined out of black Delrin. Additionally, 3 mm diameter light pipes (15 mm in length and bonded to the other face of the prisms) provided offset for hair penetration and visual inspection of mark locations. Light pipe baffling all the way to the skin surface protected the measurements from ambient light exposure. The light pipes fit snugly through holes punched in hard rubber array holders as shown in Fig. 2. The array holders were designed such that each source-light pipe assembly could be individually adjusted with its own Velcro strap to allow for an individualized fit. The detector’s light pipe was inserted through the central hole.

Fig. 2.

Head probe arrays for the DLPFC (left) and the MFG (lower right). Prisms and light pipe assemblies (top right) were used with optical fibers.

Fig. 3.

Schematic of the optical components used in the light pipe assemblies.

The light intensity reaching a detector decreases exponentially as the distance from the source increases. Therefore, sources with shallow sensitivity at 1 cm may exceed the dynamic range. This may cause photo-damage to the detectors at gain settings appropriate for sources at 3 cm due to the lack of signal attenuation over their relatively shorter optical path length. To avoid this outcome without changing laser source intensity during the trial while the participant was wearing the probes, we reduced the delivered optical intensity for the shallow channel sources. Adjustment on a per-participant basis was effected quickly by layering optically absorbent pigment on partially-transmissive cosmetic tape between the ends of the fiber probe tips and the skin. Velcro straps as seen in Fig. 2 were adjusted for each source probe, and intensities were checked in an iterative fashion. If adjustments were required to facilitate the clearance of hair, the addition or removal of attenuating material over the shallow source probes, or the reattachment of probes such that they contacted the skin, each source could be adjusted independently (this dressing process was lengthy and inappropriate for operational situations). Participants tolerated indentations in the skin due to the probes. However, multiple indentations per probe were not seen upon removal, indicating the probes remained stationary.

2.3 fNIRS data processing methods

We wished to determine which fNIRS processing methods would provide the highest state prediction accuracy. We therefore describe here the temporal filtering and regression techniques that we used to process the time traces and thereby prepare them for use in classification. We implemented six different processing methods: (1) minimally-processed as-measured, (2) static regression, (3) adaptive regression, (4) physiological, (5) physiology-cleaned only static, and (6) physiology-cleaned only adaptive.

In the static and adaptive regression methods described in sections 2.3.2 and 2.3.3 below, we relied upon our knowledge of the task being performed (e.g., stimulus onset times) to clean physiological noise and other artifacts. Investigating methods that make use of knowledge of the task being performed allowed us to quantify the capability of our attentional state prediction system in “best case scenarios” wherein this information is available.

To explore the “real world” capability of our attentional state prediction system, we also estimated classification accuracy when our system was not provided with a priori knowledge of the stimulus onset times. Processing methods that did not make use of such knowledge were the as-measured (section 2.3.1), physiological (section 2.3.4), and both “physiology-cleaned only” (pco) cases (sections 2.3.5 and 2.3.6). In each case, functional traces were produced for use as inputs in the classification to be described in section 2.4. As described next, the functional traces were cleaned of noise and of uninformative activity to varying degrees. We then used these cleaned traces to represent changes in functional brain activity in all subsequent analyses. Notably, for all of the methods below, we did not remove physiological effects in the band-pass frequency range that were not apparent in the superficial tissue.

2.3.1 fNIRS data processing case: as-measured

Relative [HbO] and [HbR] changes were calculated using the filtered raw intensity measurements from the deep (3cm) signals as described in section 2.2 and then normalized by the signal variance [59]. Temporal band-pass filtering was used to focus on sustained task activations while removing very slow drift and higher-frequency physiological and motion contributions. More specifically, we employed a fourth-order zero phase Butterworth filter. The range from 0.008 Hz to 0.1 Hz was included to retain frequency components below 0.1 Hz, which contribute to sustained task signals and to resting state hemodynamic signals of interest, while excluding slow drift. Since the hemodynamic response lasts much longer than an individual 2 s trial, we did not attempt to resolve hemodynamic responses to individual stimuli. Instead, we focused on the sustained task response across an entire block of trials. We were also interested in low-frequency hemodynamic and resting functional connectivity signal content [3, 7, 65]. Therefore, the processing described above for the “as-measured” method was also employed in the five remaining processing methods. As described next, however, the five remaining methods also employed additional processing procedures.

2.3.2 fNIRS data processing case: static regression

In the static regression case, we employed standard linear regression (i.e., a general linear model, GLM) to remove the contributions of nuisance variables to the as-measured signal. For example, better estimates of brain activity in the deep signal can be obtained by removing noise from the shallow signal. As described next, the GLM consisted of two types of regressors.

First, we created “expected” functional task activity regressors by convolving a boxcar activity on-off function with a canonical hemodynamic response function (HRF) [66]. We predicted that expected task activity would include [HbO] increases and [HbR] decreases at the DLPFC location during the MSIT, and [HbO] increases and [HbR] decreases at the MFG location during rest. Put another way, while functional activity for the DLPFC channels was on during the task periods and off during the rest periods, functional activity for the MFG channels was off during the task periods and on during the rest periods. Therefore, the boxcar activity on-off function for [HbO] at the DLPFC was identical to that for [HbR] at the MFG. Analogously, the boxcar activity on-off function for [HbR] at the DLPFC was identical to that for [HbO] at the MFG. To the extent that the measured [Hb] changes reflected these predicted boxcar functions, we expected that the beta parameter estimates for the “expected” task activity regressors would be greater than zero.

Second, we created additional “nuisance” regressors. To do so, we applied the same temporal band-pass filtering described in section 2.3.1. to the signal sources described in section 2.2, which were sensitive to shallow signals particular to each probe array [50, 63]. The resulting “nuisance” regressors allowed the removal of physiological noise (and other artifacts such as gross probe motion and ambient light exposure) from estimates of the sustained “task-related” signal coming from deeper signal measurements. Thus, the estimates of the functional task activity of interest (the functional traces to be used as classifier input features) were derived from a GLM that coded four signals in four independent regressors: (1) the expected task activity, (2) the shallow [HbO] trace, (3) the shallow [HbR] trace, and (4) a constant to model DC (or constant) offset.

Cleaning signals via regression may help to prevent a researcher from interpreting low-frequency physiological noise (e.g. Mayer waves [7, 67]) as reflecting low-frequency functional brain activity (either task-related or spontaneous). Accordingly, we removed unwanted physiological contributions to the signals of interest by subtracting a fraction of the shallow signal, which was determined by the GLM beta fit parameters for the respective nuisance regressors. These fractions were determined once for the full time series in the static case described here. This is the principal difference between the static case and the adaptive case described in section 2.3.3, wherein the parameters change time point by time point.

The static removal method is most appropriate when there is a sufficient correlation between the shallow signal and the deep signal [46]. However, the shallow signal may contain task-evoked responses originating in the superficial tissue due to the influence of the sympathetic nervous system on blood vessel diameter during cognitive responses [68], or due to some partial volume of sampled brain. Therefore, to avoid removing the effect of interest, we used two separate standard linear regression steps. First, after smoothing the measured shallow trace using a 6-timepoint (1 s) moving average, we employed regression to remove task-like responses from this trace. This was accomplished by modeling expected task activity as a nuisance regressor in a GLM wherein the measured shallow signal was the dependent measure. The expected task activity regressor weighted by the resulting beta fit parameter was subtracted from the measured shallow signal. The second regression step removed the residuals resulting from the first regression step (assumed to be noise) from the deep signal.

Although the static removal method is typically performed within-species, with separate [HbO] and [HbR] filtering [46], shallow and deep traces can be produced by channels that sample different mixes of arterial and venous compartments. A probe’s sensitivity to one species or the other depends on whether it mostly samples the arterial or the venous compartment [69], which is likely to vary between probe applications due to changes in probe location. Additionally, physiological interference has been shown to be inhomogeneous in space [70, 71]. Since the shallow and deep probes sample nearby but different locations, they likely do not sample the same mix of arterial and venous compartments. Thus, the noise on the longer separation channels may represent a different mixture (i.e., linear combination) of [HbO] and [HbR] information compared to the shorter channels. To address this issue, we implemented the shallow trace removal with across-species terms. That is, the oxygenated and deoxygenated [Hb] traces from the short source-detector separation channel were regressed out of the as-measured traces of each Hb species from the long source-detector separation channel on the same detector array.

In sum, the steps for calculating the functional traces were as follows. First, the expected task activity time trace was determined by convolving the HRF with the boxcar signal particular to each brain region (DLPFC, MFG) and Hb species ([HbO], [HbR]). Second, we created a design matrix with four regressors: (1) the expected task activity trace, (2) a DC offset trace, (3) a shallow [HbO] signal, and (4) a shallow [HbR] signal. The measured deep signal was set equal to the design matrix multiplied by beta (a 4-element column vector). The pseudo inverse function in MATLAB [57] was used to solve for beta (i.e., the four beta fit parameters). The functional traces that became the classifier features were determined by subtracting the three nuisance regressors weighted by their respective beta fit parameters from the measured deep signal. Finally, the beta fit parameter for the expected task activity regressor quantified the degree to which the functional response fit our model of the expected task activity.

2.3.3 Adaptive regression methods

As in the static regression case, we employed standard linear regression to remove the contributions of shallow nuisance variables from the deep as-measured signal. However, unlike in the static regression case, the GLM fit parameters varied time point by time point (cf. in the static case, these parameters were set once for all time points) using the adaptive regression methods described above. To differentiate this method from the static case introduced in section 2.3.2, we call it adaptive regression.

To conduct the adaptive regression, we used a discrete Kalman filter [72]. Kalman filtering is commonly used to estimate the non-stationary underlying state of a system. Its recursive nature makes it attractive for real-time autonomous applications. For a detailed introduction, the reader is referred to Welch and Bishop [73]. In brief, however, Kalman filter estimates of the model parameters at the current time point are based on a combination of (a) updates of these parameters from the immediately preceding time point and (b) the current experimental measurement. From one time point to the next, the model parameters are allowed to vary in a range around their previous values. The simplest model, and the one used in this work, assumes that these parameters are taking an isotropic random walk from one time point to the next with the covariance of the possible step sizes defined as Q. Q is called the process noise. At each time point, the estimate of the parameters is predicted from the preceding point (i.e. it is allowed to “wander” from its previous value) and this prediction is then compared to the actual measured data. The model parameter is updated based on the probability of this predicted value given the covariance of the parameter’s step in the random walk (Q) and the difference between the expectation of a measurement based on this prediction and the actual experimental data.

The Kalman gain determines how much the model statistically favors the prediction made from the random walk verses the actual measurements, and depends on the process noise (Q) and the measurement noise (R). If the process noise (Q) is large, then the model is allowed to take big steps in this random walk and the actual measurement is more influential in estimating the model. When the process noise is small, the model takes very tiny steps and is slowly pulled over time by the actual measurements. In this later case, sudden large changes in the measurements such as those due to motion artifacts will have less of an effect on the model estimate. When Q is zero, the parameters are constant and the Kalman filter converges to the static regression solution. When R is small, the experimental measurements may be over-trusted and dynamic filtering will not be employed. At the other extreme, a very large R does not allow the experimental measurements to contribute to the estimate.

In general, Kalman filters are usually tuned (by setting Q and R) somewhere between the two extremes to give performance that balances the use of dynamic filtering with use of the experimental measurements. For our study, a variety of values for Q and R were tested with an idealized response and actual experimental physiological measures. We selected values of Q and R that allowed for periods when the measurement was tracked and for periods when it was not tracked. Also, we selected values that avoided steeply-spiked state estimate traces, which are unexpected for hemodynamic responses. Q was set to 0.1 times the variance of the shallow physiological traces. The measurement noise covariance (R) was set to 10 times the variance of the difference between the measurement trace and the expected functional task activity. These settings were based on the entire time traces prior to adaptive regression, yet allow for some adjustment based on the actual experimental data for each participant and each run. We note that, for online processing, these quantities may be based on recent windows of data to base Q and R on real variance in the time-local noise.

In our adaptive model, the [HbO] or [HbR] measurement is set to the observation matrix times the state, plus noise (with covariance R) associated with the measurement method itself. Stated in GLM terms, the observation matrix is the design matrix, and the state is a vector of the beta fit parameters. The measured signal, as in the static case, is the as-measured trace (filtered to include 0.008 Hz to 0.1 Hz). The observation matrix is four columns wide and the state vector has four components. The columns are populated with four regressors, the last three of which are nuisance regressors. These four column vectors are: (1) the expected task activity, (2) the shallow [HbO] trace, (3) the shallow [HbR] trace, and (4) a constant to model DC (or constant) offset (i.e., the same four regressors that we used in the static case).

2.3.4 fNIRS data processing case: physiological

Typically, systemic physiological confounds must be removed to avoid false positive results [74], as we have done in this study. However, if physiology detected in the shallow signal is due to task engagement, then these signals may be useful on their own as classifier input features. Indeed, task-evoked changes in systemic blood pressure and autonomic nervous system responses do manifest in the skin layer [68], to which fNIRS is highly sensitive. For example, systolic blood pressure has been shown to increase and peak with task demand, and then decreases once the task is too challenging [75]. We call the signals simultaneously recorded using sources with shallow sensitivity the physiological traces. They are used without the first regression step described in section 2.3, which removed task effects. To test the possibility of predicting task engagement using detected physiology alone, these physiological fNIRS traces were used as classifier inputs. All four available [Hb] traces were used in this case; that is, the [HbO] and [HbR] traces on each of the two channels on which shallow signals were detected.

2.3.5 fNIRS data processing case: physiology-cleaned only static

To further explore the real world capability of an attentional state prediction system based on our methods, we explored static regression using nuisance regressors alone. We call this a “physiology-cleaned only” (“pco”) static case, since no a priori knowledge of task stimulus onset times is used in the processing. The shallow traces only are used as nuisance regressors without the first regression step described in section 2.3, which removes task effects. This case is abbreviated as “pco” and should not be confused with the physiology case introduced in section 2.3.4, wherein the shallow traces themselves are used as classifier inputs. Static GLM analysis as described in section 2.3.2 was employed, but with no expected task response regressor. The functional traces used as classifier input features for this case were generated using three nuisance regressors: the shallow [HbO] trace, the shallow [HbR] trace, and a constant to model offset.

2.3.6 fNIRS data processing case: physiology-cleaned only adaptive

The physiology-cleaned only (“pco”) adaptive case was similar to the physiology-cleaned only static case described in section 2.3.5. However, the GLM fit parameters were allowed to vary time point by time point using the adaptive methods described in section 2.3.3.

2.4 Classification methods

Classification was performed using the time traces produced as described in section 2.3 as input features to Support Vector Machines (SVMs). Scripts were implemented in MATLAB [57] using LibSVM [76]. For a brief introduction, the reader is referred to Burges [77] or Chang and Lin [78]. We choose SVMs for good performance with ease of implementation, flexibility in the number of input features, processing speed once trained (in the interest of future real-time application), and the ability to use tuning parameters to optimize feature separation for each participant. SVMs have shown potential for high accuracy during sustained activity with minimal training, and have been implemented in real-time fMRI methods [79].

A SVM classifier was trained (producing a SVM model) to discriminate relatively high (during the MSIT) from relatively low (during rest) levels of external task engagement (two classes of attentional state) using three of each participant’s four runs (20 minutes of training data). Its prediction accuracy was tested via leave-one-out methods on the participant’s fourth run. That is, the fourth run was “left out” of the training data set. All permutations were computed for each participant for each SVM model, such that the prediction accuracy could be determined for each of the 4 runs. The classifier output was defined to be −1 for rest if the prediction data were determined to be on the “rest” side of the hyperplane determined by the training data, and 1 if the prediction data were on the task, or “work,” side. The truth labels used for training and accuracy determination purposes were taken from the boxcar task function (see section 2.3.2), but shifted 4 seconds later to account for the delay of the hemodynamic response. In all cases, the data used for prediction were completely independent from the training data that were used to create the model. Training and prediction were conducted within each participant. Finally, the training data were processed in the same manner as the to-be-predicted data.

A total of twelve time-trace features (six optodes by two [Hb] species each) were available across both probe arrays. We pruned the number of features used for the purposes of improving accuracy [80]. Classification using fewer input feature traces may increase or decrease accuracy depending on the discriminatory information they contain. Classification including the lowest-ranked feature traces would allow more noise into the classification process, decreasing accuracy. Six traces were selected in each participant based on how well the static functional traces from the same optode-species combinations in the training data discriminated the task. This task discrimination was quantified using the F score [80]. Briefly, the numerator quantifies inter-class variance while the denominator is the sum of the within-class variances. A larger difference between the classes and less variance within each class indicates better discrimination. The F score considers each training feature independently. Ranking according to this discrimination score was performed across all training runs used. In other words, we did not restrict the selection, for example, to four traces from the DLPFC array and two traces from the MFG array. The six optode-species combinations with the greatest discrimination scores were selected. Then, the same optode-species combinations were used for both training and predicting. All four available [Hb] traces were used in the physiological case (of section 2.3.4).

There are two tuning parameters that must be selected prior to training. The optimal SVM model for each participant depends on selecting these parameters accurately. The first tuning parameter is c, which multiplies the cost of misclassifications during SVM model training. A lower c can produce a more flexible and generalizable SVM model by reducing the impact of misclassifications in exchange for finding a wider separation margin between the two classes. The second is Gaussian kernel parameter gamma (g), which determines the non-linearity associated with mapping the few input features into a new, multidimensional feature space [81] wherein the classes may be more separable. Not optimizing these parameters based on the training data may result in non-optimal classifier performance (poor predictive power where acceptable performance is achievable given the same training data).

To determine the best possible prediction accuracy achievable for each participant in this study, c and g were tested at various selected values via leave-one-out methods to optimize accuracy. The highest classification accuracies produced, using the same set of parameters across all four runs (the same c and g for all permutations), were reported for each participant. The optimal c and g parameter pairs were not expected to be identical across participants. Tuning classifier parameters between participants allows individual differences to be taken into account for optimal accuracy. The fNIRS signals, and therefore the classifier input features and associated optimal classifier parameters, will be different for each participant. Since the optimal parameters depend on (1) the separability of the data and (2) the shape of the boundary between data points in the two conditions, or classes, the optimal c-g pair might vary across participants or optode applications. There is no reason to force the threshold separating the two classes to be the same across participants, unless one seeks to generalize and apply SVM models across participants, which was not the goal of the present study.

Accuracy was determined by comparing the work or rest state predicted by the classifier for each instance to the known behavioral states (i.e., performing the task or resting) at that time. All statistical tests on classification accuracy values were one-tailed, with comparisons paired by participant.

2.5 Spectral analysis methods

The spectral content of the residual error traces was quantified for the as-measured, static and adaptive regression methods to check for components that were not effectively removed by the GLM described in section 2.3.2. The residuals (containing anything not explained by the model) were determined by subtracting all regressors (nuisance and expected activity) times their beta fit parameters from the measured signal. All residual traces were averaged across the four runs for each participant prior to this analysis. The amplitude spectrum was computed via a Fast Fourier Transform (FFT) with 0.00152 Hz resolution. The largest peak in the frequency range of 0.0076 Hz to 0.0168 Hz was identified to investigate the amplitude of observable very low frequency components. The amplitudes for the static and adaptive cases were normalized to those of the as-measured trace for each participant.

3. Results

3.1 Behavioral results

Seven participants completed four runs of the MSIT. As expected, mean behavioral accuracy was relatively high at 97.6% (SD = 2.3%, N = 7). Also as expected, performance was worse in incongruent than in congruent trials. A random effects analysis revealed that mean reaction time was significantly higher in the incongruent condition (M = 0.761 s, SD = 0.126 s) than in the congruent condition (M = 0.680 s, SD = 0.106 s), (t(6) = 7.6, p < 0.0005). Likewise, mean error rate was significantly higher in the incongruent condition (M = 3.91%, SD = 3.03%) than in the congruent condition (M = 1.43%, SD = 2.25%), (t(6) = 3.3, p < 0.01). Errors of omission were rare. One subject made a maximum of three omissions per run while all others made two or fewer omissions per run.

3.2 Functional results

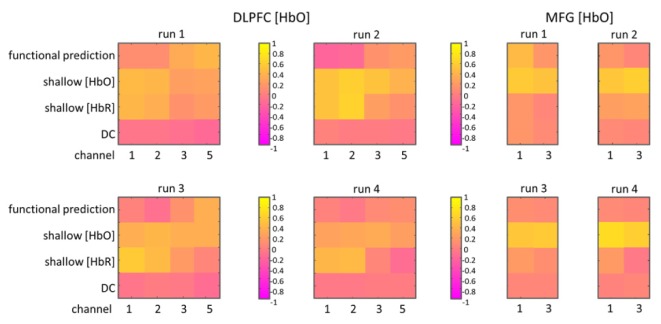
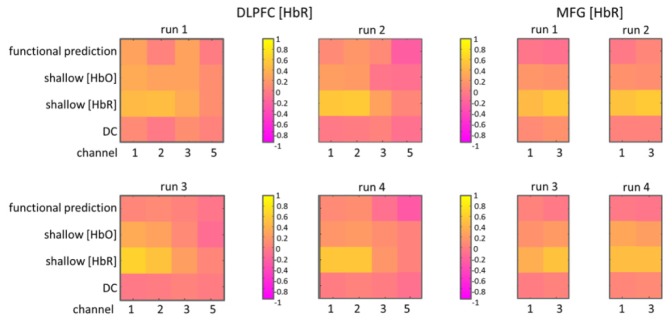
The values of the static regression beta fit parameters (from case 2, static regression described in Section 2.3.2) quantify the activation and nuisance found on each channel. These parameters (averaged across seven participants) are presented in Fig. 4 ([HbO] traces) and Fig. 5 ([HbR] traces). They are organized by probe array location, species of Hb, run, and array channel. To produce these parameters, the measured [Hb] change time traces were regressed against the predicted functional task activity and nuisance regressors. Positive beta fit parameters from the GLM analysis would indicate that the measured changes in [Hb] reflected the predicted activity or nuisance activity that was modeled by each regressor.

Fig. 4.

Average beta fit parameters quantifying the predicted activation and nuisance found on each channel for the static regression processing case are shown for [HbO] measures by location and run. Column numbers in each image scale plot correspond to probe array channel numbers.

Fig. 5.

Average beta fit parameters quantifying the predicted activation and nuisance found on each channel for the static regression processing case are shown for [HbR] measures by location and run. Column numbers in each image scale plot correspond to probe array channel numbers.

As described earlier, we hypothesized that task-evoked functional activity would differ between the DLPFC and MFG locations. At the DLPFC location, we hypothesized that performing the MSIT would be associated with [HbO] increases and [HbR] decreases relative to the rest condition. At the MFG location, we predicted that performing the MSIT would be associated with [HbO] decreases and [HbR] increases relative to the rest condition. As described next, both of these hypotheses were confirmed.

In Figs. 4 and 5, there are 16 image scale plots (two species by two array locations by four runs) with parameter values ranging from −1 to + 1. Columns 1, 2, 3 and 5 correspond to channels 1, 2, 3 and 5 on the DLPFC array. Columns 1 and 3 correspond to channels 1 and 3 on the MFG array. Orange and yellow colors indicate parameter values greater than zero for a given channel, regressor, run, location and species being cleaned. The first rows of each plot (labeled “functional prediction”) show the parameter values for the predicted functional task activity. Not all channels showed the predicted functional task activity, and the species that did show activity was not consistent across channels. However, in line with our predictions above, Channels 3 and 5 showed the predicted functional task activity (i.e., positive beta values) for [HbO] on the DLPFC array. Also consistent, Channel 1 showed the predicted functional task activity for [HbO] on the MFG array. Finally, Channels 1 and 3 showed the predicted functional task activity for [HbR] on the DLPFC array. The magnitude of predicted functional task activity for [HbR] on the MFG array was not consistent across runs.

The second, third and fourth rows of each plot show the parameter values for the shallow nuisance and constant offset to be removed. As discussed in section 2.3.2, we hypothesized that both the [HbO] and the [HbR] static regression beta fit parameters for the shallow physiological nuisance regressors would be greater than zero independent of the species of the measured trace being cleaned. Indeed, the measured traces may contain nuisance contributions stemming from variations in either species of [Hb] to varying degrees across locations. As predicted, the parameters were greater than zero for both species of the shallow nuisance regressors for both locations and both species of the measured traces of interest. However, this was most pronounced for the [HbO] traces of interest on the DLPFC array. These results can be seen by inspecting the yellow and orange colors in the second and third rows of the plots in Fig. 4 ([HbO] measures) and Fig. 5 ([HbR] measures).

Activity in the very low frequency range (around 0.01Hz) was observed in both the static and adaptive regression residual traces. This is potentially attributable to intrinsic activity in resting-state, functionally connected networks [5, 65] or to very low frequency physiological confounds such as local vasomotion of the cerebrovasculature [82], either of which may contribute to signal content in this frequency range (0.01 Hz to 0.1 Hz). Aside from such signal content being treated as nuisance via the shallow traces, covariates in this frequency range were not included in our models. The spectral amplitude of this activity (calculated as described in section 2.5) was found to be significantly greater in the static (M = 0.86, SD = 0.06) than in the adaptive residual traces (M = 0.27, SD = 0.08, (t(6) = 16.0, p<0.0005).

To further characterize the effect of the different processing methods, we present below the state prediction results enabled by each of the processed functional traces.

3.3 State prediction results

Our main goals were to (a) determine which fNIRS pre-processing method provides the highest accuracy of state prediction and (b) quantify classifier performance for each method employed. In these ways, we hoped to improve the ability to use brain activity to predict a person’s level of task engagement. Recall that we explored static and adaptive regression techniques as well as techniques that did or did not use a priori knowledge of the stimulus onset times. Processing methods that did not make use of the stimulus onset times were the as-measured, physiological and physiology-cleaned only cases. Further, two distinct physiology-cleaned only cases were investigated: static and adaptive.

The resulting mean accuracies, standard deviations (SD) and statistical significance with respect to chance prediction at 50% (averaged across all 7 participants) are presented for each case in Table 1, where they are ordered by decreasing mean accuracy and labeled according to the scheme provided in Section 2.3. The range of percent accuracy of the SVM model within each participant in the adaptive case was 12% +/− 4% across c = 0.001, 0.01, 0.1, 1 for g = 0.1, and 11% +/− 6% across c = 0.001, 0.01, 0.1, 1 for g = 0.5. The best c-g pair was not consistent across participants. This underscores the importance of the tuning parameter optimization and selection described in section 2.4 on a participant-by-participant basis. As shown in Table 1, all of the functional feature traces generated classification accuracies that were significantly greater than chance prediction regardless of the processing method and regardless of the use of task knowledge. Thus, consistent with hypotheses, combining information about relative increases of [HbO] in the DLPFC and relative increases of [HbR] in the MFG, allowed us to classify whether participants were performing the MSIT or resting at above-chance levels of accuracy. We now discuss the results of each processing method in greater detail.

Table 1. State prediction accuracy and statistics for various fNIRS processing methods and features.

processing method:	% accuracy	SD		t(6)	p <
(3) adaptive	83.8	5.7		20.58	0.0005
(2) static	71.8	14.8		6.11	0.0005
(1) as-measured *	70.2	11.3		6.98	0.0005
(4) physiological *	65.1	12.3		3.96	0.005
(5) pco static *	64.7	7.4		5.23	0.005
(6) pco adaptive *	62.0	9.5		3.32	0.01

* no task knowledge used pco: physiology-cleaned only SD: standard deviation

Both the static and the adaptive cases used knowledge of the task, via the expected task activity regressors, to produce the functional traces used as input classifier features. As shown in Table 1, the functional traces produced via static regression generated a classification accuracy of 71.8% +/− 14.8% when averaged across all seven participants. This value was significantly greater than chance accuracy, (t(6) = 6.109, p<0.0005), but only 1.6% greater than the classification accuracy in the as-measured case. The functional traces produced via adaptive regression yielded a classification accuracy of 83.8% +/− 5.7%. This value was significantly greater than chance accuracy and 13.6% greater than the classification accuracy in the as-measured case. In fact, the adaptive case represents the best classification accuracy observed in the present study. All feature types produced via adaptive regression produced mean accuracies that were statistically significantly different from chance prediction. The classification accuracy for each participant and processing method is presented in Fig. 6.

Fig. 6.

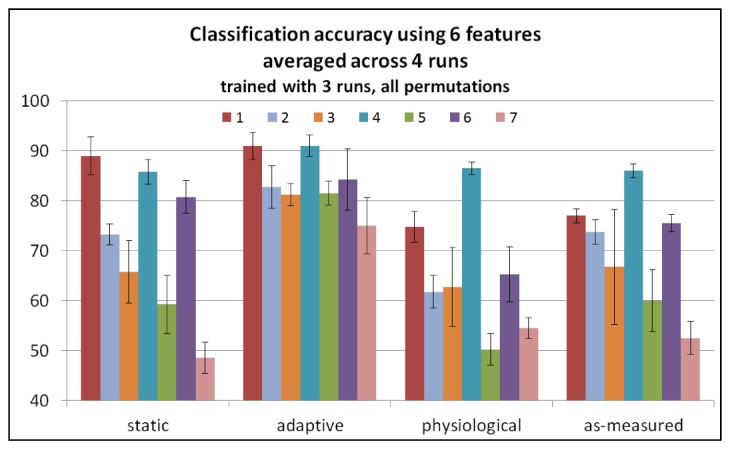
State prediction accuracy for seven participants with each bar representing one participant, for various fNIRS processing methods: as-measured, static, adaptive and physiological. Error bars show the standard deviation across the 4 runs.

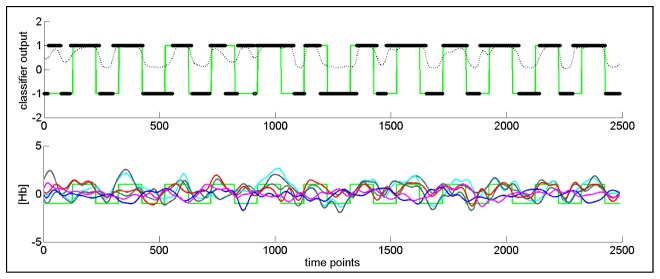
Exemplary plots of prediction data in the static case and the corresponding classifier outputs at every time instance for one run are presented in Fig. 7. Prediction accuracy was 74.8% for this run, and three training runs were used to train the classifier. In the top panel, black markers at + 1 indicate the classifier output for a more engaged, ‘working’ state, while those at −1 indicate the classifier output for a less engaged, ‘resting’ state. A prediction is made at every instance. The dotted black line indicates the probability estimates of the classifier predictions. In the bottom panel, the six classifier input features (the processed data, selected as described in section 2.4) are plotted. Truth labels are indicated by the green task function in both the top and the bottom panels.

Fig. 7.

In the top panel, black markers at + 1 indicate a classifier output of a more engaged or ‘working’ state, while those at −1 indicate a less engaged or ‘resting’ state. A prediction is made at every instance. The dotted black line indicates the probability estimates of the classifier predictions. In the bottom panel, the six classifier input features generated using static processing are plotted. Truth labels are indicated by the green task indicator function in both the top and bottom panels.

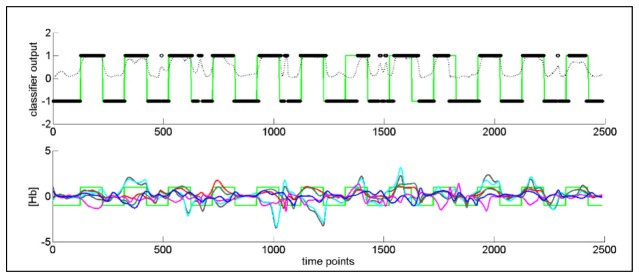
Exemplary plots of prediction data in the adaptive case and of the corresponding classifier outputs at every time instance for one run are presented in Fig. 8 using the same markings as in Fig. 7. Prediction accuracy was 87.5% for this run, and three training runs were used. This is the same participant and run as in Fig. 7, and the same markers are used.

Fig. 8.

In the top panel, black markers at + 1 indicate a classifier output of a more engaged or ‘working’ state, while those at −1 indicate a less engaged or ‘resting’ state. A prediction is made at every instance. The dotted black line indicates the probability estimates of the classifier predictions. In the bottom panel, the six classifier input features generated using adaptive processing are plotted. Truth labels are indicated by the green task indicator function in both the top and bottom panels.

The physiological traces - produced via method 4 described in Section 2.3.4 - were produced using no information about the task being performed and yielded the second-best accuracy in cases where no knowledge of the task was employed. The physiological traces generated a classification accuracy of 65.1% +/− 12.3% when averaged across all seven participants. This result was significantly greater than chance accuracy (t(6) = 3.963, p<0.005).

The as-measured traces, discussed in section 2.3.1, produced the best classification accuracy of all cases in which no information about the task being performed was used. As shown in Table 1, classification accuracy was 70.2% +/− 11.3% when averaged across all seven participants and differed significantly from chance, (t(6) = 6.978, p<0.0005).

The physiology-cleaned only functional traces produced via static and adaptive regression, respectively, generated classification accuracies of 64.7% +/− 7.4% and 62.0% +/− 9.5%, when averaged across all seven participants. The accuracy for each participant is not shown in the figures for these low-accuracy cases.

After re-running the adaptive, static and as-measured classifications using only one run (6.7 minutes) of training data, classification accuracies were lowered by less than 3%. Further, the ranking by performance of these methods (from highest to lowest classification accuracy) was unchanged.

The feature traces selected, as described in section 2.4, varied by participant and by run. All twelve possible traces appeared at least once in the top three most useful features (out of the six used) for at least one participant, and the same top three traces contributed in the same rank order for at least two of the four runs for every participant. Consistent with prior findings [13], neither [HbO] nor [HbR] traces dominated, and both brain regions (DLPFC, MFG) contributed informative features to the classification. More specifically, there were 93 features from the HbO species and 75 features from HbR species. In addition, there were 103 features from the DLPFC and 65 features from the MFG.

4. Discussion

4.1 Main findings

The present study followed up on prior work showing it is possible to predict a person’s level of task engagement (i.e., performing a task or resting) by monitoring brain activity in the DLPFC (a core region of the task-positive network) and the MFG (a core region of the task-negative network) [35]. In particular, we investigated which of several methods for processing fNIRS data, when combined with pattern classification methods, would yield the highest state prediction accuracy. Next, we describe our findings from each of these methods.

We begin with the as-measured and physiology-cleaned only (pco) cases, which represent “real world” applications wherein information about stimulus onset times is generally not available. Among these cases, accuracy was highest in the as-measured case (70% +/− 11%), consistent with prior findings [13, 35]. Thus, the least pre-processed of the fNIRS signals was found to provide the best performance when knowledge of the task being performed (e.g., stimulus onset times) was not used. The physiological and pco cases provided lower accuracy, likely resulting from the lesser amount of information in the classifier input features due to higher noise content. Consistent with this finding, the removal of shallow signals can reduce signal contrast if (1) it is applied inappropriately (e.g., when the signal is not dominated by physiological confound) [46] or (2) task effects (arising from skin or brain layers) cannot be removed from the nuisance regressors (as in the pco cases). Thus, it is perhaps not surprising that the physiological and both pco methods were outperformed by the minimally-processed as-measured traces. Given that greater physiological noise due to Mayer waves is to be expected when participants are sitting, pco methods may perform better due to all signals being more dominated by the same noise [46]. However, the lack of a strong model of the expected task activity would still be a hindrance to the pco methods. The shallow fNIRS traces themselves (method 4, physiological) produced the second-best accuracy for cases wherein no knowledge of the task was used. High levels of classifier performance in this particular case may be in part attributable to task-evoked effects in the superficial tissue, which have been reported elsewhere [68]. However, these effects were not reliable for all participants in our study. They may also be in part attributable to the short-separation distance being 1.6mm greater than the nominally optimal distance [64], resulting in unintended brain signal detection. Performance of 65% is above chance but still quite low. Therefore, this difference in distance was of limited impact.

Moving on, classifier features that were produced using processing methods that employed knowledge of the stimulus onset times yielded the highest state prediction accuracy. Among these methods, dynamic filtering of noise via adaptive regression produced the highest accuracy. Within-participant classification accuracy for distinguishing between task engagement and rest was 84% +/− 6% with just 20 minutes of training data. Using a strong model for the expected brain activity in each brain region being interrogated, noise was more effectively removed and classifier performance was enhanced.

While such a model may not appear applicable in the real world, information for such a model could be available during operational simulations and in intelligent operational environments of the future. Moreover, the increase of 14% in state prediction accuracy (relative to the as-measured case discussed above) may motivate efforts to obtain information about task timing from, for example, algorithms and sensors that detect specific brain activation patterns or even overt physical actions. On a related note, fewer training runs did not change the relative performance of the classification based on the processing methods. This is important to know when considering time-limited applications of these methods in the field.

Further regarding classification results, feature ranking produced informative results. The selected, contributing traces (the six selected from the 12 available) were reasonably consistent across runs within participants, neither species dominated, and both regions contributed. This underscores the usefulness of employing multiple channels across the head for monitoring purposes, and discourages dismissing the [HbR] signal as less useful due to increased noise levels relative to [HbO]. Finally, we note that the superior performance of the adaptive filtering method indicates that information extraction is more likely to be limited by the non-stationary nature of physiological noise [44, 45, 47, 48] than by regional optode localization precision.

While the functional results of the study supported our predictions and explained the positive classification results we obtained, the degree to which this support was observed varied across channels. This variability may indicate that not all deep channels have sensitivity profiles that are equally overlapping the brain volume of interest. It could also indicate that data quality varies across optodes, wavelengths, runs, and/or participants, thereby affecting the ability to extract activation information equally from every channel. Finally, it could indicate that some channels (e.g. channel 5 on the DLPFC array) more often overlapped arterial compartments across participants while other channels (e.g. channel 1 on the DLPFC array) more often overlapped venous compartments. Future studies should be conducted to identify methods to further improve data quality [83] and reduce the variability we observed.

Despite the variance across channels, data quality was improved by superficial noise removal and the reduction of very low frequency activity. As we predicted, in the static regression case evidence of mixing of the shallow contributions from each Hb species was seen for both species and at both the DLPFC and MFG regions. This mixing was most pronounced for the [HbO] traces at the DLPFC, and may be due to unequal sampling of arterial and venous compartments by each channel. Regressor beta fit parameters for both of the shallow nuisance regressors were found to be non-zero. Therefore, both contributed to each of the traces of interest, regardless of Hb species. This finding suggests that including only within-species shallow nuisance regressors in the static regression, as in some prior studies [45, 46, 50, 63], may be sub-optimal. Despite this improvement in the model used for shallow nuisance regression, static regression provided only a minimal increase in state prediction accuracy over the as-measured case across participants, and was far out-performed by the adaptive regression method.

We also observed a significant reduction of the amplitude of very low frequency activity in the adaptive regression residuals as compared to the static regression residuals. This may indicate that peaks in the very low frequency range of the static regression residual traces are mostly due to un-modeled time-varying physiology, which is effectively removed by the adaptive processing method. An example of such physiology is vasomotion present in the vasculature of the shallow tissue. The fNIRS technique is very sensitive to changes in the superficial tissue, as its non-invasive nature inherently involves sensing of the vasculature in the skin and through the skull. Thus, it is highly sensitive to both systemic Mayer waves and local vasomotion [82]. Intrinsic resting state activity may also contribute to signal content in this frequency range, and such a contribution cannot be ruled out in the present study. If behavioral metrics, which are influenced by functional network activity [6, 12], correlated with low frequency activity, then low frequency activity could be attributable to functional network activations. However, we did not observe such a correlation, suggesting that the observed low frequency activity is not attributable to functional network activity. Whether variability in the very low frequency range is due to physiology or to varying intrinsic resting state functional activity, adaptive filtering effectively removed it, thereby allowing us to focus on task effects.

4.2 Novelty and contributions

The present work improves on prior methods [13] for predicting task engagement with fNIRS, which did not employ adaptive filtering. In particular, we report an extensive exploration of attentional state prediction based on various fNIRS processing methods and features that sheds light on how different processing methods perform. Quantification of classifier performance differences among these methods informs analysis decisions for future state prediction studies. We successfully applied existing adaptive filtering methods [44, 50], using both measured physiological nuisance traces from short-separation optodes and measured task-evoked hemodynamic responses as in [51], to the simultaneous detection of cognitive attentional responses in multiple regions of the brain in the context of functionally-connected networks. Of importance, cognitive responses are not as reliable, robust and well-characterized as motor and visual responses. Also, superficial tissue and the depth of the cortex of interest are inhomogeneous across regions of the brain. The effectiveness of adaptive techniques should not be assumed to be the same across tasks and regions without testing, as we have done here for an attentional task using the DLPFC and the MFG. Finally, we improved upon existing within-species physiological correction methods (separate [HbO] and [HbR] filtering) [46] to account for inhomogeneous sampling of arterial and venous vascular compartments across optodes as explained in section 2.3.2, and have shown that each species of nuisance regressor makes some contribution to both species of the [Hb] signals of interest.

4.3 Pros and cons of using a simple behavioral task model

The adaptive regression method removes dynamic noise and performs well using our behavioral task model. This approach is especially useful in the present exploration of the TPN and the TNN, because functional connectivity involving these networks is dynamic. Put another way, activations in these networks are variable in both time and frequency. This may be due to noise or to variations in cognitive state on the scale of seconds to minutes [84–86]. Notably, such variability, if not modeled, can confound the measurement of task effects. Indeed, short time windows have been used to assess the correlation of fMRI Blood-Oxygen-Level Dependent (BOLD) time series in these networks to better understand the relationship between variable network connectivity and behavior [87]. Also, the temporal synchronicity of functionally connected networks, which would have to be variable to function as such, has been proposed as an integrating mechanism for introspective and extrospective functions [88]. Dynamic filtering, by means of adaptive regression, allows such variable activations to be accounted for, thereby improving the removal of noise and the detection of activation changes that are due to variations in internal and external attention.

However, some limitations of the present study result from the simplicity of our model for expected task-evoked network activation. In particular, the model does not allow flexibility for states other than the two expected ones. Thus, higher state prediction accuracy in the adaptive case may stem from the fact that we are forcing the classifier features (i.e., the functional traces and the features created using these traces), via GLM analysis at each time point, to adhere more closely to the expected two-state system.

Such a model, accounting for only negative correlation in either of the on-task or off-task states, is perhaps too basic. Internally-guided thought and the dynamic nature of functional connectivity between the TPN and TNN should be considered in the task model rather than discarding the related activations as noise. Internally-guided or task-unrelated thoughts were uncontrolled in the present study beyond instructing the participant to perform the task or to “think of nothing in particular.” Corrections for variability due to mind wandering [89, 90] during task execution were not employed. This is important because network co-activation, and therefore positive correlation, is expected during internally-guided thought [91, 92].

Finally, network correlation may differ depending on the time scale across which it is measured. This dynamic nature of functional connectivity [84–87, 93] presents further complications for making moment-to-moment predictions using a model based on static or larger time scale measures. Hemodynamic activations in the TPN and TNN are not neatly driven to be more or less anti-correlated in the on-task vs. off-task state at the single-participant, moment-to-moment level. Indeed, Kelly et al. [6] describe tightly-coupled anti-correlated network activations that explain the variance of overall participant performance levels, not participant performance on a moment-to-moment or time-windowed basis. Thus, accounting for network co-activation and for the possibility of dynamic functional connectivity both provide useful avenues for improving the behavioral task model that we employed in the present study.

5. Conclusion and future work

By employing various fNIRS processing methods and multivariate pattern classification techniques, we successfully distinguished between periods of task performance and periods of rest. We also applied adaptive regression techniques for fNIRS to the recovery of real cognitive task-evoked responses at multiple regions from measures that were contaminated by dynamic physiological artifacts. These artifacts and nuisance signal contributions were prominent on both hemoglobin species, likely originating in superficial tissue to which fNIRS is highly sensitive. Our cross-species correction techniques may therefore be used to improve the predictive power of attentional state monitoring and other fNIRS-based systems. Interesting future work includes quantifying and comparing functional response recovery with and without the cross-species correction.

Classification accuracies of 84% in the present study were achieved using SVMs, a known model of expected task activity, and improved noise-removal techniques relative to prior work [13]. This represents the maximal capability of an attentional state monitoring system based on the present methods. These results may be useful for informing decisions and warranting future investments in the development and use of such systems. Further, it would appear that classification accuracy is limited more by the availability of appropriately-complicated task models and the removal of dynamic noise than by regional optode localization precision. The ability to identify noise and remove it while leaving the activation of interest sufficiently intact is limited without a model of task activity. Without such a model, the highest classification accuracy we observed was 70%. This level of accuracy is likely insufficient for monitoring and predicting cognitive state using fNIRS alone in real-world applications. Given that participants were lying in an MRI scanner during data collection, contributions from confounding Mayer waves are expected to be greater when participants are seated, and greater still while they are standing [43]. Ambient light and motion artifacts can be expected to be greater as well. Therefore, further work must be done to assess physiological nuisance removal and the resulting cognitive state classification performance in these contexts.

Improvements in accuracy could be made in several ways. First, measuring task activity for the purposes of modeling it could aid noise removal and thus improve classification accuracy. This could be done by detecting behavioral performance or physical activity during task performance. Second, increasing the amount and quality of training data could improve classification accuracy, although the relatively small reduction in accuracy that we observed with shorter classifier training time is encouraging for more time-efficient and simpler operational use. Third, using multi-modal sensing in ensemble classification could provide additional information to the classifier, which could lead to improved classification performance. Fourth, future work implementing a more complicated model of network activity could improve classification accuracy. Finally, other classification methods should be explored, addressing cross-time and cross-task generalizability of the classifier models. Regardless of these potential improvements, we note that the present techniques are ready for investigations in which hemodynamic measures synergistically complement EEG and other psychophysiological measures in multimodal classification schemes [94].

The improved ability to monitor cognitive state for low levels of task engagement that we demonstrate here may also be applied in increasingly realistic simulations, and toward assessing the efficacy of countermeasures aimed at improving operational performance. Further, the portability of fNIRS, especially when coupled with real-time signal analysis and classification, enables the use of task engagement detection in clinical outpatient monitoring or treatment protocols, biofeedback training, or other brain-computer interface (BCI) applications [43, 95]. We conclude that fNIRS could prove quite useful for monitoring cognitive state in many real-world settings.