A Computational Tool for the Microstructure Optimization of a Polymeric Heart Valve Prosthesis

Abstract

Styrene-based block copolymers are promising materials for the development of a polymeric heart valve prosthesis (PHV), and the mechanical properties of these polymers can be tuned via the manufacturing process, orienting the cylindrical domains to achieve material anisotropy. The aim of this work is the development of a computational tool for the optimization of the material microstructure in a new PHV intended for aortic valve replacement to enhance the mechanical performance of the device. An iterative procedure was implemented to orient the cylinders along the maximum principal stress direction of the leaflet. A numerical model of the leaflet was developed, and the polymer mechanical behavior was described by a hyperelastic anisotropic constitutive law. A custom routine was implemented to align the cylinders with the maximum principal stress direction in the leaflet for each iteration. The study was focused on valve closure, since during this phase the fibrous structure of the leaflets must bear the greatest load. The optimal microstructure obtained by our procedure is characterized by mainly circumferential orientation of the cylinders within the valve leaflet. An increase in the radial strain and a decrease in the circumferential strain due to the microstructure optimization were observed. Also, a decrease in the maximum value of the strain energy density was found in the case of optimized orientation; since the strain energy density is a widely used criterion to predict elastomer’s lifetime, this result suggests a possible increase of the device durability if the polymer microstructure is optimized. The present method represents a valuable tool for the design of a new anisotropic PHV, allowing the investigation of different designs, materials, and loading conditions.

Introduction

In the surgical treatment of aortic valve diseases, PHV prostheses have the potential to combine the hemodynamics and the low thrombogenicity of biological prostheses, with the durability of mechanical prostheses. Yet, no PHV is currently used in clinical practice; several PHV prototypes, mainly composed of polyurethane-based materials, have been developed since 1960s [1] but, despite their promising short-term outcomes [2–6], none have shown satisfactory long-term reliability, due primarily to calcification and tearing of the leaflets [7–10]. The achievement of an adequate device lifetime remains the main challenge in the development of a clinically viable polymeric prosthesis. In this context, the geometry and material design are critical for obtaining optimal mechanical performance of the device.

In the literature, many authors have highlighted the importance of material anisotropy on aortic valves’ behavior. In fact, natural valve leaflets are characterized by the presence of collagen bundles basically oriented in the circumferential direction, embedded in an elastic matrix [11–14]. As a consequence of this particular architecture, the leaflet circumferential stiffness is significantly larger than the radial stiffness (about 15 MPa versus 2 MPa [11,15]). Even if the mechanisms underlying this tissue arrangement are not completely understood, it surely influence the valve mechanical behavior and failure mechanism [13,16–20]. The anisotropic tissue structure allows the valve to open easily due to the low resistance of collagen fibers to bending and increases the material stiffness and strength during valve closure. Some authors have tried to mimic the anisotropic structure of the natural valve in PHV prostheses, mainly by using reinforcement fibers in the leaflets [21–23]; however, a clear improvement in prosthesis lifetime with such devices has not been proven, and none of these devices reached a clinical evaluation stage.

Recently, different polymers characterized by good biostability and biocompatibility have been developed as possible materials for the development of PHVs [24]; among them, block copolymers represent a promising class of material [25,26]. In particular, the good biocompatibility and the suitable mechanical properties of styrene-based block copolymers for application in heart valve prostheses have been demonstrated [3,9,27–30]. Further, our group has recently shown the possibility of tuning the microstructure and, consequently, the mechanical properties of this type of polymer by compression and slow injection molding: the investigation of thin molded films of poly(styrene-block-isoprene-block-styrene), a block copolymer characterized by a cylindrical morphology, revealed a layered orientation of the cylinders which depends on the conditions during the manufacturing process (i.e., flow rate and temperature) [31,32]; this layered structure leads to a strong anisotropy of the material, as demonstrated by mechanical tests of material samples. Thus, following a mechanism similar to the native valve where the collagen bundles sustain most of the stress, the optimization of the cylinders’ orientation in the valve leaflets could enhance the long-term performance of the PHV, making this class of material an excellent candidate for the development of a new polymeric aortic valve prosthesis [33]. We have already tested some PHV prototypes made of polystyrene-containing block copolymer in continuous and pulsatile flow conditions, as prescribed by the ISO 5840 Standard. A custom-made pulse duplicator was used to test the prototypes at different flow rate and frequency conditions; pressure and flow signals were recorded and pressure drops, effective orifice area (EOA), and regurgitant volume were computed. All the tested PHVs met the requirements defined by the ISO 5840 Standard (EOA > 1 cm² and regurgitant volume < 10% of the stroke volume), indicating good device hydrodynamics under the prescribed conditions [34,35]. However, these valves were not optimized in terms of material microstructure and determining the optimum cylinders’ orientation of the PHV is one of the main challenges to solve in the development of a new anisotropic valve. The aim of this work was to develop a computational tool for the optimization of the PHV microstructure. The basic idea was to orient the polymer microstructure in the leaflets along the maximum principal stress direction, to allow the cylinders to act as reinforcements in the most stressed direction. The optimization procedure herein presented has general validity and could easily be applied to different type of valves, materials, and loading conditions.

Methods

A computational model of the PHV leaflet was developed; the simulations’ outcomes allowed the identification of the maximum principal stress directions in the leaflet, while a custom routine was implemented to optimize the material microstructure. Only one leaflet was considered due to the valve’s geometric periodicity (120 deg); the presence of the other leaflets and of a rigid stent was taken into account by applying suitable boundary conditions. The study was focused on valve closure, since during this phase the fibrous structure of the leaflets must bear the greatest load. For the sake of clarity, the description of the optimization procedure and of the finite-element (FE) model implementation is presented below in different sections: Leaflet Geometry, Material Description, Experimental Protocol, Material Microstructure Optimization, and Boundary and Other Simulation Conditions.

Leaflet Geometry

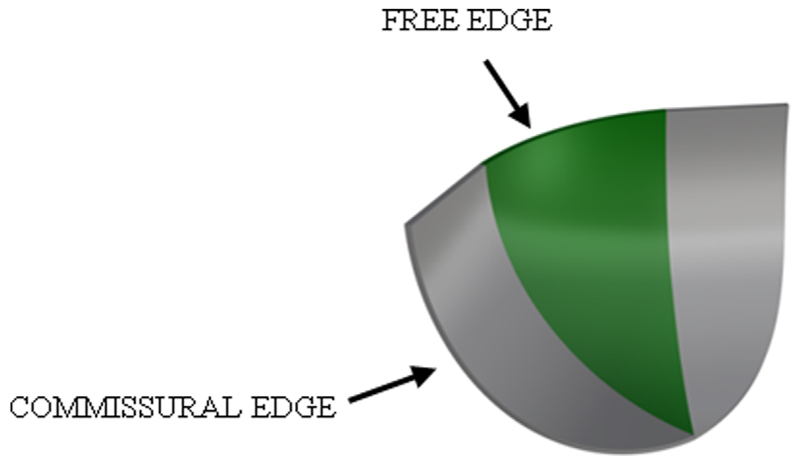
A 3D model of the PHV leaflet was designed by means of the computer-aided design (CAD) software RHINOCEROS 5 (Rhinoceros, Robert McNeel and Associates, Seattle, WA). The valve design, and particularly the leaflet shape, is fundamental for ensuring correct valve opening and closing under physiological blood pressure. For this reason, the aortic valve geometry has been investigated by different authors [36–38]. In this work, a trileaflet symmetric valve with constant leaflet thickness and identical material properties in each leaflet was assumed. The leaflet shape consists of a central spherical region where the circular free edge is extended tangentially to connect the leaflet with the valve stent; the commissural edge is cut in a cylindrical shape (Fig. 1). The valve internal diameter was set at 23 mm, the leaflet height at 11 mm, while the leaflet thickness was constant and equal to 0.3 mm.

Fig. 1.

CAD design of the valve leaflet; the central spherical region is highlighted. Geometrical parameters: valve diameter = 23 mm; leaflet height = 11 mm; and leaflet thickness = 0.3 mm.

Material Description

The mechanical behavior of block copolymers is characterized by a nonlinear stress–strain relationship which is strongly dependent on the microdomain architecture [39,40]. In fact, block copolymers with cylindrical domains can show either isotropic or anisotropic behavior, depending on the orientation of the material [40]. The mechanical behavior of block copolymers can be well described by a hyperelastic constitutive law, where the material response is determined by a strain energy function ψ. Under the hypothesis of material incompressibility (namely, volume ratio in the deformation process J = det(F) = 1), the strain energy can be written as

$$\psi =\psi \left(\mathbf{\text{C}}\right)-p(J-1)$$ (1)

where C is the right Cauchy–Green tensor, and p is the hydrostatic pressure.

The strain energy can be further divided into an isotropic and an anisotropic contribution to take into account the material’s anisotropic microstructure by considering

$$\psi (\mathbf{\text{C}})={\psi }_{\text{iso}}\left(\mathbf{\text{C}}\right)+{\psi }_{\text{aniso}}(\mathbf{\text{C}})$$ (2)

For the isotropic part of the potential, a Mooney–Rivlin stress–strain relationship was assumed; in terms of the principal invariants of C, it can be written as

$${\psi }_{\text{iso}}={\psi }_{\text{iso}}\left(I_1,I_2\right)=c_1\left(I_1-3\right)+c_2\left(I_2-3\right)$$ (3)

where c₁ and c₂ are the material parameters to be identified.

Finally, the anisotropic contribution of ψ has been defined as [41]

$${\psi }_{\text{aniso}}={\psi }_{\text{aniso}}\left(I_4\right)=k_4{\log }^2\sqrt{I_4}$$ (4)

where k₄ is a parameter to be determined from mechanical tests of the material. I₄ is a pseudo-invariant of C which takes account of the cylinders’ orientation by the unit vector a

$$I_4={\mathbf{\text{a}}}_0\cdot {\mathbf{\text{Ca}}}_0={\mathbf{\text{a}}}^{\text{T}}\cdot \mathbf{\text{a}}$$ (5)

in Eq. (5), a₀ defines the cylinders’ direction in the undeformed configuration, while a defines the cylinders’ direction in the deformed configuration. In fact, I₄ measures the square of the stretch along the cylinders’ direction.

Summarizing, the proposed strain energy function has the form

$$\psi =c_1\left(I_1-3\right)+c_2\left(I_2-3\right)+k_4{\log }^2\sqrt{I_4}-p\left(J-1\right)$$ (6)

this material constitutive law was implemented in the software by using the UANISOHYPER subroutine. The stress is computed from the strain energy by derivation with respect to the right Cauchy–Green tensor C as

$$\mathbf{\sigma }=2J^{-1}\mathbf{\text{F}}\frac{\partial \psi (\mathbf{\text{C}})}{\partial \mathbf{\text{C}}}{\mathbf{\text{F}}}^{\text{T}}$$ (7)

which, for the constitutive law defined in Eq. (6), gives

$$\mathbf{\sigma }=2\left[\left(\frac{\partial \psi }{\partial I_1}+I_1\frac{\partial \psi }{\partial I_2}\right)\mathbf{\text{b}}-\frac{\partial \psi }{\partial I_2}{\mathbf{\text{b}}}^2+\frac{\partial \psi }{\partial I_4}\mathbf{\text{a}}\otimes \mathbf{\text{a}}\right]-p\mathbf{\text{I}}$$ (8)

where b is the left Cauchy–Green tensor (for a detailed description of hyperelastic material modeling, refer to Holzapfel et al. [42]).

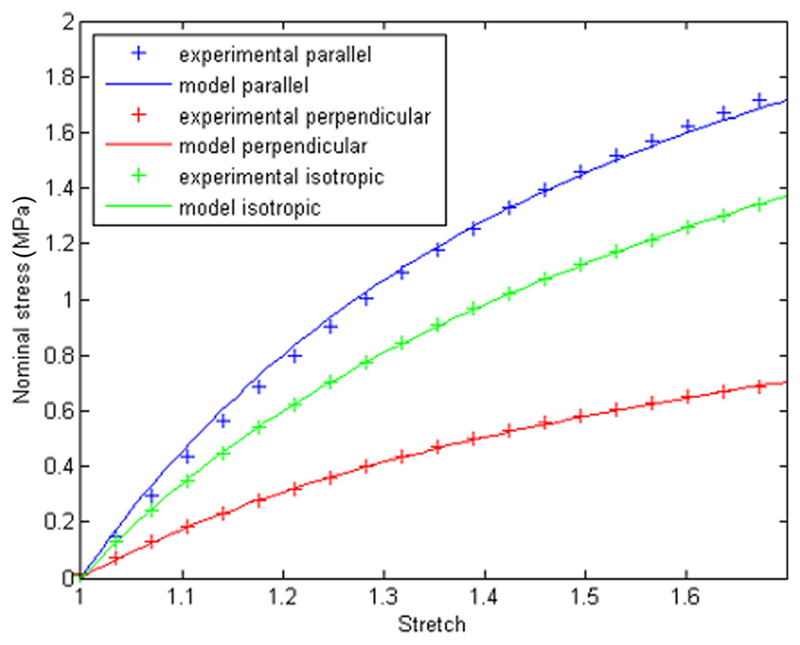
In the case of isotropic material, the anisotropic contribution was dropped; thus, three material parameters have to be identified for the anisotropic case (c₁, c₂, and k₄) and two parameters for the isotropic case (c₁ and c₂). In both cases, the parameters were optimized using the nonlinear least-square algorithm to match data from experimental mechanical tests, by means of a custom MATLAB (MATLAB, The MathWorks, Inc.) routine (Fig. 2).

Fig. 2.

Experimental and modeled stress–strain relationship for the isotropic and the anisotropic case. For the anisotropic case, both the direction parallel and perpendicular to the principle strain direction are presented.

Experimental Protocol

Uniaxial tensile tests (Texture Analyser, Stable Microsystems, UK) were performed on dogbone samples (length = 100 mm, width = 4 mm, and thickness = 0.7 mm) up to 70% elongation at a speed of 1 mm/s, according to the ASTM standard D882. About 100 preconditioning cycles were performed in order to reach a reproducible stress–strain behavior between two subsequent cycles. Both the isotropic and anisotropic materials were tested; for the anisotropic case, two cylinder orientations were considered: parallel and perpendicular to the principle strain direction. A minimum of three samples were tested for each material. The isotropic samples were obtained by solvent casting, while the anisotropic samples were fabricated via compression molding at 160 °C, as previously described by Stasiak et al. [43]. The specific block copolymer used to fabricate the samples was poly(styrene-block-ethylene/propylene-block-styrene), a linear block copolymer characterized by a cylinder length of 200–500 nm. The results of the experimental tests and the optimized material model are shown in Fig. 2; the optimized material parameters for the isotropic and anisotropic materials are presented in Table 1.

Table 1. Optimized material parameters.

	c1 (MPa)	c2 (MPa)	K4 (MPa)
Anisotropic	0.15	0.18	1.62
Isotropic	0.3	0.36	—

Material Microstructure Optimization

The cylinders’ orientation was set in the material model by defining the vector a₀, which describes the material microstructure in the reference configuration (Eq. (5)). The microstructure vector a₀ can be set in both the Cartesian (e) and material $(\tilde{\mathbf{e}})$ reference systems, the two systems being related by the relationship

$$\widetilde{\mathbf{\text{e}}}=\mathbf{\text{Qe}},\hspace{0.17em}\mathbf{\text{e}}={\mathbf{\text{Q}}}^T\widetilde{\mathbf{\text{e}}}$$ (9)

where Q is an orthogonal tensor and is referred to as the transformation matrix.

The orientation of a₀ was optimized by an iterative procedure which, starting from an initial guess, aligns the cylinders’ direction with the maximum principal stress direction. For this purpose, a custom MATLAB routine was implemented. The routine defines the cylinders orientation’ in the nth iteration based on the results of the (n − 1)th iteration in terms of maximum principal stress directions; each iteration consists of an FE simulation aimed at finding the maximum principal stress direction in the leaflet from the Cauchy stress tensor (see Boundary and Other Simulation Conditions section for a description of the FE model implementation).

Specifically, for each element of the leaflet mesh a different local reference system was defined; this local system was rotated between the (n − 1)th and the nth iteration to align one axis of the new reference system (the axis along which the microstructure vector a₀ is oriented) with the maximum principal stress direction obtained in the previous iteration. Thus, calling r₀ the microstructure vector at the (n − 1)th iteration, the vector a₀ at the nth iteration was obtained by

$${\mathbf{\text{a}}}_0={\mathbf{\text{R}}}_0{\mathbf{\text{r}}}_0$$ (10)

where R₀ represents the rotation matrix, defined from the angle between the vector r₀ and the maximum principal stress direction in the (n − 1)th iteration (Fig. 3). Finally, the routine transforms a₀ such that it refers to the undeformed configuration, in order to find the cylinders’ orientation at the beginning of the next iteration.

Fig. 3.

Schematic representation of the cylinders’ reorientation procedure: for each element, the first axis of the reference system in the (n − 1)th iteration is rotated via the matrix R₀, which superimposes this axis with the maximum principal stress direction of iteration n − 1. Thus, the new reference system to be used in the nth iteration is obtained.

The optimization process ends when the percentage of the element’s local reference systems which are rotated more than 5 deg between two subsequent iterations is less than 1%. Different starting orientations were set to ensure the robustness of the reorientation procedure, indicating that the starting orientation did not affect the optimized microstructure; hence, for the sake of simplicity a starting orientation in the x global axis direction was chosen.

Boundary and Other Simulation Conditions

A rigid valve stent was assumed; to simulate the effect of the rigid stent on the leaflet dynamics, no displacements at the commissural surface were permitted. To mimic the presence of the other two leaflets of the valve, two rigid planes were defined and a frictionless contact was implemented between each of these planes and the ventricular surface of the leaflet. Preliminary simulations comparing the one and the three leaflets case ensured the suitability of this boundary condition in the presence of a rigid stent. These simulations showed how for the case of a flexible stent the twisting in the middle of leaflets during closing can influence the mechanical response of the valve; however, no twisting has been found in the case of a rigid stent, thus the modeling of a single leaflet was adequate for the aim of this study. A uniform pressure load was applied on the aortic surface of the leaflet; different backpressures have been modeled in the range specified by the ISO Standard 5840 as operational environment for an aortic valve prosthesis (95–185 mm Hg). Since the results of the optimization procedure are similar in all the simulated cases, for the sake of brevity the only case of pressure equal to 135 mm Hg is presented hereinafter. A quasi-static loading condition was assumed [44–46]; the nonlinear implicit FE algorithm provided by abaqus was used to solve the numerical problem. The leaflet geometry was discretized in 15,330 hexahedral linear elements to perform the FE analyses. Specifically, three elements were placed across the leaflet’s thickness to correctly model the structure bending. Simulations with an increasing number of elements up to about 60,000 elements were performed to ensure the independence of the results from the mesh size.

Results and Discussion

The result of the optimization process is shown in Fig. 4. Starting from the initial configuration where the cylinders are aligned along the x global axis (identified as the baseline), the optimal microstructure obtained by our procedure shows primarily circumferential orientation within the valve leaflet, except for a region close to the commissural edge where the orientation is more radial. No discontinuities are present in the cylinders’ orientation across the thickness, since the maximum stress direction is quite constant over the three layers in which the geometry was discretized (see “Boundary and Other Simulation Conditions” section). Three iterative steps were necessary to reach this optimum material microstructure according to the criterion described in the Material Microstructure Optimization section; however, as highlighted in Fig. 5, most of the cylinders’ reorientation is completed after the first iteration. Interestingly, the optimized architecture just described reproduces quite well the structure of a native aortic valve leaflet [16], where the collagen bundles exhibit a pattern which is similar to the optimum distribution of cylinders in the PHV (Fig. 4). This evidence further confirms, as highlighted by other studies [47,48], that the natural leaflet is well adapted by remodeling during growth to withstand the pressure load exerted by the blood during valve closure. It is worth noting that in our case, the maximum stress direction is aligned with the maximum strain direction; thus, a strain-driven optimization criterion such as that hypothesized by Driessen et al. [48] for the native aortic valve would lead to the same result in terms of material microstructure.

Fig. 4.

Cylinder orientation within the leaflet at the beginning (baseline, left) and at the end (optimized, middle) of the optimization process. Right: collagen fiber architecture in a native porcine aortic valve [16].

Fig. 5.

Percentage of rotated local systems in the model for each iteration. After three iterations, the cylinder orientation changes in fewer than 1% of the total elements of the leaflet.

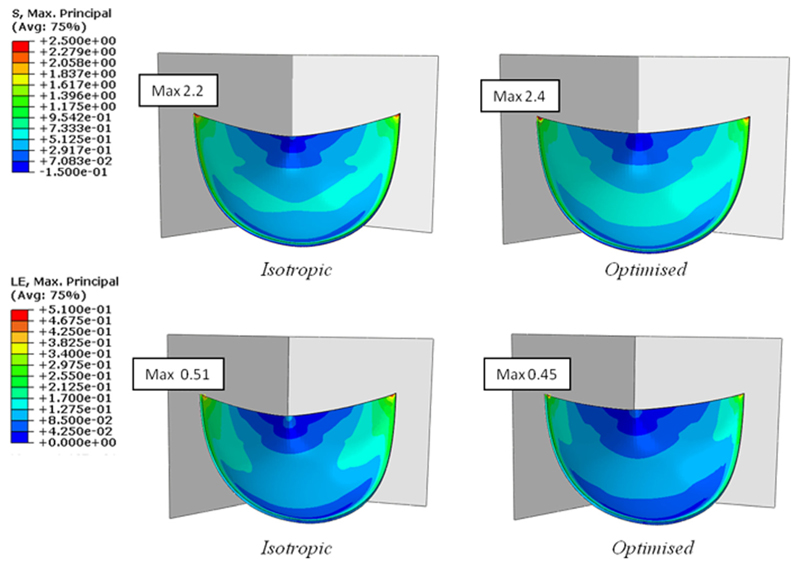
In order to study in more detail the effect of the material microstructure on the leaflet mechanics, the stress and strain distributions in the PHV leaflet for both optimized and isotropic material were analyzed (Fig. 6).

Fig. 6.

Maximum principal stress (top) and maximum principal logarithmic strain (bottom) distributions in the leaflet in the case of isotropic and anisotropic material

The comparison between optimized and isotropic material demonstrates a similar stress distribution with the maximum stress location at the top of the commissural edge (Fig. 6, top); the maximum stress is about 8% greater when the material is optimally oriented compared to the nonoriented material. This result is in agreement with other published studies, where the material anisotropy contributes to an increase in the maximum stress present in the leaflet, because of the higher stiffness in the loading direction [22,45,49]. However, in Luo et al. [45] and Li et al. [49] a change of the maximum stress location, from the top of the commissures to a point along the commissural edge, was also reported when an anisotropic leaflet material was considered. This difference to our results could be due to several factors, since the aforementioned studies were focused on porcine heart valves characterized by a different geometry, material properties, and fibers orientation and distribution, to those used in this study.

As expected, the strain pattern shows an inverse trend (Fig. 6, bottom): the optimized leaflet is characterized by a smaller maximum principal strain when compared to the isotropic material. Also, due to the material’s mechanical behavior, the difference in the maximum strain is larger than for the stress: the maximum strain is about 14% lower for optimized cylinder orientation than isotropic material.

In accordance to observations by Li et al. [49], the macroscopic effect of the decrease in maximum strain is a reduction in the vertical displacement of the central point of the free edge, which is equal to 2.1 mm in the anisotropic case and 2.8 mm in the isotropic case.

However, the material stiffening in the maximum stress direction due to the cylinders’ orientation does not affect the valve macroscopic closing: the coaptation area between the leaflets decreases only 2% when the material is oriented compared to the isotropic case.

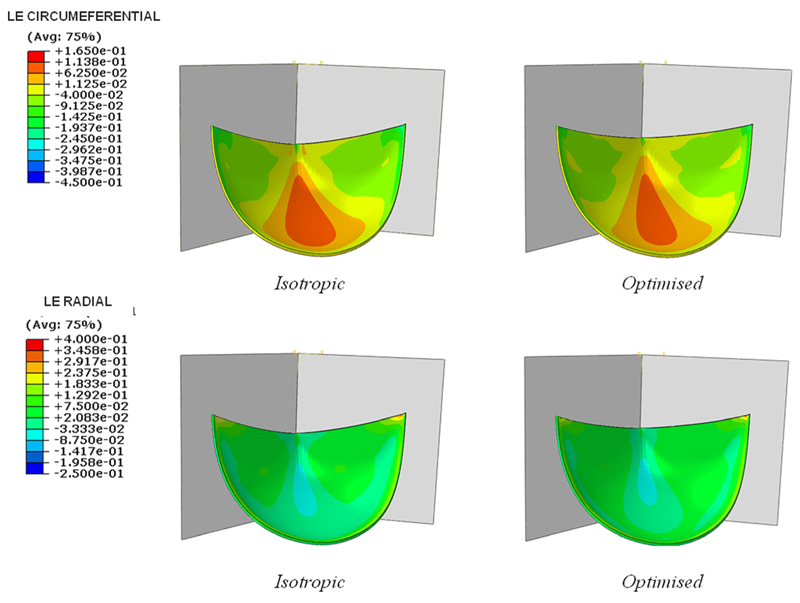
Further, the circumferential and radial strains were analyzed (Fig. 7).

Fig. 7.

Circumferential (top) and radial (bottom) logarithmic strain in the isotropic and optimized cases

The optimized microstructure leads to a smaller circumferential strain and a higher radial strain than those found in an isotropic valve, in accordance with the studies of Billiar et al. [16,50], and Martin et al. [51] on the native valve, which highlighted how the natural tissue is mainly stretched in the radial direction due to the collagen fibers organization.

A similar result was also obtained by Loerakker et al. [18] with a model of tissue engineered heart valves, where a larger radial and smaller circumferential strain were found with an increased material anisotropy.

Hence, the results presented so far mainly show that an optimized polymer microstructure can enhance the material response to the pressure load, in fact mimicking the native valve’s mechanical behavior. However this data, while promising, does not in itself clarify whether an improvement in the fatigue life of the valve prosthesis will be achieved by properly controlling the polymer microstructure.

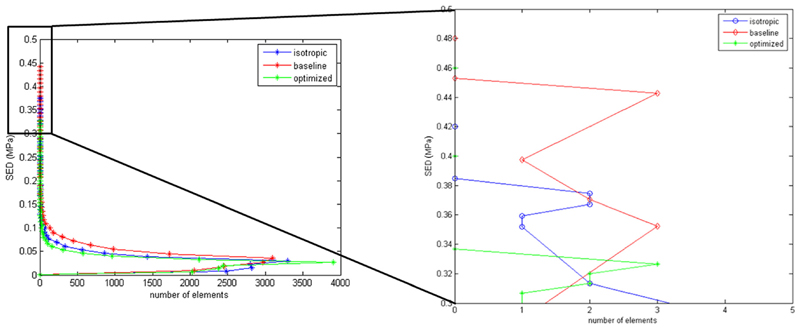
In the literature, different criteria have been proposed to predict elastomer’s lifetime under cyclic loading; among them, the strain energy density is one of the most widely used parameters to investigate the fatigue behavior of rubbers [52,53]. Thus, to better understand the effect of the cylinders’ orientation on the valve lifetime, the strain energy density was calculated for all the elements of the valve leaflet at the maximum applied pressure for the isotropic and anisotropic materials (Fig. 8). For comparison purpose, the result for the baseline configuration is also shown (Fig. 8); even if the baseline structure does not have any physical meaning, as it only represents the starting point of the optimization procedure, it can be useful to understand the effect of a possible “accidental” material orientation due to an uncontrolled manufacturing process.

Fig. 8.

Strain energy density calculated for all the leaflet elements for isotropic and anisotropic cases. For the anisotropic material, both the baseline and the optimized configuration are presented.

The results show a decrease of about 14% of the maximum value of the strain energy density when the material microstructure is optimized. Assuming that the valve failure mechanism is more likely to be initiated at points of high strain energy density, this finding suggests an improved long-term mechanical response for an optimized valve compared to an isotropic valve. Also, this result highlights the negative effect of a nonoptimized oriented material microstructure, since the baseline configuration exhibits the highest value of strain energy density among the analyzed configurations (+25% when compared to the optimized case).

Conclusions

In this work, a computation tool for the optimization of a new polymeric aortic valve prosthesis made of styrene-based block copolymers is presented. An optimization procedure was developed to align the cylindrical domains along the maximum stress direction, thus mimicking the effect of the collagen bundles in the native valve. As for the natural valve, the optimization of the leaflet microstructure is responsible for a reduction in the circumferential strain and an increase in the maximum stress. Further, the material stiffening along the most stressed direction does not negatively affect the valve regurgitation, as demonstrated by the leaflets’ coaptation area which is almost the same in the case of isotropic or optimized microstructure. As in the native valve, the opening should not be significantly influenced by the material orientation either, due to the very small resistance of the cylinders to the leaflet bending.

Furthermore, when the material is properly oriented, the maximum strain energy density is reduced, suggesting an improvement in the prosthesis’ lifetime; however, experimental fatigue tests are required to confirm the validity of this result. The presented method can be of great value for the development of a reliable PHV, in which valve geometry and material properties must be simultaneously optimized.

We have already demonstrated the possibility of orienting the material microstructure in compression and injection molded flat samples [31,40]. Also, we have fabricated compression molded valves that showed acceptable hydrodynamic behavior; although, in these valves, the material microstructure was not optimized. Based on the results of this work, we have fabricated injection molded valves with the aim of controlling the cylinders’ orientation by the polymer flow during processing. The first results are encouraging, since a mainly circumferential orientation of the cylinders has been obtained in the leaflets. In this context, the model can also be used to predict the influence of small defects on the prosthesis behavior, giving important indications about the valve manufacturing.

Some assumptions were made in the implementation of the computational model. First, the viscoelastic properties of the polymer were neglected; although loading–unloading cycles performed on the material have shown only limited hysteresis and sensitivity to strain rate, progressive creep of the polymer chains during stretching could influence the mechanical response of anisotropic samples. Also, the material characterization was obtained via uniaxial tensile tests; however, due to the polymer anisotropy and the valve loading conditions, biaxial tests would lead to more accurate results in terms of mechanical response of the material. Further, the solvent cast method ensures a random planar polymer chain distribution (namely, a transverse isotropy), but some degree of anisotropy is still to be expected in the off-plane direction. Furthermore, a perfect alignment of the cylinders along the specified direction was considered, while some tests [43] highlighted a dispersion of the cylinders around the main orientation which could influence the mechanical behavior of the material. Finally, only the closing phase was considered, since during this phase the fibers must bear the maximum load; the simulation of the valve opening will give further indications for the material optimization and leaflet thickness. Despite these limitations, the present model represents an extremely valuable tool for the design of any anisotropic valve, since each feature of the numerical model can be easily modified to understand the optimum material microstructure for different geometries, materials, and boundary conditions.