Extensions to a manifold learning framework for time-series analysis on dynamic manifolds in bioelectric signals

Abstract

This paper addresses the challenge of extracting meaningful information from measured bioelectric signals generated by complex, large scale physiological systems such as the brain or the heart. We focus on a combination of the well-known Laplacian Eigenmaps machine learning approach with dynamical systems ideas to analyze emergent dynamic behaviors. The method reconstructs the abstract dynamical system phase-space geometry of the embedded measurements and tracks changes in physiological conditions or activities through changes in that geometry. It is geared to extract information from the joint behavior of time traces obtained from large sensor arrays, such as those used in multiple-electrode ECG and EEG, and explore the geometrical structure of the low dimensional embedding of moving time-windows of those joint snapshots. Our main contribution is a method for mapping vectors from the phase space to the data domain. We present cases to evaluate the methods, including a synthetic example using the chaotic Lorenz system, several sets of cardiac measurements from both canine and human hearts, and measurements from a human brain.

I. Introduction

In both medicine and biology, there are many types of bioelectric signals of potential interest, such as those arising from the heart (electrocardiography, ECG) or the brain (electroencephalography, EEG). Many of these signals can be characterized as having nonlinear dynamics, and thus have been studied using nonlinear analysis methods. In general, such analyses may allow for a characterization of the nonlinear phenomena present in these signals, which in turn may lead to a better understanding of the underlying physical mechanisms driving the signals. Studies of bioelectric phenomena in nonlinear science broadly fall into one of two categories: mechanistic or phenomenological analyses. Mechanistic analyses are based on the idea that measured bioelectric signals can be modeled as having been produced by complex systems of generators (e.g., cellular ionic models [1, 2], neural mass models [3], etc). Often these analyses are performed as simulation studies, in which mathematical parameters of source models are tuned to produce signal patterns mimicking previous observations of the phenomena of interest (e.g., cardiac fibrillation [1], epileptiform activity [4]). Phenomenological analyses by contrast produce descriptors, through signal processing and analysis steps, that reveal consistently occurring patterns associated with a controlled experimental phenomenon (e.g., a particular disease state)[5–15]. Among these phenomenological approaches are those based on nonlinear science that have been used to test the data for the existence of geometric properties associated with nonlinear dynamical systems [8, 10–12, 14, 15].

Studies offering insights into mechanistic behaviors associated with dynamic descriptions have been limited, in part due to the inherent difficulty of processing and interpreting high-dimensional bioelectric data that result from making many simultaneous electrode measurements at high sampling rates and for long durations of time. That said, developments in machine learning during the past 10-15 years, on the topics of manifold learning and nonlinear dimensionality reduction, have made it possible to uncover relatively low-dimensional parameterizations of such datasets when it may be assumed that the data were sampled from a low-dimensional manifold embedded in the high-dimensional data domain [16–21]. Here we contribute new methods for analyzing the geometric structure underlying dynamic bioelectric signals, with the ability to connect phenomenological analyses back to the signal changes that caused them.

While advances in theory and methods related to manifold learning suggest that the field of nonlinear analysis of bioelectric signals could potentially benefit from that area of work, there are presently a number of practical and theoretical challenges potentially impeding their widespread acceptance. First, the computational burden of applying many of these techniques is too high when faced with a large number of data points. Second, they are not designed to (and are not typically used to) analyze time series, although there is progress on this topic [22, 23]. Third, in the field of nonlinear bioelectric signal analysis, there has been little validation of the claim that these methods represent the manifold geometry of the phase space of the underlying, generating dynamical system. The last point is perhaps the most important, because a lack of validation – or even a lack of a method for validation – is a serious hindrance to the adoption of any novel methods by the broader community of scientists and clinicians.

In an effort to address some of these limitations, we focused on one nonlinear dimensionality reduction method in particular, namely Laplacian Eigenmaps (LE). We describe here three contributions to the LE framework with the goal of making this approach more suitable for the analysis of nonlinear dynamics in bioelectric signals. The first two of these are preliminary contributions which enable the third – our main contribution. First, we describe how by applying LE to delay-embedded multivariate time series data, motivated by classical results on the reconstruction of the topology of dynamical manifolds (e.g., Takens-Mane embedding theorem [24, 25]), the method can be used to study the geometric structure associated with the underlying dynamics. Second, we reinterpret the basic LE algorithm (in which the mapping between manifolds is implicit) as a procedure for learning the parameters of an explicit, nonlinear, deterministic mapping from the original data domain to a low-dimensional space. As a result, we present an explicit mapping function, and this allows us to separate the algorithm into an initial training step in which the usual LE algorithm is applied to training data, followed by a mapping step in which the remaining data is mapped to the low-dimensional LE space. Third, as our main contribution, we differentiate the explicit mapping function and use it to map vectors from the original signal domain to the low-dimensional LE domain, or inversely from the LE domain back to the original signal domain.

As is the case with any sensor-data analysis and interpretation method, our goal is to overcome the compound challenges of an ill-posed inverse problem, sensor noise, and source signal irregularities by focusing on a dominant feature of the observed bioelectric signal, i.e., the dynamic patterns of leading LE coordinates. We note that the algorithm considered here makes no effort to explicitly model time-varying dynamics, such as from a non-autonomous [26] or chronotaxic [27] system, and as such it may be regarded as implicitly adopting the model of an autonomous dynamical system. In practice, however, the algorithm is readily applied to data with time-varying dynamics by assuming that a static manifold underlies the data, with the consequence of increasing the dimensionality of the reconstructed phase space. Although it may be possible to obtain a more parsimonious representation with an alternative approach, in our experience the algorithm can be quite sensitive to even small signal changes [28, 29]. Moreover, in general, it would be useful to have a method to validate that the changes in LE coordinates can be directly attributed to meaningful changes in the bioelectric signals themselves. Our proposed vector mapping approach makes it possible to perform this kind of validation by estimating the causes of LE domain changes in the bioelectric signal domain (i.e., by mapping vectors representative of these changes between the two domains), and then confirming that the estimated signal changes match those that were known a priori. In our analyses, we used this approach to validate that LE is sensitive to a number of important signal changes in both ECG and EEG data, which are known to exhibit time-varying behavior [28–30]. Of course, the same methods can be used for data exploration when there is no a priori knowledge of what causes changes in the data. For example, one can use these methods to evaluate whether a particular dynamical model, such as those employed by a dynamical inference method, is suitable for describing the signal changes that are visualized in LE coordinates [31–35].

In the remaining sections, we begin with some background on Laplacian Eigenmaps in Sec. IIA and present our new methods in Sec. II B-II D. We describe our analyses and results in Sec. III. We conclude the paper in Sec. IV with a summary of our claims and contributions, as well as some remarks about future work.

II. Methods

A. Laplacian Eigenmaps

A problem that has attracted great interest in the machine learning literature for over a decade is the identification of low-dimensional manifold structure of a set of data. Typically the assumption is that the data is unlabeled, that is, that no a priori information about relationships between data points is given. There have been a number of proposed solutions to this problem in the literature [16–20]. In general, the methods attempt to identify subsets of the high-dimensional data which can be taken to be locally flat, and then map them to a Euclidean space while preserving the local topology of the points around each data point. Laplacian Eigenmaps, by Belkin & Niyogi [16], is one such dimensionality reduction method that finds functions that minimize the graph Laplacian of a graph constructed from the set of data points. The graph Laplacian is taken as a surrogate for the Laplace-Beltrami operator on a manifold [36]. We refer readers to the literature for a more extensive review of the manifold learning problem. Here we describe our version of the Laplacian Eigenmaps algorithm, which we used for the present study.

Given a set of points assumed to be sampled from a manifold embedded in a higher-dimensional vector space, $P={\{p_k\}}_{k=1}^K$, we perform the following procedure:

1. Compute a matrix, R, of pairwise distances between all points in the data set, with elements R_i,j = ‖p_i − p_j‖₂, and choose a tuning parameter, σ (here set equal to the largest element in R).

2. Compute a matrix, W, which emphasizes local topology represented in R by deemphasizing its larger values (corresponding to longer distances), with elements $W_{i,j}=exp(-R_{i,j}^2/{\sigma }^2)$. Use W to compute a degree matrix, D = diag(Σ_iW_i,:) (where W_i,: denotes the i-th row of W), whose diagonal entries are an estimate of the local sampling densities on the putative manifold, as inferred from the points in the dataset.

3. Solve for the singular value decomposition of D⁻¹W = USV′. The columns of V correspond to the coordinate directions in the Laplacian Eigenmaps space into which points are being mapped. Therefore row k of V contains the LE coordinates of the point p_k.

The singular values on the diagonal of S provide a statistical ranking of the significance of each of the new co-ordinates in the LE space. A low-dimensional mapping is obtained by retaining only the first few columns of V, which correspond to the largest values of S. The first column is typically constant up to numerical precision and thus is discarded. We duly refer to coordinates starting from the second column of V as the “first” coordinates. The σ tuning parameter controls the effective support of the inverse exponential functions, which in turn affects the extent of the local geometry considered by the LE algorithm. Here we set this parameter to be the largest distance between input data points, and this is sufficient for the inverse exponential to decay rapidly enough to emphasize local geometry.

We note that although we are interested here in dynamic behavior, the time corresponding to each data point is ignored in the mapping; it pays attention only to spatial relationships as coded in the distance matrix R. We also note that the way in which we have stated the Laplacian Eigenmaps algorithm is different from its original form, as stated by Belkin and Niyogi in [16]. We elaborate on the relationships between our form of the algorithm and theirs in the Appendix. Finally, this method was not designed to deal with the time-variability of the systems that produce the data. Such data is expected to result in a higher dimensional manifold and to be dealt with accordingly by the user when selecting the number of coordinate directions to be retained by the algorithm.

B. Delay Embedding

Delay embedding is a technique that can be used to reconstruct dynamical attractors from time series data. Specifically, let h be a generic scalar observation function of a state, x, of a dynamical system on a d-dimensional manifold, ℳ. Takens-Mane Theorem [24, 25] states that the trajectory x(t) can be diffeomorphically embedded in a Euclidean vector space of dimension greater than 2d, by forming vectors of at least 2d + 1 appropriately delayed samples of h(x(t)). For a particular choice of the delay constant, τ, this embedding takes the form:

$$\stackrel{\sim }{x}(t)=\left[\begin{array}{c}h(x(t))\\ h(x(t-\tau ))\\ ⋮\\ h(x(t-2d\tau ))\end{array}\right].$$ (1)

In this paper, we will only consider observations in discrete time that are regularly sampled, and always take the delay constant to be equal to 1 sample (i.e., τ equals the sampling period). With the multichannel (that is, multi-electrode) measurements at hand, we can either embed them in their “natural” space without incorporating delays, or we can concatenate a sequence of delayed measurements in a multichannel extension of classical embedding (i.e., taking h to be a multivariate observation function). Thus we can use Laplacian Eigenmaps to learn the manifold structure underlying the sequence of observations, x(1), x(2), …, x(T), by applying the algorithm to the delay-embedded set of points $P={\{\stackrel{\sim }{x}(t)\}}_{t=2d\tau +1}^T$.

C. Laplacian Eigenmaps as an Explicit Mapping Function

The Laplacian Eigenmaps (LE) algorithm in Sec. IIA can be interpreted as a training step in which not only the mapping of the training points are learned, but also the parameters that define an explicit mapping from the original data domain to the resulting LE coordinate system. The idea of an explicit mapping is akin to a so-called “out-of-sample extension” of Laplacian Eigenmaps, as described in [37], which builds on the relationship between LE and kernel principal component analysis (PCA) [38] to posit a probabilistic relationship between the set of points P from Sec. IIA and then extend that to a point not in that set, x ∉ P. However, unlike in [37], in the sequel we will treat the out-of-sample extension conceptually as a mapping between manifolds, and thus we describe an explicit deterministic mapping to the putative manifold learned by the Laplacian Eigenmaps algorithm described in Sec. II A.

For a set of training points, the approach we describe next is equivalent to splitting the algorithm in Sec. IIA into a two-step process consisting of a training procedure followed by an explicit mapping procedure. As noted above, the benefit of doing this is that the explicit mapping can be applied to points that aren't in the training set. Assume that we are given a choice of tuning parameter, σ, a set of training points, $P={\{p_k\}}_{k=1}^K$, and a new point, x, in the same space. Then the training procedure consists of applying the LE algorithm in Sec. IIA to the training points, but instead of keeping the usual output (i.e., the contents of the matrix V), we are only concerned with the D, U, and S matrices, which we take as the outputs instead. To assist in the statement of the explicit mapping function, we define the function g(x) as

$$g(x)={[exp(-\frac{{\Vert x-p_1\Vert }_2^2}{{\sigma }^2})\cdots exp(-\frac{{\Vert x-p_K\Vert }_2^2}{{\sigma }^2}\left)\right]}^{\mathrm{T}}.$$

Then, given the degree matrix, D, and the matrices U and S from the training procedure, we define the explicit mapping function, f(x), from points in the original domain to their LE coordinates, as

$$f(x)=S^{†}{U}^{\prime }{D}^{-1}g(x),$$ (2)

where S^† denotes the Moore-Penrose pseudo-inverse of the diagonal matrix S. It is readily verified that applying the mapping to any training point, p_k, yields the appropriate column of the matrix V′ (i.e., $V_{k,:}^{\prime }=f(p_k)$), which establishes the equivalence of this two-step procedure to the LE algorithm in Sec. IIA for the training points. Insofar as the LE algorithm is able to discover a manifold, this function can be regarded as a mapping between manifolds (from the embedded submanifold to LE coordinates).

D. Differential of the Explicit Mapping

When a mapping between manifolds is differentiable, it is possible to map vectors between the tangent spaces of the manifolds using the differential of the mapping [39]. We are motivated to do so, as we will demonstrate in our results, because this offers the possibility of analyzing changes to signals of interest on one manifold as they are represented on another manifold (e.g., analyzing changes to bioelectric signals based on changes to their representation in LE coordinates). The differential of the explicit mapping function (2) from the previous section is

$${\partial }_{x}f(x)=-\frac{2}{{\sigma }^2}\text{diag}(f(x))\left[\begin{array}{c}{(x-p_1)}^{\mathrm{T}}\\ ⋮\\ {(x-p_K)}^{\mathrm{T}}\end{array}\right].$$

Note that the function f(x) appears in its own differential, in the diagonal of a matrix. The remaining multiplicative terms are also differentiable with respect to x. This establishes that ∂_xf(x) itself is differentiable, and from its recursive definition it follows that f(x) is C^∞. The properties of ∂_xf(x) (e.g., its determinant, rank, etc.) can be used to analyze the geometric properties of the manifolds to/from which f(x) maps. As stated above, here we will primarily be concerned with ∂_xf(x) as a mapping between tangent spaces, but in principle the differential is not limited to this purpose, and we refer the reader to the many available texts on differential geometry (e.g., [39, 40]) for a review of its other uses.

The differential, ∂_xf(x), maps a vector, υ_x, in the tangent space of the manifold at the point, x, to a vector, υ_f(x) = ∂_xf(x)υ_x, in the tangent space of the LE coordinates at the point, f(x). The inverse of the differential, when it exists, maps vectors in LE coordinates to those in the data space. In practice, however, the differential may not be invertible and there may be infinitely many vectors in the data space that map to a single vector in LE coordinates. In that case, the Moore-Penrose pseudo-inverse of the differential, ∂_xf(x)^†, is useful because it maps a vector in LE coordinates to its minimum norm inverse in data space, υ̂_x = ∂_xf(x)^†υ_f(x). Any vector in the data space, υ_x, that maps to the vector in LE coordinates can be expressed as a linear combination, υ_x = υ̂_x + υ_⊥, of the minimum norm inverse, υ̂_x, and a vector orthogonal to the column space of the pseudo-inverse, υ_⊥. In other words, any vectors in the data space that map to the same vector in LE coordinates must have the subspace spanned by υ̂_x in common, and therefore they must also have the dynamical changes represented by that vector in common.

III. Results

In this section, we present analyses that highlight the contributions that were described in the previous section. We performed four sets of analyses in total, on both simulated and real data, with the methods in our extended Laplacian Eigenmaps (LE) framework. The first two analyses were concerned with the preliminary contributions of this work: the use of delay coordinates within the LE framework, and the explicit mapping function. The last two analyses highlighted the utility of our main contributions: the differential of the explicit mapping function, and the vector mapping approach.

First we used the simulated data example to demonstrate that, using delay embedding of a scalar time series and a relatively small set of training points, LE is capable of reconstructing a phase space attractor, even from noisy observations. For this analysis, we reconstructed the well-known Lorenz system, recognizable by its butterfly-shaped chaotic attractor. Then we showed how it was possible to use LE to reconstruct the dynamical trajectories of real multi-electrode ECG measurements without requiring delay embedding. Demonstrating the use of our preliminary contributions – the explicit mapping function, both with and without delay embedding – was the main purpose of these two analyses.

In the third and fourth analyses we used real data to show how the differential can be used to identify important bioelectric signal changes. We performed the differential analysis on ECG data without delay embedding in the third analysis, and used EEG data with delay embedding in the fourth analysis. In each case, the proposed vector mapping approach was used to identify signal changes that correspond to prominent changes in LE coordinates.

A. Lorenz System with Noise

We applied Laplacian Eigenmaps (LE) with delay embedding to univariate observations from the Lorenz system, both noise-free and with additive noise. The purpose of these analyses was to demonstrate that the technique can be used to reconstruct the phase space of a system with complex trajectories, even when the observations are perturbed by a considerable amount of noise. The univariate observations themselves are clearly not high-dimensional, but delay-embedding with a large window of consecutive samples can make them so. For our analyses with the Lorenz system, we chose an arbitrarily large number of consecutive delay samples for our delay-embedding procedure (100 samples), which is much larger than the dimension of the Lorenz system. Our goal was to test whether LE could identify and form a low-dimensional representation of the Lorenz system embedded in the vector space, ℝ¹⁰⁰.

We synthesized the Lorenz system from the equations

$$\frac{\mathrm{d}x}{\mathrm{d}t}=\sigma (y-x),\frac{\mathrm{d}y}{\mathrm{d}t}=x(\rho -z)-y,\frac{\mathrm{d}z}{\mathrm{d}t}=xy-\beta z,$$

using the classical parameters ρ = 28, σ = 10, β = 8/3 [41], and sampled the variables x, y, and z at a rate of 200Hz, producing 20482 samples of each variable. In the noiseless case, we took x as the univariate observation from the system. In the two noisy cases, we added pseudorandom noise from a normal distribution with standard deviations equal to 1 and 5, respectively, to each of the variables independently and took the noisy x values as the univariate observations. The phase space trajectories of the Lorenz system, observed with and without noise, are shown in the first row of Fig. 1 ((a) no noise, (b) noise standard deviation equal to 1, (c) noise standard deviation equal to 5). The corresponding observations of the x time series are plotted in the second row, directly below the phase space trajectories. As the noise standard deviation increases, the phase space trajectories of the Lorenz system become less recognizable as forming a butterfly-shaped attractor. Also, as the plots of the progressively noisier observations show, the noise amplitude is roughly 1/4 of the signal amplitude when the noise standard deviation is 5, which corresponds to a signal-to-noise ratio of approximately 12 dB.

Fig. 1.

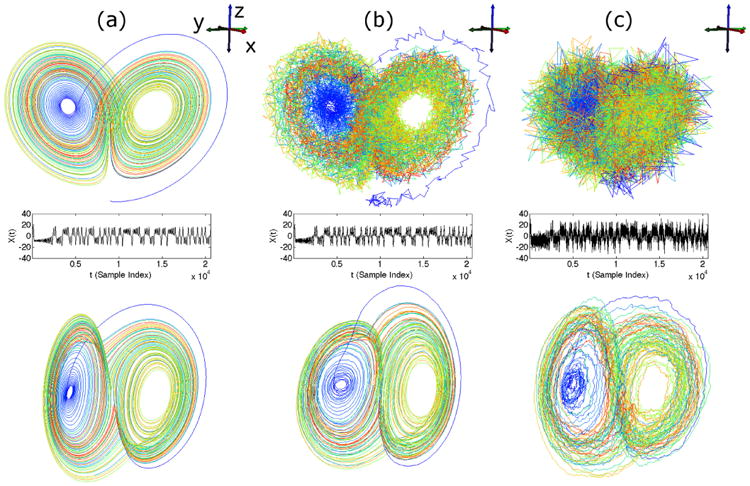
Reconstruction of classical Lorenz system using Laplacian Eigenmaps applied to delay coordinates of x component, demonstrated with increasing levels of noise added to observations. The Lorenz system ((a), top row), was synthesized using classical parameter choices (see text), and increasing levels of zero-mean noise (standard deviations of 0, 1, and 5) were added for each analysis (see (a), (b), and (c), respectively, in the top row). The noisy x component time series was taken as the only observation in each case (see (a), (b), and (c) in the middle row), and reconstructions were performed using delay embedding (taking 100 consecutive samples) and Laplacian Eigenmaps (taking the first three LE coordinates, see (a), (b), and (c) in the bottom row).

To perform our analyses, we delay embedded the observations of x with 100 consecutive samples (i.e., delay constant τ = 0.005s), and then applied the training step of LE to 1000 randomly-chosen time samples of the delay-embedded sequence. We then mapped the full set of time samples (20383 samples after delay-embedding) to LE coordinates using the learned explicit mapping. We visualized the first three LE coordinates resulting from these mappings in the third row of Fig. 1, directly below their corresponding observations. In both the original and reconstructed phase space trajectories, color is used to show the progression of time.

In the noiseless case, our approach reconstructed the Lorenz attractor successfully. This result is similar to the classical attractor reconstruction result by Takens, but instead of using 3 delay samples as the coordinate directions, we used 100 delay samples and relied on LE to find 3 coordinate directions for us. Furthermore, when using delay samples as coordinate directions, selecting an appropriate delay constant, τ, is typically regarded as an open problem [42–44]. Our results suggest that it may be possible to use more delay samples than are theoretically necessary, with the smallest available delay constant (equal to the sampling rate), and then let a dimensionality reduction algorithm such as LE find which coordinate directions are needed to represent the geometry of the manifold that is embedded within the high-dimensional vector space formed by the delay coordinates.

In the noisy cases, our procedure was still able to reconstruct the Lorenz attractor, although these reconstructions were more noisy than the one from the noise-free data. Remarkably, the amount of noise of the reconstruction in LE coordinates is visibly less than that of the observations of the original phase space. This is most noticeable in the case where the noise standard deviation was 5, as the Lorenz attractor is unrecognizable from the noisy observations (even though x, y, and z are being visualized together), whereas the trajectory in LE coordinates can still be recognized as the butterfly attractor, despite only observing x. This robustness to noise is important for the analysis of bioelectric data, which we will consider in the remaining analyses, because observations of any real bioelectric system will always contain some amount of noise.

B. Torso Surface ECG Signals

We applied LE to multiple, simultaneously-recorded ECG measurements from the body surface of a subject during a routine clinical procedure. Heart beats were paced by applying electrical stimuli to the interior walls of the left and right ventricular (LV and RV) blood chambers at multiple sites with the tip of an ablation catheter. Several beats (between 20-30) were paced from each location (17 locations in LV and 5 in RV), and electric potentials were measured from 120 leads on the subject's torso, sampled at 2 kHz. The purpose of this analysis was to demonstrate that, using multiple electrodes and without using delay embedding, LE could reconstruct trajectories that represent the expected propagation of electrical excitation along the heart surface. In particular, the spread of the excitation wavefront outward from the point of stimulation is expected to be similar for two distinct but nearby pacing sites. Furthermore, the wavefront spreads until all of the reachable and excitable muscle tissue has been excited, known as the QRS complex, followed by a refractory period during which the tissue is not excitable. Each instance of this recurring pattern conceptually forms a loop in phase space, which is the basis for its analysis with a long-standing approach, known as vectorcardiography [45], that represents this loop in physical space.

For our analysis, we took the concurrent measurements during QRS from the 120 leads and created a time-dependent vector, x(t) = [x₁(t), …, x₁₂₀(t)]^T, as the multivariate observation time series. We applied LE to all such vectors at the available sample times and visualized them using the first three LE coordinate directions. In the first row of Fig. 2, we show 4-5 example beats from each pacing location, which we grouped and then highlighted with different colors. Examples of beats paced from within the RV are highlighted on the left, and examples from the LV are on the right (both visualizations contain points from both the LV and RV, but in each case the contralateral points are colored copper/silver, and provided as a reference). The LE coordinate trajectories in Fig. 2 appear to be loops, which matches our conceptual understanding of the dynamics of the QRS complex.

Fig. 2.

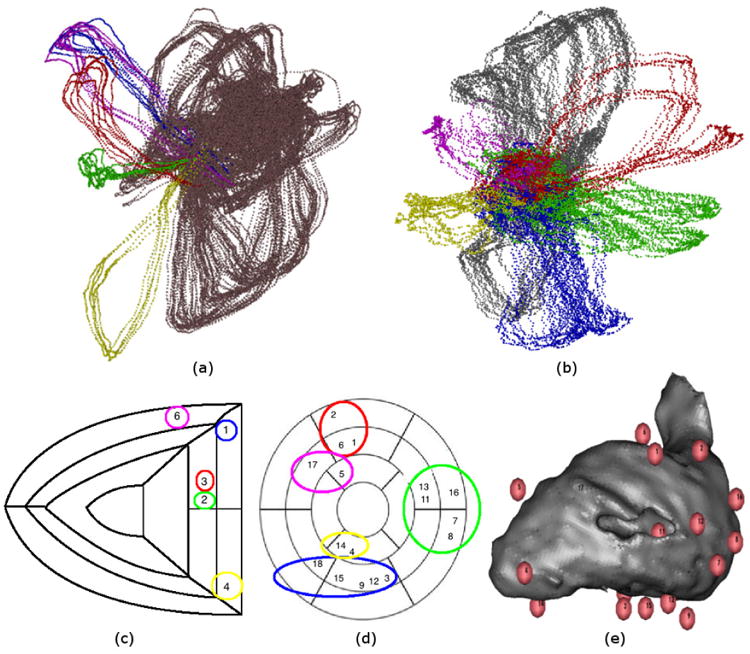
ECG trajectories resulting from left ventricular (LV) and right ventricular (RV) pacing. (a) and (b) show two different views of the same Laplacian Eigenmaps (LE) visualization, highlighting collections of trajectories according to their pacing locations. We retain the convention often used in medicine of presenting results in the coordinate system facing the subject, so that left from the viewer's perspective corresponds to the subject's right. Thus (a) shows RV-paced trajectories highlighted with yellow, green, red, blue, and purple points, and all trajectories for contralaterally-paced beats shown with copper points. (b) shows LV-paced trajectories highlighted with red, green, blue, yellow, purple points, and all trajectories for contralaterally-paced beats shown with silver points. (c) and (d) show RV/LV pacing locations overlaid on maps of RV/LV segments. Colors used to group location indices correspond to those used to highlight LE trajectories. (e) shows a visualization of the LV blood volume with spheres indicating LV pacing locations. Indices correspond to those shown on map of LV segments. Omitted indices (#10 in LV and #5 in RV) correspond to data discarded due to mistimed pacing stimuli.

The groups of pacing locations are shown in the second row of Fig. 2. In (e), we show a visualization of the LV blood chamber as a gray volume, with pacing locations shown as numbered spheres (as reported by the CARTO XP catheter tracking system (Biosense Webster, Diamond Bar, California)). A similar set of locations was obtained for the RV, whose volume visualization is not shown here. We mapped the pacing locations reported from the CARTO XP system to segmented maps of the interior walls of the ventricles (similar to those used by the American Heart Association (AHA)). In (c) and (d) we show the numbered pacing locations for the RV and LV on their AHA segments. We circled groups of pacing locations with the same colors that they were highlighted with in the LE visualizations (i.e., (a) and (c) have matching colors, as do (b) and (d)). Due to the small number of pacing locations in the RV, we took all beats from each location as their own group. Our visualizations in Fig. 2 show that, for both the LV and RV, beats paced from nearby locations map to nearby trajectories in LE coordinates.

C. Heart Surface Electrograms

In our remaining two analyses, we used the differential of LE for vector mapping, to link changes in LE coordinates to physiological changes that were identified a priori. For the analysis presented here, we applied LE to heart surface electrograms (similar to ECGs, but direct measurements of cardiac potentials) from a canine undergoing controlled interventions for an ischemia study. Measurements were sampled at a rate of 1 kHz from 247 electrodes woven into a nylon sock (“sock electrodes”) that was wrapped around the ventricles of the canine heart in situ. Throughout the study, beats were paced by stimulating the right atrial appendage at regular intervals. Interventions were performed to induce a form of ischemia. Specifically, each intervention involved completely occluding blood flow in the left anterior descending artery for a controlled period of time, inducing downstream ischemia due to insufficient blood supply. Each intervention was followed by a recovery period. Thus the protocol for the study consisted of an initial rest period and 10 ischemia interventions, whose durations were increased from one intervention to the next. The data from the full experiment, which lasted several hours, was divided into 1.2 minute intervals and a single representative beat was hand-selected (for having the fewest artifacts and least noise) and retained for analysis from each such interval. This resulted in 330 heartbeats for analysis, which we further restricted to include only the time samples from their QRS complexes.

We created a time-dependent vector of concurrent measurements from the 247 electrodes, as in Sec. III B, and we applied LE to the set of vectors resulting from the available sample times. In Fig. 3 (a)-(c), we show one sphere for each sample time, whose location comes from the first three LE coordinates, and show the full set of points from three orthogonal views. For comparison, we extracted the time of electrical excitation – known henceforth as the “activation time” – at each electrode location for each beat (taken as the time at which the most-negative temporal derivative occurs during QRS [46]). Isochrone maps of activation times are a common way to visually analyze the spread of the excitation wavefront along the measurement surface – in this case, the ventricular epicardium. In the second row of Fig. 3, we show the activation times (relative to the start of QRS) averaged over normal beats (i.e., prior to any interventions) in (d), beats occurring during ischemia intervention #5 in (f), and those occurring during ischemia intervention #8 in (h). Opposite views (front/back) of each isochronal map are shown. Directly below each pair of views is a visualization of the LE coordinates for all beats, in red, with those from the corresponding segment of the experiment highlighted in yellow (i.e., (d) goes with yellow points in (e), (f) with (g), and (h) with (i)).

Fig. 3.

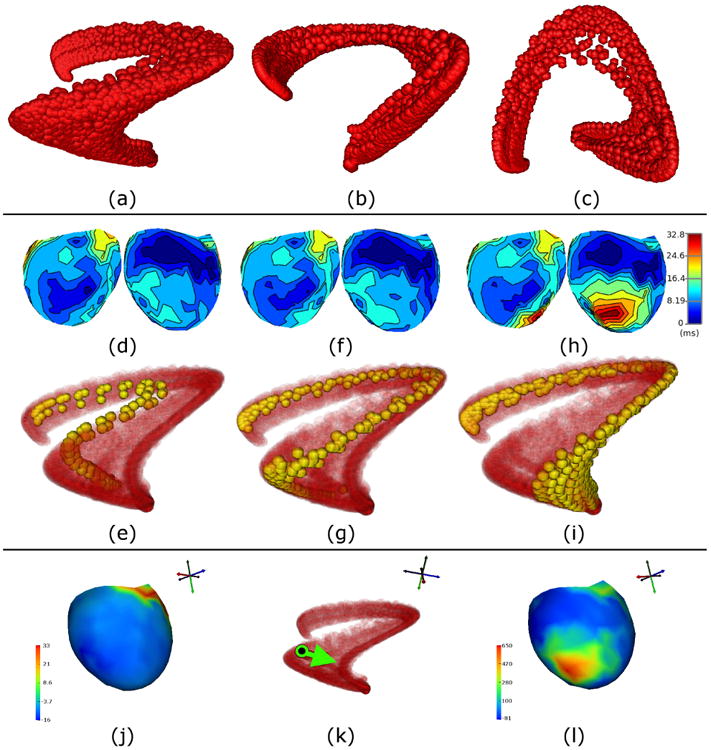
Electrograms from canine ventricular surface (epicardial) during QRS: three orthogonal views ((a), (b), and (c)) of points in LE coordinates. Each sphere represents a single time instant of data. Changes in activation times on epicardial surface of ventricles ((d), (f), and (h), showing front/back views of isochronal maps) are compared to changes in trajectories in LE coordinates ((e), (g), and (i)) during three stages of the ischemia experiment (ordered, with time increasing left-to-right). Interventions were performed to restrict blood supply and induce downstream ischemia. Normal beats are shown in (d) and (e), beats from the 5th intervention are shown in (f) and (g), and beats from the 8th intervention are shown in (h) and (i). Relevant LE trajectories for each intervention are colored yellow, with the rest of the data shown as semi-transparent red points. An analysis using the differential is shown in the fourth row ((j), (k), and (l)). The differential was evaluated at a point during a normal beat (corresponds to potentials measured on heart surface, shown as isopotential (j), and black point in LE coordinates (k)). In LE coordinates, a change vector was chosen to represent the direction of trajectory changes (green arrow in (k)) during the experimental stages (yellow trajectories from (e) to (g) and then (i)). A change map corresponding to this change vector was obtained using the proposed vector mapping approach, and visualized as an isopotential map (l). The change map shows one dominant region near the apex that changes the most. This region is the same one that suffers from late activations after 8 ischemia interventions (h).

The average activation times change very little from the normal beats to those occurring during ischemia intervention #5. The effect of the ischemia interventions can be seen more clearly in the isochrone map for intervention #8, which shows that a large region near the bottom of the ventricles activated much later than it had previously activated during intervention #5. It is likely that this region was damaged and thus was unable to activate normally by this stage of the experiment. On the other hand, we see that there was left-to-right movement of the highlighted trajectories in LE coordinates, from normal beats to ischemia intervention #5, and then again from intervention #5 to #8. That suggests that the measured electric potentials may have been changing during these interventions, but they did not result in changes in activation times. The left-to-right progression of the trajectories happened during each of the interventions, including those not shown here.

While the changes in the highlighted trajectories suggest that LE may be more sensitive to the signal changes due to these ischemia interventions, the results we have presented so far were not sufficient to support such a claim. One approach to supporting such a claim would be to show that the left-to-right changes of trajectories in LE coordinates are predictive of what is known a priori about the changes in the original signals (or in their activation times, i.e., the emergence of the region with late activations). For this purpose, we used the differential of LE as a method of mapping change vectors from LE coordinates to the original signal domain. To select a reference point, we chose a sample time from a normal heartbeat, whose sampled electric potentials are shown in Fig. 3 (j), and whose location in LE coordinates is marked with a black dot in (k). We computed the differential of the LE mapping at this point. From this location in LE coordinates, we chose a vector (shown pointing rightward in (k)), consistent with the left-to-right movement of the highlighted trajectories shown in (e), (g), and (i). We used the pseudo-inverse of the differential, as described in Sec. II D, to map this vector back to the domain of the measured electric potentials. The result is the change map shown in Fig. 3 (l).

The change map has features that support the claim that the left-to-right trajectory changes in LE coordinates were caused by the same signal changes that caused late activations during intervention #8, and that these LE coordinates were more sensitive to these signal changes than isochrone maps of average activation times. First, we have verified that a rightward movement away the point in the normal beat (in (k)) locally corresponds to a positive change in heart surface potentials in a region near the bottom of the ventricles. For the electrical reference and polarity of this experiment, normal depolarization/activation happens when a negative change in potentials occurs, and thus the positive part of the LE change map is indicative of a failure of this region to activate normally. Second, the timing of this predicted change map is also worth noting, as the abnormality only becomes apparent in activation times later in the experiment, during ischemia intervention #8, and LE coordinates were even sensitive to this change earlier than ischemia intervention #5. In summary, we were able to use our vector mapping approach to validate that LE coordinates were sensitive to some of the key features that changed as a result of changing experimental conditions.

D. Scalp Surface EEG Signals

For our final analysis, we applied our methods to EEG measurements from the scalp of a patient undergoing routine monitoring of frequent epileptic activity. The data, which were sampled at a rate of 250 Hz from 128 electrodes, contained frequent epileptiform discharges – hereafter referred to as “spikes” or “spike-and-wave complexes” – which indicate an increased risk for having seizures [47]. The spikes were identified and classified a priori by an expert epileptologist (i.e., before analysis with LE). The spikes considered here are referred to as “interictal,” because they occurred between seizures, and each one was classified as belonging to one of two types. The first type is called a “slow wave,” found mainly in the delta frequency band, and the second type is called a “sharp wave,” lasting between 70-200 ms. The relationship between these two types of spikes is not well-understood, and in general, it would be useful to have methods that enable one to explore the dynamic patterns in the data. Here we focus on the differences between the two spike types that appear in LE coordinates.

For each identified spike, we took segments of data lasting 62 samples, with the spike at the center of each segment. There were a total of 173 segments labeled as “slow waves” and 120 segments labeled as “sharp waves.” In Fig. 4 (a), we show plots of the mean time series (from electrode #4 only) for each spike type. The shaded regions represent the standard deviations about the means. We can see that taking the mean of many segments can reveal distinctive shapes for each spike type, but also that there is a considerable amount of variation about each mean, which makes it difficult to ascertain whether these shapes can be identified in individual segments.

Fig. 4.

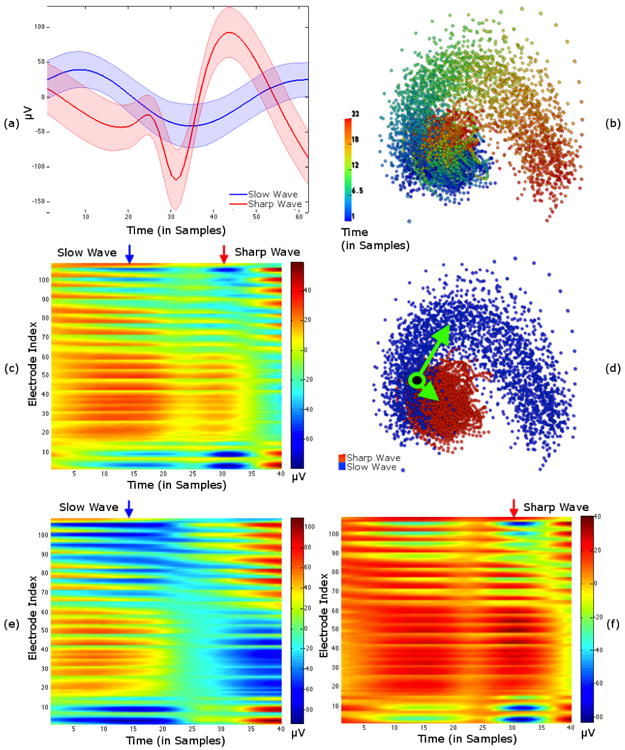
Scalp EEGs recorded during interictal epileptic spikes: two different spikes types, slow and sharp waves, were identified and labeled in the dataset. (a) shows mean signals of time-aligned spikes from a single electrode with standard deviation bounds. (b) and (d) show two visualizations of LE coordinates resulting from delay-embedding all spikes and all electrodes. In (b) color shows the progression of time, and in (d) color shows the type of spike. The voltage map in (c) of the example point (shown as black with green border in LE coordinates in (d)) shows both spike types. Voltage maps in (e) and (f) were synthesized by adding voltage maps corresponding to LE coordinate vectors (green arrows in (d)) to voltage map in (c). The vector in (d) pointing towards the slow waves was used to create the voltage map with a pronounced slow wave in (e). The other vector, pointing towards sharp waves, resulted in the pronounced sharp wave in (f).

Before applying Laplacian Eigenmaps, we delay embedded using 40 consecutive samples, resulting in 23 delay-embedded time points from each data segment. LE was applied to the combined set of delay-embedded points from both spike types (6739 points in total) by first training on 1000 randomly-chosen points and then applying the learned mapping to the remaining points. In Fig. 4 (b) and (d), we show two identical sets of points in the first three LE coordinates, with each set colored to highlight a different feature of the data. The set of points in (b) is colored to show the time at which the first delay-embedded sample occurs, relative to the start of each segment of data. In (d) color indicates which type of spike the data contained. These two visualizations show that the two different types of spikes result in data segments that cluster apart from each other, and that there is a clockwise rotation in this set of LE coordinates as time progresses within each segment (regardless of spike type).

That the segments containing different spike types cluster separately suggests that LE coordinates are able to represent differences between them. However, there is some overlap between the clusters, and it would be useful to understand why some trajectories in LE coordinates fall within this overlapping region. We selected several points in this region of LE coordinates and looked at their corresponding data domain representations as voltage maps (electrodes × time). For example, in Fig. 4 (d), we show the location of one such point with a green/black point superimposed on the LE visualization. The voltage map corresponding to this point is shown in (c). A key observation is that this point contains both slow and sharp waves within its 40 sample delay embedding window (appearing as elongated blue regions, and shorter blue regions, respectively), which could explain why the point lies in the region where the two spike clusters overlap.

To investigate the differences between these clusters, we chose vectors pointing from the green/black point (where they overlap) to the center of each cluster. We used our vector mapping approach to obtain estimates of how the voltages corresponding to the green/black point would change if we were to move in those directions in LE coordinates. We added the estimated voltage changes to the green/black point's voltages and visualized the results as voltage maps in Fig. 4 (e) and (f). In general this operation is not equivalent to moving along the manifold represented by LE coordinates, and should only be regarded as a first-order approximation (i.e., in the local tangent space) to moving along the manifold. Nevertheless, the voltage maps show that the changes represented by these two vectors are effectively suppressing one type of spike while accentuating the other. For example, the voltage map in (e) only shows a slow wave, whereas the sharp wave is most prominent in the voltage map in (f). Note that these changes were calculated using only the first three coordinate directions from LE, and ignoring the rest, which implies that there exists a local three-dimensional subspace of the data domain, with the green/black point at its origin, that captures the essential differences between the two clusters of spikes. Most importantly, this shows that the differences in LE coordinates between the clusters are representative of the known differences between spike types in the data domain.

IV. Conclusions

We have presented a number of techniques for studying the nonlinear dynamics underlying bioelectric signals using Laplacian Eigenmaps (LE), a manifold learning method established in the machine learning literature. Using both simulated and real data, we have demonstrated that LE coordinates are sensitive to important dynamical changes in the phase spaces underlying these data. Furthermore, by taking the differential of the LE mapping and then mapping vectors between the data and LE domains, we were able to validate that the changes in LE coordinates were caused by the expected changes in the data domain. We believe that this vector mapping approach can be used to explore datasets in which dynamical changes are known to be occurring, but are yet to be fully characterized, and elucidate the underlying dynamical changes.

While this paper focuses on using Laplacian Eigen-maps, it is important to note that there are large number of alternative methods that have been proposed for the manifold learning problem and it is a very active area of research. It is likely that many of these other approaches could be modified and extended in a manner similar to what we have done, and likewise they could be used to study the nonlinear dynamics of bioelectric signals. In our experience, a key feature of LE that has allowed for the successful analysis of these data is the emphasis on retaining local geometric features (e.g., pairwise distances) while mapping to a low-dimensional space. Perhaps one enabling property of our version of LE, that is not necessarily available with other methods, is the ability to define an exact function that is equivalent to the algorithm's mapping from the data domain to low-dimensional coordinates. Moreover, the differentiability of this function is another key property of the vector mapping approach we have proposed. It is not clear whether all manifold learning algorithms are amenable this type of extension, but it is known that many of them admit out-of-sample extensions (by approximation, at least) that may also be differentiable.

As mentioned in the introduction, the ability to explicitly connect the data domain to LE coordinates can also be used as a way to connect phenomenological and mechanistic analyses. One way in which this can be done is by observing that dynamical changes can be seen in an LE visualization, and then posing an optimization problem in which the system parameters of a mechanistic, generative model are tuned to recreate the phenomena identified in LE coordinates. Obtaining solutions to such optimization problems numerically – at least locally optimal ones – are made possible by the explicit mapping and its differential, which can be used within a Gauss-Newton iterative framework in a straightforward manner. In future work, it may be useful to explore the connection between the different levels of analyses further, with possible clinical applications in both ECG and EEG.

Appendix

The Laplacian Eigenmaps (LE) algorithm that we present in Sec. IIA has three key differences from the original algorithm by Belkin & Niyogi. The first difference is that Belkin & Niyogi performed their spectral analysis on the graph Laplacian matrix, L = D − W (using the notation from Sec. II A), a symmetric, positive semi-definite matrix. Specifically, this involves finding the generalized eigenvalue and eigenvector pairs, (λ, υ), that satisfy Lυ = λDυ. By performing a few algebraic steps, we can see that this is directly related to our algorithm:

$$\begin{array}{c}L\upsilon =(D-W)\upsilon =\lambda D\upsilon \\ W\upsilon =(1-\lambda )D\upsilon \\ D^{-1}W\upsilon =(1-\lambda )\upsilon .\end{array}$$

Thus the generalized eigenvectors of L and the eigenvectors of D⁻¹W are the same, which are also the same as the right singular vectors of D⁻¹W.

The second difference relates to the ordering of eigenvalues and eigenvectors. Belkin & Niyogi used the eigenvectors corresponding to the smallest eigenvalues (discarding the first one, with eigenvalue equal to zero) as their LE coordinates. In our case, as the corresponding eigenvalues would be 1 − λ, the order would be reversed and we would need to take the largest eigenvalues (discarding the first one, with eigenvalue equal to one) to get the same result. When 0 ≤ λ < 1, this is the same as taking the largest singular values.

The third difference concerns the σ parameter, which Belkin & Niyogi suggest should be small in order to emphasize the relationships between nearby points over far away points in the matrix W. Furthermore they argue that this is theoretically justified because, as σ → 0, the inverse exponential becomes a closer approximation to the Green's function for a system of partial differential equations based on the Laplace-Beltrami operator, often used to model heat flow on a manifold [36]. In our algorithm the parameter σ is chosen as the maximum value of R (i.e., the maximum of the pairwise distances between training points). While this is larger than recommended by Belkin & Niyogi, our results suggest that it is still small enough to emphasize local geometry, and it suggests that the algorithm is robust to this parameter choice.