FINEMAP: efficient variable selection using summary data from genome-wide association studies

Abstract

Motivation: The goal of fine-mapping in genomic regions associated with complex diseases and traits is to identify causal variants that point to molecular mechanisms behind the associations. Recent fine-mapping methods using summary data from genome-wide association studies rely on exhaustive search through all possible causal configurations, which is computationally expensive.

Results: We introduce FINEMAP, a software package to efficiently explore a set of the most important causal configurations of the region via a shotgun stochastic search algorithm. We show that FINEMAP produces accurate results in a fraction of processing time of existing approaches and is therefore a promising tool for analyzing growing amounts of data produced in genome-wide association studies and emerging sequencing projects.

Availability and implementation: FINEMAP v1.0 is freely available for Mac OS X and Linux at http://www.christianbenner.com.

Contact: christian.benner@helsinki.fi or matti.pirinen@helsinki.fi

1 Introduction

Genome-Wide Association Studies (GWAS) have identified thousands of genomic regions associated with complex diseases and traits. Any associated region may contain thousands of genetic variants with complex correlation structure. Therefore, one of the next challenges is fine-mapping that aims to pinpoint individual variants and genes that have a direct effect on the trait. This step is crucial for fully exploiting the potential of GWAS: to unveil molecular biology of complex traits and, eventually, provide targets for therapeutic interventions. For a recent review on fine-mapping, see Spain and Barrett (2015).

A standard approach for refining association signals is a step-wise conditional analysis, an iterative procedure that conditions on the Single-Nucleotide Polymorphisms (SNPs) with the lowest P-value of association until no additional SNP reaches the pre-assigned P-value threshold. While conditional analysis is informative about the number of complementary sources of association signals within the region, it fails to provide probabilistic measures of causality for individual variants. To overcome this problem, many recent fine-mapping methods have adopted a Bayesian framework.

Approaches for Bayesian analysis of multi-SNP GWAS data include exhaustive search as implemented in software BIMBAM (Servin and Stephens, 2007), MCMC algorithms (Guan and Stephens, 2011), variational approximations (Carbonetto and Stephens, 2012) and stochastic search as implemented in software GUESS (Bottolo and Richardson, 2010, Bottolo et al., 2013) and GUESSFM (Wallace et al., 2015). Bayesian fine-mapping has also been conducted under a simplified assumption of a single causal variant in the region (WTCCC et al., 2012). Common to these approaches is that they require original genotype-phenotype data as input, which is becoming impractical or even impossible as the size of current GWAS meta-analyses rises to several hundreds of thousands of samples (Wood et al., 2014). For this reason, fine-mapping methods have recently been extended to use only GWAS summary data together with a SNP correlation estimate from a reference panel. To our knowledge, the existing fine-mapping implementations using GWAS summary data are PAINTOR (Kichaev et al., 2014, Kichaev and Pasaniuc, 2015), CAVIAR (Hormozdiari et al., 2014) and CAVIARBF (Chen et al., 2015).

PAINTOR is an EM-algorithm to jointly fine-map several associated regions by utilizing functional annotation information of individual variants. As a special case of only a single region without annotation information, PAINTOR tackles the standard fine-mapping problem. CAVIAR differs from PAINTOR by modeling the uncertainty in the observed association statistics. This might be a reason why CAVIARBF, a more efficient implementation of CAVIAR, has been reported to be more accurate than PAINTOR in prioritizing variants when no annotation information is available (Chen et al., 2015).

Although PAINTOR, CAVIAR and CAVIARBF are very useful methods for performing fine-mapping on GWAS summary data, we think that their implementation via an exhaustive search through all possible causal configurations is likely to hinder their use in several settings. For example, it becomes computationally slow or even impossible to run these methods by allowing more than three causal variants on dense genotype data with thousands of variants per region. Thus, these methods are unlikely to make full use of unprecedented statistical power to discern complex association patterns provided by ever increasing GWAS sample sizes and genome sequencing technologies.

We introduce FINEMAP, a novel software package to improve the performance of GWAS summary data based fine-mapping. The statistical model of FINEMAP is similar to CAVIAR and CAVIARBF while the important difference is the computational algorithm. FINEMAP uses a Shotgun Stochastic Search (SSS) algorithm (Hans et al., 2007) that explores the vast space of causal configurations by concentrating efforts on the configurations with non-negligible probability. We compare FINEMAP with the exhaustive search algorithm implemented in CAVIARBF. The comparisons to two other GWAS summary data based fine-mapping methods CAVIAR and PAINTOR are not shown in this paper since CAVIARBF is more efficient but equally accurate as CAVIAR and more accurate than PAINTOR without annotation information (Chen et al., 2015). In this paper we show that

• FINEMAP is thousands of times faster than CAVIARBF while still providing similar accuracy in the examples where CAVIARBF can be applied.

• FINEMAP is more accurate than CAVIARBF when the number of causal variants in CAVIARBF needs to be restricted for computational reasons.

Our examples are based on genotype and lipid level data of the Finnish population (Borodulin et al., 2015) as well as summary statistics from GWAS on Parkinson’s disease (UKPDC and WTCCC2, 2011).

2 Model

We are interested in fine-mapping a genomic region using GWAS summary data instead of original genotype-phenotype data as input. The building blocks of our Bayesian approach are the likelihood function (Section 2.1), priors (Section 2.2), efficient likelihood evaluation (Section 2.3) and efficient search algorithm (section 3). At each step we describe how our choices differ from the existing methods PAINTOR and CAVIARBF.

2.1 Likelihood function

For a quantitative trait, we assume the following linear model

$$\mathit{y}=\mathit{X}\mathit{\lambda }+\mathbf{ϵ},$$

where y is a mean-centered vector of values of a quantitative trait for n individuals, X a column-standardized SNP genotype matrix of dimension n × m and $p(\mathbf{ϵ})=\mathrm{N}(\mathbf{ϵ}|\mathbf{0},{\sigma }^2{\mathit{I}}_n)$. The Maximum Likelihood Estimate (MLE) of the causal SNP effects $\mathit{\lambda }$ depends on X and y only through the SNP correlation matrix $\mathit{R}=n^{-1}{\mathit{X}}^{\text{T}}\mathit{X}$ and single-SNP z-scores $\hat{\mathit{z}}={\left(n{\sigma }^2\right)}^{-1/2}{\mathit{X}}^{\text{T}}\mathit{y}$

$$\hat{\mathit{\lambda }}={({\mathit{X}}^{\text{T}}\mathit{X})}^{-1}{\mathit{X}}^{\text{T}}\mathit{y}=n^{-1/2}\sigma {\mathit{R}}^{-1}\hat{\mathit{z}}$$

$$\mathbb{V}[\hat{\mathit{\lambda }}]={\sigma }^2{({\mathit{X}}^{\text{T}}\mathit{X})}^{-1}=n^{-1}{\sigma }^2{\mathit{R}}^{-1}.$$

Thus, it is possible to approximate the likelihood function for $\mathit{\lambda }$ by $\mathrm{N}(\hat{\mathit{\lambda }}|\mathit{\lambda },\mathbb{V}[\hat{\mathit{\lambda }}])$ using a SNP correlation estimate from a reference panel and single-SNP z-scores from a standard GWAS software, as previously done in GCTA (Yang et al., 2011), PAINTOR and CAVIARBF. Note that with z-scores for quantitative traits we can assume that ${\sigma }^2=1$ without any loss of generality. For binary traits, a similar approximation applies with z-scores originating from logistic regression and ${\sigma }^2\approx 1/\{\phi (1-\phi )\}$, where $\phi$ is the proportion of cases among the n individuals (Pirinen et al., 2013).

When m is large but $\mathit{\lambda }$ has only very few non-zero elements, the MLE alone is not ideal since it does not account for the sparsity assumption (Fig. 1). Thus, we take a Bayesian approach with a prior distribution that induces sparsity among causal effects.

Fig. 1.

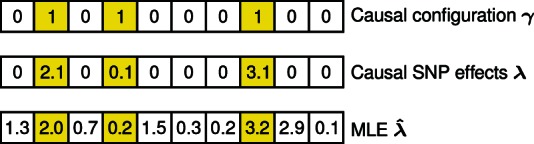
The binary indicator vector $\mathit{\gamma }$ determines which SNPs have non-zero causal effects (). The corresponding causal (linear) model for a quantitative trait assumes only few SNPs with a causal effect. The Maximum Likelihood Estimate (MLE) of the causal SNP effects $\hat{\mathit{\lambda }}$ can be computed by using only the SNP correlation matrix and single-SNP z-scores. However, the MLE is not ideal because it does not account for the sparsity assumption

2.2 Priors for $\mathbf{\lambda }$ and $\mathbf{\gamma }$

Let a binary indicator vector $\mathit{\gamma }$ determine which SNPs have non-zero causal effects (${\gamma }_{\ell }=1$ if the $\ell$th SNP is causal and 0, otherwise; see top panel in Fig. 1). For the causal effects, we use the prior

$$p(\mathit{\lambda }|\mathit{\gamma })=\mathrm{N}(\mathit{\lambda }|\mathbf{0},s_{\lambda }^2{\sigma }^2{\mathit{\Delta }}_{\gamma }),$$

where $s_{\lambda }^2$ is the user given prior variance for the causal effects in units of ${\sigma }^2$, with ${\sigma }^2=1$ for quantitative traits and ${\sigma }^2=1/\{\phi (1-\phi )\}$ for binary traits, and ${\mathit{\Delta }}_{\gamma }$ a diagonal matrix with $\mathit{\gamma }$ on the diagonal. In our examples for quantitative traits, we have set $s_{\lambda }^2={0.05}^2$. This means that with 95% probability a causal SNP explains less than 1% of the trait variation. When available z-scores originate from logistic regression, a value of $s_{\lambda }^2={(005/\sigma )}^2={0.05}^2\phi (1-\phi )$ means that with 95% probability the effect of a causal SNP on the odds-ratio scale is less than 1.15 for common variants (MAF = 0.5) and less than 2.0 for low-frequency variants (MAF = 0.01), where MAF is the minor allele frequency. Robustness to the values of $s_{\lambda }$ has been studied previously by Chen et al. (2015).

To define the prior for each causal configuration, we use a general discrete distribution for the number of causal SNPs

$$p_k=\text{Pr}(\#\text{of causal SNPs is}k),k=1,\dots ,K,$$

where $K<<m$ is the maximum number of SNPs in the causal configuration. Note that we assume that the region to be fine-mapped includes at least one causal SNP, i.e. $p_0=0$. For a fixed value of k, we assume the same probability for each configuration with k causal SNPs. Thus, a priori,

$$p(\mathit{\gamma })=p_k/\left(\begin{array}{c}m\\ k\end{array}\right)\text{\hspace{1em}when}{\displaystyle \sum _{\ell =1}^m{\gamma }_{\ell }}=k.$$

PAINTOR does not use an explicit prior on k but restricts $k\le 3$ in practice. The default prior used by CAVIARBF builds on that of CAVIAR and assumes that each SNP is causal with probability $1/m$ and that $k\le 5$. This is a special case of our prior when we set

$$p_k=\left(\begin{array}{c}m\\ k\end{array}\right){\left(\frac{1}{m}\right)}^k{\left(\frac{m-1}{m}\right)}^{m-k}$$

and renormalize for K = 5 except that CAVIARBF assigns non-zero prior also for the null configuration k = 0.

2.3 Marginal likelihood for $\mathbf{\gamma }$

We now show how the marginal likelihood for the causal configuration $\mathit{\gamma }$ can be computed efficiently.

2.3.1 Integrating out causal effects $\mathit{\lambda }$

The likelihood function $p(\mathit{y}|\mathit{\lambda },\mathit{X})$ of the causal SNP effects is (proportional to) a Normal density $\mathrm{N}(\hat{\mathit{\lambda }}|\mathit{\lambda },{\sigma }^2{(n\mathit{R})}^{-1})$. This enables an analytic solution for the marginal likelihood of $\mathbf{\gamma }$ eliminating the causal effects

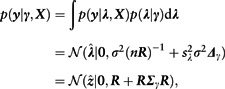where we defined ${\mathit{\Sigma }}_{\gamma }\equiv n{s}_{\lambda }^2{\mathit{\Delta }}_{\gamma }$. Importantly, an evaluation of the marginal likelihood requires only single-SNP z-scores and SNP correlations from a reference panel and does not depend on ${\sigma }^2$. This elimination of $\mathit{\lambda }$ is similar to the one used by CAVIAR and CAVIARBF and differs from PAINTOR that fixes those values based on the observed z-scores. Next, we describe two implementations to evaluate $\mathrm{N}(\hat{\mathit{z}}|\mathbf{0},\mathit{R}+\mathit{R}{\mathit{\Sigma }}_{\gamma }\mathit{R})$ with high computational efficiency.

2.3.2 Reducing the complexity from $\mathrm{O}\left(m^3\right)$ to $\mathrm{O}\left(k^3\right)$

Option 1

Let $C=\{1,\dots ,k\}$ and $N=\{k+1,\dots ,m\}$ be respectively the set of causal and non-causal SNPs. Consider the quadratic form

$$Q={\hat{\mathit{z}}}^{\text{T}}{(\mathit{R}+\mathit{R}{\mathit{\Sigma }}_{\gamma }\mathit{R})}^{-1}\hat{\mathit{z}}={\hat{\mathit{z}}}^{\text{T}}{({\mathit{I}}_m+{\mathit{\Sigma }}_{\gamma }\mathit{R})}^{-1}\mathit{a}$$

inside the exponential function in $\mathrm{N}(\hat{\mathit{z}}|\mathbf{0},\mathit{R}+\mathit{R}{\mathit{\Sigma }}_{\gamma }\mathit{R})$, where $\mathit{a}={\mathit{R}}^{-1}\hat{\mathit{z}}$ can be precomputed. We solve the linear system $({\mathit{I}}_m+{\mathit{\Sigma }}_{\gamma }\mathit{R})\mathit{b}=\mathit{a}$ for b by observing that the m – k elements in b corresponding to non-causal SNPs (${\gamma }_{\ell }=0$) are $b_{\ell }=a_{\ell }$ and the remaining elements result from solving a system of k equations

$$({\mathit{I}}_k+n{s}_{\lambda }^2{\mathit{R}}_{CC}){\mathit{b}}_C={\mathit{a}}_C-n{s}_{\lambda }^2{\mathit{R}}_{CN}{\mathit{a}}_N,$$

where ${\mathit{R}}_{CC}$ is the k × k correlation matrix of the causal SNPs and ${\mathit{R}}_{CN}$ the $k\times (m-k)$ submatrix of R corresponding to the correlations between the causal and non-causal SNPs. In addition, we observe that $\text{det}({\mathit{I}}_m+{\mathit{\Sigma }}_{\gamma }\mathit{R})$ is simply $\text{det}({\mathit{I}}_k+n{s}_{\lambda }^2{\mathit{R}}_{CC})$ after expanding with respect to the rows corresponding to non-causal SNPs. Computationally, these computations require one Cholesky decomposition with complexity $\mathrm{O}(k^3)$ and provide thus a considerable saving compared to the naive way of decomposing the whole m × m matrix with complexity $\mathrm{O}(m^3)$.

This derivation differs from the one used by CAVIARBF that is similar to our option 2 below. It also differs from PAINTOR that fixes $\mathit{\lambda }$ based on the observed z-scores and performs once a Cholesky decomposition of the whole m × m SNP correlation matrix that is used repeatedly in each likelihood evaluation. Note that option 1 cannot be used in case of collinearity among the SNPs, because the correlation matrix R is not invertible if two SNPs are perfectly correlated and is unstable with nearly perfectly correlated SNPs.

Option 2

We partition the observed z-scores into components ${\hat{\mathit{z}}}_C$ and ${\hat{\mathit{z}}}_N$ and permute rows and columns of the SNP correlation matrix and covariance matrix ${\mathit{\Sigma }}_{\gamma }$ such that

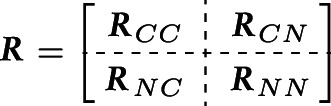
and ${\mathit{\Sigma }}_{\gamma }=\text{diag}\left\{{\sigma }_{\ell }\right\}\text{with}{\sigma }_{k+1}=\cdots ={\sigma }_m=0$. This partitioning entails a block structure in the covariance matrix of $\mathrm{N}(\hat{\mathit{z}}|\mathbf{0},\mathit{R}+\mathit{R}{\mathit{\Sigma }}_{\gamma }\mathit{R})$

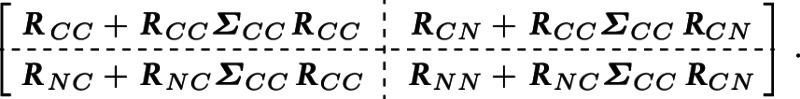
Using properties of the multivariate Normal distribution, the conditional expectation and covariance matrix of ${\hat{\mathit{z}}}_N$ given ${\hat{\mathit{z}}}_C$ are readily available

$$\mathbb{E}[{\hat{\mathit{z}}}_N|{\hat{\mathit{z}}}_C]={\mathit{R}}_{NC}{\mathit{R}}_{CC}^{-1}{\hat{\mathit{z}}}_C$$

$$\mathbb{V}\text{[}{\hat{\mathit{z}}}_N|{\hat{\mathit{z}}}_C]={\mathit{R}}_{NN}-{\mathit{R}}_{NC}{\mathit{R}}_{CC}^{-1}{\mathit{R}}_{CN}$$

and do not depend on ${\mathit{\Sigma }}_{\gamma }$. We rewrite the marginal likelihood $p(\mathit{y}|\mathit{\gamma },\mathit{X})=\mathrm{N}(\hat{\mathit{z}}|\mathbf{0},\mathit{R}+\mathit{R}{\mathit{\Sigma }}_{\gamma }\mathit{R})$ in terms of the marginal distribution of ${\hat{\mathit{z}}}_C$ and conditional distribution of ${\hat{\mathit{z}}}_N$ given ${\hat{\mathit{z}}}_C$ to obtain the following expression

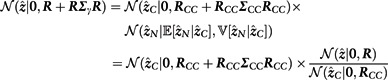This means that we can compute the Bayes factor for assessing the evidence against the null model by using only the causal SNPs

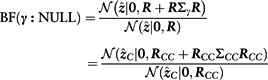and that the marginal likelihood is proportional to this expression. CAVIARBF utilizes this result, although without a mathematical derivation explicitly shown in Chen et al. (2015). Note that the correlation submatrix ${\mathit{R}}_{CC}$ is not invertible if there is almost perfect collinearity among the SNPs in C. To handle this case, we have implemented an option in FINEMAP to set the posterior probability of a causal configuration to zero if it contains at least one SNP pair with absolute correlation greater or equal to some specified threshold.

2.4 Posterior for $\mathbf{\gamma }$

According to the Bayesian paradigm, we want to base our inference on the posterior of causal configurations $p(\mathit{\gamma }|\mathit{y},\mathit{X})$. The unnormalized posterior can be evaluated by combining the prior with the marginal likelihood (option 1) as

$$p_1^{\ast }(\mathit{\gamma }|\mathit{y},\mathit{X})={\left(\begin{array}{c}\mathit{m}\\ \mathit{k}\end{array}\right)}^{-1}{\mathit{p}}_{\mathit{k}}\times \mathit{p}(\mathit{y}|\mathit{\gamma },\mathit{X}),$$

where k is the number of causal SNPs in configuration $\mathbf{\gamma }$. In addition, we can compute unnormalized posterior by using the Bayes factor (option 2)

$$p_2^{\ast }(\mathit{\gamma }|\mathit{y},\mathit{X})={\left(\begin{array}{c}\mathit{m}\\ \mathit{k}\end{array}\right)}^{-1}{\mathit{p}}_{\mathit{k}}\times \text{BF}(\mathit{\gamma }:\text{NULL}).$$

We observed that option 2 was faster than option 1 and therefore option 2 is used by default in FINEMAP. Ideally, $p^{\ast }(\mathit{\gamma }|\mathit{y},\mathit{X})$ were normalized over all ${\sum }_{k=1}^K\left(\begin{array}{c}m\\ k\end{array}\right)$ causal configurations. Unfortunately, this is computationally intractable already for modest values of K > 5. However, as we show in the results section, typically a large majority of the causal configurations have negligible posterior probability and hence a good approximation for the posterior can be achieved by concentrating on only those with non-negligible probability. We explore the space of causal configurations with a Shotgun Stochastic Search (SSS) algorithm (Hans et al., 2007) that rapidly evaluates many configurations and is designed to discover especially those with highest posterior probability.

3 Shotgun stochastic search

We use SSS to efficiently evaluate many causal configurations and discover especially those with highest posterior probability. SSS conducts a pre-defined number of iterations within the space of causal configurations. In each iteration (Fig. 2), the neighborhood of the current causal configuration is defined by configurations that result from deleting, changing or adding a causal SNP from the current configuration. The next iteration starts by sampling a new causal configuration from the neighborhood based on $p^{\ast }(\mathit{\gamma }|\mathit{y},\mathit{X})$ normalized within the neighborhood. All evaluated causal configurations and their unnormalized posterior probabilities are saved in a list ${\Gamma }^{\ast }$ for downstream analyses. The aim of the algorithm is that ${\Gamma }^{\ast }$ contains all relevant causal configurations, that is, those with non-negligible posterior probabilities.

Fig. 2.

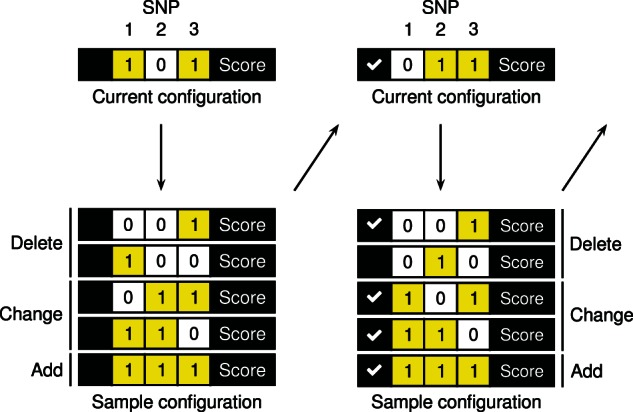
Shotgun stochastic search rapidly identifies configurations of causal SNPs with high posterior probability. In each iteration, the neighborhood of the current causal configuration is defined by configurations that result from deleting, changing or adding a causal SNP () from the current configuration. The next iteration starts by sampling a new causal configuration from the neighborhood based on the scores normalized within the neighborhood. The unnormalized posterior probabilities remain fixed throughout the algorithm and can thus be memorized () to avoid recomputation when already-evaluated configurations appear in another neighborhood

The posterior probability that SNPs in configuration $\mathit{\gamma }$ are causal is computed by normalizing over ${\Gamma }^{\ast }$

$$p(\mathit{\gamma }|\mathit{y},\mathit{X})={\mathit{p}}^{\ast }(\mathit{\gamma }|\mathit{y},\mathit{X})/{\displaystyle \sum _{\mathbf{\gamma }\in {\Gamma }^{\ast }}{\mathit{p}}^{\ast }(\mathit{\gamma }|\mathit{y},\mathit{X})}.$$

We compute the marginal posterior probability that the $\ell$th SNP is causal, also called single-SNP inclusion probability, by averaging over all evaluated configurations

$$p({\mathit{\gamma }}_{\ell }=1|\mathit{y},\mathit{X})={\displaystyle \sum _{\mathbf{\gamma }\in {\Gamma }^{\ast }}1({\mathit{\gamma }}_{\ell }=1)p(\mathit{\gamma }|\mathit{y},\mathit{X})}.$$

In addition, we compute a single-SNP Bayes factor for assessing the evidence that the $\ell$th SNP is causal as

$$\text{BF}({\gamma }_{\ell }=1:{\gamma }_{\ell }=0)=\frac{p({\gamma }_{\ell }=1|\mathit{y},\mathit{X})}{p({\gamma }_{\ell }=0|\mathit{y},\mathit{X})}/\frac{p({\gamma }_{\ell }=1)}{p({\gamma }_{\ell }=0)},$$

where the prior probability of the $\ell$th SNP being causal is

$$p({\gamma }_{\ell }=1)={\displaystyle \sum _{k=1}^K\left(\frac{k}{m}\right)}{p}_k.$$

PAINTOR, CAVIAR and CAVIARBF do not perform a stochastic search but enumerate all causal configurations with $k=1,\dots ,K$. When m is large but there are only few true causal SNPs, the exhaustive search is computationally expensive and inefficient since most configurations make a negligible contribution to the single-SNP inclusion probabilities.

3.1 Computational implementation

For $1<k<K$, the number of causal configurations to be evaluated in each iteration is:

• k for deleting,

• $k(m-k)$ for changing,

• m – k for adding a causal SNP

Computing $p^{\ast }(\mathit{\gamma }|\mathit{y},\mathit{X})$ requires a Cholesky decomposition with complexity $\mathrm{O}(k^3)$ that is fast when $K<<m$. Importantly, each unnormalized posterior probability remains fixed throughout the algorithm. This means that we can use a hash table (std::unordered_map in C ++) to avoid recomputing $p^{\ast }(\mathit{\gamma }|\mathit{y},\mathit{X})$ when already-evaluated configurations appear in another neighborhood. Inserting to and retrieving from the hash table requires constant time on average. Hash table lookups reduce the dominant computational cost of the algorithm: exploring the vast space of causal configurations. This renders SSS computational efficient because it traverses the space of causal configurations by moving back and forth to configurations with high posterior probability and overlapping neighborhoods.

4 Test data generation

We obtained real genotype data on 18 834 individuals from the National FINRISK study (Borodulin et al., 2015). The genotype data comprise a 500 kilobase region centered on rs11591147 in PCSK9 gene on chromosome 1 with 1920 polymorphic SNPs with pairwise absolute correlations less than 0.99. To assess the computational efficiency and fine-mapping accuracy, we considered the following scenarios:

• Scenario A

• Increasing number of SNPs $(m=750,1000,1250,1500)$ considering causal configurations with up to K = 3 or K = 5 SNPs.

• Scenario B

• Fixed number of m = 150 SNPs considering causal configurations with increasing maximum number of SNPs $(K=1,2,3,4,5)$.

We generated datasets where causal SNPs had highly correlated proxies since this is a setting where an in-exhaustive search could theoretically have problems. Five hundred datasets were generated under each combination of m and K in scenarios A and B using the following linear model:

$$\mathit{y}={\displaystyle \sum _{c\in C}{\beta }_c}{\mathit{g}}_c+\mathrm{N}(\mathbf{ϵ}|\mathbf{0},{\sigma }^2\mathit{I}),$$

where C is the set of causal SNPs, ${\mathit{g}}_c$ the vector of genotypes at the cth causal SNP, β_c and f_c respectively the effect size and minor allele frequency of the cth causal SNP and ${\sigma }^2=1-\sum _{c\in C}2f_c(1-f_c){\beta }_c^2$. The number of causal SNPs was five in scenario A and B. In each dataset, the causal SNPs were randomly chosen among those variants that had highly correlated proxies (absolute correlation greater than 0.5) among the other variants. The effect sizes of the causal SNPs were specified so that the statistical power at a significance level of $5\times {10}^{-8}$ was approximately 0.5. Single-SNP testing using a linear model was performed to compute z-scores. Each set of z-scores was then analyzed with CAVIARBF (default parameters) and FINEMAP (100 iterations saving the top 50 000 evaluated causal configurations). For both methods, the prior standard deviation of the causal effects was set to 0.05 and the prior distribution of each configuration with k causal SNPs was specified as

$$p(\mathit{\gamma })\propto {\left(\frac{1}{m}\right)}^k{\left(\frac{m-1}{m}\right)}^{m-k},\text{for}k=1,\dots ,K.$$

This required excluding the null configuration (k = 0) from the output of CAVIARBF.

5 Results

The main difference between FINEMAP and CAVIARBF is the search strategy to explore the space of causal configurations. We compare the computational efficiency and fine-mapping accuracy of FINEMAP with CAVIARBF to assess the impact of replacing exhaustive with stochastic search. We also illustrate FINEMAP on data from 4q22/SNCA region that contains a complex association pattern with Parkinson’s disease (UKPDC and WTCCC2, 2011) as well as on data from 15q21/LIPC region associated with HDL-C (Surakka et al., 2015).

5.1 Computational efficiency

The top panel of Figure 3 shows that FINEMAP is thousands of times faster than CAVIARBF when considering causal configurations with up to three SNPs in Scenario A. The difference in processing time becomes even larger when the maximum number of possible causal SNPs increases (Scenario B) in the bottom panel of Figure 3. CAVIARBF slows down quickly due to the exhaustive search but FINEMAP’s processing time does not increase considerably with increasing K. Importantly, there is no need to restrict the number of causal SNPs in FINEMAP to small values ($K\le 5$) as is necessary for CAVIARBF.

Fig. 3.

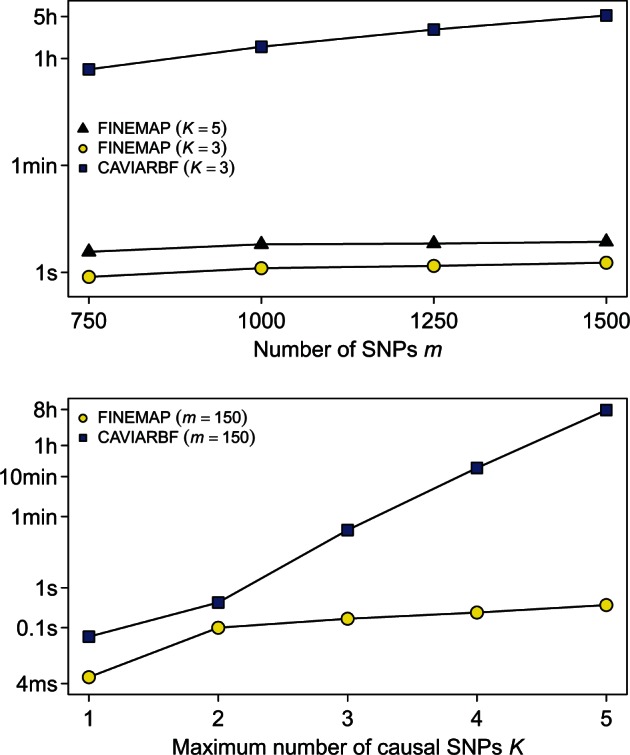
Processing time of one locus with FINEMAP and CAVIARBF on log₁₀ scale. Top panel: Scenario A with increasing number of SNPs allowing K = 3 or K = 5 causal SNPs. Bottom panel: Scenario B with 150 SNPs considering causal configurations with different maximum numbers of SNPs. All processing times are averaged over 500 datasets using one core of a Intel Haswell E5-2690v3 processor running at 2.6 GHz

5.2 Fine-mapping accuracy

We computed the maximum absolute differences between the single-SNP inclusion probabilities in each dataset under scenario B to assess the fine-mapping accuracy of FINEMAP and CAVIARBF (Table 1). The small differences (max < 0.11, median $<6\times {10}^{-4}$) show that for practical purposes FINEMAP achieves similar accuracy as CAVIARBF despite concentrating only on a small but relevant subset of all possible causal configurations (see Discussion). Figure 4 shows details of those SNPs in Scenario B for which the difference between the methods is larger than 0.01. We see that by ignoring the large majority of very improbable configurations, FINEMAP slightly overestimates the largest probabilities, that typically belong to the truly causal SNPs, and underestimates smaller probabilities, that most often belong to the non-causal SNPs.

Table 1.

Percentiles of absolute maximum differences between FINEMAP’s and CAVIARBF’s single-SNP inclusion probabilities in Scenario B

$\mathrm{m=150}$ |K	1	2	3	4	5a
Max	$\mathrm{5}\text{e}-\mathrm{7}$	$\mathrm{8}\text{e}-\mathrm{3}$	$\mathrm{2}\text{e}-\mathrm{2}$	$\mathrm{1}\text{e}-\mathrm{1}$	–
99th percentile	$\mathrm{4}\text{e}-\mathrm{7}$	$\mathrm{2}\text{e}-\mathrm{3}$	$\mathrm{8}\text{e}-\mathrm{3}$	$\mathrm{4}\text{e}-\mathrm{2}$	–
95th percentile	$\mathrm{3}\text{e}-\mathrm{7}$	$\mathrm{5}\text{e}-\mathrm{4}$	$\mathrm{3}\text{e}-\mathrm{3}$	$\mathrm{1}\text{e}-\mathrm{2}$	–
Median	$\mathrm{4}\text{e}-\mathrm{8}$	$\mathrm{4}\text{e}-\mathrm{7}$	$\mathrm{2}\text{e}-\mathrm{5}$	$\mathrm{6}\text{e}-\mathrm{4}$	–

^aCAVIARBF could not compute single-SNP inclusion probabilities due to a memory allocation failure (std::bad_alloc).

Fig. 4.

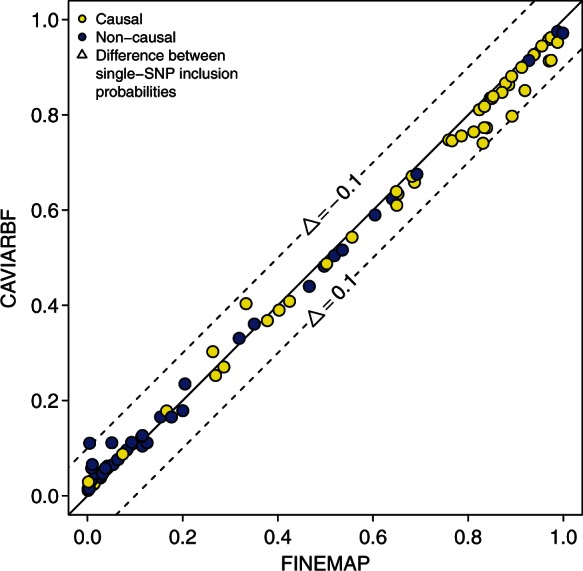
Single-SNP inclusion probabilities of all SNPs in Scenario B with absolute difference larger than 0.01 between FINEMAP and CAVIARBF

In addition to considering only causal configurations with up to three SNPs under scenario A, we also ran FINEMAP with K = 5 to demonstrate the increase in fine-mapping performance in this case where the true number of causal SNPs was five. We determined the proportion of causal SNPs that are included when selecting different numbers of top SNPs on the basis of ranked single-SNP inclusion probabilities (Fig. 5). FINEMAP and CAVIARBF had the same performance when considering causal configurations with up to three SNPs in genomic regions with 1500 SNPs. (Similar performance was also observed for genomic regions with different numbers of SNPs.) As expected, FINEMAP showed better fine-mapping performance when considering causal configurations with up to five SNPs.

Fig. 5.

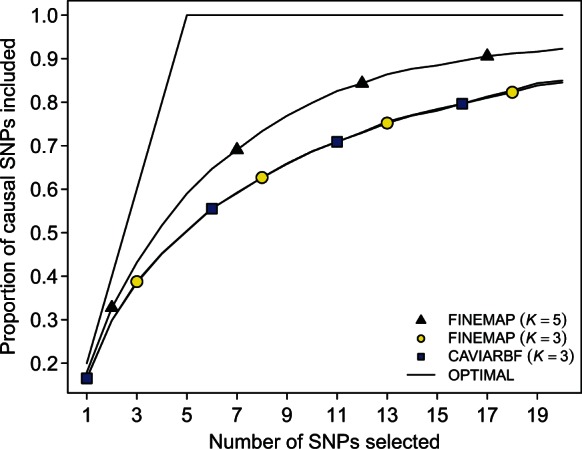
Fine-mapping accuracy of FINEMAP and CAVIARBF on data with five causal SNPs, allowing either K = 3 or K = 5 causal SNPs. The proportion of causal SNPs included is plotted against the number of top SNPs selected on the basis of ranked single-SNP inclusion probabilities. Proportions are averaged over 500 datasets with 1500 SNPs. Case K = 5 is computationally intractable for CAVIARBF

5.3 4q22/SNCA association with Parkinson’s disease

Using single-SNP testing, the UKPDC and WTCCC2 (2011) found evidence for an association with Parkinson’s disease in the 4q22 region with the lowest P-value at rs356220. A conditional analysis on rs356220 revealed a second SNP rs7687945 with P-value $3\times {10}^{-5}$ that in the single-SNP testing had only a modest P-value of 0.13. These two SNPs are in low Linkage Disequilibrium (LD) ($r^2=0.168$ in the original data) but the LD was sufficient enough to mask the effect of rs7687945 in single-SNP testing. This complex pattern of association was replicated in an independent French dataset (UKPDC and WTCCC2, 2011).

To test whether FINEMAP is able to pick up this complex association pattern, we extracted a 2 megabase region centered on rs356220 with 363 directly genotyped SNPs from the original genotype data. Single-SNP testing using a logistic model implemented in SNPTEST was performed to compute z-scores. The dataset was then analyzed with FINEMAP using 100 iterations and prior parameter value of $s_{\lambda }^2={0.05}^2$. Top panel of Figure 6 shows that the evidence that rs356220 and rs7687945 are causal is the largest among all SNPs. In addition, the causal configuration that simultaneously contains both rs356220 and rs7687945 has the highest posterior probability (0.132). The second most probable (0.113) causal configuration contains rs356220 and rs2301134. High correlation between rs7687945 and rs2301134 ($r^2=0.974$) explains why these two SNPs are difficult to tell apart. We conclude that FINEMAP was able to identify the complex association pattern at the second SNP that only became identifiable after the first SNP was included in the model. As opposed to the standard conditional analysis, FINEMAP provides posterior probabilities for all SNPs in the region and is thus able to simultaneously identify many causal variants without a step-wise procedure.

Fig. 6.

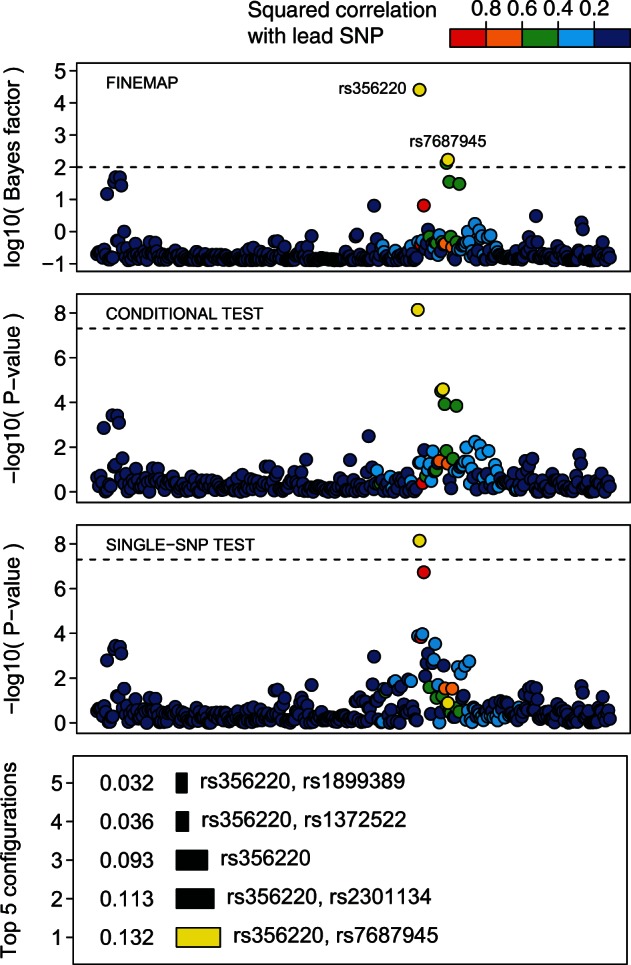
Fine-mapping of 4q22/SNCA region associated with Parkinson’s disease. Associated SNPs rs356220 and rs7687945 are highlighted by and their configuration by . Dashed lines correspond respectively to a single-SNP Bayes factor of 100 and P-value of $5\times {10}^{-8}$. Squared correlations are shown with respect to rs356220

5.4 15q21/LIPC association with high-density lipoprotein cholesterol

Using single-SNP testing and conditional analysis, evidence for multiple independent association signals with high-density lipoprotein cholesterol was found in the 15q21 region (Holmen et al., 2014; Surakka et al., 2015). A conditional analysis using genotype data on 19 115 individuals from the National FINRISK study (Borodulin et al., 2015) revealed three independent associations at rs2043085, rs1800588 and rs113298164. We extracted a 6 megabase region centered on rs2043085 with 8612 polymorphic SNPs and pairwise absolute correlations less than 0.99 from the original genotype data. Single-SNP testing using a linear model implemented in SNPTEST was performed to compute z-scores. The dataset was then analyzed with FINEMAP using 100 iterations allowing for at most five causal variants and prior parameter value of $s_{\lambda }^2={0.05}^2$. Top panel of Figure 7 shows that the functional lipid SNPs rs113298164 (missense variant, Durstenfeld et al., 1994) and rs1800588 (affecting hepatic lipase activity, Deeb and Peng, 2000) are among the variants with largest evidence of being causal. Rs2043085 that had the lowest P-value in single-SNP testing showed less evidence of being causal than rs7350789 ($r^2=0.81$). Indeed, there is substantial evidence that the configuration from standard conditional analysis (rs2043085, rs1800588 and rs113298164) is not the causal one; the top 3 configurations from FINEMAP have between 50 and 190 times higher likelihood values. This demonstrates the importance of jointly modeling the SNPs in the region. Given that FINEMAP completes in less than 30 s (Intel Haswell E5-2690v3 processor running at 2.6GHz) while the exhaustive search implemented in CAVIARBF is estimated to run over 300 years on these data, this example demonstrates the utility of FINEMAP as a tool to carry out future fine-mapping analyses.

Fig. 7.

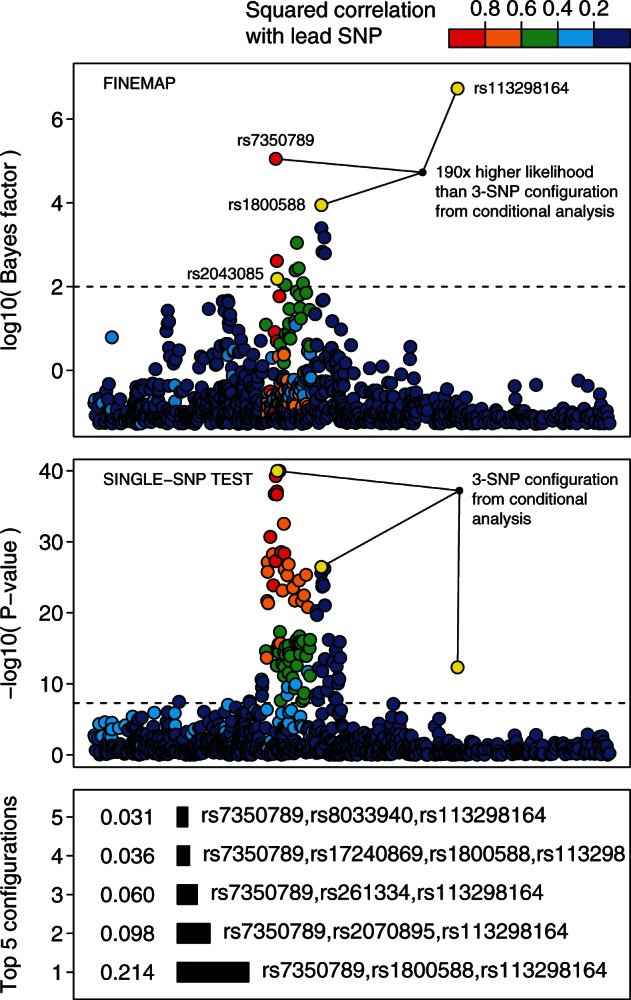
Fine-mapping of 15q21/LIPC region associated with high-density lipoprotein cholesterol. Independent association signals in conditional analysis are highlighted by . Dashed lines correspond respectively to a single-SNP Bayes factor of 100 and P-value of $5\times {10}^{-8}$. Squared correlations are shown with respect to rs2043085

6 Discussion

GWAS have linked thousands of genomic regions to complex diseases and traits in humans and in model organisms. Fine-mapping causal variants in these regions is a high-dimensional variable selection problem complicated by strong correlations between the variables. We introduced a software package FINEMAP that implements an important solution to the problem: a stochastic search algorithm to circumvent computationally expensive exhaustive search. In all datasets we have tested, FINEMAP achieves similar accuracy as the exhaustive search but uses only a fraction of processing time. For example, fine-mapping a genomic region with 8612 SNPs allowing for at most five causal variants completes in less than 30 s using FINEMAP while the exhaustive search implemented in CAVIARBF is estimated to run over 300 years. Computationally efficient algorithms are a key to handle the ever-increasing amount of genetic variation captured by emerging sequencing studies as well as to scale up the analyses to whole chromosomes or even to whole genomes.

FINEMAP uses a Shotgun Stochastic Search (SSS) algorithm (Hans et al., 2007). SSS has been inspired by Markov Chain Monte Carlo (MCMC) algorithms that are widely used for Bayesian inference. For a review on MCMC, see Andrieu et al. (2003). Standard MCMC methods, such as the Metropolis-Hastings algorithm (Hastings, 1970; Metropolis et al., 1953) and Gibbs sampler (Geman and Geman, 1984), perform a sequence of steps in the parameter space via a stochastic transition mechanism that ensures a valid approximation to the target distribution. MCMC can often quickly reach an interesting region of the parameter space, but, at each step, it only considers one of the possible neighboring states. This means that MCMC is often slow to explore a high-dimensional state space. To improve on this, SSS generates a whole set of neighboring configurations at each iteration and saves them all for further use in probability calculations. This way a large number of parameter configurations with relatively high probability is quickly explored.

FINEMAP is accurate when the set of causal configurations explored captures a large majority of the total posterior probability. Our results show that this is the case in all datasets we have tested: the maximal error in any single-SNP inclusion probability is smaller than 0.11 across all 2000 datasets of Scenario B. Using exhaustive search, we observed in genomic regions with 750 SNPs of which five were truly causal that on average only the top 123 (median = 14) causal configurations out of all possible $70.3\times {10}^6$ already cover 95% of the total posterior probability. (Similar results were also observed for genomic regions with different numbers of SNPs.) This explains why an efficient stochastic search can achieve accurate results in a tiny fraction of the processing time of an exhaustive search. Our datasets were generated by requiring that the causal SNPs had highly correlated proxies (absolute correlation greater than 0.5) among the other variants. The high accuracy of FINEMAP throughout these tests makes us believe that FINEMAP is accurate in typical GWAS data with complex correlation structure among the SNPs.

Although we have not encountered any dataset where FINEMAP would not have performed well, theoretically, it remains possible that an in-exhaustive search could miss some relevant causal configurations. A simple way to assess possible problems is to run many searches in parallel and compare and combine their outcomes. Another way is parallel tempering (Geyer, 1991) where several searches are run in parallel in different ‘temperatures’. Intuitively, increasing temperature flattens the likelihood function and hence a search in a higher temperature moves around more freely than one in a colder temperature. Such an approach, together with complex global transition mechanisms to escape from local modes, was introduced in an evolutionary stochastic search algorithm by Bottolo and Richardson (2010) that was later tailored for genetic analyses of multiple SNPs and multivariate phenotypes in the software package GUESS (Bottolo et al., 2013). These two papers could give ideas how FINEMAP could be further modified if trapping into local modes of the search space were encountered in real data analyses of GWAS regions.

Summary data based fine-mapping methods require a high-quality correlation estimate. Ideally, the correlation matrix is computed from the same genotype data from which the z-scores originate. In that case, for quantitative traits, the equations in Section 2.1 connecting original genotype-phenotype data and GWAS summary data are exact and hence no information is lost by working with summary data. For case-control data, a normal approximation to the logistic likelihood causes some difference between the two approaches but the difference is expected to be small with current GWAS sample sizes (Pirinen et al., 2013). For some populations, sequencing of many thousands of individuals have either already been carried out or will complete soon. Such reference data allow reliable fine-mapping down to low-frequency variants also when the original genotype data are not available. A more challenging problem is large meta-analyses that combine individuals from varying ancestries. Assuming that the causal variants are included in the data and have the same effect sizes across the ancestral backgrounds, FINEMAP can be run with the sample size weighted SNP correlation matrix. If these assumptions are not met, then a hierarchical model allowing separate SNP correlation structures in each ancestry would perform better (Kichaev and Pasaniuc, 2015).

Summary data based fine-mapping methods assume that the causal variants are included in the data. Recent advances in z-score imputation (Lee et al., 2013; Pasaniuc et al., 2014) help to satisfy this requirement also when a causal variant might not be genotyped. However, some SNPs are difficult to impute because they are not tagged well by the SNPs in the data. We do not expect to capture well the association signal from such SNPs either through imputation or indirectly through other SNPs in the data.

The output from FINEMAP is a list of possible causal configurations together with their posterior probabilities and Bayes factors similar to CAVIARBF. These probabilities contain all the information from the model needed for downstream analyses. Examples of useful derived quantities are the single-SNP inclusion probabilities, single-SNP Bayes factors, credible sets of causal variants (WTCCC et al., 2012) and a regional Bayes factor to assess the evidence against the null model where none of the SNPs are causal (Chen et al., 2015). We believe that FINEMAP, or related future applications of shotgun stochastic search to GWAS summary data, enables unprecedented opportunities to reveal valuable information that could otherwise remain undetected due to computational limitations of the existing fine-mapping methods.

Funding

This work was financially supported by the Doctoral Programme in Population Health (C.B.), the Academy of Finland [257654 and 288509 to M.P.; 251217 and 255847 to S.R.] and a Wellcome Trust Career Development Fellowship to C.C.A.S [097364/Z/11/Z]. S.R. was further supported by the Academy of Finland Center of Excellence for Complex Disease Genetics, EU FP7 projects ENGAGE (201413), BioSHaRE (261433), the Finnish Foundation for Cardiovascular Research, Biocentrum Helsinki and the Sigrid Jusélius Foundation.

Conflict of Interest: C.C.A.S. is a founder and shareholder of GENOMICS plc, a company that develops genome analytics.