A Practical Approach to Quantitative Processing and Analysis of Small Biological Structures by Fluorescent Imaging

Abstract

Standards in quantitative fluorescent imaging are vaguely recognized and receive insufficient discussion. A common best practice is to acquire images at Nyquist rate, where highest signal frequency is assumed to be the highest obtainable resolution of the imaging system. However, this particular standard is set to insure that all obtainable information is being collected. The objective of the current study was to demonstrate that for quantification purposes, these correctly set acquisition rates can be redundant; instead, linear size of the objects of interest can be used to calculate sufficient information density in the image. We describe optimized image acquisition parameters and unbiased methods for processing and quantification of medium-size cellular structures. Sections of rabbit aortas were immunohistochemically stained to identify and quantify sympathetic varicosities, >2 μm in diameter. Images were processed to reduce background noise and segment objects using free, open-access software. Calculations of the optimal sampling rate for the experiment were based on the size of the objects of interest. The effect of differing sampling rates and processing techniques on object quantification was demonstrated. Oversampling led to a substantial increase in file size, whereas undersampling hindered reliable quantification. Quantification of raw and incorrectly processed images generated false structures, misrepresenting the underlying data. The current study emphasizes the importance of defining image-acquisition parameters based on the structure(s) of interest. The proposed postacquisition processing steps effectively removed background and noise, allowed for reliable quantification, and eliminated user bias. This customizable, reliable method for background subtraction and structure quantification provides a reproducible tool for researchers across biologic disciplines.

INTRODUCTION

There exists a need for standardized, unbiased methods for reproducible processing and quantifying objects of interest in fluorescent imaging.^1–5 A variety of data processing and quantification options have been described,^6–10 but standard procedures have yet to be agreed upon. A routine approach is manual counting or reliance on built-in automatic quantification algorithms, without evaluating the appropriateness of the method. This often results in researchers violating the requirements for reliable quantification and/or acquiring excess volumes of data, leading to large data files and irreproducible analyses.

Our group was recently challenged by a necessity to quantify small, clustered, immunostained nerve varicosities (>2 µm in diameter, with an average intervaricosity distance of 5 µm^{11, 12}) in highly autofluorescent tissue samples in several hundred slides. The study was designed to detect and quantify sympathetic nerve termini in vascular tissue, identified by the colocalization of 2 immunofluorescently labeled proteins. Structures of this size are ∼10 times larger than the theoretical limits of conventional microscopy.

The combination of small, low-contrast structures of interest with interfering background in a large-scale imaging project forced us to examine carefully the critical parameters impacting the outcome of quantification analysis. The current protocol is a result of that examination; beginning with the first step of image acquisition, reproducible image processing options are described and quantification demonstrated, along with the effects of variations from the suggested method. Each parameter is discussed to aid the researcher in making a grounded decision if and when modifications are needed. The current method was applied to images acquired using a confocal microscope. Data from individual fluorescent channels were processed independently to reduce background noise and were then binarized and watershedded. Colocalization of the 2 channels identified the particles of interest that were subsequently counted.

MATERIALS AND METHODS

Animal Model

Aortas from 2 different strains of rabbit—the New Zealand White (NZW) that is resistant to the development of atherosclerotic disease and the Watanabe Heritable Hyperlipidemic (WHHL) that is genetically prone to developing atherosclerosis—were examined and regional differences compared within and across strains. To evaluate innervation density between study groups, ∼300 slides were imaged and analyzed. Differences in the nature of the vascular tissue (e.g., presence of disease) introduced considerable variability in staining intensity and background, requiring a valid, reproducible method to process and analyze the generated data.

All procedures were approved by the Animal Care and Use Committee of the University of Miami. The aim of the current experiment was to identify and quantify the density of sympathetic nerve termini within vascular tissue, identified by the immunologic colocalization of 2 proteins present in the sympathetic nerve termini. Aortas obtained from 46 WHHL (n = 22) and NZW (n = 24) rabbits were formalin fixed and embedded in paraffin for cross-sectional slicing. Standard immunohistochemical procedures were used to prepare and stain 10 µm sections.

Immunohistochemistry

Before staining, slides were deparaffinized using an automated instrument (Leica Jung Autostainer XL; Leica Biosystems, Buffalo Grove, IL, USA). We performed antigen retrieval by placing slides in citrate solution (0.01 M citric acid, 0.05% Tween 20, pH = 6) and heating under pressure for 20 min at 120°C. Slides were cooled for 30 min, rinsed with H20 and then PBS, and finally washed with wash buffer (BioGenex, Fremont, CA, USA). A universal blocking solution was used to reduce nonspecific background staining (BioGenex Power Block).

Slides were washed again with wash buffer, incubated with blocking solution against proteins from the secondary antibody host (e.g., donkey serum), and incubated overnight at 4°C with primary antibodies or nonimmune antibody isotype controls (1 µg/ml; Jackson ImmunoResearch Laboratories, West Grove, PA, USA) for the primary antibody host (e.g., chicken and guinea pig) diluted in antibody diluent (1% BSA). We used the following primary antibodies to identify sympathetic varicosities: chicken α-tyrosine hydroxylase (1:500; Millipore, Billerica, MA, USA), an enzyme precursor for catecholamines, and guinea pig α-synapsin (1:250; “Synaptic” Systems, Goettingen, Germany), a protein axonal marker. Immunostaining was visualized using the following secondary antibodies: tyrosine hydroxylase, detected using donkey α-chicken AlexaFluor 594 nm (1:300; Jackson ImmunoResearch Laboratories), and synapsin, detected with donkey α-guinea pig AlexaFluor 647 nm (1:450; Jackson ImmunoResearch Laboratories).

After an overnight primary incubation, slides were washed with buffer and incubated with secondary antibodies for 2 h, washed again with buffer and PBS, mounted with ProLong Gold with DAPI to stain cell nuclei (Thermo Fisher Scientific Life Sciences, Waltham, MA, USA), and allowed to cure 24 h before sealing. Images were acquired using a Leica SP5 spectral confocal inverted microscope (Leica Microsystems, Buffalo Grove, IL, USA) and equipped with a motorized stage, standard- and high-resolution Z-focus, and laser lines (405, 458, 476, 488, 496, 514, 561, 594, and 633 nm).

RESULTS

Optimizing Acquisition

In large-scale experiments, appropriate but not excessive data acquisition is the goal. For microscopes, a common best practice is to use the Abbe resolution limit to set the information density.¹³ However, if the objects to be resolved are much larger in size than the highest possible resolution of the microscope, then this approach will lead to unnecessarily large files, increased acquisition time, and increased risk of photo bleaching. For this reason, we argue that acquisition parameters should be determined based on the size of the object(s) of interest or distance between structures—whichever value is smallest.¹⁴

A confocal microscope will likely include a set of lenses, with numerical aperture (NA) values ranging from 0.4 to 1.4. This means that the theoretical lateral resolution of the system will range from 0.25 to 0.75 µm; the estimated value for a perfectly aligned system is (0.51 × λ)/NA, where λ is the wavelength of the excitation light, and NA is obtained from the selected objective lens.¹⁵ This estimation will provide the highest resolution of the imaging system, given a particular lens.

However, we have argued that for the quantification purposes, the highest resolution of an imaging system can be substituted with the lowest linear size of the structure of interest. How is that translated into the scale of the cellular environment? The aim of the current study was to count nerve termini as small as 2 µm.¹² In this case, even the lowest NA lens of the microscope (10×/0.4 NA) provided sufficient resolving power for the task [e.g., (0.51 × 500)/0.4, with a resultant 0.638 µm resolution]. However, higher NA increases light transmission and therefore, may increase photo bleaching, thereby affecting image intensity.

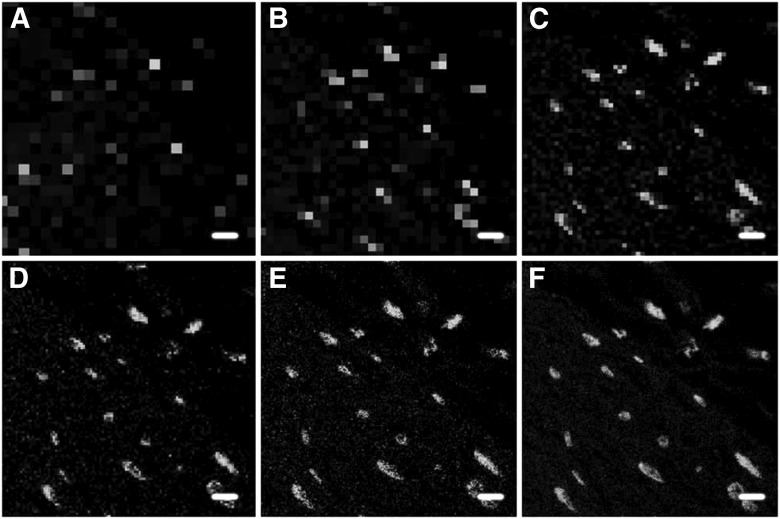
After determination of the optimal lateral resolution, the next step is to define the sampling density for the experiment, represented as pixels per micrometer in the resulting image. Nyquist criterion is often used to determine the minimal sampling density, where one must sample the 2-dimensional (2D) spatial object with 2 (2.3 for real-life samples) times the highest frequency of the signal.^{16, 17} Thus, the required sampling density for images in the current study was estimated to be ∼0.86 µm/pixel (i.e., assuming a diameter of 2 µm nerve termini, divided by 2.3). The effect of differing sampling densities on the quality of a resultant image is demonstrated (Fig. 1). Increasing resolution improves image quality and detection of objects of interest; however, the goal is to identify the resolution that provides reliable quantitation without oversampling.

Figure 1.

Sampling density affects the appearance of the final image. Images represent a typical field of view, showing several nerve termini identified by the localization of tyrosine hydroxylase. All images were acquired with a 20×/0.7 NA objective lens using different sampling rates. Pixel length for each panel: A) 6 µm; B) 3 µm; C) 1.5 µm; D) 0.75 µm; E) 0.37 µm; F) 0.09 µm. Original scale bars, 6 µm.

Addressing and optimizing axial (also known as Z) resolution is also important. Two inter-related concepts—axial resolution and optical slice thickness (OST)—need to be distinguished. Axial resolution is defined solely by the NA of the objective lens and is roughly 3 times lower than the lateral resolution of the same lens. In wide-field microscopy, each lens has a defined axial resolution, but there is no control over the OST. In confocal microscopy, by introducing a pinhole, it is possible to limit the light that comes from above and below the focal plane of the objective, thus introducing optical sectioning of the sample and improving the signal-to-noise ratio. OST is the product of the NA value of the lens, presence and characteristics of immersion fluids, and pinhole size. OST is always greater than the axial resolution of the objective lens used.

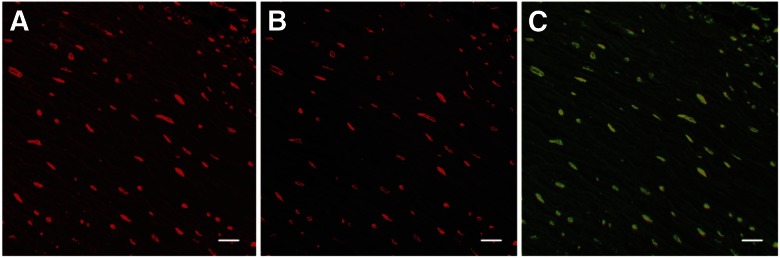
As the detection plane is normally perpendicular to the x–y axes, axial resolution is especially relevant when acquiring a 3D image, objects are densely crowded, or the signal-to-noise ratio is low. For these situations, the adjustment of the OST, by modifying lens selection, can improve data accuracy and image quality. The effect of different NA and OST values on a generated image is demonstrated (Fig. 2). Although both images identified the same structures (evidenced by the merged image; Fig. 2C), there was a noticeable enhancement in the signal-to-noise ratio when using a higher NA objective lens, resulting from improved resolution and light transmission, thereby increasing the signal-to-noise ratio. We have chosen to use a higher (20× vs. 10×) objective lens for the current project to improve the signal-to-noise ratio.

Figure 2.

Signal-to-noise ratio increases through the reduction of OST, achieved here by changing the objective lens, increasing both magnification and the NA. A) 20×/0.7 NA lens; B) 63×/1.4 NA lens, same field of view; C) overlay of A and B, where green represents the 20× channel. Original scale bars, 20 µm.

Data Processing

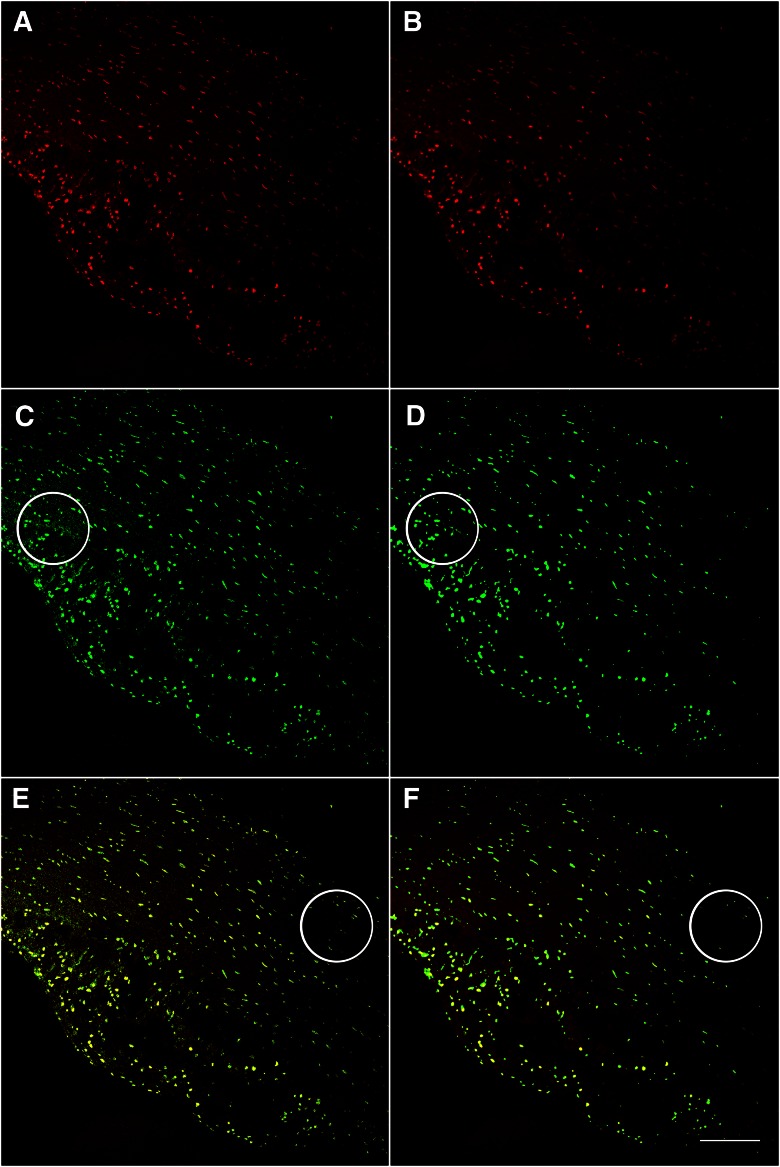
Background and noise are common issues in microscopy and may be a result of many factors, including acquisition settings, autofluorescence, or nonspecific staining. However, they have the potential to interfere with accurate image quantification^{14, 18} and therefore, must be addressed before quantification. One of the recurring problems in confocal imaging stems from photomultiplier (PMT) noise, also known as “salt and pepper” noise. This type of noise is acquisition mediated and appears as individual bright pixels on an overall lower-intensity background. During acquisition, the reduction of the voltage of the PMT and acquisition of several images in averaging or summing mode can reduce this type of noise. Postacquisition, PMT noise can be removed effectively from the image using a smoothing filter, preferably the median filter, which essentially replaces a pixel value with the median value of its neighboring pixels, the “neighborhood” of which is referred to as a “kernel.” The larger the kernel, the larger the number of pixels included in the replacement value. The power of applying a filter to diminish noise in the acquired image is illustrated (Fig. 3). The binarization of a raw image resulted in background pixels interpreted as signal. Application of a median filter improved the signal-to-noise ratio; however, low-intensity objects were lost.

Figure 3.

Application of a median filter improves object and background segmentation. Image acquired with 20×/0.7 NA objective lens, 1024 × 1024 frame size. The raw image (A) was directly binarized using the maximum entropy FIJI/ImageJ algorithm (U.S. National Institutes of Health, Bethesda, MD, USA; C) with the result overlaid onto the original image (E). Note that use of this approach resulted in background pixels interpreted as signal, indicated by a large circle in C. B) The result of a median filter applied to the original image, subsequent binarization using the maximum entropy method (D), and overlay (F). Note the improvement of signal-to-noise segmentation by removing background before binarization in D compared with C, indicated by large circles. However, both approaches failed to identify low-intensity objects, designated by circles in E and F. Original scale bar, 120 µm.

Another common source of noise is autofluorescence of the tissue. Autofluorescence can be managed pre- and postacquisition. For example, pre-exposure to intense light¹⁹ or chemical pretreatment has been shown to reduce autofluorescence in some cases (e.g., CuSO₄ in ammonium acetate buffer or Sudan Black B in 70% ethanol,²⁰ NaBH₄,²¹ or Pontamine sky blue).²²

Autofluorescence is a property of the sample and is relatively independent of acquisition method. Autofluorescence is usually characterized by uniformity in signal intensity across the sample. During acquisition, autofluorescence is often excluded from the final image by adjusting the offset of the system; however, this approach does not work well when the signal intensities of the target objects are low. Postacquisition, 1 common option to reduce autofluorescence is background subtraction; in the simplest implementation, the mean intensity of background is measured in every imaging channel and subtracted from the pixel values in the image. Alternatively, spectral unmixing algorithms could be applied to images. However, autofluorescence may spatially present in a nonuniform distribution, limiting the use of those approaches. Vascular tissue used in the current study exhibited such nonuniform autofluorescence, originating from connective tissue and extracellular matrix fibers.

In cases of high autofluorescence, the Gaussian blur filter is the preferred method for processing an image to reduce autofluorescence, as it retains specific features better than mean or median filters. However, if there is a nonuniform spatial autofluorescence distribution, a more sophisticated approach, known as the unsharp mask, is required.²³ The approach stemmed from the idea that target structures in a well-focused image are characterized by higher frequencies and higher intensities, whereas the noise is not as structured. Thus, one can blur the image using a filter to preserve the overall intensity map and subtract the blurred image from the original image. The blurred image will contain close intensity values approximating any area that is background. The true objects in this blurred image are then represented by pixels of several-fold lower intensity values compared with the original image. Thus, the subtraction of this blurred duplicate image reduces most of the background, whereas only slightly changing the intensity of the true object pixels. The resultant image intensity values can be normalized, that is, multiplied by a number to bring the highest intensities in the image to the upper value limit (e.g., 255 in an 8-bit image).

Variability in intensities is another concern and should be avoided but still often occurs among images acquired at different time points or with different settings, attempting to adjust for nonuniformity in signal intensities. To avoid this potential bias, an object-based, rather than intensity-based, approach was used to identify targets in our images. Each image was binarized (i.e., each pixel was assigned a value of 0 or 1), and then a watershed algorithm (i.e., a geometrical approach segmented elements into distinct objects) was applied to define object limits. The binarization of an image defines pixels that represent the signal, separating them from the background. There are multiple thresholding algorithms available that can be accessed through the Auto Threshold and Auto Local Threshold plug-ins of FIJI/ImageJ.²⁴ The chosen option should be selected as appropriate for segmenting objects of interest and must be applied to all images, as certain algorithms are more or less conservative in segmentation and could influence the quantification outcome. The default binary algorithm was found to be sufficient for the current study, as it preserved low-intensity structures. The watershed method worked well for the current study, however, there are many specimens that give highly erroneous segmentation following the watershedding, and the use of the algorithm should be carefully evaluated in other sample types.

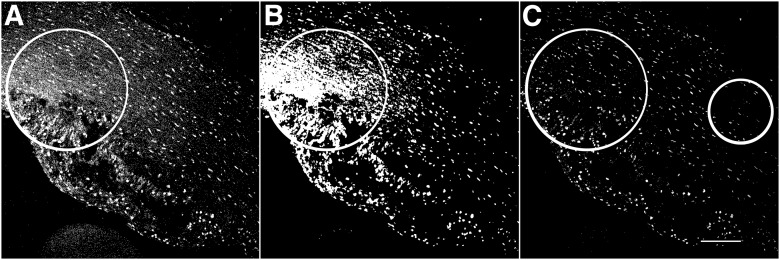
The use of different methods to eliminate nonuniform background, while concurrently preserving low-intensity signals, is demonstrated (Fig. 4). Direct binarization of raw images resulted in false-positive structures (Fig. 4A). The commonly used median filter resulted in merging of individual objects and was insufficient for removal of nonuniform background (Fig. 4B). Note the increased separation of signal and noise and the retention of structures of interest when using the proposed method of Gaussian blur-derived background subtraction and object segmentation (Fig. 4C). This approach is not novel, and technical aspects of this background correction method have been described.²³ The current method describes and demonstrates its validity with the aim of proposing its widespread use before image quantification.

Figure 4.

Quantification outcome is affected by postacquisition image processing. The original image contains an intensity gradient consisting of both signal and background pixels. A) Raw image binarized directly. The large circle indicates the retention of background pixels in the image (see also Fig. 3C), potentially affecting quantification (see Table 1). B) Application of a median filter (radius 2) to the image, the result of which was binarized with the standard default FIJI/ImageJ binary algorithm. Note the creation of large artifact fusion particles indicated by the large circle. C) Complete processing according to the proposed protocol. Note the elimination of background (large circle), as well as preservation of low-intensity particles for quantification (small circle). Original scale bar, 120 µm.

Quantification

Once the background is reduced, quantification can be accomplished using readily available options, as appropriate for their ability to identify the structure(s) of interest. FIJI/ImageJ includes several options for counting particles (e.g., Analyze Particles, 3D Object Counter, Nucleus Counter, and Cell Counter), and a comprehensive list of available analysis plug-ins has been catalogued recently.²⁵ For the purposes of the current study, the basic Analyze Particles algorithm was ideal, as it provided a simple method for quantifying objects within a specific size range. Sampled properly, structures of interest should be represented by at least 2 pixels in any dimension; thus, the lower size limit was set to an area representing the size of 4 squared pixels.

The effects of varying sampling rates and processing methods on quantification were evaluated (Table 1). Images were acquired with a 20×/ 0.7 NA objective lens using 7 different sampling rates over the same 775 × 775 µm field of view, within the same focal plane. Termini counts for all iterations were compared with the highest lateral resolution image. Sampling rate is shown as frame size in column A (e.g., the first line represents an image sampled at 8192 × 8192 pixels, 0.09 µm pixel length). The optimal sampling rate was determined using the structures of interest, where the calculated 0.86 µm or less/pixel size was achieved by using 950 × 950 resolution on a 775 × 775 µm field. Column H shows the difference in file size compared with the optimized setting and reflects a substantial increase in processing and acquisition time. Compared with the optimal setting needed for reliable quantification, the file size for the highest resolution was 74 times larger with a concomitant increase in acquisition time.

TABLE 1.

Differences in Termini Counts among Different Micrometers per Pixel and Image Processing Iterations

Line number	A	B	C	D	E	F	G	H
	Lines/frame at scanning	Target particle size (pixel2)	Original image (counts)	Median filter (counts)	Optimized method (counts)	Gaussian filter (sigma values)	Percent of counts relative to highest resolution	Relative data file size
1	8192	≥320	641	558	470	100	100%	74×
2	4096	≥80	935	584	522	100	111%	18.7×
3	2048	≥20	1456	578	508	50	108%	4.6×
4	950	≥4	1915	986	552	50	117%	1×
5	512	≥1	2307	485	765	25	163%	0.29×
6	256	≥1	685	70	494	25	105%	0.07×
7	128	≥1	353	11	248	25	53%	0.02×

Seven images, representing an identical tissue area of 775 × 775 µm, were acquired using a 20×/0.7 NA objective lens with varying sampling rates. Images were acquired stepwise with an ∼4-fold change in pixel area at each step. For every frame size, the lower limit of the particle size was defined according to the micrometer/pixel size of the image, and the cutoff was set at 2 µm where applicable. Line 4 represents the optimal lateral resolution, based on the structures of interest. Column A, Sampling rate shown as frame size; column B, particle size used for quantification; columns C–E, quantification results across several background processing iterations [column C, original image, no processing; column D, application of a median filter (radius = 2); column E, application of the proposed method]; column F, sigma radius values for the “generate blurred image” step; column G, percentage of counts in column E compared with the highest resolution image (line 1, column E); column H, difference in file size compared with the optimized setting. Note the increase in false counts with inappropriate processing when pixel size approaches target structure size.

In column C, particle counts were obtained from raw images that were directly binarized without background correction. In column D, particle counts were determined after a median filter was applied to the original image before binarization. In the oversampled images (lines 1–3), the variability among counts was minor. However, as the target size range becomes closer to the pixel size, a decrease in identifiable objects was shown. Column E represents the particle counts after complete processing of the image by the proposed method.

The optimized method involves the following steps: FIJI/ImageJ was used to process each fluorescent channel from the acquired image upon which the Gaussian blur filter was used to create a blurred image representing background, the result of which was subtracted from the raw image, thereby reducing a nonuniform background while preserving a low-intensity signal. Objects were then segmented using binarization and watershed algorithms. The 2 fluorescent channels were overlaid, and colocalized particles were detected and quantified. In fully processed images, a consistency in counts was observed among optimized versus oversampled images; however, higher sampling rates led to larger files (Table 1, column H). Conversely, images sampled below the calculated optimal sampling rate demonstrated a decrease in the number of objects detected. Overall, generation of false structures in nonprocessed images was clearly demonstrated; a 407% increase in counts was shown when comparing the nonprocessed, optimally sampled image (Table 1, line 4, column C) with the fully processed, oversampled image (Table 1, line 1, column E). Although image quality and appearance change with varying imaging settings (Figs. 1 and 2), it was demonstrated that quantification results remain consistent once the imaging parameters are optimized and postacquisition data are processed correctly.

Reliability of the Method

Three slides were quantified for each tissue (spatially separated by ∼100 µm) from 46 rabbits and from each of 2 aortic locations (e.g., arch and thorax). Nerve termini were quantified in 2 specific regions of the cross-sectional sample (i.e., intima and media) and summed to identify the total number of counts in each sample using the proposed image acquisition and data processing protocol. Pearson’s correlation coefficients (r) were calculated to examine the linear relationship between data generated from multiple slides. Adjacent regions from the same rabbit in the aortic arch and thoracic aorta were evaluated. Coefficients were high, ranging from 0.883 to 0.937, P < 0.05, for all comparisons (Table 2), illustrating the reliability of the current method as an unbiased, reproducible approach to image processing and quantification

TABLE 2.

Reliability of the Current Method

		Correlation coefficient
Aortic area	Comparison slide	Slide 2	Slide 3
Arch
Intima	Slide 1	0.919	0.920
	Slide 2	0.937
Media	Slide 1	0.905	0.883
	Slide 2	0.884
Total	Slide 1	0.908	0.896
	Slide 2	0.899
Thorax
Intima	Slide 1	0.918	0.930
	Slide 2	0.929
Media	Slide 1	0.896	0.902
	Slide 2	0.901
Total	Slide 1	0.915	0.923
	Slide 2	0.921

Pearson’s correlation coefficient (r) values for comparisons of varicosity counts between subregions of adjacent cross-sectional tissue samples within the aortic arch or thoracic aorta. Reliability between measurements is demonstrated by high correlations, supporting the reproducibility of the proposed method for image acquisition, data processing, and quantification.

DISCUSSION

A practical, easy-to-follow protocol for imaging and analyzing small biologic objects was presented, addressing 3 concerns in biologic microscopy: 1) acquisition, 2) noise and background, and 3) quantification. Relevant theoretical considerations and data processing options were described in the context of real-life situations that the user would likely encounter, while demonstrating how variations in acquisition or processing parameters impact the data generated. Pertinent conditions for optimization were suggested and discussed. A limitation of this object- based method is that it is insufficient for intensity-based analyses, wherein researchers will need to use other methods when identifying spectral overlap and colocalization or quantifying intensity values. However, the basic image acquisition guidelines can still be applied with modifications made to data processing (e.g., by eliminating binarization and watershed steps).

In conclusion, the current method emphasizes the importance of defining image acquisition parameters based on the structure(s) of interest. Once defined, the proposed postacquisitional processing steps effectively remove background and noise and allow for reliable quantification. Standardized background correction, data processing, and quantification techniques were used to eliminate user bias. The method, amenable to quantifying a variety of structures using readily available tools, was shown to be reliable across sequentially sampled tissue slides and could serve as a starting point in other experimental designs or when analyzing larger volumes of data.