Computational Models of Protein Kinematics and Dynamics: Beyond Simulation

Abstract

Physics-based simulation represents a powerful method for investigating the time-varying behavior of dynamic protein systems at high spatial and temporal resolution. Such simulations, however, can be prohibitively difficult or lengthy for large proteins or when probing the lower-resolution, long-timescale behaviors of proteins generally. Importantly, not all questions about a protein system require full space and time resolution to produce an informative answer. For instance, by avoiding the simulation of uncorrelated, high-frequency atomic movements, a larger, domain-level picture of protein dynamics can be revealed. The purpose of this review is to highlight the growing body of complementary work that goes beyond simulation. In particular, this review focuses on methods that address kinematics and dynamics, as well as those that address larger organizational questions and can quickly yield useful information about the long-timescale behavior of a protein.

1. INTRODUCTION

Proteins are involved in many biological processes, including metabolism, signal transmission, storage of energy, defense against intruders, and muscle buildup. The ability to carry out these functions depends simultaneously on the possible conformational changes of the folded protein and on the dynamics of these deformations. A complete understanding of protein function therefore requires an understanding of both the dynamic behavior of a protein and its static structural features. Physics-based simulations (1–3) offer a direct method to study proteins by describing physical interactions among atoms and numerically solving the associated equations of motion. They constitute a central investigatory tool in molecular and structural biology, allowing for analysis in areas that are difficult, expensive, or unfeasible to probe experimentally. The purpose of this review, however, is to highlight the growing body of work that goes beyond simulation. Such methods attempt to quickly answer questions about protein kino-dynamics, as well as larger organizational questions, by generating information about the long-timescale behavior of a protein (4, 5).

Proteins are sequential assemblies of amino acids (a few dozen to several hundred), termed residues, that are joined by peptide bonds; they range from hundreds to tens of thousands of atoms in size. Under normal physiological conditions, a protein usually folds into a compact yet flexible structure. Such a structure is referred to as the protein's folded state and is defined by a three-dimensional (3D) arrangement of secondary structure elements (helices and strands connected by loops). Although this structure is generally not fully rigid, its main features and overall shape are uniquely determined by the protein's amino acid sequence. It is widely accepted that the function of a folded protein is highly dependent on its structure and its ability to deform (6, 7).

For example, in structure-based drug design, one must take protein flexibility into consideration to correctly predict the interaction between a protein and a potential drug molecule (8, 9). Knowledge of the folded state is also useful for testing energy functions (10); gaining insights into free energy and key determinants of protein stability (11, 12); and modeling structural heterogeneity from nuclear magnetic resonance (NMR), cryo-electron microscopy (cryo-EM), and X-ray crystallography data (13, 14). The ability to predict the folding motion of a protein of a given sequence also has important potential applications in the design of new proteins (15) and in the discovery of cures for neurodegenerative diseases (16). However, for a given protein, only a small number of folded conformations can be determined experimentally.

As of August 2011, the most popular experimental method, X-ray crystallography, has been used to determine 65,195 of the 74,732 protein structures deposited in the Protein Data Bank (PDB) (17). This method provides relatively high resolution data and is applicable to large proteins, but it requires the creation of a high-quality crystal of the protein of interest, an operation that may not be feasible for some proteins. Additionally, a crystallographic experiment allows the determination of only a single conformation. Software techniques (13, 14, 18, 19) and/or multiple experiments with independently created crystals may produce distinct folded conformations, but these are often produced in too small a number to adequately characterize the flexibility of the folded protein. The next two most widely used experimental methods, NMR spectrometry (9,014 entries in the PDB) and cryo-EM (373 entries), allow for observation of a protein in solution and make it possible to determine several conformations. However, despite recent progress (20), cryo-EM still often produces relatively low resolution results, yielding ambiguous conformational models, and NMR can be applied only to small proteins.

Computational physics–based methods offer a clear advantage for understanding protein flexibility, as they can characterize dynamic systems and require little prior knowledge. In this context, molecular dynamics (MD) simulation models physical interactions among atoms by a potential function and solves Newton's, Lagrange's, or Langevin's equations of motion (1). Unfortunately, the solutions to these systems are complicated (6, 21): Not only is the potential function made up of many terms, but the equations of motion must also be solved at a time step (on the order of a femtosecond) that is much shorter than that of atomic fluctuations in order to reduce cumulative integration errors. MD simulation is thus a computationally intensive process. Modern computers can generate roughly a few nanoseconds of simulation in a day for a medium-sized protein—a timescale that is insufficient for capturing most biologically relevant transitions and events. Distributed computing (22) and specialized architectures (23, 24) speed up MD simulation with no loss of accuracy, but computational time remains an issue; furthermore, the sheer amount of the data generated becomes a greater hurdle, complicating biological insights. One may also achieve faster simulation by using coarser representations (e.g., by grouping atoms together) and approximate or heuristic potentials, but the resulting methods—which include, among others, coarse-grained force fields (25), multiscale models (26), improved sampling (27), replica exchange (28), normal-mode analysis (29–31), elastic network models (32–34), and Monte Carlo sampling (35, 36)—are less accurate and still produce staggering amounts of data.

Physics-based simulation offers high-resolution spatial and time-dependent information about the conformational neighborhoods of a subset of protein states. Although this information is needed to answer some biological questions, structural biologists and bioengineers deal with an increasing diversity of problems that often require computational tools to quickly generate compact, pertinent data that may be obtained from lower-resolution representations of the conformational landscape. For example, a pharmaceutical engineer may want to quickly screen a large database of ligands to identify those that have a reasonable chance to bind to a protein and select “leads” for a new drug. Alternatively, a biologist may want to explore the conformation space of a folded protein to find low-potential conformations or to simply characterize the range of feasible deformations of a protein. These goals may be better achieved by different methods, in particular, by deliberately avoiding the modeling of fast-frequency motions, which are responsible for the high computational complexity of physics-based simulation methods. In such cases, a compromise is made between accuracy and speed or storage requirements. If higher accuracy is eventually desired, the results of these methods can also be used as a launching point for physics-based simulations. This review focuses on methods aimed at quick generation of useful information about the long-timescale behavior of a protein, without explicit simulation. It consists of three main sections that address the following representation and algorithmic issues.

1. Section 2 reviews a simplified representation of the kinematics of a protein, termed the linkage model, which is used by several methods discussed in the other sections of this article. The linkage model naturally eliminates atomic fluctuations by enforcing distance and angular constraints among covalently bonded atoms. These constraints drastically reduce the number of degrees of freedom (DOFs; the number of variables required to describe a system) of a protein, which makes it easier for other procedures to explore the conformation space. However, because the atoms can no longer move independently of one another, manipulating this representation raises a challenging question: How can one change atom positions without breaking the constraints? This question is often referred to as the inverse kinematics problem, and Section 2 also reviews methods developed to solve it.

2. Section 3 considers conformational sampling. That is, given a set of constraints provided by a kinematic model, how can valid (i.e., biologically relevant) conformations be generated? This question is of fundamental interest because of the close relationship between protein conformation and function (37–39). Section 3 focuses on the use of geometric constraints in reducing the computational complexity of generating valid protein conformations. Such geometric constraints implicitly encode dominant energy terms. Their use therefore produces a twofold benefit, in that geometric constraints are also present in a favorable format that yields efficient algorithms. Section 3 considers loop sampling as well as the protein conformational sampling problem generally.

3. Regardless of the method used to find novel protein conformations, a set of valid conformations alone provides no comparative information about the relationships between protein states. Section 4 describes two broad organizational frameworks designed to answer questions about the collective properties of protein conformation space: probabilistic road maps (40), which characterize the local connectivity of a space, and Markov models (41), which describe probabilistic and long-timescale characteristics of the behavior of a protein. These methods are complementary and are designed to answer large-scale questions concerning the ensemble properties of proteins (e.g., folding rate, mean first-passage time, and probability of folding) without performing explicit physics-based simulation.

2. KINEMATIC MODELING OF A PROTEIN

2.1. Kinematic Linkage Model

A straightforward representation of a protein conformation is a list of the 3D coordinates of the atom centers in a reference coordinate frame. This representation yields a conformation space of dimensionality 3n, where n is the number of atoms in the protein. As this representation makes it possible to study protein motion at all timescales, it is not surprising that it is used by most MD simulators.

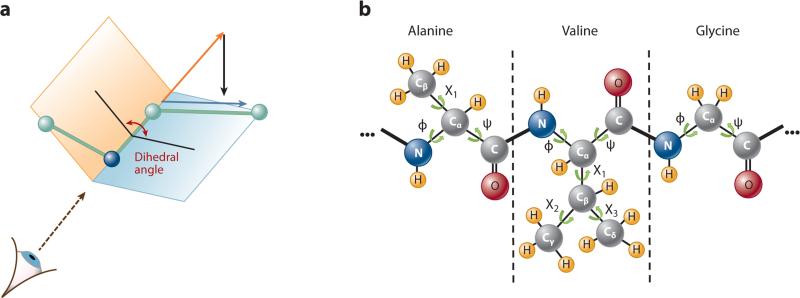
However, once high frequencies have been smoothed out over picosecond timescales (42), one may observe that the lengths of covalent bonds, angles between adjacent covalent bonds, and dihedral angles around nonrotatable bonds (double, partially double, and peptide bonds) remain almost constant (43). This observation allows one to model a protein's long-term kinetics by a kinematic linkage (44), where—in kinematics terminology (45)—atoms or small groups of atoms are links and rotatable bonds are joints. Such joints constitute the DOFs of the model and are typically parameterized by dihedral angles (also known as internal coordinates) (Figure 1a). The resulting model (Figure 1b) is a kinematic linkage that consists of a long chain—the protein main chain—in which each residue contributes two DOFs (the so-called ϕ and ψ angles around the N–C_α and C_α–C bonds, respectively) and short side chains, each of which has zero to six DOFs (the χ angles). By keeping bond lengths and angles fixed, the linkage model provides a conformational representation that naturally eliminates uncorrelated high-frequency atomic fluctuations and emphasizes so-called slow DOFs. In this model, each conformation c is defined by the values of the ϕ, ψ, and χ angles and can be considered representative of the small region spanned by uncorrelated atomic fluctuations around c in the higher-dimensional conformation space parameterized by the 3D coordinates of all atoms. The dimensionality of the conformation space of the linkage model is upper-bounded by (2 + k) × p, where p is the number of residues and k is the maximum number of χ angles in a side chain. For most proteins, (2 + k) × p is much smaller than 3n. Some works have extended MD simulation to the linkage model (46, 47) to reduce the number of variables and increase the integration time step. However, this approach introduces additional computational costs due to the complicated intrinsic properties of dihedral angle dynamics.

Figure 1.

Linkage kinematic model. (a) Dihedral angle around a covalent bond. (b) Model of a protein fragment.

2.2. Inverse Kinematics Problem

In some respects, however, the linkage model is more difficult to manipulate because the atomic positions can no longer be independently modified. This issue raises the following inverse kinematics (IK) problem: finding conformations of protein fragments that are geometrically consistent with the rest of the main-chain conformation (48).

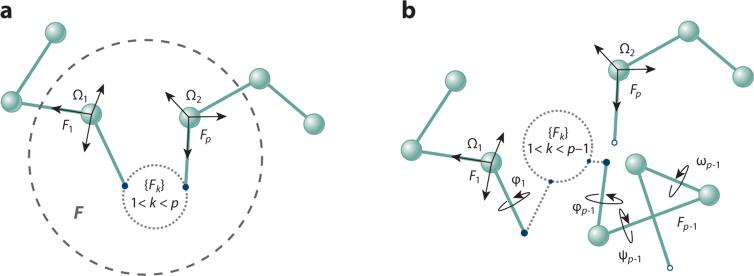
More formally (44), consider a given conformation c of some protein P. Let F be an inner fragment of p consecutive residues in P. One can attach two Cartesian coordinate frames, Ω₁ and Ω₂, to F's N and C termini, respectively (Figure 2a). F is said to be in a closed conformation when the pose Π_cl (position and orientation) of Ω₂ relative to Ω₁ is fully determined by the conformation c of P. In general, arbitrary choices of the values of the ϕ and ψ angles in F produce poses of Ω₂ relative to Ω₁ that differ from Π_cl (Figure 2b). Conformations of F that are not geometrically consistent with the rest of P are said to be open. Thus, the IK problem is to determine the values of the ϕ and ψ angles in F that result in a closed conformation of F.

Figure 2.

(a) Coordinate frames Ω₁ and Ω₂ are placed with origins relative to the centers of the appropriate terminus atoms of a protein fragment F (composed of p consecutive residues F_k, where k = 1, . . ., p); orientations are defined relative to the bonds that connect the atom to its two neighboring atoms in the main chain. (b) When Ω₂ and Ω₁ are consistent with the coordinate frames of their attachment points to the protein body P, F is geometrically consistent with P. Arbitrary choices of ϕ and ψ angles produce inconsistent (open) conformations; note that the last atom of F_p–1 does not connect to the next sequential atom of F_p.

It is well known from the fields of kinematics and robotics (45, 49, 50) that, while the space of all conformations of F's main chain has dimensionality n = 2p (the total number of ϕ and ψ angles in F), the subspace closed(Π_cl) of closed conformations of F for a given pose Π_cl has dimensionality n–6, except for critical values of Π_cl that form a subset of zero measure in the 6D space R³ × SO(3) of all the poses of Ω₂ relative to Ω₁. Here, R is the set of real numbers and SO(3) is the special orthogonal group of 3D rotations. So, in general, given a pose Π_cl of Ω₂ relative to Ω₁, F may admit closed conformations only if n ≥ 6, that is, if it consists of at least three residues. If n = 6, the number of IK solutions is finite and varies between 0 and 16 (51–53). If F consists of more than three residues, the number of IK solutions is in general (i.e., except for critical values of Π_cl) either zero or infinite; in the second case, it is possible to deform the fragment continuously without breaking closure.

2.3. Inverse Kinematics Methods

Analytical IK methods have been proposed for three-residue fragments (48, 54). In Reference 54, the problem is reduced to solving a transcendental equation, whereas the polynomial formulation described in Reference 48 makes it possible to accurately enumerate all possible solutions. The method applies to any fragment of three or more residues in which the ϕ and ψ angles of only three (possibly nonconsecutive) residues are allowed to vary. Another polynomial formulation is proposed in Reference 55, but the polynomial equations are solved with a subdivision algorithm, which yields approximate solutions. Along a related line of research, the structure of the IK map over R³ × SO(3) is studied in Reference 56, which shows that the critical poses of Ω₂ relative to Ω₁ decompose R³ × SO(3) into regular regions, such that over each such region the number of IK solutions is constant. This decomposition leads to a constructive proof of the existence of a region in which the theoretical maximum of 16 solutions is attained. This region may not be accessible in practice, however, as it may correspond to high-energy conformations with clashes among side chains.

When the protein fragment F contains p > 3 residues and all ϕ and ψ angles in F are allowed to vary, the IK problem may have an infinite number of solutions, and no analytical method is known to compute them. The solutions then span a (2p–6)-dimensional space closed(Π_cl), in which F can deform continuously without breaking closure. Several methods have been proposed to sample conformations in closed(Π_cl). The random loop generator (RLG) method (57) first chooses p–3 pairs of ϕ and ψ angles in F at random and then uses an IK method (e.g., Reference 48) to determine the remaining six angles. However, RLG considers only position accessibility and ignores orientation accessibility, meaning that angular values may be selected that do not allow Ω₂ to eventually reach Π_cl. By running RLG repeatedly with different values of the p–3 pairs of ϕ and ψ angles, one can sample multiple conformations in closed(Π_cl).

Another way to sample conformations in closed(Π_cl) is to use an iterative optimization method. The general idea is to iteratively modify all the ϕ and ψ angles in F to reduce the distance between the current pose of Ω₂ and its desired pose Π_cl. The popular cyclic coordinate descent (CCD), initially proposed in Reference 58, is applied in Reference 59 by defining the N and C anchors as the two fixed residues of the protein that bracket the deforming fragment F on its N and C termini, respectively. A fictitious residue M is added at the C terminus of F. Given any initial conformation of F (picked at random or otherwise), the CCD method iteratively modifies the ϕ and ψ angles in F until M matches the fixed C anchor. To do so, it minimizes the sum S = ∥N^MN∥² + ∥C_α^MC_α∥² + ∥C^MC∥², where ∥X^MX∥ (X = N, C_α, or C) is the Euclidean distance between the X atom of M and the X atom of the C anchor. CCD considers each of the ϕ and ψ angles in the fragment in some sequence and resets its value to the one that minimizes S. This value can also be computed analytically (59). CCD iterates until S has been reduced below a small threshold, but convergence is not guaranteed.

2.4. Incorporating Additional Distance Constraints

It is sometimes useful to constrain the linkage model further to maintain certain features. For instance, hydrogen bonds (H bonds) are known to play a key role in both the formation and the stabilization of protein structures (60–62). H bonds involving atoms from residues that are close along the protein main chain stabilize secondary structure elements, whereas H bonds between atoms from distant residues stabilize the protein's tertiary structure and shape loops and other features that often participate in functional sites. To prevent strong H bonds from breaking during linkage deformation, one may constrain the linkage model by adding distance equality constraints to the model presented in Section 2.1.

The effect of these constraints is to rigidify atom groups. The method developed in References 63–66 derives a distance constraint graph from both the linkage model and the geometry of the H bonds that must not be broken. The nodes of the graph are the atoms in the protein, and each edge represents an equality distance constraint. For instance, a constant angle between two consecutive bonds A–B and B–C leads to an edge between the nodes representing the atoms A and C. An individual H bond yields three distance constraints. The constraint graph is then processed by a 3D variant of an algorithm, known as the pebble game (67, 68), to identify all the groups of atoms made rigid by the graph edges. This algorithm is based on Laman's theorem, which was initially developed to study the rigidity of planar structures made of bars connected by hinges (69). The result yields a new kinematic linkage model of the protein in which each link is now a rigid group of atoms. Every pair of adjacent links shares exactly two atoms connected by a rotatable covalent bond or an H bond. Only the dihedral angles around these shared bonds are variable in the new linkage, which allows for less mobility than the original nonconstrained linkage. However, such a model may contain up to several dozen closed kinematic cycles, some of which may share dihedral angles. The values of the angles in the cycles can no longer be chosen independently of one another (as discussed in Section 3.3).

3. GEOMETRIC CONFORMATION SAMPLING

3.1. Goal

The goal of geometric conformation sampling—as opposed to physics-based sampling, a review of which can be found in Reference 70—is to explore the range of deformations of a protein (usually a folded one), taking only kinematic and geometric constraints into account. Most geometric conformation sampling methods use the kinematic linkage model of Section 2. This model is usually augmented by inequality interatomic distance constraints (or volume exclusion constraints) that prevent large overlaps (or clashes) between atoms. By modeling each atom as a hard sphere, with van der Waals radii reduced by a multiplication factor of 0.7 to 0.8, these distance constraints can be preserved by forbidding any two spheres to overlap. A brute-force algorithm to detect violation of this constraint (by comparing every pair of atoms) runs in quadratic time in the number of atoms. However, the grid method analyzed in Reference 71 and used in many implementations takes only linear time. It consists of indexing all atom centers in a 3D grid of small cubes and checking only pairs of atoms whose centers fall in the same cube or in neighboring cubes. A conformation that satisfies the volume exclusion constraints is said to be clash-free. The attractiveness of a geometric approach derives from the fact that geometric constraints have a favorable format that yields efficient algorithms. They do not require explicit potential functions, which in some cases are difficult to provide (for instance, when a protein may interact with as-yet-unknown molecules). They also make it possible to sample broadly distributed accessible conformations. They do not, however, address the problem of recognizing functional conformations in the generated distribution. If a potential function or structure-based function prediction software (72) is available, sampled conformations may then be filtered in a postprocessing phase. Alternatively, results from geometric conformation sampling may serve as the launching point for local physics-based simulation, producing high-resolution time-resolved information from the output of broad low-resolution exploration.

Geometric conformation sampling may apply to an entire protein or, instead, may be restricted to a fragment of a protein, typically a flexible loop. In the following subsections, we first consider loop sampling, then protein sampling.

3.2. Loop Conformation Sampling

Loop/fragment conformation sampling has a wide range of applications, for example, to predict deformations that allow ligand binding (73), interpret noisy regions in electron density maps (74), fill gaps in homology modeling (75, 76), create fragment moves in Monte Carlo simulations (77), and tweak main-chain positions for energy optimization (78). Although loop sampling involves relatively few variable dihedral angles, it is still a challenging problem as it requires dealing with two potentially conflicting constraints: A valid loop conformation must be both clash-free and closed (Section 2.2) to be consistent with the rest of the protein (assumed rigid). Basic strategies such as CCD (Section 2.3) can be employed here, but recent literature offers alternatives tailored to proteins. The loop conformation sampler is characterized mainly by the strategy it uses to achieve these two constraints.

RAPPER (79) iteratively builds up a loop conformation from its N terminus toward its C terminus. At each step, it selects the values of the ϕ and ψ angles in each successive residue at random from a precomputed table of residue-specific values derived from a large collection of diverse protein structures. It also checks (a) that the added residue does not clash with the rest of the protein or the portion of the loop built so far and (b) that the residue's C_α atom is not further away from the loop's C anchor than a certain threshold that would prevent loop closure. When a complete conformation has been generated, there remains a potentially large gap between the loop's last residue and its anchor on the protein. RAPPER runs an iterative minimization procedure to close this gap, checking volume exclusion at each iteration.

RLG (57) successively samples closed conformations using the RLG IK method (Section 2.3) and rejects each sampled conformation that is not clash-free. The rejection ratio tends to be high because clash-free conformations usually span a small subset of the closed conformation space.

The method described in Reference 80 and LoopTK (81) decompose a loop into three fragments, independently sample clash-free conformations of the two fragments rooted at the N and C anchors, and close the loop with the middle fragment. LoopTK uses SCWRL3 (82) side chains and includes an efficient method to deform any sampled conformation c and generate more conformations around it. This method consists of computing the tangent space of the closed conformation space at c, a technique often used in robotics (83), and moving by small increments in that space. LoopTK has been used to determine loops with up to 25 residues, and its combination with a functional site prediction program (72) made it possible to generate and recognize calcium-binding loop conformations.

Finally, some procedures sample loop conformations by using libraries of fragments obtained from previously solved structures (84–86). However, they do not check that sampled conformations satisfy the volume exclusion constraints.

3.3. Protein Conformation Sampling

Sampling entire protein conformations is more complicated than loop sampling, as it involves many more variable dihedral angles. Most methods surveyed below assume that a folded conformation of a protein is given and explore the protein's folded state (or a subset of it) by sampling new conformations obtained by deforming previously sampled conformations (initially, the given folded conformation).

ROCK (rigidity-optimized conformational kinetics) (66) transforms covalent bonds, H bonds (with potential energy lower than a given threshold), and hydrophobic contacts into equality distance constraints between atoms (Section 2.4). Using the pebble game algorithm (68), it identifies rigid groups of atoms. The resulting kinematic model of the protein is made of rigid groups connected by variable dihedral angles around rotatable bonds. It usually contains many closed cycles. To sample new conformations, ROCK performs a random walk starting at the given conformation. At each step, it perturbs variable dihedral angles that are not contained in any cycle at random. It also perturbs at random all variable dihedral angles in each cycle except for six, which are then solved with an IK procedure. As ROCK closes cycles sequentially, the closure of each cycle results in breaking the previously treated cycles with which it shares variable dihedral angles. Once all cycles have been treated, ROCK uses a minimization procedure to reduce to zero a gap function measuring cycle breakup. Due to conflicting cycle closure constraints, this function can have local minima; therefore, the minimization process may become trapped into a local minimum. If all cycles are successfully closed, the resulting conformation is checked for atomic clashes.

FRODA (for framework rigidity-optimized dynamic algorithm) (63, 65) performs the same rigidity analysis as does ROCK. It also performs a random walk, but it differs in the way it samples each new conformation. The positions of all the atoms are first independently perturbed at random. Then iterative optimization is used to fit the relative positions of the atoms in every rigid group R back to the geometric template associated with R, while avoiding clashes between atoms from different groups. This process has the indirect effect of achieving cycle closure. Experiments with FRODA show that each step of the random walk is 100 to 1,000 times faster than in ROCK. However, FRODA's steps may be small, as the process of fitting back atoms to templates often tends to partially cancel out the initial deformation. In addition, the method is not well suited for generating deformations in which large groups of atoms perform correlated moves. The sampling strategies of both ROCK and FRODA can be biased to sample a sequence of conformations between two given protein states and therefore to determine pathways between these conformations (65).

KGS (for kino-geometric sampling) (87) performs the same rigidity analysis as ROCK and FRODA but uses a different sampling strategy and a different method to deform a conformation into a new one. Random walks used by ROCK and FRODA (in their unbiased mode) have an inherently slow diffusion rate and hence are slow to explore a folded state. Instead, KGS uses a diffusive strategy that guides exploration toward less-visited space (88). In addition, its deformation method aims at keeping all cycles closed to avoid having to close them back later. KGS consists of computing the tangent space of the space of conformations in which all cycles are closed (83) and moving in that space. This procedure requires nontrivial computations due to the large potential number of interdependent cycles, but it allows the sampler to make relatively big deformation steps. In particular, KGS has successfully explored the folded states of cyanovirin-N, a potent HIV-inactivating protein, and the periplasmatic L-lysine/L-arginine/L-ornithine protein (LAO) (89). Each of these two proteins has two distinct substates (PDB IDs: 2EZM and 1L5E for cyanovirin-N; 2LAO and 1LAF for LAO). Transition from one state to the other involves a hinge and a twist motion between two domains.

The protein ensemble method (PEM) (90) accepts as input a 3D protein structure, such as one taken from the PDB. It computes an ensemble of conformations that collectively characterize the mobility of the entire protein at equilibrium. Such a computation is done by generating and combining ensembles of conformations for consecutive overlapping fragments (sequences of consecutive amino acids). PEM finds geometrically feasible conformations of each fragment by use of CCD (Section 2.3). The approach blends geometric exploration of conformation space with a statistical mechanics formulation to generate an ensemble of physical conformations on which thermodynamic quantities can be measured as ensemble averages. It has been developed for proteins that do not exhibit correlated motion and has been validated on proteins for which ensemble data exist from NMR experiments.

In Reference 91, new conformations are sampled in the context of a graph-based model (Section 4). The procedure starts with a given set of valid conformations (possibly containing only a single conformation) and generates new reasonable conformations by expanding from the original ones. In essence, a tree of conformations is generated with some notion of succession or propagation of one conformation from another. The way propagation, and hence exploration, is done is guided by low-dimensional projections of the conformations generated so far. These projections are spatially partitioned into cells, and a given projection is selected relative to a weighting scheme that favors larger, less dense cells to promote conformation exploration. The conformation associated with this projection then serves as the starting point for expansion of the exploration. The expansion first applies a series of random perturbations, essentially a short random walk, to the known valid conformation and then applies a selection filter (based on energy) to the result. If the resulting conformation is valid, it is added to the set of valid conformations; otherwise it is discarded. In either case, the process repeats from the beginning to generate new low-energy conformations and to characterize the energy landscape of the protein.

In case the protein structure is not completely known, Rosetta (92) performs a fragment-level construction by using template fragments drawn from libraries of known motifs from homologous and other structures. Conformations resulting from this construction are then optionally post-modified with a Monte Carlo search or other randomized optimization designed to expand the range of the search space. All resulting conformations are then energetically minimized. Although computationally intensive, this method has recently been used to produce detailed maps of the energy landscapes of numerous protein domains (93).

Finally, for many of the approaches described above (e.g., References 90 and 91), ensuring that conformations are drawn from a representative sampling of the free-energy landscape of a protein system (while avoiding oversampling) is of critical importance, both for good coverage and for speed. Dimension reduction—the approximate low-dimensional representation of high-dimensional systems—can be useful in efficiently guiding several algorithms to representative or unique regions of a conformation space. In Reference 94 the free-energy landscape of DecaAlanine is characterized in two dimensions by applying principal component analysis (PCA) directly on dihedral angles under a Cartesian transform. In Reference 95, the free-energy landscape of an SH3 domain is characterized in two and three dimensions [reduced from the original (171)], with very low residual error, by use of nonlinear dimension reduction (the ScIMaP algorithm). With both methods, conformations with similar features aggregate into well-separated minima in the lower-dimensional representations. Such representations could be used to heuristically guide a sampling scheme as it progresses while periodically updating results to include newly generated conformations.

4. GRAPH-BASED MODELS OF PROTEIN MOTION

4.1. Introduction

Conformation sampling provides information about the accessible conformation space, but it does not describe conformational changes over time. Here, we review methods that take a set of conformations as input and build a directed graph modeling the long-timescale motion behavior of a protein. The input conformations may be sampled using geometric or potential-based methods. The nodes of the computed graph represent individual conformations of a protein or groups of conformations. Its arcs represent the transitions between them. The goal is to capture a huge number of possible long-timescale motion paths into a compact and explicit representation that can then be analyzed by efficient computational tools. In particular, graph-based methods make it possible to compute ensemble properties—such as folding rate, mean first-passage time, transition-state ensemble, P_fold values (96), and dominant ordering on secondary structure formation—that characterize protein behavior over a myriad of motion paths without performing any explicit simulation.

There has recently been a surge of interest in graph-based models. This trend started with the adaptation of probabilistic road maps developed for robot motion planning (40) to represent molecular motion. Then road maps evolved into point-based Markov models and, more recently, into cell-based and hidden Markov models. We review this line of work below (that discussion is derived in part from Reference 4).

4.2. Road Maps

In a classical robot motion planning problem, a robot must move among obstacles without colliding with any of them. A configuration¹ of the robot is said to be valid if the robot at that configuration does not collide with any obstacle. It is usually prohibitively expensive to compute the space of valid configurations of a robot (the robot's valid space), but there are efficient techniques to check whether a given configuration or a given motion path is valid. Probabilistic road map (PRM) planning exploits such observations by computing an approximate representation of the valid space in the form of an undirected graph, the probabilistic road map (40). Each node of the road map corresponds to a valid robot configuration sampled randomly from the robot configuration space, and each edge between two nodes represents a simple valid path between the corresponding configurations (usually, a linear interpolation between them). A PRM planner constructs a road map until it connects a start configuration to a goal configuration. Under assumptions that are generally satisfied in practice, the probability that PRM planning finds a motion path between two configurations converges to one exponentially in the number of nodes of the road map (97). In other words, a probabilistic road map provides a good approximation of the connectivity of the space of valid configurations. PRM planning and its variants are currently the most widely used way to plan the motions of complex articulated robots.

The PRM approach has been adapted to model and analyze the motion of a flexible ligand binding with a protein assumed to be rigid (98). The adaptation relies on an analogy between valid (nonvalid) configurations for robots and low-energy (high-energy) conformations for molecules. However, whereas the configuration space of a robot is cleanly divided between valid and non-valid configurations, the energy landscape over the conformation space of a molecule or a group of molecules does not provide such a clear-cut division. Moreover, whereas in robotics one is interested in finding a single reasonably good motion path, in biology one is interested in characterizing the behavior of a molecule over a representative set of motion paths. To address these differences, the method in Reference 98 proceeds as follows. It attaches a Cartesian frame, P, to the protein (assumed to be rigid) and another one, L, to a rigid group of three atoms in the flexible ligand. It defines the conformation of the ligand by six parameters that represent the position and orientation of L relative to P, plus p dihedral angles around the ligand's rotatable bonds. It then samples at random many conformations of the ligand such that the origin of L is within some predefined distance of the protein. Each sampled conformation c is retained as a node of the road map with the following probability distribution:

$$P\left(c\text{is retained}\right)=\{\begin{array}{cc}0\hfill & \text{if}E\left(c\right)\ge E_{\max }\hfill \\ \frac{E_{\max }-E\left(c\right)}{E_{\max }-E_{\min }}\hfill & \text{if}{E}_{\min }<E\left(c\right)<E_{\max }\hfill \\ 1\hfill & \text{if}E\left(c\right)\le E_{\min }\hfill \end{array}\phantom{\}},$$ (1)

where E(c) is the potential energy of the ligand consisting of van der Waals and electrostatic terms, and E_max and E_min are input thresholds. So, this method leads to a greater density of nodes in the low-energy regions of the ligand's conformation space. Next, each node is connected to its k nearest neighbors by a linear-interpolation path. The path between two nodes, c and c′, is discretized into a sequence of conformations, c₀ = c, c₁, . . ., c_i, . . ., c_s = c′, such that in any two successive conformations, c_i and c_i+1, no two corresponding atoms are further apart than 1 Å. The path is accepted only if all the discretized conformations along the path have energy below a maximum energy threshold. If the path is accepted, the road map nodes c and c′ are connected to each other by two road map arcs of opposite directions. The arc from c to c′ is labeled by a weight w(c → c′) that measures the energetic difficulty of traversing the path from c to c′. For any three successive conformations c_i–1, c_i, and c_i–1, with potential values E_i–1, E_i, and E_i+1, the following equation is used to estimate the probability that the ligand at conformation c_i moves next to c_i+1:

$$P(c_i\to c_{i+1})=\frac{e^{\frac{E_{i+1}-E_i}{\mathrm{k}T}}}{e^{\frac{E_{i+1}-E_i}{\mathrm{k}T}}+e^{\frac{E_{i-1}-E_i}{\mathrm{k}T}}}.$$

Here, k is the Boltzmann constant and T is the absolute temperature. The weight w(c → c′) is computed as follows:

$$w(c\to c^{\prime })=-\sum _{i=0}^{s-1}\log \left[P(c_i\to c_{i+1})\right].$$

Similarly, the arc from c′ to c is labeled by $w(c^{\prime }\to c)=-{\sum }_{i=1}^s\log \left[P(c_{i+1}\to c_i)\right]$. So, the road map represents a distribution of plausible paths of the ligand through the space surrounding the receptor protein.

Once constructed, a road map is used (98) to predict an active binding site from a given collection of potential binding sites, all with low potential energies. Such a prediction is performed by computing the N (where N ≈ 100) most favorable paths in the road map that enter each site from distant conformations and the N most favorable paths that leave each site. It was observed on several protein-ligand complexes that the active binding site is often not the one with the lowest potential energy, but the one for which both the entering and leaving paths have the highest weights on average. This result suggests the presence of an energy barrier around the active site.

This method was extended in Reference 99 to protein folding to predict the dominant order of secondary structure formation. The protein is modeled using the linkage model of Section 2.1 with fixed χ angles (i.e., rigid residues), and a road map is computed by sampling conformations in this model. A key difference with the method of Reference 98 is the sampling strategy. Here, the strategy creates a wave front of conformations expanding from the given folded conformation. Each new conformation c is obtained by perturbing every ϕ and ψ angle in a previously sampled conformation by use of a Gaussian distribution. It is retained as a new node of the road map with the probability distribution defined in Equation 1, where E is now an energy function that rejects conformations containing collisions among side chains and favors hydrogen and disulfide bonds in secondary structure elements, as well as hydrophobic interactions. The nodes of the road map are sorted into bins on the basis of the number of native contacts, where a native contact is defined as a pair of residues whose C_α atoms are less than 7 Å apart in the folded conformation. The sampling strategy fills the bins starting with the bin with all native contacts. Once a bin contains at least a certain number of nodes, sampling is performed around conformations in that bin to fill bins with fewer native contacts. Thus, the density of road map nodes over the conformation space is a decreasing function of the distance from the input folded conformation.

The method in Reference 99 then computes the N best paths to the folded conformation from conformations in the zero-native-contact bin. Along each path, the appearance time for a secondary structure element is measured as the mean appearance time for all of its contacts. The predicted secondary structure formation order is the order with the greatest frequency over all paths. The method was tested on a set of 14 proteins ranging from 56 to 110 residues in size. It correctly predicted the order of secondary structure formation in all cases in which laboratory data were available.

This work is extended in Reference 100 to analyze proteins for which laboratory experiments show that secondary structures form in different dominant orders. In Reference 101, a new sampling strategy based on rigidity analysis is proposed (Section 2.4). This strategy scales up better to large proteins than does the previous, bin-based strategy.

4.3. Point-Based Markov Models

To capture the stochasticity of molecular motion, the road map model was transformed (102) into a Markov model by treating each road map node as a state and assigning each arc c → c′ a transition probability P(c → c′) derived from the energetic difference between the conformations c and c′ and inspired by the Metropolis criterion. A self-transition is added to each node with probability such that all transition probabilities at this node add up to one. The resulting graph is treated as a Markov model in the following sense: The probability of transitioning from c to c′ is a constant that does not depend on the protein's history before reaching c. The graph is known as a point-based Markov model (PMM), as each state represents a single conformation.

In principle, a PMM makes it possible to perform a random walk similar to a Monte Carlo simulation. However, the most interesting feature of a PMM is that it allows the computation of ensemble properties, without performing any explicit simulation or computing any specific path, by use of a technique known as first-step analysis. In Reference 102, this technique is used to efficiently compute the P_fold value, a theoretical measure on the progress of protein folding (96). Let F (respectively, U) denote the set of nodes that correspond to conformations that are considered folded (respectively, unfolded). The value P_fold(c) at any node c is the probability that from c the protein will reach F before U. By definition P_fold(c) = 1 if c ∈ F and 0 if c ∈ U. Computing P_fold(c) at each other node by use of simulation would require performing many runs from c. Instead, with first-step analysis, one can write the following equation, which corresponds to performing a single simulation step for many simulation runs all at once:

$$P_{\text{fold}}\left(c\right)=\sum _{c^{\prime }\in F}P(c\to c^{\prime })\times 1+\sum _{c^{\prime }\in U}P(c\to c^{\prime })\times 0+\sum _{c^{\prime }\notin F\cup U}P(c\to c^{\prime })\times P_{\text{fold}}\left(c^{\prime }\right).$$

This step leads to a sparse system of linear equations, one for each node not in F ∪ U. A linear system solver computes the P_fold values at all nodes simultaneously. This computation takes all the paths encoded in the road map into account. The method was applied to a monomer of repressor of primer (PDB ID: 1ROP) and an engrailed homeodomain (1HDD). A simplified kinematic model and the H–P energy model were used to create the PMM. The P_fold values computed with a PMM converge quickly toward the values computed through the performance of many MC simulation runs, when the number of nodes in the PMM increases. However, computation with the PMM is several orders of magnitude faster than with MC simulation. The method was later extended to predict experimental measures of folding kinetics, such as folding rates, transition-state ensembles, and Φ values of residues (103).

In Reference 104, an improved sampling method is proposed to generate the nodes of a PMM. The nodes are obtained by subsampling conformations of a protein along short trajectories obtained with MD simulation and merging conformations that are close to each other in terms of their root-mean-square distance. This approach makes it possible to assign transition durations to the arcs of the model (in addition to transition probabilities). So, it not only provides a more energy-pertinent coverage of the conformation space but also adds temporal information that potentially allows more accurate computation of dynamic properties.

This method has been tested on the 12-residue tryptophan zipper β hairpin, which had previously been simulated on Folding@Home (105). The PMM was built by subsampling 22,400 conformations along 1,750 independent trajectories. The mean first-passage time from the unfolded state to the folded state and the folding rate were compared with those from the resulting model by use of first-step analysis. Their values agreed well with experimental results from fluorescence and IR.

A method is proposed in Reference 106 to estimate the uncertainty in the set of transition probabilities in a PMM derived from MD simulation runs and to identify the nodes whose arcs have the largest uncertainty. Then one may reduce uncertainty by performing more simulations from these nodes.

4.4. Cell-Based and Hidden Markov Models

All Markov models to represent protein motion depend on a key assumption: The future state of a protein depends only on its current state s and not on its history prior to reaching s. This assumption enables a Markov model to be compact and yet capture the main features of the underlying dynamics. However, single conformations rarely contain enough information to guarantee this assumption. So, a PMM may not have the ability to represent well protein motion over time. One way to alleviate this problem is to construct large PMMs by sampling many nodes, but doing so makes them more difficult to analyze and understand.

This drawback has led to cell-based Markov models (CMMs) (5), in which each node is a collection of sampled conformations that roughly matches an attraction basin (cell) in the protein's energy landscape. The protein interconverts rapidly among different conformations within a basin s before it overcomes the energy barrier and transitions to another basin s′. The assumption is that after many interconversions within s, the protein “forgets” the history of how it entered s and transitions into s′ with a probability that depends on s alone. MD simulation is used to generate the data for building a CMM (5). Conformations subsampled along MD trajectories are first grouped into clusters so that self-transition probabilities for the states in the CMM are maximized; that is, intrastate transitions are frequent (hence, fast), whereas interstate transitions are rare (slow). Recent work builds CMMs at multiple resolutions through hierarchical clustering (107).

Related models, termed transition networks, are described in References 108 and 109. A preliminary form of CMM was initially proposed to analyze a simplified lattice protein model (110). The data for model construction were obtained by solving the master equation instead of performing MD simulation.

CMMs achieve the dual objectives of better satisfying the Markovian assumption and reducing the number of states. However, they still violate the Markovian assumption in a subtle way. Consider a protein at a conformation c near the boundary of an energy basin. The future state of the protein depends not only on c but also on the protein's velocity—hence, on past history. By requiring each conformation to belong to a single state, CMMs violate the Markovian assumption, especially near cell boundaries and in cells corresponding to shallow energy basins. To address this problem, in Reference 111 a state is modeled by a probabilistic distribution over the collection of sampled conformations. Each conformation c now belongs to all states in the model, but with different probabilities (some very small). Conversely, for each state s, the model—a hidden Markov model (HMM)—gives a probability distribution over the conformation space. A major advantage of such an HMM over a CMM is that it can be scored by well-established tools that compute its likelihood for a test data set of MD trajectories. This scoring method makes it possible to determine automatically the optimal number of states. This approach has been tested on two extensively studied peptides, alanine dipeptide and the villin headpiece subdomain (HP-35 NleNle), to estimate kinetic and dynamic folding quantities. The results were consistent with available experimental measurements. Also, although a widely accepted thermodynamic model of alanine dipeptide contains six states, a simpler model with only three states was demonstrated to be almost as good at predicting long-timescale motions.

Markov models derived from MD data are currently limited by the cost of MD simulation. So far, they have been applied only to small proteins. However, faster computers and algorithms should eventually alleviate this limit. It will be possible to generate more data at faster rates, but the resulting data sets will remain difficult to understand because of the sheer size of the data in high-dimensional spaces. The future challenge will be to gain biological insights from simulation data by deriving simple and yet powerful models. In that respect, CMMs and HMMs are promising possibilities.

5. CONCLUSION

Physics-based simulation is a valuable tool for investigating protein dynamics at high resolution. Many complementary methods that focus on lower-resolution aspects of a protein's global conformation space have nonetheless shown significant utility in answering many questions of biological importance—with considerable advantages in performance. Further, the two approaches, which focus on differing aspects of a conformational landscape, may be used together to focus on key areas of interest to researchers.