Feature Augmentation via Nonparametrics and Selection (FANS) in High-Dimensional Classification

Abstract

We propose a high dimensional classification method that involves nonparametric feature augmentation. Knowing that marginal density ratios are the most powerful univariate classifiers, we use the ratio estimates to transform the original feature measurements. Subsequently, penalized logistic regression is invoked, taking as input the newly transformed or augmented features. This procedure trains models equipped with local complexity and global simplicity, thereby avoiding the curse of dimensionality while creating a flexible nonlinear decision boundary. The resulting method is called Feature Augmentation via Nonparametrics and Selection (FANS). We motivate FANS by generalizing the Naive Bayes model, writing the log ratio of joint densities as a linear combination of those of marginal densities. It is related to generalized additive models, but has better interpretability and computability. Risk bounds are developed for FANS. In numerical analysis, FANS is compared with competing methods, so as to provide a guideline on its best application domain. Real data analysis demonstrates that FANS performs very competitively on benchmark email spam and gene expression data sets. Moreover, FANS is implemented by an extremely fast algorithm through parallel computing.

1 Introduction

Classification aims to identify to which category a new observation belongs based on feature measurements. Numerous applications include spam detection, image recognition, and disease classification (using high-throughput data such as microarray gene expression and SNPs). Well known classification methods include Fisher’s linear discriminant analysis (LDA), logistic regression, Naive Bayes, k-nearest neighbors, neural networks, and many others. All these methods can perform well in the classical low dimensional settings, in which the number of features is much smaller than the sample size. However, in many contemporary applications, the number of features p is large compared to the sample size n. For instance, the dimensionality p in microarray data is frequently in thousands or beyond, while the sample size n is typically in the order of tens. Besides computational issues, the central conflict in high dimensional setup is that the model complexity is not supported by limited access to data. In other words, the “variance” of conventional models is high in such new settings, and even simple models such as LDA need to be regularized. We refer to Hastie et al. (2009) and Bühlmann and van de Geer (2011) for overviews of statistical challenges associated with high dimensionality.

In this paper, we propose a classification procedure FANS (Feature Augmentation via Non-parametrics and Selection). Before introducing the algorithm, we first detail its motivation. Suppose feature measurements and responses are coded by a pair of random variables (X, Y), where X ∈ 𝒳 ⊂ ℝ^p denotes the features and Y ∈ {0, 1} is the binary response. Recall that a classifier h is a data-dependent mapping from the feature space to the labels. Classifiers are usually constructed to minimize the risk P(h(X) ≠ Y).

Denote by g and f the class conditional densities respectively for class 0 and class 1, i.e., (X|Y = 0) ~ g and (X|Y = 1) ~ f. It can be shown that the Bayes rule is 1I(r(x) ≥ 1/2), where r(x) = E(Y|X = x). Let π = P(Y = 1), then

$$r(\mathit{x})=\frac{\pi f(\mathit{x})}{\pi f(\mathit{x})+(1-\pi )g(\mathit{x})}.$$

Assume for simplicity that π = 1/2, then the oracle decision boundary is

$$\{\mathit{x}:f(\mathit{x})/g(\mathit{x})=1\}=\{\mathit{x}:\text{log}f(\mathit{x})-\text{log}g(\mathit{x})=0\},$$

Denote by g₁, ⋯, g_p the marginals of g, and by f₁, ⋯, f_p those of f. Naive Bayes models assume that the conditional distributions of each feature given the class labels are independent, i.e.,

$$\text{log}\frac{f(\mathit{x})}{g(\mathit{x})}=\sum _{j=1}^p\text{log}\frac{f_j(x_j)}{g_j(x_j)}.$$ (1.1)

Naive Bayes is a simple approach, but it is useful in many high-dimensional settings. Taking a two class Gaussian model with a common covariance matrix, Bickel and Levina (2004) showed that naively carrying out the Fisher’s discriminant rule performs poorly due to diverging spectra. In addition, the authors argued that independence rule which ignores the covariance structure performs better than the Fisher’s rule in some high-dimensional settings. However, correlation among features is usually an essential characteristic of data, and it can help classification under suitable models and with relative abundance of the sample. Examples in bioinformatics study can be found in Ackermann and Strimmer (2009). Recently, Fan et al. (2012) showed that the independence assumption can lead to huge loss in classification power when correlation prevails, and proposed a Regularized Optimal Affine Discriminant (ROAD). ROAD is a linear plug-in rule targeting directly on the classification error, and it takes advantages of the un-regularized pooled sample covariance matrix.

Relaxing the two-class Gaussian assumption in parametric Naive Bayes gives us a general Naive Bayes formulation such as (1.1). However, this model also fails to capture the correlation, or dependence among features in general. On the other hand, the marginal density ratios are the most powerful univariate classifiers and using them as features in multivariate classifiers can yield very powerful procedures. This consideration motivates us to ask the following question: are there advantages of combining these transformed features rather than untransformed feature? More precisely, we would like to learn a decision boundary from the following set

$$𝒟=\{\mathit{x}:{\beta }_0+{\beta }_1\text{log}\frac{f_1(x_1)}{g_1(x_1)}+\cdots +{\beta }_p\text{log}\frac{f_p(x_p)}{g_p(x_p)}=0,{\beta }_0,\cdots ,{\beta }_p\in ℝ\}.$$ (1.2)

(All coefficients are 1 in the Naive Bayes model, so optimization is not necessary.) For univariate problems, properly thresholding the marginal density ratio delivers the best classifier. In this sense, the marginal density ratios can be regarded as the best transforms of future measurements, and (1.2) is an effort towards combining those most powerful univariate transforms to build more powerful classifiers.

This is in a similar spirit to the sure independence screening (SIS) in Fan and Lv (2008) where the best marginal predictors are used as probes for their utilities in the joint model. By combining these marginal density ratios and optimizing over their coefficients β_j ’s, we wish to build a good classifier that takes into account feature dependence. Note that although our target boundary 𝒟 is not linear in the original features, it is linear in the parameters β_j ’s. Therefore, any linear classifiers can be applied to the transformed variables. For example, we can use logistic regression, one of the most popular linear classification rules. Other choices, such as SVM (linear kernel), are good alternatives, but we choose logistic regression for the rest of discussion.

Recall that logistic regression models the log odds by log

$$\text{log}\frac{P(Y=1|\mathit{X}=\mathit{x})}{P(Y=0|\mathit{X}=\mathit{x})}={\beta }_0+\sum _{j=1}^p{\beta }_j{x}_j,$$

where the β_j’s are estimated by the maximum likelihood approach. We should note that without explicitly modeling correlations, logistic regression takes into account features’ joint effects and levels a good linear combination of features as the decision boundary. Its performance is similar to LDA, but both models can only capture decision boundaries linear in original features.

On the other hand, logistic regression might serve as a building block for the more flexible FANS algorithm. Concretely, if we know the marginal densities f_j and g_j, and run logistic regression on the transformed features {log(f_j(x_j)/g_j(x_j))}, we create a decision boundary nonlinear in the original features. The use of these transformed features is easily interpretable: one naturally combines the “most powerful” univariate transforms (building blocks of univariate Bayes rules) {log(f_j(x_j)/g_j(x_j))} rather than the original measurements. In special cases such as the two-class Gaussian model with a common covariance matrix, the transformed features are not different from the original ones. Some caution should be taken: if f_j = g_j for some j, i.e., the marginal densities for feature j are exactly the same, this feature will not have any contribution in classification. Deletion like this might lose power, because features having no marginal contribution on their own might boost classification performance when they are used jointly with other features. In view of this defect, a variant of FANS augments the transformed features with the original ones.

Since marginal densities f_j and g_j are unknown, we need to first estimate them, and then run a penalized logistic regression (PLR) on the estimated transforms. Note that some regularization (e.g., penalization) is necessary to reduce model complexity in the high dimensional paradigm. This two-step classification rule of feature augmentation via nonparametrics and selection will be called FANS for short. Precise algorithmic implementation of FANS is described in the next section. Numerical results show that our new method excels in many scenarios, in particular when no linear decision boundary can separate the data well.

To understand where FANS stands compared to Naive Bayes (NB), penalized logistic regression (PLR), and the regularized optimal affine discriminant (ROAD), we showcase a simple simulation example. In this example, the choice is between a multivariate Gaussian distribution and some componentwise mixture of two multivariate Gaussian distributions:

• Class 0: $N({(5\times {\mathbf{1}}_{10}^T,{\mathbf{0}}_{p-10}^T)}^T,\mathbf{\Sigma })$,

• Class 1: $\mathit{w}◦N({\mathbf{0}}_p,{\mathit{I}}_p)+(1-\mathit{w})◦N({(6\times {\mathbf{1}}_{10}^T,{\mathbf{0}}_{p-10}^T)}^T,\mathbf{\Sigma })$, where p = 1000, ◦ is the element-wise product between matrices, Σ_ii = 1 for all i = 1, ⋯, p, Σ_ij = 0.5 for all i, j = 1, ⋯, p and i ≠ j, and w = (w₁, ⋯, w_p)^T, in which w_j ~^iid Bernoulli(0.5).

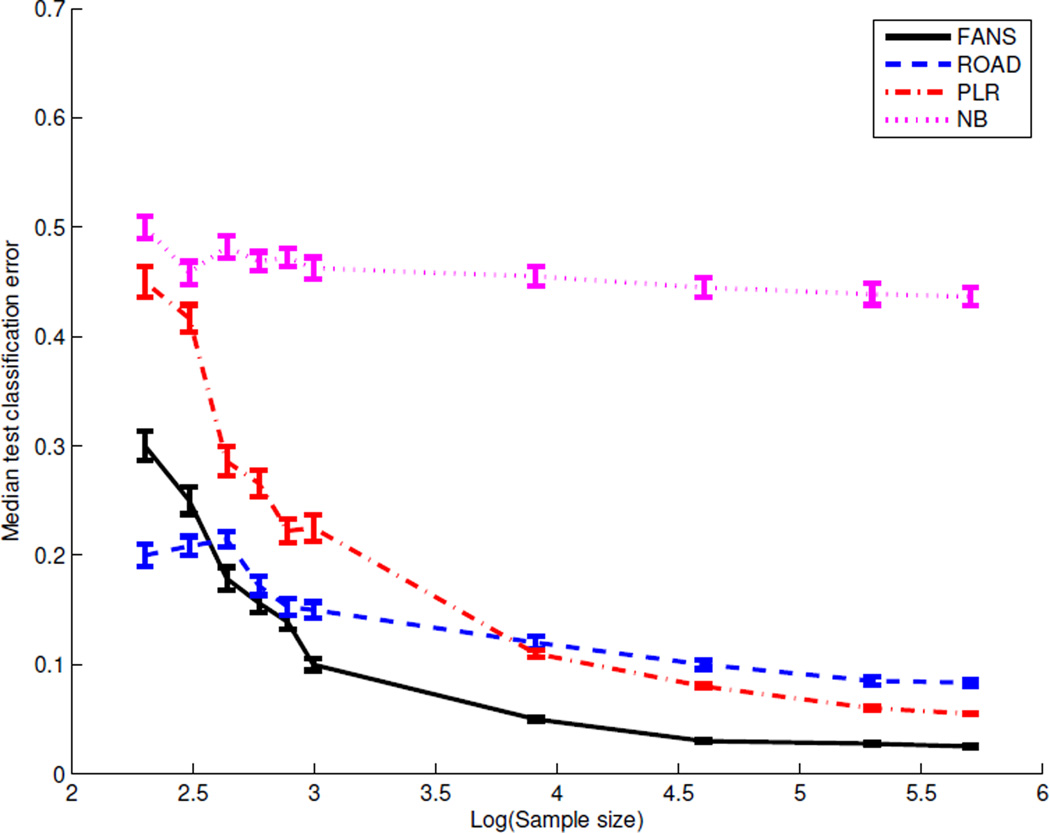
The median classification error with the standard error shown in the error bar for 100 repetitions as a function of training sample size n is rendered in Figure 1. This figure suggests that increasing the sample size does not help NB boost performance (in terms of the median classification error), because the NB model is severely biased in view of significant correlation presence. It is interesting to compare PLR with ROAD. ROAD is a more efficient approach when the sample size is small; however, PLR eventually performs better when the sample size becomes large enough. This is not surprising because the underlying true model is not two class Gaussian with a common covariance matrix. So the less “biased” PLR beats ROAD on larger samples. Nevertheless, even if ROAD uses a misspecified model, it still benefits from a specific model assumption on small samples. Finally, since the oracle decision boundary in this example is nonlinear, the newly proposed FANS approach performs significantly better than others when the sample size is reasonably large. The above analysis seems to suggest that FANS does well as long as we have enough data to construct accurate marginal density estimates. Note also that ROAD is better than FANS when the training sample size is extremely small. Figure 1 shows that even under the same data distribution, the best method in practice largely depends on the available sample abundance.

Figure 1.

The median test errors for Gaussian vs. mixture of Gaussian when the training data size varies. Standard errors shown in the error bars.

A popular extension of logistic regression and close relative to FANS is the additive logistic regression, which belongs to the generalized additive model (Hastie and Tibshirani, 1990). Additive logistic regression allows (smooth) nonparametric feature transformations to appear in the decision boundary by modeling

$$\text{log}\frac{P(Y=1|\mathit{X}=\mathit{x})}{P(Y=0|\mathit{X}=\mathit{x})}=\sum _{j=1}^p{h}_j(x_j),$$ (1.3)

where h_j’s are smooth functions. This kind of additive decision boundary is very general, in which FANS and logistic regression are special cases. It works well for small-p-large-n scenarios, while its penalized versions adapt to high dimensional settings. We will compare FANS with penalized additive logistic regression in numerical studies. The major drawback of additive logistic regression (generalized additive model) is the heavy computational complexity (e.g., the backfitting algorithm) involved in searching the transformation functions h_j(·). Moreover, the available algorithms, e.g., the algorithm for penGAM (Meier et al., 2009), fail to give an estimate when the sample size is very small. Compared to FANS, the generalized additive model uses a factor of K_n more parameters, where K_n is the number of knots in the approximation of every additive components ${\{h_j(·)\}}_{j=1}^p$. While this reduces possible biases in comparison with FANS, it increases variances in the estimation and results in more computation cost (see Table 2). Moreover, FANS admits a nice interpretation of optimal combination of optimal building blocks for univariate classifiers.

Table 2.

Computation time (in seconds) comparison for FANS, SVM, ROAD and penGAM. The parallel computing technique is applied. Standard errors are in the parentheses.

Ex(ρ)	FANS	FANS(para)	SVM	ROAD	penGAM
1(0)	12.0(2.6)	3.8(0.2)	59.4(12.8)	99.1(98.2)	243.7(151.8)
1(0.5)	12.7(2.1)	3.5(0.2)	81.3(19.2)	100.7(89.3)	325.8(194.3)
2(0.5)	16.0(3.1)	4.0(0.2)	77.6(18.1)	106.8(90.7)	978.0(685.7)
2(0.9)	22.0(4.6)	4.5(0.3)	75.7(17.8)	98.3(83.9)	3451.1(3040.2)
3(0)	12.1(2.1)	3.4(0.2)	152.1(27.4)	96.3(68.8)	254.6(130.0)
3(0.5)	11.9(2.0)	3.4(0.2)	342.1(58.0)	95.9(74.8)	298.7(167.4)
4	22.4(3.9)	6.6(0.4)	264.3(45.0)	75.1(54.0)	4811.9(3991.7)

Besides the aforementioned references, there is a huge literature on high dimensional classification. Examples include principal component analysis in Bair et al. (2006) and Zou et al. (2006), partial least squares in Nguyen and Rocke (2002), Huang (2003) and Boulesteix (2004), and sliced inverse regression in Li (1991) and Antoniadis et al. (2003). Recently, there has been a surge of interest for extending the linear discriminant analysis to high-dimensional settings including Guo et al. (2007), Wu et al. (2009), Clemmensen et al. (2011), Shao et al. (2011), Cai and Liu (2011), Mai et al. (2012) and Witten and Tibshirani (2012).

The rest of the paper is organized as follows. Section 2 introduces the FANS algorithm. Section 3 is dedicated to simulation studies and real data analysis. Theoretical results are presented in Section 4. We conclude with a discussion in Section 5. Longer proofs and technical results are relegated to the Appendix.

2 Algorithm

In this section, an efficient algorithm (S1 – S5) for FANS will be introduced. We will also describe a variant of FANS (FANS2), which uses the original features in addition to the transformed ones.

2.1 FANS and its Running Time Bound

• S1Given n pairs of observations D = {(X_i, Y_i), i = 1, ⋯, n}. Randomly split the data into two parts for L times: D_l = (D_l1, D_l2), l = 1, ⋯, L.
• S2On each D_l1, l ∈ {1, ⋯, L}, apply kernel density estimation and denote the estimates by f̂ = (f̂₁, ⋯, f̂_p)^T and ĝ = (ĝ₁, ⋯, ĝ_p)^T.
• S3Calculate the transformed observations Ẑ_i = Z_{f̂, ĝ}(X_i), where Ẑ_ij = log f̂_j(X_ij) − log ĝ_j(X_ij), for each i ∈ D_l2 and j ∈ {1, ⋯, p}.
• S4Fit an L₁-penalized logistic regression to the transformed data {(Ẑ_i, Y_i), i ∈ D_l2}, using cross validation to get the best penalty parameter. For a new observation x, we estimate transformed features by log f̂_j(x_j)−log ĝ_j(x_j), j = 1, …, p, and plug them into the fitted logistic function to get the predicted probability p_l.
• S5Repeat (S2)–(S4) for l = 1, ⋯, L, use the average predicted probability $\mathit{\text{prob}}=L^{-1}{\sum }_{l=1}^L{p}_l$ as the final prediction, and assign the observation x to class 1 if prob ≥ 1/2, and 0 otherwise.

A few comments on the technical implementation are made as follows.

Remark 1

1. In S2, if an estimated marginal density is less than some threshold ε (say 10⁻²), we set it to be ε. This Winsorization increases the stability of the transformations, because the estimated transformations log f̂_j and log ĝ_j are unstable in regions where true densities are low.

2. In S4, we take penalized logistic regression, but any linear classifier can be used. For example, support vector machine (SVM) with linear kernel is also a good choice.

3. In S4, the L₁ penalty (Tibshirani, 1996) was adopted since our primary interest is the classification error. We can also apply other penalty functions, such as SCAD (Fan and Li, 2001), adaptive LASSO (Zou, 2006) and MCP (Zhang, 2010).

4. In S5, the average predicted probability is taken as the final prediction. An alternative approach is to make a decision on each random split, and listen to majority vote.

In S1, we split the data multiple times. The rationale behind multiple splitting lies in the two-step prototype nature of FANS, which uses the first part of the data for marginal nonparametric density estimates (in S2) and (transformation of) the second part for penalized logistic regression (in S4). Multiple splitting and prediction averaging not only make our procedure more robust against arbitrary assignments of data usage, but also make more efficient use of limited data. This idea is related to random forest (Breiman, 2001), where the final prediction is the average over results from multiple bootstrap samples. Other related literature includes Fu et al. (2005) which considers estimation of misclassification error with small samples via bootstrap cross-validation. The number of splits is fixed at L = 20 throughout all numerical studies. This choice reflects our cluster’s node number. Interested readers can as well leverage their better computing resources for a larger L. However, we observed that further increasing L leads to similar performance for all simulation examples. Also, we recommend a balanced assignment by switching the role of data used for feature transformation and for feature selection, i.e., D_2l = (D_(2l−1),2, D_(2l−1),1) when D_2l−1 = (D_(2l−1),1, D_(2l−1),2).

It is straightforward to derive a running time bound for our algorithm. Suppose splitting has been done. In S2, we need to perform kernel density estimation for each variable, which costs O(n²p)¹. The transformations in S3 cost O(np). In S4, we call the R package glmnet to implement penalized logistic regression, which employs the coordinate decent algorithm for each penalty level. This step has a computational cost at most O(npT), where T is the number of penalty levels, i.e., the number of times the coordinate descent algorithm is run (see Friedman et al. (2007) for a detailed analysis). The default setting is T = 100, though we can set it to other constants. Therefore, a running time bound for the whole algorithm is O(L(n²p + np + npT)) = O(Lnp(n + T)).

The above bound does not look particularly interesting. However, smart implementation of the FANS procedure can fully unleash the potential of our algorithm. Indeed, not only the L repetitions, but also the marginal density estimates in S2 can be done via parallel computing. Suppose L is the number of available nodes, and the cpu core number in each node is N ≥ n/T. This assumption is reasonable because T = 100 by default, N = 8 for our implementation, and sample sizes n for many applications are less than a multiple of TN. Under this assumption, the L predicted probabilities calculations can be carried out simultaneously and the results are combined later in S5. Moreover in S2, the running time bound becomes O(n²p/N). Henceforth, a bound for the whole algorithm will be O(npT), which is the same as that for penalized logistic regression. The exciting message here is that, by leveraging modern computer architecture, we are able to implement our nonparametric classification rule FANS within running time at the order of a parametric method. The computation times for various simulation setups are reported in Table 2, where the first column reports results when only L repetitions are paralleled, and the second column reports the improvement when marginal density estimates in S2 are paralleled within each node.

2.2 Augmenting Linear Features

As we argued in the introduction, features with no marginal discrimination power do not make contribution in FANS. One remedy is to run (in S4) the penalized logistic regression using both the transformed features and the original ones, which amounts to modeling the log odds by

$${\beta }_0+{\beta }_1\text{log}\frac{f_1(x_1)}{g_1(x_1)}+\dots +{\beta }_p\text{log}\frac{f_p(x_p)}{g_p(x_p)}+{\beta }_{p+1}{x}_1+\dots +{\beta }_{2p}{x}_p.$$

This variant of FANS is named FANS2, and it allows features with no marginal power to enter the model in a linear fashion. FANS2 helps when a linear decision boundary separates data reasonably well.

3 Numerical Studies

3.1 Simulation

In simulation studies, FANS and FANS2 are compared with competing methods: penalized logistic regression (PLR, Friedman et al. (2010)), penalized additive logistic regression models (penGAM, Meier et al. (2009)), support vector machine (SVM), regularized optimal affine discriminant (ROAD, Fan et al. (2012)), linear discriminant analysis (LDA), Naive Bayes (NB) and feature annealed independence rule (FAIR, Fan and Fan (2008)).

In all simulation settings, we set p = 1000 and training and testing data sample sizes of each class to be 300. Five-fold cross-validation is conducted when needed, and we repeat 50 times for each setting (The relative small number of replications is due to the long computation time of penGAM, c.f. Table 2). Table 1 summarizes median test errors for each method along with the corresponding standard errors. This table omits Fisher’s classifier (using pseudo inverse for sample covariance matrix), because it gives a test error around 50%, equivalent to random guessing.

Table 1.

Median test error (in percentage) for the simulation examples. Standard errors are in the parentheses.

Ex(ρ)	FANS	FANS2	ROAD	PLR	penGAM	NB	FAIR	SVM
1(0)	6.8(1.1)	6.2(1.2)	6.0(1.3)	6.5(1.2)	6.6(1.1)	11.2(1.4)	5.7(1.0)	13.2(1.5)
1(0.5)	16.5(1.7)	16.2(1.8)	16.5(5.3)	15.9(1.7)	16.9(1.6)	20.6(1.7)	17.2(1.6)	22.5(1.8)
2(0.5)	4.2(0.9)	2.0(0.6)	2.0(0.6)	2.5(0.6)	3.7(0.9)	43.5(11.1)	25.3(1.6)	5.3(1.1)
2(0.9)	3.1(1.1)	0.0(0.0)	0.0(0.0)	0.0(0.0)	0.2(1.4)	46.8(8.8)	30.2(1.9)	0.0(0.1)
3(0)	0.0(0.0)	0.0(0.0)	49.6(2.4)	50.0(1.3)	0.0(0.1)	50.4(2.2)	50.2(2.1)	31.8(2.4)
3(0.5)	3.4(0.7)	3.4(0.7)	49.3(2.4)	50.0(1.3)	3.7(0.8)	50.0(2.1)	50.2(2.0)	19.8(2.4)
4	0.0(0.0)	0.0(0.0)	28.2(1.8)	50.0(10.7)	0.0(0.0)	41.0(1.1)	34.6(1.4)	0.0(0.0)

Example 1

We consider the two class Gaussian settings where Σ_ii = 1 for all i = 1, ⋯, p and Σ_ij = ρ^|i−j|, μ₁ = 0₁₀₀₀ and ${\mathit{\mu }}_2={({\mathbf{1}}_{10}^T,{\mathbf{0}}_{990}^T)}^T$, in which 1_d is a length d vector with all entries 1, and 0_d is a length d vector with all entries 0. Two different correlations ρ = 0 and ρ = 0.5 are investigated.

This is the classical LDA setting. In view of the linear optimal decision boundary, the nonparametric transformations in FANS is not necessary. Table 1 indicates some efficiency (not much) loss due to the more complex model FANS. However, by including the original features, FANS2 is comparable to the methods (e.g., PLR and ROAD) which learn boundaries linear in original features. In other words, the price to pay for using the more complex method FANS (FANS2) is small in terms of the classification error.

An interesting observation is that penGAM, which is based on a more general model class than FANS and FANS2, performs worse than our new methods. This is also expected as the complex parameter space considered by penGAM is unnecessary in view of a linear optimal decision boundary. Surprisingly, SVM performs poorly (even worse than NB), especially when all features are independent.

Example 2

The same settings as Example 1 except the common covariance matrix is an equal correlation matrix, with a common correlation ρ = 0.5 and ρ = 0.9.

Same as in Example 1, FANS and FANS2 have performance comparable to PLR and ROAD. Although FAIR works very well in Example 1, where the features are independent (or nearly independent), it fails badly when there is significant global pairwise correlation. Similar observations also hold for NB. This example shows that ignoring correlation among features could lead to significant loss of information and deterioration in the classification error.

Example 3

One class follows a multivariate Gaussian distribution, and the other a mixture of two multivariate Gaussian distributions. Precisely,

• Class 0: $N({(3\times {\mathbf{1}}_{10}^T,{\mathbf{0}}_{p-10}^T)}^T,{\mathbf{\Sigma }}_p)$,

• Class 1: $0.5\times N({\mathbf{0}}_p,{\mathit{I}}_p)+0.5\times N({(6\times {\mathbf{1}}_{10}^T,{\mathbf{0}}_{p-10}^T)}^T,{\mathbf{\Sigma }}_p)$,

where Σ_ii = 1, Σ_ij = ρ for i ≠ j. Correlations ρ = 0 and ρ = 0.5 are considered.

In this example, Class 0 and Class 1 have the same mean, but have different marginal densities for the first 10 dimensions. Table 1 shows that all methods based on linear boundary perform like random guessing, because the optimal decision boundary is highly nonlinear. penGAM is comparable to FANS and FANS2, but SVM cannot capture the oracle decision boundary well even if a nonlinear kernel is applied.

Example 4

Two classes follow uniform distributions,

• Class 0: Unif (A),

• Class 1: Unif (B\A),

where A = {x ∈ ℝ^p : ‖x‖₂ ≤ 1} and B = [−1, 1]^p. Clearly, the oracle decision boundary is {x ∈ ℝ^p : ‖x‖₂ = 1}. Again, FANS and FANS2 capture this simple boundary well while the linear-boundary based methods fail to do so.

Computation times (in seconds) for various classification algorithms are reported in Table 2. FANS is extremely fast thanks to parallel computing. While penGAM performs similarly to FANS in the simulation examples, its computation cost is much higher. The similarity in performance is due to the abundance in training examples. We will demonstrate with an email spam classification example that penGAM fails to deliver satisfactory results on small samples.

3.2 Real Data Analysis

We study two real examples, and compare FANS (FANS2) with competing methods.

3.2.1 Email Spam Classification

First, we investigate a benchmark email spam data set. This data set has been studied by Hastie et al. (2009) among others to demonstrate the power of additive logistic regression models. There are a total of n = 4, 601 observations with p = 57 numeric attributes. The attributes are, for instance, the percentage of specific words or characters in an email, the average and maximum run lengths of upper case letters, and the total number of such letters. To show suitable application domains of FANS and FANS2, we vary the training proportion, from 5%, 10%, 20%, ⋯, to 80% of the data while assigning the rest as test set. Splits are repeated for 100 times and we report the median classification errors.

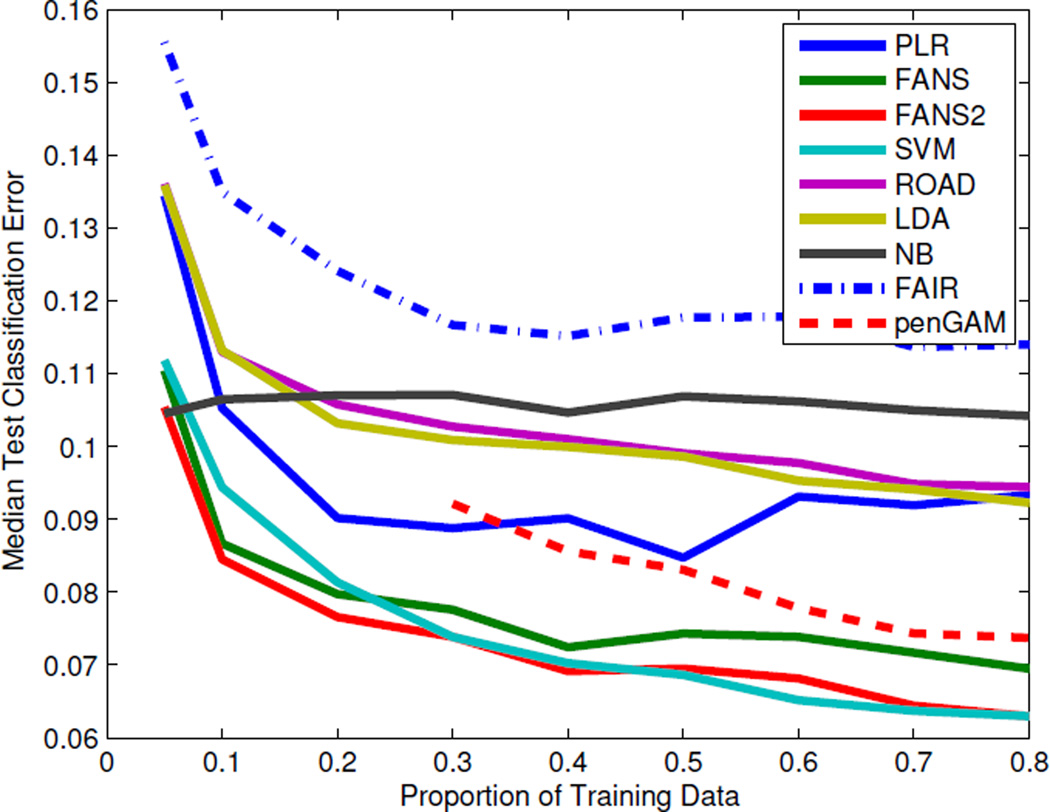
Figure 2 and Table 3 summarize the results. First, we notice that FANS and FANS2 are very competitive when training sample sizes are small. As the training sample size increases, SVM becomes comparable to FANS2 and slightly better than FANS. In general, these three methods dominate throughout different training proportions. The more complex model penGAM failed to yield classifiers when training data proportion is less than 30% due to the difficulty of matrix inversion with the splines basis functions. For larger training samples, penGAM performs better than linear decision rules; however, it is not as competitive as either FANS or FANS2. Also interestingly, when the training sample size is 5%, Naive Bayes (NB) performs as well as the sophisticated method FANS2 in terms of median classification error, but NB has a larger standard error. Moreover, the median classification error of NB remains almost unchanged when the sample size increases. In other words, NB’s independence assumption allows good training given very few data points, but it cannot benefit from larger samples due to severe model bias.

Figure 2.

The median test classification error for the spam data set using various proportions of the data as training sets for different classification methods.

Table 3.

Median classification error (in percentage) on e-mail spam data when the size of the training data varies. Standard errors are in the parentheses.

%	FANS	FANS2	ROAD	PLR	penGAM	LDA	NB	FAIR	SVM
5	11.1(2.6)	10.5(1.1)	13.6(0.9)	13.5(1.7)	-	13.6(1.1)	10.5(5.0)	15.6(1.7)	11.2(0.8)
10	8.7(2.4)	8.5(0.9)	11.3(0.8)	10.5(1.1)	-	11.3(0.9)	10.7(4.2)	13.5(0.9)	9.4(0.7)
20	8.0(2.1)	7.7(0.7)	10.6(0.6)	9.0(0.8)	-	10.3(0.6)	10.7(5.3)	12.4(0.7)	8.1(0.7)
30	7.8(1.7)	7.4(0.5)	10.3(0.4)	8.9(0.6)	9.2(0.6)	10.1(0.5)	10.7(4.0)	11.7(0.4)	7.4(0.6)
40	7.2(2.2)	6.9(0.5)	10.1(0.5)	9.0(0.6)	8.6(0.5)	10.0(0.4)	10.5(5.1)	11.5(0.6)	7.0(0.5)
50	7.4(2.2)	7.0(0.5)	9.9(0.5)	8.5(0.6)	8.3(0.5)	9.9(0.4)	10.7(4.1)	11.8(0.6)	6.9(0.5)
60	7.4(2.2)	6.8(0.5)	9.8(0.6)	9.3(0.6)	7.8(0.6)	9.5(0.5)	10.6(4.8)	11.8(0.7)	6.5(0.6)
70	7.2(1.6)	6.4(0.6)	9.5(0.7)	9.2(0.7)	7.4(0.7)	9.4(0.6)	10.5(4.6)	11.4(0.7)	6.4(0.7)
80	6.9(1.6)	6.3(0.7)	9.4(0.6)	9.3(0.9)	7.4(0.8)	9.2(0.6)	10.4(4.7)	11.4(0.8)	6.3(0.9)

3.2.2 Lung Cancer Classification

We now evaluate the newly proposed classifiers on a popular gene expression data set “Lung Cancer” (Gordon et al., 2002), which comes with predetermined, separate training and test sets. It contains p = 12, 533 genes for n₀ = 16 adenocarcinoma (ADCA) and n₁ = 16 mesothelioma training vectors, along with 134 ADCA and 15 mesothelioma test vectors.

Following Dudoit et al. (2002), Fan and Fan (2008), and Fan et al. (2012), we standardized each sample to zero mean and unit variance. The classification results for FANS, FANS2, ROAD, penGAM, NB, FAIR and SVM are summarized in Table 4. FANS and FANS2 achieve 0 test classification error, while the other methods fail to do so.

Table 4.

Classification error and number of selected genes on lung cancer data.

	FANS	FANS2	ROAD	PLR	penGAM	NB	FAIR	SVM
Training Error	0	0	1	0	0	6	0	0
Testing Error	0	0	1	6	2	36	7	4
No. of selected genes	52	52	52	15	16	12533	54	12533

4 Theoretical Results

In this section, an oracle inequality regarding the excess risk is derived for FANS. Denote by f = (f₁, ⋯, f_p)^T and g = (g₁, ⋯, g_p)^T vectors of marginal densities of each class with f₀ = (f_0,1, ⋯, f_0,p)^T and g₀ = (g_0,1, ⋯, g_0,p)^T being the true densities. Let ${\{({\mathit{X}}_i,Y_i)\}}_{i=1}^n$ be i.i.d. copies of (X, Y), and the regression function be modeled by

$$P(Y_1=1|{\mathit{X}}_1)=\frac{1}{1+\text{exp}(-m({\mathit{Z}}_1))},$$

where Z₁ = (Z₁₁, ⋯, Z_1p)^T, each Z_1j = Z_1j(X₁) = log f_j(X_1j) − log g_j(X_1j), and m(·) is a generic function in some function class ℳ that includes the linear functions. Now, let 𝒬 = {q = (m, f, g)} be the parameter space of interest with constraints on m, f and g be specified later. The loss function we consider is

$$\rho (q)=\rho (m,\mathit{f},\mathit{g})={\rho }_q({\mathit{X}}_1,Y_1)=-Y_{1}m({\mathit{Z}}_1)+\text{log}(1+\text{exp}[m({\mathit{Z}}_1)]).$$

Let m₀ = arg min_m∈ℳ Pρ(m, f₀, g₀). Then the target parameter is q* = (m₀, f₀, g₀). We use a working model with m_β(Z₁) = β^TZ₁ to approximate m₀. Under this working model, for a given parameter q = (m_β, f, g), let

$${\pi }_q({\mathit{X}}_1)=P(Y_1=1|{\mathit{X}}_1)=\frac{1}{1+\text{exp}(-{\mathit{\beta }}^T{\mathit{Z}}_1)}.$$ (4.4)

With this linear approximation, the loss function is the logistic loss

$$\rho (q)={\rho }_q({\mathit{X}}_1,Y_1)=-Y_1{\mathit{\beta }}^T{\mathit{Z}}_1+\text{log}(1+\text{exp}[{\mathit{\beta }}^T{\mathit{Z}}_1]).$$

Denote the empirical loss by $P_n\rho (q)={\sum }_{i=1}^n{\rho }_q({\mathit{X}}_i,Y_i)/n$, and the expected loss by Pρ(q) = Eρ_q(X, Y). In the following, we take ℳ as linear combinations of the transformed features so that m₀ = m_β0, where

$${\mathit{\beta }}_0=\text{arg}\underset{\mathit{\beta }\in {ℝ}^p}{\text{min}}P\rho (m_{\mathit{\beta }},{\mathit{f}}_0,{\mathit{g}}_0).$$

In other words, q₀ = (m_β0, f₀, g₀) = q*. Hence, the excess risk for a parameter q is

$$ℰ(q)=P[\rho (q)-\rho (q^{*})]=P[\rho (q)-\rho (q_0)].$$ (4.5)

As described in Section 2, densities f₀ and g₀ are unavailable and must be estimated. Theorem 2 will establish the excess risk bound for the L = 1 base procedure, which implies that the logistic regression coefficient and density estimates are close to the corresponding true values. Therefore, we expect for each l = 1, ⋯, L, the predicted probability p_l is close to the oracle π_q*(·). This further implies that $p=1/L{\sum }_{l=1}^L{p}_l$ is close to π_q*(·). Given the above analysis, we fix L = 1 in the FANS algorithm (i.e., only one random splitting is conducted) throughout the theoretical development.

Suppose we have labeled samples $\{{\mathit{X}}_1^{+},\cdots ,{\mathit{X}}_{n_1}^{+}\}$ (used to learn f₀) and $\{{\mathit{X}}_1^{-},\cdots ,{\mathit{X}}_{n_1}^{-}\}$ (used to learn g₀; theory carries over for different sample sizes), in addition to an i.i.d. sample {(X₁, Y₁), ⋯, (X_n, Y_n)} (used to conduct penalized logistic regression). Moreover, suppose {(X₁, Y₁), ⋯, (X_n, Y_n)} is independent of $\{{\mathit{X}}_1^{+},\cdots ,{\mathit{X}}_{n_1}^{+}\}$ and $\{{\mathit{X}}_1^{-},\cdots ,{\mathit{X}}_{n_1}^{-}\}$. A simple way to comprehend the above theoretical set up is that the sample size of 2n₁ + n has been split into three groups. The notations P and E are regarding the random couple (X, Y). We use the notation Pⁿ to denote the probability measure induced by the sample {(X₁, Y₁), ⋯, (X_n, Y_n)}, and notations P⁺ and P⁻ for the probability measures induced by the samples $\{{\mathit{X}}_1^{+},\cdots ,{\mathit{X}}_{n_1}^{+}\}$ and $\{{\mathit{X}}_1^{-},\cdots ,{\mathit{X}}_{n_1}^{-}\}$.

The density estimates f̂ = (f̂₁, ⋯, f̂_p)^T and ĝ = (ĝ₁, ⋯, ĝ_p)^T are based on samples $\{{\mathit{X}}_1^{+},\cdots ,{\mathit{X}}_{n_1}^{+}\}$ and $\{{\mathit{X}}_1^{-},\cdots ,{\mathit{X}}_{n_1}^{-}\}$:

$${\hat{f}}_j(x)=\frac{1}{n_{1}h}\sum _{i=1}^{n_1}K\left(\frac{X_{ij}^{+}-x}{h}\right)\text{and}{ĝ}_j(x)=\frac{1}{n_{1}h}\sum _{i=1}^{n_1}K\left(\frac{X_{ij}^{-}-x}{h}\right)\text{for}j=1,\cdots ,p,$$

in which K(·) is a kernel function and h is the bandwidth. Then with these estimated marginal densities, we have an “oracle estimate” q₁ = (β₁, f̂, ĝ), where

$${\mathit{\beta }}_1=\text{arg}\underset{\mathit{\beta }\in {ℝ}^p}{\text{min}}P\rho (m_{\mathit{\beta }},\hat{\mathit{f}},\mathit{ĝ}).$$

It is the oracle given marginal density estimates f̂ and ĝ, and is estimated in FANS by

$${\hat{\mathit{\beta }}}_1=\text{arg}\underset{\mathit{\beta }\in {ℝ}^p}{\text{min}}{P}_n\rho (m_{\mathit{\beta }},\hat{\mathit{f}},\mathit{ĝ})+\lambda {\Vert \mathit{\beta }\Vert }_1.$$

Let q̂₁ = (m_β̂1, f̂, ĝ). Our goal is to control the excess risk ℰ(q̂₁), where ℰ is defined by (4.5). In the following, we introduce technical conditions for this task.

Let Z⁰ be the n × p design matrix consisting of transformed covariates based on the true densities f₀ and g₀. That is $Z_{ij}^0=\text{log}{f}_{0,j}(X_{ij})-\text{log}{g}_{0,j}(X_{ij})$, for i = 1, ⋯, n and j = 1, ⋯, p. In addition, let ${\mathit{Z}}^0={({\mathit{Z}}_1^0,{\mathit{Z}}_2^0,\dots ,{\mathit{Z}}_n^0)}^T$. Also, denote by |S| the cardinality of the set S, and by ‖D‖_max = max_ij |D_ij| for any matrix D with elements D_ij.

Assumption 1 (Compatibility Condition)

The matrix Z⁰ satisfies compatibility condition with a compatibility constant ϕ(·), if for every subset S ⊂ {1, ⋯, p}, there exists a constant ϕ(S), such that for all β ∈ ℝ^p that satisfy ‖β_S^c‖₁ ≤ 3‖β_S‖₁, it holds that

$${\Vert {\mathit{\beta }}_S\Vert }_1^2\le \frac{1}{n{\varphi }^2(S)}{\Vert {\mathit{Z}}^0\mathit{\beta }\Vert }^2|S|.$$

A direct application of Corollary 6.8 in Bühlmann and van de Geer (2011) leads to a compatibility condition on the estimated transform matrix Ẑ, in which Ẑ_ij = log f̂_j(X_ij) − log ĝ_j(X_ij).

Lemma 1

Denote by E = Ẑ − Z₀ the estimation error matrix of Z₀. If the compatibility condition is satisfied for Z₀ with a compatibility constant ϕ(·), and the following inequalities hold

$$\frac{32{\Vert \mathit{E}\Vert }_{\text{max}}|S|}{\varphi {(S)}^2}\le 1,\mathit{\text{for every}}S\subset \{1,\cdots ,p\},$$ (4.6)

the compatibility condition holds for Ẑ with a new compatibility constant ${\varphi }_1(·)\ge \varphi (·)/\sqrt{2}$.

The Compatibility Condition can be interpreted as a condition that bounds the restricted eigenvalues. The irrepresentable condition (Zhao and Yu, 2006) and the Sparse Riesz Condition (SRC) (Zhang and Huang, 2008) are in similar spirits. Essentially, these conditions avoid high correlation among subsets where signals are concentrated; such high correlation may cause difficulty in parameter estimation and risk prediction.

To help theoretical derivation, we introduce two intermediate L₀-penalized estimates. Given the true densities f₀ and g₀, consider a penalized theoretical solution $q_0^{*}=({\mathit{\beta }}_0^{*},{\mathit{f}}_0,{\mathit{g}}_0)$, where

$${\mathit{\beta }}_0^{*}=\text{arg}\underset{\mathit{\beta }\in {ℝ}^p}{\text{min}}3P\rho (m_{\mathit{\beta }},{\mathit{f}}_0,{\mathit{g}}_0)+2H\left(\frac{4\lambda \sqrt{s_{\mathit{\beta }}}}{\varphi (S_{\mathit{\beta }})}\right),$$ (4.7)

in which H(·) is a strictly convex function on [0,∞) with H(0) = 0, s_β = |S_β| is the cardinality of S_β = {j : β_j ≠ 0}, and ϕ(·) is the compatibility constant for Z⁰. Throughout the paper, we consider a specific quadratic function² H(υ) = υ² / (4c) whose convex conjugate is G(u) = sup_υ{uυ − H(υ)} = cu². Then, equation (4.7) defines an L₀-penalized oracle:

$${\mathit{\beta }}_0^{*}=\text{arg}\underset{\mathit{\beta }\in {ℝ}^p}{\text{min}}3P\rho (m_{\mathit{\beta }},{\mathit{f}}_0,{\mathit{g}}_0)+\frac{8{\lambda }^2{s}_{\mathit{\beta }}}{c{\varphi }^2(S_{\mathit{\beta }})}.$$ (4.8)

Similarly, with density estimate vectors f̂ and ĝ, we define an L₀-penalized oracle estimate $q_1^{*}=(m_{{\mathit{\beta }}_1^{*}},\hat{\mathit{f}},\mathit{ĝ})$, where

$${\mathit{\beta }}_1^{*}=\text{arg}\underset{\mathit{\beta }\in {ℝ}^p}{\text{min}}3P\rho (m_{\mathit{\beta }},\hat{\mathit{f}},\mathit{ĝ})+\frac{8{\lambda }^2{s}_{\mathit{\beta }}}{c{\varphi }_1^2(S_{\mathit{\beta }})}.$$ (4.9)

To study the excess risk ℰ(q̂₁), we consider its relationship with $ℰ(q_1^{*})$ and $ℰ(q_0^{*})$.

Assumption 2 (Uniform Margin Condition)

There exists η > 0 such that for all (m_β, f, g) satisfying ‖β − β₀‖_∞ + max_1≤j≤p ‖f_j − f_0,j‖_∞ + max_1≤j≤p ‖g_j − g_0,j‖_∞ ≤ 2η, we have

$$ℰ(m_{\mathit{\beta }},\mathit{f},\mathit{g})\ge c{\Vert \mathit{\beta }-{\mathit{\beta }}_0\Vert }_2^2,$$ (4.10)

where c is the positive constant in (4.8).

The uniform margin condition is related to the one defined in Tsybakov (2004) and van de Geer (2008). It is a type of “identifiability” condition. Basically, near the target parameter q₀ = (m_β0, f₀, g₀), the functional value needs to be sufficiently different from the value on q₀ to enable enough separability of parameters. Note that we impose the uniform margin condition in both the neighborhood of the parametric component β₀ and the nonparametric components f₀ and g₀, because we need to estimate the densities, in addition to the parametric part. A related concept in binary classification is called “Margin Assumption”, which was first introduced in Polonik (1995) for densities.

To study the relationship between ℰ(q̂₁) and $ℰ(q_1^{*})$, we define

$${\upsilon }_n(\mathit{\beta })=(P_n-P)\rho (m_{\mathit{\beta }},\hat{\mathit{f}},\mathit{ĝ})\text{and}{W}_M=\underset{\Vert \mathit{\beta }-{\mathit{\beta }}_1^{*}\Vert \le M}{\text{sup}}|{\upsilon }_n(\mathit{\beta })-{\upsilon }_n({\mathit{\beta }}_1^{*})|.$$

Denote by

$$2{\epsilon }^{*}=3ℰ(m_{{\mathit{\beta }}_1^{*}},\hat{\mathit{f}},\mathit{ĝ})+\frac{8{\lambda }^2{s}_{{\mathit{\beta }}_1^{*}}}{c{\varphi }_1^2(S_{{\mathit{\beta }}_1^{*}})}.$$

Set M* = ε*/λ₀ (λ₀ to specified in Theorem 1) and

$${𝒥}_1=\{W_{M*}\le {\lambda }_0{M}^{*}\}=\{W_{M*}\le {\epsilon }^{*}\}.$$

The idea here is to choose λ₀ such that the event 𝒥₁ has high probability.

A few more notations are introduced to facilitate the discussion. Let τ > 0. Denote by ⌊τ⌋ the largest integer strictly less than τ. For any x, x′ ∈ ℝ and any ⌊τ⌋ times continuously differentiable real valued function u on ℝ, we denote by u_x its Taylor polynomial of degree ⌊τ⌋ at point x:

$$u_x(x\prime )=\sum _{|s|\le \lfloor \tau \rfloor }\frac{{(x\prime -x)}^s}{s!}{D}^{s}u(x).$$

For L > 0, the (τ, L, [−1, 1])-Hölder class of functions, denoted by Σ(τ, L, [−1, 1]), is the set of functions u : ℝ → ℝ that are ⌊τ⌋ times continuously differentiable and satisfy, for any x, x′ ∈ [−1, 1], the inequality:

$$|u(x\prime )-u_x(x\prime )|\le L{|x-x\prime |}^{\tau }.$$

The (τ, L, [−1, 1])-Hölder class of density is defined as

$${𝒫}_{\mathrm{\Sigma }}(\tau ,L,[-1,1])=\{p:p\ge 0,\int p=1,p\in \mathrm{\Sigma }(\tau ,L,[-1,1])\}.$$

Assumption 3

Assume that β₁ is in the interior of some compact set 𝒞_p. There exists an ε₀ ∈ (0, 1) such that for all β ∈ 𝒞_p and f_j, g_j ∈ 𝒫_Σ(2, L, [−1, 1]), j = 1, ⋯, p, ε₀ < π_(mβ,f,g)(·) < 1 − ε₀.

Assumption 4

‖Z⁰‖_max ≤ K for some absolute constant K > 0, and ‖β₀‖_∞ ≤ C₁ for some absolute constant C₁ > 0.

Assumption 5

The penalty level λ is in the range of (8λ₀, Lλ₀) for some L > 8. Moreover, the following holds

$$\frac{8K{L}^2{(e^{\eta }/{\epsilon }_0+1)}^2}{\eta }\frac{{\lambda }_0{s}_{{\mathit{\beta }}_1^{*}}}{{\varphi }_1^2(S_{{\mathit{\beta }}_1^{*}})}\le 1,$$

where η is as in the uniform margin condition.

Assumption 3 is a regularity condition on the probability of the event that the observation belongs to class 1. Since the FANS estimator is based on the estimated densities, we impose the constraints in a neighborhood of the oracle estimate β₁ (when using f̂ and ĝ). Assumption 4 bounds the maximum absolute entry of the design matrix as well as the maximum absolute true regression coefficient. Assumption 5 posits a proper range of the penalty parameter λ to guarantee that the penalized estimator mimics the un-penalized oracle.

Assumption 6

Suppose the feature measurement X has a compact support [−1, 1]^p, and f_0,j, g_0,j ∈ 𝒫_Σ(2, L, [−1, 1]) for all j = 1, ⋯, p, where 𝒫_Σ denotes a Hölder class of densities.

Assumption 7

Suppose there exists ε_l > 0 such that for all j = 1, ⋯, p, ε_l ≤ f_0,j, $g_{0,j}\le {\epsilon }_l^{-1}$. Also we truncate estimates f̂_j and ĝ_j at ε_l and ${\epsilon }_l^{-1}$.

Assumption 8

$$n_1^{\frac{7}{20}-\frac{3}{4}\alpha }{(\text{log}(3p))}^{\frac{3}{4}}{(\text{log}{n}_1)}^{\frac{1}{10}}=o(1),$$

and,

$$n_1^{\frac{1}{10}-\alpha }{(\text{log}(3p))}^{\frac{1}{2}}{(\text{log}{n}_1)}^{\frac{2}{5}}=o(1),$$

for some constant α > 7/15.

Assumption 6 imposes constraints on the support of X and smoothness condition on the true densities f₀ and g₀, which help control the estimation error incurred by the nonparametric density estimates. Assumption 7 assumes that the marginal densities and the kernel are strictly positive on [−1, 1]^p. Assumption 8 puts a restriction on the growth of the dimensionality p in terms of sample size n₁.

We now provide a lemma to bound the uniform deviation between f̂_j and f_0,j for j = 1, ⋯, p.

Lemma 2

Under Assumptions 6–8, taking the bandwidth $h={\left(\frac{\text{log}{n}_1}{n_1}\right)}^{1/5}$, for any δ₁ > 0, there exists $N_1^{*}$ such that if $n_1\ge N_1^{*}$,

$$P^{+-}(\underset{1\le j\le p}{\text{max}}{\Vert {\hat{f}}_j-f_{0,j}\Vert }_{\infty }\ge m)\le {\delta }_1,\mathit{\text{and}}{P}^{+-}(\underset{1\le j\le p}{\text{max}}{\Vert {ĝ}_j-g_{0,j}\Vert }_{\infty }\ge m)\le {\delta }_1,$$

for $m=C_2\sqrt{\frac{2\text{log}(3p/{\delta }_1)}{n_1^{1-\alpha }}}$, and C₂ is an absolute constant.

Denote by

$${𝒥}_2=\{\underset{1\le j\le p}{\text{max}}{\Vert {\hat{f}}_j-f_{0,j}\Vert }_{\infty }\le \eta /2,\underset{1\le j\le p}{\text{max}}{\Vert {ĝ}_j-g_{0,j}\Vert }_{\infty }\le \eta /2\},$$

where η is the constant in the uniform margin condition. It is straightforward from Lemma 2 that

$$P^{+-}({𝒥}_2)\ge 1-\frac{6p}{\text{exp}({\eta }^2{n}_1^{1-\alpha }/4C_2^2)}.$$

The next lemma can be similarly derived as Lemma 2, so its proof is omitted.

Lemma 3

Under Assumptions 6–8, taking the bandwidth $h={\left(\frac{\text{log}{n}_1}{n_1}\right)}^{1/5}$, for any δ > 0, there exists $N_2^{*}$ such that if $n_1\ge N_2^{*}$,

$$P^{+-}({\Vert \mathit{E}\Vert }_{\text{max}}\ge m)\le \delta ,$$

where E is the estimation error matrix as defined in Lemma 1 and $m=C_3\sqrt{\frac{2\text{log}(3p/\delta )}{n_1^{1-\alpha }}}$ for some absolute constant C₃.

Corollary 1

Under Assumptions 6–8, take the bandwidth $h={\left(\frac{\text{log}{n}_1}{n_1}\right)}^{1/5}$. On the event ${𝒥}_3=\{{\Vert \mathit{E}\Vert }_{\text{max}}\le C_3\sqrt{\frac{2\text{log}(3p/\delta )}{n_1^{1-\alpha }}}\}$ (regarding labeled samples) with P⁺⁻(𝒥₃) > 1 − δ, there exists $N_2^{*}\in \mathbb{N}$ and C₄ > 0 such that if $n_1\ge N_2^{*},|F_{kl}|=|{Ẑ}_{1k}-Z_{1k}^0|·|{Ẑ}_{1l}-Z_{1l}^0|\le C_4{b}_{n_1}$ uniformly for k, l = 1, ⋯, p, where $b_{n_1}=2\text{log}(3p/\delta )/n_1^{1-\alpha }$. Denote by

$${𝒥}_4=\{32{\Vert \mathit{E}\Vert }_{\text{max}}\underset{S\subset \{1,\dots ,p\}}{\text{max}}\frac{|S|}{\varphi {(S)}^2}\le 1\}.$$

On the event 𝒥₄, the inequality (4.6) holds, and the compatibility condition is satisfied for Ẑ if we assume Assumption 1 (by Lemma 1). Moreover, it can be derived from Lemma 3 by taking a specific δ,

$$P^{+-}({𝒥}_4)\ge 1-3p\text{exp}\{-n_1^{1-\alpha }/(2048C_3^2{A}_p^2)\},$$

where A_p = max_{S⊂{1,⋯,p}}|S|/ϕ(S)². Combining Lemma 2 and the uniform margin condition, we see that for given estimators f̂ and ĝ, the margin condition holds for the estimated transformed matrix Ẑ involved in the FANS estimator β̂¹. Following similar lines as in van de Geer (2008) delivers the following theorem, so a formal proof is omitted.

Theorem 1 (Oracle Inequality)

In addition to Assumptions 1–8, assume ${\Vert m_{{\mathit{\beta }}_1^{*}}-m_{{\mathit{\beta }}_0}\Vert }_{\infty }\le \eta /2$ and $ℰ(m_{{\mathit{\beta }}_1^{*}},\hat{\mathit{f}},\mathit{ĝ})/{\lambda }_0\le \eta /4$. Then on the event 𝒥₁ ∩ 𝒥₂ ∩ 𝒥₃ ∩ 𝒥₄, we have

$$ℰ(m_{{\hat{\mathit{\beta }}}_1},\hat{\mathit{f}},\mathit{ĝ})+\lambda {\Vert {\hat{\mathit{\beta }}}_1-{\mathit{\beta }}_1^{*}\Vert }_1\le 6ℰ(m_{{\mathit{\beta }}_1^{*}},\hat{\mathit{f}},\mathit{ĝ})+\frac{16{\lambda }^2{s}_{{\beta }_1^{*}}{(e^{\eta }/{\epsilon }_0+1)}^2}{c{\varphi }_1^2(S_{{\beta }_1^{*}})}.$$

Moreover, when $n_1\ge \text{max}(N_1^{*},N_2^{*})$ and under the normalization condition that ‖Z_1j‖_∞ ≤ 1 for all j = 1, ⋯, p, it holds that

$$\mathbb{P}({𝒥}_1\cap {𝒥}_2\cap {𝒥}_3\cap {𝒥}_4)\ge 1-\text{exp}(-t)-6p\text{exp}\{-{\eta }^2{n}_1^{1-\alpha }/(4C_2^2)\}-\delta -3p\text{exp}\{-n_1^{1-\alpha }/(2048C_3^2{A}_p^2)\},$$

for

$${\lambda }_0:=4{\lambda }^{*}+\frac{tK}{3n}+\sqrt{\frac{2t}{n}(1+8{\lambda }^{*})},$$

where 𝕡 is the probability with regards to all the samples and

$${\lambda }^{*}=\sqrt{\frac{2\text{log}(2p)}{n}}+\frac{K\text{log}(2p)}{3n}.$$

Theorem 1 shows that with high probability, the excess risk of the FANS estimator can be controlled in terms of the excess risk of $q_1^{*}$ when using the estimated density functions f̂ and ĝ plus a term of explicit order. Next, we will study the excess risk of $q_1^{*}$.

Assumption 9

Let ${\mathit{Z}}_1^0({\mathit{\beta }}_1)$ be the subvector of ${\mathit{Z}}_1^0$ corresponding to the nonzero components of β₁, and $b_{n_1}=\text{log}(3p/{\delta }_1)/n_1^{1-\alpha }$. Assume s_β1 ≤ a_n1 for some deterministic sequence {a_n1}, and a_n1 · b_n1 = o(1). In addition, $0<C_5\le {\lambda }_{\text{min}}(P\{{\mathit{Z}}_1^0({\mathit{\beta }}_1){\mathit{Z}}_1^0{({\mathit{\beta }}_1)}^T\})$, for some absolute constant C₅.

Assumption 9 allows the number of nonzero elements of β₁ to diverge at a slow rate with n₁. Also, it demands a lower bound of the restricted eigenvalue of the sub-matrix of Z⁰ corresponding to the nonzero components of β₁.

Lemma 4

Let Q(β) = Pρ(m_β, f̂, ĝ) + λ‖β‖₀, and β̄₁ = min{|β_1,j| : j ∈ S_β1}. Under Assumptions 3, 6, 7, 8 and 9, on the event 𝒥₃, there exists a constant $N_3^{*}$ such that, if $n_1\ge N_3^{*}$ and the penalty parameter $\lambda <0.5C_5{\epsilon }_0(1-{\epsilon }_0){\overline{\mathit{\beta }}}_1^2$, the L₀ penalized solution coincides with the unpenalized version; that is ${\mathit{\beta }}_1^{*}={\mathit{\beta }}_1$.

Theorem 2 (Oracle Inequality)

In addition to Assumptions 1–9, suppose $4C_1{C}_4{s}_{{\mathit{\beta }}_0}^2{b}_{n_1}\le {\lambda }_0\eta$, the penalty parameter λ ∈ (8λ₀, min(Lλ₀, 0.5C₅ε₀(1 − ε₀) · min_j:β1,j ≠0(|β_1,j|))), where C₅ is defined in Assumption 9, ${\Vert m_{{\mathit{\beta }}_1^{*}}-m_{{\mathit{\beta }}_0}\Vert }_{\infty }\le \eta /2$ and $n_1\ge \text{max}(N_1^{*},N_2^{*},N_3^{*})$. Taking the bandwidth $h={\left(\frac{\text{log}{n}_1}{n_1}\right)}^{1/5}$, on the event 𝒥₁ ∩ 𝒥₂ ∩ 𝒥₃ ∩ 𝒥₄ as in Theorem 1, we have

$$ℰ(m_{{\mathit{\beta }}_1^{*}},\hat{\mathit{f}},\mathit{ĝ})\le C_1{C}_4{s}_{{\mathit{\beta }}_0}^2{b}_{n_1}.$$

Then in view of Theorem 1, we have

$$ℰ(m_{{\hat{\mathit{\beta }}}_1},\hat{\mathit{f}},\mathit{ĝ})\le \frac{16{\lambda }^2{s}_{{\beta }_1}^{*}{(e^{\eta }/{\epsilon }_0+1)}^2}{c{\varphi }_1^2(S_{{\beta }_1^{*}})}+6C_1{C}_4{s}_{{\mathit{\beta }}_0}^2{b}_{n_1}.$$

This theorem finale requires quite some conditions. We now de-convolute them by providing a high level description of the motivations behind these conditions. Because FANS is essentially a two step procedure, we need both steps to do well in order to have the theoretical performance guarantee. The first step is to estimate the transformed features. In this step, we need regularity conditions on the class conditional densities f₀ and g₀, and regularity conditions on the kernel density estimate components, such as the kernel K. Also, the sample size need to be big enough so that the kernel density estimate is close to the truth. The second step is penalized logistic regression using the estimated transformed features. In this step, usual conditions on the penalty level, design matrix and signal strength are needed. Moreover, some conditions that link nonparametric and parametric components, i.e., the first and second steps, such as the uniform margin condition should be in place.

From Theorem 2, it is clear that the excess risk of the FANS estimator is naturally decomposed into two parts. One part is due to the nonparametric density estimation while the other part is due to the regularized logistic regression on the estimated transformed covariates. When both the penalty parameter λ and the bandwidth h of the nonparametric density estimates f̂ and ĝ are chosen appropriately, the FANS estimator will have a diminishing excess risk with high probability. Note that one can make explicit λ to obtain a bound on the excess risk in terms of the sample sizes n and n₁, and the dimensionality p. Also, it is worth noting that the development of oracle inequality of the FANS procedure β̂₁ is accomplished via an important bridge of the L₀-regularized estimator ${\mathit{\beta }}_1^{*}$.

The oracle inequality for FANS2 can be developed along similar lines. In particular, the parameter under the working model will be changed to q₂ = (m_(β,γ), f, g) and the success probability given X₁ will be modeled by a modified logistic function

$${\pi }_{q_2}({\mathit{X}}_1)=P(Y_1=1|{\mathit{X}}_1)=\frac{1}{1+\text{exp}(-{\mathit{\beta }}^T{\mathit{Z}}_1-{\mathit{\gamma }}^T{\mathit{X}}_1)},$$ (4.11)

where we note that in addition to the transformed features, the original features are also included. We would like to emphasize that X₁ is observed and therefore there is no need to control its estimation error as we did for Z₁. The conditions for the theory of FANS can be adapted to establish an oracle inequality for FANS2. We omit the details to avoid duplication of similar conditions and arguments.

5 Discussion

We propose a new two-step nonlinear rule FANS (and its variant FANS2) to tackle binary classification problems in high-dimensional settings. FANS first augments the original feature space by leveraging flexibility of nonparametric estimators, and then achieves feature selection through regularization (penalization). It combines linearly the best univariate transforms that essentially augment the original features for classification. Since nonparametric techniques are only performed on each dimension, we enjoy a flexible decision boundary without suffering from the curse of dimensionality. An array of simulation and real data examples, supported by an efficient parallelized algorithm, demonstrate the competitive performance of the new procedures.

To verify our methods’ performance against model misspecification, we evaluate different classifiers on the following example that has non-additive optimal decision boundary. Similar to Example 4, FANS and FANS2 perform the best among all competing methods (penGAM performs slightly worse with a larger standard error).

Example 5

Non-additive decision boundary. In particular, for x ~ N(0_p, I_p), let $y=1\mathrm{I}\{x_1^2\sqrt{x_2^2+x_3^4+1}\ge 0.75\}$.

One problem in applications we are faced with is whether we should use FANS or FANS2. While we do not have a universal rule, a rule of thumb might shed some insight. From the simulation examples, we see when the sample size is small and/or decision boundary is highly nonlinear, FANS is recommended over FANS2. Otherwise, FANS2 is recommended. Admittedly, in real data applications, it is often impossible to know a priori how the oracle decision boundary looks like. Data abundance can be a rough guideline in these scenarios.

A few extensions are worth further investigation. For example, an extension to multi-class classification is an interesting future work. Beyond a specific procedure, FANS establishes a general two-step classification framework. For the first step, one can use other types of marginal density estimators, e.g., local polynomial density estimates. For the second step, one might rely on other classification algorithms, e.g., the support vector machine, k-nearest neighbors, etc. Searching for the best two-step combination is an important but difficult task, and we believe that the answer mainly depends on the specific applications.

We can further augment the features by adding pairwise bivariate density ratios. These bivariate densities can be approximated by the bivariate kernel density estimates. Alternatively, we can restrict our attention to bivariate ratios of features selected by FANS. The latter has significantly fewer features.

Dimensions of data sets (e.g., SNPs) in many contemporary applications could be in millions. In such ultra-high dimensional scenarios, directly applying the FANS (FANS2) approach could cause problems due to high computational complexity and instability of the estimation. It will be beneficial to have a prior step to reduce the dimensionality in the original data. Notable works towards this effort on the theoretical front include Fan and Lv (2008), which introduced the sure independence screening (SIS) property to screen out the marginally unimportant variables. Subsequently, Fan et al. (2011) proposed nonparametric independence screening (NIS), an extension of SIS to the additive models.

Table 5.

Median test error (in percentages) for Example 5. Standard errors are in the parentheses.

Ex	FANS	FANS2	ROAD	PLR	penGAM	NB	FAIR	SVM
5	6.7(1.1)	6.9(1.1)	50.2(2.1)	50.0(1.4)	8.0(2.3)	50.2(2.3)	49.7(2.1)	50.0(2.0)

Appendix

The appendix contains technical proofs and Lemma 5.

Proof of Lemma 2

For any r, m > 0,

$$P^{+-}(\underset{1\le j\le p}{\text{max}}{\Vert {\hat{f}}_j-f_{0,j}\Vert }_{\infty }\ge m)\le e^{-rm}{E}^{+-}\text{exp}\left(\underset{1\le j\le p}{\text{max}}r{\Vert {\hat{f}}_j-f_{0,j}\Vert }_{\infty }\right)=e^{-rm}{E}^{+-}\left(\underset{1\le j\le p}{\text{max}}\text{exp}r{\Vert {\hat{f}}_j-f_{0,j}\Vert }_{\infty }\right)\le e^{-rm}\sum _{j=1}^p{E}^{+-}\left(\text{exp}r{\Vert {\hat{f}}_j-f_{0,j}\Vert }_{\infty }\right).$$

Since we assumed that all f̂_j and f_0,j are uniformly bounded by ${\epsilon }_l^{-1}$, ‖f̂_j − f_0,j‖_∞ is bounded by ${\epsilon }_l^{-1}$ for all j ∈ {1, ⋯, p}. This coupled with Lemma 1 in Tong (2013), provides a high probability bound for ‖f̂_j − f_0,j‖_∞, gives rise to the following inequality,

$$E^{+-}\text{exp}\left(r{\Vert {\hat{f}}_j-f_{0,j}\Vert }_{\infty }\right)\le \text{exp}\left(r\sqrt{\frac{\text{log}(n_1/{\delta }_2)}{n_{1}h}}\right)+\text{exp}(r{\epsilon }_l^{-1})·{\delta }_2,$$

where δ₂ plays the role of ε in Lemma 1 of Tong (2013)(taking constant C = 1 for simplicity).

Finding the optimal order for r does not seem to be feasible. So we plug in $r=n_1^{1-\alpha }m$ and ${\delta }_2=\text{exp}(-r{\epsilon }_l^{-1})$, then

$$P^{+-}(\underset{1\le j\le p}{\text{max}}{\Vert {\hat{f}}_j-f_{0,j}\Vert }_{\infty }\ge m)\le p\text{exp}(-n_1^{1-\alpha }{m}^2)\{1+\text{exp}(n_1^{1-\alpha }m\sqrt{\frac{\text{log}{n}_1}{n_{1}h}+\frac{n_1^{1-\alpha }m{\epsilon }_l^{-1}}{n_{1}h}}\left)\right\}\le p\text{exp}(-n_1^{1-\alpha }{m}^2)\{1+\text{exp}[\sqrt{2}{n}_1^{1-\alpha }m\left(\sqrt{\frac{\text{log}{n}_1}{n_{1}h}+}\sqrt{\frac{m{\epsilon }_l^{-1}}{n_1^{\alpha }h}}\right)\left]\right\}\le p\text{exp}(-n_1^{1-\alpha }{m}^2)\{1+\text{exp}[\sqrt{2}{n}_1^{1-\alpha }m{\left(\frac{\text{log}{n}_1}{n_1}\right)}^{\frac{2}{5}}+\sqrt{2}{m}^{\frac{3}{2}}{\epsilon }_l^{-\frac{1}{2}}{n}_1^{\frac{11}{10}-\frac{3}{2}\alpha }{(\text{log}{n}_1)}^{\frac{1}{10}}\left]\right\},$$

where in the last inequality we have used the bandwidth $h={\left(\frac{\text{log}{n}_1}{n_1}\right)}^{1/5}$.

The results are derived by taking $m=\sqrt{\frac{2\text{log}(3p/{\delta }_1)}{n_1^{1-\alpha }}}$ (so ${\delta }_1=3p\text{exp}(-n_1^{1-\alpha }{m}^2)$, and by taking Assumption 8. Note that we need to introduce α > 0 because the consistency conditions do not hold for α = 0. In fact, we need at least α > 7/15. Under this assumption, there exists a positive integer $N_1^{*}$ such that if $n_1\ge N_1^{*}$,

$$1+\text{exp}[2^{\frac{5}{4}}{\epsilon }_l^{-\frac{1}{2}}{n}_1^{\frac{7}{20}-\frac{3}{4}\alpha }{(\text{log}(3p/{\delta }_1))}^{\frac{3}{4}}{(\text{log}{n}_1)}^{\frac{1}{10}}+2n_1^{\frac{1}{10}-\alpha }{(\text{log}(3p/{\delta }_1))}^{\frac{1}{2}}{(\text{log}{n}_1)}^{\frac{2}{5}}]\le 3.$$

Therefore, for $n_1\ge N_1^{*}$,

$$P^{+-}(\underset{1\le j\le p}{\text{max}}{\Vert {\hat{f}}_j-f_{0,j}\Vert }_{\infty }\ge m)\le {\delta }_1,\text{for}m=\sqrt{\frac{2\text{log}(3p/{\delta }_1)}{n_1^{1-\alpha }}}.$$

Lemma 5

For any vector θ₀ = (θ_0,1, ⋯, θ_0,p)^T, let S_θ0 = {j : θ_0,j ≠ 0}, and let the minimum signal level be θ̄₀ = min{|θ_0,j| : j ∈ S_θ0}. Let g(θ_j) = c_j(θ_j − θ_0,j)² + λ‖θ_j‖₀, where c_j > 0. If $\lambda \le c_j{\overline{\mathit{\theta }}}_0^2$, g(θ_j) achieves the unique minimum at θ_j = θ_0,j.

Proof of Lemma 5

For θ_0,j = 0, the result is obvious. For θ_0,j ≠ 0, we have j ∈ S_θ0 and

$$g({\theta }_j)\ge \lambda {\Vert {\theta }_j\Vert }_{0}I({\theta }_j\ne 0)+c_j{({\theta }_j-{\theta }_{0,j})}^{2}I({\theta }_j=0)=\lambda {\Vert {\theta }_j\Vert }_{0}I({\theta }_j\ne 0)+c_j{\theta }_{0,j}^{2}I({\theta }_j=0).$$

If $\lambda {\Vert {\theta }_{0,j}\Vert }_0\le c_j{\overline{\mathit{\theta }}}_0^2$,

$$g({\theta }_j)\ge \lambda {\Vert {\theta }_j\Vert }_{0}I({\theta }_j\ne 0)+\lambda {\Vert {\theta }_{0,j}\Vert }_{0}I({\theta }_j=0)=\lambda {\Vert {\theta }_{0,j}\Vert }_0.$$

Since g(θ_0,j) = λ‖θ_0,j‖₀, the lemma follows.

Proof of Lemma 4

Denote Q₀(β) = Pρ(m_β, f̂, ĝ). Then we have β₁ = arg min_β∈ℝ^p Q₀(β): Since ∇Q₀(β₁) = 0 and

$${\nabla }^2{Q}_0(\mathit{\beta })=P\{{\mathit{Ẑ}}_1{\mathit{Ẑ}}_1^T\text{exp}({\mathit{Ẑ}}_1^T\mathit{\beta }){(1+\text{exp}({\mathit{Ẑ}}_1^T\mathit{\beta }))}^{-2}\}\ge {\epsilon }_0(1-{\epsilon }_0)P\{{\mathit{Ẑ}}_1{\mathit{Ẑ}}_1^T\}⪰0.$$

By Taylor’s expansion of Q₀(β) at β₁,

$$Q(\mathit{\beta })=Q_0({\mathit{\beta }}_1)+0.5{(\mathit{\beta }-{\mathit{\beta }}_1)}^T{\nabla }^2{Q}_0(\tilde{\mathit{\beta }})(\mathit{\beta }-{\mathit{\beta }}_1)+\lambda {\Vert \mathit{\beta }\Vert }_0,$$ (6.12)

where β̃ lies between β and β₁. Let M̂ = P{Ẑ₁(β₁)Ẑ₁(β₁)^T}, where Ẑ₁(β₁) is the subvector of Ẑ₁ corresponding to the nonzero components of β₁, and $\mathit{M}=P\{{\mathit{Z}}_1^0({\mathit{\beta }}_1){\mathit{Z}}_1^0{({\mathit{\beta }}_1)}^T\}$, where ${\mathit{Z}}_1^0({\mathit{\beta }}_1)$ is the subvector of ${\mathit{Z}}_1^0$ corresponding to the nonzero components of β₁. Let F = M̂ − M (a symmetric matrix). From the uniform deviance result of Lemma 3, with probability 1 − δ regarding the labeled samples, there exists a constant C₄ > 0 such that |F_kl| ≤ C₄b_n1 uniformly for k, l = 1, ⋯, s_β1, where $b_{n_1}=2\text{log}(3p/\delta )/n_1^{1-\alpha }$.

Hence, ‖F‖₂ ≤ ‖F‖_F ≤ C₄s_β1b_n1 ≤ C_4an1b_n1. For any eigenvalue λ(M̂), by the Bauer-Fike inequality (Bhatia, 1997), we have min_1≤k≤sβ1 |λ(M̂) − λ_k(M)| ≤ ‖F‖₂ ≤ C₄a_n1b_n1, where λ_k(A) denotes the k-th largest eigenvalue of A. In addition, in view of Assumption 9, there exists k ∈ S_β1 such that

$${\lambda }_{\text{min}}(\hat{\mathit{M}})\ge {\lambda }_k(\mathit{M})-C_4{a}_{n_1}{b}_{n_1}\ge {\lambda }_{\text{min}}(\mathit{M})-C_4{a}_{n_1}{b}_{n_1}\ge C_5-C_4{a}_{n_1}{b}_{n_1}.$$

Since a_n1b_n1 = o(1), there exists $N_3^{*}(\delta )$ such that when $n_1>N_3^{*}(\delta )$, we have λ_min(M̂) > 0.

Let ${\mathit{\beta }}_1^{(1)}$ be the subvector of β₁ consisting of the nonzero components. Then by (6.12) and Lemma 5 for each j ∈ S_β1 with λ < 0.5C₅ε₀(1−ε₀)β̄₁², we have

$$Q(\mathit{\beta })\ge Q_0({\mathit{\beta }}_1)+0.5(C_5-C_4{a}_{n_1}{b}_{n_1}){\epsilon }_0(1-{\epsilon }_0){\Vert {\mathit{\beta }}^{(1)}-{\mathit{\beta }}_1^{(1)}\Vert }^2+\lambda {\Vert \mathit{\beta }\Vert }_0\ge Q_0({\mathit{\beta }}_1)+\sum _{j\in S_{{\mathit{\beta }}_1}}\{0.5(C_5-C_4{a}_{n_1}{b}_{n_1}){\epsilon }_0(1-{\epsilon }_0){({\beta }_j-{\beta }_{1,j})}^2+\lambda {\Vert {\beta }_j\Vert }_0\},$$ (6.13)

where β_j and β_1,j are the j-th components of β and β₁, respectively. For $n_1\ge N_3^{*}(\delta )$,

$$Q(\mathit{\beta })\ge Q_0({\mathit{\beta }}_1)+\lambda \sum _{j\in S_{{\mathit{\beta }}_1}}{\Vert {\beta }_{1,j}\Vert }_0=Q_0({\mathit{\beta }}_1)+\lambda {\Vert {\mathit{\beta }}_1\Vert }_0.$$

By (6.12), we have

$$Q_0({\mathit{\beta }}_1)=Q_0({\mathit{\beta }}_1)+\lambda {\Vert {\mathit{\beta }}_1\Vert }_0.$$

Therefore, β₁ is a local minimizer of Q(β). It then follows from the convexity of Q(β) that β₁ is the global minimizer ${\mathit{\beta }}_1^{*}$.

Proof of Theorem 2

For simplicity, denote by ρ(m(Z₁), Y₁) the loss function ρ_q(X₁, Y₁) = −Y₁m(Z₁) + log(1 + exp(m(Z₁)). Note that

$$\frac{\partial \rho (m({\mathit{Z}}_1),Y_1)}{\partial m({\mathit{Z}}_1)}=-Y_1+\frac{\text{exp}(m({\mathit{Z}}_1))}{1+\text{exp}(m({\mathit{Z}}_1))}=-Y_1+{\pi }_{m,{\mathit{f}}_0,{\mathit{g}}_0}({\mathit{X}}_1),$$

and

$$\frac{{\partial }^2\rho (m({\mathit{Z}}_1),Y_1)}{{[\partial m({\mathit{Z}}_1)]}^2}=\frac{\text{exp}(m({\mathit{Z}}_1))}{{[1+\text{exp}(m({\mathit{Z}}_1))]}^2}.$$

By the second order Taylor expansion, we obtain that

$$\rho (m_{\mathit{\beta }}({\mathit{Ẑ}}_1),Y_1)=\rho (m_{{\mathit{\beta }}_0}({\mathit{Z}}_1^0),Y_1)+[\partial \rho (m_{{\mathit{\beta }}_0}({\mathit{Z}}_1^0),Y_1)/\partial m_{\mathit{\beta }}({\mathit{Z}}_1)](m_{\mathit{\beta }}({\mathit{Ẑ}}_1)-m_{{\mathit{\beta }}_0}({\mathit{Z}}_1^0))+\frac{1}{2}\frac{{\partial }^2\rho (m^{*},Y_1)}{{[\partial m_{\mathit{\beta }}({\mathit{Z}}_1)]}^2}{(m_{\mathit{\beta }}({\mathit{Ẑ}}_1)-m_{{\mathit{\beta }}_0}({\mathit{Z}}_1))}^2,$$ (6.14)

where m* lies between m_β(Ẑ₁) and $m_{{\mathit{\beta }}_0}({\mathit{Z}}_1^0)$. Since

$$P\left[\frac{\partial \rho (m_{{\mathit{\beta }}_0}({\mathit{Z}}_1^0),Y_1)}{\partial m_{\mathit{\beta }}({\mathit{Z}}_1)}\right]=0$$ (6.15)

and 0 < ∂²ρ(m*, Y₁)/[∂_mβ(Z₁)]² < 1, taking the expectation we obtain that

$$|P\rho (m_{\mathit{\beta }}({\mathit{Ẑ}}_1),Y_1)-P\rho (m_{{\mathit{\beta }}_0}({\mathit{Z}}_1^0),Y_1)|<0.5P[{(m_{\mathit{\beta }}({\mathit{Ẑ}}_1)-m_{{\mathit{\beta }}_0}({\mathit{Z}}_1^0))}^2]=0.5P[{({\mathit{Ẑ}}_1^T\mathit{\beta }-{({\mathit{Z}}_1^0)}^T{\mathit{\beta }}_0)}^2].$$

Hence, from Corollary 1, on the event 𝒥₃,

$$|P\rho (m_{{\mathit{\beta }}_0}({\mathit{Ẑ}}_1),Y_1)-P\rho (m_{{\mathit{\beta }}_0}({\mathit{Z}}_1^0),Y_1)|\le 0.5{\mathit{\beta }}_0^{T}P[({\mathit{Ẑ}}_1-{\mathit{Z}}_1^0){({\mathit{Ẑ}}_1-{\mathit{Z}}_1^0)}^T]{\mathit{\beta }}_0\le C_1{C}_4{s}_{{\mathit{\beta }}_0}^2{b}_{n_1},$$

where s_β = |S_β| is the cardinality of S_β = {j : β_j ≠ 0}. Naturally, $P\rho (m_{{\mathit{\beta }}_0}({\mathit{Ẑ}}_1),Y_1)\le P\rho (m_{{\mathit{\beta }}_0}({\mathit{Z}}_1^0),Y_1)+C_1{C}_4{s}_{{\mathit{\beta }}_0}^2{b}_{n_1}$.

In addition, by definition of β₁, Pρ(m_β1(Ẑ₁), Y₁) = min_β Pρ(m_β (Ẑ₁), Y₁). As a result, Pρ(m_β1(Ẑ₁), Y₁) ≤ Pρ(m_β0 (Ẑ₁), Y₁). Thus, we have

$$P\rho (m_{{\mathit{\beta }}_1}({\mathit{Ẑ}}_1),Y_1)\le P\rho (m_{{\mathit{\beta }}_0}({\mathit{Z}}_1^0),Y_1)+C_1{C}_4{s}_{{\mathit{\beta }}_0}^2{b}_{n_1}.$$ (6.16)

In addition, by (6.14) and (6.15), for any β we have $P\rho (m_{\mathit{\beta }}({\mathit{Ẑ}}_1),Y_1)\ge P\rho (m_{{\mathit{\beta }}_0}({\mathit{Z}}_1^0),Y_1)$. Then, setting β = β₁ on the left side leads to

$$P\rho (m_{{\mathit{\beta }}_1}({\mathit{Ẑ}}_1),Y_1)\ge P\rho (m_{{\mathit{\beta }}_0}({\mathit{Z}}_1^0),Y_1).$$ (6.17)

Combining (6.16) and (6.17) leads to

$$|P\rho (m_{{\mathit{\beta }}_1}({\mathit{Ẑ}}_1),Y_1)-P\rho (m_{{\mathit{\beta }}_0}({\mathit{Z}}_1^0),Y_1)|\le C_1{C}_4{s}_{{\mathit{\beta }}_0}^2{b}_{n_1}.$$ (6.18)

As a result, we have

$$ℰ(m_{{\mathit{\beta }}_1},\hat{\mathit{f}},\mathit{ĝ})\le C_1{C}_4{s}_{{\mathit{\beta }}_0}^2{b}_{n_1}.$$ (6.19)

(6.19) combined with Lemma 4 $({\mathit{\beta }}_1^{*}={\mathit{\beta }}_1)$ leads to

$$ℰ(m_{{\mathit{\beta }}_1^{*}},\hat{\mathit{f}},\mathit{ĝ})\le C_1{C}_4{s}_{{\mathit{\beta }}_0}^2{b}_{n_1}.$$ (6.20)

Recall the oracle estimator

$${\mathit{\beta }}_1^{*}=\text{arg}\underset{\mathit{\beta }\in ℬ}{\text{min}}\{ℰ(m_{\mathit{\beta }},\hat{\mathit{f}},\mathit{ĝ})+\frac{8\lambda s_{\beta }}{c{\varphi }_1^2(S_{\beta })}\}.$$

Then by Theorem 1,

$$ℰ({\hat{q}}_1)=ℰ(m_{{\hat{\mathit{\beta }}}_1},\hat{\mathit{f}},\mathit{ĝ})\le 6ℰ(m_{{\mathit{\beta }}_1^{*}},\hat{\mathit{f}},\mathit{ĝ})+\frac{16{\lambda }^2{s}_{{\beta }_1^{*}}{(e^{\eta }/{\epsilon }_0+1)}^2}{c{\varphi }^2(S_{{\beta }_1^{*}})}.$$ (6.21)

Therefore, by (6.20) and (6.21),

$$ℰ({\hat{q}}_1)\le \frac{16{\lambda }^2{s}_{{\beta }_1^{*}}{(e^{\eta }/{\epsilon }_0+1)}^2}{c{\varphi }^2(S_{{\beta }_1^{*}})}+C_1{C}_4{s}_{{\mathit{\beta }}_0}^2{b}_{n_1}.$$