Spatial and rotational quality assurance of 6DOF patient tracking systems

Abstract

Purpose:

External tracking systems used for patient positioning and motion monitoring during radiotherapy are now capable of detecting both translations and rotations. In this work, the authors develop a novel technique to evaluate the 6 degree of freedom 6(DOF) (translations and rotations) performance of external motion tracking systems. The authors apply this methodology to an infrared marker tracking system and two 3D optical surface mapping systems in a common tumor 6DOF workspace.

Methods:

An in-house designed and built 6DOF parallel kinematics robotic motion phantom was used to perform motions with sub-millimeter and subdegree accuracy in a 6DOF workspace. An infrared marker tracking system was first used to validate a calibration algorithm which associates the motion phantom coordinate frame to the camera frame. The 6DOF positions of the mobile robotic system in this space were then tracked and recorded independently by an optical surface tracking system after a cranial phantom was rigidly fixed to the moveable platform of the robotic stage. The calibration methodology was first employed, followed by a comprehensive 6DOF trajectory evaluation, which spanned a full range of positions and orientations in a 20 × 20 × 16 mm and 5° × 5° × 5° workspace. The intended input motions were compared to the calibrated 6DOF measured points.

Results:

The technique found the accuracy of the infrared (IR) marker tracking system to have maximal root-mean square error (RMSE) values of 0.18, 0.25, 0.07 mm, 0.05°, 0.05°, and 0.09° in left–right (LR), superior–inferior (SI), anterior–posterior (AP), pitch, roll, and yaw, respectively, comparing the intended 6DOF position and the measured position by the IR camera. Similarly, the 6DOF RSME discrepancy for the HD optical surface tracker yielded maximal values of 0.46, 0.60, 0.54 mm, 0.06°, 0.11°, and 0.08° in LR, SI, AP, pitch, roll, and yaw, respectively, over the same 6DOF evaluative workspace. An earlier generation 3D optical surface tracking unit was observed to have worse tracking capabilities than both the IR camera unit and the newer 3D surface tracking system with maximal RMSE of 0.69, 0.74, 0.47 mm, 0.28°, 0.19°, and 0.18°, in LR, SI, AP, pitch, roll, and yaw, respectively, in the same 6DOF evaluation space.

Conclusions:

The proposed technique was found to be effective at evaluating the performance of 6DOF patient tracking systems. All observed optical tracking systems were found to exhibit tracking capabilities at the sub-millimeter and subdegree level within a 6DOF workspace.

1. INTRODUCTION

Recent studies have shown that in addition to monitoring patient motion along the left–right (LR), superior–inferior (SI), and anterior–posterior (AP) directions, it is also important to consider rotational motion along the pitch (around LR), roll (around SI), and yaw (around AP) axes.^1–4 Taking all three translational and three rotational directions into account during patient motion monitoring is termed 6 degree of freedom (6DOF) tracking, and failure to consider all movement directions and orientations can result in poor dose conformity during radiation therapy (RT). This is especially true for highly conformal modalities, such as frameless stereotactic radiosurgery (SRS), where removal of the frame in favor of light immobilization demands the need for continuous real-time 6DOF head motion tracking.^5,6

Patient motion monitoring systems can be either classified as internal or external in nature, and many clinical tracking systems now have the capacity to monitor both translational and rotational motion. Internal 6DOF tracking systems typically use kilovoltage (kV) imaging to track patient anatomy or markers which have been embedded into or a target site.^7,8 However, due to the invasiveness of marker insertion and the potential high cost of imaging dose to the patient, use of kV tracking is often limited to occasional snapshots or short periods of fluoroscopy.^7,9,10 Magnetic field imaging can also be used to track embedded transponders in 6DOF in patients,² though such techniques are similarly invasive and cannot be used in many treatment modalities.¹¹ Optical 6DOF tracking systems do not require the use of ionizing radiation and can provide continuous real-time patient tracking over long periods of time.^12,13 Two such external optical tracking systems which have observed expanding clinical use in radiotherapy include infrared (IR) marker tracking^14,15 and 3D optical surface imaging.^16,17 Among these external tracking modalities, 3D surface image based imaging offers a potential ease-of-use advantage in that it does not require the addition of IR markers for tracking, which may accelerate patient setup and prevent marker reproducibility issues.

Many current radiotherapy treatment techniques rely on 6DOF tracking systems to perform critical functions such as intrafractional patient motion monitoring or gating the radiation treatment beam. Failure of such devices to operate within designed specifications could lead to improper dose coverage, poor clinical outcomes, and patient injury. However, while 6DOF optical patient monitoring is widespread in radiotherapy, as of yet there are no quality assurance (QA) methods to fully quantify their full 6DOF operating performance. Previous research which has explored the capabilities of such systems has typically focused only on translational degrees of movement or has relied on limited reference standards for angular accuracy evaluation.^{1,6,11,17–21} In order to effectively examine both the angular and translational accuracy of these motion monitoring devices, a precise calibration technique must be used to be able to compare intended to output motion, including regions outside of Linac isocenter due to the nature of real patient motion. Such a technique has been historically difficult to develop and generalize to various tracking system configurations.²²

In this work, we present a comprehensive method for calibrating and evaluating the full 6DOF performance of patient motion tracking units. Here, we have coupled a robust and generalizable calibration methodology together with a highly accurate robotic motion phantom in order to enable the evaluation of multiple points located throughout a 6DOF workspace quickly and accurately.²³ We demonstrate the method by investigating the translational and rotational accuracies of an IR marker tracking unit and two 3D optical surface units.

2. METHODS AND MATERIALS

2.A. Experimental setup

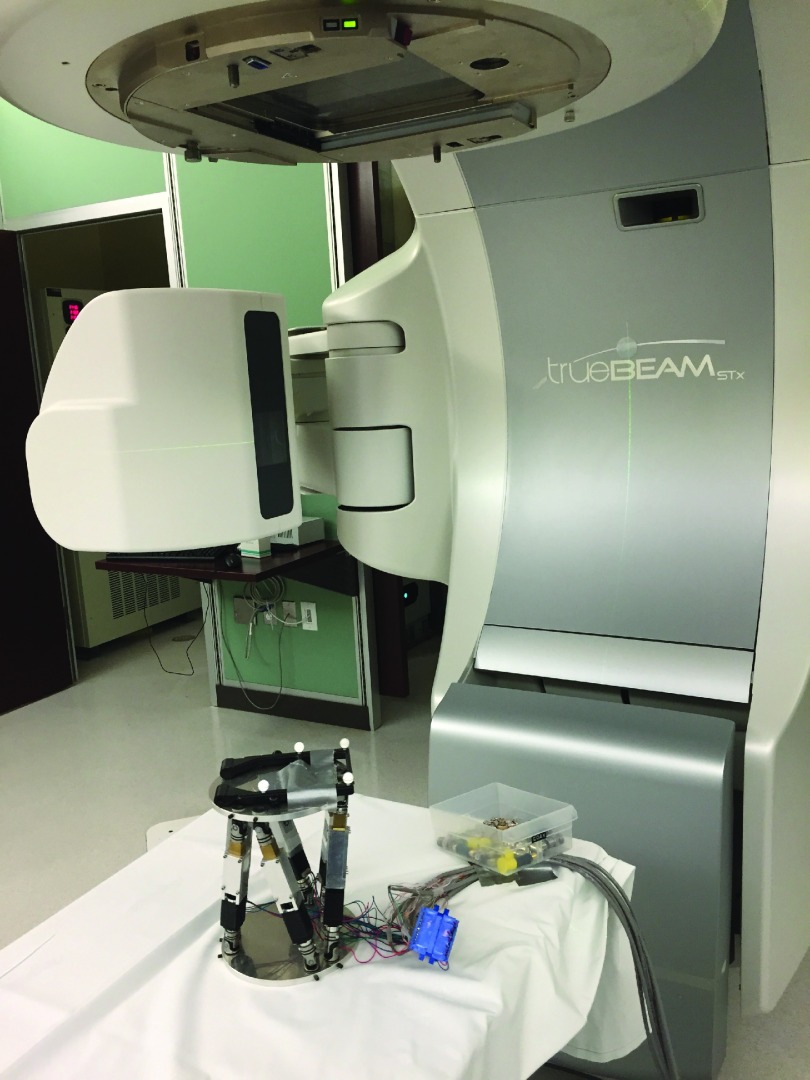
To effectively evaluate the tracking accuracy of a 6DOF patient tracking system, care must be taken to connect the camera and control coordinate frames, particularly, when translations and rotations are both monitored. In this work, these two coordinate systems are the camera coordinate frame and the 6DOF robotic motion phantom (Fig. 1) system, which was used to perform motions spanning a comprehensive 6DOF workspace.²³ This robotic motion phantom follows the Stewart–Gough platform archetype and uses inverse kinematics to control a mobile top platform relative to a stationary bottom platform both translationally and rotationally by precisely modulating the six struts, or linear actuators, which connect the two platforms.^24,25 Previous research focused on the design, production, and evaluation of this system demonstrated the control capabilities to be less than 0.22 mm translationally and 0.16° rotationally.²³ As such, the highly precise robotic motion phantom control is considered as the reference; this control point, or control coordinate system, was used as the reference baseline against which the camera point, or tracking coordinate system, is compared.

FIG. 1.

Parallel kinematics robotic motion phantom used to perform the precise 6DOF motion trajectories, which were employed to evaluate the external optical tracking system.

As an initial step to evaluate the performance of the optical tracking systems, a calibration methodology was developed and verified in order to associate the camera and control coordinate frames effectively. To this end, a formalism for the calibration was first established and tested with an IR marker tracking system (Polaris, NDI), which had been used previously with the robotic motion phantom.^23,26 The calibration was then applied to the 3D surface camera case, which differed slightly to the IR camera case because of the geometrical setups discussed later. The calibration methodology is presented below.

2.B. Calibration methodology

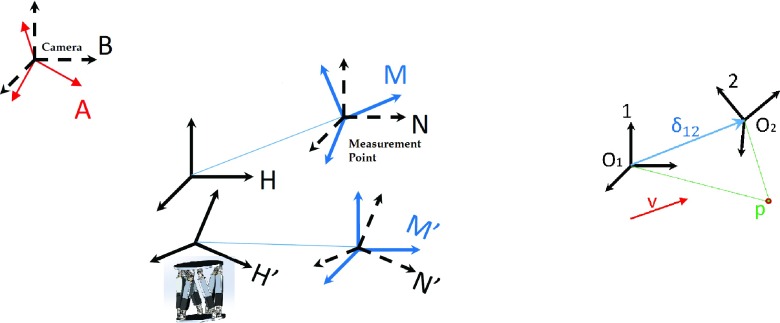
One must first consider the coordinate frame setup of the camera tracking system (Fig. 2, left). This setup includes the inherent camera reference coordinate frame (A), the inherent robotic motion phantom control frame (H), and the inherent virtual point, or measurement, frame (M); these three unprimed coordinate frames are not fundamentally associated mathematically and can be considered as the initial conditions before the motion is performed. As the virtual point frame (M) represents the origin of the tracked coordinate frame, and the elements which are tracked by either the IR camera or the optical surface map are rigidly connected to the top platform of the robotic motion phantom, the coordinate frames M and H are also necessarily rigidly connected. The orientation of these coordinate systems is not initially aligned, but the translational vector connecting the origins of these two frames, which we call δ_HM, is immutable in magnitude. The notation δ₁₂ can be understood as the 3D vector connecting the origins of two arbitrary coordinate systems 1 and 2, in the frame of reference of 1. Similarly, we introduce the 3 × 3 rotation matrix R₁₂ which defines the orientation of coordinate frame 2 in reference to coordinate frame 1. With this established, it can be seen that some point p in coordinate frame 1 can be transformed to be represented in another coordinate frame 2 by Eq. (1) (Fig. 2, right). Further, a vector v represented in one coordinate frame can be represented in another frame simply through the application of the requisite rotation matrix [Eq. (2)],

$${\displaystyle {\mathbf{p}}_2={\mathbf{\delta }}_{21}+{\mathbf{R}}_{21}{\mathbf{p}}_1,}$$ (1)

$${\displaystyle {\mathbf{v}}_2={\mathbf{R}}_{21}{\mathbf{v}}_1.}$$ (2)

FIG. 2.

The assembly of coordinate systems considered for motion control, calibration and tracking evaluation (left), and the point and vector representation in two coordinate frames (right). Here, coordinate frames A and B are the camera frames, M and N are the measurement coordinate frames, H is the control frame for the phantom, and the primed analogs are these latter coordinate frames after motions were performed by the H control frame.

Returning to the tracking system cases, we can also define the B and N frames as coordinate systems which share an origin with the camera frame A and the virtual point frame M, respectively, but which are oriented to the inherent control coordinate frame H (Fig. 2, left).

Motions are performed by the robotic motion phantom (H), moving this control coordinate system to the H′ frame. As the H frame is rigidly connected to the M (and N) frame, H′ is necessarily connected to the resultant M′ (and N′) frames, and so as motions are performed, H → H′, M → M′, and N → N′, with the orientation of N′ continuing to match the orientation of H′ by geometrical requirement. Subsequently, as trajectory inputs are fed into the robotic motion phantom, the measurement coordinate system M′ is moved in reference to the camera system A. In order to be able to compare the input motion of the phantom to the measured motion of the frame M′, several geometrical relations must be established; to this end, a calibration methodology was employed, which served to primarily compute R_HA, R_NM, and δ_HN. This methodology is presented below, under the assumption that motion control of the phantom was done so precisely, namely, that δ_HH′ and R_HH′ are known.

In order to compute R_HA, one must utilize both the input intended motions, as given by δ_HH′ and R_HH′, and the measurement output, as given by δ_AM′ and R_AM′. An input trajectory spanning a set of 15 translational points were first performed by the robotic phantom in a 1.5 × 1.5 × 1.5 cm workspace, and monitored using the tracking system. Comparing the measured values for these points to the intended values using singular value decomposition yielded a rotation matrix R_HA, which shows the orientation relationship between these two coordinate systems. Furthermore, utilizing this matrix and the average values of both the intended and measured motions, one can extract the translational vector between the camera frame and the measurement frame, δ_BM using Eq. (3). Using the measured angular data R_AM′, which is uniform throughout this translation-only trajectory, the rotation matrix R_AM is also found,

$${\displaystyle {\mathbf{\delta }}_{\mathrm{BM}}=-\left({\mathbf{R}}_{\mathrm{HA}}\cdot \text{mean}\left({\mathbf{\delta }}_{{\mathrm{AM}}^{\prime }}\right)\right)+\text{mean}\left({\mathbf{\delta }}_{{\mathrm{HH}}^{\prime }}\right).}$$ (3)

Then, to evaluate δ_HN, a trajectory consisting of a set of six angles were performed—two each of pitch (around LR), roll (around SI), and yaw (around AP)—and the measurement data were once again compared to the intended input angles. In practice, as this angular motion is performed by the robotic phantom, and given the displacement δ_HN between the virtual point M (or N) and the control point H, the translations δ_AM′ are measured by the camera system and used analytically to compute this unknown displacement δ_HN, described as follows:

$${\displaystyle {\mathbf{\delta }}_{\mathrm{HN}}={\left({\mathbf{R}}_{{\mathrm{HH}}^{\prime }}-{\mathbb{1}}^{3\times 3}\right)}^{-1}\left({\mathbf{\delta }}_{{\mathrm{NN}}^{\prime }}-{\mathbf{\delta }}_{{\mathrm{HH}}^{\prime }}\right).}$$ (4)

In this equation, we are given the angular trajectory input (moving the control coordinate frame from H to H′) in the form of R_HH′ and δ_HH′, and δ_NN′ is acquired from measurements and the consideration of the following equations:

$${\displaystyle {\mathbf{\delta }}_{{\mathrm{BN}}^{\prime }}={\mathbf{\delta }}_{{\mathrm{BM}}^{\prime }}={\mathbf{R}}_{\mathrm{BA}}{\mathbf{\delta }}_{{\mathrm{AM}}^{\prime }}={\mathbf{R}}_{\mathrm{HA}}{\mathbf{\delta }}_{{\mathrm{AM}}^{\prime }}}$$ (5)

$${\displaystyle {\mathbf{\delta }}_{{\mathrm{NN}}^{\prime }}={\mathbf{\delta }}_{{\mathrm{BN}}^{\prime }}-{\mathbf{\delta }}_{\mathrm{BN}}\text{where}{\mathbf{\delta }}_{\mathrm{BN}}={\mathbf{\delta }}_{\mathrm{BM}}.}$$ (6)

This calibration series was implemented in matlab (The Mathworks, 2013b) and used for proper coordinate frame alignment prior to evaluation of the optical surface tracking system. An L₂ optimization form was used to compute δ_HN from the set of input data, transformed to δ_NN′.

2.B.1. IR marker tracking calibration

To validate this calibration methodology, the calibration trajectory was performed using the robotic motion phantom, and the resultant motion was tracked using a Polaris stereoscopic IR camera with capture rate of 8 frames/s. In this setup, the origins of the camera and measurement coordinate frames were separated by several meters, and the orientations of the frames of reference were not initialized prior to the start of motion, that is, δ_AM was nonzero, and R_AM, R_HM, and R_HA were not unit matrices. The four reflective markers shown fixed to the robotic motion phantom in Fig. 3 defined a virtual point coordinate frame M which was tracked with the IR camera frame A. A successful calibration then allowed for the proper evaluation of the camera systems.

FIG. 3.

Experimental setup for the test of the calibration methodology using an IR marker tracking system. Shown are the robotic motion phantom with a set of four reflective IR markers fixed to the top platform, which were tracked using the stereoscopic IR camera (not shown). The arrangement of the four markers produces a virtual point for tracking, which is called the M frame of reference.

2.B.2. Optical surface tracking calibration

In the optical surface map tracking regime, the setup differs slightly from the IR marker tracking system. Here, the camera coordinate frame A is not considered, as the measurement output data are represented relative to the virtual point M, that is, the collected motions are δ_MM′ rather than δ_AM′, since δ_AM is zero. Furthermore, R_AM is the unit matrix in this setup, again due to the nature of the recorded motion file reporting the motion as δ_MM′ and the angles of R_MM′. In this way, the calibration methodology for optical surface mapping can be considered as a specific and simplified case of the general calibration technique presented above, so the same techniques as used in the IR marker tracking case can be applied.

2.C. 6DOF camera evaluation

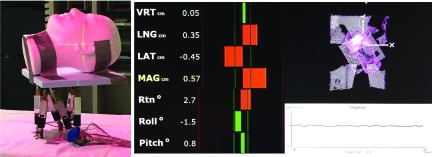
Upon verifying the calibration methodology with the IR marker tracking system, the optical surface mapping system, HD AlignRT (VisionRT, London, UK; software version 5.0.1747) system was evaluated using a comprehensive 6DOF trajectory. This trajectory was composed of a set of points in a 3D cube about isocenter: a straight line in the SI and LR directions spanning ±10 and ±8 mm in AP. At each of these 12 points, and at isocenter, a series of seven angular motions were performed: 1° and 5° of rotation each for pitch (around LR), roll (around SI), and yaw (around AP), as well as the no-angle case. This 6DOF workspace was selected to cover a range of motions typically observed in intracranial SRS procedures, as well as other typical tumor trajectories.⁶ As in the calibration procedure, the robotic motion phantom moved to each point in this trajectory and rested for 15 s to permit adequate averaging. A Styrofoam head was rigidly fixed to the top platform and served as the surface region of interest (ROI) used for the purposes of motion tracking (Fig. 4). The ROI was selected to cover a region spanning the forehead to the bridge of the nose, to provide a good balance of spatial and temporal resolution, while mimicking an ROI which could be clinically used for an open-face thermoplastic mask during brain disorder treatments.¹⁷ The motion capture frame rate was 4 frames/s with this ROI selection. This trajectory was performed twice under surveillance by the HD AlignRT system— with room lights ON and OFF in order to compare the effectiveness of 6DOF tracking with different ambient light conditions.

FIG. 4.

Experimental setup for the evaluation of the AlignRT system. A Styrofoam head was rigidly connected to the top platform of the robotic motion phantom (left), and a region of interest on the head was selected for tracking (right). The optical surface contour is tracked, and relate to tracking virtual point, which is located at room isocenter.

The measured output motion was recorded by the HD AlignRT system and analyzed using matlab (The Mathworks, 2013b). For each translational position and corresponding angular motion, a root-mean squared error (RMSE) analysis was performed for all six degrees of freedom to evaluate both the translational and rotational precision within this workspace. To demonstrate the accuracy of the system, the 13 intended input points were compared directly to the calibrated measured points. The same primary evaluation trajectories were also independently performed under the tracking of the IR camera system and an older generation of the AlignRT system. These results were analyzed in the same manner as above, considering both precision and accuracy, and compared quantitatively to the HD AlignRT system. In the case of the two AlignRT generations, the same collection software version was used to permit a fair comparison.

3. RESULTS

3.A. 6DOF calibration

The calibration trajectory was performed using the robotic motion phantom and tracked with the IR marker camera, and the calibration formalism was employed to verify the efficacy of the technique. The maximal errors across the entire calibration procedure are less than 0.22 mm translationally and 0.25° rotationally, and it is therefore considered effective, as this is on the same order as the Polaris tracking noise.¹⁷ Specifically, the translational error in calculating δ_HN was 0.14, 0.22, and 0.20 mm in LR, SI, and AP, respectively; the maximum angular error comparing intended angular motion to an appropriately transformed measured output was 0.20°, and comparing δ_HH′ to the transformed δ_AM′ → δ_NN′ data by Eqs. (3)–(6) yielded a maximum translational error of 0.23 mm after calibration.

3.B. 6DOF optical tracking system evaluation

In the room lights ON case, the calibration methodology was performed effectively, with average translational errors of 0.29 mm; the maximum angular error after the application of the R_HA rotation matrix to measured data was less than 0.3°, considering all three angular degrees of freedom. The RMSE analysis was performed on the appropriately transformed measurement data. At isocenter, RMSE was 0.29 mm in LR, 0.37 mm in SI, and 0.31 mm in AP, with rotational RMSE at 0.03° in pitch (around LR), 0.06° in roll (around SI), and 0.07° in yaw (around AP). As the robotic motion phantom positioned itself distally along LR, SI, and AP independently, the RMSE analysis generally degraded, with RMSE for LR, SI, and AP reaching up to 0.46, 0.61, and 0.54 mm, respectively, for motions which occur along the three translational axes (Table I).

TABLE I.

RMSE analysis for three optical tracking systems, for a set of points along the three primary axes in a 6DOF workspace, in mm for translations and degrees for rotations. Within each box, the RMSE values are displayed for the HD AlignRT system (top), the previous generation AlignRT system (middle), and the Polaris IR marker tracking system (bottom). All results here were performed with room lights ON.

	RMSE X	RMSE Y	RMSE Z	RMSE pitch	RMSE roll	RMSE yaw	System
(0,0,0)	0.29	0.37	0.31	0.03	0.06	0.07	HD AlignRT
	0.32	0.2	0.33	0.21	0.09	0.04	AlignRT
	0.03	0.05	0.04	0.03	0.02	0.03	Polaris
(±5,0,0)	0.31	0.31	0.45	0.06	0.07	0.07	HD AlignRT
	0.69	0.41	0.45	0.18	0.13	0.13	AlignRT
	0.05	0.05	0.05	0.03	0.04	0.04	Polaris
(±10,0,0)	0.46	0.49	0.54	0.06	0.11	0.07	HD AlignRT
	0.51	0.62	0.46	0.22	0.17	0.18	AlignRT
	0.13	0.05	0.06	0.05	0.05	0.04	Polaris
(0,±5,0)	0.33	0.45	0.4	0.05	0.08	0.07	HD AlignRT
	0.42	0.31	0.4	0.21	0.13	0.12	AlignRT
	0.12	0.07	0.06	0.02	0.03	0.07	Polaris
(0,±10,0)	0.34	0.52	0.44	0.04	0.08	0.07	HD AlignRT
	0.46	0.51	0.47	0.28	0.17	0.16	AlignRT
	0.18	0.25	0.07	0.04	0.04	0.05	Polaris
(0,0,±5)	0.37	0.55	0.32	0.04	0.09	0.06	HD AlignRT
	0.48	0.65	0.39	0.21	0.19	0.14	AlignRT
	0.08	0.05	0.05	0.02	0.03	0.07	Polaris
(0,0,±10)	0.46	0.6	0.32	0.04	0.07	0.08	HD AlignRT
	0.5	0.74	0.36	0.23	0.18	0.15	AlignRT
	0.09	0.06	0.06	0.02	0.03	0.09	Polaris

In a direct accuracy comparison between the intended input points and the transformed measured data points, the minimum translational errors occurred when no angular motions were performed: the average angle-free error was found to be 0.14 mm in LR, 0.27 mm in SI, and 0.15 mm in AP. When angular motions in the workspace were confined to 1°, these magnitudes increased slightly, to 0.24° in LR when 1° roll was performed, 0.51 mm in SI when a 1° yaw was performed, and 0.27 mm in AP when a 1° roll was performed. However, once a 5° rotation was performed, in any orientation, the average discrepancies between the input and transformed measured data reached up to 1.1 mm in LR, 1 mm in SI, and 1 mm in AP. In Fig. 5, the intended translational points are compared directly in 3D space to the transformed measured data, separated by the angular motions performed at each of these 13 points in the workspace.

FIG. 5.

HD AlignRT comparison between intended (x) and measured (o) points in the 6DOF workspace, separated by angular motions performed at each of the 13 translational positions, as well as 8 positions in combinations of the three translational degrees of freedom. No rotations (top), pitch (around LR) of 1°(top left) and 5°(top right), roll (around SI) of 1°(middle left) and 5°(middle right), and yaw (around AP) of 1°(bottom left) and 5°(bottom right).

Across this entire 6DOF workspace, analysis on the angular data produced average RMS errors of less than 0.1° consistently, even at extreme translations. This analysis considered rotations of up to 5° in pitch, roll, and yaw. For all positions and rotations, the maximal angular discrepancy was less than 0.3° for this case with room lights ON. Important to note is that the largest observed angular RMSEs occurred for roll, around the SI axis, and the smallest angular error occurred for pitch, around the LR axis (Table I).

In the lights OFF case, the translational and angular RMSEs were slightly but noticeably larger. At isocenter, the RMSE was 0.38 mm for LR, 0.71 mm for SI, 0.23 mm for AP, 0.12° for pitch, 0.10° for roll, and 0.08° for yaw. These RMSE values reached up to 0.70 mm in LR, 1.62 mm in SI, and 0.66 mm in AP across the same evaluation trajectory as described above. Compared to the lights ON case, the angular results were slightly worse in almost all cases, excluding when a 5° roll was performed.

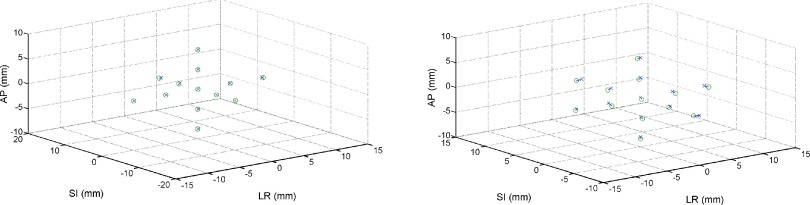
The IR marker system produced similar motion tracking results to the HD AlignRT system. The analysis for this case yielded maximal translational RMSE of 0.18 mm and maximal angular RMSE of 0.10°. In a direct comparison between the tracking efficacies of the two systems, the HD AlignRT system had slightly improved angular resolution but worse spatial resolution, compared to the Polaris IR marker tracking system (Table I). Examining the true translational difference between the intended and measured data, the Polaris system showed better translational tracking compared to the AlignRT system (Fig. 6, left).

FIG. 6.

Direct comparison of the accuracy of the IR marker tracking system (left) and the older generation of the optical surface mapping system (right). Both plots show the intended translational position (x) compared to the transformed measured data (o) in the case when no angular motions were performed at each of the points in the 6DOF workspace.

Comparing the newer HD AlignRT system to the older AlignRT system showed improved tracking accuracy and an increased 6DOF tracking volume for the newer system. For the older generation AlignRT system, RMSE analysis found LR errors to range from 0.32 mm at isocenter and up to 0.69 mm at the most extreme translational movements, occurring with 5° rotations; SI errors ranged from 0.20 mm at and up to 0.74 mm at the more distal positions in the 6DOF workspace, when large angular motions were also performed; AP errors ranged from 0.33 mm at isocenter and up to 0.47 mm at the most extreme translational motions with large rotations (Table I). Angular RMSEs were similar to that of the HD AlignRT system, with errors ranging from 0.21°, 0.09°, and 0.04° at isocenter up to 0.28°, 0.19°, and 0.18° in pitch, roll, and yaw, respectively, at locations more distal to isocenter. A direct comparison between the intended position and the appropriately transformed measured position for the rotation-free case is presented in Fig. 6 (right).

4. DISCUSSION

This work presents a novel method for validating the accuracy of external tracking systems for use in radiation therapy. The method is not inherently limited to external optical tracking systems and may be used to evaluate the performance of any 6DOF patient tracking system, such as stereoscopic x-ray imaging or CBCT. With increased use of 6DOF patient motion tracking devices in radiotherapy, this method provides a rigorous technique for performing QA in order to guarantee that such devices are operating within designed specifications. The methodology for camera system calibration and evaluation presented in this work has the potential to serve as a foundation for such an evaluation. The calibration methodology will be applied initially, and then using a robotic device as the motion control phantom, one can perform an exhaustive trajectory covering a desired 6DOF workspace, such as the one presented earlier in this work.

In a direct 6DOF comparison between the AlignRT systems and the Polaris IR marker tracking system, it was found that both 3D optical mapping systems had worse translational tracking capabilities and similar rotational errors to the latter, based on the quantitative RMSE results for precision and the accuracy results comparing the intended and measured outputs. The reason behind the difference between the IR and 3D surface map paradigms is potentially in the fundamental nature of how these systems track points during treatment. The virtual point coordinate system characterized by the reflective IR marker set may be more precisely defined by the careful marker configuration, compared to the array of approximately 500 vertex points.¹⁷

Compared to the previous generation AlignRT, the HD AlignRT system performed better in most cases. Given the overall end-to-end clinical standards of 1–2 mm accuracy for highly conformal cases such as SRS, it is best to maintain sub-millimeter camera accuracy such that its contribution to total error is small.²⁷ In most cases, the HD AlignRT system was able to meet this clinical requirement and was able to meet this requirement when motions were limited to 5 mm and 1°. This subset of points is more typical for motions observed during frameless SRS treatments.⁶ For a highly conformal treatment modality such as SRS, failure to achieve sub-millimeter accuracy can result in improper dose coverage and significant normal tissue irradiation, due to the high-dose low-fraction characteristics of this technique. However, in several cases, both the HD and older optical surface mapping systems reached a threshold of angular motion, beyond which the system was unable to effectively track the ROI contour, in either translations or rotations. This contributed substantially to the accuracy and precision of the device, especially in the cases when RMS errors exceeded 1 mm.

As shown in Fig. 5, when the phantom positioned itself further from isocenter, the viable 6DOF tracking workspace decreased noticeably, that is, as the phantom moved distally from isocenter, the threshold angular motion beyond which the HD AlignRT camera system could not effectively identify true motions decreased, when rotations were performed in pitch (around LR) and roll (around SI). For this HD AlignRT system, within the presented workspace, however, no such failures were observed before rotations in pitch and roll reached approximately 3°, and none of these issues were present when yaw (around AP) rotations were performed, up to 10°. In the older AlignRT system, the viable rotational workspace was similar but smaller still, and yaw rotations at the 10° mark experienced such failures. In the 6DOF volume examined, the Polaris IR camera did not observe issues of this nature. Such failure-to-track events are particularly concerning in a highly conformal case such as SRS, and monitoring of the clinical stuff will still be required when observed motions begin to deviate over the course of treatment. However, under the sub-millimeter and subdegree patient positioning conditions for SRS, deviations from isocenter over 1 mm or 1° would not be observed clinically, and within this 6DOF workspace subset, no such failure-to-track errors were observed. Still, such events motivate the necessity of clinical oversight when using these systems.

A quantitative and qualitative comparison between the room lights ON and OFF cases was also performed, and in most cases, tracking accuracy was improved when the room lights were ON, which is the condition typically used with patients. Because of the nature of the 3D optical tracking paradigm, we explored the potential for ambient light to affect tracking accuracy. We found that the two conditions yielded similar results, while the room lights ON case, which is more common clinically, yielded slightly better tracking performance. In addition to this examination, future work aims to evaluate the dynamic capabilities of 6DOF systems.

5. CONCLUSION

The combined application of an effective calibration methodology and a precise 6DOF robotic motion phantom permitted the complete evaluation of three optical tracking systems. Quality assurance using this procedure offers the advantage of off-center evaluation, and complete examination of tracking capabilities in 6DOF. This QA procedure can be set up quickly and is highly automatic, and can therefore be used as a daily QA, or potentially immediately before a procedure. This exhaustive evaluation of the Polaris IR marker tracking system, and two AlignRT systems, was performed across a clinically relevant 6DOF workspace, and the accuracy of the tracking was found to be within clinical tolerances for intracranial SRS in most cases. Based on this level of translational and rotational accuracy, effective motion monitoring during such highly conformal procedures may be possible at the sub-millimeter and subdegree level with the systems explored in this work.

CONFLICT OF INTEREST DISCLOSURE

The authors have no COI to report.