Crowding in the S-cone pathway

Abstract

The spatial extent of interference from nearby object or contours (the critical spacing of “crowding”) has been thoroughly characterized across the visual field, typically using high contrast achromatic stimuli. However, attempts to link this measure with known properties of physiological pathways have been inconclusive. The S-cone pathway, with its ease of psychophysical isolation and known anatomical characteristics, offers a unique tool to gain additional insights into crowding. In this study, we measured the spatial extent of crowding in the S-cone pathway at several retinal locations using a chromatic adaptation paradigm. S-cone crowding was evident and extensive, but its spatial extent changed less markedly as a function of retinal eccentricity than the extent found using traditional achromatic stimuli. However, the spatial extent agreed with that of low contrast achromatic stimuli matched for isolated resolvability. This suggests that common cortical mechanisms mediate the crowding effect in the S-cone and achromatic pathway, but contrast is an important factor. The low contrast of S-cone stimuli makes S-cone vision more acuity-limited than crowding-limited.

1. Introduction

The physiological locus of crowding—the difficulty identifying objects when they are surrounded by other objects (flankers), especially in peripheral vision — remains elusive. Since this phenomenon is a factor limiting vision, understanding how to mitigate its effects is important, motivating research toward unveiling the underlying mechanisms. Early work identified that the origin of crowding is not at the retinal level, based on evidence from contralateral effects (Flom et al., 1963). In these experiments, Flom et al. (1963) showed that eye of origin was not a factor in crowding effects. Specifically, when the target was presented to one eye, and the flanker(s) to the other eye, crowding was just as strong as when both the target and flankers were presented to the same eye, a finding confirmed by Tripathy and Levi (1994). Due to the anatomical architecture of the visual system, this demonstrated that crowding happens after the signals from the two eyes are combined—in primary visual cortex (V1) or later.

Since then, however, progress in pinpointing a neural locus has been inconclusive. Using psychophysics, Liu et al. (2009) claimed than signal modulation due to crowding was unlikely to happen in V1, as this would require propagation across the vertical meridian. Such propagation is unlikely as cross-meridian objects are quite distant anatomically. These authors instead posited that crowding occurs beyond V3, proposing hV4 or LOC (lateral occipital cortex) as possible sites. Using EEG, Chicherov et al. (2014) showed that changes in the N1 signal (modulations arising from high-level visual areas such as lateral occipital, posterior temporal, and inferior parietal cortex) are associated with crowding. Others who champion a locus beyond V1 for crowding include Freeman and Simoncelli (2011) and Freeman et al. (2011), who identify V2 as the possible site, using psychophysics, fMRI, and computational modeling. Finally, Motter (2009) identified area V4 as the possible site based on electrophysiology with non-human primates. Using functional magnetic resonance imaging, however, Millin et al. (2014) did see a suppression of signals in V1 due to crowding. Additional neuroimaging results from the same lab confirmed this (Kwon et al., 2014). With EEG and fMRI, Chen et al. (2014) also found modulation of signals in V1, believing early suppression to be a large contributor to crowding. Lastly, Anderson et al. (2012) found signal changes in the BOLD response across all of occipital visual cortex from V1 to V4, with the largest magnitudes in later areas.

Beyond a specific location, the neural mechanism(s) that contribute to crowding are equally mysterious. Several proposed theories are reviewed by Levi (2008). Of relevance to the current study are those models that involve specific hypotheses concerning the spatial extent of cortical signals, either due to the organization of “integration fields,” or due to the lateral spread of neural activity, hypothesized to originate from horizontal connections. Perceptually, the spatial zone within which flankers impede correct recognition of a target is called the crowding zone. Its spatial extent, called the critical spacing, has been extensively quantified (Bouma, 1970; Levi et al., 1985; Pelli et al., 2004; Strasburger et al., 1991; Toet and Levi, 1992), usually with a constant that determines the change in critical spacing as a function of eccentricity. Although this measure (the “Bouma constant”) can vary amongst individual subjects (Pelli et al., 2007) and the stimuli used (Rosen et al., 2014), its value, especially the linear relationship with eccentricity (Bouma, 1970; Jacobs, 1979; Pelli et al., 2004; Toet and Levi, 1992), can be used to evaluate within-subject differences resulting from changes in the stimulus. For example, reducing contrast (Coates et al., 2013a) or shortening the stimulus duration (Chung and Mansfield, 2009; Kooi et al., 1994; Tripathy and Cavanagh, 2002; Tripathy et al., 2014; Wallace et al., 2013) have both been found to cause an enlargement of the crowding zone, yielding possible clues in determining the neural basis of crowding.

One way to test theories of crowding is to utilize an alternate afferent pathway in the visual system, such as the koniocellular pathway, which originates primarily from S-cones (Hendry and Reid, 2000). This pathway remains segregated from the traditional luminance and red/green pathways in the retina, LGN, and the input layers of primary visual cortex—Layers 4Cα, 4Cβ, and 4A for the luminance, red/green, and koniocellular pathway respectively (Chatterjee and Callaway, 2003). Characteristics of this pathway have been extensively studied anatomically, both to better understand color vision (Dacey, 2000) and as a stereotypical example of parallel processing in the central nervous system (Nassi and Callaway, 2009; Casagrande, 1994). There has also been recent interest from neuroscience in studying the functional properties of this pathway. For example, koniocellular LGN neurons have receptive fields that are relatively larger, and typically more variable in size, than those in the magnocellular and parvocellular pathways (Xu et al., 2001). One recent study (Sceniak et al., 2006) used electrophysiology to quantify the lateral spread of surround-suppression signals in the three retinal-driven input layers of primary visual cortex, finding that the spatial extent of the classical receptive field, as well as the extent of surround suppression was similar between the three pathways.

Human psychophysical experiments targeting the S-cone pathway have also become popular, for a variety of reasons, summarized by Smithson (2014). Practically, it has been known for some time that measuring basic visual functions like perimetry or acuity while isolating the S-cone pathway may yield diagnostic information about certain retinal diseases, including diabetic retinopathy, glaucoma, and retinitis pigmentosa (Johnson et al., 1993; Adams et al., 1987; Sandberg and Berson, 1977; Greenstein et al., 1989). Due to the neural site of damage from these diseases, visual function in the S-cone pathway is reduced prior to other symptoms, leading to the introduction of clinical procedures such as the SWAP test of S-cone pathway perimetry.

There is varied theoretical interest in S-cone psychophysics as well, as it is an ideal platform for relating function and structure (Metha and Lennie, 2001). The reduced spatial resolution of the S-cone pathway is the most well-known result (Anderson et al., 2002; Green, 1972; Swanson, 1989), reflecting both S-cone undersampling and neural deficiencies (Green, 1968). A diverse array of additional visual functions have been tested. A study of spatial summation with S-cone stimuli showed a constant ratio of the size of Riccò’s area (the area of complete spatial summation) and S-cone pathway ganglion cell dendritic fields, with equal S-cone contrast thresholds across the visual field for stimuli of these sizes (Vassilev et al., 2005). Other psychophysical results include stronger surround-suppression in the S-cone pathway (Xiao and Wade, 2010), binocular rivalry between S-cone stimuli and luminance stimuli (O’Shea and Williams, 1996), and the observation that S-cone stimuli produce attentional cueing effects but not saccade distraction, unlike luminance stimuli (Sumner et al., 2002).

One of the appeals of S-cone psychophysics is the ease with which this separate anatomical pathway can be isolated using purely psychophysical methods. The most straightforward technique involves the presentation of blue stimuli on a bright yellow background that adapts the L- and M-cones (Anderson et al., 2002; Redmond et al., 2013; Rabin and Adams, 1990), which we employed in the present study. As far as we know, there has not been previous measurement of crowding using an S-cone isolation paradigm. Therefore, results from the present study would enhance our understanding of the functional capabilities of the S-cone pathway, and any functional differences between the S-cone and the luminance pathways. Furthermore, differences in the spatial extent of crowding mediated by the S-cone pathway versus results using traditional luminance-defined stimuli could help constrain models of crowding.

An important consideration with this paradigm is the fact that contrast sensitivity is reduced in the S-cone pathway (Green, 1968). This reduction could be significant, since contrast is known to modulate the size of the crowding zone (Coates et al., 2013b). Several studies have examined how differences in contrast between the target and flankers affect the critical spacing of crowding (Chung et al., 2001; Kooi et al., 1994; Pelli et al., 2004; Rashal and Yeshurun, 2014), or have used threshold contrast as the dependent variable to study crowding (Levi et al., 2002; Strasburger et al., 1991). However, a complete characterization of the relationship between overall stimulus contrast and the extent of the crowding zone is lacking, although there are several clues from the literature. A careful examination of the results of Kooi et al. (1994) reveals that the crowding zone for stimuli having target and flanker contrast of 29% is significantly larger than that for stimuli having a target and flanker contrast of 83%. More recently, our laboratory reported marked increases in the size of the crowding zone for stimuli with contrasts below 10–20% (Coates et al., 2013a). Therefore, in the present study we also included a control condition with low contrast achromatic stimuli in the experimental setup.

2. Methods

2.1. Subjects

Five young subjects (aged 18–20) with normal vision participated in the experiment. All had normal vision (at least 20/20 in each eye) with their habitual distance corrections. Subjects viewed the stimulus with their right eye. Their left eye was occluded with an eye patch. Subjects were seated, with their head placed in a chin rest. At the beginning of each condition, subjects were given a few minutes to adapt to the new luminance level from the projector and the computer monitor (see below). All subjects practiced each condition at each eccentricity at least once before data collection. All subjects gave informed oral and written consent before the commencement of data collection. The research followed the tenets of the Declaration of Helsinki and was approved by the Institutional Review Board at the University of California, Berkeley.

2.2. Experimental apparatus

The experimental setup comprised a projector, a computer screen, and an optical bench with a beam splitter and various optical filters to yield the desired experimental conditions for S-cone isolation. A schematic diagram illustrating the setup is shown in Figure 1. In our design of the apparatus we followed the examples of several classic papers from the literature that isolate S-cones (Rabin and Adams, 1990; Swanson, 1989; Anderson et al., 2002, 2003). The goal was to create a display in which blue stimuli were presented against a bright orange/yellow background designed to adapt the L- and M-cones of the subjects. To achieve this, the output from a Kodak Ektagraphic III A Projector was projected through a Wratten 16 long-pass filter, a neutral density (ND) filter with an optical density of 1.4 (ND1.4), and an aperture, onto a diffusing screen made from tracing paper mounted on a clear glass plate. The luminance of the diffused orange/yellow background was 275 cd/m², measured on the diffusing screen with a Minolta LS100 photometer. For the control experiment, combinations of ND filters were used in place of the ND1.4 filter, as described in Section 3.1.

Figure 1.

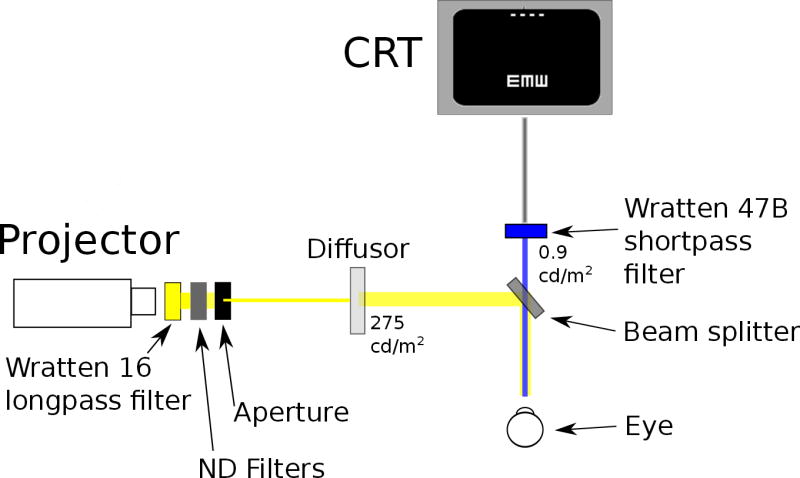
A schematic figure of the experimental setup.

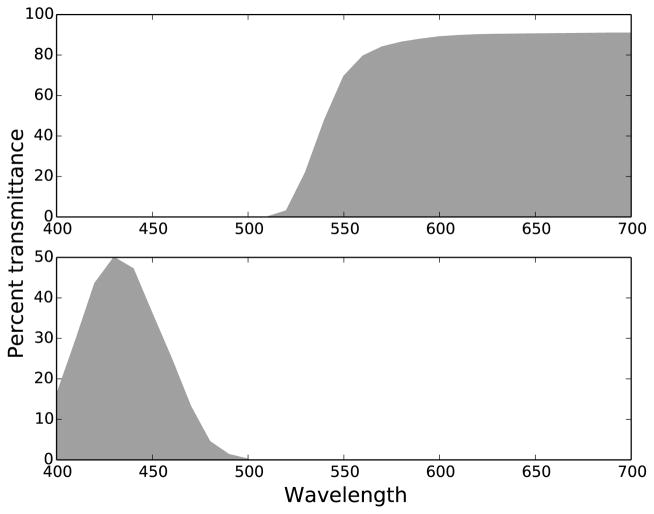
A beam splitter, located directly in front of the subject’s testing eye, combined the orange/yellow adapting background in a 50/50 ratio with the filtered output from a 15” CRT computer screen (Compaq/HP cv7500) with a resolution of 1024×768 pixels. Directly in front of the beam splitter a Wratten 47B short-pass filter was used to limit the stimuli to short wavelength light. The transmittances of the two Wratten filters used in this study are shown in Figure 2. This figure plots the data provided in numerical form in the “Transmission of Wratten Filters” guide from the Eastman Kodak Company. The computer displayed high contrast white stimuli on a black background. The target had a luminance of 0.9 cd/m², measured after passing through the Wratten 47B filter, before entrance into the beam splitter. The distance of the computer monitor to the beam splitter was 108 cm, and its image (subtending 17°×13°) was completely superimposed by the background. The experiment was conducted in a totally dark room.

Figure 2.

Transmittance curves for Wratten filters used in experiment. Top plot: Wratten 16 for the adapting yellow/orange background. Bottom plot: Wratten 47B for the short-wavelength-limited stimulus. Plotted from numerical data from the “Transmission of Wratten Filters” guide from the Eastman Kodak Company.

2.3. Stimuli

Stimuli comprised Tumbling-E patterns that satisfied Sloan specifications (NAS-NRC Committee on Vision, 1980). They were rendered and presented using custom software written in Python with the PsychoPy psychophysics library (Peirce, 2008). Threshold letter size (defined as the height (or width) of the entire letter) was measured when the target Es were presented alone (unflanked condition), or in the presence of two or four flankers. Flankers consisted of additional Tumbling Es in random orientations. For the two-flanker conditions, two flankers were positioned at equal distance on the left and right of the target E. For the four-flanker conditions, the flankers were positioned at equal distance above, below, to the left and right of the target E. Flanker spacing, measured from the center of the target to the center of the flanker, was specified in nominal units, relative to the stimulus size. Five spacings were tested for the two-flanker conditions: 1.5×, 1.75×, 2×, 3×, and 6× the stimulus size. For the conditions with four flankers, an additional condition with a spacing of 1.25× was tested. Subjects were tested at the fovea and at 3°, 5°, and 8° eccentricity in the lower visual field. When testing in the periphery, a fixation line (1° wide) appeared near the top of the CRT display, with the stimuli centered at 3°, 5°, or 8° below the fixation line. When testing at the fovea, the stimuli were centered on the display, and no fixation line was shown. Stimuli were presented for 150 milliseconds, after which subjects responded with the arrow keys on a standard computer keyboard to indicate the direction of the three bars of the target E (up, down, right or left). Immediately after the subjects responded for a trial, the next stimulus appeared.

There were five stimulus conditions in the main experiment of the study, summarized in Table 1. Luminance values indicate the luminance in the optical path before entering the beam splitter. Two conditions used the S-cone isolating setup described above, with either two (S2) or four (S4) flankers. For two other conditions without the yellow adapting background (N2 for two flankers and N4 for four flankers), the projector was turned off, yielding blue stimuli on a black background as seen by the subjects. The purpose of these conditions was to target the luminance pathway.

Table 1.

Summary of conditions

Code	Background condition	Number of flankers	Stimulus		Background
			Filter	Luminance	Filter	Luminance
S2	S-cone isolation	2	Wratten 47B	0.9 cd/m2	Wratten 16	275 cd/m2
N2	No background	2	Wratten 47B	0.9 cd/m2	(off)
S4	S-cone isolation	4	Wratten 47B	0.9 cd/m2	Wratten 16	275 cd/m2
N4	No background	4	Wratten 47B	0.9 cd/m2	(off)
LC4	Low contrast	4	ND1.8	0.9 cd/m2	ND2	100 cd/m2

The fifth condition (LC4) presented four flankers with the stimuli at a reduced contrast, thus providing a comparison with conventional crowding stimuli using achromatic targets. Note that the contrast for this condition was chosen such that the threshold sizes for un-flanked foveal LC4 stimuli were similar to those in the S2 and S4 condition. Other possible ways to normalize performance across conditions are considered in the Discussion. To reduce contrast, the projector was used with an ND2 filter instead of the Wratten 16 filter, resulting in a bright white background. Furthermore, the CRT screen luminance was reduced by replacing the Wratten 47B filter with a ND1.8 filter. With this ND filter, the luminance of the stimulus entering the beam splitter matched the luminance in the main experiment: 0.9 cd/m². The luminance of the white background as measured on the diffusing screen was 100 cd/m².

The letters were displayed in positive contrast on the CRT (white characters on a black background) and the beam splitter combined the CRT and projector background in equal proportion. Contrast values are determined by Equation 1. Mathematically, all luminance values are multiplied by one half due to the beam splitter, but these one half terms cancel in the ratio.

$$\text{Weber}\text{contrast}=\frac{(L_{\text{CRT}\text{target}}+L_{\text{projector}})-(L_{\text{CRT}\text{background}}+L_{\text{projector}})}{(L_{\text{CRT}\text{background}}+L_{\text{projector}})}$$ (1)

For the N2 and N4 conditions, the contrast was high: 0.9/0.0084=107. (L_{CRT target}=0.9 cd/m², L_{CRT background}=0.0084 cd/m², L_projector=0 cd/m²).

For the S2 and S4 conditions, the contrast was low: 0.9/275=0.0033 (0.33%). (L_{CRT target}=0.9 cd/m², L_{CRT background}=0.0084 cd/m², L_projector=275 cd/m²). However, the traditional measure of contrast (such as measured by a photometer) reflects responses in the luminance (L- and M-cone) pathway. Instead, a more relevant quantity is “S-cone contrast,” which determines contrast in the S-cone pathway in isolation. To estimate this measure requires the cone fundamentals of Smith and Pokorny (1975), the transmission curves in Figure 2, and stereotypical CRT spectral distributions. Interpolating from the data of Anderson et al. (2002) in a similar apparatus yields an effective contrast in the isolated S-cone pathway of approximately 0.74 (74%).

Finally, the contrast for the LC4 condition was low: 0.9/100 (0.9%). (L_{CRT target}=0.9 cd/m², L_{CRT background}=0.0084 cd/m², L_projector=100 cd/m²).

Note that a direct comparison between contrast values in the luminance and S-cone pathways is not necessarily straightforward. It is known that contrast sensitivity is lower for the isolated S-cone pathway than for the luminance pathway, for example. Stimuli targeting the luminance pathway (L- and M-cones) have a maximum contrast sensitivity of approximately 1.8 log units, whereas S-cone stimuli have a maximum contrast sensitivity of approximately 0.9 log units (Rabin, 1996). This was an additional motivation for our use of unflanked foveal acuity as the normalizing measure across conditions, as discussed later.

2.4. Psychophysical procedure

For all subjects, the two-flanker conditions were tested first, with S2 and N2 presented in a random order. Next, the four-flanker conditions (S4, N4, and LC4) were presented in a random order. Within each condition, the testing order of the four eccentricities was randomized. Then for each eccentricity, the different flanker spacings were tested in a random order in separate blocks of trials. For a given set of stimulus parameters (background, eccentricity, spacing), a three-down, one-up staircase was used to determine the smallest stimulus size that could be identified at 79% correct. Each staircase began with a stimulus that was well above threshold. To determine the final threshold, the last eight out of ten reversals were averaged using the arithmetic mean. Each threshold letter size reported in this paper represents the average of the thresholds determined from at least two staircases, tested on separate days.

2.5. Control Experiment: Validation of S-cone isolation

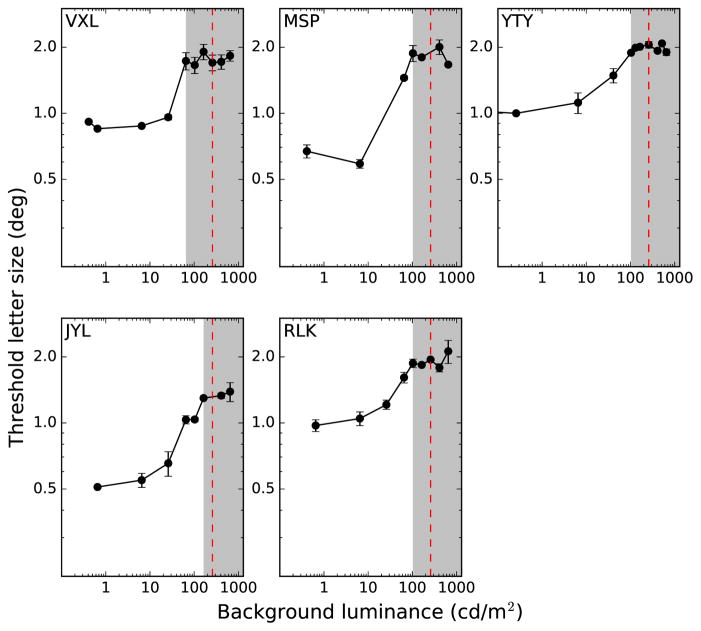
To confirm that our experimental paradigm successfully isolated S-cones, we followed the approach of Rabin and Adams (1990), Anderson et al. (2002), and Redmond et al. (2013). When the threshold is plotted as a function of the luminance of the yellow adapting background, there is an initial steeply rising portion over which threshold increases with the background luminance, followed by a plateau at higher luminances. The steeply rising portion represents the range of luminances where the task is mediated by L- and M-cones, while the plateau indicates S-cone involvement. Results from our control experiment, shown in Figure 3, illustrate this concept. The shaded regions at the right of each panel indicate the S-cone isolation regime. The plateau occurs because S-cone acuity is no longer affected by the background. Rabin and Adams (1990) noted that this shape illustrates the involvement of the underlying Stiles π mechanisms at each “branch.” Anderson et al. (2002) confirmed this effect at various locations in the visual field, including the fovea, and at 10°, 20°, 25°, and 35° eccentricity in the nasal and temporal retina. At every location in the visual field in their study, the shape of the curve was similar. Importantly, the critical luminance—the background luminance at which each curve started to flatten—shifted to higher values further in the periphery.

Figure 3.

Threshold letter size for identifying the orientation of a single blue Tumbling E is plotted as a function of the luminance of the yellow background. Results show the average and standard deviation of two staircases. Vertical red dashed lines indicate the luminance of the yellow adapting background used in the main experiment. Gray regions indicate S-cone isolation regimes, determined by the location of the plateaus.

In our control experiment, we measured the threshold letter size for identification of a single Tumbling-E stimulus presented against the yellow adapting background, for a range of background luminances. As in the main experiment, subjects viewed the target through a Wratten 47B filter so that it appeared blue (see Figure 1). Neutral density filters were placed between the Wratten 16 filter and the aperture to vary the luminance of the yellow adapting background. A range of luminances were tested, from very dim background levels to several that were brighter than the level used in the main experiment. On each trial, the Tumbling-E stimulus was presented at 8° eccentricity in the lower visual field. We used the same three-down, one-up staircase procedure to determine the threshold letter size, as in the main experiment. Since Anderson et al. (2002) showed that the critical luminance to achieve S-cone isolation increases with eccentricity, determination of the plateau at the largest eccentricity (8°) was sufficient validation that the luminance of the yellow background was high enough to isolate S-cones at all of the eccentricities tested in the main experiment.

3. Results

3.1. Control Experiment: Validation of S-cone isolation

Figure 3 presents our results from this control experiment for each subject. Threshold letter size was measured for a range of luminances of the yellow adapting background. The plateau for each curve was identified manually, and is indicated by the left edge of the gray region. The red dashed line in each panel in Figure 3 indicates the luminance of the background used in the main experiment (275 cd/m²). For all subjects, the threshold letter size measured at this luminance fell within the plateau region corresponding to the S-cone regime, confirming that the luminance of the yellow background used in the main experiment was high enough to isolate S-cones.

3.2. Main Experiment

Figure 4 plots representative results for the main experiment, showing all four eccentricities of one subject for the N2 condition (blue-on-black two-flanker stimuli). Each colored curve shows the threshold letter sizes as a function of flanker spacings at a given eccentricity. For all flanker spacings, threshold letter size (on the ordinate) increases progressively as the stimulus appears further in the periphery. Threshold letter size also increases when the flankers are closer to the target (smaller x-values), the hallmark of crowding.

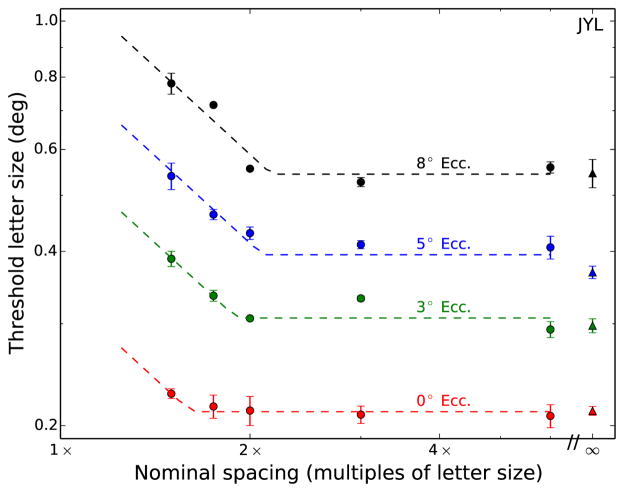
Figure 4.

Representative results of threshold letter size as a function of nominal spacing are plotted for all eccentricities for one stimulus condition (N2) and one subject. Data points indicate the mean threshold of two (or more) staircases, and error bars represent the standard deviation. Dashed lines indicate constrained two-line fits (see text for details). The infinity symbol denotes the no-flanker condition.

We fit our data with two hinged lines having fixed slopes of −1 and 0 on logarithmic axes. The fits were performed with custom software written in Python, with the Numpy/Scipy scientific libraries (Oliphant, 2007), using iterative nonlinear minimization of squared error. The x-coordinate of the intersection point of the two lines represents the nominal critical spacing, while the y-coordinate of this point indicates the threshold letter size. This fit has been employed successfully in describing and helping with the interpretation of data obtained in a variety of crowding studies, including studies using low contrast stimuli (Coates et al., 2013b), studies with patients lacking central vision (Chung, 2014), and studies with amblyopes and apperceptive agnosics (Song et al., 2014). The rationale of the fit is the following. The portion to the right of the critical spacing (the intersection point) is flat, since flankers outside the critical spacing have no effect on threshold letter size. Within the critical spacing (to the left of the intersection point), threshold letter size increases as the nominal critical spacing becomes smaller. The −1 slope in this region implies that there is a complete trade-off between threshold letter size and nominal critical spacing. This is a direct consequence of the fact that the critical spacing for a given stimulus condition at a given eccentricity has a fixed absolute size (in degrees of visual angle).

The two variables estimated from the fit are the unflanked threshold letter size and the critical spacing. The unflanked threshold letter size is defined by the ordinate value of the at portion, while the critical spacing is determined as the abscissa of the intersection point. Note that there is little crowding for the foveal condition in Figure 4, even at the smallest spacing tested (1.5×). This was true of all subjects, motivating the addition of a closer spacing (1.25×) for the four-flanker conditions.

3.2.1. Bootstrap procedure

To determine confidence intervals for the two fitted parameters, we performed the following bootstrap resampling procedure. For each subject, condition, and eccentricity, 1000 bootstrap samples of the data were created. Specifically, for each bootstrap sample, the appropriate subset of data (all measurements at every flanker spacing) was sampled with replacement, resulting in a new dataset. No constraints were placed on the resampling process, so any combination of flanker spacings could have been randomly chosen. For each of these samples, the best two-line function was determined for the data, yielding an estimate for the threshold unflanked letter size and critical spacing. The distributions of these 1000 estimates were used to characterize the fitted parameters, with the point estimate defined by the median.

3.2.2. Threshold letter size

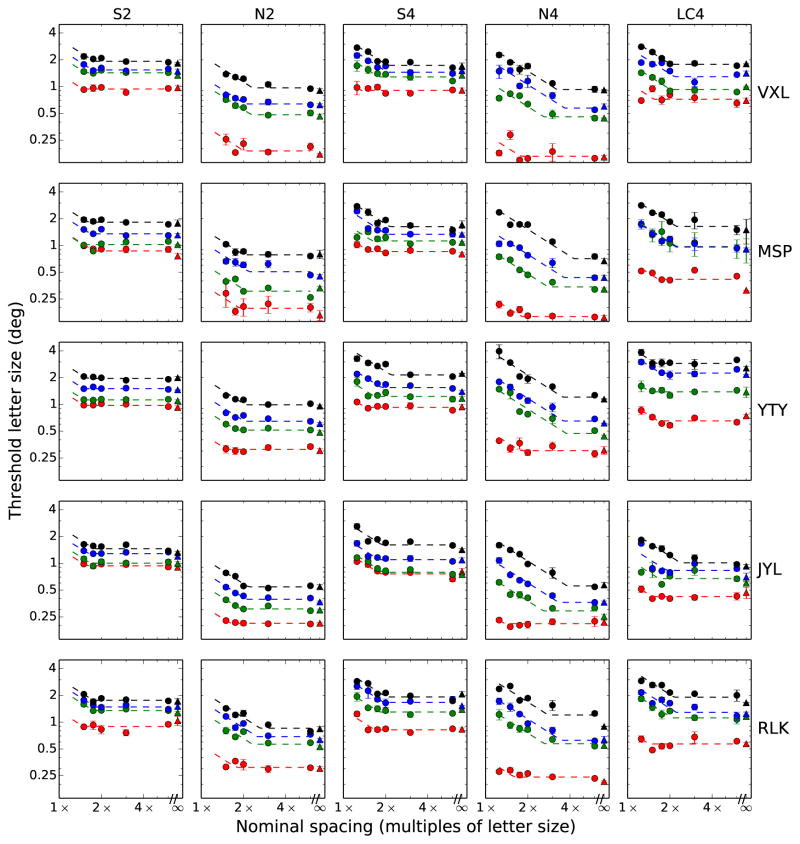
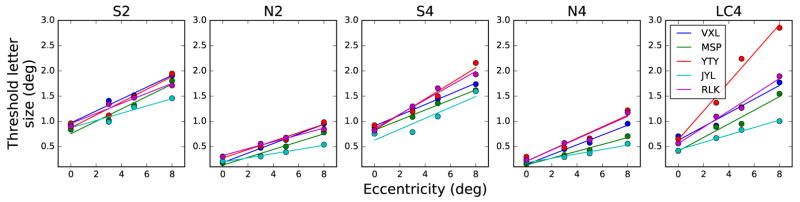
The entire set of results for the main experiment is shown in Figure 5. Each column corresponds to a different stimulus condition, while each row corresponds to a subject, as indicated. First, the systematic increase in thresholds as a function of eccentricity is evident for all subjects and conditions as the “stacking” of the parallel curves at successive eccentricities. To examine the change in threshold letter size with eccentricity, we first derived the unflanked threshold letter size (the ordinate of the at portion of each curve) as described earlier. The unflanked threshold letter sizes versus eccentricity for each of the five conditions are plotted in Figure 6. The linear change in size thresholds versus eccentricity is in good agreement with classic results (Jacobs, 1979; Latham and Whitaker, 1996; Toet and Levi, 1992; Weymouth, 1958). These studies noted a linear relationship between resolution thresholds (threshold letter size) and eccentricity for single achromatic letters, at least within the central 10° of the visual field.

Figure 5.

Threshold letter size as a function of nominal flanker spacing. Rows indicate subjects, columns indicate condition, from left: S-cone (2 flankers), Blue-on-black (2 flankers), S-cone (4 flankers), Blue-on-black (2 flankers), Low contrast (4 flankers). Eccentricities are colored as in Figure 4.

Figure 6.

Unflanked threshold letter size versus eccentricity, for the five stimulus conditions. Individual subject data are given in each panel. Colored curves depict best fitting lines, as described in the text.

A traditional method of quantifying these data is the E₂ measure, a value which indicates the eccentricity at which the foveal value doubles (Levi et al., 1984; Levi and Klein, 1985). We use the form stated in Toet and Levi (1992). Thresholds (T) at different eccentricities are fit by an equation of the form T=T₀(1+E/E₂), where T₀ is the foveal threshold and E is the eccentricity in degrees. There are two ways to determine E₂ and T₀ for the data in Figure 6. One way is to simply fit a regression line to the data points and use the resultant slope (m) and intercept (b), where T₀=b and E₂=b/m. The other technique is to perform optimization on the equation for T directly, such as an iterative non-linear regression method of minimizing least-squares. For our data the two methods yield virtually identical results.

The first two rows in Table 2 show the E₂ and T₀ values corresponding to the change in unflanked threshold letter size with eccentricity in the normal periphery, for the different stimulus conditions. Each value shown is the average and standard deviation across our five subjects. Our N4 and N2 conditions (blue stimuli on a black background) were designed to target the luminance channel, yielding results comparable to the literature, which typically used high-contrast, achromatic stimuli (Jacobs, 1979; Toet and Levi, 1992; Latham and Whitaker, 1996). For the N4 condition, the E₂ is 2.30±0.97, a value in the typical range of 1.0–3.0 reported for resolution tasks such as grating acuity or letter identification (Herse and Bedell, 1989; Virsu et al., 1987; Levi et al., 1985; Latham and Whitaker, 1996; Toet and Levi, 1992; Strasburger et al., 2011). The E₂ of 3.30±1.31 for condition N2 also agrees with previous findings. The solid colored lines in Figure 6 illustrate the best-fit lines for each subject in each condition.

Table 2.

E₂ and T₀ values averaged across the five subjects for the five stimulus conditions

		S2	N2	S4	N4	LC4
Unflanked threshold letter size (deg)	E2	8.62±2.13	3.30±1.31	6.84±1.35	2.30±0.97	3.87±1.29
	T0	0.89±0.08	0.22±0.07	0.81±0.10	0.18±0.03	0.54±0.09
Critical spacing (deg)	E2	7.17±1.35	2.26±0.58	4.54±0.98	0.73±0.24	2.47±0.49
	T0	1.39±0.08	0.39±0.11	1.28±0.14	0.25±0.11	0.85±0.20

E₂ has not been previously quantified for S-cone stimuli. However, resolution thresholds for S-cone stimuli across the visual field were reported by Anderson et al. (2002). These authors determined the threshold for resolving oblique gratings using a similar S-cone isolation setup, in the fovea and in the nasal and temporal visual fields at 10°, 20°, 25° and 35° eccentricity. Our threshold letter sizes are slightly larger than predictions based on that study. Specifically, we interpolated their threshold grating acuity measured at the fovea and at 10° eccentricity in three observers (their Figure 3). Conversion from grating acuity (in cycles/deg) to threshold letter size was computed by assuming that each Tumbling E stimulus comprised 2.5 cycles of gratings. This procedure yielded values that could be compared to our results.

Their S-cone threshold letter sizes at 8° eccentricity were 1.15°±0.15, averaged across three observers. Our S-cone threshold letter sizes at 8° eccentricity ranged from 1.5° to 2.2° for our five observers (mean±SD of 1.8°±0.18 for condition S2 and 1.8°±0.21 for condition S4), as shown in Figure 6, Panel 1 and Panel 3. There are several plausible explanations for this discrepancy, relating to differences in the experimental paradigms. Their stimuli were gratings, presentation time was longer (1 second total, with a 0.3 second sinusoidal rise and fall), and they tested on the horizontal meridian. Acuity measured on the inferior visual meridian is approximately 25% worse than acuity measured on the horizontal meridians (Phelps, 1984). Despite these differences, the studies are in good agreement that the resolution thresholds for S-cone stimuli at 8° eccentricity are approximately twice the foveal thresholds. Formally, estimating E₂ from the foveal and 10° eccentricity data of Anderson et al. (2002) yields an E₂ of 7.67±1.03 for their three subjects, which is very similar to the E₂ for our S-cone conditions: 8.62±2.13 and 6.84±1.35 for S2 and S4, respectively.

3.2.3. Critical spacing

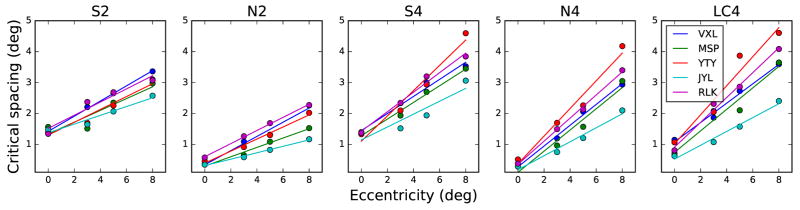
Next, we evaluate the critical spacings derived from the data. Since the critical spacing for crowding (in absolute units) in the normal periphery is independent of the size of the target (Levi et al., 2002; Pelli et al., 2004; Tripathy and Cavanagh, 2002), absolute critical spacing, in degrees of visual angle, is the desired measure and are used for all further analyses. Absolute critical spacings were obtained by multiplying the nominal critical spacings with the unflanked threshold letter sizes. Absolute critical spacing is plotted as a function of eccentricity for the five conditions in Figure 7. Again a linear relationship with eccentricity is evident, which is consistent with previous studies (Bouma, 1970; Latham and Whitaker, 1996; Toet and Levi, 1992). A comparison between Figure 6 and Figure 7 shows that the rate of incease in critical spacing with eccentricity is much faster than the rate of increase in threshold letter size with eccentricity (Figure 6), as reported for achromatic stimuli in previous studies (e.g. Toet and Levi (1992); Latham and Whitaker (1996)).

Figure 7.

Critical spacing as a function of eccentricity for the five stimulus conditions. Individual subject data are given in each panel. Colored curves depict best fitting lines, as described in the text.

Condition N4 (comprising a blue stimulus on a black background) is the condition most readily comparable to previous studies because it does not target the S-cone pathway. The critical spacing E₂ calculated for this condition is 0.73±0.24. With two flankers, the critical spacing E₂ increased to 2.26±0.58. In other words, the critical spacing increases with eccentricity at a faster rate when there were more flankers. Similarly, the critical spacing E₂ for the S4 condition is smaller (4.54±0.98) than that of the S2 condition (7.17±1.35). These results are expected, as crowding increases with the number of flankers (Põder and Wagemans, 2007; Strasburger et al., 1991), especially when the additional flankers are oriented along the (radial) line connecting the target and the fovea.

3.2.4. Bouma’s law: critical spacing linear fits

The rule-of-thumb known as “Bouma’s law” refers to the linear change in critical spacing as a function of eccentricity (Bouma, 1970; Pelli et al., 2004, 2007; Rosen et al., 2014; Strasburger, 2005; Strasburger et al., 2011). The precise expression specifying critical spacing in terms of center-to-center target-flanker spacing is d=b×E+w, where b is the slope or “Bouma constant,” w is the y-intercept, and E is the target eccentricity in degrees. The intercept corresponds to the foveal critical spacing, which is typically negligible, and often limited by the threshold letter size at the fovea.

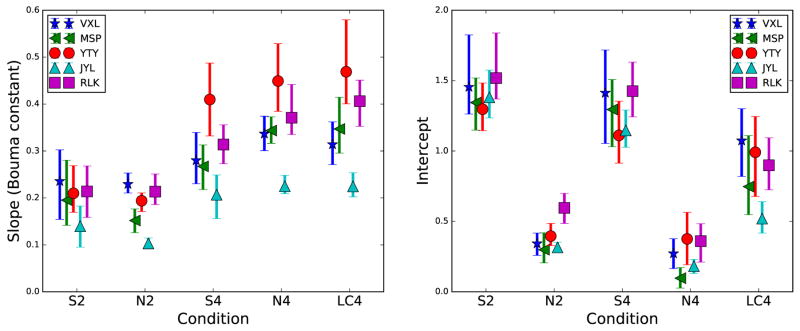
The parameters for the linear fits of the individual critical spacings versus eccentricity are shown in Figure 8. The left panel indicates the fitted slopes, while the right panel indicates the fitted intercepts. To calculate the error bars, the bootstrap procedure described in Section 3.2.1 was used. Specifically, 1000 bootstrap estimates of the critical spacing at each eccentricity were generated. Then, the best linear fit through the four bootstrapped critical spacing estimates was determined, resulting in 1000 estimates of the slope and intercept. The error bars in Figure 8 indicate the 95% confidence intervals from this procedure.

Figure 8.

Parameters from the individual linear fits of Figure 7 (critical spacing versus eccentricity) are plotted as a function of condition for each subject. Left panel indicates the slope of each line. Right panel shows the y-intercept of each line. Error bars are 95% confidence intervals determined from bootstrap resampling.

The values from Figure 8 reveal two different types of per-condition groupings. First, the slopes group based on the number of flankers. The two-flanker conditions result in smaller values (0.14–0.24 and 0.10–0.23 for S2 and N2, respectively), while the four-flanker conditions have larger (steeper) slopes (0.21–0.41, 0.23–0.45, and 0.22–0.47, for S4, N4, and LC4, respectively). These values are in excellent agreement with a wealth of results from the literature, with the number typically referred to as the “Bouma constant,” with a value of 0.3–0.5 for many experiments (Chung et al., 2001; Pelli et al., 2004; Strasburger et al., 2011). The smaller constants for the tangential two-flanker conditions are as expected, as mentioned earlier.

The intercept terms group differently. They are small for the two achromatic conditions (ranges of 0.30–0.59 and 0.10–0.37 for N2 and N4, respectively), large for the S-cone conditions (1.30–1.52 and 1.11–1.41 for S2 and S4, respectively), and intermediate (0.52–1.06) for the low contrast condition. The significance of these two types of clustering of results will be mentioned further in the Discussion section.

3.3. Fitted summary results

Due to the variability of the data ranges for our subjects and conditions, the variation in the previous literature, and the novelty of our paradigm, it is challenging to find a framework to support the analysis of these data. However, it has been shown previously that plotting the absolute critical spacing versus the threshold letter size reveals patterns in the data. Specifically, for several studies, data pooled across subjects and eccentricities plotted in this way are collinear within a condition. The slope of the corresponding line is diagnostic, reflecting either the stimulus condition such as stimulus contrast (Coates et al., 2013a), or subject population, such as patients with macular degeneration (Chung, 2014) or type of amblyopia (Song et al., 2014).

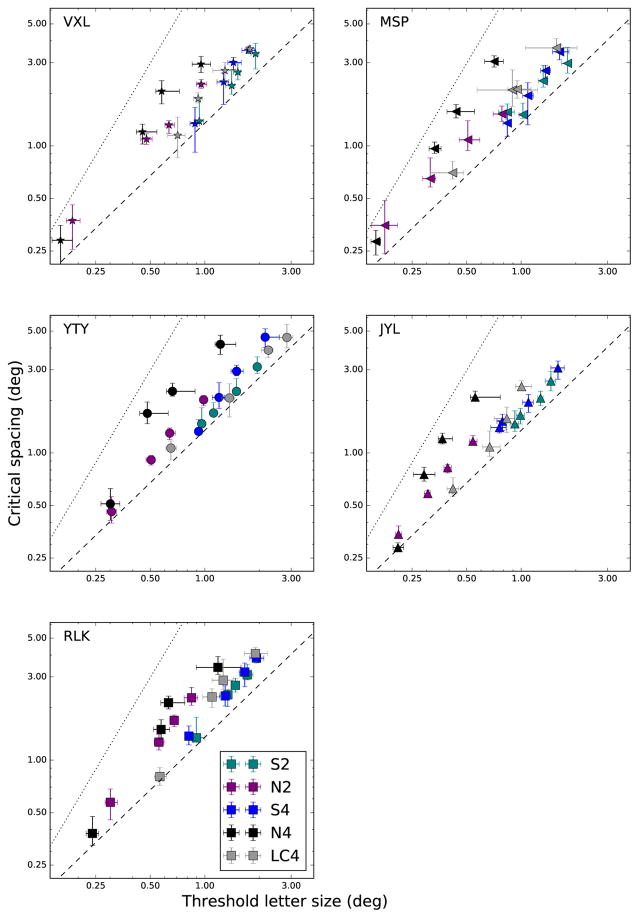
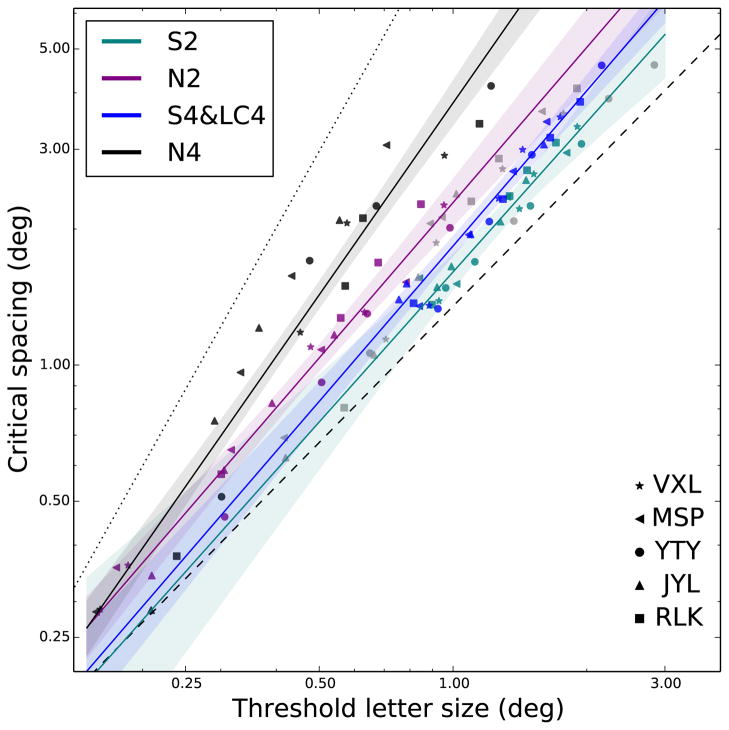
Figure 9 shows this approach, with a separate plot for each subject. Each data point in each plot represents a single eccentricity and condition. The conditions are color coded as indicated in the figure legend. Error bars indicate the 95% confidence intervals determined from the fitting procedure. The dotted line to the upper left of each plot indicates the line log(y)=1.75×log(x)+1.0, which corresponds to results for high-contrast peripheral targets in normal observers (Chung, 2014; Song et al., 2014). The dashed line near the middle of each plot indicates the line log(y)=log(x)+0.13, which corresponds to results for blurred foveal targets with normal observers (Song et al., 2014) or low-contrast stimuli with normal observers (Coates et al., 2013a). The former line illustrates the well-known result that the critical spacing for crowding typically grows more quickly than the threshold letter size as eccentricity increases. The latter line, on the other hand, indicates that in some conditions critical spacing grows more closely in tandem with threshold letter size, such as at the fovea. We refer to these two lines as “crowding-limited” and “acuity-limited,” respectively. Clearly, our results lie between these two extremes. Most importantly, the same-colored points, indicating the four eccentricities for each condition, appear collinear.

Figure 9.

Critical spacing (absolute size in deg) is plotted as a function of threshold letter size (deg). Each data point represents the critical spacing and threshold letter size (derived from the fitting procedure in Figure 5, and are plotted in Figures 6 and 7) for one condition and at one eccentricity. Conditions are color-coded as shown in legend. Error bars represent 95% confidence intervals determined from the fitting procedure. Dotted line indicates results from previous studies that used high-contrast targets in the normal periphery. Dashed lines shows previous results with blurred foveal targets.

To determine the significance of this per-condition linearity, we performed model comparison using the statistical package R (Ihaka and Gentleman, 1996). A full model comprises five independent lines, each with unique slope and intercept (a total of 10 parameters). Simpler models yoke the parameters of lines across subsets of the conditions, identifying groups that are not statistically different. Only one model was superior to the saturated (full) model of a separate line for each of the five conditions. The model that combined the low contrast, 4-flanker condition (LC4) with the S-cone 4-flanker (S4) condition could not be rejected (F-ratio test: F(89,2)=1, p=0.37). All other models were significantly inferior (p<0.05) to the full model, based on F tests. The adjusted R² of this combination model (S4+LC4) was 0.954. Note that there was greater variability in the S-cone and the low-contrast stimuli than the achromatic stimuli.

Figure 10 shows the results of the model fitting, plotting the data pooled across subjects and the fitted regression lines. The equations for the four lines, sorted by decreasing steepness, are: log(y)=1.41×log(x)+0.58 (N4: no background, 4 flankers), log(y)=1.14×log(x)+0.3 (N2: no background, 2 flankers), log(y)=1.14×log(x)+0.22 (S4: S-cone, 4 flankers and LC4: low contrast, 4 flankers) and finally, log(y)=1.09×log(x)+1.03 (S2: S-cone, 2 flankers). Shaded regions indicate 95% confidence regions from the regressions. The dotted and dashed lines represent results from the literature, included here for reference, as in Figure 9. All data lie within the ranges found previously with other experimental paradigms. In summary, the lines fitting the two-flanker conditions are flatter than the corresponding four-flanker conditions, and the S-cone conditions (and the low contrast condition) are flatter than the corresponding no-background conditions. The significance of these observations concerning the slope will be described in the Discussion section.

Figure 10.

Critical spacings are plotted as a function of threshold letter sizes. Data are replotted from Figure 9. Data from the five subjects are pooled, and different conditions are fit with colored lines as described in the text. Shaded regions around each line represent 95% confidence intervals estimated from linear fits. The dashed and dotted lines represent results from previous studies using blurred stimuli presented at the fovea (dashed line, representing acuity-limitation), or high-contrast stimuli presented in the normal periphery (dotted line, representing crowding-limitation).

4. Discussion

This paper presented experiments measuring foveal and peripheral crowded acuity under an S-cone isolation paradigm. First, we found that the constrained two-line model, previously used to determine the critical spacing in standard achromatic paradigms, fit our data for the different conditions well, as shown in Figure 4 and Figure 5. This validates the finding that within the crowding zone, there is a perfect trade-off between size and spacing. Thus, this characteristic of crowding holds even for stimuli that are mediated by the koniocellular pathway.

Figure 10 helps connect this work to previous findings obtained using traditional paradigms. The intuition of this plot is that although individual subjects vary in their acuities and crowding amounts, the relationship between these two measures, and the correlated change in the two values is similar across subjects, independent of eccentricity, and indicative of the stimulus condition. The dotted line, with a slope (on log-log axes) of 1.75, represents results that have been reported for crowding in the normal periphery using high-contrast targets (Chung, 2014; Coates et al., 2013a; Song et al., 2014). The dashed line, with a slope of 1, represents results of crowding limited by blur at the fovea (Song et al., 2014) or crowding with low-contrast peripheral targets (Coates et al., 2013a). Song et al. (2014) found that the results for anisometropic amplyopes were located near the foveal line, while results for strabismic amblyopes followed the peripheral line. Additionally, Chung (2014) showed that results for patients with age-related macular degeneration can fall on either of the lines, or lie between them. The adoption of a region in the peripheral retina as the new reference locus to replace the fovea as an adaptation to the loss of central vision was one possible explanation for those subjects whose data do not fall on the peripheral line.

Together, these results confirm the notion that the normal periphery is “crowding-limited,” while the normal fovea is “acuity-limited,” and a variety of conditions can be differentiated based on their slopes on this type of plot (Chung, 2014; Song et al., 2014). These terms refer to the fact that a steeper line indicates that the crowding zone grows rapidly with eccentricity, and crowding will be more of a limiting factor than letter resolution for crowded acuity tasks. Flatter lines, on the other hand, correspond to situations in which the critical spacing changes more slowly, perhaps barely exceeding the threshold letter size. In these cases it will be the size of each letter, not interference from the flankers, that is the limiting factor as eccentricity increases (Chung, 2014).

For our stimulus conditions, the lines were positioned between the two extremes. The two conditions without the yellow adapting background (N2 and N4) were more crowding-limited, having a larger slope closer to the dotted line, while the S-cone isolation conditions (S2 and S4) were more acuity-limited, closer to the dashed line with a slope of 1. Furthermore, the pattern of results agreed with those of previous studies in that points were constrained between the two lines, implying that S-cone crowding is not qualitatively different from the variety of conditions and patient groups that have been characterized previously using the techniques illustrated in Figure 10. The statistical indistinguishability of the low-contrast (LC4) and the S-cone (S4) results further suggest that there is also no quantitative difference between S-cone crowding and that of stimuli of suitably low contrast. One possible alternative explanation is that the combined model fit was superior due to the larger variability of both the S-cone and the low-luminance stimuli versus the achromatic stimuli, both within and across subjects. This variability could have been due to proximity to subjects’ contrast detection thresholds, which we did not measure.

Note that we chose the contrast of the LC4 stimuli such that foveal letters at the un-flanked identification threshold had roughly comparable sizes in that condition, in relation to the S-cone size thresholds (condition S2 and S4). Other than this method of equating unflanked foveal acuity, there are at least two other possible ways to normalize performance across conditions. The first method involves measuring each subject’s contrast detection threshold, and then determining size thresholds for identification at a certain multiple of the contrast level for detection. This would have tested stimuli with equivalent “visibility.” An alternative approach is to exactly equate the cone contrasts across conditions, which would have yielded stimuli with the same theoretical pathway excitation. Both of these methods would likely have resulted in different threshold stimulus sizes, since the contrast sensitivity function (CSF) for S-cone stimuli is both reduced and shifted to lower spatial frequencies relative to the luminance CSF (Mullen, 1985). It is conceivable that the critical spacing for crowding may also be sensitive to the method of equating baseline performance, which is an interesting topic for future study.

The pattern of results from Figure 8 (analyzing critical spacing versus eccentricity) lend additional support to the claim that crowding in the S-cone isolation paradigm does not differ significantly from crowding in traditional achromatic paradigms, except for the effects of lowered contrast. Specifically, although the baseline critical spacings for the S-cone stimuli were much greater than the critical spacings for the high-contrast stimuli (Figure 8, right panel), the intermediate critical spacing of the low-contrast stimuli suggests that this effect could be due to the lower contrast sensitivity in the S-cone pathway. The slopes (or Bouma constants), on the other hand, had very similar values between conditions when they were grouped based on the number of flankers (Figure 8, left panel). This property, reflecting the known finding that more flankers generally cause more crowding, suggests a similar mechanism underlying crowding for the two pathways.

Our results are also in agreement with the neurophysiological results of Sceniak et al. (2006) in macaques. These authors found that neither the spatial extent of excitatory summation, nor the spatial extent of the suppressive surround (from the non-classical receptive field) differed significantly among neurons in the input layers of V1 (corresponding to the achromatic, red/green, and koniocellular pathways.) Therefore, the signals for stimuli in these pathways have the same cortical extent, and thus the neural theories typically invoked for crowding—large receptive fields or excessive signal propagation—would occur over identical distances. In all, this converging evidence suggests that the deleterious effects of crowding, including its neural “signature,” affect stimuli in the achromatic and the koniocellular pathways similarly. However, the current results do not allow distinguishing between whether crowding is localized within the channels (but with equal extent), or whether crowding occurs after the chromatic channels are combined.

• Spatial crowding was studied in an S-cone isolation paradigm

• The Bouma constant for critical spacing matched classic achromatic results

• The larger baseline critical extent matched low-contrast achromatic stimuli

• S-cone crowding appears similar to low-contrast luminance crowding