A graphical model method for integrating multiple sources of genome-scale data

Abstract

Making effective use of multiple data sources is a major challenge in modern bioinformatics. Genome-wide data such as measures of transcription factor binding, gene expression, and sequence conservation, which are used to identify binding regions and genes that are important to major biological processes such as development and disease, can be difficult to use together due to the different biological meanings and statistical distributions of the heterogeneous data types, but each can provide valuable information for understanding the processes under study. Here we present methods for integrating multiple data sources to gain a more complete picture of gene regulation and expression. Our goal is to identify genes and cis-regulatory regions which play specific biological roles. We describe a graphical mixture model approach for data integration, examine the effect of using different model topologies, and discuss methods for evaluating the effectiveness of the models. Model fitting is computationally efficient and produces results which have clear biological and statistical interpretations. The Hedgehog and Dorsal signaling pathways in Drosophila, which are critical in embryonic development, are used as examples.

1 Introduction

Individual types of genomic data give only an incomplete picture of the mechanisms of regulation and expression; multiple data sources are necessary to understand the process of expression from transcription factor (TF) binding to transcription. For example, binding data tell us where DNA-binding proteins such as TFs are bound to the genome, but not how, which, or even whether genes are regulated by these proteins. Expression data provides direct evidence of gene regulation, but does not reveal the mechanisms of that regulation. Sequence conservation indicates possible functional conservation, but not the specific function being conserved. Taking advantage of the information present in all of these data sources should produce a high-quality list of genes whose products are critical to a particular pathway or phenotype.

We present here a method with explicit statistical models for univariate and multivariate data sources, good computational efficiency, and easily interpretable results. Our motivating examples involve embryonic development in Drosophila melanogaster, using data for TF binding, gene expression, and DNA sequence conservation. For the first example, we wish to identify genes in the hedgehog (Hh) pathway which are targets of the cubitus interruptus (Ci) TF involved in regulation of almost all Hh-responsive genes (Von Ohlen et al., 1997). For the second example, we wish to identify targets of the dorsal (Dl) TF, which controls dorsal-ventral patterning in early embryogenesis. We intend our method to be generally applicable to a wide variety of problems and data sources.

Our method fits layered and chained graphical mixture models, which are special cases of Bayesian belief networks, to the data. Model fitting is simultaneous, estimating the parameters of the model from all available data, as opposed to a sequential or filtering approach in which portions of data of one type are discarded based on analysis using data of another type. Because no non-target genes are definitively known, we use an unsupervised approach. We show that our combined models are more effective than models using a single data source at identifying target genes, and are also more effective than other combined-data models.

2 Related work

The general approach of hierarchical mixture modeling, which we apply here to genomic data, has been applied in other contexts, usually to represent a random- or fixed-effects model. For example, Vermunt and Magidson (2005) present a model for categorical data and apply it to employee-satisfaction surveys from nursing home and home-care employees. Here groups of employees are nested within clusters of teams; the model fitting procedure finds the appropriate number of classes at each level and estimates the characteristics of each class. Lourme and Biernacki (2013) present a model for continuous data and apply it to classification of shearwaters (a type of seabird) from geographically dispersed populations using morphological data, and show that clusters of birds within each population have similar characteristics. In the bioinformatics realm, Jörnsten and Keleş (2008) study the relationships between clusters of time-series gene expression data from different cell lines, while Li et al. (2010) discuss protein identification from mass spectrometry data with a nested model in which observed spectra are generated by hidden peptide data, which are in turn generated by hidden protein data.

A characteristic of all these models is that although the groups are heterogeneous, the data are homogeneous; that is, each mixture component, at each level of the hierarchy, represents a grouping of the same type of observations. The use of hierarchical mixture models in which the lower level of the hierarchy is heterogeneous, representing groups of different types of data, as described here in Section 3, does not appear to be common in genomics or elsewhere. A broad overview of existing approaches to genomic data integration is given in Hawkins et al. (2010), and specific applications abound. We give here a few examples in domains related to the problem at hand.

Integration of binding and expression has been successfully applied to finding TF targets in Qin et al. (2011). Sequence-based data, although it provides less direct functional evidence than do binding and expression, is often a useful addition to other data types. DNA sequence conservation is used in Ortiz-Barahona et al. (2010) for TF target prediction. De Bie et al. (2005) and Xie et al. (2010) integrate binding site motif scores with binding and expression for the same purpose. Multiple sequence-based measures are used in Seringhaus et al. (2006) for essential gene prediction. Expression and copy number are integrated in Tyekucheva et al. (2011) for functional gene set analysis. Of these, only Xie et al. (2010) present a mixture model approach. Our approach is conceptually similar to theirs, but extends the modeling strategy for multivariate data with more flexible choices of topology, and is computationally less complex. We discuss the difference between the approaches in more detail in Section 3.3.

An important conclusion from these works is that integrated analysis is more effective than looking at data sources in isolation. In particular, simultaneous approaches are preferred to the sequential or filtering approach (De Bie et al., 2005; Hoffman et al., 2012). Simultaneous approaches provide more insight into the biological processes which generate the joint distribution of the data (Lemmens et al., 2006) and help reduce the effect of noise and increase power to detect signal (Tyekucheva et al., 2011).

Much of the work in genomic data integration has focused on supervised (Seringhaus et al., 2006) or partially supervised (Ortiz-Barahona et al., 2010; Tyekucheva et al., 2011) classification approaches which require high-quality training sets with both positive and negative controls. However, when available training data sets are small, unreliable, or incomplete, unsupervised methods are required (Lemmens et al., 2006; Xie et al., 2010; Qin et al., 2011; Hoffman et al., 2012) and this is the approach we follow here.

3 Models

The layered and chained models used for integrating the various data sources are described here. We first give an overview of the layered and chained model topologies and discuss the desired output of the model. Next, we describe the marginal models which are components of the joint model, and model fitting and selection procedures. We then describe the joint model fitting procedure and discuss the ways in which it extends the standard EM algorithm for mixture model parameter estimation. Finally, we discuss details of interpretation for the fitted model.

3.1 Overview of the joint model

We describe the relationship between target status (for the current problem, target vs. non-target) and observed data with a hierarchical generative model. Here a “top-level” hidden variable generates “intermediate” hidden variables, which in turn generate the observed data. In the current model, the hidden variables are categorical, while the observed data are continuous; we can also model discrete observed data with the appropriate choice of distribution.

Let the top-level hidden random variable ${\mathcal{Y}}_0$ denoting target status, take on integer values from 1 to K₀ for some integer K₀>1. Now for some integer Z>1 denoting the number of different data sources, and z=1,…, Z, let the intermediate hidden random variables ${\mathcal{Y}}_z$ take on integer values from 1 to K_z for some integer K_z>1. In the current problem, Z=3 and the data sources in order are binding (z=1), expression (z=2), and conservation (z=3). Also define the observed random variables ${\mathcal{X}}_1,\dots {\mathcal{X}}_Z$ (each ${\mathcal{X}}_Z$ may be multivariate) where the distribution of ${\mathcal{X}}_z$ depends only on the value of ${\mathcal{Y}}_z$.

We consider here two topologies for representing the relationships between these variables. The first is the layered mixture model shown on the left side of Figure 1, in which ${\mathcal{Y}}_0$ generates $\mathcal{Y}=({\mathcal{Y}}_1,\dots ,{\mathcal{Y}}_Z)$. This model treats all observed variables as equally important to estimating the distribution of ${\mathcal{Y}}_0$. The second is the chained model shown on the right side of Figure 1, in which the top-level hidden variable ${\mathcal{Y}}_0$ generates the hidden variable ${\mathcal{Y}}_1$, which in turn generates the observed variable ${\mathcal{X}}_1$ and the next hidden variable ${\mathcal{Y}}_2$, etc.

Figure 1.

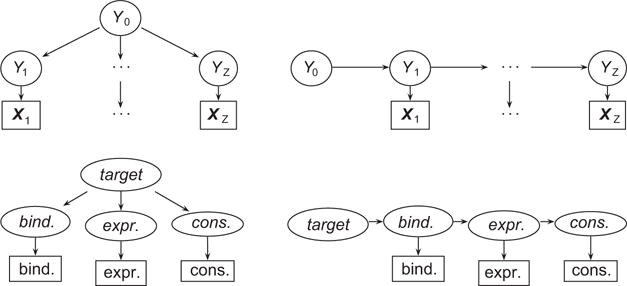
The layered (left) and chained (right) mixture models. The general model is shown in the upper row. Ovals indicate hidden variables, while rectangles indicate observed variables. Arrows show generative relationships, which account for all dependencies between variables. The specific model is shown in the lower row, with binding corresponding to z=1, expression to z=2, and conservation to z=3. Names of hidden data are in italics, while upright typeface indicates observed data.

For the current problem, the chained model reflects the flow of biological information, from binding to expression to conservation. That is, binding regulates expression, and changes in expression lead to phenotypic differences which are subject to selective pressure. More generally, the chained model is also appropriate when the data types can be arranged in order of specificity to the problem at hand – here, for example, binding data is the most specific to TF target identification and conservation the least specific, with expression in the middle.

Note that the chained model is a heterogeneous hidden Markov chain, in contrast to the more common homogeneous variety; that is, the ${\mathcal{Y}}_z\mathrm{s}$ are not all drawn from a single alphabet. Generally, the sample spaces $\mathrm{\Omega }({\mathcal{Y}}_i)\ne \mathrm{\Omega }({\mathcal{Y}}_j)$ when i≠j, nor does equality of sample space imply equality of distribution.

The distributions of the ${\mathcal{Y}}_z’\mathrm{s}$ depend – directly or indirectly, depending on the model topology – on the value of ${\mathcal{Y}}_0$. In the problem at hand, K₀=2 with ${\mathcal{Y}}_0=1$ indicating target and ${\mathcal{Y}}_0=2$ indicating non-target. Given N genes, for n=1,…, N the estimated posterior probability that the nth gene is a target is $\text{Pr}(y_{0,n}=1|{\mathit{x}}_{.,n},\widehat{\theta })$ Here y_{0, n} is the nth hidden target status variable, that is, a realization of ${\mathcal{Y}}_0$. Similarly, x_{., n}=(x_{1, n},…, x_{z, n}) is the observed data for the nth gene, with x_{z, n} being a realization of ${\mathcal{X}}_z$. Finally, $\widehat{\theta }$ denotes the estimated parameters of the model.

The interpretation of the ${\mathcal{Y}}_z\mathrm{s}$ depends on the value of K_z for each z. In the current problem, if K₁=2, then ${\mathcal{Y}}_1=1$ indicates a bound cis-regulatory region while ${\mathcal{Y}}_1=2$ indicates unbound; if K₂=3, then ${\mathcal{Y}}_2=1$ indicates over-expression, ${\mathcal{Y}}_2=2$ no differential expression, and ${\mathcal{Y}}_2=3$ underexpression; and if K₃=2, then ${\mathcal{Y}}_3=1$ indicates high conservation while ${\mathcal{Y}}_3=2$ indicates low conservation. The distribution of ${\mathcal{X}}_z$ given ${\mathcal{Y}}_z$ reflects these interpretations: for example, in the case of binding, $\mathrm{E}[{\mathcal{X}}_1|{\mathcal{Y}}_1=1]>\mathrm{E}[{\mathcal{X}}_1|{\mathcal{Y}}_1=2]$, as seen in Figure 2. Supplementary Figure 1 shows similar distributions for the other data sources.

Figure 2.

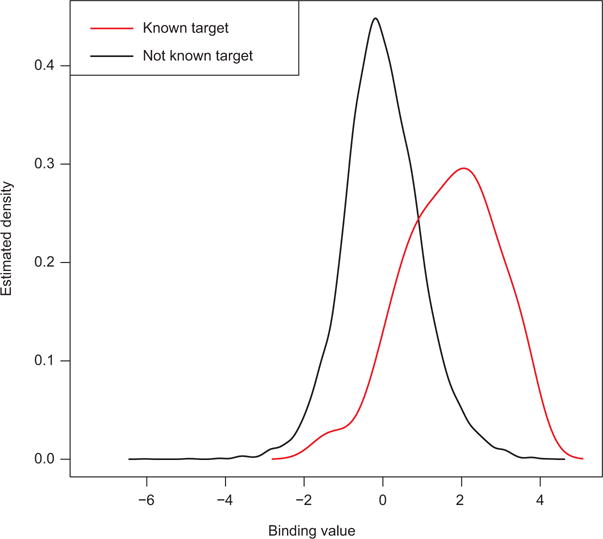
Nonparametric density estimates for binding data, for known Ci target genes and genes of unknown target status (see Section 5.1 and Supplementary Figure 1).

3.2 Marginal models

For each data source, we may fit a standard mixture model to that data source alone. This is referred to as the “marginal model” because it deals only with one data source at a time, as opposed to the “joint model” described in Section 3.1. We do this to choose the number of components K_z and marginal distribution for each data source, which are then used in the joint model fitting procedure discussed in Section 3.3. Here we describe the marginal modeling procedure in detail and introduce notation used in following sections.

A natural choice for modeling data of dimension D≥1 on (−∞, ∞)^D is a mixture of (multivariate) normal distributions, in which all the genes have the same mean and variance within each component, but different means and variances across components. Let mixture component membership be represented by $\mathcal{Y}$, a categorical random variable taking on values from 1 to some integer K>1 (the number of components) with distribution parameter p=(p₁,…, p_k) being the component probabilities, such that Σ_kp_k=1 for k=1,…, K. Here $\mathcal{Y}$ may represent target status or some more specific categorization such as bound vs. unbound, etc. Then the component-specific distribution of $\mathcal{X}$ is f_y(x|θ) = ϕ(x|μ_y, Σ_y), where ϕ is the normal density. The joint distribution of $\mathcal{X}$ and $\mathcal{Y}$ is therefore

$$\mathrm{f}(\mathit{x},y|\theta )=p_y{\mathrm{f}}_y(\mathbf{x}|\theta ).$$ (1)

From this, for a sample X=(x₁,…, x_N), we use the EM algorithm (Dempster et al., 1977; McLachlan and Krishnan, 2008, pp. 61–66) to estimate the parameters and find the posterior probabilities ${\widehat{w}}_{n,y}=\text{Pr}(y_n=y|{\mathit{x}}_n,\widehat{\theta })$. Specifically, the EM algorithm finds the maximum likelihood estimate $\widehat{\theta }$ by iterative maximization of the “Q-function,” or the conditional expected log-likelihood

$$\mathrm{Q}(\theta |{\theta }^{(i-1)})={\mathrm{E}}_{\mathcal{Y}}\left[{\displaystyle \sum _n\text{log}\mathrm{f}({\mathit{x}}_n,y_n|\theta )|\mathit{X},{\theta }^{(i-1)}}\right]$$ (2)

where θ⁽ⁱ⁻¹⁾ is the previous iteration’s estimate for the parameters. For the model given in Equation (1),

$$\mathrm{Q}(\theta |{\theta }^{(i-1)})={\displaystyle \sum _{n,k}{w}_{n,k}\{\text{log}{p}_k+\text{log}{\mathrm{f}}_k({\mathit{x}}_n|{\theta }^{(i-1)})\}}$$ (3)

where

$$w_{n,y}=\text{Pr}(y_n=y|{\mathbf{x}}_n,{\theta }^{(i-1)})=\frac{p_y^{(i-1)}{\mathrm{f}}_y({\mathit{x}}_n|{\theta }^{(i-1)})}{{\displaystyle \sum _k{p}_k^{(i-1)}{\mathrm{f}}_k({\mathit{x}}_n|{\theta }^{(i-1)})}}.$$ (4)

For the problem at hand, w_{n, 1} is the probability that the nth gene is a target (y_n=1) based on the particular data source (binding, expression, or conservation) being used.

To allow greater flexibility in modeling, we also consider the situation in which each gene has its own variance, with only the component means being common between the genes. The gene-specific variance model leads to the heavy-tailed Pearson Type VII (PVII) distribution, a generalization of the t-distribution. Let ${\mathcal{S}}_y$ be a gamma-distributed random variable with shape α_y>0 and rate 1, representing a scaling factor applied to the variance of the individual gene within each component. That is, let $\mathcal{X}$ given ${\mathcal{S}}_y$ and $\mathcal{Y}$ have the normal distribution with mean μ_y and variance ${\sum }_y/{\mathcal{S}}_y$. The usefulness of this distribution in mixture modeling is shown in Sun et al. (2010), in which marginal distributions and methods for distribution-specific parameter estimation are also discussed.

To choose the the value of K (number of mixture components) and the distribution family (normal or PVII) which best models the observed data for each data source, we use the ICL-BIC criterion of Biernacki et al. (2000). Where the BIC of Schwarz (1978) is defined as $\text{BIC}=2{\mathcal{L}}_{\mathit{X}}(\widehat{\theta })-|\mathrm{\Theta }|\text{log}N$, with ${\mathcal{L}}_{\mathit{X}}(\widehat{\theta })$ being the log-likelihood of the estimated parameters given the observed data and |Θ| being the size of the parameter space, ICL-BIC is defined as $\text{ICL}-\text{BIC}=2{\mathcal{L}}_{\mathit{X},\widehat{\mathit{Y}}}(\widehat{\theta })-|\mathrm{\Theta }|\text{log}N$ with $\widehat{\mathit{Y}}$ being the maximum a posteriori (MAP) estimate of the value of the hidden data. Thus ICL-BIC may be interpreted as the most probable value of BIC if all data were observed. All other things being equal, the model with the higher (often “less negative”) ICL-BIC is preferred. See Ji et al. (2005) for an application of this criterion to models of gene expression, and Viroli (2010) for an extensive comparison to other model selection criteria, where it is found that ICL-BIC generally outperforms AIC, BIC, and other criteria in selecting the correct mixture model. Note that with respect to the joint model, the marginal model selection procedure is only used to choose the K_z’s and distribution families, and does not imply any categorization of the observed data before fitting the joint model. The investigator may, of course, choose the numbers of components and the distribution families a priori to answer specific questions rather than relying on the model selection procedure.

3.3 Joint model specifics

In both the layered and chained models, the unconditional target status probability is $p_{0,y_0}=\text{Pr}({\mathcal{Y}}_0=y_0)$. In the layered model, ${\mathcal{Y}}_0$ generates the distribution for the ${\mathcal{Y}}_z’\mathrm{s}$, and the component probability given target status is $q_{z,y_0,y_z}=\text{Pr}({\mathcal{Y}}_z=y_z|{\mathcal{Y}}_0=y_0)$. In the chained model, ${\mathcal{Y}}_0$ generates the distribution for ${\mathcal{Y}}_1$, which then generates the distribution for ${\mathcal{Y}}_2$, etc., and the component probability for ${\mathcal{Y}}_z$ given ${\mathcal{Y}}_{z-1}$ is $q_{z,y_{z-1},y_z}=\text{Pr}({\mathcal{Y}}_z=y_z|{\mathcal{Y}}_{z-1}=y_{z-1})$. Given parameters θ⁽ⁱ⁻¹⁾, denote the nth element of the zth hidden component data vector by y_{z, n} and the conditional probabilities for the hidden variables by

$$\begin{array}{l}{u}_{n,y_0}=\text{Pr}(y_{0,n}=y_0|{\mathit{x}}_{\cdot ,n},{\theta }^{(i-1)}),\\ v_{z,y_0,n,y_z}=\text{Pr}(y_{0,n}=y_0,y_{z,n}=y_z|{\mathit{x}}_{\cdot ,n},{\theta }^{(i-1)})\text{or}\\ v_{z,y_{z-1},n,y_z}=\text{Pr}(y_{z-1,n}=y_{z-1},y_{z,n}=y_z|{\mathit{x}}_{\cdot ,n},{\theta }^{(i-1)}),\\ w_{z,n,y_z}=\text{Pr}(y_{z,n}=y_z|{\mathit{x}}_{\cdot ,n},{\theta }^{(i-1)})\end{array}$$ (5)

with $v_{z,y_0,n,y_z}$ for the layered model and $v_{z,y_{z-1},n,y_z}$ for the chained model. For observed data X=(X₁,…, X_z) where X_z=(x_z,1,…,x_z,n), and hidden data Y=(y₁,…,y_z) where y_z=(y_{z, 1},…, y_{z, n}) with y₀=(y_{0, 1},…, y_{0, n}), the complete data log-likelihood is

$$\begin{array}{l}{\mathcal{L}}_{X,Y,y_0}(\theta )={\displaystyle \sum _{n,k_0}\mathrm{I}(y_{0,n}=k_0)}\text{log}{p}_{0,k_0}\\ +{\displaystyle \sum _{n,z,(k),k_z}(\mathrm{I})\text{log}{q}_{z,(k),k_z}}\\ +{\displaystyle \sum _{n,z,k_z}\mathrm{I}(y_{z,n}=k_z)\text{log}{\mathrm{f}}_{k_z}}({\mathit{x}}_{z,n}|\theta ).\end{array}$$ (6)

where (k) denotes k₀ in the layered model and k_z−1 in the chained model. Similarly, let I( $\mathcal{P}$) denote the indicator function which returns 1 when proposition $\mathcal{P}$ is true and 0 when $\mathcal{P}$ is false, and (I) denotes I(y_{0, n}=k₀, y_{z, n}=k_z) in the layered model, I(y_{z−1, n}=k_z−1, y_{z, n}=k_z) in the chained model. The Q-function is thus

$$\begin{array}{l}\mathrm{Q}(\theta |{\theta }^{(i-1)})={\displaystyle \sum _{n,k_0}{u}_{n,k_0}\text{log}{p}_{0,k_0}}\\ +{\displaystyle \sum _{n,z,(k),k_z}{v}_{z,(k),n,k_z}\text{log}{q}_{z,(k),k_z}}\\ +{\displaystyle \sum _{n,z,k_z}{w}_{z,n,k_z}\text{log}{\mathrm{f}}_{k_z}}({\mathit{x}}_{z,n}|{\theta }^{(i-1)}).\end{array}$$ (7)

Then the steps of the model fitting procedure, including the EM algorithm as adapted for the model topologies, are

1. Marginal model selection: for each z=1,…, Z, choose the best distribution and K_z for the zth data source as described in Section 3.2. (We could fit all possible choices to the layered and chained joint models, but this is combinatorially explosive.) Then initialize the parameters for the joint model based on the selected marginal models.

2. E-step: for the ith iteration, using the previous iteration’s parameter estimates θ⁽ⁱ⁻¹⁾, estimate the conditional probabilities defined in Equation (5). In the layered model, these are

   $$\begin{array}{l}{u}_{n,y_0}=\frac{p_{y_0}^{(i-1)}{\displaystyle \prod _z{\displaystyle \sum _{k_z}{q}_{z,y_0,k_z}^{(i-1)}{g}_{z,n,k_z}}}}{{\displaystyle \sum _{k_0}{p}_{k_0}^{(i-1)}}{\displaystyle \prod _z{\displaystyle \sum _{k_z}{q}_{z,k_0,k_z}^{(i-1)}{g}_{z,n,k_z}}}},\\ v_{z,y_0,n,y_z}=u_{n,y_0}\frac{q_{y_0,y_z,k_z}^{(i-1)}{g}_{z,n,y_z}}{{\displaystyle \sum _{k_z}{q}_{z,y_0,k_z}^{(i-1)}{g}_{z,n,k_z}}},\\ w_{z,n,y_z}={\displaystyle \sum _{k_0}{v}_{z,k_0,n,y_z}}\end{array}$$ (8)

   where $g_{z,n,y_z}={\mathrm{f}}_{y_z}({\mathit{x}}_{z,n}|{\theta }^{(i-1)})$. Estimation in the chained model uses a version of the Baum-Welch algorithm (Baum et al. 1970; McLachlan and Krishnan 2008, pp. 290–293) modified to handle the heterogeneity of the ${\mathcal{Y}}_z’\mathrm{s}$. See Appendix B in the Supplementary Materials for details.

3. M-step: estimate the current iteration’s parameters, θ⁽ⁱ⁾=argmax_θ Q(θ|θ⁽ⁱ⁻¹⁾). This is a straightforward maximum likelihood estimation for the p’s and q’s, and a weighted MLE for the parameters relating to the observed variables, using weights ${\mathbf{w}}_z,\dots {,}_{y_z}$ and data X_z.

4. Repeat steps 2 and 3 until convergence.

5. Report the final estimated parameters $\widehat{\theta }$ and posterior target probabilities $\widehat{\mathit{U}}$, the N×K₀ matrix of which the (n, y₀)th element is ${\widehat{u}}_{n,y_0}=\text{Pr}(y_{0,n}=y_0|{\mathit{x}}_n,\widehat{\theta })$. Specifically, ${\widehat{u}}_{n,1}$ is the estimated probability, given the data and the final estimated parameters, that the nth gene is a target.

Simulation testing (Section 4) indicates that BIC is more effective than ICL-BIC for choosing between the layered and chained topologies. As with marginal model selection, the desired topology may also be selected a priori if one topology is clearly more applicable to the problem at hand; however, the results discussed in Sections 4 and 5 indicate that using a formal model selection procedure to choose between the topologies will generally give better results.

As mentioned in Section 1, of the previous models for similar applications, ours is most similar to that of Xie et al. (2010). Our model differs from theirs in two major ways. First, their model is fully Bayesian, with prior distributions on all parameters, and uses MCMC for model fitting, leading to what they describe as an “extensive computation load” even for a fairly small data set. Second, their model topology is similar to our chained model, but uses the estimated “internal” posterior weight matrix ${\widehat{\mathit{W}}}_{\mathrm{z}}$ for some z∈[1,…, Z} as the reporting variable in the chained model, rather than $\widehat{\mathit{U}}$ as in our method. We show in Section 4 that the use of $\widehat{\mathit{U}}$ as the reporting variable is generally preferred.

3.4 Fitted model interpretation

The simplest interpretation of the fitted model is as a MAP classifier: if ${\widehat{w}}_{n,y}=max{\widehat{\mathit{w}}}_{n,}$. in the marginal model, assume x_n was generated by the yth component, and similarly for ${\widehat{u}}_{n,y_0}=max{\widehat{\mathit{u}}}_{n,}$. and the y₀th component in the joint model. However, we may wish to consider subsets of the components as “alternative” and “null,” as in the current case in which y₀=1 indicates target status and y₀=2 indicates non-target. Thus the classification of the nth gene may be viewed as a hypothesis test, ${\mathcal{H}}_{n,A}:y_n=1$ (the nth gene is a target) vs. ${\mathcal{H}}_{n,\mathrm{Ø}}:y_n\ne 1$ (the nth gene is not a target). This interpretation requires a multiple testing approach.

Various approaches to false discovery rate (FDR) control which are applicable to mixture model classification have been proposed in the literature, including the empirical method of Newton et al. (2004), the resampling-based method of Storey (2002), and the semiparametric method of Strimmer (2008). However, the “local false discovery rate” of Efron (2007), denoted “fdr,” provides a particularly elegant parametric solution in the mixture model case. The local false discovery rate for the nth gene is simply defined as

$${\text{fdr}}_n=\text{Pr}({\mathcal{H}}_{n,\mathrm{Ø}}|{\xi }_n)$$ (9)

for some test statistic ξ_n. If we take ξ_n = x_n, that is, we use the nth observation itself as the test statistic, then this is

$$fd{r}_n=\{\begin{array}{l}1-{\widehat{w}}_{n,1}\text{marginal model}\\ 1-{\widehat{u}}_{n,1}\text{joint model}.\end{array}$$ (10)

Then for whatever is the desired false discovery rate cutoff q^*, we classify as targets whatever genes have ${\widehat{w}}_{n,1}\ge 1-q\ast$ in the marginal model or ${\widehat{u}}_{n,1}\ge 1-q^{\ast }$ in the joint model. As shown in Section 4, this approach outperforms the others given above.

4 Simulation

Here we use simulated data with known characteristics to assess the validity of BIC for topology selection, to show that performance is best when the correct model is chosen, and to show that both joint models are superior to the marginal models for target detection. We also examine the effectiveness of the marginal model selection procedure and the computational complexity of the joint model fitting algorithm. In each of 300 simulation runs, we generate data from both topologies for N=10,000 genes, with 300 genes being targets and the remainder being non-targets (p_{0, 1}=0.03). For simplicity, we simulate all data sources from the normal model, that is, ${\mathrm{f}}_{y_z}(\mathit{x}|\theta )=\varphi (\mathit{x}|{\mathit{\mu }}_{z,y},{\sum }_{z,y})$ for each z=1,…, Z. Recall that here Z=3, with z=1 corresponding to binding, z=2 to expression, and z=3 to conservation, in keeping with the Ci and Dl data sets.

Like both the Ci and Dl data sets, the simulated data contains a mix of univariate and multivariate data sources. Binding and conservation are both simulated as univariate data with the simulation parameters given in Supplementary Table 1, which are chosen to give similar results to the model fits to the Ci data. Expression data are simulated as multivariate data, and the simulation parameters (Supplementary Table 1) are also chosen to give similar results to the model fits to the Ci data, but are simpler than the fitted model parameters (see Section 5.2). For example, the simulated expression data has only three dimensions and a simple covariance matrix in which the first dimension has fairly strong positive correlation with the second and weak negative correlation with the third, and the second and third are uncorrelated. This is similar to, but simpler than, the Ci data in which each of the four dimensions of the expression data represents the log-ratio of wild-type expression to expression in a particular type of mutant. The purpose of the simulation parameters is not to simulate a specific data set but to enable simulation of the general type of data set we have developed our methods to address.

BIC for layered and chained fits to data generated from the layered and chained topologies is shown in Table 1a. As expected, BIC tends to select the “native” topology, that is, the same topology from which the data are generated. Table 1b and the first row of Figure 3 show receiver operating characteristic (ROC) area under the curve (AUC) for layered, chained, and marginal fits to the simulated data. Again, the best performance is found with the joint model fitted to its native topology. The chained model seems to be somewhat more sensitive to topological misspecification than is the layered model; that is, the chained fit to data generated from the layered topology performs worse than does the layered fit to data generated from the chained topology. In all cases, each of the joint models is superior to any of the marginal models.

Table 1.

BIC and ROC AUC results for joint model fits to simulated data. Compare to Supplementary Table 2.

(a) Mean (and standard error) of BIC for layered and chained fits to data generated from layered and chained topologies. Higher (less negative) values are preferred. The “difference” row shows the difference between BIC s for correct vs. incorrect fit topologies.
	Layered gen.	Chained gen.
Layered fit	–145970.6 (21.9)	–145429.8 (22.6)
Chained fit	–145995.9 (21.9)	–145414.3 (22.6)
Difference	25.3 (0.8)	15.5 (2.0)

(b) Mean (and standard error) of ROC AUC for layered and chained fits, joint fit selected by BIC, and marginal fits to data generated from layered and chained topologies. See also the first row of Figure 3.
	Layered gen.	Chained gen.
Layered fit	0.881 (0.0007)	0.854 (0.0009)
Chained fit	0.838 (0.0009)	0.877 (0.0008)
Selected fit	0.881 (0.0007)	0.875 (0.0009)
Binding only	0.727 (0.0010)	0.820 (0.0009)
Expression only	0.737 (0.0011)	0.753 (0.0010)
Conservation only	0.715 (0.0010)	0.671 (0.0009)

(c) Proportions of correct choices for layered and chained fits to data generated from the corresponding topologies (BIC, ROC AUC) and of the fit selected by BIC being best by ROC AUC (“conditional”).
	BIC	ROC AUC	Conditional
Layered fit	0.997	1.000	0.917
Chained fit	0.910	0.993	0.989

Figure 3.

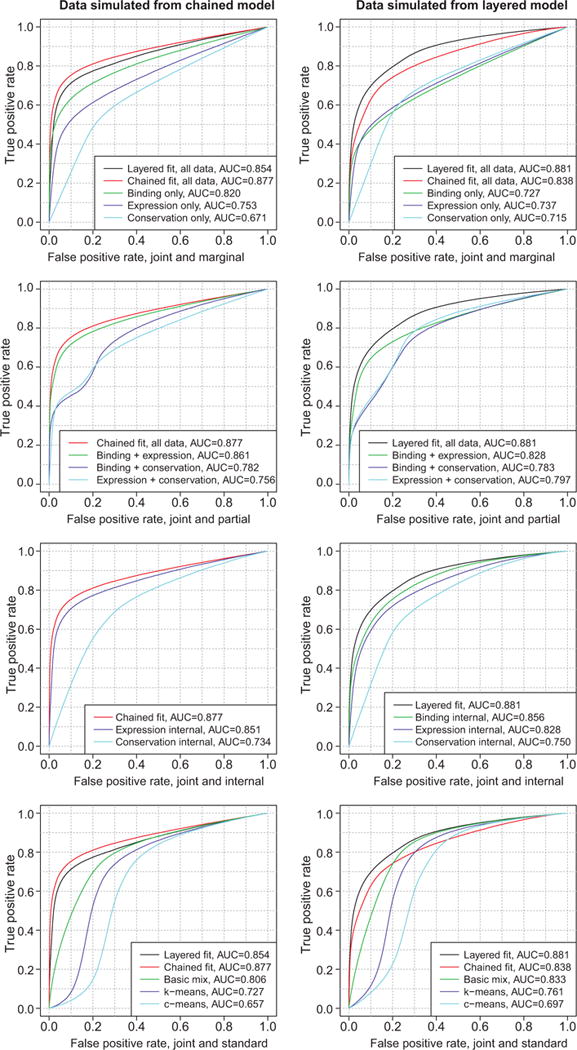
ROC curves for joint models compared to alternatives, for data simulated from the chained (left) and layered (right) topologies. Compare to Figure 5.

The chained model is preferred when a meaningful order exists among the individual data sources, for example in terms of problem specificity or information flow; otherwise the layered model provides a robust alternative, and is preferred if no clear order exists. In the chained model, dependence is stronger between ${\mathcal{Y}}_0$ and those ${\mathcal{Y}}_z\mathrm{s}$ with lower values of z, while in the layered model, the dependence between ${\mathcal{Y}}_0$ and all of the ${\mathcal{Y}}_z\mathrm{s}$ is roughly the same. This can be seen by comparing the ROC AUC values for the marginal fits.

Although we can see from Table 1a and b that means for measures of both model selection (BIC) and model performance (ROC AUC) are highest with the native topology, in many cases the difference is fairly small. We therefore wish to know how reliably the model selection procedure will choose the correct topology. The first two columns of Table 1c show the proportion of correct choices – that is, the proportion of cases in which the layered fit is superior with layered data, and the chained fit is superior with chained data – for BIC and ROC AUC. These results show that both model selection (BIC) and model performance (ROC AUC) are quite likely to favor the correct topology.

We also wish to know how frequently the selected topology will outperform the alternative. The “conditional” column of Table 1c shows the proportion of cases in which a particular topology is superior by ROC AUC given that it is superior by BIC, or in other words, the probability that the selected topology will provide better prediction of target status, regardless of the topology from which the data are actually generated. We see here that BIC is very likely to select the best-performing topology, as measured by ROC AUC, whatever the underlying model.

Including all data sources, rather than using only a partial subset of the data such as only binding and expression, leads to stronger predictions, as seen in the second row of Figure 3. This is particularly the case when the strongest marginal predictor, which here is binding, is left out of the model. However, the inclusion of even the weakest marginal predictor, which here is conservation, noticeably improves overall performance when the correct topology is chosen.

As mentioned in Section 3.3, although the internal posteriors ${\widehat{\mathit{W}}}_z$ of the joint models for both univariate and multivariate data sources are better predictors of target status than are the marginal posteriors, they are generally less effective than the joint posterior $\widehat{\mathit{U}}$, as can be seen in the third row of Figure 3. Here we interpret the internal posteriors in the same way as the joint posteriors: for the zth internal posterior ${\widehat{\mathit{W}}}_z$, we predict target status for the nth gene using ${\widehat{w}}_{z,n,1}$ just as we use ${\widehat{u}}_{n,1}$ in the joint posterior. (In the chained model, the special case of ${\widehat{\mathit{W}}}_1$ is equivalent to $\widehat{\mathit{U}}$ because ${\mathcal{Y}}_0$ depends on ${\mathcal{Y}}_2,\dots ,{\mathcal{Y}}_z$ only through ${\mathcal{Y}}_1$) Using the internal posteriors from the chained model as the reporting variable corresponds to the method of Xie et al. (2010). Using the internal posterior from the layered model does not correspond to any known method, but results are shown for comparison. For both topologies, the joint posterior is generally the better choice as indicated by the simulation results.

We also compare our method to some standard methods for unsupervised learning in which we combine all data sources into one wide matrix: the “basic” marginal mixture model with K=2 on the combined matrix, and K-means (Hartigan and Wong, 1979) and C-means (Bezdek et al., 1984) clustering, each with two clusters. The output of the C-means algorithm is a membership matrix analagous to the posterior probability matrix $\widehat{\mathit{W}}$ for the basic mixture model, with the same interpretation. For the K-means algorithm, for the nth gene and for each estimated cluster center ${\widehat{\mathit{\mu }}}_{\mathit{y}}$, we calculate the inverse squared Euclidean distance ${\delta }_{n,y}^{-2}=1/{\Vert {\mathit{x}}_n-{\widehat{\mathit{\mu }}}_{\mathit{y}}\Vert }^2$, where x_n is the nth row of the combined data matrix. Then the posterior probability of target status under K-means is ${\delta }_{n,1}^{-2}/({\delta }_{n,1}^{-2}+{\delta }_{n,2}^{-2})$ for δ_{n, 1}>0, or 1 in the event that δ_{n, 1}=0. The results shown in the fourth row of Figure 3 indicate that the correctly specified joint mixture model strongly outperforms the standards. Furthermore, even the joint mixture model with the incorrect topology is generally somewhat better than the basic mixture model, which is the best of the standard methods tested.

Table 2 shows that local FDR control (“fdr”) is superior to the other methods discussed in Section 3.4. For each method, we control at q^*=0.20, and calculate the true false discovery rate for those samples called as targets, that is, fp/(tp+fp) where fp is the number of false positives and tp is the number of true positives. The ideal method would yield a true FDR of 0.20 using this approach. All methods other than fdr have much larger false discovery rates; fdr is not conservative enough for the layered model, and is slightly too conservative for the chained model, but comes closer to the ideal than any of the other methods. The results of the other methods are all very similar to each other and quite different from those of fdr.

Table 2.

Means (and standard errors) of true false discovery rate by various methods of FDR control at q*=0.20.

	Local (fdr)	Empirical	Resampling	Semiparametric
Layered	0.255 (0.0045)	0.408 (0.0034)	0.399 (0.0034)	0.400 (0.0034)
Chained	0.185 (0.0020)	0.319 (0.0023)	0.318 (0.0022)	0.318 (0.0023)

We perform another set of simulations to test the marginal model selection procedures using ICL-BIC as opposed to BIC, as described in Section 3.2. Here we simulate univariate data from both the normal and PVII distributions, with two and three well-separated components, to compare the effectiveness of these criteria for marginal model selection. Table 3 shows that for data generated from the normal distribution, both criteria perform well (with BIC being better when K=2 and ICL-BIC being slightly better when K=3) but for PVII data, ICL-BIC far outperforms BIC, which is strongly biased toward the normal model. Thus ICL-BIC is our preferred criterion.

Table 3.

Proportions of correct marginal model selection choices, by BIC and ICL-BIC, for data generated from various models. Simulation component probabilities are (0.05, 0.95) for K=2 and (0.05, 0.90, 0.05) for K=3, with components having equal variance, and means separated by three standard deviations.

	Normal, K=2	Normal, K=3	PVII, K=2	PVII, K=3
BIC	0.973	0.897	0.110	0.000
ICL-BIC	0.670	0.933	0.990	0.843

Finally, another set of simulations is performed to determine the computational efficiency of the method. Here we simulate very simple data from the joint model using both topologies, with components of uniform size separated by three standard deviations, and iterate through various values of sample size (N), dimensionality (D₁=…=D_z=D for some D), number of data sources (Z), and number of components (K₀=K₁=…=K_z=K for some K), while holding other values fixed. Results are shown in Figure 4.

Figure 4.

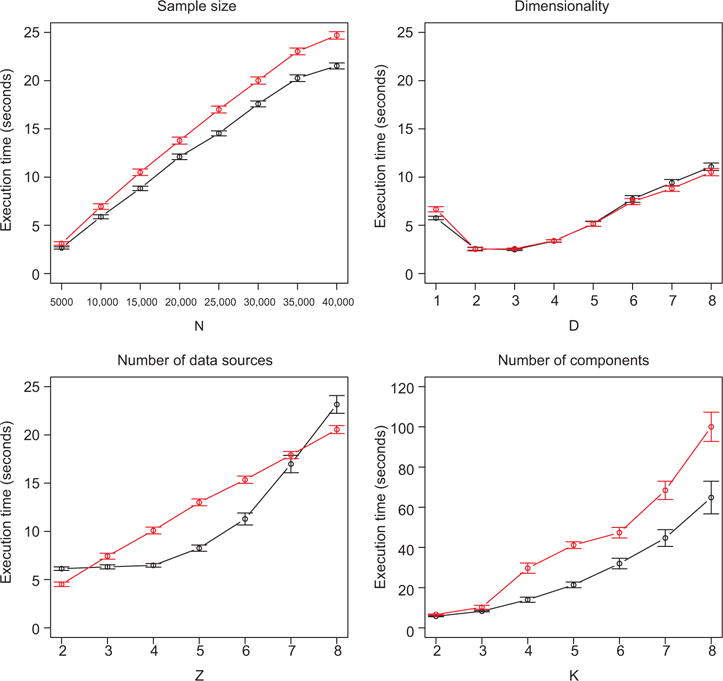
Mean execution times across simulations for layered (black) and chained (red) data, for various model specifications. Error bars show 95% confidence bounds based on standard error. Default values are N=10,000, D=1, Z=3, and K=2, unless otherwise specified. Note that the y-axis scale for the “number of components” plot differs from the others.

Execution times are approximately $\mathcal{O}(N)$ and $\mathcal{O}(D)$, that is, linear in sample size and dimensionality, with the exception of D=1, which may be explained by the fact that different estimation procedures are used for univariate and multivariate normal distributions. Times are linear in number of data sources for the chained model and approximately $\mathcal{O}(Z^2)$ for the layered model, although Z has to grow quite large before the layered model is significantly slower. The number of components in the mixtures makes the largest difference to performance. Execution times are approximately $\mathcal{O}(K^2)$ and increase considerably as K grows large. This is unsurprising if we consider that the number of free parameters relating to the hidden variables is (K₀−1)+K₀Σ_z(K_z−1) in the layered model and (K₀−1)+Σ_zK_z−1(K_z−1) for the chained model; with the same K throughout, this simplifies to K²Z−KZ+K−1 for both models, and for large values of K the K² term dominates the number of calculations required for each iteration.

The layered model tends to be somewhat faster than the chained model. This may be explained by the fact that certain computations in the chained model E-step are necessarily sequential, and cannot be performed in parallel as in the layered model. See Appendix B in the Supplementary Materials for details.

Overall, the simulation results indicate that the goals of the joint models are met. Our model selection procedures are effective at choosing the best model, model fitting is computationally efficient, the joint models are superior to the marginal models and to standard unsupervised learning methods in identifying targets, and incorporating even fairly weak marginal data sources improves joint model prediction.

5 Application to data

Here we describe the application of the techniques developed in Section 3 to the Ci and Dl data. We first describe the data in detail and give the preprocessing steps used to prepare the data for analysis. We then describe the results of the model selection and model fitting procedures. Finally, we interpret the gene lists generated from the fitted models.

5.1 Data and preprocessing

The number of genes used in the Ci analysis is N=10,244. Ci binding data are a univariate vector of length N representing log-ratios of Ci binding in the regulatory regions of genes vs. background binding. Expression values are multivariate, as a N×D (width D=4) matrix of log-ratios of expression in mutant vs. wild-type embryos, mutants being homozygous null for one of four proteins known to affect Ci’s regulatory function. The proteins are smoothened (Smo), patched (Ptc), and Ci and Hh themselves. Data are described in Biehs et al. (2010) and available from the NCBI GEO database (Barrett et al., 2009; National Center for Biotechnology Information, 2013) under accession number GSE24055.

In the Dl data, both binding and expression are N×D matrices where N=13,326 and D=2. Binding data represent the log-ratios of binding in regulatory regions vs. background for dorsal and snail (Sna), a TF which is an early target of Dl and plays an important role in the dorsal-ventral patterning process (Zeitlinger et al., 2007). These data are available under GEO accession number GSE26285. Expression data represent log-ratios of gene expression for different mutant strains with varying levels of Dl throughout the embryo (pipe⁻/pipe⁻ vs. Toll^10B and pipe⁻/pipe⁻ vs. Toll^rm9/Tollrm¹⁰). They are described in Biemar et al. (2006) and are available under GEO accession number GSE5434.

For both the Ci and Dl analyses, cross-species gene sequence conservation is calculated from Phast-Cons (Siepel et al., 2005) using 12 fly species with one species each of mosquito, honeybee, and beetle as outgroups. The conservation values used in the analysis are a univariate vector of length N calculated from the sums of PhastCons highly conserved element (HCE) scores for HCEs which overlap genes. These scores are available from the UCSC Genome Browser (Fujita et al., 2010; University of California, Santa Cruz, 2013).

The initial preprocessing step for both data sets is to remove genes which do not appear in all data sources, leading to the gene counts given above. Next, we impute missing values using regression-based imputation as discussed in Hastie et al. (1999). (A small number of genes have no conservation values, while about a tenth of the genes in the Ci data set are missing one or two expression values.) Finally, all data are standardized to have mean 0 and standard deviation 1.

5.2 Main results

Model selection results for both data sets are summarized in Table 4. For the number of components for each data source, we choose between K_z=2 and K_z=3. Greater values of K_z could of course be evaluated, but it would be difficult to assign biological meaning to these groupings. Our choices for K_z are generally supported by the data for the current application: in most cases, two components were chosen for the marginal models, although the structure of the Ci expression data is sufficiently complicated that it requires a three-component model. The default normal model is preferred for Dl binding and for expression from both data sets, while PVII is preferred for Ci binding and for conservation from both data sets.

Table 4.

Joint model topologies, marginal distribution families, and marginal numbers of components (K_z) for Ci and Dl models. See Supplementary Tables 3–6 for complete model selection results and parameters from the fitted models.

	Ci data	Dl data
Joint	Chained	Layered
Binding (z=1)	PVII, K1 = 2	Normal, K1 =2
Expression (z=2)	Normal, K2 =3	Normal, K2 =2
Conservation (z=3)	PVII, K3 =2	PVII, K3 =2

The topology selection results for the Ci data bear out the idea of information flow and specificity inherent in the chained model. On the other hand, the layered model is preferred for the Dl data, perhaps because, as the marginal “quasi- ROC” curves discussed below indicate, conservation is a particularly strong predictor for Dl target status. We hypothesize that because dorsal-ventral patterning is such a fundamental process in the development of viable embryos, Dl targets tend to be even more highly conserved than Ci targets or other developmental genes.

From previous literature and annotation, 68 genes are known to be Ci targets (The Gene Ontology Consortium, 2000, 2013; Biehs et al., 2010), and 49 genes are known to be Dl targets (Biemar et al., 2006; Tomancak et al., 2007; Zeitlinger et al., 2007; Berkeley Drosophila Genome Project, 2013). Because true negatives for both data sets are unknown, true ROC curve analysis is impossible, but we can assume that the vast majority of genes are not targets and plot quasi- ROC curves of the rate of true positives (known targets) vs. all positives. That is, if n_t is the number of known target genes, n_c is the number of genes called as targets, and n_{c, t} is the number of known target genes called as targets, then the true positive rate is n_{c, t}/n_t and the all positive rate is n_c/N. These are shown in Figure 5.

Figure 5.

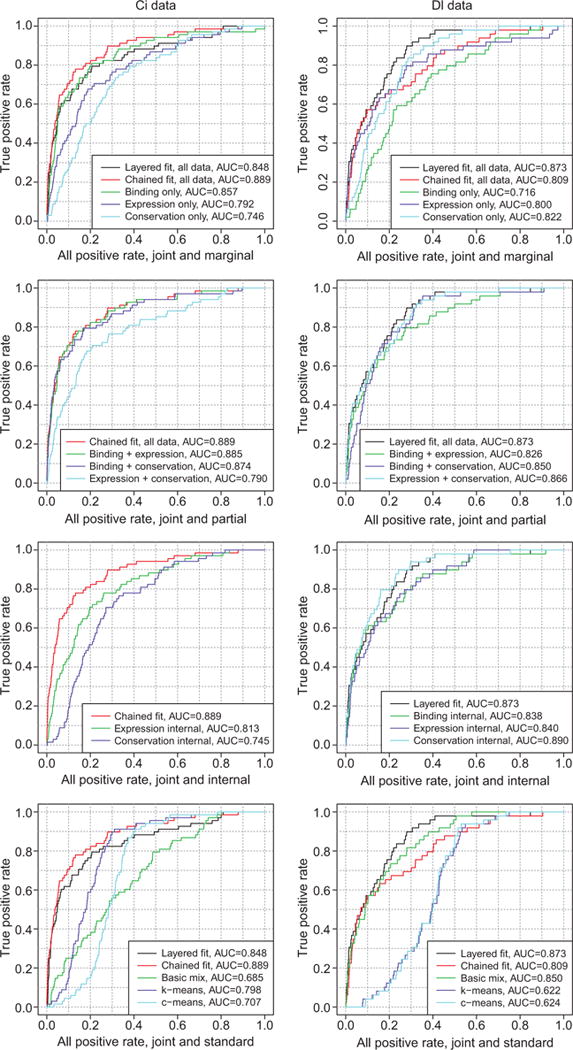
Quasi-ROC curves for joint models compared to alternatives, for Ci (left) and Dl (right) data. Compare to Figure 3.

As we would expect from the simulation results, the joint models outperform each of the marginal models. The plots in the first row of Figure 5 show that the selected joint model topologies, chained for Ci and layered for Dl, also outperform the alternate topologies, layered for Ci and chained for Dl. The other plots in Figure 5 show comparisons of the performance of these selected topologies to various alternative methods of prediction.

Again as expected from the simulation results, inclusion of conservation data very slightly improves performance with the Ci data set and more strongly improves performance with the Dl data set, as shown in the second row of Figure 5. It is clear that conservation data has a part to play in the identification of developmental genes, albeit much more so in some data sets than in others. The joint posterior outperforms the internal posteriors for the chained model fitted to the Ci data, as shown in the third row of Figure 5. For the layered model fitted to the Dl data, the internal posterior for conservation is actually superior to the joint posterior. This somewhat surprising result is most likely due to the strength of conservation as a predictor for Dl target status; in general, unlike binding and expression, conservation is not specific to the problem at hand. Finally, as shown in the fourth row of Figure 5, the joint models with the selected topologies outperform the standard methods.

5.3 Interpretation of results

To interpret the model fit results, we wish to analyze gene lists of equal size for each of the marginal data sources (binding, expression, and conservation) and for the joint model fitted to the entire data set. Arbitrarily, we select the top 200 genes – that is, the 200 genes with the greatest posterior probability of being targets – from the marginal and joint fits. (See Supplementary Table 7 for the posterior probability cutoffs.) We also select genes by fdr with q^*=0.20. We then use the DAVID tool (Huang et al., 2009a,b) to find “enriched” Gene Ontology (GO) biological process (BP) terms (The Gene Ontology Consortium, 2000, 2013) and pathways from the Kyoto Encyclopedia of Genes and Genomes or KEGG (Kanehisa and Goto, 2000; Kanehisa et al., 2012) in these gene lists. Here we describe the results.

Analysis of the Ci data reveals several genes ranked highly by the joint list relative to the rankings determined by the marginal methods. Most notably, hedgehog (hh) appears very near the top of the joint list, while it is much further down in the marginal lists, as shown in Table 5.

Table 5.

Ranks for KEGG Hedgehog pathway genes in top 200 genes by joint model for Ci data set. See also Supplementary Table 8.

	Joint	Binding	Expression	Conservation
hh	12	79	111	2461
wg	40	407	99	754
smo	71	570	182	1450
wntd	127	848	339	3287

Hh is a secreted protein and signals non-cell-autonomously to neighboring cells. Activation of hh expression via Hh signaling can occur in the eye disk (Heberlein et al., 1995). While not commonly described, activation of the pathway via a positive regulatory loop may be an underlying feature of Hh signaling in other organ systems. Other genes in the KEGG Hedgehog pathway which are identified by the joint model have similar relative ranks; wingless (wg) is perhaps the best-studied Hh target to date and lends validation to our joint list.

GO terms and KEGG pathways generated by the DAVID analysis for Ci are given in Supplementary Tables 9–14. Because the number of GO terms generated by DAVID analysis may be very large, up to several hundred for each list, we show only the top 50 GO terms for each list.

The top 200 genes identified from the the joint model fit to all data (Supplementary Table 9) are highly enriched in terms having to do with the mechanisms by which Hh signaling exerts its influence over the developing animal, as well as terms that describe which organ systems require Hh signaling for morphogenesis. For example, “leg disc development” requires biological mechanisms such as “regionalization” to set aside tissue that will become the leg disc. Thus, the joint model appears valuable in predicting where and how Hh signaling functions in the developing animal.

Genes identified from the binding data alone (Supplementary Table 10) are more enriched in terms having to do with the mechanisms of development, particularly (and unsurprisingly) those involving functions previously ascribed to Hh signaling such as cell fate commitment. Genes identified from the expression data (Supplementary Table 11) are highly enriched in terms having to do with pattern formation. As expected, genes identified from the conservation data are enriched in less specific terms, most of which are not specific to development, although in accordance with Siepel et al. (2005), developmental genes do tend to be highly conserved and this can be seen in some of the terms in Supplementary Table 12.

234 genes are selected by fdr from the joint model fit. Because these are nearly the same as the top 200 genes, enriched terms for the fdr-selected genes, shown in Supplementary Table 13, are nearly the same as those for the top 200 genes shown in Supplementary Table 9. The relevant terms do appear to be slightly more strongly enriched, as measured by p-value, in the fdr-selected list than in the top-200 list.

Most interesting are those “overenriched” terms (terms with boldface IDs in Supplementary Table 9) which are enriched in the joint list but not in the marginal lists, or are enriched more strongly in the joint list. These terms, such as “sensory organ development,” “leg disc development,” and “imaginal disc morphogenesis,” reflect the universal nature of Hh signaling in the development of organs and match well with curated phenotypes associated with hh loss of function mutations (McQuilton et al., 2012; The FlyBase Consortium, 2013). This result indicates that the integrated analysis succeeds in its goal of identifying target genes better than analysis of any individual data source. Similarly, in the KEGG pathways (Supplementary Table 14) genes identified from the integrated analysis are more strongly associated with the Hh pathway than are genes identified from analysis of any of the individual data sources.

For the Dl data (Supplementary Tables 15–20) GO terms overenriched in the joint model top-200 list (Supplementary Table 15) such as “embryonic morphogenesis,” “blastoderm segmentation,” and “embryonic pattern specification” are specific to developmental processes in which Dl plays a major role. Interestingly, all of the top 50 terms, including very general but relevant terms such as terms “pattern specification process” and “cell fate commitment,” are overenriched as compared to the marginal lists in Supplementary Tables 16–18. The list of enriched terms from fdr-selected genes in Supplementary Table 19 is very similar to the list in from top-200 genes in Supplementary Table 15, even though a much larger gene list, comprising 1650 genes, is selected by fdr. This indicates that the model effectively ranks the genes in order of importance, and that the most significant genes will be present in any reasonably sized list of selected genes.

The joint models are also strongest in identification of the KEGG Hh pathway, as seen in Supplementary Table 20. Although Dl is not considered part of the Hh pathway, the mediating transcription factors of each pathway can be regulated by the same co-activator (Bantignies et al., 2002) and may contribute to activation of the same genes during different developmental contexts. Similar Hh-pathway enrichment results were found for the lists of Dl targets given by Biemar et al. (2006) and Zeitlinger et al. (2007), as shown in Supplementary Tables 20(f) and 20(g), where the Hh pathway is the most strongly enriched KEGG pathway for both lists. Thus the joint model best identifies the relevant terms and pathways overall.

6 Discussion

Mixture models have long been recognized as a powerful tool for unsupervised probabilistic classification. We have shown that hierarchical mixture models with flexible topologies, using simple, efficient algorithms to fit the models to univariate and multivariate data sources, can be an effective addition to the mixture modeling toolbox. The adaptability of the method should allow it to be used with any reasonable combination and number of biologically relevant data sources, and the results are easily interpreted.

Our method is particularly useful when the relevance of the various data sources to answering the biological question of interest is not known in advance. For example, the performance improvement made by including sequence conservation in the model, particularly with the Dorsal data, shows that data not specific to the problem domain may provide a considerable amount of useful information. Both the layered and chained models perform well when the appropriate topology is unknown, and steadily improve in performance as more data sources are added. Furthermore, the selection procedure is quite effective at finding the strongest model.

There are several opportunities for future methodological work, among which is extending the range of marginal distributions available for modeling observed data. An increasing amount of genomic data is not continuous, but discrete; “next generation” methods such as RNA-seq produce data which are most effectively modeled with discrete distributions (Kvam et al., 2012). We will therefore incorporate multivariate discrete distributions, such as those given by Xu (1996), which allow modeling dependence structures. We will also consider additional continuous distributions such as those reviewed in Azzalini (2005) to allow more flexible modeling of a wide variety of data. We may add Bayesian methods for estimation of the posterior distribution of the parameters so long as the computational efficiency of the current approach, important for dealing with ever-growing volumes of data, can be maintained.

Another avenue will be the development of semi-supervised models, as suggested by Alexandridis et al. (2004) for cases where a partial training data set is available, as in the case of the known targets for Ci and Dl discussed here. Early testing for the marginal models suggests this may be an effective approach for the problem at hand, with significant improvement over the unsupervised models but with a lesser penalty for training set error than is found in fully supervised approaches. Future work will involve applying this approach to the joint models.

We will also apply our method to other questions of biological and medical interest. The overall approach we have developed here is intended and expected to be generally applicable to many problems in data modeling and analysis.

The R package lcmix is available at http://r-forge.r-project.org/projects/lcmix/ and implements the methods described. Code for analysis and simulations specific to the paper is available from the corresponding author upon request.