Coil compression in simultaneous multislice functional MRI with concentric ring slice-GRAPPA and SENSE

Abstract

Purpose

Simultaneous multislice (SMS) imaging is a useful way to accelerate fMRI. As acceleration becomes more aggressive, an increasingly larger number of receive coils are required to separate the slices, which significantly increases the computational burden. We propose a coil compression method that works with concentric ring non-Cartesian SMS imaging and should work with Cartesian SMS as well. We evaluate the method on fMRI scans of several subjects and compare it to standard coil compression methods.

Methods

The proposed method uses a slice-separation k-space kernel to simultaneously compress coil data into a set of virtual coils. Five subjects were scanned using both non-SMS fMRI and SMS fMRI with 3 simultaneous slices. The SMS fMRI scans were processed using the proposed method, along with other conventional methods. Code is available at https://github.com/alcu/sms.

Results

The proposed method maintained functional activation with a fewer number of virtual coils than standard SMS coil compression methods. Compression of non-SMS fMRI maintained activation with a slightly lower number of virtual coils than the proposed method, but does not have the acceleration advantages of SMS fMRI.

Conclusion

The proposed method is a practical way to compress and reconstruct concentric ring SMS data and improves the preservation of functional activation over standard coil compression methods in fMRI.

Introduction

Simultaneous multislice (SMS) parallel imaging is frequently used in fMRI to accelerate acquisition while maintaining the necessary TE for BOLD contrast. However, many coils are desired for slice separation, which can increase the computational load by several factors during reconstruction. One way to reduce the amount of data used in processing is to exploit the redundancy of the signal from different coils through coil compression. By combining the original coil data into a new, reduced set of virtual coils, the amount of data is decreased by several factors, which reduces the computational burden for reconstruction. We propose GeneRalized Autocalibrating partially parallel acquisitions-Based Simultaneous-Multislice-Acquired Coil Compression (GRABSMACC), a method that uses the slice-separation kernel to simultaneously compress the k-space data before it is transformed into the image domain. Similarly to GRAPPA (1), GRABSMACC does not rely on accurate sensitivity maps for reconstruction, which is an advantage over SENSE (2) in parallel imaging.

In fMRI, efficient single-shot k_x-k_y trajectories such as a spiral-in have been recommended for fMRI due to their shorter readout times and improved signal recovery in the presence of susceptibility-induced gradients (3, 4). However, the spiral-in is not well-suited for GRAPPA because of the irregularity of the sampling pattern in both the angular and radial directions. In addition, the use of a readout z-gradient (5) in SMS imaging further disrupts the regularity in a spiral readout, as shown in Figure 5b of Ref. (6) and Figure 2d of Ref. (7). These figures show that the z-gradient blips create large gaps in each spiral platter. We propose an out-to-in concentric ring trajectory that has good sampling regularity for a GRAPPA kernel, but still retains most of the susceptibility benefits of the more established spiral-in. The concentric ring trajectory requires more samples than a spiral-in, but is still more efficient than Cartesian patterns such as EPI. In this work, GRABSMACC is demonstrated with the non-Cartesian concentric ring sampling pattern, but should also work with Cartesian trajectories such as EPI.

King et al. (8, 9) implemented coil compression in hardware by changing the image signal basis to one composed of the eigenvectors of the noise covariance matrix. The hardware implementation has SNR benefits, but lacks the flexibility of software coil compression, especially with varying levels of acceleration in different directions. On the software side, Buehrer et al. (10) developed a method that reduces image noise in parallel MRI by taking advantage of coil noise covariance and the coil sensitivities for aliased voxels. Not only does this method rely on sensitivities and the issues that go along with the acquisition and accuracy of sensitivity maps, but it requires the undersampling to produce a simple point spread function for it to be practical. Huang et al. (11) used Principle Component Analysis in the k-domain, circumventing the need for coil sensitivities and noise covariance. More recently, Zhang et al. (12) reduced the number of required virtual coils by performing a Singular Value Decomposition (SVD) to compress data in a hybrid image-k-domain. This method was implemented by Cauley et al. and shown to work well with a blipped-EPI trajectory in SMS (13). However, the method relies on a Fourier Transform in a fully sampled direction to obtain hybrid space, which is not possible for many non-Cartesian trajectories, such as our implementation of a concentric ring readout. Beatty et al. (14) have proposed a new method that combines the k-space reconstruction kernel with a coil compression kernel. This method is similar to GRABSMACC in that the unaliasing process is also responsible for coil compression. However, in the current work, we extend this general idea to SMS imaging with non-Cartesian trajectories.

Because GRABSMACC uses the slice-separation kernel to simultaneously compress k-space data, the kernel convolution step for slice separation uses a larger dataset when compared to standard SVD coil compression, which only operates on pre-compressed data. Although this comes at an increased computation cost when compared to standard SVD compression, we show that GRABSMACC preserves functional activation better at higher levels of compression, thus enabling a fewer number of virtual coils to be used when compared to standard compression. Furthermore, the main computational burden in this non-Cartesian SMS reconstruction lies not in the slice separation process, but in the transformation of unaliased k-space data for each coil into the image domain prior to coil combination. Therefore, the reduction in the number of required coils for GRABSMACC results in significant computational time savings, especially when reconstructing multiple fMRI studies.

This work provides several novel contributions: (a) the development of a blipped, concentricring-in k-space trajectory with the sampling regularity necessary for implementation of slice-GRAPPA, (b) the development and evaluation of GRABSMACC, a practical method for coil compression and reconstruction of both Cartesian and non-Cartesian SMS fMRI, and (c) the analysis of coil compression performance and computation time in fMRI with both non-SMS and SMS imaging. With coil compression in fMRI, care must be taken to ensure that the functional activation in an fMRI scan is not reduced in exchange for data compression. In this paper, we present the methodology of GRABSMACC and analyze fMRI scans of several subjects to compare activation performance, image artifacts, SNR, and reconstruction speed for different levels of coil compression using GRABSMACC, standard coil compression in GRAPPA-based and SENSE-based SMS reconstruction, and coil compression in traditional, non-SMS imaging.

Methods

Along with GRABSMACC, all algorithms, reconstruction methods, and coil compression methods described in this section are available at https://github.com/alcu/sms.

Concentric Ring Trajectory

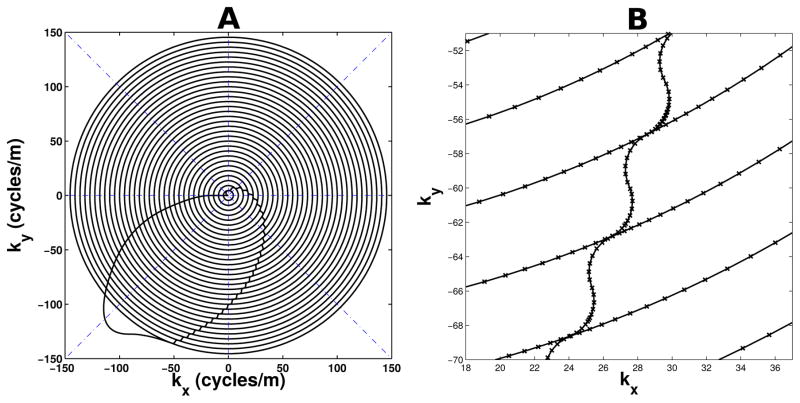
The out-to-in concentric ring trajectory was developed using a numerical algorithm based on Ref. (15). As shown in Figure 1a, the k_x-k_y trajectory follows the path of multiple centered, concentric circles with radii spread evenly along the radial direction, along with a sample at the k-space origin. Transitions between circles follow a path created using 2 quarter-circles tangent to the main concentric rings, as shown in Figure 1b. All reconstruction and coil compression operations, including ones for GRAPPA, SENSE, non-simultaneous multislice imaging, and their associated field maps and calibration scans, used data obtained only in the concentric rings and origin, ignoring data sampled during all transitions. In order to provide better sampling regularity for GRAPPA, the transition paths were not started until each concentric circle was entirely complete. The numerical algorithm samples points along the k-space path with step sizes that are as a large as possible, while still satisfying maximum gradient amplitude and slew rate hardware constraints. It does this by using the maximum slew rate at each step until the curvature of the path is too great. When this happens, the algorithm re-samples a previous point with a smaller step size, equivalent to backing up and slowing down the trajectory. The result is an efficient and accurate trajectory that is consistent with hardware limits.

Figure 1.

(a) k_x-k_y components of the concentric ring k-space trajectory used in this work. Boundaries of angular sectors for GRAPPA are shown with dash-dotted blue lines. (b) Close-up of ring transitions with “x” markers indicating where samples were acquired.

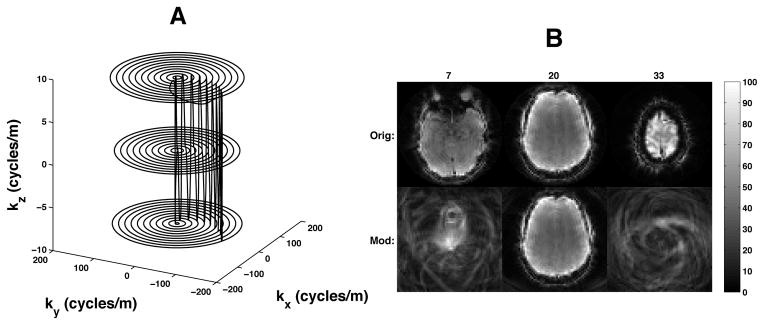
In order to decrease the geometry factor in SMS imaging (5), z-gradient blips were used during the concentric ring readout. The z blips were timed to occur only during the k_x-k_y transitions between rings so that the entirety of each concentric ring remained in a single k_z plane, as shown in Figure 2a. The readout z-gradient consisted of a repeating set of (n_slc − 1) positive blips followed by a rewinder negative blip and were designed according to the necessary Fourier requirements for n_slc simultaneously acquired slices (multiband factor), each separated by a distance of n_acqd_slc, where n_acq is the number of SMS acquisitions per TR, and d_slc is the distance between adjacent individual slices (6). Figure 2b shows the aliasing pattern produced by the blipped concentric ring trajectory. The middle slice is located at z-isocenter, and therefore is not modulated. The use of tangent quarter-circles for the transition paths may not be optimal in terms of speed, but because it was desired to have the z blips entirely within each transition, the quarter-circle transitions were more than adequate to achieve the minimum time needed for each z blip.

Figure 2.

(a) Three-dimensional concentric ring k-space trajectory. (b) Modulation pattern resulting from a blipped concentric ring trajectory for 3 simultaneous slices. The numbers at the top indicate the slice number, where contiguous slices in the volume are numbered 1 through 39. The 20th slice is acquired at z-isocenter, assuming an axial acquisition. The top row shows the original, non-modulated, 3 simultaneous slices. The bottom row shows what the blipped modulation does to the various slices. Slice 20 is unaffected because it is acquired at z-isocenter. The blipped-EPI equivalent of slices 7 and 33 would be a simple FOV shift.

Slice-GRAPPA and Split Slice-GRAPPA

For each SMS fMRI run, a calibration scan was necessarily acquired for slice separation and reconstruction. The calibration scan consisted of non-simultaneous slices acquired at the same z locations as the SMS acquisitions. The calibration acquisitions used exactly the same k_x-k_y-k_z trajectory as the SMS acquisitions did, but with a conventional non-simultaneous RF pulse. The calibration scan used the same TR as the SMS fMRI scan to preserve image contrast and was acquired shortly before each fMRI run.

In addition to the calibration scan, field maps were obtained by acquiring non-simultaneous slices at the same z locations as the SMS acquisitions, with the same k_x-k_y concentric ring trajectory. No readout z-gradient was used for the field maps. The brain volume was acquired two times, with one time frame having an echo time delayed by 2 ms with respect to the other so that the phase difference could be used for a standard field map computation.

A slice-GRAPPA (SG) reconstruction process based on Refs. (16) and (5) was developed to separate and reconstruct the SMS data. First, all acquired data from all coils were linearly interpolated to a constant angular velocity trajectory. Next, the interpolated data were divided into angular sectors as depicted in Figure 1a. Interpolated data from each angular sector were unwrapped and arranged into a Cartesian grid according to the radial and angular location of each sample. SG was then applied separately to each sector according to the equation

$${\mathit{S}}_{\text{src}}\mathit{W}={\mathit{S}}_{\text{trg}},$$ [1]

where S_src is a “source” matrix containing interpolated data from all coils for one SMS acquisition, W is a matrix of GRAPPA kernels, and S_trg is a “target” matrix containing interpolated non-simultaneous calibration data. Split slice-GRAPPA (SP-SG) (17) was also implemented and applied to each sector according to Eq. [1], but with different dimensions for S_src and S_trg when compared to SG.

For each SMS fMRI run, a simulated SMS acquisition was generated for S_src by summing calibration slices, and the original, non-summed calibration slices were used for S_trg. The kernels in W were then computed from S_src and S_trg in Eq. [1] using least squares. To separate the simultaneous slices in the SMS fMRI run, the acquired data from each time frame was used for S_src, and Eq. [1] was used again, this time to compute k-space data for each separate slice in S_trg.

Data from each k-space sector were then reassembled back into their original interpolated concentric ring locations and demodulated with the negative of the phase imparted by the blipped read-out z-gradient. Finally, conjugate gradient using a non-uniform fast Fourier transform (NUFFT) (18, 19) with B₀ inhomogeneity correction (20) and finite difference regularization was used to transform k-space data into coil images, and the coil images were combined using the standard square-root-sum-of-squares method.

Standard Coil Compression in Slice-GRAPPA and Split Slice-GRAPPA

Standard coil compression in SG and SP-SG compresses the SMS k-space data before the entire GRAPPA process described previously. Each acquisition in a time frame is compressed separately, resulting in n_acq compression matrices. First, n_stack number of time frames, located in the middle of the fMRI run, are stacked into a matrix S_stack, with data from each coil arranged along a single column of S_stack. The dimensions of S_stack are n_stackn_dat-by-n_coil, where n_dat is the number of samples located only in the concentric rings, and n_coil is the full number of coils in the receive array. The compression matrix, V_comp, is calculated by computing the SVD of S_stack, described by

$${\mathit{S}}_{\text{stack}}=\mathit{U}\mathbf{\sum }{\mathit{V}}^{\ast },$$ [2]

and using the first n_vcoil columns of V as V_comp, where n_vcoil is the number of virtual coils to which the data should be compressed.

To compress each fMRI time frame, each SMS acquisition from that frame is assembled into a matrix S_full and multiplied by the corresponding V_comp for that SMS acquisition to obtain

$${\mathit{S}}_{\text{comp}}={\mathit{S}}_{\text{full}}{\mathit{V}}_{\text{comp}},$$ [3]

where S_comp contains the compressed SMS acquisition and has dimensions n_dat-by-n_vcoil. The matrix S_full is constructed in the same manner as S_stack, except with data from only one time frame, and therefore has dimensions n_dat-by-n_coil. Before calculating W in Eq. [1], the calibration data must be compressed with the same V_comp matrices before being interpolated and arranged into S_trg. Specifically, the calibration scan has n_tot = n_slcn_acq acquisitions, and the n_slc non-simultaneous calibration acquisitions that match the excitation locations of a single SMS acquisition should each use the same V_comp as that single SMS acquisition. Once the SMS and calibration data are compressed, the previously described SG or SP-SG process is performed with a reduced coil dimension of n_vcoil for all matrices in Eq. [1].

GRABSMACC

In contrast, our proposed method for coil compression, GRABSMACC, only compresses the “target” data and not the “source” data, and uses the GRAPPA kernel for both slice separation and coil compression. In this method, the non-simultaneous acquisitions from the calibration scan are used to compute the compression matrices V_comp. Specifically, the calibration data is used for S_stack in Eq. [2], and the first n_vcoil columns of V are used to construct V_comp. Since there are n_tot = n_slcn_acq calibration acquisitions, or equivalently, slices, there are n_tot number of V_comp matrices, one for each slice. Each slice of the calibration scan is arranged into an S_full, and each S_full is then compressed using Eq. [3].

Once the calibration data is compressed to n_vcoil coils, it is used in Eq. [1] as S_trg for computation of W. No coil compression is done on data used for S_src. Therefore, in GRABSMACC, the source data matrix has full coil dimensions, the target matrix has compressed coil dimensions, and the kernel has both. Specifically, in SG the dimensions of S_src are n_rep-by-n_kernn_coil, those for S_trg are n_rep-by-n_slcn_vcoil, and those for W are n_kernn_coil-by-n_slcn_vcoil, where n_rep is the number of GRAPPA kernel repetitions and n_kern is the number of weights in the kernel for a single coil. In SP-SG, the dimensions of S_src are n_repn_slc-by-n_kernn_coil, those for S_trg are n_repn_slc-by-n_slcn_vcoil, and those for W remain unchanged from SG.

To separate the slices in GRABSMACC, uncompressed k-space data from each acquisition of each time frame is used for S_src, and Eq. [1] is used to compute the compressed, separated slices in S_trg. Hence, multiplication by W performs a simultaneous slice separation and compression of k-space data. Finally, the slice-separated data can be transformed into images by the same conjugate gradient and square-root-sum-of-squares process described previously.

SENSE

The discretized SENSE (2) reconstruction model for one acquisition of one time frame is given by

$$\left[\begin{array}{c}{\mathit{s}}_1\\ {\mathit{s}}_2\\ ⋮\\ {\mathit{s}}_{n_{\text{coil}}}\end{array}\right]=\left[\begin{array}{cccc}{\mathit{M}}_1{\mathit{Q}}_1{\mathit{C}}_{1,1}& {\mathit{M}}_2{\mathit{Q}}_2{\mathit{C}}_{1,2}& \cdots & {\mathit{M}}_{n_{\text{slc}}}{\mathit{Q}}_{n_{\text{slc}}}{\mathit{C}}_{1,n_{\text{slc}}}\\ {\mathit{M}}_1{\mathit{Q}}_1{\mathit{C}}_{2,1}& {\mathit{M}}_2{\mathit{Q}}_2{\mathit{C}}_{2,2}& \cdots & {\mathit{M}}_{n_{\text{slc}}}{\mathit{Q}}_{n_{\text{slc}}}{\mathit{C}}_{2,n_{\text{slc}}}\\ ⋮& ⋮& \ddots & ⋮\\ {\mathit{M}}_1{\mathit{Q}}_1{\mathit{C}}_{n_{\text{coil}},1}& {\mathit{M}}_2{\mathit{Q}}_2{\mathit{C}}_{n_{\text{coil}},2}& \cdots & {\mathit{M}}_{n_{\text{slc}}}{\mathit{Q}}_{n_{\text{slc}}}{\mathit{C}}_{n_{\text{coil}},n_{\text{slc}}}\end{array}\right]\left[\begin{array}{c}{\mathit{x}}_1\\ {\mathit{x}}_2\\ ⋮\\ {\mathit{x}}_{n_{\text{slc}}}\end{array}\right],$$ [4]

where s_u is k-space data from coil u, x_v is simultaneous slice v, C_u,v contains the sensitivity of coil u to simultaneous slice v, Q_v is the 2-dimensional Fourier transform operator with B₀ inhomogeneity correction for slice v, M_v contains the phase imparted by the z-gradient modulation to slice v, and n_slc is the number of simultaneously acquired slices for each SMS acquisition. For reconstruction, the x_v vector was solved for in Eq. [4] using conjugate gradient with finite difference regularization. Because x_v contains multiple slices, the finite difference operator was constructed to only take differences within each slice and not across simultaneous slices. The Q_v matrices were implemented by a NUFFT (18, 19) with B₀ inhomogeneity correction (20).

ESPIRiT (21) was used to generate sensitivity maps from data acquired during the non-delayed field map acquisition. First, individual coil images were reconstructed with conjugate gradient using NUFFTs, inhomogeneity correction, and finite difference regularization. Then, a 2-dimensional Fourier transform was done on each coil image to obtain Cartesian k-space data. ESPIRiT was then used on this field-corrected k-space data to obtain sensitivity maps. Only the primary set of n_coil maps from ESPIRiT was used for all SENSE reconstructions.

Standard Coil Compression in SENSE

Standard coil compression for SENSE was done exactly the same as for standard coil compression in SG and SP-SG, described previously. However, a new set of virtual coil sensitivities need to be computed for use in Eq. [4]. This was done by first compressing the k-space data from the non-delayed field map acquisition before performing the previously-described ESPIRiT process to generate n_vcoil sensitivity maps. Similar to the GRAPPA calibration data, n_acq number of V_comp matrices must be used appropriately for n_tot = n_slcn_acq non-simultaneous slices. Finally, Eq. [4] with n_coil = n_vcoil is used to reconstruct the separated slices by using the compressed SMS acquisitions for s_u and the virtual coil sensitivities for C_u,v.

fMRI Experiment Design and Analysis

For each of five healthy subjects, both a concentric ring SMS fMRI scan and a non-simultaneous multislice (non-SMS) concentric ring fMRI scan were performed in accordance with the University of Michigan Institutional Review Board using a GE Discovery MR750 3.0 Tesla MRI scanner and a Nova Medical 32-channel receive head coil. The SMS and non-SMS scans each had a total acquisition time of 240 s for the entire run. Each fMRI scan had 20-second blocks of both visual and motor stimuli alternating with 20-second blocks of rest. The visual stimulus consisted of a flashing checkerboard pattern, and subjects were instructed to tap the fingers on only their right hand while the visual stimulus was present.

Functional activation for all scans was computed using the General Linear Model on detrended magnitude data using a paradigm model waveform based on SPM’s canonical hemodynamic response function (22). Maps of t-scores were computed using Ref. (23), which accounts for degrees of freedom in the time-series data, and a threshold of t > 6 was used to determine voxel activation in all scans. Counts of activated voxels were performed by manually masking visual and left motor cortex areas, then counting the number of activated voxels within those masked regions. A different mask was created for each subject, but all methods performed on data from one subject used the same mask for that subject.

SMS Scan Parameters

Each SMS fMRI time frame consisted of n_acq = 13 acquisitions per TR of n_slc = 3 simultaneous slices, each of which were 3 mm thick and acquired n_acqd_slc = 39 mm apart with no space between contiguous acquisitions. The SMS TR and TE were 663 ms and 31 ms, respectively. The SMS RF pulse was created using a sum of 3 Hamming-windowed sincs, each of which was frequency-modulated to create the 39 mm gap between simultaneous slices. The SMS RF pulses for all 5 subjects were 6.4 ms in length, and the Ernst angle for gray matter was used for the flip angle.

The calibration TR and TE in all cases were 663 ms and 31 ms, respectively. To match the SMS scans, each calibration time frame had n_tot = n_slcn_acq = 39 slices. Because the SMS scans used the minimum TR for 13 acquisitions, only 13 slices of the entire volume could be acquired per TR in the calibration scans. Therefore, a total of n_slc = 3 TRs were needed for the calibration data. The RF pulse used for the calibration scan for each subject was the corresponding single non-modulated sinc used for the SMS scan for that subject. The calibration RF pulses for all 5 subjects were 6.4 ms in length.

Trajectory Parameters

The out-to-in concentric ring k_x-k_y trajectory was designed to produce a 64-by-64 image with a 22 cm FOV, and consisted of 32 equally spaced concentric circles with a sample at the k-space origin, as shown in Figure 1a. All gradients were designed to use 150 mT/m/ms for the maximum slew rate and 40 mT/m for the maximum amplitude. The blipped z-gradient consisted of a repeating pattern of positive-negative-positive blips to obtain a k_z trajectory that starts out at 1/FOV_z for the outermost k_x-k_y ring, goes to −1/FOV_z for the next ring, then 0 for the next ring, and continues with that pattern until the k_x-k_y-k_z origin is reached, where FOV_z = n_totd_slc is the SMS field of view in the through-plane direction. The scanner gradient sampling interval was 4 μs, resulting in 6612 samples for the entire concentric ring trajectory, including the initial path from the origin to the outermost ring and the final origin sample. The number of samples located only in the concentric rings was n_dat = 5892.

GRAPPA Reconstruction Parameters

For all the GRAPPA-based reconstructions, each ring was interpolated to a constant angular velocity trajectory of 208 samples, then separated into 8 angular sectors, as depicted in Figure 1a. The GRAPPA kernel for each sector of each coil consisted of a 3-by-3 grid that weights 3 consecutive rings and 3 consecutive interpolated points in the angular direction, resulting in n_kern = 9. For each sector of each coil, an additional asymmetric kernel was computed for the outermost and innermost rings, respectively. Instead of computing additional asymmetric kernels for the angular edges, each sector was created with an overlap of 1 point along both angular edges so that the original, non-asymmetric kernel could be used to compute all data points up to the non-overlapped angular edge. Finally, for the sample at the k-space origin, another kernel was constructed that uses 8 evenly spread data points from each of the innermost 3 rings. Coil compression for SG and SP-SG used n_stack = 10. For GRABSMACC, only the calibration frame was used to compute coil compression matrices, so n_stack = 1.

Conjugate gradient with 5 iterations and finite difference regularization was used to transform k-space data into the image domain. Theory from Ref. (24) was used to choose the regularization parameter in terms of the desired spatial resolution in the reconstruction. The regularization parameter for a point spread function with a full width at half maximum of 1.35 was determined, which results in a slight degree of smoothing. However, the same regularization parameter was used for all methods including all the GRAPPA-based, SENSE, and non-SMS reconstructions, so all methods should have the same degree of smoothing from regularization.

SENSE Reconstruction Parameters

Each SMS scan was also reconstructed using SENSE. Conjugate gradient with 10 iterations was used, along with the same field map, regularization parameter, and NUFFT parameters used in the SG and SP-SG conjugate gradient computation. The number of iterations was determined by examining the change in the solution with each iteration and using the number that resulted in a change similar to using 5 iterations with non-SMS reconstruction. The ESPIRiT process used a kernel of size 3-by-3 on only the central 32-by-32 region of the 64-by-64 Cartesian k-space, a threshold of 0.02 times the largest singular value to determine the ESPIRiT calibration matrix null space, and an eigenvalue threshold of 0.95 for the final eigenvector sensitivity maps. Coil compression in SENSE was done with n_stack = 10.

Non-SMS Scan Parameters

The non-SMS fMRI scans had n_tot = n_slcn_acq = 39 slices per time frame to match the SMS scans. However, the non-SMS scans used a TR of 1989 ms and a TE of 31 ms. The same RF pulse used for the SMS calibration scans was used for the non-SMS scans, but with a different Ernst flip angle for gray matter because of the longer TR. A separate field map acquisition was also acquired. Conjugate gradient using NUFFTs with inhomogeneity correction and finite difference regularization was used for reconstruction, and the coil images were combined using square-root-sum-of-squares. The same regularization parameter and NUFFT parameters used in SG and SP-SG were used with 5 iterations. It was found that further iterations did not produce significant changes in the solution for non-SMS data. The non-SMS scans were also coil-compressed before reconstruction for comparison with the SMS reconstructions. Specifically, n_stack = 10 time frames from the middle of the scan were used in a similar manner as in standard coil compression of SG and SP-SG, with the only difference being that there were n_tot = 39 different V_comp matrices, one for each slice.

Image Artifacts

The interslice leakage artifact and intraslice artifact using the Linear System Leakage Approach (17) were computed for all SMS reconstruction methods by taking non-SMS data consisting of only the middle n_acq = 13 slices of the non-SMS scan of subject 5 and reconstructing them with each of the various SMS methods. In the notation of Ref. (17), the interslice leakage metric of (L_2→1 + L_2→3) was computed, along with the intraslice artifact of (I_2→2 − I₂). The interslice leakage artifact metric is defined as Σ_w(|p_w,1|² + |p_w,3|²)/Σ_w(|p_w,1|² + |p_w,2|² + |p_w,3|²), where p_w,v is the complex value of pixel w in slice v of the 3 simultaneous slice reconstruction, and w ranges through the number of pixels in each slice. Here, v = 1 indicates all of the 13 inferior slices in the 39 total slices, v = 2 indicates the middle 13 slices, and v = 3 indicates the superior 13 slices. The intraslice artifact metric is defined as Σ_w(|p_w,2|² − |q_w,2|²)/Σ_w(|p_w,1|² + |p_w,2|² +|p_w,3|²), where q_w,v is the complex value of the ground truth (non-SMS) voxel. The total image artifact of (L_1→2 +I_2→2 +L_3→2 − I₂) was computed by synthesizing SMS data from all 39 slices of the non-SMS scan of subject 5, then reconstructing and comparing the SMS reconstruction with the original, ground truth non-SMS slices. The total image artifact is defined as Σ_w(|p_w,2|² − |q_w,2|²)/Σ_w(|q_w,2|²). All artifact computations were performed on 10 time frames of the non-SMS scan of subject 5, and the resulting metrics and maps were computed on the average of those 10 frames.

Retained SNR

The Pseudo Multiple Replica method (25) was used to compute the retained SNR, which is equivalently defined as 1/g, where g is the geometry factor in SMS reconstructions. In order to use this method, a noise-only scan was performed on one subject, and the same process described in Ref. (5) was used to generate a 250 image pseudo-time-series for each of non-SMS and SMS imaging with a full 39 slices for each time frame. Finally, average 1/g values were computed over a brain-like region of interest.

Results

Activated Voxel Counts

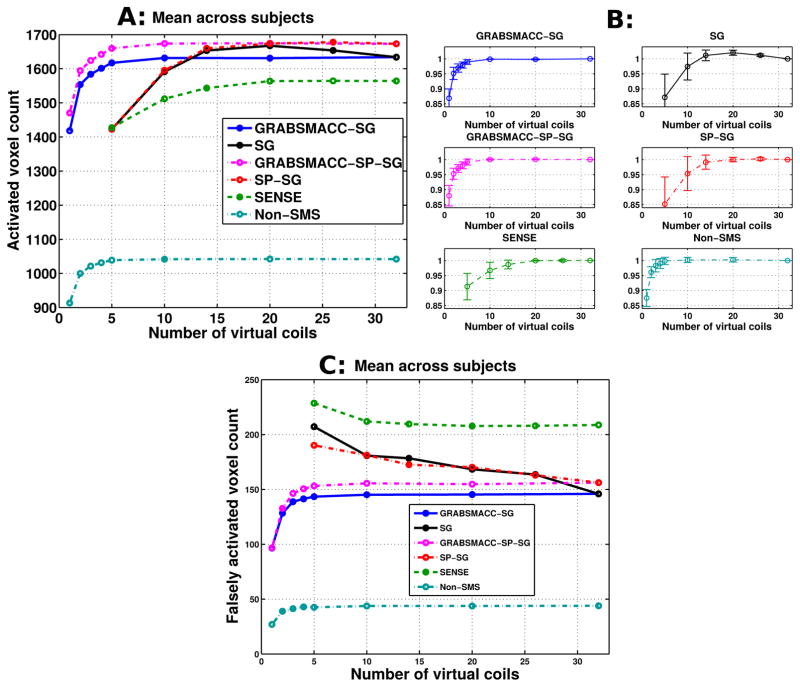
Figure 3a shows the mean of activated voxel counts across all 5 subjects in the visual and motor cortex ROIs for different acquisition and reconstruction methods versus number of virtual coils. Since n_coil = 32 for all experiments, 32 indicates no coil compression. In the Results section and in all the Figures, the terms “SG” and “SP-SG” by themselves refer to standard coil compression in SG and SP-SG, respectively. The terms “GRABSMACC-SG” and “GRABSMACC-SP-SG” refer to the use of GRABSMACC in SG and SP-SG, respectively. Looking at Figure 3a, the activated count for both GRABSMACC-SG and GRABSMACC-SP-SG remains unaffected until the number of virtual coils is reduced to around 5. The count for SP-SG initially tracks that of GRABSMACC-SP-SG, but has a drop at just 14 virtual coils and quickly drops far lower than the GRABSMACC-SP-SG count. The count for SG increases towards the count for SP-SG as the number of virtual coils decreases and similarly drops back down at 14 virtual coils. The SENSE count also begins to decrease at 14 virtual coils. Coil compression in non-SMS imaging performed similarly to both GRABSMACC-SG and GRABSMACC-SP-SG, with a decrease in count starting at around 4 virtual coils.

Figure 3.

(a) Activated voxel counts: mean across all 5 subjects. (b) Normalized activated voxel counts: mean across all 5 subjects with error bars indicating 95% confidence intervals. Before taking the mean across subjects, the count for each method was normalized by the count using all 32 coils. (c) Falsely activated voxel counts: mean across all 5 subjects. Falsely activated voxels are defined as active brain voxels that are outside the visual and motor cortex areas used for the activated voxel counts in (a) and (b). A t-score threshold of 6 was used for all methods.

The counts for each method were also normalized by dividing by the count using all 32 coils. Figure 3b shows the mean across subjects of the normalized counts for each method, along with error bars indicating 95% confidence intervals for each mean. The normalized counts for all four methods exhibit similar trends as they do in Figure 3a. Of note, the error bars around the normalized counts for GRABSMACC-SG, GRABSMACC-SP-SG, and non-SMS are very small, especially for 10 to 32 virtual coils, indicating excellent reproducibility between subjects. The error bars around the counts for SENSE are also small, but for a reduced range of 20 to 32 virtual coils. For SG and SP-SG, the error bars are relatively large below 20 virtual coils.

Figure 3c shows the mean of “falsely” activated voxel counts across all 5 subjects in the visual and motor cortex areas for different acquisition and reconstruction methods versus number of virtual coils. Falsely activated voxels are defined as active brain voxels that are outside the visual and motor cortex ROIs used for the activated voxel counts in Figures 3a and 3b. The most striking feature of Figure 3c is that SG and SP-SG exhibit increased false activation with just a small amount of compression. SENSE does as well, but to a lesser extent. However, the false activation level does not change appreciably for GRABSMACC-SG, GRABSMACC-SP-SG, and non-SMS until approximately 5 virtual coils.

Activation Maps

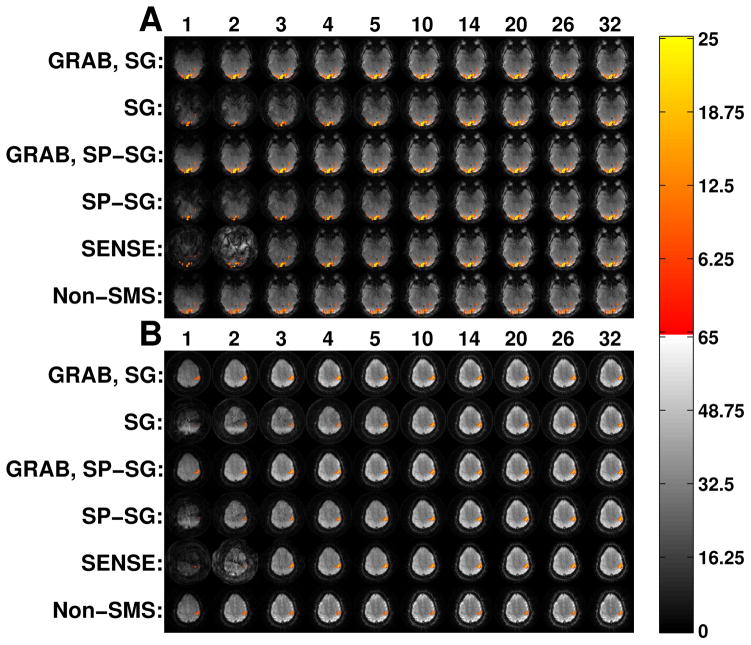
Figure 4a shows the quantitative t-score activation map for one visual cortex slice of subject 5 for different combinations of method (listed at the left) and number of virtual coils (listed at the top). The same visual cortex slice from the same fMRI time frame was reconstructed using the indicated combination of method and virtual coils, and is shown underneath the activation map in each entry. In other words, the underlying background image is the actual result using the indicated reconstruction method. The non-SMS images are from a different fMRI run and are intensity windowed differently from the SMS images due to the differing TR. Figure 4b shows the same data as 4a, but for one motor cortex slice of subject 5.

Figure 4.

(a) Visual and (b) motor cortex activation maps over reconstructed images for subject 5. The underlying background image is the actual result using the indicated reconstruction method. A t-score threshold of 6 was used for all methods. The top of each column lists the number of virtual coils for that column. For each of (a) and (b), the same visual or motor cortex slice is pictured for all methods and number of virtual coils. The activated voxel color scale is the t-score.

The visual and motor cortex activation maps are very similar between all the SMS methods, which is expected since they are all reconstructed using the same data. The non-SMS activation pattern, however, is still quite similar to the SMS reconstruction results, indicating good functional reproducibility in SMS fMRI. Comparing between different numbers of virtual coils, the activation map for each method does not change much in terms of shape or location; the only noticeable difference is a smaller activation size when the number of virtual coils becomes very small. In this regard, these results corroborate those in Figures 3a and 3b.

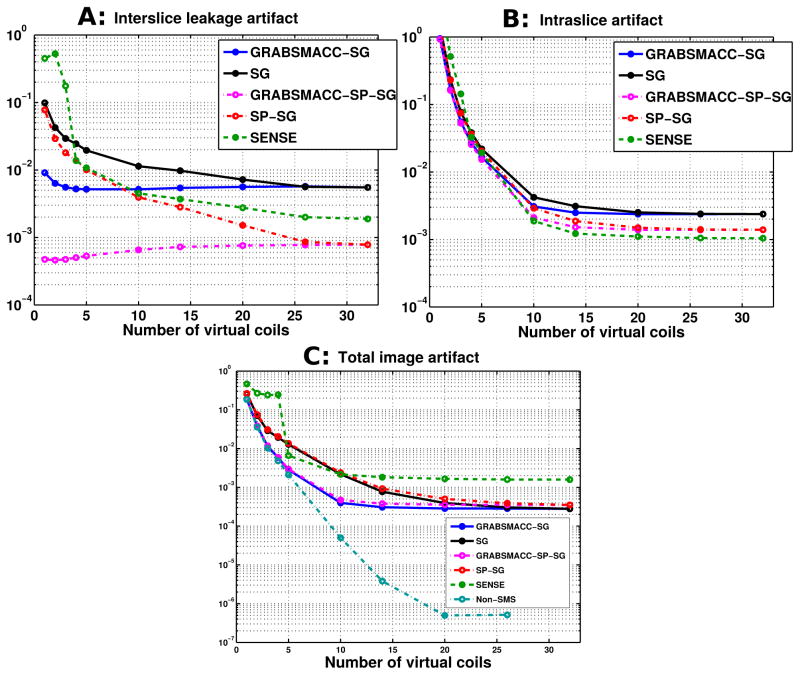
Image Artifacts

Figure 5 shows the interslice leakage (L_2→1+L_2→3), intraslice (I_2→2 − I₂), and total image artifact (L_1→2 + I_2→2 + L_3→2 − I₂) metrics for different acquisition and reconstruction methods versus number of virtual coils. The metrics were computed using the full set of 39 slices in each time frame. From Figure 5a, it is clear that GRABSMACC-SP-SG has the least interslice leakage out of all the methods. The intraslice artifact shown in Figure 5b has approximately the same behavior in all methods, except for a differing baseline level for each method. In Figure 5c, GRABSMACC-SG and GRABSMACC-SP-SG are the best performing SMS methods in terms of total image artifact.

Figure 5.

(a) Interslice leakage artifact metric (L_2→1+L_2→3), (b) intraslice artifact metric (I_2→2 − I₂), and (c) total image artifact metric (L_1→2 + I_2→2 + L_3→2 − I₂) for the middle slices of a 3-simultaneous-slice-acquired volume of 39 total axial slices.

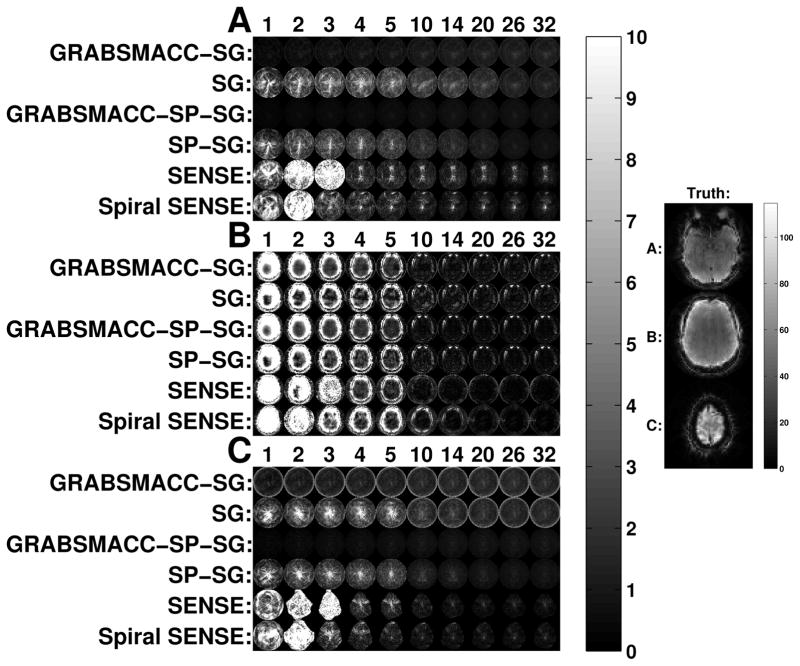
Figure 6 shows the actual interslice leakage, intraslice, and total image artifact maps for the 3 simultaneously acquired slices labeled as “Truth” on the right side. These images parallel the results in Figure 5; GRABSMACC-SP-SG has the least overall interslice leakage, with similar intraslice artifact behavior in all SMS methods. The intraslice artifact in GRABSMACC-SP-SG is larger than in SENSE, but the intraslice artifact in GRABSMACC-SP-SG is mostly near the eyes and not as much in the brain, which is the area that matters the most in fMRI.

Figure 6.

(a) Interslice leakage artifact for the inferior slice (L_2→1), (b) intraslice artifact for the middle slice (I_2→2 − I₂), and (c) interslice leakage artifact for the superior slice (L_2→3) from the middle slice of a 3 simultaneous slice acquisition. The image on the right shows the ground truth inferior (a), middle (b), and superior (c) slices.

In Figure 5a, SP-SG exhibits less interslice leakage when compared to SG, confirming the results of Ref. (17), while SENSE falls somewhere between SG and SP-SG. Figure 5a clearly shows the benefit of GRABSMACC on both SG and SP-SG in terms of reduced interslice leakage artifacts with larger amounts of compression. In particular, GRABSMACC-SG and GRABSMACC-SP-SG are the only SMS reconstruction methods that do not have increased interslice leakage with larger amounts of compression. In Figures 6a and 6c, both GRABSMACC-SG and GRABSMACC-SP-SG reduce the amount of interslice leakage compared to SG and SP-SG, respectively. GRABSMACC-SP-SG does particularly well with almost no visible interslice leakage signal, especially when com-pared to the other 4 methods shown. In addition, Figures 6a and 6c illustrate the importance of interslice leakage on functional activation; for all methods, the leakage signal tends to concentrate more in the center of the image where brain matter is likely to be present, potentially affecting activation in the areas of most interest.

The intraslice artifact, shown in Figures 5b and 6b, is very similar between all 5 SMS reconstruction methods, and particularly so between SG and GRABSMACC-SG and between SP-SG and GRABSMACC-SP-SG. Using 20 to 32 coils, there is very little difference between SG and GRABSMACC-SG and between SP-SG and GRABSMACC-SP-SG. When going below 20 virtual coils, the GRABSMACC methods have slightly less intraslice artifact than their non-GRABSMACC counterparts. The intraslice artifact results again mirror the results in Ref. (17) in that SP-SG has reduced intraslice artifact compared to SG.

All the GRAPPA-based methods have similar total image artifact with all 32 coils, as shown in Figure 5c. However, SG has slightly less total image artifact compared to SP-SG, again consistent with Ref. (17), which explains that SP-SG trades off higher total image artifact for reduced leakage. Using GRABSMACC for compression reduces the total image artifact to very similar levels for both SG and SP-SG.

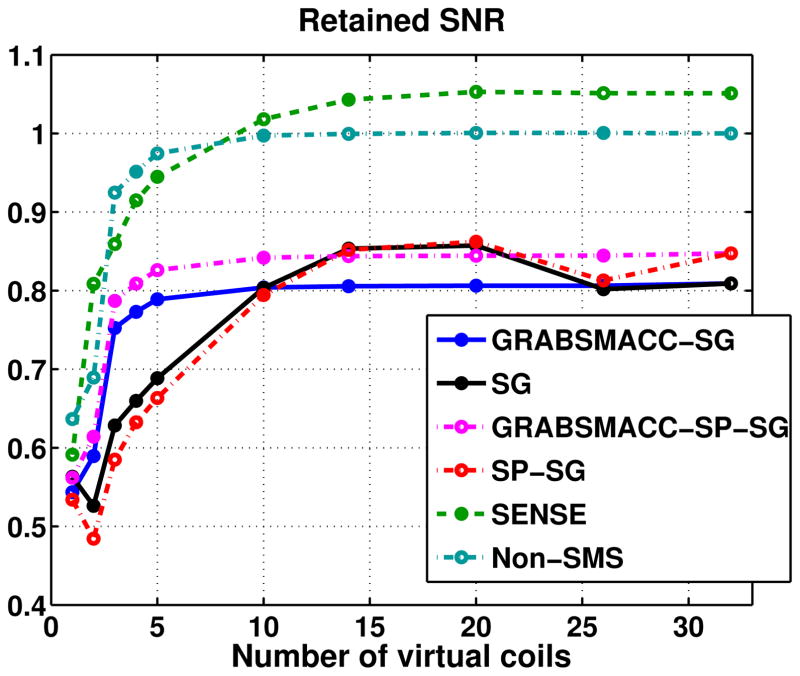
Retained SNR

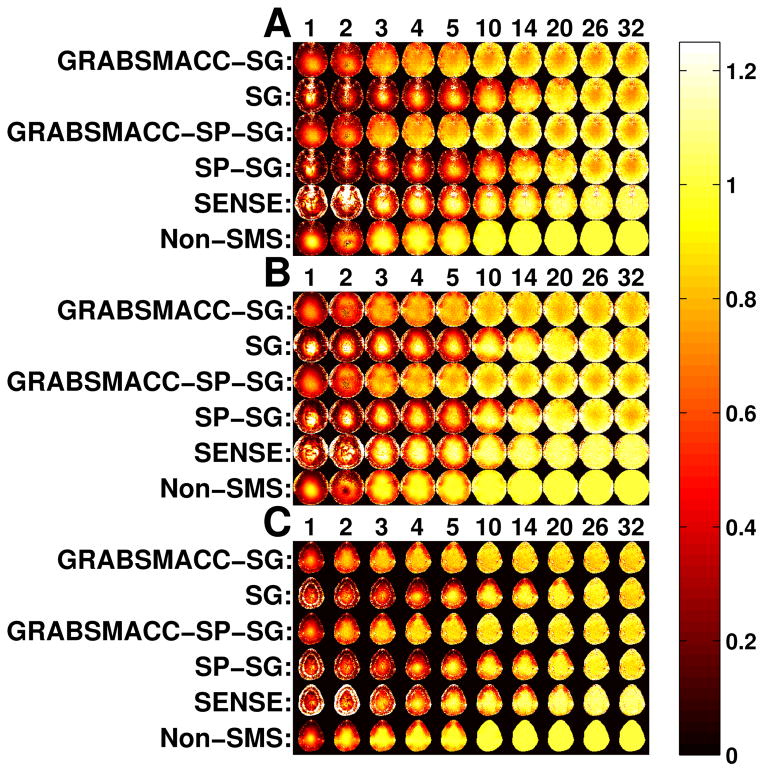
Figure 7 shows the average retained SNR, or equivalently, average 1/g-factor within a brain ROI that covers all 39 slices in each time frame. The GRABSMACC-SG and GRABSMACC-SP-SG plots behave the most similarly to the non-SMS plot; all three have constant SNR until around 5 virtual coils. The SNR using all 32 coils for SENSE starts out at a higher level than non-SMS, but begins to fall earlier around 14 virtual coils. The plots for SG and SP-SG are almost the same, with an increase in SNR with 20 and 14 virtual coils. In general, the GRAPPA-based methods have a baseline retained SNR of around 0.8 to 0.85. Figure 8 shows retained SNR maps of the same 3 simultaneous slices used in Figure 6.

Figure 7.

Average retained SNR, or equivalently, average 1/g-factor within brain voxels.

Figure 8.

Maps of retained SNR, or equivalently, 1/g-factor of the same slices used in Figure 6. (a) Inferior slice, (b) middle slice, and (c) superior slice.

Computational Speed

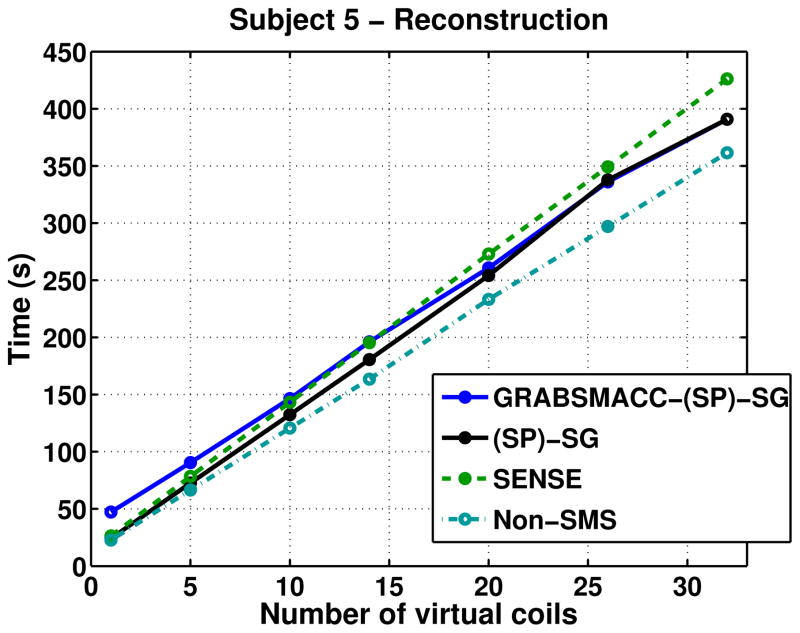
Figure 9 shows the time needed for a single computer with an Intel Xeon E3-1230 3.20 GHz processor to reconstruct the first time frame of fMRI runs of subject 5, and includes the time needed for coil compression. The times for SG and SP-SG were virtually identical, as were the times for GRABSMACC-SG and GRABSMACC-SP-SG, so each of the pairs were combined into a single plot, as shown in the legend of Figure 9. Construction of field maps, sensitivity maps, and GRAPPA kernels are only done once per fMRI scan, so they were not included in the times. While not insignificant, the time needed for them does not contribute as much relative to the overall time needed for reconstruction of the entire fMRI scan. In all methods, the reconstruction time increases linearly with the number of virtual coils used. The time needed for kernel computation was around 100 seconds and 256 seconds for GRABSMACC-SG and GRABSMACC-SP-SG, respectively, regardless of the number of virtual coils used. The time needed for kernel computation ranged linearly from 4 to 100 seconds in SG, and linearly from 11 to 256 seconds in SP-SG as the number of virtual coils increased from 1 to 32.

Figure 9.

Reconstruction times of the first time frame of fMRI scans of subject 5. The time needed for field map, sensitivity map, and GRAPPA kernel generation is not included in these reconstruction times. The time needed for coil compression is included.

Discussion

The concentric ring trajectory provides better sampling regularity for GRAPPA than a spiral, but is longer: the readout length for the same FOV and image size using a typical spiral-in is around 20.224 ms, whereas the readout length of the proposed concentric ring trajectory was 26.044 ms. The increase in length is mainly caused by the need to sample k-space with shorter intervals along the trajectory right before and after the ring transitions, as shown in Figure 1b, in order to satisfy maximum gradient slew rate constraints. In addition, each ring is sampled fully along the entire circle before transitioning to the next smaller ring. Potential time savings could be had if one were to start the transition before reaching the end of the full circle, although at decrease in sampling regularity for the GRAPPA kernel. However, this readout time increase does not prevent the use of a suitable TE for BOLD imaging.

Unlike a simple FOV shift obtained with blipped-CAIPI EPI, blips using concentric rings result in a blur, as shown in Figure 2b. Qualitatively, when compared with blipped-CAIPI, there is potentially less signal overlap of simultaneous slices because the signal is blurred throughout the entire FOV, whereas in blipped-CAIPI, there is a discrete shift. Less overlap potentially results in a better g-factor. However, using GRAPPA with non-Cartesian trajectories inevitably introduces certain distortions in the reconstruction due to the Cartesian approximation of a non-Cartesian trajectory that occurs when unwrapping the constant angular velocity rings into Cartesian grids. In Ref. (5), the 1/g maps for blipped-CAIPI SE-EPI with 3 simultaneous slices averaged around 0.997, whereas the non-blipped version averaged around 0.68. Using our blipped concentric rings, GRABSMACC-SP-SG resulted in an average 1/g of around 0.85, which is not as high as the blipped-CAIPI results in Ref. (5), but still higher than non-blipped SMS. Using SENSE resulted in an average 1/g of over 1 using our blipped concentric rings, possibly because the conjugate gradient algorithm was not run quite to convergence, which could result in slight smoothing not obvious visually. Thus, it is likely that the Cartesian approximation in the GRAPPA-based methods reduced the retained SNR. The retained SNR, a measure of thermal noise, is not the only metric that should be considered when evaluating a method for fMRI. While the decrease in 1/g is not insignificant, Ref. (26) argues that physiological noise and not thermal noise dominates in many studies. As shown in Figure 5a, GRABSMACC-SP-SG results in less interslice leakage compared to SENSE, with fewer false activations in neighboring simultaneous slices. In addition, signal recovery in the presence of in-plane susceptibility-induced gradients may show that the concentric-ring-in trajectory may have utility when imaging in inferior regions of the brain.

In this work, a concentric ring trajectory was chosen to enhance sampling regularity for GRAPPA compared to non-Cartesian trajectories such as spirals. Another benefit of concentric rings is that they are amenable to in-plane acceleration using GRAPPA. Single-shot acquisitions can easily be constructed for higher sampling density, while multishot acquisitions would better match B₀ phase evolution. If multiple interleaves are acquired, gross movement or physiological motion between excitations can easily degrade the quality of the calibration, although recent work has reduced the sensitivity losses from these issues in accelerated parallel EPI (27).

Comparing the activation counts of SG and GRABSMACC-SG in Figure 3a, SG appears to outperform GRABSMACC-SG since the count for SG increases as the number of virtual coils is decreased from 32. One explanation is that autocorrelation in the data for SG increased as the number of virtual coils initially decreased from 32, resulting in a reduction in the effective degrees of freedom and a difference in the actual t-score significance threshold. Since the threshold was fixed at t > 6, this resulted in an artificially increased number of activated voxels for SG. Comparing SP-SG and GRABSMACC-SP-SG in Figure 3a and 3c, GRABSMACC-SP-SG is clearly superior to SP-SG in both true and false activation counts. The false activation behavior seems to be strongly related to the interslice leakage artifact results in Figures 5a, 6a, and 6c, since activation from one slice can leak into another.

Although interslice leakage can affect the false activation, intraslice artifacts also contribute. For example, in Figure 3c, GRABSMACC-SG exhibits less false activation than SP-SG at all levels of compression, while in Figure 5a, GRABSMACC-SG has a higher amount of interslice leakage than SP-SG for ≥ 10 virtual coils. However, the total image artifact shown in Figure 5c, which contains both interslice and intraslice artifacts, shows that GRABSMACC-SG has less total artifact than SP-SG for all levels of compression, similar to the false activation results. It should also be mentioned that the false activation in Figure 3c is computed from all 39 slices, whereas the artifact results in Figure 5 are not computed from all the slices; in Figure 5a the interslice leakage is from the middle block of 13 slices out to the superior and inferior blocks of 13, Figure 5b displays the intraslice leakage for just the middle block of 13 slices, and Figure 5c contains interslice leakage from the superior and inferior blocks into the middle block of 13, along with intraslice leakage for the middle block.

Also of importance is the general trend of false activation for each method in Figure 3c. With GRABSMACC-SG and GRABSMACC-SP-SG, it is reassuring that activation results will likely not be falsely elevated with coil compression. Excessive amounts of compression will likely hinder GRABSMACC’s ability to detect true activation, but it does not seem to cause false activation and lead to false positive conclusions on brain function. On the other hand, SG, SP-SG, and SENSE all result in increased false activation with increasing compression. Also interesting is how similar the shape of the curves for GRABSMACC-SG and GRABSMACC-SP-SG are to the shape of the curve for non-SMS in Figures 3a and 3c. In this respect, GRABSMACC mimics the non-SMS ideal much better than the other SMS reconstruction methods.

In Figure 5a, the interslice leakage mostly increases with a decreasing number of virtual coils, but this is not the case for GRABSMACC-SG and GRABSMACC-SP-SG, both of which exhibit a very slight decrease in interslice leakage when the number of virtual coils is very low. As explained by Ref. (17), there is a trade off between interslice and intraslice artifacts for SMS imaging. Compared to SP-SG, SG trades off higher interslice error for lower total artifact error, whereas SP-SG trades off higher total artifact error for lower interslice error. Furthermore, the interslice and intraslice error trade off can be tuned with weighting parameters in SP-SG. In Figure 5a, the very slight decrease in interslice leakage with lower numbers of virtual coils in GRABSMACC-SG and GRABSMACC-SP-SG are likely coming at the expense of increased intraslice error. The monotonically increasing total image artifact with decreasing coils shown in Figure 5c confirms this effect for all methods. Perhaps the virtual coil sensitivities created by the GRABSMACC methods at low numbers of virtual coils exhibit very good variation in the through-plane direction, but not as adequately in-plane, which generates better slice separation but worse intraslice artifact.

In general, the SNR plots in Figure 7 behave similarly to the activation count plots in Figure 3a. Perhaps the most surprising feature of the SNR plots is that the SNR for SG and SP-SG is higher at 14 and 20 virtual coils when compared to using all 32 coils. The SNR for SENSE also increases slightly at 20 virtual coils, although to a lesser extent than SG and SP-SG. This behavior is perhaps explained by the interslice leakage of these methods. It is possible that the increased interslice leakage artifact for these methods creates an artificial, “stationary” signal in the images, resulting in a higher signal with the same level of standard deviation and hence a higher calculated SNR. However, once the number of virtual coils is reduced below 14, the overall degradation in the underlying image begins to outweigh any of the artificial changes that the interslice leakage produced. Notice that GRABSMACC-SG and GRABSMACC-SP-SG exhibit no increases in interslice leakage from 32 to 5 coils, and so the SNR remains almost constant from 32 to 5 coils. In particular, note that non-SMS has absolutely no interslice leakage, and the shape of the SNR plot for non-SMS in Figure 7 is very similar to the shape of the SNR plots for GRABSMACC-SG and GRABSMACC-SP-SG.

Taking into account all the results, GRABSMACC-SP-SG likely has the best preservation of activation out of all the SMS reconstruction methods for the purposes of most fMRI studies. SG, SP-SG, and SENSE exhibit worrying false activation and increased interslice leakage with compression. GRABSMACC-SP-SG has the least interslice leakage, which is perhaps the most important out of all the artifacts since it has the most potential for generating erroneous activation. In terms of SNR, SENSE comes out on top. However, the amount of SNR that GRABSMACC-SP-SG does possess is clearly enough to detect activation in a normal functional study. Furthermore, the SNR is better preserved with higher amounts of compression when compared to SENSE.

The better compression for GRABSMACC and non-SMS can be explained from the V_comp matrices. With these two methods, a different V_comp matrix is computed for each of the n_tot = n_slcn_acq number of individual slices. The SVD selects the best possible set of linear combinations of coils to use for each individual slice, in fact tailoring the compression for each target solution. However, with SENSE, SG, and SP-SG, only n_acq number of V_comp matrices are used, which amounts to one V_comp matrix for each set of n_slc = 3 individual slices. The V_comp matrices are computed from “source” data consisting of the sum of 3 slices, which may not result in the best set of linear combinations to use for the individual target slices. In SMS imaging, the n_slc = 3 simultaneously acquired slices are separated from each other by some distance in the through-plane direction for decreased geometry factor. This separation in space results in an SMS signal that is the sum of 3 very different objects.

Although GRABSMACC outperforms standard coil compression in SMS reconstruction, it does not decrease the amount of storage needed for raw data archival, if desired. The full set of original 32 coils are used in GRABSMACC to reconstruct images in a virtual coil basis, so the raw k-space data cannot be compressed and saved at a smaller size for later reconstruction. On the other hand, with standard coil compression, raw data can be compressed and saved, but the standard process is still a form of lossy compression. If enough of the signal of interest is not maintained, it cannot be recovered once the original data is deleted.

The reconstruction times for GRABSMACC shown in Figure 9 do not differ much from SG and SP-SG at 26 and 32 coils, and actually increase slightly above the times needed for SG and SP-SG as the number of virtual coils is reduced below 26. This is because the W matrix has bigger dimensions in GRABSMACC than in standard coil compression, resulting in slightly slower k-space separation. However, the W matrix only needs to be determined once per fMRI run or once for the entire fMRI study. The main bottleneck for image reconstruction in GRABSMACC, SG, and SP-SG is the iterative conjugate gradient routine that transforms separated k-space data into the image domain, and not the k-space domain slice separation process using the kernels in W, which is just a simple matrix vector multiplication. For example, in GRABSMACC-SP-SG with all 32 coils using a single computer with an Intel Xeon E3-1230 3.20 GHz processor, the kernel convolution step takes a total of around 21 seconds for 1 time frame, and the remaining 370 seconds is used for multiple conjugate gradient routines transforming k-space data for each coil into the image domain. Therefore, at each matching virtual coil position in Figure 9, GRABSMACC takes longer than SG and SP-SG, but not by much compared to the total time needed. On the other hand, unlike the GRAPPA-based methods, SENSE uses conjugate gradient once, albeit on a larger problem, to separate the slices directly into the image domain. For this reason, GRABSMACC becomes ever so slightly slower than SENSE at 14 virtual coils and below. We also note that while non-Cartesian SENSE most likely requires the use of an iterative reconstruction, GRABSMACC can easily be implemented with a non-iterative reconstruction like the conjugate phase reconstruction (28), which would substantially decrease the reconstruction time even further.

The main benefit of GRABSMACC over standard coil compression in SG, SP-SG, and SENSE is better preservation of activation with the reduction in number of virtual coils. Since activation is preserved so much better in GRABSMACC versus the other methods, a much smaller number of virtual coils can be used in GRABSMACC with equivalent activation performance but less computational burden. For example, GRABSMACC-SP-SG with 10 virtual coils results in essentially the same activation as with all 32 coils, no increase in false activation, no increase in interslice leakage, no decrease in SNR and negligible increase in intraslice and total image artifact. For SENSE, one would need 20 virtual coils for activation and SNR to remain unaffected compared to using all 32 coils, although the interslice leakage is increased. From Figure 9, GRABSMACC-SP-SG with 10 virtual coils takes about 54% as long as SENSE with 20 virtual coils, which translates to time savings on the order of several hours when reconstructing multiple fMRI studies. A similar argument can be made when comparing GRABSMACC-SP-SG to SP-SG, with the added fact that SP-SG has even more interslice leakage when compared to using 32 coils, and likely more false activation as well.

Buehrer et al. (10) proposed a coil compression method that uses Principle Component Analysis on coil sensitivities to compute compression matrices that reduce reconstructed image noise. Their method requires the formation of coil sensitivities for superimposed voxels, which is easily done for undersampled Cartesian trajectories. However, with a concentric ring and blipped z-gradient readout, the aliasing pattern is not a trivial shift in some direction, but a blur in many directions. This makes it impractical to use their method to reduce image noise in our case. On the other hand, GRABSMACC can be easily used with Cartesian SMS fMRI. Future work may involve comparing the activation performance of GRABSMACC with other noise reducing compression methods, as well as investigating the compression performance of GRABSMACC using different numbers of simultaneous slices.

Conclusions

Coil compression is frequently used to reduce the computational time and memory required to reconstruct parallel imaging data and becomes increasingly beneficial as the number of coils increases. GRABSMACC is a practical method for coil compression in SMS fMRI and retains functional activation better than standard coil compression techniques used with SMS imaging and reconstruction. Experiments presented indicate that SMS fMRI scans using 32 receive coils and 3 simultaneous slices can be compressed down to approximately 31% of their original size without any significant loss of functional activity.