Oscillatory lower body negative pressure impairs task related functional hyperemia in healthy volunteers

Oscillatory cerebral blood flow is associated with reduced functional hyperemia and neurovascular coupling in postural tachycardia syndrome. Evoked by central hypovolemia, it may interfere with neurovascular coupling at the neurovascular unit. This study shows that forced induction of oscillatory cerebral blood flow using oscillatory lower body negative pressure causes neurovascular unit dysfunction.

Abstract

Neurovascular coupling refers to the link between an increase in neural activity in response to a task and an increase in cerebral blood flow denoted “functional hyperemia.” Recent work on postural tachycardia syndrome indicated that increased oscillatory cerebral blood flow velocity (CBFv) was associated with reduced functional hyperemia. We hypothesized that a reduction in functional hyperemia could be causally produced in healthy volunteers by using oscillations in lower body negative pressure (OLBNP) to force oscillations in CBFv. CBFv was measured by transcranial Doppler ultrasound of the left middle cerebral artery. We used passive arm flexion applied during eight periodic 60-s flexion/60-s relaxation epochs to produce 120-s periodic changes in functional hyperemia (at 0.0083 Hz). We used −30 mmHg of OLBNP at 0.03, 0.05, and 0.10 Hz, the range for cerebral autoregulation, and measured spectral power of CBFv at all frequencies. Arm flexion power performed without OLBNP was compared with arm flexion power during OLBNP. OLBNP power performed in isolation was compared with power during OLBNP plus arm flexion. Cerebral flow velocity oscillations at 0.05 Hz reduced and at 0.10 Hz eliminated functional hyperemia, while 0.03 Hz did not reach significance. In contrast, arm flexion reduced OLBNP-induced oscillatory power at all frequencies. The interactions between OLBNP-driven CBFv oscillations and arm flexion-driven CBFv oscillations are reciprocal. Thus induced cerebral blood flow oscillations suppress functional hyperemia, and functional hyperemia suppresses cerebral blood flow oscillations. We conclude that oscillatory cerebral blood flow produces a causal reduction of functional hyperemia.

NEW & NOTEWORTHY

Oscillatory cerebral blood flow is associated with reduced functional hyperemia and neurovascular coupling in postural tachycardia syndrome. Evoked by central hypovolemia, it may interfere with neurovascular coupling at the neurovascular unit. This study shows that forced induction of oscillatory cerebral blood flow using oscillatory lower body negative pressure causes neurovascular unit dysfunction.

during mental challenges, the velocity of blood flow in the middle cerebral artery (MCA) increases in healthy control subjects in the absence of blood pressure (BP) or end-tidal CO₂ (ET_CO2) changes (32). This increase is called “functional” or “neural activity related hyperemia.” Neurovascular coupling (NVC) (1) refers to the link between the increase in neural activity in response to a neural activation task and an increase in cerebral blood flow (CBF), denoted “functional hyperemia” (12). Functional hyperemia can be measured by transcranial Doppler ultrasound (TCD) in the MCA in healthy volunteers (29). Research has shown that NVC involves interactions among the neurons, blood vessels, and glia comprising the neurovascular unit (17).

Our recent work demonstrated increased low-frequency oscillations (≤0.1 Hz) of CBF velocity (CBFv; OCBFv) in young patients with postural tachycardia syndrome (POTS), a form of chronic orthostatic intolerance, during upright posture (22, 33). OCBFv was highly coherent with and phase locked to oscillations in mean arterial pressure (MAP) (OAP) at low frequencies, indicating impaired cerebral autoregulation. OCBFv was amplified compared with that in healthy volunteers, with larger transfer function gain (22), increased monotonically with orthostatic stress during graded tilt test (33), and was associated with reduced functional hyperemia not observed in healthy controls (33, 34).

However, this work showed an associative rather than a causal relationship between increased oscillatory CBF (OCBF) and reduced functional hyperemia/NVC. We considered whether imposing increased OCBF in the low-frequency range would cause reduced functional hyperemia, even in healthy volunteer subjects. If so, enhanced low-frequency OCBF would be causing the reduction in functional hyperemia. Such reduction could be frequency dependent because of the countering effect of cerebral autoregulation, which exerts its control at very low frequencies (41). In the present work, we used oscillatory lower body negative pressure (LBNP; OLBNP) to drive low-frequency oscillations and arm flexion as a somatosensory stimulus to produce neural activation to test the hypothesis that increased low-frequency OCBF power results in a frequency-dependent reduction in functional hyperemia in healthy volunteers.

METHODS

Outline.

We measured CBFv in the left MCA by TCD ultrasound to assess their functional hyperemic response. As in previous work, this was quantitated as the percent change in CBFv divided by the time-averaged CBFv to compensate for individual differences in the angles of insonation for each subject (33).

To remove intellectual components or perceptual differences between subjects, and to provide a highly repeatable stimulus (30), we used the response to a somatosensory stimulus as the neural activation task. We adapted a simple brain activation paradigm from the work of Salinet et al. (31) in which passive arm flexion and reextension at a rate of 1 flexion/s was performed for 60 s, followed by a 60-s resting period. This was repeated for a total of eight complete 120-s cycles. Time-averaged CBFv was taken over the eight cycle epoch. While each arm flexion produced an individual increase in CBFv, this was typically small; larger increments were produced by the 60-s flexion task. Flexion was performed on the right arm, and the responses were detected by measuring CBFv on the contralateral side. Arm flexion was performed by the same individual on all subjects to minimize stimulus variation. While in the past our laboratory assessed functional hyperemia by using the change in slope or amplitude of each activation period (35), in the present study we employed a periodic activation task so that we could use Fourier methods (see below) to measure changes in average amplitude during OCBF functional hyperemia. Thus functional hyperemia was cycled with a period of 120 s (fundamental frequency of 0.0083 Hz), increasing during periods of flexion and decreasing during periods of rest. In this way, we generated a 960-s-long epoch of oscillating functional hyperemia.

Since the frequency resolution is equal to the inverse of the time duration during which a signal is being observed, the prolonged recording results in a frequency resolution slightly <0.001 Hz. Our measure of functional hyperemia was obtained by using Simpsons rule (14) to integrate the power spectral density over a 0.01-Hz band encompassing 0.0083 Hz, which is equivalent to multiplying the mean over the interval by 0.01 Hz in spectral power.

During the eight-cycle flexion and nonflexion epochs, we used the protocol of Taylor (9–11, 37) and applied OLBNP to drive frequency oscillations in MAP and CBFv at 0.03, 0.05, and 0.10 Hz. These frequencies correspond to observed spontaneous oscillations that relate to cerebral autoregulation (5). OLBNP was accomplished by varying negative pressure between 0 mmHg and −30 mmHg at each of these frequencies using a pressure gauge and manual pressure release valve. This generated a mean LBNP change of −15 mmHg.

Thus to obtain a 0.10-Hz oscillation, the vacuum was turned on for 5 s, then off for 5 s; to obtain a 0.05-Hz oscillation, the vacuum was turned on for 10 s and off for 10 s; and for 0.03-Hz oscillation, the vacuum was turned on for 15 s and off for 15 s. OLBNP was imposed at a given frequency for 16 min, which was maintained during arm flexion for an additional 16 min.

When arm flexion was complete, OLBNP was turned off, and the subject was allowed to recover for 30 min. At each frequency of OLBNP, including the absence of OLBNP, we measured spectral power contained within a 0.01-Hz band encompassing 0.03 Hz (0.025–0.035 Hz), 0.05 Hz (0.045–0.055 Hz), and 0.10 Hz (0.95-0.105 Hz), as well as power at the frequency of arm flexion 0.0083 Hz (0.0033–0.0133 Hz).

Subjects.

We enrolled 12 consecutive healthy volunteers. Subjects were 19–27 yr old (median age 23.5 yr, 6 women, 6 men). Healthy volunteers were nonsmoking individuals with no previously known medical conditions, free of systemic illness, with a normal physical exam and electrocardiogram. Healthy female subjects were enrolled without regard to their use of oral contraceptives or the phase of their menstrual cycle. Healthy volunteers were included only if they had never experienced orthostatic intolerance of any type, including orthostatic hypotension, POTS, and syncope. We also excluded subjects with a history of respiratory disease, sleep apnea, heart disease, renal disease, systemic hypertension, diabetes, acute or chronic inflammatory disease, neoplasm, immune-mediated disease, past head trauma, obesity, congenital heart disease, or peripheral vascular disease.

Subjects took no medications, including nonprescription medications, for at least 2 wk before the study, with the exception of contraceptive medications. None of the subjects had ever received cardioactive or vasoactive medications. All subjects were required to stop ingestion of xanthine-, caffeine-, and alcohol-containing substances 72 h before the study. A light breakfast was permitted on testing day if eaten ≥2 h before testing.

The Institutional Review Board of New York Medical College reviewed and approved this protocol. Each subject received a detailed description of all protocols and was given an opportunity to have their questions answered. Signed, informed consent was obtained from all participants.

Instrumentation.

All subjects were instrumented in a similar fashion by the same operators. Height and weight were measured. During instrumentation, all subjects lay supine on a bed. Beat-to-beat BP was monitored using finger arterial plethysmography (Finometer; FMS, Amsterdam, The Netherlands) on the left middle or index finger. Finometer data were calibrated to brachial artery pressure. A single-lead ECG measured heart rate (HR). A nasal cannula was connected to a capnograph to measure ET_CO2, and a pulse oximeter to measure O₂ saturation (Smiths Medical, Waukesha, WI). We used TCD (Neurovision; Multigon, Yonkers, NY) to measure CBFv in the left MCA at a depth of 5–6 cm using a 2-MHz probe fixed to the subject's head by a custom-made headband. All analog signals were digitized at 200 Hz with custom signal processing software and analyzed off-line.

OLBNP.

Subjects were placed in the supine position into the LBNP box such that their lower bodies (legs and hips up to the level of iliac crest) were placed in a sealed air-tight chamber (the LBNP box) and instrumented. The subject was then sealed within the box with a rubber diaphragm hermetically fitted around the iliac crest that did not compress the abdomen. Suction was provided by a vacuum pump capable of rapidly producing changes in negative pressure. Negative pressure was set with a variable autotransformer calibrated against an electronic manometer. A manual pressure release valve was used to control the timing of pressure pulses.

Protocol.

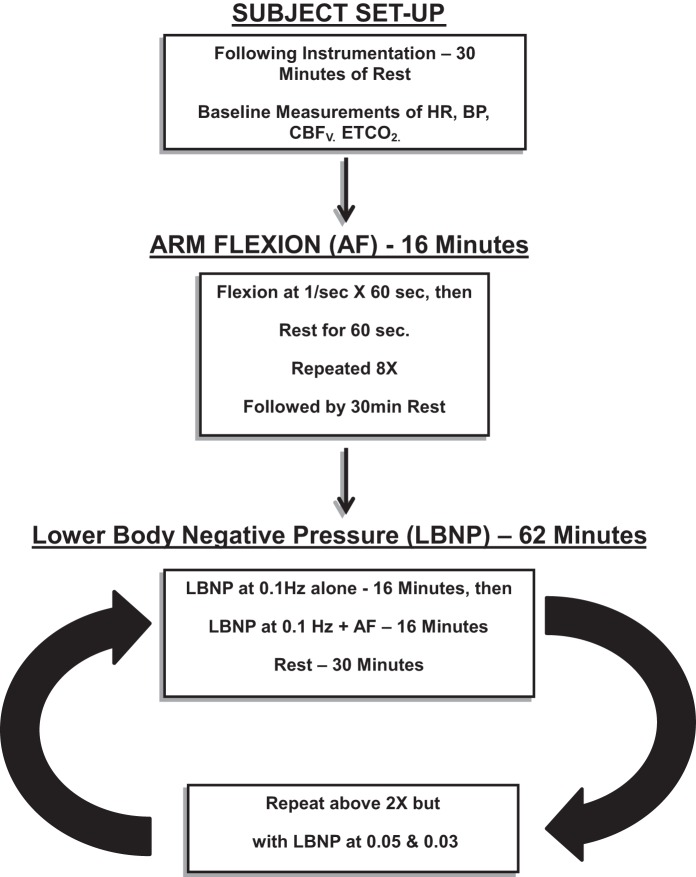
All subjects arrived at 9:30 AM. Following instrumentation, subjects remained supine and were placed within the LBNP box. We familiarized subjects with passive arm flexion and LBNP box function, including changes in vacuum pressure. There was a minimum of 30 min of equilibration after instrumentation and LBNP installation. Baseline measurements of arterial pressure, CBFv, HR, and ET_CO2 were taken over the next 16 min. Arm flexion for 16 min as outlined above was performed at baseline in the absence of OLBNP. Subjects rested 30 min and were exposed to OLBNP at 0.03, 0.05, and 0.10 Hz in random order. OLBNP without arm flexion at each frequency was performed for 16 min, after which arm flexion commenced. At the end of arm flexion, OLBNP was turned off, and the subjects were allowed to recover for 30 min. The duration of the experiment was ∼4 1/2 h. Figure 1 is a schematic diagram of the study design.

Fig. 1.

A schematic diagram of the study designed employed in these determinations. CBFv, cerebral blood flow velocity; ET_CO2, end-tidal CO₂; AF, arm flexion; LBNP, lower body negative pressure; HR, heart rate; BP, blood pressure.

A priori stopping criteria (end test) were in place, including signs and symptoms of presyncope, defined as a decrease in systolic BP to 80 mmHg; a decrease in systolic BP to 90 mmHg associated with symptoms of lightheadedness, nausea, sweating, or diaphoresis; or progressive symptoms of orthostatic intolerance accompanied by a request to discontinue the test. All subjects completed the protocol.

Data analysis.

All data were continuously sampled at 200 Hz and were converted with an analog-to-digital converter (DI-720 DataQ Ind, Milwaukee, WI) connected to a personal computer and analyzed offline. NCSS 2007 (NCSS, LCC, and Kaysville) statistical software was used in the statistical analysis.

Time-averaged CBFv, MAP, HR, and ET_CO2.

Averaged CBFv, MAP, HR, and ET_CO2 tabulated at baseline periods (no OLBNP and no arm flexion), during arm flexion alone (no OLBNP), OLBNP alone at each frequency of oscillation, and arm flexion plus OLBNP at each frequency of oscillation and were compared by one-way ANOVA.

OCBF and OAP.

We time-averaged CBFv and arterial pressure over each cardiac cycle. We anti-alias filtered the signals using a zero-phase eighth-order low-pass Butterworth filter at 0.4 Hz. Power spectral density curves (periodograms) were computed using the squared amplitudes of a Hanning windowed fast Fourier transform (FFT) for each time series (CBFv, MAP, and HR), at each oscillatory LBNP frequency (0.03, 0.05, 0.10 Hz) during 16-min intervals, with and without flexion. We include baseline as no OLBNP.

We are detecting extremely low-frequency oscillations. Often FFT analyses employ data detrending, which can influence estimated power spectra particularly at the lowest frequencies (8), especially if high-order detrending is employed (25). Therefore, we only subtracted mean values from our time series (15).

Before computing the FFT, we applied a tapered Hanning window to the entire data set to limit spectral leakage caused by the finite nature of the data (13), after which FFT was computed. To deal with the high order of variance in the periodogram, we chose to average data in the frequency domain over the 0.01-Hz interval that encompasses each frequency of interest (2). Thus, at each frequency and flexion condition, oscillatory power was determined by integrating the appropriate power spectrum density curve over the 0.01-Hz band encompassing each tabulated frequency (0.0083, 0.03, 0.05, 0.10 Hz). Data were approximately log-normal. Results for comparison were expressed as the difference of logarithms base 10 multiplied by 10 in units of decibels. Parametric analysis based on the log-transformation is an accepted approach and, indeed, will enhance the statistical validity of the comparisons when data are severely skewed (e.g., follows a log-normal distribution). The transformation may address not only the skewness of the data, but the heterogeneity of the variances. The difficulty with the log-transformation occurs when the results are back-transformed to yield clinically interpretable results. Means and confidence limits (even error bars) for back-transformed data may require complicated conversions to yield unbiased estimates (42, 43). However, if the results are interpretable on the log scale, then back-transformation is not necessary.

We focused on the effects of flexion on baseline power at 0.0083 Hz, our measure of functional hyperemia, and how the addition of OLBNP may alter that response, i.e., whether OLBNP blunts functional hyperemia. We also investigated the effects of OLBNP without flexion on baseline power at 0.03, 0.05, and 0.10 Hz, and how the addition of flexion may alter those responses. The effects of frequency of OLBNP and arm flexion on neuronal activation of CBFv (function hyperemia) at the frequency of flexion were evaluated by repeated measures two-way ANOVA with a Tukey post hoc correction for significant differences at P < 0.05. Graphical data were depicted as means ± SE. Significance was set at P < 0.05.

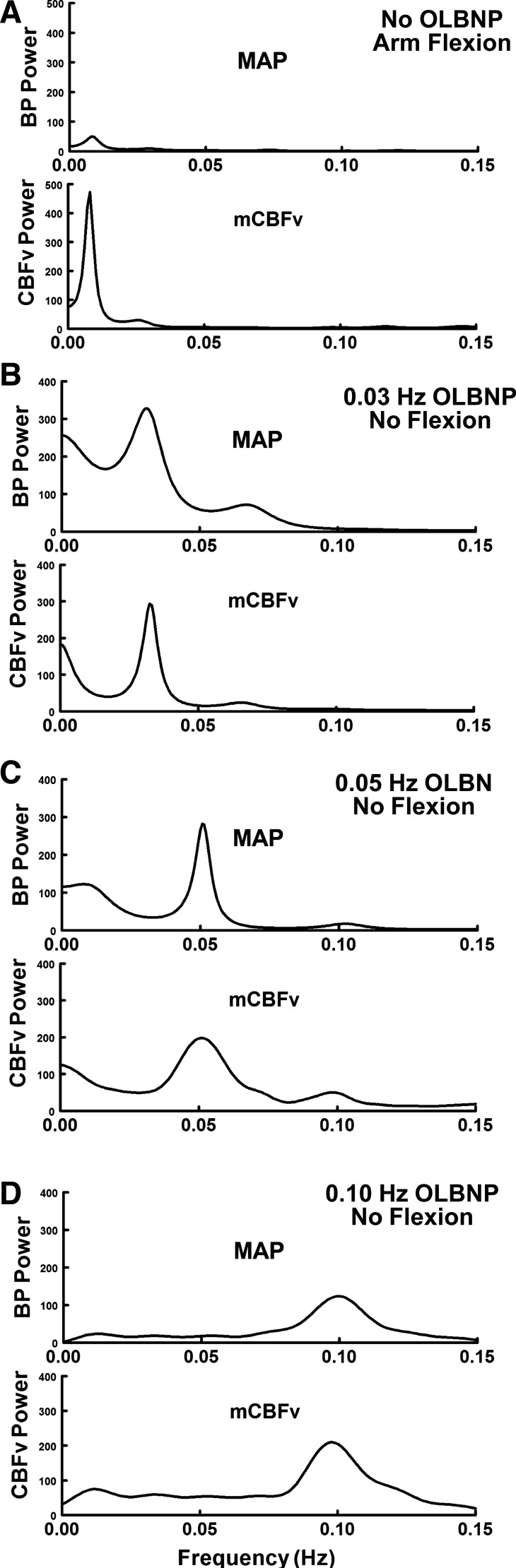
Please note that we employed autoregressive spectral estimation methods, a parametric method, to obtain the spectral estimates of Fig. 3. This was done for illustrative purposes only to offer smoother autospectra to the reader. We followed the methods of Montano et al. (23). The Levinson-Durbin algorithm on the Yule-Walker equations was followed by Anderson's test, choosing the order of the model that minimized Akaike's final prediction error (15).

Fig. 3.

Paired power spectral densities of MAP (OAP) and CBFv (OCBF) during AF without oscillations in LBNP (OLBNP; A) and during OLBNP without AF [0.03 (B), 0.05 (C), and 0.10 Hz (D)] at each of the LBNP box oscillatory frequencies. The figure illustrates the spectral structure of individual signals at the different frequencies employed. Spectral estimates were obtained using an autoregressive method. AF had little effect on MAP spectrum with a small “bump” near 0.0083 Hz. However, AF marked increased OCBFv power centered at 0.0083 Hz. OLBNP produced large changes in both BP and CBFv at the LBNP box frequency.

RESULTS

Baseline data.

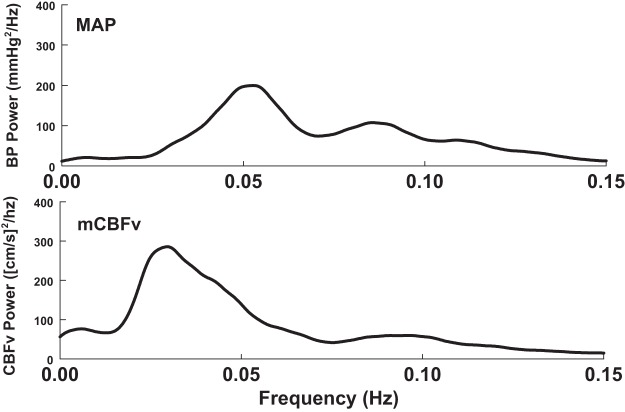
To appreciate the effects of arm flexion and OLBNP, we first obtained baseline data that were recorded in the absence of these stimuli. Figure 2 shows this baseline data; the left panel depicts smoothed baseline MAP and mean CBFv power spectral densities (periodograms) averaged over subjects in the absence of arm flexion and without LBNP.

Fig. 2.

Baseline data obtained in the absence of AF and LBNP. Depicted are mean arterial pressure (MAP; top) and mean CBFv (mCBFv; bottom) power spectral densities [periodograms, oscillations in MAP (OAP) and oscillatory cerebral blood flow (OCBF), respectively] averaged over subjects and smoothed.

The effects of LBNP oscillations and arm flexion on time-averaged values of MAP, CBFv, HR, and ET_CO2.

As shown in Table 1, the averaged hemodynamic data were unaffected by OLBNP, with or without arm flexion.

Table 1.

Mean values during OLBNP with and without arm flexion

			OLBNP Frequency
	No OLBNP		0.03 Hz		0.05 Hz		0.10 Hz
Arm flexion	No	Yes	No	Yes	No	Yes	No	Yes
MAP, mmHg	67 ± 3	67 ± 3	73 ± 4	76 ± 4	76 ± 5	77 ± 5	70 ± 4	72 ± 5
mCBFv, cm/s	75 ± 4	73 ± 3	69 ± 4	69 ± 4	71 ± 4	72 ± 4	69 ± 4	69 ± 4
HR, beats/min	63 ± 3	64 ± 3	65 ± 2	66 ± 2	65 ± 3	66 ± 2	62 ± 3	62 ± 2
ETCO2, Torr	42 ± 1	42 ± 1	43 ± 1	43 ± 1	43 ± 1	42 ± 1	43 ± 1	43 ± 1

Values are means ± SE.

MAP, mean arterial pressure; mCBFv, beatwise mean cerebral blood flow velocity; HR, heart rate; ET_CO2, end-tidal CO₂; OLBNP, oscillations in lower body negative pressure.

The effect of isolated arm flexion and LBNP oscillations on MAP and CBFv power spectra.

Figure 3 shows power spectral densities of OAP and OCBF during arm flexion alone in the top panel in the absence of OLBNP, and to OLBNP at the frequencies shown in the subsequent panels. Arm flexion has little effect on OAP spectrum, but produces a small “bump” near 0.0083 Hz. On the other hand, arm flexion markedly increases OCBF power centered at 0.0083 Hz with low power “blips” at higher harmonics. Small oscillations in arterial pressure during arm flexion are unlikely to drive large changes in OCBFv. In contrast, OLBNP oscillations produce large changes in OAP and OCBF at the LBNP box frequency. Again, low-power higher harmonics were sometimes observed. Although we computed variability in HR and ET_CO2 in our experiments, there was little consistency in the relation of their oscillatory power as related to arm flexion. Arm flexion had little effect on oscillatory HR or ET_CO2, nor did oscillations in HR and ET_CO2 affect 0.0083-Hz frequency power. However, OLBNP at 0.03, 0.05, and 0.10 Hz increased the logarithm of HR oscillatory power by 7–8 dB, corresponding to approximately five- to sixfold change in the absolute amplitude of HR oscillations.

Suppression of functional hyperemia (arm flexion power near 0.0083 Hz) by OLBNP.

Figure 4 shows the effect of OLBNP on the response to arm flexion in the time domain from a representative subject. While blunting approached significance for 0.03 Hz, functional hyperemia was significantly blunted at 0.05 Hz and was effectively eliminated at 0.10 Hz (P < 0.001).

Fig. 4.

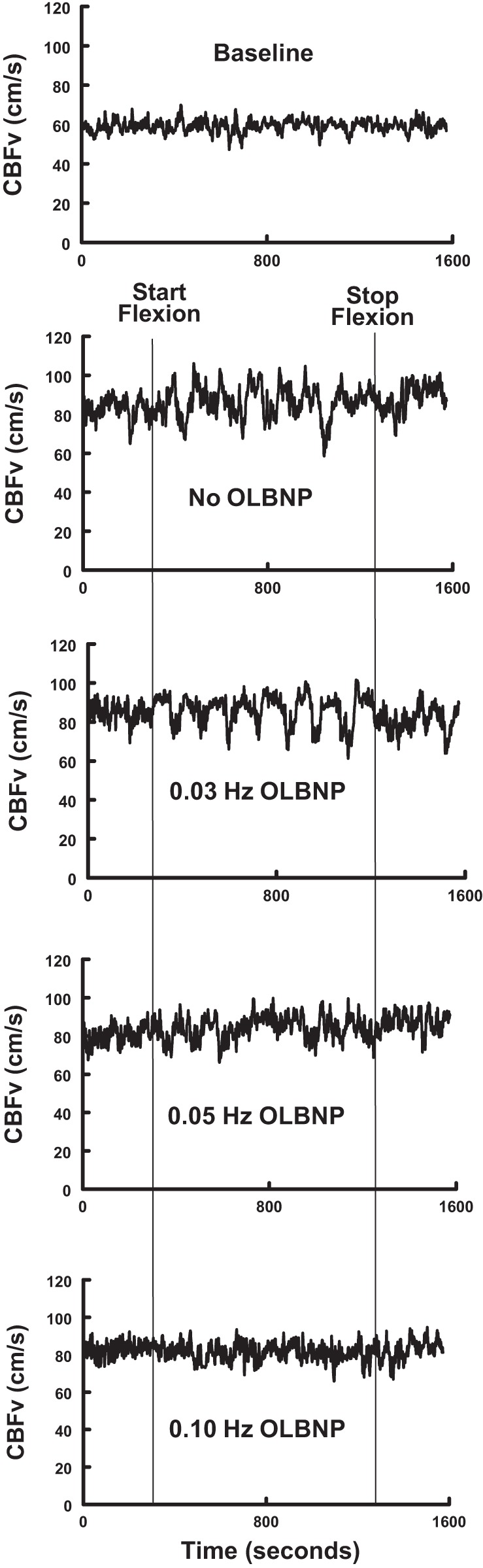
The effects of OLBNP imposed at the frequencies shown, and AF on CBFv for a representative subject. The top panel (Baseline) shows CBFv in the absence of either AF or OLBNP. Note the diminution of CBFv oscillations with increasing OLBNP frequency.

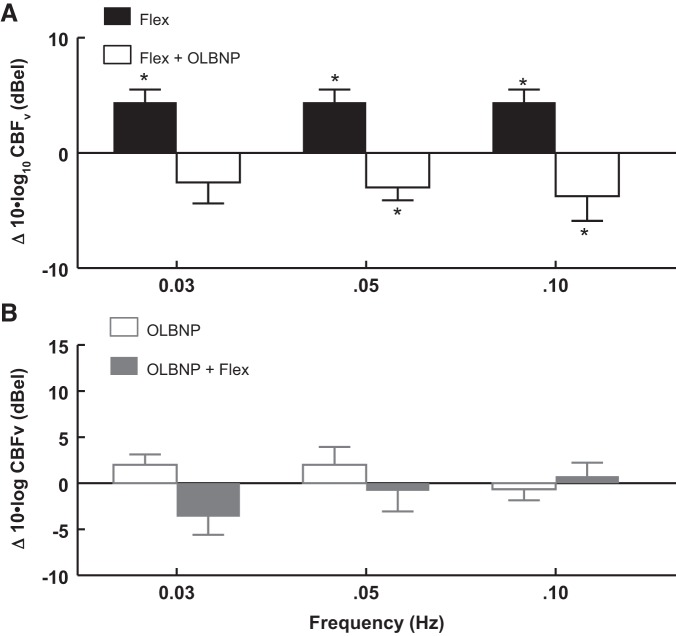
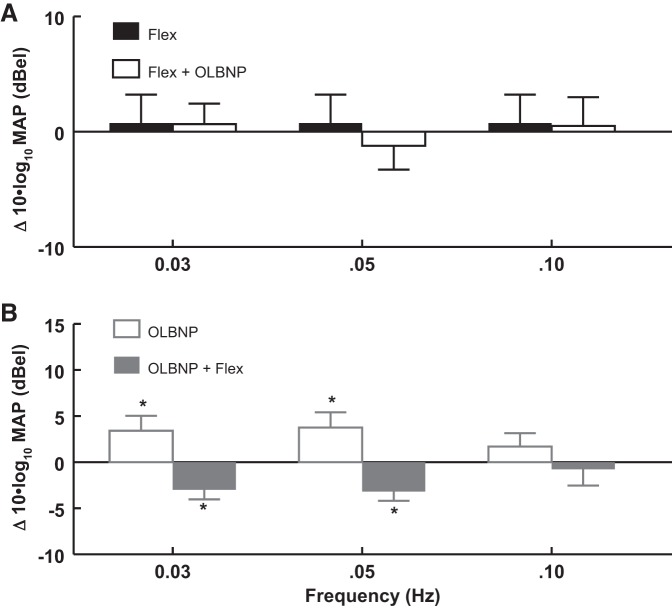
Figure 5 and Table 2 show the effects of OLBNP on functional hyperemia. Functional hyperemia corresponds to OCBF power at 0.0083 Hz in response to arm flexion averaged over all subjects. Arm flexion OCBF power is shown before and after application of OLBNP at specific frequencies.

Fig. 5.

The effects of OLBNP at 0.03, 0.05, and 0.10 Hz on functional hyperemia measured by the OCBF power near 0.0083 Hz due to AF. Data are averaged over all subjects. A: AF is compared with the absence of flexion (baseline, solid bars) and is shown as a log₁₀ of OCBF power during flexion − log₁₀ of OCBF power at baseline, or equivalently 10 × log₁₀(flexion/baseline) in decibels. Similarly, OLBNP with AF is compared with AF alone (open bars) = 10 × log₁₀(OLBNP + flexion/flexion), which is a negative quantity (OLBNP reduces flexion power). The net effect of first flexion and then OLBNP + flexion is equal to the sum of the logarithmic effects = log₁₀(flexion/baseline) + log₁₀(OLBNP + flexion/flexion) = log₁₀(OLBNP + flexion/baseline) and is close to zero. Therefore, oscillatory power is reduced nearly to baseline by 0.05 Hz (P < 0.01) and 0.10 Hz (P < 0.001) LBNP oscillations. B: the effect on OCBF power near 0.0083 Hz of adding AF (open bars) after first applying and maintaining OLBNP at 0.03, 0.05, and 0.10 Hz (shaded bars). There is no significant direct effect of OLBNP oscillations alone on OCBF power at 0.0083 Hz, and no significant effect of AF on OCBF power at 0.0083 Hz in the presence of OLBNP. Values are means ± SE. *Significant difference of the comparison.

Table 2.

Change in 10 × log₁₀ CBFv power at 0.0083 Hz

OLBNP Frequency, Hz	Flexion Alone	Flexion + OLBNP
0.03	4.06 ± 1.07	−2.56 ± 1.72
0.05	4.06 ± 1.07	−3.01 ± 1.12
0.10	4.06 ± 1.07	−3.76 ± 2.01
	OLBNP Alone	OLBNP + Flexion
0.03	2.01 ± 1.07	−3.64 ± 1.96
0.05	2.04 ± 1.07	−0.82 ± 2.24
0.10	−0.65 ± 1.07	0.76 ± 1.47

Values are means ± SE.

In Fig. 5A, baseline arm flexion is followed by OLBNP with continued arm flexion; a logarithmic comparison of power is shown. The solid bars compare arm flexion near 0.0083 Hz (functional hyperemia) to baseline. The open bars compare arm flexion during OLBNP at 0.03, 0.05, and 0.10 Hz to arm flexion alone (functional hyperemia). Oscillatory power is reduced nearly to baseline by 0.05 Hz (P < 0.01) and 0.10 Hz (P < 0.001) oscillations. The reduction of power does not reach significance during 0.03-Hz oscillations.

Figure 5B shows the effect of adding arm flexion after first applying OLBNP at 0.03, 0.05, and 0.10 Hz. Again, oscillatory power is only measured near 0.0083 Hz, the frequency of arm flexion (functional hyperemia). There is no significant direct effect of OLBNP oscillations alone on functional hyperemia power. But there is also no significant effect of arm flexion on OCBF power at 0.0083 Hz in the presence of OLBNP. OLBNP at 0.03, 0.05, and 0.10 Hz effectively suppress functional hyperemia.

A similar analysis was used in relation to OAP in Fig. 6 and Table 3. Figure 6A illustrates that arm flexion exerts no significant effects on OAP power at the frequencies shown. In contrast, Fig. 6B shows that when OLBNP is applied first, MAP power at 0.0083 Hz is increased at 0.03 (P < 0.025) and 0.05 Hz (P < 0.05). These increases are reversed by arm flexion. Referencing Fig. 5, changes in MAP are not reflected in changes of OCBFv at the same oscillatory frequencies.

Fig. 6.

The effects of OLBNP at 0.03, 0.05, and 0.10 Hz on OAP power at 0.0083 Hz due to AF. Data are averaged over all subjects and are logarithmic as in Fig. 5, with results expressed as decibels. A: AF alone compared with baseline (solid bars) has no effect on OAP power at OLBNP frequencies. AF is followed by OLBNP (open bars), while flexion continues. B: OLBNP is first applied (open bars) and maintained during subsequent AF. Logarithmic OAP power at 0.0083 Hz is increased at 0.03 (P < 0.025) and 0.05 Hz (P < 0.05). Increased power is reversed by the addition of AF to LBNP (shaded bars). Values are means ± SE. *Significant difference of the comparison.

Table 3.

Change in 10 × log₁₀ MAP power at 0.0083 Hz

OLBNP Frequency, Hz	Flexion Alone	Flexion + OLBNP
0.03	0.75 ± 2.47	0.66 ± 1.78
0.05	0.75 ± 2.47	−1.22 ± 2.07
0.10	0.75 ± 2.47	0.52 ± 2.50
	OLBNP Alone	OLBNP + Flexion
0.03	3.41 ± 1.62	−3.00 ± 1.03
0.05	3.76 ± 1.65	−3.19 ± 0.99
0.10	1.70 ± 1.45	−0.78 ± 1.76

Values are means ± SE.

Effect of functional hyperemia (via arm flexion at 0.0083 Hz) on oscillatory power at 0.03, 0.05, and 0.10 Hz.

Since oscillations in LBNP interfere with functional hyperemia, we investigated whether arm flexion interferes with oscillatory power at LBNP oscillatory frequencies.

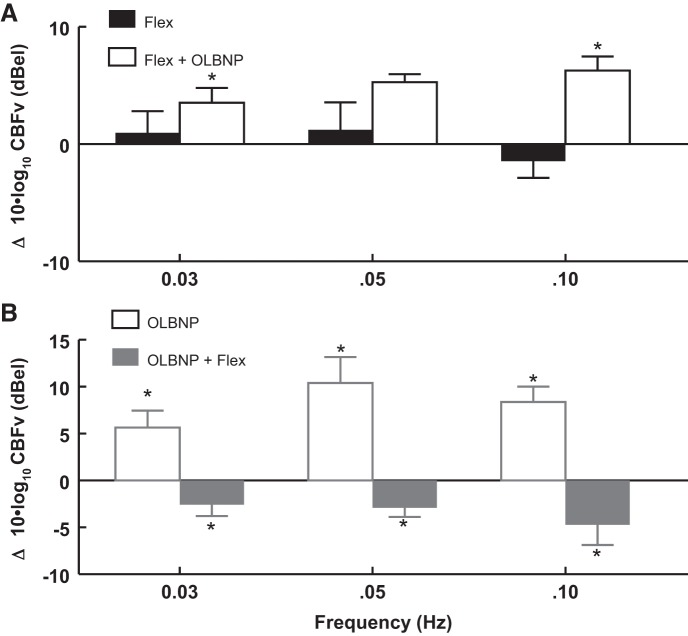
Figure 7 and Table 4 show the effect of arm flexion (at 0.0083 Hz) on OLBNP power at 0.03, 0.05, and 0.10 Hz. Figure 7A shows that arm flexion alone has no effect on power at OLBNP frequencies. Figure 7B shows the effect of OLBNP on power when it is applied first followed by arm flexion. Comparing the OLBNP power in A and B shows that prior arm flexion blunts subsequent OLBNP power.

Fig. 7.

The effect of AF (at 0.0083 Hz) on logarithmic OCBF velocity (OCBFv) power at 0.03, 0.05, and 0.10 Hz. A: AF alone compared with baseline (solid bars) has no effect on logarithmic power at OLBNP frequencies. AF is followed by OLBNP (open bars) while flexion continues. B: the effect of OLBNP compared with baseline (open bars) on OCBFv power when it is applied first. The addition of AF follows (shaded bars). Comparing OCBFv power in A and B suggests that it is reduced by AF at each frequency of OLBNP. Values are means ± SE. *Significant difference of the comparison.

Table 4.

Change in 10 × log₁₀ CBFv power at OLBNP frequency

OLBNP Frequency, Hz	Flexion Alone	Flexion + OLBNP
0.03	0.96 ± 1.84	3.52 ± 1.26
0.05	1.21 ± 2.34	5.27 ± 0.68
0.10	−1.46 ± 1.42	6.27 ± 1.21
	OLBNP Alone	OLBNP + Flexion
0.03	5.63 ± 1.81	−2.58 ± 1.22
0.05	10.39 ± 2.76	−2.92 ± 0.97
0.10	8.36 ± 1.64	−4.73 ± 2.15

Values are means ± SE.

Oscillatory power is reduced by arm flexion at each frequency of OLBNP. OCBFv power is smallest at 0.03 Hz, which may help to explain why OLBNP at 0.03 Hz failed to significantly suppress functional hyperemia (Fig. 5A).

DISCUSSION

The interactions between OLBNP-driven CBFv oscillations and arm flexion-driven CBFv oscillations are reciprocal. Thus induced CBF oscillations suppress functional hyperemia, and functional hyperemia suppresses CBF oscillations. During oscillatory LBNP, CBFv, and MAP are highly coherent (9). Here both OAP and OCBF are forced by the OLBNP, which entrains both OCBF and OAP at the frequency of OLBNP; there need not be a direct relation between OCBF and OAP.

However, our laboratory has previously shown that impaired dynamic cerebral autoregulation in the absence of forcing also produces OCBFv and suppressed functional hyperemia at very low frequencies secondary to entrainment by OAP (22). Generalizing our present and past observations, we propose that low-frequency OCBF power blunts functional hyperemia and, therefore, NVC.

It is interesting to note from Figs. 6 and 7 that the change in logarithmic power when arm flexion is followed by arm flexion plus OLBNP is different from the change in logarithmic power when initial OLBNP is followed by OLBNP plus arm flexion. The effects did not commute. This is consistent with nonlinear coupling in which effects are not simply additive.

Our laboratory's previous observations of increased OCBFv and reduced functional hyperemia were made in POTS patients. There were two problems in generalizing these observations: 1) association is not causation; and 2) patients are not healthy volunteers. Thus our prior observations in POTS may represent pathophysiology rather than physiology. The present data indicate that OCBF can blunt functional hyperemia in healthy subjects and that blunting is causal. One might consider this as a type of “vasoneural coupling” akin to the hemo-neural hypothesis (24) and believed to result from the effects of shear stress and vasodilating signal molecules on astrocytes and neurons within the neurovascular unit (3, 4, 7). Conversely, we have also shown that functional hyperemia (at least when cyclic) reduces OCBFv, which could relate to the known interaction of astrocytes and pericytes surrounding capillaries that are functionally linked to astrocytic processes surrounding pial vessels. Thus downstream astrocyte-derived signals from within the neurovascular unit can be transmitted to the pial arterioles and modulate cerebral autoregulation (40).

In the present study, for the sake of simplicity, we used an effort-independent means to produce hyperemia via a passive afferent motor stimulus. This required no effort on the part of the subject and removed interindividual variation in perceptual abilities, intelligence, and volitional components from the analysis. The use of the passive motor paradigm also has the advantage of producing a greater hyperemic response compared with active motor activity or motor imagery and compared with cognitive tasks that our laboratory has used (31). Unfortunately, using the present study design, we were unable to address issues of higher cortical function, such as cognition, which are considerably more complex.

Excessive OCBF blunts NVC in animals.

Investigations (27) using in vivo near-infrared spectroscopy and extracellular recordings in the visual thalamus of the cat showed that CBFv oscillations suppress NVC, and that NVC was restored once oscillations abated. In these studies, OCBF at 0.14 Hz interfered with functional hyperemia measured by an increase in oxyhemoglobin during visual sensory stimulation. OCBF blunted NVC and was in turn reduced by stimulation, implying mutual interaction of activity-related flow (functional hyperemia) with OCBF.

In animal models, vasoneural coupling and NVC activation of astrocytic receptors by neuronal glutamate induce increased intracellular calcium, resulting in arteriolar vasodilation mediated by prostaglandins, epoxyeicosatrienoic acids, nitric oxide, and inhibited by 20-hydroxyeicosatrienoic acid (6, 16, 44). While neural activity controls local CBF via NVC, vasoneural coupling suggests that local CBF reciprocally affects neuronal activity. OCBF could, therefore, exert direct effects on neurons and axons, or indirect effects via astrocytes. For example, microvascular shear stress-driven endothelial cells can directly affect neurons by nitric oxide, epoxyeicosatrienoic acids, and prostaglandin signaling, resulting in axon depolarization (7). Also, astrocytes can depolarize due to vascular deformation (3) linked to the release of vascular mediators, including angiotensin-dependent NADPH oxidase promoting oxidative stress (36), glutamate, d-serine, ATP promoting neuronal activity, and arachidonic acid metabolites. Since oscillatory shear stress couples vascular deformation to astrocyte depolarization, and astrocyte depolarization to neuronal activity (18), a likely outcome of OCBF is interference with NVC and neuronal depolarization.

Increased OCBF implies reduced cerebral autoregulation.

Although CBF increases during task-related cerebral activity (28), these increases are relatively small compared with resting CBF (26), which is maintained relatively stable by cerebral autoregulation. Cerebral autoregulation comprises properties of the cerebral vasculature that, in the absence of large environmental or metabolic changes, maintains overall CBF relatively unchanged, despite changing BP (38).

We have shown a progressive reduction in cognitive performance testing and functional hyperemia and progressive increase in OCBF in POTS patients, but not controls, during stepwise incremental upright tilt (32). However, the average magnitude of CBFv decreases similarly in POTS and controls with angle of tilt. We observed stepwise increased oscillations in arterial pressure that produced larger stepwise increases in OCBF. Increased OCBF in POTS resulted primarily from enhanced low-frequency oscillatory power that occurred in POTS, and not controls, from the combined effects of increased OAP in the low-frequency band and increased low-frequency transfer gain from OAP to OCBF in POTS. Our laboratory has shown greatly increased CBFv in POTS when upright, which is protected by autoregulation (21).

In the present study, we show that induced CBF oscillations suppress functional hyperemia, and functional hyperemia suppresses CBF oscillations. We, therefore, conclude that OCBF produces a causal reduction of functional hyperemia. Since we studied the role of OCBF using the range of frequencies for cerebral autoregulation, it appears that the reduction of functional hyperemia is constrained by autoregulation. It remains to be determined, however, if these relationships may be altered in patients with POTS or syncope.

Limitations.

TCD ultrasound measures OCBFv rather than OCBF, which depends on the cross-sectional area of the insonated artery. However, MCA cross section may be relatively resistant to change during orthostatic stress (32). Also, changes in OCBFv are nearly proportionate to changes in oscillations of CBF (19). Thus, even under conditions of changing BP, cerebral autoregulation can be estimated by TCD, although its influence may be underestimated (20).

TCD only measures blood flow through specific cerebral blood vessels, such as the MCA, with good temporal resolution. The MCA was used because it is the main vessel that perfuses the area of the brain activated during passive motor testing (21).

Strictly speaking, Fourier transfer function analysis depends on linear time-independent system characteristics. While the linear hypothesis is at best an approximation, it still provides useful information. One additional concern is the relatively small range of amplitudes of arterial pressure and CBFv that are interrogated, particularly while supine.

The Welch method (39) is considered a reference standard to reduce periodogram variance. The method divides the time series into shorter segments, demeans and applies a Hanning window to each segment, and then averages over all segments. This essentially starts as a time domain procedure. Although variance decreases, so does frequency resolution. Also, the process of repeated segmental detrending of short data sequences further degrades frequency resolution at very low frequencies.

Although mean ET_CO2 did not vary with OLBNP, oscillations in ET_CO2 could potentially influence OCBF results. However, it was not feasible to make such measurements, because spurious ET_CO2 signals occurred whenever the patient opened his or her mouth and at other times as well. To account for this in calculating mean ET_CO2, we manually detected suitable ET_CO2 signals for measurement. There was no practical way to compensate adequately for such spurious signals and, therefore, no way to obtain a smooth sequence of ET_CO2. However, there is no respiratory entrainment at the imposed frequencies of OLBNP, and thus important entrained oscillations in ET_CO2 are unlikely to impact on OCBF and OAP, which were driven by the overwhelming external signal of the oscillating box.

GRANTS

Funding for this project was provided by National Heart, Lung, and Blood Institute Grants RO1-HL-112736 and RO1-HL-074873.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: J.M.S. and M.S.M. conception and design of research; J.M.S., K.B., P.V., A.T.D.P., Z.R.M., C.T., and M.S.M. interpreted results of experiments; J.M.S. prepared figures; J.M.S. and M.S.M. drafted manuscript; J.M.S., P.V., Z.R.M., and M.S.M. edited and revised manuscript; J.M.S., K.B., P.V., A.T.D.P., Z.R.M., C.T., and M.S.M. approved final version of manuscript; K.B., A.T.D.P., Z.R.M., and C.T. performed experiments; P.V. analyzed data.