Abstract
Quantum annealing (QA) serves as a specialized optimizer that is able to solve many NP-hard problems and that is believed to have a theoretical advantage over simulated annealing (SA) via quantum tunneling. With the introduction of the D-Wave programmable quantum annealer, a considerable amount of effort has been devoted to detect and quantify quantum speedup. While the debate over speedup remains inconclusive as of now, instead of attempting to show general quantum advantage, here, we focus on a novel real-world application of D-Wave in wireless networking—more specifically, the scheduling of the activation of the air-links for maximum throughput subject to interference avoidance near network nodes. In addition, D-Wave implementation is made error insensitive by a novel Hamiltonian extra penalty weight adjustment that enlarges the gap and substantially reduces the occurrence of interference violations resulting from inevitable spin bias and coupling errors. The major result of this paper is that quantum annealing benefits more than simulated annealing from this gap expansion process, both in terms of ST99 speedup and network queue occupancy. It is the hope that this could become a real-word application niche where potential benefits of quantum annealing could be objectively assessed.
Quantum Annealing
Quantum annealing is designed to mimic the process of simulated annealing1 as a generic way to efficiently get close-to-optimum solutions in many NP-hard optimization problems. Quantum annealing is believed to utilize quantum tunneling instead of thermal hopping to more efficiently search for the optimum solution in the Hilbert space of a quantum annealing device such as the D-Wave2,3. Since the introduction of D-Wave One in 2011, there has been a considerable amount of work done on its potential applications, e.g., protein folding4, determining Ramsey number5, Bayesian network structure learning6, operational planning7, power system fault detection8, graph isomorphism9, database optimization10, machine learning11, deep learning12, to name but a few. Note that of all the applications we are aware of, most were solved with small logical instance size due to hardware constraints and none of them demonstrated conclusive speedup compared to classical methods. In fact, benchmarking quantum speedup is more subtle than it appears to be. There has recently been a lot of insightful work on such a challenging question13,14,15. One conclusive remark is that no evidence for a general speedup has been found thus far, but potential speedup might exist in certain problems or upon scaling. In this paper, we introduce a new breed of graph-theoretic applications motivated by the very problem that makes the design of optimal wireless network protocols outstanding from the computational viewpoint—the interference constraints—and we show that a gap expansion technique benefits quantum annealing much more than simulated annealing, indicating a way to obtain quantum speedup.
Quantum annealing is based on the premise that the minimum energy configuration of the Ising spin glass model encodes the solution to specific NP-hard problems, including all Karp’s 21 NP-complete problems16. Such problems are written in the form of Quadratic Unconstrained Binary Optimization (QUBO) problems,
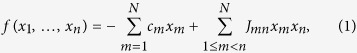 |
where xm ∈ {0, 1}, and cm, Jmn represent QUBO parameters. The latter has an equivalent Ising formulation
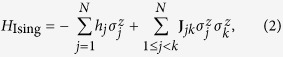 |
where 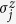 represents the z-Pauli operator of Ising spin j in the network, and hj and Jjk are local fields and coupling strengths, resp. The annealer initially prepares a initial transverse magnetic field, an equal superposition of 2N computational basis states, eigenspace of
represents the z-Pauli operator of Ising spin j in the network, and hj and Jjk are local fields and coupling strengths, resp. The annealer initially prepares a initial transverse magnetic field, an equal superposition of 2N computational basis states, eigenspace of
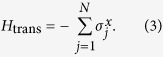 |
During the adiabatic continuation, the Hamiltonian evolves smoothly from Htrans to HIsing, that is,
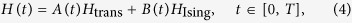 |
where A(·) decreases monotonically from 1 to 0 and B(·) increases monotonically from 0 to 1. From the adiabatic theorem, if the evolution is “slow enough”, the system would remain in its ground state. Thus, in principle, an optimal solution to the original problem could be obtained by measurements at final time17.
Network Scheduling Problem
One of the fundamental problems in multi-hop wireless networks is network scheduling. Signal-to-Interference-plus-Noise Ratio (SINR) has to be maintained above a certain threshold to ensure successful decoding of information at the destination. For example, IEEE 802.11b requires a minimum SINR of 4 and 10 dB corresponding to 11 and 1 Mbps channel, resp18. Consequently, only a subset of edges of the network can be activated within the same time slot, since every link transmission causes interference with nearby link transmissions.
Different networks and protocols use different interference models. The most commonly used model is the 1-hop interference model (node exclusive model), in which every node can transmit or receive along only one activated link abutting that node in the same time slot. This is commonly used in Bluetooth and FH-CDMA19,20, while the 2-hop interference model is sometimes used in studies of IEEE 802.11 networks21, in which no two links within 2-hop distance can be simultaneously activated. Generally, K-hop is used with K representing arbitrary hop interference model. In some cross-layer optimization studies22, the optimal K is found to vary between 1 and 3. In theory, protocol designers can set K to arbitrary value, as long as end-to-end delay, signal interference and computation cost reach a Pareto-optimal point.
There are two major methods for solving network interference: the first one is the graph based model that solves the Weighted Maximum Independence Set (WMIS) problem on a conflict graph23,24,25,26,27, the other optimizes a geometric-based SINR28,29,30,31. The former is sometimes argued as being an overly idealistic assumption; however, the WMIS problem is still involved in the latter model32 and is of interest in SA versus QA; thus we mainly consider the former model for simplicity. Several general heuristics for the WMIS problem are well-studied, including simulated annealing33, neural networks34,35,36, genetic algorithm37,38,39, greedy randomized genetic search40, Tabu search41,42,43,44. It is claimed that simulated annealing is superior to other competing methods with experimental instances of up to 70,000 nodes33.
To give formal definitions on a graph G = (V, E), let wl∈E be the wireless networking link weights in a given time slot. (They are related to queue differential and somehow the most highly weighted links should receive priority activation if interference allows.) Let dS(x, y) denote the hop distance between x, y ∈ V. Consider edges eu, ev ∈ E and let ∂eu = {u1, u2}, ∂ev = {v1, v2}. We then define
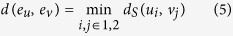 |
to be the distance between edges. Similar to the definition in the work of Sharma et al.22, a subset of edges E′ is said to be valid subject to the K-hop interference model if, for all e1, e2 ∈ E′ with e1 ≠ e2, we have d(e1, e2) ≥ K. Let SK denote the set of K-hop valid edge subsets (scheduling set). Then the network scheduling under the K-hop interference model is
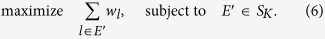 |
In the K = 1 case, the problem is a max-weight matching problem and thus has polynomial solution (Edmonds’ blossom algorithm45). However, for the case K > 1, the problem is proved to be NP-hard and non-approximable22. As already said, the network scheduling problem (6) has to be solved in every time slot; thus, the complexity of the exact scheduling problem becomes critical in time-sensitive applications.
Overview
We intend to design a quantum annealing scheduler to solve the WMIS problem and benchmark the results obtained by realistic network simulation against simulated annealing. The complete benchmarking is summarized in the following steps.
Conflict Graph
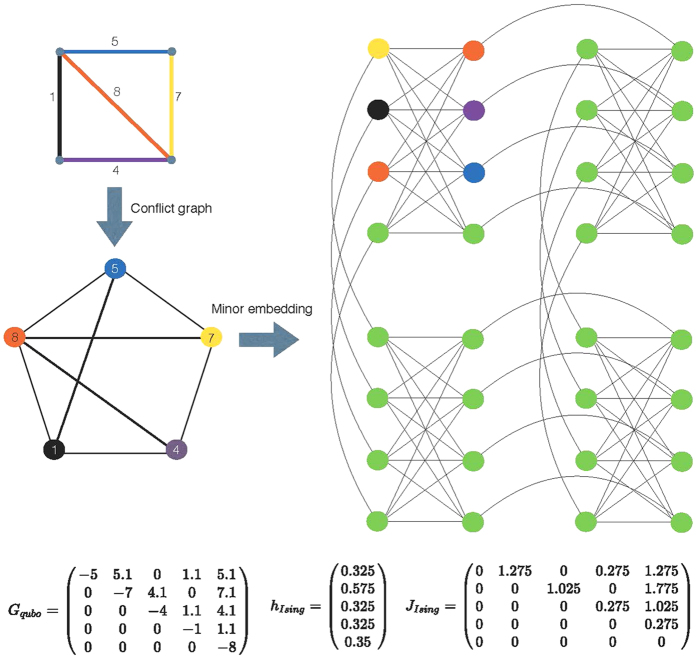
The original scheduling problem on the original graph is reformulated as a QUBO problem (1) on a conflict graph: the nodes of the conflict graph are the edges of the original graph with weights wl (=cl in QUBO), while the edges of the conflict graph are pairs of edges of the original graph in scheduling conflict, as illustrated in Fig. 1, left. As such, subject to proper choice of the Jmn (details in supplemental material), the QUBO problem (1) on the conflict graph, the WMIS problem, provides a solution to K-hop interference problem on the original graph (6).
Figure 1. An example of conflict graph conversion, QUBO generation, and minor-embedding to Chimera architecture.
The conflict graph is generated based on the 1-hop interference model. Only 4 cells of K4,4 structure of the Chimera architecture are shown. On D-Wave Two platform, 64 such cells are available, giving 512 available physical qubits. Quantum annealing is performed on such architecture to theoretically give the ground state of the configuration, and thus the network scheduling solution to the original problem. The numerical data shows the conflict graph weight structure Gqubo and how it is mapped to the Ising Hamiltonian characterized by hIsing and JIsing. The off-diagonal entries of Gqubo are chosen as 0.1 larger than the minimum of the weights of the two corresponding vertices of the conflict graph.
Gap Expansion
In the WMIS problem, some βmn scaling of Jmn is introduced as shown in (7) to open up the gap of the Ising model, resulting in less scheduling violations, especially in the QA approach.
Embedding to Hardware
The QUBO problem has to be mapped to the Ising Hamiltonian via 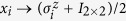 , with the constant energy shift ignored. We perform minor embedding into the D-Wave Chimera architecture, as illustrated in Fig. 1, right, or decide that it is not embeddable. This is discussed in more detail in the supplemental material. Figure 1 gives a simple numerical example of how a network is mapped to D-Wave architecture.
, with the constant energy shift ignored. We perform minor embedding into the D-Wave Chimera architecture, as illustrated in Fig. 1, right, or decide that it is not embeddable. This is discussed in more detail in the supplemental material. Figure 1 gives a simple numerical example of how a network is mapped to D-Wave architecture.
Measurement and Post-processing
We perform the annealing run a certain number of times on D-Wave, find the lowest energy configuration, and use such configuration as scheduling solution. Some commonly used algorithm techniques in adiabatic quantum computation, such as gauge transformation and majority vote on possible broken chains are not performed. See the work of King et al.46 for more discussion.
Results
In theory and practice, SA is regarded as a strong competitor of QA and their performances are often contrasted in the literature13,14,15. On the other hand, it is known that SA can also boost the overall performance of classical heuristic algorithms in solving WMIS problems33. Thus, it is worth comparing our QA results with the performance of the SA algorithm. Comparison metrics are defined later in this section. We use the gap expansion process on the quantum scheduler, defined in detail in the following section, and observe that the quantum scheduler takes better advantage of this gap expansion technique than SA.
Table 1 shows the parameters of the 2 random graphs (15 and 20 nodes) being tested on D-Wave installed at Information Sciences Institute of University of Southern California (USC). The “problem size” n is the number of nodes of the wireless network, the “QUBO size” is |E| and thus generally scales as O(n2), where E and n are the edge set and order of the problem graph, resp. The “Physical Qubits” is the number of nodes N after minor embedding in the D-Wave architecture. After minor-embedding in the case of the 20-node network, a significantly large proportion of all available qubits are utilized (405 out of 502).
Table 1. Problem size of random graphs used in experiment.
| Problem Size | QUBO Size | Physical Qubits | |
|---|---|---|---|
| Graph1 | 15 | 31 | 164 |
| Graph2 | 20 | 57 | 405 |
The third column represents the actual physical qubits used after minor embedding.
Simulated Annealing Setup
Here, we adapted a highly optimized simulated annealing algorithm (an_ss_ge_fi_vdeg)47, compiling the C++ source code with gcc 4.8.4 with MATLAB C-mex API. Additionally, a wide range of parameters were tested to ensure near optimal performance of the algorithm within a reasonable run time (see supplemental material). All the non-time-critical tests in this section were ran on the servers of the USC Center for High-Performance Computing (HPC).
Quality metrics
We compare the performance of QA and SA based on three quantitative metrics: average network delay, throughput optimality, and ST99. The first metric reflects the actual network performance; the latter two metrics reflect the accuracy and speed of QA and SA compared to exact solvers (see supplemental material for formal definitions.)
Average network delay
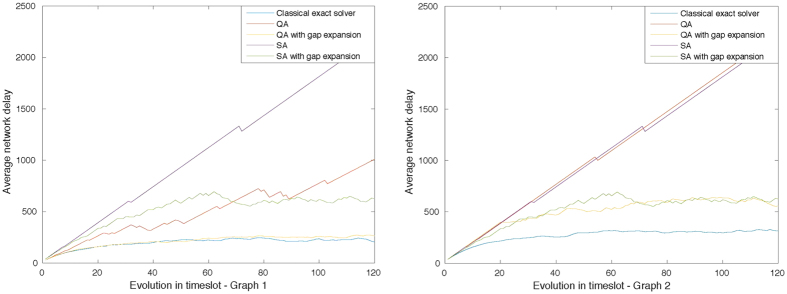
We use an optimized wireless network protocol in our experiment (see supplemental material for protocol definitions). In Fig. 2, we show that, after gap expansion, the overall performance significantly improves. As one would expect, the network delay is also improved and gets closer to the exact classical solution. It is a rather delicate issue as how to deal with non-independent solutions returned by D-Wave. In the experiment, we skip the time slot transmission if the lowest energy solution does not conform to the K-hop interference model. Sometimes, it makes sense to perform a polynomial greedy style matching when the returned result is non-independent, in which case the problem is more error-insensitive and thus more scalable. Here we consider the worst case scenario, that is, no transmission is allowed if the result is non-independent.
Figure 2. Network delay of classical exact algorithm, quantum annealing, quantum annealing after gap expansion, and simulated annealing are plotted versus time slot for two randomly generated networks.
The left one is a simpler case with 15 nodes and 31 edges where quantum annealing reaches almost as good a result as the exact solution in terms of network delay; the right one is a harder case with 20 nodes and 57 edges in total.
Throughput optimality and ST99[OPT]
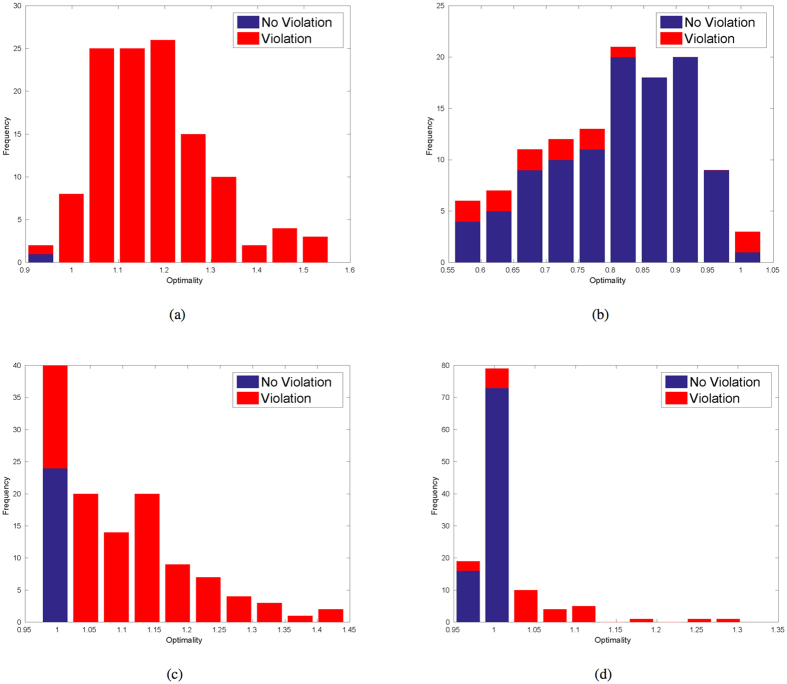
Based on our previous assumption, it is of vital importance that the solutions given by the solver satisfy the independence constraint. Here we use the optimality measure Fquantum as defined in section 5.2 of supplemental material. Briefly, if there are no violations, such measure reaches 1 if the solution is exactly optimal, and less than 1 if suboptimal. If there are violations,  if those solutions improve the throughput and
if those solutions improve the throughput and  if the violations do not even improve the throughput. In Fig. 3, we investigate the distribution of the optimality factors among all 120 time slots of Graph 2 (the harder graph). All the violations are counted inside red bars. Comparing (a) and (c) of Fig. 3 and (b) with (d) of Fig. 3, we can see that energy compression as shown in Fig. 2 results in substantially less violations of the independence constraint, and that this reduction is more pronounced in the QA case than in the SA case. This could explain the huge performance improvement before and after gap expansion in Fig. 2. The test results of SA under a particular set of parameters are shown in (c) and (d) of Fig. 3 The ranges of our tested parameters are listed in the supplemental material. It is worth making the following observations:
if the violations do not even improve the throughput. In Fig. 3, we investigate the distribution of the optimality factors among all 120 time slots of Graph 2 (the harder graph). All the violations are counted inside red bars. Comparing (a) and (c) of Fig. 3 and (b) with (d) of Fig. 3, we can see that energy compression as shown in Fig. 2 results in substantially less violations of the independence constraint, and that this reduction is more pronounced in the QA case than in the SA case. This could explain the huge performance improvement before and after gap expansion in Fig. 2. The test results of SA under a particular set of parameters are shown in (c) and (d) of Fig. 3 The ranges of our tested parameters are listed in the supplemental material. It is worth making the following observations:
QA benefits more from the gap expansion compared to SA.
SA either finds the very optimal ground state or gets trapped in very ‘deep’ local minima.
Figure 3. Number of violation (red) and nonviolation (blue) cases versus throughput optimality measure on test graph 2 (the harder instance).
D-Wave simulation runs are shown in (a,b). SA simulation runs shown in (c,d) are executed under the one set of optimal parameters we have tested (5000 sweeps, 5000 repetitions, linear schedule with initial temperature β0 = 0.1 and final temperature β1 = 10). Note that the abscissa of the blue vertical bars register Fquantum whereas the abscissa of the red vertical bars registers  as defined in supplemental material. (a) D-Wave: Before gap expansion; (b) D-wave: After gap expansion; (c) Simulated Annealing: Before gap expansion; (d) Simulated Annealing: After gap expansion.
as defined in supplemental material. (a) D-Wave: Before gap expansion; (b) D-wave: After gap expansion; (c) Simulated Annealing: Before gap expansion; (d) Simulated Annealing: After gap expansion.
There is still a relatively large number of violations in the returned results of SA even after gap expansion. This is in agreement with our previous knowledge about SA in that it is designed to find the ground state and it is not optimized to search for sub-optimal results. In addition, Table 2 shows the exact numbers related to the performances of SA and QA after gap expansion.
Table 2. Performances After Gap Expansion.
| Number of violations (out of 120) | Average optimality (without violations) | |
|---|---|---|
| Quantum Annealing | 13 | 0.8129 |
| Simulated Annealing | 31 | 0.9935 |
From the optimality data returned by D-Wave, we can plot ST99 related to the level of optimality as shown in Fig. 4. Note that our ST99 definition (see supplemental material) relies on optimality level, which could typically be 80% or 90% depending on user needs.
Figure 4. ST99, defined as 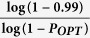 , versus required optimality level OPT specified by network, before and after gap expansion on Graph 1 and Graph 2 (the harder instance).
, versus required optimality level OPT specified by network, before and after gap expansion on Graph 1 and Graph 2 (the harder instance).
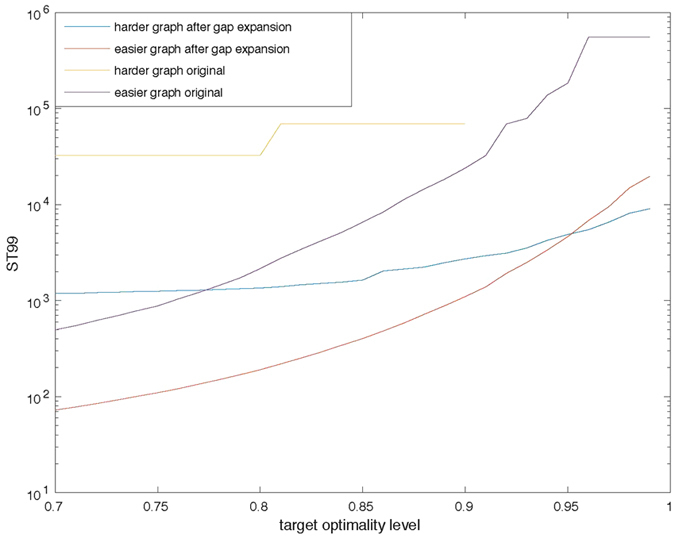
Note that the probability is calculated based on all solutions returned by D-Wave; thus, an ST99 of 103 corresponds to one set of annealing runs, which in our case costs 20 ms (1000 annealing runs with 20 μs for each run). Curve for Graph 2 before gap expansion ends at 0.9 optimality level, because there are no solutions that satisfy such optimality level after a total of 120,000 annealing runs.
In Table 3, we show how setting the penalty weight β of the gap expansion consistently with the local or global approach would affect the quality of the returned solution. We found that setting βglobal = 1 would yield the best performance so far. We do not have a quantitative explanation for the wrong solutions; potential explanations on small problems have been discussed in refs 13, 14, 15. Intuitively, as the problem size grows, it is much more difficult even to find close to ground states; indeed, as the penalty weight grows too large, the local fields begin to vanish, thus making the problem effectively more difficult since all weights have to be scaled to [−2, +2]. The problem of quantitative connection among quality measure, network stability, and throughput optimality remains open.
Table 3. Penalty weight with different β setup and resulting quality measure of returned solution averaged over 120 time slots.
| Avg. Optimality - G1 | Delay - G1 | Avg. Optimality - G2 | Delay - G2 | |
|---|---|---|---|---|
| βmn = 1 + ε | 0.781 | 384.9 | 0.077 | NC |
| βmn = 2 | 0.928 | 376.3 | 0.312 | 1213 |
| βglobal = 1 | 0.974 | 268 | 0.741 | 566.1 |
| βglobal = 1.5 | −0.165 | NC | −0.331 | NC |
| βglobal = 2 | −0.185 | NC | −0.356 | NC |
Graph 2 is a larger size instance than Graph 1. Delay refers to average network delay in steady state, and NC refers to the non-convergent case where steady state is not reached within tested time span.
Methods
Gap Expansion
We try to make the problem insensitive to quantum annealing errors by properly setting the hi and Jij terms in Eq. (2) in order to expand the final energy gap. Note that this gap is the energy gap between the eigenvalues of the Ising form at the end of the adiabatic evolution, not to be confused with the gap between ground and first excited states during the evolution. We introduce a scaling factor βmn that multiplies the quadratic part of the QUBO formulation and as such scales the various terms so as to put more penalty weight on the independence constraints:
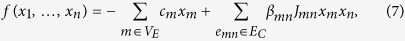 |
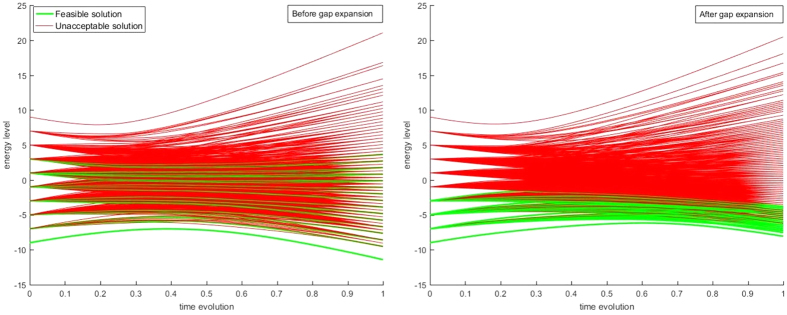
where VE and EC denote the vertex set and edge set, resp., of the conflict graph and βmn is chosen uniform. In theory, βmn = 1 would suffice as long as Jmn > min(cm, cn), as the ground state has already encoded the correct solution of the WMIS problem48. However, since measuring the ground state correctly is not guaranteed, increasing βmn becomes necessary to enforce the independence constraints, so that the energy spectrum of the non-independence states is raised to the upper energy spectrum and the feasible energy states are compressed to the lower spectrum. Figure 5 illustrates the effect of the feasible energy compression on a small random graph.
Figure 5. Hamiltonian energy level evolution with H(s) = (1 − s)Htrans + sHIsing, demonstrating the feasibility of energy compression on a small, randomly generated test wireless graph with 7 nodes on the conflict graph, plotting all 128 possible energy states in both before and after gap expansion cases.
Both Hamiltonians are rescaled to have a maximum energy level of 2 for both coupling strengths and local fields. Note that for a typical desktop computer, such plots are impossible to construct once the size of the conflict graph goes higher than 12.
A natural question regarding β would be, How large is large enough? The problem is, interestingly, another optimization problem itself. The D-Wave V7 is subject to an Internal Control Error (ICE) that gives Gaussian errors with standard deviations σh ≈ 0.05 and σJ ≈ 0.03546. Putting too large a βmn penalty would incur two problems: 1) The local fields would become indistinguishable and 2) The minimum evolution gap would become too small. Accordingly, a few parameter values have been tried out and the results are shown in Table 3, which corroborates the experimental results of the previous section indicating that gap expansion would significantly influence the optimality of the returned solution.
There exist several strategies in setting heavier penalty weights to expand the gap. We compare two different approaches to set the penalty weights:
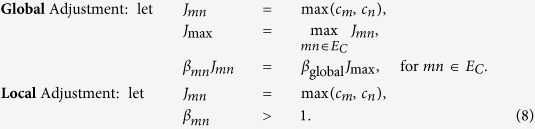 |
In the local adjustment48, the constraint on Jmn depends only on the fields at ∂mn, whereas in the global adjstment, contrary to48, Jmn depends on all fields.
Discussion
We have presented the first experimental D-Wave application of network scheduling—a problem widely investigated in the field of wireless networking understood in the classical sense. The problem is reduced to a WMIS problem, itself reformulated in the form of the minimum energy level of an Ising Hamiltonian, itself mapped to the Chimera architecture by utilizing a differential geometrical approach49 that immediately rules out cases where minor-embedding is impossible. We increased the success rate of the quantum annealer and the simulated annealer to return non-violation solutions by classically increasing the energy gap, so that the range of acceptable solutions is greatly increased.
By comparing QA with SA, though omitting Quantum Monte Carlo (QMC), we found a potential comparison point where QA outperforms SA in the sense of benefit from gap expansion as seen in Fig. 3. Gap expansion reduces by 89% the number of violation cases for QA, while it only reduces by 67.5% the number of violation cases for SA. Although, as seen from Table 2, SA has an optimality advantage in non-violation cases, it is however interesting to observe that among suboptimal solution cases QA has less violations than SA. By deliberately constructing cases suitable for suboptimal solutions, one could potentially demonstrate a quantum advantage in terms of less violations.
As far as speed is concerned, we noted that on Graph 2, and disregarding all overhead, the 1,000 runs of QA took a total of 1000 × 20 μsec = 20 msec on D-Wave II to render the solution utilized in the performance analysis. On SA on the other hand, 5,000 runs, totaling 1 minute in the adopted simulation environment, were needed to get solutions comparable with those of QA. This comparison might however be misleading as there is room for considerable speed up of SA on specialized architecture. It is also argued14,15 that even 20 μs might be too large for particular problems; however, this is the minimum programmable annealing time on D-Wave platform.
Despite encouraging results, due to the very limited experimental data, we cannot positively assert a general sizable advantage of quantum annealing against simulated annealing. However, we plan to generalize this potential advantage in the future by utilizing a broader class of graphs and the 1152-qubit chip. It is hoped that this could help resolve the speedup issue13,14,15.
The classical wireless protocols (Backpressure, Dirichlet and Heat Diffusion, see supplemental material for protocol definition) return solutions with the interference constraints always satisfied—so that there is forwarding at every time slot. Here, the QA and SA interference problem solvers allow solutions that violate the interference constraints in the interest of speed. Unfortunately, should an interference constraint be violated even at a remote corner of the network, our simulation stops the transmission, so that the Dirichlet protocol as it now stands cannot take advantage of the proposed algorithm speedup. As to whether the Dirichlet protocol could be tweaked to take advantage of the faster QA solution to the interference problem is widely open.
Additional Information
How to cite this article: Wang, C. et al. Quantum versus simulated annealing in wireless interference network optimization. Sci. Rep. 6, 25797; doi: 10.1038/srep25797 (2016).
Supplementary Material
Acknowledgments
We sincerely thank Tameem Albash, Walter Vinci, Joshua Job and Richard Li for helpful discussions, and Prof. Daniel Lidar for providing critical comments on the paper. Many thanks also go to Prof. Paul Bogdan for helpful remarks on the paper. This work was supported in part by ARO MURI Contract W911NF-11-1-0268 and in part by NSF grant CCF-1423624. Huo Chen was supported by an Annenberg Fellowship.
Footnotes
Author Contributions C.W. formulated the quantum computation formulation of the interference problem and developed the quantum annealing experiments. H.C. ran the simulated annealing experiments. E.J. developed the Heat Diffusion wireless protocol and managed the overall project.
References
- Kirkpatrick S., Gellatt C. D. & Vecchi M. P. Optimization by simulated annealing. Science 220, 671–680 (1983). [DOI] [PubMed] [Google Scholar]
- Ray P., Chakrabarti B. K. & Chakrabarti A. Sherrington-Kirkpatrick model in a transverse field: absence of replica symmetry breaking due to quantum fluctuations. Phys. Rev. B 39, 11828 (1989). [DOI] [PubMed] [Google Scholar]
- Kadowaki T. & Nishimori H. Quantum annealing in the transverse Ising model. Phys. Rev. E 58, 5355–5363 (1998). [Google Scholar]
- Perdomo-Ortiz A., Fluegemann J., Narasimhan S., Biswas R. & Smelyanskiy V. N. Finding low-energy conformations of lattice protein models by quantum annealing. Sci. Rep. doi: 10.1038/srep00571 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bian Z. et al. Experimental determination of Ramsey numbers. Phys. Rev. Lett. 111, 130505 (2013). [DOI] [PubMed] [Google Scholar]
- O’Gorman B., Perdomo-Ortiz P., Babbush R., Aspuru-Guzik A. & Smelyanskiy V. N. Bayesian network structure learning using quantum annealing. Euro. Phys. J. 224(1), 163–188 (2015). [Google Scholar]
- Rieffel E. G. et al. A case study in programming a quantum annealer for hard operational planning problems. Quan. Info. Proc. 14(1), 1–36 (2015). [Google Scholar]
- Perdomo-Ortiz A., Fluegemann J., Narasimhan S., Biswas R. & Smelyanskiy V. N. A quantum annealing approach for fault detection and diagnosis of graph-based systems. Euro. Phys. J. 224(1), 131–148 (2015). [Google Scholar]
- Zick K. M., Shehab O. & French M. Experimental quantum annealing: case study involving the graph isomorphism problem. Sci. Rep. doi: 10.1038/srep11168 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trummer I. & Koch C. Multiple query optimization on the D-Wave 2X adiabatic quantum computer. arXiv: 1501.06437.
- Pudenz K. & Lidar D. A. Quantum adiabatic machine learning. Quan. Info. Proc. 12, 2027–2070 (2013). [Google Scholar]
- Benedetti M. et al. Estimation of effective temperatures in a quantum annealer and its impact in sampling applications: A case study towards deep learning applications. arXiv:1510.07611.
- Boixo S. et al. Quantum annealing with more than one hundred qubits. Nature Phys. 10, 218–224 (2014). [Google Scholar]
- Rønnow T. F. et al. Defining and detecting quantum speedup. Science 345, 420–424 (2014). [DOI] [PubMed] [Google Scholar]
- Hen I. et al. Probing for quantum speedup in spin glass problems with planted solutions. Phys. Rev. A 92, 042325 (2015). [Google Scholar]
- Lucas A. Ising formulation of many NP problems. Frontiers in Phys. 2, 5 (2014). [Google Scholar]
- Farhi E. et al. A quantum adiabatic evolution algorithm applied to random instances of an NP-complete problem. Science 292, 472–475 (2001). [DOI] [PubMed] [Google Scholar]
- The Working Group for WLAN Standards. IEEE 802.11 Wireless Local Area Networks available at http://www.ieee802.org/11/ (Accessed 23th March, 2016).
- Baker D. J., Wieselthier J. & Ephremides A. A distributed algorithm for scheduling the activation of links in a self-organizing mobile radio network. IEEE ICC 2F.6.1–2F.6.5 (1982). [Google Scholar]
- Miller B. & Bisdikian C. Bluetooth Revealed: The Insider’s Guide to an Open Specification for Global Wireless Communications (Prentice Hall, 2000). [Google Scholar]
- Balakrishnan H., Barrett C. L., Kumar V. S. A., Marathe M. V. & Thite S. The distance-2 matching problem and its relationship to the MAC-layer capacity of ad hoc wireless networks. IEEE JSAC 22(6), 1069–1079 (2004). [Google Scholar]
- Sharma G., Mazumdar R. & Shroff N. On the complexity of scheduling in wireless networks. MobiCom’06 Los Angeles, USA, doi: 10.1145/1161089.1161116 (2006, Sep. 24–29). [DOI] [Google Scholar]
- Jain K. et al. Impact of interference on multi-hop wireless network performance. MobiCom’03 ACM, San Diego, USA, doi: 10.1145/938985.938993 (2003, Sep. 14–19). [DOI] [Google Scholar]
- Alicherry M., Bhatia R. & Li L. E. Joint channel assignment and routing for throughput optimization in multiradio wireless mesh networks. IEEE JSAC 24, 1960–1971 (2006). [Google Scholar]
- Kodialam M. & Nandagopal T. Characterizing the capacity region in multi-radio multi-channel wireless mesh networks. MobiCom’05 ACM, Cologne, Germany (2005, Aug. 28-Sep. 2). [Google Scholar]
- Sanghavi S. S., Bui L. & Srikant R. Distributed link scheduling with constant overhead. ACM Sigmetrics 35, 313–324 (2007). [Google Scholar]
- Wan P. J. Multiflows in multihop wireless networks. MobiHoc’09 ACM, Beijing, China, doi: 10.1145/1530748.1530761 (2009. Sep. 20–25). [DOI] [Google Scholar]
- Blough D. M., Resta G. & Sant P. Approximation algorithms for wireless link scheduling with SINR-based interference. IEEE Trans. on Networking 18, 1701–1712 (2010). [Google Scholar]
- Chafekar D., Kumar V. S. A., Marathe M. V., Parthasarathy S. & Srinivasan A. Capacity of wireless networks under SINR interference constraints. J. Wireless Networks 17, 1605–1624 (2011). [Google Scholar]
- Moscibroda T., Wattenhofer R. & Zollinger A. Topology control meets SINR: the schedling complexity of arbitrary topologies. MobiHoc’06 ACM, Florence, Itay, doi: 10.1145/1132905.1132939 (2006). [DOI] [Google Scholar]
- Gupta P. & Kumar P. R. The capacity of wireless networks. IEEE Trans. on Info. Theory 46(2), 388–404 (2000). [Google Scholar]
- Andrews M. & Dinitz M. Maximizing capacity in arbitrary wireless networks in the SINR model: complexity and game theory. INFOCOM’09 Rio de Janeiro, Brazil, doi: 10.1109/INFCOM.2009.5062048 (2009, Apr. 19–25). [DOI] [Google Scholar]
- Homer S. & Peinado M. Experiments with polynomial-time clique approximation algorithms on very large graphs. Cliques, Coloring, and Satisfiability 147–167 (AMS, 1996). [Google Scholar]
- Grossman T. Applying the INN model to the max clique problem. Cliques, Coloring, and Satisfiability 125–145 (AMS, 1996). [Google Scholar]
- Jagota A. Approximating maximum clique with a Hopfield network. IEEE Trans. Neural Networks 6, 724–735 (1995). [DOI] [PubMed] [Google Scholar]
- Jagota A., Sanchis L. & Ganesan R. Approximately solving maximum clique using neural networks and related heuristics. Cliques, Coloring, and Satisfiability 169–176 (AMS, 1996). [Google Scholar]
- Bui T. N. & Eppley P. H. A hybrid genetic algorithm for the maximum clique problem. Proceedings of the 6th International Conference on Genetic Algorithms 478–484 (Morgan Kaufmann, 1995).
- Hifi M. A genetic algorithm - based heuristic for solving the weighted maximum independent set and some equivalent problems. J. Oper. Res. Soc. 48, 612–622 (1997). [Google Scholar]
- Marchiori E. Genetic, iterated and multistart local search for the maximum clique problem. Applications of Evolutionary Computing 2279, 112–121 (Springer-Verlag, 2002). [Google Scholar]
- Feo T. A. & Resende M. G. C. A greedy randomized adaptive search procedure for maximum independent set. J. Oper. Res. 42, 860–878 (1994). [Google Scholar]
- Battiti R. & Protasi M. Reactive local search for the maximum clique problem. Algorithmica 29, 610–637 (2001). [Google Scholar]
- Friden C., Hertz A. & de Werra D. Stabulus: A technique for finding stable sets in large graphs with tabu search. Computing 42, 35–44 (Springer-Verlag, 1989). [Google Scholar]
- Mannino C. & Stefanutti E. An augmentation algorithm for the maximum weighted stable set problem. Comput. Optim. Appl. 14, 367–381 (1999). [Google Scholar]
- Soriano P. & Gendreau M. Tabu search algorithms for the maximum clique problem. Cliques, Coloring, and Satisfiability 221–244 (AMS, 1996). [Google Scholar]
- Edmonds J. Paths, trees, and flowers. Canad. J. Math. 17, 449–467 (1965). [Google Scholar]
- King A. D. & McGeoch C. C. Algorithm engineering for a quantum annealing platform. arXiv:1410.2628.
- Isakov S. V., Zintchenko I. N., Rønnow T. F. & Troyer M. Optimized simulated annealing for Ising spin glasses. arXiv:1401.1084. [Google Scholar]
- Choi V. Minor-embedding in adiabatic quantum computation: I. the parameter setting problem. Quan. Info. Proc. 7, 193–209 (2008). [Google Scholar]
- Wang C., Jonckheere E. & Brun T. Ollivier-Ricci curvature and fast approximation to tree-width in embeddability of QUBO problems. ISCCSP IEEE, Athens, Greece, doi: 10.1109/ISCCSP.2014.6877946 (2014, May 21–23). [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.