Three Approaches to Modeling Gene-Environment Interactions in Longitudinal Family Data: Gene-Smoking Interactions in Blood Pressure

Abstract

Background

Blood pressure (BP) has been shown to be substantially heritable, yet identified genetic variants explain only a small fraction of the heritability. Gene-smoking interactions have detected novel BP loci in cross-sectional family data. Longitudinal family data are available and have additional promise to identify BP loci. However, this type of data presents unique analysis challenges. Although several methods for analyzing longitudinal family data are available, which method is the most appropriate and under what conditions has not been fully studied.

Methods

Using data from three clinic visits from the Framingham Heart Study, we performed association analysis accounting for gene-smoking interactions in BP at 31,203 markers on chromosome 22. We evaluated three different modeling frameworks: generalized estimating equations, hierarchical linear modeling, and pedigree-based mixed modeling.

Results

The three models performed somewhat comparably, with multiple overlaps in the most strongly associated loci from each model. Loci with the greatest significance were more strongly supported in the longitudinal analyses than in any of the component single-visit analyses. The pedigree-based mixed model was more conservative, with less inflation in the variant main effect and greater deflation in the gene-smoking interactions. The generalized estimating equations, but not the other two models, resulted in substantial inflation in the tail of the distribution when variants with minor allele frequency < 1% were included in the analysis.

Discussion

The choice of analysis method should depend on the model and the structure and complexity of the familial and longitudinal data.

INTRODUCTION

Elevated blood pressure (BP) increases risk for cardiovascular disease and is the leading cause of global health burden [Lim, et al. 2012]. However, despite an estimated heritability of 30%, less than 3% of BP variation has been attributed to particular genetic variants [Ehret 2010]. Gene-environment interactions have been suggested as one source of the genetic contribution to BP variability [Manolio, et al. 2009], and BP-associated factors such as age [Shi, et al. 2009a], sex [Ramirez-Lorca, et al. 2007], and alcohol [Simino, et al. 2013] have been investigated for potential interactions with genes affecting blood pressure.

For studying gene-environment interactions, longitudinal family studies have desirable properties by combining the features of repeated measures and family studies. A conventional longitudinal study involves the repeated evaluation of one or more measurable traits in a series of unrelated individuals. The repeated measurements help reduce error, increase statistical power, and provide a means to study the pattern and determinants of systematic changes in a phenotype of interest over time. In contrast, a cross-sectional family study utilizes phenotypic similarities and differences amongst close relatives to disentangle the genetic and environmental contributions to the trait under study [Khoury and James 1993]. A longitudinal family study further increases the power to resolve the genetic and environmental determinants of traits associated with complex diseases and also to study the corresponding determinants of change in such traits over time [Burton, et al. 2005].

However, analysis of longitudinal phenotypes in family data is much more challenging due to two sources of dependence among their observations: familial relatedness across subjects and the longitudinal correlation across visits within a single subject. Several software packages readily handle either one of these sources of correlation, allowing the use of a variety of covariance structures to model their form. However, for analysis of longitudinal family data with both familial and longitudinal correlations, most software does not allow for the fully flexible modeling of both covariance structures. There are three R software packages implementing the three approaches: geepack [Halekoh, et al. 2006] implementing generalized estimating equations, nlme [Pinheiro J 2015] implementing hierarchical linear modeling, and pedigremm [Vazquez, et al. 2010] implementing pedigree-based mixed modeling. Some packages including pedigreemm can facilitate modeling familial covariance using the kinship matrix, and other packages including nlme have highly structured covariance structures implemented for the longitudinal component (such as an auto-regressive structure). To our knowledge, no currently-available software does both.

In the present study, we evaluated three analysis options for the longitudinal family data while considering gene-smoking interactions for association with BP using data in the Framingham Heart Study (FHS). Cigarette smoking is a risk factor for cardiovascular disease [Lubrano and Balzan 2015] with complex effects on BP, including increased BP from acute exposure and decreased BP from longer-term exposure [Green, et al. 1986]. We recently investigated interactions between genes and cigarette smoking for association with BP using a cross-sectional data from FHS [Sung, et al. 2014]. FHS is a longitudinal study from 1948, constituting a seminal contribution to the field and a heavily documented population. Analysis of longitudinal data for gene-smoking interactions may provide greater power than cross-sectional analysis by taking advantage of the greater number of observations and strength of longitudinal trends. We focused our analysis at 31,203 SNPs on chromosome 22 based on our findings with a cross-sectional subset of data from FHS study [Sung, et al. 2014]. We evaluated several issues including the extent to which results show agreement, control over type I error, sensitivity to low minor allele frequencies, and utility relative to cross-sectional analysis.

METHODS

Subjects

These analyses were based on Framingham SNP Health Association Resource (SHARe) data released in 2005 from the database of Genotypes and Phenotypes (dbGaP; http://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000342.v12.p9). The Framingham Heart Study is a longitudinal study founded in 1948 with the recruitment of the first of three cohorts (the ‘Original’ cohort). The Original cohort returned for follow-up visits every 4 to 8 years, accumulating over 30 clinic visits. In 1971, the offspring, spouses, and children of the Original cohort were enrolled (‘Offspring’ cohort) and this cohort completed 7 clinic visits through 2005. The ‘Third Generation’ cohort, consisting of the biological and adopted offspring of the Offspring cohort, was recruited in 2002 and completed its first visit in 2005.

Table I shows the sample size by cohort and visit. All 7 visits of the Offspring cohort are shown, along with the single Third Generation visit, whose average visit date best matches Offspring visit 7, and the 7 Original cohort visits whose average visit date most closely matches each of the 7 Offspring visits. For the current study we analyzed data from visits 1, 4, and 7 for computational ease as these had the largest sample size and span the length of time for which data on multiple cohorts was available. All analyzed subjects had complete genotyped and imputed SNP data for chromosome 22 and systolic blood pressure (SBP), cigarettes per day (CPD), age, sex, and use of anti-hypertension medication. Descriptive statistics for the sample are shown for each of the three analyzed visits in Table II.

Table I.

Number of subjects by visit and cohort

Cohort	Visit 1	Visit 2	Visit 3	Visit 4	Visit 5	Visit 6	Visit 7
Original	917	0	797	772	648	510	305
Offspring	3534	2985	3066	3278	3200	3108	2967
Third Generation	0	0	0	0	0	0	3793
Total	4451	2985	3863	4050	3848	3618	7065

Table II.

Study Sample Descriptive Statistics

	Visit 1	Visit 4	Visit 7
Sample Size	4,451	4,050	7,066
CPD	11.4 ± 14.6	4.6 ± 10.7	8.8 ± 12.6
Age, years	40.6 ± 14.0	55.7 ± 13.1	50.8 ± 15.3
Male, %	45.3 (2014)	46.0 (1861)	46.1 (3260)
Taking Anti-hypertensive meds, %	5.9 (261)	22.4 (905)	21.3 (1505)
SBP, mm Hg	122.8 ± 16.1	130.0 ± 20.2	132.4 ± 17.2

Data presented as % (n) or mean ± standard deviation

Most cross-sectional data analysis for longitudinal data often chooses a single visit with the largest sample size. For this reason, we particularly included visit 7 in our longitudinal analysis. Although age and the proportion of medication users usually increase with visits in most longitudinal studies, our data in visit 7 have somewhat lower ages and a smaller proportion of medication users than data in visit 4. This is because the Third Generation, a younger generation, only participated in visit 7.

The combination of cohorts does raise complications in the structure of the population and in the appropriate terminology (e.g. ‘longitudinal’ vs ‘cross-sectional’). Even in a fully ‘rectangular’ dataset (most subjects measured at all visits, missing data distributed randomly) the presence of some subjects missing observations such that they were only measured once would not invalidate that label ‘longitudinal’ for the study as a whole. In this case the ‘missing’ data are for the most part distributed non-randomly (by cohort). We wanted to explore the extent to which a longitudinal analysis of this Framingham Heart Study data, which constitutes a seminal contribution to the field and a heavily documented population, would be possible with various methodologies in spite of this complication.

Phenotypes and Genotypes

Three SBP readings (one taken by a nurse/technician and two by a physician) were averaged for the analysis. Although efficacy of anti-hypertensive medication is not the same, detailed data on the number and kinds of medications was not available for large numbers of the subjects to allow this type of analysis. It’s also worth noting that often times subjects are given a 2^nd (or 3^rd) class of anti-hypertensive medication specifically because the 1^st class had a weak (or no) effect, and as such the relationship between the degree of blood pressure reduction and the number of medications taken is not straight-forward or linear. Following a standard medication adjustment for blood pressure, the SBP value was adjusted for subjects taking anti-hypertension medication by adding 15 mm Hg.

As the measure of smoking we used cigarettes per day (CPD), the number of cigarettes that the subject smoked on average per day if he/she smoked at the time of each visit. Pack-years is another smoking measure, the average number of packs smoked per day times the total number of years a subject smoked during his/her lifetime. The CPD reflects the rate/intensity of smoking, whereas the pack-years information represents the total volume of smoking in one’s life (up to that time), which therefore is a function of one’s age. Pack-years information may be preferred for analysis of other traits, for example, cancer risk, which accumulates with continued smoking and does not decrease after cessation. However, we chose CPD for our analysis of blood pressure because the effects of smoking on blood pressure are relatively short-lived, largely disappearing within a year of smoking cessation. We used zero value of CPD for former smokers based on our understanding of the underlying physiology.

Framingham Heart Study participants were genotyped using the GeneChip Human Mapping 500K Array Set (Affymetrix, Santa Clara, CA) which assays 487,988 SNPs; an additional 2.5 million SNPs were imputed based on HapMap using MACH [Li, et al. 2010]. SNPs with fewer than 2 minor alleles or poor imputation quality (r² > 0.3) were removed from the analysis. We focus our analysis on chromosome 22 because an association between BP and a region on chromosome 22 was detected in a previous analysis including gene-smoking interactions in a cross-sectional subset of these data [Sung, et al. 2014]. This resulted in 31,203 imputed SNPs.

Analysis

Three modeling frameworks were implemented in R packages available on the Comprehensive R Archive Network (CRAN): generalized estimating equations (GEE) in geepack [Halekoh, et al. 2006], a hierarchical linear model (HLM) in nlme [Pinheiro J 2015], and a pedigree-based mixed model implemented in pedigreemm (pedMM) [Vazquez, et al. 2010]. Each approach used the same set of predictors but differed in their modeling of the covariance structure across visits within individuals and across individuals within families. The basic model included a SNP-CPD interaction term as well as age and sex as covariates:

$$\mathit{SBP}={\beta }_0+{\beta }_1\ast \mathit{Age}+{\beta }_2\ast \mathit{Sex}+{\beta }_3\ast \mathit{CPD}+{\beta }_4\ast \mathit{SNP}+{\beta }_5\ast \mathit{SNP}\ast \mathit{CPD}$$

Although body mass index (BMI) is a well-known risk factor, we elected not to include BMI as a covariate. The choice of whether to include BMI as a covariate in a genetic analysis of blood pressure is not straight-forward. This is because, unlike the covariates age and sex, BMI itself has a genetic component, and adjusting for BMI will likely have the effect of eliminating or substantially diminishing the effects of variants whose mechanism of influence on blood pressure is via an influence on BMI. As our model also includes cigarette smoking, which has a complicated effect on blood pressure that includes an effect on BMI as one of its mechanisms, genetic variants acting on blood pressure through BMI were of particular interest in these analyses. Therefore, while we sacrificed some power for variants NOT acting through BMI, we chose not to include BMI in the baseline analysis.

To compare three modeling frameworks, we performed three tests. First, we tested the genetic main effect in the presence of SNP-CPD interaction effect by using Wald test statistic that follows a chi-squared distribution with 1 degrees of freedom (df) under the H₀: β₄=0. Second, we performed the standard approach to identify SNP-CPD interactions by using the Wald test statistic that follows a chi-squared distribution with 1 df under the H₀: β₅=0 (i.e., testing for the interaction effect in the presence of the genetic main effect). Finally, we performed the 2df test that jointly tests the genetic main and SNP-CPD interaction effects [Kraft, et al. 2007]. In particular, we used a Wald test statistic that follows a chi-squared distribution with 2 df under the H₀: β₄=β₅=0. This Wald test statistic is based on estimates of β₄ and β₅ and their corresponding 2×2 covariance matrix.

The GEE approach treated each family as an independent cluster, using an ‘exchangeable’ (or compound symmetric) working correlation to model the covariance between all observations from any subject and any visit within the family. The other two models each treat the longitudinal and family correlations separately. The HLM model used compound symmetry for the covariance among family members, while the covariance across visits within a single subject was modeled with a first order auto-regressive (AR1) structure (implying a decaying correlation as the time between visits increases). The pedMM model incorporated a fully-specified kinship matrix for the covariance across family members, and used compound symmetry to model the covariance across visits within subjects. All participants in the Framingham Heart Study population were used to build the kinship coefficient matrix. These models are referred to as GEE-CS, HLM-AR1, and pedMM-CS, respectively.

In addition to these three primary models, three other analyses were performed. These included two analyses, one with HLM and one with pedMM, using no modeling of the longitudinal correlation (i.e. across visits within subjects). These models retained their treatment of the familial correlation (compound symmetry and kinship, respectively) for these analyses and are referred to as HLM-NoLong and pedMM-NoLong. Finally, an additional analysis used the HLM approach and modeled the correlation across visits using an auto-regressive moving average (ARMA) structure; it is referred to as HLM-ARMA. The covariance structures employed for both the familial and longitudinal components of each of the six analyses are summarized in table III.

Table III.

Familial and Longitudinal Covariance Structure by Analysis

Primary Analyses	Familial Covariance	Longitudinal Covariance
GEE-CS	Compound Symmetry (joint with longitudinal)	Compound Symmetry (joint with familial)
HLM-AR1	Compound Symmetry	First Order Auto-Regressive
pedMM-CS	Kinship	Compound Symmetry
Secondary Analyses
HLM-NoLong	Compound Symmetry	Independence
pedMM-NoLong	Kinship	Independence
HLM-ARMA	Compound Symmetry	First Order Auto-Regressive Moving Average

RESULTS

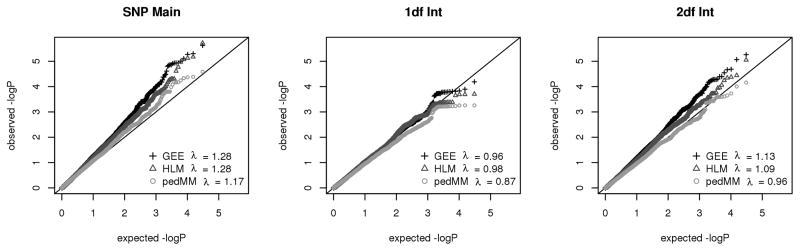
For each of the six analyses, table IV shows the genomic inflation factor λ for the SNP main effect, 1df SNP-CPD interaction, and 2df joint test of the SNP main effect and SNP-CPD interactions. QQ plots for the three primary analyses are shown in Figure 1. All three analyses show substantial inflation in the SNP main effect (λ_SNP 1.17–1.28) and deflation in the SNP-CPD interaction (λ_SNP-CPD 0.87–0.98).

Table IV.

Genomic Control (λ)

Model	SNP Main	1df Int	2df Int
HLM-AR1	1.27	0.98	1.09
HLM-ARMA	1.28	1.00	1.11
HLM-NoLong	1.9	1.23	1.53
GEE-CS	1.29	0.96	1.13
pedMM-CS	1.18	0.86	0.96
pedMM-NoLong	0.73	1.26	0.87

For each model, Table IV shows the genomic control λ value for the SNP main effect, 1df SNP*CPD interaction, and 2df joint test of the SNP main effect and SNP*CPD interaction.

Figure 1.

Figure 2 shows the Manhattan plots for SNPs with MAF > 1% for the three primary analyses and for the SNP main effect, 1df interaction test and 2df joint test. Table V summarizes the strongest association signals. No loci showed significant (p<1.7e-6) results in any model with any test. Several suggestive (p<1.7e-5) associations were found in 2df and main effect tests in the HLM-AR1 and GEE-CS models; the number of loci implicated by these associations are shown in Table VI. The GEE-CS model showed a suggestive 2df association in a PARVB intron which appears to be driven by main effects, and a second suggestive 2df association in a FAM227A intron which is driven primarily by the 1df SNP-CPD interaction (p=1.27e-4). In addition to the PARVB locus, the GEE-CS model also detected 3 other suggestive main effects: in FAM19A5, DERL3, SLC35E4. The HLM-AR1 model detected a subset of these suggestive loci: the 2df association with PARVB and the main effects in PARVB, FAM19A5 and DERL.

Figure 2.

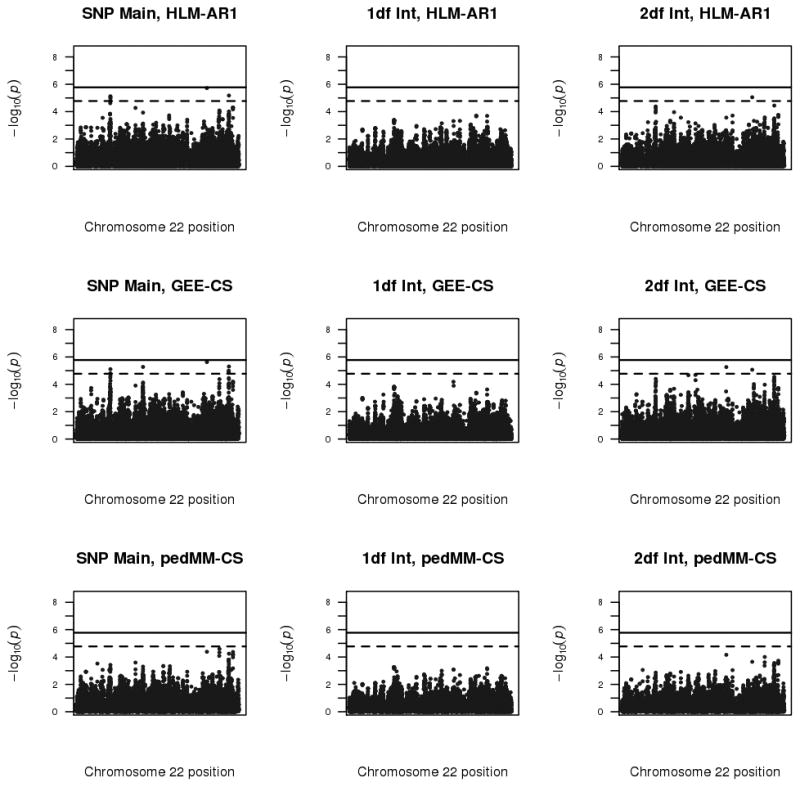
Table V.

Top Association Signals

Locus	Model	rs#	MAF	pMAIN	p1df	p2df	Beta Main	se Main	Beta Int	se Int
DERL3	HLM-AR1	rs5760061	0.21	7.52E-06	7.26E-02	4.22E-05	1.50	0.33	−0.03	0.02
DERL3	GEE-CS	rs5760061	0.21	7.79E-06	7.94E-02	4.03E-05	1.49	0.33	−0.03	0.02
DERL3	pedMM-CS	rs5760061	0.21	3.78E-04	3.68E-01	1.38E-03	1.26	0.35	−0.02	0.02
SLC35E4	HLM-AR1	rs1076301	0.48	1.18E-04	1.10E-01	5.93E-04	−1.13	0.29	0.02	0.02
SLC35E4	GEE-CS	rs1076301	0.48	5.34E-06	1.18E-01	2.15E-05	−1.37	0.30	−0.27	0.02
SLC35E4	pedMM-CS	rs1076301	0.48	5.04E-04	9.58E-02	2.33E-03	−1.07	0.31	0.03	0.02
FAM227A	HLM-AR1	rs9610989	0.02	4.48E-01	1.12E-03	2.74E-04	−1.13	1.49	−0.26	0.08
FAM227A	GEE-CS	rs9610989	0.02	5.75E-01	1.27E-04	5.47E-06	−0.83	1.48	−0.27	0.07
FAM227A	pedMM-CS	rs9610989	0.02	2.27E-01	8.41E-04	6.93E-05	−1.90	1.57	−0.27	0.08
PARVB	HLM-AR1	rs2267606	0.09	1.91E-06	1.29E-01	8.91E-06	−2.23	0.47	0.04	0.02
PARVB	GEE-CS	rs2267606	0.09	2.38E-06	1.18E-01	8.57E-06	−2.35	0.50	0.04	0.02
PARVB	pedMM-CS	rs2267606	0.09	4.13E-05	7.99E-02	2.24E-04	−2.01	0.49	0.04	0.03
GRAMD4	HLM-AR1	rs6008948	0.08	8.21E-05	2.06E-01	3.55E-04	2.09	0.33	−0.04	0.02
GRAMD4	GEE-CS	rs6007952	0.07	4.20E-05	3.20E-01	1.07E-04	2.33	0.57	−0.03	0.03
GRAMD4	pedMM-CS	rs6007952	0.07	2.58E-05	2.62E-01	9.90E-05	2.25	0.54	−0.03	0.03
FAM19A5	HLM-AR1	rs4925403	0.10	6.67E-06	1.95E-02	3.61E-05	−2.80	0.30	0.08	0.02
FAM19A5	GEE-CS	rs4925403	0.10	5.00E-06	5.46E-02	2.84E-05	−2.84	0.62	0.06	0.03
FAM19A5	pedMM-CS	rs4925403	0.10	5.73E-05	3.83E-02	2.74E-04	−2.63	0.65	0.07	0.03
BRD1	HLM-AR1	rs3810643	0.22	5.01E-05	9.55E-03	1.89E-04	1.34	0.33	−0.05	0.02
BRD1	GEE-CS	rs1883110	0.21	6.59E-05	3.36E-03	1.89E-04	−1.29	0.32	0.06	0.02
BRD1	pedMM-CS	rs1883111	0.24	4.28E-05	1.76E-02	1.86E-04	−1.41	0.34	0.04	0.02

Table VI.

Number of Loci Suggestively Associated by Model and Test

	HLM-AR1	GEE-CS	pedMM-CS
Main	3	4	0
1df	0	0	0
2df	1	2	0

The pedMM-CS analysis did not detect any suggestive or significant associations. However, pedMM-CS provided the strongest support for two other main effect loci, one in a GRAMD4 intron (p=2.6e-5) and one near BRD1 (p=4.3e-5), which also received modest support from the HLM-AR1 (p=8.2e-5 and p=5.0e-5) and GEE-CS (p=4.2e-5 and p=6.6e-5). The pedMM-CS main effects also lent additional support (p<1e-4) to the PARVB and FAM19A5 loci.

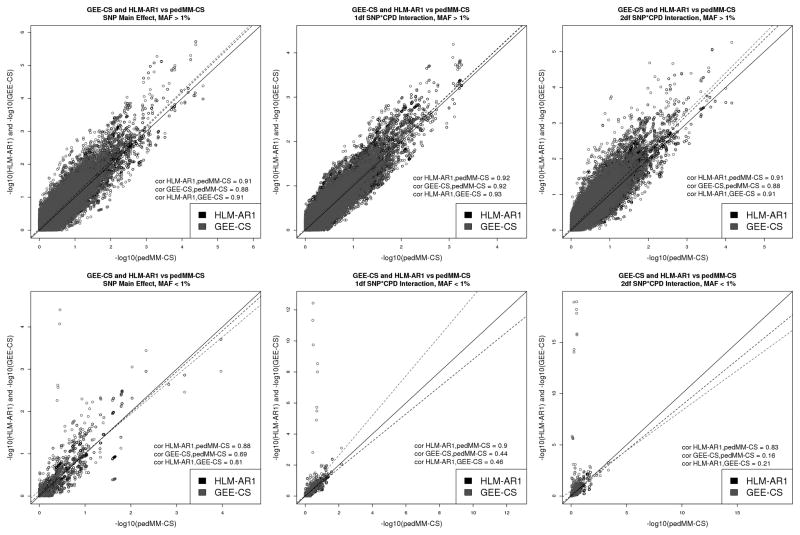
Figure 3 shows the p-value comparisons for each test and model for all SNPs with MAF greater than 1% in the top row and for all SNPs with MAF less than 1% in the bottom row. Approximately one dozen rare and low frequency variants gave rise to strong interaction signals (both 1df and 2df) in the GEE analysis but not in the HLM or pedMM analyses. Inclusion of rare and low frequency variants did not give rise to apparent inflation of SNP main effects for any analysis.

Figure 3.

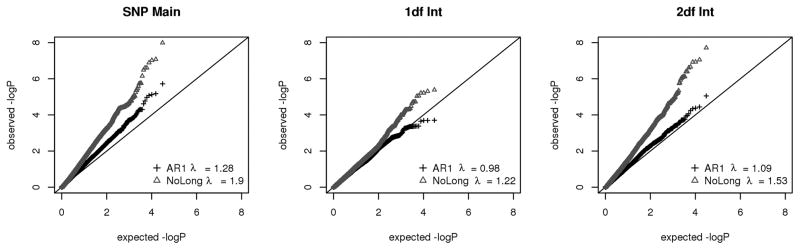
The QQ plots in Figure 4 compare the HLM model with AR1 longitudinal covariance structure to the HLM model assuming independence among the visits (HLM-AR1 vs HLM-NoLong). The independence model is dramatically inflated relative to the AR1 model for the SNP main effect and both 1df and 2df joint tests of the SNP-CPD interaction (Table IV). Comparison of the HLM-AR1 model with an HLM model using the ARMA covariance structure to model longitudinal correlations revealed minimal differences in the resulting p-values (supplemental Figure 1). As the AR1 structure is more parsimonious, using one parameter instead of the two used by ARMA, we focus here on the HLM-AR1 model.

Figure 4.

DISCUSSION

These analyses were motivated by the desire to leverage longitudinal data to detect BP loci missed by single visit analyses, as predicted in simulations [Shi, et al. 2009b]. Suggestive evidence in the longitudinal data was found by more than one model for several loci lacking evidence of association from single-visit analyses. At the FAM227A locus, for example, rs9619089 was implicated by the 2df joint test in the GEE-CS model at p = 5.47e-6 (and supported by the HLM-AR1 and pedMM-CS models at p = 2.74e-4 and 6.93e-5, respectively, Table IV) but gave rise to a 2df p-value of 2.69e-1, 7.88e-3, and 3.18e-4 for the GEE-based analyses run separately on visits 1, 4, and 7, respectively. Similarly, the 2df interaction involving rs2267606 at the PARVB locus was associated at 8.57e-6 in the GEE-CS model (8.91e-6 from HLM-AR1 and 2.24e-4 from pedMM-CS) but the single visit HLM 2df p-values were 2.69e-1, 7.88e-3, and 3.18e-4 for analysis of visits 1, 4, and 7, respectively. These results demonstrate the additional contributions longitudinal data can make relative to cross-sectional data. To effectively make use of these data, it was important to model the repeated measures as correlated. We note that the results from the GEE-CS model at the two loci may be due to incorrect covariance structure, leading to inflation of type I error. Figure 4 shows QQ plots contrasting the HLM-AR1 model (which assumes that the correlation between clinic visits decreases over time) with the HLM-NoLong model (which assumes no correlation between the visits). The SNP main effect and both 1df and 2df interaction tests were all dramatically inflated in the NoLong model relative to the AR1 model.

Although the three models differ substantially in their handling of familial and longitudinal correlations, their overall results are quite comparable, with similar patterns of inflation (Figure 1) and highly correlated p-values (Figure 3) for the main effect and both interaction tests. There was also considerable overlap among the most strongly associated loci (Figure 2, Table V). In general, pedMM-CS was the most conservative model, which in the present analysis most likely reflects relatively less inflation for SNP main effects and the 2df interaction test as well as some deflation for the 1df interaction test. The other major distinction apparent in these results is in the handling of low frequency SNPs (those with MAF less than 1%). The HLM-AR1 and pedMM-CS models show strong agreement for these SNPs, with p-value correlations across all three tests greater than 0.8. The GEE-CS model, however, shows strong 1df and 2df interaction signals for a number of rare SNPs that are not supported by the other two models, resulting in much lower correlations with those models (Figure 3). Given the agreement between the other two models and the fact that GEEs have previously been shown to have convergence problems and increased type I error for low frequency variants in other contexts [Chen, et al. 2011], we interpret these results to reflect increased type I error rather than increased power. Although the FHS includes a small subset of non-European subjects, our analysis restricted to subjects with European ancestry. We performed main-effect only analysis for the data, confirming the absence of population stratification.

The power gained relative to single visit analyses and the convergent results across modeling frameworks support the use of longitudinal family data for gene discovery. To choose from among the available approaches, the investigator must weigh the complexity of the family structures against the complexity of the repeated measures. Large multi-generational families will include a wide variety of relationships ranging from no correlation (mother-father) to high correlation (parent-child, sibling-sibling). Assuming a single covariance across all intra-family pairs of subjects (as the HLM and GEE models do) may introduce substantial familial mis-specification, and the pedMM model, which instead uses the kinship matrix to model familial covariance, may be more suitable. Some studies, however, have a more uniform set of relationships within their families, such as those designed around first degree relatives. The single covariance assumed by the HLM and GEE models may be adequate in such cases, and the use of the HLM model allows for a more finely structured specification of the longitudinal correlations. Similarly, a finely specified longitudinal covariance matrix may not be necessary for studies with just a few closely spaced visits, for which a single longitudinal covariance term (as is used by pedMM) may fit the data well. If there are numerous widely spaced visits in a study, however, the correlation between any two observations may depend on the distance between them and it may be necessary to use a structured covariance matrix (such as AR1) rather than assume a single constant correlation.

The GEE approach has been useful and will continue to do so, as it provides robust standard errors to protect against mis-specification of the mean model [Tchetgen Tchetgen and Kraft 2011; Voorman, et al. 2011]. For analysis of longitudinal family data, the GEE approach treats each family as a cluster and all pairs of observations across family members and visits as equally correlated. Because of this, the GEE approach provided different results from two other model-based approaches that we evaluated. This approach may be most suitable when both the familial and longitudinal complexity is low. For studies such as FHS with a high degree of complexity in both the families and the repeated measures, no existing software allows the finely structured modeling of both sources of dependence. Although this limitation may contribute to the inflation observed in the SNP main effect in all three models, concordance of results across these models suggests that it is not a fatal flaw. The increased association signal observed relative to single visit analyses supports the need to develop analysis methods for longitudinal family data.

Limitations

FHS has large, multi-generational families and numerous widely separated visits, both of which reduce the suitability of the compound symmetric covariance structures implemented in the three modeling frameworks discussed. The results reported here may therefore have limited generalizability to other study designs with smaller families or fewer, more closely spaced measurements. These analyses only include subjects of European ancestry, also potentially limiting the applicability of these results to other racial and ethnic groups. The smoking trait (cigarettes per day) was based on self-reports spanning more than 30 years; the impact of social desirability bias on self-reported data may have changed as attitudes regarding smoking have evolved over that period.