Abstract
Recent single cell studies show extensive molecular variability underlying cellular responses. We evaluated the impact of molecular variability in the expression of cell signaling components and ion channels on electrophysiological excitability and neuromodulation. We employed a computational approach that integrated neuropeptide receptor-mediated signaling with electrophysiology. We simulated a population of neurons in which expression levels of a neuropeptide receptor and multiple ion channels were simultaneously varied within a physiological range. We analyzed the effects of variation on the electrophysiological response to a neuropeptide stimulus. Our results revealed distinct response patterns associated with low versus high receptor levels. Neurons with low receptor levels showed increased excitability and neurons with high receptor levels showed reduced excitability. These response patterns were separated by a narrow receptor level range forming a separatrix. The position of this separatrix was dependent on the expression levels of multiple ion channels. To assess the relative contributions of receptor and ion channel levels to the response profiles, we categorized the responses into six phenotypes based on response kinetics and magnitude. We applied several multivariate statistical approaches and found that receptor and channel expression levels influence the neuromodulation response phenotype through a complex though systematic mapping. Our analyses extended our understanding of how cellular responses to neuromodulation vary as a function of molecular expression. Our study showed that receptor expression and biophysical state interact with distinct relative contributions to neuronal excitability.
Keywords: Neuromodulation, Biophysics, Neurophysiology, Dynamical System
1 Introduction
Neuromodulation is critical for functions of neural systems in both health and disease. Hence, the physiological and behavioral implications of neuromodulation have been intensively studied in both experimental and computational investigations [1–5]. Peptide modulators operate by triggering intracellular signaling cascades involving enzymatic reactions and calcium mobilization. This signaling results in tuning of ion channel properties [3] and feedback regulation of functional membrane receptor levels [6]. It has recently been shown that anatomically defined neurons exhibiting specific electrophysiological phenotypes have remarkable molecular heterogeneity in the expression levels and properties of ion channels [7]. G-protein coupled receptor (GPCR) expression also varies substantially in defined cell types [8]. However, few studies have addressed the question of how variability in GPCR levels and excitability properties influences the effects of neuromodulation [9]. The aim of this work was to investigate the role of variability in molecular expression levels – reflecting phenotypic diversity and genetic heterogeneity – in determining the electrophysiological response to neuropeptide-mediated GPCR stimulation.
The peptide Angtiotensin-II (AngII) regulates autonomic nervous system activity via its effects within the brainstem [10–14]. Binding of AngII to the G-protein coupled type-1 Angiotensin Receptor (AT1R) in brainstem autonomic nuclei influences the inotropic and chronotropic drive of the heart [15, 16]. Aberrations of AngII signaling in the brainstem has been implicated in the pathology underlying neurogenic hypertension [17–19]. Thus, deciphering the mechanisms of AngII-mediated regulation of neuronal behavior is critical to our understanding of cardiovascular homeostasis and diseases thereof.
The electrophysiological response to neuromodulators such as AngII jointly depend on the biophysical state of the neuron, characterized by the balances of ionic conductance expression levels, as well as the activation of GPCR signaling. Expression levels of both ion channels and GPCRs are highly regulated. Functional expression levels of GPCRs at the membrane surface can be modulated at timescales from seconds to days, due to post-translational modifications, endocytosis, and transcriptional regulation [6, 20]. Ion channels are regulated on short time scales by post-translational modifications following the activation of GPCR signaling, and on longer time scales by trafficking and transcriptional regulation [21, 3]. Functional states and expression levels of receptors and ion channels are dynamically regulated and subject to modification under chronic disease conditions [22–24]. However, the relative contributions of neuromodulator receptors and intrinsic membrane ion channels to neuromodulation response phenotypes have not been elucidated.
While expression levels of both neurotransmitter receptors and membrane ion channels have been shown to vary substantially at the single neuron level [25], disparate molecular configurations can generate identical physiological phenotypes [26, 7]. Such results are consistent with molecular degeneracy in neural networks [27–30], often mediated by compensatory mechanisms involving ion channel expression correlations [31]. For instance, using a mathematical model of synaptic plasticity it was shown that multiple ion channel configurations support identical synaptic plasticity profiles [32]. In vertebrate neurons, it was shown that neuromodulator receptor stimulation evokes consistent response phenotypes across a population of neurons with varied ion channel expression configurations [33]. However, some cells departed from the average population response such that neuromodulation evoked an opposing effect on neuronal excitability relative to the mean response. Further, in vivo data from mammalian species have shown variable physiological responses to AT1R stimulation [34]. Thus, it is currently unclear if and how variability in GPCR and ion channel expression results in bidirectional responses to neuromodulation.
To examine the mechanistic basis of a physiological phenotype and assess its mapping to molecular variables, two distinct through complementary approaches exist: forward and inverse problem solving [35]. In biophysics, the forward approach entails manipulating ion channel function and assessing the effects on cellular behavior [36]. In contrast, the inverse approach involves characterizing the properties of ion channel populations that underlie cellular phenotypes of interest through reverse engineering [37, 38]. Both approaches address the question of how an electrophysiological phenotype is determined by ion channels and their properties [35]. The computational implementations of forward and inverse approaches are analogous to experimental approaches in systems genetics [39]. For example, the contributions of particular ion channels to neuronal membrane properties can be assessed through simulated channel knockouts in Hodgkin-Huxley models [40]. Complementary inverse approaches have been applied through the global analysis of how electrophysiological parameters constrain Hodgkin-Huxley models to exhibit specific electrophysiological properties [41, 40].
We employed a multi-scale computational modeling approach to study the neuromodulation of brainstem neurons using both forward and inverse approaches. Our investigations examined neuromodulator-mediated effects on excitability in populations of simulated neurons exhibiting phenotypic variability. We simulated the effects of molecular variability on neuromodulation in the context of AngII-mediated regulation of excitability in brainstem autonomic neurons. Our model integrated the activation of AT1R, downstream regulation of Ca2+ homeostasis and kinase activation, and subsequent effects on electrophysiological excitability [42] based on previous work [43–46]. This approach facilitated the systematic variation of neuronal phenotype – characterized by functional expression levels of AT1R and six ion channels – in a manner which would be impractical experimentally. Our results showed that AT1R and conductance levels distinctively control AngII–response directionality.
2 Methods
Dynamic neuromodulation-mediated biochemical signaling model
Our biochemical signaling model captures the transduction of AngII-AT1R binding by enzyme-mediated phospholipid metabolism, Ca2+ regulation, and protein kinase activation [42]. This model is based on a previously published model of neuronal Ca2+ signaling induced by GPCR binding [43]. However, our model integrates biochemical signaling dynamics with a model of cardiorespiratory neuron electrophysiology [46]. Our signaling model is comprised of 13 signaling pathways that are collectively represented by 164 ordinary differential equations (code to implement the basic model is available through modelDB [47], http://senselab.med.yale.edu/ModelDB, accession number: 156830). The model simulates phospholipase C activation phosphoinositide (IP) hydrolysis, IP3-mediated Ca2+ release from the endoplasmic reticulum, and Ca2+-mediated activation of PKC and CaMKII. Details of the biochemical reactions included in our model are available at the Database of Quantitative Cellular Signaling (http://doqcs.ncbs.res.in, accession number: 23). Documentation on the modeling and parameter values of the 13 pathways are in Supplementary Tables S1,2,4 of [42].
Computational modeling of membrane electrophysiology
We employed our computational model of integrated AngII/AT1R signaling in rat brainstem neurons. Model details are presented in [42]. In brief, our model represents a single compartment neuron with voltage-gated ion channels (Na, CaL, KDR, KA), a voltage-gated and calcium-activated channel (KAHP), and a voltage-independent leak channel. Membrane potential dynamics were modeled by the current balance equation:
| (1) |
| (2) |
where C is the membrane capacitance, V is the voltage across the membrane. For each ion channel i, gi is the conductance, Ei is the reversal potential, ḡi is the maximal conductance, mi is the activation variable, hi is the inactivation variable, and Mi and Hi are suitable parameters that are dependent on the kinetics of the channel activation/inactivation.
Hodgkin-Huxley equations were used to model the gating variables underlying the Na and CaL conductances as follows [48] :
| (3) |
| (4) |
where αi and βi are voltage-dependent rate constants describing the state transition rates. The time course for approaching the equilibrium value of the gating variable (m∞,i) is described by the time constant τi as follows:
| (5) |
| (6) |
and thus, we write equations 3 and 4 as follows:
| (7) |
| (8) |
Note that h∞,i and τm,i are modeled as in equations 5,6. While we used an Ohmic formulation to model the CaL current, which is a common convention [46], the GHK formulation may be more biophysically appropriate [49].
A modified Hodgkin-Huxley formalism was used to model the gating dynamics of the potassium conductances, where the steady-state gating variables were modeled using Boltzmann functions:
| (9) |
| (10) |
where V1/2 is the half-activation voltage and k activation (or inactivation) curve slope factor. A detailed description of the electrophysiological model and parameter values is available in Supplementary Table S3 of [42].
We modeled AngII-mediated AT1R stimulation as a bimolecular interaction between receptor and ligand characterized by mass action kinetics. We modeled AngII-induced reductions in gKDR, following channel phosphorylation by PKC and CaMKII, as follows:
| (11) |
| (12) |
where KU represents the fraction of un-phosphorylated channels, KP represents the fraction of channels with n sites phosphorylated, and KT is the total conserved number of channels. For this reaction, kp and kdp are the phosphorylation and de-phosphorylation rates, respectively. Kinases PKC and CaMKII were assumed to act independently on distinct phosphorylation sites. The parameter n = 4 was set assuming that each of four channel subunits were phosphorylated. In the complete model, the total population of phosphorylated channels is
| (13) |
and the effects of channel phosphorylation were simulated as follows:
| (14) |
Details of the system of equations representing our phosphorylation model appear in the Supplementary Materials. Our model was implemented in MATLAB (Natick, MA) using ode15s and code to run model simulations and perform key analyses from this paper is available through modelDB [47], http://senselab.med.yale.edu/ModelDB, accession number: 185300).
Synaptic stimulus and phasic neuromodulation
Brainstem cardiorespiratory neurons receive phasic barrages of synaptic input modulated by the sinus rhythm [50, 51]. We simulated this afferent input profile by applying a sinusoidal current [52] with superimposed synaptic noise [53]. We applied a sinusoidal stimulus with a frequency of 400 beats per minute (see equation 16), corresponding to the heart rate of the adult Sprague-Dawley rat [54]. The synaptic noise conductance gn was represented as follows [55, 53]:
| (15) |
where dt = 0.5 ms is the time step for updating the synaptic input, τn is the synaptic time constant, σn is a deviation term that scales the noise amplitude, and ξ is a normally distributed random variable random variable (mean=0, sd=1). The full synaptic noise model Isyn(t) was formulated as follows:
| (16) |
| (17) |
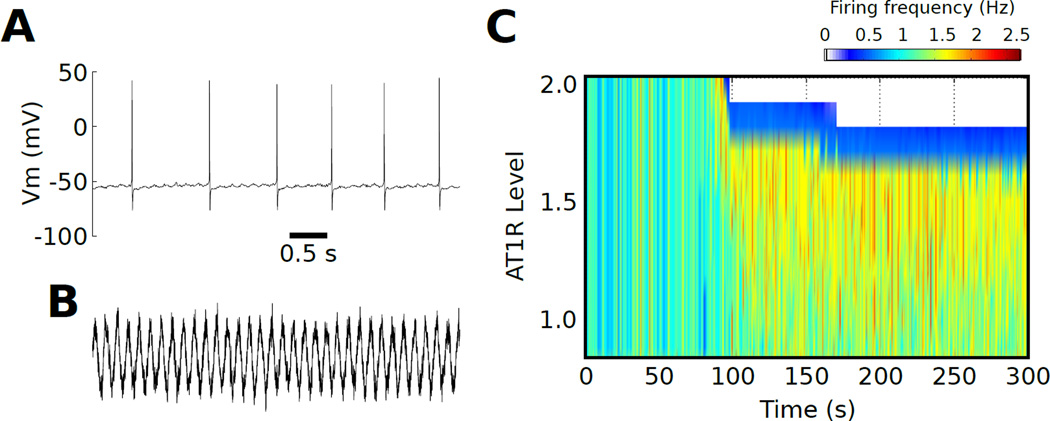
We set τn = 2.73 ms and En = −10 mV based on [53], and we optimized the oscillating current amplitude A and the noise scaling term σn to achieve firing rates of ~1 Hz (A=1.55×10−1, σn=1×10−4; Fig 2A,B). A phasic AngII stimulus was generated similarly according to equations 15–17 (A=100 nM, σn=1×10−3).
Fig. 2. Phasic input drives an AT1R-dependent firing rate bifurcation.
(A) Firing patterns consistent with physiological data occur with phasic synaptic input. (B) Temporal profile of the fluctuating synaptic stimulus (timescale as in (A)). (C) A firing rate separatrix is generated as a function of AT1R expression following phasic AngII stimuli.
Phenotype classification and cluster analysis
Based on visual inspection of our forward engineering simulation results, we developed a phenotype classification scheme based on firing rate properties including the baseline firing rate (pre-AngII), steady state firing rate (following prolonged AngII stimulation), the peak firing rate following AngII application, and the fractional change in firing rate. Details on this classification scheme are presented in the Results below.
To determine if the AngII response phenotypes could be related to expression of AT1R and peak channel conductance based differences between Euclidean expression state vectors, unsupervised hierarchical clustering was applied using the Euclidean distance metric. Expression levels of molecular species (x) were represented as Z scores:
| (18) |
where x̄ and σ̂x denote the empirical mean and standard deviation of x, respectively.
Global parameter variation analysis
Following previous computational studies of electrophysiological variability [56, 29], we globally varied maximal ionic conductances and AT1R receptor level. We varied these molecular species over a two-fold range (0.5×–2×) such that a multivariate uniform distribution of parameter values was generated (Supplementary Materials Fig S1). The two-fold variation range falls within the physiological range of variation for ion channel mRNA [57], the expression of which has been shown to correlate with corresponding channel peak conductance [58]. We generated a set of 10,000 parameters and selected parameter sets that gave physiological firing rates for brainstem cardiorespiratory neurons (>0.1 Hz, <5 Hz [59,60]) for further evaluation of the AngII response.
Regression analysis of firing rate properties
We implemented multivariate linear regression analyses based on previous studies that related ion channel expression to electrophysiological properties [56, 61]. Z-scores were used for both predictor and response variables. We split the data set into training (70%) and testing (30%) sets based on neuromodulation response phenotype (see Results). We first determined model complexity (linear, quadratic, or cubic) by applying 10-fold cross-validation on the training set. For all predictor variables, cubic fits were relatively optimal. For our model fits, we applied stepwise term inclusion/exclusion based on Bayesian information criteria using the Linear Model.stepwise function in MATLAB. Final model fits were evaluated using the testing data set, as described in the Results.
Random forest classification
To classify electrophysiologically defined neuromodulation response phenotypes, we applied a supervised, non-parametric, random forest (RF) classification approach. The RF algorithm assembles a population of classification trees (i.e., a “forest”) based on a set of bootstrap samples. Out of sample predictions are made by aggregation the sample predictions across the entire forest [62]. We randomly split the Z score data into training (70%) and testing (30%) sets based on neuromodulation response phenotype (see Results). Training was implemented with k-fold cross-validation (k = 10 with 10 repeats). Classifier performance was evaluated by standard metrics including accuracy, sensitivity, and specificity. Further analysis entailed depiction of how much each classification variable contributed to prediction error rate [63]. We implemented our RF analyses using the caret and random Forest packages developed in R [64,65,62]. Further details regarding the theory and implementation of RF analysis are in the Supplementary Materials.
Partial least squares regression
Partial least squares regression (PLSR) analysis employs the mathematical underpinnings of principal components analysis (PCA). The methods described here are based on previous explanations [66–68]. PCA is a data reduction technique in which high-dimensional data are projected onto a lower dimensional subspace that captures the majority of variance within the data. This type of analysis is often used for the purpose of data visualization [41]. If X is a data matrix with rows representing cell phenotypes and columns representing molecular expression levels, PCA is implemented by the following computations:
| (19) |
| (20) |
where eig(XTX) denotes a matrix with eigenvectors of the correlation matrix, organized according to decreasing eigenvalues. These are orthonormal vectors with numbers of elements corresponding to the number of molecular expression variables in the data set. Hence, P forms a new set of axes (know as loading vectors or loadings) onto which the data are projected to generate the scores T. In particular, the dimensionality of the loading matrix chosen such that the data are represented in fewer dimensions than the number of molecular variables. In many cases, three dimensions are sufficient to account for the majority of the variance in the data such that the residuals primarily contain noise. PLSR is accomplished by performing PCA on both the conductance data matrix X (predictor variables) and the firing rate property data matrix Y (response variables). The principal components representation of the firing rate matrix is as follows:
| (21) |
| (22) |
where Q and U denote the loadings and scores generated by the PCA of Y, respectively. As described in detail elsewhere [66, 68], PLSR relates Y to X by finding a rotation of the loading vector coordinate system P that maximizes the covariance between the X and Y scores, T and U, respectively (see equation 24). The X data can then be visualized as the projection onto the new coordinate system:
| (23) |
Tnew and Pnew were computed according to the optimization of the following objective function (J):
| (24) |
where cov(Unew, Tnew) is the covariance between Unew and Tnew. We implemented PLSR in R [64] using the pls package and the plsr function [69]. The PLSR model was generated using 10-fold cross-validation.
Results
GPCR expression variability partitions neuropeptide-induced firing rate phenotypes
Recent single neuron gene expression data showed variation in abundances of transcripts related to AngII signaling and membrane electrophysiology [25]. Such variation occurs over a 4–6 fold range [25, 7]. To test the hypothesis that variation in AT1R expression level modulates action potential firing rate responses to AngII, we varied the AT1R level from 0.5 to 2 times the reference model level (0.5× – 2×). We then stimulated the population of neuronal phenotypes with AngII and examined the effect of AT1R expression on excitability. For all receptor levels, our model neurons were tuned to fire at a physiological rate under baseline conditions (i.e., ~ 1.0 Hz) [42]. Our simulation results revealed that AngII application to phenotypes with low AngII receptor level yielded increased firing rate. In contrast, for relatively higher receptor expression levels, AngII elicited an opposing effect in which the stimulus suppressed action potential firing (Fig 1A). For a 100 nM AngII stimulus, neurons showed firing rate increases for AT1R levels up to ~ 1.3×. At AT1R ~ 1.5× a transient firing rate increase was followed by a sustained excitability decrease (Fig 1A).
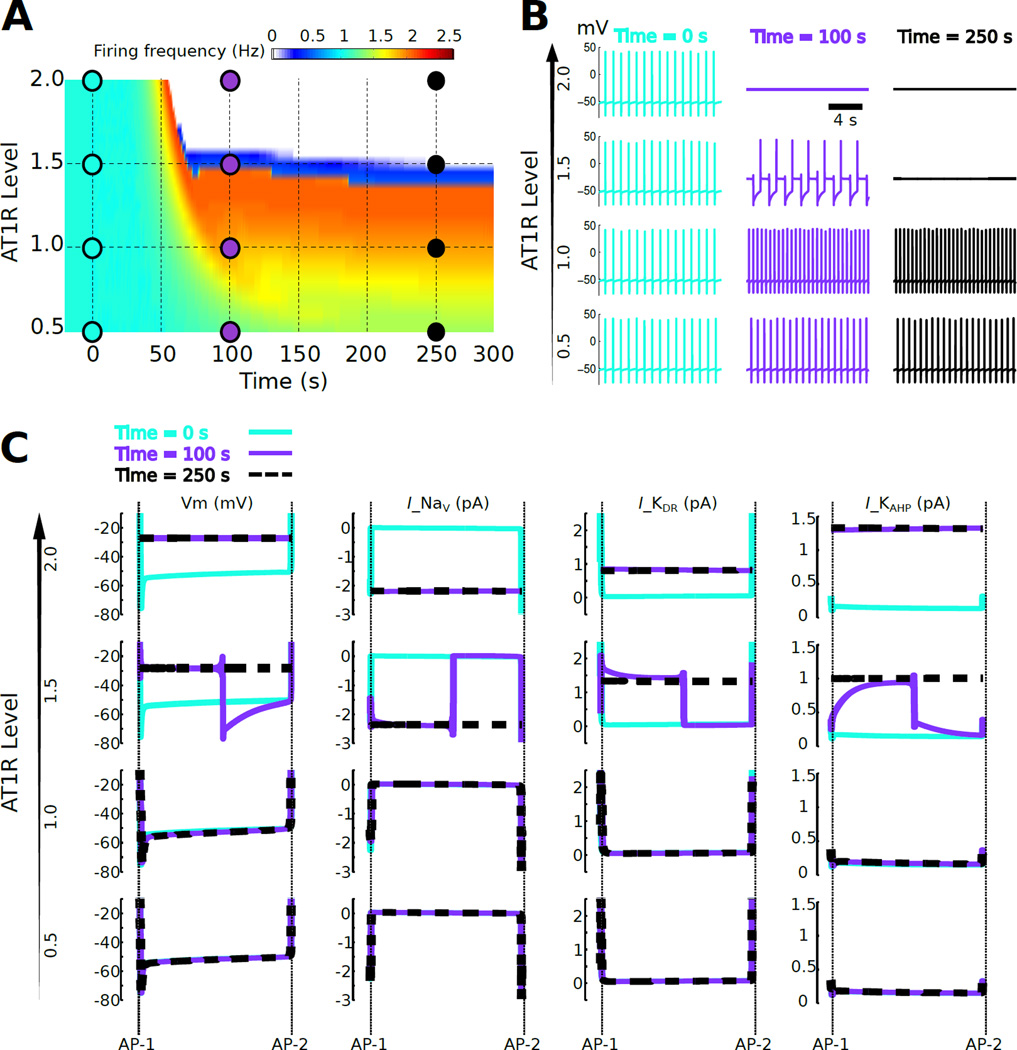
Fig. 1. Bifurcation of firing rate response to AngII as a function of AT1R level.
(A) Firing rate response to continuous 100 nM AngII application starting at time = 0 as a function of time for a population of cells exhibiting variation in AT1R level. The AT1R level was varied from 0.5 to 2 times the reference level. A narrow region of AT1R levels (~ 1.5×, blue) separates firing rate increases (<1.5×) from firing rate cessation (>1.5×). This narrow region of AT1R levels is referred to as a separatrix. (B) Membrane potentials are shown at three time points (t = 0, 100, and 250 sec) for four AT1R levels (0.5×, 1×, 1.5×, and 2×). (C) Inter-AP potentials and currents corresponding to the times and AT1R levels from panel B. Vm denotes membrane potential and Ix denotes the ionic current due to channel x. Only currents that showed detectable changes following AngII application are shown: INa, IKDR, and IKAHP. The data indicate that the separatrix occurs because increased AT1R signaling results in depolarization resulting from re-balancing of Na+ and K+ currents, with consequent abrogation of AP firing.
When AT1R levels were increased above 1.5×, there was a cessation of firing. These two divergent response patterns, increased versus decreased excitability, were separated by a narrow receptor level range forming a discrete boundary (i.e., a separatrix). Analysis of the membrane potential at times t = 0 s (preceding the response), t = 100 s (transient response), and t = 250 s (steady-state response) showed that cessation of firing at 1.5× and 2× AT1R levels corresponds to depolarized membrane potentials of ~−30 mV (Fig 1B). These results suggest that AngII can produce either an increase or decrease in firing rate in an AT1R expression-dependent manner, thereby yielding a separatrix distinguishing divergent neuromodulator response profiles.
As shown previously, firing rate changes following neuromodulation occur as a result of adjustments in membrane ion channel currents during the intervals between action potential spikes (inter-spike intervals) [42]. To elucidate the ionic contributions to the response patterns distinguished by the separatrix, we analyzed channel currents during inter-spike intervals (Fig 1C). This analysis suggested that AngII-mediated membrane potential depolarization prevented action potential firing. At AT1R = 2×, elevated depolarizing Na+ current was balanced by elevations in hyperpolarizing KDR and KAHP currents (compare traces at t = 100 s versus t = 250 s). The increase in Na+ channel conductance was implicated in depolarization–mediated suppression of excitability. This result agrees with in vitro data from patch-clamp recordings showing suppressed firing associated with K+ current reduction, along with depolarized membrane potentials [70, 71]. This indicates depolarization–mediated sodium channel inactivation repressed the cell’s ability to fire Na+ channel–dependent action potentials [72].
To examine whether the AT1R dependent separatrix could be observed in response to physiologically relevant synaptic stimuli, we applied randomized synaptic input [53], tuned to a sinusoidal current used to mimic the phasic baroreceptor input received by brainstem cardiorespiratory neurons [52], and measured the neuronal response to a phasic 100 nM AngII stimulus (Fig 2). Our results showed that the AT1R-dependent separatrix occurred for synaptic stimuli (Fig 2C). We observed that the cessation of firing, in response to AngII, extended up to AT1R = 3.5× (data not shown). Analysis of firing rate response to phasic AngII stimuli as a function of AT1R expression level revealed a separatrix that was similar to that observed for the tonic AngII stimulus (Fig. 1A). These data suggest that AT1R-dependent separatrix is not stimulus-specific and the separatrix is a physiologically plausible phenomena that is not selective to square step AngII stimuli.
Forward engineering of biophysical variability yields divergent neuropeptide response phenotypes
To analyze the effects of biophysical variability on firing rate responses to AngII, we explored pairwise variations in peak channel conductance levels. Ion channel peak conductance levels have been shown to correlate with channel gene expression levels, even in single neurons [58, 73]. We varied pairs of depolarizing (Na and CaL) and hyperpolarizing (KDR, KAHP, and KA) channel conductances. We modified one depolarizing and one hyperpolarizing conductance to generate nine distinct biophysical state phenotypes. Peak conductance variations were 0.5 to 1.4 times baseline values (0.5× – 1.4×). We generated nine biophysical phenotypes that were grouped into three sets based on baseline firing rate (Fig 3A–C). Our simulations of 100 nM AngII-induced firing rate responses showed that the nine biophysical phenotypes rendered firing rates within the physiological range observed for cultured brainstem neurons in vitro (~ 0.3 – 3.0 Hz) [59].
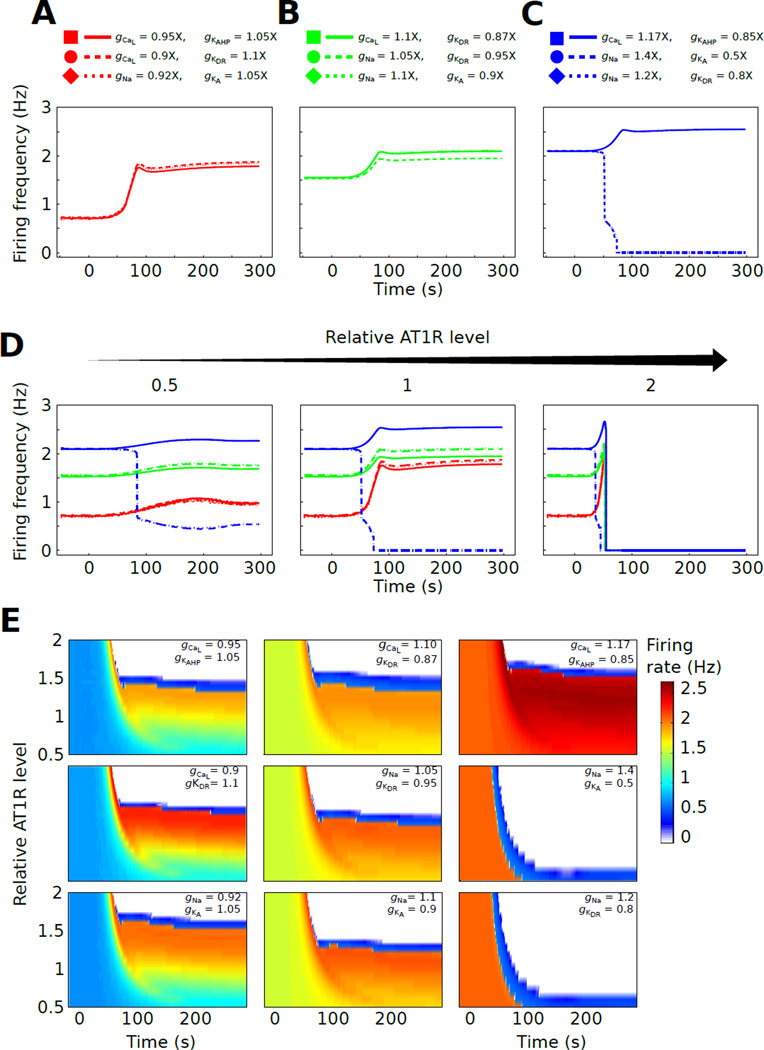
Fig. 3. Biophysical state tunes the AT1R-dependent firing rate separatrix.
(A–C) Nine phenotypes defined by sets of conductance ratios (depolarizing:hyperpolarizing) were generated. Three conductance ratio sets gave baseline firing rates of 0.6 Hz (A), three sets gave baseline rates of 1.5 Hz (B), and three sets gave baselines of 2.1 Hz (C). All nine phenotypes were stimulated by 100 nM AngII at t = 0 and the firing rate responses are shown. (D) Each phenotype from panel A was simulated with three AT1R receptor levels: half the receptor concentration of the reference model from figure 1 (0.5× AT1R, left), identical AT1R concentration to the reference model (1× AT1R, middle), and double the reference AT1R concentration (2× AT1R, right). Annotation for the traces is in panel A. (E) The nine biophysical phenotypes were simulated with 24 AT1R levels (0.5× –2×). Firing frequency responses to 100 nM AngII in heatmap representations are presented with one map for each biophysical state. This analysis shows that receptor-dependent separatrix was tunable by biophysical state as determined by conductance balance.
The AngII-mediated firing rate changes were baseline firing rate-dependent. Neurons with lower basal firing showed relatively larger and faster increases in firing following AngII application (Fig 3A). For phenotypes with similar baseline firing rates, different conductance balances led to different AngII-mediated responses. For phenotypes with 1.5 Hz baseline firing (Fig 3B), one particular cell (gCaL = 1.1×, gKDR = 0.87×) showed less responsiveness to AngII relative to the others. Phenotypes with 2.1 Hz baseline firing showed disparate AngII-mediated responses in which two of the variants exhibited nearly identical firing decreases followed by cessation of firing, while the third showed a firing rate increase (gCaL = 1.17×, gKAHP = 0.85×, Fig 3C). These results suggest that molecular phenotypes defined by biophysical state can also distinguish increased versus decreased excitability responses to AngII.
We next investigated whether interactions between biophysical state and AT1R level influence the aforementioned separatrix. We generated three AT1R level variants (0.5×, 1×, and 2×) for each of the nine biophysical phenotypes. Simulations of AngII-mediated responses in these variants showed that AT1R and conductance levels jointly influenced the firing rate separatrix (Fig 3D). High AT1R level (2×) uniformly produced decreased excitability. At lower AT1R level (0.5× – 1.5×), channel conductance balances could tune the response properties in diverse ways (Fig 3D). At these AT1R levels, increases in excitability were greater for phenotypes with relatively low initial firing rates.
After independently examining the roles of variability in AT1R levels and biophysical state, we investigated how an expanded range of simultaneous variations could impact neuromodulator responsiveness. We varied the AT1R level within a two fold range (0.5× – 2×) for all nine biophysical phenotypes. A total of 240 model variants were used for our forward engineering analyses. For each biophysical phenotype, the AT1R level separatrix was observed (Fig 3E). These simulation results showed that the AT1R level at which the separatrix occurred was sensitive to the biophysical state. Our results indicate that peak channel conductance level and AT1R levels jointly tune the separatrix position. For instance, the AngII induced firing rate profile for one phenotype with an initial firing rate of 2 Hz (gCaL = 1.17×, gKAHP = 0.85×) exhibited a firing rate separatrix at ~ 1.5× AT1R (Fig 3E, top panel of right column), while the other phenotypes with the same initial firing rate showed separatrices around 0.5× AT1R (right column). Likewise, within other groups of phenotypes with similar initial firing rates, the separatrix position varied with biophysical phenotype.
Neuromodulator response profiles reveal phenotype classes based on response amplitude and kinetics
Our next goal was to determine the relative contributions of AT1R level and ionic conductance to AngII-dependent firing responses. We categorized firing rate waveforms depicting the 100 nM AngII response of 240 neurons with varied conductance balances and AT1R levels into six neuromodulation response phenotypes (Fig 4A):
increased firing with adaptation
increased firing without adaptation
biphasic firing with a large transient increase
biphasic firing with a small transient increase
monotonic firing decrease
no change in firing rate
Classes 1–5 showed >10% changes in firing rate, while class 6 was defined by <10% firing rate change. We applied the following criteria for this categorization: (1) steady-state final rate at 285 s <90% of the peak rate, (2) steady-state final rate at 285 s >90% of the peak rate, (3) bi-phasic responses with increases followed by a decrease in firing rate, such that the magnitude of the increase was greater than that of the decrease relative to baseline, (4) bi-phasic responses with increases lower in magnitude than those of decreases relative to baseline, and (5) responses with monotonic decreases in firing rate. For this forward analysis, the sixth class (no change in firing rate) was observed in only 4/240 cases (<2%) and we do not further discuss this phenotype in our forward analysis. Note that phenotype 6 was highly represented in our reverse analysis (see below). We applied unsupervised hierarchical clustering to facilitate the visualization of the firing rate profiles for each neuromodulation response phenotype (1–5). Our results showed a spectrum of excitability responses within each phenotype (Fig 4A). Phenotypes 1 and 2 were below the separatrix whereas phenotypes 3, 4, and 5 contained profiles that were either on or above the separatrix.
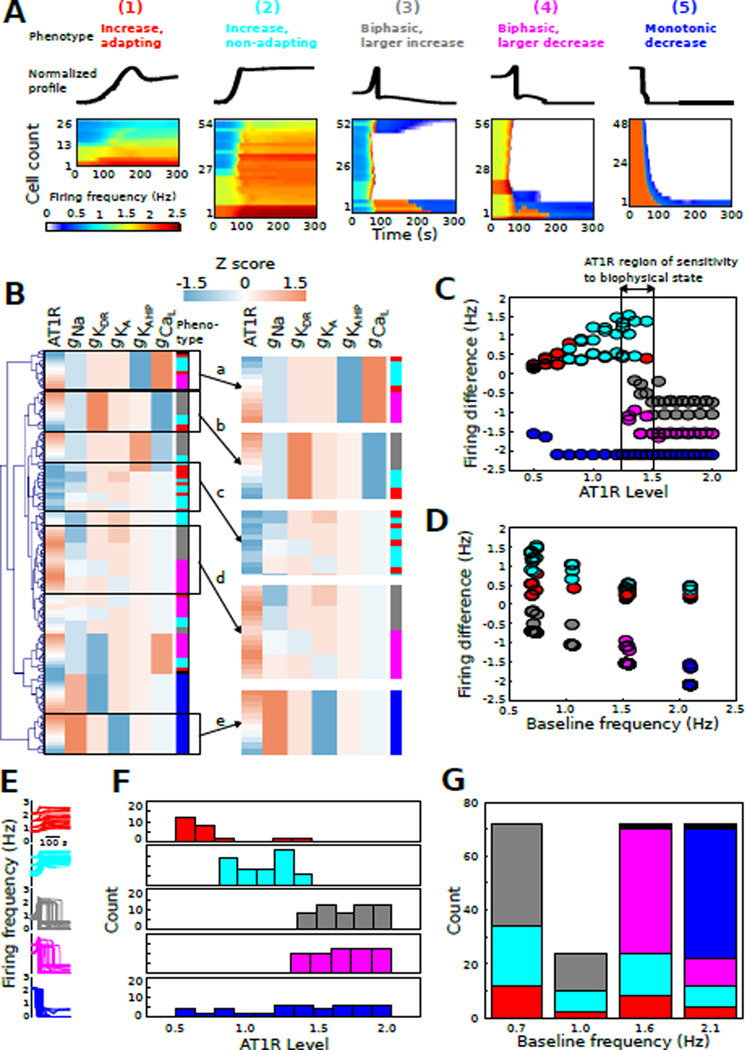
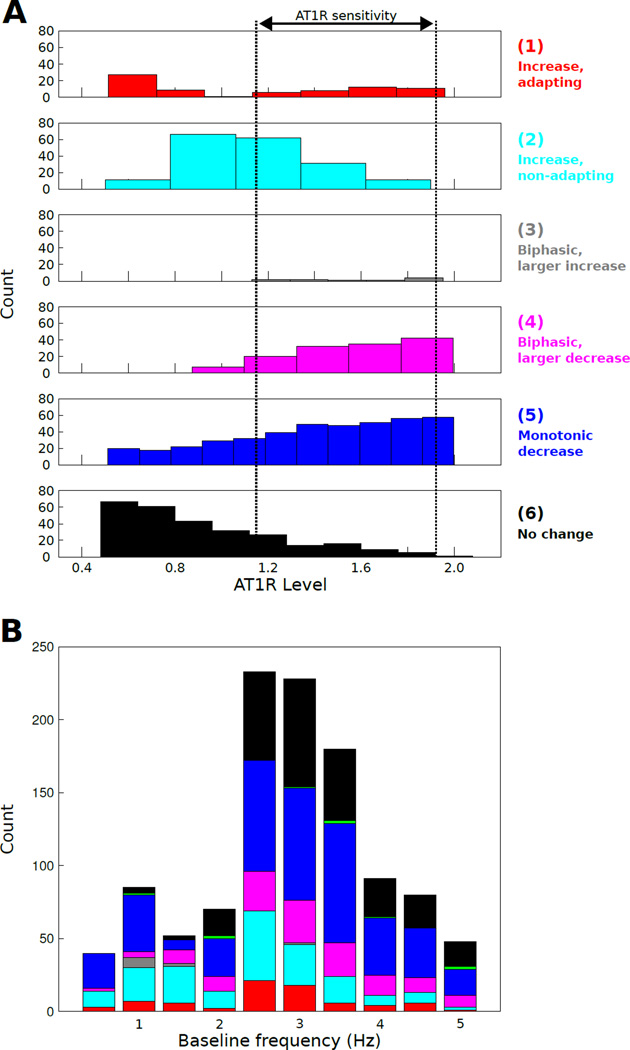
Fig. 4. AngII response phenotypes revealed by classification of neuronal responses.
(A) AngII response profiles (N = 240) were grouped into the following phenotypes based on electrophysiological criteria: (1) increased firing with adaptation, (2) increased firing without adaptation, (3) biphasic firing with a large transient increase, (4) biphasic firing with a small transient increase, (5) monotonic firing decrease, and (6) no change in firing rate. Normalized waveforms are shown for phenotypes 1–5. All voltage time series profiles were organized by hierarchical clustering for visualization. The resulting heatmaps show firing frequency plotted as a function of time (AngII applied starting at t = 0). (B) Molecular expression Z scores for AT1R and channels were grouped by hierarchical clustering and annotated according to phenotype as described in panel A. A set of subclusters is highlighted in the right panel: (a,b) some biophysical states show phenotype-dependence on AT1R level, (c) set of biophysical states associated with low AT1R expression and phenotypes 1 and 2, (d) set of biophysical states associated with high AT1R expression and phenotypes 3 and 4, (e) biophysical state associated with phenotype 5 irrespective of AT1R level. (C) Firing frequency difference (final – initial) as a function of AT1R level for all phenotypes. This analysis shows a range of AT1R level with all phenotypes, indicating an AT1R expression range associated with AngII response sensitivity to biophysical state. (D) Firing frequency difference as a function of baseline firing frequency, representative of biophysical state, for all phenotypes. (E) Firing rate temporal profiles colored based on phenotype class. (F) Cell counts as a function of AT1R level for each AngII response class. (G) Counts of neuromodulation response phenotypes at each baseline firing rate. Note that phenotype 6 is represented by black in this figure.
To visualize potential influences of AT1R and channel expression on the neuromodulation response phenotype, we performed hierarchical clustering of the Z scores for AT1R level and peak conductance (Fig 4B). The application of such clustering techniques has shown utility in facilitating the visual assessment of structure within complex data sets [61]. We contrast the use of clustering with the application of multivariate analytic approaches presented below in our reverse engineering analysis. A number of informative clusters emerged from our analysis (Fig 4B, right). (a) One biophysical state was associated with phenotypes 1, 2, and 4 such that AT1R level determined phenotype. (b) One biophysical state was associated with phenotypes 1, 2, and 3 such that AT1R level determined phenotype. (c) A set of biophysical states, with similar low AT1R levels, was associated with phenotypes 1 and 2. (d) A set of biophysical states, with similar high AT1R levels, was associated with phenotypes 3 and 4. (e) One biophysical state was associated with phenotype 5 irrespective of AT1R level. This analysis indicates that for some molecular cell states, neuromodulation response phenotype is influenced primarily by AT1R level (Fig 4Ba,b), whereas for other cell states the phenotype is influenced primarily by conductance balance (Fig 4Bc,d). For a third biophysical state, phenotype is independent of AT1R level (Fig 4Be). Thus, the phenotypes appear to be shaped by a non-linear interdependence between AT1R level and biophysical state.
We further assessed the relation between AT1R level and neuromodulation response phenotype by analyzing the firing frequency difference (final firing rate at 290 s post initiation of AngII stimulation minus baseline firing rate) as a function of AT1R level for all phenotypes (Fig 4C). The graphical analysis revealed that phenotypes 1 and 2 were observed exclusively for AT1R levels below ~ 1.5×. Phenotypes 3 and 4 were observed exclusively for AT1R levels above ~ 1.2×. In contrast, phenotype 5 was independent of AT1R level, as indicated by cluster analysis. Interestingly, there was a range of AT1R levels in which all phenotypes were observed (~ 1.2 – 1.5×, Fig 4C). To further elucidate the contributions of biophysical state to phenotype, we analyzed firing frequency difference as a function of baseline firing rate, an indicator of biophysical state (Fig 4D). In contrast to the effects of AT1R level, biophysical state did not appear to prominently influence phenotypes 1 and 2. However, phenotype 3 was only observed for baseline firing below 1.4 Hz, whereas phenotype 4 was only observed above 1.4 Hz. Phenotype 5 was only observed at the highest basal firing rate of ~ 2.1 Hz. These results suggest that AT1R level and biophysical state exert distinct influences on phenotype.
Despite the complexity of the interactions amongst receptors and channels, the data suggest an underlying molecular structure to our neuromodulation response phenotype classification. To highlight this structure, we analyzed counts of each phenotype with respect to AT1R level (Fig 4F). These data showed that increases in firing rate were associated with low AT1R levels (phenotypes 1 and 2). Profiles with increases followed by decreases in firing were associated with relatively high AT1R levels (phenotypes 3 and 4). Monotonic firing decreases were apparently independent of AT1R level (phenotype 5, Fig 4F). To examine the contributions of biophysical state to the classification of AngII-mediated response profiles, we analyzed the relationship between neuromodulation response phenotype and baseline firing frequency (Fig 4G). Phenotypes 1 and 2, which were observed at low AT1R levels, were represented across basal firing rates. In contrast, phenotype 3 was observed at lower firing rates while phenotype 4 was observed at higher rates, even though these phenotypes were nearly identical in terms of their relation to AT1R levels. Phenotype 5, which was unrelated to AT1R level, was observed only in phenotypes with the highest basal firing rate.
Reverse engineering of biophysical variability reveals a structured parametric basis for neuromodulation response phenotype
We next tested the extent to which the results of our forward analysis could generalize to a randomly sampled spectrum of physiological phenotypes. We simulated the neuronal firing rate for 10,000 randomly sampled parameter sets. All parameters were varied independently to generate multivariate uniform distribution (Supplementary Fig S1). Out of the 10,000 parameter sets, 1,107 parameter sets resulted in physiological firing rates (>0.1, <5 Hz) [59, 60]. We then simulated the response to 100 nM AngII in the 1,107 variants and classified the neuromodulation response phenotype. We found that 99.2% of the neuromodulation responses could be classified as described above (neuromodulation response phenotypes 1–6). The remaining neuromodulation responses (9/1107) were all found to belong to a ‘transient response’ phenotype. This transient response phenotype was characterized by a transient firing rate change following AngII application, followed by a relaxation to the baseline firing rate. This phenotype will not be discussed further with the exception that it will be represented by green in the remaining figures. In contrast to our forward engineering analysis, neuromodulation response phenotype 3 was relatively underrepresented (10/1107). This result highlights the fact that forward engineering analyses can identify rare phenotypes.
Consistent with our forward analysis, we observed a region of AT1R levels for which the spectrum of phenotypes could be observed (Fig 5A, Supplementary Fig S2A; compare with Fig 4C,F). Interestingly, this AT1R range was relatively protracted for the reverse analysis. Furthermore, similar to our forward analysis, we found that neuromodulation response phenotype 3 was predominantly expressed for relatively low baseline firing rates compared to phenotypes 4 and 5 (Fig 5B, Supplementary Fig S2B). These data show that phenotype distributions differ substantially with respect to AT1R level as well as baseline firing rate. We revisit these distributions below the the context of further analyses presented below (Fig 9).
Fig. 5. Unbiased sampling supports forward engineering results.
(A) The AT1R histogram replicates phenotype-specific AT1R distributions with a region of neuromodulation response sensitivity to biophysical state. (B) Neuromodulation response phenotype distributions as a function of baseline firing rate.
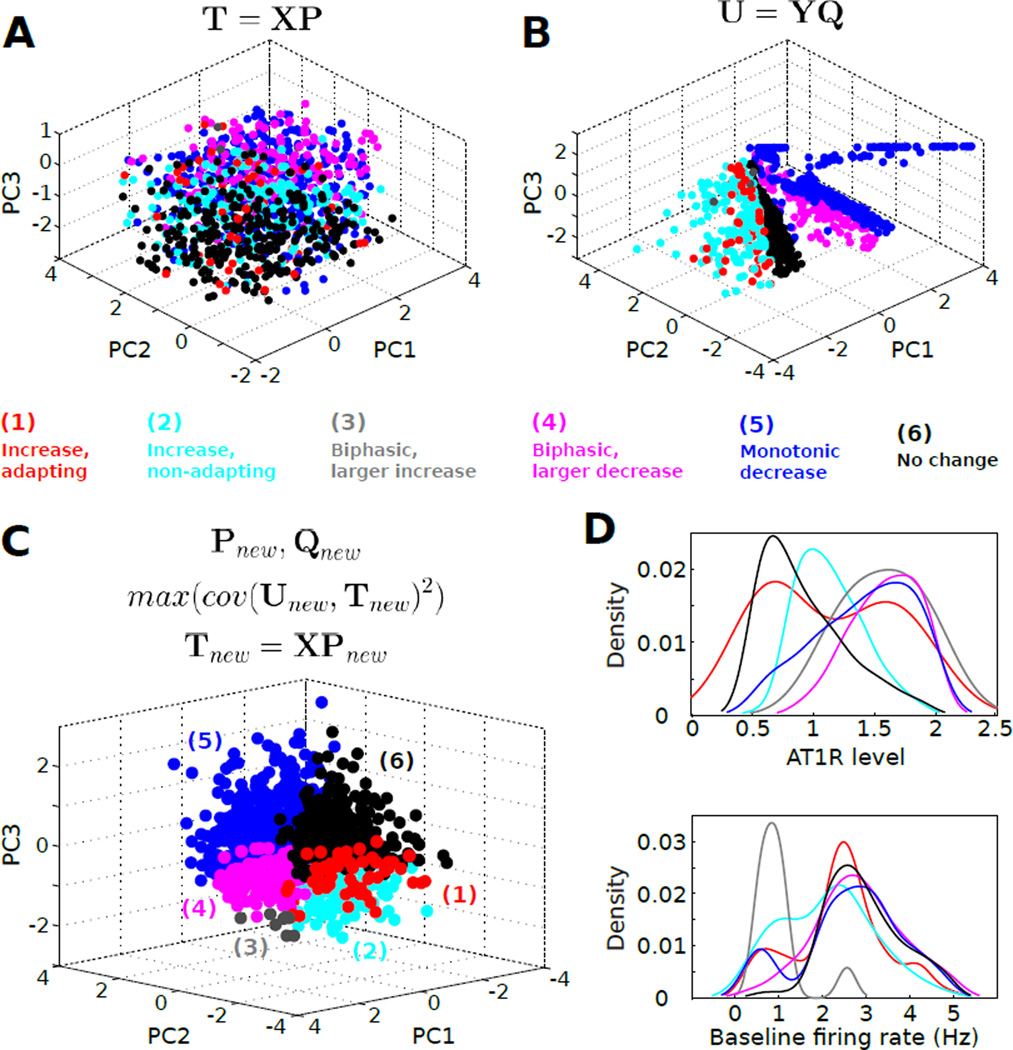
Fig. 9. Molecular state space contains phenotype-specific sub-manifolds.
(A) Principal component analysis (PCA) scores for the molecular expression data set. Colored data points correspond to the respective sample phenotypes (see panel C). (B) PCA scores for the firing rate property data set. (C) Principal component scores generated by the application of partial least squares regression (PLSR) to the molecular expression and firing rate property data sets shown in panels A,B. (D) Kernel density histograms, constructed from the data in Fig 5, depict the complex relations between AT1R expression and phenotype, and between baseline firing rate and phenotype. Note that baseline firing rate is an indicator of the overall conductance expression state of the neuron.
Given that a plethora of conductance states underlie similar electrophysiological behavior, it is possible that pairwise correlations, higher-order interactions, or both, regulate electrophysiological homeostasis [31]. To determine which of these possibilities may be the case, we assessed all pairwise channel expression relationships across the entire population of 1,107 physiological models (Supplementary Fig S3), and for each neuromodulation response phenotype (Supplementary Figs S4–9). We found that gKDR was positively correlated with gNa for most phenotypes (Pearson correlation >0.4, Bonferroni corrected p-value <0.05; Fig 6A). However, the position of respective data cloud in gKDR–gNa expression space differed with respect to phenotype. For instance, phenotypes 1, 2, and 6 generally showed higher gKDR expression relative to gNa expression, as compared to phenotypes 4 and 5 (Fig 6A). These data suggest that the mechanistic basis of phenotype determination, in part, involves a ratio of depolarizing to hyperpolarizing drive. Phenotypes with relatively less repolarization reserve [74] showed less capacity for firing rate augmentation.
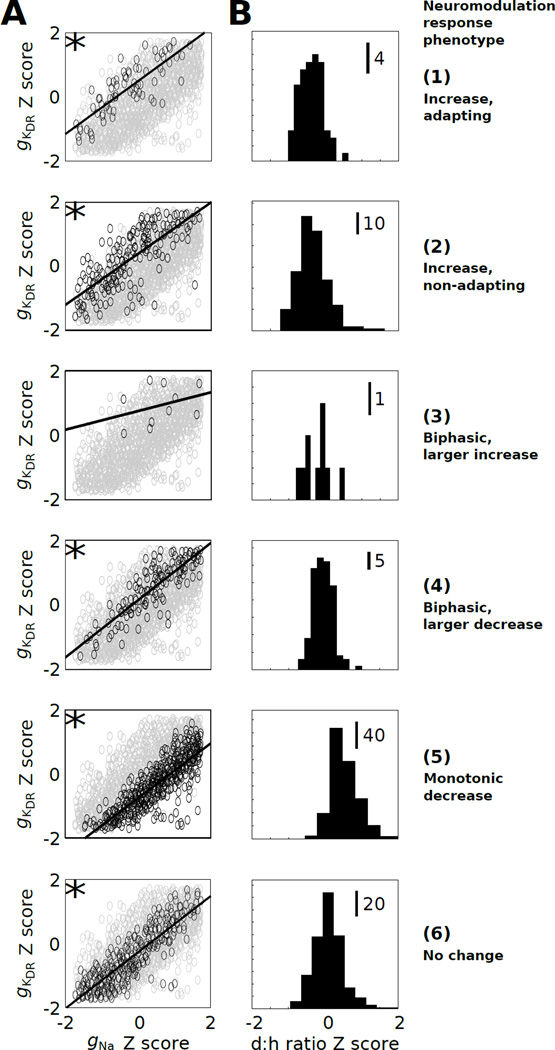
Fig. 6. The balance of depolarizing versus hyperpolarizing channel level influences neuromodulation response phenotype.
(A) Pairwise expression Z-score relationships between gKDR and gNa. Solid lines corresponding to linear regression relations. The asterices (*) indicate absolute correlations >0.4 with p-values <0.05 (Bonferroni corrected).(B) Histograms illustrate d:h ratio Z-score distributions for phenotypes 1–6.
Overall, distinct phenotypes partitioned separate portions of the physiological expression space, based on single conductance histograms analyzed for each phenotype, consistent with defined relationships between conductance state and neuromodulation response phenotype. We next addressed whether the ratio of summed depolarizing (gNa, gCaL) to summed hyperpolarizing (gKDR, gKA, gKAHP) conductance expression levels predicts neuromodulation response phenotype. We evaluated the relationship between this ratio (d:h ratio) and each conductance expression level, and we analyzed d:h ratio histograms for each phenotype (Fig 6B, Supplementary Fig S10). Consistent with our correlation analysis, the d:h ratio showed phenotype specificity, suggesting that the balance between depolarizing and hyperpolarizing drive influences the neuromodulation response (see below).
Statistical and functional analyses of channel effects on firing rate properties
To evaluate the impact of channel expression states on the firing rate properties used to classify the neuromodulation response phenotypes, we applied a multivariate linear regression approach [56, 61]. We determined that cubic fits with interactions exceeded the quality of linear, quadratic, and quadratic + interaction fits, based on cross-validation. However, even cubic fits failed to provide convincing predictions of our data. While channel expression could predict baseline firing rate (adjusted R2 = 0.95 for the testing data set), AngII stimulation-dependent firing rate response properties were not well predicted by cubic models (adjusted R2 < 0.7 for the testing data set, Supplementary Table 1). However, the accurate fit of baseline firing rate suggests that this metric is representative of the overall conductance expression state of the neuron. (Note that for baseline fit, the stepwise algorithm removed all regression coefficients related to AT1R, as should be the case given that AngII does not influence the baseline rate in our simulations.)
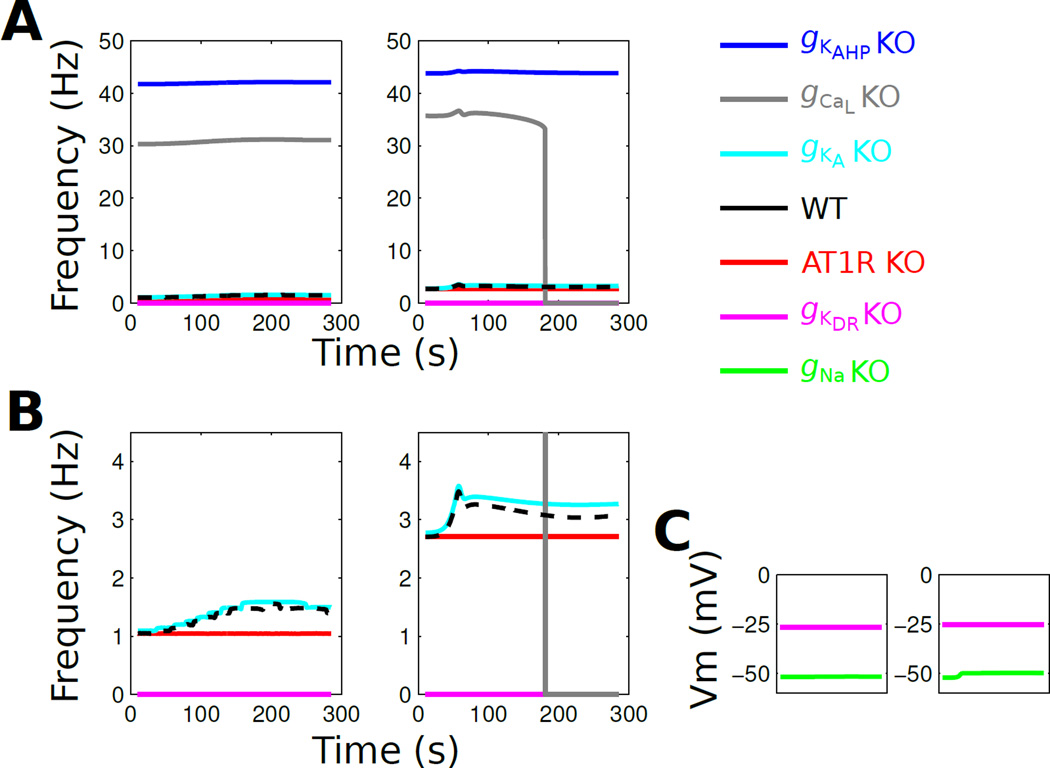
Our pairwise correlation analysis suggested that pairwise channel degeneracy may be able to induce compensation if one channel is occluded. To examine the effects of functional channel occlusion on the neuromodulation response, we studied the effects on AngII on ‘virtual knockout models’ (VKMs) in which channels were individually removed from the model by setting their peak conductance to zero [40].We applied the virtual knockout to AT1R, gNa, gKDR, gKA, gKAHP, and gCaL in multiple instances (6–10) of each neuromodulation response phenotype (Supplementary Figs S11–16). Overall, we found consistent effects of the VKM for an individual channel across phenotypes. For instance, VKMs for gKAHP and gCaL resulted in augmented firing rates and either no change or cessation of firing in response to AngII (Fig 7A). VKMs for gKA led to mild effects on the baseline firing rate and AngII-mediated response (Fig 7B). Whereas VKMs for both gNa and gKDR elicited the cessation of firing, the mechanisms were distinct (Fig 7C). The VK of gNa stabilized the membrane at a subthreshold potential whereas the VK of gKDR stabilized the membrane at a suprathreshold potential (Fig 7C). The latter effect is consistent with that observed for phenotypes above the separatrix discussed previously (Fig 1). These results suggest that the compensatory mechanisms associated with pairwise, and possibly higher order, channel expression correlations are insufficient to enforce phenotypic homeostasis if a channel is completely occluded, with the exception of gKA.
Fig. 7. Virtual knockouts show that molecular expression constraints are insufficient to compensate for complete channel occlusion.
Two representative VKMs from neuromodulation response phenotype 1 are shown. (A) Firing rate profiles in response to 100 nM AngII (continuous administration starting at t=0). The left and right panels correspond to the same set of knockouts for two different instances of phenotype 1. Note that the frequency scale is determined by the high firing rates from the gKAHP and gCaL KO conditions. (B) Data from panel A and shown with a reduced frequency scale. (C) Membrane potential is shown for gNa and gKDR KO phenotypes, which do not fire action potentials. These results generalize to other VKMs from phenotype 1 as well as phenotypes 2–6.
Classification and dimensionality reduction analyses reveal a complex though structured mapping from expression space to neuromodulation response
While our analyses presented thus far were directed to relate molecular expression to individual firing rate properties, we wanted to determine if we could predict the neuromodulation response phenotype from the molecular expression state. Decision tree analysis is highly effective in predicting response classes of multivariate data sets [75]. Decision trees were recently applied in classification analysis of electrophysiological data [76]. We utilized the random forest (RF) paradigm for decision tree analysis, in which a population of decision trees is used to generate class predictions. We applied the RF analysis with and without the electrophysiological variables used for neuromodulation response phenotype classification (Fig 8A). The RF analysis generates a set of statistical performance metrics for each phenotype including accuracy, sensitivity, specificity, positive predictive value, and negative value (Supplementary Table 2). When only the conductance Z-scores and d:h ratio were considered in the analysis, phenotype prediction accuracy was sub-optimal (0.5 – 0.89, Supplementary Table 2). However, performance statistics improved substantially when firing rate properties were included as prediction variables (accuracy range 0.79 – 1.0, Supplementary Table 3).
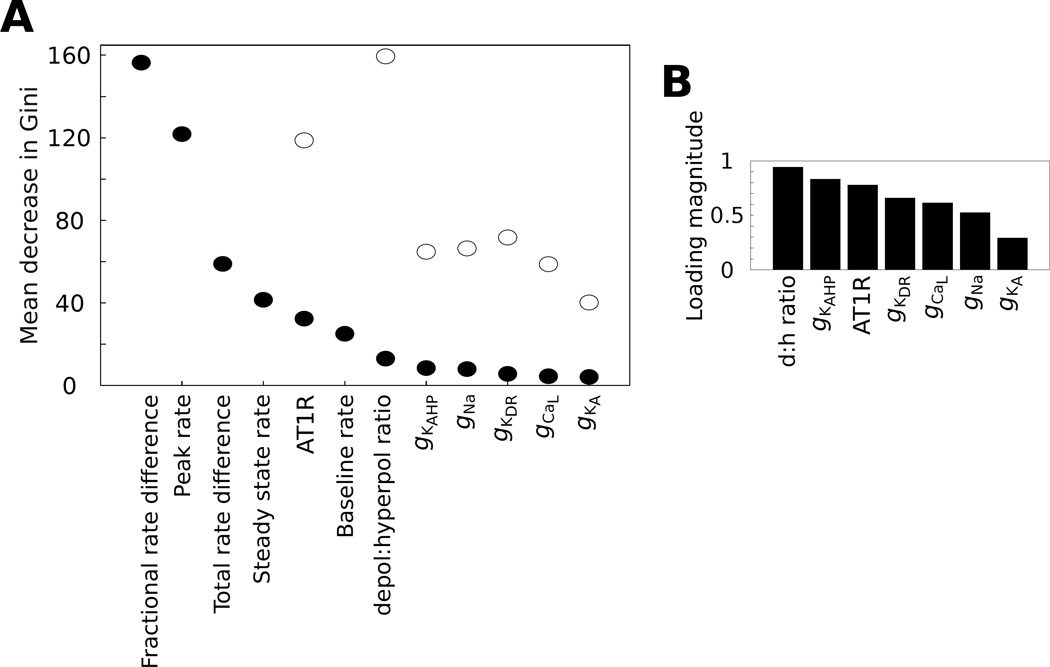
Fig. 8. Structured molecular interactions underlie neuromodulation response phenotype.
(A) The mean decrease in Gini score is a metric of variable importance (VIP) from the random forest analysis. These VIP scores are shown for RF models with and without the inclusion of firing rate properties (filled and open circles, respectively). (B) Loading magnitudes are shown for components of the PLSR loading vectors from each molecular variable in the model, including the depolarizing to hyperpolarizing (d:h) ratio. The loading magnitudes refer to Euclidean norms of the respective components from the loading vectors (Pnew, equation 23) of the PLSR model (see Fig 9C).
RF analysis also gives a classification variable importance (VIP) ranking known as the mean decrease in the Gini score (Fig 8A, see details in Supplementary Materials). This VIP score indicates the relative contribution of each variable in generating predictions from the classification model (i.e., the population of decision trees). Our RF analysis indicated that firing rate properties out ranked conductance expression properties in VIP contribution to neuromodulation response phenotype classification (Fig 8A). However, AT1R expression and the d:h ratio where the two top ranking VIP scores when considering only molecular expression, regardless of whether firing rate properties were included in the classification model. This analysis indicates, consistent with the above results, that molecular expression contributes to neuromodulation response phenotype in a complex manner that is conditioned by firing rate properties.
To extend our analysis, we evaluated whether molecular expression profiles could be related to neuromodulation response phenotype if the expression data were analyzed with dimensionality reduction (i.e., the reduction of dimensions of molecular expression variables to three dimensions for presentation in Cartesian coordinates) [41,77,78,61]. We applied principal components analysis (PCA) to our molecular expression data set and plotted the data in three dimensions with phenotype annotated by color (Fig 9A). This visualization showed a modest separation of phenotype with respect to expression space. Phenotypes 4 and 5 (blue and magenta) appeared to be separated from phenotypes 1, 2, and 5. We next performed PCA on the firing rate property data set and found stronger evidence for phenotype separation in reduced firing rate property space, as expected given that these properties were applied in phenotype classification (Fig 9B).
We further examined whether molecular expression state could provide a more precise mapping to neuromodulation response phenotype. For instance, molecular expression states commonly form manifolds in their subspaces [79], and a variety of computational approaches exist for visualizing such relations [78, 80]. Considering the complex nature of the mapping between molecular expression and neuromodulation response phenotype, we utilized partial least squares regression (PLSR). This approach takes into account both the molecular expression and physiological variables in determining the projection of the conductance data set onto a subspace of reduced dimensionality. This approach has shown utility in the analysis of multidimensional data from molecular studies [81]. The results of our PLSR analysis demonstrated that rotating the coordinate system onto which expression states were projected, based on the corresponding firing rate property vectors, results in partial segregation of neuromodulation response phenotypes as a function of expression state (Fig 9C). These phenotype-specific clusters in PC space represent molecular expression sub-manifolds [79]. Furthermore, the ranking of Euclidean norm magnitudes of the PLSR loading vectors matched the RF VIP rankings such that the d:h ratio, gKAHP level, and AT1R level were the highest contributors to the expression data projection (Fig 8B, compare with Fig 8A). However, it should be noted that for both the RF and PLSR analyses, the molecular contributions showed a graded pattern with a shallow slope (Fig 8), indicating that there are not sharp boundaries between molecular species that show high versus low predictive value for phenotype classification. This interpretation is consistent with the phenotype-dependent densities of AT1R expression level and baseline firing rate, which show substantial overlap across phenotypes (Fig 9D). Nevertheless, our PLSR results support the conclusion that molecular expression state is highly predictive of neuromodulation response phenotype, based on a mapping that is facilitated by information regarding firing rate geometry.
Discussion
We examined to relative influences of GPCR-mediated signaling strength and voltage gated ion channel composition on the electrophysiological response to dynamic neuromodulation. We simulated AngII-mediated neuromodulation of membrane electrophysiology based on PKC- and CaMKII-mediated phosphorylation of KDR channels. Available evidence suggests that such phosphorylation occurs on Kv2.1 and Kv2.2 channels [82, 83]. However, it has also been shown that putative PKC and CaMKII sites exist on Kv1.4 channels mediating the KA current [84]. We previously simulated the effects of KA channel phosphorylation and found that this mechanism did not influence the neuronal firing rate [42]. These results are consistent with our VKM analyses. Hence, we omitted KA channel phosphorylation from our model.
We simulated AngII-mediated responses over a range of AT1R levels and observed a separatrix across the AT1R axis which distinguished increased versus decreased excitability responses. The biophysical basis of the separatrix was reduction of hyperpolarizing K+ currents balanced by increased Na+ current at a depolarized equilibrium. Such phenomena were shown in other experiments and model simulations [70, 72]. These data suggested that aberrant increases in K+ conductance can result in depolarization block via inactivation of Na+ channels [42].
A wealth of recent data demonstrate single cell variability in functional expression of ion channels [25, 57,73] and GPCRs [8]. Gene expression data indicate that voltage-gated ion channel transcripts vary approximately two- to six-fold [7]. However, few studies have examined the effects of molecular variability on neuronal responses to neuromodulation [33]. Our simulations of AT1R variability in a population of phenotypes show that a firing rate separatrix is tunable in the conductance–AT1R expression level state space. A restricted range of AT1R level is associated with maximal tunability by relative conductance balances. Analysis of the simulation data suggest that distinct AngII response profiles, characterized by firing rate response kinetics and amplitude, partition the neuromodulation response phenotype into distinct regions of multidimensional molecular expression state space, thereby generating a set of sub-manifolds [79]. We note here that the term sub-manifold has a very specific formal meaning [85–87]. Our use of the term is relaxed in mathematical specificity to indicate data grouping in low dimensional space based on [79].
Consistent with the notion of homeostatic mechanisms of neurophysiological phenotype degeneracy [7, 27,28], resulting from coordinated control over ion channel expression variability across channel species [88–90], we found that multiple biophysical states produced firing frequencies within the physiological range of brainstem neurons [28, 26]. However, despite similar baseline firing rates, different conductance balances led to differential responsiveness to neuromodulation, as observed in experimental studies [8,91,92]. These divergent neuromodulation response profiles were associated with different pairwise molecular correlations, indicating that compensatory interactions support robust phenotypes [31]. However, our VKM analysis indicated that these correlations were not sufficient for the compensation of complete channel occlusion.
Amongst biophysical state variants with physiological baseline firing rates, only some combinations yield a typical response to AngII, based on the finding that AngII consistently evokes firing rate increases in vitro [59]. These findings contrast with reports suggesting that neuromodulation typically evokes consistent responses in diverse cell populations [33]. Our finding of divergent neuromodulation response profiles could be explained in two ways: (1) there is variability in the in vivo AngII-mediated response within a heterogeneous population of brainstem neurons, and (2) regulatory constraints on molecules involved in AngII signaling and membrane electrophysiology maintain brainstem neurons within a sector of multidimensional functional expression space that ensures reliable AngII responses. There is evidence in favor of both interpretations, though we note that the AT1R-dependent separatrix is currently a hypothesized construct, as experimental data demonstrating its existence have not been obtained. However, it has been shown that AngII can exert both inhibitory and excitatory effects in the brainstem [93, 34], consistent with a distribution of phenotypes that traverses a separatrix. Our recent data suggest that phenotypic diversity in autonomic brainstem regions is highly plastic and is coordinated by anatomical connectivity [25], as found in other studies of neuromodulator response in in vivo [91]. Further, it has been shown that constraints at the gene regulatory level, mediated by particular combinations of transcription factors, coordinate physiological processes [94]. Ion channels are known to be regulated by combinations of transcription factors [95]. Recent computational modeling work supports a role of gene regulatory constraints in shaping the homeostasis of excitability phenotype [89,90]. Such regulation presumably occurs in adult cells to balance phenotypic variability with organismal homeostasis [96,90,57, 97,98]. However, studies with an intact in situ rat brainstem-heart preparation show that, for a particular range of doses, AngII microinjection into the brainstem nucleus of the solitary tract elicits inconsistent sympathetic responses [34]. Thus, physiological constraints may ensure optimal responsiveness to neuromodulators, while cell-to-cell variability may be implicated in regulating network responses.
It has recently become common to study the relations between molecular expression and excitability phenotype using populations of Hodgkin Huxley models [99,100,29,30]. Such approaches have facilitated the understanding of relationships between molecular and electrophysiological phenotypes in the context of epilepsy research [101]. Our study expands this line of work by demonstrating that neuromodulation can operate in a switch-like manner with a complex dependence on molecular expression. There are several future directions that can be taken using our neuromodulation framework. For instance, our framework could be applied to the quantitative study of neuromodulation in the context of morphologically reconstructed neurons with spatially distributed receptors and channels [102]. While neuromodulatory responses have been shown to be generally consistent within specific neural circuits [33], our results support the possibility that neuromodulation responsiveness is tunable in particular contexts [34]. We propose that molecular constraints can tune neuronal behavior in an adaptive manner to optimize physiological function.
Supplementary Material
Acknowledgements
This study was supported by National Heart, Lung, and Blood Institute grant No. R01 HL111621 to RV.
References
- 1.Marder E. Neuron. 2012;76(1):1. doi: 10.1016/j.neuron.2012.09.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Dayan P. Neuron. 2012;76(1):240. doi: 10.1016/j.neuron.2012.09.027. [DOI] [PubMed] [Google Scholar]
- 3.Levitan I. Annual Review of Physiology. 1994;56:193. doi: 10.1146/annurev.ph.56.030194.001205. [DOI] [PubMed] [Google Scholar]
- 4.Nadim F, Bucher D. Current Opinion in Neurobiology. 2014;29C:48. doi: 10.1016/j.conb.2014.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Finkel L. Annual Review of Biomedical Engineering. 2000;2:577. doi: 10.1146/annurev.bioeng.2.1.577. [DOI] [PubMed] [Google Scholar]
- 6.Ritter SL, Hall RA. Nature Reviews Molecular Cell Biology. 2009;10(12):819. doi: 10.1038/nrm2803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Marder E. Proceedings of the National Academy of Sciences of the United States of America. 2011;108(Suppl 3):15542. doi: 10.1073/pnas.1010674108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Spaethling J, Piel D, Dueck H, Buckley P, Morris J, Fisher S, Lee J, Sul J, Kim J, Bartfai T, Beck S, Eberwine J. FASEB journal. 2014;28(2):771. doi: 10.1096/fj.13-240267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Marder E, O’Leary T, Shruti S. Annual Review of Neuroscience. 2014;37:329. doi: 10.1146/annurev-neuro-071013-013958. [DOI] [PubMed] [Google Scholar]
- 10.Sumners C, Fleegal M, Zhu M. Clinical and Experimental Pharmacology & Physiology. 2002;29(5–6):483. doi: 10.1046/j.1440-1681.2002.03660.x. [DOI] [PubMed] [Google Scholar]
- 11.Ferguson A, Washburn D, Latchford K. Experimental Biology and Medicine (Maywood, NJ) 2001;226(2):85. doi: 10.1177/153537020122600205. [DOI] [PubMed] [Google Scholar]
- 12.Phillips M, Sumners C. Regulatory Peptides. 1998;78(1–3):1. doi: 10.1016/s0167-0115(98)00122-0. [DOI] [PubMed] [Google Scholar]
- 13.Hogarty D, Speakman E, Puig V, Phillips M. Brain Research. 1992;586(2):289. doi: 10.1016/0006-8993(92)91638-u. [DOI] [PubMed] [Google Scholar]
- 14.McCubbin J, DeMoura R, Page I, Olmsted F. Science (New York, NY) 1965;149(3690):1394. doi: 10.1126/science.149.3690.1394. [DOI] [PubMed] [Google Scholar]
- 15.Accorsi-Mendonca D, Machado B. Autonomic Neuroscience: Basic & Clinical. 2013;175:3. doi: 10.1016/j.autneu.2012.12.002. [DOI] [PubMed] [Google Scholar]
- 16.Guyenet P. Nature Reviews Neuroscience. 2006;7:335. doi: 10.1038/nrn1902. [DOI] [PubMed] [Google Scholar]
- 17.Shan Z, Zubcevic J, Shi P, Jun J, Dong Y, Murca T, Lamont G, Cuadra A, Yuan W, Qi Y, Li Q, Paton J, Katovich M, Sumners C, Raizada M. Hypertension. 2013;61(6):1328. doi: 10.1161/HYPERTENSIONAHA.111.00156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cuadra A, Shan Z, Sumners C, Raizada M. Pharmacology & Therapeutics. 2010;125(1):27. doi: 10.1016/j.pharmthera.2009.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Paton J, Wang S, Polson J, Kasparov S. Journal of Molecular Medicine (Berlin, Germany) 2008;86(6):705. doi: 10.1007/s00109-008-0324-4. [DOI] [PubMed] [Google Scholar]
- 20.Mitra AK, Gao L, Zucker IH. American Journal of Physiology. Cell physiology. 2010;299(3):C561. doi: 10.1152/ajpcell.00127.2010. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- 21.Smyth JW, Shaw RM. Heart Rhythm : The Official Journal of the Heart Rhythm Society. 2010;7(8):1135. doi: 10.1016/j.hrthm.2010.05.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Penela P, Murga C, Ribas C, Tutor AS, Peregrn S, Mayor F. Cardiovascular Research. 2006;69(1):46. doi: 10.1016/j.cardiores.2005.09.011. [DOI] [PubMed] [Google Scholar]
- 23.Kaczorowski GJ, McManus OB, Priest BT, Garcia ML. The Journal of General Physiology. 2008;131(5):399. doi: 10.1085/jgp.200709946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hbner CA, Jentsch TJ. Human Molecular Genetics. 2002;11(20):2435. doi: 10.1093/hmg/11.20.2435. [DOI] [PubMed] [Google Scholar]
- 25.Park J, Brureau A, Kernan K, Starks A, Gulati S, Ogunnaike B, Schwaber J, Vadigepalli R. Genome Research. 2014;24(6):930. doi: 10.1101/gr.161802.113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Foster WR, Ungar LH, Schwaber JS. Journal of Neurophysiology. 1993;70(6):2502. doi: 10.1152/jn.1993.70.6.2502. [DOI] [PubMed] [Google Scholar]
- 27.Edelman G, Gally J. Proceedings of the National Academy of Sciences of the United States of America. 2001;98(24):13763. doi: 10.1073/pnas.231499798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bhalla US, Bower JM. Journal of Neurophysiology. 1993;69(6):1948. doi: 10.1152/jn.1993.69.6.1948. [DOI] [PubMed] [Google Scholar]
- 29.Rathour RK, Narayanan R. Proceedings of the National Academy of Sciences of the United States of America. 2014;111(17):1787. doi: 10.1073/pnas.1316599111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Rathour RK, Narayanan R. The Journal of Physiology. 2012;590(22):5629. doi: 10.1113/jphysiol.2012.239418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hudson AE, Prinz AA. PLoS Computational Biology. 2010;6(7):e1000838. doi: 10.1371/journal.pcbi.1000838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Anirudhan A, Narayanan R. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience. 2015;35(11):4691. doi: 10.1523/JNEUROSCI.4223-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Grashow R, Brookings T, Marder E. Proceedings of the National Academy of Sciences of the United States of America. 2009;106(28):11742. doi: 10.1073/pnas.0905614106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Paton J, Kasparov S. The Journal of Physiology. 1999;521(Pt 1):213. doi: 10.1111/j.1469-7793.1999.00213.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Cannon RC, D’Alessandro G. PLoS Computational Biology. 2006;2(8):e91. doi: 10.1371/journal.pcbi.0020091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Prescott SA, De Koninck Y, Sejnowski TJ. PLoS Computational Biology. 2008;4(10):e1000198. doi: 10.1371/journal.pcbi.1000198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Torben-Nielsen B, Stiefel KM. PLoS Computational Biology. 2010;6(9):e1000932. doi: 10.1371/journal.pcbi.1000932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Torben-Nielsen B, Stiefel KM. Network (Bristol, England) 2009;20(2):69. doi: 10.1080/09548980902984833. [DOI] [PubMed] [Google Scholar]
- 39.Moresco EMY, Li X, Beutler B. The American Journal of Pathology. 2013;182(5):1462. doi: 10.1016/j.ajpath.2013.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Rathour RK, Narayanan R. Proceedings of the National Academy of Sciences of the United States of America. 2014;111(17):E1787. doi: 10.1073/pnas.1316599111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Taylor AL, Hickey TJ, Prinz AA, Marder E. Journal of Neurophysiology. 2006;96(2):891. doi: 10.1152/jn.00367.2006. [DOI] [PubMed] [Google Scholar]
- 42.Makadia HK, Anderson WD, Fey D, Sauter T, Schwaber JS, Vadigepalli R. Biophysical Journal. 2015;108(1):211. doi: 10.1016/j.bpj.2014.11.1851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Mishra J, Bhalla U. Biophysical Journal. 2002;83(3):1298. doi: 10.1016/S0006-3495(02)73901-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Bhalla US, Iyengar R. Science (New York, N.Y.) 1999;283(5400):381. doi: 10.1126/science.283.5400.381. [DOI] [PubMed] [Google Scholar]
- 45.Vadigepalli R, Doyle FJ, Schwaber JS. Neural Computation. 2001;13(10):2239. doi: 10.1162/089976601750541796. [DOI] [PubMed] [Google Scholar]
- 46.Rybak I, Paton J, Schwaber J. Journal of Neurophysiology. 1997;77(4):1994. doi: 10.1152/jn.1997.77.4.1994. [DOI] [PubMed] [Google Scholar]
- 47.Hines ML, Morse T, Migliore M, Carnevale NT, Shepherd GM. Journal of Computational Neuroscience. 2004;17(1):7. doi: 10.1023/B:JCNS.0000023869.22017.2e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Hodgkin A, Huxley A. The Journal of Physiology. 1952;117(4):500. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Koch C. Biophysics of Computation: Information Processing in Single Neurons. Oxford University Press; 1998. [Google Scholar]
- 50.Mifflin SW, Spyer KM, Withington-Wray DJ. The Journal of Physiology. 1988;399:349. doi: 10.1113/jphysiol.1988.sp017085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Lipski J, McAllen RM, Spyer KM. The Journal of Physiology. 1975;251(1):61. doi: 10.1113/jphysiol.1975.sp011081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Rogers RF, Rybak IA, Schwaber JS. Brain Research Bulletin. 2000;51(2):139. doi: 10.1016/s0361-9230(99)00242-7. [DOI] [PubMed] [Google Scholar]
- 53.Destexhe A, Rudolph M, Fellous JM, Sejnowski TJ. Neuroscience. 2001;107(1):13. doi: 10.1016/s0306-4522(01)00344-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Azar T, Sharp J, Lawson D. Journal of the American Association for Laboratory Animal Science : JAALAS. 2011;50(2):175. [PMC free article] [PubMed] [Google Scholar]
- 55.Kndgen H, Geisler C, Fusi S, Wang XJ, Lscher HR, Giugliano M. Cerebral Cortex (New York, N.Y.: 1991) 2008;18(9):2086. doi: 10.1093/cercor/bhm235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Taylor AL, Goaillard JM, Marder E. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience. 2009;29(17):5573. doi: 10.1523/JNEUROSCI.4438-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Schulz D, Goaillard J, Marder E. Proceedings of the National Academy of Sciences of the United States of America. 2007;104(32):13187. doi: 10.1073/pnas.0705827104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Toledo-Rodriguez M, Blumenfeld B, Wu C, Luo J, Attali B, Goodman P, Markram H. Cerebral Cortex (New York, N.Y.: 1991) 2004;14(12):1310. doi: 10.1093/cercor/bhh092. [DOI] [PubMed] [Google Scholar]
- 59.Wang D, Gelband CH, Sumners C, Posner P. Journal of Neurophysiology. 1997;78(2):1013. doi: 10.1152/jn.1997.78.2.1013. [DOI] [PubMed] [Google Scholar]
- 60.Donoghue S, Garcia M, Jordan D, Spyer KM. The Journal of Physiology. 1982;322:337. doi: 10.1113/jphysiol.1982.sp014040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Tripathy SJ, Burton SD, Geramita M, Gerkin RC, Urban NN. Journal of Neurophysiology. 2015;113(10):3474. doi: 10.1152/jn.00237.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Liaw A, Wiener M. R News. 2002;2(3):18. [Google Scholar]
- 63.Qi Y. In: in Ensemble Machine Learning. Zhang C, Ma Y, editors. US: Springer; 2012. pp. 307–323. [Google Scholar]
- 64.R Development Core Team, R. A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; 2008. URL http://www.R-project.org. ISBN 3-900051-07-0. [Google Scholar]
- 65.Kuhn M. Journal of Statistical Software. 2008;28(5):1. doi: 10.18637/jss.v028.i07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Wold S, Sjstrm M, Eriksson L. Chemometrics and Intelligent Laboratory Systems. 2001;58(2):109. [Google Scholar]
- 67.Ogunnaike BA. Random Phenomena: Fundamentals of Probability and Statistics for Engineers. CRC Press; 2009. [Google Scholar]
- 68.Jensen KJ, Janes KA. Physical Biology. 2012;9(4):045004. doi: 10.1088/1478-3975/9/4/045004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Mevik Bh, Wehrens R. Journal of Statistical Software. 2007:1–24. [Google Scholar]
- 70.Guan D, Armstrong W, Foehring R. The Journal of Physiology. 2013;591(19):4807. doi: 10.1113/jphysiol.2013.257253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Liu P, Bean B. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience. 2014;34(14):4991. doi: 10.1523/JNEUROSCI.1925-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Kispersky TJ, Caplan JS, Marder E. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience. 2012;32(32):10995. doi: 10.1523/JNEUROSCI.2045-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Schulz D, Goaillard J, Marder E. Nature Neuroscience. 2006;9(3):356. doi: 10.1038/nn1639. [DOI] [PubMed] [Google Scholar]
- 74.Roden DM. Circulation. 2008;118(10):981. doi: 10.1161/CIRCULATIONAHA.108.798918. [DOI] [PubMed] [Google Scholar]
- 75.Kingsford C, Salzberg SL. Nature Biotechnology. 2008;26(9):1011. doi: 10.1038/nbt0908-1011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Hadzipasic M, Tahvildari B, Nagy M, Bian M, Horwich AL, McCormick DA. Proceedings of the National Academy of Sciences of the United States of America. 2014;111(47):16883. doi: 10.1073/pnas.1419497111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.McGarry LM, Packer AM, Fino E, Nikolenko V, Sippy T, Yuste R. Frontiers in Neural Circuits. 2010;4:12. doi: 10.3389/fncir.2010.00012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Cunningham JP, Yu BM. Nature Neuroscience. 2014;17(11):1500. doi: 10.1038/nn.3776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.O’Leary T, Wyllie DJA. The Journal of Physiology. 2011;589(Pt 20):4811. doi: 10.1113/jphysiol.2011.210179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Li L. Methods in Molecular Biology (Clifton, N.J.) 2010;620:417. doi: 10.1007/978-1-60761-580-4_14. [DOI] [PubMed] [Google Scholar]
- 81.Janes KA, Yaffe MB. Nature Reviews Molecular Cell Biology. 2006;7(11):820. doi: 10.1038/nrm2041. [DOI] [PubMed] [Google Scholar]
- 82.Gelband CH, Warth JD, Mason HS, Zhu M, Moore JM, Kenyon JL, Horowitz B, Sumners C. Circulation Research. 1999;84(3):352. doi: 10.1161/01.res.84.3.352. [DOI] [PubMed] [Google Scholar]
- 83.Misonou H, Mohapatra DP, Park EW, Leung V, Zhen D, Misonou K, Anderson AE, Trimmer JS. Nature Neuroscience. 2004;7(7):711. doi: 10.1038/nn1260. [DOI] [PubMed] [Google Scholar]
- 84.Hagiwara K, Nunoki K, Ishii K, Abe T, Yanagisawa T. Biochemical and Biophysical Research Communications. 2003;310(2):634. doi: 10.1016/j.bbrc.2003.09.062. [DOI] [PubMed] [Google Scholar]
- 85.Song Y, Nie F, Zhang C, Xiang S. Pattern Recognition. 2008;41(9):2789. [Google Scholar]
- 86.Lee SM, Araman P, et al. in IEEE Conference on Computer Vision and Pattern Recognition, 2007; 2007. pp. 1–7. [Google Scholar]
- 87.Sun K, Marchand-maillet S. In: Jebara T, Xing EP, editors. Proceedings of the 31st International Conference on Machine Learning (ICML-14; 2014. pp. 1–9. [Google Scholar]
- 88.Tobin A, Cruz-Bermdez N, Marder E, Schulz D. PLoS ONE. 2009;4(8):E6742. doi: 10.1371/journal.pone.0006742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.OLeary T, Williams AH, Caplan JS, Marder E. Proceedings of the National Academy of Sciences of the United States of America. 2001;110(28):2239. doi: 10.1073/pnas.1309966110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.OLeary T, Williams AH, Franci A, Marder E. Neuron. 2014;82(4):809. doi: 10.1016/j.neuron.2014.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Svoz-Couche C, Spyer KM, Jordan D. British Journal of Pharmacology. 2000;131(7):1445. doi: 10.1038/sj.bjp.0703722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Guenther E, Schmid S, Hewig B, Kohler K. Brain Research. 1996;718(1–2):112. doi: 10.1016/0006-8993(96)00077-7. [DOI] [PubMed] [Google Scholar]
- 93.Dampney RaL, Tan PSP, Sheriff MJ, Fontes MaP, Horiuchi J. Current Hypertension Reports. 2007;9(3):222. doi: 10.1007/s11906-007-0040-4. [DOI] [PubMed] [Google Scholar]
- 94.di Sanguinetto S, Dasen J, Arber S. Current Opinion in Neurobiology. 2008;18(1):36. doi: 10.1016/j.conb.2008.04.002. [DOI] [PubMed] [Google Scholar]
- 95.Wolfram V, Southall TD, Gnay C, Prinz AA, Brand AH, Baines RA. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience. 2014;34(7):2538. doi: 10.1523/JNEUROSCI.4511-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Temporal S, Lett KM, Schulz DJ. Current Biology. 2014;24(16):1899. doi: 10.1016/j.cub.2014.06.067. [DOI] [PubMed] [Google Scholar]
- 97.Ramocki MB, Zoghbi HY. Nature. 2008;455(7215):912. doi: 10.1038/nature07457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.LeMasson G, Marder E, Abbott LF. Science (New York, N.Y.) 1993;259(5103):1915. doi: 10.1126/science.8456317. [DOI] [PubMed] [Google Scholar]
- 99.Sarkar AX, Christini DJ, Sobie EA. The Journal of Physiology. 2012;590(11):2555. doi: 10.1113/jphysiol.2011.223313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Marder E, Taylor AL. Nature Neuroscience. 2011;14(2):133. doi: 10.1038/nn.2735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Klassen T, Davis C, Goldman A, Burgess D, Chen T, Wheeler D, McPherson J, Bourquin T, Lewis L, Villasana D, Morgan M, Muzny D, Gibbs R, Noebels J. Cell. 2011;145(7):1036. doi: 10.1016/j.cell.2011.05.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Kotaleski JH, Blackwell KT. Nature Reviews Neuroscience. 2010;11(4):239. doi: 10.1038/nrn2807. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.