Broadband Tunable, Polarization-Selective and Directional Emission of (6,5) Carbon Nanotubes Coupled to Plasmonic Crystals

Abstract

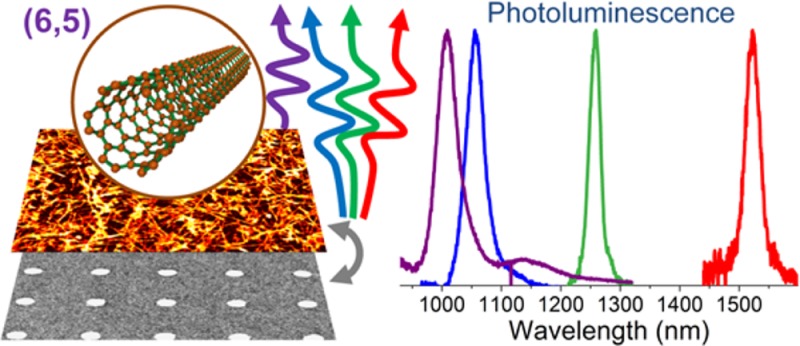
We demonstrate broadband tunability of light emission from dense (6,5) single-walled carbon nanotube thin films via efficient coupling to periodic arrays of gold nanodisks that support surface lattice resonances (SLRs). We thus eliminate the need to select single-walled carbon nanotubes (SWNTs) with different chiralities to obtain narrow linewidth emission at specific near-infrared wavelengths. Emission from these hybrid films is spectrally narrow (20–40 meV) yet broadly tunable (∼1000–1500 nm) and highly directional (divergence <1.5°). In addition, SLR scattering renders the emission highly polarized, even though the SWNTs are randomly distributed. Numerical simulations are applied to correlate the increased local electric fields around the nanodisks with the observed enhancement of directional emission. The ability to control the emission properties of a single type of near-infrared emitting SWNTs over a wide range of wavelengths will enable application of carbon nanotubes in multifunctional photonic devices.

The outstanding optical and electrical properties of semiconducting single-walled carbon nanotubes (SWNTs) make them promising candidates for applications as light sources¹⁻³ especially at the single photon level,⁴⁻⁶ in nonlinear optics,^7,8 as detectors,^9,10 in photovoltaics,^11,12 integrated circuits,^13,14 and optoelectronic devices in general.^15,16 The spectral position of their very narrow excitonic emission depends on their chirality vector (n,m). Thus, using SWNTs with different chiralities would provide coverage of the entire near-infrared range.¹⁷ However, there are still several challenges preventing widespread use of SWNTs in actual devices. First, the emission efficiency of SWNTs must be improved and it should be directional for maximum collection/detection efficiency. Second, although the variation of (n,m) in principle provides an attractive approach to spectrally tune the emission, it remains difficult to purify large amounts of monochiral samples with a specific chirality despite numerous efforts toward controlled growth¹⁸ or postgrowth sorting by density gradient centrifugation, chromatography, or polymer wrapping.¹⁹⁻²¹

Instead of changing the chirality of the SWNTs in order to obtain a certain emission wavelength, one could also alter their environment to control the optical response. For example, various plasmonic nanostructures can be used to increase the electronic transition rates (e.g., absorption or spontaneous emission) in regions of extremely intense local fields that form in the proximity of metallic nanostructures supporting local plasmon resonances (LPRs). So far only a few reports have successfully demonstrated implementation of plasmonic structures with SWNTs enhancing their absorption,²² emission,²³ or Raman scattering.^24,25 The main limitation of this approach is the need for precise positioning of the SWNTs to obtain a strong effect. In contrast to that, nonplasmonic, photonic cavities have modes that are spatially more extended (although at the expense of the field intensity) and have been used to tune and enhance light emission from single SWNTs.^2,26 In order to take advantage of the favorable features of plasmonic and photonic cavities, metallic structures supporting LPRs (e.g., rods, spheres, disks, etc.) can be arranged in a periodic manner. This leads to constructive coupling in the far-field (via diffraction²⁷ or waveguiding²⁸) and to the formation of new hybrid photonic-plasmonic modes called surface lattice resonances (SLRs). These modes are less localized than pure plasmonic modes and thus less demanding in terms of the positioning requirements for the emitters while providing even higher local fields than individual metallic structures.²⁹ SLRs and the plasmonic crystals supporting them have been used mostly with organic emitters (e.g., rhodamine 6G) and have already led to such fascinating phenomena as lasing³⁰⁻³² and strong light-matter coupling³³⁻³⁵ that may lead to Bose–Einstein condensation. Interestingly, despite the fundamental and applied interest there are no reports on SLRs operating in the 1000–1500 nm range. This gap is most likely due to the lack of suitable near-infrared emitters beyond 900 nm. Moreover, with regard to potential optoelectronic devices semiconducting SWNTs with their large ambipolar carrier mobilities, photostabilty and narrow photoluminescence and electroluminescence linewidths³⁶ are particularly advantageous compared to common organic dyes. From this perspective, the integration of the SWNTs with plasmonic structures supporting SLRs is promising for further exploration of the intriguing effects of plasmonic crystals and tailoring SWNT emission.

Here, we demonstrate that periodic arrays of gold nanodisks (NDs) transform thin films of monochiral (6,5) SWNTs that emit at around 1000 nm into a broadly tunable light source (∼1000–1500 nm emission range). As confirmed by 3D finite-difference time-domain (FDTD) simulations, the observation of narrow (∼20–40 meV) but broadband tunable light emission is caused by the significant enhancement of directed emission via the Purcell effect. Additional angle-dependent spectroscopic studies reveal that light emission is exceptionally directional with a divergence of ∼1.5° due to the dispersive nature of the SLRs. Finally, the observed emission is polarized despite the random orientation of SWNTs in the film. We believe that these results will boost the development of efficient SWNT-based light-emitting devices with new and expanded capabilities.

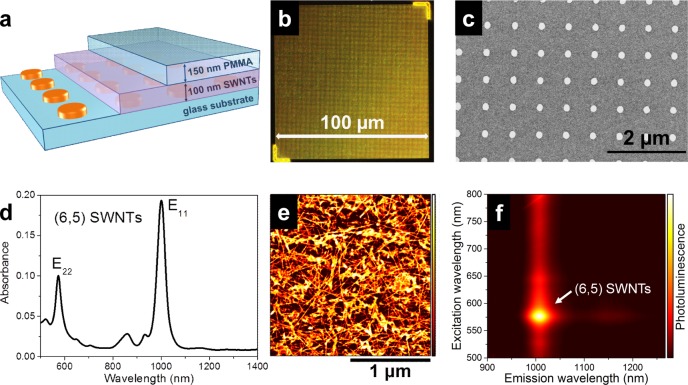
To demonstrate tuning of SWNT emission, we fabricated samples consisting of a glass substrate, a rectangular array of 25 nm high gold NDs covered by a 100 nm thick film of randomly oriented (6,5) SWNTs (sorted by polymer wrapping),³⁷ and a 150 nm poly(methyl methacrylate) (PMMA) top layer as illustrated in Figure 1a. The plasmonic crystals were fabricated by electron-beam lithography (see Supporting Information for details of sample fabrication). The square symmetry was chosen to simplify interpretation of the spectral features and round NDs were selected because small deviations in their shape only have a weak impact on the overall expected effect. The resonance energy of the SLRs can be tuned via the interdisk distance, that is, periodicity or pitch of the plasmonic crystals, given that the scattering efficiency of the LPRs is strong enough in this spectral range. For the purpose of varying the main resonance in the range from 1000 nm up to 1500 nm, we prepared three different samples with a pitch of a = 670, 830, and 1000 nm, and diameters D = 160–180, 220, and 280 nm, respectively. A large scale dark-field image under white light illumination of a typical 100 × 100 μm² patterned area is shown in Figure 1b. The total area of these structures represents a trade-off between electron-beam writing time and the magnitude of SWNTs-plasmonic crystal interaction. The latter increases as more scattering components couple with each other and thus scales with the number of NDs. A representative scanning electron micrograph of the 670 nm pitch sample with square periodic arrangement and 160–180 nm diameter round NDs is shown in Figure 1c (see Supporting Information Figure S1 for 830 and 1000 nm pitches). (6,5) SWNTs were used as they represent one of the few chiralities that can be dispersed with very high purity and in large amounts without requiring costly and complicated purification techniques. Drop casting of a highly concentrated toluene dispersion of (6,5) SWNTs yielded a 100 nm thick layer, which we found to be sufficient to illustrate the versatility of the approach. For a reasonable effect there is no need for precise nanopositioning of SWNTs with respect to the NDs. The absorption spectrum of the obtained SWNT layer is shown in Figure 1d. One can clearly see that the main spectral features at 1000 and 580 nm nicely correlate with the expected E₁₁ and E₂₂ transitions of (6,5) SWNTs, including a phonon sideband at 850 nm. The length of the SWNTs is about 1 μm as illustrated in the atomic-force micrograph in Figure 1e. The SWNT film and plasmonic crystals were covered by a 150 nm PMMA layer, which is sufficiently thick to homogenize the dielectric environment around the NDs for maximum far-field coupling (see ref (38) and Supporting Information Figure S2) but thin enough to exclude additional waveguide contributions.³⁹

Figure 1.

(a) Schematic illustration of a sample consisting of a glass substrate, gold nanodisk array, a 100 nm layer of random (6,5) SWNTs and a 150 nm PMMA layer on top. (b) Dark-field microscopy image of nanodisk array under white-light illumination and (c) scanning electron micrograph of periodic array of gold nanodisks with 670 nm pitch (diameter 160–180 nm). (d) Representative absorption spectrum, (e) atomic-force micrograph, and (f) photoluminescence excitation map of a 100 nm thick (6,5) SWNT layer.

In order to investigate light emission from the pure SWNTs on the prepared samples (away from the plasmonic crystals), we recorded photoluminescence (PL) excitation maps (Figure 1f) by varying the excitation wavelength of a supercontinuum laser source (see Supporting Information for details). The optical response is dominated by the E₁₁ and E₂₂ transitions of the (6,5) SWNTs at 1010 and 580 nm, respectively. The absence of other emission peaks again highlights the purity of the prepared SWNT films. The only other spectral feature at 1150 nm for resonant E₂₂ excitation is attributed to the vibrionic D-mode phonon sideband shifted by ∼150 meV with respect to the lowest excitonic transition.⁴⁰ The measured photoluminescence efficiency of ∼0.1% of the SWNT film and the theoretically predicted exciton radiative lifetime of a few nanoseconds agree well with the experimental exciton lifetime of a few picoseconds (resolution limited, see Supporting Information Figure S3 for details).

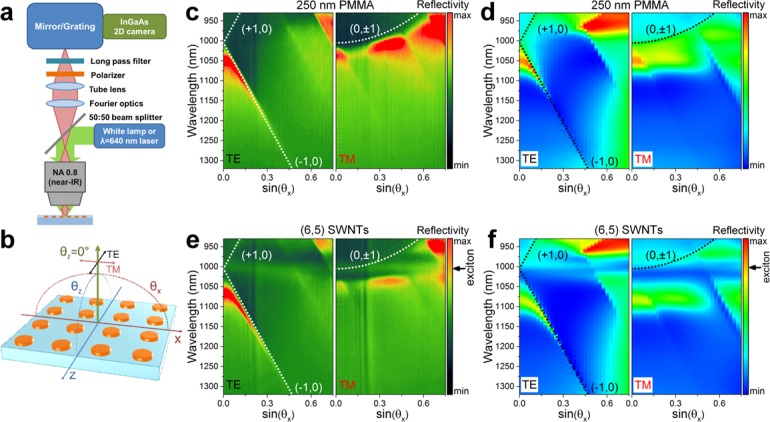
To precisely characterize the dispersive (i.e., angle and wavelength dependent) interaction between the periodic arrays and the SWNT film, we used a Fourier-space imaging setup, as illustrated in Figure 2a. Depending on the type of the measurement, that is, reflectance or PL spectroscopy, a collimated white light source or laser beam (λ = 640 nm; continuous wave power 10 mW) was passed through a 50:50 beam splitter and then focused on the sample by a 100× near IR objective with 0.8 numerical aperture. This yielded a spot size of ∼1.5 μm. The angle of incidence/detection determined by the objective was ±52°. The back-focal plane of the objective was projected via Fourier optics and a tube lens onto the entrance slit of a spectrometer (IsoPlane SCT-320, Princeton Instruments) equipped with a cooled 2D InGaAs camera (640 × 512 pixels NIRvana 640ST, Princeton Instruments). With this configuration, we were able to simultaneously acquire wavelength and angle distribution of the reflected/emitted light. An additional polarizer was placed in front of the spectrometer to select TE (transverse electric) or TM (transverse magnetic) light polarization. Any scattered laser excitation was blocked by a long pass filter with a 850 nm cutoff wavelength. The collection angles θ_x and polarization direction with respect to the entrance slit of the spectrometer (which was oriented along the X-axis) and the periodic arrays are depicted in Figure 2b. Ideally, the collection angle perpendicular to the entrance slit, θ_z, should be fixed to zero to achieve maximum angular resolution. However, an integration of about 1.5° was the practical limit due to the finite size of the entrance slit. For θ_x = 0° there should be no difference between TE and TM polarizations due to the square symmetry of the arrays.

Figure 2.

Schematic layout of (a) experimental setup for angle-resolved reflectivity and photoluminescence measurements, and (b) collection angles θ_x and θ_z, and polarization direction with respect to the periodic array and entrance slit of spectrometer oriented along the X-axis. Experimental and 3D-FDTD calculated angle- and polarization-dependent reflectivity spectra of samples with a nanodisk pitch of 670 nm without (c,d) or with (e,f) SWNTs. Analytical dependencies for corresponding Rayleigh anomalies are indicated with white/black dotted lines.

First, we characterized bare periodic ND arrays covered only with 250 nm PMMA without any SWNTs. The typical reflectivity, defined as the difference in signal from regions with and without periodic structures and divided by the lamp spectrum is shown in Figure 2c for the sample with pitch 670 nm (see Supporting Information Figure S4b and S4c for samples with pitches 830 and 1000 nm). It is easy to see that for the two polarizations the optical response is quite different. For example, TE-polarized light is dominated by the fast (in terms of dispersion, i.e., high dλ/dθ) components emerging due to the far-field coupling of the LPRs with (+1,0) and (−1,0) Rayleigh anomalies (RAs). These are indicated as the white dotted lines according to⁴¹

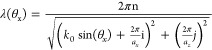1

, where k₀ is the free space wavevector, n is the surrounding refractive index, n = 1.5 for the glass and PMMA layer, a_x = a_z = a = 670 nm corresponds to the pitch, and i, j are the diffraction orders, that is, 0, +1, −1, and so forth.

As expected for the TM polarization, the optical response follows orthogonal (0, ± 1) RAs. It is important to note that the dispersion curves of SLRs usually do not exactly follow analytical trends due to variable spectral overlap and coupling rates between broad LPRs and narrow RAs. To compare the experimental values with more rigorous theoretical calculations we performed 3D-FDTD simulations of the reflectivity as shown in Figure 2d (see Supporting Information Figure S2 for details). A good qualitative agreement between the experimental and simulated trends is found. Although the TE and TM-polarized light normal to the surface of the sample (θ_x = 0°) is the same in the simulated spectra, a slight discrepancy (∼10 nm) is present in the experimental values. This is possibly a result of a slight ellipticity of the NDs and small angle integration (see above) caused by the finite size of the entrance slit of the spectrometer, which leads to a different response for two orthogonal polarizations.

Upon introduction of the SWNTs into the proximity of the plasmonic crystal (see layout in Figure 1a) the experimental and simulated reflectance spectra reveal slight changes as shown in Figure 2e,f, respectively. A 20–30 nm shift, especially pronounced in TM polarization at around sin(θ_x) = 0.45, implies a high energy exchange rate between SLR and excitons in SWNTs. This may indicate the formation of plasmon–exciton polaritons that were recently investigated for other materials and configurations.³³⁻³⁵ Although intriguing, this effect is beyond the scope of the present work. The important outcome of the reflectivity data shown here is that the narrow and angle-dependent SLRs are defined solely by the geometry (i.e., pitch and ND diameter) of the plasmonic crystal and are barely influenced by the SWNTs. This dependence enables broadband tunability of emission from the (6,5) nanotubes with pronounced differences in TE/TM polarizations (see Supporting Information Figure S4e,f for additional reflectivity data of samples with pitches 830 and 1000 nm).

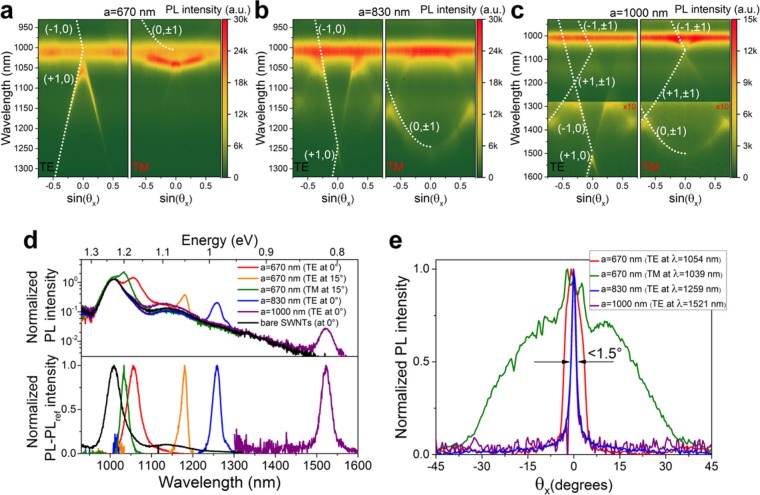
In order to demonstrate that tunable SLRs are able to tailor and modify the light emission properties of SWNTs networks, we performed angle-dependent PL measurements as shown in Figure 3a–c for samples with pitch 670, 830, 1000 nm, respectively. We find that all spectra show dispersionless excitonic transitions at 1010 nm by the SWNTs that are not efficiently coupled to the periodic arrays. Some variation of the intensity of the excitonic signal for different samples is attributed to the variation of density and/or thickness of the drop-cast SWNT film. Nevertheless, the characteristic spectral features due to the SLRs are clearly visible. As expected from the random distribution of the SWNTs, the signal at 1010 nm is nonpolarized while the polarization state of light emission affected by the periodic arrays differs significantly. We excluded any direct radiative contribution from the metal nanostructures itself by performing additional measurements of samples without SWNTs (see Supporting Information Figure S5).

Figure 3.

(a–c) Angle- and polarization-dependent photoluminescence spectra of samples with pitch 670, 830, and 1000 nm (intensity is multiplied 10 times in (c) for regions beyond 1280 nm for clarity), respectively. Analytical dependencies for corresponding Rayleigh anomalies at negative angles are marked with white dotted lines. (d) Normalized (to E₁₁ transition, top) and normalized differential (bottom) PL spectra of pure SWNTs (black) and TE-polarized emission normal to the sample surface with pitch 670, 830, and 1000 nm, TE and TM polarizations at ±15° for pitch 670 nm. (e) Angle dependence of normalized PL for TM-polarized emission for pitch 670 nm (at 1039 nm, green) compared to TE-polarized light at peak positions 1054 (red), 1259 (blue), and 1521 nm (purple) corresponding to the three samples with pitch 670, 830, and 1000 nm.

To better visualize the appearance of new broadband tunable and polarization-selective emission peaks, we extracted a few representative PL spectra normalized to the E₁₁ transition: for pure SWNTs, TE polarization normal to the surface of the samples with ND pitch 670, 830, and 1000 nm, TE and TM polarizations at ±15° for ND pitch 670 nm (Figure 3d, top). New emission peaks arise in addition to the excitonic transition at 1010 nm.

Here, it is important to emphasize a few key points. First, emission at 0° is nonpolarized, but tunable via changing the pitch of the periodic arrays. Second, by only minor variation of the selected detection angle, the polarization state of two spectrally separated (by ∼150 nm) PL peaks is completely changed, which is important for applications where the light generation under a particular angle is of interest, for example, light in-coupling and guiding. Finally, as shown by the normalized differential (i.e., after subtraction of the pure SWNTs spectrum) PL spectra (Figure 3d, bottom) all new spectral features exhibit exceptionally narrow linewidth (∼20–40 meV), which is comparable to the excitonic transitions of pure (6,5) SWNTs.

The highly dispersive behavior of SLRs has one additional implication, that is, the directionality of the emission. Figure 3e shows the normalized PL intensity as a function of emission angle for TE-polarized light at the peak positions 1054, 1259, and 1521 nm corresponding to three samples with pitch 670, 830, 1000 nm, respectively. Additional TM-polarized emission for pitch 670 nm (at 1039 nm) is also included. Highly directional emission within 1.5° is observed for TE-polarized light for pitches 830 and 1000 nm. The slightly higher divergence (∼6.5°) for the 670 nm pitch sample is due to a spectrally broader PL peak. Its position is more red-shifted from the region where the RAs intersect and where divergence is narrower as seen in Figure 3a. In contrast to the TE polarization, the TM emission is much broader due to the smaller dispersion for TM SLRs. The highly directional and spectrally narrow emission highlights the potential for practical integration of plasmonic crystals with SWNTs into devices.

One can achieve high quality SLRs by fine-tuning the structural parameters for the rather small areas of 100 × 100 μm². Even for smaller areas of 50 × 50 μm² the resonance quality remains as high (see Supporting Information Figure S6). It is important to keep in mind that the new apparent spectral features are the results of the Purcell effect, that is, increased emission rate of SWNTs at particular wavelengths where SLRs occur and are not caused by the formation of new emitting states in SWNT. The barely detectable broad SWNTs emission in the 1050–1500 nm range (visible in logarithmic scale of Figure 3d, top) is enhanced at 0° by 7.8, 7.3, and 14.9 times for 670, 830, and 1000 nm pitches. This emission tail is most likely related to multiphonon-assisted decay.⁴²

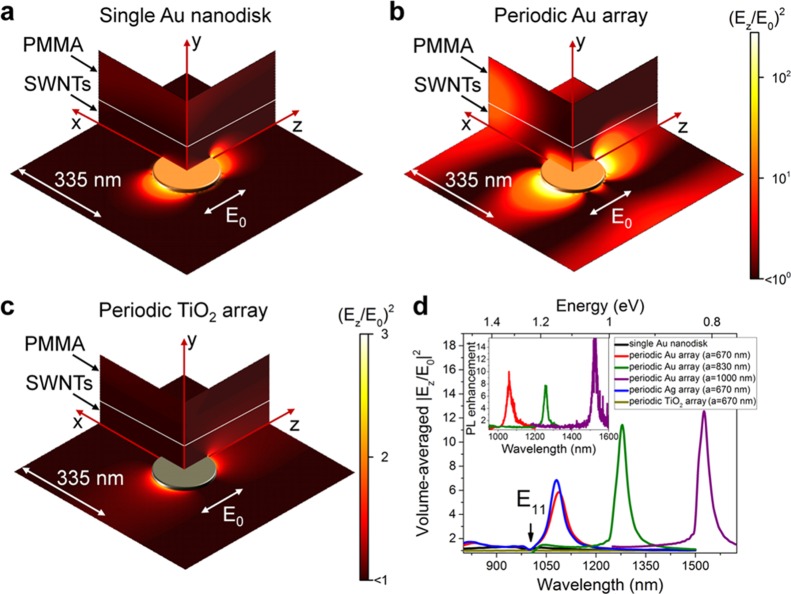
To investigate the origin of the observed enhancement further, we performed simulations of the local field intensity enhancement around NDs at λ = 1085 nm for the plane wave propagating normal to the surface (see Supporting Information B and Figure S2 for details) for a few representative configurations (see Figure 4a–c). The field intensity enhancement leads to higher radiative decay rates and thus power emitted in the reciprocal direction.^43,44 For the LPRs of single gold ND components (Figure 4a) reasonable enhancement is achieved only when emitters (i.e., quantum dots, molecules, SWNTs, etc.) are precisely positioned in the nanometer-sized hot spots. However, when NDs are arranged in a periodic array (Figure 4b) not only the intensity enhancement is higher for the localized fields (up to ∼300–500-fold) but also one can notice the delocalized high-field regions (especially at large ±X values). This is a direct manifestation of the fact that SLRs are both plasmonic and photonic in nature. Therefore, despite the low-field regions in the film where SWNTs are unaffected, the overall contribution of localized and delocalized fields ensures significant PL enhancement even for a rather thick SWNTs layer.

Figure 4.

Electric field intensity enhancement distribution (X–Y, X–Z, and Y–Z planes) at λ = 1085 nm around (a) a single gold nanodisk, (b) gold, and (c) TiO₂ nanodisks in a periodic array with pitch 670 nm. (d) Volume-averaged (over SWNTs layer, i.e., 100 nm thick) intensity enhancement for single gold nanodisk (black), gold (red), silver (blue), and TiO₂ (dark yellow) periodic nanodisk array with pitch 670 nm, and gold periodic nanodisk array with pitch 830 nm (green) or 1000 nm (purple) (inset: corresponding experimental PL enhancement at 0°).

Dielectric structures may also provide reasonable enhancement of quantum emitters without the metal-related quenching close to the surface.^45,46 However, the simulated enhancement around periodically arranged high-refractive index titanium oxide NDs of the same size is much lower compared to the metal NDs as shown in Figure 4c. The reason for such a low enhancement is that far-field coupling cannot take place efficiently due to the insufficient scattering cross-section of titanium oxide NDs in this spectral range.

In addition to the magnitude of the maximum field enhancement, it is important to estimate the volume-averaged values of the SWNT film as directly observed in the far-field experiments. As shown in Figure 4d, the expected PL enhancement from the 670 × 670 × 100 nm³ box of SWNTs depends on the system. We also included the simulation of a periodic array of silver NDs due to their lower intrinsic losses compared to gold NDs. The estimated enhancement for the LPR of a single gold ND is broad with a maximum of 1.3 times. However, for the silver and gold ND periodic arrays enhancement is much narrower with values of up to 5.8–6.8 times that are close to the experimental results (see inset in Figure 4d). Reasonable correlation between experimental and simulated emission enhancement is also visible for the gold ND arrays with pitches of 830 and 1000 nm. For the dielectric ND arrays, almost no enhancement is found. Possible experimental evidence for the Purcell effect being responsible for the PL enhancement would be the shortening of the exciton lifetime due to a higher radiative decay rate. However, owing to the already resolution-limited lifetime of SWNTs (<10 ps), faster exciton decay cannot be resolved.

The wavelength-dependent intensity enhancement shows a dip around 1000 nm that correlates with the excitonic E₁₁ transition and represents cancelation of the emission enhancement by the concurrent process of enhanced absorption by the SWNTs, sometimes also discussed in terms of Fano resonances.⁴⁷ The effect is especially pronounced for SWNTs due to their minimal Stokes shift of only few nanometers. This also has an important implication for applications where absolute PL intensity of SWNTs (i.e., brightness) is of interest. The energy position of plasmon resonances should be slightly detuned from the E₁₁ transition as in the case of the sample with pitch 670 nm (compare the absolute PL intensity in Figure 3a–c). Moreover, the maximum angle-integrated brightness is expected for the TM polarized emission due its lower dispersion compared to the TE emission (Figure 3a). Alternatively, to lower the energy exchange rate between SLRs and the SWNT film one may consider decreasing the density of SWNTs and/or tuning the distance between NDs and SWNTs as a trade-off between high local field intensity enhancement closer to the NDs and low coupling rate for larger separations.

The proposed concept can also be applied directly to emitters with substantially different optical properties. For example, instead of SWNTs NDs were covered with a near-IR emitting diketopyrrolopyrrole copolymer⁴⁸ with a larger Stokes shift and much broader emission band (∼250 nm). The optical response is still governed by the dispersion properties of SLRs (see Supporting Information Figure S7). However, for semiconducting polymers the charge carrier mobilities are orders of magnitude lower than for SWNT networks and thus not very suitable for optoelectronic applications.

In conclusion, we have shown how monochiral (6,5) SWNT films can be combined with periodic arrays of plasmonic nanodisks to achieve narrow emission over a wide spectral range in the near-infrared. The strong directionality and polarization of the emission follow the expected dispersion properties of the plasmonic crystals. FDTD simulations confirm that the main origin of the observed narrow spectral features is the increased spontaneous emission rate of SWNTs via coupling to SLRs. Changing the periodicity of the arrays or the shape of the building blocks directly alters the anisotropic response of the emitting SWNTs. Further adjustments of parameters like SWNT density may reveal additional interesting phenomena such as plasmon-exciton polaritons or SWNT lasing. The high charge carrier mobility and picosecond exciton lifetimes of SWNTs may enable fast, directional, and broadband tunable electroluminescent devices in the near-infrared.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.6b00827.

• Methods: SWNTs dispersion preparation and characterization, fabrication and characterization of plasmonic crystals. Additional data and analysis: SEM images, PL lifetime of SWNTs, reflectivity of samples with 830 and 1000 nm pitches (with and without SWNTs), 3D-FDTD calculations, angle-dependent PL of bare plasmonic crystals, SLRs quality comparison for 50 × 50 μm² arrays and reliability test of the effect with a near-infrared emitting polymer. (PDF)

The authors declare no competing financial interest.