Semiempirical Quantum Mechanical Methods for Noncovalent Interactions for Chemical and Biochemical Applications

Abstract

Semiempirical (SE) methods can be derived from either Hartree–Fock or density functional theory by applying systematic approximations, leading to efficient computational schemes that are several orders of magnitude faster than ab initio calculations. Such numerical efficiency, in combination with modern computational facilities and linear scaling algorithms, allows application of SE methods to very large molecular systems with extensive conformational sampling. To reliably model the structure, dynamics, and reactivity of biological and other soft matter systems, however, good accuracy for the description of noncovalent interactions is required. In this review, we analyze popular SE approaches in terms of their ability to model noncovalent interactions, especially in the context of describing biomolecules, water solution, and organic materials. We discuss the most significant errors and proposed correction schemes, and we review their performance using standard test sets of molecular systems for quantum chemical methods and several recent applications. The general goal is to highlight both the value and limitations of SE methods and stimulate further developments that allow them to effectively complement ab initio methods in the analysis of complex molecular systems.

1. Introduction: Noncovalent Interactions in (Bio)Chemistry and the Values of Quantum Mechanical Models

Noncovalent interactions are crucial in chemistry, biochemistry, and materials science. They govern the structure and conformational dynamics of molecular systems and are therefore also crucial to reactive properties. The ability to understand and predict noncovalent interactions is thus indispensable to theoretical and computational studies of complex molecules.

In many computational studies, a classical potential function (i.e., a molecular mechanical force field) is used to describe noncovalent interactions. This is based on the assumption that, in the absence of chemical reactivity and therefore any change in covalent bonding, the potential function can be expressed as a sum of a set of relatively simple functional forms. For the noncovalent component, for example, the typical force field includes Coulombic terms between point charges or higher-order multipoles,¹ Lennard-Jones terms for van der Waals interactions, and sometimes polarizable dipoles,^1,2 fluctuating charges,³ or charge transfer terms.⁴ Classical force fields are vital for condensed-phase simulations due to their computational efficiency; their accuracy for certain properties (e.g., population of various conformations) can be rather high for well-calibrated systems.

Despite the success of force fields, there is still tremendous interest in developing efficient quantum mechanics (QM) based methods for treating noncovalent interactions due to several considerations. First, the parametrization of a force field is often a laborious process that requires extensive tests and refinement of parameters that are not easily decoupled. In the recent years, there has been progress regarding the development of “ab initio” force fields in which parameters are computed rather than fitted.⁵⁻⁷ Although this is an exciting and promising direction, there are still technical challenges, such as the balance of bonded and nonbonded contributions in the treatment of polymeric systems. Second, most force fields, including those based on first-principles calculations, use rather simple functional forms, which may not be able to capture subtle effects such as hyperconjugation, charge transfers, and other many-body effects.⁸⁻¹⁰ Third, due to the various approximations in classical force fields, they are likely most suitable for a particular set of molecules under a specific range of conditions. For example, the stability of ion-pair interactions in a protein’s interior is likely overestimated by typical nonpolarizable force fields.¹¹

These considerations have led to the development of various linear-scaling QM methods,¹²⁻¹⁴ which hold the promise to treat both covalent and noncovalent interactions for large molecules. In practice, however, linear-scaling QM calculations remain computationally expensive whenever ab initio QM or density functional theory (DFT) methods are used. This is a particularly serious limitation for the study of biomolecules and other soft matter, where adequate conformational sampling is imperative. For many biological applications,^15,16 for example, molecular dynamics simulations on a nanosecond to microsecond scale are required, which involve millions to billions of energy and force evaluations.

It is in this context that semiempirical (SE) methods, which have a long history in quantum chemistry,¹⁷ have come back into the spotlight in recent years. The most prevalent SE methods are those based on approximations (e.g., neglect of diatomic differential overlap, NDDO) to the Hartree–Fock (HF) theory, leading to methods such as AM1,¹⁸ PM3,¹⁹ MNDO/d,²⁰ and OMx.²¹ Another approach that has become popular in the past decade is the density functional tight binding (DFTB) approach,²²⁻²⁴ which was derived in the framework of DFT based on a Taylor expansion of the energy with respect to a reference density. Both sets of SE methods use minimal basis sets and involve various approximations to electron integrals, leading to an increase of computational efficiency by a factor of 100 to 1000 over typical implementations of ab initio QM and DFT methods. As a result, with the same computational resources, SE methods can be used to study systems 10 times larger or to carry out 1000 times longer sampling.²⁵ These enhancements can be further improved by integrating SE approaches with modern computational architectures (e.g., GPUs)^26,27 and computational algorithms (e.g., linear-scaling/fragmentation techniques,^{12−14,28,29} faster diagonalizations, and/or extended Lagrangian MD algorithm).³⁰

These considerations, however, raise the following critical question: Are the SE methods sufficiently accurate for the description of structure, dynamics, and reactivity of complex molecular systems? The development of SE methods has focused on the description of the chemical bond traditionally; therefore, there is vast literature on the parametrization and benchmark of SE methods for heats of formation, structures, and other properties of mostly small molecules.³¹⁻³⁴ The description of larger systems, in which noncovalent interactions like van der Waals forces and hydrogen bonds are important, poses different challenges. In this review, we focus on this aspect of SE methods.

Along this line, we note three major sources of error for SE methods in general. The first source is limitations of the “parent” approach, which is HF for the NDDO-based methods and DFT within the generalized gradient approximation (GGA) for DFTB. HF lacks electron correlation; thus, dispersion interactions are absent entirely. Popular GGA functionals do not describe dispersion properly also and are often problematic for the description of Pauli repulsion. The second source of error is the use of a minimal basis set, which is important to computational efficiency but also introduces errors in electronic polarizability, van der Waals interactions, and hydrogen bonding. The third source of error is integral approximations, which also lead to errors in nonbonded interactions. In recent years, various empirical corrections or extension to SE methods have been proposed to ease the errors due to these approximations; they range from somewhat ad hoc empirical fixes to physical enhancements that explicitly modify the electronic structure (i.e., electron density) of molecules.

In the following, we first briefly review the formalism of HF-based (NDDO) and DFT-based (DFTB) SE methods. Then, we discuss the various correction schemes/extensions proposed for the SE methods for the treatment of noncovalent interactions. We then summarize the performance of SE methods and the correction schemes/extensions by reviewing the results for various standard test sets and recent applications. Finally, we conclude with a few remarks concerning future developments.

2. Semiempirical Molecular Orbital Theory

In standard electronic structure methods, the molecular orbitals (MOs, {ψ_i}) are approximated by a linear combination of basis functions represented by atomic orbitals (AOs, {χ_μ}):

1

The conventional HF theory usually expands all electrons in the AO basis, while SE methods typically only treat the valence shell electrons and assume these in the field of the nuclei and the (unpolarizable) inner-shell electrons. Commonly, SE methods expand the valence electron density in a minimal set of Slater-type orbitals.

The molecular orbital coefficients C_μi are obtained by solving the Roothaan–Hall equations, which can be written in the form of a generalized eigenvalue problem,

2

where F, C, and S are the Fock, MO-coefficient, and overlap matrices, respectively, and ϵ is the diagonal matrix containing the orbital energies. The Fock matrix (F) can be separated into its one-electron (h) and two-electron parts (G), the elements of which are given by

3

4

Approximations to these matrix elements are discussed next.

2.1. Approximations to Matrix Elements

The bedrock of the large family of SE MO methods is the neglect of certain integrals that make up the computational bottleneck in a conventional HF calculation.

In the zero-differential overlap (ZDO) approximation, only two-electron integrals of the type (μμ|νν) are calculated.³⁵ This conveniently reduces the scaling behavior of the two-electron part of the Fock matrix in eq 4 from to 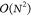in the number of atoms.

In the complete neglect of differential overlap (CNDO) family of SE methods, the ZDO approximation is used, and the Mataga–Nishimoto approximation is further applied to parametrize the retained integrals as³⁶

5

which ensures the correct convergence to 1/R_AB in the long-range limit and to 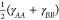in the short-range limit. Since the Mataga–Nishimoto expression only depends on the atomic parameters γ_AA and γ_BB, there is little directionality in the integrals; for instance, p-orbitals are treated equally to s-orbitals, and relative energies, such as rotational barriers, etc., are described only crudely.

The intermediate neglect of differential overlap (INDO) approximation is similar to CNDO, but integrals centered on the same atom are parametrized. Several extensions to INDO have been proposed with a focus on excited-state properties.³⁷⁻³⁹ While INDO methods are still widely used for simulating molecular properties related to electronic excitations, these are not recommended for computing energetics.⁴⁰

The neglect of differential-diatomic overlap (NDDO) approximations extend INDO by further including two-electron integrals of the type (μν|λσ), where μ and ν are AOs centered on one atom, and λ and σ are AOs centered on another atom.⁴¹ The integrals retained in NDDO greatly improve the description of rotational barriers and relative energies, compared to the predecessors of the method.⁴² Although a larger number of two-electron integrals have to be computed in NDDO, the number of integrals still scales as .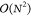

In the one-electron part of the Fock matrix (eq 3), the scaling behavior is reduced to 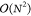by employing the following rules:

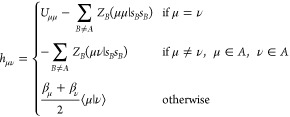6

Here, U_μμ is a free parameter related to the ionization potential, (μν|s_Bs_B) is an electron–core integral that models the interaction of orbitals centered on atom A with the unpolarizable core of atom B represented by an s-orbital-like density, and β_μ and β_ν are resonance integrals similar to those in the Hückel theory.¹⁷

The last approximation in NDDO is that core–core interactions are described with

7

rather than with an interaction between classical point charges, as done in HF. The reasoning behind this is to simulate the interaction between not only the two nuclei but also the electronic core.

2.2. Simplifications to the Roothaan–Hall Equation

The Roothaan–Hall equations are normally solved by first applying an orthogonalization transformation and solving a standard eigenvalue problem in the orthogonal basis denoted by λ,

8

and then transforming the coefficient matrix back into the AO basis, from where new density and Fock matrices can be built. In NDDO, the computational time of matrix operations is substantial compared to building the Fock matrix, and the approximation is made in NDDO theory such that

9

where F^(NDDO) is the NDDO Fock matrix that is assumed to be a priori orthogonal. In this case, the Roothaan–Hall equation takes a simple form

10

which avoids the orthogonalization procedure entirely. The diagonalization procedure required to calculate the eigenvalues and eigenvectors thus remains the bottleneck in NDDO calculations, as it inherently scales as 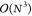, and techniques such as pseudodiagonalization are often applied to reduce the scaling of this step.⁴³

The assumption of an orthogonal AO basis set goes hand-in-hand with the NDDO approximation, as the neglected three- and four-center two-electron integrals can be shown to be small in this basis.⁴⁴ The error is, however, much larger for the one-electron part of the Fock matrix,⁴⁵ as discussed later in this chapter.

It is worth noting that most SE methods with an origin in the NDDO formalism are fitted to reproduce the heats of formation of molecules, rather than absolute energies

11

where ΔH_A^f indicates the heat of atomization of element A at 298 K. This implies that thermal corrections are absorbed by the parametrization. Therefore, in principle, appropriate thermodynamical corrections should always be taken into consideration when comparing results obtained using this class of methods to those obtained via other approaches.

2.3. Modified Neglect of Diatomic Overlap (MNDO)

The MNDO method introduced by Dewar and Thiel⁴⁶ has formed the foundation of recent advances in SE methods with great success, as will be detailed in the next section. MNDO improves upon NDDO in two main respects: (i) the two-center two-electron integrals are replaced by approximate integrals derived from multipole interactions, and (ii) there are improved core–core interaction terms in the one-electron operator.

To ease the implementation and increase the computational efficiency, Dewar and Thiel introduced an SE model for the two-center two-electron integrals in NDDO.⁴⁷ Briefly described, the integrals are approximated by the classical interaction between the multipole moments of the two charge distributions

12

where l_n is the order of the multipole moment and m describes the orientation of the multipoles. Each multipole is in turn approximated by a configuration of 2^l_n point charges, and the Dewar–Sabelli–Klopman–Ohno approximation⁴⁸ is used to calculate the interaction between the point charges, ensuring the correct behavior of the integral in the short- and long-range limits. In the long-range limit, the integral converges to the classical interaction, while in the short limit, the integral also compensates for the missing electron correlation to some degree. The overlaps required for the one-electron part of the Fock matrix are still described by the overlap of Slater functions in MNDO.

Using the NDDO theory as ansatz, the core–core repulsion is too weak due to the unpolarizable core, and bond lengths become too short. To account for this deficiency and also to take the Pauli repulsion into account approximately, the MNDO core–core repulsion energy is given by

13

where α_A and α_B are empirical, element-specific parameters, which must be obtained via fitting to reference data.

2.3.1. Extensions to the MNDO Method

Several extensions and modifications to MNDO exist, and some of the most successful ones are briefly detailed in this section.

The AM1 (Austin model 1) method¹⁸ developed in the groups of Dewar and Stewart is a further refinement to MNDO. Apart from being a complete reparametrization of MNDO, AM1 also alleviates problems with short-range interactions by adding up to four Gaussian functions to the core–core repulsion term:

14

As a result, the number of fitting parameters is increased greatly compared to the MNDO method. One of the major improvements in AM1 was that hydrogen bonds were more stable than predicted from MNDO, which generally describes hydrogen bonds poorly.^18,49

The PM3 (parametric method 3) method by Stewart¹⁹ is essentially a reparametrization of AM1 using a different parametrization strategy and only two Gaussian functions to correct the core–core repulsion. AM1 has also recently been reparametrized using a more complete set of training data in a model named RM1 (Recife model 1).⁵⁰

Motivated by the availability of a steadily increasing amount of reference data, the approach of the AM1 and PM3 models was further refined by Stewart in the PM6 (parametric model 6) method.⁵¹ Besides using a much larger set of reference data to fit the parameters, PM6 also introduced several improvements in the core–core terms. Replacing the Gaussian core–core corrections of AM1 and PM3, PM6 uses a core–core correction term originally introduced by Voityuk and Rösch,⁵² which employs pairwise parameters rather than element-specific parameters.

PM6 further uses different core–core repulsion potentials for N–H, O–H, C–C, and Si–O pairs to correct for specific weaknesses in the parametrization. Lastly, the PM6 method also adds d-orbitals in the atomic basis to certain elements, much like the MNDO/d method does.²⁰

The most recent of the PMx models by Stewart is PM7,⁵³ which further includes a dispersion correction⁵⁴ and a hydrogen-bond correction based on the H⁺ correction.⁵⁵ In addition, several semiempirical integrals are modified by switching functions to enforce convergence to the classical result at longer distances.

Several empirical correction schemes have been devised to increase the accuracy of the core–core repulsion potential further. The PDDG (pairwise distance directed Gaussian) modification by the Jorgensen group⁵⁶ adds additional Gaussian functions to the core–core repulsion term, while the PIF (parametrized interaction functions) and MAIS (method adapted for intermolecular studies) methods add longer-range functions to increase the accuracy further in the case of nonbonded interactions, such as hydrogen bonds.^57,58

Clearly, the minimal valence-only basis set approximation makes it difficult to describe interatomic polarization accurately. Different approaches have been developed accordingly to improve polarizability and interactions that rely on a proper treatment of polarization; see section 6 for more details.

2.3.2. Orthogonalization-Corrected Methods

As mentioned previously, the NDDO-type methods solve the Roothaan–Hall equations while assuming that the AO basis is orthogonal. Although this approximation is justified by the NDDO approximations in the two-electron part of the Fock matrix, it may give rise to more severe errors arising from the one-electron part.⁴⁵ The MSINDO method and the family of orthogonalization-corrected methods (OMx) seek to correct this by applying an approximate orthogonalization correction to the one-electron part of the Fock matrix.^21,59 Briefly, MSINDO and OMx employ an expansion of the explicit Löwdin orthogonalization to the second order

15

16

where h is the one-electron part of the Fock matrix and S′ is the overlap matrix with zeroed diagonal elements. From this ansatz, a semiempirical orthogonalization correction Δ^λh is derived

17

such that ^λh can be assembled approximately without performing any explicit orthogonalization at all. In the OM1 method, only one- and two-center terms are included in the correction, while three-center terms are included in OM2 additionally. OM3 also includes up to three-center terms but omits certain small terms. The OMx methods also introduce a few other modifications to the MNDO integrals, such as the addition of a Pauli-repulsion term, an effective core potential (ECP), and scaling of certain integrals by a Klopman–Ohno term.²¹

2.4. Limitations of NDDO/MNDO

2.4.1. Limitations Due to the Hartree–Fock Origin

Since HF is a mean-field theory, effects due to dynamical electron correlation are not described. Most prominent is the lack of dispersion interactions in HF, which is inherited in the SE methods derived from HF. In contrast to DFTB, which aims to derive its parameters from “first-principles” DFT, the NDDO/MNDO class of SE methods involve parameters that can be adjusted to accommodate dynamical correlation effects in an approximate way. The MNDO type of SE methods use a Slater-type basis set, but the two-center two-electron integrals are calculated using the SE multipole approximations via the Dewar–Sabelli–Klopman–Ohno approximation.⁴⁶ These integrals are shallower at shorter range compared to the corresponding analytical integrals, and this can be viewed as inclusion of some correlation effect. While this approach adds some flexibility not present in HF, it is however clear that simply adjusting parameters is not adequate for a proper treatment of dispersion interactions. Several dispersion correction schemes are discussed later in this review.

2.4.2. Limitations Due to Parametrization Data

The large number of parameters in NDDO/MNDO semiempirical methods are determined by fitting to collections of empirical data. A prominent property to which the parameters are fitted is the experimental gas-phase heat of formation at 298 K, first and foremost because these data are relatively abundant.

For instance, the original MNDO method used about 100 data points, while PM3 used 800, and PM6 used 9000 data points. This seems adequate for methods that describe only a few common elements (e.g., H, C, N, and O). For methods aiming to general applicability, however, larger amounts of data are required for the parameter optimization to reach a well-defined global optimum, especially if diatomic (pairwise) parameters are present in the model. The assembly and thorough validation of such large data sets remain a bottleneck. For instance, PM6 and PM7 are parametrized for 70 elements, each with 10–20 parameters, so the need for more data to fit diatomic parameters is dire.

The transferability of a parameter set is in part dictated by the training data. The PM7 method was fitted using the S22 data set^60,61 to increase the amount of data that pertains to nonbonded effects. This practice has not been the norm, however, because the calculations necessary to obtain such data sets have only recently become feasible.

Stewart suggested two strategies to overcome the mentioned problems: (i) experimental data should be combined with data from high-accuracy theoretical calculations (e.g., CCSD(T)/CBS), which could greatly increase the amount of diatomic data, and (ii) a scheme that involves calculating the parametric Hessian should be used to check convergence in the parameter space.⁵³

2.4.3. Limitations Due to Minimal Basis Set Approximations

The minimal, valence-only basis set used in NDDO/MNDO methods is required for the fastest possible calculations, but it is also the main reason that molecules appear less polarizable in these theories. Intermolecular polarization is underestimated by 25%,⁶² which in turn leads to a systematic underbinding of noncovalent interactions (see section 7.2 for examples.)

Some work has been put into SE methods with extended AO basis sets, such as the SINDO1 and PMO family of methods.^63,64 These methods have shown a substantial increase in accuracy for polar bonding, such as in hydrogen bonds, as well as for isotropic molecular polarizabilities.⁶⁵⁻⁶⁷ It has also been noted that d-functions might play a non-negligible role in bonding for certain chemical substitutes where the d-orbital contributes to the occupied MOs, such as nitro groups.⁶⁸ However, simply increasing the AO basis comes at the cost of lower computational throughput. Other approaches to increase the amount of intermolecular polarization involve adding an auxiliary polarizing density separate from the AO basis. Such approaches have shown promising results and are discussed in more detail in section 6.

It has been shown for the water dimer that a careful optimization of the 1s orbital exponent has a crucial impact on the description of hydrogen bonds. While too compact 1s functions actually prevent hydrogen bonds to form at all, less compact 1s functions are able to yield correct hydrogen-bonding geometries.⁶⁸

At shorter range, Pauli repulsion is also not described properly. This is in part due to the lack of basis functions, but even more so due to the integral and orthogonality approximations in the NDDO/MNDO methods. Additionally, the inner-shell electrons are neglected completely. The effects of missing Pauli repulsion and the missing (unpolarizable) inner-shell electrons must be compensated for to a large extent by careful tuning of the core–core repulsion terms, as discussed in section 2.3.1 above.

2.4.4. Limitations Due to Orthogonal Basis and Integral Approximations

The error caused by the neglect of the three- and four-center integrals in the two-electron part of the NDDO/MNDO Fock operator in the ZDO approximation is reduced in the orthogonal basis somewhat, because these integrals are small in this basis set and much smaller than the effects of orthogonality.⁴⁴ The error due to orthogonality in the one-electron part can be reduced by orthogonality corrections to some degree, as seen in the OMx methods.²¹

The orthogonality error is short-ranged in nature, and the most prominent negative effect is the large underestimation of rotational barriers, which is ascribed to the lack of Pauli repulsion largely.⁴⁵ While this can be alleviated empirically by functional forms of the core–core repulsion to some extent, this practice also introduces a substantial number of new parameters. In light of the limited data available for parametrization, such corrections might reduce the transferability of the developed models. Appropriate orthogonality corrections seem to be recommendable for future developments in this regard.

3. DFTB Theory

Similar to the NDDO/MNDO methods, DFTB calculations run 2–3 orders of magnitude faster than standard DFT-GGA approaches. In addition to the use of a minimal AO basis set and the treatment of exclusively valence electrons, such high computational efficiency results from integral approximations that allow the AO Hamiltonian matrix elements to be determined beforehand, once for all, so that they do not have to be computed during a molecular calculation. The Taylor expansion as described below does not pose a crucial approximation,^69,70 being merely a formulation to cast the DFT total energy in a form suitable for the subsequent DFTB approximations.

Several recent reviews have already focused on the DFTB formalism,^23,24 benchmark, performance, and known problems,²⁴ as well as on its unique values in applications to complex biological problems.²⁵ In the following, we first summarize the aspects of the methodology that are relevant to the description of noncovalent interactions. Then, we discuss how approximations made in the underlying DFTB methods impact the description of noncovalent interactions. More detailed benchmarks and further extensions are discussed in later sections.

3.1. DFTB Energy Expressions

To derive the DFTB models from DFT, a reference density ρ₀ is chosen as the superposition of neutral atom densities ρ₀ = ∑_Aρ₀^A, and the DFT total energy is written in terms of density deviations δρ from this reference. Expanding the exchange–correlation energy with respect to these density deviations,^71,72 the total energy can be written as

18

The DFTB models are classified as DFTB1, DFTB2 (also referred to as SCC-DFTB),⁷³ and DFTB3, due to the respective highest orders in the density deviations δρ considered. Several approximations to the integrals are applied, and the resulting approximate energy reads

19

where the indices A and B denote atoms, μ and ν denote AOs, and i denotes MOs with occupation numbers n_i. The individual terms play different roles in the description of noncovalent interactions, which will be explained in the following.

20

E⁰[ρ₀] consists of the DFT double-counting terms (see p 147 of ref (74)), and it only depends on the reference density. Therefore, it covers not only a Coulomb interaction (core–core repulsion) like in the NDDO SE methods but also the difference of electron–electron and core–core Coulomb interactions, plus the difference of exchange–correlation energy and the integrated exchange–correlation potential. It takes the form of a short-ranged function with exponential decay for any GGA functional. In practice, the pairwise functions V_AB^rep depend only on distances of nearest-neighbor bonding interactions, while they vanish in the noncovalent region. Therefore, these potentials play a crucial role for all of the covalent-bonding properties, e.g., atomization and reaction energies, bond lengths, and vibrational frequencies, but they do not affect nonbonding properties in any major way^24,75 (also see section 8.4). The parametrization as short-ranged two-body potentials, being determined by fitting to ab initio or experimental data, has three consequences: (i) possible long-range contributions are missing as well as (ii) multicenter contributions, which is discussed below in more detail. (iii) Further, the repulsive potentials V_AB also compensate for errors arising from approximations of E¹, E², and E³ through the fitting procedure.

21

This is a first-order term in the density due to the Kohn–Sham orbitals {ψ_i}. Note that the Hamiltonian involves the zeroth-order density; therefore, only first-order terms in the density appear in the Coulomb and exchange–correlation integrals. The main approximations involved here are the two-center approximation for the Hamiltonian matrix elements

22

(μ ∈ A and ν ∈ B) and, importantly, the use of a minimal Slater-type AO basis set {μ}. The basis functions are obtained from a DFT calculation involving an external confining potential during the DFTB parametrization procedure, to avoid an overly diffuse character of orbitals that occurs in free atoms, which would be inappropriate for the description of electron density in covalent bonds (between two atoms). Unfortunately, this leads to a less accurate description of the electron density at longer distances from the atom centers, affecting the description of noncovalent interactions.

23

In the second-order term, the deviations δρ from the reference density are approximated in terms of charge density monopoles,^22,73 which in turn are represented by atomic point charges obtained from the Mulliken population analysis. The integral in the calculation of charge–charge interactions is substituted by an analytical function γ_AB^h (see the next subsection for additional discussions), which converges to 1/R_AB for large distances of atoms A and B carrying the point charges, and it accounts for the deviation from 1/R_AB for short interatomic distances properly. For the on-site electron repulsion (i.e., for γ_AA), a Hubbard parameter U_A related to the atomic hardness is involved and can be obtained from a DFT calculation of an isolated atom.

24

If an anion shall be described rather than a neutral atom, the atomic electron density is expected to be more diffuse. In the DFTB framework, without including any diffuse basis functions explicitly, this phenomenon may be taken into account by considering U_A to be a function of atomic charge. The corresponding energy contribution appears in the third-order term E³, in which Γ_AB depends on the charge derivative of the Hubbard parameter.⁷²

3.2. Limitations of DFTB for Noncovalent Interactions

3.2.1. Limitations Due to the DFT-GGA Origin

DFTB is derived from DFT, and its present parametrization uses the PBE exchange–correlation functional.⁷⁶ Therefore, DFTB models inherit the limitations of GGA in general⁷⁷⁻⁷⁹ and those of PBE in particular. We discuss the limitations relevant to the discussion of noncovalent interactions briefly.

First, there is the delocalization error. In HF, the exact exchange functional compensates for the electron self-interactions (SI) stemming from the mean-field Hartree term exactly, but this is not the case in DFT because approximate exchange functionals are used. Thus, the electron–electron repulsion is overestimated, and so is the delocalization of electron density in extended systems. DFTB inherits this problem, and a recent analysis⁸⁰ indicated that the first-order term of the DFTB Taylor expansion is free of SI, while the second-order terms (quadratic in density, or atom charges) are responsible for the deviation from the “straight-line” behavior.⁷⁷ The delocalization error manifests itself in conjugated organic molecules in particular, but also in hydrogen-bonded complexes, as demonstrated, for example, with vibrational frequency shifts of C=O in strongly hydrogen-bonded complexes.⁸¹ DFT-PBE, as well as DFTB (parametrized on the basis of PBE), yields a red shift of the same magnitude upon hydrogen-bonding, amounting to as much as 80 cm^–1 in strongly hydrogen-bonded complexes. This value is overestimated grossly compared to higher-level calculations due to the overestimated charge transfer, which is caused by the delocalization error.

Second, there is the issue of van der Waals (vdW) interactions. Usually, only dispersion energy is discussed in this context, representing the attractive part of the vdW interactions. In fact, both Pauli repulsion and dispersion contributions carry significant errors with DFT-GGA, as discussed in detail previously.^82,83 DFT yields the true ground-state electron density in principle; thus, the exact DFT functional would be able to describe vdW interactions, and this is the basis for the search of new vdW functionals. In practice, however, popular approximate (LDA or GGA) functionals exhibit an exponential decay of interaction potential with distance, so they cannot account for the 1/R⁶-like dependence of dispersion, by construction. As discused in detail in ref (82) (see also references therein), the commonly used exchange functionals (e.g., PW91, PBE) underestimate the short-range Pauli repulsion and bind vdW dimers already at the exchange-only level, while the Becke exchange functionals overestimate repulsion.

For DFTB, this has two consequences: (i) an empirical dispersion contribution has to be added,⁸² and (ii) the Pauli repulsion is underestimated due to both the use of PBE and the application of a confined minimal basis set (see below). The practical impact is that DFTB tends to describe soft matter with too high a density. For discussion of possible solutions, see section 5.

3.2.2. Limitations Due to Integral Approximations

The zeroth-order contributions in eq 20 decay exponentially with interatomic distance within the DFT-GGA framework.⁸² On the basis of a correct exchange–correlation functional, they could contain long-range interactions like Pauli repulsion and dispersion interactions due to the E_xc[ρ₀] – ∫v_xcρ₀ term. Since this is omitted by describing eq 20 with short-range repulsive interactions truncated between the first- and second-nearest neighbor distances, the long-range contributions have to be included by an additional correction term, as described below.

In addition, the treatment of the zeroth- (eq 20) and first-order (eq 21) terms is based on a two-center approximation; therefore, the multicenter nature of these contributions is neglected. The DFTB integral approximations have previously been analyzed using density functional expansion methods.⁸⁴ While the expansion itself does not imply a major approximation, the neglect of multicenter contributions in the zeroth- and first-order terms do so. The errors introduced have to be compensated by an appropriate choice of the repulsive potentials. Those neglected three-center, four-center, and higher-order many-body contributions can be important for dense materials⁸⁵ and possibly also for a higher accuracy in bonding interactions.^24,84 For noncovalent interactions, three-body interactions can be included in the dispersion corrections, as discussed below, and they seem to be important for an accurate treatment of larger systems.

The second-order contributions in eq 23 involve several integral approximations and are essential to the description of noncovalent interactions. (i) The differential charge densities δρ are approximated by monopole terms; i.e., the dipole, quadrupole, and higher contributions are neglected. This affects all noncovalent properties for which orbital resolution plays a significant role, such as interactions involving lone pairs. (ii) The charge monopoles are represented by point charges obtained from a Mulliken analysis, leading to inaccurate molecular dipole moments. This may be improved by application of more sophisticated charge analysis schemes like the empirical CMn model.⁸⁶⁻⁸⁸ Furthermore, since the interaction of electron densities is modeled by point charges, subtle effects like the halogen bonding due to the presence of a σ-hole are not treated (see section 5). (iii) The atom-centered point charges interact according to the Coulomb law (1/R) for large distances, and the function γ models the deviation from the 1/R behavior due to the overlap of electron densities and exchange–correlation effects at short distances. For vanishing R, i.e., the interactions on one atom, the function converges to a certain value U, which is related to the chemical hardness of the respective atom. Thus, the deviation from 1/R at short distances, which depends on the “size of the atom”, is modeled by the chemical hardness of the atom, which was proposed to be inversely proportional to the atom size.^89,90 This relation is a good approximation for many main-group elements, but it fails for hydrogen. For this reason, a modification of γ was suggested to be used for interactions involving a hydrogen atom.^91,92 This modified function γ^h introduces a new parameter, which was fitted to reproduce the interaction energy of the water dimer. The application of γ^h constructed in this way yields substantially more accurate hydrogen-bonding energies than the original DFTB2 model.^92,93 (iv) As discussed in section 6, the inclusion of some of the on-site exchange-like integrals, which are neglected in standard DFTB models, was shown to improve the description of hydrogen bonding.⁹⁴ Formally, these integrals appear in the second-order energy contribution.

3.2.3. Limitations Due to the Minimal Basis Set

In DFTB, a minimal basis set is used for computational efficiency. Although a part of the basis set effect (e.g., larger size of an anion) is captured via the third-order term in DFTB3, the use of a minimal basis set may impact the treatment of noncovalent interactions significantly. Specifically, we have the following considerations.

First, for the treatment of hydrogen bonds, which are prevalent in biomolecules and aqueous solutions, the calculation is known to be sensitive to the quality of basis set due to at least two considerations: (i) molecular multipoles (dipole, quadrupole) are crucial to the description of the electrostatic component, but the accuracy is limited with small basis sets, and (ii) the sizable basis set superposition error (BSSE) leads to largely overestimated binding energies. With DFTB, BSSE does not occur because the matrix elements H_μν⁰ in the first-order term are precalculated. Thus, the integrals that describe the interaction of two atoms A and B (H_μν) are unaffected by the basis functions of any other atom C. Further, the second-order terms, which are responsible for the electrostatic interactions, are not basis-set dependent. Thus, it is possible to obtain good accuracy in hydrogen bonding with DFTB despite the use of a minimal basis set, as long as the Mulliken charges represent the charge distribution properly and γ_AB^h is tuned well.

For interactions that involve highly polarizable moieties, however, an additional challenge is the adequate description of polarizability, which tends to be underestimated with minimal basis sets. This is best demonstrated in a planar molecule. While the in-plane polarizability is qualitatively correct, the out-of-plane polarizability vanishes with a minimal basis set. The reason is that only one p-function in the out-of-plane orientation is located on every second-row atom, which is insufficient to represent electron density that is asymmetric in the out-of-plane direction; thus, an adequate description of out-of-plane polarization requires additional s- or d-functions. Obviously, this limitation greatly affects intermolecular interactions for which polarization is important. For instance, DFTB performed poorly for the description of charged complexes in the benchmark set by Grimme.⁹⁵ As discussed in section 6 further, one possible strategy to improve the description while avoiding larger basis sets is to apply an auxiliary polarizing basis set and compute the resulting polarization response.

The use of a minimal basis set impacts the description of short-range Pauli repulsion also. In particular, we note that the parametrizations of DFTB models involve confining potentials in atomic calculations. The confining potential modifies the electron density at distances relevant to noncovalent interactions and therefore the description of Pauli repulsion at these distances. The general trend is an underestimated Pauli repulsion and therefore underestimated intermolecular distances. For example, the older “mio” parameter set^22,73 consistent with DFTB2 uses a more strongly confined AO basis than the newer “3OB” set⁷⁵ consistent with DFTB3. Consequently, the predicted intermolecular distances tend to be shorter at the DFTB2/mio level than at DFTB3/3OB.

4. Comparison of NDDO/MNDO and DFTB Models

The NDDO/MNDO and DFTB models share many common approximations: the use of a minimal valence basis set, use of (two-center) integral approximations, and being the descent from HF or DFT as approximate theories with their respective limitations. Nevertheless, there are also important differences, which we summarize in the following.

With the density matrix P_μν = ∑_iC_μiC_νi^* in the AO basis set {χ_μ}, the ground-state density may be written as

25

Representing the DFTB reference density ρ₀ by the zeroth-order density matrix P_μν⁰, the differential density may be expressed as

26

with δP_μν = P_μν – P_μν⁰.

With these expressions, the DFTB matrix elements (with μ ∈ A, ν ∈ B) can be written as⁹¹

27

where δv_xc is the functional derivative of the exchange–correlation energy with respect to the electron density. In DFTB, the terms in the parentheses are combined in the γ function rather than evaluated individually; the above separation serves merely the purpose of comparison with the NDDO/MNDO approaches.

The NDDO/MNDO Hamiltonian, on the other hand, can be written as

28

Several differences are noteworthy. (1) H_μν⁰ and h_μν in the matrix elements in eqs 27 and 28 are different quantities. While h_μν represents one-electron terms only, H_μν contains also the electron–electron (e–e) interaction for the reference density. Therefore, DFTB provides a very accurate account of the e–e interactions for systems with small charge transfer between atoms, while NDDO/MNDO approximates the e–e interactions from the beginning. These e–e interactions are contained in the two-electron contributions, which are the last two terms in the respective equations. While these terms look similar in NDDO/MNDO and DFTB formally, there are two important differences between the treatments: (i) DFTB treats only the difference density on this level, while NDDO/MNDO covers the complete e–e interaction with these terms. Thus, a better accuracy in cases of small charge transfer may be expected with DFTB, in principle. (ii) The two-electron terms are subject to a monopole approximation in DFTB, while NDDO/MNDO applies a distributed charge approximation (eq 12), so that higher multipoles are included. Indeed, it was shown that DFTB performs like a point-charge model for large distances where the overlap vanishes,^69,96 while NDDO/MNDO may cover multipole effects in principle. (2) While the derivation from approximate methods leads to some common limitations (like the missing dispersion interaction), HF and DFT-GGA show deficient behavior with opposite trends for other properties. For instance, HF overestimates band gaps, while DFT-GGA underestimates them. This and other problems can be related to deviations from the correct “straight-line” behavior of the dependence of energy on excess charge, leading to a delocalization error in DFT-GGA and a localization error in HF.⁷⁷ This may affect the description of large molecular complexes in which charge transfer is involved. Both methods miss the description of dispersion interactions, and this is usually resolved by the addition of a damped empirical dispersion term. The damping functions, however, have slightly different meanings in HF and DFT because DFT includes correlation effects in the density-overlapping region partly, while HF does not. (3) The DFTB formalism involves an overlap matrix, while standard NDDO/MNDO methods do not. An exception is the OMx class of methods, which introduce the effects of nonorthonormality. The nonorthonormality is important for Pauli repulsion,⁹⁷ and this can be shown using two AOs in a molecule as an example: Let us consider two AOs that couple and split energetically to form a pair of a bonding and an antibonding MO. In an orthogonal method, the orbital energies split symmetrically, while a nonorthogonal method yields a larger positive shift of the antibonding orbital and a smaller negative shift of the bonding orbital. If both orbitals are doubly occupied, which is the case relevant for vdW interactions, the larger energy shift of the antibonding orbital leads to a larger repulsion. The standard NDDO/MNDO schemes miss this effect and therefore tend to underestimate Pauli repulsion further.^21,45

5. Empirical Post-SCF Correction Schemes

5.1. Dispersion Corrections

A crucial deficiency in the SE approaches described in the previous sections is their origin in theories that lack a description of dynamical electron correlation. Dispersion is a long-range, nonlocal correlation effect, which means that HF (being a mean-field theory) and standard semilocal and hybrid density functionals (e.g., PBE) do not describe such effects. For this reason, DFTB- and NDDO-based methods are unable to describe dispersion interactions properly.

While the effects of dispersion interactions are much smaller than, for example, hydrogen bond interactions and ionic and covalent bonds, they are ubiquitous in nature. Dispersion forces are the dominant forces in a variety of situations, such as π–π stacking of aromatic molecules, binding between lipids, and binding to graphene. Even in very polarized systems, such as bulk water, it is well-known that an accurate description of dispersion is crucial,^98,99 and it also plays a major role in binding to halogen atoms.¹⁰⁰

In what follows, we highlight several recent approaches to augment SE methods such that they describe dispersion interactions in a cost-effective manner. To avoid costly additions to the QM calculations, these are post-SCF in nature. Further, they do not depend on the electron density, but rather on atom coordinates, in similar fashion to molecular mechanics (MM). Besides the fast evaluation of energy, the MM-like nature also allows the gradients to be low in complexity and evaluated quickly.

Commonly, this class of dispersion corrections builds on various interpretations of the London dispersion energy between two atoms, derived from second-order perturbation theory,¹⁰¹

29

where I_A and I_B are the ionization potentials of atoms A and B, and α_A and α_B are the polarizabilities of the respective atoms. To include the dispersion in SE and other QM methods, several authors have adopted an empirical expression consisting of an R^–6 term that is dampened at short distances

30

where f(R_AB) is a damping function that removes the otherwise unphysical dispersion energy at short ranges, and C_6,AB is a diatomic constant calculated from atomic polarizabilities via the Slater–Kirkwood relations. This approach was first added to DFTB2 by Elstner and co-workers⁸² and allowed for a correct description of nucleic acid base stacking, which is impossible to achieve with the uncorrected DFTB2 due to the lack of dispersion.

Several very similar dispersion corrections have been developed by other groups: Clark and co-workers developed such a dispersion correction for NDDO methods and demonstrated the importance of dispersion for small complexes, such as the benzene dimer and the methane–ethane dimer;^68,102 the atomic polarizabilities in the C₆ coefficients were solved in a variational fashion. Hillier and co-workers adopted the dispersion correction for AM1 and PM3 and showed a great improvement in the description of DNA systems¹⁰³ and also sulfur-containing molecules.¹⁰⁴ Likewise, in the OMx-D method by Thiel and co-workers, a dispersion correction is added to the OMx family of methods. For OM3-D, the root-mean-square deviation (RMSD) of the interaction energy is reduced from 5.4 to 1.7 kcal/mol for a set of 145 complexes of small molecules, and similar improvements are seen for OM1-D and OM2-D.¹⁰⁵ Zhenchkov and co-workers developed a Lennard-Jones-type potential that uses the parameters of the UFF force field, and they saw similar improvements to interactions between H₂ and bulk graphene and polycyclic aromatic hydrocarbons for DFTB.¹⁰⁶

Perhaps the most widely adopted dispersion-correction scheme for SE methods is the family of dispersion corrections by Grimme. The first- and second-generation D and D2 corrections use an expression similar to eq 30, scaled by a factor, s₆, close to unity.^107,108 In the most recent development, the third-generation D3 correction, also a R^–8 term is included, and the coordination number of each atom is taken into account.¹⁰⁹ The constants are calculated from atomic polarizabilities obtained with time-dependent DFT, but the values of scaling factors and the limits of the switching functions are free parameters that must be fitted for the specific QM method to which the D3 correction is added.

Some additional work has been put into the functional form of the short-range damping function of the D3 method.¹¹⁰ In the original formulation, the dispersion energy vanishes at R_ab = 0 using the “zero-damping” function introduced by Jurečka and co-workers⁵⁴ A more physically motivated damping function is proposed by Becke and Johnson; at R_ab →0, it converges to a finite value that corresponds to the total dispersion energy of the atom pair.^111−113

Similar to the two-body D3 term, a three-body dispersion term has been developed by Grimme and co-workers based on the Axilrod–Teller–Muto dispersion term^114,115 derived from a third-order perturbation theory

31

Some recent results suggest that three-body interactions are required for accurate treatment of larger systems, such as the L7 data sets, but they are generally negligible for calculations with less than 10 atoms.^95,116 D3 parameters have been published for around 100 elements, and the free parameters in the D3 model have been fitted for many DFT functionals and SE methods. For example, DFTB3 without dispersion corrections exhibits an RMSD of 3.0 kcal/mol for the dimerization energies in the S66 data set, while this error can be reduced to 1.1 kcal/mol by including the D3 correction.¹¹⁷ For larger systems, the effects are even more dramatic: for a number of water clusters,¹¹⁸ the RMSD in total binding energy is reduced from 14.2 to 2.0 kcal/mol by including the D3 correction, and the RMSD for the L7 data set can be reduced from 15.9 to 2.3 kcal/mol.¹¹⁷

The D3 correction has been benchmarked thoroughly for SE methods and has been implemented in several QM programs. It seems unrivaled in both adoption and widespread use currently and is thus generally recommendable for all studies at the SE, DFT, or HF levels of theory.

A more recent development by Petraglia and co-workers is the dDsM dispersion correction.¹¹⁹ Here, an expression similar to eq 30 is used, but the values of C_6,AB depend on the Mulliken charges of the molecule. This in turn introduces a direct dependence on the underlying electron density, although the dDsM correction is still added as a post-SCF correction using the converged Mulliken charges, as it was shown that the effects of self-consistency were negligible.¹²⁰ Since the Mulliken charges are robust for small and minimal basis sets, the method seems especially attractive for SE methods. dDsM was parametrized for DFTB3 and PM6 and showed encouraging improvement over the D3 correction for dissociation energies and stacking configurations of aromatic biomolecules. However, as the value of C_6,AB depends on the Mulliken charges, the gradient has an electronic contribution, and only an approximate gradient that neglects this contribution has been published currently, although the error seems small.

As discussed earlier in this review, the effects of Pauli repulsion are underestimated in SE methods, primarily due to the use of a minimal basis set. While this affects covalent bonding (e.g., rotational barriers are underestimated), it also affects noncovalent interactions. The effect of dispersion corrections is a stronger attractive potential, which accentuates the lack of Pauli repulsion at shorter distances to some degree. Řezáč and Hobza introduced a repulsive term between hydrogen atoms, to obtain a description of binding between hydrocarbons in the D3H4 correction that is a balance between the strictly attractive D3 potential and missing Pauli repulsion.¹²¹

5.2. Hydrogen Bond Corrections

As discussed earlier in this review, the lack of polarizing functions in a valence-only AO basis set causes the intermolecular polarization to be underestimated. A direct consequence is that the strength of an intermolecular interaction between polar functional groups is underestimated. During the past decade, a number of post-SCF hydrogen-bonding corrections have been proposed to alleviate this shortcoming of SE (NDDO) methods.

Some recent developments are the H, H2, H2X, H+ H4, and H4X corrections.^55,121−126 These are essentially MM terms that depend on hydrogen-bonding distances and important bond angles. In general, these take the form

32

where c is a scaling factor, f_DHA is a function that takes into account the structure of the donor–hydrogen–acceptor complex, and f_damp is a damping function that enforces a correct behavior in the long-range and short-range limits. Most commonly, these are combined with an empirical dispersion correction, such as D3; see the previous section.

The parameters of these combined dispersion and hydrogen-bond corrections are fitted to reproduce dissociation energies obtained from high-level QM calculations.¹²⁷ A subtle consequence of this is that NDDO/MNDO methods that are postcorrected with a hydrogen-bond term are no longer an approximation to the standard enthalpy of formation, an important realization for certain thermochemical calculations.¹²⁸ This is not an issue for those NDDO/MNDO methods that include the hydrogen-bond term during method development and parametrization, such as PM7.⁵³

The first- and second-generation of hydrogen bond corrections^122,123 use functional forms that do not have a continuous second derivative; therefore they may be problematic for the simulation of processes such as proton transfer, and further, they may hinder the convergence of geometry optimizations. Another problem with these corrections is that even though they are additive and of post-SCF nature, they still depend on the partial charges of the atoms involved formally. Consequently, the SCF energy is no longer a variational minimum. Although the error is small in most cases, this becomes a problem for geometry optimizations because the point of vanishing force no longer coincides with the minimum of energy.⁵³

The third-generation hydrogen-bonding H+ correction⁵⁵ uses a functional form that has removed the dependence on partial charges, thus allowing for smooth proton transfers, and the H4 correction¹²¹ further removes problems with certain linear conformations that were present in H+.^121,125 These hydrogen bond corrections are comparable in accuracy for model dimer systems, such as the S22 and S66 data sets. When used in conjunction with D3, the interaction energies of complexes involving one hydrogen bond are predicted with an SE method typically within an RMSD of 1 kcal/mol compared to CCSD(T)/CBS, while the RMSD is typically around 0.5 kcal/mol for dispersion-dominated complexes.^121,125

For the binding free energies in a test set of 30 large host–guest complexes, Sure and Grimme found little difference between the accuracy of four different hydrogen-bonding corrections using hydrogen-bond- and dispersion-corrected PM6.¹¹⁶ For a set of nine complexes that involve ionic interactions, the RMSD of 9 kcal/mol with uncorrected PM6 only improves to 6 kcal/mol with PM6-D3H4, and the RMSD of 4 kcal/mol with DFTB-D3 even increases slightly to 5 kcal/mol with DFTB3-D3H4.¹¹⁷

In an extensive review of PMx, DFT, and SAPT methods, Gilson and co-workers compared the accuracy of PM6-DH+, PM6-DH2, PM6-DH2X, and PM7 on seven data sets.¹²⁹ In most cases, no consistent differences in accuracy were found among the PMx-based methods. For complexes involving a charged moiety, PM7 was found to be 0.2–0.5 kcal/mol more accurate. However, some inconsistencies were revealed in the treatment of halogen bonds. Large errors around 10 kcal/mol were found for complexes involving an HF molecule with all methods, and also the binding between bromobenzene and nitrogen gave errors of similar size for the PM6-based methods. For short halogen bonds, the X-correction was found to increase the accuracy substantially;¹²⁴ This correction is discussed in more detail in sections 5.3 and 7.2.4.

While hydrogen bond corrections to SE methods improve the accuracy of dimerization energies greatly, they do not solve the underlying problem of missing polarization, as they do not modify the underlying wave function. This means also that cooperative effects are not taken into account explicitly. For example, for a set of 15 water clusters containing 6–17 water molecules,¹¹⁸ the DFTB3-D3 model exhibits a remarkably low RMSD of total interaction energies of only 2.0 kcal/mol, compared to a CCSD(T)/aug-cc-pVTZ reference. However, this RMSD increases to 23.9 kcal/mol with DFTB3-D3H4,¹¹⁷ demonstrating that great care has to be taken whenever methods created from gas-phase models are used to simulate the condensed phase.

In short, the accuracy of dispersion- and hydrogen-bond-corrected SE methods for dissociation energies of dimer complexes is very close to that of DFT with modestly sized basis sets.^95,116,117 The accuracy is unclear, however, for larger systems where cooperative effects are crucial, and great care needs to be taken when using hydrogen-bonding corrections. This is also the reason why this strategy has never been adopted for DFTB widely. Initial tests showed that binding energies of dimers can be improved quite substantially indeed.²² Still, the additional potential is not very transferable and is usually fitted for weak hydrogen bonds with relatively long hydrogen bonding distances. For strong hydrogen bonds and in particular when cooperative bonding effects are present, an additive potential is no longer sufficient. An analysis of hydrogen bonding showed that the problem is rather electrostatic in nature, leading to the modification of the γ-function^83,91 as described above in section 3.2.2. Note that Clark an co-workers performed a similar analysis for the NDDO type of methods.⁶⁸

5.3. Halogen Bond Correction

Halogen bonds are noncovalent interactions between an electron donor and a halogen atom covalently bound to an electron acceptor. Compared to the hydrogen atom in a hydrogen bond, the electron density around a halogen atom is much more anisotropic, and a positively charged region exists along the covalent bonding axis of the halogen atom, the so-called σ-hole. This region interacts with the lone pair of the electron donor, forming the halogen bond. Riley and Hobza used symmetry-adapted perturbation theory to show that this interaction accounts for approximately half of the halogen bond energy, while the rest of the interaction energy is mostly due to dispersion interaction.¹⁰⁰ Halogen bonds are badly reproduced by minimal basis set SE methods, which systematically overestimate the interactions. Řezáč and Hobza have devised the halogen bond “X-correction” term for PM6, which is combined with Grimme’s D2 dispersion corrections to yield the D2X correction.¹²⁴ The halogen bond correction adds a repulsive potential to alleviate the overestimated interaction energy

33

where a and b are empirically fitted parameters. For a small data set, the mean error in interaction energies for PM6-D2X was 0.4 kcal/mol. The X-correction was recently merged with the more recent D3H4 correction, yielding the D3H4X correction.¹²⁶

Kubillus and co-workers have recently derived a more refined halogen bond correction, much similar in spirit to the X-correction by Hobza for use with dispersion-corrected DFTB3¹³⁰

34

where c₁, c₂, and c₃ are universal parameters for the model and d_AB is a pair-specific parameter. Furthermore, a screening function is applied to ensure that the artificial σ-hole is switched off at covalent-bonding distances. Protein–ligand binding energies were found to be similar to those obtained with DFT using modest basis sets, and only minor deviations in halogen-bonding geometries were observed. As discussed in section 7.2.4, these X-corrections improve the description of halogen bonds by SE methods substantially, leading to errors on the order of merely ∼1 kcal/mol compared to high-level ab initio calculations.

5.4. Empirically Corrected Small-Basis-Set Methods

Pioneered by the Grimme group, empirical corrections have also been applied to ab initio methods with small but highly specialized basis sets. In terms of accuracy and computational cost, the resulting methods lie somewhere in between conventional ab initio methods and the SE methods that are the focus of this review. While SE methods are 100–1000 times faster than DFT and HF with reasonably sized basis sets, these methods are 10–50 times faster.⁹⁵ These methods are defined by the addition of several empirical corrections, such as a dispersion corrections, and additional corrections for limitations related to the finite basis set. To maximize accuracy, the involved empirical parameters are fitted only for the specific method and basis set.

In the HF-3c method (HF with three corrections), the minimal basis set MINIX is used. The HF energy is augmented by the D3 dispersion correction using the Becke–Johnson damping and, additionally, by the gCP (geometrical counterpoise) and the SRB (short-range bonding) corrections.¹³¹ gCP is a pairwise correction for BSSE, which only depends on the nuclear coordinates.¹³² In a similar, pairwise fashion, SRB corrects for the overestimation of bond lengths with small basis sets.¹³¹ This empirical approach contains a total of only nine parameters, and it retains an accuracy close to DFT with large basis sets while the computational cost is low owing to the minimal basis set. HF-3c has been refined further into the HF-3cv method, which involves a valence-only basis set with an ECP, causing only a minor decrease in accuracy.⁹⁵

Most recently, the ideas of the corrected HF methods have been adopted for DFT with a double-ζ basis set. In the PBEh-3c method, a slighty reparametrized version of the PBE0 functional is used with the Ahlrichs-type def2-SV(P) basis set, with an ECP for heavier atoms, and the D3 and gCP corrections are applied together.¹³³ For noncovalent interactions, PBEh-3c was found comparable in accuracy to DFT with medium-sized and large basis sets and vastly improved compared to DFT with similarly sized basis sets.

6. Quantum Mechanical Extensions to Semiempirical Methods

Although the empirical corrections described in the previous section alleviate some limitations of popular SE models, they are not coupled with the electronic structure of the molecule; therefore, their transferability to more complex systems is not warranted. For example, we have recently observed¹¹⁷ that the empirical hydrogen-bonding correction at the DFTB3 level, while valuable for small water clusters, leads to substantially overestimated binding energy of larger water clusters. Therefore, it is worth pursuing extension of SE methods such that the electronic structure is affected (possibly modified) by noncovalent interactions explicitly.

6.1. Electrostatics

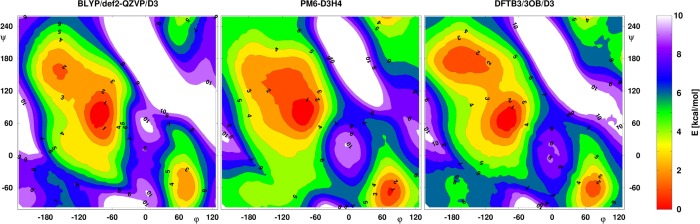
Electrostatic interactions make up a major contribution to noncovalent interactions between many molecules. To ensure an accurate description of electrostatics at all distances, it is important that multipole moments of molecules are described well. Along this line, it is worth noting that the two-electron integrals in NDDO/MNDO methods are evaluated on the basis of multipole models of the AOs (e.g., see eq 12); thus, the angular distribution of atomic charge densities is maintained for interactions at all distances. In DFTB, short-range effects are described by both H_μν⁰ terms (eq 21) and the second-order term (eq 23), while long-range effects are solely described by second/third-order terms (eqs 23 and 24). In the latter, the atomic charge distributions are approximated in the current implementation by monopoles (Mulliken charges); thus, the angular dependence of charge distribution is lost. Consequently, while the angular dependence of hydrogen-bonding interactions is properly described at the DFTB3 level around equilibrium distances, larger errors occur at longer distances^96,134 (see Figure 1). To what degree such an error impacts key properties in the condensed-phase remains to be analyzed thoroughly; dynamical properties of hydrogen-bonded systems are likely to be affected.

Figure 1.

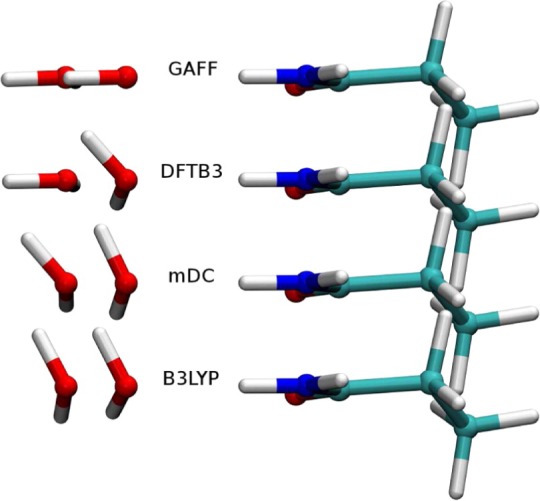
Effect of multipoles on hydrogen-bonding interactions at different distances. Although the angular dependence of the water–amide interaction is described by DFTB3 at short distance correctly, the description reduces to that of an MM force field at longer distances due to the use of charge monopoles in the second-order term. Reproduced from ref (134). Copyright 2014 American Chemical Society.

To alleviate the errors associated with the monopole approximation, York and co-workeres have developed a QM force field model (referred to as modified divide-and-conquer, mDC).^29,135 Here, the monomer units (e.g., individual water molecules or amino acids) are treated with DFTB3/3OB (although other QM methods can also be used), while the interactions between them are treated with a parametrized multipolar charge model complemented by Lennard-Jones interactions

35

Here, q_lm is the atomic multipole moment on atom A, p_lm is a multipolar potential at atom A due to the multipoles on all of the other (B ≠ A) atoms,

36

37

and C_lm(r) are real regular solid harmonics.

The mDC model is similar in spirit to the Xpol model of Gao and co-workers²⁸ in terms of the fragmentation philosophy, although the current Xpol implementation treats the monomer–monomer electrostatic interactions at a QM/MM level using point charges for one of the monomers. The mDC model has been parametrized for water and biomolecules and also implemented for simulations with periodic boundary conditions using the multipolar particle–mesh Ewald method.^96,134 The results obtained from simulations of bulk water under different conditions, protein–ligand interactions, and molecular crystals suggest that the mDC model is a promising approach that warrants continuing developments. In a separate line of work,¹³⁶ the density variations in the DFTB framework (Δq_A from eq 19 onward) have been extended to include higher multipolar contributions, although no complete implementation and parametrization of such a multipolar model has yet been reported.

The Mulliken treatment of two-electron integrals, which sets every differential overlap of atomic orbitals as 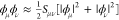, also leads to the neglect of certain on-site contributions due to the orthogonality of AOs centered on the same atom. Another piece of improvement of DFTB⁹⁴ was motivated by this realization, having derived an on-site correction that includes exchange-like one-center two-electron integrals (μν|μν) with μ, ν ∈ A and μ ≠ ν. The effect of including these integrals on the energy is that the variation of off-diagonal elements of the dual density matrix connecting orbitals ϕ_μ and ϕ_ν residing on the same atom is now considered. The standard DFTB model only involves the variation of diagonal elements of the dual density matrix (i.e., the Mulliken populations). The tests performed on water clusters indicate that the on-site integral corrections improve the hydrogen-bonding interactions substantially indeed, without the need for any special modification of γ for HX pairs⁹¹ as discussed in section 3.2. Moreover, the on-site-corrected DFTB3 (without modified γ) appears to treat water–hydroxide interactions better than other DFTB models. So, while DFTB3/3OB overbinds the clusters (OH)⁻(H₂O)_n (n = 1–4) by 6–8 kcal/mol, the error is reduced to 1–2 kcal/mol with the on-site correction. Since the repulsive potentials were not reoptimized after the inclusion of the new on-site integrals, the robustness and transferability of the on-site DFTB model remain to be explored systematically.

6.2. Polarization and van der Waals Interactions

A major limitation of SE methods is the use of a minimal basis set, which leads to underestimated van der Waals interactions and polarization, typically. It is possible to alleviate this limitation by augmenting the basis with, for example, p functions on the hydrogen atoms. Indeed, this was done in the SINDO1 method⁶³ and the PMO suite of methods by Gao and Truhlar and their co-workers.^64,66,67 This was emphasized by Clark and co-workers¹³⁷ as being seminal for the treatment of polarizability in organic molecules. Hydrogen-bonding geometries and energies were observed to improve in SINDO1⁶⁵ and PMO,⁶⁶ and the PMO2 method further reduced errors in molecular polarizabilities by 80%.⁶⁷ Also, DFTB2 was augmented with p-orbitals on hydrogen with similar improvements in energetics and geometries.^22,138

From the computational perspective, including p functions on hydrogen atoms can be costly; for biomolecules, this increases the size of the basis set by a factor of roughly 2, which leads to an increase of computational cost of nearly an order of magnitude, due to the 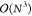scaling for standard implementations. Moreover, including p functions on hydrogen may also lead to an imbalance in the basis set. In previous studies,^22,63 for example, the contribution from the p-orbitals needed to be truncated beyond a certain distance. These considerations ignited a search for alternative approaches to improve the polarization.

One approach is based on the principle of chemical potential equalization (CPE), in which the SE density [ρ_SE(r)] is augmented by an additional, polarizable response density^139−141

38

where the CPE basis functions φ_i^CPE(r) are, for example, p-type Gaussian functions. The expansion coefficients c_i are solved by a variational minimization of the total energy

39

where

40

Here q indicates QM partial charges and M and N represent the interactions between the QM/CPE and CPE/CPE charge distributions, respectively. The simplest model invokes Coulombic interactions in M and N, and short-range effects (e.g., kinetic energy contribution) are approximated by employing a distance-dependent scaling function. Since the CPE and SE SCF equations are solved in a sequential fashion, the increase in computational cost is rather modest.

The CPE approach has been combined with the MNDO/d method^141,142 and, more recently, with the DFTB2⁶⁹ and DFTB3 methods⁸⁷ to improve the molecular polarizability. Errors in the isotropic molecular polarizability were reduced substantially, although any further improvements in the anisotropy likely require larger CPE basis sets. In the latest work by Christensen and co-workers,¹¹⁷ the CPE approach was coupled with the DFTB3/3OB method for the description of noncovalent interactions. It will be shown in section 7 that it was possible to improve the molecular polarizability and intermolecular interactions simultaneously, with a modest number of parameters. As expected, the impact of CPE is most significant for interactions that involve polar and charged molecules. Moreover, it was observed that the CPE model is substantially more transferable among molecules of different sizes and charge states compared to pure MM corrections to SE methods. For example, the overstabilization of large water clusters observed for empirical hydrogen-bonding corrections does not occur with the DFTB3/CPE model.

Notably, for the CPE model to be sufficiently flexible for molecules of different charge states, it was found crucial to allow the exponent of the CPE basis functions (ζ_i) to vary as a function of the atomic partial charge (Δq_A). An analysis of the charge-dependence of atomic polarizabilities led Giese and York¹⁴¹ to propose an exponential dependence model

41

where z_A (not nuclear charge) and B_A are element-dependent parameters.

A related approach is SCP-NDDO, in which the NDDO energy is augmented by an additional, self-consistent polarizing (SCP) contribution^143,144

42

where ΔE_SCP depends on a multipolar polarization density matrix

43

There are both additional polarization and dispersion contributions; the polarization density matrix is solved self-consistently together with the NDDO density matrix (P_λσ), while the dispersion contribution is included in a post-SCF fashion. SCP-NDDO has been mainly parametrized for water,^143,144 with PM3 serving as the reference method that provided the starting parameters; an additional p-type function is also included for hydrogen. The SCP-PM3 model was shown to provide a much improved description for both water clusters (with an RMSD of interaction energies of 0.19 kcal/mol relative to the MP2/CBS estimates for n = 2–6 and 8) and bulk water (see section 8.4), compared to PM3. It is interesting to note that a similar SCP approach has been introduced to improve DFT methods as well.¹⁴⁵

7. Benchmark Calculations

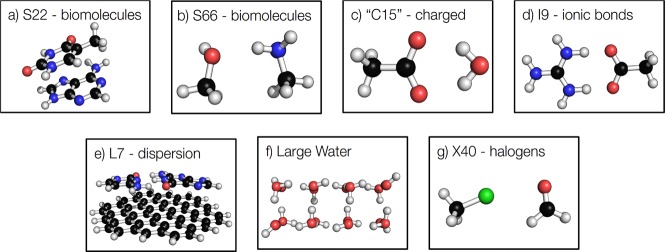
In this section, we review some of the recent advances in the data sets for the benchmarking and validation of quantum chemical methods for the prediction of noncovalent interactions. Many of these sets were developed for calibrating ab initio/DFT methods, although they have also recently been used to benchmark SE methods. First, we detail the common strategies for calculating accurate interaction energies briefly and then we summarize a number of the most useful and accurate data sets.

7.1. Standard Test Sets for Molecules

Often touted as the “gold standard” of computational chemistry, the coupled cluster method with single, double, and perturbative triple excitations, CCSD(T), in the complete basis set limit (CBS) has become the go-to method for very accurate calculations of interaction energies, and the only notable shortcomings are essentially systems where multireference and relativistic effects are pronounced.^146,147 Here, we detail briefly the CCSD(T)/CBS approach used to generate some of the most recent and most accurate data sets currently available. We refer the reader to the reviews in refs (148) and (149) for more information.

Noncovalent interactions are most frequently evaluated by calculating the dissociation energy between two or more individual molecules in a cluster. For example, the dissociation energy of the dimer complex AB consisting of the molecules A and B can be calculated as

44

where E_AB, E_A, and E_B are the calculated energies of the complex and the two monomers, respectively. The same formula can be generalized to molecular clusters of three or more molecules.¹⁵⁰

Accurate estimates of these energies can be done by using extrapolation techniques: these approaches exploit the fact that the remaining correlation energy beyond MP2 converges quite rapidly.¹⁵¹ Thus, the CCSD(T)/CBS energy can be approximated as the sum of the MP2/CBS energy and a small CCSD(T) correction

45

46

where E_MP2^CBS is the MP2 energy extrapolated to the CBS limit, and E_CCSD(T) and E_MP2^{small–basis} are the CCSD(T) and MP2 energies evaluated with a smaller basis set. Extrapolation schemes such as that by Halkier and co-workers can be used to extrapolate the MP2 energy to the CBS limit.¹⁵² Řezáč and co-workers recommended using at least aug-cc-pVDZ as the small basis set and preferably aug-cc-pVTZ and aug-cc-pVQZ to extrapolate the MP2 energy to the CBS limit, and the Boys–Bernardi counterpoise correction¹⁵³ should be used to remove any BSSE.¹⁵⁴ For dimer interaction energies calculated using eq 45, the error is estimated to be around 1%, and such energies are thus appropriate as validation and benchmark data for SE methods.¹⁴⁶

We noted recently that a high accuracy of an SE method in the gas-phase does not necessarily guarantee the transferability of the method to the condensed phase.¹¹⁷ For this reason, it is necessary to create data sets containing larger molecular clusters, such as trimers, host–guest complexes, and water clusters. In addition, a treatment such as eq 45 is trivial for smaller molecules, but the steep scaling of the CCSD(T) correction becomes prohibitive for large complexes quickly. The use of localized molecular orbitals (LMOs) with cutoffs in coupled cluster methods have led to methods with greatly reduced scaling compared to canonical coupled clusters, and these methods are very attractive for use in the study of large molecular assemblies. For instance, the DLPNO-CCSD(T) method¹⁵⁵ has recently been applied to the L7 data set, which contains complexes with up to 112 atoms.⁹⁵ We expect these LMO methods to constitute the basis of future data sets with larger molecular assemblies.

7.1.1. Common Data Sets for Biological Nonbonded Interaction

Several data sets have been created to model noncovalent interactions in biomolecules. One of the first data sets of CCSD(T)/CBS quality was the S22 set created by Hobza and co-workers in 2006.⁶⁰ S22 contains CCSD(T)/CBS-extrapolated interaction energies for 22 dimer complexes with a range of organic molecules that mimic biologically relevant interactions, such as pairs of amino acid side chains and of DNA bases. S22 has been updated with more accurate interaction energies^61,156 and extended into the S26 data set,¹⁵⁷ and dissociation curves have also been published.^158,159 The S66 data set also by Hobza and co-workers contains 66 dimers of organic molecules and is more balanced in terms of different interaction motifs than S22.¹⁶⁰ Dissociation curves and interaction energies for angularly displaced conformations have been published for S66.¹⁵⁴ In a similar fashion, Hobza and co-workers have created data sets for dimer complexes with ionic bonds¹²¹ and the X40x10 set that contains halogenated molecules.¹²⁶ The A24 data set, which also includes relativistic effects and coupled-cluster energies with up to quadruple excitations, is an attempt to assess the errors introduced by the CCSD(T) level of theory and nonrelativistic Hamiltonians.¹⁴⁶ For the 24 dimers in the A24 set, the error in CCSD(T) compared to CCSDT(Q) was found to be 0.95% of the total interaction energy, while relativistic effects accounted for 0.14% of the total interaction energy.

Two data sets by other groups, similar to the sets mentioned already, are those by Mintz and Parks, consisting of small organic dimers containing divalent sulfur,¹⁶¹ and the I9x8 set by Christensen and co-workers, containing interactions between ionic side chain analogues.¹¹⁷ Sherill and co-workers have established the HSG database,¹⁶² which considers intermolecular contacts for fragments taken from the crystal structure of indinavir bound to the HIV-II protease. Also, the performance of various correlated methods for describing noncovalent interactions was examined carefully.^163,164 Together with the sets mentioned earlier, these extend the space of benchmark data sets to cover virtually all interactions found in organic biomolecules.

7.1.2. Water Clusters

As water has been notoriously difficult to model due to the complex electronic structure of its hydrogen bonding and the non-negligible role of cooperative effects, several groups have created collections of water clusters of various sizes. These are some of the most recent ones: the set of water clusters by Truhlar and co-workers,¹¹⁸ with 15 water clusters ranging from 6 to 17 molecules; the WATER27 set by Goddard and co-workers,¹⁶⁵ with 27 clusters of up to 20 water molecules, of which 6 clusters contain a hydronium ion and 7 contain a hydroxide ion; and the water clusters by Shields and co-workers, consisting of 38 clusters with 2–10 water molecules.¹⁶⁶

7.1.3. Supersets

Some of the work by Hobza and co-workers is collected in the Benchmark Energy and Geometry Database (BEGDB) for molecular clusters and complex molecular systems.¹²⁷ Similar collections or “supersets” of nonbonded interactions have been put together by other groups. For instance, Friesner and co-workers collected a total of 2027 CCSD(T)-quality interaction energies from the literature into a set used to parametrize their B3LYP-MM model.¹⁶⁷ The GMTKN30 superset by Goerigk and Grimme collects 30 data sets of general main-group thermochemistry, kinetics, and noncovalent interactions and contains S22 and WATER27 along with a number of additional data sets that probe noncovalent interactions.¹⁶⁸ Zhao and Truhlar assembled a database for general ground-state properties, such as thermochemistry, barrier heights, noncovalent interaction energies, and spectroscopy.¹⁶⁹ A subset of this database, named NCIE53, contains the interaction energies of 53 dimers that model noncovalent interactions in biomolecules.

7.1.4. Large Complexes

The data sets mentioned so far consist of small model dimers, and it is therefore difficult to assess the role of many-body interactions and cooperative effects in the noncovalent bonding. Řezáč and co-workers have created the 3B-69 set consisting of 69 trimer structures for which the three-body energy, defined as the difference between the total energy of the trimer and the sum of the individual monomer energies and the two-body energies, is extrapolated to the CCSD(T)/CBS limit.

The L7 data set by Hobza and co-workers seeks to model systems where large dispersion forces are dominant, such as circumcoronenes, alkanes, and stacked base pairs, and contains complexes with up to 112 atoms.¹⁷⁰ Extrapolated DLPNO-CCSD(T)/CBS interaction energies have recently been calculated by Grimme and co-workers.⁹⁵ Other data sets for large, supramolecular assemblies have been created: The S12L set by Grimme and co-workers and its recent extension, S30L, are models of large host molecules that bind a smaller ligand molecule.^116,171 For these data sets, the experimental binding free energies have been back-corrected to theoretical binding energies and have been used to benchmark the applicability of a number of DFT functionals and SE methods for such calculations.

7.1.5. Molecular Crystals

While the data sets already mentioned in this section are based on a gas-phase type of interaction, molecular crystals can be used to simulate condensed-phase calculations. Since the “gold standard” CCSD(T) treatments as suggested in eq 45 are currently not affordable for obtaining electronic lattice energies routinely, experimental sublimation enthalpies are back-calculated by careful subtraction of thermal and zero-points effects evaluated at the dispersion-corrected DFT level.

For instance, Ortero-de-la Roza and Johnson constructed the C21 data set, which contains the geometries and sublimation enthalpies for 21 molecular crystals.¹⁷² C21 has been expanded by Reilly and Tkatchenko in the X23 data set.¹⁷³ The chemical diversity of C21 and X23 is much like that of the S66 and S22 sets and includes dispersion-dominated, hydrogen-bonded, and mixed-type molecular crystals. Similarly, the ICE10 data set, consisting of 10 ice polymorphs, has been created by Grimme and co-workers.¹⁷⁴ Despite the inaccuracies introduced by the combined experimental and theoretical approach to calculate interaction energies, X23 and ICE10 currently serve as rigorous benchmarks for interaction energies in solids and the condensed phase.¹⁷⁵

7.2. Benchmark of Popular SE-QM Methods

In this section, we summarize the benchmarks of some of the most recent SE methods mentioned above, by comparison to high-level CCSD(T) calculations carried out on the data sets in the previous section. Additionally, we compare the accuracy of the ever-popular DFT functional B3LYP^176,177 with the essentially converged basis set def2-QZVP,¹⁷⁸ as well as with the more modestly sized 6-31G(d)¹⁷⁹ basis set. More computational details are presented in section 7.3.

A number of data sets are discussed in section 7.1, which all probe different types of noncovalent interactions and thus provide insight into the specific shortcomings and strengths of the methods we are benchmarking. We focus on the following data sets.

General performance: For a general overview of each method, the S22 and S66 sets^60,160 are used, which probe a variety of dispersion and polar interactions, such as hydrogen bonding.

Nonpolar interactions: The L7 set¹⁷⁰ and the dispersion dominated subset of S66 probe the accuracy of describing dispersion-type interactions.

Polar interactions: The polar-interaction subset of S66, the data set of 15 charged hydrogen-bonded complexes by Hobza and co-workers¹²¹ (referred to as “C15” hereafter), and the I9 set,¹¹⁷ which models ionic side-chain interactions, are used to probe the accuracy of strong polar interactions. Furthermore, a set of water clusters by Truhlar and co-wokers¹¹⁸ (referred to as “large water” hereafter) are used to elucidate cooperative bonding effects. These systems pose a challenge to the balanced description of polar and nonpolar intermolecular forces, as well as cooperative binding effects.

Halogen bonds: The X40 set¹⁸⁰ is used to assess the accuracy of binding to halogenated molecules.

The accuracy of interaction energy estimates for the data sets mentioned here is presented in Table 1, while the results for the halogen bonds in X40 are presented separately in Table 2. A graphical overview of the data sets considered is shown in Figure 2, and an overview of the accuracy of selected methods is shown in Figure 3.

Table 1. Calculated Interaction Energies Are Compared to “Gold Standard” CCSD(T) Binding Energies for 10 Methods Using 8 Different Data Sets, Which All Probe Different Types of Interactions^a.

	S22		S66		S66 (disp)c		L7
method	RMSD	MSD	RMSD	MSD	RMSD	MSD	RMSD	MSD
DFTB3b	4.1	3.4	3.0	2.7	3.4	3.1	15.9	14.1
DFTB3-D3b	1.5	0.7	1.1	0.4	0.6	–0.4	2.3	–1.4
DFTB3-D3H4b	1.2	0.5	0.9	0.3	0.5	0.3	2.6	0.8
DFTB3/CPE(q)-D3b	1.1	0.5	0.6	0.0	0.7	–0.3	2.1	–0.6
PM6b	4.2	3.4	3.0	2.7	2.8	2.6	12.8	10.9
PM6-D3H4b	0.8	0.4	0.6	0.2	0.4	0.1	3.4	–1.1
OM2	3.7	3.1	2.9	2.6	3.2	3.1	16.1	14.0
OM2-D3	1.4	0.9	1.1	0.6	0.4	0.1	2.6	0.6
B3LYP/6-31G(d)	3.7	1.6	2.7	1.3	4.0	3.8	18.7	15.6
B3LYP-D3/6-31G(d)	2.9	–2.4	2.3	–2.1	1.6	–1.5	7.9	–7.5
B3LYP/def2-QZVP	5.0	3.7	3.8	3.2	5.4	5.2	22.7	20.1
B3LYP-D3/def2-QZVP	0.6	–0.3	0.4	–0.3	0.2	–0.2	3.2	–3.0

	S66 (pol)d		C15e		I9		large water
method	RMSD	MSD	RMSD	MSD	RMSD	MSD	RMSD	MSD
DFTB3b	2.9	2.6	6.0	4.8	5.6	4.7	14.2	11.1
DFTB3-D3b	1.8	1.3	5.0	3.6	3.9	2.6	2.0	–1.4
DFTB3-D3H4b	1.0	–0.2	4.1	2.2	4.7	2.7	23.9	–20.3
DFTB3/CPE(q)-D3b	0.6	0.1	1.5	0.6	1.7	0.5	3.0	–1.9
PM6b	3.8	3.2	4.6	4.3	9.1	8.5	34.8	27.9
PM6-D3H4b	0.6	0.0	1.5	0.8	6.0	5.6	11.0	8.9
OM2	3.0	2.9	3.2	2.9	(5.7)f	(6.1)f	26.0	20.4
OM2-D3	1.9	1.7	2.3	1.9	(4.1)f	(4.6)f	14.0	10.9
B3LYP/6-31G(d)	1.4	–1.2	3.5	–3.2	10.0	–8.7	53.0	–44.8
B3LYP-D3/6-31G(d)	3.3	–3.2	5.2	–5.0	12.8	–12.0	72.5	–60.4
B3LYP/def2-QZVP	1.6	1.4	1.0	0.9	1.3	1.2	10.5	6.7
B3LYP-D3/def2-QZVP	0.7	–0.6	1.0	–0.9	2.3	–2.1	9.7	–8.9

^aThe root-mean-squared deviation (RMSD) and the mean signed deviation (MSD) between the calculated and reference energies are given in units of kcal/mol. A positive MSD value implies a tendency to the underbinding of complexes.

^bDFTB and PM6 values from ref (117).

^cOnly the “dispersion” subset of S66 is considered here.

^dOnly the “polar” subset of S66 is considered here.

^e“C15” refers to the set of 15 charged hydrogen-bonding complexes from ref (121).

^fDue to lack of OM2 parameters for sulfur, three complexes are left out of the OM2 and OM2-D3 statistics for the I9 set.

Table 2. Performance of Tested SE Methods as Well as Representative DFT Methods for the Halogen-Bonded Complexes in the X40 Set (complexes 13–26)^a.

method	RMSD	MSD
PM6-D3H4	2.1	–0.9
PM6-D3H4X	0.5	+0.3
DFTB3/3OB/D3	3.7	–3.3
DFTB3/3OB/D3Xb	0.6	+0.1
B3LYP/def2-SVP	0.6	+0.4
B3LYP/def2-SVP/D3	1.9	–1.8
B3LYP/def2-QZVP	2.1	+2.2
B3LYP/def2-QZVP/D3	0.3	–0.1

^aRoot-mean-squared deviation (RMSD) and mean signed deviation (MSD) are in kcal/mol.

^bCalculations performed for complexes 13–24 only because the X corrections were not parametrized for sulfur–X contacts, which are involved in complexes 25 and 26.

Figure 2.

Representative systems from the data sets discussed in Tables 1 and 2. The data sets are discussed in detail in section 7.1.

Figure 3.

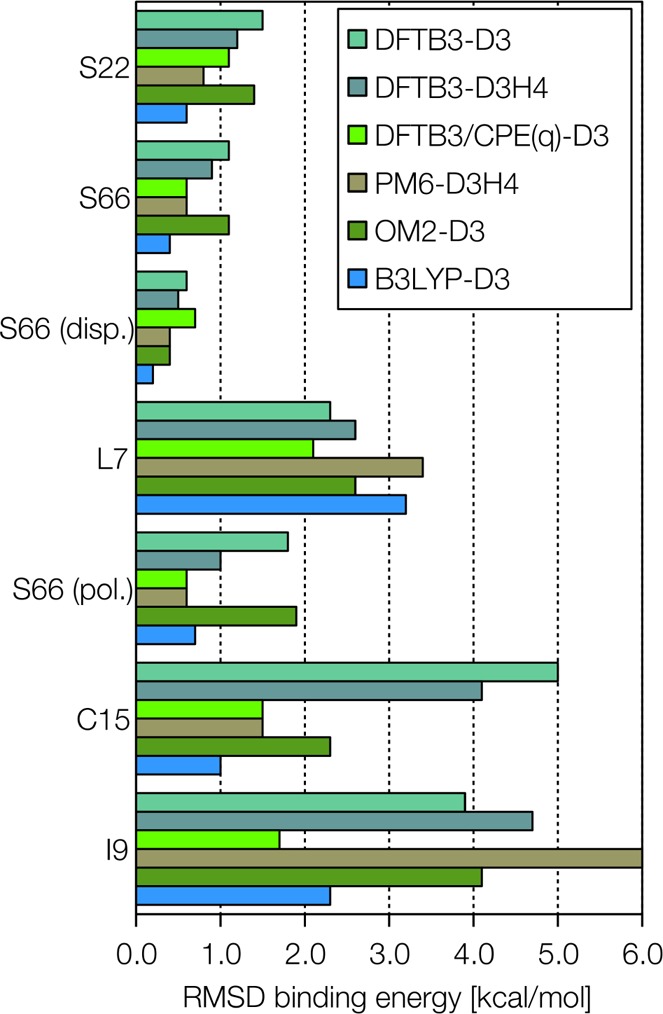
Root-mean-squared deviation (RMSD) of the binding energy for seven different data sets is shown for five selected semiempirical methods involving the empirical corrections D3 and D3H4. Results obtained with B3LYP/def2-QZVP/D3 are shown for reference.

7.2.1. General Performance

For the S22 and S66 data sets, the error in the binding energy for the uncorrected SE methods DFTB3, PM6, and OM2 are comparable, with RMSDs of 3.7–4.1 kcal/mol for S22 and of 2.9–3.0 kcal/mol for S66, with respect to the CCSD(T)/CBS reference. In all cases, the mean signed deviations imply a systematic underbinding of around 3 kcal/mol for the uncorrected methods. The addition of the two-body correction D3 to DFTB3 and OM2 decreases the RMSD for the S22 data set to 1.5 and 1.4 kcal/mol for the two methods, respectively, while the RMSD for S66 is 1.1 kcal/mol with both methods.

For DFTB3 and PM6, we show the effect of adding the combined dispersion and hydrogen-bond correction, D3H4. For DFTB3-D3H4, this correction yields a decrease of RMSD by 0.2–0.3 kcal/mol, compared to solely using the D3 correction. Especially in the case of PM6-D3H4, the RMSD values of 0.8 and 0.6 kcal/mol for the S22 and S66 sets, respectively, are the lowest of any of the corrected SE methods presented. The DFTB3/CPE(q)-D3 method is close to PM6-D3H4 with an RMSD of 1.1 and 0.6 kcal/mol for S22 and S66, respectively.

For reference, we also calculate the interaction energies with B3LYP and dispersion-corrected B3LYP-D3 using the large, essentially converged def2-QZVP basis set. With no dispersion correction, the errors are quite large, at 5.0 and 3.8 kcal/mol for the S22 and S66 sets, respectively. A dramatic increase in accuracy is observed with the dispersion correction: RMSD is reduced to 0.6 and 0.4 kcal/mol, respectively.

Thus, it is quite apparent that a large portion of the errors observed here can be attributed to the lack of dispersion, and the two-body D3 dispersion correction is indeed very effective at correcting for dispersion, despite its mechanical post-SCF character.

7.2.2. Nonpolar Interactions

To probe nonpolar interactions more closely, we look at the dispersion-dominated subset of S66 (S66 disp) and the L7 set. The complexes in consideration here lack any substantial binding between polar molecular groups and are thus dominated by dispersion forces completely, and any error in predicted interaction energy can be attributed to the intrinsic lack of dispersion in the method used.

In all cases, uncorrected methods exhibit quite large errors in the range of 2.8–5.4 kcal/mol for S66 disp. In contrast, all methods that are augmented with the D3 dispersion correction display very good agreement with the CCSD(T)/CBS references, with RMSD values in the range of 0.4–0.7 kcal/mol for S66 disp. B3LYP-D3, in comparison, is slightly closer to the reference, with RMSD of only 0.2 kcal/mol for S66 disp. For the large complexes in the L7 set, the errors are found to be larger compared to those for S66, in the range of 12.8–22.7 kcal/mol. Remarkably, RMSD is reduced to as little as 2.1–3.2 kcal/mol for all methods when the D3 dispersion correction is applied. Apparently, the error is quite small and only a few tenths of a kcal/mol larger than that of dispersion-corrected DFT with a large basis set, across all dispersion-corrected SE methods.

7.2.3. Polar Interactions

Some stronger noncovalent interactions often encountered in biomolecules are hydrogen bonds, charged hydrogen bonds, and ionic bonds. To assess these three categories of polar binding, we look at the polar subset of the S66 data set (S66 pol), the C15 set, and the I9 set. Typical interaction energies for complexes in these data sets are 10, 20, and 120 kcal/mol, respectively. We note that dispersion only makes a small contribution in these data sets; for example, the typical magnitude of the D3 dispersion contribution is only 1–2 kcal/mol.

For S66 pol, the methods DFTB3/3OB, PM6, and OM2 with no corrections yield comparable RMSD values of ca. 3 kcal/mol. In the case of the C15 set featuring charged motifs, the RMSD values are 6.0, 4.6, and 3.2 kcal/mol for the three methods, respectively. In the case of DFTB3, the large RMSD is dominated by complexes with hydrogen bonds to the nitrogen lone pair of a methylamine molecule, a previously reported shortcoming of DFTB3/3OB.¹¹⁷ In the cases of PM6 and OM2, there are no similar large outliers, and OM2-D3 exhibits a relatively small error for C15, corresponding roughly to double the RMSD value with B3LYP-D3. The D3H4 correction is capable of reducing the PM6-D3H4 RMSD to 1.5 kcal/mol, only 0.5 kcal/mol higher than the RMSD of B3LYP-D3. D3H4 does not solve the nitrogen-related problem of DFTB3 completely, however, and the RMSD for DFTB3-D3H4 is 4.1 kcal/mol. The DFTB3/CPE(q)-D3 method, on the other hand, was parametrized with this problem in mind and seems to work well; the RMSD values for the S66 pol subset and the C15 set are among the lowest observed.

The ionic bonds in the I9 set are substantially stronger than those in C15. For DFTB3 and OM2, the RMSD interaction energies are comparable, at 5.6 and 5.7 kcal/mol, respectively, while these values for DFTB3-D3 and OM2-D3 are 3.9 and 4.1 kcal/mol, respectively. Note that OM2 does not have parameters for sulfur, so three complexes are left out of the statistics for I9 and OM2. For PM6, however, the RMSD for I9 is 9.1 kcal/mol, and all of the complexes are predicted to bind rather weakly, especially those complexes involving methyl acetate. Adding the D3H4 correction to PM6 gives a moderate decrease in RMSD to 6.0 kcal/mol. However, adding the D3H4 correction to DFTB3 actually increases the RMSD by 0.8 kcal/mol compared to DFTB3-D3. DFTB3/CPE-D3, by contrast, gives a small RMSD of 1.7 kcal/mol, almost comparable to B3LYP with a large basis set.

Another important view of polar interactions in larger systems is gained from looking at systems that are condensed-phase-like, such as large water clusters, which feature substantial polar interactions, non-negligible dispersion forces, and strongly cooperative hydrogen bonding.

Here we focus on the set of large water clusters by Truhlar and co-workers.¹¹⁸ It is apparent that no method without dispersion correction can predict the binding energy of the large water clusters properly. Indeed, the RMSD values for DFTB3, PM6, and OM2 are quite large, and underbinding in the range of 14–35 kcal/mol is observed. Adding the D3 dispersion correction brings the RMSD for DFTB3-D3 and OM2-D3 down to 2.0 and 14.0 kcal/mol, respectively.

While OM2 and DFTB3 have comparable accuracy on small dimers, such as those in the S22 and S66 data sets, it is apparent that this does not necessarily guarantee good performance in the condensed phase. The situation is illustrated for DFTB3-D3H4 even better: while the RMSD for DFTB3-D3 is 2.0 kcal/mol, this actually increases to 23.9 kcal/mol for DFTB3-D3H4 due to strong overbinding. Interestingly, PM6-D3H4 underestimates the binding with an RMSD of 11.0 kcal/mol. We speculate that this is primarily due to the lack of cooperativity in the H4 correction, which is entirely mechanical in nature and parametrized on small, gas-phase model systems.

In contrast, the DFTB3/CPE(q)-D3 method scales well, by design, with an RMSD of 3.0 kcal/mol for large water clusters. In comparison, B3LYP with no correction predicts underbinding with an RMSD of 10.5 kcal/mol. Adding a dispersion correction for B3LYP-D3 leaves the RMSD practically unchanged at 9.7 kcal/mol, though, but the complexes are overbound instead.

For comparison, we also computed the binding energies with the B3LYP functional using the modestly sized 6-31G(d) basis set. In all the data sets presented so far, the binding energy is overestimated strongly due to a substantial BSSE. Adding the D3 dispersion correction only adds further to the systematic overbinding, and in general, we actually find that the errors (RMSD and MSD) of interaction energy are smaller for dispersion-corrected SE methods than for B3LYP/6-31G(d). However, adding the D3 dispersion correction to B3LYP with the def2-QZVP basis set leads to errors that are roughly half that of the dispersion-corrected SE methods. These observations are in line with our recent results obtained with the PBE functional.¹¹⁷ For the large water clusters, B3LYP-D3 has an RMSD of interaction energy of ca. 10 kcal/mol, but we note that other dispersion-corrected functionals, such as RPBE-D3, revPBE-D3, or BLYP-D3, might provide a better description of strong hydrogen bonding.

In short, the discussion of water cluster results illustrates the need for considering not only gas-phase dimers but also systems representative of the condensed phase, for which SE methods are often applied. Generally, models parametrized for gas-phase model systems cannot be assumed to be transferable to molecular systems in the condensed phase.

7.2.4. Halogen Bonds

As described in section 5.3, due to their electronegativity, halogen atoms attract the electron density in molecules, inducing a negative electric field in the surroundings. However, a halogen atom, usually iodine or bromine in an organic molecule, may feature a somewhat anisotropic electron density distribution, and the region of positive electric potential on its surface is then called a σ-hole.¹⁸¹ The σ-hole may interact attractively with an electronegative atom or group (see Figure 4), and this is the nature of halogen bonding (X-bonding).^182,183

Figure 4.

Halogen bond in the complex F₃C–Br···O=CH₂. The electrostatic potential on the surface of the molecules is color-coded (red, negative; blue, positive). The light blue cap on the bromine atom is the σ-hole. Note the nonlinear orientation of the molecules, such that the σ-hole can point directly at one of the lone pairs of the formaldehyde oxygen atom.

Apart from the electrostatic interaction, dispersion also makes important contributions. This is due to the large polarizabilities of the atoms in contact, the halogen and the negatively charged partner. Heavier halogens exhibit stronger X-bonds, and X-bonding in general is somewhat tunable.¹⁸⁴ A dedicated review of X-bonding may be found in another contribution to this issue.¹⁸⁵

The σ-hole can only be described with QM as long as a basis set larger than minimal is used. Since SE methods rely on the application of (sub)minimal basis sets, they fail to render the σ-hole on the halogen atom, and thus they cannot capture X-bonding. Specifically with PM6, noncovalent interactions are too attractive because of underestimated repulsion. The problem was rather intriguing because the PM6 interaction energies in minimum-energy structures were in rather good agreement with ab initio references; as soon as the distance dependence of interaction energies was analyzed, however, the qualitatively wrong description of the interaction was unraveled.¹²⁶ As summarized in section 5.3, an additional repulsive contribution was proposed in the exponential form a exp[−bR]¹²⁴ and was later reparametrized.¹⁸⁶ The situation with DFTB is similar to that with the NDDO-based methods like PM6: halogen bonds are overbound strongly in DFTB due to the missing residual Pauli repulsion. In analogy to PM6, the recent parametrization of DFTB3/3OB for halogens¹³⁰ was complemented with an additional repulsive contribution in the form of a exp[−b(R – d_ij)^c] for each pair of atoms i, j constituting a halogen bond. (We note that ways to describe X-bonding in MM force fields were proposed also. An elegant possibility is to introduce a virtual atom close to the halogen atom, which makes it possible to capture the anisotropy of the electric field correctly, provided the parametrization is properly done.^187−189)

The performance of corrected PM6 and DFTB3 is assessed and compared to DFT in Table 2. As for the full-DFT approaches, the B3LYP calculations performed with a quadruple-ζ basis set and a dispersion correction agree perfectly with the CCSD(T)/CBS reference. The remaining B3LYP results illustrate the problems of DFT calculations in general: the overbinding due to BSSE whenever a smaller basis set is used (e.g., double-ζ) and the underbinding due to the missing dispersion interaction whenever the method is uncorrected for this failure. The small deviations obtained with dispersion-uncorrected B3LYP/def2-SVP are a consequence of a fortuitous cancellation of these errors. Coming to the tested SE methods, both PM6-D3H4 and DFTB3/3OB/D3 overbind the X-bonded complexes if they are uncorrected for X-bonding. With all relevant corrections applied, i.e., those for dispersion, H-bonding, and X-bonding, the accuracy of PM6-D3H4X is very close to that of DFT-D, a much more computationally costly approach.¹⁸⁶ Much the same, the description of X-bonding with DFTB3 is improved largely upon application of an X-bonding correction DFTB3/3OB/D3X. The interaction energies of X-bonded complexes in the X40 set are obtained with an RMSD of less than 1.0 kcal/mol with both PM6-D3H4X and DFTB3/3OB/D3X. It may be generalized that these corrected SE models provide results of a similar or better quality than DFT methods with double-ζ basis sets. This is true even for chemically difficult systems, such as the very strong halogen bonds of fluorinated compounds.

Regarding the angular dependence of X-bonding, see also another review in this issue.¹⁸⁵ The X-bonding is an interaction with a clear directionality: the σ-hole always points in the direction of a lone pair of the interaction partner, as seen in the case of the F₃C–Br···O=CH₂ complex in Figure 4, which adopts a nonlinear Br–O–C geometry in the minimum-energy structure. The energy landscape along the angular degree of freedom is very flat, however. The performance of the empirically corrected methods for this effect does not seem to be investigated yet, and additionally, the benchmark sets available to-date concentrate on the distance dependence of the interaction energy rather than on any angular dependence.

7.3. Computational Methodology

For calculations not involving halogen atoms, B3LYP and PM6 calculations were carried out in Gaussian 09,¹⁹⁰ and OM2 calculations were carried out in the MNDO99 program.⁴⁶ For B3LYP-D3 and OM2-D3, the dispersion corrections were calculated using the Becke–Johnson damping function (D3-BJ). For the OM2-D3 calculations, the two-body D3 dispersion correction was calculated in the DFTD3 program supplied by Grimme and co-workers^109,110 with the parameters from ref (95), while Gaussian 09 was used to calculate B3LYP-D3-corrected energies using the default parameters implemented in Gaussian 09. B3LYP calculations were carried out using the def2-QZVP basis set, for which the D3 parameters have been parametrized, and with the smaller 6-31G(d). The counterpoise correction was not used in any calculations. Although no new DFTB3 calculations are carried out on complexes not involving halogen atoms, it is worth mentioning that all presented DFTB3 calculations (including those with the various corrections) use the 3OB parameter set,⁷⁵ as well as the hydrogen γ_XH-correction.

The calculations of X-bonded complexes were performed with TurboMole 7^191,192 (B3LYP), Mopac 2012¹⁹³ (PM6), and DFTB+ ¹⁹⁴ (DFTB3). As for the DFT calculations, the D3 correction was used in conjuction with D3-BJ and the functional-specific parameters implemented in the TurboMole package. The DFTB3 calculations involved the 3OB parameter set as well as the D3-BJ and X corrections, as described in ref (130). The same methods and programs were used for the calculation of the potential energy surface (PES) of alanine dipeptide and alanine tetrapeptide in sections 8.2.1 and 8.2.2, respectively. TurboMole was used for calculations on the small peptides with aromatic side chains in section 8.2.3 as well as for RI-MP2 calculations in section 8.2.2. The metadynamics QM/MM simulations in section 8.2.4 were performed with a recent DFTB3 implementation¹⁹⁵ in Gromacs 5,¹⁹⁶ which involves the D3-BJ correction.

8. Applications

8.1. Nucleic Acids

8.1.1. Nucleobases

Historically, the extension of DFTB2 accounting for the dispersion interaction was first applied to describe both H-bonded and stacked DNA base pairs;⁸² these kinds of contacts between DNA bases are depicted in Figure 5. H-bonded nucleobase pairs were shown to be described well with most QM methods;¹⁹⁷ SE methods capture H-bonding qualitatively, while underestimating the interaction energy as discussed earlier in this review. Upon application of the dispersion correction, a balanced description of H-bonding and stacking interaction was achieved: the RMSD for H-bonded base pairs was 1.1 kcal/mol over the considered set of 26 complexes, and all of the stacked base pairs were overbound slightly by 1.5 kcal/mol systematically. The dependence of interaction energies on the twist angle was reproduced well for the stacked pairs. A recent systematic study suggested that the interaction energies of both H-bonded and stacked nucleobase pairs are underestimated by a larger margin of ca. 5 kcal/mol, however.¹⁹⁸ This is likely due to the use of an improved ab initio reference compared to the initial work by Elstner and co-workers in 2001. The performance of SE methods for these very strongly H-bonded complexes thus needs to be investigated further, considering the newer corrections discussed in previous sections.

Figure 5.

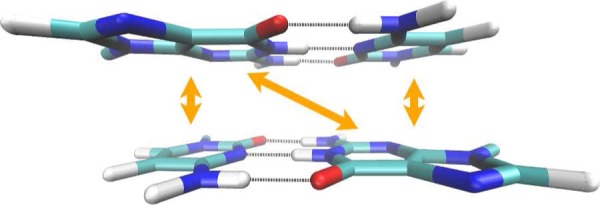
A DNA base pair step in the B-DNA configuration, viewed from the major groove. Major noncovalent interactions highlighted are hydrogen bonds (gray shaded lines) and dispersion contacts (orange arrows).

The corrected DFTB2-D method was further used to characterize the interactions in the complex of a molecule intercalating into a double-stranded DNA oligomer.¹⁹⁹ The obtained interaction energies agreed with the ab initio reference, indicating that the (dominant) dispersion contribution was accounted for properly. Also, DFTB2-D was used to prune many-body contributions to the complex interaction between several base pairs and the intercalator molecule. They were found to be negligible, however, providing justification for the application of a pairwise additive method like an MM force field. Still, a modified force field was required in order to compensate for the missing description of a charge-transfer interaction, which was large in the case of cationic intercalators.

8.1.2. Carbohydrates

Apart from the nucleobases and the phosphate groups, the ribose or deoxyribose moiety is the remaining component of nucleic acids. Application of SE methods to carbohydrates has a long tradition, as exemplified by a study of the stereochemistry of glucopyranosides in solution,²⁰⁰ which used the method perturbation configuration interaction using localized orbitals (PCILO)²⁰¹ with an implicit solvent model. The current computational state of the art to describe the isomerism of monosaccharides was reviewed,²⁰² and it was stated that the failure of commonly used SE methods—MNDO, AM1, and PM3—to capture dispersion interaction makes them unable to reproduce relative energies of carbohydrate conformations; the different sugar ring conformations for an example of guanine deoxyribonucleoside are shown in Figure 6. Much like in the case of peptide conformation (see below), modern MM force fields, which incorporate the dispersion explicitly, can often provide a better description of noncovalent interactions in carbohydrates, outperforming the more computationally costly SE methods. Although MM force fields may come into trouble as well, in particular for anomeric effects,²⁰³ it was concluded that they were still the method of choice, especially for MD studies, in particular MM3, GROMOS, and the dedicated GLYCAM06.²⁰⁴

Figure 6.

Relevant conformations of the sugar ring of guanine deoxyribonucleoside: the two energy minima (Min1 and Min2) as well as the lower-energy transition state (TS).

A similar conclusion was arrived at in a study of the three-dimensional structure of a glycosaminoglycan,²⁰⁵ which applied an MM force field as well as two QM/MM setups involving SE methods. The calculated properties were compared with experimental references (vicinal couplings, nuclear Overhauser enhancements and glycosidic linkage geometries). Among the QM/MM approaches, PM3-CARB1 (carbohydrate-specific parametrization of PM3)²⁰⁶ complemented with the TIP3P MM water model and DFTB2-D/TIP3P showed the best performance for a few of the monitored structural aspects. However, the fully classical MM approach GLYCAM06/TIP3P provided the best overall result, with the most accurate description of monosaccharide puckering, three-dimensional structure, and solvent interactions.

Barnett and Naidoo considered the quality of reproduction of ring pucker to assess the accuracy of several SE methods (with QM/MM approaches) for the description of carbohydrate structure.²⁰⁷ Among AM1, PM3, PM3CARB-1, and DFTB2, DFTB2 provided a free energy surface that was different from the NDDO methods (AM1, PM3, and PM3CARB-1), while it was similar to the surface yielded by ab initio methods. In their further work, a new method was proposed to cut polar glycosidic bonds in QM/MM simulations, such that complex glycans could be simulated with sufficient accuracy with this simple link atom hybrid saccharide (SLASH) method.²⁰⁸ Also developed was a new SE reparametrization, AM1/d-CB1, which provides means to simulate glycosylation reactions more accurately.²⁰⁹

York and co-workers revisited the pertaining problem of SE methods, the unsatisfactory description of sugar pucker, concentrating on sugars that occur in nucleic acids.²¹⁰ As a benchmark, the gas-phase two-dimensional PES along the puckering coordinates was generated with an ab initio method. Then, the considered NDDO and DFTB2 were corrected by means of an empirical correction in the form of B-splines. Much like the other recent empirical corrections for SE methods, this was fitted to the difference between the ab initio reference and the particular uncorrected method. The corrected SE methods reproduce the reference energy profiles, including the transition state observed in the ab initio data, and are expected to perform well in QM/MM simulations of nucleic acids.

8.1.3. Outlook

In short, for the treatment of nucleic acid systems, dispersion-corrected SE methods such as DFTB2-D already provide rather reliable descriptions for many applications. For carbohydrates, however, current SE methods remain qualitative in nature and require empirical corrections to improve the description of the underlying PES. At a more fundamental level, this suggests that a better description of Pauli repulsion is crucial. Other issues worth further tests for a reliable description of nucleic acids in general include the description of the highly charged phosphate group and its interaction with water and ions.

8.2. Peptides and Proteins

Noncovalent interactions, such as hydrogen bonding and dispersion, are important to the conformational properties of peptides and proteins. Therefore, a balanced treatment of bonded (torsional) and nonbonded interactions is needed for a reliable description of these systems.

8.2.1. Alanine Dipeptide in Vacuo

The so-called alanine dipeptide or dialanine (CH₃CO–NHCH(CH₃)CO–NHCH₃, referred to as “AD” hereafter) is one of the smallest molecules featuring a peptide-like pair of (φ, ψ) angles, and as such, it has been the subject of computational chemistry studies for 25 years.^211−213 It was suggested to involve the main principles of protein backbone conformation^214,215 while representing a merely two-dimensional problem, and thus, AD is an ideal molecule to show and analyze the performance of protein simulation methods.

In the gas phase, the PES of AD exhibits six stationary points, on the levels of B3LYP/6-31G* and MP2/6-31G*.²¹⁶ The three lowest-energy conformers possess intramolecular H-bonds (see Figure 7, top). The conformers C₇^ax and C₇ contain a seven-membered ring created by the H-bond, and they differ in the orientation of the alanine side chain (methyl group), which is perpendicular to the ring in C₇^ax and it is in the plane of the ring in C₇. In C₅^ext, a weak H-bond is formed between the amino hydrogen and the carboxyl oxygen of the central alanine, forming a five-membered ring. These conformations are visible clearly on the PES of AD (Figure 8) as well as on the free energy surface obtained with DFTB3/3OB (section 8.2.4). The higher-energy conformers contain no H-bonds. These are the β-turn-like conformation, β₂, as well as the right- and left-handed α-helical conformations, α and α_L.

Figure 7.

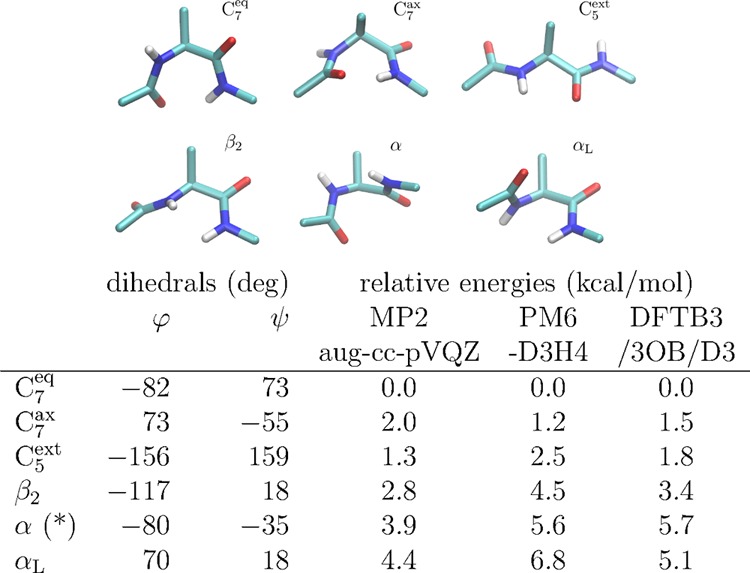
Considered gas-phase structures of alanine dipeptide. The relative conformational energies were obtained with dispersion-corrected PM6 and DFTB3, as well as with RI-MP2 for reference. Prior to that, the geometries were optimized on the DFT level BLYP/def2-TZVP/D3. (*) The structure α is not a stationary point on the BLYP/D3 PES; therefore, the geometry was obtained with restrained minimization to keep the dihedrals φ and ψ fixed.

Figure 8.

Potential energy surface of AD in the space of dihedral angles φ and ψ: (left) BLYP/def2-QZVP/D3 (reference), (center) PM6-D3H4, (right) DFTB3/3OB/D3. Energies from single-point calculations performed with the respective methods on structures obtained from restrained optimization on the B3LYP/def2-TZVP level.

In a study of SE performance to describe the AD molecule,²² these six (meta)stable structures were considered as starting structures for energy minimizations with the DFTB2, AM1, and PM3 methods. Both AM1 and PM3 produced distorted structures of C₅^ext, where the intramolecular H-bond disappeared. The energy of α-helical structures is too low compared to the H-bonded ones. This was explained by the underestimated strength of H-bonds in C₅ and C₇, leading to too weak stabilization of C₅^ext and C₇ compared to α. β₂ was not a stationary point on the DFTB2, AM1, and PM3 PESs. It was shown that AM1 and HF calculations with a double-ζ basis set do not predict turn structures to be stable conformers.²¹⁷ Also, AM1 and PM3 did not reproduce the energy ranking and structures of secondary structural motifs.^218,219 On the other hand, DFTB2 seemed to describe the structure of AD reliably and the energetics semiquantitatively. Secondary structural motives, like β-sheets, helices, and turn structures, were predicted as stable conformers, in agreement with B3LYP results.

To assess the performance of up-to-date corrected SE methods, the φ–ψ space of AD was scanned with both PM6-D3H4 and DFTB3/3OB/D3; all of the degrees of freedom except φ and ψ were subject to optimization on the DFT level B3LYP/def2-TZVP. The resulting energy maps are shown in Figure 8, together with the BLYP/def2-QZVP/D3 energies for reference. The features of the DFT PES are reproduced by the SE methods in general. C₇^eq is the global minimum, and there is a clear minimum at C₇; however, it is visibly deeper than in the reference. The barrier between C₇^eq and C₇ is only slightly lower with both SE methods. Interestingly, while DFTB3/3OB/D3 reproduces the local minimum at C₅^ext, PM3-D3H4 fails to do so. The resolution of this study (6° for both φ and ψ) does not make it possible to locate any other (metastable) minima, but still it illustrates well how the SE methods describe the peptide bond: the main features are reproduced well, and DFTB3/3OB/D3 provides even details like the C₅ minimum.

8.2.2. Longer Peptides in Vacuo

Alanine oligopeptides are a traditional benchmark or showcase for computational methods. The energetics of these larger molecules may already involve a competition among H-bonding, dispersion, and steric strain. Looking for applications of SE models, we found the study “Stability of α-helical structure of poly(l-alanine)”, dating back to 1973,²²⁰ although the applied “semiempirical” energy function was actually an MM force field. Up-to-date research, on the other hand, keeps reporting constantly on peptides that are inherently difficult to describe with computational chemistry. As an example, Rizzo and co-workers have investigated a heptapeptide (Ace-Phe-Ala₅-Lys-H) for which “experiment and theory struggle to agree”.²²¹ This peptide turned out to be also a “validation challenge” for DFT methods.²²² Since there are four confomers very close in energy, high accuracy is needed to reproduce their ranking. While this particular molecule is definitely an extreme case, peptides represent this kind of challenge in general: there always seem to be several conformations with rather similar energies, and since different kinds of covalent and noncovalent interactions play different roles in the individual conformations, all of them need to be described quite accurately.

This led to conformational ensembles of simple peptides being used to test the performance of various QM methods, including SE methods. Friesner and co-workers compiled a set of 10 conformations of alanine tetrapeptide in the gas phase, complemented with a dimer of AD in a β-sheet arrangement.²²³ With the primary purpose of testing various force fields, this set contains various structures that range from extended to compact. Importantly, these involve different numbers of intramolecular hydrogen bonds, arranged in sequences of several C₅^ext and C₇ pseudocycles (i.e., “rings” composed of five or seven atoms that are closed by a H-bond). This work formulated how the number of intramolecular H-bonds drives the structure of peptides in the gas phase: because of one more hydrogen bond in the same molecule, a 3₁₀-helix would be favored over an α-helix in the gas phase, generally. The number of H-bonds is maximized in a periodic conformation built from C₇^eq pseudocycles, which features one additional H-bond in comparison with the 3₁₀-helix.

Here, we use the set of alanine tetrapeptide structures to illustrate the performance of the recently corrected SE methods, PM6-D3H4 and DFTB3/3OB-D3. Three additional conformers are considered: α- and 3₁₀-helical as well as a sequence of three C₇^eq pseudocycles (note that α does not represent a stationary point on the PES). All of the structures are reoptimized with the same method as used in the original work (HF/6-31G**),²²³ and the energies are obtained on the level RI-MP2/aug-cc-pVQZ; the use of the large basis set is expected to minimize BSSE, which would be difficult to eliminate for conformers involving intramolecular H-bonds otherwise. The resulting relative energies are shown in Figure 9; the RMSD of relative energies over this set of 13 conformers are 2.9 and 1.4 kcal/mol for PM6-D3H4 and DFTB3/3OB-D3, respectively.

Figure 9.

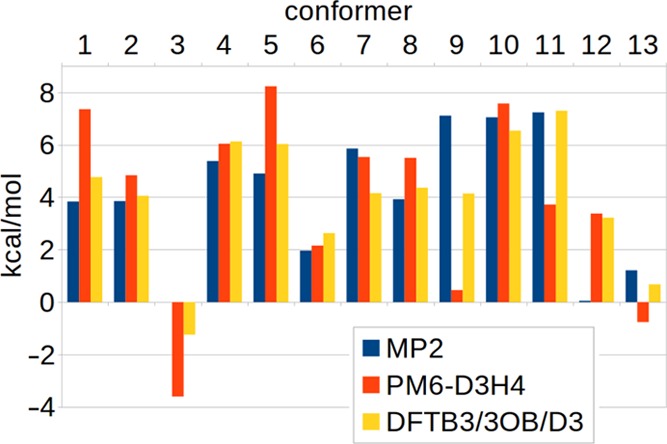
Energies of the conformers of alanine tetrapeptide obtained with the considered SE methods as well as on the ab initio level RI-MP2/aug-cc-pVQZ. Conformers 1–10 are those considered by Friesner and co-workers, while 11, 12, and 13 are the α- and 3₁₀-helical conformations and the sequence of three C₇^eq pseudocycles, respectively. Following the work of Friesner and colleagues, the MP2 energy of conformer 3 was set to zero arbitrarily, and the PM6 and DFTB3 energies were shifted to minimize the root-mean-squared deviation from the MP2 data.

For even longer peptides, the work by Elstner and co-workers on oligopeptide conformations was reviewed earlier.²²⁴ A conformational study of peptides Ace-Ala_n-Nme (n = 1–20) considered important secondary structural elements: α-helix, 3₁₀-helix, and C₅^ext.²¹⁸ Energy minimizations were performed with DFTB2, AM1, and full DFT (B3LYP/6-31G*, for n ≤ 11). DFTB2 energies and geometries agreed well with B3LYP for n ≤ 11, making it possible to extrapolate for n = 11, 14, 17, and 20. α-Helical structures relaxed to 3₁₀ for shorter helices (n < 8), while the α-helix remained stable in the center of longer chains with the termini assuming a 3₁₀ conformation. As stated above, the domination of 3₁₀-helix over α, in the gas phase, was likely the effect of one more H-bond in the 3₁₀-helix. The situation was expected to change when the peptide is immersed in a polar solvent with competing H-bond donors and acceptors; dispersion was also shown to be important in this context, favoring the more compact α form over the 3₁₀-helix.²²⁵

The following work focused on model peptides with up to eight glycines or alanines, and DFTB2, AM1, and PM3 results were compared to ab initio references.²¹⁹ DFTB2 underestimated energy differences between conformers consistently, while pilot calculations with an ab initio method corrected for the BSSE hinted that the comparison may actually be more favorable for DFTB2. The energy ranking of the conformers was in accordance with the B3LYP results. Dipole moments were only slightly underestimated relative to the B3LYP/6-31G* values, meaning that the electrostatic interaction of the peptide with other molecules could be described well. The structures of the various conformers were reproduced reliably, and all of the considered secondary structure elements corresponded to stationary points on the DFTB2 PES (except for one, high-energy structure). There were also failures, most notably concerning the overestimated pyramidalization at the nitrogen atom of glycine. It was commented that even various ab initio methods disagreed with each other and that the PES was extremely flat, such that a tiny deviation of energy led to a sizable deviation of the pyramidalization angle.

Also considered in this study were the SE methods AM1 and PM3, and their description of extended, helical, and turn conformations was rather troublesome. Many of the important secondary structure elements were predicted to be either distorted or intrinsically unstable. This indicates that AM1 and PM3 render a wrong topology of the PES at these conformers. The turn structures were especially problematic, and the extended structures were distorted. There were further difficulties with 3₁₀- and α-helices: PM3 tended to unwind helices by virtue of breaking the intramolecular H-bonds. AM1, favoring bifurcated H-bonds, predicted helices that were halfway in between the 3₁₀- and α-conformation. Thus, AM1 and PM3 were not recommended for peptide applications.

Dedicated to the SE methods was the study of secondary structure elements of peptides by Thiel and co-workers.²²⁶ In addition to the calculations with then established AM1 and PM3, as well as ab initio reference methods, the methods OM1 and OM2 were employed. The set of molecules considered included AD, triglycine and trialanine in β-turn structure, the tetraalanine set by Friesner’s group,²²³ and oligoalanine series up to Ace-(Ala)₆-Nme. The calculated geometries and relative stabilities of the conformers were improved by OM1/2 with respect to AM1 and PM3 considerably, although there were still certain deviations from ab initio data in some cases. DFTB2 was tested on this set of molecules by Thiel and co-workers as well,³³ and it performed better than AM1 and OM2 for relative energies of conformers and backbone dihedral angles, while the H-bond lengths deviated from the reference with all of the SE methods by some margin; the numerical data are reprinted in Table 3. (We are unaware of any similar study that has performed the benchmark with the up-to-date, corrected SE methods discussed in this review.)

Table 3. Performance of Selected SE Methods for the Energies and Structures of Peptides in the Set Considered by Thiel and Co-Workers^226 a.

	AM1	OM2	DFTB2/mio
relative energies (kcal/mol)	2.0	1.7	1.1
backbone H-bond lengths (Å)	0.22	0.34	0.26
backbone dihedral angles (deg)	17	12	9

^aPresented are mean unsigned deviations from the respective references; data are taken from ref (33).

8.2.3. Aromatic Side Chains

The stability of peptide conformation is often determined by intramolecular noncovalent interactions, mainly hydrogen bonds, when present, and the dispersion energy, in peptides containing aromatic amino acid residues. Here, the paradigmatic class of model compounds are isolated (gas-phase) di- and tripeptides containing an aromatic side chain (of Phe, Trp, or Tyr). Noncovalent interactions between the aromatic side chain and a peptide bond play a crucial role, and the description of dispersive interactions is vital.

The groups of Hobza and de Vries combined their efforts to investigate the PES of the Phe-Gly-Gly tripeptide in the gas phase by means of QM and statistical thermodynamics calculation and by IR/UV double-resonance spectroscopy.²²⁷ The PES featured more than 1000 minima; thus, an efficient energy-screening strategy was required before high-level correlated ab initio calculations could be performed. To this account, the computations started with an MD/quenching simulation using DFTB2-D, which yielded a set of correct lowest-energy conformers, an achievement that was missed by simulations based on MM force fields. The most stable conformers involved H-bonds as well as electrostatic and dispersion interactions between the phenyl ring and the carboxy group or the Gly–Gly peptide bond. This illustrated the need for a balanced description of the various kinds of noncovalent interactions, a rather difficult task that can be solved with an application of empirically corrected DFTB or other SE methods.

A following study of Trp-Gly and Trp-Gly-Gly peptides confirmed these findings.²²⁸ The obtained conformer structures were assigned to the previously measured IR spectra. The combination of DFTB2-D MD/quenching simulations with high-level correlated ab initio QM calculations proved to be a valuable and efficient tool to sample the conformational space of small peptides. Also, it was shown that the ranking of conformers differed on the free energy surface from the ranking on the PES, pointing out the importance of free energy analysis (via, for example, thermal corrections from statistical thermodynamics). Interestingly, the need of performing thermal corrections was emphasized in a recent study of the Tyr-Gly dipeptide.²²⁹ While the most stable conformer was a folded and H-bonded one at 0 K, thermal corrections at 400 K made non-H-bonded conformers more stable. This finding was in accordance with spectroscopic results, which did not find any H-bonded conformers.

Hobza and co-workers then compiled their reference data on small peptides in a benchmark database;²³⁰ included were peptides Trp-Gly, Trp-Gly-Gly, Phe-Gly-Gly, Gly-Gly-Phe, and Gly-Phe-Ala. These test cases proved to be sensitive, such that few methods yielded satisfactory accuracy. Standard MM force fields failed here, which was possibly linked to the use of fixed atomic charges (independent of conformation). It was emphasized again how important it was to have a QM method at hand that was both reliable and efficient, such that an initial screening of the conformation space could be performed. Ideally, that would be an SE method such as DFTB, and DFTB2-D was used again here. This database did not include any interactions between two aromatic amino acid side chains, and this was included in a following study of the Phe-Gly-Phe peptide.²³¹ DFTB2-D yielded geometries of the conformers with small deviations from the CCSD(T)/CBS reference, and the method was recommended for application to this kind of interaction.

NDDO methods have been applied in studies of small peptides as well, also involving empirical corrections for dispersion and other noncovalent interactions. The study of the complex conformational space of the Trp-Ser peptide involved dispersion-corrected PM3.²³² Although this method showed relatively large errors in relative energies of conformers, the lowest-energy conformer was still predicted correctly. The NDDO method was determined to be only useful for the purpose of crude initial screening of favorable conformers, which shall be later treated with more reliable QM methods. On the other hand, the application of PM6-DH to a large group of various molecules and complexes, which included the above-mentioned set of structures of small peptides,¹²² led to a much more favorable appraisal of the SE method. Chemical accuracy (error below 1 kcal/mol) was achieved as soon as geometry optimization was performed. The accuracy in terms of error was comparable to that obtained at the considerably more expensive MP2/cc-pVTZ level.

As an illustration, we apply the two most recently corrected SE methods to study the conformational energies of small peptides published in the BEGDB and compare the results to the available high-level ab initio data [CCSD(T)/CBS]. The RMS deviation is 1.6 and 1.2 kcal/mol with PM6-D3H4 and DFTB3/3OB/D3, respectively (see Table 4). The results illustrate how these methods can be useful to describe the interactions of bulky aromatic side chains with each other as well as with the peptide bonds.

Table 4. RMSD from CCSD(T)/CBS Data of Relative Energies of Various Conformers of Five Different Small Peptides, Obtained with Two Representative SE Methods Involving Empirical Corrections for Noncovalent Interactions (kcal/mol).

peptide	PM6-D3H4	DFTB3/3OB/D3
Trp-Gly	1.4	0.9
Trp-Gly-Gly	2.0	1.8
Gly-Gly-Phe	1.5	0.9
Gly-Phe-Ala	0.7	0.9
Phe-Gly-Gly	2.2	1.2
whole set	1.6	1.2

8.2.4. Alanine Dipeptide in Aqueous Solution

Solvation plays a crucial role in the stability of the different peptide conformations. For example, with a reaction field model at the level HF/6-31G*, the α-conformation was stabilized with respect to C₇^eq significantly, even though α was still not a minimum on the PES.²³³ Both the α and polyproline-II (PPII) conformers became stationary points on the PES as soon as explicit water molecules were included in the quantum system.²³⁴ This observation was in accordance with available Raman, vibrational circular dichroism, and Raman optical activity spectra. Free energy calculations performed with empirical MM force fields also found stable (and dominant) α and PPII conformers in solution.²³⁵ DFTB was also shown to describe the changes of the PES upon solvation, namely the stabilization of α due to favorable dipole–solvent interaction.²³⁶

As for AD itself, the effect of water on its conformation was characterized with NMR,²³⁷ and a large amount of work was aimed to show the difference in conformation between the gas phase and aqueous solution. Experimental reports agreed that PPII dominates in alanine oligopeptides^238,239 and other small model peptides.²⁴⁰ Other relevant conformations were α and the extended conformation β (or C₅^ext).

An early study compared the structure of AD yielded by various MM force fields and by DFTB-based QM/MM,²⁴¹ and the solvated AD was also used as an example application in the presentation of DFTB-QM/MM in the Amber package²⁴² as well as just recently in Gromacs.¹⁹⁵ The states α and PPII-β dominate both with MM and with QM/MM. While up-to-date MM force fields predicted PPII as the most favored conformation, in agreement with the above-mentioned experimental reports, QM/MM simulations with DFTB2 or DFTB3 showed a reversed trend. Obviously, the small difference in the depth of the PPII-β and α basins (less than 1 kcal/mol) makes it very difficult to get the conformational equilibrium right.

Unlike the small difference of the depth of minima, the height of the barrier between them was markedly different: ca. 1.5 kcal/mol with QM/MM, while it was higher with the considered MM force fields (ca. 2.5 kcal/mol with Amber and more than 3.5 kcal/mol with CHARMM).¹⁹⁵ The barrier between PPII and β seems to be either overestimed by force fields or underestimated by DFTB. If the former is true, then this may be possibly an effect of the harmonic character of the MM force fields, as noted earlier.²⁴² On the other hand, as discussed in sections 2.4.3, 3.2.3, and 5.1, the use of a minimal basis set in DFTB leads to underestimated Pauli repulsion and thus to underestimated rotational barriers.

A comprehensive QM/MM study of solvated AD considered a number of SE methods (MNDO, AM1, PM3, RM1, PDDG/MNDO, PDDG/PM3, and DFTB2) plugged in a QM/MM scheme.²⁴³ Investigated were their abilities to predict the structural ensemble of AD in aqueous solution. Free energy surfaces were obtained from replica-exchange MD simulations, and results were compared to both experiment and classical MM simulations with the Amber ff99SB force field. The Amber force field was able to outperform the SE methods (except for RM1), in much the same way as mentioned above for the case of DFTB2. The QM/MM interactions between the AD molecule and water were reported to differ little between the QM/MM simulations performed with different QM methods, and it was concluded that the differences came from the QM description of the interactions within the AD molecule. The good performance of RM1 may have stemmed from its way of parametrization biased toward biological molecules.

A new QM/MM implementation in Gromacs makes it possible to perform simulations with the newest incarnation of DFTB, namely, DFTB3 with the 3OB parameter set and the D3 dispersion correction.¹⁹⁵ Well-tempered metadynamics simulations of AD both in the gas phase and in aqueous solution were performed with this software, and the resulting free energies are shown in Figure 10. The gas-phase free energies match the PES closely, with C₇^eq being the global minimum, separated from C₅ by a low barrier, while the two paths from C₇^eq to C₇ cross higher barriers. For AD in aqueous solution, the QM/MM simulation yields the α-helical and the PPII+β basins as similarly deep dominant minima and a secondary minimum in the left-handed α-helical conformation.

Figure 10.

Free energy maps of alanine dipeptide obtained from well-tempered metadynamics simulations performed with DFTB3/3OB/D3: (left) AD in a vacuum (Helmholtz function) and (right) AD in aqueous solution simulated with QM/MM using TIP3P water (Gibbs function). The color codes the free energy, ΔF or ΔG, in kcal/mol.

It may be difficult to interpret these findings in terms of the performance of the applied SE method, however. The structural preferences of AD stem from a competition and compensation of noncovalent interactions (i) within the AD molecule, (ii) between AD and the surrounding water, and (iii) within the bulk water. These interactions are described with very different models: (i) with the SE method, (ii) with the applied QM/MM Hamiltonian, and (iii) with the water MM force field. Further investigation of these relations is desirable.

Larger peptides were also simulated with DFTB-based QM/MM schemes. The presentation of the QM/MM implementation with DFTB in CHARMM included MD simulations of penta- and octaalanine peptides in aqueous solution.²⁴⁴ The 3₁₀-conformation was unstable and converted to α rather quickly; the α-helix itself was observed to be stable. The termini, however, exhibited a 3₁₀-like conformation, and all of these observations were in accordance with NMR spectroscopy reports.

A divide-and-conquer QM/MM implementation of DFTB2 was applied to simulate crambin, a 46-residue protein, in water over 350 ps, a remarkably long time span for QM-based calculations in 2000.²⁴⁵ It was observed that α-helices transformed to a 3₁₀-conformation unless an empirical dispersion correction was switched on. Using the complete QM/MM method including dispersion correction, geometrical details were reproduced better than with any MM force field. Another point that showed the usefulness of a QM/MM approach was the significant charge transfer between the N- and C-termini, a feature that cannot be predicted even with a polarizable MM force field.

Finally, we note that DFTB2/MM has also been used to explore conformational properties of non-natural peptides, such as β-peptides.²⁴⁶ As summarized in ref (25), the DFTB2 model was found to give rather reliable structures as compared to B3LYP calculations, and DFTB2/MM simulations were valuable for validating MM models for these non-natural peptides.^246,247

8.2.5. Outlook

We have reviewed the performance of SE methods for the description of peptides and proteins, attempting to isolate the various features of protein structure. AD served to benchmark the description of backbone degrees of freedom, and it became evident that SE methods do fine here, with DFTB being slightly superior to PM6. Small improvements remain desirable for the description of rotational barriers, and it seems that this can be achieved by correcting for the underestimated Pauli repulsion.

Longer alanine-based peptides have also been used to manifest the strength of intrabackbone H-bonding and the trade-off between H-bonding and steric strain, which gives rise to secondary structure preferences. Much the same as for AD, the SE description of PES for the larger peptides is reasonable, and it is worth mentioning the generally encouraging performance of DFTB3/3OB/D3.

The noncovalent interactions between side chains and the backbone, as well as those between various side chains, are determinant for a higher level of structural arrangements of proteins. These electrostatic and dispersion interactions are described well with contemporary corrected SE methods, as demonstrated by the examples of small peptides with aromatic side chains. We note that the performance of corrected SE methods in this context was also reviewed briefly in a recent work.²⁴⁸

The situation appears less clear when SE methods are combined with MM models to describe peptides and proteins in solution. Due to interactions with solvent molecules, many peptide/protein conformations are close in energy; thus, a well-balanced treatment of various noncovalent interactions becomes even more important. Therefore, it is equally important to calibrate QM/MM interactions carefully.²⁴⁹

In the long run, the problem of protein folding requires extraordinarily efficient computational approaches, and SE methods may prove to be a valuable alternative to empirical force fields. Accordingly, Wollacott and Merz proposed new, SE-based scoring functions to rank unfolded and folded structures correctly, using a large decoy set containing the native protein structure. They showed that these scoring functions can distinguish decoys from the native structure with sufficient accuracy.²⁵⁰ Here, the enthalpy contribution to the folding free energy was obtained with PM3 or AM1. The folding problem was also presented as a showcase application of an efficient PM6-DH+ implementation.²⁶

8.3. Scoring Functions for Molecular Docking

All of the various scoring functions (SFs) used in computer-aided drug design to evaluate drug candidates rely on a rapid and accurate evaluation of intermolecular interactions between the drug and the receptor. Therefore, the SF must be able to describe all relevant types of noncovalent interactions,²⁵¹ such as dispersion, hydrogen bonding,²⁵² and halogen bonding.²⁵³ Application of calibrated SE methods is a good way to meet these conditions.²⁵⁴ For recent dedicated reviews on the application of SE methods in ligand scoring, refer to refs (255−257).

The possibility of applying a QM method in the framework of an SF was investigated by Vasilyev and Bliznyuk in 2004.²⁵⁸ They applied an efficient implementation of AM1/COSMO to estimate the binding energies for a series of RNA···theophylline-analog complexes, and the approach was found useful, although preliminary. Another SE study of ligand–protein interactions aimed to reproduce experimental binding enthalpies of several complexes using PM3.²⁵⁹ The results from calculations agreed well with the experiment, with an error of up to 2 kcal/mol. A different idea was exploited in a docking study in which PM6-based atomic charges instead of empirical charges were used in the SF; the scoring results improved markedly.²⁶⁰

In 2005, Raha and Merz developed an SE-based SF, QMScore,²⁶¹ which involves the standard AM1 method with a force-field dispersion correction and an implicit solvation model (Poisson-Boltzmann). Their showcase was the study of zinc ion-mediated ligand binding to protein.²⁶² In what followed, different variations of the SE setup (AM1 or PM3) were validated on ca. 200 noncovalently bound complexes, and QMScore was shown to outperform other SFs.²⁶¹ The AM1-based SF complemented with a QM/MM scheme was applied further to metalloprotein–ligand complexes with a fair performance.²⁶³ The pairwise additivity of the protein–ligand interaction energy was investigated on the binding of indinavir to the HIV-II protease (PR).²⁶⁴ The sum of the pairwise interaction energies accumulated more than 95% of the total interaction energy with both the PM6-DH2 SE method and the M06-L density functional used as a reference; the contribution of the three-body interactions was negligible, amounting to 1.4% and 3.8%, with PM6-DH2 and M06-L, respectively. The basic principle of pairwise additivity is considered generally and utilized in fragment-based drug design approaches in particular.

The SE-based scoring has been developed further by Hobza and co-workers, who have complemented the SE-based SF with advanced empirical corrections to the SE methods.²⁶⁵ Much like the previous work by Merz and co-workers,^266,267 the SF by Hobza and co-workers relies on a phenomenological, idealized decomposition of the process of binding, which in turn leads to the approximation of binding free energy by the sum of several contributions with a clear physical meaning. These individual contributions are the gas-phase interaction energy, the solvation/desolvation free energy, the change of the conformational free energies of the protein and ligand, and the entropy change upon binding. The values of the contributions and their comparison may provide additional insight into the nature of the protein–ligand binding. Unlike the case of an empirical SF, none of the contributions are fitted, for example, to experimental data in any way. The idea is to use the most accurate methods for the respective terms, however, in such a way that they are balanced with the other terms, in terms of both accuracy and computational cost. Still, two of the terms in the SF, the protein deformation energy and the binding entropy, would need prohibitively long calculation times to be evaluated accurately, and thus, they are evaluated largely approximately. Consequently, the SF shall provide merely relative values of the binding free energy, and the goal is a (linear) correlation of the score with the real, experimental binding free energy.

The gas-phase interaction energy is calculated using geometries obtained with SE energy minimization in the solution phase, and its magnitude is usually the largest among all of the contributions to the SF, amounting to as much as several hundred kcal/mol (for charged ligands). It is, however, compensated for largely by the change of solvation free energies upon binding. Consequently, even small deviations may lead to large deviations in the final score, and special care is needed here. The gas-phase interaction energy is calculated with a corrected PM6 method—most recently, PM6-D3H4X—which was shown to be the most accurate among SE methods, outperforming even the costly ab initio MP2 method.

The first application was a study of a series of inhibitors of HIV-1 protease, which were docked with UCSF DOCK and rescored by the SF based on PM6-DH2, which covers both dispersion and H-bonding reliably.²⁶⁵ The rescoring brought on significantly improved results, distinguishing between correct binding poses and non-native ones and also improving the relative strength of binding of the inhibitors. This dramatic improvement supports the rescoring based on an SE method as a tool for drug design that is valuable and computationally inexpensive at the same time; this is particularly important when diverse types of ligands (neutral/charged) need to be evaluated.^268,269

Although the main motivation to use an SE method in the scoring may be the improved accuracy with respect to empirical schemes, there are also situations in which any empirical scheme would come into trouble for principal reasons: (i) There is a chemical element (or binding situation) that is difficult to parametrize in MM. (ii) A covalent bond is formed between the receptor and the ligand. (iii) Another process that cannot be described with MM takes place; an example is a halogen bond due to the presence of a σ-hole. In any of these cases, the application of an SE-based SF is clearly superior.

The study of inactivation of Schistosoma mansoni cysteine peptidase by vinyl sulfone inhibitors may serve as an example of case ii.²⁷⁰ Here, the SF and the docking procedure were extended to describe covalent binding of ligands; there are two additional features: (a) quantum chemical energy minimization is involved to describe any breakage and formation of covalent bonds and (b) a new term is added to the noncovalent contribution to SF to describe the free energy difference between the covalent and noncovalent complexes. In other words, the development concerns both the computation of SF (in b) and a protocol to evaluate and design the inhibitors that exhibit covalent bonding and a conserved binding mode (in a).

For case iii, a typical example is the study of ligands that form halogen bonds with the receptor. The study of halogenated inhibitors of protein kinase CK2 showed an MM-based SF to fail due to its inability to describe halogen bonding.²⁷¹ The application of empirical corrections to PM6-DH2 (yielding PM6-DH2X) led to correct geometries of the complexes as well as quantitative correlation of the obtained score with the inhibition constants. A following study aimed to quantify how halogenations of a ligand modulates—possibly, increases—the strength of binding to aldose reductase.²⁷² A series of inhibitors was tested, and the factors that determine the strength of the halogen bond were identified as being (a) the bromine–iodine substitution and (b) the fluorination of the aromatic ring of the inhibitor in various positions. An SE method was used also to perform free energy calculations designed to explain the role of the halogen bond in the ligand binding. Some of the proposed substitions caused an increase of the interaction energy, which led to a decrease of IC₅₀ of as much as an order of magnitude.

Related is the approach based on the AM1 calculation of local property fields, which then replace an MM force field in the description of the interaction with the receptor.²⁷³ A showcase application on two classes of ligands brought new insights that could not have been obtained with a method based on an MM force field.

In ligand docking and scoring studies, it is valuable to combine SE methods with computational approaches of miscellaneous sorts. To illustrate such possibilities, some other applications are mentioned below.

It was investigated how the conformational and desolvation free energies are affected if only a single conformer of a flexible inhibitor of HIV protease was considered.²⁶⁹ To provide reference data, sufficient sampling was guaranteed by means of extensive MD simulation (using an MM force field). The error caused by the limited treatment of ligand flexibility amounted to ca. 5% of the total range of the scores. It was concluded that an approach restricted to a single conformer represents a reasonable, viable compromise between accuracy and computational efficiency.

The PM6-DH+ method was coupled with the COSMO implicit solvation model to rescore a set of docked guest complexes in a cucurbit[7]uril host.²⁷⁴ Coupled with the mining minima (MM2) algorithm, the method reproduced experimental binding energies; also shown was that the SE method was superior to an MM model.

In a study of protein–ligand complexes containing three different proteins,²⁷⁵ a few corrected SE methods (AM1, RM1, and PM6) were combined with an MD/MM-GB/PBSA setup. These methods yielded binding affinities that correlated well with the experiment; still, an improved treatment would be desirable for some terms other than interaction energies, such as entropic contributions. The SE scoring was computationally efficient, causing only a modest increase of total computational time as compared to MM-based scoring.

Other studies used binding poses generated by standard docking approaches and rescored them with the PM6-DH2 method. The application to a vitamin D receptor showed a good correlation with experiment,²⁷⁶ a study of InhA inhibitors was able to retrieve bioactive conformations,²⁷⁷ and the binding affinities of specifically binding and nonspecific DNA sequences to the zinc-finger protein were distinguished.²⁷⁸

The recent study of pyrazolo[1,5-a]pyrimidine inhibitors of cyclin-dependent kinase 2 involved a double-layer SE/MM as well as triple-layer QM/SE/MM approaches,¹⁸⁶ aiming to describe the innermost part of the complex on an even more accurate level, DFT-D. A ligand-building protocol provided a good correlation with experimental inhibition constants, while a docking protocol did not. It was concluded that the former approach is preferable whenever the chemical changes of ligands are small, because no dramatic change of the binding mode may be expected upon such a modification.

Finally, the work on searching for ligand binding sites on the surface of a protein molecule constitutes another interesting application of SE methods.²⁷⁹ Molecular orbitals of the protein obtained with AM1 were sorted according to their spatial delocalization, and this was considered as a basis for the identification of a possible binding site.

8.4. Bulk Water Properties

Water is arguably the most important solvent in chemistry and biology.²⁸⁰ Therefore, many models have been developed for bulk water at both classical (MM)^1,281−283 and quantum mechanical levels. Since water properties depend on the interplay of hydrogen-bonding, polarization, and van der Waals interactions, many QM models in fact do a rather poor job describing bulk water. For example, it was well-documented that popular GGA functionals such as BLYP do not capture water structures at the ambient conditions and that including empirical dispersion is crucial.^98,99,284 At the SE level, it is thus not surprising that most models in their original form do not describe water properties well. For example, the coordination number of the first solvation shell in water at ambient conditions is described by several standard SE models poorly: while the experimental value is 4.5–4.7, PM3¹⁴⁴ gives a value of ∼2.75, PM6¹⁴⁴ a value of ∼7.79, DFTB2^285,286 (without the modified γ for HX) a value of ∼8.4, and DFTB3/3OB²⁴⁹ a value of 5.6. Many factors may contribute to the errors of these methods. For example, the lack of a reliable treatment of dispersion in the standard SE methods (and popular DFT methods) is an important limitation. The underestimated polarization is likely important also; the average molecular dipole moment in liquid water has been estimated^287−289 to be in the range 2.5–3 D, while PM3, PM6, and DFTB3/3OB give values of 1.9, 2.3, and 2.4 D, respectively. The heat of vaporization is also underestimated by these SE methods grossly, by 2–5 kcal/mol. These methods also tend to overestimate diffusion constants; the value is 0.78, 1.28, and 0.44 Ų/ps with PM3, PM6, and DFTB3/3OB, respectively, compared to the experimental value of 0.23 Ų/ps.

Motivated by these observations, several revised SE models have been developed for bulk water. Monard and co-workers²⁹⁰ applied PM3-PIF⁵⁷ and PM3-MAIS⁵⁸ to study bulk water using a divide-and-conquer implementation and found major improvement over PM3. The SCP-NDDO method¹⁴⁴ discussed in section 6.2 improves the polarization of PM3 and also includes a post-SCF dispersion contribution. The performance of the model for water is satisfactory for both bulk water and also the air/water interface under ambient conditions. Han and co-workers parametrized the XP3P model²⁹¹ in the Xpol framework using the MNDO-based PMO methodology;^64,66,67 a set of diffusion p functions is added on the hydrogen atoms and a damped dispersion model is included. XP3P was shown to give reliable properties for bulk water over a fairly broad set of temperatures, with a density maximum at ca. −25 °C. An advantage of XP3P over the popular MM models is that it handles the dipole derivative of water with respect to OH stretch properly, and this property is likely important to a flexible water model. In the same vein, the mDC model by York and co-workers⁹⁶ also shows impressive performance for bulk water over a range of temperatures and exhibits good structural (radial distribution functions), thermodynamic (heat of vaporization, heat capacity, and compressibility), and dynamical (diffusion) properties; the temperature of density maximum is also rather close to the experimental value. The only quantity slightly underestimated is the dielectric constant, which was 48 as compared to the experimental value of 78 at 298 K. This may reflect the underestimated polarizability of the DFTB3/3OB model.^87,117

In addition, there are several other models based on somewhat brute-force or ad hoc modifications of SE models by adjusting parameters to fit experimental bulk properties or ab initio data directly. We would consider them along the line of “specific reaction parameters” pioneered by Rossi and Truhlar.²⁹² These include the modified PM3 model for studying proton transfer in bulk water by Thiel and co-workers,²⁹³ the modified DFTB2 model by Roethlisberger and co-workers,²⁹⁴ the modified DFTB3/3OB model by two of us,²⁴⁹ and the modified PM6 model by Van Voorhis and co-workers.²⁹⁵ The parametrizations were done either by reverse Monte Carlo^296,297 to fit experimental observables (e.g., radial distribution function) or by force-matching^298,299 to ab initio calculations of fairly large water clusters. Encouraging results are obtained almost by construction in these methods, which make them useful in very specific applications; in other words, at least in the near future, considering the potential increase in computational cost associated with a more robust integral approximation, the DFTB3 framework discussed here remains attractive. Transferability of these empirically modified parameters, however, is not apparent. For example, we modified the O–H repulsive potential in DFTB3/3OB to improve the structural properties of bulk water under ambient conditions.²⁴⁹ Rather modest changes, on the order of k_BT, were required to improve the radial distribution functions substantially; this improvement also was transferable to solvated proton and hydroxide in water clusters and in bulk water to some degree. The hydroxide ion, however, remains oversolvated in the bulk,^249,300 and the heat of vaporization of bulk water remains underestimated substantially. This exercise suggested that more transferable improvements of SE models require physical modifications of the underlying electronic Hamiltonian, as discussed in section 6.

8.5. Metal–Ligand Interactions

Metal–ligand interactions are tremendously important in chemistry and biology. In many cases, there are significant changes in the electronic structure of the metal ion upon complexation, especially when transition-metal ions are involved. Therefore, metal–ligand interactions often fall out of the scope of “noncovalent interactions”, representing a topic that warrants a thorough discussions in its own right indeed. Nevertheless, we briefly comment on several recent studies that highlight both the value and limitation of SE methods for the treatment of metal–ligand interactions, limiting most of the discussions to our own recent research.

According to a recent survey,^301,302 the most prevalent metal ions in enzymes include Mg²⁺, Ca²⁺, Mn²⁺, Fe²⁺, and Zn²⁺; other ions include cobalt and copper, while Na⁺ and K⁺ are rich in the cellular milieu. Thus, for biological applications, treating the ligation of these ions is of particular importance. As for NDDO methods, PM3 and PM6 have been parametrized for quite a few metal ions by Stewart,^51,303 and by Merz and co-workers for several ions.^304,305 At the DFTB level, Na⁺, K⁺, and Ca²⁺ have been parametrized within the framework of DFTB3/3OB.¹³⁰ In general, structural properties such as metal–ligand distances are described well, especially for charge-neutral ligands, while binding energies may have errors on the order of a few to 10 kcal/mol.^130,304,305 Other than these parametrizations, however, we are not aware of any extensive and systematic benchmark for these ion parameters. A recent study³⁰⁶ attempted to conduct a comparative study of Na⁺, K⁺, and Ca²⁺ binding to proteins by force fields (both the nonpolarizable CHARMM36 force field and the polarizable Drude force field),² DFTB3/3OB, and a collection of DFT methods. MD simulations for 30 cation-selective proteins with high-resolution X-ray structures were carried out to generate active site models, and the binding energy of the metal ions was characterized. Rather large errors were observed with the nonpolarizable force field, especially for Ca²⁺, while DFTB3/3OB and the Drude force field provided largely comparative descriptions for the binding energies, usually within 10% compared to DFT calculations with a decent basis set. Notably, DFTB3/3OB was able to capture qualitatively the polarization and charge transfer effects that may propagate to the second coordination shell of the metal ion; these effects are particularly evident for Ca²⁺, suggesting that a QM treatment might be more important for divalent ions.

For additional “simple” divalent ions like Mg²⁺ and Zn²⁺, which do not adopt open shells, many SE methods, such as AM1, PM3, and PM6, have been parametrized; Zn²⁺ contains valence d electrons, and thus, MNDO(d)²⁰ has been parametrized. In the DFTB framework, both DFTB2^307,308 and DFTB3³⁰⁹ have been parametrized for Mg²⁺ and Zn²⁺. Cai and co-workers³⁰⁷ found that magnesium–ligand lengths computed from AM1^303,310 and PM3, MNDO, and MNDO/d³⁰³ deviate by ca. 0.1 Å on average in comparison to B3LYP/6-311++G** for small Mg complexes. The AM1/d parameters³¹¹ for magnesium provided a clear improvement in accuracy compared to AM1 by incorporating d orbitals. For zinc,³¹² the mean absolute deviations (MAD) of metal–ligand distances with AM1,³¹³ PM3 and PM3(ZnB),³⁰⁵ MNDO/d,³¹⁴ and PM6⁵¹ are larger than 0.05 Å with respect to CCSD(T) values for small zinc-containing molecules. With the latest parametrization of DFTB3/3OB,³⁰⁹ the structural properties are described very well as compared to B3LYP/aug-cc-pVTZ; the MAD of metal–ligand distances, for example, is in the range of 0.01–0.02 Å for a fairly broad set of Mg²⁺ and Zn²⁺ containing molecules relevant to biochemistry. In terms of metal–ligand interaction energies, the MAD in comparison to high-level ab initio or DFT calculations (e.g., G3B3 for Mg²⁺ and B3LYP/aug-cc-pVTZ for Zn²⁺) is in the range of 3–5 kcal/mol, which corresponds to a low percentile of the ligand binding energies typically. It is worth noting that single-point energy calculations at the DFTB3/3OB structures usually lead to much smaller deviations from the G3B3 or B3LYP calculations, with MAD on the order of 1 kcal/mol, highlighting the high quality of the DFTB3 structures again. The importance of a reliable treatment of zinc sites to the description of enzyme catalysis is illustrated by our recent study of alkaline phosphatase,^315,316 where we showed that the previous AM1/d-PhoT/MM calculations^317,318 likely led to incorrect transition states due to distortions of the bimetallic zinc motif.

For transition metals that involve open shells, the treatment of electron correlation is very important, and the development of SE methods has been much limited, with only modest success. MNDO(d),²⁰ PM3(TM),³¹⁹ and AM1* ³²⁰ represent an NDDO/MNDO family of methods that have been parametrized for a range of transition-metals ions; they are most successful for structural properties, although AM1* has also modest success in many ion–ligand interactions. The PM6 method, which has been recently updated and reparametrized in PM7, has also shown an increased accuracy in the prediction of structures and heats of formations compared to earlier methods. McNamara and co-workers^321,322 reported a specific parametrization of PM3 for iron and observed encouraging results for a series of biologically relevant compounds, such as [4Fe–4S] cubanes; the reference, however, was B3LYP/6-31G*, which is likely of limited accuracy for iron compounds.

In the framework of DFTB, Morokuma and co-workers developed DFTB2 parameters for several first-row transition metals, including Sc, Ti, Fe, Co, and Ni.³²³ It was shown that this parametrization often provides adequate structural properties, although the energetics are less satisfactory; thus, DFTB2 was mainly recommended as the intermediate layer in ONIOM calculations of organometallic and metalloenzyme applications.³²⁴ Recently, Bruschi and co-workers³²⁵ developed DFTB2 parameters for copper, although their study focused primarily on structural properties of small compounds, and a limited benchmark was reported for energetic properties or larger systems. In the context of materials science, DFTB2 parameters were developed for several transition metals (e.g., Ti, Zn and Fe) in applications that target metal oxides or nanoparticles.^326−328

In their latest work, Gaus and co-workers parametrized DFTB3/3OB for copper³²⁹ in a spin-polarized framework.^330,331 To obtain a balanced treatment of Cu(I) and Cu(II) species, it was found crucial to consider the Hubbard parameter and its charge derivative to be functions of the orbital angular momentum, thus allowing the 3d and 4s orbitals to adopt different sizes and responses to the change of charge state. In terms of comparison to PM6 and higher level ab initio or DFT methods, the trends are similar: DFTB3/3OB tends to give rather reliable structures, while larger errors are found in the metal–ligand interaction energies; single-point energy calculations at DFTB3 structures again recover the QM reference values (B3LYP/aug-cc-pVTZ; see more discussions in ref (329) regarding this choice of the reference method) with MAD in the range of 1–3 kcal/mol. Another general trend is that the errors in the ligand binding energy are larger for charged (anionic) ligands. To what degree this is due to the treatment of charge transfer or ligand polarization is an interesting topic for future study. The limitation that DFTB3 is parametrized using PBE as the “parent functional” is more transparent for a number of Cu²⁺ compounds, for which the proper description of exchange was shown to be crucial.^332,333 Therefore, including a fraction of exact exchange in DFTB seems an important direction to pursue. Nevertheless, the DFTB3/3OB model was shown to be able to capture some important features of Cu²⁺, such as Jahn–Teller distortion.^329,334

9. Concluding Remarks

In this contribution, we have reviewed semiempirical (SE) quantum mechanical methods in terms of their basic formulation, approximations, limitations, and application to noncovalent interactions in various (bio)chemical systems. In this “ab initio” era, SE methods are still of interest because they can potentially find a niche in many soft-matter applications where both the flexibility in electronic structure and the conformational samplings are important. In other words, SE methods are needed in applications for which ab initio QM methods are too expensive while conventional classical force fields are not adequate. Examples include molecular association, charge transport, and chemical reactions in biological systems or complex fluids such as room-temperature ionic liquids. Using a quantum mechanical model is also essential to the computation of many experimental observables, such as vibrational spectra.

Due to the various approximations inherent in the standard SE methods, they have limitations in the treatment of noncovalent interactions, which make them unfit for highly quantitative computational studies. As we discuss here, however, various empirical corrections and formal extensions of SE methods have improved the accuracy of popular NDDO/MNDO and DFTB models for intermolecular interactions dramatically. As a result, the applicability of SE methods to condensed-phase problems has been enhanced substantially in the recent years, and some examples are discussed here.

In terms of future directions, we emphasize several areas. First, we note that the most empirical corrections and formal extensions have been benchmarked and calibrated on relatively small systems; this is due mostly to the difficulty of conducting highly accurate QM calculations for much larger systems. Local correlation methods or embedding methods might be valuable in this context. In systems that resemble condensed phase more closely, a different balance between polarization and exchange repulsion may become important and should be taken into consideration for the calibration of SE methods, which are most useful for condensed-phase applications. Second, to describe the structural properties of macromolecules properly, it is important to balance the description of bonded and nonbonded interactions. For example, although the various corrections have improved the accuracy of SE methods for hydrogen-bonding and dispersion, substantial errors are still often found for bond rotations and steric interactions, leading to errors in the relative (free) energies of different conformers and isomerization barriers. Along this line, improving the description of Pauli repulsion appears to be particularly important, especially for the DFTB models. Finally, for SE methods to be competitive with advanced classical force fields, it is important to make them scale well with respect to system size and take full advantage of modern computational hardware; efforts along the line of fragmentation and extended Lagrangian molecular dynamics seem particularly promising. Hybrid SE/MM simulations are another approach for accessing larger systems and longer time scales, and a careful calibration of SE–MM interactions using condensed-phase systems is needed for reliable results. With intense efforts from many groups on these fronts, to quote Grimme and co-workers,⁹⁵ “the future for low-cost quantum chemical methods for investigating noncovalent interactions in all of their aspects seems bright”.

Biographies

Anders S. Christensen received a degree in nanoscience from the University of Copenhagen (2010) and a Ph.D. in theoretical chemistry from the University of Copenhagen (2014) working with protein folding under the supervision of Prof. Jan H. Jensen. In 2014 he joined the group of Prof. Qiang Cui at the University of Wisconsin—Madison, where he is working as a postdoc developing faster and more accurate semiempirical quantum mechanical methods to simulate biological systems. He is interested in developing and implementing theoretical computational methods with applications in biomolecular chemistry, in particular to rapidly elucidate and study the structure and function of large biomolecules.

Tomáš Kubař graduated from Charles University in Prague with a M.Sc. in physical chemistry in 2003 and with a Ph.D. in physical chemistry in 2007. After three years of postdoctoral research at Technische Universität Braunschweig, he moved to Karlsruhe Institute of Technology (KIT). Tomáš has been a member of the Center for Functional Nanostructures at KIT since 2015. His research focuses on the development and implementation of multiscale simulation schemes and free energy techniques, with applications including electron transfer and proton transfer processes, as well as interaction of peptides and proteins with biological membranes.

Qiang Cui received a B.S. (1993) in chemical physics from the University of Science and Technology of China and a Ph.D. (1997) in chemical physics from Emory University, working with Prof. Keiji Morokuma. Following postdoctoral studies at Harvard University with Prof. Martin Karplus, in 2001, he joined the University of Wisconsin—Madison, where he has remained since as a professor of chemistry. He is interested in developing theoretical/computational methods for the analysis of biomolecular systems, especially concerning chemical reactions in enzymes, energy transduction in biomolecular machines, and, more recently, interaction among biomolecules, lipids, and inorganic materials.

Marcus Elstner received a degree in physics from Technische Universität Berlin in physics in 1993 and graduated with a Ph.D. in theoretical physics from the University of Paderborn in 1998. After a postdoctoral stay at Harvard University, he moved to the University of Paderborn in 2000, where he finished his habilitation in 2003. Marcus became a professor at Technische Universität Braunschweig in 2006, and accepted his current position at Karlsruhe Institute of Technology in 2009. He is interested in method developments with focus on DFTB and its integration into multiscale methods and applications to photoactive biomolecules, electron-transfer in biomolecules and organic materials, and interaction of peptides with biological membranes.

The authors declare no competing financial interest.