One hundred and fifty years of sprint and distance running – Past trends and future prospects

Abstract

Sprint and distance running have experienced remarkable performance improvements over the past century. Attempts to forecast running performances share an almost similarly long history but have relied so far on relatively short data series. Here, we compile a comprehensive set of season-best performances for eight Olympically contested running events. With this data set, we conduct (1) an exponential time series analysis and (2) a power-law experience curve analysis to quantify the rate of past performance improvements and to forecast future performances until the year 2100. We find that the sprint and distance running performances of women and men improve exponentially with time and converge at yearly rates of 4% ± 3% and 2% ± 2%, respectively, towards their asymptotic limits. Running performances can also be modelled with the experience curve approach, yielding learning rates of 3% ± 1% and 6% ± 2% for the women's and men's events, respectively. Long-term trends suggest that: (1) women will continue to run 10–20% slower than men, (2) 9.50 s over 100 m dash may only be broken at the end of this century and (3) several middle- and long-distance records may be broken within the next two to three decades. The prospects of witnessing a sub-2 hour marathon before 2100 remain inconclusive. Our results should be interpreted cautiously as forecasting human behaviour is intrinsically uncertain. The future season-best sprint and distance running performances will continue to scatter around the trends identified here and may yield unexpected improvements of standing world records.

1. Introduction

Sprint and distance running have experienced remarkable performance improvements for more than a century. Approaches to quantify and forecast these improvements share an almost similarly long history (Liu, 2004) and are typically based on: (1) the assessment of human physiology and metabolic capacity (e.g., Joyner, 1991; Joyner, Ruiz, & Lucia, 2011; Senator, 1982), (2) probabilistic modelling (e.g., Godsey, 2012; Tryfos & Blackmore, 1985) or (3) time series analysis (e.g., Nevill & Whyte, 2005; Whipp & Ward, 1992). The available time series analyses plot running velocity or running time as a function of the year in which a performance was established and typically cover short time periods only.

Here, we seek to expand the existing time series analyses in a step-wise approach: First, we establish sets of performance data that cover up to one and a half centuries and apply an exponential time series analysis. Second, we contrast this analysis by establishing so-called experience curves that explain the improvements in running performances with the accumulation of experience. In a third step, we use the rates of performance improvements identified in the first two steps to forecast running performances until the year 2100. This analysis allows us to address interesting but controversial questions such as:

• Will women soon outrun men?

• When will 9.50 s over 100 m be broken?

• Will humans run a marathon in under two hours before the year 2100?

The notion of experience has received little attention in the analysis of running performances and merits a short introduction. In econometrics, it has long been recognised that production costs in the manufacturing industry do not decline merely by the passing of time but due to the accumulation of experience. In 1966, the Boston Consulting Group first modelled the dynamics of costs as a power-law function of cumulative experience, i.e., production output. When presented on a double-logarithmic plot, the resulting regression line is referred to as an experience curve (Henderson, 1973). Since then, experience curves have been widely used for production management (Dutton & Thomas, 1984) and for the cost assessment of novel energy technologies (e.g., Weiss, Patel, Junginger, & Blok, 2010). We argue here that improvements in sprint and distance running may likewise follow experience curve patterns and could be understood as the outcome of experience accumulated by athletes, coaches and the manufacturers of equipment, nutrition and drugs. We justify this argument as follows:

• Like manufacturing, sprint and distance running operate in a competitive environment in which performance improvements are essential for success.

• Scale effects are critical in both manufacturing and running.

• Mechanisms such as learning-by-doing, learning-by-searching and learning-by-interacting reduce production costs in manufacturing and improve running performances.

2. Methods

2.1. Data collection

We collect data for the women's and men's season-best outdoor sprint and distance running performances, as published by the International Association of Athletics Federation (IAAF, 2011, 2012, 2015). We include performances established before 31 December 2014 in the Olympic running events of: 100 meters (m), 200 m, 400 m, 800 m, 1500 m, 5000 m, 10,000 m and the marathon (see Note 1 and Tables S1 and S2 in the Supplemental Data). We transform all performance data, expressed by IAAF (2011, 2012, 2015) in units of time, prior to analysis into units of speed (m/s).

Although it is straightforward to collect data on season-best running performances, it is more challenging to identify a suitable parameter to approximate experience. In econometrics, there is wide agreement in using cumulative production as a proxy for the experience. Here, by analogy, one could sum the number or distance of races run by all athletes throughout history in each event. However, pertinent data are unavailable. Likewise, it is infeasible to approximate experience based on, e.g., the cumulative income generated by runners or the cumulative expenditures of equipment manufacturers because data are unavailable for sufficiently long-time horizons at the required level of detail. Therefore, we choose to approximate experience by the cumulative number of Olympic participants in the respective sprint and distance running events, covering all modern Olympic Games between 1896 and 2012 (SR, 2012; see Tables S3 and S4 in the Supplemental Data). Although subject to uncertainty, our approximation implicitly accounts for variability of the interest in sprint and distance running in particular, the low interest in running during the First and Second World Wars.

2.2. Data analysis

2.2.1. Exponential time series analysis

We begin by plotting season-best sprint and distance running performances as a function of the year in which they were established. We fit the data with a three-parameter exponential function (Liu, 2004; Liu & Schutz, 1998; see also Note 2 in the Supplemental Data):

(1)

Here, V_s,i represents the running performance (m/s) in year i for event s, V _s,∞ represents the estimated asymptotic limit of V_s,i as i approaches infinity. The improvement parameter b_s measures how quickly the season-best performances converge towards their asymptotic limit V _s,∞. The parameter i_{s ,0} accounts for both the year of the first performance recorded in our data sets and the respective running performance in that year.

Based on equation 1, we quantify the average yearly improvement rate IR_s (%) at which the performance for each event s converges toward the asymptotic limit V _s,∞ as:

(2)

We uniformly estimate the uncertainty margin of improvement rates based on the standard error of the asymptotic fit.

2.2.2. Experience curve analysis

We follow the notion of Henderson (1974) and propose a power-law relationship for each Olympic running event s between experience E_s and running performance V_s (m/s):

(3)

Here, V_{s ,0} represents the first season-best running performance (m/s) ever established and p_s represents the experience index. While we assume that the cumulative number of participants in the Olympic Games in a specific event s is a good proxy for the acquired experience E_s, we must also consider that runners had already acquired a certain level of experience prior to the adoption of a running event by the Olympic Games. Therefore, E_s in equation 3 consists of two components representing the experience acquired: (1) prior to the adoption of an event by the Olympic Games (Z_{s ,0}) and (2) after the adoption of an event by the Olympic Games, which we approximate by the cumulative number of Olympic participants (Z_s). The relationship between the running performance V _s (m/s) and the cumulative number of Olympic participants Z_s can then be written as:

(4)

Here, V˜ _s,0 represents a coefficient that is proportional to V_{s ,0} in equation 3. Introducing the parameter Z_{s ,0} avoids infinitely small values of V_s before a running event was adopted by the Olympic Games and allows us to account for the experience women acquired from men's running prior to the adoption of their own running events by the Olympic Games. Note that equation 4 does not contain an asymptotic parameter towards which running performances converge (for more details, see Note 3 in the Supplemental Data).

By using a nonlinear least-squares Marquardt-Levenberg algorithm, we find the parameters V˜ _s,0, Z_{s ,0} and p_s with which equation 4 fits our data best for V_s and Z_s. The resulting experience curve yields declining performance improvements with each additional unit of experience. We plot all experience curves on a double-logarithmic scale; the resulting graphical representation is a straight line with slope p_s.

Following the standard experience curve approach (Henderson, 1974), we quantify the improvement of running performances with each doubling of cumulative experience by calculating the learning rate LR_s (%), for each event s as:

(5)

We estimate the uncertainty margin of learning rates based on the standard error of the slope parameter p_s.

We have explained in Section 2.1 that we use the cumulative number of participants in the selected Olympic running events Z_s as a proxy for experience. To derive an experience indicator, two considerations are important. First, Olympic Games only take place every four years. We therefore try to account for the experience gained in the years between Olympic Games by interpolating available participation numbers. Moreover, personal communication with runners suggests that athletes typically seek to improve their performance by adopting novel training methods from shorter events. An 800 m runner, for example, may benefit from new approaches to sprinting; a 10,000 m runner may benefit from interval workouts adopted by 5000 m runners. Moreover, with increasing age, middle-distance runners tend to shift their focus to longer distances. We account for these observations by calculating the experience in each event as presented in Table I. Although track athletes can become successful marathon runners, we would consider experience in marathon running unique and separately from track running, as the marathon is more than four times longer than the longest track event. To also include the performances established in 2013 and 2014 into our experience curve analysis, we estimate the experience for these two years as described in Section 2.2.3.

Table I. Estimating the cumulative experience in a particular Olympic event; women's and men's running is treated separately.

Event	Events used to calculate cumulative experience
100 m	60 ma + 100 m + 200 m
200 m	60 ma + 100 m + 200 m
400 m	100 m + 200 m + 400 m
800 m	400 m + 800 m
1500 m	800 m + 1500 m
5000 m	1500 m + 5000 m
10,000 m	5000 m + 10,000 m
Marathon	Marathon

^aEvent was only part of the Olympic Games in 1900 and 1904.

2.2.3. Performance forecasts

We use the rates of performance improvements established in our time series and experience curve analyses to forecast sprint and distance running performances until 2100. To do so, the experience curve analysis also requires forecasting Olympic participation numbers. In line with the trends observed in the past two decades, we assume that the number of women and men participating in the Olympic sprint and distance running events will remain constant until 2100 at the average participation level observed for each event between 1992 and 2012 (see Tables S3 and S4 in the Supplemental Data). We abstain from estimating the uncertainty of our forecasts based on the error margins of the fit parameters in equations 1 and 4 because the small value range covered by the historic performances (i.e., the weakest and strongest performances typically differ by less than a factor of two from each other) often leads to large error margins of the fitted parameters, even though the sums of the residuals of the fitted models are small. Following the general convention, we uniformly present and discuss all forecasted performances in terms of running time.

3. Results

3.1. Time series analysis

The season-best sprint and distance running performances of women and men, expressed in terms of speed, have improved by 67% ± 40% and 25% ± 8% in the time horizons covered, translating into average yearly improvement rates of 0.5% ± 0.1% and 0.2% ± 0.1%, respectively (Figure 1; Table S5 in the Supplemental Data). The marginal yearly performance improvements tend to decline. In fact, the women's sprint and middle-distance performances have not improved at all in the past two decades (Figure 1).

Figure 1. Exponential time series analysis of the women's and men's season-best sprint and distance running performances; axes are scaled linearly; solid lines represent the best fit to the data according to equation 1; dashed lines for the 10,000 m and marathon events represent the best fit for performances established after 1945; dotted horizontal lines represent the current world record (Data sources: IAAF, 2011, 2012, 2015).

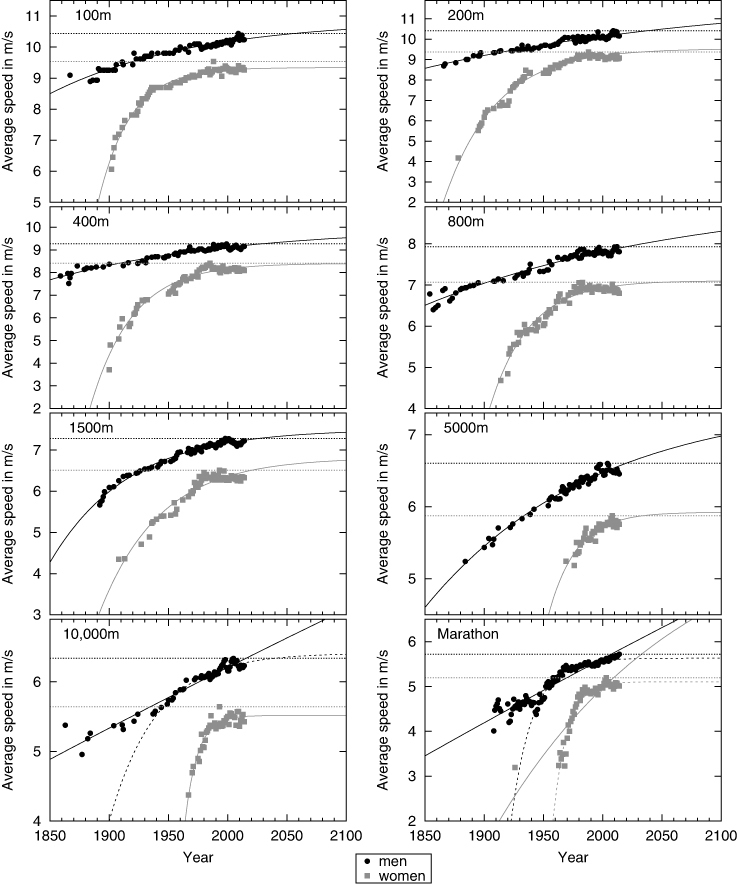
Our results suggest that the women's and men's sprint performances generally follow time exponentially. Exceptions represent the men's 10,000 m as well as the women's and men's marathon events (Figure 1). Fitting equation 1 to all performance data for these events results in unrealistic asymptotic season-best performances V _s,∞. To obtain a realistic fit, we excluded for these three events in an additional analysis all performances established prior to 1945 (see dashed lines in Figure 1). After this correction, the coefficients of determination (R ²), which indicate the goodness of fit of our exponential time series analysis, reach on average 0.94 ± 0.04 and 0.95 ± 0.02 for women's and men's performances, respectively. The women's performances appear to approach their asymptotic limit V _s,∞ at higher rates (4% ± 3% per year) than the men's performances (2% ± 2% per year) do. The modelled yearly improvement rates for individual events range from 0.4% ± 0.1% for the men's 200 m and 800 m to 9.0% ± 1.0% for the women's 10,000 m (Figure 1; Table S6 in the Supplemental Data). The differences in the yearly rates of performance improvements between women and men may be explained by the comparatively low performance levels in the early years of women's running. Moreover, women were excluded from long distance events until the second half of the twentieth century and may have afterward disproportionately benefited from the experience already acquired by men.

Figure 1 suggests that the sprint and distance running performances of women and men converged until the 1980s. Since then, however, differences in the performance level remained on average at 10% ± 1%. The standing women's world records are identical to the men's records established around the years 1927 ± 21. In line with these findings, the modelled asymptotic limit of season-best performances V _s,∞ suggests that differences in the running velocities of women and men continue to prevail at 19% ± 7% (Table S6).

3.2. Experience curve analysis

Using the data displayed in Figure 1, we establish experience curves that cover the time horizons in which individual running events have been part of the Olympic Games (Figure 2). The sprint and distance running performances of women and men improve on average at 3% ± 1% and 6% ± 2%, respectively, with each doubling of cumulative experience. The identified learning rates range from 0.8% ± 0.4% for the women's 10,000 m to 10.9% ± 1.5% for the men's marathon (see Note 3 and Table S7 in the Supplemental Data). The fitted experience curves show a coefficient of determination (R ²) of 0.76 ± 0.19 and 0.92 ± 0.04 for the women's and men's performances, respectively (Table S7 in the Supplemental Data). Based on the goodness of fit, we argue that running performances can be modelled with the experience curve approach, albeit with limitations discussed in Section 4.1.

Figure 2. Experience curves of the women's and men's season-best sprint and distance running performances; the axes are scaled logarithmically; solid lines represent the best fit to the data according to equation 4; dotted horizontal lines represent the current world record (Data sources: IAAF, 2011, 2012, 2015).

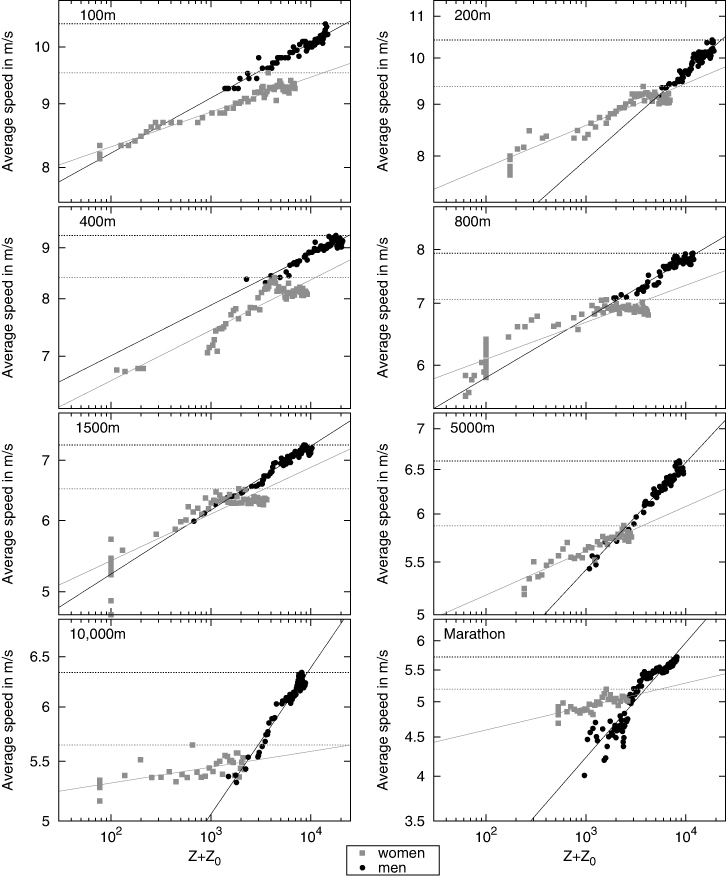
3.3. Forecasting running performances

We use both the exponential time series analysis and the experience curve analysis to forecast running performances until 2100. The trend in the time series analysis of women's performances suggests little improvement throughout the twenty-first century, while men's performances may continue to improve. By contrast, our experience curve analysis suggests that improvement potential for both women's and men's performances exists (Figures 1 and 2; Tables S9 and S10 in the Supplemental Data). A sensitivity analysis conducted with a four-parameter experience curve model supports the forecasts of the exponential time series analysis and generally suggests limited improvement potential for women's performances (with notable exception of the 10,000 m and marathon events) but considerable improvement potential for men's performances (Table S11 in the Supplemental Data). We argue here that the time series analysis and the four-parameter experience curve analysis both account to a larger degree than our standard experience curve analysis for the stagnation of women's performances in the past two decades. Note that forecasting season-best performances does not allow us to predict when precisely a world record will be broken. Instead, we interpret the point where a fitted curve crosses the current world record as an indication of the year in which it is on average likely that the world record will be broken. In this way, we predict based on the time series analysis that four out of eight women's world records may be broken within this century; our experience curve analysis suggests that seven of the current women's world records may be broken by the end of this century, while the sensitivity analysis suggests that only three out of eight records may be broken by the end of this century (Table II; Tables S9–S11 in the Supplemental Data). The time series analysis suggests that men may break all but the marathon world record by the end of the century; the experience curve forecast expects that all world records, including the one for the marathon, will be broken in the near future. The consistency in the time series and experience curve forecasts of men's performances may be explained by a more homogeneous improvement of men's performances compared to women's performances.

Table II. Forecasts of the year in which the current world record may be broken.

			Year in which the trend line of the fitted models reaches the current world record
	Event	World record as of 31 December 2014	Exponential time series analysis	Experience curve analysis
Women	100 m	10.49 s	–	2067
	200 m	21.34 s	2032	2027
	400 m	47.60 s	–	2026
	800 m	1:53.28 min	2051	2013
	1500 m	3:50.46 min	2020	2013
	5000 m	14:11.15 min	2034	2024
	10,000 m	29:31.78 min	–	>2100
	Marathon	2:15:25 h	–a	2055
Men	100 m	9.58 s	2057	2060
	200 m	19.19 s	2039	2038
	400 m	43.18 s	2029	2029
	800 m	1:40.91 min	2020	2021
	1500 m	3:26.00 min	2026	2016
	5000 m	12:37.35 min	2020	2025
	10,000 m	26:17.53 min	2040a	2020
	Marathon	2:02:57 h	–a	2007

^aForecasts are based on performances established from 1945 onward.

–World record as of 2014 represents a higher running speed than the asymptotic parameter V _s,∞ and may not be reached until the end of this century.

Extending past trends suggests that men will likely break 9.50 s and 1:40 min over the 100 m and 800 m events only around the years 2100 and 2035, respectively. Following our time series analysis, the forecasted season-best performances of the women's 100 m, 400 m, and 10,000 m events, as well as the women's and men's marathon do not reach the current world records. However, this does not mean that the world record will never be broken as the realized season-best performances will fluctuate statistically around the trend identified here.

4. Discussion

4.1. Strengths and weaknesses of the analysis

4.1.1. Strengths of the analysis

The data sets compiled here cover longer time periods and reveal more robust insights into the dynamics of sprint and distance running performances than the data sets used in previous studies (e.g., Tryfos & Blackmore, 1985; Whipp & Ward, 1992). Our data sets are made available in the Supplemental Data and may provide the empirical basis for further quantitative analyses of running performances.

Our findings suggest that running performances tend to improve by following an exponential function of time as well as experience curve patterns. The experience curve approach has, so far, not been applied to the field of sports sciences. By including experience as an explanatory variable, we explicitly account for the declining interest in competitive running during the First and Second World Wars. The exponential time series analysis has strong empirical merits but cannot capture such effects. We argue that experience curves are specifically useful for analysing and forecasting the dynamics of parameters whose explanatory variable does not follow time homogeneously. Specifically, for the women’s 10,000 m as well as for the women’s and men’s marathon events, the experience curve analysis fits the data better than the time series analysis does; the latter only represents the data well if performances established before 1945 are neglected. We recommend expanding experience curve analyses by (1) covering additional sport events, (2) applying alternative proxies of experience and (3) conducting scenario analyses by assuming a range of plausible rates of experience accumulation in the future.

4.1.2. Limitations of the analysis

Modelling and forecasting human behaviour is intrinsically uncertain. The identified patterns of performance improvement may only persist if socio-economic conditions in the future remain similar to those observed in the past. The stagnation of women's sprint and middle-distance performances after the end of the cold war may illustrate how political factors affect competitive running at the top level. Moreover, the identified exponential and experience curve patterns: (1) only apply within the boundaries of well-established competitive sprint and distance running, (2) do not explicitly account for human physiology and bio-kinetics and (3) cannot single out the contribution of individual factors behind the observed performance improvements. Sporadically occurring innovation in equipment (such as the introduction of synthetic running surfaces in the late 1960s and automatic timing in 1977), medication and training methods have been affecting running performances in the past and will continue to do so in the future. As a consequence, the future season-best sprint and distance running performances will continue to scatter around the trends identified here and may also result of the unexpected improvements of the standing world records.

Our experience curve analysis provides a first, but still incomplete, step towards a more detailed explanation of long-term trends in sprint and distance running. While it is reasonable to assume that experience increases with the cumulative number of Olympic participants, it is unclear whether the relationship between both parameters is linear (as assumed here) or of any other nature. Approximating experience solely by the cumulative number of Olympic participants partially disregards a multitude of explanatory factors, such as an increasing human population, changing shares of the population with opportunities for competitive running, improved medication and nutrition or variability in the opportunity costs for taking up a running career.

A specific caveat of our experience curve analysis relates to the potentially insufficient capturing of the steep initial improvement and the later stagnation of women's performances, resulting in a potential overestimation of future progress (see also Section 4.2). Introducing a fourth asymptotic parameter into our experience curve model addresses this shortcoming and may thus provide a more reliable forecast of future running performances (see Table S11 in the Supplemental Data).

4.2. Discussion of historic improvement rates and future performance forecasts

Our analysis has shown that marginal performance improvements tend to decline and may even cease to exist. The most pronounced examples represent the women's sprint and middle-distance events for which high initial improvement rates are followed by two decades of stagnation. The observed dynamics may be explained by the fact that women have initially over-proportionally benefitted from men's experience (e.g., in training methods, equipment, nutrition, medication) and the rapid expansion of opportunities for competitive running in the decades after the Second World War. With the end of the cold war era, however, political factors may have contributed to more restrictive doping tests, declining marginal innovation in training methodology and sports equipment, as well as increased opportunity costs of choosing a running career. In the context of doping, it may be interesting to note that women naturally possess a lower muscle-weight to body-weight ratio than men do. Anabolic drugs that tend to increase the muscle-weight to body-weight ratio may thus benefit women more than they benefit men. Consequently, we would expect the stagnation or decline of performance levels following the decreased use of anabolic drugs to be more pronounced for women than for men; this expectation appears to be confirmed by our data.

Our results generally support the findings of the logistic regression analysis conducted by Nevill and Whyte (2005) but not the conclusions of Whipp and Ward (1992). The latter authors identify a linear increase in running speed until the late 1980s and project based on this observation that women's and men's performances will converge, e.g., for the marathon in 1998 at a time of 2:01:59 h. By analysing longer data series, our analyses suggest declining performance improvements over time and a persisting gap between women's and men's performances.

Controversial discussions among runners and sports enthusiasts have motivated us to conduct the present analysis. We conclude that if the past trends persist, we may witness (see Tables S9–S11 in the Supplemental Data):

• men still running faster than women by the end of the twenty-first century;

• a sub 9.50 s run over 100 m around the end of the twenty-first century;

• a sub 1:40 min run over 800 m around the year 2040;

• a new world record in the women's 1500 m and 5000 m events within the next two decades;

• new world records over the men's 200 m, 400 m, 1500 m, 5000 m and 10,000 m within the next two to three decades.

We obtain inconclusive results regarding the prospects of a sub-2 hour marathon. Despite recent improvements in the men's marathon record, we regard a marathon in less than 2 h as unlikely to happen before the year 2100. Moreover, we are sceptical about the optimistic forecasts obtained from our experience curve analysis for most of the women's and men's sprint and distance running events (see Note 4 in the Supplemental Data). Over the past two decades, no woman has reached the sprint and middle-distance performances of the 1980s and early 1990s; likewise, none of the recent men's performances have come close to the standing 5000 m and 10,000 m world records. Although it appears questionable that any of the long-standing world records will be broken soon, the statistical analysis of Denny (2008) suggests that, unlike for animal races, there may still be potential for an increase in running performances across all events. Denny (2008) argues that other constraints than physiological and mechanical factors limit human running performances. This argument again points to experience and innovation as drivers behind running performances and sports performances in general. We are looking forward to seeing our results challenged by scientists and the global running community.

Disclosure statement

The views expressed here are those of the authors and may not be regarded as an official position of the European Commission. Neither the authors nor the employers of the authors have any financial interest in or a financial conflict with the subject matter or materials discussed in this article.

Supplemental data

Supplemental data for this article can be accessed here (http://dx.doi.org/10.1080/17461391.2015.1042526).