On-Chip Integrated, Silicon–Graphene Plasmonic Schottky Photodetector with High Responsivity and Avalanche Photogain

Abstract

We report an on-chip integrated metal graphene–silicon plasmonic Schottky photodetector with 85 mA/W responsivity at 1.55 μm and 7% internal quantum efficiency. This is one order of magnitude higher than metal–silicon Schottky photodetectors operated in the same conditions. At a reverse bias of 3 V, we achieve avalanche multiplication, with 0.37A/W responsivity and avalanche photogain ∼2. This paves the way to graphene integrated silicon photonics.

Over the past decade, silicon photonics¹ has progressed toward miniaturization and on-chip integration of optical communication systems, where data are encoded by light signals and distributed over waveguides rather than conventional metal-based electronic interconnects.^2,3 So far, a variety of passive and active photonic devices in Si have been demonstrated including low-loss (∼0.3 dB/cm) waveguides,^4,5 high-quality factor optical cavities (∼10⁶),⁶⁻⁸ high-speed (tens of GHz)⁹⁻¹¹ electro-optic modulators, and Si light sources based on Raman gain.^12,13 The wealth of devices, together with the well established complementary metal-oxide–semiconductor (CMOS) fabrication processes make Si photonics a promising technology for short-range (board-to-board, chip-to-chip, or intrachip)¹ optical communications.

The photodetector (PD) is one of the basic building blocks of an optoelectronic link, where it performs optical-to-electrical signal conversion. Development of Si PDs for telecom wavelengths (1.3–1.6 μm) based on the mature CMOS technology is an essential step for monolithic, on-chip, optoelectronic integration.¹ While Si PDs are widely employed in the visible spectral range¹⁴ (0.4–0.7 μm), they are not suitable for detecting near-infrared (NIR) radiation above 1.1 μm, because the energy of NIR photons at telecom wavelengths (0.78–0.95 eV) is not sufficient to overcome the Si bandgap (indirect, 1.12 eV) and induce photogeneration of electron–hole (e–h) pairs, i.e., no photocurrent (I_ph) is generated. Over the years, the Si photonics industry has developed solutions to overcome this deficiency by combining Ge (bandgap 0.67 eV) with Si¹⁵⁻¹⁷ and integrating compound (III–V) semiconductors on the Si chip^18,19 using wafer bonding techniques.²⁰ While these approaches provide a path toward photodetection in the telecom spectral range,¹ they either require advanced and complex fabrication processes in the case of SiGe devices²¹ or rely on III–V materials systems not compatible with standard CMOS technology.¹⁴ Motivated by the need of developing Si-based PDs for telecom wavelengths, several approaches were proposed to date. These include two-photon absorption (TPA),^22,23 defect mediated band-to-band photogeneration via midbandgap localized states,²⁴⁻²⁶ deposition of polysilicon²⁷ for NIR absorption, and enhancement by optical cavities.^23,25−29 However, in the cases of defect-mediated and poly-Si PDs, the overall concentration of defects in the Si lattice affects both I_ph and the leakage (dark) current I_dark,^14,24,25 i.e., a higher defects density increases both the sub-bandgap optical absorption and thermal generation processes,¹⁴ thus increasing both I_ph and I_dark.^14,24,25 As a result, PDs with reduced defects concentration are typically needed,^24,25 coupled to optical resonators to amplify the optical power and to enhance the absorption without increasing either device length or defect density. On the other hand, nonlinear optical process, such as TPA, could potentially contribute to all-Si NIR-PDs,¹ but this approach requires increased optical power²³ with respect to linear absorption, or PD integration with high quality factor cavities, to achieve enhanced photon density.²³

An alternative exploits internal photoemission (IPE) in a Schottky diode.^14,30,31 In this configuration, photoexcited (“hot”) carriers from the metal are emitted to Si over a potential Φ_B, called Schottky barrier (SB), that exists at the metal–Si interface.^14,32 In Si, the injected carriers are accelerated by an electric field in the depletion region of a Schottky diode and then collected as a photocurrent at the external electrical contacts. Typically, a SB is lower (0.2–0.8 eV) than the Si bandgap,¹⁴ thus allowing photodetection of NIR photons with energy hν > Φ_B. The advantages of Schottky PDs are the simple material structure, easy and inexpensive fabrication process, straightforward integration with CMOS technology, and broadband (0.2–0.8 eV) operation.¹⁴ The main disadvantage is the limited IPE quantum yield, i.e., the number of carriers emitted to Si divided by the number of photons absorbed in the metal, typically <1%.^33,34 This is mainly due to the momentum mismatch between the electron states in the metal and Si, which results in specular reflection of hot carriers upon transmission at the metal–Si interface.^33,34 The quantum yield is often called internal quantum efficiency (IQE)¹⁴ so that IQE = I_ph/P_abs × hν/q, where P_abs is the absorbed optical power, hν is the photon energy, q is the electron charge, and I_ph/P_abs is the PD responsivity (R_ph) in units of A/W. One way to improve the R_ph and IQE in Schottky PDs is to confine light at the metal–Si interface by coupling to plasmonic modes.^35,36 The role of plasmonic confinement in enhancing the IPE efficiency in Si Schottky PDs was intensively studied³⁷⁻⁴⁶ in various M–Si plasmonic structures. Several NIR Si plasmonic Schottky PDs have been demonstrated, exploiting both localized plasmons³⁷⁻⁴⁰ and guided surface plasmons polaritons (SPP).⁴¹⁻⁴⁶ Yet, in these devices, the R_ph reported to date does not exceed few tens mA/W with maximum IQE ∼ 1%.⁴³ These values are significantly below that of SiGe PDs (R_ph ∼ 0.4–1 A/W and IQE ∼ 60–90%).¹⁵⁻¹⁷ Consequently, R_ph of Schottky PDs should be further improved both by developing advanced device designs or using novel CMOS-compatible materials.

Graphene is appealing for photonics and optoelectronics because it offers a wide range of advantages compared to other materials.⁴⁷⁻⁵² A variety of prototype optoelectronic devices exploiting graphene have already been demonstrated, such as transparent electrodes in displays,⁵³ photovoltaic modules,^54,55 optical modulators,⁵⁶⁻⁵⁸ plasmonic devices,⁵⁹⁻⁶³ and ultrafast lasers.⁵¹ Amongst these, a significant effort has been devoted to PDs due to a number of distinct characteristics of graphene.^47−50,52 Single-layer graphene (SLG) is gapless. This enables charge carrier generation by light absorption over a very wide energy spectrum. In addition, SLG has ultrafast carrier dynamics,⁶⁴ wavelength-independent absorption,^65,66 tunable optical properties via electrostatic doping,^67,68 high mobility,⁶⁹ and the ability to confine electromagnetic energy to unprecedented small volumes.^49,50 The high carrier mobility enables ultrafast conversion of photons or plasmons to electrical currents or voltages.^70,71 By integration with local gates, this process is in situ tunable^72,73 and allows for submicron detection resolution and pixelization.⁷⁴ SLG absorbs 2.3% of the incident light,^65,66 which is remarkably high for an atomically thin material. This is an appealing property for flexible and transparent optoelectronic devices.⁴⁷

The most common SLG PDs exploit the metal–graphene–metal (MGM) configuration, in which a SLG channel is contacted between source and drain electrodes.^70−72,75 MGM devices are easy to fabricate,^70,71 they are able to operate over a broadband wavelength range,^70,71 and have demonstrated ultrahigh (∼230 GHz)⁷⁶ operation speed. However, for visible and NIR wavelengths, free-space illuminated MGM PDs have R_ph ∼ a few mA/W.^70,71 This is primarily because of the finite optical absorption^65,66 and limited photoactive area (A_photo).⁷⁷ In the MGM configuration, the built-in electric field that separates the photoexcited e–h pairs is localized in very narrow (∼100–200 nm)⁷⁷ regions next to the edges of the SLG–metal contacts, while the rest of the SLG channel area does not contribute to I_ph. One way to increase R_ph is to apply a voltage between source-drain electrodes and increase the electric field penetration into the SLG channel.^70,71 However, this will drive a current into SLG (dark current, I_dark), which could be of the same order or even larger than I_ph.^70,71 Thus, this approach can significantly reduce the signal-to-noise ratio (SNR) and increase power consumption. Another way consists of combining MGM devices with metal nanostructures^63,78 and enabling light coupling to localized and SPP modes, thus enhancing light–graphene interaction and light absorption. MGM-PDs can be also integrated with microcavities,^79,80 where at resonance the optical absorption in graphene is amplified by multiple light round trips.^79,80 High R_ph can be achieved using a hybrid configuration, in which a MGM structure is combined with semiconductor quantum dots (QD) as light absorbing media.⁸¹ This gave R_ph ∼ 10⁷ A/W⁸¹ with a photoconducitve gain (i.e., the number of detected charge carriers per single incident photon, G_ph) up to 10⁷. Similar performances to graphene–QD hybrid devices were also demonstrated in graphene tunneling PDs,⁸² comprising two SLGs separated by a thin (<10 nm) dielectric layer. However, in both QDs-integrated or tunneling-based PDs, the typical response time is limited to ms,^81,82 not suitable for high-speed (tens of GHz) optical communications.

Another important performance metric of PDs is the normalized photo-dark-current ratio, NPDR = R_ph/I_dark.⁸³ The larger the NPDR, the better PD noise rejection and ability to perform when interference (noise) is present. To achieve higher NPDR, I_dark must be reduced and R_ph must be increased. However, since SLG has no gap, a trade-off between improving R_ph by using source-drain bias and minimizing I_dark exists in all MGM-PDs.⁵² In telecom applications, where power consumption and SNR are parameters of great importance for achieving energy efficient data transmission with reduced errors rate,¹ MGM-PDs should be operated near zero bias, which, in turn, limits R_ph. Even though MGM-PDs can perform in photovoltaic mode at zero bias with zero dark current,^52,84 the conductance of graphene can lead to enhanced thermal noise as a result of reduced channel resistance.⁸⁴ A promising route to increase R_ph, while minimizing I_dark, is to create a Schottky junction with rectifying characteristics (i.e., a diode) at the SLG–Si interface.⁸⁵⁻⁸⁹ By operating a Schottky diode in reverse bias (photoconductive mode), I_dark is suppressed compared to I_ph, while the entire Schottky contact area contributes to photodetection.⁸⁵⁻⁸⁹

Several PDs have been reported to date, operating at telecom wavelengths and integrating on-chip graphene with Si photonics, based on MGM structures evanescently coupled to Si waveguides.⁸⁹⁻⁹³ In these cases, the guided mode approach enables longer interaction between SLG and the optical waveguide modes than free-space illumination.⁵² This raises the optical absorption in PD beyond 2.3% and, by increasing the interaction length, 100% light power can be absorbed and contribute to I_ph.⁹¹ Nevertheless, because of the evanescent coupling, the typical length needed to achieve nearly complete absorption in MGM-PDs is ∼40–100 μm.⁸⁹⁻⁹³ However, for on-chip optoelectronic integration, where scalability, footprint, and cost play an important role, the development of miniaturized, simple to fabricate, Si-based PDs for telecoms, with R_ph comparable to the SiGe devices currently employed in Si photonics, is needed.¹

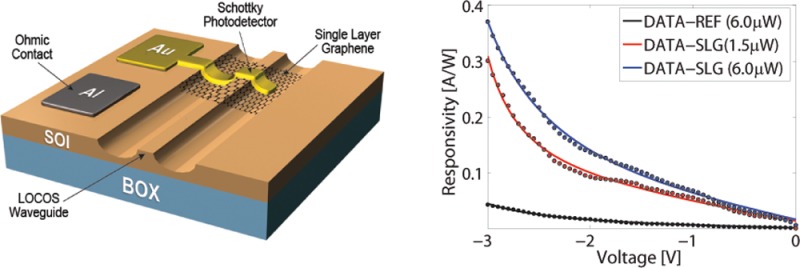
Here, we report a compact (5 μm length), waveguide integrated, plasmonic enhanced metal/graphene/Si (M–SLG–Si) Schottky PD with R_ph ∼ 0.37A/W at 1.55 μm. The M–SLG–Si structure supports SPP guiding and benefits from optical confinement at the Schottky interface. Our data show that graphene integration in M–SLG–Si PDs increases R_ph by one order of magnitude compared to the standard M–Si configuration without SLG. The SLG-integrated device has R_ph ∼ 85 mA/W at 1 V reverse bias, with I_dark ∼ 20 nA. By taking advantage of the Shottky diode operation in the reverse bias, R_ph can be further increased up to ∼0.37 A/W at 3 V. To the best of our knowledge, this is the highest R_ph reported so far for waveguide-integrated Si-PDs operating at 1.55 μm, and it is comparable to state-of-the-art SiGe devices.¹⁵⁻¹⁷ This is a simple, inexpensive, easy-processed approach for high responsivity Si PDs in the telecom spectral range and paves the way to graphene–Si optoelectronic integration.

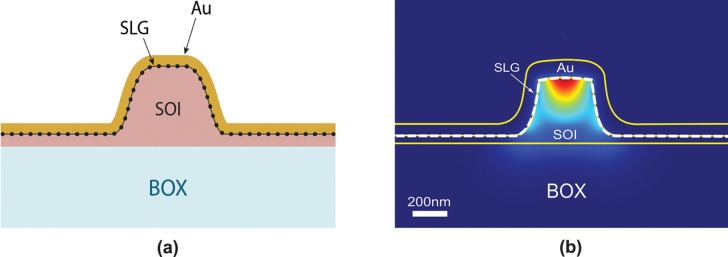
Our PD is schematically shown in Figure 1a. The device consists of a Si-waveguide coupled to a SLG/Au contact that electrically forms a Schottky diode. The M–SLG–Si structure supports the fundamental SPP waveguide mode (Figure 1b). SPP guiding in a similar M–Si waveguide was experimentally demonstrated in ref (43) using a near-field scanning optical microscope. Introducing a subnanometre SLG layer at the interface is not expected to perturb the SPP guiding, as confirmed by the simulation in Figure 1b. The M–SLG–Si SPP waveguide mode benefits from optical confinement at the Schottky interface, where the IPE process takes place. This maximizes the optical intensity in SLG and enhances light–graphene interaction, increasing the absorption adjacent to the Schottky interface and, as a result, enhancing R_ph.

Figure 1.

(a) Schematic M–SLG–Si Schottky PD. SOI: silicon-on-insulator. BOX: buried oxide. (b) Finite element (COMSOL Multiphysics)⁹⁴ simulated optical intensity profile of a SPP waveguide mode supported by a M–SLG–Si structure.

The fabrication process is discussed in Methods. We prepare on the same chip two types of devices: (1) M−SLG−Si Schottky PDs (our target devices) and (2) reference M−Si PDs. Figure 2 shows a scanning electron microscope (SEM) picture of a representative M–SLG–Si Schottky PD integrated with locally oxidized⁵ Si waveguides. The PD length is ∼5 μm, and the Si waveguide width is ∼310 nm.

Figure 2.

(a) SEM micrograph of Schottky PD coupled to a Si photonic waveguide. False colors: brown, Si; yellow, Au. (b) Layout of waveguide integrated Schottky PD.

Figure 3 plots a typical current–voltage (I–V) characteristic of our devices, measured using a probe station and a parameter analyzer (Keithley 4200). The device shows electrical rectification (i.e., diode behavior). The current in forward bias is limited by the series resistance,¹⁴ while at reverse bias, the leakage current I₀ is limited by thermionic emission from Au/SLG to Si. In reverse bias, I₀ grows with increasing temperature, consistent with what expected for thermionic-emission in a Schottky diode.¹⁴ In the thermionic regime, the variations of I₀ are reflected in the forward bias region, where the forward current also increases (Figure 3). By using the I–V characteristics in forward bias, and following the procedure described in refs (95 and 96), we extract the M–SLG–Si devices Schottky barrier height Φ_B ∼ 0.34 and a diode ideality factor n ∼ 1.8 (defined as the deviation of the measured I–V curve from the ideal exponential behavior).¹⁴ For the reference M–Si devices, we get Φ_B ∼ 0.32 and n ∼ 1.7, similar to M–SLG–Si. This indicates that SLG does not significantly affect the electrical properties of the Schottky contact.

Figure 3.

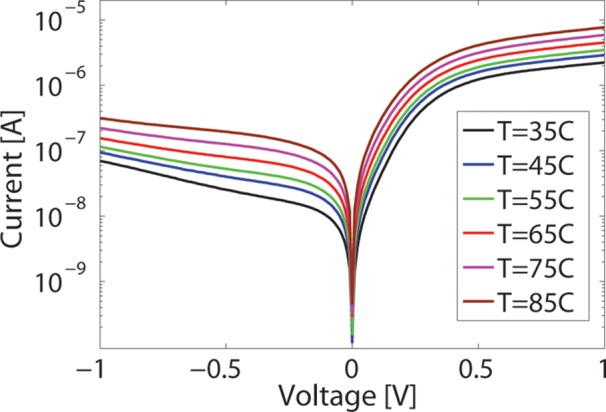
I–V characteristics of a representative M–SLG–Si Schottky PD for various temperatures.

For optoelectronic characterization, we use a 1.55 μm continuous wave (CW) transverse-magnetic (TM) polarized light from a tunable laser source (Agilent 81680A). The optical signal is butt-coupled to the waveguide using a polarization-maintaining (PM) tapered fiber with a mode size ∼2.5 μm. The device under test is placed on a fixed vacuum holder, while the lensed fiber is aligned with respect to the waveguide facet under a microscope using a high precision (0.1 μm step) XYZ translation stage. Figure 2b shows that our device has a symmetric Y-branch to split the optical signal between the active arm with integrated Schottky PD and the reference waveguide. This is continuously monitored to avoid optical power fluctuations during the experiment. At the output facet of the reference waveguide, the light is collected with a similar fiber and detected by an external InGaAs power meter (Agilent 81634a). After optimizing the optical coupling conditions by adjusting the positions of both input and output lensed fibers, and maximizing the optical power reading in the InGaAs power meter, we measure the I–V characteristics of the Schottky PD. To do so, we place probes on the contacts pads of the Schottky device under the microscope by using micromanipulators. Since we perform a steady-state DC characterization using a CW laser, no special arrangements for impedance matching are required. We use standard TRIAX/BNC cables to interface between the needle-based electrical probes and the SMU unit (Keithley 4200).

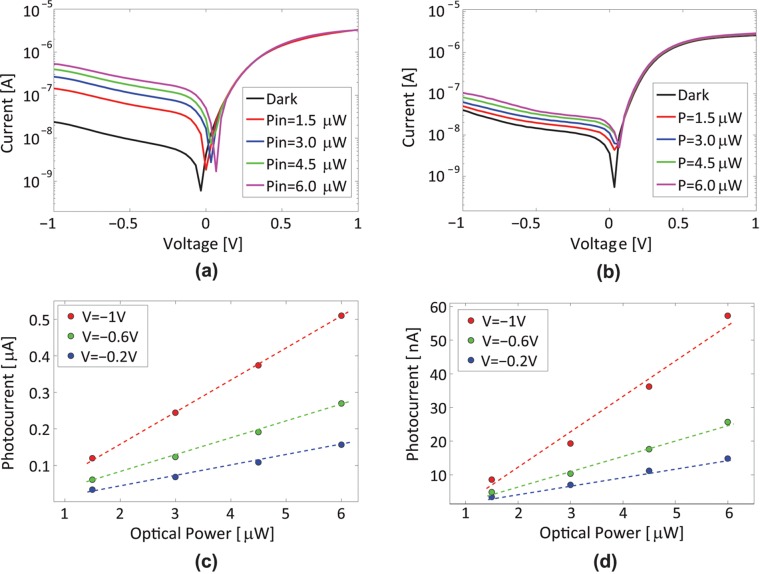
To test the optoelectronic response, we measure the I–V curves of the graphene-integrated M–SLG–Si and reference M–Si devices at different P_opt values inside the SPP waveguide. For each P_opt, we perform three independent measurements and plot in Figure 4a,b the average results, with a maximal standard deviation ∼5%. The PDs operate in photoconductive mode,¹⁴ when a P_opt increase results in larger reverse current, since I_ph acts as an external current source added to the Schottky diode I₀.

Figure 4.

I–V characteristics of (a) graphene-integrated and (b) reference M–Si PDs for different optical powers coupled to the Schottky region. Measured photocurrent in (c) graphene-integrated and (d) reference M–Si PDs as a function of optical power coupled to the Schottky region. The slope of the lines in (c,d) corresponds to R_ph.

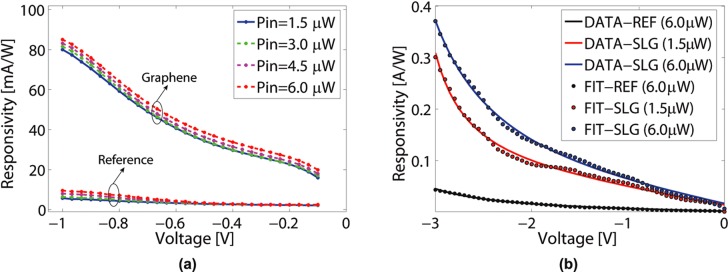
Figure 4c,d plot I_ph as a function of P_opt as derived from the I–V curves in Figure 3. I_ph grows linearly with P_opt, and the slope corresponds to R_ph, i.e., I_ph = R_ph × P_opt. We estimate P_opt inside the Schottky PDs by taking into account a coupling loss of ∼18.5 dB (98.5%) between the external tapered fiber and the Si waveguide (as measured by monitoring the output signal in the reference waveguide), a propagation loss (scattering + free carriers) ∼ 1.5 dB/mm (29% per mm) in the waveguide, ∼3 dB (50/50) power splitting, and ∼1.5 dB (29%) power loss in the Y-branch. Consequently, on the basis of our I–V measurements and our P_opt, we calculate and plot R_ph as a function of reverse voltage V_R in Figure 5a.

Figure 5.

(a) R_ph of M–SLG–Si and reference M–Si PDs as a function of reverse bias for different optical powers coupled to the Schottky region; (b) R_ph of M–SLG–Si and reference M–Si PDs for 0 < V_R < 3 V. Colored solid lines show a fit of the bias dependent R_ph based on combined thermionic-field emission and avalanche multiplication processes.

We get maximal R_ph ∼ 85 mA/W (±5%) with I₀ ∼ 20 nA at V_R = 1 V. The former corresponds to IQE ∼ 7%. By using the values of device resistance R_D = dV/dI, the responsivity R_ph and the dark current I₀ at V_R = 1 V, we estimate a noise equivalent power NEP ∼ 1.1 × 10^–12 W/Hz^0.5. For the reference M–Si PD, we get R_ph ∼ 9 A/W (±5%) and NEP ∼ 1.2 × 10^–11 W/Hz^0.5, similar to state of the art Si Schottky PDs at 1.55 μm.⁴¹⁻⁴⁶ We conclude that the presence of SLG at the Schottky interface improves both R_ph and NEP by one order of magnitude compared to our reference M–Si PDs. The improvement is significantly larger than the ±5% error bar in the measurements. We attribute this to light absorption in the SLG adjacent to the Schottky barrier, where the IPE process takes place. The absorption is enhanced by SPP optical confinement at the M–SLG–Si interface (Figure 1b). The significant increase of R_ph in SLG-integrated devices could be due to an higher transmission probability of hot carriers from SLG to Si when compared to the M-to-Si photoemission process.

We then measure R_ph for V_R > 1 V. Figure 5b shows that R_ph grows monotonically up to V_R ∼ 2 V and then abruptly increases to ∼0.37 A/W at V_R = 3 V. To the best of our knowledge, this is the highest R_ph reported so far for waveguide-integrated Si-PDs at 1.55 μm, and it is comparable to state-of-the-art Si–Ge devices currently employed in Si photonics.¹⁵⁻¹⁷ We attribute this to the combined effect of two processes that can enhance I_ph. First: thermionic-field emission (TFE), i.e., tunneling of photoexcited carriers from the M–SLG contact to Si at energies E_F < E < Φ_B. The relative contribution of TFE with respect to IPE depends on Si doping, operation temperature, and the electric field applied to the Schottky junction.^14,97 TFE tends to dominate at higher (>10¹⁸ cm^–3) doping levels,^14,97 and its voltage dependence is 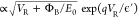, where E₀ and ϵ′ are two analytically defined constants.^14,97 In our device, with Si doping ∼7 × 10¹⁷ cm^–3 at room temperature, we calculate using eqs 3 and 4 (see Methods) E₀ and ϵ′ to be ∼1.04 V and ∼2.1 eV, respectively.¹⁴ Second: avalanche multiplication of photoexcitepd carriers inside the Si depletion region, where the electrons (or holes) can lose their energy upon scattering with the Si lattice creating other charge carriers (i.e., impact ionization). This process can be empirically modeled by M = 1/[1 – (V_R/V_BD)^k],¹⁴ where M is the avalanche multiplication factor, V_BD is the breakdown voltage at which M goes to infinity, and k is a power coefficient that empirically acquires values between 2 < k < 6.¹⁴ As first order approximation, we assume independent contribution of each process. We show in Figure 5b that our data are well fitted by R_ph (V) ∝ TFE × M with V_BD and k as free parameters. From the fit we get V_BD ∼ 3.75 V and k ∼ 3.2, corresponding to M ∼ 2 at V_R = 3 V. We note that, under avalanche conditions, the dark current also increases (∼3 μA), and operation at elevated V_R (>2.5 V) reveals a trade-off between improving R_ph and higher dark current.

In summary, we demonstrated on-chip, compact, waveguide-integrated metal–graphene–silicon plasmonic Schottky photodetectors operating at 1.55 μm. The presence of graphene at the Schottky interface significantly improves the responsivity. The devices reach 85 mA/W responsivity at 1 V reverse bias, corresponding to 7% internal quantum efficiency. This is one order of magnitude higher compared to reference metal–Si photodetectors under the same conditions. We attribute this improvement to the combined effect of light confinement and graphene absorption at the metal–graphene–silicon Schottky interface, as well as enhanced carriers injection from graphene-to-silicon as compared to the metal–silicon interface. Avalanche multiplication for higher (>2 V) reverse biases allows us to reach a responsivity ∼0.37 A/W, corresponding to a photogain ∼2. Our device paves the way toward graphene integrated silicon photonics.

Methods

Si–SLG Schottky PD Fabrication

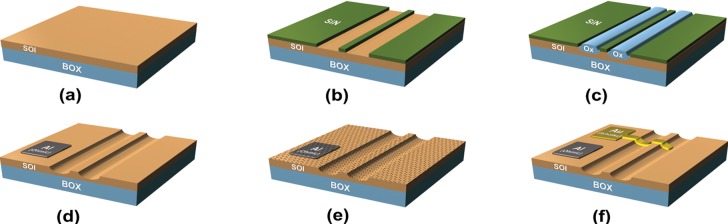
Figure 6 outlines the fabrication process of our devices. We start with a commercial silicon on insulator (SOI, from SOITEC) substrate with a 340 nm p-type (7 × 10¹⁷ cm^–3) Si layer on top of a 2 μm buried oxide (BOX). First, a 100 nm SiN mask is deposited by plasma enhanced chemical vapor deposition (PECVD, Oxford PlasmaLab100) onto the SOI substrate at 300 °C (Figure 6b). Next, a Si photonic waveguide and the PD area are defined by electron beam lithography (EBL, Raith eLine 150) using positive e-beam resist (ZEP 520A). The EBL pattern is subsequently transferred to SiN by reactive ion etching (RIE) (Oxford Plasmalab 100) with a CHF₃/O₂ gas mixture. Then the SOI substrate is locally oxidized (wet, 1000 °C) to grow a SiO₂ layer only in localized patterns defined by EBL where Si is exposed to O₂, while at the same time a SiN mask prevents O₂ diffusion into the Si in protected areas (Figure 6c). After oxidation, the sacrificial SiN mask layer is etched in hot phosphoric acid (H₃PO₄, 180°) followed by SiO₂ removal in a buffered oxide etch (BOE) solution. The ohmic contact to Si is realized by Al evaporation followed by metal lift-off and thermal alloying at 460 °C in a forming gas (H₂/N₂, 5%/95%) environment. This fabrication process is based on the technique of local-oxidation of Si (LOCOS) in which a Si waveguide is defined by oxide spacers⁵ rather than RIE. The LOCOS process enables the realization of low-loss (∼0.3 dB/cm)⁵ Si photonic waveguides coupled to a Schottky PD using the same fabrication step.

Figure 6.

Fabrication process of Si–SLG Schottky PDs integrated with photonic waveguides. (a) Planar SOI substrate; (b) PECVD deposition and patterning of SiN mask; (c) local oxidation; (d) etching of SiN and SiO₂ Al ohmic contact to Si; (e) SLG transfer; (f) formation of Schottky contact and consequent SLG etching.

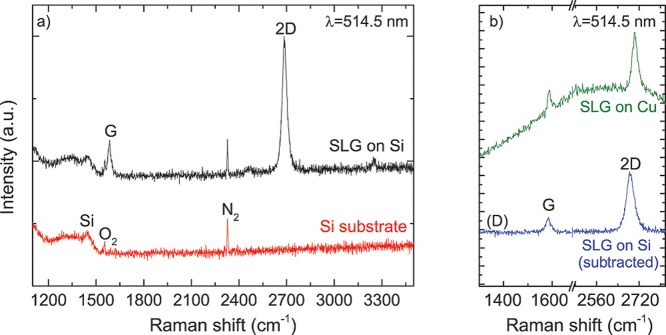
SLG is grown on a 35 μm Cu foil following the process described in ref (98). The substrate is annealed in hydrogen atmosphere (H₂, 20 sccm) up to 1000 °C for 30 min. Then 5 sccm CH₄ is added to initiate growth.^98,99 The substrate is subsequently cooled in vacuum (1 mTorr) to room temperature and removed from the chamber. After growth, the quality and uniformity of SLG are monitored by Raman spectroscopy using a Renishaw InVia equipped with a 100× objective (numerical aperture NA = 0.85). The Raman spectrum of SLG on Cu at 514 nm is shown in Figure 7b (green curve). This has a negligible D peak, thus indicating negligible defects.^100−104 The 2D peak is a single sharp Lorentzian with full width at half-maximum, FWHM(2D) ∼ 29 cm^–1, a signature of SLG.¹⁰⁰ Different (∼20) point measurements show similar spectra, which indicate uniform quality. The position of the G peak, Pos(G), is ∼1589 cm^–1, with FWHM(G) ∼ 13 cm^–1. The 2D peak position, Pos(2D) is ∼2698 cm^–1, while the 2D to G peak intensity and area ratios, I(2D)/I(G) and A(2D)/A(G), are 2.6 and 5.8, respectively, indicating a p-doping ∼300 meV,^105,106 which corresponds to a carrier concentration ∼5 × 10¹² cm^–2.

Figure 7.

(a) Raman spectra of (red curve) Si substrate and (black curve) SLG transferred on Si. (b) Raman spectra of (green curve) SLG on Cu, and (blue curve) after normalized, point-to-point subtraction of the Si substrate spectrum (shown in (a), red curve) from the spectrum of SLG transferred on Si (shown in (a), black curve).

SLG is then transferred onto the SOI with Si waveguides. A ∼500 nm thick layer of poly(methyl methacrylate) (PMMA) is spin coated on the SLG/Cu sample and then placed in a solution of ammonium persulfate (APS) in DI water until Cu is completely etched.^98,107 After Cu etching, the PMMA membrane with attached SLG is transferred to DI water for cleaning APS residuals.

To obtain a Schottky interface between the Si waveguide and SLG without the native oxide layer, we perform the transfer in diluted hydrofluoric acid (HF) and DI water (1:100). After cleaning from APS residuals, a SLG/PMMA membrane is placed on a plastic beaker containing 5 mL/500 mL HF and DI water. Next, the target SOI chips are first dipped in BOE for 5 s to etch the Si native oxide and then used to lift the floating SLG/PMMA membrane from diluted HF. As a result, during drying, the presence of HF at the SLG/Si interface prevents Si oxidation and allows formation of “oxide free” SLG/Si Schottky contacts. After drying, PMMA is removed in acetone, which leaves SLG to entirely cover the SOI. We also transfer SLG from the same Cu foil with the same transfer procedure onto Si. This is used to check the SLG quality after transfer by Raman spectroscopy.

The Raman spectrum of SLG transferred on Si is shown in Figure 7a (black line). This is measured at 514.5 nm and with laser power below 300 μW to avoid possible heating effects or damage. The D peak region overlaps the bands at ∼1200–1500 cm^–1, attributed to third order Raman scattering from TO phonons in the Si substrate.¹⁰⁸ The peaks at ∼1550 and ∼2330 cm^–1 in the Raman spectrum of Si substrate (red line) arise from molecular vibrations of ambient oxygen (O₂)¹⁰⁹ and nitrogen (N₂).¹¹⁰ The Raman spectra of the transferred SLG film (black line) and reference Si substrate (red line) are acquired using identical exposure time and laser power. After the intensity of the third order Si peak at ∼1450 cm^–1 in the Si reference spectrum (red line) is normalized to the same peak in the spectrum of the transferred SLG film (black line), a point-to-point subtraction is implemented (Figure 7b, blue line). The resulting spectrum shows I(D)/I(G) ∼ 0.04, indicating negligible defects.^100−104 The 2D peak retains its single-Lorentzian line-shape with FWHM(2D) ∼ 33 cm^–1, validating that SLG has been successfully transferred. Pos(G) ∼ 1584 cm^–1, FWHM(G) ∼ 17 cm^–1, and Pos(2D) ∼ 2687 cm^–1, while I(2D)/I(G) and A(2D)/A(G) are 3.2 and 5.9, respectively, suggesting a p-doping ∼4 × 10¹² cm^–2 (∼200 meV).^105,106

After SLG transfer, we use an additional EBL step followed by O₂ plasma etching to selectively remove SLG from the substrate area containing five waveguides and dedicated to the reference M–Si devices. Then a Schottky contact is prepared by evaporation and liftoff of an 3 nm/100 nm Cr/Au metal strip intersecting the Si waveguide with SLG on top (Figure 6f) (or without SLG for reference devices) and forming a Schottky interface for photodetection. Finally, the samples are placed in a reactive O₂ plasma to remove superfluous SLG.

Thermionic Field Emission

The TFE current is given by¹⁴

1

where A** is the effective Richardson constant, k is the Boltzmann constant, T is the temperature, and q is the electron charge. The contribution of TFE to charge injection across the M–Si interface can be evaluated by comparing the thermal energy kT to E₀₀, defined as¹⁴

2

where ℏ is the reduced Planck constant, N is the Si doping, m* is the effective mass of the charge carriers in Si, and ϵ_s is the dielectric permittivity of Si. When kT ∼ E₀₀, the TFE process mainly contributes to charge carriers injection across the Schottky interface.¹⁴ The parameters E₀ and ϵ′ are analytically defined as¹⁴

3

4

In our case, for Si doping 7 × 10¹⁷ cm^–3 using eq 2, we get E₀₀ ∼45 meV, comparable to the thermal energy at room temperature of 26 meV, reflecting a significant TFE contribution to carriers injection at the Schottky interface. Hence, we calculate E₀ and ϵ′ to be ∼1.04 V and ∼2.1 eV, respectively.

The authors declare no competing financial interest.