Long-term training modifies the modular structure and organization of walking balance control

Abstract

How does long-term training affect the neural control of movements? Here we tested the hypothesis that long-term training leading to skilled motor performance alters muscle coordination during challenging, as well as nominal everyday motor behaviors. Using motor module (a.k.a., muscle synergy) analyses, we identified differences in muscle coordination patterns between professionally trained ballet dancers (experts) and untrained novices that accompanied differences in walking balance proficiency assessed using a challenging beam-walking test. During beam walking, we found that experts recruited more motor modules than novices, suggesting an increase in motor repertoire size. Motor modules in experts had less muscle coactivity and were more consistent than in novices, reflecting greater efficiency in muscle output. Moreover, the pool of motor modules shared between beam and overground walking was larger in experts compared with novices, suggesting greater generalization of motor module function across multiple behaviors. These differences in motor output between experts and novices could not be explained by differences in kinematics, suggesting that they likely reflect differences in the neural control of movement following years of training rather than biomechanical constraints imposed by the activity or musculoskeletal structure and function. Our results suggest that to learn challenging new behaviors, we may take advantage of existing motor modules used for related behaviors and sculpt them to meet the demands of a new behavior.

years of deliberate physical practice are required for motor actions to become truly proficient (Crossman 1959; Ericsson et al. 1993). This proficiency is accompanied by detectable changes in the central representations (Elbert et al. 1995; Pascual-Leone et al. 1993) and biomechanics of trained movements (Furuya et al. 2011; Furuya and Kinoshita 2008; Verrel et al. 2013), as well as related motor behaviors (Gentner et al. 2010). Yet how such long-term training affects the neural control of motor behaviors is not well understood. Therefore, our goal was to determine how the structure and organization of neuromotor outputs for walking and balance are affected by long-term training. Identifying how long-term training affects the construction, storage, and execution of movement may provide valuable insight into yet unknown mechanisms of motor coordination and motor learning that could guide future rehabilitation efforts.

Evidence suggests that motor modules reflect underlying neural mechanisms for coordinating movement. Motor modules, a.k.a., muscle synergies, are groups of coactive muscles with a fixed spatial structure that can have time-varying activation patterns (Torres-Oviedo and Ting 2007). Motor modules may transform movement goals into biomechanical outputs (Chvatal et al. 2011; Chvatal and Ting 2012, 2013; Hayes et al. 2014; Lee 1984; Neptune et al. 2009), acting as building blocks that can be scaled, shifted and recombined to coordinate purposeful goal-directed actions (Flash and Hochner 2005; Ting et al. 2015) across a variety of contexts (Chvatal et al. 2011; Chvatal and Ting 2013; d'Avella and Bizzi 2005; Weiss and Flanders 2004). It is debated whether this structure reflects neural control mechanisms (Berger et al. 2013; Byadarhaly et al. 2012) or emerges from biomechanical constraints imposed by musculoskeletal structure and function (Kutch et al. 2008; Kutch and Valero-Cuevas 2012; Valero-Cuevas et al. 2009). Behavioral evidence suggests that motor modules reflect the structure of neural output, as their spatial structure is preserved across motor behaviors (Tresch and Jarc 2009), despite differences in sensory states (Cheung et al. 2005; Torres-Oviedo 2006), biomechanical contexts (Cappellini et al. 2006; Chvatal et al. 2011; Chvatal and Ting 2013; d'Avella and Bizzi 2005; Oliveira et al. 2012; Routson et al. 2014; Torres-Oviedo and Ting 2010), and loading conditions (Cheung et al. 2009a; Ivanenko et al. 2004; McGowan et al. 2010). Several animal studies have combined motor module analyses with neural recording, imaging, and stimulation techniques to identify motor circuits in the motor cortex (Asavasopon et al. 2014; Overduin et al. 2012, 2014), brain stem (Chvatal et al. 2013; Roh et al. 2011), and spinal cord (Hart 2004; Hart and Giszter 2010; Tresch et al. 1999) that may be involved in expressing motor modules and generating functional motor behaviors.

If motor modules represent neural control mechanisms to coordinate movement, how might their structure and organization change with long-term training? The greatest evidence for differences in motor module structure across levels of motor ability comes from studies of motor impairment, not expertise (Kristiansen et al. 2013; Turpin et al. 2011). These results suggest that the spatial structure, reflected in motor module number and composition, as well as temporal structure or module recruitment, are related to impairments in walking and balance ability. Specifically, motor module number is generally reduced (Clark et al. 2010; Fox et al. 2013; Rodriguez et al. 2013), the number of coactive muscles per module is increased (Clark et al. 2010; Fox et al. 2013; Gizzi et al. 2011; Hayes et al. 2014), and temporal recruitment becomes broader (Hayes et al. 2014) and more variable (Routson et al. 2014). However, just as motor module structure is altered during motor development (Dominici et al. 2011), deficits in the spatial and temporal structure of motor modules may be remediated via motor rehabilitation (Routson et al. 2013). Therefore, it is likely that long-term training in unimpaired individuals may induce changes in the spatial and temporal structure of motor modules. Whether these changes in structure alter the neural control of movement across related motor behaviors is unknown. For example, in many motor behaviors, including walking and balance, motor modules are recruited from a common pool (Cappellini et al. 2006; Oliveira et al. 2012; Torres-Oviedo 2006). This versatility, or generalizability, of motor modules in movement suggests that a change in the control of one behavior could also alter the neural control of a different behavior. However, this has not yet been studied in relation to differences in motor ability.

We hypothesized that long-term training leading to skilled motor performance alters muscle coordination during challenging as well as nominal everyday motor behaviors. Specifically, we examined the structure and organization of motor modules during walking balance behaviors. We compared motor modules between professionally trained ballet dancers and untrained novices while walking overground and across a narrow beam. We predicted that experts would 1) use more motor modules than novices; 2) have modules composed of fewer coactive muscles; 3) recruit more distinct motor modules with greater spatial and temporal consistency during beam walking; and 4) share a larger pool of motor modules between beam and overground walking, revealing greater versatility in their motor patterns.

METHODS

Participant Recruitment

Two groups of participants were recruited: experts (professional trained ballet dancers) and novices (no dance or gymnastic training). Inclusion criteria for all participants was age greater than 18 yr. Experts were required to have at least 10 yr of ballet training and were recruited from the professional development program of the Atlanta Ballet Center for Dance Education, as well as from the Company of the Atlanta Ballet. Novices were required to have no formal dance or gymnastic training. Exclusion criteria for both groups were self-reported medical conditions that could impair walking and balance. Written, informed consent was obtained from each subject. The Institutional Review Board of the Georgia Institute of Technology approved all protocols.

Experimental Procedures

All participants completed four experimental conditions (narrow beam-walking, wide beam-walking, overground walking at preferred gait speed, and overground walking at slow speed). First, balance performance was assessed with a narrow beam-walking test previously shown to detect differences in walking balance proficiency across the spectrum of motor ability (Sawers and Ting 2015). During beam walking, the center of pressure under the foot is restricted to a narrow region. As a result, the lateral ankle strategy for maintaining balance (Hof et al. 2010) cannot be of much assistance. Similarly foot placement, another strategy to maintain balance (Hof et al. 2010; Winter 1995) is limited by the width of the beam. Therefore, the main balance strategy left to participants during beam walking is the lateral hip strategy (Winter 1995); where slight lateral motions of the trunk about the hips are used to maintain and/or restore balance. Participants were asked to walk in a heel-to-toe pattern along a beam that was 3.8 cm wide and 3.66 m long while keeping their arms crossed over their chest. In an effort to reduce the effect of postural threat (Brown et al. 2006; Carpenter et al. 1999) on walking balance performance, beam height was kept low (3.25 cm). No explicit instructions were given regarding walking speed or stepping pattern (i.e., step length or cadence), as previous work has demonstrated that stepping pattern has little effect on beam-walking performance (Speers et al. 1998). Participants attempted to walk across the beam and were instructed to stop if they uncrossed their arms or stepped off the beam (i.e., balance failure).

Next, as a control condition, participants were asked to walk across a wider beam (20.3 cm) using the same heel-to-toe gait pattern. The wider beam condition was added to examine the influence of task difficulty on the sharing of motor modules between behaviors. Finally, overground walking was performed at two speeds: 1) a preferred self-selected speed, and 2) a self-selected slow speed. The slow overground-walking speed condition was selected to better match beam-walking speeds. Overground motor modules were only extracted from the slow-walking condition to determine the degree to which they were shared with the beam conditions. Electromyography (EMG) from the preferred walking speed trials were used to normalize beam- and slow-walking EMG data. All experimental conditions were randomized. Participants performed six trials of each condition while wearing standardized footwear.

Data Collection and Processing

Kinematic data.

Marker coordinate data were collected at 120 Hz using an eight-camera motion capture system (Vicon, Centennial, CO) and a 25-marker set that included head-arms-trunk, pelvis, thigh, shank, and foot segments based on the Vicon Plug-in-Gait model. Marker coordinate data were interpolated using a cubic spline interpolation to remove gaps from the data, filtered with a low-pass Butterworth filter (third-order) at 20 Hz, and combined with subject-specific anthropometric data to build an eight-segment whole body model. Whole body center-of-mass (CoM) position was estimated using a weighted sum approach.

Electromyographic data.

Surface EMG activity was recorded at 1,080 Hz from 16 muscles on the right leg and trunk of each participant. The muscles that were recorded included the following: tibialis anterior, peroneus longus, medial gastrocnemius, soleus, vastus medialis, vastus lateralis, biceps femoris long head, semimembranosus, gluteus maximus, gluteus medius, rectus femoris, tensor fasciae latae, adductor magnus, rectus abdominus, external obliques, and erector spinae. EMG signals were high-pass filtered at 35 Hz (third-order Butterworth), de-meaned, rectified, and low-pass filtered at 40 Hz (third-order Butterworth) using custom Matlab routines (Figs. 1A and 2A).

Fig. 1.

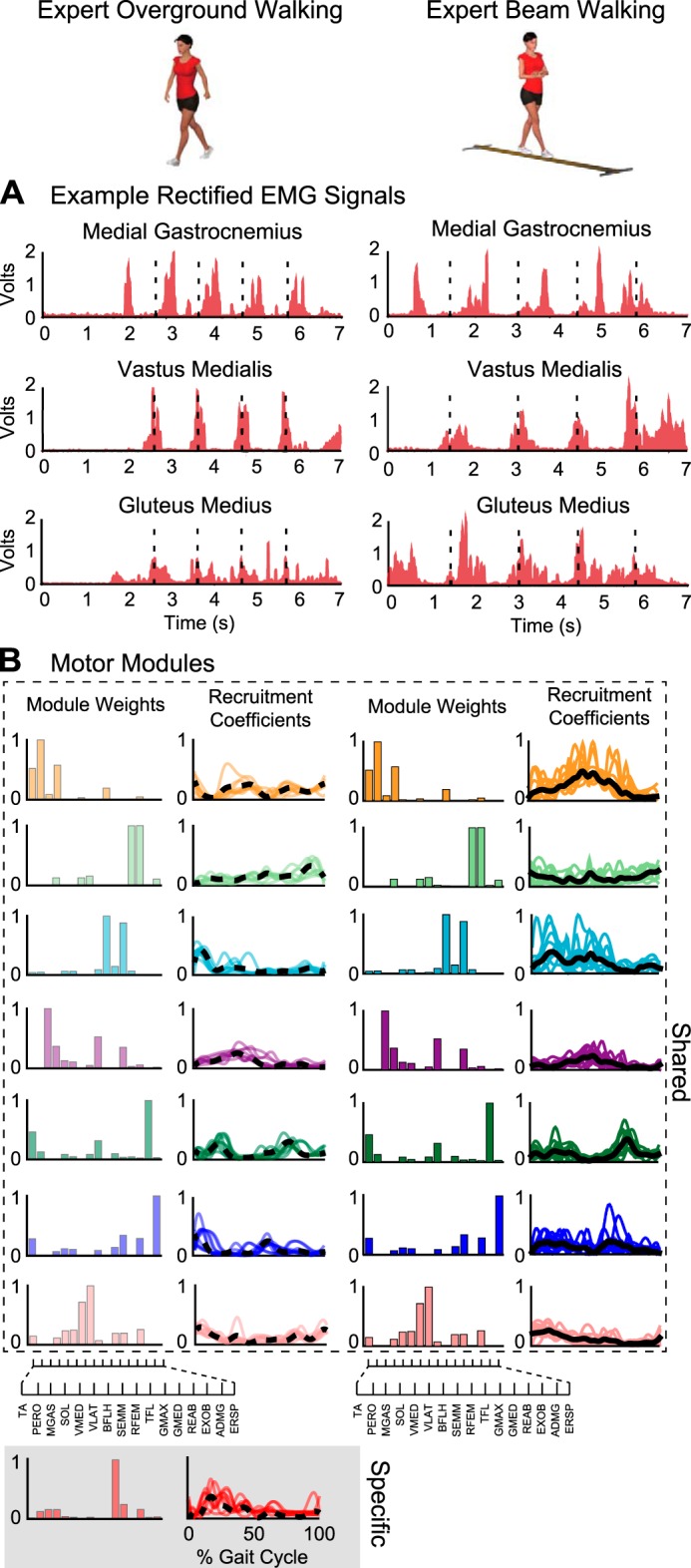
Example electromyography (EMG) and motor modules during overground and beam walking of a professionally trained ballet dancer (expert). A: examples of EMG recordings from select muscles during overground and beam walking (dashed lines denote ipsilateral heel-strikes). EMG data for each individual and behavior were binned into 50-ms windows and used for subject-specific and behavior-specific motor module analysis, capturing step-to-step variations in muscle activity. EMG data were not averaged across steps or individuals. B: examples of motor module weights which illustrate spatial structure, and recruitment coefficients that denote temporal structure extracted from overground and beam walking. Shared motor modules are indicated in the white box, and behavior-specific motor modules are indicated in the gray box. In this expert, all motor modules used in beam walking were also recruited during overground walking, with one extra module for overground walking. Motor module recruitment coefficients increased in magnitude and variation during beam walking, yet showed little to no change in shape. Thick lines represent average recruitment coefficient across steps (dashed for overground walking, solid for beam walking), and thin lines are cycle-by-cycle coefficients. TA, tibialis anterior; PERO, peroneus longus; MGAS, medial gastrocnemius; SOL, soleus; VMED, vastus medialis; VLAT, vastus lateralis; BFLH, biceps femoris long head; SEMM, semimembranosus; RFEM, rectus femoris; TFL, tensor fasciae latae; GMAX, gluteus maximus; GMED, gluteus medius; REAB, rectus abdominus; EXOB, external obliques; ADMG, adductor magnus; ERSP, erector spinae.

Fig. 2.

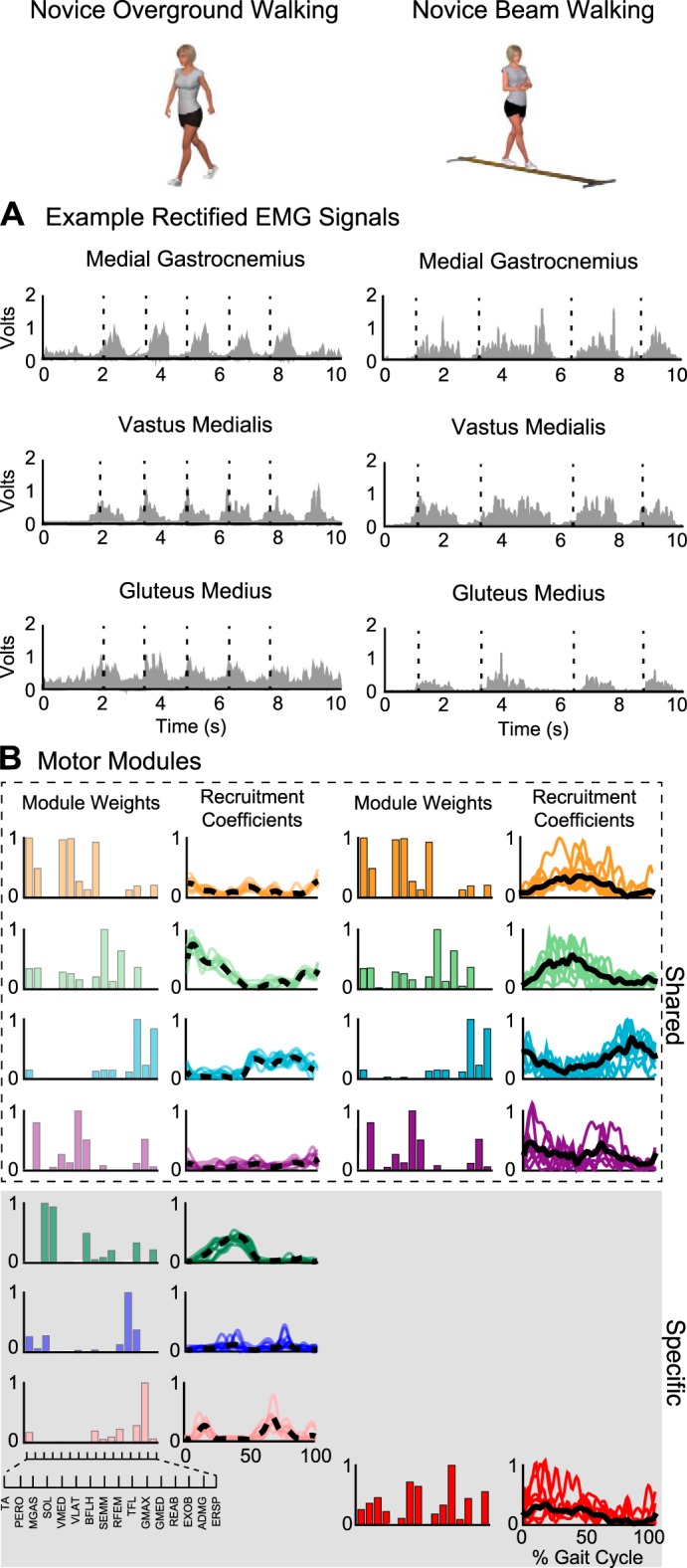
Example EMG and motor modules during overground and beam walking of an untrained participant (novice). A: examples of EMG recordings from select muscles during overground and beam walking (dashed lines denote ipsilateral heel-strikes). EMG data for each individual and behavior were binned into 50-ms windows and used for subject-specific and behavior-specific motor module analysis, capturing step-to-step variations in muscle activity. EMG data were not averaged across steps or individuals. B: examples of motor modules weights (spatial structure) and recruitment coefficients (temporal structure) extracted from overground and beam walking. Shared motor modules are indicated in the white box, and behavior-specific motor modules are indicated in the gray box. In this novice, 50% of the motor modules were shared between beam and overground walking. Temporal structure increased in magnitude and variation, with more notable differences in the shape of the recruitment coefficient between overground and beam walking compared with experts. Thick lines represents average recruitment coefficient (dashed for overground walking, solid for beam walking), and thin lines are cycle-by-cycle coefficients.

Subject-specific EMG data matrices were generated for each walking condition. All trials were cropped to exclude the first and last strides (i.e., initiation and termination), as well as any balance failures. Next, EMG data were downsampled by averaging the data in 50-ms time bins (Chvatal and Ting 2012; Hayes et al. 2014). Previous studies have shown that using 50-ms time bins is sufficient to identify the number and composition of the motor modules during walking (Chvatal and Ting 2012). EMG data from all trials were then concatenated rather than averaged to create data matrices that were 16 (number of muscles) × n (number of time bins) in size for each participant. Ten to twelve gait cycles, identified using vertical heel marker position, were included in the analysis for each participant (Oliveira et al. 2014). No time normalization procedures were performed on the EMG data. As a result, the size of the data matrices (i.e., the length of n) varied between participants. A minimum of 321 data points was used in each EMG matrix. The EMG data matrices were then normalized to the maximum activation observed during overground walking at preferred walking speed, and each row in the data matrices (i.e., muscle vector) was scaled to have unit variance so that equal weighting was applied to each muscle in the extraction process. The unit variance was removed after module extraction to restore the original scaling and facilitate comparison of motor modules (Hayes et al. 2014; Torres-Oviedo and Ting 2007).

Motor module extraction.

To test our prediction that experts would have a larger pool of motor modules that are shared across motor behaviors, we extracted motor modules from the EMG data in two stages (Cheung et al. 2005; Roh et al. 2011). In the first stage, motor modules were extracted from the EMG data of each behavior independently. The objective of this stage was to determine the number of motor modules used in each behavior. In the second stage, the EMG data from each behavior were pooled, and motor modules were extracted from both behaviors simultaneously. The goal of this second stage was to determine the number of shared and behavior-specific motor modules.

STAGE 1: INDEPENDENT MOTOR MODULE EXTRACTION.

Motor modules were initially extracted from overground- and beam-walking EMG data matrices separately using nonnegative matrix factorization (NNMF) (Lee and Seung 1999). Importantly, motor modules were extracted from the whole data set of EMG for each participant rather than an averaged stride cycle. This is important because it helps to capture the consistent patterns underlying step-to-step variability of the EMG data better than averaged data (Oliveira et al. 2014). NNMF is a computational technique that has been used extensively for motor module analysis (Cheung et al. 2009b; Chvatal and Ting 2013; Clark et al. 2010; Ting and Macpherson 2005). NNMF extracts motor modules assuming that each recorded muscle activation pattern, M, is the product of a small number of modules, W_i that are each activated by a module recruitment coefficient, c_i. In this formulation a given muscle activation pattern, M, would be represented by:

$$\text{M}=c_1\stackrel{\rightharpoonup }{W_1}+c_2\stackrel{\rightharpoonup }{W_2}+\cdots +c_n\stackrel{\rightharpoonup }{W_n}$$

where W_i indicates the relative contributions of each muscle in module i. In this model, each motor module is considered to be a spatially fixed time-invariant pattern with recruitment coefficients that vary over time (Hart 2004; Torres-Oviedo 2006). This allows for modules to be flexibly combined and produce a variety of different motor behaviors (Ting and McKay 2007).

To determine the number of motor modules needed to account for the recorded EMG data in each walking condition, we first extracted 1 to 16 modules. The goodness of fit of the data reconstruction for each number of motor modules was then quantified by the variance accounted for (VAF). The VAF describes how much of the variability in the original EMG data is accounted for by the EMG reconstructed from the motor modules and their recruitment coefficients (Zar 1999). To help ensure consistency in selecting the number of motor modules embedded within the EMG data sets, we calculated the 95% confidence interval (CI) for the VAF of the reconstructed EMG at each module number (1–16) (Cheung et al. 2009a; Hayes et al. 2014). This was accomplished by implementing a bootstrapping procedure where the EMG data sets were resampled 500 times with replacement, and the VAF of the reconstructed EMG was recalculated after each resampling. 95% CIs were then constructed from the bootstrapped VAF values at each module number, and the number of modules was selected as the minimum number of modules at which the lower bound of the 95% CI exceeded 90% VAF (Cheung et al. 2009a; Chvatal et al. 2011).

STAGE 2: SHARED AND SPECIFIC MOTOR MODULE EXTRACTION.

To determine the number of shared and behavior-specific motor modules, we used a modified version of the NNMF algorithm (Cheung et al. 2005; Roh et al. 2011) that simultaneously extracts motor modules that are shared across beam and overground walking and those that are specific to each behavior from a data matrix containing EMG from both conditions. A shared motor module is defined as one that is recruited in both behaviors, and therefore has non-zero recruitment coefficients, C in both behaviors. To identify behavior-specific motor modules, the coefficients, C, corresponding to beam walking are set to zero, and vice versa for overground walking. This modification takes advantage of the multiplicative update rule such that any components of W or C that are set to zero prior to NNMF will remain at zero after extraction

First, for each subject, EMG data from beam and overground walking was concatenated into a single matrix so that both behaviors could be analyzed simultaneously. This allowed for the extraction of motor modules that are shared between behaviors, as well as those that are specific to beam or overground walking. For the first iteration of the algorithm, the total number of motor modules to be extracted was set to the sum of the number of motor modules extracted from each behavior independently in stage 1. This iteration assumes no shared motor modules. For example, if five motor modules were extracted in stage 1 for beam walking and six were extracted for overground walking, the total number of modules initially extracted in stage 2 would be 11. During the initial iteration of the algorithm, the recruitment coefficients specific to beam walking were set to zero for overground walking and vice versa. The total number of motor modules extracted is then iteratively reduced by one, which increases and decreases the number of shared motor modules and behavior-specific motor modules by one, respectively. This iterative process of increasing the number of shared motor modules was continued until the total number of modules was equal to the minimum number of motor modules for the individual behavior that was found to have the fewest modules in the independent extraction (i.e., all modules for one behavior are shared with the other behavior).

As in stage 1, the number of shared vs. specific motor modules for each participant was determined by the minimum number of total motor modules that were required so that the lower bound of the 95% CI of the overall reconstructed EMG VAF exceeded 90%. We defined the percentage of shared motor modules between beam and overground walking as the ratio of the number of shared modules over the number of total motor modules across the two behaviors (Figs. 1B and 2B). This approach to identify shared and behavior-specific motor modules was selected because it addresses a number of the shortcomings when comparing the similarity of motor modules extracted independently from data sets of different behaviors, such as underestimating the number of modules in either condition (Cheung et al. 2005).

Data Analysis

Beam-walking performance.

Normalized distance walked was used to quantify beam-walking proficiency (Sawers and Ting 2015). The normalized distance walked is calculated as the ratio of the sum of the distance walked across all six-beam trials and the total possible distance (i.e., 6 trials × 3.68 m/trial = 22.08 m). A normalized distance of 1.0 would be reported for perfect performance on all beam trials. To test our prediction that experts would have better walking balance proficiency than novices, differences in normalized distance walked were compared with a two-sided t-test (α = 0.05).

Walking speed for beam and overground trials were calculated from processed C7 marker coordinate data and trial time. Whole body medial-lateral CoM control was characterized using the margin of stability. The margin of stability quantifies the distance between the extrapolated CoM and the lateral base of support (Hof et al. 2005). The variable b_min is the minimum margin of stability within a gait cycle. The extrapolated CoM is calculated as the vertical projection of the CoM plus its horizontal velocity, divided by a constant related to stature. The lateral base of support was estimated using the position of the lateral malleolus marker, a technique that has been previously utilized when center-of-pressure data are not available (Gates et al. 2013). Since the lateral malleolus was used as the limit of the base of support and not the center-of-pressure or the edges of the beam, the margin of stability that was calculated may be slightly larger than it otherwise would be. The effect of group (expert vs. novice) and condition (beam vs. overground) on walking speed and margin of stability (b_min) was examined with a two-way mixed-design ANOVA (α = 0.05) for each variable. Step width was also calculated during overground walking as the distance between the lateral malleoli at right heel-strike. Differences in step width were examined using a two-sided t-test (α = 0.05).

Kinematics.

To characterize the kinematic movement patterns of experts and novices during beam and overground walking, sagittal and frontal plane segment angle trajectories of the leg and trunk were calculated with respect to the horizontal from processed marker coordinate data. These trajectories were compared between and within groups using a wavelet functional ANOVA, which compares the shape and magnitude of a signal rather than discrete time points without sacrificing statistical power (McKay et al. 2013). To describe the variability of the kinematic movement patterns, the root mean square error (RMSE) of each segment angle trajectory was calculated. RMSE values were compared between experts and novices, as well as between beam and overground walking using a two-way mixed-design ANOVA (α = 0.05).

Spatial patterns of muscle coactivity.

To test our prediction that experts would use more motor modules than novices, the number of motor modules that were independently extracted for each behavior was compared between experts and novices as well as between beam and overground walking using a two-way mixed-design ANOVA (α = 0.05). To test our prediction that experts would have a larger pool of common motor modules between beam and overground walking, we compared the percentage of motor modules that were identified as shared between walking behaviors from the shared/specific extraction using a two-sided t-test (α = 0.05).

Motor module composition was quantified with two metrics of muscle coactivity, W_mus and W_sum. W_mus is the number of significantly active muscles per module (Hayes et al. 2014). Significantly active muscles were computed by establishing 95% CIs for the contribution, i.e., the values of the elements w_ij, to each muscle i in each module j extracted from the bootstrapped versions of the EMG datasets created in stage 1. Significantly active muscles were considered those whose 95% CI did not include zero. W_sum measures the overall level of muscle activity in a module, calculated as the sum of the contributions, w_ij, of significantly active muscle within a module (Hayes et al. 2014). W_sum and W_mus may reflect the efficiency of the motor modules, providing a description of module sparseness. To test our prediction that experts would exhibit less coactivity than novices, W_mus and W_sum were compared between experts and novices, as well as between beam and overground walking using a two-way mixed-design ANOVA (α = 0.05).

Cluster analysis techniques were utilized to characterize motor module separation, consistency, and distinctness. Sammon's mapping, a two-dimensional nonlinear mapping technique, was used to map and plot each subject's 16 dimensional modules (i.e., 16 muscles) in two-dimensional space (De Marchis et al. 2013). This procedure generates a new set of k N-dimensional vectors (N = 2 dimensions) from a set of k M-dimensional vectors (M = 16 dimensional space of the motor modules), while conserving the structure (point-to-point Euclidean distance) of the original data set by minimizing differences in the distance between points from the two data sets (Sammon 1969). Sammon's mapping was applied to a matrix that contained all of the data: specifically, all of the motor modules from the bootstrapped EMG data sets of beam and overground walking of all participants. This allowed us to compare Euclidean distances in the two-dimensional maps across individuals and behaviors. K-means clustering was then used to organize the resulting two-dimensional Sammon's map values into clusters and identify the centroid location of each cluster. For each participant and behavior, the number of clusters was set equal to the number of modules that were identified in the independent module extraction (stage 1). Each data point in a cluster is a two-dimensional representation of one of the bootstrapped motor modules. Module separation (s) was quantified as the average distance between the centroids corresponding to each motor module, module consistency (R95) was quantified as the radius of a circle that encompassed all of the cluster points in that module to 95% confidence, while module distinctness (d) was defined as the mean distance between R95 circles:

$$\overline{d}=\frac{1}{N}{\sum }_{ij}\overline{s}-\left(R{95}_i+R{95}_j\right)$$

To test our prediction that experts would have greater spatial consistency and distinctness in their motor module structure, each of these metrics were compared between experts and novices, as well as between beam and overground walking using a two-way mixed-design ANOVA (α = 0.05).

Temporal patterns of muscle coactivity.

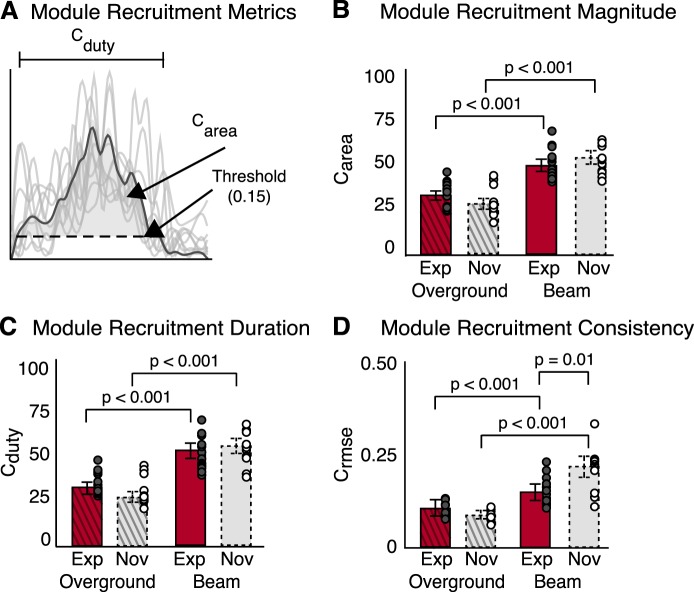
To characterize the temporal patterns of muscle coactivity, we calculated three metrics from the motor module recruitment coefficients (see Fig. 9A). Module recruitment magnitude (C_area) was defined as the area under the curve of the mean recruitment coefficient, the duration of module recruitment (C_duty) was defined as the percentage of the gait cycle for which the recruitment coefficient was above a given threshold (15% of max activation) (Hayes et al. 2014), and the consistency of module recruitment (C_rmse) was measured as the RMSE of each recruitment coefficient. To test our prediction that experts would have smaller, shorter, and more consistent module recruitment, C_area, C_duty, and C_rmse were compared between experts and novices, as well as between beam and overground walking using a two-way mixed-design ANOVA (α = 0.05). All statistical analyses were conducted using SPSS (version 21; SPSS, Chicago, IL).

Fig. 9.

Motor module temporal structure during overground and beam walking for experts and novices. A: metrics used to characterize temporal recruitment of motor modules. C_duty is the duration that a recruitment coefficient is greater than threshold (0.15). C_area is a measure of recruitment magnitude and is calculated as the area under the mean recruitment coefficient curve that is above threshold. C_rmse is the consistency of the recruitment coefficient with respect to the mean. For the both experts and novices, motor module recruitment magnitude (B), duration (C), and consistency (D) were significantly greater during beam compared with overground walking (P < 0.001). D: recruitment consistency during beam walking was significantly greater in experts (red bar, solid border) than novices (gray bar, dashed border) (P = 0.01). Values are means ± SD.

RESULTS

Participants

Thirteen experts (professionally-trained ballet dancers) and 10 untrained novices participated in the experiment. Dance experience among the experts ranged from 12 to 20 yr. Average height (mean ± 1 SD) (experts: 1.64 ± 0.07 m; novices: 1.66 ± 0.05 m), weight (experts: 55 ± 7 kg; novices: 64 ± 10 kg), and age (experts: 24 ± 2 yr; novices: 22 ± 3 yr) did not differ between the cohorts (P > 0.05). All participants were women.

We Measured Differences in Performance on the Balance Beam between Experts and Novices

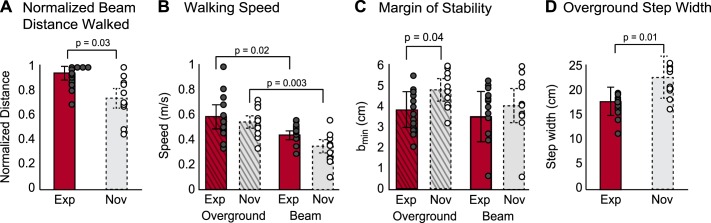
Consistent with our expectation that experts would have better walking balance proficiency, experts walked farther than novices on the balance beam (Fig. 3A, experts: 0.91 ± 0.06; novices: 0.71 ± 0.09; P = 0.03). This difference in balance proficiency was not accompanied by a difference in beam- or overground-walking speed between cohorts (Fig. 3B, expert overground: 0.59 ± 0.11 m/s; novice overground: 0.57 ± 0.05 m/s; expert beam: 0.43 ± 0.03 m/s; novice beam: 0.34 ± 0.06 m/s; P > 0.05). However, within both groups, beam-walking speed was significantly reduced compared with overground-walking speed (Fig. 3B, experts: P = 0.02; novices: P = 0.003). These results confirmed that experts had distinguishable differences in balance proficiency compared with novices, justifying further analysis of EMG data.

Fig. 3.

Motor performance metrics for beam and overground walking. A: normalized distance walked on the narrow beam was greater among experts (red bar, solid border) than novices (gray bar, dashed border). Individual averages across 6 attempts are denoted by the circles (experts: gray-filled circles; novices, open circles). B: walking speed did not differ between experts and novices during beam or overground walking. However, walking speed was lower in beam compared with overground walking among experts and novices (experts: P = 0.02; novices: P = 0.003). C: margin of stability was significantly smaller among experts compared with novices during overground walking (P = 0.04), but not during beam walking. There were no differences in the margin of stability across walking conditions within either group. D: step width was significantly smaller among experts compared with novices during overground walking (P = 0.006). Values are means ± SD.

Experts had a significantly smaller margin of stability compared with novices during overground walking (Fig. 3C, experts: 3.91 ± 0.9 cm; novices: 4.89 ± 0.5 cm; P = 0.02), but not beam walking (Fig. 3C, experts: 3.70 ± 1.2 cm; novices: 4.06 ± 0.9 cm; P > 0.05) (Fig. 3C). However, within either group, the margin of stability did not differ significantly between beam and overground walking (Fig. 3C, experts: P > 0.05; novices: P > 0.05). Therefore, the margin of stability in beam walking did not reflect differences in balance proficiency, but may reflect the smaller available base of support in beam walking. Experts had a smaller step width during overground walking compared with novices (Fig. 3D, experts: 17.3 ± 2.75 cm; novices: 21.8 ± 4.3 cm; P = 0.006), indicating that the reduced margin of stability that was observed during overground walking among experts was due the smaller base of support.

Leg and Trunk Kinematics Were Similar in Experts and Novices during Overground and Beam Walking

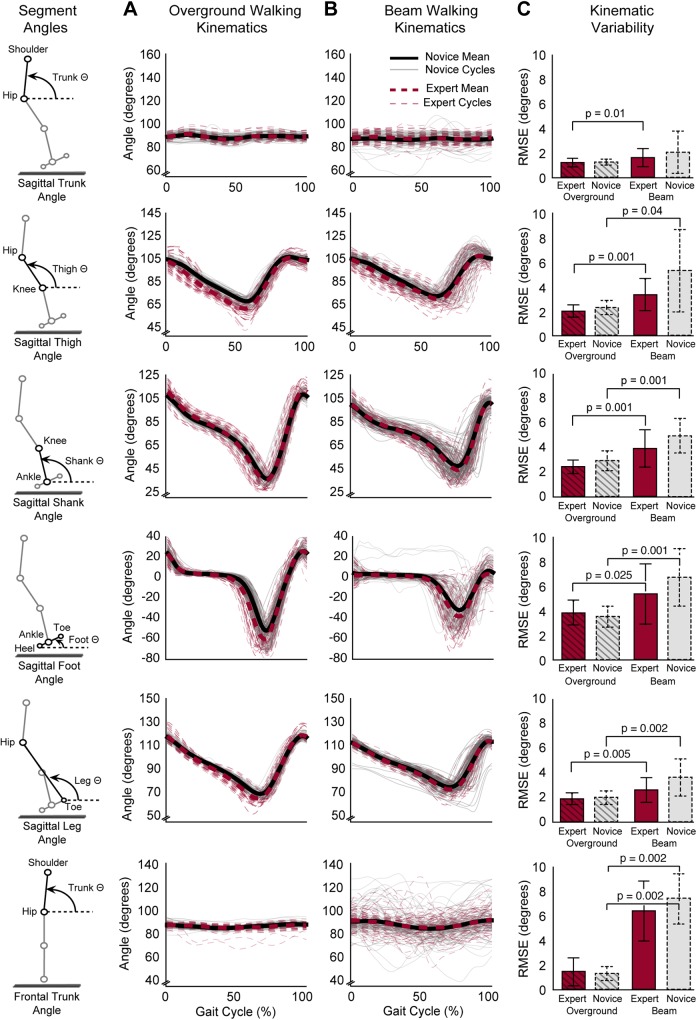
Segment angle trajectories of the leg and trunk in the sagittal and frontal plane were not significantly different between experts and novices during beam (P > 0.05) or overground walking (P > 0.05) (Fig. 4, A and B). However, within both groups, significant differences in segment angle trajectories were observed between overground and beam walking (experts: P < 0.005; novices: P < 0.005) (Fig. 4, A and B). Similarly, segment kinematic variability, evaluated by RMSE, did not differ between experts and novices during beam (P > 0.05) or overground walking (P > 0.05), but was significantly greater during beam vs. overground walking for all but the sagittal plane trunk angle in both groups (experts and novices: P < 0.04) (Fig. 4C).

Fig. 4.

Segment angle kinematics during overground and beam walking for experts and novices. A and B: body segment angle trajectories did not differ between experts (red dashed lines) and novices (black solid lines) during overground (A) or beam (B) walking. However, for both experts and novices, body segment angle trajectories differed between overground and beam walking (P < 0.005). C: body segment angle root mean square error (RMSE) (means ± SD) did not differ between experts and novices during overground or beam walking. However, in experts and novices, body segment angle RMSE was greater during beam compared with overground walking for most angles (P < 0.025).

Experts Used More Motor Modules in Beam Walking than Novices

Consistent with our prediction that more motor modules would accompany long-term training, experts had more modules than novices during beam walking [Fig. 5B, expert: 6.69 ± 0.60 (range: 6–8); novice: 5.60 ± 1.15 (range: 4–8); P = 0.009]. However, there were no differences in the number of modules used by experts and novices during overground walking [Fig. 5A; expert overground: 7.00 ± 0.82 (range: 6–8); novice overground: 6.30 ± 1.16 (range: 5–8); P > 0.05]. Moreover, within each group, there were no significant differences in the number of modules used in beam vs. overground walking (Fig. 5, A and B, P > 0.05). Example VAF plots in Fig. 5 illustrate that there was no overlap between original data and random data, demonstrating that there was significant structure in the EMG data that was characterized by motor modules. Moreover, trial-by-trial variability in the EMG data was well accounted for when reconstructed using motor modules (original vs. reconstructed EMG in Fig. 5).

Fig. 5.

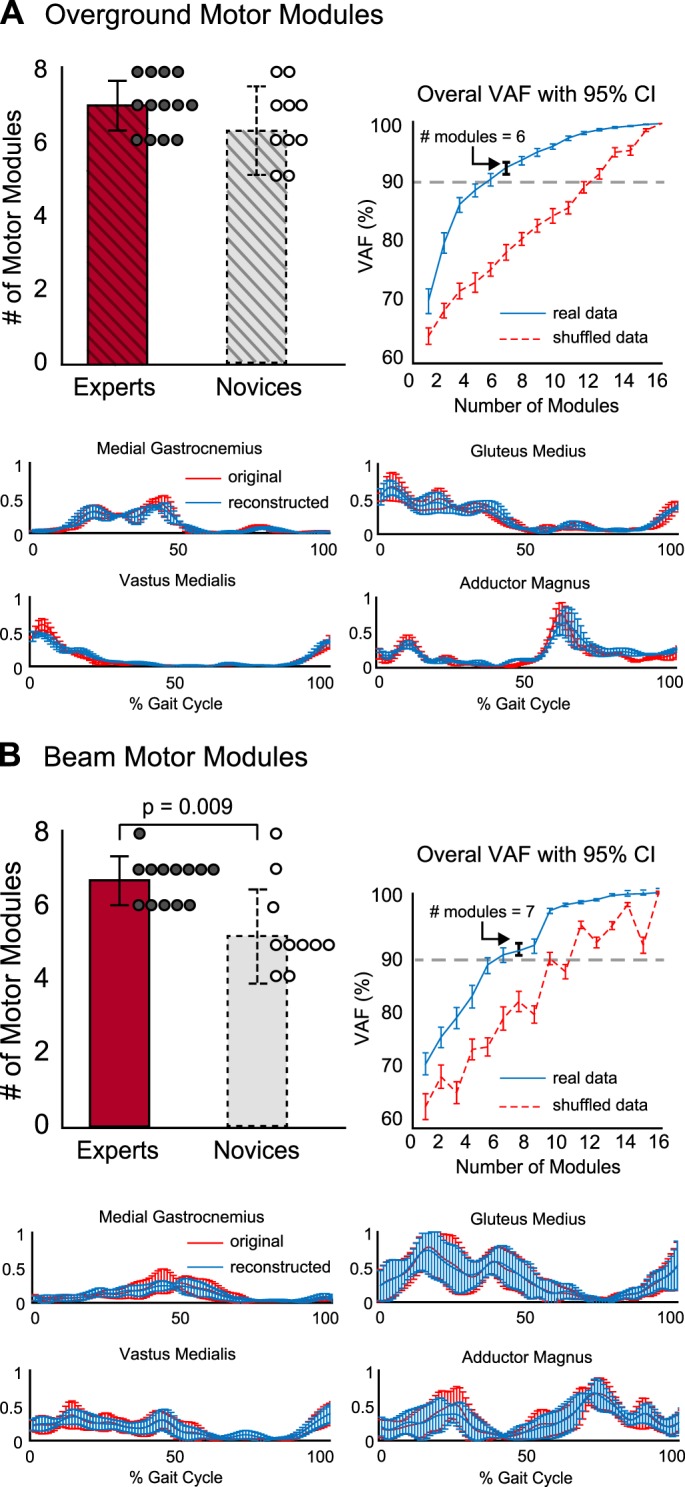
Number and goodness of fit for motor modules in overground and beam walking for experts and novices. A, top left: the number of motor modules (mean ± SD) used during overground walking did not differ between experts (red bar, solid border) and novices (gray bar, dashed border). Average number of motor modules per subject are denoted by the circles (experts: gray-filled circles; novices, open circles). A and B, top right: the number of motor modules selected accounted for ≥90% of the overall variability accounted for (VAF) during overground beam walking as depicted by plots from an example subject. Bottom: the extracted motor modules reconstructed the original overground EMG data (example from single individual; red: original EMG, blue: reconstructed EMG). B, top left: the number of motor modules (mean ± SD) used during beam walking was significantly greater among experts than novices (P = 0.009). Bottom: as with overground walking, EMG signals during beam walking were well reconstructed using the extracted motor modules as depicted in the example original vs. reconstructed EMG plots from a single subject. CI, confidence interval.

Experts Shared More Modules across Overground and Beam Walking than Novices

Not only did experts use more motor modules than novices during beam walking, but as predicted, experts also had a larger pool of subject-specific motor modules that were shared across walking behaviors. Specifically, a larger percentage of motor modules were shared across overground and narrow beam walking in experts compared with novices (Fig. 6A, experts: 82 ± 18%; novices: 54 ± 22%; P = 0.02). To explore whether this overlap in motor modules would also be observed in novices when performing a less challenging balance behavior, we evaluated the percentage of motor modules common to overground and wide-beam walking. We found that both experts and novices shared a considerable percentage of motor modules between the two behaviors (>85%), with no difference between groups (Fig. 6B, experts: 85 ± 18%; novices: 96 ± 9%; P > 0.05).

Fig. 6.

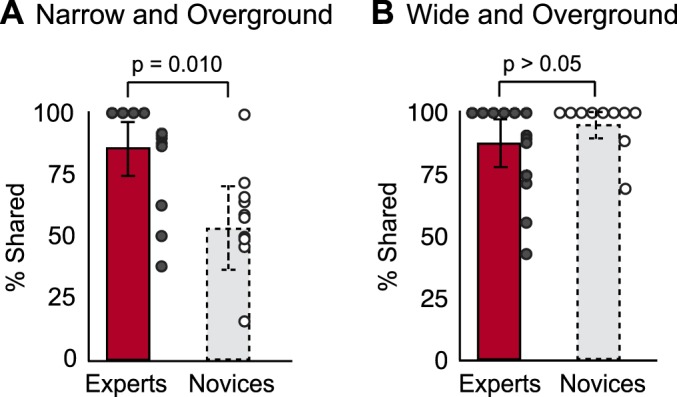
Percentage of motor modules shared between overground- and beam-walking conditions. A: experts (red bar, solid border) shared a larger percentage of motor modules than novices (gray bar, dashed border) between narrow beam and overground walking (P = 0.02). Average number of shared motor modules per subject are denoted by the circles (experrather than creating de novo, behavior-specific ts: gray-filled circles; novices, open circles). B: experts and novices shared an equal percentage of motor modules between wide beam and overground walking. Values are means ± SD.

Motor Module Spatial Structure Was More Sparse, Consistent, and Distinct in Experts Compared with Novices

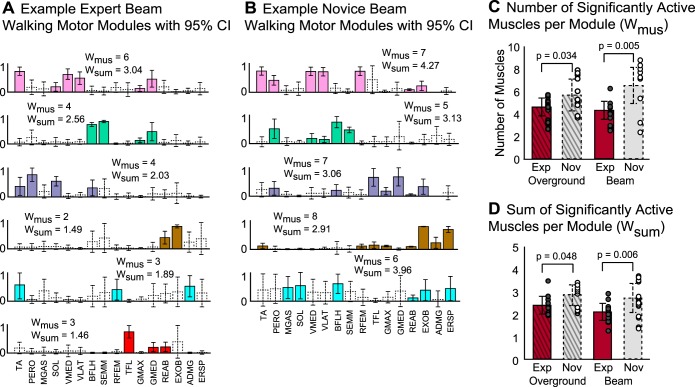
As predicted, the W_mus (Fig. 7C, experts: 4.50 ± 1.13; novices: 6.30 ± 1.65; P = 0.005) and the W_sum (Fig. 7D, experts: 2.21 ± 0.37; novices: 2.82 ± 0.57; P = 0.006) was lower among experts compared with novices during beam walking. Interestingly, in the less skilled, more automatic overground-walking activity, W_mus (Fig. 7C, experts: 4.76 ± 0.92; novices: 5.84 ± 1.36; P = 0.034) and W_sum (Fig. 7, C and D, experts: 2.35 ± 0.40; novices: 2.73 ± 0.46; P = 0.048) were also significantly lower among experts compared with novices. Within either group, W_mus and W_sum did not differ between overground and beam walking (Fig. 7, C and D, experts P > 0.05; novices P > 0.05).

Fig. 7.

Motor module coactivity for experts and novices during overground and beam walking. A and B: example expert (A) and novice (B) motor modules. Coactivity was quantified as the average number of significantly active muscles per module (W_mus), as well as the average sum of those significantly active muscles per module (W_sum). Significantly active muscles (filled bars, solid border) represent those whose activation was consistently greater than zero, despite step-to-step variations. Muscles were classified as significantly active if their 95% CI did not include zero, whereas nonsignificantly active muscle (open bars, dashed border) had 95% CIs that included zero. C: W_mus was lower among experts (red bar, solid border) than novices (gray bar, dashed border) in overground and beam walking (overground: P = 0.034, beam: P = 0.005). W_mus did not differ between overground and beam walking for experts or novices. Average W_mus per subject is denoted by the circles (experts: gray-filled circles; novices, open circles). D: W_sum was also lower among experts compared with novices during overground and beam walking (overground: P = 0.048, beam: P = 0.006). In both experts and novices, W_sum did not differ between overground and beam walking. Values are means ± SD.

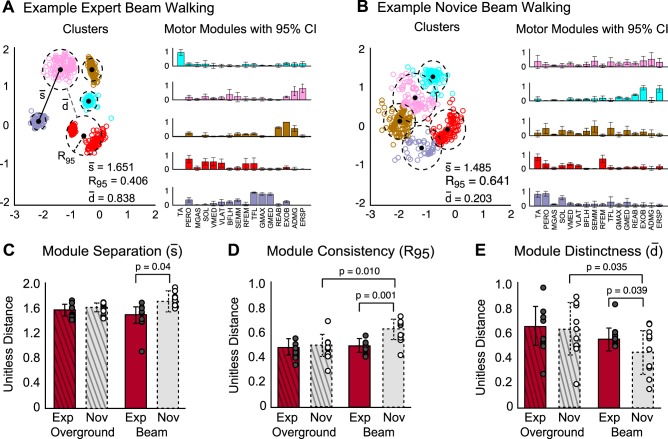
Lending further support to differences between experts and novices in motor module spatial structure, greater consistency and distinctness were observed in expert module clusters (Fig. 8, A and B). Specifically, while the separation between clusters (i.e., mean centroid-to-centroid distance, s) was larger among novices than experts during beam walking (Fig. 8C, experts: 1.51 ± 0.11; novices: 1.65 ± 0.18; P = 0.04), their consistency (i.e., lower mean radius of the 95% CI, R95) was significantly greater in experts compared with novices during beam walking (Fig. 8D, experts: 0.49 ± 0.05; novices: 0.60 ± 0.08; P = 0.001). As a result, experts had more distinct clusters than novices during beam walking (Fig. 8E, experts: 0.57 ± 0.09; novices: 0.45 ± 0.18; P = 0.039). No significant differences in any of the cluster metrics were observed for overground walking. Within either group, only cluster consistency (R95) was significantly different between overground and beam walking for novices (Fig. 8D, beam: 0.60 ± 0.08; overground: 0.49 ± 0.09; P = 0.01). The error, or Sammon's stress, in conserving the original point-to-point distances in the projected data set from Sammon's mapping was 0.042, indicating that the structure of the original data was adequately preserved in the transformation from 16 to two-dimensional space.

Fig. 8.

Cluster analysis of motor module spatial structure during overground and beam walking for experts and novices. A and B: example expert (A) and novice (B) motor modules and cluster plots depicting motor module separation (s), consistency (R95), and distinctness (d). Each data point in a cluster is a two-dimensional representation of one of the bootstrapped motor modules. C: motor module separation was greater among novices (gray bar, dashed border) than experts (red bar, solid border) during beam (P = 0.009) but not overground walking. Average motor module separation per subject is denoted by the circles (experts: gray-filled circles; novices, open circles). D: motor module consistency was greater among experts than novices during beam (P = 0.001) but not overground walking. Module consistency was lower during beam vs. overground walking among novices (P = 0.001) but not experts. E: motor module distinctness was greater among experts than novices during beam (P = 0.039) but not overground walking. Values are means ± SD.

Temporal Recruitment of Motor Modules Was More Consistent in Experts Compared with Novices

Among the metrics used to quantify the temporal recruitment of motor modules, only the variability in module recruitment (C_rmse) was found to differ between experts and novices. C_rmse was lower among experts compared with novices, but only during beam (Fig. 9D, experts: 0.138 ± 0.04; novices: 0.193 ± 0.06; P = 0.01), not overground, walking (Fig. 9D, experts: 0.0.082 ± 0.02; novices: 0.063 ± 0.01; P > 0.05). In contrast to our prediction, there was no significant difference between experts and novices in the magnitude (C_area) or duration (C_duty) over which modules were recruited during beam or overground walking (Fig. 9, B and C; P > 0.05). In comparison, the magnitude (C_area), duration (C_duty), and variability (C_rmse) were all greater during beam vs. overground walking in experts (P < 0.001) and novices (P < 0.001) (Fig. 9, B–D).

DISCUSSION

Here we demonstrate that years of ballet training altered the structure of muscle coordination patterns in walking and balance behaviors. The differences in motor modules between experts and novices could not be explained by differences in kinematics, and, therefore, may reflect changes in the neural control of movement following years of training, rather than biomechanical constraints imposed by the activity or musculoskeletal structure and function. This supports our hypothesis that long-term training leading to skilled motor performance alters muscle coordination during challenging as well as nominal everyday motor behaviors. Moreover, the greater overlap of motor modules between beam and overground walking in experts suggests that, to learn challenging new behaviors, we may take advantage of existing motor modules used for related behaviors (e.g., overground walking) and sculpt them to meet the demands of a new behavior (e.g., beam walking). Additionally, since ballet dancers do not train on balance beams, the observed differences in muscle coordination are unlikely to be task-specific modifications to the neural control of movement. Rather they may reflect general changes to handle balance challenges.

Motor Modules Reflect Differences in Neural Control of Movement

The observed differences in motor modules between experts and novices may reflect changes in neural control of movement (Ting et al. 2015). This interpretation is strengthened by two observations. First, among experts similar motor modules were used during beam and overground walking, despite differences in their kinematic movement trajectories and increased kinematic variability in the frontal plane during beam walking. The increased lateral trunk variability during beam walking suggests that there was an increased reliance on a lateral hip strategy to maintain balance during beam walking. Therefore, the similarity in motor modules cannot be attributed to similar movement kinematics, implicating differences in the underlying neural control (Tresch and Jarc 2009). Second, motor modules were different in experts and novices during beam walking, even though kinematic movement trajectories and the variability in those movement trajectories were similar between groups. Surprisingly, the variability in lateral trunk movements during beam walking did not differ between experts and novices, although presumably experts would have had to make those lateral movements more effectively, given the greater distance they walked on the beam. Thus the differences in motor modules between groups cannot be attributed to differences in movement kinematics, once again implicating changes in the neural control of movement after years of training. Note that we did not observe kinematic differences in beam or overground walking between experts and novices, whereas prior work has demonstrated differences in kinematics between expert and novice musicians (Furuya and Altenmüller 2013; Verrel et al. 2013). One reason may be that prior studies have specifically observed trained movements, i.e., playing an instrument, whereas we examined a behavior that experts had not specifically practiced, but was likely to be affected by ballet training, i.e., walking across a narrow beam. In contrast to fine motor skills (McNemar 1933), balance proficiency is affected more by training than hereditary factors (Williams and Hearfield 1973), highlighting the need for a mechanistic understanding of improvements in balance control that can be implemented in rehabilitation. Differences in motor modules between experts and novices may thus underlie the differences in balance proficiency as a result of changes in the neural control of movement owing to long-term training.

Long-term Training May Create a Larger Motor Repertoire

Long-term motor training may expand the size of one's motor repertoire, increasing the set of available motor actions. While motor training during rehabilitation has been shown to increase the number of motor modules in individuals with sensorimotor deficits (Routson et al. 2013), ours is the first demonstration that long-term training may increase the number of motor modules in unimpaired adults. Prior studies have not found differences in motor module number between experts and novices, likely because they were focused on constrained athletic activities requiring high power output (e.g., cycling, weightlifting) (Kristiansen et al. 2013; Turpin et al. 2011). In contrast, beam walking is a challenging balance behavior that requires precise control of movement. Moreover, the body is upright and not kinematically constrained, allowing more motor variability in the coordination of the body's degrees of freedom (Steele et al. 2015; Ting and Chvatal 2010). Experts may, therefore, have more flexibility in achieving motor goals because of a larger motor repertoire, something that may be particularly useful under such challenging conditions. For example, an expanded motor repertoire may have allowed experts to produce additional biomechanical functions that novices could not produce, and which serve a particular (or important) function in maintaining balance on the beam. Another explanation is that experts may decompose a behavior into more precise biomechanical functions than novices, such that they use multiple motor modules for executing a biomechanical function that novices would execute with a single motor module. Finally, experts may have multiple motor modules for executing the same function in different movement contexts. However, distinguishing between these interpretations would require more detailed biomechanical analyses involving ground reaction forces, and possibly more experimental conditions and/or musculoskeletal modeling techniques.

At present we are unable to comment on possible differences in the neural control of interlimb coordination as it relates to balance proficiency, and how that may influence our understanding of the size of the motor repertoire. While interlimb coordination is critical to maintaining balance (Berger et al. 1984; Dietz et al. 1989; Moyer et al. 2009; Oliveira et al. 2012), the present study only examined motor modules in a single leg to collect and analyze a sufficient number of muscles to capture the complexity of limb control during such an intricate behavior as beam walking. While it is unlikely that this affected the number of motor modules and their composition during overground walking, this may have reduced the number of motor modules extracted during beam walking, as the left leg may have been involved in executing unique neuromotor patterns that were not performed by the right leg. Such differences may be critical to understanding neuromotor mechanisms of balance impairment.

Motor Module Efficiency Increases with Long-Term Training

Our results suggest that long-term training leading to skilled motor performance results in more efficient muscle coordination, such that fewer muscles are coactive during challenging as well as everyday motor behaviors. Specifically, we found that the spatial structure of muscle activity was sparser in experts compared with novices during beam and overground walking. Interestingly, it was only the sparseness of the muscle activity per module that differed between experts and novice during the overground walking, not the number of motor modules. However, the number of motor modules is more likely to reflect the task mechanics of a motor behavior (Steele et al. 2015; Ting et al. 2015) than the efficiency of the muscle coordination used in the execution of those motor behaviors. Therefore, the differences in the efficiency of everyday movements may be reflected in the coactivity of muscle coordination patterns, not the number of motor modules that are recruited. This efficiency in the structure of the motor output is consistent with studies demonstrating that long-term training results in more efficient generation of neuronal activity in primary motor cortex (Picard et al. 2013), more efficient use of cortical resources (Jäncke et al. 2000; Naito and Hirose 2014), and contraction of motor maps (Krings et al. 2000; Molina-Luna et al. 2008; Pascual-Leone et al. 1994; Tennant et al. 2012) that initially expand with skill learning (Nudo et al. 1996; Pascual-Leone et al. 1995). Additionally, with extended physical practice, subcortical circuits may take on greater independence for coordinating motor patterns, suggesting a role for the motor cortex as a tutor to subcortical circuits (Kawai et al. 2015), a development that would be consistent with increased automaticity and movement efficiency among experts (Leavitt 1979). Training due to rehabilitation may also improve spatial efficiency of muscle activity (Routson et al. 2013), which is degraded among individuals with sensorimotor impairments (Clark et al. 2010; Fox et al. 2013; Gizzi et al. 2011; Hayes et al. 2014; Routson et al. 2013). In contrast, improvements in walking with mechanical assistive devices (e.g., cane, walker) do not affect motor module efficiency, only temporal recruitment (Hayes et al. 2014). Patients with notable performance deficits may also have impaired temporal recruitment of motor modules, suggesting they are unable to appropriately recruit motor modules to meet task demands. As our participants were young and healthy, we did not observe differences in the temporal efficiency of motor module recruitment.

Experts Are More Consistent

Experts may have better balance proficiency than novices due to the consistency with which they can transform movement goals into motor actions (Schmidt 1975). Our results show that experts had high temporal and spatial consistency in the structure of their muscle activity during challenging beam-walking conditions. Trial-by-trial consistency in the spatial structure of motor modules was higher during beam walking in experts than novices, but similar in experts and novices during overground walking. Experts also exhibited greater consistency in the temporal recruitment of motor modules during beam walking compared with novices. The lower spatial and temporal consistency in motor modules among novices during beam walking may result from exploring the space of potential actions (Haith and Krakauer 2013) to find more effective motor solutions (Loeb 2012). It is also possible the lower consistency among novices may be due to the novel beam-walking activity requiring motor patterns that lie outside of the range of motor modules available to novices, or that novices were required to engage in more corrections to near losses of balance than experts. By having to engage in more discrete corrections to prevent a loss of balance during beam walking, novices may have relied more heavily on the recruitment of aperiodic muscle activity. This aperiodic muscle activity may be quantified by the greater variation in the recruitment coefficients (i.e., temporal variability) of the motor modules of novices during beam walking. Such aperiodic muscle activity in motor modules for the control of walking balance has been observed previously in response to discrete perturbations to walking (Chvatal and Ting 2012), but has not been well characterized. Since the activation of motor modules can be influenced by sensory inflow (Cheung et al. 2005), the differences in temporal consistency between experts and novices may be due to differences in how sensory information is processed to recruit motor modules. The consistency of motor module spatial structure among experts resulted in more distinct motor modules compared with novices during beam walking. This distinctness suggests that experts were allocating unique muscle combinations to each motor module, which may have increased the consistency and efficacy with which related biomechanical subtasks were executed, leading to better walking balance proficiency.

Shared Motor Modules Suggest a Backward-Compatible Motor Learning Mechanism

To learn challenging new behaviors, we may take advantage of existing motor modules used for related behaviors and sculpt them to meet the demands of a new behavior (Georgopoulos and Grillner 1989; Grillner and Wallén 2004). These modified motor modules may be “backward compatible” in that they continue to be recruited when performing previously learned behavior(s), extending the capabilities of the motor repertoire without increasing its size. The difference between experts and novices may be the degree of practice-dependent tuning of existing motor modules that extends their versatility from nominal to more challenging behaviors. For example, ballet dancers used a common set of motor modules across narrow-beam, wide-beam, and overground walking. In contrast, novices exhibited common motor modules only between wide-beam and overground-walking conditions, suggesting that their motor modules are also robust and backward compatible, but across a smaller range of task difficulty. Therefore, long-term ballet training may sculpt existing overground-walking motor modules for use during challenging balance tasks (represented in our study by beam walking), and these modified motor modules then continue to be used for overground walking, thereby creating the greater overlap in motor modules observed in experts. Conversely, if experts had less overlap (i.e., more balance challenge-specific motor modules), this would have suggested that, rather than modifying existing motor modules which then continue to be used for overground walking, new balance challenge-specific (i.e., beam walking) motor modules would be created with long-term training. Consistent with the idea of sculpting existing motor modules to improve performance, early stages of skill learning in animals also involve reconfiguring existing rather than creating de novo, behavior-specific motor patterns (Kargo and Nitz 2003; Nudo et al. 1996). Sharing motor modules across behaviors may facilitate learning (Clune et al. 2013; McKay and Ting 2012) by permitting new motor behaviors to be performed with a nominal level of proficiency and allow motor modules to be shaped over the course of training to improve performance (Mussa-Ivaldi and Bizzi 2000). This would bias learning toward behaviors that are compatible with the existing motor repertoire (Berger et al. 2013; Sadtler et al. 2014), which may explain why some individuals appear to be “naturals” or have an affinity for a particular sport or activity. This selection and repetition of successful motor modules from the motor repertoire may strengthen the connectivity between certain sets of neurons while others are weakened, altering synaptic efficacy. This may result in a biasing of neural circuitry, such that trained motor patterns become more robust and are recruited more consistently (Monfils 2005) to execute common biomechanical subtasks, regardless of context. The effect of training for one behavior on the control of another (Gentner et al. 2010; Mouchnino et al. 1993; Pedotti et al. 1989) may be an important consideration in rehabilitation, as remediating specific movement deficits could influence the control of other motor behaviors (Fox et al. 2013).

The small pool of motor behaviors that are typically studied limits our understanding of the role motor modularity plays in the control of movement. While modularity is often considered a strategy to simplify the control of movement by reducing the degrees of freedom (d'Avella et al. 2003; Ting and Macpherson 2005), this is only true within the context of the motor behaviors examined during an experiment, and not necessarily representative of the expansive range of behaviors that we regularly perform (Ting et al. 2015; Zelik et al. 2014). It is also possible that the motor modules that were considered beam specific may actually be shared with other motor behaviors that were not examined in the present study. A thorough characterization of the scope of the motor repertoire used for locomotor behaviors would be required to test this idea. Additionally, rather than modifying existing motor modules, new behavior-specific motor modules may develop, particularly during training for specific athletic or artistic activities, increasing the size of the motor repertoire to extend its capabilities. Therefore, the number of motor modules that make up each individual's motor repertoire may be much larger than we have traditionally considered. Rather than reducing the dimensions of all possible movements, modularity may only reduce dimension in the context of specific behaviors by mapping motor intentions into motor patterns.

GRANTS

This study was supported by National Science Foundation (Emerging Frontiers in Research and Innovation) Grant 1137229, and National Institutes of Health Grants HD-46922 and T32 NS-007480-14.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: A.S. and L.H.T. conception and design of research; A.S. performed experiments; A.S. and J.L.A. analyzed data; A.S., J.L.A., and L.H.T. interpreted results of experiments; A.S. prepared figures; A.S. drafted manuscript; A.S., J.L.A., and L.H.T. edited and revised manuscript; A.S., J.L.A., and L.H.T. approved final version of manuscript.