Sodium MRI in human heart: a review

Abstract

This paper offers a critical review of the properties, methods and potential clinical application of sodium (²³Na) magnetic resonance imaging (MRI) in human heart. Because the tissue sodium concentration (TSC) in heart is about ~40µmol/g wet wt, and the ²³Na gyromagnetic ratio and sensitivity are respectively about 1/4^th and 1/11^th that of hydrogen (¹H), the signal-to-noise ratio of ²³Na MRI in heart is about 1/6000^th that of conventional cardiac ¹H MRI. In addition, as a quadrupolar nucleus, ²³Na exhibits ultra-short and multi-component relaxation behavior (T₁~30ms; T₂ ~0.5–4ms and 12–20ms), that requires fast, specialized, ultra-short echo-time MRI sequences, especially for quantifying TSC. Cardiac ²³Na MRI studies from 1.5–7 T measure a volume-weighted sum of intra- and extra-cellular components present at cytosolic concentrations of 10–15 mM and 135–150 mM in healthy tissue, respectively, at a spatial resolution of about 0.1–1 ml in 10 min or so. Presently, intra- and extra-cellular sodium cannot be unambiguously resolved without the use of potentially toxic shift reagents. Nevertheless, increases in TSC attributable to an influx of intra-cellular sodium and/or increased extra-cellular volume have been demonstrated in human myocardial infarction consistent with prior animal studies, and arguably might also be seen in future studies of ischemia, and cardiomyopathies–especially those involving defects in sodium transport. While technical implementation remains a hurdle, a central question for clinical use is whether cardiac ²³Na MRI can deliver useful information unobtainable by other more convenient methods, including ¹H MRI.

Graphical abstract

The properties, methods and clinical potential of sodium MRI in human heart are reviewed. The myocardial sodium concentration is about ~40µmol/g.wet.wt., and its signal-to-noise ratio is about 1/6000^th of conventional proton MRI. Sodium’s short multi-component relaxation behavior necessitates fast, ultra-short-echo MRI sequences, especially for quantification. Presently, intra- and extra-cellular sodium cannot be unambiguously resolved, but increased sodium primarily attributable to sodium influx, is demonstrated in human myocardial infarction. The added value of cardiac ²³Na MRI vs. existing methods remains key.

INTRODUCTION

Sodium plays a vital role in myocyte function and integrity. The sodium concentration is 8–10 times higher in the extracellular vs. the intracellular space, with the trans-membrane sodium flux and osmotic balance regulated by the sodium-potassium pump. The sodium channel mediates the rapid upbeat of the cardiac action potential and calcium exchange, which are critical to cardiac excitability, conduction and muscular contraction (1–4). Alterations in tissue sodium concentration (TSC) and in trans-membrane sodium flux occur in ischemic heart disease and myocardial infarction (MI)(5,6). Sodium channel dysfunction is also linked to dilated and hypertrophic cardiomyopathies (7–12). While serum sodium levels are routinely measured in patients and may be independent predictors of outcome for certain heart failure etiologies (11), these measures can only detect electrolyte imbalances that affect the entire blood pool. Except for sodium (²³Na) magnetic resonance imaging (MRI), direct in vivo sampling of cardiac sodium is only possible via myocardial biopsy during cardiac surgery or image-guided intervention undertaken for other purposes (12). This makes ²³Na MRI a uniquely noninvasive tool for accessing myocardial sodium in vivo.

PROPERTIES

Signal-to-noise ratio (SNR)

Fifty years have passed since the first ²³Na nuclear magnetic resonance (MR) studies of sodium in muscle (13). ²³Na MRI of isolated rodent hearts (14), and the first human cardiac ²³Na MRI (15,16) were reported in the 1980s following the innovation of 1.5 T whole-body scanners, which provided the requisite signal-to-noise ratio (SNR) unavailable to early 0.04–0.3 T scanners (17). Indeed, after accounting for the myocardial sodium tissue concentration of ~40 mmol/kg wet weight, the lower ²³Na MR sensitivity and gyromagnetic ratio (©) of about 1/4^th that of ¹H, the SNR of ²³Na MRI is some 6000 times lower than that of conventional cardiac proton (¹H) MRI under optimum but equivalent detection conditions for both nuclei (Table 1, bottom row). Overcoming this severe, intrinsic SNR handicap to perform ²³Na MRI, demands considerable effort.

Table 1.

NMR properties and predicted sensitivity of ²³Na MRI in tissue relative to ¹H.

	1H MRI in tissue	23Na MRI in tissue
Magnetic moment (in nuclear magnetons)	2.7927	2.2161
Spin quantum number	1/2	3/2
NMR frequency @ 1 Tesla	42.577	11.262
Sensitivity* @ constant field per nucleus ∝ υ3I(I+1)	1	0.0925
Relative SNR at constant B0/nucleus*	1	0.35
In vivo concentration (mol/kg)	42.8	0.04
In vivo conc. of nucleus (mol/kg)	85.6	0.04
SNR of moiety in tissue	85.6	0.014
SNR relative to 1H of tissue water†	1	1.64 × 10−4

^*υ =NMR frequency,

I =nuclear spin quantum number.

^†Assumes SNR ∝ υ¹.

Optimized detectors, and front-end scanner electronics are certainly essential for ²³Na MRI: they are already near-optimal for ¹H MRI. Field strength (B₀) is important, but the increase in SNR anticipated from higher B₀ is at best only linear in B₀, assuming that all detectors satisfy the condition that coil noise is negligible compared to sample noise (18). Adjusting the ²³Na MRI operating parameters, on the other hand, can have far greater impact. Reducing spatial resolution from 0.5×0.5×3 mm (0.0075 ml)–typical for a ¹H MRI study–to 5×5×10 mm or 0.25 ml for ²³Na MRI, for example, yields a 333-fold increase in SNR, which can cut the SNR deficit from 6000 to just 18. Being able to image sodium, the prime mover in cellular ion transport, at sub-milliliter resolution by ²³Na MRI, is by no means unattractive.

No formal experimental comparison of the B₀-dependence of ²³Na SNR under equivalent conditions yet exists, but published ²³Na images of human heart acquired at 1.5 T (19–22), 3 T (23–25) and 7 T (26,27) clearly benefit from the huge SNR advantage gained by cutting spatial resolution compared to ¹H MRI. Of the most recent human cardiac data, ²³Na SNRs of 11–24 are reported in the septum at 3T with a resolution of 4×4×10 mm at 3 T in ~9 min acquisitions (25). Sodium images acquired from heart patients in ~12 min at 1.5 T had 6 mm isotropic resolution, permitting myocardial TSC measurements with an accuracy of ~10% in control subjects (22). The 7T results suggest a SNR of ~24 with 5×5×40 mm resolution in 11 min acquisitions (26), and 10-phase cardiac cine ³Na MRI with 6mm isotropic revolution in ~19 min (27).

Thus, much of the remaining SNR deficit for ²³Na–that factor of 18 compared to ¹H MRI–is dealt with by signal averaging for 10 minutes or so, as compared to the seconds typically required for ¹H MRI with comparable SNR per pixel. The ability to accommodate many averages in practical scan times–the acquisition efficiency–depends critically on the tissue ²³Na spin-lattice (T₁) and spin-spin (T₂) relaxation times.

Relaxation times

Initially, it was thought that only 30%–40% of the total tissue sodium was MR-visible (13,28) due to nuclear quadrupolar interactions of this spin-3/2 nucleus (29), and/or interactions with tissue macromolecules. In fact, ²³Na commonly exhibits multi-exponential T₂ relaxation in intact biological tissue, with fast (T_2f) and slow (T_2s) spin-spin relaxation times (30). The T_2f component comprises about 40% of the total ²³Na signal depending on tissue type (30,31), and is attributable on theoretical grounds, to the motion-averaged electrostatic field gradients arising from reorienting water molecules and charged sites on macromolecules in the vicinity of the ions (29, 32). Experimental data showing a T_2s component representing 68±15% of the sodium signal in muscle (32), isolated perfused rat hearts, frog hearts (33), and canine hearts studied in vivo (34), is consistent with this theory. In healthy skeletal and cardiac muscle T_2f falls in the range 0.5–4 ms, while T_2s is 12–32 ms and contributes 68±15% of the total ²³Na heart signal (6,24,34–37). Consequently, a major portion of the T_2f signal component is lost when spin-echo or gradient-echo times (TE) are longer than about 3 ms. This signal loss and the effect of short T₂s on the useful signal bandwidth (BW), reduces SNR and confounds quantification of absolute TSC. Nevertheless, TSC measured by short-TE ²³Na MRI, appears to match tissue [Na] measured by assay (34).

On the plus side, the factors responsible for short ²³Na T₂s also produce short T₁ relaxation times of around 10–40 ms (34,35). This means that MRI experiments performed with pulse sequence repetition times TR~60 ms, are essentially fully-relaxed. Some published ²³Na MR T₁ and T₂ relaxation times for tissues encountered in the chest and heart are summarized in Table 2 (6, 24, 28, 32–45).

Table 2.

Some reported T₁ and T₂ relaxation times for ²³Na in intact muscle, heart and blood.

Tissue/Sample	T1(ms) a	T2f (ms) a	T2s (ms) a	Bo (T)	Ref
Blood plasma (human)	30 ±1		17 ±1	4.7	38
Blood plasma		12	49.5	1.5	39
Blood plasma	37.3 ±1.0		24.5 ±0.8	8.5	40
Blood, human in vivo			20.9 ±6.0	1.5	41
Blood, human	30.8 ±1.3	3.25 ±0.29	18.1 ±1.3	1.5	35
Blood, human LV, in vivo	31.1 ±7.5		19.3 ±3.3	1.5	36,37
Blood, human heart	31.9±4.1		20.1 ±1.3	3T	24
Red blood cells	30.1 ±3.1	4.3 ±1.2	19.9 ±1.8	1.5	35
Red blood cells	30 ±3		14 ±3	4.7	38
Red blood cells		6.3	27.2, 17.3b	1.5	42
Rat muscle	18.3 ±0.5	1.59 ±0.16	16.1 ±2.6	2.3	32
Rat muscle	12 ±1		15 ±8	0.89	28
Rat muscle hindlimb		3–4	21–37	7.05	43
Human skeletal muscle		1.2 ±0.2	32.5 ±8.2	1.91	44
Human skeletal muscle		0.6–2.5	21.2–23.1	2	45
Human skeletal muscle	32.3 ±0.5	0.46 ±0.21	12.3 ±1.9	1.5	35
Canine heart-viable tissue	34.2 ±0.9	3.6 ±0.6c	31.5 ±0.8	4.7	6
-non-viable	26.2 ±1.5	2.2 ±0.2 c	21.9 ±1.2	4.7	6
Canine heart-normal		2.44 ±0.4	15.2 ±1.8d	1.5	34
-infarcted		2.04 ±0.2	22.7 ±3.4d	1.5	34
Human heart	31.6±7.0		13.3±4.3	1.5	36,37
Human heart	19.9±6.2		12.4±1.8	3	24

^aValues are mean±SD. Empty cells: values not determined or not reported

^bComposite T_2s relaxation reported.

^cSignificant decrease in non-viable vs. viable tissue

^dSignificant elevation in infarcted vs. normal state (p <0.004)

Because ²³Na T₁s are about 1/25^th of the typical proton (¹H) T₁s, ²³Na experiments can potentially be conducted ~25 times faster than a conventional ¹H study for the same MR saturation level. This should result in a gain in SNR efficiency of about √25 ~5. If in addition the BW is cut 4-fold vs. ¹H (compromise to the detection of the T_2f component, notwithstanding), the combined effect reduces the residual SNR deficit by √(25×4) =10-fold, from 18 to about 2 (46).

Intra- and extra-cellular sodium

The total tissue sodium concentration, [Na]_tissue, is a composite of the disparate intra- and extra-cellular sodium concentrations, [Na]_intra and [Na]_extra (34):

$${[\mathit{\text{Na}}]}_{\mathit{\text{tissue}}}^{\mathit{\text{mmol}}/\mathit{\text{kg}}}=(V_{\mathit{\text{intra}}}{[\mathit{\text{Na}}]}_{\mathit{\text{intra}}}^{\mathit{\text{mM}}}+V_{\mathit{\text{extra}}}{[\mathit{\text{Na}}]}_{\mathit{\text{extra}}}^{\mathit{\text{mmol}}/\mathit{\text{kg}}})W^{l/\mathit{\text{kg}}}$$ [1]

Here [Na]_intra is typically 10–15 mM and [Na]_extra is 135–150 mM in the cytosol. The V’s are the corresponding tissue volume fractions with V_extra =1-V_intra, and W (in liters/kg or ml/g wet weight) is the tissue water content.

As an example, V_intra occupies about 75% of the water space of cardiac tissue (6,47,48), which in turn is about 77% water (6, 49). Thus, use of Eq. [1] yields a tissue TSC of 0.77×(0.75×15+0.25×145) =37 µmol/g wet weight. This excludes contributions from intravascular blood which occupies 8–10% (50) of the tissue but carries a TSC of ~84 µmol/g (38). If a separate 9% intravascular blood component is accounted for, [Na]_tissue increases to (37+0.09×84)/1.09 =41 µmol/g, consistent with a measured value of 43 µmol/g for human heart (21).

Ordinarily, the naturally abundant ²³Na resonance is a singlet in biological tissue, and [Na]_intra and [Na]_extra are not resolvable by ²³Na NMR. However, introducing a chemical shift reagent such as dysprosium or thulium into the extra-cellular space can peel off the extra-cellular pool into a separate resonance (51,52), resulting in two resonances–one for each. ²³Na NMR spectroscopy can then be used to study ion transport between the two pools, for example, under normal and ischemic conditions (52). Unfortunately, these heavy-metal shift reagents are ultimately toxic and unsuitable for human or non-terminal animal studies in their present form.

Note that the mere existence of dual-component ²³Na T₂ values has long fueled speculation that each T₂ component might be separately assigned to [Na]_intra and [Na]_extra (53,54). The hypothesis that each or either T₂ component can be wholly assigned to intra- or extra-cellular sodium is presently unproven. Moreover, there is some evidence against it. This includes ²³Na studies of frog heart that show that when the intracellular sodium signal determined from shift reagent experiments, is subtracted from the total signal, the remaining extra-cellular interstitial sodium remains biexponential with the same T₂s (T_2f≈1–2ms and T_2s≈17ms; 33). Hence the conclusion that the extra-cellular “interstitium contains sodium relaxation times that are similar to the relaxation times found for intracellular sodium” (33). Similarly, studies of fresh rat skeletal muscle up to 24 hrs post-biopsy elicited no significant differences in relaxation components despite equalization of the intra- and extra-cellular sodium concentrations (32). The conclusion was that muscle sodium is “satisfactorily described as distributed in a single compartment” from the NMR standpoint (32). While frog heart and rat muscle are not mammalian heart muscle, observations that neither T_2f and T_2s nor their relative fractions change in acute reperfused MI vs. healthy canine myocardium measured in vivo despite a doubling of [Na]_tissue, are consistent with the same conclusion (34). Thus, from the NMR standpoint, it seems that the view from the Na⁺ ion is somewhat similar from inside the cell, as it is from the outside.

This is not to say that [Na]_intra, [Na]_extra, or T_2f, and T_2s and their relative fractions can never change under various stresses or disease states. Changes in TSC (or [Na]_tissue) in response to stress, ischemic disease, infarction, disorders affecting ion transport, therapeutic intervention due to ion pump failure, increased membrane permeability, and/or cell rupture will generally reflect changes in [Na]_intra, if [Na]_extra, is maintained in homeostasis by the blood pool. Changes in cellular volume V_intra, or vascular volume, due to edema, injury or even exercise would also affect TSC. While this renders ²³Na MR sensitive to many cellular level disturbances, it also means that measurements of [Na]_tissue alone may not permit resolution of those contributory factors in Eq. [1] that may be causal.

There is hope that newer triple-quantum filtered (TQF) ²³Na MRI techniques might help distinguish intra- and extra-cellular cardiac sodium pools, but as in the case of T_2f and T_2s, support for a hypothesis that it could provide unambiguous resolution of [Na]_intra and [Na]_extra is presently lacking. Since there are presently no human cardiac TQF ²³Na data, we will not address this here.

METHODS

²³Na MRI pulse sequence

Table 2 shows that the ²³Na tissue MR signal can have multiple contributing T₂ components ranging from 0.5 to 33 ms. It is unclear to what extent the scatter in these values reflect real physiological variability, or just the difficulty and error in measuring them by ²³Na MR. Certainly, the use of ultra-short ²³Na MRI TEs (21,24,25,55–58) would avoid the uncertainty in T₂ and minimize the SNR loss from T₂ decay. It would also permit quantitative measurements of TSC. Indeed, the presence of the T_2f component not only argues against spin-echo MRI (5,59), but also gradient-refocused echo sequences with TE delays of ≥3 ms (6,46,56). Ultra-short TE ²³Na MRI pulse sequences and their associated reconstruction algorithms generally require customized programming that can present a hurdle to clinical studies.

The simplest approach to detecting and imaging the T_2f component with ultra-short TE is to eliminate both the slice-selection and phase-encoding gradients with their associated delays, altogether. A three-dimensional (3D) projection reconstruction reminiscent of the original MRI experiment (60) fits this bill. Such a sequence comprises a short, hard excitation pulse, followed by a constant radial gradient that is reoriented in subsequent applications, to generate a 3D set of angular projections. To optimize the SNR, the projections can be incremented by an angle (111°) related to the “golden ratio” (61,24,27). By this means, TEs as short as 0.2–0.4ms are possible (57,62)–just short enough to catch a few time points of a T_2f ~0.5ms signal (Table 2). The constant gradient radial projections do over-sample the central low-spatial resolution Fourier components, and under-sample the high spatial frequency components. This is not the most efficient trajectory for covering image k-space.

Spiral (25), and “twisted projection imaging” or TPI (56) are alternative k-space trajectories that have been used for human cardiac ²³Na MRI. Spirals have been used widely in ¹H MRI, while the TPI method is responsible for nearly all quantitative measurements of [Na] in humans (63). In TPI, the constant radial projection gradient is replaced by variable spiral-like k-space trajectories that uniformly sample image k-space in 3D, as illustrated in Fig. 1(a) (56). Combined with a 400µs hard excitation pulse, TEs of ~400µs are possible, measured to the center of the pulse, since 200µs must still be allowed for turning on the TPI gradient (34,35,56,58).

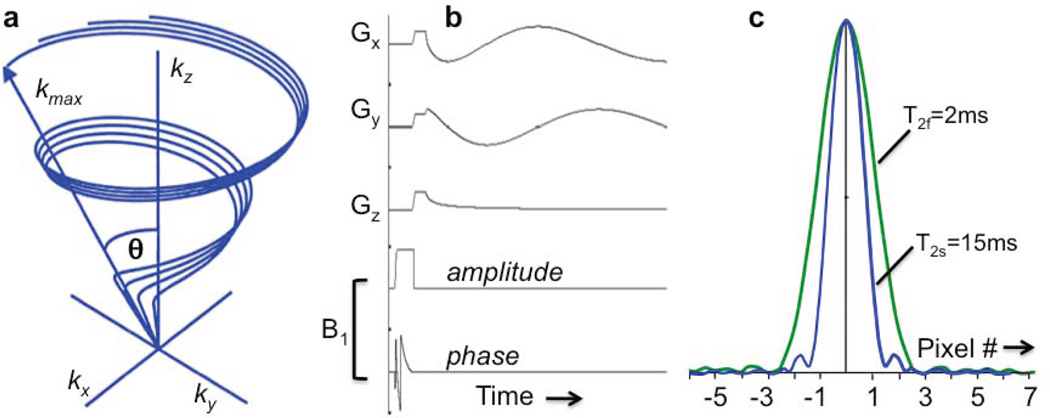
Figure 1.

(a) Partial k-space sampling scheme for twisted projection imaging (TPI). The maximum k forms a sphere of radius k_max, and the projections lie on a surface of a cone whose twist is adjusted to maintain critical sample density (56). (b) The TPI pulse sequence with adiabatic half passage excitation. The hard pulse of the original TPI sequence (56) is replaced by an amplitude (amp.) and phase modulated AHP pulse, but the gradient waveforms, G_x, G_y, and G_z, are the same, and depicted for one of the projections (21). (c) Simulated point spread function for T_2f =2ms and T_2s =15ms signal components excited by a TPI sequence with TE=0.36ms, a 31.3 kHz bandwidth, 12 ms readout, 22cm FOV, 44×44×44 array size, and Δx =5mm nominal isotropic spatial resolution (58). The T_2s component has a full-width at half-maximum (fwhm) of about 1.5Δx (7.5 mm), while the fwhm of the T_2f component is 2.4Δx (12.0 mm). (Adapted from Refs. 21,56, 58).

One significant problem with all sequences using hard pulses, is the effect of RF field (B₁) inhomogeneity. This may arise, for example, when using surface coils for exciting the cardiac ²³Na MR signal. The resultant spatially-varying excitation flip-angle (FA) could be addressed by calibrating the spatial B₁ distribution, or by replacing the hard pulse with an adiabatic pulse to provide substantially B₁-independent excitation (21). Presently, the most power-efficient adiabatic pulses are adiabatic half-passage (AHP; FA=90°) pulses whose TE period nominally commences at the end of the pulse (vs. the middle of the hard pulse). Use of AHP thus cuts TE by a further half pulse-length (21). A TPI sequence with AHP excitation is depicted in Fig. 1(b).

Of course, while the T_2f signal may be detectable at the start of the acquisition window, it is long gone 2 or 3 T_2f periods later, so that the spatial information corresponding to the k-space traversed towards the end of the acquisition window–the high spatial frequency components–is still not encoded into the T_2f component. Consequently, the image point spread function (PSF) is different for T_2f vs. T_2s (58), depending on the acquisition parameters (BW, gradient strength, etc). The result can be a blurred ²³Na image comprised of a low-resolution T_2f image superimposed on a high-resolution T_2s image. A comparison of human cardiac images acquired at TEs of 0.4ms and 3.6ms (62) might exemplify such an effect. If spatial resolution is more important than quantifying TSC, setting TE ≥3 ms should eliminate any blurring due to T_2f. Fig. 1(c) depicts simulated PSFs for T_2f =2 ms and T_2s =15ms components excited by a TPI sequence with TE=0.36ms and 12ms readout (58).

For two-dimensional (2D) or restricted 3D ²³Na MRI employing slab-selection, the duration of the slice-selection pulse can be cut using truncated selective excitation pulses, achieving TEs as small as 1–1.5ms (24,25). The cost of truncating slice selection is non-uniform slice profiles, which must be accounted for if quantification is the goal.

A final complication for cardiac ²³Na MRI pulse sequencing is cardiac motion. In conventional cardiac ¹H MRI this is addressed by electro-cardiographic (ECG) gating. If ²³Na MRI acquisitions were prospectively gated at a TR equal to the heart-rate, almost the entire SNR advantage of sodium’s short T₁ would be lost. Retrospective ECG-gating (24,27) wherein only those frames acquired during active cardiac contraction are omitted, or the acquisition of multiple frames during a timing window limited to a motion-quiet period of say ≤80% of the cardiac cycle (19,20,22,25,55), offer less SNR-costly alternatives. Yet another option is to acquire thousands of projections ungated and bin them into, say, a 10-phase cardiac cine stream (27).

Cardiac ²³Na MRI coils

While ²³Na MRI can be performed on clinical scanners equipped with broad-band MR transmit/receive capabilities, the limited availability of suitable detection coils and receiver hardware presents another hurdle for patient studies. The usual route after purchasing a ²³Na MR channel for the clinical scanner and developing a ²³Na MRI pulse sequence capability, is to build (15,21,46) or purchase (20,57) a custom set of ²³Na transmit/receive coil systems tailored to the specific application.

The best detectors are those that provide the optimum SNR. From 1.5T to 7T, the ²³Na MR frequency ranges from only 16.9 to 79 MHz–a regime ruled by conventional loop detectors. For cardiac ²³Na MRI, the choice is invariably surface coils. The diameter of individual surface coils should approximately equal the depth of interest, say 10–15cm for the center of the heart (46). Phased-arrays of surface coils will extend the size of the region of optimum SNR, but require multi-channel ²³Na MRI receiver hardware (including preamplifiers, transmit/receive switches, and MR receivers) and phased-array reconstruction, that may or may not be available to the scanner (23,26,46).

Photographs of custom surface and flexible phased-array ²³Na MRI coils for human cardiac use at 1.5 T are shown in Fig. 2 (21,22,46). The low ²³Na MR frequency at 1.5T necessitates the use of multiple windings and distributed tuning capacitance to achieve the desirable “sample-dominant noise” condition (18). The receiver coils can also be used for MR excitation. Optimized individual surface coils have intrinsically nonuniform B₁s, which must be dealt with for quantitative work (e.g. with the aforementioned AHP pulses; 21). Phased-arrays require either multi-channel excitation (typically unavailable for human cardiac ²³Na MRI), or a large separate transmit coil (46). Fig. 3 shows sodium images of the human heart acquired in 4 s and 200 s at 1.5T with the 4-channel cardiac phased-array in Fig. 2, and a separate 40cm surface transmit coil (46).

Figure 2.

Custom-built coils for human cardiac ²³Na MRI at 1.5 Tesla (16.9 MHz). (a) Square 25×25 cm three-turn transmit/receive surface coil used for quantitative cardiac TSC studies employing adiabatic excitation (21). The coil has 3 embedded vials of saline gel to serve as sensitivity references, and a mount permitting exchange with a conventional cardiac ¹H coil for cardiac MRI (21,22). (b) A 4-channel ²³Na phased-array constructed from 15-cm, 3-turns coils for increased inductance at the lower ²³Na frequency (46). The detectors were fabricated on 0.25-mm thick flexible printed circuit board, with a separate 40-cm square single-turn transmit coil for excitation.

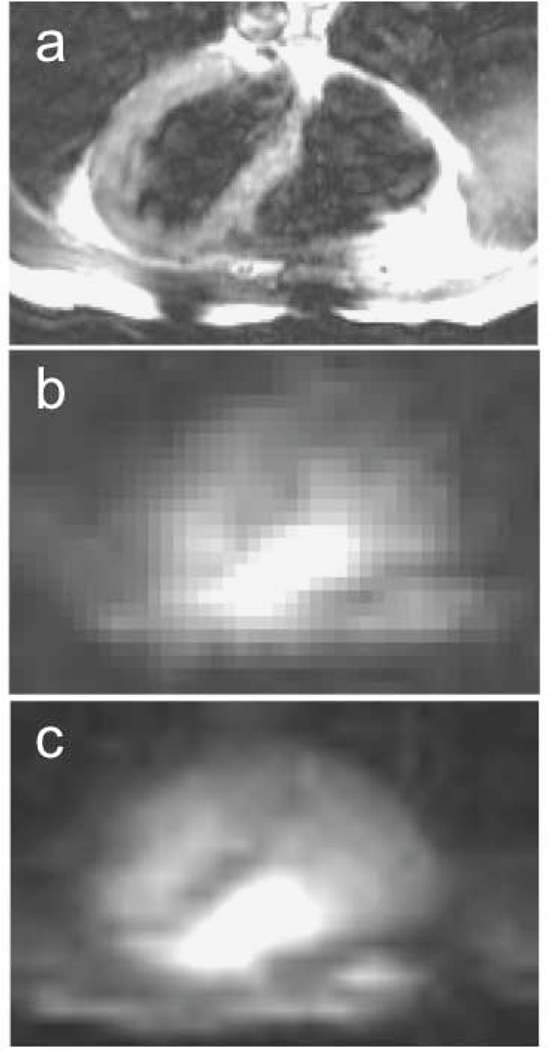
Figure 3.

(a) Conventional ¹H trans-axial image, and (b) corresponding single slice ²³Na MRI of the human heart acquired with the phased-array in Fig. 2(b) using a slice-selective gradient refocused echo (GRE) sequence in 4s, and (c) 200s (array size, 32 × 32; resolution, 1 × 1 × 4 cm³; TR/TE= 33/5 ms; from Ref. 46).

RF power deposition

Another down-side of ²³Na’s low gyromagnetic ratio (©) is that it requires 4-times the B₁ for the same FA and duration, yet short pulses are needed to avoid T_2f losses. In addition, the RF power deposited in biological tissue, measured as the specific absorption rate, SAR in W/kg, is proportional to [υB₁]² (64). Consequently, the SAR for a ²³Na study done with the B₁ required to produce the same FA, pulse length, and TR as a ¹H MR study at a 4-fold higher MR frequency in the same magnet, is essentially the same, although RF penetration effects will be less for ²³Na due to the lower ²³Na RF (64). The benefit of faster scanning due to the short ²³Na T₁ may thus be limited in practice by potential RF heating concerns in vivo, especially as one moves to higher B₀ in search of higher SNR.

Note also that surface coil excitation has a much greater potential for causing local heating than whole-body excitation due to the presence of high SAR gradients close to the surface coil. In addition, the MRI scanner’s inbuilt protections on RF power deposition typically overstate SAR (65). Because the cardiac ²³Na coils are likely to be custom-built anyway (Fig. 2), the most prudent course for ensuring safety probably includes testing the coil set for heating using a body phantom of saline gel (23,66).

Quantification

In ²³Na MRI signals are quantified as relative changes in signal intensity, or absolute concentration–TSC. Measuring changes in ²³Na image intensity is subject to the confounding effects of T₁, T_2s and T_2f relaxation, nonuniform B₁, and nonuniform detection sensitivity, on reproducibility and the interpretation of any results. Generally, it is prudent to eliminate as many variables as possible (eg, FA variations, T₁ saturation etc.) through experimental design and observing a rigorous protocol. Signal differences can be measured relative to adjacent uninvolved or healthy tissue in a sample region over which sensitivity and/or FA is essentially constant. While such changes cannot be conclusively attributed to changes in TSC, the ²³Na MRI signal is often linearly correlated with tissue [Na], for example, as seen in MI (34,46, 67–69).

Absolute TSC at a location (x, y, z) can be measured from the ratio of the ²³Na image signal intensity $(S_{x,y,z}^{\mathit{\text{tissue}}})$ to that in the same location of a reference phantom of known concentration recorded with the same resolution and FA (21). Saline is a typical concentration reference. In general, the tissue and reference signals require corrections for T₁ saturation and T₂ decay, and for differences in the coil sensitivity (ϕ) that occur when the coil is loaded with the body vs. the reference phantom. The TSC in the tissue at (x,y,z) is given by:

$${[\mathit{\text{Na}}]}_{x,y,z}^{\mathit{\text{tissue}}}=\frac{S_{x,y,z}^{\mathit{\text{tissue}}}{F}_{x,y,z}^{\mathit{\text{tissue}}}{E}_{x,y,z}^{\mathit{\text{tissue}}}\varphi .{[\mathit{\text{Na}}]}^{\mathit{\text{ref}}}}{S_{x,y,z}^{\mathit{\text{ref}}}{F}^{\mathit{\text{ref}}}{E}^{\mathit{\text{ref}}}}.$$ [2]

Here, superscripts tissue and ref denote factors associated with sample and reference acquisitions; and F and E are the T₁ saturation and T₂ decay correction factors, respectively. The coil loading,ϕ, can be determined from the ratio of ²³Na signals from a small phantom embedded in the coil, recorded during tissue and reference experiments (21). For a TPI or projection sequence employing TE ≤0.4ms, and TR >60ms, the relaxation corrections E and F approximate unity, so only the signals and loading factors need be measured.

An alternative to measuring TSC that avoids the separate reference acquisition, is to use an external concentration reference in the field-of-view of the ²³Na acquisition, at some location, say (x₁, y₁, z₁). Then, although loading is the same, ϕ must be replaced in Eq. (2) by the ratio, Ψ, of the coil sensitivity at (x₁, y₁, z₁) to that at (x, y, z). Note that except for uniform detectors, Ψ =Ψ(x₁, y₁, z₁, x, y, z) is not a scalar. The reference phantom can also be replaced by an internal reference of known [Na] that changes minimally between subjects. While the ratio of myocardial to ventricular blood ²³Na signals has been reported as a potentially useful semi-quantitative measure (55), extending this to absolute TSC measurements with corrections for differences in spatial sensitivity and relaxation times has yet to be validated.

In the event that FA differs between the reference and tissue acquisitions, or that FA at the tissue differs from its value at the reference location, the signal and F terms in Eq. [2] will be modulated accordingly. In the simple case of TR>>T₁, Eq. [2] is multiplied by the ratio [sin{α(x₁, y₁, z₁)}/sin{α(x, y, z)}], where α is the FA at the two locations. For TR~T₁, the correction would need to be modified further to reflect the FA dependence of the steady-state magnetization of a partial saturation experiment. The potential effects of nonuniform B₁ and partial saturation effects on the accuracy of TSC measurements, are an argument for performing studies at TR>>T₁ with constant FAs provided by separate large excite coils or adiabatic pulses (21,22).

Table 3 summarizes in vivo measurements of TSC in chest and heart likely to be encountered in a ²³Na MRI study (21, 34, 35, 58, 70–73). Note that cardiac TSC measurements are prone to partial volume errors from voxels close to high-TSC blood (22,50). The canine ²³Na MRI measurement of TSC was confirmed by post-mortem atomic absorption spectrophotometry (34).

Table 3.

Some in vivo ²³Na MRI measurements of total sodium content in normal tissue.

Tissue	n	[Na] mmol/kg wet wt	Ref.	MRI method
Human skeletal muscle	10	28.4 ±3.6	35	TPI
	5	26.2 ±3.3	58	TPI
	5	26 ±4	70	3DGRE
Canine heart	6	34.4 ±2.8	34	TPI
Human heart	10	43 ±4	21	TPI
Human adipose tissue	10	17 ±4	21	TPI
		20 ±2	71	TPI
Human ventricular blood	10	79 ±8	21	TPI
Human breast, fibrous	9	28 ro	71	TPI
	19	33 roua	72	TPI
	2	57 ±14	73	3DDR

Values are mean ±SD; TPI=twisted projection imaging; 3DGRE=three-dimensional (3D) gradient refocused echo; 3DDR=3D density-adapted radial acquisition.

^aConverted from mmoles/liter of wet tissue assuming a specific gravity of 1.04 (46).

CLINICAL AND PRE-CLINICAL RESEARCH

Cardiac ²³Na MRI is presently limited to patients with chronic MI (19,20,22). The findings are that ²³Na MRI shows areas of elevated myocardial signal that correlate with wall-motion abnormalities identified by ¹H MRI in 30 subjects studied at 8 days and 6 months post-MI (19). An additional 10 patients studied on days 9, 14, and 90 post-MI revealed a decline in the level of sodium signal elevation from 39%, to 31% to 28% at the three times, respectively, in infarcted vs non-infarcted tissue (20). Another study measuring absolute TSC found 30% elevations in 20 patients with chronic MI measured ≥90 days post-onset (59 ±10 vs 45 ±5 µmol/g in non-MI and 43 ±4µmol/g in controls; 22). This study confirmed that changes in ²³Na MR relaxation times were not a confounding factor in the two earlier studies (19,20) that reported changes in sodium signal levels in MI.

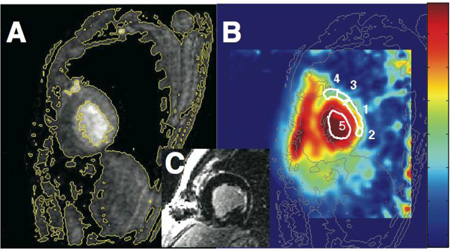
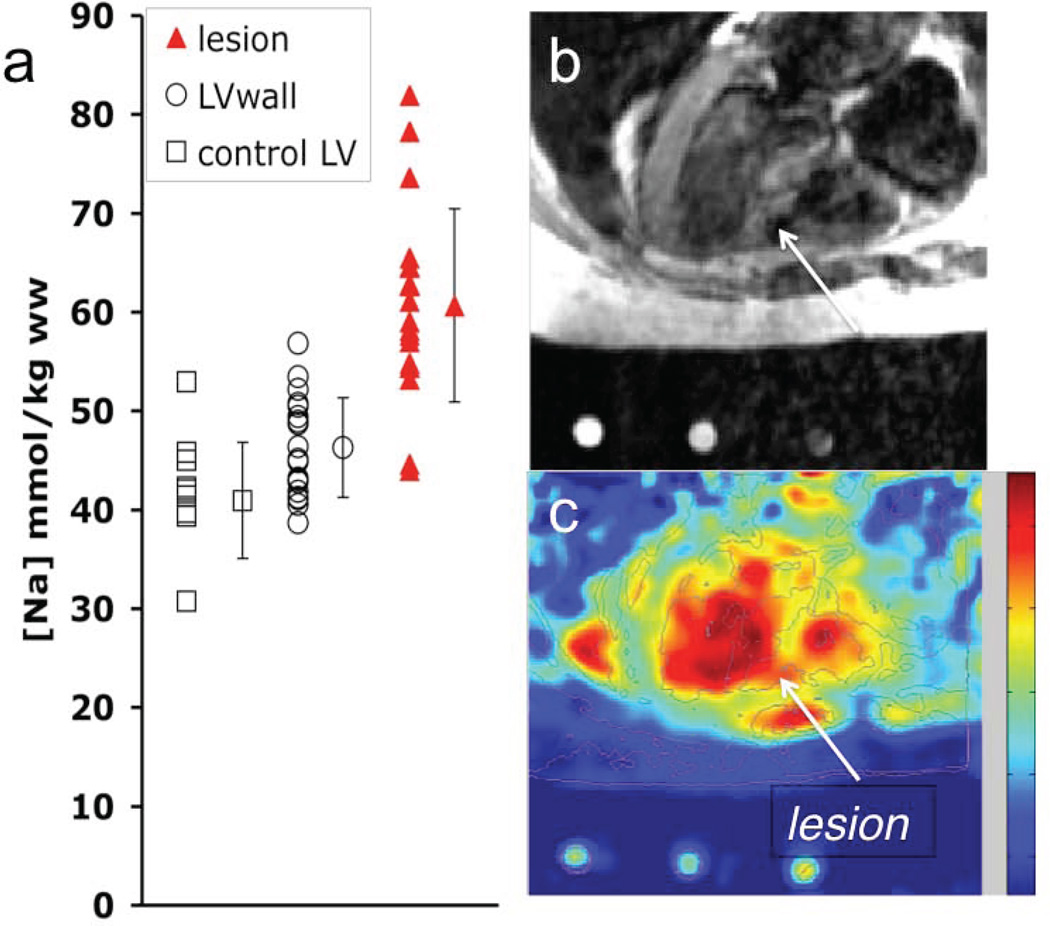
Fig. 4 shows TSC levels in normal, MI, and adjacent tissues in the cohort of 20 MI patients, and a ²³Na image showing elevated TSC in a patient with a septal MI (22). This study also showed that the magnitude of the TSC increases in MI identified by contrast-enhanced ¹H MRI, was unrelated to infarct age or size after 90 days post-onset, or to global ventricular function. An intermediate elevation in TSC was also reported in viable tissue immediately adjacent to the infarction (22). Although intracellular sodium is important for myocellular excitability, TSC measured at rest in these chronic MI patients was not closely associated with an increased risk of arrhythmia, as assessed by electro-physiologic testing for inducibility of monomorphic ventricular tachycardia (22).

Figure 4.

(a) TSC values in infarcted and remote myocardium in 20 MI patients, and in adjacent tissue in 11 of the patients. Vertical bars denote means ±SD. TSC is significantly increased in MI vs remote tissue (P <0.001). (b) Trans-axial gated ¹H fast spin-echo image, and (c) corresponding ²³Na image from a 3D TPI data set (TR/TE=85/0.4 ms; isotropic spatial resolution =6 mm) from a 61-year-old man with a remote septal MI (arrow). Color scale is proportional to TSC and includes B₁ correction; LV=left ventricle. (Adapted from Ref. 22).

The result that sodium ²³Na MR levels are elevated in MI is consistent with prior animal work (5,6,67–69). For example, canine studies of acute MI show TSC levels increasing by up to two-fold or more in the first 8–9 hrs following reperfusion (69). To the extent that the local extracellular sodium pool is buffered at or near 140mM by residual perfusion or diffusion routes, the elevated TSC observed in acute MI as it relates to Eq. [1] is attributable to either: (i) increased [Na]_intra due to energetically compromised cellular Na⁺/K⁺ pump activity; or (ii) an increase in V_extra associated with edema, myocyte necrosis or intra-myocardial hemorrhage; or (iii) a combination of both.

Of these, insight on the role of the intracellular component is provided by ²³Na MR spectroscopy studies of rodent hearts using shift reagents, which demonstrate huge increases of up to 5-fold in [Na]_intra following 30 min of ischemia and dysfunction (74,75). Histochemical measurements suggest that the increase in the V_intra factor is, on the other hand, much smaller: up to about 13% in the first hour post-occlusion in isolated canine heart (3,4). On the extracellular side of Eq. [1], microscopic analysis using diffusible markers suggests that about 12–19% of the total myocardial tissue volume in rodents is extracellular (1,67,75), with microscopy evidence that V_extra is little-changed in acute reperfused MI (67). Increases in total tissue water content, W, are even more modest: 2–6% increases in reperfused canine MI up to 26 hours post-onset (2,4), or no significant difference from non-MI in acute (57) or chronic MI (49). Thus, these studies in aggregate, point to the bulk of the change in TSC following MI being borne by an increased [Na]_intra, at least in the acute phase (69).

CONCLUSIONS AND FUTURE

Despite the 6000-fold SNR hit compared to ¹H MRI, ²³Na is the second most viable nucleus for performing routine human MRI in its natural endogenous form. Yet, cardiac applications remain quite limited. Undoubtedly a declining appetite for supporting non-¹H nuclei by the scanner manufacturers has taken a toll: the specialized technical requirements of pulse sequences, detectors and image reconstruction can present insurmountable obstacles for many would-be clinical ²³Na MRI researchers. But there are other issues as well. To be useful in a clinical setting, cardiac ²³Na MRI needs to add value by providing functional information relating to diagnosis and/or prognosis that is not obtainable by regular ¹H MRI or other more convenient means.

Because changes in the tissue ²³Na MRI signal primarily reflect changes in intracellular sodium concentration and/or the extracellular volume fraction when the extra-cellular sodium is in homeostasis with the blood pool, ²³Na MRI may be particularly sensitive to disorders affecting sodium-potassium pump function, channelopathies (54), as well as injuries or interventions that disrupt the extra-cellular space. Thus, while cardiac applications are presently limited to MI patients, future ²³Na MRI studies could reveal altered myocardial TSC associated with sodium pump dysfunction in some cardiomyopthies (7–12). If serum sodium can independently predict outcomes in certain forms of heart failure (11), then TSC measured directly in the heart, might be even more outcome sensitive. Also, just as arm and leg exercise in healthy subjects causes TSC to increase in skeletal muscle (31,70,76)–due to hyperaemia and a net Na⁺ influx into the myocytes (1)–it is conceivable that exercise stress could elicit changes in cardiac TSC as well, which might find value in patients with symptoms of myocardial ischemia.

Of course, the potential for false positive detections of altered TSC in the myocardial wall is also high. The adjacent blood pool has twice the sodium; the myocardial wall is relatively thin compared to the spatial resolution of ²³Na MRI, and is thinner still in dilated cardiomyopathy and chronic MI; while exercise tends to introduce motion artefacts. All too often, the main competition to ²³Na MRI is ¹H MRI which, in its many forms–including contrast enhancement, cine, functional tagging, etc.–is already a sensitive, high resolution diagnostic tool for probing cardiac function.

Abbreviations

TSC

tissue sodium concentration

MI

myocardial infarction

SNR

signal-to-noise ratio

TE

echo-time

BW

bandwidth

FA

flip-angle

TPI

twisted projection imaging

PSF

point spread function

AHP

adiabatic half passage

ECG

electro-cardiographic

T₁

spin, lattice relaxation time

T₂

spin-spin relaxation time

TR

pulse sequence repetition time