Body mass scaling of passive oxygen diffusion in endotherms and ectotherms

Significance

Biologists have long sought to understand how differences in the structure of vertebrate respiratory systems are related to differences in oxygen consumption rates associated with metabolism. In particular, they have sought to understand how structural constraints on passive oxygen diffusion through gills or lungs are related to the nonlinear body mass scaling of oxygen consumption rates. Here we show that the body mass dependence of oxygen diffusion capacity, which is governed by the area and thickness of respiratory surfaces, matches the body mass dependence of respiration in diverse endothermic (birds and mammals) and ectothermic (reptiles, amphibians, and fishes) vertebrates. These results provide a step toward a more complete understanding of the structural differences that underlie changes in oxygen consumption rates with body size.

Abstract

The area and thickness of respiratory surfaces, and the constraints they impose on passive oxygen diffusion, have been linked to differences in oxygen consumption rates and/or aerobic activity levels in vertebrates. However, it remains unclear how respiratory surfaces and associated diffusion rates vary with body mass across vertebrates, particularly in relation to the body mass scaling of oxygen consumption rates. Here we address these issues by first quantifying the body mass dependence of respiratory surface area and respiratory barrier thickness for a diversity of endotherms (birds and mammals) and ectotherms (fishes, amphibians, and reptiles). Based on these findings, we then use Fick’s law to predict the body mass scaling of oxygen diffusion for each group. Finally, we compare the predicted body mass dependence of oxygen diffusion to that of oxygen consumption in endotherms and ectotherms. We find that the slopes and intercepts of the relationships describing the body mass dependence of passive oxygen diffusion in these two groups are statistically indistinguishable from those describing the body mass dependence of oxygen consumption. Thus, the area and thickness of respiratory surfaces combine to match oxygen diffusion capacity to oxygen consumption rates in both air- and water-breathing vertebrates. In particular, the substantially lower oxygen consumption rates of ectotherms of a given body mass relative to those of endotherms correspond to differences in oxygen diffusion capacity. These results provide insights into the long-standing effort to understand the structural attributes of organisms that underlie the body mass scaling of oxygen consumption.

Since the classic debates of Krogh and Bohr (1), the relationship of passive oxygen diffusion to oxygen consumption has remained the focus of considerable research (2). Still, we have much to learn about how oxygen diffusion across respiratory surfaces relates to whole-organism oxygen consumption (3). In particular, we have much to learn about how the structural constraints on oxygen diffusion capacity, namely the thickness and area of respiratory surfaces, relate to the body mass scaling of oxygen consumption in vertebrates—a pattern that reflects the scaling of species’ energy use (3).

Studies on the body mass dependence of oxygen diffusion have been undertaken over the last century in all major classes of vertebrates, typically using respiratory surface area as a metric of diffusion capacity (2, 3). Less commonly, studies have also considered potentially relevant changes in respiratory barrier thickness with mass (4). In many cases, these studies have concluded that the body mass scaling of oxygen diffusion relative to that of oxygen consumption differs between endotherms and ectotherms (3, 5, 6). This has led to very different conclusions regarding the structure and function of respiratory systems among classes of vertebrates, as explained below.

Among endotherms, particularly mammals, researchers have concluded that a mismatch exists between the body mass scaling of oxygen diffusion and oxygen consumption (6). Oxygen diffusion capacity is thought to scale linearly with body mass (or nearly so) in these groups, whereas oxygen consumption is thought to increase less than proportionally with mass (3, 6–8). Thus, when these relationships with body mass are expressed as power law functions of the form Y = M^b, the scaling exponent “b” is about 1 for diffusion, but about 2/3 to 8/10 for consumption (9–12). This apparent mismatch has confounded modeling efforts to explain the body mass dependence of oxygen consumption rates in mammals and other vertebrates (e.g., refs. 8 and 13). It has also been used as evidence that the structure of respiratory systems has evolved to optimize performance at maximum rather than minimum rates of oxygen consumption. This is because maximum consumption seems to scale more steeply with body mass, like respiratory surface area (14). More generally, this apparent mismatch in the scaling of oxygen diffusion and consumption has been used to argue against the evolutionary optimization principle of symmorphosis (15) in complex biological systems such as the respiratory system (16, 17).

In contrast, among some classes of ectotherms, previous work has concluded that the body mass scaling of oxygen diffusion capacity roughly matches that of oxygen consumption (3, 5, 18). In fishes, for example, the relationships of both oxygen consumption and respiratory surface area are thought to scale to the 0.6–0.8 power of body mass (5). These observations have led to the argument that passive oxygen diffusion is a rate-limiting step in oxygen consumption, and that the size or thickness of respiratory surface areas arise from evolutionary tradeoffs in animal design (5, 19).

Within studies of both endotherms and ectotherms, researchers have noted that species with greater oxygen diffusion capacity and larger respiratory surface areas tend to show higher levels of aerobic activity or “athleticism” (19–22). Between these two groups, however, it remains unclear to what extent respiratory surface area and/or other physiological differences (e.g., mitochondrial density) may correspond to the substantially lower oxygen consumption rates of ectotherms vs. endotherms at a given body mass (22). General quantitative relationships between the structural constraints on oxygen diffusion and oxygen consumption have not been established across vertebrates.

Thus, here we quantitatively examine the body mass dependence of the two primary structural constraints on oxygen diffusion capacity in ectotherms and endotherms, namely respiratory surface area and respiratory barrier thickness (air–blood barrier in lungs and water–blood barrier in gills). Based on these results, we then predict the overall rate of oxygen diffusion as a function of body mass in ectotherms and endotherms using Fick’s law of diffusion (23). Finally, we compare the predicted scaling relationships of oxygen diffusion to observed relationships for oxygen consumption in these two groups. Analyses of the thickness and area of respiratory surfaces, as well as oxygen consumption rates, include species from all major classes of vertebrates (birds, mammals, fishes, amphibians, and reptiles).

Model Development

Following from Fick’s law of diffusion (23), oxygen diffusion can be modeled as a passive, two-dimensional process that is structurally constrained by two factors: the total respiratory surface area (RSA, in square centimeters) over which gas exchange occurs and the respiratory barrier thickness of that barrier (RBT, in centimeters). In this formulation, diffusion rate is the product of the oxygen flux per unit respiratory surface area $\left(\frac{\mathrm{\Delta }\text{pO}2*\text{K}}{\text{RBT}}\right)$ multiplied by the total RSA such that

$$\frac{\text{mL}\hspace{0.17em}{\text{O}}_2}{\text{hour}}=\left(\frac{\mathrm{\Delta }\text{pO}2*\text{K}}{\text{RBT}}\right)\left(\text{RSA}\right),$$ [1]

where ΔpO2 is the partial pressure gradient of oxygen (mm Hg) and K is Krogh’s diffusion constant (cm²⋅h⁻¹⋅mL O₂⋅cm⁻³ tissue⋅mm Hg⁻¹). Both K and ΔpO2 are assumed here to be independent of body mass, consistent with previous work (6, 24). Thus, the body mass dependence in Eq. 1 arises from the body mass dependence of RSA and RBT, which can be described by power laws of the form RSA = aM^α and RBT = bM^β, where M is body mass (grams) (4, 25). Substituting these equations for RSA and RBT into Eq. 1 yields a general expression for the body mass dependence of diffusion rate:

$$\frac{\text{mL}\hspace{0.17em}{\text{O}}_2}{\text{hour}}=\left(\frac{a}{b}\right)\left(\mathrm{\Delta }\text{pO}2*\text{K}\right)\left(M^{\beta -\alpha }\right),$$ [2]

where the overall mass dependence is determined by the difference between the scaling of RSA and RBT $\left(M^{\beta -\alpha }\right)$. Note that although Eq. 2 describes a passive process, active processes to enhance oxygen delivery may contribute to diffusion through effects on ΔpO2 (26).

Eq. 2 can be parameterized to yield quantitative predictions for oxygen diffusion rate as a function of body mass at the whole organism level. We do so below for endotherms and ectotherms based on reported values of ΔpO2 and K, and the empirical relationships of RSA and RBT to body mass presented here.

Methods

RBT and RSA.

Published data were compiled on RBT and RSA for all major classes of vertebrates (birds, mammals, amphibians, fishes, and reptiles), which includes both air-breathing species with lungs and water-breathing species with gills. Data broadly represent the taxonomic diversity, body sizes, body temperatures, and aerobic activity levels that occur in each class (SI Appendix, Appendix 1). As such, these data include species from all major ecosystems (marine, freshwater, and terrestrial), using all major forms of locomotion (swimming, flying, and walking) and exhibiting a broad range of life histories. However, efforts were made to restrict analyses to adult or subadult individuals because respiratory features may change through ontogeny (4, 27). Body mass estimates corresponding to RBT and RSA values were taken from the original studies or, if unavailable, from other published sources (SI Appendix, Appendix 1).

Standard morphometric measures of RBT and RSA were used in all analyses. RBT is described using the harmonic mean distance, which is considered the most relevant measure with respect to gas exchange (4). For air-breathing species, this represents the air–blood barrier distance and for water breathers the water–blood barrier distance. Measures reported as arithmetic mean thickness (AMT) were converted to harmonic mean thickness (HMT) based on the published equation HMT = 2/3 × AMT for species other than birds (28). Respiratory surface areas were measured on whole lungs or gills, upon removal and fixation, following standard procedures (25).

Quantifying RBT and RSA in amphibians presents unique challenges because oxygen diffusion occurs through the lungs, mouth cavity, and skin to varying degrees (29). Thus, it was necessary to approximate RBT and RSA in amphibians in a manner that differed from other species considered here in two respects. First, RSA in amphibians was based on the total respiratory capillary surface areas in the lungs, mouth cavity, and skin. For anuran amphibians, this estimate was based on the total length of respiratory capillaries for each species, and the relationship between total capillary length and total capillary area described for caudate amphibians (30). Second, for RBT, a single mean value from lungs was used for all caudates (n = 4) (4), and species-specific estimates from lungs were used for all anurans. Given these approximations, we present statistics for ectotherms both with and without amphibians.

ΔpO2 and Diffusion Rate.

Data were compiled on the partial pressure difference of oxygen across the respiratory barrier for endotherms and ectotherms at rest (SI Appendix, Appendix 2). For species with lungs, ΔpO2 estimates represent the partial pressure difference between the air sacs of lungs on one side of the barrier and blood vessels on the other. This equates to the alveolar-to-arterial pO2 difference in mammals or, for vertebrate classes lacking alveoli, the difference between blood pressure and the partial pressure of air in comparable lung structures [e.g., parabronchi in birds; see ref. 31). For species with gills, ΔpO2 represents the difference between the partial pressure of oxygen in inhaled water and that in afferent blood vessels.

The Krogh’s diffusion constant (K; cm²⋅h⁻¹⋅mL O₂⋅cm⁻³ tissue⋅mm Hg⁻¹) used in determining overall oxygen diffusion rates for both endotherms and ectotherms represents the product of the rate of diffusion (cm²/h) multiplied by the solubility of oxygen in tissue (mL O₂⋅cm⁻³ tissue⋅mm Hg⁻¹) (32). The value used here was based on in vivo measures of oxygen diffusion using phosphorescence quenching microscopy (32). Although this estimate is considerably lower than Krogh’s original estimate (33), it is within two- to threefold of many current estimates from various tissues—particularly those using in vivo methods (34–46). The diffusion constant was adjusted for temperature to 38 °C in our analysis of endotherms and to 25 °C for ectotherms, based on a reported Q10 of 1.1 (47).

Oxygen Consumption Rates.

For oxygen consumption of endotherms at rest, we relied primarily on two recent compilations of data (48, 49). For oxygen consumption rates of ectotherms at rest, we relied exclusively on the compilation of (48) (SI Appendix, Appendix 3). Because this dataset often included multiple points for a single species, we included only the individual(s) at the largest body mass and highest constant temperature. For both endotherms and ectotherms, most oxygen consumption measures were taken from subadult or adult individuals.

Statistical Analyses.

Statistical models were fit to natural log-transformed data using both ordinary least squares (OLS) and phylogenetic generalized least squares [PGLS (50); regression with R version 3.0 (51)] (Table 1). For PGLS, because no well-resolved phylogeny exists for all vertebrates, we constructed our own phylogenetic supertree based on recent phylogenies of each vertebrate class [fishes (52), mammals (53), amphibians (54), birds (55), and reptiles (56–59); see also ref. 60]. The tree was constructed using the matrix representation with parsimony (MRP) approach (61, 62) and the Baum–Ragan coding procedure (63). Execution of the final MRP matrix was performed in TNT under the defaults for “traditional search” (64), and conversions between tree formats were performed in Mesquite 2.75 (65). This approach to supertree construction is widely used and has been shown to be effective (66).

Table 1.

Summary of OLS and PGLS regression analyses for the body mass dependence of RBT, RSA, and oxygen consumption rates in endothermic (birds and mammals) and ectothermic (fishes, amphibians, and reptiles) vertebrates

Models	N	df	I	95% CI	P	M	95% CI	P	R2
RBT, μm
Endotherms
PGLS (Fig. 1B)	56	54	0.13	(0.09,0.21)	**	0.1	(0.06,0.14)	**	0.32
OLS	59	57	0.13	(0.1, 0.17)	**	0.11	(0.08,0.15)	**	0.43
Ectotherms
PGLS (Fig. 1B)	33	31	1.85	(1.05,3.25)	0.04	−0.04	(-0.11,0.03)	0.27	0.03
PGLS-NoA	18	16	2.97	(1.15,7.69)	0.04	−0.11	(-0.23,0.01)	0.1	0.12
OLS	44	42	1.91	(1.27, 2.91)	**	−0.04	(-0.12,0.04)	0.08	0.02
RSA, cm2
Endotherms
PGLS(Fig. 1A)	48	46	58.55	(31.5,109.9)	**	0.89	(0.83,0.95)	**	0.98
OLS	51	49	57.97	(45.6,74.44)	**	0.9	(0.86,0.93)	**	0.98
Ectotherms
PGLS(Fig. 1A)	24	22	6.88	(2.69,17.63)	**	0.78	(0.65,0.9)	**	0.81
PGLS-NoA	12	10	3.53	(0.81,13.59)	0.12	0.85	(0.64,1.06)	**	0.91
OLS	33	31	8.93	(5.15,15.33)	**	0.76	(0.64,0.87)	**	0.85
O2 consumption, mL O2/h
Endotherms
PGLS (Fig. 2A)	580	578	3.28	(1.95,5.58)	**	0.75	(0.73,0.78)	**	0.95
OLS	580	578	4.09	(3.78,4.39)	**	0.7	(0.69,0.71)	**	0.95
Ectotherms
PGLS (Fig. 2B)	249	247	0.13	(0.02,0.63)	**	0.84	(0.8,0.89)	**	0.80
OLS	249	247	0.10	(0.08,0.13)	**	0.9	(0.85,0.95)	**	0.82
O2 diffusion
Endotherms			4.78	(3.71,5.55)		0.79	(0.77,0.81)
Ectotherms			0.15	(0.1,0.21)		0.82	(0.76,0.87)

The character “I” represents the intercept of the scaling relationship and “M” represents the scaling exponent. P values of P < 0.001 are noted with asterisks. Statistics listed as “NoA” represent those without amphibians (Methods). Data and sources are listed in SI Appendix, Appendixes 1 and 3.

For the PGLS analyses, we treated polytomies as soft (67) and assumed equal branch lengths given the uncertainty in divergence times within and across classes of vertebrates (68).The expected covariance among species was estimated using the corBrownian function in the APE package for R (69), which assumes a Brownian motion model of trait evolution (70, 71). In Table 1, we present the results of both OLS and PGLS analyses because some subset of species were not present in the phylogeny.

Results

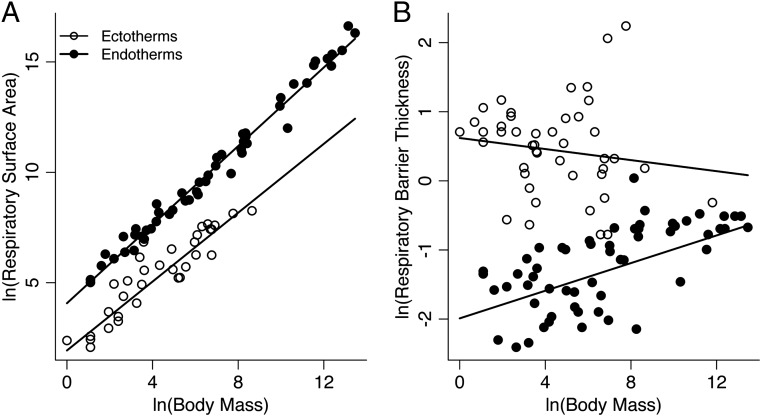
Analyses reveal stark differences in the relationships of RSA and RBT to body mass between ectotherms and endotherms, after accounting for any influence of evolutionary relatedness among species. RSA shows strong, positive relationships with mass in both groups but increases more steeply with mass in endotherms than in ectotherms (RSA ∝ M^0.89 vs. RSA ∝ M^0.78; Fig. 1A and Table 1). In contrast, RBT increases modestly with body mass in endotherms and shows no significant increase with mass in ectotherms (RBT ∝ M^0.1 in endotherms vs. RBT ∝ M^−0.04 in ectotherms; Fig. 1B and Table 1). For a given body mass, RBT is about 13-fold higher, and RSA is about 8- to 10-fold lower, in ectotherms than in endotherms (Fig. 1, Table 1, and SI Appendix, Appendix 1). Body mass also explained substantially more variation in RSA than RBT across species (Table 1).

Fig. 1.

The relationships of (A) RSA (square centimeters) and (B) RBT (micrometers) to body mass (grams) in endotherms (birds and mammals) and ectotherms (reptiles, fishes, and amphibians). Statistics for the lines, fit using PGLS regression, are given in Table 1. Data and sources are listed in SI Appendix, Appendix 1.

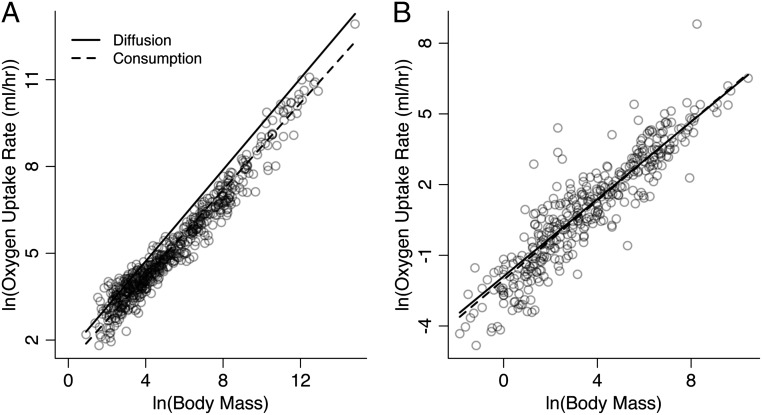
The overall body mass dependence of oxygen diffusion rate in endotherms and ectotherms is estimated based on the relationships for RSA and RBT shown in Fig. 1. For endotherms at rest, the relationship of oxygen diffusion to body mass is estimated to be mL O₂/h = 4.78⋅M^0.79, based on a mean ΔpO2 value of 4.28 (n = 11), and K = 2.48 × 10⁻⁷ cm²⋅h⁻¹⋅mL O₂⋅cm⁻³ tissue⋅mm Hg⁻¹ at 38 °C (Methods). For ectotherms at rest, the relationship is estimated to be mL O₂/h = 0.15⋅M^0.82, based on a mean ΔpO2 value of 19.03 (n = 13, SI Appendix, Appendix 2), and K = 2.19 × 10⁻⁷ cm²⋅h⁻¹⋅mL O₂⋅cm⁻³ tissue⋅mm Hg⁻¹ at 25 °C. These relationships for the body mass dependence of oxygen diffusion are statistically indistinguishable from those of oxygen consumption in endotherms and ectotherms, based on the 95% confidence intervals (CI) (Table 1). PGLS regression analysis of the body mass dependence of oxygen consumption rates for endotherms at rest yields a fitted line (mL O₂/h = 3.28⋅M^0.75, n = 580) that is similar in both slope and intercept to that predicted for diffusion (mL O₂/h = 4.78⋅M^0.79; Fig. 2A and Table 1). The relationship of oxygen consumption rate to body mass in ectotherms also yields a fitted line (mL O₂/h = 0.13⋅M^0.84, n = 249) that closely matches that of diffusion rate (mL O₂/h = 0.15⋅M^0.82; Fig. 2B and Table 1).

Fig. 2.

The observed body mass dependence of oxygen consumption and the predicted body mass dependence of oxygen diffusion for (A) endotherms at rest (birds and mammals; n = 580) and (B) ectotherms at rest (reptiles, fishes, and amphibians; n = 249). Dashed lines are fitted to the oxygen consumption rate data using PGLS regression (Table 1). Solid lines are the predicted relationships of oxygen diffusion (milliliters of O₂ per hour) to body mass (grams) following Eq. 1. Data and sources are listed in SI Appendix, Appendixes 1–3.

Discussion

Our results yield estimates of the body mass dependence of passive oxygen diffusion in endothermic and ectothermic vertebrates using Fick’s law (23). The body mass dependence of the flux per unit area (∝ 1/RBT) multiplied by the total respiratory area (RSA) combine to determine the scaling of oxygen diffusion shown in Eq. 1. The slopes (i.e., scaling exponents) of these relationships arise from the body mass scaling of respiratory surface area and, to a lesser extent, the scaling of respiratory barrier thickness. In endotherms, RSA scaled to the 0.89 power of body mass, but diffusion scaled to the 0.79 power given the scaling of RBT with mass. In ectotherms, the scaling of diffusion (slope = 0.82) more closely matched the scaling of respiratory surface area (slope = 0.78) (Table 1). The nearly 15-fold variation in the RBT of ectotherms was significantly greater than that of endotherms and showed a much weaker correlation with body mass (Fig. 2 and Table 1).

Difference in the intercepts of the relationships of diffusion with body mass, whereby diffusion rates were roughly 30-fold lower in ectotherms than in endotherms (Fig. 2), also arose largely from differences in RSA and RBT between groups. However, these differences were offset somewhat by the 4.4-fold higher value of ΔpO2 in ectotherms than in endotherms (19.03 mm Hg vs. 4.28 mm Hg; SI Appendix, Appendix 2). The weak temperature dependence of Krogh’s diffusion constant, K, has only a very minor effect on the observed difference in intercepts.

The estimated scaling of oxygen diffusion, based on the scaling of RSA and RBT, was statistically indistinguishable from that of oxygen consumption for both endotherms and ectotherms—consistent with the concept of symmorphosis (15). Incorporating the body mass dependence of RSA and RBT into Fick’s law, along with estimates of K and ΔpO₂, predicts both the slopes and intercepts of the oxygen consumption relationships shown in Fig. 2—there are no free parameters. In endotherms, previous models of oxygen consumption in mammals have assumed a linear scaling of diffusion capacity based on available data (8, 20, 72), and thus a mismatch between diffusion and consumption. To address this mismatch, these models further assumed ΔpO2 scales to the −1/12 power of body mass without supporting data (24). The scaling of oxygen diffusion (slope = 0.79) we observed in endotherms was consistent with the 3/4 scaling of resting oxygen consumption rates found here, but also with the most recent estimate of the scaling of maximum oxygen consumption rates in mammals (slope = 0.83; CI: 0.79–0.89) (73). This observation also does not seem consistent with the argument that the structure of respiratory systems has evolved to optimize performance at maximum rather than minimum oxygen consumption rates. Moreover, differences in the intercepts between minimum and maximum oxygen consumption rates could potentially be explained solely based on differences in ΔpO2. The three- to sixfold difference between minimum and maximum oxygen consumption (12) seems to correspond with a change in ΔpO2 of similar magnitude from rest to activity in mammals (74–76). In ectotherms, although the scaling of diffusion and consumption matched, both differed significantly from the previously proposed values of 2/3 and 3/4—consistent with previous work (48). OLS and PGLS models of these and other relationships yielded similar results, although they are not strictly comparable (Methods).

However, our results should not be viewed as pointing to structural constraints on oxygen diffusion as the single rate-limiting step of oxygen consumption. Passive diffusion is just the first step in the complex system that governs the acquisition and delivery of oxygen. Moreover, we recognize that our use of Fick’s law does not account for the many structural and functional differences among species that may affect diffusion (31). We might expect, however, structures relevant to the delivery of oxygen “downstream” of diffusion to show corresponding relationships with mass. For example, we speculate that the size and number of oxygen-carrying red blood cells may be related to the flux per unit area and total area of respiratory surfaces. It is perhaps no coincidence that species with thicker respiratory barriers (e.g., salamanders, lungfish, and tortoises) also tend to have larger cells (77). Passive diffusion may be just one of many colimiting steps on oxygen consumption (78).

Still, the results presented here show how the thickness and area of respiratory surfaces combine to match the body mass dependence of oxygen diffusion to oxygen consumption in endothermic and ectothermic vertebrates. Future work examining the functional tradeoffs associated with differences in RSA and RBT among species may provide insights into the evolutionary forces that have ultimately constrained diffusion rates and perhaps oxygen consumption rates. For example, perhaps the sizes of RSA and RBT are the result of a tradeoff between maximizing gas exchange and minimizing respiratory water (or ion) loss (79). Respiratory water loss may constitute a significant fraction of total water loss among vertebrates (80), and it seems from our data that species facing greater challenges with respect to water loss (e.g., desert tortoises, lungfish, and salamanders) have relatively small respiratory surface areas and/or relatively thick respiratory barriers. A closer look at diffusion in this way may prove valuable to answering the long-standing question of why oxygen consumption rate, and thus species’ energy use (i.e., metabolic rate), scales with body mass.