Gelada vocal sequences follow Menzerath’s linguistic law

Significance

Human language follows a variety of structural principles, known as linguistic laws. One of these, Menzerath’s law, states that, the larger the size of the construct (e.g., the size of a word in terms of syllable number), the smaller the size of the individual constituent parts (e.g., syllables). We show for the first time (to our knowledge) that Menzerath’s law also holds in the vocal communication of a nonhuman species. In the gelada (Theropithecus gelada), a primate living in the highlands of Ethiopia, longer vocal sequences produced by adult males were associated with shorter individual calls. This result suggests that general—perhaps universal—principles underpin the structure of vocal communication in our own species and others.

Abstract

Identifying universal principles underpinning diverse natural systems is a key goal of the life sciences. A powerful approach in addressing this goal has been to test whether patterns consistent with linguistic laws are found in nonhuman animals. Menzerath’s law is a linguistic law that states that, the larger the construct, the smaller the size of its constituents. Here, to our knowledge, we present the first evidence that Menzerath’s law holds in the vocal communication of a nonhuman species. We show that, in vocal sequences of wild male geladas (Theropithecus gelada), construct size (sequence size in number of calls) is negatively correlated with constituent size (duration of calls). Call duration does not vary significantly with position in the sequence, but call sequence composition does change with sequence size and most call types are abbreviated in larger sequences. We also find that intercall intervals follow the same relationship with sequence size as do calls. Finally, we provide formal mathematical support for the idea that Menzerath’s law reflects compression—the principle of minimizing the expected length of a code. Our findings suggest that a common principle underpins human and gelada vocal communication, highlighting the value of exploring the applicability of linguistic laws in vocal systems outside the realm of language.

Identifying fundamental principles that underpin diverse natural phenomena is a central goal of the life sciences (1, 2). The existence of such principles, revealed by the occurrence of common statistical patterns, can shed light on the basic processes shaping biological systems (3). In recent years, exploration of the universality of the statistical laws of human language has proved a fruitful starting point for identification and investigation of these fundamental principles (4, 5). The power of such an approach is illustrated by recent studies of the generality of Zipf’s law of abbreviation (6). This linguistic law, also commonly known as Zipf’s law of brevity, states that more frequently used words tend to be shorter, and it has been found to hold true in all languages assessed to date (5). Analyses of the nonvocal surface behavioral repertoire of dolphins (7), the vocal repertoire of Formosan macaques (8), close-range calls of common marmosets (9), and social calls of four species of bats (10) reveal that they too conform to an inverse general relationship between magnitude (e.g., duration) and frequency of use. This common pattern provides evidence that compression—the information-theoretic principle of minimizing the expected length of a code—is a general principle of animal (including human) behavior, reflecting selection for energetic efficiency (5, 11).

Further evidence of compression in human language—this time, not at the level of individual elements, but at the level of elements combined into sequences—may come from studies of another linguistic law, Menzerath’s law, which states simply that “the greater the whole, the smaller its constituents” (12–14). Traditionally, this law has been used to explore the structuring of language in written text, and evidence supports this law at different scales of analysis: the longer a word in terms of syllable number, the shorter on average are its constituent syllables (e.g., ref. 13), and the longer a sentence in terms of number of clauses, the shorter on average those clauses are (e.g., ref. 15). Although Menzerath’s law was originally induced as a linguistic law, it has since been applied to a wide range of systems beyond human language: a negative correlation between construct and constituent size has been found in domains such as music (16) and at the molecular level, with species that have a larger number of chromosomes tending to have a smaller mean chromosome size (4, 17–20), genes that have a higher number of exons having shorter exons on average (21, 22), and proteins with a higher number of domains having on average shorter domains (23). This broad adherence to Menzerath’s law can be interpreted as a manifestation of self-organization (24) and compression of information (14, 25), and suggests that these processes may be widespread in shaping multilevel systems as diverse as macromolecules, language, and music.

To date, no study has tested Menzerath’s law in the vocal communication of any species except our own. Carrying out such studies is essential if the generality of this law across different communication systems is to be evaluated. Such an investigation would also contribute to our understanding of the multifaceted nature of animal vocal signaling; identifying the processes by which animals take singular sounds and combine them into diverse sequences is a key goal for those wanting to quantify, compare, and explain variation in vocal complexity across taxa, including humans (26). Moreover, finding conformity to Menzerath’s law in animal vocal behavior would highlight an important commonality between human language and the vocal systems of other animals, with respect to the basic structural patterns underpinning how sounds are combined into larger units and structures. This commonality would provide evidence for selection acting on the communicative systems of these disparate taxa, either to constrain them to a common ancestral state, or to drive their convergent evolution (5).

Here, we test Menzerath’s law in the vocal communication of wild geladas (Theropithecus gelada), a gregarious primate species with a well-described vocal repertoire, and in which individuals—typically adult males—produce long and complex vocal sequences during affiliative contexts (27–30). The constituent parts of these sequences are discrete, individual calls, and six different call types in total are seen in sequences. Playback experiments indicate that sequences composed of only the most common call type—grunts—elicit weaker responses from receivers than do more varied sequences; furthermore, regardless of composition, playbacks of sequences composed of multiple call types elicit similar strong responses from receivers (31). These results suggest that, in contrast to what happens when words are combined to form sentences, geladas do not seem to combine elements into sequences to convey a different meaning. Instead, these vocal sequences may function similarly to bird song in that increasing the diversity of calls within them provides a more effective way to convey the same message (32).

First, we test for (i) a negative correlation between the number of calls in a sequence and the average duration of these calls; this provides a test of Menzerath’s law in the gelada vocal system. Patterns consistent with Menzerath’s law could result from one or more different processes, which we explore in further analyses. One such process would be energetic or breathing constraints on vocal production leading to shorter vocal utterances being made later in sequences (and more of these shortened calls being seen in sequences with more calls overall); we therefore assess whether (ii) durations of calls become shorter later in sequences. Patterns consistent with the law could also occur if sequences with more calls contain a higher proportion of the shorter call types in the repertoire; therefore, we test whether (iii) sequence composition changes with the number of calls. Another possible process underlying emergence of this law would be calls of a particular type being shortened in duration in sequences with more calls; we explore this possibility by testing whether (iv) within specific call types, durations are shorter in sequences containing a larger number of calls. We then extend our analyses to explore the silences between calls (intercall intervals) testing whether (v) Menzerath’s law also holds for silences, such that intercall intervals are shorter in sequences with more calls, and (vi) durations of intercall intervals become shorter later in sequences. Finally, as a link between Menzerath’s law and the principle of compression has previously been proposed (14, 25), but not systematically established, we (vii) use a mathematical approach to provide formal support for this link and (viii) put forward a unified explanation for the origins of both Menzerath’s law and Zipf’s law of abbreviation.

Results

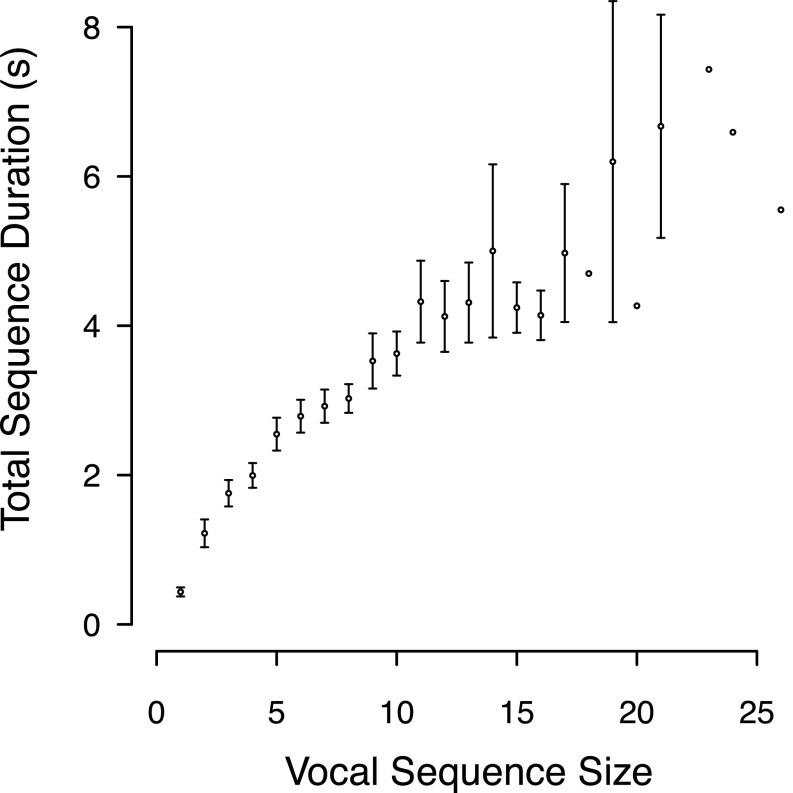
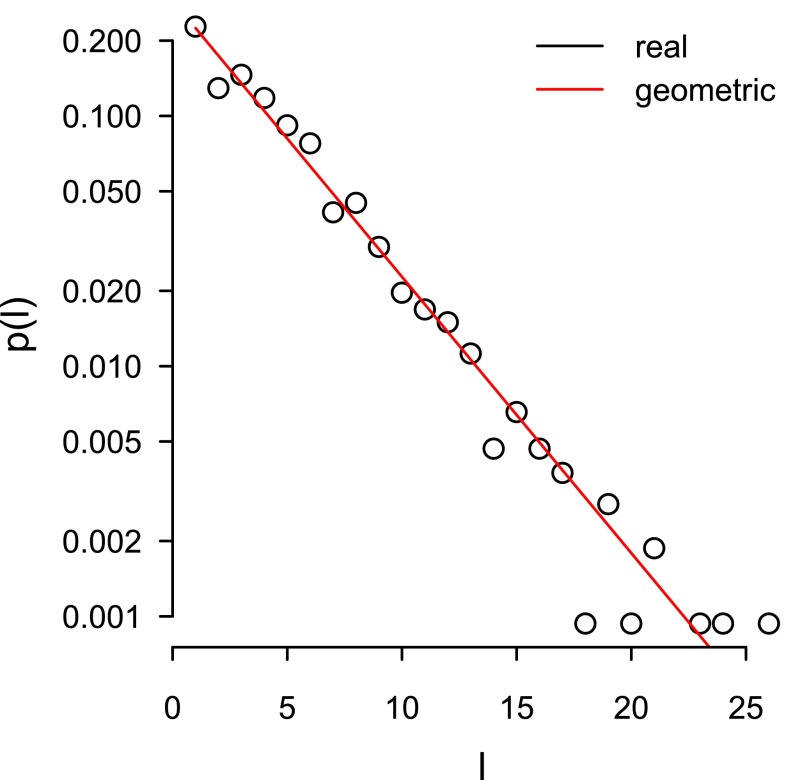
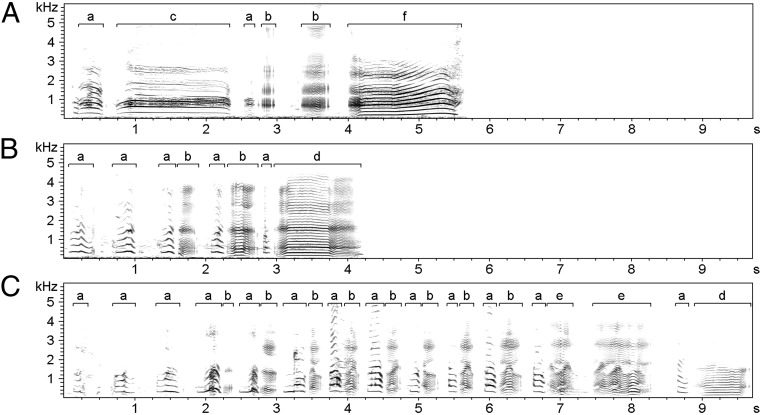
We analyzed 1,065 vocal sequences (composed of 4,747 individual calls) recorded from 57 study males (1–113 sequences per male). The sequence sizes ranged between 1 and 26 calls (242 single call sequence recordings, 1–156 recordings for sequences with two or more calls, with 1–24 recordings per male per sequence size). There were no recordings available for sequences of 22 calls or 25 calls. Because 242 sequences were composed of a single call, this means that 823 sequences were used in the analyses involving intercall intervals. Total sequence duration averaged 1.97 s (SEM: 0.05 s; range: 0.12–8.33 s), and the distribution of the sequence sizes was consistent with a geometric distribution, suggesting that the probability of sequence termination is not dependent on sequence size (see Supporting Information for further details about the variation of sequence duration and size; Figs. S1 and S2). Example spectrograms of short and long vocal sequences from the same male, showing each of the six call types, are shown in Fig. 1. Audio for these spectrograms are available in Audio Files S1–S3.

Fig. S1.

Relationship between vocal sequence size and sequence duration (i.e., total duration of sequence from start of first call to end of last call). Points and whiskers indicate mean ± 2 SEM, and lack of whiskers indicates that there was a sample size of one sequence.

Fig. S2.

The distribution of the vocal sequence size (black) against a geometric distribution (red) where the parameter (π = 0.224) has been obtained by maximum likelihood. p(l) is the probability that a sequence consists of l calls.

Fig. 1.

Example spectrograms of (A) a 6-call vocal sequence, (B) an 8-call sequence, and (C) a 24-call sequence from the same study male. Brackets on the spectrograms denote the start and end of each call, and the lowercase letters above the brackets represent different call types: (a) exhale grunt, (b) inhale grunt, (c) exhale moan, (d) inhale moan, (e) wobble, and (f) yawn. Spectrograms were made in Avisoft SAS Lab-Pro (version 5.1.12; Avisoft Bioacoustics).

i) Is Call Duration Negatively Correlated with Sequence Size?

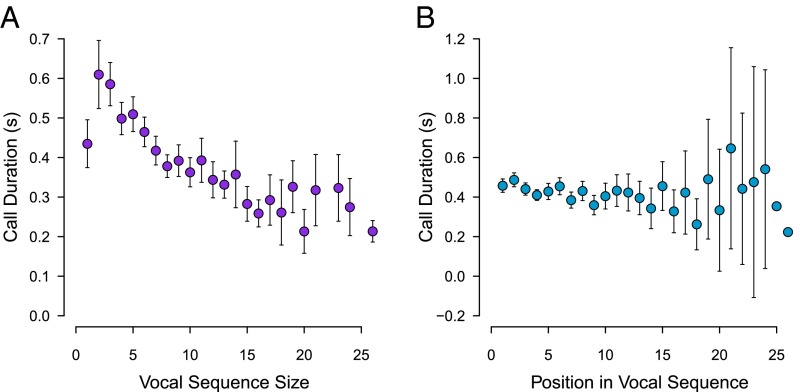
To test whether there is a negative association between construct size and the duration of constituent parts, we tested for a correlation between sequence size and the duration of individual calls. Supporting Menzerath’s law, individual call duration was negatively correlated with sequence size (r_s = −0.229, n = 4,747, P < 0.0001; Fig. 2A). This finding was further supported by a linear mixed model (LMM) that included individual call duration as the dependent variable, sequence size, call position, and call type as fixed effects, and male identity and sequence recording (i.e., the vocal sequence that a call was from) as random effects (P < 0.0001; Table 1).

Fig. 2.

Relationship between call duration and (A) vocal sequence size (i.e., number of discrete calls) and (B) call position in a vocal sequence. Points and whiskers indicate mean ± 2 SEM, and lack of whiskers indicates that there was a sample size of 1 sequence.

Table 1.

Results of LMM used to test for relationships between call duration and sequence size, call position, and call type

Factor	Estimate	SEM	t	P*
Intercept	0.333	0.009	35.228	<0.0001
Sequence size	−0.006	0.001	−5.041	<0.0001
Call position	0.003	0.001	1.841	0.0658
Call type†
Exhaled moan	1.280	0.015	85.754	<0.0001
Inhaled grunt	−0.037	0.010	−3.836	0.0001
Inhaled moan	0.535	0.013	40.636	<0.0001
Wobble	0.673	0.039	17.235	<0.0001

^*Bolded values indicate P < 0.05.

^†Exhale grunt was the reference level for call type.

ii) Does Call Duration Get Shorter Later in the Sequence?

To test whether such a Menzerath’s law effect could be due to constraints on vocal production, resulting in shorter calls toward the end of a sequence, we explored the role of call position in the LMM (Table 1). Call position was not associated with call duration, indicating that calls were relatively similar in duration throughout an entire vocal sequence (Fig. 2B). This finding was corroborated by an LMM showing that the duration of first-position calls was negatively associated with sequence size (estimate ± SEM: −0.020 ± 0.005, t = 4.151, P < 0.0001), indicating that the duration of calls in the beginning of sequences reflected sequence size.

iii) Do Proportions of Call Types Change with Sequence Size?

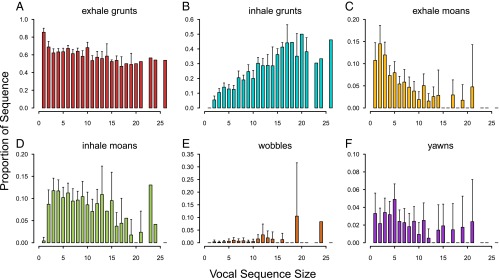
To test whether a Menzerath’s law effect could be due to a varying proportion of shorter or longer call types in sequences of different sizes, we explored differences in duration across the six call types and examined associations between sequence size and proportions of each call type given in each sequence size. There was marked variation in duration among the six call types (Table 2). On average, inhale grunts were the shortest of the call types, exhale grunts were the second shortest call type, followed by inhale moans, wobbles, yawns, and exhale moans (Tables 1 and 2). The proportions of both exhale grunts (estimate ± SEM: −0.019 ± 0.002, t = 8.130, P < 0.0001) and exhale moans (estimate ± SEM: −0.008 ± 0.002, t = 4.747, P < 0.0001) in vocal sequences were negatively associated with sequence size (Fig. 3). The proportions of inhale grunts (estimate ± SEM: 0.023 ± 0.001, t = 20.173, P < 0.0001), inhale moans (estimate ± SEM: 0.005 ± 0.001, t = 3.979, P = 0.0001), and wobbles (estimate ± SEM: 0.001 ± 0.000, t = 4.676, P < 0.0001) in vocal sequences were positively associated with sequence size (Fig. 3). The proportion of yawns in vocal sequences was unrelated to sequence size (estimate ± SEM: −0.001 ± 0.001, t = 1.351, P = 0.1772; Fig. 3).

Table 2.

Duration of the call types used in gelada male vocal sequences

Call type	N	Mean, s	SEM	Range, s
Exhale grunt	2,982	0.296	0.002	0.064–0.766
Exhale moan	300	1.597	0.430	0.770–4.153
Inhale grunt	872	0.244	0.004	0.029–0.511
Inhale moan	435	0.840	0.012	0.514–1.985
Wobble	41	0.948	0.127	0.261–4.250
Yawn	117	0.996	0.037	0.200–2.406

Fig. 3.

Relationship between proportions of specific call types and sequence size. Bars and whiskers indicate the mean proportion + 2 SEM of the specific call type in vocal sequences of that given size, and lack of whiskers indicates that there was no variation in the proportion values. Call types are (A) exhale grunts, (B) inhale grunts, (C) exhale moans, (D) inhale moans, (E) wobbles, and (F) yawns.

iv) Do Calls of a Particular Type Shorten in Duration in Longer Sequences?

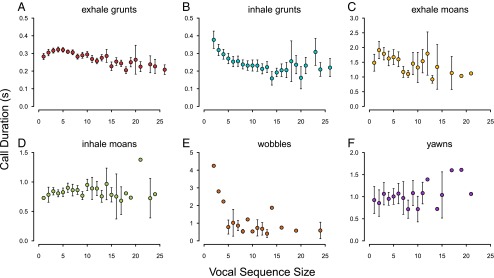
To test whether a Menzerath’s law effect could be due to the shortening of specific call types in longer sequences, we explored the relationships between call duration and sequence size within particular call types using LMMs. Individual call duration was negatively associated with sequence size for exhale grunts (estimate ± SEM: −0.002 ± 0.001, t = 2.299, P = 0.0219), exhale moans (estimate ± SEM: −0.044 ± 0.013, t = 3.471, P = 0.0006), inhale grunts (estimate ± SEM: −0.005 ± 0.001, t = 6.001, P < 0.0001), and wobbles (estimate ± SEM: −0.083 ± 0.029, t = 2.873, P = 0.0090) (Fig. 4). Call duration was unrelated to sequence size for inhale moans (estimate ± SEM: 0.003 ± 0.003, t = 0.863, P = 0.3892) and yawns (estimate ± SEM: 0.008 ± 0.010, t = 0.771, P = 0.4422) (Fig. 4). See Supporting Information and Table S1 for further analyses including call position.

Fig. 4.

Relationship between call duration and sequence size for datasets focusing on each of the six call types. Points and whiskers indicate mean ± 2 SEM, and lack of whiskers indicates that there was a sample size of one sequence. Call types are (A) exhale grunts, (B) inhale grunts, (C) exhale moans, (D) inhale moans, (E) wobbles, and (F) yawns.

Table S1.

Results of LMMs used to test for relationships between call duration and sequence size and sequence position for datasets focused on each of the six call types

Model (call type)	Factor	Estimate	SEM	t	P*
Exhale grunt	Intercept	0.306	0.007	41.655	<0.0001
	Sequence size	−0.001	0.001	−1.058	0.2904
	Call position	−0.002	0.001	−2.365	0.0181
Exhale moan	Intercept	1.832	0.084	21.748	<0.0001
	Sequence size	−0.024	0.016	−1.498	0.1353
	Call position	−0.049	0.025	−1.981	0.0488
Inhale grunt	Intercept	0.291	0.009	31.168	<0.0001
	Sequence size	−0.010	0.001	−9.238	<0.0001
	Call position	0.009	0.001	7.290	<0.0001
Inhale moan	Intercept	0.806	0.030	26.483	<0.0001
	Sequence size	−0.030	0.007	−4.250	<0.0001
	Call position	0.040	0.008	5.232	<0.0001
Wobble	Intercept	1.865	0.314	5.939	<0.0001
	Sequence size	−0.075	0.037	−1.997	0.0546
	Call position	−0.012	0.035	−0.344	0.7333
Yawn	Intercept	1.00	0.088	11.380	<0.0001
	Sequence size	−0.043	0.036	−1.182	0.2401
	Call position	0.053	0.036	1.459	0.1478

^*Bolded values indicate P < 0.05.

v) Is Intercall Interval Duration Negatively Correlated with Sequence Size?

We extended our definition of constituent parts to include the intercall intervals (the silences between calls) in vocal sequences and carried out analyses similar to those using individual call duration as a dependent variable. Supporting Menzerath’s law, individual intercall interval duration for each sequence was negatively correlated with sequence size (r_s = −0.413, n = 3,682, P < 0.0001; Fig. 5A). This finding was further supported by a LMM that included individual intercall interval duration as a dependent variable, sequence size and interval position as fixed effects, and male identity and sequence recording as random effects (P < 0.0001; Table 3).

Fig. 5.

Relationship between intercall interval duration and the (A) vocal sequence size and (B) intercall interval position in a vocal sequence. Points and whiskers indicate mean ± 2 SEM, and lack of whiskers indicates that there was a sample size of one sequence.

Table 3.

Results of LMM used to test for relationships between intercall interval duration and sequence size and interval position

Factor	Estimate	SEM	t	P*
Intercept	0.452	0.017	26.827	<0.0001
Sequence size	−0.023	0.002	−11.130	<0.0001
Interval position	−0.003	0.001	−2.271	0.0232

^*Bolded values indicate P < 0.05.

vi) Do Intercall Intervals Become Shorter Later in a Sequence?

To test whether such a Menzerath’s law effect of intercall intervals could be due to constraints on vocal production, resulting in shorter intervals toward the end of a sequence, we explored the role of interval position in the LMM (Table 3). There was support for the prediction that intercall interval duration shortens as a sequence progresses, as interval duration was negatively associated with interval position (Fig. 5B). Moreover, an LMM showed that the duration of first-position intercall intervals was negatively associated with sequence size (estimate ± SEM: −0.021 ± 0.003, t = 6.365, P < 0.0001), indicating that the intervals in the beginning of sequences also reflected sequence size.

vii) A Formal Mathematical Exploration of the Link Between Menzerath’s Law and Compression.

In quantitative linguistics, the presence of Menzerath’s law has been interpreted as a compression effect (ref. 14, p. 147; ref. 25, p. 42); however, the connection between this law and the problem of compression in information theory is not obvious and has never been formally explored mathematically. In standard coding theory, the problem of compression is based on the minimization of the mean code length (33):

$$L={\displaystyle \sum _{i=1}^V{p}_i{l}_i},$$ [1]

where p_i and l_i are, respectively, the probability and the length of the ith element of a repertoire (e.g., an alphabet) of size V. Solving the problem of compression consists of finding the lengths so as to minimize L, assuming that the probabilities of the elements are constant and that two elements cannot have the same code. The minimization of L and a negative correlation between probability and length are intimately related (11). For instance, it has been shown that the minimization of L leads to the law of abbreviation, i.e., a negative correlation between probability and length (5, 11). For Menzerath’s law in human language and the vocalizations of geladas, we propose the minimization of the following function:

$$M={\displaystyle \sum _{i=1}^T{l}_i},$$ [2]

where l_i is now the magnitude of the ith construct in a series of T constructs. For instance, l_i could be the total duration of the ith vocalization of a gelada or the length in words of the ith sentence in text (see ref. 5 for a review of costs associated to duration). Notice that there is an important difference between L and M; to illustrate this point, we borrow the concept of type and token from quantitative linguistics (34). Although L is defined as a summation over types (elements of the repertoire or vocabulary), M is defined as a summation over tokens, namely occurrences of elements of the repertoire. Interestingly, M can be expressed equivalently as the total sum of the duration of the parts of every occurrence, namely, the following:

$$M={\displaystyle \sum _{i=1}^T{\displaystyle \sum _{j=1}^{n_i}{l}_{ij}},}$$ [3]

where l_ij is the length of the jth part of the ith occurrence (token). If one assumes that, given a certain occurrence, all of the parts are identically distributed, it turns out that the expectation of M is as follows:

$$E\left[M\right]={\displaystyle \sum _{i=1}^T{n}_{i}E\left[l_{ij}|i\right]},$$ [4]

where E[l_ij|i] is the expected magnitude of the parts of the ith occurrence, assuming that parts are identically distributed for a given occurrence. Now it is easy to see that L and E[M] follow the same scheme: both are a weighted sum of the magnitude of elements from a set. Applying the arguments used to derive the law of abbreviation from the minimization of L (11), one can also derive Menzerath’s law from the minimization of E[M]. This argument relies on the simplifying assumption that parts are identically distributed, which is supported by the absence of an overall effect on duration of call position (Table 1).

viii) A Unified Explanation for the Origins of Zipf’s Law of Abbreviation and Menzerath’s Law Through a General Cost Function.

The generality of the principle of compression becomes more evident when regarding the minimization of L and E[M] as instances of the minimization of a generalized cost function:

$$K={\displaystyle \sum _i{x}_i{y}_i,}$$ [5]

where x_i and y_i are, respectively, the weight and the magnitude of the ith element of a set (we assume that all “x_i”s and “y_i”s are positive). L is a particular case of K when x_i and y_i are, respectively, the probability and the length of the ith element (in this case, K is defined over the alphabet or species repertoire). E[M] is a particular case of K when x_i is the number of parts (the number of calls) of the ith occurrence (token) and y_i is the expected magnitude of its parts; i.e., E[l_ij|i] (in that case, the set consists of occurrences or tokens). Applying the same arguments of Ferrer-i-Cancho et al. (11) to the minimization of K, a negative correlation between the weight of a unit and its magnitude is expected. To conclude, the minimization of K can be viewed as a general principle of compression, shedding light on the origins of both Zipf’s law of abbreviation and Menzerath’s law. This provides theoretical support for the intuition that Menzerath’s law is an effect of compression (14, 23, 25). Indeed, one can also conclude that minimization of K and a negative correlation between the weight of a unit and its magnitude (Zipf’s law of abbreviation, Menzerath’s law) are intimately related, based upon previous arguments for L (11).

Discussion

The complex vocal sequences of adult male geladas follow Menzerath’s law, with sequences that are larger—i.e., that contain more calls—being composed of calls with shorter duration. This finding provides support for the generality of this linguistic law beyond the realm of human language. There is currently great controversy about why diverse biological systems exhibit Menzerath’s law and related laws (4, 5, 8, 18, 20, 35), and indeed about whether such laws hold at all (9, 36). Our findings make a significant contribution to this ongoing debate, providing (to our knowledge) the first evidence for Menzerath’s law in nonhuman animal vocal systems, and complementing a growing body of comparable evidence from a range of mammalian species (7, 8, 10) that behavior can be described by another, related linguistic law—Zipf’s law of abbreviation (6). A virtue of our analysis of the presence of Menzerath’s law is that it considers the duration of individual calls within a sequence, and thus the finding of the law cannot be attributed to an artifact of using mean durations (37). Our results also provide support for the hypothesis that Menzerath’s law, as is the case for Zipf’s law of abbreviation, is an effect of compression—the information-theoretic principle of minimizing the expected length of a code.

The finding that gelada vocal sequences show the same negative relationship between the size of the whole construct and the size of its constituents, as is found in human language, suggests that equivalent principles of self-organization (24) underpin the vocal communication of our own species and another primate. Although there are elementary differences between the vocal faculties of humans and of other animals (38–40), exploring and comparing mathematical, structural properties of their communication systems can be informative (26, 41). As language is inherently sequence-based and animals of many taxa, from bacteria (42) to great apes (43), combine individual signals into sequences, identifying basic patterns of sequence structure that are shared by human and nonhuman animal communication provides evidence for evolutionary preservation, or convergent evolution, of the processes underlying the emergence of such patterns (41). Importantly, adherence to Menzerath’s law need not involve any cognitively demanding planning by the animals producing sequences of sound. Finding Menzerath’s law in gelada communication suggests that strings of sound following this law could predate the evolution of meaningful combinations.

Our further analyses revealed insights into how the negative relationship between call duration and sequence size arises in gelada vocal sequences. First, our analyses of call duration and call position in a vocal sequence suggest that conformity to Menzerath’s law cannot be explained simply by physiological or mechanical constraints on vocal production leading to shorter calls being made at the end of sequences (and more of these abbreviated calls being added to the end of longer sequences). Considering all call types together, a negative association was not seen between call position and duration as would be expected if such constraints were important; this indicates that, from the start of vocal sequences, male geladas make calls of the “appropriate” duration for that sequence size, and call duration does not then reduce predictably as the sequence progresses.

The emergence of patterns consistent with Menzerath’s law may be in part due to the composition of vocal sequences varying with the number of calls. In particular, the proportion of exhale grunts decreased and the proportion of inhale grunts increased in larger sequences. This is likely to be due to males increasing the frequency with which they make both an inhale grunt and an exhale grunt on the same breath as sequence size increases. Most significantly, once sequences exceed about 15 calls, inhale and exhale grunts—the two call types with the shortest duration—made up the vast majority of the constituent calls, and the relative proportion of each call type in the sequences varied little. Abbreviation of some individual call types in larger sequences may also underpin conformity to Menzerath’s law: the durations of inhale grunts and exhale moans (the second and third most common call types in sequences) were negatively related to the number of calls in the sequence. There is little evidence from studies of human language of a comparable effect (i.e., that the same constituent of a construct decreases in length in larger constructs), not least because Menzerath’s law is almost exclusively investigated in written texts where a given word has a fixed length. However, one of the earliest studies of this phenomenon (conducted before its formal description as a linguistic law) suggests a similar shortening of a particular spoken sound when it appears in a larger construct. Grégoire (44) found that, in spoken French, the duration of the pronunciation of the syllable pâ- decreased with increasing duration of the word or phrase that it began; the sound lasted 325 ms in pâte, but only 195 ms in pâteuse.

Conformity to Menzerath’s law in gelada vocal sequences may reflect constraints linked to the respiratory and energetic demands of signal production. The lack of a strong association between call duration and position in the sequence does not preclude the possibility that physiological or mechanical constraints are important limiting factors in gelada vocal sequences. Nonhuman primates’ relatively limited breathing control while vocalizing restricts their ability to produce long, continuous vocal sequences (45, 46), and an increase in the frequency with which vocalizations are made on both the inhale and exhale of the same breath could lead to hyperventilation (47). Additionally, as revealed both by comparative analyses (48) and single species studies (49–51), the duration of vocal signals in vertebrates can be constrained by energy availability. Although reducing signal duration can therefore save energy and/or may be a necessary result of breathing patterns, it remains an open question as to whether or not the shortening of a vocalization results in the loss of transmission fidelity. Theoretical analyses of communication indicate that transmission fidelity is increased by adding redundancy, e.g., increasing signal duration (52), and studies of human speech support this idea: when asked to speak particularly clearly, people significantly increase the duration of individual speech sounds (53). A reduction in signal length also increases the risk both of confusing different signals and of perturbation of the signal by noise in the environment (54). Menzerath’s law may therefore emerge in gelada vocal sequences as a compromise between effectiveness of communication, and the energetic demands and breathing constraints of vocal production.

Our analyses extended the standard approach of exploring Menzerath’s law by considering the gaps between constituents of a construct (intercall intervals in our study), as well as the constituents themselves (calls); to our knowledge, no study of Menzerath’s law in humans has explored these interconstituent gaps. The same negative relationship with sequence size was found for intercall interval duration as was seen for call duration. Thus, larger vocal sequences have a faster tempo—they contain calls of shorter duration, with shorter gaps in between, and therefore are delivered at a higher rate. This variation in sequence tempo may reflect the emotional arousal state of the vocalizing animal (55) and potentially signal such information to receivers (56). A promising avenue for future research will be to investigate whether these longer and faster sequences have a different communicative function from shorter and slower sequences, such as expressing affective state to potential listeners (55). Indeed, it has been proposed that the rhythm of gelada vocal sequences has important communicative function in itself (27), but this idea has never been formally tested. One advantage of longer sequences being produced at a faster tempo is that it reduces the risk of being “talked over” by other geladas; this is a serious potential problem, due to a noisy environment of conspecific vocalizations in which these animals need to communicate (30). Notably, the duration of intercall intervals was negatively related to position in the sequence; this was not the case for calls, where no such relationship was seen. This indicates that tempo increases toward the end of sequences.

Although no previous study of nonhuman animal communication has explicitly tested Menzerath’s law, results from the literature indicate that a negative relationship between sequence size and call duration is not inevitable. For example, baboons give longer sequences of grunts in infant handling compared with movement contexts, but the grunts in the longer sequences were longer, not shorter, in duration (57). Similarly, in a study of Barbary macaque female copulation calling (58), sequences given around the time of ovulation had a higher number of calls than sequences given early in the cycle, and these calls were again longer in duration. The difference between these findings and the present results may be due to the nature of the respective vocal sequences. Unlike gelada vocal sequences, sequences of baboon grunts are both homogenous and shorter, and so there may be less opportunity for Menzerath’s law to emerge. In Barbary macaques, copulation call sequences not only consist of the same call type repeated multiple times but also are very loud and appear to be aimed at distant as well as nearby receivers (59). In long-range communication, a potential reason for Menzerath’s law not to emerge is the conflict between compression and transmission success, which lead to opposing constraints; it is easier for compression to dominate when successful communication over long distances is not necessary (5). Our analysis of short-range vocalizations in geladas provides support for the hypothesis that compression prevails in short-range communication (10).

Although a connection between Menzerath's law and compression has been suggested various times (14, 25), it has not been formally investigated. Here, to our knowledge, we provide the first mathematical demonstration of the connection between compression and Menzerath’s law. We also provide (to our knowledge) the first unified explanation for both Zipf's law of abbreviation and Menzerath’s law by means of a general cost function, which could explain the recurrence of these patterns across biological systems and levels of organization. The power of the argument relies on its mathematical simplicity and its general scope: it covers both individual elements and also the (possibly recursive) sequential structures they form. Furthermore, our explanation makes no linguistic or communicative assumptions about the elements or their combinations (e.g., with respect to whether they convey meaning, or serve a particular function). Therefore, our theoretical framework can bridge gaps across a broad range of biological disciplines.

Conclusion

Quantitative methods have proved extremely powerful in the field of linguistics, for example revealing shared fundamental properties of geographically and morphologically diverse languages, which are not revealed by qualitative approaches (60, 61). The full power of linguistic laws may, however, extend far beyond the field in which they were developed (4, 5). Testing for conformity to linguistic laws in other biological systems facilitates a move from exploration of universal properties of language (62) to the development and testing of hypotheses about the fundamental principles that may explain the repeated occurrence of these statistical patterns across diverse biological contexts (4, 5). Our demonstration of a pattern consistent with Menzerath’s law in gelada vocal communication further highlights the value of exploring the full scope of linguistic laws outside the realm of language. This law can be tested wherever a structure, process, or system can be broken down into a construct and its constituents; the law’s mathematical simplicity belies its enormous potential explanatory power, and we hope our work will encourage others to test the generality of Menzerath’s law in biology. Finally, our demonstration of how a generalized principle of compression produces Menzerath’s law, in conjunction with our previous work indicating that Zipf’s law of abbreviation also reflects this principle (5), suggests that compression may underpin biological information systems in a broad sense. Compression exists not only at different levels of the chemistry of life—codons (63), proteins (23), genes (22), and entire genomes (18)—but also in multiple forms of animal behavior, from elementary patterns of behavior (7) to vocal communication in nonhumans (8, 10) and human language (4, 6, 25).

Materials and Methods

Study Site and Subjects.

Data for this study come from 57 adult male geladas across three different bands in one wild community (about 1,200 individuals) living in the Sankaber area of the Simien Mountains National Park, Ethiopia (64). Gelada bands are comprised of smaller harem-like units with a leader male, 0–3 follower males, and 1–11 females with their immature offspring (64). Male geladas were chosen as the target of the study because they produce more complex vocalizations than females (27, 30). The study males included 33 unit leaders, 14 followers, and 7 males who were a leader and a follower at different times during the study period, from across 30 reproductive units. The remaining three study males were bachelors from all-male groups in the study bands, and one of these males was a leader and a bachelor at different times during the study period (65). This population has been under intensive behavioral study since January 2006, and study subjects are fully habituated to human observers on foot (approach distances less than 3 m) (66).

The gelada research was approved by the University Committee on Use and Care of Animals at the University of Michigan and adhered to the laws and guidelines of Ethiopia.

Vocal Sequence Data Collection and Processing.

From March 2008 to June 2014, we opportunistically recorded vocal sequences during behavioral observations, using a Sennheiser ME66 directional microphone connected to a Marantz PMD 660 or 661 Digital Recorder. We define a vocal sequence (i.e., the whole construct) as one or more discrete calls (i.e., the constituent parts) made by the same individual and, for those sequences with two or more calls, separated by an intercall interval of less than 5 s (Fig. 1 and Audio Files S1–S3). Sequence size refers to the number of calls in the sequence. Call (or interval) position refers to the placement of the call (or interval) in the entire sequence (first, second, third, fourth, etc.). To control for behavioral context, we focus only on the vocal sequences made during close-range affiliative social situations. These “contact call” vocal sequences are thought to play an important role in facilitating contact with group members, and they are known to vary widely in size, composition, and complexity of individual calls (27, 30). Six call types are made during these vocal sequences: exhale grunts, exhale moans, inhale grunts, inhale moans, wobbles, and yawns (30). Call types in a vocal sequence were described at the time of the recording and reassessed during visual and auditory inspection of the spectrogram; an earlier study of gelada vocalizations, which examined calls from many of the sequences analyzed here, found 96% interobserver reliability of call type identification (30). Because grunts and moans (an elongated version of a grunt) grade into each other, density plots of call durations (log-transformed) for exhaled and inhaled grunts/moans were used to determine thresholds to distinguish between grunt and moan call types. These thresholds were defined as the minimum value between the first two peaks. By this definition, the threshold between exhaled grunts and moans was 0.768 s and the threshold between inhaled grunts and moans was 0.513 s.

Our analyses focus on vocal sequences with sufficiently high noise-to-signal ratio to categorize call types, and which are uninterrupted by a call from another adult unit member. We used Avisoft SAS-Lab Pro (version 5.1.12; Avisoft Bioacoustics) to generate spectrograms with a fast Fourier transformation (size of 1,024 points) and to label the start time, end time, and call type of all calls in a vocal sequence. These start and end times were used to calculate the call duration and intercall interval duration. Calculations of call durations, intercall interval durations, and all statistical tests were carried out in R 3.2.2 (67).

Statistical Analysis.

To explore the relationship between call duration (and intercall interval duration) and sequence size, we first used Spearman rank correlation tests, a method introduced to examine Menzerath’s law and remain objective about the exact functional dependency between the variables (22, 37, 68). In these tests, the duration of individual calls or intercall intervals for each sequence size was correlated with sequence size. Although this can help to avoid potential problems of previous research on Menzerath’s law (37), we recognize that its application with our dataset involves pseudoreplication. Therefore, LMMs were constructed to assess the relationships between call (or interval) duration and sequence size while taking call (or interval) position, call type, male identity, and sequence recording (i.e., the vocal sequence that a call was from) into account. We ran the LMMs in R 3.2.2. using the function lmer of the R package lme4 (69). The lmerTest package was implemented to determine the significance of the LMM coefficients (70). (i) First, we examined variation in individual call duration by including sequence size, call position, and call type as fixed factors and male identity and the sequence recording as random effects. (ii) An effect of call position was assessed in the LMM for part i, and to examine further the relationship between call position and individual call duration, we ran an additional LMM with duration of the first call in vocal sequences as the dependent variable, sequence size as a fixed effect, and male identity as a random effect. (iii) To examine whether the proportion of call types changes as sequence size changes, we ran six LMM models, one for each call type. For these models, the proportion of each call type was calculated for all vocal sequences as the number of calls of a given call type divided by the sequence size. Call type proportion was included as a dependent variable, with sequence size as a fixed effect and male identity as a random effect. (iv) Then, to assess whether a relationship between call duration and sequence size applied to specific call types, six LMM models were run, one for datasets limited to each of the call types. In these models, call duration was the dependent variable with sequence size as a fixed effect and with male identity and sequence recording as random effects. See Supporting Information for rationale behind the exclusion of call position as a fixed effect for the LMMs on datasets for specific call types and the results of analyses including call position (Table S1). (v) We examined variation in intercall interval duration by including sequence size, interval position, and call type as fixed effects and male identity and sequence recording as random effects. (vi) An effect of intercall interval position was assessed in the LMM for part v, and to examine further the relationship between interval position and interval duration, we ran an additional LMM with duration of the first intercall interval as the dependent variable, sequence size as a fixed effect, and male identity as a random effect. All statistical tests were assessed using a significance level of α = 0.05.

Variation of Vocal Sequence Duration and Sequence Size

To test whether there is an association between sequence size and sequence duration (the amount of time between the start of the first call and the end of the final call in a sequence), we carried out a linear mixed model (LMM) that included sequence duration as a dependent variable, sequence size as a fixed effect, and male identity as a random effect. This analysis revealed that sequence size was positively associated with sequence duration (estimate ± SEM: 0.326 ± 0.008, t = 39.988, P < 0.0001; Fig. S1).

The empirical distribution of sequence sizes is close to a straight line when taking logs on the y axis (Fig. S2), suggesting that sequence sizes follow a geometric distribution—i.e., the probability that a sequence has size l is p(l) = π (1 − π)^l−1, where π is the probability of termination, the only parameter of the distribution. The maximum-likelihood estimator of π, i.e., 1/L, where L is the mean size of the sequences (71), gives π = 0.224. With this parameter, a geometric distribution provides a high-quality visual fit to the actual distribution of sequence sizes (Fig. S2). The consistency of sequence sizes with a geometric distribution suggests that the process of generating sequences is “memoryless” (72): during the process of sequence generation, the current length does not change the probability of ending the sequence.

Additional Analyses of the Relationships Between the Duration of Particular Call Types and Sequence Size

In the main text, call position is not included as a fixed effect in the analyses on call duration and sequence size for particular call types because inhale moans, exhale moans, wobbles, and yawns are rarely produced repeatedly in a single vocal sequence. This means that our power of using repeated measures (i.e., sequence recording as a random effect) is greatly reduced, limiting the ability of the LMMs to effectively compare calls at different positions within sequences of a given size. Also, this means that call position and sequence size are not always independent. Certain call types like yawns, inhaled moans, and wobbles are frequently found near the end of vocal sequences. In these instances, “sequence size” and “call position” can be similar or the same for several of the data points. Consequently, results from the following LMMs (below)—in which call position is included as a fixed effect, and that we report for completeness' sake—should be interpreted with caution.

As a supplement to our main analyses, we ran six LMMs (one for each call type) with call duration as a dependent variable, sequence size and call position as fixed effects, and male identity and sequence recording as random effects. When including call position as a fixed effect, the LMMs show that call duration is negatively associated with sequence size only in inhaled grunts and inhaled moans (Table S1). The LMMs also show a negative association between call duration and call position for exhale grunts and exhale moans, and a positive association between call duration and call position for inhale grunts and inhale moans.