Dodecagonal quasicrystalline order in a diblock copolymer melt

Significance

Spherical objects ranging in size from metal atoms to micron-scale colloidal particles to billiard balls tend to form regular close packed arrays with three-dimensional translational symmetry. We show that nearly spherical nanoscale micelles, formed by self-assembled diblock copolymers, spontaneously evolve into a two-dimensional dodecagonal quasicrystal following rapid cooling from the disordered liquid state. This aperiodic arrangement, characterized by rotational symmetry but not translational symmetry, transforms over time into a three-dimensional Frank–Kasper σ phase with local tetrahedral particle packing. This discovery suggests that certain forms of quasicrystalline order are nonequilibrium states generated by kinetically facilitated particle clustering in the supercooled liquid. Redistribution of polymer molecules between micelles through molecular diffusion appears to play a central role in these processes.

Abstract

We report the discovery of a dodecagonal quasicrystalline state (DDQC) in a sphere (micelle) forming poly(isoprene-b-lactide) (IL) diblock copolymer melt, investigated as a function of time following rapid cooling from above the order–disorder transition temperature (T_ODT = 66 °C) using small-angle X-ray scattering (SAXS) measurements. Between T_ODT and the order–order transition temperature T_OOT = 42 °C, an equilibrium body-centered cubic (BCC) structure forms, whereas below T_OOT the Frank–Kasper σ phase is the stable morphology. At T < 40 °C the supercooled disordered state evolves into a metastable DDQC that transforms with time to the σ phase. The times required to form the DDQC and σ phases are strongly temperature dependent, requiring several hours and about 2 d at 35 °C and more than 10 and 200 d at 25 °C, respectively. Remarkably, the DDQC forms only from the supercooled disordered state, whereas the σ phase grows directly when the BCC phase is cooled below T_OOT and vice versa upon heating. A transition in the rapidly supercooled disordered material, from an ergodic liquid-like arrangement of particles to a nonergodic soft glassy-like solid, occurs below ∼40 °C, coincident with the temperature associated with the formation of the DDQC. We speculate that this stiffening reflects the development of particle clusters with local tetrahedral or icosahedral symmetry that seed growth of the temporally transient DDQC state. This work highlights extraordinary opportunities to uncover the origins and stability of aperiodic order in condensed matter using model block polymers.

The discovery of aperiodic order, today referred to as quasicrystalline order, in rapidly cooled Al–Mn alloys by Shechtman and coworkers in 1984 heralded a paradigm shift in the understanding of what constitutes long-range order in matter (1, 2). More recently, quasicrystalline order has been found in an expanding variety of soft materials including self-assembling wedge-shaped dendrimers, mixtures of ligand coated nanoparticles, concentrated solutions of surfactant and block polymer micelles, multicomponent polymer blends containing ABC-type miktoarm star polymers, and an ABA′C-type linear multiblock polymer (3–8). The underlying principles that govern the formation of quasicrystals in soft materials remain largely unresolved.

Block polymers are uniquely tunable self-assembling soft materials in which the nanoscale morphology, characteristic length scale, chemical and physical properties, and dynamics can be precisely controlled through the judicious choice of block repeat unit chemistries, block molecular weights, and molecular architecture (9, 10). Such exquisite control over structure, and the associated dynamics, makes block polymers ideal model materials for fundamental inquiries into the formation and stability of soft quasicrystals. In this article, we report the discovery of a long-lived metastable dodecagonal quasicrystalline phase (DDQC) in a (nominally) single-component poly(1,4-isoprene-b-DL-lactide) (IL) diblock copolymer melt (Fig. 1A), arguably the simplest material to exhibit quasicrystalline symmetry. This finding builds on our recent work detailing the formation of the Frank–Kasper σ phase, a large unit cell periodic approximant of the DDQC in a related IL diblock copolymer specimen (11–13).

Fig. 1.

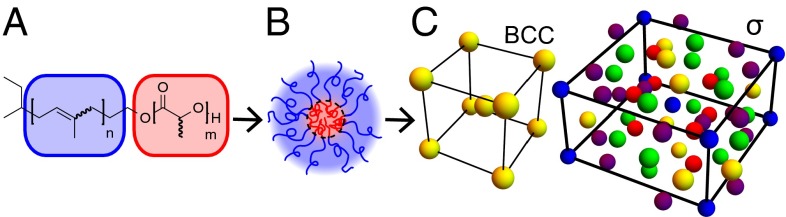
Self-assembly of asymmetric diblock copolymers. (A) Chemical structure of IL diblock copolymers. (B) Asymmetric diblock copolymers form nearly spherical point particles. (C) Below T_ODT, the point particles form various ordered structures including BCC and the Frank–Kasper σ phase. Colors in C indicate lattice sites with different local coordination environments.

Under conditions that favor block segregation, asymmetric AB-type diblock copolymers self-assemble into discrete, nearly spherical, micelle-like particles composed of hundreds of individual polymer chains, as illustrated in Fig. 1B. Upon cooling below the order–disorder transition temperature (T_ODT), the mesoscopic particles order into a body-centered cubic (BCC) crystal (Fig. 1C) through a first-order phase transition. It is important to note that the micelle-like particles do not emerge at the order–disorder transition temperature from a homogenous disordered phase as anticipated by mean-field theory (10, 14). As a consequence of relatively long-lived thermally driven composition fluctuations the disordered state just above T_ODT contains a dense array of soft but segregated micelles characterized by a distribution of shapes and sizes with a liquid-like arrangement in space (12). The ordered BCC phase, first predicted by Leibler, is widely accepted as the equilibrium morphology for asymmetric diblock copolymer melts just below the ODT (14). Recently, we demonstrated the formation of a Frank–Kasper σ phase when a particular IL diblock copolymer specimen (designated IL-15) was cooled more than about 20 °C below T_ODT = 48 °C (11–13). The σ phase structure has a large tetragonal unit cell that contains 30 particles partitioned into five crystallographically distinct symmetry related lattice sites (Wyckoff positions) with different local coordination environments and volumes (Wigner–Seitz cells) indicated by the different colored particles in Fig. 1C (11, 13). This contrasts with the single local coordination environment of the particles, one per lattice site, associated with the BCC structure. The σ phase is a periodic approximant to an aperiodic dodecagonal quasicrystal structure; reports of the DDQC in soft materials often coincide with the observation of the σ phase (3–5, 8). We have proposed that the spontaneous symmetry breaking associated with the formation of the low-symmetry σ phase in diblock copolymers, which requires a redistribution of mass between particles to accommodate the five particle sizes, is driven by a tendency to maximize the average sphericity of the particles with decreasing temperature (13).

In this article, we report the evolution of nanoscale structure in another IL diblock copolymer specimen, designed to allow rapid quenches of the disordered melt to temperatures deeply below T_ODT while remaining well above the micelle core block glass transition temperature. Upon supercooling the disordered liquid below a threshold temperature denoted T_erg, ∼25 °C under T_ODT, we document the evolution of DDQC order, using synchrotron small-angle X-ray scattering (SAXS) measurements. This quasicrystalline phase persists as a long-lived metastable state that eventually transforms to the equilibrium Frank–Kasper σ phase, where the lifetime of the DDQC phase is strongly temperature dependent. Dynamic mechanical spectroscopy (DMS) experiments conducted on the supercooled liquid reveal a spontaneous stiffening of the material when rapidly cooled below T_erg, without evidence (SAXS) of long-range order, suggesting the development of an unresolved state of local order that seeds the growth of the DDQC phase.

Results and Analysis

The experiments discussed in this article document the temperature-dependent structure and dynamics of a poly(1,4-isoprene-b-DL-lactide) diblock copolymer designated IL-5.1 synthesized by an established combination of anionic polymerization and ring-opening polymerization (12, 15). IL-5.1 has a number-average molecular weight M_n = 4,600 g/mol (dispersity M_w/M_n = 1.06) divided between the polyisoprene (PI; 3,540 g/mol) and polylactide (PLA; 1,070 g/mol) blocks, corresponding to a composition of 18% by volume PLA based on published densities (16, 17). This asymmetric block copolymer self-assembles into particles with a PLA core surrounded by a PI corona, as illustrated in Fig. 1B. The PLA blocks in the particle cores vitrify on cooling with a broad glass transition temperature T_g,PLA centered at 0 °C (spanning ∼20 °C to –20 °C as measured by DSC; SI Appendix, Fig. S1), setting the lower bound of experimental temperatures at which equilibrium can be approached. The corona PI blocks vitrify at a much lower temperature (T_g,PI = –63 °C). IL-5.1 was designed to have a slightly higher M_n but a similar asymmetric composition to IL-15 (M_n = 3,890 g/mol; 22% PLA), shown previously to form the σ phase, to elevate the T_ODT (T_ODT = 66 °C as measured by DMS; SI Appendix, Fig. S2) to enable deeper quenches while remaining well above T_g,PLA (11).

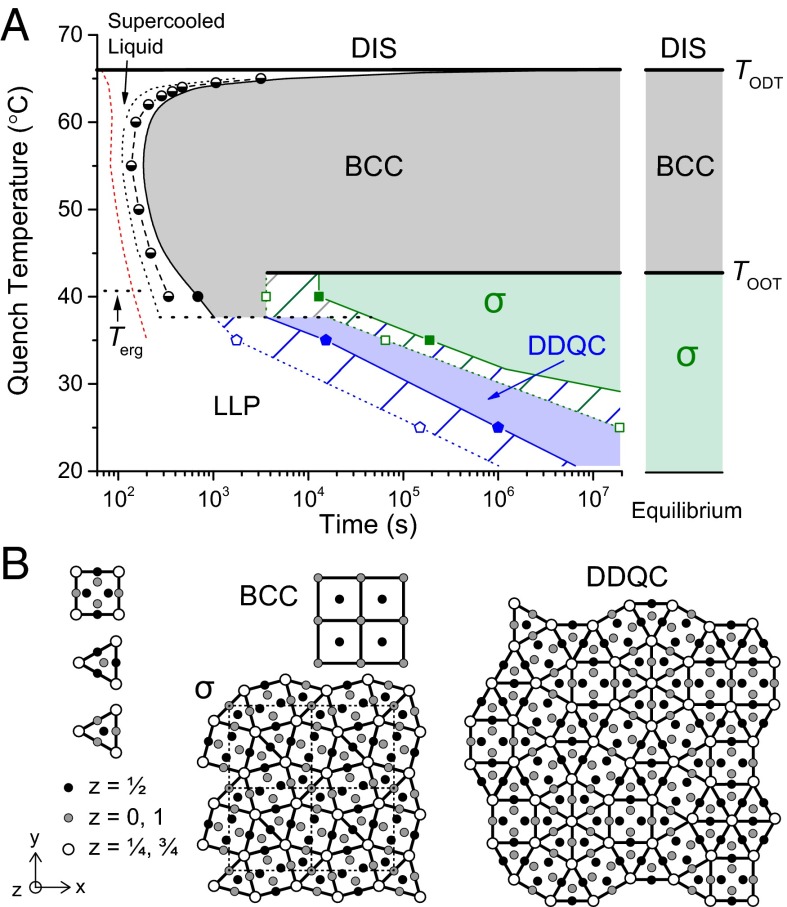
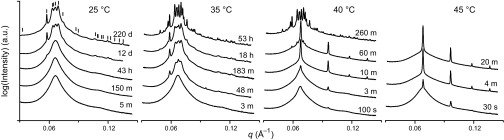
IL-5.1 exhibits three ordered morphologies and two distinct disordered states depending on temperature and time, as measured by DMS and SAXS experiments and summarized in the time–temperature–transformation (TTT) diagram in Fig. 2 (see SI Appendix for experimental details and DMS data). An equilibrium disordered state (DIS) exists at temperatures above T_ODT = 66 °C. Rapidly cooling the equilibrium disordered melt (T > T_ODT) to temperatures down to about 40 °C results in a metastable supercooled liquid that persists until the nucleation and growth of an ordered phase. Fig. 3 shows SAXS patterns recorded as a function of time following a quench to 45 °C, demonstrating the nucleation and growth of a BCC phase from the supercooled disordered state in a matter of minutes, which remains stable upon extended annealing; the corresponding SAXS pattern contains sharp Bragg reflections at relative peak positions of (q/q*)² = 1, 2, 3, 4, 5, 6, 7, …, where q* represents the leading order diffraction peak and q = 4πλ⁻¹sin(θ/2) is the magnitude of the scattering wave vector.

Fig. 2.

Time-dependent phase behavior of IL-5.1. (A) Time–temperature–transformation diagram. In the BCC-forming regions (shaded gray), dotted lines, dashed lines and half-filled circles, and solid (black) lines indicate achievement of 5%, 50%, and 95% of the maximum measured value of G′, respectively. In the complex phase region, open symbols and filled symbols indicate the first evidence of nucleation and completion of ordering in SAXS, respectively, with lines connecting these symbols being guides to the eye. The red dashed line indicates the approximate times during DMS experiments after initiation of a quench when the sample equilibrated at the target temperature. (B) The BCC, σ, and DDQC phases viewed as decorated tilings of the x–y plane. The common square and triangle tiles used to construct the periodic and aperiodic tilings of the σ and DDQC phases, respectively, are also shown.

Fig. 3.

IL-5.1 ordering kinetics measured by synchrotron SAXS. Selected time-resolved SAXS data collected at the times indicated after rapidly quenching from the disordered state above T_ODT to 25 °C, 35 °C, 40 °C, and 45 °C. See SI Appendix, Figs. S4 and S5, for SAXS patterns at additional time points at 25 °C and 35 °C, respectively. Curves have been shifted vertically for clarity. Tick marks above the 220 d scattering pattern recorded at 25 °C identify the DDQC indexing shown in SI Appendix, Fig. S9.

Upon cooling from T > T_ODT to 40 °C, a BCC phase nucleates and grows within about 10 min but is subsequently consumed by nucleation and growth of the Frank–Kasper σ phase over a period of several hours, also shown in Fig. 3; a significant number (>45) of closely spaced Bragg peaks are quantitatively accounted for based on P4₂/mnm space group symmetry (see SI Appendix, Fig. S3, and ref. 13 for detailed indexing). The ordering of IL-5.1 at 40 °C (T_ODT – T = 26 °C) mirrors the behavior of specimen IL-15 when quenched to 25 °C (T_ODT = 48 °C; T_ODT – T = 23 °C), a nearly equivalent quench depth below T_ODT. However, IL-5.1 exhibits about 5× faster ordering kinetics at comparable undercooling owing to the higher absolute ordering temperature (11, 13).

Deeper quenches from T > T_ODT, to 35 °C and 25 °C, lead to qualitatively different phase transitions as summarized in Fig. 2. At both temperatures a SAXS pattern containing four strong peaks and numerous weaker reflections at higher q evolves directly from the broad peak associated with the supercooled disordered phase (Fig. 3). Complete development of this diffraction pattern takes about 3 h at 35 °C and 10 d at 25 °C. We believe this scattering pattern reflects formation of the DDQC phase (see below), an aperiodic structure that is closely related to the Frank–Kasper σ phase as illustrated in Fig. 2B. At 35 °C the DDQC persists as a metastable state for several hours before nucleation and growth of the Frank–Kasper σ phase over the course of several days. Following its growth at room temperature (nominally taken as 25 °C), the DDQC state persists for many months.

Evidence of σ phase nucleation from the DDQC state at 25 °C can be found in a 2D SAXS pattern collected after 220 d of annealing at room temperature following a quench from T > T_ODT. Discrete diffraction spots are seen at q values consistent with the σ phase structure slightly offset from the intense Debye–Scherrer rings due to the DDQC structure (SI Appendix, Fig. S6). This reinforces the notion that the DDQC phase is metastable with respect to the σ phase, which appears to be the equilibrium ordered phase at temperatures below the order–order transition temperature 40 °C < T_OOT < 45 °C. Remarkably, the DDQC phase seems to evolve only from the supercooled disordered state. Cooling to temperatures below T_OOT from the BCC phase (grown at T_OOT < T < T_ODT) leads to the direct formation of the Frank–Kasper σ phase, i.e., without passing through the DDQC phase (SI Appendix, Figs. S7 and S8).

The x–y plane obtained by projection of the tetragonal structure of the Frank–Kasper σ phase along the z axis ([001] direction of the unit cell) can be represented as a periodic tiling of squares and equilateral triangles decorated with particles that occur at specific periodic positions along z, as illustrated in Fig. 2B. The detailed structure of the DDQC is believed to be closely related to the Frank–Kasper σ phase and represented by an aperiodic tiling of the x–y plane with the same decorated square and triangle tiles arranged in different motifs. The resulting axial 2D dodecagonal (i.e., 12-fold rotationally symmetric) quasicrystal is aperiodic in the x–y plane but periodic in the z direction. The aperiodic tiling in Fig. 2B was generated using the random Stampfli tiling approach (18).

Our identification of the DDQC phase in IL-5.1 relies on analysis of the 1D SAXS powder patterns shown in Fig. 3 (see SI Appendix, Fig. S9, for a representative high-resolution DDQC SAXS pattern). Because the specimen is polycrystalline, with grain sizes much smaller than the size of the X-ray beam, it is not possible to directly observe the 12-fold rotational symmetry associated with the x–y tiling shown in Fig. 2B. The relative peak positions and intensities in the DDQC powder SAXS patterns in Fig. 3 (and SI Appendix, Fig. S9) are nearly identical to the powder pattern of the DDQC phase reported in wedge-shaped dendrimers (SI Appendix, Fig. S10), and we have successfully identified the reflections in the experimental DDQC SAXS patterns based on the five-dimensional indexing scheme used to characterize single-domain 2D DDQC scattering patterns obtained from dendrimers and Mn-based quaternary alloys (see SI Appendix, Fig. S9, for detailed indexing of the IL-5.1 DDQC scattering pattern) (3, 19). Selected allowed DDQC reflections are indicated by tick marks above the 25 °C SAXS data in Fig. 3 and were chosen to lie in high-symmetry planes in the quasicrystal reciprocal lattice. In addition, the close proximity in parameter space of the proposed DDQC phase to the Frank–Kasper σ phase is consistent with the behavior of other soft quasicrystals, which generally are found to compete for stability with Frank–Kasper phases both experimentally and in simulations (3–8, 20, 21).

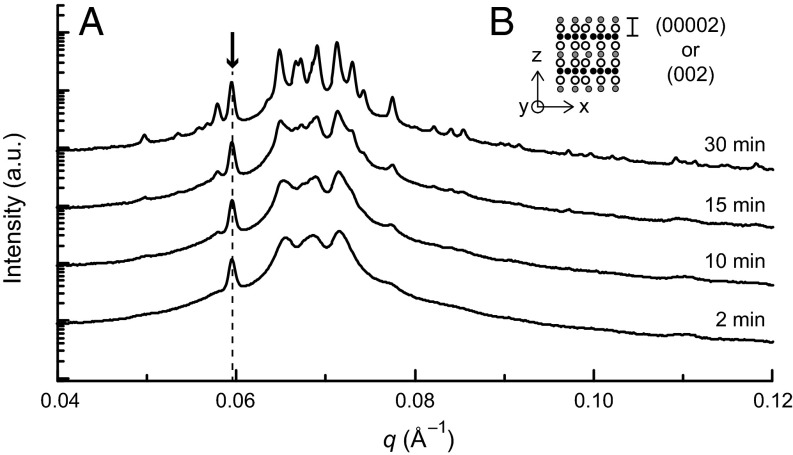
Additional insight into the stability of the DDQC phase and its relationship to the σ phase was obtained by heating the quasicrystal as shown in Fig. 4. A well-developed DDQC state was generated by annealing sample IL-5.1 for 49 d at room temperature following a quench from T > T_ODT. The sample was then heated, and SAXS patterns were collected as a function of time and temperature (see SI Appendix, Fig. S11, for complete heating experiment). The DDQC SAXS pattern persists virtually unchanged after short anneals (ca. 10 min) at 40 °C and 45 °C. At 50 °C, the DDQC eventually transforms into the equilibrium BCC phase (SI Appendix, Fig. S12). However, this transition is mediated by formation of the Frank–Kasper σ phase before transformation to the BCC state as seen in Fig. 4. Increasing the temperature accelerates the DDQC-to-σ phase transition. What takes days at 35 °C and months at 25 °C occurs in a matter of minutes at 50 °C, and nucleation and growth of the σ phase is complete in ∼30 min. The (00002) peak in the DDQC pattern corresponding to the interplanar spacing in the periodic direction of the axial quasicrystal (projection along the z direction in the structures illustrated in Figs. 2 and 4) becomes the (002) peak in the σ phase scattering pattern (which corresponds to the z direction in the analogous illustration of the σ phase in Fig. 2). Clearly, the DDQC-to-σ order–order transition occurs via a rearrangement of the particles in the x–y plane without changing the periodicity in the z direction.

Fig. 4.

Heating the DDQC. (A) Synchrotron SAXS data collected at 50 °C after annealing for the indicated times. Before heating to 50 °C, the sample was annealed at room temperature for 49 d following a quench from the disordered state to grow the DDQC. The arrow indicates the (00002) or (002) reflections in the DDQC and σ phase SAXS patterns, respectively. (B) Illustration of the equivalence of the (00002) and (002) planes in the DDQC and σ phase structures. Curves have been shifted vertically for clarity.

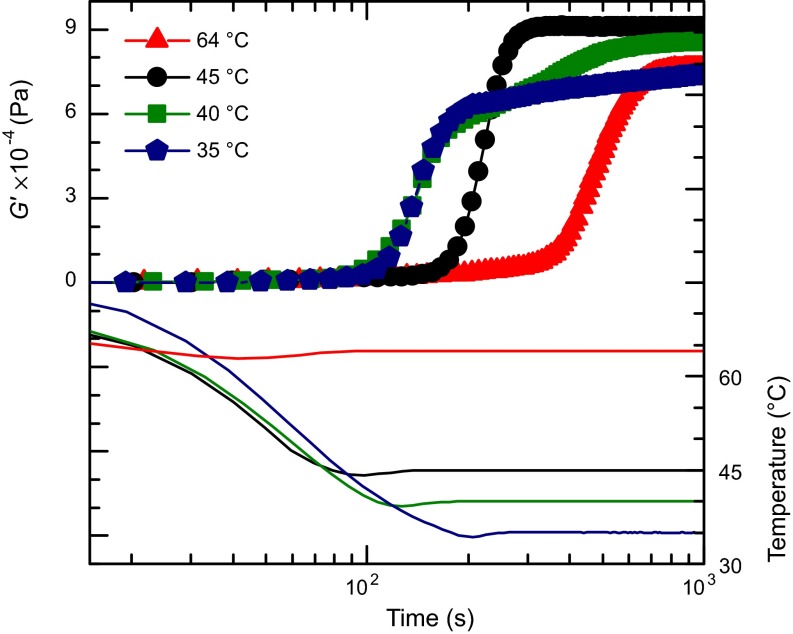
Near T_ODT, the supercooled disordered state in IL-5.1 behaves as a viscoelastic liquid with a longest relaxation time (τ) corresponding to structural relaxations on the scale of the self-assembled particles (i.e., not on the scale of individual polymer chains), as recently documented in the related polymer IL-15 (13). In this regime, the rate of ordering following rapid cooling can be monitored by recording the linear dynamic elastic modulus (G′) as a function of time at a frequency ω << τ⁻¹; ordering transforms the viscous liquid into a soft viscoelastic solid, and the fractional conversion is roughly proportional to the value of G′(t)/G′(t → ∞) (13). Representative measurements are shown in Fig. 5 for ordering at 64 °C and 45 °C (see SI Appendix, Fig. S13, for long time behavior and additional ordering temperatures). Combining such rheological measurements with time-dependent SAXS experiments allows us to map the phase behavior of IL-5.1 as a function of time following rapid temperature quenches on a TTT diagram as shown in Fig. 2A.

Fig. 5.

Linear shear storage modulus (symbols) and temperature (solid lines) during DMS measurements of the ordering process.

At approximately T_OOT, the apparent relaxation time τ of the supercooled disordered state appears to diverge (see SI Appendix, Fig. S14, for frequency-dependent viscoelastic properties), and the sample stiffens into a viscoelastic solid nearly instantaneously upon cooling below about 40 °C, as revealed by the G′ data obtained at 40 °C and 35 °C (Fig. 5). This spontaneous stiffening occurs without the development of order, as demonstrated by comparing the results in Fig. 5 with the SAXS experiments of Fig. 3. [Here we note that the time required to quench the sample on the mechanical spectrometer (∼100 s; Fig. 5) is considerably longer than what is achieved in the SAXS experiments of <5 s.] At 40 °C, the material stiffens essentially as soon as it reaches the target temperature (100–200 s), and then the modulus increases in a second step coincident with nucleation and growth of the BCC phase (≅600 s). When cooled to 35 °C, stiffening occurs just as at 40 °C. However, a second rise in G′ does not begin for about 30 min coincident with the development of DDQC order as revealed in SAXS experiments (SI Appendix). These results point to a dynamical transition in the supercooled disordered melt from a liquid (T > 40 °C) to a disordered but solid-like state referred to as “liquid-like packing” (LLP) for T < 40 °C. We identify the temperature T_erg ∼ 40 °C with the transition from ergodic liquid-like behavior to a nonergodic disordered solid state (see below). Formation of the DDQC appears to be predicated on first establishing the LLP state.

Discussion

The discovery of a DDQC phase in the (nominally) single-component IL-5.1 diblock copolymer melt marks only the third experimental single-component system to exhibit quasicrystalline order, joining supramolecular wedge-shaped dendrimers (3, 22, 23) and linear poly(styrene-b-isoprene-b-styrene-b-ethylene oxide) (SISO) tetrablock terpolymers (8); quasicrystals have only been reported in multicomponent hard materials such as binary metal alloys (24). Diblock copolymers are perhaps the simplest of these systems and are the most amenable to statistical mechanical theory. We acknowledge here that block polymers are not rigorously single-component systems, being composed of a collection of molecules that have a narrow distribution of chain lengths and compositions (i.e., dispersity) arising from the nature of the synthetic process. Nevertheless, we believe these small departures from ideality do not contribute significantly to the phenomena described herein, a supposition that can be assessed using statistical mechanical theory (25, 26).

As a result of the separation in length scales between the individual monomer units and the polymer chain as a whole, flexible AB diblock copolymers exhibit largely universal phase behavior dependent on a limited number of parameters that are easily tuned during polymer synthesis and processing: primarily composition (f) and segregation strength χN, (where χ is the segment–segment interaction parameter) and to a lesser extent the degree of polymerization (N), dispersity (Đ), and the ratio b_A/b_B of block statistical segment lengths [b = R_g/(N/6)^1/2, where R_g is the unperturbed polymer coil radius of gyration] (10, 25). Aggregation of nearly spherical micelle-like particles, each containing ∼200 polymer molecules, produces the ordered structures such as the BCC and σ phases (13). Formation of the DDQC phase in diblock copolymers cannot be rationalized based on the detailed shape or chemistry of the individual molecules, complicated interactions between preformed particles, or other such arguments. We believe the development of aperiodic order in diblock copolymers and other soft materials must stem from more fundamental and universal factors. Hence, understanding DDQC formation in diblock copolymers offers an opportunity to gain insight into the workings of nature beyond these macromolecular systems.

Recent self-consistent mean-field theory (SCFT) calculations provide supporting evidence for the universality of low-symmetry Frank–Kasper phases in block polymer self-assembly. Xie et al. predict the occurrence of two Frank–Kasper phases, σ and A15, separated from the disordered state by the BCC phase with increasing segregation strength (i.e., at higher χN) in asymmetric AB diblock copolymers and AB_m miktoarm block copolymers (26). The A15 phase ($Pm\overline{3}n$) is an additional periodic quasicrystal approximant Frank–Kasper phase formed in a variety of self-assembling soft materials (22, 27–29). The SCFT calculations implicate asymmetry in the block statistical segment lengths as a key parameter, predicting that a minimal degree of asymmetry is required (b_A > 1.5b_B for AB diblocks) for a stable σ phase window to occur at f_A < 1/2. This prediction has yet to be tested by systematic experiments but is in qualitative agreement with the modest statistical segment length asymmetry of the IL system (b_L/b_I ∼ 1.2) (12).

Recently, we argued that a tendency to maximize the average sphericity of the polyhedral particles that constitute the soft ordered crystals, imposed by the lattice symmetry under the constraint of uniform density, favors the formation of the σ phase over BCC at low temperatures in block polymer melts and other soft materials (13). Sphericity can be defined by the isoperimetric quotient, IQ = 36πV²/S³, where V and S are the particle volume and surface area, respectively; for a sphere, IQ = 1. The experimental Frank–Kasper σ phase structure formed by the IL-15 specimen reported earlier results in a calculated sphericity value (IQ)_σ = 0.762 (number- and volume-averaged), which is greater than the sphericity of the ideal BCC structure (IQ)_BCC = 0.7534 [but nearly equivalent to (IQ)_A15 = 0.7618] (13). Because the real space structure of the DDQC phase is not known in detail [the structure illustrated in Fig. 2B represents an idealized candidate structure (3)], the sphericity cannot be calculated a priori. The SAXS patterns suggest the DDQC phase in IL-5.1 has a high population of structural defects (e.g., grain boundaries, point defects, and phason strain), as evidenced by the significantly broader diffraction peak widths relative to those associated with the BCC and σ. Nevertheless, based on the underlying similarities in local tetrahedral particle packing, implicit in the common triangular and square tiling elements that govern the σ and DDQC phases (Fig. 2B), we expect similar overall sphericities (see below).

Formation of the DDQC structure as a metastable intermediate state before the formation of the equilibrium Frank–Kasper σ phase appears quite similar to the simulated phase behavior of collections of uniformly sized spherical particles governed by the Dzugotov potential, a modified Lennard–Jones interparticle potential that contains a repulsive feature that suppresses the formation of close-packed (BCC, HCP, and FCC) crystal structures (20, 30, 31). There are important differences between this computational model and the experimental polymer system, most significantly the consequences of mass exchange during the formation of the σ phase, which leads to five discrete particle shapes and volumes in the tetrahedral unit cell, features that are not represented in the hard sphere simulations. Nevertheless, the simulations demonstrate the metastable nature of the DDQC and identify icosahedral clusters as the seeds that nucleate the quasicrystals that grow to fill space before transforming to the σ phase, which is dominated by lattice sites configured as distorted icosahedral motifs (20).

In IL-5.1, the DDQC phase forms only from the stiff supercooled disordered state generated by cooling below T_erg at a sufficiently high rate to avoid intersecting the nose of the TTT diagram, thus bypassing nucleation of the BCC phase (Fig. 2). This disordered state exists well above T_g of either block (see DSC trace in SI Appendix, Fig. S1), indicating that the behavior of this soft solid is not driven by conventional particle core or matrix vitrification. We believe the transition in properties of the supercooled material from liquid-like to solid-like at T_erg is connected to the extinction of facile relaxation modes due to the effects of increasing segregation strength, resulting in a jammed or glass-like state.

Upon cooling, several changes occur in the fluctuating disordered state in asymmetric diblock copolymers. Theory (32, 33) and experiments (34, 35) show that the number density of micelle-like point particles increases with decreasing temperature, reducing the free unimer concentration and sharpening the local composition profile at the core–corona interface. The particle aggregation number (i.e., the number of diblock chains per particle) and particle volume increase slightly with decreasing temperature, as also occurs in the ordered BCC phase (36). At a certain temperature, the number density must saturate as the particles become tightly packed and the unimer concentration approaches zero. At this point, further cooling actually drives a reduction in particle number density due to the increasing core–corona interfacial tension, which favors larger spherical micelles (i.e., greater aggregation number). However, due to a high (and steeply temperature-dependent) energy penalty associated with transporting a core block through the corona region (∼exp[αχN]), single-chain diffusion across domains drops precipitously at reduced temperatures (36–38). This freezes collective particle-level reorganization necessary to accommodate the thermodynamic drive toward fewer, larger particles or the redistribution of particle volumes necessary to form the σ phase. We believe this leads to a type of jamming, analogous to what occurs in granular materials, colloidal suspensions, foams, and emulsions (39, 40), which exhibit essentially solid-like mechanical properties (i.e., frequency-independent G′) while maintaining a disordered morphology. Hence, the LLP state may be thought of as a kinetically trapped soft glass-like solid.

At temperatures below T_erg, the ergodicity temperature, the material ceases to behave like a supercooled liquid, instead taking on the characteristics of a glass (i.e., a nonequilibrium and nonergodic disordered solid) (41, 42). This falling out of local equilibrium is realized experimentally in the solid-like mechanical response evident in Fig. 5 and through the development of thermorheological complexity in the DMS data collected at 40 °C and 35 °C (SI Appendix, Fig. S14). We associate T_erg in the particle-forming IL block copolymers with the glass transition temperature, T_g, in molecular glasses. The notion that a microphase separated structure in a block polymer melt can exhibit a dynamic transition analogous to a glass transition has been anticipated by Zhang and Wang (43). Using an extension of the Fredrickson–Helfand theory (44), they identified the appearance of glass-like behavior and the emergence of broken ergodicity at high segregation strength in asymmetric diblock copolymers, coincident with the thermodynamic stability limit of the fluctuating disordered state. Whether this corresponds to T_erg remains an open question.

Perhaps the most intriguing issue raised by these results is the nature of the local structure of the LLP state. Given sufficient time, this nonequilibrium state evolves into the Frank–Kasper σ phase. This suggests that the seeds for tetrahedral packing, the local micelle coordination underpinning the σ phase, are sown soon after the liquid is cooled below T_erg. We speculate that the LLP is characterized by a disorganized array of micelle clusters with some form of short-range order. The bump in intensity evident in the scattering patterns taken immediately after quenching to 25 °C and 35 °C at ∼1.8q* (Fig. 3) evidences such particle correlations. Unfortunately, there is insufficient detail in the overall SAXS pattern to extract quantitative information regarding the detailed radial distribution function. Perhaps these reflect icosahedral clusters as suggested by molecular simulations (20, 45) and as implicated in many investigations of glass-forming systems (46, 47).

This speculation is consistent with our sphericity arguments regarding the occurrence of the σ phase (13). The central particle in a 13-particle cluster with icosahedral symmetry is forced to take a dodecahedral shape, where (IQ)_dodecahedron = 0.7547, i.e., slightly greater than (IQ)_BCC = 0.7534 but considerably larger than (IQ)_FCC = (IQ)_HCP = 0.7405. Of course, this ratio only accounts for a fraction of the collection of polyhedral particles characterized by a distribution of particle volumes that are trapped when the disordered state is rapidly quenched from T > T_ODT to T < T_erg. Clearly, this disperse set of particles will not satisfy the packing requirements of any periodic crystal structure built from a specific set of polyhedral volumes and shapes, e.g., one and five types for the BCC and σ phases, respectively. Nevertheless, the soft deformable micelles can rearrange their shapes and nearest neighbor positions without changing volume to optimize packing in the LLP state. We hypothesize that the effects of limited chain diffusion, restricted at relatively short times to short-range interparticle distances by strong segregation at reduced temperatures, facilitate local optimization of sphericity, which drives tetrahedral packing. This line of reasoning explains why the DDQC appears as a transient intermediate that eventually transforms to the σ phase.

The first new feature in the SAXS patterns that emerges as the material is annealed at T < T_erg (e.g., after 43 h at 25 °C; Fig. 3) is the (00002) reflection of the DDQC, which suggests that the clusters initially consolidate into layers with short-range order. Subsequently, the triplet of broader peaks appears at higher q, signaling development of two-dimensional aperiodic tiling as illustrated in Fig. 2B. We are designing additional diblock copolymers that may afford access to real space imaging using transmission electron microscopy to address these questions.

This work demonstrates the opportunities presented by model single-component diblock copolymers in the quest to unravel the origins of aperiodic order in condensed matter.

Materials and Methods

For details, see SI Appendix. IL-5.1 was synthesized by triethylaluminum-catalyzed ring opening polymerization of d,l-lactide initiated by a ω-hydroxyl poly(1,4-isoprene) prepared by anionic polymerization. Molecular weight, composition, and dispersity of IL-5.1 were determined by ¹H NMR and size exclusion chromatography. SAXS experiments were conducted on the DND-CAT 5-ID-D beamline at the Advanced Photon Source with samples prepared in 1.5-mm nominal diameter quartz capillary tubes. With the exception of extended annealing of samples at room temperature (nominally taken as 25 °C), temperature was controlled to within approximately ±1 °C. Rapid temperature quenches (<5 s) were achieved by quickly moving the capillary sample between temperature-controlled baths. DMS experiments were conducted in the linear viscoelastic regime using a parallel plate geometry with a TA Instruments ARES-G2 rheometer equipped with a forced convection oven.