A conceptual model of morphogenesis and regeneration

Abstract

This paper is devoted to computer modelling of the development and regeneration of multicellular biological structures. Some species (e.g., planaria and salamanders) are able to regenerate parts of their body after amputation damage, but the global rules governing cooperative cell behaviour during morphogenesis are not known. Here, we consider a simplified model organism, which consists of tissues formed around special cells that can be interpreted as stem cells. We assume that stem cells communicate with each other by a set of signals, and that the values of these signals depend on the distance between cells. Thus the signal distribution characterizes location of stem cells. If the signal distribution is changed, then the difference between the initial and the current signal distribution affects the behaviour of stem cells – e.g. as a result of an amputation of a part of tissue the signal distribution changes which stimulates stem cells to migrate to new locations, appropriate for regeneration of the proper pattern. Moreover, as stem cells divide and form tissues around them, they control the form and the size of regenerating tissues. This two-level organization of the model organism, with global regulation of stem cells and local regulation of tissues, allows its reproducible development and regeneration.

1 Introduction

Many biological organisms can regenerate some of their tissues and organs. Some species, such as hydra or planarian, can regenerate the whole organism from its small parts (Birnbaum and Alvarado, 2008; Holstein et al., 2003; Lengfeld et al., 2009; Alvarado, 2012). Other organisms, among them mammals, have more limited regeneration potential that includes wound healing (Baddour et al., 2012; Sousounis et al., 2014) but also regeneration of complex structures such as antlers (Li, 2012), liver (Mao et al., 2014), and fingertips (Illingworth, 1974).

Physiological mechanisms of regeneration are very complex and in many cases they are not completely known. However, the biggest knowledge gap concerns the overall dynamics of a large-scale anatomy which allows it to be maintained, remodelled, or regenerated toward a specific shape. Our goal is to understand what algorithm is used by cell networks to decide which activity brings the morphology closer to the correct state, and to know when that state has been reached so that growth can stop (Levin, 2011, 2012; Lobo et al., 2014; Mustard and Levin, 2014). We can group these mechanisms in two classes that can be related to large pattern formation and to cell (or tissue) memory. By pattern formation we understand here the tissue organization due to the molecular process of cell-cell communication, processes of cell growth, division and motion and other processes which use the information available at current time. Contrary to that, cell memory implies the existence of the information about some former states of the tissue, which orchestrates cellular activity towards restoring a particular anatomical configuration and allows growth and remodelling to stop when a particular goal-state has been reached.

Let us illustrate these mechanisms on the example of wound healing, in which some cytokines are produced at the injury site, they diffuse in the tissue and attract some special cells (e.g., fibroblasts) which divide and regenerate the tissue. Morphogenetic gradients, organizing centres and activator-inhibitor interaction can be involved in pattern formation and tissue regeneration. If, for example, tissue formation is controlled by an organizing centre, we can expect that the same centre will provide its regeneration assuming that the centre itself is preserved.

Experiments on planarian regeneration allow us to assume that its tissues can keep some information about their former states. Due to alteration of normal electrical connectivity among its cells, a planarian with two heads can be obtained from a normal one-headed animal (Levin and Stevenson, 2012; Levin, 2014). If two heads are amputated, then both of them will regenerate in subsequent rounds of regeneration (Levin, 2014). Hence, regenerations of one or two heads are possible. The choice between them is not determined at the genetic level because the genomic sequence is the same, and because any “reprogrammed” (epigenetically) tissues are discarded at each cut. Therefore the information about the number of heads is kept in the remaining tissue. Moreover, this memory is preserved in any part of the tissue since the amputated part can vary. There are other examples of regeneration that suggest the existence of tissue memory (Kragl et al., 2009; Levin and Stevenson, 2012; Levin, 2014).

A model of tissue regeneration based on cell memory is suggested in our previous work (Bessonov et al., 2015), where we consider a tissue as an ensemble of points on the plane, each point corresponding to a single cell. Each cell produces a signal that spreads in space and decays as a function of distance from the cell. At the same time, each cell receives the signals produced by all other cells, and consequently the total signal received by a cell depends on its location with respect to the other cells. Hence, the distribution of the total signal depends on the geometry of cell structure. We suppose that each cell keeps the value of the total signal that it receives from the other cells (memory). If a part of the cell structure is amputated, the signal distribution changes, and the difference between the old and the new signals stimulates cell proliferation. Under some additional conditions on the location of proliferation cells, the initial cell structure will be regenerated. This mechanism works for a local tissue regeneration with the characteristic size determined by the rate of signal decay in space.

In the current work we continue to model regeneration of cell structures. We suggest a model which allows a more distant regeneration. It contains two submodels – one global and one local. The main assumptions of the first submodel are similar to those in the previous work (Bessonov et al., 2015): cells exchange signals, keep the information about the values of these signals and react when these values are changed. In comparison with the previous work, we do not amputate a part of the cell structure but instead alter the positions of cells. The difference between the initial signal distribution and the new one after cell displacement initiates cell motion and returns them to the initial positions.

One of the important characteristics of multicellular regeneration is the minimal information necessary to restore the initial structure after its modification. In (Bessonov et al., 2015), all cells produce and receive the same signal. Hence, each cell is supposed to keep only one real number: the value of the total initial signal. It appears that this information is sufficient for the regeneration of cell structure when a part of it is amputated. The difference between the old and the new signals stimulate cell proliferation, and we can exactly restore the initial cell structure. In the current work we consider a more complex biological structure consisting of several different tissues, and we change its geometry. In this case, if all cells produce and receive the same signal, in general they will not return to their initial configuration. In order to characterise such structures, a more detailed pairwise cell communication is required, where each cell produces its own signal and distinguishes the signals from other cells. However, we cannot describe all individual cells of each tissue in this manner because the required information would be too large. Hence, we consider that only the cells of the first (global) submodel communicate by different signals. Those cells can be some special cells or groups of cells of the corresponding tissue (e.g. stem cells, instructor cells, or organizers (Bouwmeester, 2001; Kish et al., 2011; Rubin, 1985; Vandenberg and Levin, 2010)). Then the number of such cells corresponds to the number of tissues or organs and it is much more limited than the number of cells in the whole structure. In this case we need to complete the first (global) submodel by the second (local) submodel, which describes tissue growth around the cells of the first submodel. While a more complete and biologically realistic models can be considered, here we choose a simple and schematic mechanism of circular tissue growth in order to illustrate the principle.

Therefore, the global submodel provides configuration of tissue centres, while the local submodel creates the tissues around the centres. If some parts of the tissues are amputated but their centres are preserved, then the tissues will be regenerated. If some centres are amputated, then they should be restored by some other mechanisms which we do not consider here. The same model is able to describe morphogenesis, assuming the cells of the global submodel emerge in the embryo. In this case the tissue centres move to their equilibrium positions and generate their corresponding tissues.

2 Stem cell distribution in a plane

Consider n stem cells C₁, . . . , C_n distributed in a plane. Each stem cell C_i produces a signal s_i which decays in space as a function of distance from the stem cell, i.e. s_i(x, t) = f(d(x, x_i(t))), where f is the decay function, d is the distance function, x_i(t) is the position of the stem cell C_i at a moment of time t ≥ 0, and x is an arbitrary position in the plane. As an example of the decay function we can consider the exponential decay function f(d) = a^−d such that a > 1. Next, we can denote the intensity of the signal s_i received by cell C_j as s_ij(t), i.e.

$$s_{ij}\left(t\right)=s_i({\mathbf{x}}_j\left(t\right),t)=f\left(d({\mathbf{x}}_i\left(t\right),{\mathbf{x}}_j\left(t\right))\right).$$ (1)

By definition we have the symmetry s_ij(t) = s_ji(t). We will consider two cases - one in which signals s₁, . . . , s_n are all of the same type, and other in which each signal is of a different type.

Case 1

In the first case, all signals s₁, . . . , s_n are of the same type, hence we can express the total signal received by cell C_i at some moment t as

$$u_i\left(t\right)=\sum _{j\ne i}{s}_{ji}\left(t\right).$$ (2)

Supposing that there exists cell memory of the intensity of signal u_i, we can define the memorised intensity as

$$u_i^{\ast }=\sum _{j\ne i}{s}_{ji}\left(t_0\right),$$ (3)

for some moment t₀ > 0. The moment t₀ can be considered as the moment before some trauma which changes morphology of the tissue, like tissue removal. Alternatively, memorised signals $u_i^{\ast }$ can be considered as encoded in cells during the organism development, providing information about ideal cell distribution (target morphogenesis).

For each stem cell C_i we have defined the current total signal u_i(t) the cell receives and the memorised signal $u_i^{\ast }$. Depending on the difference between the memorised and the current signal, $u_i^{\ast }-u_i\left(t\right)$, each stem cell produces a response signal z which again decays in space as a function of distance

$$z_i\left(t\right)=(u_i^{\ast }-u_i\left(t\right))f\left(d(\mathbf{x},{\mathbf{x}}_i\left(t\right))\right).$$ (4)

The distribution of the total signal z in the plane is then given by

$$z(\mathbf{x},t)=\sum _i{z}_i\left(t\right).$$ (5)

In order to restore their ideal positions cells C₁, . . . , C_n move along the gradient of the signal z, as shown in Figure 1. Hence the equation of motion is given by

$$\frac{d{\mathbf{x}}_i}{dt}=\nabla z.$$ (6)

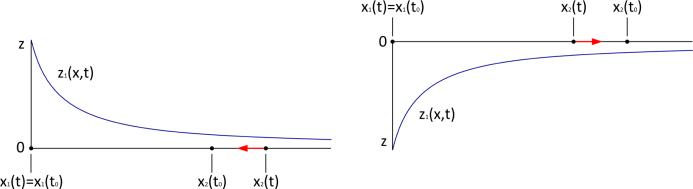
Fig. 1.

A scheme of cell motion along the gradient of signal z. Left: If at some moment t cell C₂ is farther from cell C₁ than it was initially (at the moment t₀), then $u_1^{\ast }-u_1\left(t\right)<0$, the signal z₁(t) will be decreasing and C₂ will move towards C₁. If at the moment t the cell C₂ is closer to the cell C₁ than it was initially, then $u_1^{\ast }-u_1\left(t\right)>0$, the signal z₁(t) will be increasing and C₂ will move away from C₁.

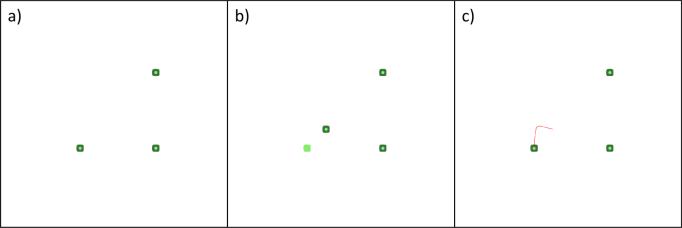
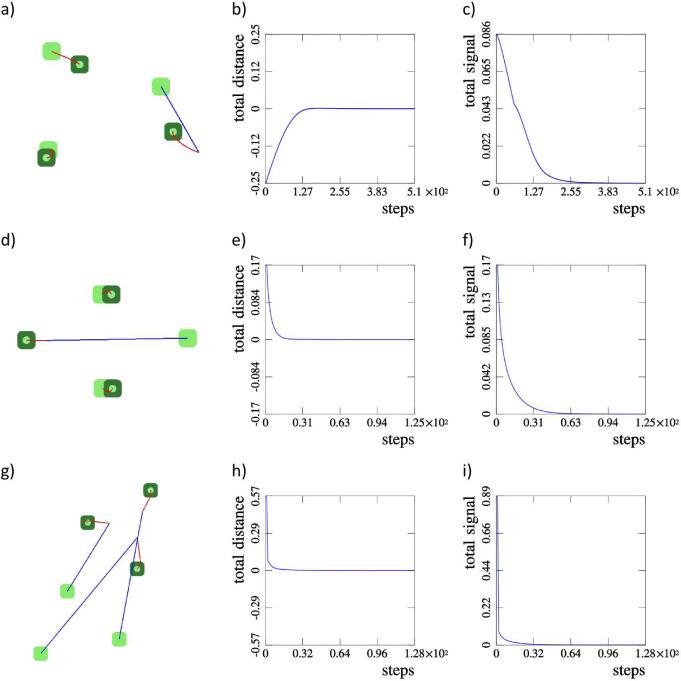
As an example let us take a configuration of three cells in a plane as shown in Figure 2. Furthermore, let us fix positions of two cells and vary the position of the third one. As we can see in Figures 2 and 3 the third cell will obtain its initial position characterised by the memorised signal intensity. This is true up to the symmetry of the configuration as shown in Figure 3 c). However, if the positions of other cells are not fixed, as well as for systems with more cells, the system cannot recover its initial configuration. This is shown in Figure 4, where the stationary distribution of a three cells system is along a straight line, although their initial configuration was triangular. We see that a single type of signal, n memorised signal intensities, and a single type of response signal do not offer sufficient information to the system in order for it to recover its initial configuration. Because of this, we consider the second case, where all signals are of different types.

Fig. 2.

Case 1. An example with three cells, two of which have fixed positions: a) the initial cell configuration, b) the leftmost cell is displaced (light green square shows the initial cell position), c) the displaced cell returns to its initial position (the red line shows the movement trace of the cell).

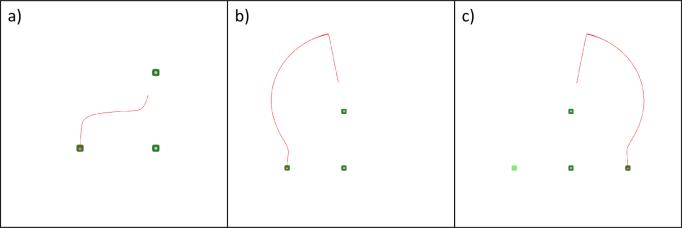
Fig. 3.

Case 1. Several examples with three cells two of which have fixed positions: a) and b) the system obtains its initial configuration, c) the system obtains a configuration symmetrical to the initial configuration.

Fig. 4.

Case 1. Example with three cells, none of which have fixed positions. Even after a small perturbation the system is unable to return to its initial configuration. For some three-cell systems cells can reach a stationary solution which differs from their initial configuration and in which they are positioned on the same line. In the remaining cases, as well as in configurations with more than three cells, system is unstable and cannot reach a stationary configuration.

Case 2

Let us consider the case where each of the signals s and each of the response signals z are of different types. Then each cell C_j will receive n – 1 different signals s from other cells. Thus for each pair {i, j} such that i ≠ j, we define the signal produced by cell C_i and received by cell C_j as

$$s_{ij}\left(t\right)=f\left(d(x_i\left(t\right),x_j\left(t\right))\right),$$ (7)

where x_i(t) and x_j(t) are the positions at the moment t of cells C_i and C_j respectively, d is the distance function, and f is the function of the signal decay. Again, by definition, we have the symmetry s_ji(t) = s_ij(t). The corresponding memorised signal we denote by $s_{ij}^{\ast }$. Depending on the difference between the current received signal s_ij(t) and the memorised signal $s_{ij}^{\ast }$, cell C_j produces the response signal z_ji coded for cell C_i. The distribution of the response signal is given by

$$z_{ji}(\mathbf{x},t)=(s_{ij}^{\ast }-s_{ij}\left(t\right))f\left(d(\mathbf{x},{\mathbf{x}}_j\left(t\right))\right).$$ (8)

In order to restore the initial configuration of the system, each cell C_i moves along the gradients of the received signals coded for it, i.e.

$$\frac{d{\mathbf{x}}_i}{dt}=\sum _{j\ne i}\left(\nabla z_{ji}\left({\mathbf{x}}_i\left(t\right)\right)\right).$$ (9)

If we consider only smooth decay functions f, which is a biologically reasonable assumption, then we can write equation (9) as

$$\frac{d{\mathbf{x}}_i}{dt}=\nabla \left(\sum _{j\ne i}{z}_{ji}\left({\mathbf{x}}_i\left(t\right)\right)\right).$$ (10)

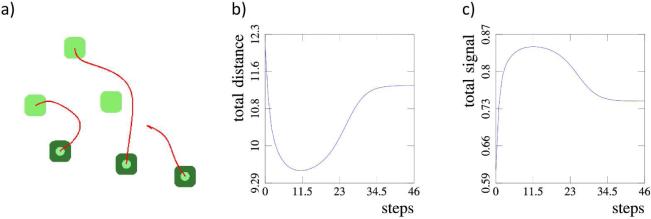
We consider three examples of three-cell configurations, presented in figure 5. In the example a) a single cell is displaced and the system returns to the initial configuration. In the example d) a single cell is displaced and the system obtains a configuration symmetrical to the initial one. In the example g) all three cells are displaced and the system again returns to its initial configuration. The corresponding graphs of the total distance b), e) and h) together with graphs of the total signal c), f) and i) show that in each example the system obtains a stationary configuration.

Fig. 5.

Case 2. a), d), g) Three examples with three cells. Initial and final positions of cells are denoted by light and dark green, respectively. Blue lines show the initial cell displacements, while red lines show cell movement traces. b), e), h) Difference between the total distance between all cells in a current and the initial configuration. c), f, i) Difference between the current (s) and the memorised (s*) total signal of all cells.

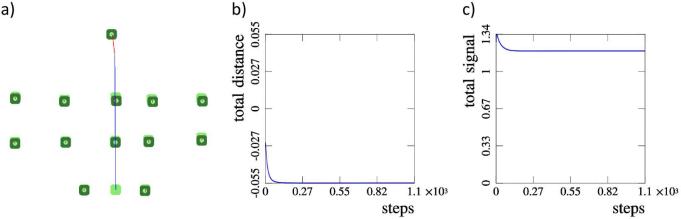
As a more complex example we take a polygon-like cell distribution with eight cells (Figure 6). A single cell is displaced from its initial position and placed on the opposite side of the configuration. In this case both the displaced cell and remaining cells rotate, but in opposite directions. The rotation continues until the system reaches its initial configuration (Figure 6 b)).

Fig. 6.

Case 2. A more complex, polygon-like, configuration with 8 cells. a) A single cell is displaced to the other side of the polygon. b) The system obtains its initial configuration, which is confirmed by the total distance and the total signal graphs c) and d).

There also exist configurations and corresponding deformations for which the system can have several different stationary solutions. An example is given in Figure 7 where a single cell is displaced to the opposite side of a 13-cell configuration. The system is not able to reach its initial configuration however it finds a local equilibrium. Therefore, we can conclude that n different signal types s_i, n corresponding types of response signals z_i and n² memorised intensities of signals $s_i^{\ast }$ offer sufficient information to the system in order for it to restore its initial configuration following non-extreme perturbations.

Fig. 7.

Case 2. A more complex configuration with 13 cells in which the system does not return to its initial configuration. a) A single cell is displaced to the opposite side of the configuration. The system finds a stable configuration which is different from the initial one. b) and c) The total distance and the total signal graphs show that, although stable, the final configuration is not equivalent to the initial configuration.

3 Tissue regeneration

Previously described model serves as a proof of a principle showing how distribution of a finite number of points C₁, . . . , C_n can be characterised in a plane. We can consider that each of those points is a centre of organisation of different type of tissue in an organism. The premise is that each such centre can organise growth or regeneration of its corresponding tissue. As the simplest model of cell tissue formation we take that each cell C_i is a stem cell which goes through asymmetric division creating a new stem cell and a differentiated cell of the corresponding tissue. In order to preserve the ability of the system to retain the distribution of stem cells, it is necessary that the daughter stem cell inherits the memory of the mother stem cell.

Cell-cell interactions

In order to describe tissue growth we consider the following model of stem cell growth and division. Consider a set of cells {C₁, . . . , C_n}. Each cell C_i in the model is represented by its mass m_i, centre of the mass x_i, and volume with radius h_i. If the distance between centres of mass of two cells C_i and C_j is less than the sum of their radii, i.e. d(x_i(t), x_j(t)) < (h_i + h_j), then a repulsion force acts between them as a result of cell deformation. Furthermore, we model the effect of cell adhesion in terms of force which acts if h_i + h_j < d(x_i(t), x_j(t)) ≤ 2 (h_i + h_j) and tries to keep cells together. Both, the repulsion and the adhesion force are described by the following equation:

$${\mathbf{F}}_{ij}\left(t\right)=\{\begin{array}{cc}{k}_F\left(\frac{h_0}{r_{ij}}-1\right)\left(\frac{2h_0}{r_{ij}}-1\right){\widehat{r}}_{ij},\hfill & 0<r_{ij}\le 2h_0,\hfill \\ 0,\hfill & 2h_0<r_{ij},\hfill \end{array}\phantom{\}}$$ (11)

where k_F is the force strength coefficient, h₀ = h_i + h_j is the equilibrium distance between the cells, r_ij = x_i – x_j is the vector from the position of cell j to the position of the cell i, r_ij = |r_ij| is the distance between the two cells, and r̂_ij = r_ij/r_ij.

Generally, we can assume that in an organism cells of one type of tissues can exhibit different levels of adhesiveness to cells of different types of tissues (Steinberg, 1964; Steinberg and Poole, 1982). In our model we consider that the cells of the same type of tissue will adhere to each other in the way described by equation (11), while cells of different tissues will have be less adhesive. Such organisation leads to separation of tissues (Steinberg and Poole, 1982) and was observed for some types of cells, like liver and retina cells (Roth and Weston, 1967). Hence we define the force acting between two cells i and j belonging to different tissues as follows:

$${\mathbf{F}}_{ij}\left(t\right)=\{\begin{array}{cc}{k}_F\left(\frac{h_0}{r_{ij}}-1\right)\left(\frac{2h_0}{r_{ij}}-1\right){\widehat{r}}_{ij},\hfill & 0<r_{ij}\le h_0,\hfill \\ \frac{k_F}{2}\left(\frac{h_0}{r_{ij}}-1\right)\left(\frac{2h_0}{r_{ij}}-1\right){\widehat{r}}_{ij},\hfill & h_0<r_{ij}\le 2h_0,\hfill \\ 0,\hfill & 2h_0<r_{ij}.\hfill \end{array}\phantom{\}}$$ (12)

The total force acting on cell C_i is then given by

$${\mathbf{F}}_i\left(t\right)=\sum _{j\ne i}{\mathbf{F}}_{ij}\left(t\right).$$ (13)

The influence of signalling on stem cells, previously described by equation (10), is now described in the model in terms of forces acting on stem cells. Let us denote the set of all cells with I and the set of all stem cells with $I_s\subseteq I$. The influence of other stem cells on stem cell C_i through signalling is given by:

$${\mathbf{H}}_i\left(t\right)=k_H\nabla \left(\sum _{\begin{array}{c}\hfill C_j\in I_s,\hfill \\ \hfill j\ne i\hfill \end{array}}{z}_{ji}\left({\mathbf{x}}_i\left(t\right)\right)\right),$$ (14)

where k_H is the coefficient of influence.

Equations of cell motion follow from

$$m_i\left(t\right)\frac{d{\mathbf{v}}_i}{dt}\left(t\right)+c{\mathbf{v}}_i\left(t\right)={\mathbf{F}}_i\left(t\right)+{\mathbf{H}}_i\left(t\right),$$ (15)

where v_i the vector of cell movement and c is the damping coefficient (viscosity). If cell C_i is not a stem cell, then H_i(t) = 0 and the mass m_i(t) of the cell is constant.

Stem cell division

We assume that a stem cells grows in regular intervals, starting from its initial volume (area in 2D), until its volume is doubled. At that moment the radius and the mass of the cell in the model are given by:

$$r_i=r_i^0\sqrt{2}\text{and}{m}_i=2m_i^0,$$ (16)

where $m_i^0$ and $r_i^0$ denote the initial mass and radius of the cell. Once the stem cell reaches its maximal size it divides in a random direction, i.e. it is destroyed and two new cells with radius $r_i^0$ and mass $m_i^0$ are created. Let us denote the random direction unit vector with ${\stackrel{‒}{v}}_{rand}$, and the centre of the mass of the stem cell at the moment of division with x₀. Then the positions x_1/2 of the two new cells are given by:

$${\mathbf{x}}_{1∕2}={\mathbf{x}}_0\pm \frac{\sqrt{2}}{2}{r}_i^0{\stackrel{‒}{v}}_{rand}.$$ (17)

One of the two cells is a new stem cell, while the other cell is differentiated. At the moment of division the direction and the rate of movement of the two daughter cells is equal to the direction and the rate of movement of the mother cell.

In order to limit tissue growth in this simplified model, we consider that each stem cell produces a survival signal which decays in space. Each differentiated cell of the tissue corresponding to stem cell C_i receives this signal, and if the intensity of the received signal is lower than some predefined threshold the cell dies (apoptosis). Due to a symmetry of the signal distribution, instead of the survival signal we can consider that each stem cell has a survival area for the tissue surrounding it.

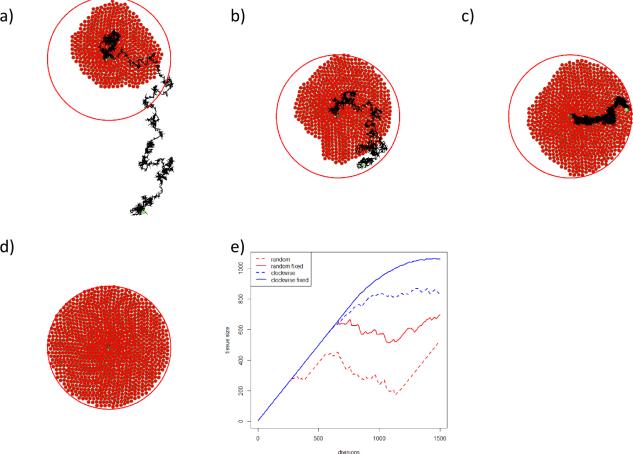
By the described mechanisms of cell division and tissue growth control, a single stem cell should be able to produce a circular tissue. However, the random choice of division direction in each of subsequent divisions, and the small spatial movement of the stem cell after division (described by equation (17)), results in a sporadic motion of the stem cell, as shown in Figure 9 a). In addition to the random direction division the stem cell motion is influenced by its physical interactions with surrounding cells (equation (11)). Figure 9 b) shows the stem cell motion in the case of the random direction division but without the influence of surrounding cells, i.e. the stem cell exerts physical force on surrounding cells, but surrounding cells do not exert forces on the stem cell. In both cases, due to the stem cell motion, the stem cell is not able to generate the corresponding tissue to its maximal size. In order to reduce the sporadic motion of the stem cell we introduce the following scheme of choosing the direction of cell division. The direction of the first division is chosen randomly, as it is described above, while in each following division the direction of division is obtained by a counter-clockwise rotation of the vector of the previous division. Figures 9 c) and d) show the stem cell motion for the counter counter-clockwise case, with and without the influence of other cells on the stem cell. Figure 9 e) gives the comparison of the four methods mentioned above. Several stages of the circular tissue formation obtained with the last method (counter-clockwise generation, without influence of surrounding cells) are given in Figure 8.

Fig. 9.

Tissue generation and stem cell motion for different methods of choosing the direction of division: a) the random method, surrounding cells exert forces on the stem cell, b) the random method, surrounding cells do not exert forces on the stem cell, c) the counter-clockwise method, surrounding cells influence the stem cell, d) the counter-clockwise method, surrounding cells do not influence the stem cell. The current stem cell position is in the centre of the tissue survival area (large circle) while the black curve shows the trace of the stem cell movement. The light green circle at the beginning of the stem cell trace shows the initial position of the cell. In e) all four methods are compared by tissue growth.

Fig. 8.

From left to right: several stages of growth of a tissue produced by a single stem cell. The stem cell is located at the centre and is denoted by larger dark green areola. The results are obtained by the counter-clockwise method for determining the direction of division, and by cancelling the physical influence of surrounding cells on the stem cell.

In configurations with more stem cells the condition that surrounding cells do not exert forces on stem cells is not longer necessary, because the stable configuration of stem cells (via signalling) reduces the motion of stem cells. Hence, in the example given in Figure 10 stem cells are influenced by their surrounding cells, but the complete tissue is still successfully generated. In cases where survival areas of two different tissues are intersected, differentiated cells of both tissues will compete in the intersected area. If the repulsion forces between them is stronger than the influence of signalling on the stem cells, the stem cells will get separate until their survival areas do not intersect any more. However, in the case presented in Figure 10 the influence of signalling is dominant, so differentiated cells continuously compete for the intersection area. This leads to the emergence of a border between two tissues which varies around the equidistance between the stem cells.

Fig. 10.

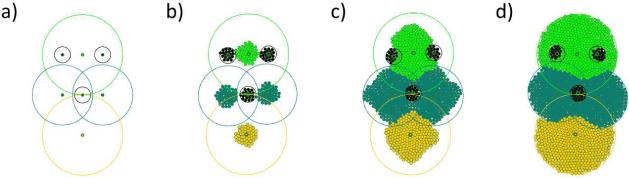
An example with seven stem cells and their corresponding tissue survival areas. Each stem cell generates different tissue: a head (green), a left and a right side of the trunk (blue), a tail (yellow), two eyes in the head and pharynx in the trunk (black). The stem cell configuration remains stable during the tissue formation, determining the final shape of the organism. The images show: a) the initial and, at the same time, the ideal configuration of stem cells, b) and c) intermediate stages of tissue formation, d) the final shape of the organism with all tissue being fully developed.

Example

We first consider an example organism with seven stem cells, as shown in Figure 10. Four of them have larger tissue survival areas and will form the head (green), trunk (blue) and tail (yellow) tissues of the example organism. The remaining three stem cells (black) have smaller survival areas and will form two eyes in the head and a pharynx in the trunk of the organism. Although the model is conceptual and unable to realistically represent any real life organisms, the configuration of stem cells in Figure 10 was intentionally created to resemble planaria - organisms which posses remarkable regenerative possibilities and which are extensively studied in the pursuit to uncover driving mechanisms of regeneration and morphogenesis. At the beginning we position the stem cells in the configuration presented in Figure 10 a). Each of the stem cells generates its corresponding tissue, as shown in Figure 10 b) and c). Tissue growth continues until the organism reaches its maximal size, which is limited by the union of tissue survival areas of all stem cells (Figure 10 d)). This example shows growth of several bordering tissues and the stability of the stem cell configuration due to the signalling between them.

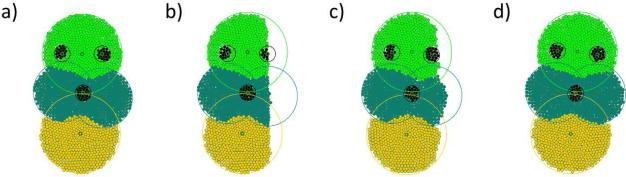
Next, we consider the same organism and remove a part of its tissues which does not contain any of the stem cells (Figure 11 a)). The amputated tissues are then successfully regenerated by their corresponding stem cells (Figure 11 b) to d)). The stem cell configuration and the organism phenotype remain stable during the process. Note that in the current model stem cells cannot be regenerated in the case of their amputation, however, the model can be extended to account for a such scenario (see Discussion section).

Fig. 11.

An example of tissue regeneration for the same stem cell configuration (organism) as in Figure 10: a) the initial organism, b) the organism after a vertical cut and the removal of the tissue, b) an intermediate stage of tissue regeneration, d) the fully regenerated organism.

4 Morphogenesis

So far we have shown that the model can describe, on an abstract level, a model organism consisting of several different tissues, and that the spatial organisation of those tissues inside the organism can be stable. Furthermore, In Figure 11 we have shown the conceptual ability of the model to regenerate missing tissues, and that the tissue organisation remains stable during the process of regeneration. However, in this state the model cannot describe the organism growth and the appearance of its shape (morphogenesis). If the stem cells would be closely grouped together, their reaction on the signalling would be too severe, leading to their rapid motion and separation. As their separation would be more rapid than the rate of generation of their corresponding tissues, the tissues would be at first separated and would reconnect only after they have almost achieved their full size.

Time dependent function

In order to introduce the possibility of gradual organism growth we add a time dependent function to the model. More precisely, instead of the equation (15) for stem cell motion we consider the following equation:

$$m_i\left(t\right)\frac{d{\mathbf{v}}_i}{dt}\left(t\right)+c{\mathbf{v}}_i\left(t\right)={\mathbf{F}}_i\left(t\right)+g\left(t\right){\mathbf{H}}_i\left(t\right),$$ (18)

where the time dependant function g(t) is an increasing function limited from above. An example of such function g is

$$g\left(t\right)=\{\begin{array}{cc}{k}_g(t-t_0),\hfill & t-t_0<{\tau }_m.\hfill \\ k_g{\tau }_m,\hfill & t-t_0\ge {\tau }_m,\hfill \end{array}\phantom{\}}$$ (19)

where k_g a positive constant, t – t₀ is the age of the organism and τ_m is the period of maturation of the organism. The function g affects only the motion of the stem cells due to the signalling between them, while the part of motion of the cells due to the physical interaction with the surrounding cells remains unaffected. Thus at the beginning of the organism growth the motion of stem cells will be slow, then it will increase as the organism grows, and finally it will reach its limit when the organism becomes mature.

Example

Let us now consider the same model organism presented in 10. We begin from the ideal stem cell configuration shown in 10 a). Next we displace stem cells from their ideal configuration and arrange them to be grouped closely together. They still posses the memory about their ideal configuration shown in Figure 12 a). Their memory in this case can be considered as “genetic memory” or “epigenetic memory” (Morozova and Shubin, 2012; Morozova and Penner, 2015). In the example shown in Figure 12 b) and c), the stem cells go to their ideal configuration, but their movement rate corresponds to the growth rate of their corresponding tissues. Hence, the tissues remain connected through the whole process of the organism growth, finally forming a full grown organism as shown in d).

Fig. 12.

An example of organism growth and formation (morphogenesis) for the same stem cell configuration (organism) as in Figure 10. The ideal configuration of stem cells is the one shown in Figure 10 a), presenting “genetic” or “epigenetic” memory. The stem cells are then displaced and grouped closely together to their initial (non-ideal) position: a) the initial stem cell configuration, b) and c) intermediate stages of the organism growth, d) the fully grown (mature) organism.

5 Discussion

We consider in this work morphogenesis and regeneration at two levels of regulation, local and global. Tissue organization and size are determined at the local level due to proliferation of stem cells. They also produce survival signals that prevent apoptosis of differentiated cells. Global regulation determines mutual locations of the tissues. It is effectuated by the signals between central cells of each tissue. This two level organization of the model organism appears to be very robust. It allows their reproducible development and regeneration.

The purpose of this work is to suggest a minimal set of assumptions to describe morphogenesis and regeneration. Though all assumptions of the model are biologically plausible, they are very simplified in comparison with realistic biological mechanisms. One benefit of this approach is that it illustrates the minimal components sufficient to achieve a degree of self-repair - an important goal for synthetic bioengineering applications attempting to construct robust biobots (Doursat et al., 2013; Doursat and Sanchez, 2014; Kamm and Bashir, 2014). At this point, we do not specify (constrain) the biological nature of the signals between cells, but any number of chemical and physical pathways could easily implement such signalling.

The notion of central cells has a direct meaning here – each tissue is organized around the corresponding self-renewing cell. In the absence of other tissues, it becomes a circle with the self-renewing cell at the center. It should be noted however that the tissue is circular under certain conditions on the direction of cell division. If the direction of division of the self-renewing cell is random, then it causes sporadic cell motion and the corresponding tissue will not be circular. Thus, in the model we suppose that the direction of cell division is regulated by some “genetic” or “epigenetic” (Morozova and Shubin, 2012; Morozova and Penner, 2015) information. As a simplified model we consider that the direction of division changes counter-clockwise with a given step. In this case the tissue becomes circular.

Limitations

There are several limitations of this model. Communication between central cells controls their mutual locations. If these locations are modified, then the cells will return back to their initial positions. However, if the perturbations are sufficiently large, it is possible that central cells will converge to some other stable configuration different from the initial one. So the initial configuration can be stable with respect to small perturbation and unstable with respect to large perturbations. We observed such behaviour in some examples. A more detailed investigation of possible non-uniqueness of stable configuration will be reported in subsequent work.

Furthermore, the model at this level does not offer the possibility of description of formation of tissues of more complex shapes. For that, a more complex model of tissue generation is necessary. Such model needs to describe two aspects - the tissue orientation inside of the organism and a possibility of a stable and robust generation a complex tissue shape. One possible concept of generation of complex-shaped tissue is presented in (Bessonov et al., 2015).

In the case of tissue removal, the model is able to regenerate the missing tissue only in the case when the removed tissue did not contain any centres of organization (stem cells). However, the model can be extended to account for stem cell removal. Here we propose one possibility. In the case a stem cell has been removed, the closest remaining stem cell will undergo through a symmetric cell division creating two new stem cells. One of the daughter cells will resume the function of the mother cell, while the other daughter will assume the function of the missing stem cell. Due to the signalling between stem cells, the latter daughter stem cell will move to its appropriate position and generate the missing tissue.

Further development

The representation of the tissue considered in this work is deliberately very simplified. More cell types can be present and stem cells can be distributed inside the tissue. In this case we cannot reduce the interaction between tissues to signalling between their central cells. Instead all cells of a given tissue can participate in the communication and some overall signal can be sent to other tissues.

Another important question concerns the regulation of cell division. We consider in this work the simplest case where each stem cell divides giving one stem cell and one differentiated cell (asymmetric division). We can also assume that it can give two stem cells or two differentiated cells. In this case we need to introduce intracellular regulation of stem cells and specify how it depends on the extracellular factors. Depending on the signals coming from other tissues or on some external perturbations, stem cells can change their division pattern. If it gives two stem cells, then they can remain together in the same tissue or they can separate and form different tissues.

Predictions

If locations of central cells and of the corresponding tissues are modified, then they will return to their initial configuration. Such behaviour is observed in some biological experiments, where significant remodelling of appendages grafted to aberrant locations is observed (Farinella-Ferruzza, 1956; French, 1980).