Segmental Analysis of Cardiac Short-Axis Views Using Lagrangian Radial and Circumferential Strain

Abstract

Accurate description of myocardial deformation in the left ventricle is a three-dimensional problem, requiring three normal strain components along its natural axis, that is, longitudinal, radial, and circumferential strains. Although longitudinal strains are best estimated from long-axis views, radial and circumferential strains are best depicted in short-axis views. An algorithm that utilizes a polar grid for short-axis views previously developed in our laboratory for a Lagrangian description of tissue deformation is utilized for radial and circumferential displacement and strain estimation. Deformation of the myocardial wall, utilizing numerical simulations with ANSYS, and a finite-element analysis–based canine heart model were adapted as the input to a frequency-domain ultrasound simulation program to generate radiofrequency echo signals. Clinical in vivo data were also acquired from a healthy volunteer. Local displacements estimated along and perpendicular to the ultrasound beam propagation direction are then transformed into radial and circumferential displacements and strains using the polar grid based on a pre-determined centroid location. Lagrangian strain variations demonstrate good agreement with the ideal strain when compared with Eulerian results. Lagrangian radial and circumferential strain estimation results are also demonstrated for experimental data on a healthy volunteer. Lagrangian radial and circumferential strain tracking provide accurate results with the assistance of the polar grid, as demonstrated using both numerical simulations and in vivo study.

Introduction

Echocardiographic strain imaging has become more widespread as an important diagnostic tool to characterize myocardial function.^1-6 Local displacements can be estimated using cross-correlation-based techniques between frames of radiofrequency (RF) echo signals over a cardiac cycle.^7,8 One-dimensional (1D) deformation tracking, sensitive to deformations along the beam direction and computationally efficient, has been commonly utilized.^9,10 However, with this approach, it is difficult to estimate deformations perpendicular to the beam direction. Two-dimensional (2D) tracking algorithms^11-14 attempt to provide 2D strain tensor information by incorporating multiple A-lines in the tracking block. Several 2D tracking algorithms have been investigated by many research groups^11-14 and provide strain information along and perpendicular to the beam propagation direction. Displacement and strain components that are perpendicular to the beam propagation direction are of relatively coarser resolution when compared with estimates along the beam direction.

However, accurate analysis of left ventricular mechanics requires strain information along the longitudinal, radial, and circumferential directions, which form the natural axes of myocardial deformation. Although longitudinal strains can be acquired through the direct estimation of cardiac deformation along the beam direction from apical two-, three- or four-chamber views,¹⁵ radial and circumferential strains, which are best depicted in a parasternal short-axis view,¹⁶ are not directly measurable from displacement and strain estimated along the beam direction. Also, an accurate description of regional myocardial deformation over a cardiac cycle requires a Lagrangian description^6,17-24 of tissue motion. In a Lagrangian description,^17-19 displacement and strain are described around a point in myocardial tissue as it traverses through space and time. Regional anomalies within the myocardial wall are better tracked under such a description when compared with a Eulerian description over a cardiac cycle,^17,18 which only focuses on fixed spatial coordinates within the 2D imaging plane. An Eulerian description can be utilized to obtain a local snapshot of the myocardial deformation. In finite strain theory, for homogeneous deformations, the difference between Lagrangian and Eulerian descriptions of strain can be observed by comparing the form of Green-Lagrange and Euler-Almansi strain tensors.^17,18

Commercial software packages from different vendors have provided radial and circumferential strain information for over a decade.^25-31 However, clinical echocardiographic strain estimation algorithms still process B-mode echo signals. B-mode images are derived from log-compressed and decimated envelope information derived from RF echo signals.^25-30 It has been previously demonstrated that strain estimated using RF signals provides a higher elastographic signal-to-noise ratio (SNR_e)^32,33 and significantly fewer strain artifacts³⁴ when compared with envelope and B-mode echo signals due to the additional phase information included in RF echo signals. These commercial algorithms track the movement of acoustic patterns or “speckle” on B-mode images, devoid of phase information reducing the accuracy and precision of the strain estimated.³³ Furthermore, different vendors use different algorithms for speckle tracking and radial and circumferential strain calculations, leading to poor agreement in strain estimated across commercial systems.^27,30,35 In addition, these algorithms are proprietary to the ultrasound system and opaque to users of the system.

Although longitudinal, radial, and circumferential strains have been evaluated using commercial B-mode-based speckle tracking–based echocardiographic strain imaging, there are relatively fewer reports on radial and circumferential echocardiographic strain imaging using RF signals in human subjects.^20,36,37 However, RF echo signal–based radial and circumferential strain estimation on animal models has been reported by several investigators.^38-40

At the same time, a large number of peer-reviewed papers have reported on results obtained on simulation models and tissue mimicking phantoms.^38,41-44 Radial strain estimates have been reported to have poor accuracy in identifying dysfunctional regions when compared with sonomicrometry.⁴¹ Heyde et al.⁴¹ reported that the assessment of global left ventricular function provides promising results; however, regional strain analysis was not fully validated. Zervantonakis et al.⁴³ investigated radial and circumferential strain for short-axis images in a polar coordinate system using a finite-element analysis (FEA) canine model at end-systole. However, details on radial and circumferential strain computation from displacement components were not presented in the paper.⁴³

Polar strain, that is, radial and circumferential strains, described in a polar coordinate system has also been investigated for vascular ultrasound strain imaging, usually with FEA-based concentric wall models.^45,46 Hansen et al.⁴⁵ investigated radial strains using a transverse cross-section of a homogeneous vessel with a concentric lumen for evaluating angular compounding, using a single quasi-static compressional state with an applied pressure of 0.532 kPa. Richards et al.⁴⁶ designed a concentric FEA model for intravascular ultrasound (IVUS) and investigated eight independent quasi-static radial and circumferential strain deformations ranging from 0.1% to 10%. They utilized a polar registration mesh for displacement interpolation. These studies, however, were mainly focused on tissue deformations at selected time instances in a cardiac cycle, and not over a continuous deformation as described in this paper.

In this paper, we demonstrate a framework to generate a Lagrangian description^17,18 of radial and circumferential strains over a cardiac cycle. A polar grid generation algorithm previously developed in our lab²⁴ was utilized. This algorithm incorporates semi-automatically tracked epi- and endocardial contours to generate a polar grid over several cardiac cycles. The alignment of points on this grid is designed to enable least squares strain estimation (LSQSE)⁴⁷ in a polar coordinate system. In our previous work, we used a Lagrangian approach to generate axial and lateral strains over several cardiac cycles.²⁴ In this paper, we extend this Lagrangian approach to perform radial and circumferential strain estimation along the natural axes of deformation of the heart. Our polar grid–based approach is not limited by poor quality lateral displacement/strain estimation. We present both a FEA-based concentric wall model and a realistic canine heart model that incorporates fiber orientation and the entire range of cardiac deformation, that is, compression, translation, and torsion,^48,49 for the purpose of validation of our algorithm. Finally, we present results obtained using experimental RF data acquired on a healthy human volunteer.

Materials and Method

Concentric Homogeneous Myocardial Wall Simulation Using ANSYS

In this study, we first utilize a cross-sectional deformation model designed to mimic cardiac applications with a cyclic tissue deformation simulating a cardiac cycle. Simulated RF data from a short-axis cross-sectional view of a concentric homogeneous wall phantom were generated using a frequency domain–based ultrasound simulation program⁵⁰ developed in our laboratory, coupled to displacement information generated from FEA software. The simulated phantom was a concentric wall phantom, constructed with an outer radius of 3.1 cm and wall thickness of 1.1 cm, and an elevational wall thickness of 1.0 cm,^51-53 to simulate the cross-sectional geometry of a left ventricular myocardial wall and 3D deformations over a cardiac cycle. Scatterers were randomly distributed in the wall with a scatterer number density of 10 scatterers/mm³ to ensure Rayleigh scattering statistics.⁵⁴ The center of the phantom was positioned at a 5 cm depth. A 1D linear array transducer with 256 rectangular elements with dimensions of 0.2 × 10 mm was modeled with a 2.5-MHz center frequency and 80% bandwidth. The elements were spaced 0.25 mm apart (center to center) and the transmit focus was also set to a depth of 5 cm.

FEA software, ANSYS (ANSYS, Inc., Pittsburgh, Pennsylvania) was utilized to generate the displacement field that was then incorporated into the ultrasound simulation. Myocardial wall with a density of 1 g/cm³ and a Young’s modulus of 20 kPa with Poisson’s ratio of 0.495⁵⁵ was used. Displacement fields were generated by applying a pressure differential to the inner surface of the simulated myocardial wall. To simulate cardiac deformations of the heart, sinusoidal pressure variations at 2 Hz and varying between 0 to 1000 Pa were applied to the inner surface to generate a cyclical deformation of the myocardial wall, whereas the pressure at the outer surface was kept at 0 Pa. In this setting, the largest deformation occurs near the inner surface and decreases outward, creating an inhomogeneous strain distribution. The Young’s modulus, Poisson’s ratio, and pressure applied ensured that strain values were within the range reported in human studies.^56,57 Displacement fields over the cardiac cycle were then extracted and bi-linearly interpolated²⁴ to guide the deformation of each individual scatterer in the myocardial wall phantom. We simulated deformations over a 1-second time period, with a frame rate of 250 Hz, to generate the RF echo signal loop. This frame rate was chosen to be consistent with the FEA-based canine cardiac simulation described later in this section. Note that the purpose of this model was to simulate the short-axis geometry and strain variations in human heart in a simplified manner to enable comparison of the accuracy of our Eulerian and Lagrangian strain estimation^17,18 with the ideal FEA variations for homogeneous and uniformly elastic tissue. In addition, only radial and circumferential strains are anticipated in this simple model. More complex cardiac deformations are investigated in the next section that utilizes a FEA-based canine cardiac simulation model.⁴⁴

FEA-Based Canine Cardiac Simulation

A 3D canine cardiac ultrasound simulation previously adapted in our laboratory was also utilized for validation.⁴⁴ Here, a 3D canine heart mechanical model developed by the Cardiac Mechanics Research Group at University of California San Diego (UCSD) was incorporated with the ultrasound simulation program developed in our laboratory.⁵⁰ This geometrically accurate model incorporates local fiber orientation that enables simulation of all movement and deformation aspects^48,49 (compression, translation, and torsion). The original deformation model includes information over four cardiac cycles with only 1296 data points that depict the deformation, at 250 frames/second.^48,49 Piecewise cubic Hermite interpolation was performed to increase the amount of the deformation points in the spatial grid to incorporate ultrasound scattering.⁴⁴ The sampling frequency of the RF echo signals simulated was 40 MHz. In this study, a mid-cavity slice of left ventricle along a short-axis view was chosen as the input to the ultrasound simulation. The description of the ultrasound simulation is the same as that presented for ANSYS-based simulation above.

Ultrasound RF Data Acquisition on Human Subjects

Echocardiographic RF echo signals from a healthy human volunteer were acquired at the University of Wisconsin (UW) adult echocardiography clinic under a protocol approved by UW– Madison Health Sciences institutional review board. Informed consent was obtained before echocardiographic scanning and RF data acquisition. The volunteer was scanned using a GE Vivid 7 system (GE Ultrasound, Waukesha, Wisconsin) with a 2.5-MHz phased array transducer. RF signals along a parasternal short-axis view along the mid-cavity were collected over several cardiac cycles. The heart rate of the volunteer was 0.81 beats/second. RF data were acquired at a frame rate of 34 Hz with a sampling frequency of 20 MHz.

Displacement Estimation in Cartesian Coordinates

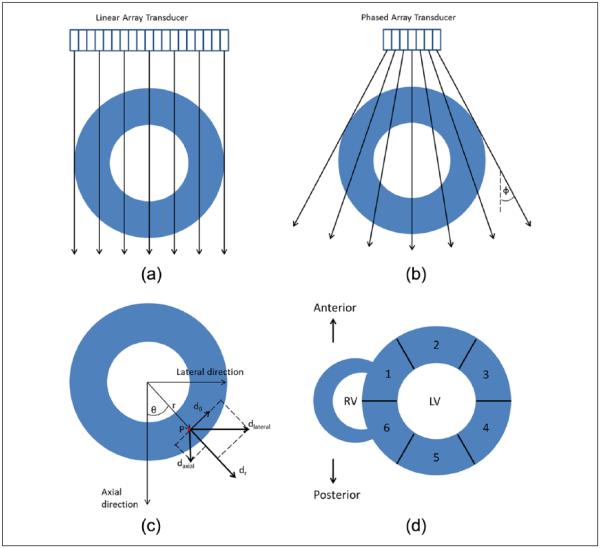
RF data generated from both ultrasound simulations and in vivo data acquisitions were processed using a multilevel speckle tracking algorithm^13,14 to generate a local displacement field. Four levels of tracking were performed using an iterative coarse-to-fine search scheme to estimate high spatial resolution displacements. The processing kernel overlap was 75% for all four levels. The final processing kernel size was 4 wavelengths by 3 A-lines. These values were empirically chosen to balance between displacement estimation accuracy, SNR, and spatial resolution of strain estimation. Displacements along and perpendicular to the beam direction in the image plane were estimated for both ANSYS and cardiac FEA linear array ultrasound simulations. For the in vivo study using a phased array transducer, due to the sector shaped acquisition pattern, the displacement information obtained perpendicular to the beam direction was sparse, especially at deeper depths. As a result, only the displacement field along each beam line was utilized. For the purpose of this study, we label orthogonal vectors in the Cartesian coordinate system as “axial” and “lateral” direction. For the linear array geometry, axial direction corresponds to the ultrasound beam direction, whereas lateral direction corresponds to the orthogonal or perpendicular direction to the beam. In this study, for phased array geometry, we avoid describing the displacement field as “axial” and “lateral” displacement vectors as beam lines propagate in different diverging directions (fan angle), and thus it does not always coincide with the definition for a Cartesian coordinate system. Figure 1(a) and (b) depicts the ultrasound beam direction and its intersection with the left ventricle for both the linear and phased array geometry, respectively. Displacement field along the beam direction generated with phased array geometry was converted to “partial” axial and lateral displacement vectors in a Cartesian coordinate system based on the angular component of each beam line using following equations:

$$\begin{array}{c}\hfill d_{\text{axial}-\text{partial}}=\text{cos}\varphi \times d_{\text{beam}}\hfill \\ \hfill d_{\text{lateral}-\text{partial}}=\text{sin}\varphi \times d_{\text{beam}},\hfill \end{array}$$ (1)

where ϕ denotes the ultrasound beam fan angle, and d_beam represents the displacement measured along ultrasound insonification direction.

Figure 1.

Illustration of the ultrasound beam direction and its intersection with a hypothetical left ventricle are shown for (a) linear array, (b) phased array geometries. The relationship between Cartesian and polar displacements is shown in (c). Segments based on the AHA criteria are shown in (d): (1) anteroseptal, (2) anterior, (3) anterolateral, (4) inferolateral, (5) inferior, and (6) inferoseptal. AHA = American Heart Association. LV=Left Ventricle; RV= Right Ventricle.

Radial and Circumferential Strain Estimation Using a Polar Grid

A Lagrangian deformation tracking algorithm using a polar grid previously developed in our lab was implemented for short-axis images to estimate radial and circumferential strain.²⁴ Here, endocardial and epicardial contour pairs were generated semi-automatically by stacking 2D echocardiographic images over two cardiac cycles into a 3D matrix. MITK 3M3 program (Mint Medical GmbH, Heidelberg, Germany) was used for piecewise linear interpolation of endocardial and epicardial wall boundaries obtained at selected three to four time steps, to cover the entire cardiac cycle. A centroid was then calculated from the donut-shaped left ventricular myocardial wall with the contour pairs for each image frame. The contour pair is then divided in an equiangular fashion along the circumferential direction with equidistant points in the radial direction to generate a polar grid. In this study, contour lines were divided into 600 sections to ensure that it was a multiple of 6. This number is the recommended number of segments of left ventricle in mid-cavity recommended by American Heart Association (AHA).⁵⁸ In addition, 40 data points along radial direction between the epi- and endocardial contours were generated for this study. In general, the number of data points can be up-sampled to improve spatial resolution, however, with increased computational costs. Displacements along and perpendicular to the beam direction are then overlaid onto the polar grid, with non-overlapping points filled in with bilinear interpolation.

Radial and Circumferential Displacement Estimation

Axial and lateral displacements in a Cartesian coordinate system have been previously computed for both the linear and phased array geometry. Radial and circumferential displacements were then estimated using a 2D rotation matrix M, defined as

$$\mathbf{M}=\left[\begin{array}{cc}\hfill \text{cos}\theta \hfill & \hfill \text{sin}\theta \hfill \\ \hfill -\text{sin}\theta \hfill & \hfill \text{cos}\theta \hfill \end{array}\right],$$ (2)

where θ denotes the counter-clockwise angle measured from a pre-defined 0° line crossing the centroid and a point on the polar grid. Radial and circumferential displacements in polar coordinates can be generated using

$${\mathbf{D}}^{\text{polar}}={\mathbf{MD}}^{\text{cartesian}},$$ (3)

where

$${\mathbf{D}}^{\text{polar}}=\left(\begin{array}{c}\hfill d_{\text{r}}\hfill \\ \hfill d_{\theta }\hfill \end{array}\right),{\mathbf{D}}^{\text{cartesian}}=\left(\begin{array}{c}\hfill d_{\text{axial}}\hfill \\ \hfill d_{\text{lateral}}\hfill \end{array}\right).$$ (4)

In Equation (4), d_r and d_θ denote the radial and circumferential displacement vector components for the polar coordinate system, whereas d_axial and d_lateral denote the displacement components for Cartesian coordinate system. Equation (3) finally reduces to

$$\begin{array}{c}\hfill d_r=\text{cos}\theta \times d_{\text{axial}}+\text{sin}\theta \times d_{\text{lateral}}\hfill \\ \hfill d_{\theta }=-\text{sin}\theta \times d_{\text{axial}}+\text{cos}\theta \times d_{\text{lateral}}.\hfill \end{array}$$ (5)

This relationship is illustrated in Figure 1(c).

Radial and Circumferential Strain Generation

After the polar displacement vector components are computed, radial and circumferential strains can be calculated using the infinitesimal strain-displacement relationship in polar coordinates:

$$\begin{array}{c}\hfill {\epsilon }_{rr}=\frac{\partial d_r}{\partial r}\hfill \\ \hfill {\epsilon }_{\theta \theta }=\frac{1}{r}\frac{\partial d_{\theta }}{\partial \theta }+\frac{d_r}{r},\hfill \end{array}$$ (6)

where r denotes the distance between the centroid and the computation point or particle. Note that we assumed infinitesimal strain because the deformation of myocardial wall between frames (on the order of 0.1 mm) is much smaller than the dimension of the simulated objects (10 mm). Also note that the contribution of the radial displacement to circumferential strain comes from the elongation or shortening of muscle in circumferential direction, when the radial deformation occurs. Along the radial direction, radial strains are computed with a 9-point least squares strain estimator (LSQSE)⁴⁷; in a similar manner for the circumferential direction, $\frac{\partial d_{\theta }}{\partial \theta }$ are also computed with a 9-point LSQSE. Note that this is achieved when the polar grid is divided equidistantly in the radial direction and equiangularly in the circumferential direction.

Lagrangian and Eulerian Description Generation with AHA Segmentation

In this study, the Lagrangian description of segmental displacement/strain curves was generated using accumulated displacement/strain along the grid points as it deforms over a cardiac cycle. A Eulerian description was generated assuming that the contour positions are unchanged over time. A segmentation scheme for the left ventricle recommended by AHA⁵⁸ was adapted in this study to calculate segmental strain variations for both the canine heart simulation and in vivo human volunteer study. This scheme divides the mid-cavity slice of the left ventricular wall into six segments based on their circumferential location relative to right ventricle and papillary muscle. The segments based on AHA criteria are as follows: (1) anteroseptal, (2) anterior, (3) anterolateral, (4) inferolateral, (5) inferior, and (6) inferoseptal as shown in Figure 1(d). To simulate the AHA segmentation scheme, the homogeneous simulated myocardial wall from ANSYS simulation was divided into six segments circumferentially, with each segment covering one-sixth of the concentric wall. We selected two segments from each study to demonstrate strain estimation results. A segment in which the deformation is predominantly along the beam direction and a segment in which the deformation is predominantly perpendicular to beam direction were selected. In ANSYS simulations, these two selections are called “axial segment” and “lateral segment,” respectively. The corresponding segments are anterior and inferolateral segments in the canine heart simulation, and anteroseptal and anterolateral segments for the in vivo study.

Results

Simulation Results with ANSYS Model

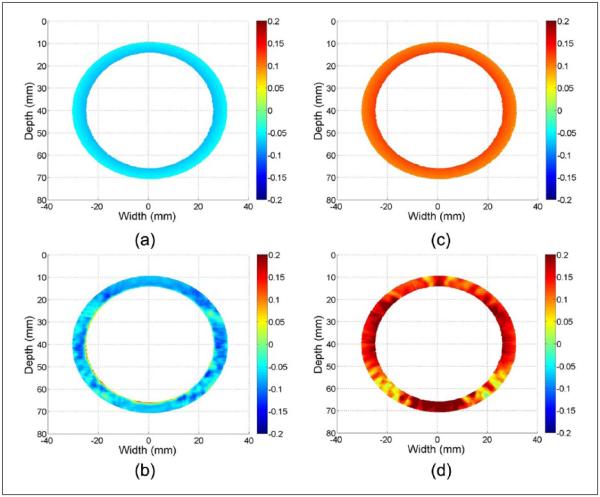
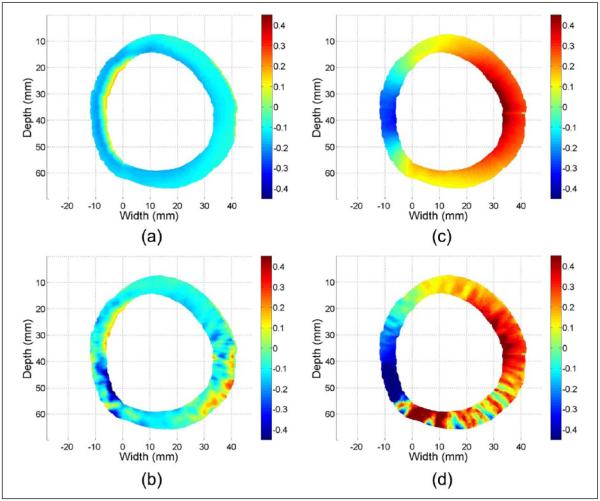
Figure 2 provides a representative example of accumulated Lagrangian strain maps obtained using the homogeneous and uniformly elastic ANSYS concentric wall model simulation, at peak strain during a sinusoidal deformation cycle. The time instant before pressure application is utilized as the start time for strain accumulation. Ideal accumulated radial and circumferential strains are shown in Figure 2(a) and (c); estimated accumulated radial and circumferential strains are shown in Figure 2(b) and (d). These strain components are calculated from axial and lateral displacement field using Equations (5) and (6). Figure 2(a) and (b) illustrates negative radial strains caused by compression along the radial direction whereas Figure 2(c) and (d) demonstrates positive circumferential strains caused by expansion of the wall in the circumferential direction.

Figure 2.

Accumulated ideal radial (a) estimated radial (b) strain, along with ideal circumferential (c) and estimated circumferential (d) strain at the peak strain obtained using ANSYS simulation of a concentric myocardial wall.

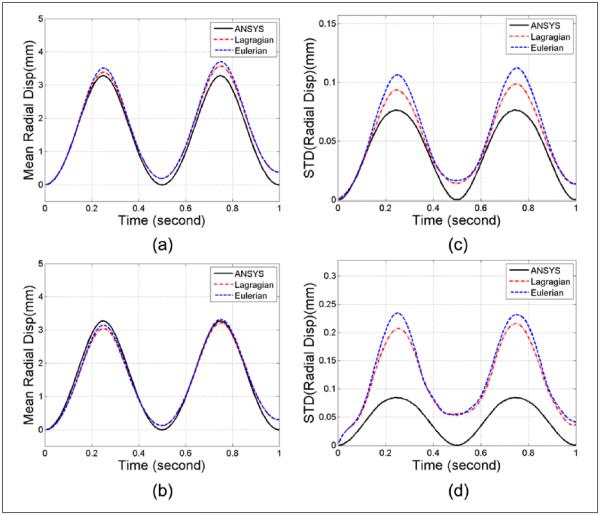
Segmental mean accumulated radial displacement variations over time estimated from the ANSYS model and subsequent ultrasound simulations are shown in Figure 3(a) and (b). Displacement variations from axial and lateral segments are shown in Figure 3(a) and (b), respectively. Ideal displacement values obtained using ANSYS along with the Lagrangian and Eulerian displacement variations over two sinusoidal cycles are plotted together for comparison. Note that ideal strain plots obtained from FEA are Lagrangian, as the Eulerian description only focuses on relative temporal locations rather than following the tissue deformation. Also, ideal radial/circumferential displacement and strain values are directly extracted from ANSYS without additional noise artifacts. Comparison of the standard deviation between the ideal ANSYS results and the Lagrangian and Eulerian displacement estimation within the axial and lateral segments are plotted separately in Figure 3(c) and (d), respectively. From Figure 3(a) and (b), both Lagrangian and Eulerian displacement variations follow the ideal ANSYS curve closely. In the standard deviation plots (Figure 3c and d), the Eulerian curve presents with the highest standard deviation values when compared with Lagrangian and ideal ANSYS curves, and the ideal ANSYS curve presents with the lowest standard deviations among the three plots as expected, because the standard deviation derived from the ideal model reflects only the physiological inhomogeneity of strain in the model whereas in the estimated curves, additional variability due to errors in deformation and strain estimation results in higher standard deviation values than the ideal case. Note that circumferential displacement and its associated standard deviations are not shown mainly because the outward cyclic pressure field utilized for the ANSYS model primarily generates deformations along the radial direction.

Figure 3.

Regional mean radial displacement from the (a) axial and (b) lateral segments, and standard deviation computed from the (c) axial and (d) lateral segments, respectively, of the ANSYS simulation.

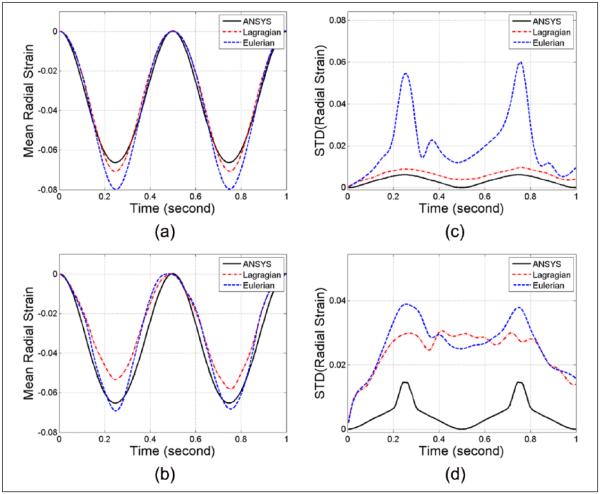
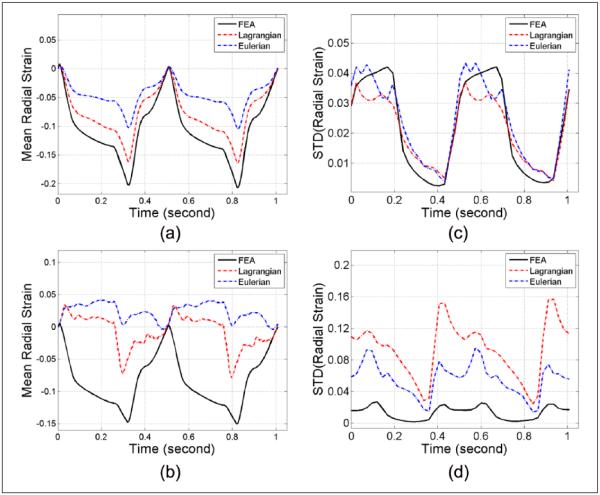
The mean accumulated radial strain variations over time estimated from the ANSYS model and subsequent Lagrangian and Eulerian strain estimated from the ultrasound simulations are shown in Figure 4(a) and (b) for the same axial and lateral segment shown in Figure 3. The corresponding standard deviations within these two segments are plotted separately in Figure 4(c) and (d), respectively. Note that for the axial segment (Figure 4a-c), the Lagrangian plot for both segmental strain variation and standard deviation closely follows the ideal ANSYS curve whereas the Eulerian curve deviates from the other two plots. However, for the lateral segment (Figure 4b-d), the Lagrangian strain estimation underestimates the results and deviates from the ideal ANSYS plots. The Eulerian strain estimates indicate an overestimation of the ideal ANSYS strain estimated. The standard deviation plots with either the Lagrangian or Eulerian estimations are both higher than that obtained from the ANSYS results.

Figure 4.

Regional mean radial strain from (a) axial and (b) lateral segments, and standard deviation computed from the (c) axial and (d) lateral segments, respectively, of the ANSYS simulation.

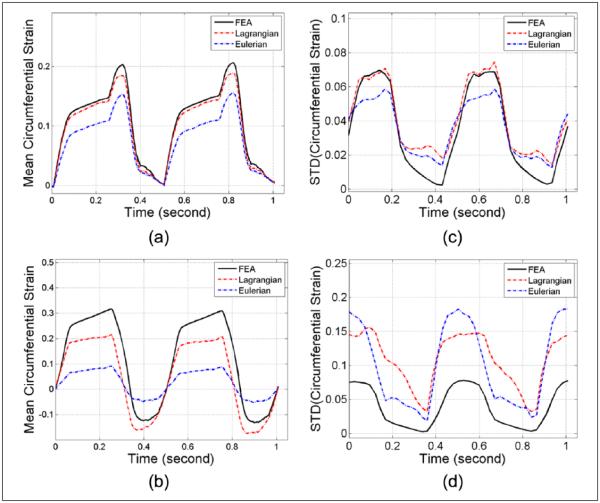
Similar to Figure 4, the mean accumulated circumferential strain variations over time estimated from the ANSYS model and subsequent Lagrangian and Eulerian strains estimated from the ultrasound simulations are shown in Figure 5(a) and (b), whereas the corresponding standard deviations within the axial and lateral segments are plotted separately in Figure 5(c) and (d), respectively. Note that for circumferential strains, both the Lagrangian and Eulerian strains and standard deviation results are comparable within the two selected segments and deviate from the ideal ANSYS plot.

Figure 5.

Regional mean circumferential strain from (a) axial and (b) lateral segments, and standard deviation computed from the (c) axial and (d) lateral segments, respectively, of the ANSYS simulation.

Simulation Results with the Canine Heart Model

Figure 6 presents radial and circumferential strain images from the cardiac simulation for a mid-cavity slice of the left ventricle for the canine heart model. Strain components are calculated from axial and lateral displacement field using Equations (5) and (6). We selected end-systole as the starting time for strain accumulation. The time instance shown in Figure 6 denotes the end-diastolic phase of the cardiac cycle. Figure 6(a) and (c) denotes ideal radial and circumferential strains whereas Figure 6(b) and (d) shows estimated values. Figure 6(a) and (b) shows negative radial strain values over most regions in the left ventricular wall, indicating compression along the radial direction. The positive strain values shown in Figure 6(c) and (d) indicate that compared with end-systole, the left ventricular wall experiences expansion along the circumferential direction whereas the ventricular septum region experiences contraction along the circumferential direction, which is demonstrated by negative strain values.

Figure 6.

Accumulated ideal radial (a) and circumferential (b) strains along with estimated radial (c) and circumferential (d) strains at the peak strain obtained using 4D canine cardiac simulation. 4D = four-dimensional.

Mean accumulated radial strain variations over time estimated from the deformations in the canine heart model and subsequent ultrasound simulation are shown in Figure 7(a) and (b), whereas corresponding standard deviation comparisons within the anterior and inferolateral segments are plotted separately in Figure 7(c) and (d), respectively. Note that only the axial and lateral displacement vectors are provided in the original canine heart model. Radial and circumferential displacements have to be estimated from the axial and lateral displacement vectors by coordinate rotation and polar strain computation. The ideal radial and circumferential strains were also generated from the ideal axial and lateral displacement vectors. Unlike ANSYS results for radial strain estimation, Eulerian mean strain curves underestimate the ideal values as shown in Figure 7(a) and (b), because unlike the ANSYS model, the canine heart model also moves in space. As the heart displaces, lower strain regions may move into the fixed region-of-interest used for the Eulerian description, thus lowering the estimated regional mean values. Also note that even the Lagrangian mean strain curves fail to track the ideal variations for the inferolateral segment (see Figure 7b). Standard deviation variations for all three curves are comparable as shown in Figure 7(c) for the anterior segment, whereas the estimated standard deviation for both Lagrangian and Eulerian strains are higher than the ideal values for the inferolateral segment, as shown in Figure 7(d), similar to that observed with the ANSYS model.

Figure 7.

Regional mean radial strain from (a) anterior and (b) inferolateral segments, and standard deviation from (c) anterior and (d) inferolateral segments, respectively, for the 4D canine cardiac simulation. These curves cover two cardiac cycles starting from end-systole. FEA = finite-element analysis; 4D = four-dimensional.

Mean accumulated circumferential strain variations over time estimated from the cardiac model and subsequent ultrasound simulations are shown in Figure 8(a) and (b), whereas standard deviation comparisons of the accumulated circumferential strains within anterior and inferolateral segments are plotted separately in Figure 8(c) and (d), respectively. Similar to that observed for the radial strain, failure to track ideal strain variations is pronounced for the Eulerian approach, as shown in Figure 8(a) and (b), while the standard deviation values are higher than ideal values for both the Lagrangian and Eulerian approaches in the inferolateral segment.

Figure 8.

Regional mean circumferential strain from (a) anterior and (b) inferolateral segments, and the standard deviation from (c) anterior and (d) inferolateral segments, respectively, for the 4D canine cardiac simulation. These curves cover two cardiac cycles starting from end-systole. FEA = finite-element analysis; 4D = four-dimensional.

Human Volunteer Results

Finally, Figure 9 presents in vivo radial and circumferential strain maps overlaid on the corresponding B-mode image for the human volunteer. Estimated displacement fields along the ultrasound insonification direction are first converted to partial axial and lateral displacements using Equation (1). Radial and circumferential strains are then calculated using Equations (5) and (6). Similar to results reported on the canine heart model, we selected end-systole as the starting time for strain accumulation. The time instance in Figure 9 corresponds to the end-diastolic phase of the cardiac cycle.

Figure 9.

Accumulated radial (a) and circumferential (b) strains at the peak strain values for a human volunteer. The segments based on the AHA criteria are as follows: (1) anteroseptal, (2) anterior, (3) anterolateral, (4) inferolateral, (5) inferior, and (6) inferoseptal. AHA = American Heart Association.

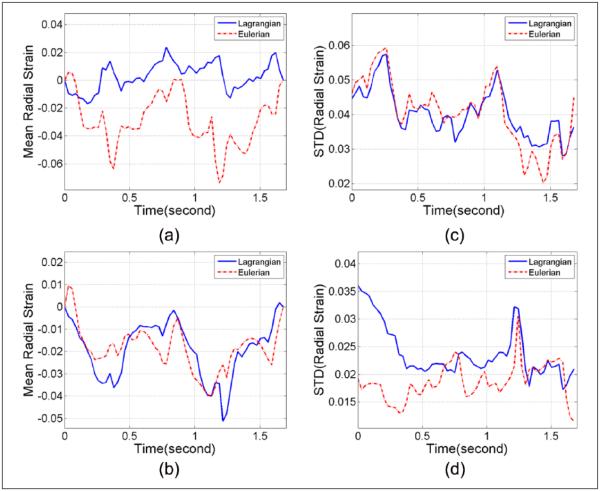
Figures 10 and 11 present radial and circumferential strains and standard deviation variations for the anteroseptal and anterolateral segments. These two segments were selected because in the in vivo short-axis images, the anteroseptal segment has smaller fan angles, with the axial deformation predominantly tracked based on Equation (1), whereas the anterolateral segment is located further away from the central beam line and has large fan angles; as a result, more lateral deformation components can be captured according to Equation (1). Although there are no ideal values to compare with for the strain analysis with the human volunteer, the estimation differences over cardiac cycles can still be appreciated between Lagrangian and Eulerian approaches.

Figure 10.

Regional mean radial strain from (a) anteroseptal and (b) anterolateral segments, and standard deviation from (c) anteroseptal and (d) anterolateral segment, respectively, for the human volunteer. These curves cover two cardiac cycles starting from end-systole.

Figure 11.

Regional mean circumferential strain from (a) anteroseptal and (b) anterolateral segments, and standard deviation from (c) anteroseptal and (d) anterolateral segments, respectively, for the human volunteer. These curves cover two cardiac cycles starting from end-systole. 4D = four-dimensional.

Discussion

In this paper, we presented an algorithm to compute radial and circumferential strains using a polar grid and Lagrangian deformation tracking previously developed on our laboratory. The innovation comes from the use of a polar grid, which has specifically designed grid locations, to generate radial and circumferential strains based on a Lagrangian description over a cardiac cycle along the natural axes of cardiac deformation. The utilization of polar grid enables the calculation of radial and circumferential strains using a least square method directly along radial and circumferential directions. This process cannot be directly realized in a Cartesian coordinate system. Interpolation errors incurred to generate a polar grid density similar to the original displacement field are significantly lower than errors incurred in the estimation of radial and circumferential strains using coordinate transformation from axial and lateral displacement vectors or strain tensors. We have also developed approaches for the 2D tracking of deformation for RF phased array data that have significantly improved spatial resolution,³⁴ which can be easily incorporated into the polar grid algorithm described in this paper.

A concentric homogeneous myocardial wall model generated using the FEA package ANSYS was utilized to compare ideal variations in the radial and circumferential strain with that estimated using Lagrangian and Eulerian approaches. Local displacements from the ANSYS software package were incorporated into a 3D ultrasound simulation program to generate RF echo signals over the sinusoidal deformation applied to the concentric heart wall model. We utilize a sinusoidal, rather than a more complicated physiological pressure pattern in an attempt to create a relatively smooth deformation pattern. This simplified pressure pattern, along with the concentric shaped myocardial wall, can be considered as a simple, but effective model for algorithm evaluation. ANSYS results provide a Lagrangian description as initial material coordinates before deformation are known with FEA simulations. However, if we compare estimation results with a specific point in the cycle without looking at the history of the deformation, we would obtain Eulerian results. As the ultrasound RF data samples the cardiac deformation at a finite frame rate, local displacement and strain estimated between two of these snapshots are referred to as the Eulerian displacement and strain. When these local displacement trajectories over a cardiac cycle are accurately tracked, accumulated, and compared with a specific location in the cardiac cycle (typically end-diastole or end-systole), we obtain a Lagrangian description of the strain. Several investigators accumulate displacement and strain without correcting for the deformation trajectory, which is referred to as accumulated Eulerian displacement and strain,^1,6 thereby differentiating it from a Lagrangian description of the strain. In this paper, we compare both these descriptions starting from a specific location in the cardiac cycle (at end-systole).

A 3D canine heart mechanics model, that provides 4D (3D + time) deformation data was then adapted as the input to the 3D ultrasound simulation for further validation. This model includes complicated deformation patterns and myocardial wall thickness variations, in contrast to the ANSYS concentric wall model. Lagrangian as well as Eulerian approaches to estimate radial and circumferential strain components over two cardiac cycles were implemented. Lagrangian and Eulerian mean strain and standard deviation variations using the AHA segmentation standard⁵⁸ were also compared with ideal strain variations obtained from the cardiac mechanics model. From the analysis of the accumulated radial and circumferential strain from the two simulations, we observe that the estimated Lagrangian strain generally yields more accurate and less noisy results when compared with Eulerian strain estimations. Note that due to anisotropy and deformation range (both directional and dimensional), the standard deviation can vary significantly, and this variation may provide important diagnostic information. In the simple homogeneous FEA model, the deformation is primarily along the radial direction due to deformation applied to the inner wall and as torsional deformation was not incorporated into the model. However, for the canine heart model, as it models the deformation of a canine heart based on data acquired with an imaging modality (magnetic resonance tagging), the entire gamut of cardiac deformations are present. This significantly increases the standard deviation of the strain within the myocardium. Similar deformations are anticipated for the normal volunteer.

Two of the segments, that is, axial and lateral segments for ANSYS simulation, anterior and anterolateral segments for 3D canine heart model, and the anteroseptal and anterolateral segments for human volunteer study were selected to evaluate the impact of radial and circumferential displacement and strain estimation accuracy on the final radial and circumferential strain computed. Lateral displacement estimation incurs more noise artifacts and is less accurate when compared with axial displacement estimation, mainly due to the lack of phase information and lower resolution in the lateral direction.^14,59

Regional strain results clearly demonstrate improved accuracy in the axial/anterior segment (see Figures 4, 5, 7, and 8a), where deformation along the beam direction is the predominant component, when compared with the lateral/anterolateral segments (see Figures 4, 5, 7, and 8b), where deformations perpendicular (lateral) to the axial deformation are also present. This is in line with relatively poor lateral displacement estimation shown in previous work.⁴⁴

The concentric ANSYS wall model was used to mimic the contours of left ventricular wall viewed along the short axis. This model with sinusoidal deformations was utilized to evaluate the ability of algorithms to estimate uniformly varying deformations in a homogeneous medium and to obtain performance metrics for the different algorithms compared. The ideal accumulated radial and circumferential strain values extracted directly from ANSYS software can be readily used to verify the effectiveness of radial and circumferential Lagrangian and Eulerian strain estimation algorithms, as shown in Figures 4 and 5. The ideal radial and circumferential strains for the canine heart model, shown in Figures 7 and 8, were generated using displacement transformations to the polar grid from the ideal axial and lateral displacements. This is due to the fact that the original canine heart model contained only Cartesian locations of the myocardial wall at each time instance over the cardiac cycle.

Note that for the cardiac simulation, additional steps, namely, coordinate rotation and polar strain computations, are needed to generate the final radial and circumferential strain maps. Additional inaccuracy caused by bilinear interpolation onto a polar grid is also generated during this computation process. In comparison, for the ANSYS simulation, ideal radial and circumferential strains are directly extracted from the software program without additional noise artifacts. As a result, when ideal standard deviation values are compared between the two simulations, ANSYS results generally provide the ideal variations without additional noise artifacts when compared with Eulerian and Lagrangian estimations (see Figures 4-5c and d). However, for the canine heart simulation, the differences in the standard deviations between ideal and estimated values are not as apparent due to the additional steps needed to calculate the ideal strain values (see Figures 7-8c and d). In general, both the mean and standard deviation are essential for a complete characterization of myocardial function. The standard deviations provide an insight into the physiological inhomogeneity and estimation variability inherent with strain estimation.

The in vivo human volunteer study utilized only the displacement field estimated along the beam direction to generate radial and circumferential displacements due to phased array geometry. This displacement field is first converted to Cartesian “partial” axial and lateral displacements using axis rotations based on the angle of the phased array beam transmitted. Cartesian displacement pairs are then converted to radial and circumferential displacements and strain fields. Although only “partial” radial and circumferential strains are produced in this process due to the lack of displacement information perpendicular to each beam line, it still has the potential to provide a useful tool to analyze the mechanical properties of the myocardial wall in its natural coordinate system. We should point out that several differences exist between the canine heart model and the in vivo study. First, linear array transducers were used in the simulations whereas a phased array transducer was used for the in vivo study. In addition, active and unpredictable physiological deformations, lower frame rates, as well as potentially higher attenuation levels in in vivo cases all may have a negative impact on the accuracy of strain estimation.

Conclusion

In this paper, we present an approach to estimate radial and circumferential displacement and strain fields using a polar grid between the epi- and endocardial boundaries of the heart along the short-axis view. This polar grid enables Lagrangian tracking by following epi- and endocardial contours over several cardiac cycles, and placing the estimated displacement at appropriate grid points between the contours. The polar grid is also designed to facilitate the calculation of radial and circumferential strains from their displacement counterpart. Radial and circumferential displacements were computed from Cartesian axial and lateral displacement vectors estimated from RF echo signal loops over several cardiac cycles. Lagrangian radial and circumferential strain components were then computed, by tracking pixel or particle deformations, after transferring the Cartesian displacements vectors onto a polar grid between the epi- and endocardial boundaries. Lagrangian accumulation of strain tensors over a cardiac cycle shows good agreement with ideal values, for both ANSYS concentric wall model and a canine heart model, whereas Eulerian results deviate from the ideal variations over a cardiac cycle. Differences between echocardiographic Lagrangian and Eulerian results are also shown using RF data acquired on a healthy human volunteer.