Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 May 17;6:26099. doi: 10.1038/srep26099

Detection of one-dimensional migration of single self-interstitial atoms in tungsten using high-voltage electron microscopy

T Amino 1, K Arakawa 2,a, H Mori 3
PMCID: PMC4869112  PMID: 27185352

Abstract

The dynamic behaviour of atomic-size disarrangements of atoms—point defects (self-interstitial atoms (SIAs) and vacancies)—often governs the macroscopic properties of crystalline materials. However, the dynamics of SIAs have not been fully uncovered because of their rapid migration. Using a combination of high-voltage transmission electron microscopy and exhaustive kinetic Monte Carlo simulations, we determine the dynamics of the rapidly migrating SIAs from the formation process of the nanoscale SIA clusters in tungsten as a typical body-centred cubic (BCC) structure metal under the constant-rate production of both types of point defects with high-energy electron irradiation, which must reflect the dynamics of individual SIAs. We reveal that the migration dimension of SIAs is not three-dimensional (3D) but one-dimensional (1D). This result overturns the long-standing and well-accepted view of SIAs in BCC metals and supports recent results obtained by ab-initio simulations. The SIA dynamics clarified here will be one of the key factors to accurately predict the lifetimes of nuclear fission and fusion materials.

Lattice defects can influence the macroscopic properties of crystalline materials. Therefore, an accurate understanding of the structure and dynamic behaviour of the defects is important to control various processes where defects can be produced, such as crystal growth, energetic particle irradiation, and plastic deformation.

Most elementary defects among the various types of defects are atomic-size point defects (self-interstitial atoms (SIAs) and vacancies). In metals with body-centred cubic (BCC) and face-centred cubic (FCC) structures, the two most probable structures of SIAs are “dumbbell,” where one lattice site is occupied by two atoms, and “crowdion,” where the strain due to the insertion of an extra atom is relaxed along the close-packed direction (crowdion axis)1. Interestingly, the difference in an SIA structure of this kind leads to differences in the manner of SIA migration because a dumbbell structure undergoes three-dimensional (3D) migration, whereas a crowdion structure undergoes one-dimensional (1D) migration along its axis. This difference in SIA migration dimension (3D or 1D) strongly influences the reaction rate between a mobile SIA and an immobile defect2,3,4,5,6,7 and that between two SIAs8,9; a lower migration dimension basically yields lower reaction rates. Therefore, the structure and migration dimension of SIAs is a key factor in processes where SIAs are produced, such as microstructural evolution with irradiation in nuclear fission and fusion systems10.

Since the 1950s, many studies have been performed on the structure of SIAs in BCC and FCC metals in the low-temperature range below the onset of stage III during the recovery processes of specimens irradiated at extremely low temperatures11,12. For BCC metals, intensive X-ray structural analysis and measurements of macroscopic properties have been carried out for iron (Fe) and molybdenum (Mo), and the structure of SIAs in these metals at low temperatures was determined to be <011> dumbbell11,12. In tungsten (W), the structure of SIAs at low temperatures was also determined to be <011> dumbbell from internal friction measurements13,14. To the best of our knowledge, these conclusions—dumbbell SIAs in BCC metals—have been widely accepted. However, conflicting results have been obtained by recent density functional theory (DFT) simulations; these simulations have shown that the most stable SIA structures were <011> dumbbell for Fe15,16 but <111> crowdion for other BCC metals, including Mo and W17,18. Thus, the most elementary issue on defects—the structure and dynamics of single SIAs—is an open question that needs to be experimentally clarified. Therefore, in the present study, we adopted W as a typical BCC metal, which will be an important component for radiation-resistant structural materials for future nuclear fusion reactors19, and we aimed to experimentally determine the migration dimension of SIAs in high-purity W. We also aimed to determine other important parameters related to the dynamics of SIAs—the activation energy for SIA migration, 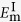Inline graphic, and the reaction radii of an SIA and a vacancy, an SIA and another SIA, and an SIA and an impurity atom, represented as rIV, rII, and rIX, respectively.

One of the most hopeful experimental methods for directly detecting the dynamics of defects within material is transmission electron microscopy (TEM), which has been successfully applied to TEM-visible nanoscale defects20,21. Additionally, the dynamics of even point defects have been directly detected when their migration rate was extremely slow and the specimens were extremely thin (e.g., carbon nanotubes)22. However, even using cutting-edge high-resolution TEM, directly tracing fast-migrating individual point defects (e.g., the jump frequency of an SIA, MI, at 16 K is estimated in this study to be greater than 2.0 × 107 Hz) within comparatively thick specimens is very difficult.

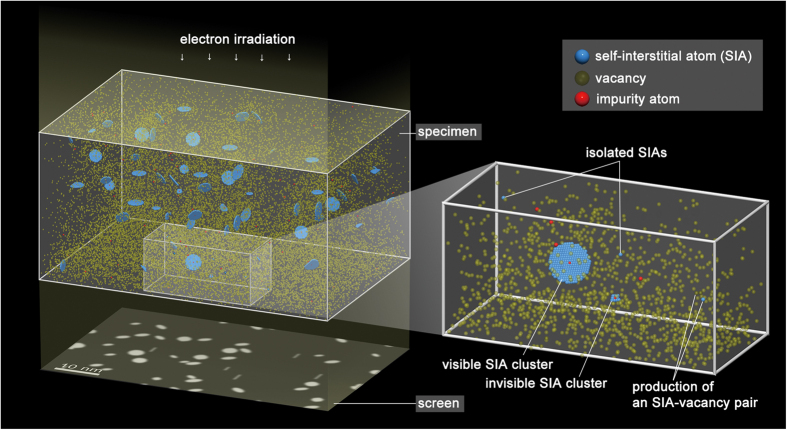
In this study, we propose an alternative method for detecting the dynamics of fast-migrating SIAs, in which high-voltage transmission electron microscopy (HVEM) is effectively combined with computer simulations. A schematic view of the system for the present study is shown in Fig. 1. Under high-energy electron irradiation, only isolated SIAs and vacancies are produced nearly spatially homogeneously during the primary damage process; therefore, the mesoscopic process of the clustering of SIAs, which can be directly observed by HVEM, must reflect SIA dynamics, including the migration dimension. In the current study, we extracted parameters related to SIA dynamics from the formation process of SIA clusters in the form of dislocation loops10 by performing both HVEM experiments and object kinetic Monte Carlo (OKMC)23,24,25,26,27 simulations of numerous point defect reactions and the resultant loop formations. In OKMC simulations, individual objects (point defects and point defect clusters) are tracked in a stochastic manner with the given input parameters. With this method, even the spatial correlation among individual objects is taken into account; hence, if the input parameters are correct, the results are expected to be correct. Needless to say, the results depend on the input parameters. In this study, using this feature of OKMC simulations, we tested a large number of parameter sets and searched for the parameter sets that would reproduce the experimental data. We will show that the range of “correct” parameter sets is strikingly narrow and that the correct parameter sets are fixed with small ambiguities.

Figure 1. Schematic view of the system for the present study.

Figure 1

Open in a new tab

Using this system, we extracted the dynamic behaviour of fast-migrating atomic-size single SIAs, which cannot be directly traced. Within a high-voltage electron microscope, under high-energy electron irradiation, pairs of an SIA and vacancy are produced spatially homogeneously at a constant rate in a tungsten specimen. Individual SIAs migrate and react with other objects, such as immobile vacancies (leading to mutual annihilation), impurity atoms (SIA–impurity complex formation), SIA–impurity complexes (heterogeneous SIA–cluster nucleation), other SIAs (homogeneous SIA–cluster nucleation), SIA clusters (SIA–cluster growth), and surfaces (SIA escape to surfaces). The formation process of nanoscale SIA clusters, which can be directly imaged by TEM, reflects numerous SIA reactions whose rates strongly depend on SIA dynamics, such as migration dimension (3D or 1D), migration frequency, and reaction radius with other objects. In the present study, the dynamics of TEM-invisible SIAs were extracted from direct observation of the formation process of TEM-visible SIA clusters. The displayed microstructure within the specimen is a snapshot (irradiation time: 331.14 s) produced by an object kinetic Monte Carlo (OKMC) simulation of SIA reactions for SIA dynamics parameters that reproduced the experimental data.

Results

HVEM experiment results

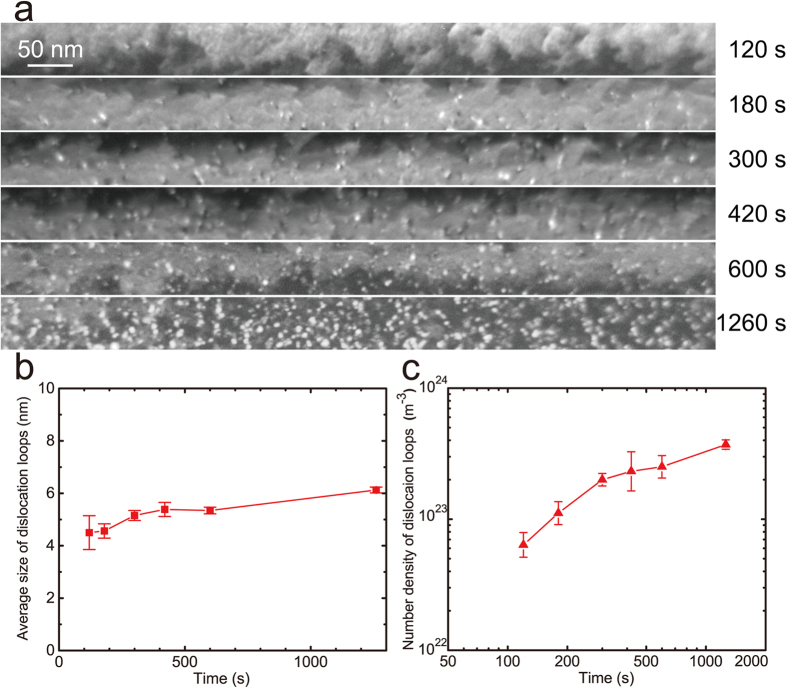
Figure 2a shows TEM images of the irradiated specimen. The white dots denote loops. Figure 2b,c show the temporal variations in the average size and number density of TEM-visible loops larger than 3 nm in diameter, respectively, which were taken from the TEM images, as shown in Fig. 2a. As shown in Fig. 2b, the average diameter of the loops at an irradiation time of 1200 s is approximately 6 nm. In addition, the maximum diameter of the loops was 10 nm at an irradiation time of 1200 s.

Figure 2. HVEM experiment results.

Figure 2

Open in a new tab

SIA clusters were produced in the form of dislocation loops, and they were grown within tungsten with high-energy electron irradiation (acceleration voltage: 2000 kV, beam flux: 3.0 × 1022 m−2s−1, temperature: 16 K, thickness: 48 nm). (a) TEM images showing the formation process of the loops. Temporal variation in (b) the average size (diameter) and (c) the number density of TEM-visible loops larger than 3 nm in diameter, taken from the TEM images as shown in panel a.

In ref. 28, the following results, which were necessary for OKMC simulations in the present study, were obtained for the same W ingot as that used in the present study (see Supplementary Note 1 for details): Loop nucleation occurred through homogeneous nucleation via the direct combination of two SIAs and heterogeneous nucleation via the formation of embryos, which are complexes of an SIA and an impurity atom. The dimension-less concentration of impurities related to the heterogeneous nucleation of loops at 16 K, CX, was evaluated to be 3.6 × 10−6 (case (1)) and 6.9 × 10−6 (case (2)). The 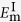Inline graphic values were evaluated to be 0.095 eV for case 1 and less than 0.040 eV for case 2.

OKMC simulation results

In OKMC simulations for both of the migration dimensions of the SIAs (3D and 1D), we initially tried to determine the parameter sets that would reproduce the experimental data shown in Fig. 2b. Next, from among the selected parameter sets, we searched for parameter sets that would reproduce the other experimental data shown in Fig. 2c.

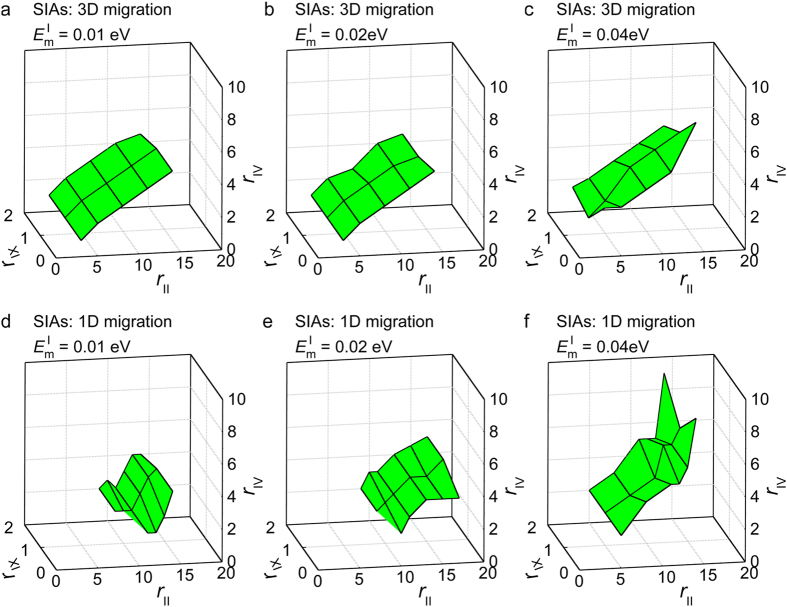
First, we found that there were multiple parameter sets capable of reproducing the experimental result shown in Fig. 2b for both migration dimensions (3D and 1D). In addition, restrictions among these parameters were present. Figure 3a–c and d–f show the relationships among the parameters reproducing the experimental results shown in Fig. 2b for SIA migration dimensions 3D and 1D, respectively. Clearly, the proper parameters for rIV, rII, and rIX are restricted to the curved foil region within the (rIV, rII, rIX) space for each fixed 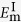Inline graphic value. The results for 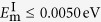Inline graphic were almost the same as those for 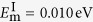Inline graphic; hence, the results for 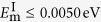Inline graphic are not shown here. When 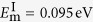Inline graphic (case (1)), parameter sets reproducing the experimental result were not obtained for either SIA migration dimension (3D and 1D). Thus, only case (2) can reproduce the experimental results (see Supplementary Note 2 and Fig. S1). Here, we touch on the origin of the correlation among the parameters shown in Fig. 3. A qualitative explanation in terms of the relationships between the individual parameters and the growth rate of the loops follows: Smaller 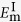Inline graphic and rIV values yield larger growth rates because of the lower reaction rates of an SIA with a vacancy and consequential higher concentrations of SIAs. Larger rII values yield larger growth rates because of the larger reaction radius between an SIA with a loop. Conversely, the rIX value did not influence the growth rate of the loops within the examined range.

Figure 3. Restrictions of the parameter sets in OKMC simulations.

Figure 3

Open in a new tab

There were multiple parameter sets capable of reproducing the experimental result shown in Fig. 2b for both migration dimensions (3D and 1D). In addition, restrictions among these parameters were present. The reproducing sets of the rII, rIV, and rIX values are shown for different 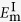Inline graphic values. The SIA migration dimensions are (a–c) 3D and (d–f) 1D. The rIV, rII, and rIX values are shown as atomic-distance units.

Next, we searched for parameter sets that reproduced the experimental results shown in Fig. 2c from among the restricted parameter sets, as shown in Fig. 3. Typical OKMC simulation results for the 3D migration of SIAs are shown in Fig. 4a for various 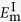Inline graphic values. As shown in this figure, in the case of the 3D migration of SIAs, the densities of the loops at the initial stages were significantly higher than those in the experimental results for any of the parameter sets under the above restrictions. Thus, the 3D migration of SIAs yielded the rapid saturation of loop densities compared to the experimental results. Here, loop density tended to decrease at later stages for the case of 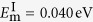Inline graphic because loops absorbed the nearby vacancies primarily owing to their significant accumulation and some of the loops shrank to less than 3 nm in diameter. Typical OKMC simulation results for the 1D migration of SIAs are shown in Fig. 4b for various 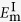Inline graphic values. When 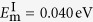Inline graphic, the loop density decreases at later stages because of the same reason as the 3D migration of SIAs. However, when 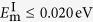Inline graphic, the experimental result is reproduced. Strikingly, the perfect parameter sets that reproduced both of the experimental results had a narrow range as follows: SIA migration dimension: 1D, 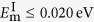Inline graphic (MI ≥ 2.0 × 107 Hz), rIV = 4.0, rII = 13.0, and rIX = 1.0 atomic-distance units. The 1D migration dimension supports the recent DFT simulation results, in which the stable structure of SIAs in W was concluded to be crowdion17,18. In addition, other obtained values are consistent with those in recent simulation studies, as shown in the next section. This verifies the method in the present study.

Figure 4. Representative OKMC simulation results.

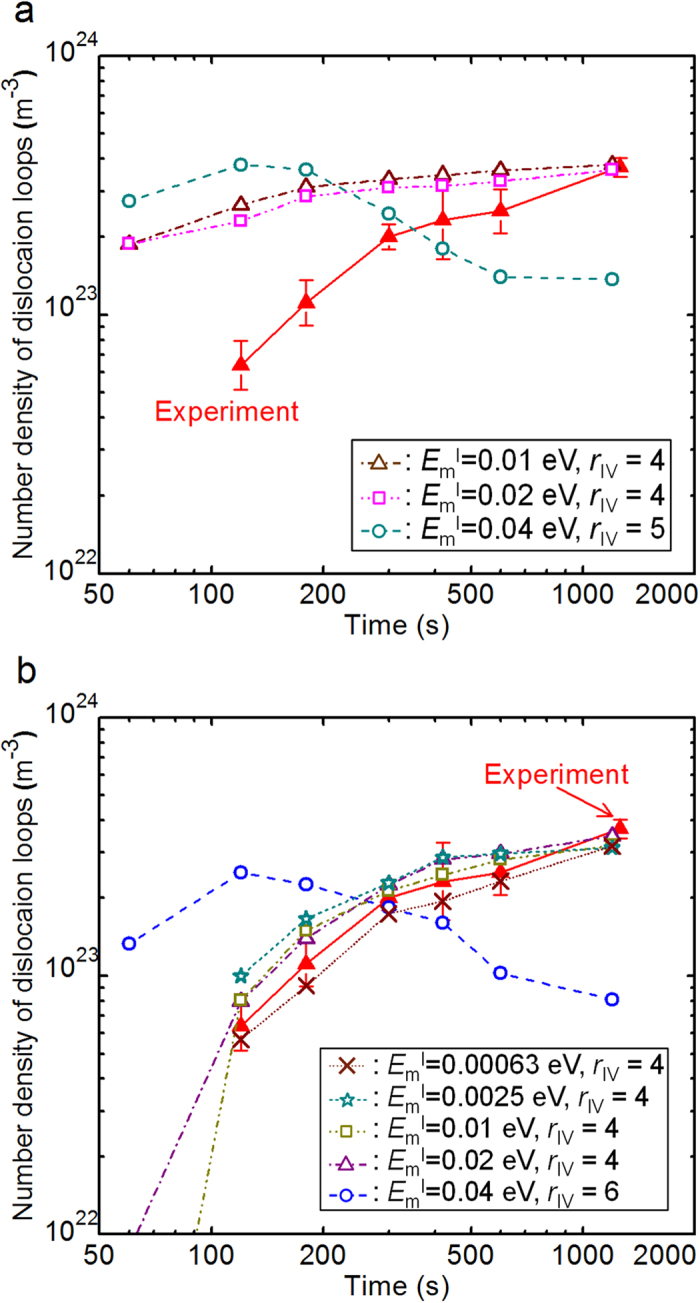
Figure 4

Open in a new tab

We searched for parameter sets reproducing the experimental result shown in Fig. 2c from among the restricted parameter sets, as shown in Fig. 3. Representative temporal variations in the number density of the dislocation loops are shown for (a) SIA migration dimension: 3D, rII = 11.0, rIX = 0.0 and (b) SIA migration dimension: 1D, rII = 13.0, rIX = 1.0. The rIV, rII, and rIX values are shown as atomic-distance units.

Discussion

The reason why loop formation is slower for the 1D migration of SIAs, as shown in Fig. 4, is qualitatively explained as follows. According to reaction-rate theory, the reaction rate of an SIA with spatially homogeneous arranged sinks is lower for the 1D migration of SIAs2,5,7,9. Therefore, the reaction rate of an SIA with another SIA or an impurity atom decreases, which makes the loop nucleation slower. From the analysis of our OKMC simulation results among all kinds of SIA reactions (see Supplementary Fig. S2), the primary reaction was that between an SIA and a vacancy. For the 1D migration of SIAs, this reaction was not homogeneous but was strongly spatially correlated and enhanced because an SIA was frequently recombined with its original counterpart vacancy, which was generated, together with the SIA, and placed within the path of the 1D-migrating SIA (Supplementary Fig. S2c). Enhanced reactions of an SIA and a vacancy also make loop nucleation slower. Thus, slower loop formation for the 1D migration of SIAs is attributed to both the decreased reactions of an SIA with another SIA (Supplementary Fig. S2a) or an impurity atom (Supplementary Fig. S2b) and the enhanced reactions of an SIA with a vacancy (Supplementary Fig. S2c).

Previous experimental studies on the structure of SIAs in W have deduced a <011> dumbbell structure using the internal-friction technique13,14, which seems inconsistent with the results obtained in the present study. However, with the measurements of macroscopic properties, it is difficult to precisely assign the origin of internal friction peaks. In addition, in reference to previous DFT simulation studies17,18, the formation energy of a crowdion is smaller than that of a dumbbell by only 0.026 eV. Therefore, even if the origin of the internal friction peak is confirmed to be SIAs, the stable SIA structure may change because of the application of stress for the internal friction measurement.

Here, we touch on a classical view of the SIA structure in the so-called “conversion-two-interstitial model,”29 which has been proposed for FCC metals. In this model, crowdion was thought to be a metastable structure which is formed from irradiation at very low temperatures and is able to convert to a stable dumbbell in stage I. To the best of our knowledge, this model has been negated for FCC metals by the “one-interstitial model,” where the SIA structure was thought to be an invariably stable dumbbell11,12. However, the results obtained in the present study require us to consider the “conversion-two-interstitial model” again. Strictly speaking, in the present study, we do not indicate whether crowdion in W is a metastable structure realized only for low temperatures or the most stable one realized even for high temperatures because the examined temperature is limited to 16 K. To clarify this problem, further similar studies at higher temperatures and with other metals are required.

In comparatively older molecular dynamics (MD) simulations, the stable structure of an SIA has been confirmed as <011> dumbbell, and 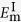Inline graphic has been evaluated to be 0.37 eV30 and 0.54 eV31, values that are significantly higher than the value of 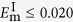Inline graphic eV obtained in the present study. However, in recent MD simulation studies using newer interatomic potentials, the stable structure of an SIA was <111> crowdion, and the evaluated 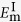Inline graphic values were comparatively lower, ranging from 0.009 eV32 to 0.061 eV33. Lower 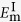Inline graphic values have also been derived from more recent studies using a combination of DFT simulations and the Frenkel–Kontrova model (0.0026 eV)34 and a molecular statics simulation (0.002 eV)35. These simulation studies imply that the 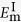Inline graphic value was originally extremely low. Conversely, evaluations of 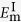Inline graphic have been performed by recovery experiments of specimens irradiated at approximately 4 K (the boiling point of liquid helium). A study of electric resistance measurements yielded an 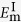Inline graphic value of 0.054 eV36, and a study of field ion microscopy observation of surface SIAs yielded a value of 0.085 eV37, which are higher than recent 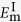Inline graphic values determined by simulations32,34,35. The value of 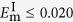Inline graphic eV obtained in the present study is more consistent with recent simulation studies.

The reaction radius values obtained in the present study are rIV = 4.0, rIX = 1.0, and rII = 13.0 atomic-distance units. There are no studies evaluating the latter two available for comparison. However, the rIV value obtained by an electric resistance recovery experiment was 3.338. Referring to a molecular statics simulation study, the reaction volume for a crowdion is an ellipsoid; the semi-major radius is 6.6, and the semi-minor radius is 2.035. By approximating this ellipsoid as a sphere, the radius becomes 3.0. The rIV value obtained in the present study (4.0) is close to the values obtained in the former studies35,38, which reflects the accuracy of the present study.

In conclusion, using a combination of HVEM experiments and OKMC simulations, we extracted the dynamics of fast-migrating single SIAs in W, which cannot be directly traced, even by cutting-edge high-resolution TEM. We revealed that the migration dimension of SIAs is not 3D but 1D, and we resolved the contradiction between the results in previous experiments and recent simulations. The SIA dynamics clarified here are key factors for predicting the lifetime of nuclear fission and fusion materials, in which SIAs are produced with high-energy particle irradiation. In addition, this study opens a new pathway for further experimental investigation of SIA dynamics for a wide range of inorganic materials and more complex point-defect dynamics such as interactions between vacancies and solute atoms, which is important to accurately understanding the responses of a wide range of metallic alloys to heat treatment.

Methods

High-voltage electron microscopy experiments

An ingot of high-purity coarse-grained polycrystalline W with a purity of 99.9999 mass% (JX Nippon Mining & Metals Co., Tokyo, Japan) was used. The impurity amounts of the ingot are shown in ref. 28. One grain of the ingot was cut and thinned to (011) disks with a thickness of 0.1 mm using spark erosion and mechanical polishing. Then, the disks were perforated at the centre by electropolishing so that the periphery of the hole became cross-sectionally wedge-shaped. The high-energy electron irradiation of the thin-foil specimens was performed within an HVEM (Hitachi H-3000) at 16 K using a liquid-helium cooling specimen holder (Oxford instruments), where thermal migration of vacancies was frozen39, and the radiation-induced microstructure was observed. The acceleration voltage for electron irradiation was 2000 kV. The beam flux was 3.0 × 1022 m−2s−1. From Fig. 6 in ref. 40, the displacement energy for the [011] electron incidence was evaluated to be 46 eV, yielding the displacement cross-section of 30 × 10−28 m2 41. Therefore, this beam flux corresponded to a displacement per atom (dpa) rate (point-defect pair generation rate) of 9.0 × 10−5 dpa s−1. TEM observation was carried out using the weak-beam dark-field technique 42 with a reflection of g = 200. Under this condition, loops with all of the Burgers vectors, b = 1/2<111> 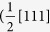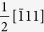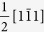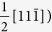Inline graphic, Inline graphic, Inline graphic, Inline graphic, with a diameter larger than approximately 3 nm were imaged. The sizes of the loops were evaluated for areas with a thickness of 48 nm, which was measured using the equal-thickness fringes43. The number densities of the loops were evaluated from the dependence of the areal densities on thickness, by taking into consideration the presence of denuded zones44.

Object kinetic Monte Carlo simulations

Conditions for OKMC simulations are as follows:

  1. Simulation cells were rectangular parallelepiped boxes composed of BCC lattice with (011) surfaces. Periodic boundary conditions were applied to the end faces of the cell except the upper and lower surfaces. The size of the cell for the evaluation of average loop size was 96.1 nm × 15.8 nm × 48.0 nm (thickness). The loop density was evaluated from the thickness dependence of the areal density of loops for cells with thicknesses of 10.0, 30.0, 48.0, and 70.0 nm, and the corresponding cell sizes were 20.1 nm × 1442.5 nm × 10.0 nm, 59.9 nm × 162.4 nm × 30.0 nm, 96.1 nm × 63.2 nm × 48.0 nm, and 139.9 nm × 29.7 nm × 70.0 nm, respectively.

  2. SIA, vacancies, and impurities were located at normal atom positions.

  3. A pair consisting of an SIA and a vacancy was produced because of knock-on displacement by one electron incidence. In ref. 40, it was shown that the displacements of atoms toward the <111> and <001> directions occur much more easily than those toward the <011> directions. Among multiple <111> and <001> directions, the most preferential displacement directions for the electron incidence in the direction of [011] were the [111] and 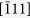Inline graphic directions, which corresponded to a minimum recoil angle of approximately 35 degrees. Therefore, for the [011] electron incidence, the initial position of an SIA was set to be displaced from the initial position of a corresponding vacancy towards the [111] or 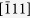Inline graphic directions by the (rIV + 1) atomic distance. The dpa rate was set to be 9.0 × 10−5 dpa s−1, as in the experiments.

  4. In the case of 3D migration, an SIA was moved in the direction of one of eight <111> directions by one atomic distance. In the case of 1D migration, an SIA underwent a back and forth motion by one atomic distance parallel to the original displacement direction. For both dimensions, the motion direction for individual motion steps was chosen randomly.

  5. SIA clusters were circular loops with b = 1/2<111> and habit planes of {110}. The spontaneous change in b of the loops20,45 was neglected.

  6. Vacancies and impurities were immobile.

  7. MD simulations and TEM studies have clarified that a loop undergoes 1D glide diffusion along its b direction by thermal energy21,46,47. Here, in reference to the MD simulation results47, the jump frequency of a loop (and a single SIA), which was composed of n SIAs and free from impurities, was set to be
    graphic file with name srep26099-m30.jpg
    where ν0 is the Debye frequency (4.05 × 1013 Hz18) and k is the Boltzmann constant. We note that it is not clear if this classical equation holds and the attempt frequency is Debye frequency for the jump of a loop (and a single SIA) even at low temperatures such as 16 K, which is considerably lower than the Debye temperature (310 K18) (see Supplementary Note 3). However, what was important here was the absolute values of MI rather than the accurate form of the equation for MI. Therefore, in the present study, we adopted this classical equation, and discretized input MI values by discretizing input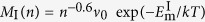 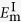Inline graphic values, as shown in condition 11. On the other hand, a single SIA and loop combined with impurities were immobile and thermally stable. A single SIA and loop moved when they were provided with an energy larger than 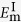Inline graphic by momentum transferred from an incident electron. It is known that de-pinning of loops from impurities is enhanced by electron irradiation48. However, this effect is not significant for low irradiation temperatures and low beam fluxes, as in this experiment; therefore, it was neglected.

  8. The reaction volume between an SIA and another object was approximated as a sphere with a corresponding radius.

  9. Combinations of a vacancy and another vacancy, a vacancy and an impurity atom, and an impurity and another impurity did not occur.

  10. The combination of two loops occurred when the minimum distance between SIAs composing each loop were equal to or smaller than rII (here, a single SIA is regarded as the minimum size loop, with b parallel to its motion direction). From MD simulations and TEM experiment studies, it was clarified that one loop basically absorbs the other one upon collision between the two loops, even those with different b values49,50,51. In the present study, a loop that was stationary at the moment just before the collision absorbed the other, and the mass centre of the new loop shifted to that of the absorbing loop. When both loops were immobilized by impurities, the smaller one was absorbed by the larger one and the impurity atom, which had pinned the absorbed one, became free. The combination of a loop with a surface, a vacancy, and an impurity atom similarly occurred depending on the values of 1/2rII, rIV, and rIX, respectively.

  11. The range of examined parameters were as follows: migration dimension of an SIA: 3D, 1D; 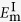Inline graphic for case (1): 0.095 eV, 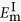Inline graphic for case (2): 0.00063, 0.0013, 0.0025, 0.0050, 0.010, 0.020, and 0.040 eV; CX for case (1): 3.6 × 10−6, CX for case (2): 6.9 × 10−6; 1.0 ≤ rIV ≤ 9.0 (0.5 step), rII: 3.0, 5.0, 8.0, 9.0, 10.0, 11.0, 12.0, 13.0, and 14.0, and 0.0 ≤ rIX ≤ 4.0 (1.0 step) in atomic-distance units. The total number of examined parameter sets was approximately 500.

  12. In comparisons of OKMC simulation results to experimental results, only loops larger than 3 nm in diameter were counted, as was done in the experimental measurements.

  13. The judgment criteria for reproduction of the experimental results shown in Fig. 2b were as follows: (i) loops larger than 3 nm in diameter appeared within the computation box by an irradiation time of 120 s (this corresponds to a situation where the number density of TEM-visible loops was greater than 1.4 × 1022 m−3), (ii) the average diameter, d, of loops at an irradiation time of 1200 s was 5.5 ≤ d ≤ 6.5 nm. Additionally, as shown in the main text, (iii) the maximum diameter of the loops was less than 10 nm even at an irradiation time of 1200 s.

Additional Information

How to cite this article: Amino, T. et al. Detection of one-dimensional migration of single self-interstitial atoms in tungsten using high-voltage electron microscopy. Sci. Rep. 6, 26099; doi: 10.1038/srep26099 (2016).

Supplementary Material

Supplementary Information
srep26099-s1.pdf (517.1KB, pdf)

Acknowledgments

This work was financially supported by Grants-in-Aid for Scientific Research (Grant No. 24360395, 24656371, 22224012, 15H04244, and 15K14109) from Japan Society for the Promotion of Science, CREST, Japan Science and Technology, and the Iron and Steel Institute of Japan Research Promotion Grant. Part of this work was supported by the “Advanced Characterization Nanotechnology Platform, Nanotechnology Platform Program” of the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan, at the Research Centre for Ultra-High Voltage Electron Microscopy (Nanotechnology Open Facilities) in Osaka University and TATARA Nanotechnology Project Centre in Shimane University. We highly appreciate the reviewers for their important suggestions.

Footnotes

Author Contributions K.A. conceived and designed the experiments and simulations. T.A. and K.A. performed the experiments. T.A. carried out the analyses and simulations. T.A., K.A. and H.M. discussed the results and commented on the manuscript.

References

  1. Corbett J. W. Electron Radiation Damage in Semiconductors and Metals. Academic Press, New York and London (1966). [Google Scholar]
  2. Frank W. Theory of Crystal Defects. In: Defects in Refractory Metals (eds. Batist R. D., Nihoul J. & Stals L.). SCK/CEN, Mol (1972). [Google Scholar]
  3. Trinkaus H., Singh B. N. & Foreman A. J. E. Glide of interstitial loops produced under cascade damage conditions: Possible effects on void formation. J Nucl Mater 199, 1–5 (1992). [Google Scholar]
  4. Borodin V. A. & Ryazanov A. I. Swelling modification by one-dimensional diffusion of cascade-produced small interstitial clusters. J Nucl Mater 256, 47–52 (1998). [Google Scholar]
  5. Barashev A. V., Golubov S. I. & Trinkaus H. Reaction kinetics of glissile interstitial clusters in a crystal containing voids and dislocations. Philosophical Magazine A 81, 2515–2532 (2001). [Google Scholar]
  6. Semenov A. A. & Woo C. H. Void lattice formation as a nonequilibrium phase transition. Physical Review B 74, 15 (2006). [Google Scholar]
  7. Jansson V., Malerba L., De Backer A., Becquart C. S. & Domain C. Sink strength calculations of dislocations and loops using OKMC. J Nucl Mater 442, 218–226 (2013). [Google Scholar]
  8. Gösele U. & Seeger A. Theory of bimolecular reaction rates limited by anisotropic diffusion. Philos Mag 34, 177–193 (1976). [Google Scholar]
  9. Amino T., Arakawa K. & Mori H. Reaction rate between 1D migrating self-interstitial atoms: an examination by kinetic Monte Carlo simulation. Philos Mag 91, 3276–3289 (2011). [Google Scholar]
  10. Gary S. W. Fundamentals of radiation Materials Science. Springer, Berlin (2007). [Google Scholar]
  11. Schilling W. Self-interstitial atoms in metals. J Nucl Mater 69–70, 465–489 (1978). [Google Scholar]
  12. Wollenberger H. J. In: Physical Metallurgy, Part II (eds. Cahn R. W. & Haasen P.). North Holland Physics Publishing, Amsterdam (1983). [Google Scholar]
  13. DiCarlo J. A., Snead C. L. & Goland A. N. Stage-I interstitials in electron-irradiated tungsten. Physical Review 178, 1059–1072 (1969). [Google Scholar]
  14. Okuda S. & Mizubayashi H. Free Migration of Interstitials in Tungsten. Physical Review Letters 34, 815–817 (1975). [Google Scholar]
  15. Domain C. & Becquart C. S. Ab initio calculations of defects in Fe and dilute Fe-Cu alloys. Physical Review B 65, 024103 (2001). [Google Scholar]
  16. Fu C.-C., Willaime F. & Ordejón P. Stability and mobility of mono- and di-interstitials in α-Fe. Physical Review Letters 92, 175503 (2004). [DOI] [PubMed] [Google Scholar]
  17. Nguyen-Manh D., Horsfield A. P. & Dudarev S. L. Self-interstitial atom defects in bcc transition metals: Group-specific trends. Physical Review B 73, 020101(R) (2006). [Google Scholar]
  18. Derlet P. M., Nguyen-Manh D. & Dudarev S. L. Multiscale modeling of crowdion and vacancy defects in body-centered-cubic transition metals. Physical Review B 76, 054107 (2007). [Google Scholar]
  19. Rieth M. et al. Review on the EFDA programme on tungsten materials technology and science. J Nucl Mater 417, 463–467 (2011). [Google Scholar]
  20. Arakawa K., Hatanaka M., Kuramoto E., Ono K. & Mori H. Changes in the Burgers vector of perfect dislocation loops without contact with the external dislocations. Physical Review Letters 96, 125506 (2006). [DOI] [PubMed] [Google Scholar]
  21. Arakawa K. et al. Observation of the one-dimensional diffusion of nanometer-sized dislocation loops. Science 318, 956–959 (2007). [DOI] [PubMed] [Google Scholar]
  22. Suenaga K. et al. Imaging active topological defects in carbon nanotubes. Nature Nanotechnolgy 2, 358–360 (2007). [DOI] [PubMed] [Google Scholar]
  23. Rottler J., Srolovitz D. J. & Car R. Point defect dynamics in bcc metals. Physical Review B 71, 064109 (2005). [Google Scholar]
  24. Souidi A. et al. Dependence of radiation damage accumulation in iron on underlying models of displacement cascades and subsequent defect migration. J Nucl Mater 355, 89–103 (2006). [Google Scholar]
  25. Ortiz C. J. & Caturla M. J. Simulation of defect evolution in irradiated materials: Role of intracascade clustering and correlated recombination. Physical Review B 75, 184101 (2007). [Google Scholar]
  26. Björkas C., Nordlund K. & Caturla M. J. Influence of the picosecond defect distribution on damage accumulation in irradiated α-Fe. Physical Review B 85, 024105 (2012). [Google Scholar]
  27. Xu D., Wirth B. D., Li M. & Kirk M. A. Defect microstructural evolution in ion irradiated metallic nanofoils: Kinetic Monte Carlo simulation versus cluster dynamics modeling and in situ transmission electron microscopy experiments. Applied Physics Letters 101, 101905 (2012). [Google Scholar]
  28. Amino T., Arakawa K. & Mori H. Activation energy for long-range migration of self-interstitial atoms in tungsten obtained by direct measurement of radiation-induced point-defect clusters. Philosophical Magazine Letters 91, 86–96 (2011). [Google Scholar]
  29. Schilling W., Burger G., Isebeck K. & Wenzl H. Annealing Stages in the Electrical Resistivity of Irradiated FCC Metals. In: Vacancies and Interstitials in Metals (eds. Seeger A., Schumacher D., Schilling W. & Diehl J.). North Holland, Amsterdam, 255–361 (1970). [Google Scholar]
  30. Guinan M. W., Stuart R. N. & Borg R. J. Fully dynamic computer simulation of self-interstitial diffusion in tungsten. Physical Review B 15, 699–710 (1977). [Google Scholar]
  31. Carlberg M. H., Münger E. P. & Hultman L. Dynamics of self-interstitial structures in body-centred-cubic W studied by molecular dynamics simulation. Journal of Physics: Condensed Matter 12, 79–86 (2000). [Google Scholar]
  32. Zhou W. H., Li Y. G., Huang L. F., Zeng Z. & Ju X. Dynamical behaviors of self-interstitial atoms in tungsten. J Nucl Mater 437, 438–444 (2013). [Google Scholar]
  33. Fikar J. & Schäublin R. Molecular dynamics simulation of radiation damage in bcc tungsten. J Nucl Mater 386–388, 97–101 (2009). [Google Scholar]
  34. Fitzgerald S. P. & Nguyen-Manh D. Peierls potential for crowdions in the bcc transition metals. Physical Review Letters 101, 115504 (2008). [DOI] [PubMed] [Google Scholar]
  35. Ahlgren T., Heinola K., Juslin N. & Kuronen A. Bond-order potential for point and extended defect simulations in tungsten. Journal of Applied Physics 107, 033516 (2010). [Google Scholar]
  36. Dausinger F. & Schultz H. Long-range migration of self-interstitial atoms in tungsten. Physical Review Letters 35, 1773–1775 (1975). [Google Scholar]
  37. Scanlan R. M., Styris D. L. & Seidman D. N. An in-situ field ion microscope study of irradiated tungsten. Philos Mag 23, 1459–1478 (1971). [Google Scholar]
  38. Biget M., Rizk R., Vajda P. & Bessis A. On the spontaneous recombination volume of Frenkel defects in irradiated b.c.c. metals. Solid State Communications 16, 949–952 (1975). [Google Scholar]
  39. Ehrhart P., Jung P. & Schultz H. & Ullmaier, H. Atomic Defects in Metals. Springer-Verlag, Berlin (1991). [Google Scholar]
  40. Maury F., Biget M., Vajda P., Lucasson A. & Lucasson P. Frenkel pair creation and stage I recovery in W crystals irradiated near threshold. Radiation Effects 38, 53–65 (1978). [Google Scholar]
  41. Oen O. S. Cross sections for atomic displacements in solids by fast electrons. In: ORNL-3813 (1965). [Google Scholar]
  42. Jenkins M. L. & Kirk M. A. Characterization of Radiation Damage by Transmission Electron Microscopy. Institute of Physics, Bristol and Philadelphia (2001).
  43. Hirsch P. B., Howie A., Nicholson R. B., Pashley D. W. & Whelan M. J. Electron Microscopy of Thin Crystals. Butterworths, London (1965).
  44. Yoshida N. & Kiritani M. Point defect clusters in electron-irradiated gold. Journal of the Physical Society of Japan 35, 1418–1429 (1973). [Google Scholar]
  45. Gao F., Heinisch H., Kurtz R. J., Osetsky Y. N. & Hoagland R. G. Migration and directional change of interstitial clusters in α-Fe: searching for transition states by the dimer method. Philos Mag 85, 619–627 (2005). [Google Scholar]
  46. Marian. J. et al. Dynamics of self-interstitial cluster migration in pure α-Fe and Fe-Cu alloys. Physical Review B 65, 144102 (2002). [Google Scholar]
  47. Osetsky Y. N., Bacon D. J., Serra A., Singh B. N. & Golubov S. I. One-dimensional atomic transport by clusters of self-interstitial atoms in iron and copper. Philos Mag 83, 61–91 (2003). [Google Scholar]
  48. Satoh Y., Matsui H. & Hamaoka T. Effects of impurities on one-dimensional migration of interstitial clusters in iron under electron irradiation. Physical Review B 77, 94135 (2008). [Google Scholar]
  49. Osetsky Y. N., Serra A. & Priego V. Interactions between mobile dislocation loops in Cu and α-Fe. J Nucl Mater 276, 202–212 (2000). [Google Scholar]
  50. Marian J., Wirth B. D. & Perlado J. M. Mechanism of formation and growth of <100> interstitial loops in ferritic materials. Physical Review Letters 88, 255507 (2002). [DOI] [PubMed] [Google Scholar]
  51. Arakawa K., Amino T. & Mori H. Direct observation of the coalescence process between nanoscale dislocation loops with different Burgers vectors. Acta Mater 59, 141–145 (2011). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep26099-s1.pdf (517.1KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES