Neural spike-timing patterns vary with sound shape and periodicity in three auditory cortical fields

Abstract

Mammals perceive a wide range of temporal cues in natural sounds, and the auditory cortex is essential for their detection and discrimination. The rat primary (A1), ventral (VAF), and caudal suprarhinal (cSRAF) auditory cortical fields have separate thalamocortical pathways that may support unique temporal cue sensitivities. To explore this, we record responses of single neurons in the three fields to variations in envelope shape and modulation frequency of periodic noise sequences. Spike rate, relative synchrony, and first-spike latency metrics have previously been used to quantify neural sensitivities to temporal sound cues; however, such metrics do not measure absolute spike timing of sustained responses to sound shape. To address this, in this study we quantify two forms of spike-timing precision, jitter, and reliability. In all three fields, we find that jitter decreases logarithmically with increase in the basis spline (B-spline) cutoff frequency used to shape the sound envelope. In contrast, reliability decreases logarithmically with increase in sound envelope modulation frequency. In A1, jitter and reliability vary independently, whereas in ventral cortical fields, jitter and reliability covary. Jitter time scales increase (A1 < VAF < cSRAF) and modulation frequency upper cutoffs decrease (A1 > VAF > cSRAF) with ventral progression from A1. These results suggest a transition from independent encoding of shape and periodicity sound cues on short time scales in A1 to a joint encoding of these same cues on longer time scales in ventral nonprimary cortices.

humans and other animals use shape and periodicity temporal cues to identify acoustic objects. Shape cues include the rising and falling slopes and the duration of change in the sound envelope amplitude and are critical for perception of intensity and timbre (Irino and Patterson 1996; Iverson and Krumhansl 1993), speech (Drullman et al. 1994), water sounds (Geffen et al. 2011), and quality of musical instruments (Paquette and Peretz 1997; Risset and Wessel 1982). Periodicity cues emerge when sounds are repeated at regular time intervals and are important for perception of rhythm at low modulation frequencies (up to ∼20 Hz) (Plomp 1983), roughness at intermediate frequencies (∼20–200 Hz) (Terhardt 1974; von Helmholtz 1863), and pitch at higher modulation frequencies (∼100 - 800 Hz) (Burns and Viemeister 1981; Joris et al. 2004; Plomp 1967; Pollack 1969).

Primary (A1) and nonprimary auditory cortices are essential for perception of temporal sound cues in mammals (Lomber and Malhotra 2008; Threlkeld et al. 2008), but how they might encode these cues remains unclear. Neurons in A1 and nonprimary auditory cortices can spike synchronously with each cycle of sinusoid amplitude-modulated (SAM) sound providing a response correlate for sound periodicity cues (Doron et al. 2002; Eggermont 1998; Joris et al. 2004; Niwa et al. 2013; Schreiner and Urbas 1988; Schulze and Langner 1997). In A1, spike rate and first-spike latency change systematically with sound envelope shape cues (Heil 1997; Lu et al. 2001a, 2001b). However, there is evidence that nonprimary cortices can be more sensitive than A1 to sound envelope shape (Schreiner and Urbas 1988). These prior studies raise the possibility that there are differences in how auditory cortical fields encode temporal sound cues.

In the present study, we investigate spike-timing responses to temporal sound cues in A1, ventral (VAF), and caudal suprarhinal (cSRAF) auditory cortical fields of the rat, because these fields have distinct sound sensitivities and thalamocortical pathways that could support unique temporal sound cue processing (Centanni et al. 2013; Higgins et al. 2010; Polley et al. 2007; Storace et al. 2010, 2011, 2012). Prior studies found that spike rate, spiking synchrony, and first-spike latency change with temporal sound cues in A1 (Heil 2004; Joris et al. 2004; Lu et al. 2001b), but these metrics do not determine absolute spike timing of sustained responses or spike-timing variation over repeated sound presentations. To overcome these limitations, in the present study we examine two forms of spike-timing variation, jitter and reliability, which are known to convey information about temporal sound cues (DeWeese et al. 2005; Kayser et al. 2010; Zheng and Escabí 2008, 2013). In all three cortical fields, we find that spike-timing jitter decreases logarithmically with the sound-shaping parameter f_c providing a neural response correlate for sound shape. Conversely, reliability decreases logarithmically with sound modulation frequency providing a neural correlate for sound periodicity cues. In A1, we find that jitter and reliability change independently with sound periodicity cues much like they do in auditory midbrain (Zheng and Escabí 2008, 2013); however, this is not the case in the ventral cortices. Finally, jitter time scales increase and modulation frequency upper cutoffs decrease with ventral progression from A1. The results indicate that A1 and ventral cortices have distinct spike-timing responses that correlate with and could provide a neural code for temporal sound cues.

METHODS

Surgical Procedure and Electrophysiology

Data were collected from 16 male Brown Norway rats (age 48–100 days). All animals were housed and handled according to a protocol approved by the Institutional Animal Care and Use Committee of the University of Connecticut. Craniotomies were performed over the temporal cortex to conduct high-resolution intrinsic optical imaging (IOI) and extracellular recording. All recordings were obtained from the right cerebral hemisphere, because we have previously examined and reported anatomic pathways to the three cortical fields in the right cerebral hemisphere (Higgins et al. 2010; Polley et al. 2007; Storace et al. 2010, 2011, 2012). Anesthesia was induced and maintained with a cocktail of ketamine and xylazine throughout the surgery and during optical imaging and electrophysiological recording procedures (induction dosages: ketamine 40–80 mg/kg, xylazine 5–10 mg/kg; maintenance dosages: ketamine 20–40 mg/kg, xylazine 2.5–5 mg/kg). A closed-loop heating pad was used to maintain body temperature at 37.0 ± 2.0°C. Dexamethasone and atropine sulfate were administered every 12 h to reduce cerebral edema and secretions in the airway, respectively. A tracheotomy was performed to avoid airway obstruction and minimize respiration-related sound, and heart rate and blood oxygenation were monitored through pulse oximetry (Kent Scientific, Torrington, CT).

Locating Auditory Fields with Intrinsic Optical Imaging

Prior studies found that IOI tone-frequency responses and their topographic organization were correlated with tone responses assessed with multiunit (Kalatsky et al. 2005; Storace et al. 2011) and surface micro-electrocorticographic (μECOG) electrophysiological measures (Escabí et al. 2014). Thus the topographic organization of cortical responses to tone frequency was mapped with high-resolution Fourier IOI to locate A1, VAF, and cSRAF auditory fields (see Fig. 1), as described in detail elsewhere (Higgins et al. 2008; Kalatsky et al. 2005; Kalatsky and Stryker 2003). Briefly, surface vascular patterns were imaged with a green (546 nm) interference filter at a 0-μm plane of focus. The plane of focus was shifted 600 μm below the focus plane for the surface blood vessels to obtain IOI with a red (610 nm) interference filter. Tone sequences consisting of 16 tone pips (50-ms duration, 5-ms rise and decay time) delivered with a presentation interval of 300 ms were presented with matched sound level to both ears. Tone frequencies were varied from 1.4 to 45.3 kHz (one-eighth-octave steps) in ascending and subsequently descending order, and the entire sequence was repeated every 4 s. Hemodynamic delay was corrected by subtracting ascending and descending frequency phase maps to generate a difference phase map (Kalatsky and Stryker 2003).

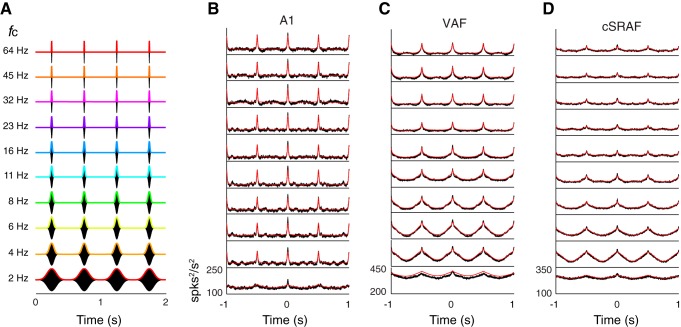
Fig. 1.

Assessing tone-response properties and organization of 3 auditory cortical fields in rat. A: primary (A1), ventral (VAF), and caudal suprarhinal fields (cSRAF) are located with intrinsic optical imaging (IOI) of metabolic responses to tone sequences (methods) as illustrated with this example from the right brain hemisphere of 1 animal. Dashed lines indicate boundaries between fields. B, D, and F: frequency-response areas (FRA) obtained from the multiunit response to tones for penetration sites from A1 (B), VAF (D), and cSRAF (F). Cortical recording positions for each site are indicated in A (filled circles). Corresponding FRA plots present spike rate for different variations in sound frequency (1.4–45.3 kHz) and level (15–85 dB SPL). Best frequency (BF; filled circles) and bandwidths (black bars) are computed and indicated for each sound level in the significant FRA (methods). C, E, and G: poststimulus time spike-rate histograms (PSTHs) and maximum responses (asterisks) of the average responses across all tones in the FRA for each neuron, corresponding to B, D, and F, respectively. H and I: rank order differences in bandwidth and peak latency across fields. H: response bandwidth (in octaves) at 75 dB SPL changes between A1, VAF, and cSRAF [F(2, 207) = 14.4, P < 0.001] with mean (SE): 2.3 (0.07), 2.1 (0.05), and 1.8 (0.08), respectively. Post hoc independent samples t-tests reveal a rank-order decrease in bandwidth with ventral progression from A1 (A1 > VAF: P < 0.05; VAF > cSRAF: P < 0.001; A1 > cSRAF: P < 0.001). I: the PSTH peak latencies increased significantly [F(2, 218) = 28.9, P < 0.001] between A1, VAF, and cSRAF: 24 (0.4), 32 (1.0), and 39 (1.9) ms, respectively. In this and subsequent figures, asterisks indicate significance level of post hoc pairwise comparisons: *P < 0.05; **P < 0.001 (methods).

An example IOI illustrates anatomic locations and frequency organizations of the three cortical fields examined in this study with cortical field borders (see Fig. 1A, dashed lines) determined as explained in detail previously (Higgins et al. 2010; Polley et al. 2007; Storace et al. 2012). Briefly, A1 and VAF were defined by low-to-high tone-frequency response gradients in the caudal-to-rostral anatomic direction; whereas cSRAF was defined by a low-to-high frequency response gradient in the opposite direction of VAF (Higgins et al. 2010). Accordingly, a high tone-frequency-sensitive region defines the border between VAF and cSRAF (see Fig. 1A, dashed line passing through 32-kHz zone). The center of the border between VAF and A1 was 1.25 mm dorsal to the center of the VAF-cSRAF border; A1 spanned 1.25 mm dorsal to the VAF-A1 border (see Fig. 1A, dashed line is dorsal border).

Sound Delivery

Responses to three sequences of sound stimuli were recorded at each cortical site to assess 1) spike-timing pattern, 2) multiunit frequency response area, and 3) intrinsic response best frequency organization. We previously demonstrated that diotic presentation elicits responses in all three cortical fields (Higgins et al. 2010). Hence, all sound stimuli were calibrated for diotic presentation via hollow ear tubes. Speakers were calibrated between 750 and 48,000 kHz (±5 dB) in the closed system with a 400-tap finite impulse response (FIR) inverse filter implemented on a Tucker Davis Technologies (TDT, Gainesville, FL) RX6 multifunction processor. Sounds were delivered through an RME audio card or with a TDT RX6 multifunction processor at a sample rate of 96 kHz.

Periodic B-Spline Shaped Noise Sequence

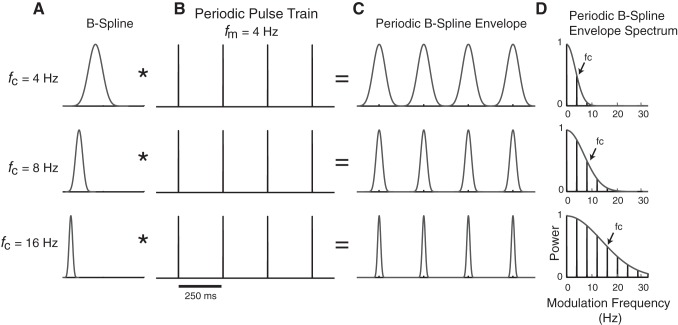
Most prior studies investigating temporal processing by auditory cortical neurons have used SAM sound sequences. As with any sinusoidal modulation, the envelope shape of a single cycle including its slope (rising and falling) and its duration vary when the modulation frequency is varied. Therefore, one cannot examine how neurons respond to independent variation in shape and modulation frequency by utilizing SAM sounds, as we previously explained (Zheng and Escabí 2008). To overcome this limitation, in this study we created a set of periodic basis spline (B-spline) sequences allowing independent control of the sound envelope shape and modulation frequency (see Fig. 2).

Fig. 2.

Generating periodic B-spline envelopes to independently control shape and periodicity sound cues. A and B: the B-spline filter function illustrated in A is convolved (*, operator) with a periodic impulse train illustrated in B that has a fixed modulation frequency (f_m = 4 Hz). Three distinct B-spline filters are shown with distinct cutoff frequency parameters (f_c = 4, 8, and 16 Hz), which control the shape of the envelope (rise and decay time, width). C: resulting sound envelopes have periodic structure where the f_m parameter controls the periodicity and f_c controls the envelope shape. D: the envelope power spectrum is low pass, has harmonic spacing equal to f_m, and has a half-power modulation frequency equal to f_c (i.e., the B-spline cutoff frequency).

Noise sequences were 2 s long in duration and were generated by modulating uniformly distributed noise with a periodic B-spline envelope [e(t), Eq. 1]. All sequences were delivered at 65 dB SPL peak amplitude and 100% modulation depth. The noise carriers were varied from trial to trial (unfrozen) to remove spectral biases in the sound and to prevent repetition of fine-structure temporal patterns between trials.

Periodic noise sequence envelopes were generated by convolving an 8th-order B-spline filter (see e.g., Fig. 2A) with an impulse train (see e.g., Fig. 2B):

$$e\left(t\right)=h_8\left(t\right)\ast {\displaystyle {\sum }_{k=1}^N}\delta \left(t-kT\right)={\displaystyle {\sum }_{k=1}^N}{h}_8\left(t-kT\right).$$ (1)

In Eq. 1, N is the number of cycles in the impulse train and T is the modulation period. The modulation period is the inverse of the envelope fundamental frequency f_m in the modulation frequency domain and ultimately determines the modulation frequency of the sound as shown in Fig. 2C. The asterisk is the convolution operator, δ( ) is the Dirac delta function, T is the modulation period (1/f_m), and h₈( ) is the 8th-order B-spline function, which is treated as a smoothing filter applied to the periodic impulse train. The B-spline filter contains a single parameter, f_c, that controls the shape (i.e., duration and slope) of the resulting periodic envelope e(t) and, as further described below, serves as a low-pass filter that limits the harmonic composition of the sound envelope.

In the time domain, the generalized pth-order B-spline filter impulse response is obtained by convolving p rectangular pulses (each with a total width = 1/a and height = a), producing a smooth function that resembles a Gaussian function (see Fig. 2A; de Boor 2001). The B-spline parameter a determines the duration and slope of the B-spline function. In the modulation frequency domain, the B-spline corresponds to a low-pass filter with transfer function

$$H_p\left(\omega \right)=\mathit{sin}c{\left(\frac{\omega }{2a}\right)}^p,$$ (2)

where sinc (x) = sin (x)/x and ω is the modulation frequency in radians. The B-spline transfer function (Eq. 2) takes on a low-pass filter profile with gain of unity [i.e., H_p(0) = 1], where the scaling parameter a is proportional to the filter bandwidth (see Fig. 2D). We define the B-spline filter upper cutoff frequency (f_c, in Hz) as the frequency where the filter power is ½ (i.e., 3-dB cutoff). This quantity was evaluated numerically by solving

$${\left|H_p\left(2\pi f_c\right)\right|}^2=sinc{\left(\frac{\pi fc}{a}\right)}^{2p}=\frac{1}{2},$$ (3)

where the 8th-order B-spline yields a relationship,

$$a=\frac{\pi f_c}{0.507}.$$ (4)

Combining Eqs. 2 and 4, the B-spline transfer function is expressed as

$$H_8\left(\omega \right)=sinc{\left(0.507\cdot \frac{\omega }{2\pi f_c}\right)}^8,$$ (5)

which consists of a unity gain low-pass filter with cutoff frequency f_c.

In the modulation frequency domain, the low-pass filtering operation limits the harmonics in the periodic sequence up to the B-spline f_c (see Fig. 2D; 3-dB upper cutoff frequency). Thus, by changing the harmonic content of the envelope, we precisely controlled the shape. The noise burst duration and rising and falling slope vary with the B-spline f_c. To illustrate these duration effects of f_c, we compute the standard deviation of the B-spline envelope as a metric of the sound duration (see Fig. 3B). Approximately 83% of the B-spline noise burst energy is contained within a ±1-standard deviation time window centered at the peak. To illustrate slope change with f_c, we calculate the derivative of the B-spline envelope, find its maximum, and convert this into units of Pascals per second (see Fig. 3C).

Fig. 3.

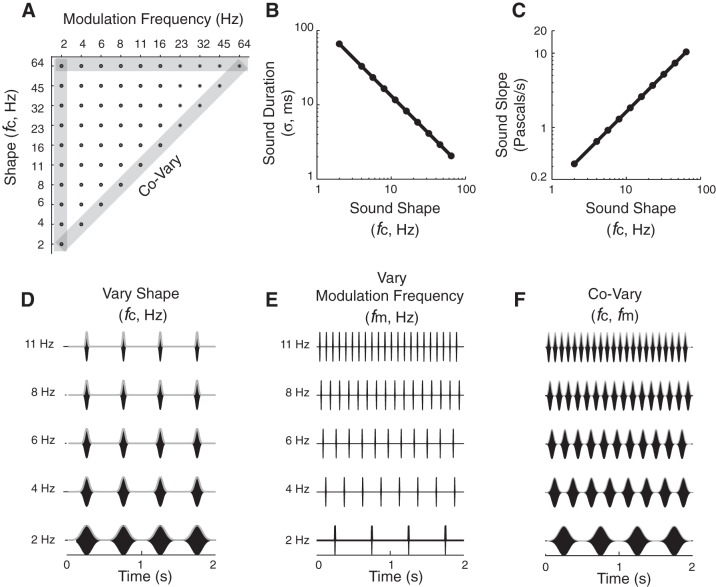
Sound ensemble used to characterize neural coding of shape and periodicity. A: sound sequences are delivered in pseudorandom order by selecting sound with different shapes (f_c) and periodicities (f_m) from 55 conditions in the sound parameter matrix. Modulation frequencies cover the perceptual ranges of rhythm (f_m < 20 Hz) and roughness (>20 Hz). All sequences use unfrozen noise carriers that were modulated by the periodic B-spline envelope as illustrated in Fig. 2 (see methods). B: the duration (filled circles) of the sound envelope decreases as a power law (straight line on a logarithmic plot) with f_c. C: the peak slope of the envelope increases following a power law with f_c. D: waveforms of example periodic noise burst sequences corresponding to the constant periodicity (f_m = 2 Hz) and variable shape (f_c = 2–11 Hz) condition (from vertical gray-shaded bar in A). E: example waveforms with constant shape (f_c = 64 Hz) and variable periodicity (f_m = 2–11 Hz) parameters (from horizontal gray-shaded bar in A). F: example waveforms in which the shape and periodicity covary with one another (diagonal gray-shaded bar in A), resembling conventional sinusoid amplitude modulated-(SAM) sound sequences.

There are several advantages to using the B-spline functions for shaping sound envelopes. Although Gaussian functions may be used, they have infinite duration that would create edge artifacts and discontinuities when synthesizing periodic sound sequences. Such abrupt discontinuities would create spectral splatter that could evoke responses in neurons. By comparison, B-splines have compact waveforms in both time and frequency (i.e., their duration and bandwidth are finite) and are continuously differentiable (up to 8th-order differentiable for the B-splines used), which prevents such discontinuities and potential sound artifacts. Raised sinusoidal (“raised sine”) functions have been used in prior physiology and psychophysics studies to shape sounds (Prendergast et al. 2010; Riquelme et al. 2006). However, this is achieved through a nonlinear operation (raising a sinusoid to an arbitrary power, n), which creates successively higher order harmonic distortions with increasing n. Although the shape varies systematically with n, the raised sine parameter lacks an intuitive interpretation that relates the shape changes directly to the spectral composition of the envelope. By comparison, the B-spline can be interpreted in terms of a simple low-pass filter operation where the B-spline parameter f_c has a direct intuitive interpretation in terms of the modulation spectrum of the sound.

A stimulus set of periodic noise sequences was created (see Fig. 3) by independently varying the modulation frequency f_m and B-spline cutoff frequency f_c. As is true with any periodic sound sequence, the duration of the periodically repeating elements limits the maximum modulation frequency that can be obtained for a given sequence, and thus the test space for f_m is constrained by the f_c parameter. For example, as the B-spline f_c decreases (see e.g., Fig. 2, f_c = 8 vs. 4 Hz) such that the sound duration increases, the minimum allowed period between consecutive noise bursts must increase. Conversely, as f_m increases, the minimum allowed f_c parameter must increase (see e.g., Fig. 2, higher f_c allows for higher f_m). Since the B-spline serves as a low-pass filter for the periodic envelope, lowering f_c limits the number of harmonics present in the modulation envelope (see e.g., Fig. 2A, top, f_c = 4 Hz). In the limiting case where f_c = f_m, the high-order harmonics are attenuated and the sound envelope primarily consists of a single harmonic, analogous to conventional SAM sound. In this study, we varied the modulation frequency parameter f_m from 2 to 64 Hz and required that f_c ≥ f_m. This produces 55 unique envelope sequences (see Fig. 3A, stimulus matrix; Fig. 3, D–F, example sound amplitude waveforms). Sounds were delivered in a pseudorandom shuffled order of f_m and f_c until 10 trials were presented under each condition. Each stimulus trial was separated by a 1-s interstimulus period.

Recording and Sorting Single Units

Recorded units were assigned to a cortical field according to IOI and stereotaxic positions. Lateral stereotaxic position (mm) relative to central fissure increased significantly [1-way ANOVA: F(2, 194) = 85.9, P < 0.001] between fields [means (SE)]: A1, 3.41 (0.06); VAF, 4.35 (0.05); and cSRAF, 4.66 (0.07) mm. This confirms position differences for the three fields described previously (Polley et al. 2007; Storace et al. 2011, 2012). Extracellular spikes were recorded with 16-channel tetrode arrays (4 × 4 recording sites across 2 shanks, with each shank separated by 150 μm along the caudal-rostral axis, 1.5–3.5 MΩ at 1 kHz; NeuroNexus Technologies, Ann Arbor, MI), using an RX5 Pentusa Base station (TDT, Alchua, FL). On average, 1.7 cortical sites (6.4 tetrode sites) per cortical field were recorded in each animal. Only data from penetration depths of 400 to 650 μm relative to the pial surface were included in the present study, because our prior studies confirmed anatomically that this corresponds to layer 4 where ventral division auditory thalamic neurons project (Storace et al. 2010, 2011, 2012). Mean depths (μm) for isolated units used in this study were not significantly different across cortical fields: A1, 577 (10.0); VAF, 555 (7.8); and cSRAF, 570 (10.2) μm [F(2,220) = 1.52, P = 0.22].

Neural responses to periodic noise sequences were spike sorted using custom cluster routines in MATLAB (The MathWorks, Natick, MA). Continuous neural traces were digitally band-pass filtered (300-5,000 Hz), and the cross-channel covariance was computed across tetrode channels. The instantaneous channel voltages across the tetrode array that exceed a hyperellipsoidal threshold of f = 5 (Rebrik et al. 1999) were considered as candidate action potentials. This method takes into account across-channel correlations between the voltage waveforms of each channel and requires that the normalized voltage variance exceeds 25 units: V^TC⁻¹V > f², where V is the vector of voltages, C is the covariance matrix, and f is the normalized threshold level. Spike waveforms were aligned and sorted using peak voltage values and first principle components with automated clustering software (KlustaKwik software) (Harris et al. 2000). Sorted units were classified as single units if the waveform signal-to-noise ratio (SNR) exceeded 3 (9.5 dB, SNR defined as the peak waveform amplitude normalized by the waveform standard deviation), the interspike intervals exceeded 1.2 ms for >99.5% of the spikes, and the distribution of peak waveform amplitudes were unimodal (Hartigan's dip test, P < 0.05). Mean spike widths (ms) of units included here were not significantly different between regions: A1, 0.39 (0.02); VAF, 0.39 (0.01); and cSRAF, 0.42 (0.02) ms [F(2,220) = 0.87, P = 0.42].

Measuring Multiunit Tone-Frequency Response Areas and Peristimulus Histograms

Although A1, VAF, and cSRAF represent overlapping ranges of tone frequencies, the multiunit responses differ in spectral resolution, optimal sound level, and response latency to tones, as described previously (Funamizu et al. 2013; Polley et al. 2007; Storace et al. 2011). In this study, we confirmed these regional differences by assessing the tone frequency response area (FRA). Sorted single-unit responses from each penetration site were combined to compute the multiunit FRA. FRAs were probed with short-duration tones (50-ms duration, 5-ms rise time) that varied over a frequency range of 1.4 to 45.3 kHz (in one-eighth-octave steps) and sound pressure levels (SPL) from 15 to 85 dB peak SPL in 10-dB steps (see Fig. 1, B, D, F). Variations in tone frequency and level were presented in pseudorandom order with an intertone interval of 300 ms. This generated 328 unique tone conditions that were presented 6 times, resulting in a total of 1,968 sounds to map each FRA. Automated algorithms (custom MATLAB routines) were used to estimate threshold and the statistically significant responses within the FRA as described in detail elsewhere (Escabí et al. 2007). Multiunit best frequency (BF) was computed as the centroid frequency of the spike rate responses to all tone frequencies for a given sound level (m) tested:

$${\text{BF}}_{\text{m}}=\frac{{\displaystyle {\sum }_{\text{k}}}{X}_{\text{k}}\cdot \text{FRA}\left(f_{\text{k}},{\text{SPL}}_{\text{m}}\right)}{{\displaystyle {\sum }_{\text{k}}}\text{FRA}\left(f_{\text{k}},{\text{SPL}}_{\text{m}}\right)},$$ (6)

where FRA(f_k,SPL_m) is the statistically significant spike rate response to a tone pip with frequency f_k and level SPL_m, and X_k = log₂ (f_k/f_r) is the distance (in octaves) of f_k with reference to f_r = 1.4 kHz. The characteristic frequency (CF) was defined as the BF at threshold, i.e., at the lowest sound level that produces statistically significant responses (relative to a Poisson distribution spike train assumption, P < 0.05).

Spectral bandwidth was estimated as the width of the FRA at each sound level. At each sound level, we computed the variance (i.e., second-order moment) about the BF and defined bandwidth as twice the standard deviation, using methods described previously (Escabí et al. 2007; Higgins et al. 2008; Storace et al. 2011).

Prior studies found that spike timing and temporal modulation sensitivities varied with the CF of neurons (Heil and Irvine 1997; Rodriguez et al. 2010). Hence, the current study only included sites with CFs ranging from 5 to 26 kHz, because these were well matched across cortical fields. The geometric mean of CF did not vary significantly between regions [F(2,220) = 2.07, P = 0.129: A1, 11.5 kHz (1.07); VAF, 13.0 kHz (1.04); SRAF, 11.6 kHz (1.05)]. FRA bandwidth was compared at a sound level of 75 dB peak SPL, as described previously (see Fig. 1H) (Higgins et al. 2008; Polley et al. 2007; Storace et al. 2011).

Finally, we verified that our population of neurons in A1, VAF, and cSRAF differed in tone-response peak latency (see Fig. 1I), as described previously (Funamizu et al. 2013; Polley et al. 2007; Storace et al. 2011). Multiunit poststimulus time histograms (PSTHs; 2-ms bin width) were generated from FRA responses as illustrated for example multiunit responses (see Fig. 1, C, E, G). The peak (maximum rate) of each PSTH was determined as illustrated for example neurons (see asterisks, Fig. 1, C, E, G). The peak latency (time of peak relative to tone onset) was determined for each multiunit and averaged for each population of cells.

Quantifying Spike-Timing Reliability and Jitter

Single-unit shuffled autocorrelogram analysis.

Although vector strength and synchronized rate are common indexes of neural synchronization to periodic sounds, they fail to characterize the absolute spike-timing precision or its reliability. In this study we adopted an alternative approach and computed the shuffled autocorrelogram (SAC) to quantify changes in spike-timing precision (i.e., jitter) and reliability of responses (Elhilali et al. 2004; Kayser et al. 2010). Our methods for computing and fitting the SAC were described in detail previously (Zheng and Escabí 2008, 2013). Briefly, initial analyses determined that the response adaptation was minimal after 500 ms in all cortical fields. Hence, the first 500 ms were removed from each spike train before analysis of the “steady-state” spike trains. The steady-state spike trains were partitioned into segments, each consisting of a modulation cycle. The steady-state SACs were obtained by computing a circular cross-correlation between all pairwise spike train segments (across trials and cycles, see Fig. 4B, blue, green, and orange correlograms):

$${\phi }_{\text{shuffled}}\left(\tau \right)=\frac{1}{N\left(N-1\right)}{\displaystyle {\sum }_{k=1}^N}{\displaystyle {\sum }_{l\ne k}}{\phi }_{kl}\left(\tau \right),$$ (7)

Fig. 4.

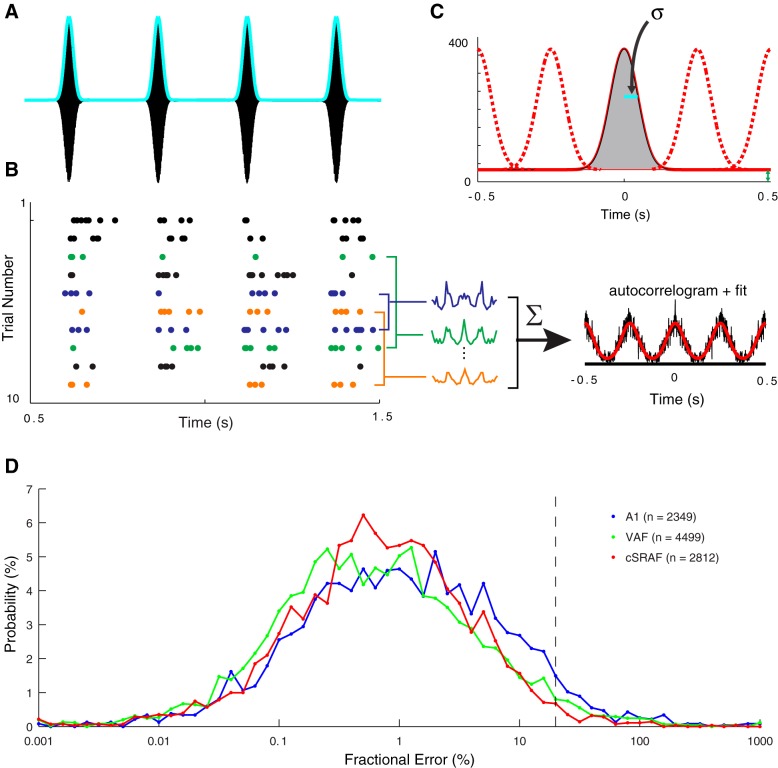
Shuffled autocorrelograms (SACs) quantify spike-timing jitter and reliability. A: the sound pressure waveform (black) and envelope (cyan) of an example noise sequence with f_c = 11 Hz, a corresponding duration of 12 ms, and f_m = 4 Hz used to probe neural responses. B: spike-timing patterns illustrated with a dot-raster plot (each dot is 1 action potential) for 10 repeated sound presentations (trials) for a single cSRAF neuron. Activity following the first 500 ms after the stimulus onset is collected to describe the steady-state response. Cross-correlations between pairs of trials are illustrated for 3 trial pairs (blue, green, and orange). SACs (black line) are computed from the average of all pairwise cross-correlations between trials over the steady-state portion of the response (see methods). Overlaid modified Gaussian model fits are shown (red line; see methods). C: the autocorrelation fit for this example single-neuron response is plotted to illustrate estimation of reliability and jitter. The reliability and spike-timing jitter (σ) parameters are derived by fitting the SAC model to the measured SAC using a least-squares approach. D: frequency distributions of SAC fractional model error in A1 (red), VAF (green), and cSRAF (blue), indicating close fitting of SACs with the Gaussian model in all 3 regions (n, no. of single-neuron response fits).

where N is the total number of cycles and φ_kl(τ) is the circular cross-correlation between the spike trains from the kth and lth cycles. This procedure was implemented using the fast algorithm described in detail elsewhere (Zheng and Escabí 2008). Spike trains sampled with 1,000 samples/s versus those with a proportional resolution scheme of 50 or 10 samples per cycle (Zheng and Escabí 2008) yielded comparable results. Hence, in this study we used SACs generated from the fixed 1,000 samples/s spike trains for simplicity (see e.g., Figs. 4 and 5, single-neuron autocorrelograms; Fig. 6, population autocorrelograms).

Fig. 5.

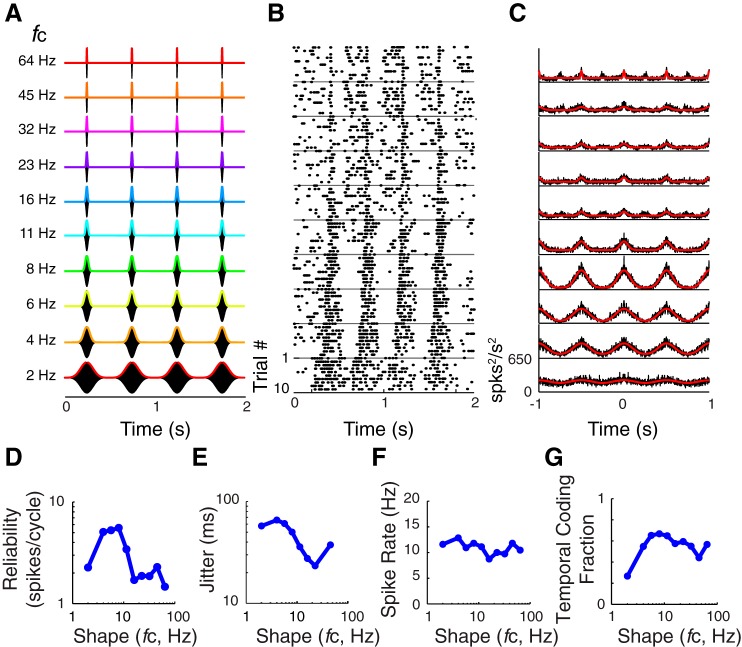
An example response from a single cSRAF neuron illustrates that spike-timing jitter can decrease with increasing sound shape f_c. A: corresponding sound waveforms (black) and envelopes (colored lines) of the 10 variations of f_c repeated 10 times to probe neural responses. The parameter f_m is fixed at 2 Hz. B: dot-raster plots depict the single-neuron responses to the sounds shown in A. When the f_c is equal to 4 Hz, the sound-evoked response follows the sound envelope and has sustained spiking throughout each noise burst cycle. As f_c increases and noise bursts become sharper and shorter in duration, the spike-time jitter during each cycle of sound becomes smaller. C: corresponding SACs (black) and modified Gaussian model fits (red) for the dot rasters in B. The decrease in response jitter with f_c is visible in the significant fits (red lines) of the SAC, mirroring the time course of modulations in the original sound envelopes (rainbow colored lines in A). D: reliability is maximal for f_c near ∼6 Hz for this neuron. E: jitter is maximal when f_c is low (4 Hz) and corresponding noise bursts are long in duration with slow rising and falling slopes. Jitter duration decreases from 70 to 20 ms when f_c increases from 4 to 45 Hz. Note the relationship follows a power law. F: spike rate does not change markedly with f_c in this example neuron (same neuron as shown in Fig. 4). G: temporal coding fraction is maximal for sound shapes f_c near ∼8 Hz for this neuron.

Fig. 6.

Population SACs follow the sound envelope in A1, VAF, and cSRAF. A: 10 different sound waveforms with varying f_c from 2 to 64 Hz. B–D: population SACs (black lines) and fits (red lines) for A1 (B), VAF (C), and cSRAF (D). Sound waveform delivered to obtain averaged SACs are shown in corresponding row in A.

Stochastic spiking model with normally distributed spike timing errors.

A stochastic spiking model was used to estimate the spike-timing precision and spiking reliability directly from the measured autocorrelograms. The phenomenological spiking model consists of a quasi-periodic spike train that contains three forms of neural variability: spike-timing jitter, reliability errors, and spontaneous or additive noise spikes. Spike-timing errors (jitter) relative to a specific phase of the stimulus are assumed to have a normal distribution with standard deviation σ. A total of x̄ reliable spikes are generated for each cycle of the stimulus so that the average stimulus-driven spike rate is λ_periodic = x̄·f_m (spikes/s). The model also contains additive noise spikes (not temporally driven by the stimulus) with a firing rate of λ_noise. Hence, the total firing rate is λ_total = λ_periodic + λ_noise = x̄·f_m + λ_noise. We previously have shown that the expected SAC for this spiking model is as follows (Zheng and Escabí 2013):

$${\phi }_{\text{shuffled}}\left(\tau \right)={\overline{x}}^2\cdot f_{\text{m}}\cdot {\displaystyle {\sum }_n}\frac{1}{\sqrt{4\pi {\sigma }^2}}{e}^{-\frac{{\left(\tau -n\cdot T\right)}^2}{4{\sigma }^2}}+2\cdot {\lambda }_{\text{period}}\cdot {\lambda }_{\text{noise}}+{\lambda }_{\text{noise}}^2.$$ (8)

Because the autocorrelogram is obtained by correlating spike trains with the above statistical distributions and periodic structure, the time-varying component of the SAC is periodic and each cycle follows a normal distribution with a standard deviation equal to $\sqrt{2}$σ. That is, the standard deviation of the SAC is $\sqrt{2}$ times larger than the standard deviation of the spike-timing errors. Furthermore, we have shown that the SAC area exceeding the baseline firing rate (2·λ_periodic·λ_noise + λ_noise²) is x̄²·f_m and is thus proportional to the squared reliability. We use least-squares optimization to fit the above equation to experimentally measured SAC to estimate the spike-timing jitter (σ) and firing reliability (x̄) as well as the driven (periodic, λ_periodic) and undriven (noise, λ_noise) firing rate parameters.

For the sound conditions that did not generate strong temporally driven neural responses (e.g., at high modulation rates, which often lack phase locking), the model fits and shuffled autocorrelogram were characterized by a constant value with no periodic fluctuations (i.e., they lack a periodic response and mostly contain random firing). Under such conditions the firing reliability is zero and the spike-timing jitter is ill conditioned and thus undefined (since there are zero temporally reliable spikes to define spike-timing errors and thus jitter can take on an infinite number of values). Jitter responses were considered significant and included for estimates of jitter in the single-unit (see Figs. 4, 5, 7, 8, and 9) and population response analyses (see Fig. 6) only if two conditions were satisfied: 1) the estimated reliability was significantly greater than the reliability of randomized Poisson spike train, as described below, and 2) the fractional model error (power of the model error vs. total response power) did not exceed 20%, as described below. Furthermore, to avoid quantifying jitter for conditions where synchrony (i.e., phase locking) was lacking, we reported jitter only if the model optimization was well defined and yielded a jitter value greater than the sampling period of the spike train (1 ms) and less than half the modulation period.

Fig. 7.

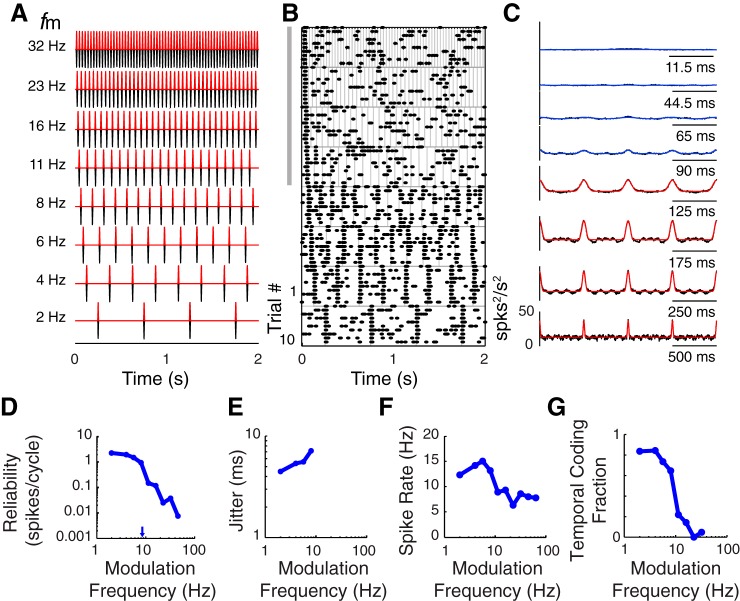
Single VAF neuron firing reliability decreases with increasing sound modulation frequency. A: sound pressure waveforms for noise burst sequences played with 8 variations of sound shape and repeated 10 times to probe neural responses. The cutoff frequency is fixed (f_c = 64 Hz) while the modulation frequency is varied (only f_m = 2–32 Hz are illustrated). B: dot-raster plots depict responses to corresponding sounds shown in A. Responses synchronize to the onset of each cycle of noise when f_m is 2–8 Hz (bottom 4 panels). When f_m is above 8 Hz, reliable synchronous spiking is only obtained for the first cycle of sound in the sequence (top 4 panels near gray bar). C: significant (red lines) and nonsignificant (blue lines) modified Gaussian model fits of the SAC (underlying black lines) obtained from spike times depicted in B. When f_m is >8 Hz and the period between noise bursts is <90 ms, the autocorrelogram magnitudes are low and not significant (see blue lines). D: reliability (reliable spikes/cycle) decreases with increasing modulation frequency. The corresponding 50% upper cutoff modulation frequency is indicted (blue arrow). E: jitter is plotted for each sound modulation frequency yielding a significant SAC (i.e., jitter changes from 3.8 to 6.2 ms). F and G: spike rate (F) and temporal coding fraction (G) decrease with sound modulation frequency for this neuron.

Fig. 8.

Changes in reliability, jitter, and temporal coding fraction with sound shape and modulation frequency in A1, VAF, and cSRAF. Geometric means are given for 223 single neurons probed with 55 sound conditions tested in the 3 cortical fields. A–D: population geometric means for jitter (A) and reliability (B) and arithmetic means for temporal coding fraction (C) and spike rate (D) for each sound shape and modulation frequency in A1. E–H and I–L show the same response summary for VAF and cSRAF, respectively. A, E, and I: changes of mean jitter with f_c and f_m in the 3 cortical fields. Color scale indicates geometric mean jitter. For f_m below 16 Hz, jitter is larger (red and orange voxels) when f_c is lower. In A1, jitter is smaller and less variable across all sound conditions as evident by the preponderance of cyan and yellow voxels in the sound response matrix in A. Significant jitter measures are often not observed for the highest modulation frequencies where f_m is above 16 Hz (white voxels). B, F, and J: geometric mean spike-time reliability for all sound shapes and modulation frequencies. Reliability is low in all 3 cortices when f_m is at or above 16 Hz (blue and cyan voxels), and for cSRAF some values of f_c and f_m above 16 Hz generate no measurable reliability (white voxels). In all 3 fields, reliability is uniformly highest when sound modulation frequency is low (f_m = 2 Hz). C, G, and K: in all 3 fields, the degree of synchronized vs. asynchronous spiking, i.e., the temporal coding fraction, varies with f_c and f_m. In all fields, a narrow range of sound conditions yields near maximal mean temporal coding fractions (i.e., red, orange, and light green voxels in A1, VAF, and cSRAF, respectively). A1 has the highest temporal coding fractions of all 3 cortices (red voxels). Asterisks indicate conditions yielding maximum temporal coding fraction for A1, VAF, and cSRAF: 0.46 (0.04), 0.34 (0.02), and 0.29 (0.02), respectively. In all fields, temporal coding fraction is negligible when f_m is 16 Hz or greater due to low reliability of spiking. D, H, and L: in all 3 fields, mean spike rates are relatively uniform across all sound conditions. In VAF, mean spike rates shift from lower (yellow voxels) to higher (orange voxels) values when f_c is decreased from 64 to 4 Hz.

Fig. 9.

Changes in jitter, reliability, temporal coding fraction, and spike rate with sound shape and modulation frequency in 3 auditory cortical fields. A: population geometric mean jitter varies with sound shape; that is, jitter decreases with increasing f_c following a power-law relationship in all 3 fields. All sounds used to generate this plot have fixed modulation frequency (f_m = 2 Hz). Insets illustrate 2 corresponding sound waveforms (f_c = 2 and 64 Hz). Linear regression fits (dashed lines) vary significantly [F(2, 2,512) = 21.15, P < 0.001] for A1, VAF, and cSRAF and have corresponding slopes of −0.30 (0.07), −0.51 (0.06), and −0.27 (0.08), respectively. All regression slopes are significantly different from zero, indicating a dependence of jitter on f_c in A1 (P = 0.001), VAF (P < 0.001), and cSRAF (P = 0.01). Linear regression slopes for fits of A1, VAF, and cSRAF vary significantly [F(2, 2,512) = 21.15, P < 0.001]. B: geometric mean jitter increases in rank order across A1, VAF, and cSRAF: 10 (1.03), 13 (1.03), and 17 (1.04) ms, respectively (**P < 0.001). C: cumulative probability distribution plots for data shown in B. D: geometric means of reliable spikes/cycle decrease with f_c in VAF and cSRAF (red and green symbols), but not in A1 (blue symbols), with correlation coefficients (r) for A1, VAF, and cSRAF of −0.001 (P > 0.999), −0.81 (P = 0.017), and −0.141 (P < 0.001), respectively. E: population response functions illustrate the decrease in spike reliability observed with increase in f_m in all 3 cortical fields. B-spline f_c is fixed at 32 Hz. Geometric mean reliability is plotted as a function of each f_m value. Insets indicate sound waveforms corresponding to f_m = 2 and 8 Hz. F: 50% upper cutoff sound modulation frequencies are rank ordered with geometric means for A1, VAF, and cSRAF of 5.9 (1.02), 5.4 (1.02), and 4.9 (1.02), respectively [F(2, 1,603) = 21.95; all pairwise post hoc t-tests are significant: **P < 0.001]. G: cumulative probability plot illustrates the high overlap in reliability upper cutoffs across all cortices. H: arithmetic means of spike rate do not change significantly with sound f_c in any field examined. Correlation coefficients for A1, VAF, and cSRAF are 0.02 (P = 0.71), −0.03 (P = 0.33), r = −0.034 (P = 0.394), respectively. I: mean (SE) measures plotted correspond to data shown in top row of Fig. 8, C, G, and K, f_c = 64 Hz. The arithmetic mean for temporal coding fraction is maximal at ∼4 Hz and decreases with increasing modulation frequency in all 3 fields. Insets indicate sound waveforms corresponding to f_m = 4 and 8 Hz. Arrows indicate 50% upper cutoffs. J: 50% upper cutoff sound modulation frequency for temporal coding fraction is significantly lower in cSRAF than in A1 or VAF [F(2, 1,579) = 12.28, P < 0.001] with means for A1, VAF and cSRAF of 6.2 (1.02), 5.9 (1.02), and 5.4 (1.02) Hz, respectively; post hoc t-tests indicate significant differences: A1 > cSRAF (**P < 0.001) and VAF > cSRAF (**P < 0.001). K: cumulative probability plot of temporal coding upper cutoff indicates a largely overlapping distribution of upper cutoff frequencies across all 3 fields. L: spike rate increases slightly with f_m in VAF but is not dependent on f_m in A1 or cSRAF. Correlation coefficients for A1, VAF, and cSRAF are −0.03 (P = 0.52), 0.07 (P = 0.02), and 0.05 (P = 0.25), respectively.

The quality of the model fit was assessed with a cross-validation procedure in which half of the neural data were used for model optimization, and the remaining half for model validation. Trials were divided between odd-numbered and even-numbered trials, to compute independent shuffled autocorrelograms for each half of the data [ϕ₁(t), ϕ₂(t)] that were used for model validation. Fractional model error (Zheng and Escabí 2013) was computed for each condition:

$$E=\frac{\mathrm{var}\left[{\varphi }_1\left(t\right)-{\varphi }_{\text{model}}\left(t\right)\right]-\frac{1}{2}\mathrm{var}\left[{\varphi }_2\left(t\right)-{\varphi }_1\left(t\right)\right]}{\mathrm{var}\left[{\varphi }_1\left(t\right)\right]-\frac{1}{2}\mathrm{var}\left[{\varphi }_2\left(t\right)-{\varphi }_1\left(t\right)\right]}\cdot 100\%.$$ (9)

In Eq. 9, fractional model errors have been corrected for estimation noise and thus account for deterministic errors between the neural data and model. Across all stimulus conditions, the model provided good fits to the SACs (Fig. 4D). Fractional model error geometric means were 1.04 (1.04)% in A1, 0.63 (1.03)% in VAF, and 0.69 (1.03)% in SRAF. For each stimulus condition, median fractional model error did not exceed 3.3% in any of the cortical regions, indicating high-quality fits to the data.

Temporal responses were considered statistically significant if the estimated reliability was greater than that of a simulated homogeneous Poisson (asynchronous) spike train with spike rate matched to recorded neuron spike rate. Ten Poisson spike trains were simulated for each condition and corresponding SACs were computed. The neural and simulated SACs were jackknifed (across trials and cycles) to determine the error bounds of the real and simulated model of SACs and the estimated parameters. The neural responses were considered significant if the estimated reliability (from the modified Gaussian model fits) exceeded the expected level for the Poisson spike train (Student's t-test, P < 0.001).

Temporal coding fraction.

The temporal coding fraction (F) is computed to quantify the fractional power in the time-varying component of spike train relative to its total power. The temporal coding fraction is computed by measuring the power in the response harmonics according to

$$\text{F}=\frac{2{\displaystyle {\sum }_{k=1}^N}\left(A_k^2\right)}{A_0^2+2{\displaystyle {\sum }_{k=1}^N}{A}_k^2},$$ (10)

where A_k is the Fourier coefficient of the kth response harmonic and A₀ is the Fourier coefficient of the response at 0 Hz. Note that for nonzero harmonics, the total power is multiplied by 2 to account for the negative frequencies in the response spectrum. Harmonics are only included if the power is significantly greater than variance of a randomized spike train with identical spike rate (Student's t-test, P < 0.001). This metric is analogous to the temporal coding fraction described previously (Zheng and Escabí 2013); however, unlike the previous metric, which only takes into account the relative proportions of the spontaneous and driven rates, this new metric captures the fractional power associated with the time-varying response component relative to the total response power.

Single-unit and population response functions.

We characterized how firing rates, jitter, and reliability vary with sound shape and modulation frequency. Single-unit steady-state spike rate responses were classified as low-pass, band-pass, high-pass, band-reject, or flat response types with respect to 20 sound stimulus conditions (f_m = 2 Hz, f_c = 2–64 Hz, and f_c = 64 Hz, f_m = 2–64 Hz) using an approach detailed elsewhere (Escabí et al. 2007; Zheng and Escabí 2008). A spike rate decrease relative to the maximum was used to determine the response type. For example, a “band-pass” type VAF single-unit rate response is illustrated in Fig. 7F. No single units were classified as “flat” response type because spike rate varied by more than 10% across the 10 periodicities, and across the 10 shapes for all single units. Rate responses to sound f_m had simple “tuning” (i.e., high pass, low pass, band pass, or band reject) for 67%, 45%, and 45% of single units in A1, VAF, and cSRAF, respectively, whereas the remaining had complex tuning, comparable to multiunit modulation transfer functions reported previously (Escabí et al. 2007).

When all single-unit spike rate responses were averaged, they generated essentially flat population spike rate response functions (results; see Fig. 9, H and L). Therefore, the systematic changes of jitter and reliability across shape and modulation frequency, respectively (see Fig. 9, A and E), are not mirrored in the population spike rate. In a prior study, which included onset and steady-state responses, we found the population f_m vs. rate response had a peak at ∼6 Hz for rat A1 neurons (Escabí et al. 2007). The lack of a peak in the population rate function in this study was possibly due to differences in response regime examined (i.e., steady-state vs. onset), anesthesia (i.e., ketamine vs. pentobarbital), spontaneous spike rates, or the number of neurons used to generate the population response function.

Scaling and slopes of response functions.

All response functions were plotted on scales appropriate for the corresponding response distribution. Temporal coding fraction and spike rate response distributions were approximately normally distributed on a linear scale; hence, these data were plotted on linear scales. In contrast, jitter and reliability distributions were approximately normal on a logarithmic scale; hence, these were plotted on logarithmic scales for all illustrations. Means and parametric tests were computed using the logarithmic transformation for variables with a logarithmic distribution. For modulation frequency response functions, 50% upper cutoff frequency was calculated by interpolating consecutive points. The 50% upper cutoff frequency was determined as the lowest f_m above the peak f_m that yields 50% of the peak value.

To quantify the relationship between jitter and reliability across multiple sound parameter spaces, we determined the correlation coefficient with an outlier robust function (Pernet et al. 2012; Wilcox 1994) and used an outlier robust linear regression function (MATLAB) to fit jitter and reliability (see Fig. 10). This employs a bisquare weighting function to compute the parameters of the fit.

Fig. 10.

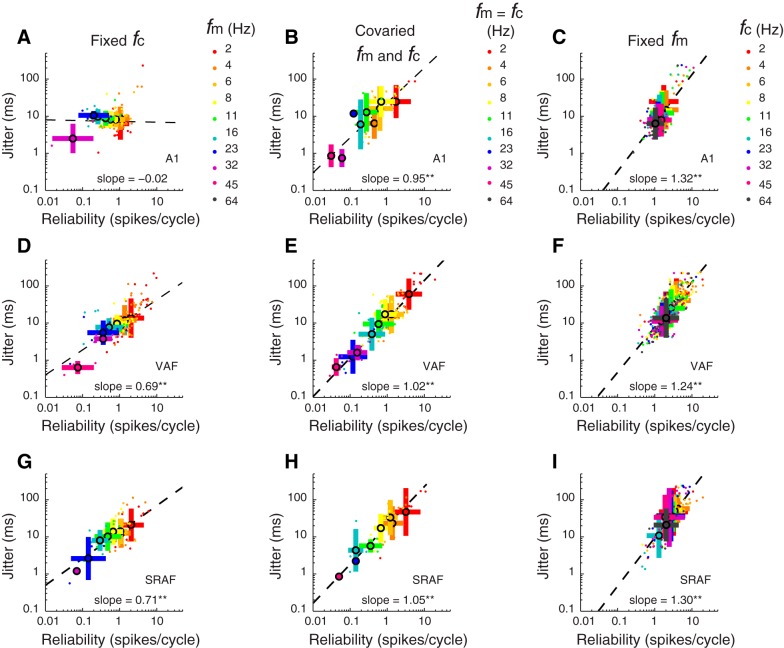
Spike-timing jitter and reliability covariation in the 3 auditory cortical fields. In all plots, color indicates the sound parameter varied (as indicated by the color keys given in A–C, right). Small colored dots indicate single-neuron data; large colored dots and bars indicate population mean and SD, respectively. A, D, and G: reliability vs. jitter plotted for responses to each of 10 different sound f_m for A1, VAF, and cSRAF, respectively. Sound f_c is fixed at 64 Hz. In A1 (A), as f_m is decreased from high (purple dots) to low values (red dots), spike-time reliability increases from 0.1 to ∼2 spikes/cycle, but jitter does not change appreciably. In VAF (D) and cSRAF (G), as f_m is decreased from high (purple and pink dots) to low values (red dots), spike-time reliability and jitter both increase (**P < 0.001). B, E, and H: in all fields, jitter varies with reliability when sound shape and periodicity are covaried (see sound parameters on diagonal of Fig. 3A). Jitter and reliability are significantly (all fields **P < 0.001) correlated (A1, VAF, cSRAF: r = 0.72, 0.87, and 0.82, respectively) when shape and periodicity cues are covaried as with SAM sounds, with mean slope for A1, VAF, cSRAF of 0.95 (0.13), 1.02 (0.05), and 1.05 (0.09), respectively [F(2, 182) = 0.30, P = 0.73]. C, F, and I: jitter and reliability covary when f_m is fixed (2 Hz) and sound shape f_c is varied in all 3 fields (**P < 0.001). Regression slopes are not significantly different [F(2, 568) = 0.39, P = 0.68] across cortical fields for A1, VAF, and cSRAF: 1.32 (0.10), 1.24 (0.05). and 1.30 (0.08), respectively. Note that jitter and reliability (methods) are used to generate plots throughout this figure.

RESULTS

Identifying Cortical Fields

Like many mammals, rats have multiple auditory cortical fields defined by topographic organization of sound frequency responses (Hackett 2011; Polley et al. 2007; Storace et al. 2010, 2011, 2012). An IOI illustrates tone response organization for A1, VAF, and cSRAF auditory cortical fields that span collectively over 3 mm along the dorsoventral axis of temporal cortex in the rat (Fig. 1A). After cortical fields were located, multiunit spike rate responses to 328 combinations of tone intensity and frequency were acquired to measure FRAs (Fig. 1, B, D, F) and the peak latency of tone response (e.g., Fig. 1, C, E, G, asterisks). Sensitivities to sound frequency were assessed by computing BF and bandwidth from the FRA at each sound level (methods; e.g., Fig. 1, B, D, F, filled circles and lines, respectively). We found that A1 neurons typically have broad bandwidths at high sound levels (Fig. 1B, bandwidths indicated with black lines), as shown previously (Polley et al. 2007; Sally and Kelly 1988; Storace et al. 2011). In contrast, VAF and cSRAF neurons typically respond to a more narrow range of tone frequencies across all sound levels (e.g., Fig. 1, D and F, black lines). Accordingly, there is a rank-order decrease in mean tone-response bandwidths at 75 dB with A1 > VAF > cSRAF (Fig. 1H), as described previously (Centanni et al. 2013; Polley et al. 2007; Storace et al. 2011). The peak latency of the spike rate response to tone increases between cortical fields with A1 < VAF < cSRAF (Fig. 1I), as previously reported (Centanni et al. 2013; Funamizu et al. 2013; Polley et al. 2007; Storace et al. 2012). These differences in spectral and temporal response characteristics confirm that the populations of cells we designate as belonging to A1, VAF, and cSRAF are consistent with those described previously.

Relationship Between Spike-Timing Variability and Temporal Sound Cues

The spike-timing variability of central auditory neurons can vary independently with sound shape and periodicity cues (Zheng and Escabí 2008, 2013). Hence, in this study we independently varied sound envelope shape and modulation frequency in a set of 55 B-spline shaped periodic noise sequences (methods; Figs. 2 and 3). The B-spline cutoff frequency f_c (Fig. 2) was varied to create different sound shapes. The sound duration decreased (Fig. 3B) and the slope increased (Fig. 3C) linearly with the B-spline f_c. Thus, in our sound set, we varied these two shape cues by changing the B-spline f_c from 2 to 64 Hz (Fig. 3D, subset of sounds). Periodicity cues were varied with the sound modulation frequency f_m from 2 to 64 Hz (Fig. 3E, subset of sounds). Envelope period and shape covary along the diagonal of our sound matrix (Fig. 3, A and F, where f_c = f_m), as is the case for SAM sounds used in many prior physiological studies of cortical responses to sound.

Two forms of spike-timing variability, jitter and reliability, are thought to play an important role in the encoding of temporal sound cues (Buran et al. 2010; DeWeese et al. 2005; Kayser et al. 2010; Stein et al. 2005; Zheng and Escabí 2008, 2013). In this study, we quantified differences in spike-timing jitter and reliability across three cortical regions using an approach described previously (methods). The procedure is illustrated for a single cSRAF neuron stimulated repeatedly with a noise burst sequence with a fixed shape and modulation frequency parameter (Fig. 4). This neuron responds to each burst of sound with one to six spikes (Fig. 4B, dots) with a characteristic spike-timing jitter of 6.75 ms. The neuron's response is reliable, because it responds with 1.6 reliable spikes per cycle, on average, and it only fails to spike once over the 4 noise bursts and 10 sequence repetitions (Fig. 4B, trials 1–10). These spike-timing patterns were quantified by computing all pairwise cross-correlations between trials (e.g., Fig. 4B, blue, green, orange lines) and computing the averaged SAC (Fig. 4B, black line). The SAC was fitted to a normally distributed spike train model (Fig. 4B, red line) to estimate jitter and reliability (methods; Fig. 4C).

Spike-Timing Patterns Change with Shape and Periodicity Cues

In auditory midbrain, spike-timing jitter varies primarily with sound shape and not with sound modulation frequency (Zheng and Escabí 2008, 2013). In this study, we questioned whether a similar principle holds for cortical neurons. For the same example cSRAF neuron as described in Fig. 4, we illustrate responses to a fixed modulation frequency of 2 Hz and 10 sound shape variations (Fig. 5A). The dot raster plots illustrate how spike timing varies with B-spline f_c (Fig. 5B). Corresponding SACs (Fig. 5C, black lines) and significant fits (Fig. 5C, red lines) were generated to quantify the spike-timing variability elicited by each sound shape. In this cSRAF neuron, reliability is maximal (>5 spikes/cycle) when f_c is between 4 and 8 Hz and reliability decreases to a minimum level (<2 spikes/cycle) when f_c is above 8 Hz (Fig. 5D). Over the same range of sound shapes, jitter decreases approximately threefold (65 to 23 ms; Fig. 5E). In contrast, mean spike rate varies to a lesser degree with sound shape (Fig. 5F). To examine the degree of synchronous relative to asynchronous spiking, we computed a temporal coding fraction as the proportion of the spike train power that is temporally synchronized with the sound (methods). For the example cSRAF neuron, temporal coding fraction varies across sound f_c and is maximal for f_c near 8 Hz (Fig. 5G). Thus, over the range of sound shapes where jitter changes precipitously (Fig. 5E), the neuron spikes with similar temporal synchrony. These results suggest that spike-timing jitter and reliability are better indicators of sound shape than spike rate or temporal coding fraction alone in a single cSRAF neuron.

The population SAC, computed as the arithmetic mean of all single-unit SACs, indicates that spike timing changes with sound shape on a population level in all three cortical fields (Fig. 6) with notable differences between fields. In A1, the population SACs has sharp narrow peaks for all the sound shapes, indicating relatively precise spike timing and smaller jitter (Fig. 6B). In contrast, the population SACs from VAF and cSRAF have broad correlations, indicating a more sustained response with less precise spike timing and higher jitter (Fig. 6, C and D, respectively).

Prior studies found that cortical neuron response strength decreased with increasing sound modulation frequency when examined with SAM sounds (Joris et al. 2004). In the present study we found a similar response relation when sound modulation frequency was increased without altering sound shape (Fig. 7). Raster plots (Fig. 7B) illustrate the response spike times of an example VAF neuron to eight different variations in f_m (Fig. 7A, 10 trials for each condition). When f_m is 8 Hz or less, the neuron reliably generates one to four spikes (black dots) per each noise burst (i.e., cycle) of sound (Fig. 7B). When f_m is greater than 8 Hz, this neuron responds with synchronous reliable spiking to the onset of the first cycle of the sound sequence only (Fig. 7B, gray bar indicates reliable onset responses only). Consequently, the steady-state SAC is not significant for f_m above 8 Hz (methods; Fig. 7C, blue lines). The reliability decreases from 1 to <0.01 spikes/cycle when f_m is increased from 2 to 64 Hz (Fig. 7D). The 50% modulation frequency upper cutoff for this neuron is 7 Hz (methods; Fig. 7D, arrow), indicating that this neuron can only reliably respond to sounds with modulation frequencies below 7 Hz. For this example neuron, jitter is plotted for responses to sound modulation frequencies up to 8 Hz (Fig. 7E), because the steady-state SAC is significant for these conditions only. Jitter increases by a factor of 1.6 from ∼4 to 7 ms when sound modulation frequency increases from 2 to 8 Hz (Fig. 7E). Finally, spike rate changes by a factor of 2.5 over the range of modulation frequencies examined. However, reliability and temporal coding fraction change more dramatically than spike rate, as reflected by the low-pass response functions (Fig. 7, D and G, respectively). This illustrates how steady-state reliability, spike rates, and temporal coding fractions all can decrease with increasing modulation frequency in single cortical neurons.

Jitter and Reliability Change with Sound Shape and Periodicity Cues

To answer the question of whether jitter changes similarly with sound cues in each auditory field, mean jitter was determined for each of the 55 noise sequences in our sound stimulus set and for all neurons in each auditory cortical field (Fig. 8, A, E, I). As noted above, an accurate estimate of jitter requires a temporally modulated response; therefore, mean jitter was only computed for conditions where the reliability was significantly above that of a random spike train (methods). The number of cells with significant jitter decreases with higher modulation frequencies such that for some sounds we are unable to report any jitter measures (Fig. 8, A, E, and I, white voxels). In A1, jitter is greatest when f_c is 8 Hz or below (Fig. 8A; note high numbers of yellow and orange voxels corresponding to 15 and 25 ms, respectively); jitter is relatively small when f_c is above 8 Hz (note higher numbers of cyan and green voxels corresponding to ∼10 ms). When the modulation frequency is >32 Hz, there are few significant fits of the SAC and mean jitter is at its lowest (Fig. 8A, blue and white voxels). In A1, jitter ranges from ∼2 ms (Fig. 8A, blue voxels) to 25 ms (orange voxels) across the 55 noise sequences examined. In contrast, in VAF and cSRAF, jitter ranges from ∼2 ms (Fig. 8, E and I, blue voxels) to as much as ∼70 ms (red voxels). This indicates that spike-timing jitter changes with the type of noise sequence played and tends to be higher in the ventral cortical fields, consistent with the population SACs (Fig. 6).

In response to 55 noise sequences in our stimulus set, spike-timing reliability decreases with sound modulation frequency but changes minimally with sound shape. In all three fields, reliability is maximal at ∼10 spikes/cycle for all sound shapes when sound modulation frequency is 2 Hz (Fig. 8, B, F, and J, red voxels). Reliability decreases two orders of magnitude from 10 to ∼0.1 spikes/cycle when sound modulation frequency is increased to 8 Hz in the ventral fields (Fig. 8, F and J) and to 11 Hz in A1 (Fig. 8B). This precipitous drop in reliability with sound modulation frequency is consistent with prior studies of auditory cortical neurons using SAM sounds (Fitzpatrick et al. 2009; Malone et al. 2007; O'Connor et al. 2010, 2011; Scott et al. 2011; Ter-Mikaelian et al. 2007).

Jitter Varies with Sound Shape Cues

Changes in spike-timing jitter could serve as a neural code for sound shape (Zheng and Escabí 2013). To illustrate this, we have plotted a subset of all the mean jitters corresponding to a fixed f_m of 2 Hz (i.e., data from first column in each response matrix of Fig. 8, A, E, and I, are plotted in Fig. 9). Figure 9A illustrates how mean jitter decreases as sound f_c increases in all three cortical fields. The proportional decrease in jitter follows a power-law relationship (linear on a doubly logarithmic plot) with sound shape parameter (i.e., f_c) as indicated by the linear regression fits (Fig. 9A, dashed lines). This is meaningful, because it indicates that jitter could be used to identify sound shape. Corresponding sound waveforms are plotted for two conditions to emphasize how jitter changes with sound shape (Fig. 9A, insets). Note that noise burst duration decreases as the B-spline f_c increases (Fig. 3B). Hence, in all three cortical fields the decrease in jitter is proportional to a decrease in noise burst duration. Corresponding regression slopes are more negative in VAF than in A1 and cSRAF, indicating that change in sound shape introduces a larger change in spike-timing jitter in VAF (Fig. 9A). The jitter predicted by the regression model for a f_c of 1 Hz is lower in A1 than in either ventral field, and the corresponding y-intercepts for jitter in A1, VAF, and cSRAF are 23 (1.2), 85, (1.2) and 68 (1.2) ms, respectively (Fig. 9A). Furthermore, across all sound sequences presented, the average jitter and area under the cumulative probability distributions increase in rank order across cortical fields with A1 < VAF < cSRAF (Fig. 9, B and C).

Reliability Varies with Sound Modulation Frequency

Prior work in primate A1 suggests that the reliable spikes per cycle of SAM sound decrease with increasing sound modulation frequency (Malone et al. 2007). In the present study, we found the same relationship in rodent A1, VAF, and cSRAF when independently varying sound modulation frequency. To illustrate this, we have plotted a subset of reliability means corresponding to a fixed f_c of 32 Hz (i.e., data from the third row in each response matrix of Fig. 8, B, F, and J, are plotted in Fig. 9E). In all three fields, reliable spikes per cycle of sound drops to 50% of its maximum at sound modulation frequencies below 10 Hz (Fig. 9E, arrows). Mean 50% modulation frequency upper cutoffs for reliable spiking are rank ordered with A1 > VAF > cSRAF (e.g., Fig. 9F) and decrease with ventral progression across fields [F(2, 1,603) = 21.9, P < 0.001]. This indicates that the most reliable spiking is observed for a slightly broader range of sounds in A1, compared with VAF or cSRAF. This difference is evident as a small shift to the right in corresponding cumulative probability distribution curves (Fig. 9G). In A1, reliability does not vary systematically with sound shape (Fig. 9D, blue symbols), whereas it has a decreasing trend with f_c in VAF and cSRAF (Fig. 9D, green and red symbols). Note that the ventral fields have more reliable spikes per cycle of sound (Fig. 9D, green and red symbols) than A1 (Fig. 9D, blue symbols) when f_c is low (4, 6, 8 Hz), and the corresponding noise burst duration is long (e.g., σ = 30, 20, 15 ms). This can be attributed to the sustained spike train response associated with larger jitter in VAF and cSRAF under these conditions (e.g., Fig. 5B). It follows that A1 and ventral nonprimary cortices are most reliable for a distinct set of temporal sound cues.

Minimal Spike Rate Variation with Temporal Cues

Cortical neuron spike rates can change with temporal sound cues (Krebs et al. 2008; Liang et al. 2002; Lu and Wang 2004; Niwa et al. 2013; Schulze and Langner 1997), leading us to question whether population changes in jitter and reliability are associated with similar population changes in spike rate. In this study we found that band-pass, low-pass, high-pass, and band-stop types of spike rate response change with sound shape and modulation frequency (methods). Single-neuron spike rates vary by up to 1.6-fold with changes in sound shape or modulation frequency in all cortices (e.g., VAF single neuron, Fig. 7F). This net change is less than that of single-neuron jitter or reliability with the same temporal sound cues (e.g., Figs. 5E and 7D, respectively). In all three fields, population spike rates vary minimally (i.e., 1.1-fold, Fig. 9H), whereas spike-timing jitter changes up to 4.5-fold (i.e., 450%, Fig. 9A), with change in sound shape parameter. Change in population spike rates are minimal (i.e., < 20%, 1.2-fold) with sound modulation frequency (Fig. 9L) and are only significant in VAF (Fig. 9L, green symbols). Hence, spike rate change is not likely to account for the marked changes in reliability over the same range (Fig. 9E). The relatively flat population spike rate response relations we observed in this study reflect an averaging of a wide range of single-unit spike rate responses across sound conditions. Together, these results indicate that the marked changes in population jitter and reliability with temporal sound cues do not stem from changes in population spike rate.

Temporal Coding Fraction Varies with Sound Modulation Frequency

The cortical responses observed in this study contain both synchronous and asynchronous spikes. A high temporal coding fraction is observed when the power of the synchronized response is larger than the power of the asynchronous response (methods). In A1, the mean temporal coding fraction is maximal for a noise burst with f_c of 64 Hz, duration of 2 ms, and f_m of 4 Hz (Fig. 8C, asterisk). Thus temporal coding is maximal for relatively brief noise burst durations with slow modulation frequencies. In VAF and cSRAF, temporal coding fraction is maximal for sound with f_c of 6 Hz, duration of 23 ms, and f_m of 2 Hz (Fig. 8, G and K, asterisks). This indicates that maximal temporal coding is obtained in VAF and cSRAF with noise burst durations that are longer than those eliciting maximal temporal coding in A1. The f_c inducing maximal temporal coding fraction (i.e., the best f_c) decreases significantly [F(2, 220) = 5.3, P = 0.006] between A1, VAF, and cSRAF: 24 (1.1), 17 (1.1), and 13 (1.2) Hz, respectively. This indicates that sound shape sensitivities contribute to the relative synchronization of responses. Figure 9I illustrates how temporal coding fraction changes with sound modulation frequency when sound shape is fixed. For a short-duration noise burst (f_c = 64 Hz), the temporal coding fraction increases with modulation frequency up to 4 Hz in all fields (Fig. 9I) and is highest in A1 (Fig. 9I, blue symbols). For modulation frequencies above 4 Hz, the temporal coding fraction decreases logarithmically with increasing modulation frequency in all fields. The modulation frequency upper cutoff measured at 50% maximal temporal coding fraction varies significantly among regions [F(2, 1,579) = 12.28, P < 0.001] and is higher for A1 and VAF than it is for cSRAF (Fig. 9, J and K). Collectively, these results indicate that temporal synchrony of responses to short-duration noise bursts at interburst intervals around 250 ms is higher in A1 and VAF than in cSRAF.

Jitter and Reliability Covariations Differ Across Cortical Fields

Although jitter and reliability are both metrics of spike-timing variability, they can vary independently (Buran et al., 2010; Zheng and Escabí, 2013). In this study, we found this is true for A1 neurons, because reliability varies with sound modulation frequencies but jitter does not (Fig. 10A, for fixed f_c of 64 Hz). Thus reliability is high (∼1.5 spikes/cycle) when sound modulationcycle) when sound modulation frequency is low (f_m = 2 Hz; Fig. 10A, red symbols), and reliability is lowest (<0.1 spikes/cycle) when sound modulation frequency is higher (f_m = 32 Hz; Fig. 10A, purple symbols). In contrast, jitter does not change with sound modulation frequency in A1 (Fig. 10A). As a consequence, there is insignificant correlation (r = 0.15, P = 0.10) between jitter and reliability, and the corresponding regression slope is not significantly different from zero [slope = −0.02 (0.04)], indicating a sound-induced variation of reliability independent of jitter in A1. For VAF and cSRAF, jitter and reliability both increase as sound modulation frequency is varied from lower (Fig. 10, D and G, red symbols) to higher values (Fig. 10, D and G, purple and pink symbols), and they are strongly correlated (VAF and cSRAF: r = 0.64 and r = 0.55, respectively; both P < 0.001). Corresponding regression slopes are significantly different [ANCOVA: F(2, 380) = 58.1, P < 0.001] across cortical fields [A1, VAF, and cSRAF slope: −0.02 (0.04), 0.69 (0.04), and 0.71 (0.1), respectively]. These results indicate distinct spike-timing mechanisms for sensing sound modulation frequency in A1 vs. ventral cortical fields.

When sound shape and periodicity cues are jointly varied, as in the case of SAM sounds, there are significant correlations between jitter and reliability in all cortical fields (A1, VAF, and cSRAF: r = 0.72, r = 0.87, and r = 0.82, respectively; all P < 0.001; Fig. 10, B, E, H). Corresponding regression slopes are steep and not significantly different across A1, VAF, and cSRAF [mean slope: 0.95 (0.13), 1.02 (0.05), 1.05 (0.09); F(2, 182) = 0.30, P = 0.73; Fig. 10, B, E, H]. The covariation of jitter and reliability is unsurprising for VAF and SRAF responses given that jitter and reliability vary jointly with sound modulation frequency (Fig. 10, D and G). However, the covariation of jitter and reliability in A1 with SAM like sounds is surprising given the lack of covariation shown in Fig. 10A. This result in A1 could be attributed to sound shape sensitivities (Fig. 9A), because the sound shape and modulation frequency are changing proportionally for data in Fig. 10, B, E, H. Together, these results indicate that independence of reliability and jitter cannot be determined for these cortical fields if responses are probed with sounds that covary shape and periodicity cues, as is the case with SAM sounds.

As already demonstrated for all cortical fields, jitter decreases when sound f_c increases but modulation frequency is fixed (Fig. 9A). Under these same conditions we found that reliability increases as jitter increases such that the two are significantly correlated with correlation coefficients for A1, VAF, and cSRAF: r = 0.56, r = 0.85, and r = 0.82, respectively (for all comparisons P < 0.001). The steep regression slopes also indicate a strong covariation (Fig. 10, C, F, I). As illustrated in spike-time dot raster plots of single-neuron responses (e.g., Fig. 5B), the number of spikes decreases along with the jitter as sound f_c increases. By definition, reliability decreases as the number of spikes per cycle decreases (methods); thus the observed covariation in jitter and reliability under these conditions is expected. We found the covariation regression slopes are not significantly different across cortical fields (Fig. 10, C, F, I). This is consistent with our observation that all cortical fields display a power-law dependence of jitter on sound f_c.

DISCUSSION

Spike-Timing Changes with Temporal Sound Cues in Primary and Nonprimary Auditory Cortex

Prior studies have reported changes in relative response synchrony with sound periodicity cues (Doron et al. 2002; Eggermont 1998; Joris et al. 2004; Niwa et al. 2013; Schreiner and Urbas 1988; Schulze and Langner 1997). However, response synchrony measures (e.g., vector strength and correlation indexes) from these studies do not distinguish the response variation (i.e., jitter) to sound onsets from its reliability over repeated trials. As we have demonstrated in this study for A1 neurons and previously for midbrain neurons, spike-timing jitter and reliability can vary independently to potentially encode distinct temporal sound cues (Zheng and Escabí 2008, 2013). This indicates that jitter and reliability are useful metrics, because they can decompose and independently quantify two forms of response variability. Moreover, these metrics have widespread utility, because they can be determined for neural responses to aperiodic sounds (Chen et al. 2012; Elhilali et al. 2004; Miller et al. 2002; Sen et al. 2001). We report novel population wide trends in three auditory cortices of the rat (A1, VAF, and cSRAF) consisting of logarithmic decreases in jitter and reliability with sound envelope shape and periodicity parameters (Fig. 9, A and E). Comparable changes in firing rate with changing sound shape and periodicity were not observed in the three neural populations (Fig. 9, H and L, respectively). This is meaningful because spike-timing reliability and jitter provide neural correlates of periodicity and shape cues, respectively. Moreover, it suggests spike-timing jitter may provide a temporal code for the perceptual qualities of sound shape including timbre, intensity, and duration.

In all three cortical fields examined in this study, we found a decrease in the spike-timing reliability with increasing sound modulation frequency (Fig. 9E). This is consistent with prior reports for midbrain and A1 neurons (Malone et al. 2007; Zheng and Escabí 2008, 2013). We also found that changes in reliability with sound modulation frequency were not associated with changes in jitter in A1. Hence, jitter and reliability did not covary for A1 neurons (Fig. 10A). Importantly, this independence suggests distinct underlying biological sources for jitter and reliability and is consistent with independent jitter and reliability sensitivities observed at the first synapse of the auditory pathway (Buran et al. 2010) and in auditory midbrain (Zheng and Escabí 2013). This is also important because it suggests that the reliability of a response can be reduced at high sound modulation frequencies without altering the response timing precision within each cycle of sound. This result contrasts with a prior study of A1 neurons that found first-spike jitter does change with sound level and modulation frequency (Phillips et al. 1989). Such differences could be attributed to the fact that the latter study included only the transient first spike in the analysis, whereas the present study includes first and any other subsequent spikes. Such changes in jitter with sound modulation frequency might be attributed to response adaptations that occur during the non-steady-state portion of the response. The lack of covariation between steady-state jitter and reliability reported in this article for A1 may be a characteristic property of early levels of the auditory pathway given it is also observed in auditory midbrain (Zheng and Escabí 2013).

In VAF and cSRAF, spike-timing jitter and reliability did not vary independently. Instead, they covaried with sound modulation frequency (Fig. 10, D and G) and shape (Fig. 10, F and I). This is significant because it indicates that jitter could only convey information about the combined shape and modulation frequency of a sound sequence in these cortices. Given that VAF and cSRAF have larger jitter, and therefore more sustained responses to sound shape, one may predict that spike rate is a better metric of their sensitivities. However, population spike rates did not change with sound shape in any of the three fields and only varied minimally with sound modulation frequency, and only in VAF (Fig. 9, H and I). These results indicate that population spike-timing pattern, and not simply spike rate, has the capacity to encode temporal sound cues in A1 and ventral nonprimary cortices.

It is functionally significant that ventral cortices, VAF and cSRAF, had more sustained responses and longer sound encoding times than A1, as indicated by their longer jitter time scales. A neuron's “encoding time” is the time window over which it responds in a temporally precise manner to changes in sound, and it is estimated as twice the jitter (Chen et al. 2012; Theunissen and Miller 1995). Conceptually, one can think of jitter and encoding time as the time scale over which a neuron's spiking pattern conveys information needed to parse or discriminate sounds. In this study we found that A1 had the shortest mean jitter, on the order of 10 ms (e.g., Fig. 9B, blue bar), and therefore the shortest mean encoding time, on the order of 20 ms. This is consistent with steady-state jitter and sound encoding times for A1 neurons reported for other species and probed with dynamically modulated sounds (Chen et al. 2012; Elhilali et al. 2004; Miller et al. 2002; Sen et al. 2001). In contrast, the first-spike jitter of A1 neurons in response to repetitive sound sequences was much shorter, typically <2 ms, and closer to the time scale of that observed in the auditory nerve (Heil 1997; Phillips 1993; Phillips and Hall 1990). In this study, we found that mean jitter of the steady-state response was rank ordered and increasing across cortical fields: A1 < VAF < cSRAF (Fig. 9B). This goes hand in hand with an upward shift in the power-law relationship and total range of jitter observed with progression from A1 to cSRAF (Fig. 9A and Fig. 10, C, F, I). In cSRAF, the mean jitter and encoding times for the 55 sounds examined were ∼15 and 30 ms, respectively. A single noise burst with duration of 70 ms (i.e., f_c = 2 Hz) induced mean jitter and encoding times of 70 and 140 ms, respectively, in cSRAF (e.g., Fig. 9A, red symbols, 2-Hz f_c). In contrast, mean jitter and encoding times were as little as 20 and 40 ms, respectively, for the same 70-ms duration noise burst in A1 (Fig. 9A, blue symbols, 2-Hz f_c). Thus cSRAF neurons have the capacity to encode, parse, or group sound features over a time window that is 100 ms longer than in A1 neurons. Although mean steady-state jitter and encoding times increased almost twofold on average between A1 and cSRAF, this is not as great as the 10-fold increase observed between auditory midbrain and A1 in the cat (Chen et al. 2012).

A transformation to longer steady-state jitter time scales could determine how caudal-ventral cortices in the rat encode extended sound sequences containing both shape and periodicity cues. By analogy, the posterior (PAF) nonprimary auditory cortex in the cat can readily follow slow but not fast sound envelope transients, and this limitation is attributed to “the large jitter in response timing of these neurons” (Heil 2001). This indicates that response jitter can limit the range of sound shapes to which a neuron or cortical field may respond. In addition, models of neural spiking suggest that an increase in response duration and jitter should limit response synchronization and the capacity to temporally encode sound modulation frequency (Escabí and Read 2003; Lu and Wang 2004; Rabang and Bartlett 2011). Accordingly, we found the proportion of response power with synchronized spiking (i.e., the maximum temporal coding fraction) decreased almost twofold between A1 and cSRAF (e.g., Fig. 9I), mirroring the almost twofold increase in jitter time scales. Thus fields that have higher jitter, and therefore longer encoding times, have reduced capacity to temporally encode high envelope modulation frequencies. This apparent trade-off between response encoding time and temporal coding fraction may also explain why ventral-posterior cortices in the cat (PAF and VPAF) are more sensitive to sound envelope shape than to periodicity (Schreiner and Urbas 1988). It is feasible that the different jitter time scales of A1, VAF, and cSRAF allow the regions to encode unique combinations of sound shape and modulation frequency. Accordingly, we found cSRAF neurons had their highest temporal coding fraction in response to a periodic noise burst sequence with slow temporal onsets, long burst durations, and a low modulation frequency (Fig. 8K, asterisk). In contrast, A1 neurons had their highest temporal coding fraction in response to a sound sequence with a faster onset and a higher modulation frequency (Fig. 8C, asterisk). Thus primary and ventral nonprimary cortical fields spike with maximal temporal synchrony to unique combinations of sound shape and periodicity cues. The current and previous results are consistent with a framework where jitter time scales ultimately determine the combination of sound shape and modulation frequency cues that a given cortical field may encode with the spike timing of their response.

Candidate Biological Mechanisms Contributing to Spike-Timing Variability

Several biological mechanisms may contribute to the differences in spike-timing precision and reliability observed across the cortical fields. The type of vesicular glutamate transporters expressed at input neuron synapses can contribute to spike-timing variability. For example, synaptic transmitter release probability is higher at synapses that contain two types of vesicular glutamate transporter as opposed to one; this results in more reliable postsynaptic potentials and spiking in the postsynaptic targets (Fremeau et al. 2004; Wilson et al. 2005; Wojcik et al. 2004). The latter could in principle contribute to the higher temporal coding fractions (Fig. 9I) and reliability upper cutoffs (Fig. 9, F and G) in A1, given that we find thalamic neurons projecting to A1 express two glutamate transporters, whereas those projecting to cSRAF express only one (Storace et al. 2012).

A potential source of jitter is the variability in the probabilistic opening and closing of membrane ion channels (i.e., channel noise) on postsynaptic membrane that contributes to variable membrane excitability and, ultimately, spike-timing jitter (Marsalek et al. 1997; Schneidman et al. 1998). Sensory systems can regulate such sources of jitter through neuromodulator action on postsynaptic neurons (Billimoria et al. 2006). However, the time scales for postsynaptic membrane jitter are small even in neocortical neurons. For example, spike-timing jitter is on the order of 1 ms in neocortical neurons in response to time-varying current injections (Mainen and Sejnowski 1995). Accordingly, postsynaptic membrane excitability is unlikely to explain the long steady-state jitter and encoding times and their differences across auditory cortical fields reported in this study. Another potential source of jitter is the synaptic response variability due to short-term plasticity (e.g., synaptic depression and facilitation) that occurs with repetitive activation (Mohan et al. 2013; Reyes 2011). In this study, we minimize the contribution of short-term plasticity by analyzing the steady-state response to ongoing sound repetition (methods).

Differences in the synaptic input source and pathway convergence to auditory cortical fields likely contribute to differences in spike-timing precision between cortices observed in this study. For example, computational models suggest that pooling of synaptic inputs and synaptic network dynamics could generate synaptic input variability that in turn contributes to spike-timing jitter in recipient neurons (Butts and Goldman 2006; Siegel and Read 2001). Accordingly, for the rat, it is plausible that differences in sound-evoked jitter in auditory cortical neurons stem from differences in their corresponding thalamocortical (Storace et al. 2010, 2011, 2012) or corticocortical inputs (Mascagni et al. 1993; Romanski and LeDoux 1993; Shi and Cassell 1997). For example, the rat ascending thalamic pathways to physiologically defined A1 and VAF arise from different caudal-rostral sections of thalamus and have different spectral resolution that could result in different network convergence patterns onto corresponding cortical target neurons (Polley et al. 2007; Storace et al. 2011). Populations of neurons within thalamus have varying degrees of onset, sustained, and offset spike train responses to sound (Bartlett and Wang 2007; He 2002; Rabang and Bartlett 2011; Rabang et al. 2012; Scholl et al. 2010), and these spike-timing differences could be passed onto cortex or even transformed through pathway convergence to construct new sound-related spike-timing response jitter and other response sensitivities (Chen et al. 2012; Miller et al. 2001).

Encoding Envelope Pitch Cues

The present study does not address how shape or periodicity cues may be encoded when sound modulation frequencies are above 100 Hz and perceived as pitch. Primates and rodents clearly detect and have selective cortical responses to pitch cues (Kelly et al. 2006; Long and Clark 1984; Lu et al. 2001b; Schulze and Langner 1997; Walker et al. 2011), and yet we found limited responses with modulation frequencies above 10 Hz. It is plausible that the lack of responses to pitch cues is due to use of ketamine anesthesia, which blocks excitatory N-methyl-d-aspartate (NMDA) receptors (Monaghan et al. 1989) and can alter spike timing and the range of sound modulation frequencies to which a neuron responds (Felix et al. 2012). However, anesthesia is not the only factor determining such limits, because other studies have observed similar sound modulation frequencies limits for synchronized neural responses in awake primate A1 (Malone et al. 2007). The present study found a decline in synchronous responses with sound modulation frequency (e.g., Fig. 9I) and in this respect is consistent with frameworks proposing that low and high sound modulation frequencies are encoded with synchronous vs. asynchronous responses in cortex (Bendor and Wang 2005; Lu et al. 2001b; Schulze and Langner 1997).

Conclusion

Prior studies support the notion that cortical neurons can keep track of sound rhythms by ticking off synchronized spikes with each beat of the rhythm, like the ticktock of a metronome (Joris et al. 2004). On the other hand, the timing precision of the first spike of a response has the capacity to encode sound envelope shape (Heil 2001, 2003). The present study extends these previous conceptualizations and indicates that spikes beyond the first spike and their corresponding jitter have the potential to encode sound envelope shape cues. We find that A1 has the capacity to independently encode shape and rhythm sound cues much like lower stations of the auditory pathway (Buran et al. 2010; Zheng and Escabí 2008). In contrast, we find that spike-timing jitter and reliability covary in the ventral nonprimary auditory cortices and have the capacity to encode combined features of sound shape and periodicity cues. This raises the intriguing possibility that ventral auditory cortices form a specialized stream for encoding combinations of sound shape and rhythm cues.

GRANTS

We acknowledge funding support from National Science Foundation (NSF) Award 1355065 (to H. L. Read and M. A. Escabí), NSF Integrative Graduate Education Research Training Grant I1144399 (to H. L. Read, core faculty), and the University of Connecticut research foundation.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

C.M.L. and A.F.O. performed experiments; C.M.L., M.A.E., and H.L.R. analyzed data; C.M.L., M.A.E., and H.L.R. interpreted results of experiments; C.M.L. and H.L.R. prepared figures; C.M.L., M.V., M.A.E., and H.L.R. edited and revised manuscript; C.M.L., A.F.O., M.V., M.A.E., and H.L.R. approved final version of manuscript; M.A.E. and H.L.R. conception and design of research; H.L.R. drafted manuscript.