Synaptic refinement during development and its effect on slow-wave activity: a computational study

Abstract

Recent evidence suggests that synaptic refinement, the reorganization of synapses and connections without significant change in their number or strength, is important for the development of the visual system of juvenile rodents. Other evidence in rodents and humans shows that there is a marked drop in sleep slow-wave activity (SWA) during adolescence. Slow waves reflect synchronous transitions of neuronal populations between active and inactive states, and the amount of SWA is influenced by the connection strength and organization of cortical neurons. In this study, we investigated whether synaptic refinement could account for the observed developmental drop in SWA. To this end, we employed a large-scale neural model of primary visual cortex and sections of the thalamus, capable of producing realistic slow waves. In this model, we reorganized intralaminar connections according to experimental data on synaptic refinement: during prerefinement, local connections between neurons were homogenous, whereas in postrefinement, neurons connected preferentially to neurons with similar receptive fields and preferred orientations. Synaptic refinement led to a drop in SWA and to changes in slow-wave morphology, consistent with experimental data. To test whether learning can induce synaptic refinement, intralaminar connections were equipped with spike timing-dependent plasticity. Oriented stimuli were presented during a learning period, followed by homeostatic synaptic renormalization. This led to activity-dependent refinement accompanied again by a decline in SWA. Together, these modeling results show that synaptic refinement can account for developmental changes in SWA. Thus sleep SWA may be used to track noninvasively the reorganization of cortical connections during development.

cortical circuits are formed over successive stages of development in the brain (Espinosa and Stryker 2012) that underlie ongoing cognitive maturation (Craik and Bialystok 2006). An early and critical developmental phase is the formation of selective connectivity among neurons that receive related sensory inputs (Ko et al. 2011; White and Fitzpatrick 2007; Yoshimura et al. 2005). An important question is the extent to which these selective circuits are formed through synaptic pruning, a net reduction in synapses and connections, or by synaptic refinement, the selective reorganization of an initially homogenous connectivity without a change in the net number of synapses (Innocenti and Price 2005; Tau and Peterson 2010).

The primary visual cortex (V1) is a model region for studying developmental changes in cortical connectivity. In the adult V1 lateral axons are clustered, connecting to neurons with similar receptive fields (RFs) and preferred orientations (POs) (Gilbert and Wiesel 1983). The reorganization of lateral cortical connections into such a selective pattern, from an initially homogenous state, is thought to occur early on in development (Callaway and Katz 1991). Recent experiments on synaptic refinement in mice have revealed that after the establishment of feedforward connections, lateral connections reorganize through two processes that appear to balance each other so that the overall connectivity rate stays constant (Ko et al. 2013). In one process, neurons with similar visual responses become preferentially connected to each other, a phenomenon that occurs largely independent of visual experience; in the other, neurons that do not respond reliably to visual stimuli become less interconnected, a process that does not occur with dark rearing (Ko et al. 2013, 2014). Additionally, there is recent evidence that synaptic refinement occurs not just through the formation and elimination of synaptic connections but also through changes in the strengths of existing synapses. Thus mouse V1 neurons with similar RFs and POs are more likely to have stronger excitatory connections (Cossell et al. 2015).

Once adolescence starts in humans and adultlike cognitive capacities appear, the brain's metabolism falls off sharply, along with its ability to recover function after injury (Feinberg 1983; Spear 2000). Over this period from pre- to postadolescence, the total number of synapses as well as the corresponding gray matter volume is thought to follow an inverted U-shaped curve, peaking at preadolescence and then decreasing over the course of adolescence (Blakemore and Choudhury 2006; Lenroot and Giedd 2006). Intriguingly, a similar inverted U-shaped curve also has been observed in slow-wave activity (SWA) during non-rapid eye movement (NREM) sleep. NREM SWA (defined as EEG power in the 0.5- to 4-Hz range) also peaks at the end of childhood and then decreases over the course of adolescence (Kurth et al. 2010b). It has been suggested that the decline in the total number of synapses may be the cause of the observed decrease in SWA (Campbell and Feinberg 2009; Feinberg 1983). This hypothesis is consistent with computer models showing that the amount of SWA correlates with overall synaptic strength (Esser et al. 2007). However, there is actually little direct experimental evidence that significant synaptic pruning occurs in human adolescents at the time of the decline of SWA (Paus et al. 2008; Petanjek et al. 2011).

A decrease of SWA from pre- to postadolescence was also observed in mice (de Vivo et al. 2014) and rats, in which SWA follows an inverted U-shaped curve similar to the one in humans (Olini et al. 2013). In mice, however, it is clear that most synaptic pruning occurs long before the developmental drop in SWA, and over the period from pre- to postadolescence there is no substantial change in the number of synapses in the whole brain (De Felipe et al. 1997; de Vivo et al. 2014). On the other hand, during the same period there is major synaptic refinement, at least in the primary visual cortex (Ko et al. 2013), which seems to coincide in time with the reduction in SWA. Therefore, an intriguing possibility is that cortical synaptic refinement, rather than synaptic pruning, may play a role in the developmental decline in SWA.

To investigate if and how synaptic refinement is sufficient to explain observed changes in SWA during development, we resorted to computer simulations in which we could systematically manipulate synaptic refinement while assessing the resulting effects on SWA. The simulations were performed by taking advantage of a large-scale model of the primary visual cortex and associated thalamic regions that reproduces accurately cortical activity during wake and sleep (Esser et al. 2005, 2007; Hill and Tononi 2005; Olcese et al. 2010). In the present work, neural activity in the model was assessed in its wake and sleep mode both before and after synaptic refinement was implemented in a way that mimicked physiological data (Ko et al. 2013). We show that when we rewired lateral corticocortical connections such that neurons with similar POs and RFs were linked more selectively (hardwired refinement), there was invariably a marked decline in SWA in accord with experimental data in different species. We further show that an equivalent decline of SWA could be obtained by achieving synaptic refinement through spike timing-dependent plasticity (STDP), where connections underwent repeated cycles of potentiation through exposure to visual stimuli in the wake mode, followed by synaptic renormalization.

MATERIALS AND METHODS

The large-scale model used in this study was first introduced by Hill and Tononi (2005). The following describes the organization, connectivity, and cellular and synaptic parameters of the version used herein. Previous model versions have been used to 1) produce realistic wake and sleep dynamics (Hill and Tononi 2005), 2) reproduce realistic responses to both visual stimuli (Hill and Tononi 2005) and transcranial magnetic stimulation (Esser et al. 2005), 3) predict the breakdown of effective connectivity during sleep (Esser et al. 2009), 4) assess the effects of changes in synaptic strength on SWA and slope (Esser et al. 2007), and 5) observe the effects of homeostatic synaptic renormalization on learning and memory (Olcese et al. 2010). The present model version closely resembles that of Esser et al. (2007) in parameters and connectivity. However, in this model only V1 is simulated, with some adaptations so that local excitatory connections could undergo synaptic refinement similar to that observed in vivo. Lists of all network connections and model parameters are provided in Tables 1–3.

Table 1.

Thalamocortical connectivity

									Delay
Source Layer	Cell Type	Target Layer	Cell Type	Transmitter	Style	Pmax (height)	Radius or Size	Strength	Mean	SD
Optic nerve	Exc	LGN	Exc, Inh	AMPA	Gaussian	0.75	1	10	2	1
Thalamic
LGN	Exc	NRT	Exc	AMPA	Gaussian	1	2	2	2	0.25
LGN	Inh	LGN	Exc, Inh	GABAA	Gaussian	1	2	2	1	0.25
NRT	Inh	NRT	Inh	GABAA	Gaussian	0.5	12	2	1	0.25
NRT	Inh	LGN	Exc, Inh	GABAA	Gaussian	0.15	12	2	2	0.25
NRT	Inh	LGN	Exc, Inh	GABAB	Gaussian	0.05	12	2	2	0.25
M cells	Exc	M cells	Exc, Inh	AMPA, NMDA	Rectangular	0.03	10 × 10	1	2	0.25
M cells	Inh	M cells	Exc, Inh	GABAA	Gaussian	0.3	2	2.9	2	0.25
Thalamocortical
LGN	Exc	IV, Infra	Inh	AMPA	Gaussian	0.1	5	3.5	3	0.25
LGN	Exc	IV, Infra	Exc	AMPA	Rectangular	0.5	8 × 1	3.5	3	0.25
M cells	Exc	Supra, Infra	Exc, Inh	AMPA	Gaussian	0.1	12	0.3	7	0.2
Corticothalamic
Infra	Exc	NRT	Inh	AMPA	Gaussian	0.5	5	0.5	8	0.5
Infra	Exc	LGN	Exc, Inh	AMPA	Gaussian	0.25	7	0.33	8	0.5
Infra	Exc	M cells	Exc, Inh	AMPA	Gaussian	0.1	12	0.62	5	1
V1 intraareal
Supra	Exc	Supra	Exc	AMPA	Rectangular	0.064	10 × 10	1	2	0.25
Supra	Exc	Supra	Exc	NMDA	Rectangular	0.064	10 × 10	0.75	2	0.25
Supra	Exc	Supra	Inh	AMPA	Gaussian	0.05	12	0.6	2	0.25
Supra	Inh	Supra	Exc, Inh	GABAA	Gaussian	0.025	7	0.5	2	0.25
Supra	Inh	Supra	Exc, Inh	GABAB	Gaussian	0.5	2	0.5	2	0.25
IV	Exc	IV	Exc	AMPA	Rectangular	0.0384	10 × 10	1	2	0.25
IV	Exc	IV	Inh	AMPA	Gaussian	0.05	12	0.6	2	0.25
IV	Inh	IV	Exc, Inh	GABAA	Gaussian	0.025	7	0.5	2	0.25
Infra	Exc	Infra	Exc	AMPA	Rectangular	0.0384	10 × 10	1	2	0.25
Infra	Exc	Infra	Inh	AMPA	Gaussian	0.05	12	0.6	2	0.25
Infra	Exc	Infra	Exc, Inh	GABAA	Gaussian	0.025	7	0.5	2	0.25
V1 interareal
Supra	Exc	Infra	Exc, Inh	AMPA	Gaussian	1	2	1	2	0.25
Supra	Exc	Infra	Exc	NMDA	Gaussian	1	2	1	2	0.25
Supra	Inh	IV, Infra	Exc, Inh	GABAB	Gaussian	0.5	2	0.5	2	0.25
IV	Exc	Supra	Exc, Inh	AMPA	Gaussian	1	2	2.21	2	0.25
Infra	Exc	Supra	Exc, Inh	AMPA	Gaussian	1	2	2.21	2	0.25
Infra	Exc	IV	Exc, Inh	AMPA	Gaussian	1	2	2.21	2	0.25

Parameters for the connectivity profiles used to construct the thalamocortical network. Connection profiles are listed per layer and neuron type for the large-scale model. Gaussian connections are selected according to a Gaussian distribution (σ = 7.5) with a peak of P_max. Rectangular connections are selected by the maximum probability P_max within a rectangular area. The radius of the Gaussian connections and size (area) of rectangular connections are measured in no. of neurons (so 10 × 10 means a probability distribution over a square of 10 neurons). Strength (expressed in no. of simultaneous PSPs per connection) is a modifier of the synaptic currents defined in materials and methods. The mean delay of the spike impulse from the source cell to the target cells and its SD are measured in ms.

Exc, excitatory; Inh, inhibitory; Infra, infragranular; Supra, supragranular.

Table 3.

Intrinsic neuronal currents

		Conductance,
Channel	Neurons	Waking	Sleeping
gNaP	Exc/Inh	0.5	1.25
gh	Exc	0.5	4.0
gT	30% Exc	0.5	4.0
gDK	Exc/Inh	0.5	0.8
gKL	Exc/Inh	1.0	1.85

Peak conductance (g_peak) of intrinsic neuronal currents for different channel types during wake and sleep. Conductances are implicitly normalized by a leak membrane conductance and thus adimensional.

Overall organization.

The large-scale model (Fig. 1) consists of a section of V1 (14,400 simulated neurons) along with an associated section of thalamus (2,400 neurons). The model design enables realistic physiological responses, such as edge detection, when presented with simulated retinal stimuli embedded in noise (Esser et al. 2007; Hill and Tononi 2005).

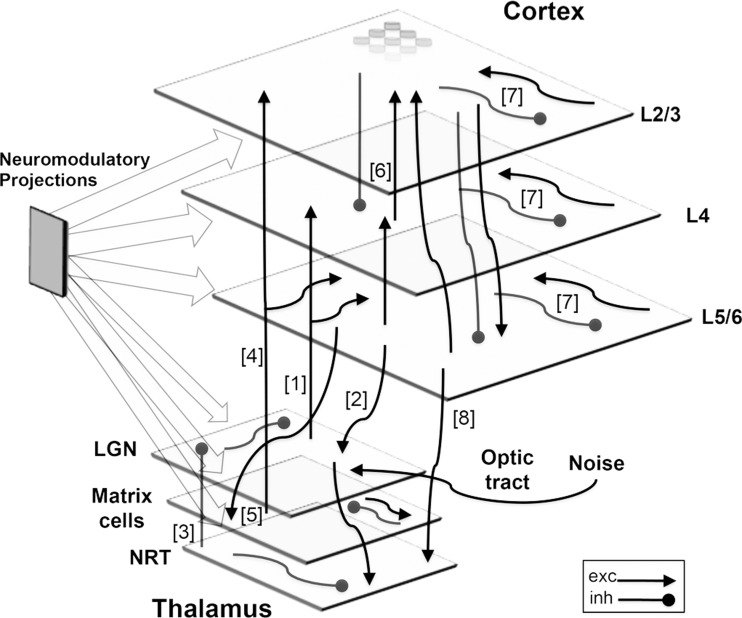
Fig. 1.

Schematic diagram. V1 and a thalamic area consisting of the LGN, matrix cells, and NRT. Visual inputs of either presented stimuli or background noise are projected onto the LGN via the optic tract (right). Thalamocortical loops are implemented by projections from the LGN to L4 and L5/6 [1] and by excitatory back connections from L5/6 to the LGN [2]. The NRT sends inhibitory projections diffusely to neurons in the LGN [3]. Matrix cells provide broad excitation to both L2/3 and L5/6 [4] and receive diffuse excitatory feedback from L5/6 [5]. These loops, along with broad lateral excitatory connections between matrix cells, allow matrix cells to act as a global oscillator coupled to the cortex. Cortical interlaminar loops constructed of highly specific columnar projections [6] go from L4 to L2/3, from L2/3 to L5/6, and then from L5/6 back to L2/3 and L4, enacting vertical interlaminar processing. Cortical intralaminar lateral connections [7], both excitatory and inhibitory, span each layer. Feedback connections from the cortex [8] regulate the activity of the thalamus. There are numerous diffuse neuromodulatory connections (left). Network not drawn to scale. Exc, excitatory; inh, inhibitory.

The simulated cortex has three layers: the supragranular layer (L2/3), layer 4 (L4), and the infragranular layer (L5/6), each with its own inter- and intralaminar connectivity. Cortical columns are represented by groups of nine model neurons (2 excitatory and 1 inhibitory neuron per layer; Mountcastle 1997). The simulated V1 area is retinotopically structured and corresponds to ∼0.6 cm² of striate cortical surface (equating to a monocular patch of 6° × 6° in the parafoveal visual field). This means that locations on the cortex have corresponding locations in the thalamus and retina, a relationship mediated by afferents from the model lateral geniculate nucleus (LGN). These afferents converge onto individual neurons in both L4 and L5/6 (creating 8 × 1 RFs) and enforce POs. Four different POs of bars are explicitly implemented in the model: 0° (vertical), 45° (right-slanting diagonal), 90° (horizontal), and 135° (left-slanting diagonal).

The thalamus is composed of three distinct cellular populations, each with its respective function: core cells in the LGN, matrix cells, and intrathalamic inhibitory cells in the nucleus reticularis of the thalamus (NRT). Each topographic location in the LGN is composed of two neurons: one that acts as an X-relay cell and the other as an inhibitory interneuron. For simplicity, only the ON portion of the RFs of the thalamic neurons is modeled. Matrix cells project diffusely to cortex (Jones and Hendry 1989). Hence, model matrix cells diffusely target L2/3 and L5/6, receive feedback via excitatory corticothalamic connections from L5/6, and assist global synchronization during sleep. The NRT also receives corticothalamic feedback from L5/6, as well as excitatory inputs from the LGN, while at the same time providing the LGN with inhibitory feedback.

Connectivity.

Presynaptic neurons connect probabilistically to postsynaptic neurons. Connection profiles are either Gaussian spatial density profiles (as for local inhibitory connections) or rectangular, uniformly distributed profiles (as for the thalamocortical afferents that implement POs and specified RFs). There are two categories: focused (area < 8 × 8; for example, interlaminar connections) or diffuse (area ≥ 8 × 8; for example, lateral inhibitory connections). Although the ratio of excitatory to inhibitory neurons in the model is 2:1, to resemble in vivo data, the ratio of excitatory to inhibitory synapses is 80:20 (White and Keller 1989). Conduction delays are taken into account in the connection profiles. Full details of connections profiles are given in Table 1.

Model neurons.

The model is composed of single-compartment spiking neurons implementing Hodgkin-Huxley-style currents. The simplified dynamics of the fast spiking currents (I_Na and I_K) preserve the efficiency of integrate-and-fire neurons for large-scale simulations (Hill and Tononi 2005). The change in subthreshold membrane potential V for each neuron is given by

$$\frac{dV}{dt}=\left[-g_{NaL}\left(V-E_{Na}\right)-g_{KL}\left(V-E_K\right)-I_{syn}-I_{\mathrm{int}}\right]/{\tau }_m-g_{spike}\left(V-E_K\right)/{\tau }_{spike\mathrm{.}}$$

The Na⁺ leak conductance (g_NaL = 0.4; E_Na = 30 mV) and K⁺ leak conductance (g_KL = 1.0; E_K = −90 mV) are the primary contributors to the resting membrane potential. All neural parameters are from Hill and Tononi (2005), including the activation of a fast K⁺ current during a spike in the form of a brief pulse (in which g_spike = 1 for a duration t_spike), the governing time for the fast hyperpolarizing current (τ_spike), the threshold time constant (τ_θ) that determines the time to return to the equilibrium threshold, and the membrane time constants (τ_m), all summarized in Table 2. The membrane potential is influenced by synaptic input (I_syn) and intrinsic currents (I_int). A spike occurs when the membrane potential V reaches threshold, which drives V to the sodium reversal potential E_Na. After a spike, neurons enter a refractory period of length τ_θ. Rapid synaptic depression occurs through depletion of presynaptic vesicle pools (Hill and Tononi 2005; Zucker and Regehr 2002).

Table 2.

Neuron spike parameters

Neuron Type	θeq, mV	τθ, ms	tspike, ms	τspike, ms	τm, ms
Cortical Exc	−51	2	2	1.75	16.0
Cortical Inh	−53	1	1	−0.5	8.0
Thalamic	−53	0.75	1	0.75	8.0

Parameters for membrane potential equation, defined in materials and methods, Model neurons, specified for each neuronal type.

I_syn is a summation of all incoming currents from synaptic channels:

$$I_{syn}={\displaystyle \sum _{i,j}{g}_j^i\left(t\right)\left(V-E_j\right)}.$$

The amplitude and time course of each current are defined by the time-varying conductance g(t) for each afferent i on each channel j. The reversal potential E_j for each channel determines its sign. Each current has a rise and decay time constant (τ₁ and τ₂, respectively). Excitatory current comes from voltage-independent (AMPA) and voltage-dependent (NMDA) channels, whereas inhibition occurs via fast (GABA_A) and slow (GABA_B) channels. Specifically, synaptic parameters are as follows: AMPA (τ₁ = 0.5 ms, τ₂ = 2.4 ms, E_rev = 0 mV), NMDA (τ₁ = 4.0 ms, τ₂ = 40.0 ms, E_rev = 0 mV), GABA_A (τ₁ = 1.0 ms, τ₂ = 7.0 ms, E_rev = −70 mV in the cortex and −80 mV in thalamic cells), and GABA_B (E_rev = −90 mV). The synaptic parameters of GABA_B are fully explicated in Esser et al. (2009) and are designed to undergo nonlinear changes in conductance in response to consistent activation, based on a previous channel model (Destexhe and Sejnowski 1995). Except for the updated GABA_B channels, all parameters are as described in Hill and Tononi (2005). However, the peak conductance values of the model neurons were adapted to sustain single excitatory postsynaptic potentials of ∼1-mV amplitude and inhibitory postsynaptic potentials of 1- to 1.5-mV amplitude (see values in Table 3).

I_int also influence the firing dynamics of all cortical and thalamic neurons (as described in Hill and Tononi 2005). The conductances of these intrinsic currents are listed in Table 3. Briefly, the currents included in the model are 1) a noninactivating hyperpolarization-activated cation current (I_h), which underlies a depolarizing “pacemaker” potential in thalamic and cortical cells (Huguenard and McCormick 1992; McCormick and Bal 1997), 2) a low-threshold fast-activating Ca²⁺ current (I_T), involved in burst firing in the thalamus (Huguenard and McCormick 1992), 3) the persistent Na⁺ current (I_NaP), which activates at a subthreshold voltage and inactivates on the order of seconds, 4) a depolarization-activated K⁺ current (I_DK), which acts as a generalized Na⁺- or Ca²⁺-activated K⁺ current and is known to play an important role in the UP and DOWN states of slow waves (Sanchez-Vives and McCormick 2000; Steriade 2003), and 5) the K⁺ leak current (I_KL), which is critical for the transition between wake and sleep modes of firing (Hill and Tononi 2005).

Transitioning from wake to sleep is triggered by the simulated change in neuromodulator levels, which act on cholinergic, noradrenergic, serotonergic, histaminergic, and glutamatergic metabotropic receptors in cortex and thalamus (McCormick 1992). The corresponding changes in model parameters are given in Table 3. The primary driver of the wake to sleep transition is the increase in g_KL (from 1.0 to 1.85), which simulates the effect of reduced release of arousal neuromodulators such as acetylcholine and norepinephrine during sleep. The model does not currently include sleep stages, and so it cannot explain the dependence of SWA on sleep depth.

Sources of spontaneous activity and visual stimuli.

Background noise in the model originates from spontaneous optic tract firing. This firing is modeled as 400 separate Poisson processes and is independent of the wake-sleep cycle. The optic nerve cells project onto the LGN. From there, the background noise percolates throughout the network, producing irregular spontaneous activity in all layers of the model (see Fig. 2). Another source of noise are “minis,” spontaneously released neurotransmitter quanta (Vautrin and Barker 2003).

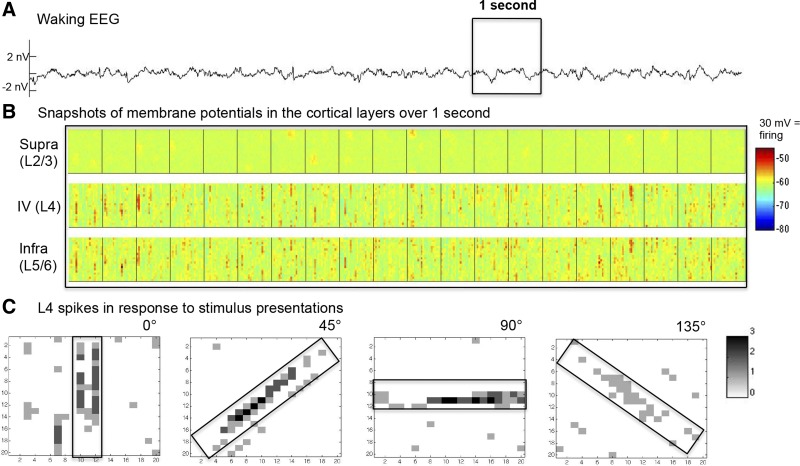
Fig. 2.

Simulated waking activity before refinement: spontaneous and evoked. Synaptic currents and membrane potentials for all neurons were recorded during a 10-s simulation under the waking mode. A: EEG during spontaneous activity without stimulus presentation. The EEG signal is derived from the sum of individual postsynaptic currents in supragranular neurons (modeled at the nV scale). B: membrane potential snapshots of a 20 × 20 neuron cortical patch over the boxed 1 s, with an image captured every 50 ms from excitatory populations in L2/3, L4, and L5/6. C: matrix plots show the summed spiking response of four 20 × 20 populations of excitatory L4 neurons during the 100 ms after their preferred stimulus was presented through the optic tract (size and shape of the bar presented are indicated by the rectangle over the analogous retinotopic area on the cortex).

Visual stimuli were presented over retinothalamic projections onto the LGN with a strength (w) of 50 for a duration of 100 ms. This caused strong responsive firing of a topographic section of the thalamus the same size and shape as the presented bar.

Synaptic refinement.

Synaptic refinement is implemented in the thalamocortical model by modifying intralaminar lateral connections. In a first set of simulations, connections in all cortical layers were rewired in a predefined manner to reflect experimental data (Ko et al. 2013). In the prerefinement model, the lateral intralaminar excitatory connections among cortical neurons are distributed uniformly, irrespective of PO and only diffusely connected over RFs. Comparatively, in the postrefinement model, neurons connect preferentially to neurons with similar POs and RFs (details in results). Inhibitory connections were not altered during refinement, since inhibitory cells in the adult cortex show significantly less orientation selectivity in their lateral connections than excitatory cells do (Kisvarday 1997).

In a second set of simulations, excitatory intralaminar cortical connections in all cortical layers were augmented with a version of STDP. To generate refinement via activity-dependent plasticity, visual stimuli were presented, bringing about a shift in synaptic strength profiles (see results). The STDP rules were taken from Olcese et al. (2010), where they were used to examine the homeostatic regulation of synaptic strength. Long-term potentiation is thought to involve the AMPA receptor (Collingridge et al. 2004), along with the NMDA receptor as a triggering mechanism (Brader et al. 2007). Therefore, STDP is modeled to affect the synaptic strength w of postsynaptic AMPA and NMDA receptors, which in turn modulates the synaptic peak conductances (g_peak) of excitatory connections (Abbott and Nelson 2000; Dan and Poo 2004). The particular STDP weight-change equation is adopted from Standage et al. (2007):

$$\Delta w_{p,d}=k_{p,d}{m}_{p,d}\left(w\right)e^{-c_{p,d}\Delta t}$$

where Δw is the change in synaptic weight, subscripts p and d stand for potentiation and depression, respectively, k is the learning rate, Δt is the time difference between the post- and presynaptic spikes, and m is a weight-dependent factor that ensures small synapses will have greater percent changes than large ones. In particular,

$$m_{p,d}=a_{p,d}{w}^{b_{p,d}}$$

with a_p = 431, a_d = −59, b_p = 0.4, b_d = 0.1, c_p = 0.039, c_d = 0.043, k_p = 6e⁻⁵, and k_d = −6e⁻⁵ (Standage et al. 2007).

Plastic changes can depend on the intracellular Ca²⁺ level (entering via NMDA receptors; Brader et al. 2007). Thus, as in Olcese et al. (2010), no plastic changes occur for low levels of Ca²⁺ currents; at the level typical of spontaneous activity, the standard STDP rule applies and there can be both potentiation and depression, whereas at a higher Ca²⁺ concentration, only potentiation occurs.

Reduced model of isolated supragranular cortex section.

To examine a range of connectivity changes and their effect on SWA, we simulated sleep activity in a smaller scale cortical model: 2,700 neurons from supragranular cortex of the large-scale model in isolation. Strengths of individual connections were adjusted to ensure similar wake and sleep behavior as in the large-scale model (Table 4). Inputs from the rest of the cortex were substituted with noise in the form of 900 separate Poisson processes. Initially, every neuron connected to every other neuron with equal probability. Starting from this condition of complete homogeneity, connection selectivity was gradually increased and the resulting effects on SWA were observed (see results for details).

Table 4.

Small-scale model connectivity

									Delay
Source Layer	Cell Type	Target Layer	Cell Type	Transmitter	Style	Pmax (height)	Radius or Size	Strength	Mean	SD
Cortical noise	Exc	Cortex	Exc, Inh	AMPA	Gaussian	0.75	1	7.5	2	1
Cortex
Cortical sheet	Exc	Cortical sheet	Exc, Inh	AMPA	Rectangular	0.01	30 × 30	1	2	0.25
Cortical sheet	Exc	Cortical sheet	Exc, Inh	NMDA	Rectangular	0.01	30 × 30	0.35	2	0.25
Cortical sheet	Inh	Cortical sheet	Exc, Inh	GABAA	Rectangular	0.01	30 × 30	1.5	2	0.25
Cortical sheet	Inh	Cortical sheet	Exc, Inh	GABAB	Rectangular	0.01	30 × 30	0.5	2	0.25

Parameters for the connectivity profiles used to construct the small-scale network. Connection profiles are listed per layer and neuron type for the small-scale model as in Table 1.

Data gathering and analysis.

In all the simulations, models were started with identical initial states. The membrane potentials of cortical and thalamic neurons, as well as the synaptic currents of cortical neurons, were recorded at every simulation time step (4,000 Hz). Recording began after 10 s of the sleep mode to let the simulation settle to its equilibrium behavior.

Because the cortical EEG is believed to reflect mainly postsynaptic currents in cortical pyramidal cells (Buzsáki et al. 2012), an approximate EEG of the model's V1 was derived by summing individual postsynaptic currents over all V1 model neurons. To analyze SWA and detect individual slow waves, the EEG was bandpass filtered (at 0.5–30 Hz; stopband edge, frequencies 0.5–80 Hz; stopband minimal attenuation, 10 dB) using a Chebyshev type II filter design as in Esser et al. (2007). The total simulation of 20 s was broken into nonoverlapping epochs of 4 s in length. To detect individual slow waves, the EEG signal of each epoch was centered around zero by subtracting the mean value. Slow waves were defined as positive (>0) deflections between two consecutive negative (<0) peaks. Wave amplitude was measured as the maxima within the positive deflection. Waves with amplitudes below 20% of the global peak amplitude for that epoch were excluded to prevent small fluctuations around the zero-line counting as slow waves. The slope of a wave was defined as the average of the slope of the first wave segment (from the preceding negative peak to the positive peak) and second wave segment (from the positive peak to the subsequent negative peak).

Simulation techniques.

Simulations were run using Synthesis, an object-orientated neural simulator (https://github.com/Caanon/Synthesis). Using a Quad-Core Mac Pro running MacOS 10.4 with 9 GB of RAM, each second of simulation took around 30 min to compute. The Runge-Kutta fourth-order method was used to perform numerical integration over a step size of 0.25 ms. Running at a lower step size did not affect previous results (Esser et al. 2009). In this work, changes in initial conditions and small percentile changes to synaptic parameters and connectivity numbers did not alter the main experimental findings. The software package MATLAB (The Math Works, Natick, MA) was used for analysis.

RESULTS

In the following simulations we show that synaptic refinement impacted both the waking and sleeping behavior of the thalamocortical model, resulting in a drop in SWA and changes in slow-wave morphology. Synaptic refinement affected the lateral intralaminar excitatory connections of all three cortical layers in the model and was accomplished by rewiring in a predefined manner. Next, in a further set of simulations, we investigated how synaptic plasticity can bring about synaptic refinement by changing profiles of synaptic strength. Finally, a smaller model was used to make a general case that the greater amount of synaptic refinement there is, the larger the drop in SWA.

Sleep/wake activity prior to synaptic refinement.

The prerefinement thalamocortical model (Fig. 1; described in materials and methods) corresponds to a preadolescent period early on in brain development. During the wake mode, the model engages in low-voltage spontaneous activity, which resembles physiological waking activity in the EEG (Fig. 2A). Cellular membrane potentials fluctuate rapidly around −60 mV and rarely hyperpolarize below −70 mV. Spontaneous activity differs in frequency and intensity across cortical layers. Deep layers fire more frequently during wake, whereas superficial layers show sparser firing (Fig. 2B), as observed in the real brain (Niell and Stryker 2010; Sakata and Harris 2012).

In the prerefinement model, the POs and RFs of cortical neurons are already in place due to selective thalamocortical feedforward connections. Local cortical connections, however, are still aspecific (Espinosa and Stryker 2012). Topographic plots of poststimuli neuronal spikes demonstrate that the RFs and POs of simulated cortical neurons are indeed intact and functional before refinement (Fig. 2C). Since V1 is retinotopic, when a bar is presented to the optic nerve, the population response of neurons with a matching PO reflects the shape of the bar. The presentation of a 0° bar, for example, generated activity in the population of L4 neurons with a PO of 0° (Fig. 2C). Neurons not selective for the stimulus do not show any evoked response above baseline spontaneous activity.

The same retinothalamic afferents that carry information about visual stimuli also originate spontaneous activity. For this reason, POs and RFs were reflected in the spontaneous cortical firing. In Fig. 2B, for example, snapshots of the membrane potential of populations in L4 and L5/6 with a preference for 0° (vertical) bars are shown and exhibit subthreshold fluctuations in the form of vertical bars. This result is in line with experimental data from the visual cortex in nonhuman primates showing that cellular membrane potentials of a neuronal population during spontaneous activity reflect the functional properties of that population (Kenet et al. 2003; Tsodyks 1999).

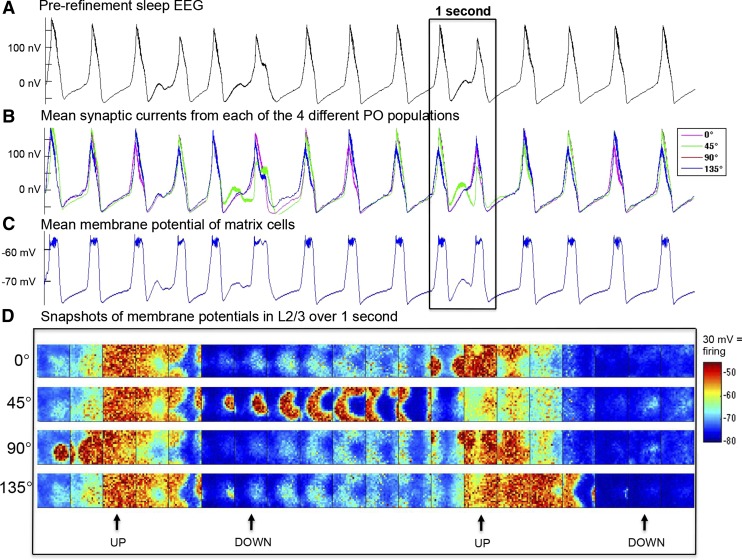
In the sleep mode, the prerefinement model exhibits high-amplitude SWA. Figure 3A shows the persistent generation of oscillations in the simulated EEG, a prototypical slow-wave pattern with clearly delineated negative and positive phases. The EEGs from populations of neurons with different POs are synchronous (Fig. 3B), and the entire thalamocortical system participates in these slow waves, assisted by matrix cells, which act in the thalamus to help widely excite cortical neurons into the UP state (Fig. 3C). The negative phase of the EEG slow waves correspond to the DOWN states at the cellular level, characterized by network silence (no or little firing) and globally hyperpolarized membrane potentials (approximately −80 mV). The positive phase of the EEG slow waves correspond instead to the UP states, characterized by globally depolarized membrane potentials (approximately −58 mV) and elevated firing throughout the network. These two states are visualized in the snapshots of the membrane potentials (taken every 50 ms for 1 s of sleep) across the different populations with distinct POs (Fig. 3D). This behavior is characteristic of the bistability of neuronal activity during deep sleep (Steriade et al. 2001; Tononi and Massimini 2008).

Fig. 3.

Simulated activity during sleep before refinement. Synaptic currents and membrane potentials for all neurons were recorded during a 20-s simulation in the sleep mode. A: 10 s of EEG. B: mean synaptic current of the populations in the supragranular layer with different POs, plotted individually. C: mean membrane potential of thalamic matrix cells. D: snapshots of the supragranular membrane potential of 20 × 20 populations over 1 s, with an image captured every 50 ms from the 4 populations with different POs. Snapshots show the origination and termination of UP states (with an average membrane potential of around −60 mV). A neuron fires when its membrane potential crosses its dynamic threshold, after which its membrane potential is set to +30 mV. The neurons that fired in each snapshot can thus be identified as the darkest red dots. Note that only a small subset of neurons is firing at any given time during the UP state.

Reorganization of connections simulates synaptic refinement.

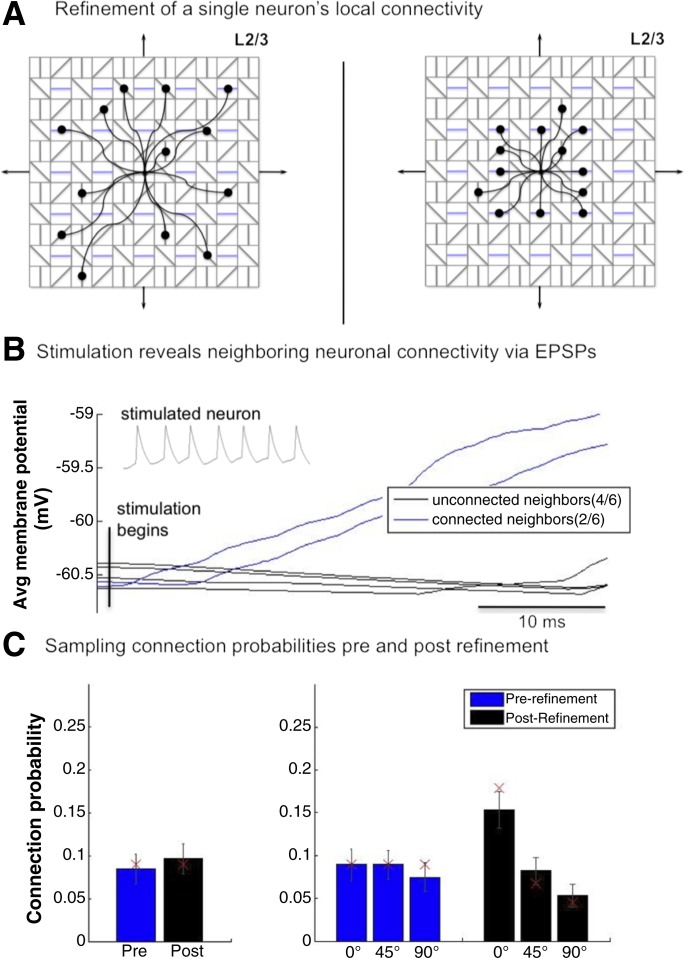
To reflect a postadolescent period in brain development, the intralaminar connections of the model were refined. This refinement, which was done by rewiring the connections, was based on physiological data from the mouse visual cortex (Ko et al. 2013). Accordingly, the postrefinement model was created from the prerefinement model by manipulating the model's probabilistic connectivity profiles, keeping all other parameters identical. In the prerefined model, which has highly homogenous lateral connectivity, neurons connect with equal probability over a local cortical area (10 × 10) and are insensitive to their targets' POs (25% to each of the 4 POs on average). Refinement consisted of rewiring these intralaminar connections so that the probability of a neuron being connected to the same PO doubled from 25% to 50%, whereas connection probabilities to neurons with 45° and 90° differences decreased from 25% to 19% and 11%, respectively. Crucially, the overall net number of connections remained unchanged (Fig. 4A). In addition, lateral connections were refined from a diffuse to a focused connectivity profile by decreasing the profile area by ∼50% (from 10 × 10 to 7 × 7). Since similar RFs are spatially proximal to each other, this leads to a postrefinement increase in the likelihood of connections between neurons with more similar RFs (Fig. 4A). These wiring changes were applied to excitatory neurons in all cortical layers.

Fig. 4.

Refinement of neural connectivity. A: topographic schematic of the refinement of a representative L2/3 neuron (center) with a 90° PO. Prerefinement (left), the neuron's 13 local excitatory connections were probabilistically distributed uniformly across all 4 distinct POs (25% each) over a 10 × 10 area around the neuron. Postrefinement (right), the neuron has doubled its connections to neurons that share its PO (in blue) while decreasing its connections to those with a different PO. Additionally, the area of local connectivity has been reduced by ∼50% to 7 × 7, increasing the probability of the neuron to connect to neurons with similar RFs. B: mean responses of 6 neurons adjacent to a neuron that was repeatedly stimulated (to trigger an action potential) for 40 ms across 15 stimulation trials. Recordings aligned to stimulus onset. C: mean connection probabilities of 140 randomly selected supragranular neurons with respect to 6 nearby neurons (connections assessed directly). Error bars denote SE. Red × symbols denote the absolute probabilities of lateral excitatory connections.

Ko et al. (2013) assessed refinement by studying supragranular neurons in the visual cortex of mice at different stages of development. Critically, those same neurons were then identified in slices so as to assess local connectivity. This was done by stimulating target neurons and finding evoked EPSPs in their neighbors (2–6 proximal neurons within 50 μm). The local connectivity of neurons became more selective for neurons with similar RFs and POs over development. To demonstrate that the changes in connectivity profiles in the model are congruent with these experimental observations, a similar experiment was conducted: a single target neuron was stimulated to fire for 40 ms while the membrane potentials of 6 neighboring cells were recorded (Fig. 4B). Two of the six neighboring neurons showed rising responses during stimulation. Since in the model the connectivity matrices of all connection types are available, it could be verified that these two neighbors (Fig. 4B, blue) indeed received lateral excitatory connections from the target cell, whereas the other 4 (black) had no connections. This demonstrates that, as in vivo, the model's individual excitatory connections can be identified via single-cell stimulations. To further verify that the model's true connection probabilities can, in principle, be inferred from local recordings (as done in Ko et al. 2013), lateral excitatory connections of 140 randomly selected supragranular neurons were examined with respect to 6 nearby neurons (Fig. 4C). The mean probability of finding a connection (postrefinement: mean 0.10, SE 0.017; prerefinement: mean 0.07, SE 0.017) was not significantly different before and after refinement (P = 0.08, 2-sample t-test). Before refinement, lateral excitatory connectivity showed no significant preference for similar POs (F = 0.92, P = 0.4; ANOVA). After refinement, neurons were found to connect preferentially to their own orientation and aversely to their opposite orientation (F = 0.92, P < 0.0001; ANOVA). The locally assessed connection probabilities for both the pre- and postrefinement models overlap with the actual imposed model values used in the model's construction (marked as red × symbols in Fig. 4C, right). The total connection probabilities are similar to those observed experimentally (Ko et al. 2013), although connectivity is overall sparser in the model. Our results show that locally derived connection probabilities indeed approximate the true values.

Responsiveness to stimuli in the postrefinement model.

Although spontaneous waking activity in the postrefinement model is similar to the prerefinement model (low amplitude and variable), we examined whether refinement changed how the model responds to stimuli. Both the pre- and postrefinement models were presented with a series of 15 vertical (0°) bars over their retinothalamic afferents. This reliably resulted in selective responses in L4 (after propagation through the LGN). The total number of spikes within the appropriate retinotopic zone of L4 was recorded for 100 ms after each bar presentation (postrefinement: mean evoked spikes 151.5, SD 57.57; prerefinement: mean evoked spikes 142, SD 60.47). To assess whether information transmission changed due to refinement, the signal-to-noise ratio (SNR) of the response was defined as

$$SNR=\frac{mean\left(evoked\hspace{0.17em}spikes\right)}{SD\left(spontaneous\hspace{0.17em}spikes\right)}.$$

Only spikes of neurons with the appropriate PO and within the appropriate retinotopic area were included. The appropriate retinotopic areas were defined as a 3 × 20 patch of L4 in the population with the PO that matched the presented bar. This patch corresponded topographically to where the bar was presented (as in Fig. 2C). The SNR for the prerefinement condition was 14.76, whereas the postrefinement SNR increased to 17.97. By focusing lateral connectivity and increasing the connectivity between more similar POs, synaptic refinement may affect neuronal evoked responses, increasing the SNR of signal transmission.

Synaptic refinement leads to a reduction in SWA.

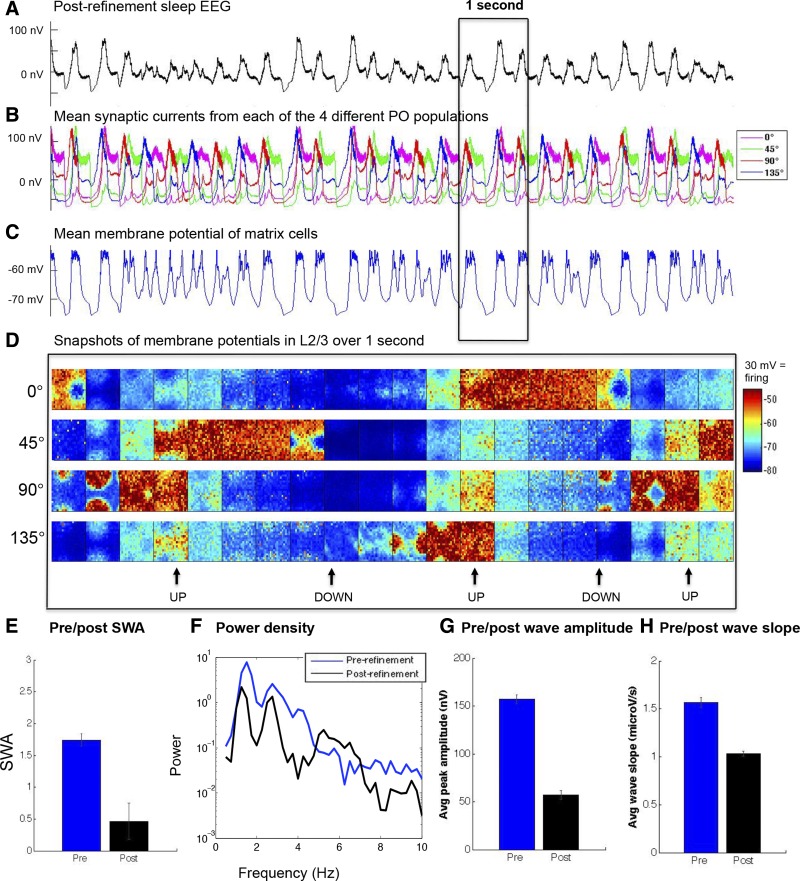
The postrefinement model shows, on average, smaller slow waves in the cortical EEG (Fig. 5A). The reason is that in the postrefinement model, supragranular populations with different POs enter UP and DOWN states less synchronously (Fig. 5B). However, global slow waves could still be observed during periods of greater synchrony, as can be seen in the EEG and in the response of the thalamic matrix cells coupled to the cortex (Fig. 5C). Yet, depolarization (approximately −58 mV) during the UP states and hyperpolarization (approximately −80 mV) during the DOWN states is less global, as can be seen in the membrane potential rasters (Fig. 5D).

Fig. 5.

Simulated activity during postrefinement sleep. A: 10 s of EEG, showing smaller slow waves. B: mean synaptic currents of the populations in the supragranular layer with different POs, plotted individually. Populations are much less synchronous in their activity, as well as more variable in the timing of their UP states, than in the prerefinement model (compare with Fig. 3B). C: mean membrane potential of the thalamic matrix cells. D: snapshots of the supragranular membrane potential of 20 × 20 populations over 1 s, with an image captured every 50 ms from the 4 populations with different POs. E: postrefinement model shows a decrease in SWA. F: the lower frequency power spectrum of the pre- and postrefinement conditions averaged across sleep epochs. G and H: amplitude (G) and slope (H) of the slow waves have decreased postrefinement. Error bars denote SE.

SWA was measured over 20 s of simulation, subdivided into 5 epochs (see materials and methods). SWA significantly decreased in the postrefinement model (Fig. 5E), a reduction to 27% of the original prerefinement SWA value (postrefinement: SWA mean 0.47, SE 0.28; prerefinement: SWA mean 1.74, SE 0.01; P < 0.01, 2-sample t-test). As can be seen in Fig. 5F, this decrease applies to most low frequencies.

There is evidence that the morphology of individual slow waves reflects the cortical dynamics underlying the EEG. Decreased amplitude and slope signify a decreased ability of the slow wave to recruit neurons and spread along the cortex (Esser et al. 2007). Indeed, the decrease in SWA in the course of sleep is accompanied by a decrease in amplitude and slope of the slow waves in both adult humans (Riedner et al. 2007) and rats (Vyazovskiy et al. 2007), as well as in human infants (Fattinger et al. 2014).

To analyze these waveform properties, individual slow waves in the simulated EEGs were identified (see materials and methods). Slow waves in both the pre- and postrefinement conditions (prerefinement: n = 55; postrefinement: n = 27) were evaluated in terms of amplitude and slope. Refinement decreased the average wave amplitude to 33% of the prerefinement value (Fig. 5G; postrefinement: peak amplitude mean 50.72 nV, SE 4.45 nV; prerefinement: peak amplitude mean 157.24 nV, SE 4.39 nV; P < 0.01, 2-sample t-test). The slope of the individual waves also decreased significantly after refinement (Fig. 5H; postrefinement: mean slope 1.03 μV/s, SE 0.026 μV/s; prerefinement: mean slope 1.57 μV/s, SE 0.053 μV/s; P < 0.01, 2-sample t-test).

Because experimental data on synaptic refinement were obtained from the supragranular layer only (Ko et al. 2013), it is not yet clear to what extent refinement occurs in all cortical layers. For this reason, we also created a postrefinement model wherein solely the L2/3 lateral excitatory connections were rewired in the manner described. As before, the result was a decline in SWA during the sleep mode, although the decrease was attenuated compared with when all the layers were refined (just L2/3 refinement; postrefinement: SWA mean 0.61, SE 0.02; prerefinement: SWA mean = 1.74, SE 0.01; P < 0.01, 2-sample t-test). Similarly, refining just L2/3 reduced wave amplitude (postrefinement: peak amplitude mean 69.71 nV, SE 3.78 nV; prerefinement: peak amplitude mean 157.24 nV, SE 4.39 nV; P < 0.01, 2-sample t-test) and slope (postrefinement: mean slope 0.9 μV/s, SE 0.057 μV/s; prerefinement: mean slope 1.57 μV/s, SE 0.053 μV/s; P < 0.01, 2-sample t-test), but to a lesser degree than refining all three cortical layers.

Modeling the developmental process of synaptic refinement via STDP.

It has been shown that an increase in the selectivity of connections during development can occur via synaptic plasticity, because changes in synaptic strength are forerunners for changes in connectivity (Sanes and Yamagata 2009). Indeed, there is evidence that synaptic refinement involves a rearrangement in the strengths of connections, because neurons in adult mouse V1 with similar RFs and POs have stronger excitatory synaptic connections (Cossell et al. 2015). To explore this aspect of synaptic refinement, a second set of simulations tested whether the implementation of STDP in the lateral excitatory connections of the prerefinement model could lead, after a period of learning, to synaptic refinement, and whether this in turn would result in a drop in SWA (see materials and methods for details).

During normal development, learning takes place over many cycles of wake followed by sleep. According to the synaptic homeostasis hypothesis (SHY; Tononi and Cirelli 2003, 2014), wake leads to a net increase in synaptic strength in many brain areas, and then, during sleep, there is synaptic renormalization in the form of a net reduction of synaptic strength back to a baseline level. This renormalization is best performed during sleep, when the brain is offline and spontaneous activity can sample the brain's extant knowledge in a statistically unbiased manner (Tononi and Cirelli 2014). Thus learning according to SHY involves both local potentiation and global renormalization across a repeating wake-sleep cycle.

To mimic this process, we used the previously defined prerefinement model (now referred to as prelearning) and trained it over 11 wake sessions. In each training session the model was presented with 70 3 × 20 bar stimuli of all 4 POs at different topographical locations. Each training session led to net potentiation. After each one of the 11 sessions, we renormalized the average total synaptic weight back to its starting value presession, mimicking the effect of a period of sleep. This renormalization was done by decreasing the strength w of all neurons in a population with a shared PO proportionally to that population's increase in strength w during the prior training session. Renormalization was implemented only over the same lateral connections augmented with STDP. Critically, this meant that at the end of the 11 sessions, the total synaptic strength of these connections was unchanged.

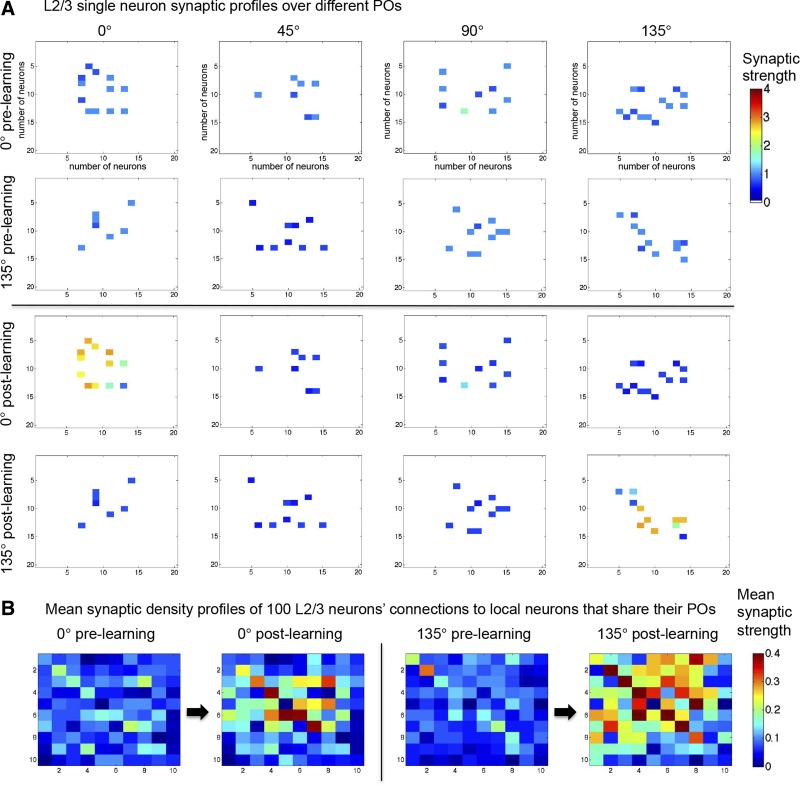
The result of these 11 sessions was synaptic refinement in the form of a rearrangement of synaptic strength without a change in the total amount. Neurons in all layers began, prelearning, with a mean homogeneous connection strength profile [25%, 25%, 25%, 25%] to neurons with POs of 0°, 45°, 90°, and 135° difference to their own PO. Postlearning in the supragranular layer, this distribution shifted to a mean connection strength profile of 46%, 16.4%, 19.5%, and 16.3%. Other layers showed near-identical results. Thus learning via STDP resulted in neurons connecting most strongly to other neurons with shared PO (0° difference), as can be seen in Fig. 6A.

Fig. 6.

Learning-induced changes in synaptic strength. A: synaptic strength profiles of the connections of 2 individual L2/3 neurons with POs of 0° and 135°, respectively. Plots show the changes to the local connections of 2 individual neurons, one with a 0° PO and the other with a 135° PO, to neighboring neurons of all the different POs, pre- and postlearning. Each row shows the neuron's projections and synaptic strength over its 20 × 20 nearest neighbors of each particular PO. Prelearning (top), the strength of the connections of both neurons was uniform across POs (mean strength 1, SD 0.25). Postlearning (bottom), the 2 neurons connect preferentially to neurons that share their POs. Total synaptic strength remains the same. B: mean synaptic density profiles of the local excitatory connectivity of 100 neurons with a PO of 0° and another 100 with a PO of 135°. Sampling was over a 10 × 10 area centered on each neuron and was conducted both pre- and postlearning. This sampling reveals the focusing of lateral connectivity via learning.

In the previous set of simulations (Figs. 4 and 5), synaptic refinement was accomplished by directly rewiring the model's connections. To compare the two cases, in the rewired model the mean connection profile shifted from being homogeneous in prerefinement [25%, 25%, 25%, 25%] to 50%, 19%, 11%, and 19% in the postrefinement model. If an increase of 1% in a synapse's strength corresponds to an increase of 1% in the chance that another connection is added, the refinement in the form of a rearranged synaptic strength is very similar to the refinement done by rewiring (as in Fig. 4). STDP also potentiated local connections between topographically, and thus functionally, closer neurons. Synaptic renormalization also led to a renormalization of connections between topographically, and thus functionally, distant neurons (Fig. 6B). The result was, again, similar to the focusing of local excitatory connectivity when synaptic refinement was accomplished by rewiring (Fig. 4A).

Effects of learning on SWA.

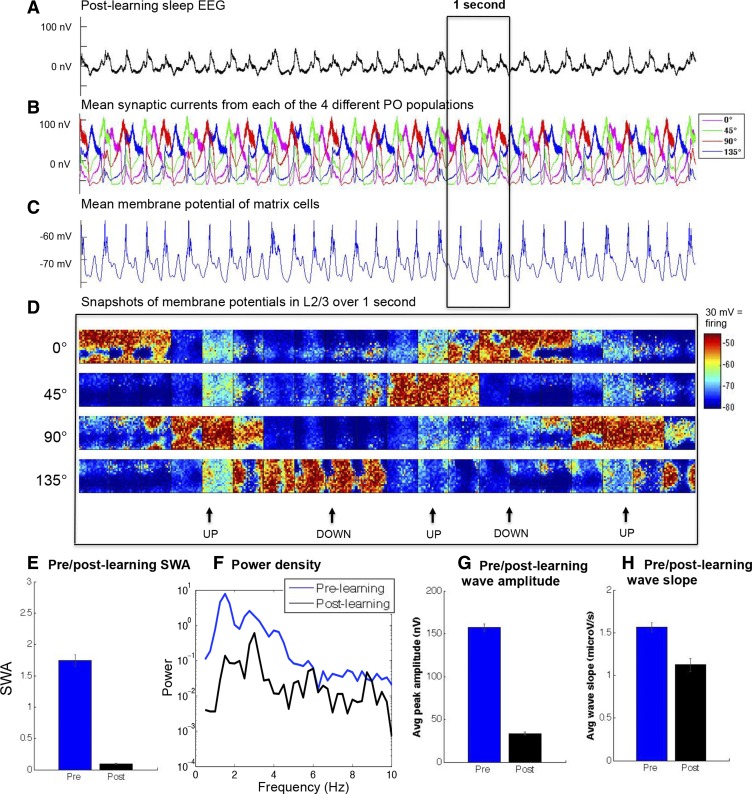
After synaptic refinement was brought about via learning across multiple wake-sleep cycles, STDP was disabled and the postlearning model was run in the sleep mode for 20 s while all synaptic currents and membrane potentials were recorded. Just as in the postrefinement model, slow waves in the postlearning model decreased in amplitude (Fig. 7, A–H). When the same analysis was performed over five 4-s epochs of the sleep mode, the postlearning model also showed a drastic decrease in the amount of SWA (postlearning: SWA mean 0.093, SE 0.008; prelearning: SWA mean 1.74, SE 0.01; P < 0.01, 2-sample t-test). Resultant slow waves (postlearning: n = 69; prelearning: n = 27) were analyzed in terms of amplitude and slope, both of which showed significant reductions (postlearning: peak amplitude mean 33.44 nV, SE 1.47 nV; prelearning: peak amplitude mean 157.24 nV, SE 4.39 nV; P < 0.01, 2-sample t-test; postlearning: mean slope 1.13 μV/s, SE 0.08 μV/s; prelearning: mean slope 1.57 μV/s, SE 0.053 μV/s; P < 0.01, 2-sample t-test). These results suggest that a set of cycles of potentiation followed by renormalization can lead to synaptic refinement, and this can have a profound effect on SWA.

Fig. 7.

Refinement via synaptic plasticity reduces SWA. A: EEG of 10 s of slow-wave sleep postlearning. B: similar to the postrefinement condition, in postlearning sleep the mean synaptic currents from populations with different POs are more asynchronous. C: mean membrane potential of thalamic matrix cells. D: snapshots of the supragranular membrane potential of a 20 × 20 population over 1 s, with an image captured every 50 ms from populations with POs of 0°, 45°, 90°, and 135°, respectively. Note the similarity in dynamics to Fig 5D. E: SWA drops postlearning. F: the lower frequency power spectrum of the prelearning and postlearning conditions averaged across sleep epochs. G and H: both amplitude (G) and slope (H) of sleep slow waves have decreased in the postlearning condition. Error bars denote SE.

Examining the effects of topographic and orientation refinement in a model section of the supragranular layer.

In the large-scale thalamocortical model, it would be computationally unfeasible to systematically explore how changes in the size and type of refinement impact SWA. To that end, a 2,700-neuron section of the supragranular layer of the large-scale model was excised and modified so that it displayed normal wake-sleep behavior (see materials and methods; see Table 4 for details). As in the large-scale model, only lateral excitatory connections were rewired during refinement.

Synaptic refinement, as modeled here, has two aspects: a focusing of lateral connectivity, which increases topographic selectivity (Callaway and Katz 1991) and an increase in orientation selectivity of connections (Ko et al. 2013). Initial connectivity of the L2/3 cortical section was homogeneous: each neuron connected diffusely to the entire 30 × 30 model area (100% network coverage), and no neuron had a preference for any PO.

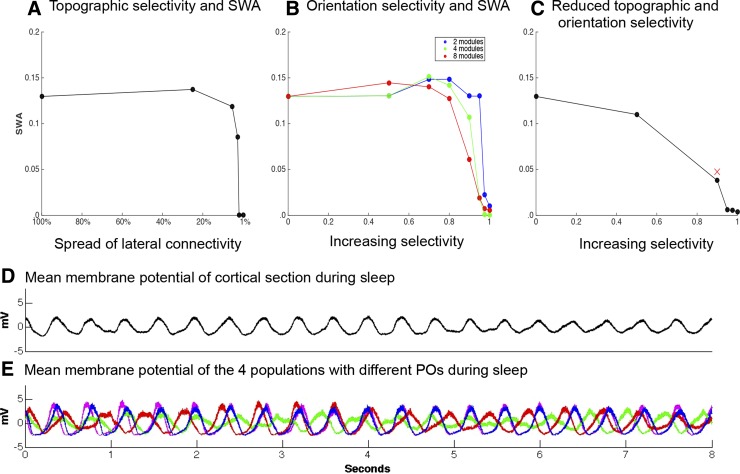
To isolate the effect of focusing lateral connectivity on SWA, the area that neurons connected to in a probabilistic manner was reduced from 30 × 30 to 15 × 15, 7 × 7, 5 × 5, 4 × 4, and 3 × 3. However, the net number of connections remained constant across all conditions. The average membrane potential (used in lieu of the EEG because the signals are nearly identical) was recorded in each condition of varying connectivity over a 10-s period of sleep. The first 2 s of activity were excluded from analysis to allow the simulation to settle. The focusing of lateral connections caused SWA to drop off sharply once the spread of the lateral connections was smaller than 5 × 5 (Fig. 8A).

Fig. 8.

Refining by degrees. A: effects of decreasing the spread of lateral connectivity on SWA. B: effects of increasing the selectivity between populations with different POs. C: with lateral connectivity fixed at 5% coverage, a 4-PO network was run through conditions of increasing orientation selectivity. In this combined condition, the decline in SWA occurs earlier and is more pronounced than in the conditions in A and B. D: mean membrane potential of the entire network over 8 s of sleep for the condition marked as a red × in C. E: in the same condition, mean membrane potentials of the 4 populations with distinct POs. Note the asynchrony of UP and DOWN states.

The second aspect of synaptic refinement modeled herein is the increase in orientation selectivity. Selectivity is when populations of neurons have a greater amount of connectivity among themselves than with the rest of the brain; across entire brain regions this is typically referred to as modularity (Meunier et al. 2009). Such modules can be groups of neurons that share an orientation, but they also can be any commonly activated or functionally similar groups. To formalize this, we define the selectivity (S) of a network with discrete populations as a ratio between two connectivity values: the difference between the number of actual connections established by groups of neurons and the number of connections that those neurons would establish if the network were randomly wired, compared with the maximum possible difference. Complete homogeneity, or random connectivity, thus corresponds to S = 0, whereas at S = 1, neurons only have connections to other neurons in their population.

To investigate the effect of increasing orientation selectivity, neurons in the L2/3 section were randomly assigned to different populations with different POs (representing different modules). The S of the network was then increased in stages from S = 0 to S = 0.5, 0.9, 0.95, 0.975, and 1 for conditions of 2, 4, and 8 distinct populations with different POs. Again, the total number of neuronal connections stayed the same in all cases, but in this case the distance of the lateral connections also stayed the same. Increasing S decreased SWA (Fig. 8B) and did so more effectively the higher the number of distinct POs. With only 2 POs, SWA remained basically unchanged up to S = 0.95, whereas when the section had 8 distinct POs, SWA decreased substantially starting from S = 0.5.

To test the interaction between these two aspects of synaptic refinement, we reduced the lateral connectivity of the section to the area it was in the postrefinement thalamocortical model (7 × 7, which in this case is 5% network coverage by each neuron). The network was given four POs and run through increases in S. Combining the two aspects of refinement hastened the reduction in SWA (Fig. 8C).

The decreases in SWA were the result of asynchrony between neural populations. Figure 8D shows the average membrane potentials of the 4 populations with different POs in the S = 0.9, 7 × 7 lateral connectivity condition (marked by a red × in Fig. 8C). This condition is, in the dynamics of its slow waves, closest to the large-scale postrefinement model. As can be directly seen, slow waves decreased in amplitude due to averaging effects.

Note that the increase in selectivity required for a reduction in SWA comparable to experimental data (∼50%; de Vivo et al. 2014; Jenni and Carskadon 2004) is higher (0.9) in the small-scale model than in the large-scale model. In the large-scale model, refinement was implemented as a doubling of connections to the same preferred orientation, consistent with the findings of Ko et al. (2013), corresponding to a value of increased selectivity of ∼0.33. This difference is not surprising given the smaller size and the lack of thalamocortical and corticocortical feedback of the reduced model. Nevertheless, the small-scale model allows us to make a general point: the greater the selectivity, the greater the reduction in SWA.

DISCUSSION

We have shown that synaptic refinement as implemented in our simulations is sufficient to cause a marked decrease in SWA. Specifically, simulating synaptic refinement by rewiring the model's connections directly (Fig. 4) led to a 27% reduction in SWA (Fig. 5). This decline is close in magnitude to the 50% reduction in SWA observed in the frontal and parietal cortices in adolescent mice (de Vivo et al. 2014), as well as to the 47% drop in SWA observed in EEG recordings during adolescent development in humans (Jenni and Carskadon 2004). Additionally, the decline in amplitude and slope of slow waves was also similar in magnitude to that seen in humans (Kurth et al. 2010a). Of note, refinement in the model led to a drop in EEG power that was not restricted to SWA but extended to all frequencies below 10 Hz, a finding also consistent with results in vivo in both rodents (de Vivo et al. 2014; Olini et al. 2013) and humans (Buchmann et al. 2011).

Experimental data indicate that synaptic refinement requires visual experience and that it is the corticocortical connectivity that is refined post eye-opening, not the feedforward thalamocortical connectivity (Ko et al. 2013). For example, in dark-reared rats, cortical networks do not fully develop the appropriate corticocortical selective connectivity (Ishikawa et al. 2014). To explore how visual experience might bring about synaptic refinement, we implemented STDP in the local excitatory connections of the model. Molecular, anatomical, and physiological studies have shown that synaptic plasticity during waking experience leads to a net increase in synaptic strength, whereas periods of sleep lead to synaptic renormalization (Tononi and Cirelli 2014). To mimic this process, we exposed the model to stimuli in a “wake” mode, leading to net synaptic potentiation. Exposure to stimuli was then followed by synaptic renormalization. This cycle was repeated over multiple sessions. The results of the simulations suggest that a series of wake-sleep cycles can bring about the selective reorganization of synaptic strength that accompanies synaptic refinement (Cossell et al. 2015), which is in turn associated with a drop in SWA (Figs. 6 and 7). Previous work has indicated that such repeated patterns of synaptic potentiation during wake and then renormalization during sleep can also have beneficial effects on memory at both the system level (Nere et al. 2013) and at the level of individual neurons (Hashmi et al. 2013).

Overall, the present results support the hypothesis that synaptic refinement may contribute significantly to the drop in SWA observed during adolescence and outline a mechanism of action in the form of daily cycles of potentiation/renormalization. An important remaining question is whether the developmental decrease in SWA parallels the time courses of synaptic refinement. Evidence from mice shows decreases in SWA from at least postnatal day 20 (P20) onward (de Vivo et al. 2014), a period of time overlapping with the occurrence of synaptic refinement (P13–P26; Ko et al. 2013). In our simulations, SWA tracks refinement nonlinearly, beginning to decrease only once a critical amount of refinement has occurred (Fig. 8). Thus refinement may be ongoing throughout brain development but only become relevant to SWA after it reaches a critical level.

Across cortex, refinement during development is most likely not restricted to groups of neurons with similar orientation selectivity and receptive fields but will affect many functional groups of neurons. The fact that a greater number of different groups of neurons facilitates the drop in SWA (Fig. 8B) indicates that in cortical areas that are very heterogeneous or contain many modules, smaller increases in selectivity may be required to account for the drop in SWA seen in vivo.

The model was designed to be as physiologically realistic as possible (see materials and methods), and our results are compatible with the evidence from intracellular recordings performed in cats, which showed that neuronal activity is less rhythmic and synchronous across cortical regions in sleep relative to anesthesia (Chauvette et al. 2011). The general results of this study also proved insensitive to small manipulations of the experimental parameters. Yet, the model has limitations. Thus the duration of the intracellular DOWN states of neurons in the model (∼150–200 ms) are the same as those observed during slow-wave sleep in vivo (Chauvette et al. 2011), but the durations of the UP states (150–250 ms) are shorter. Moreover, the declines in SWA after refinement or after sleep tend to be larger than those seen in vivo. One reason for these discrepancies is likely that the parameters were necessarily taken from different species, and whereas the model was originally interpreted as a small portion of cat V1, the empirical parameters to emulate synaptic refinement were based on mice, and the rate of slow waves in the EEG is close to that found in rodents (Vyazovskiy et al. 2007). Moreover, we are modeling only a single region, V1, which limits slow waves in their spread. Nevertheless, few other models are capable of producing physiologically realistic SWA together with appropriate visual responses in wake, as well as STDP. For example, the small model used by Ko et al. (2013) to examine synaptic refinement did not generate slow waves. Additionally, the model's robustness was tested by systematically varying the relevant parameters and initial conditions (amounting to over 3 yr of central processing unit time) when it was first introduced (Hill and Tononi 2005). The same model, under conditions similar to those in the present study, has previously been used for studying SWA (Esser et al. 2007; Hill and Tononi 2005; Olcese et al. 2010). One of these studies showed that the amount of SWA tracks global synaptic strength in the model (Esser et al. 2007). We build on these results by showing that changes in the local distribution of synaptic strength, from homogeneous to heterogeneous, can have similar effects. These effects may combine, or one or the other may dominate at different times, to drive developmental changes in SWA.

Of course, computer simulations cannot by themselves prove that synaptic refinement is the ultimate cause of the developmental decline in SWA, and it remains possible that other developmental processes such as synaptic pruning play a major role. However, the present results are consistent with the idea that it is possible to indirectly track the maturation of cortical connectivity during development by monitoring the progressive decline of SWA, a relatively simple, noninvasive procedure that can be performed at multiple time points (Cirelli and Tononi 2015; Ringli and Huber 2011; Ringli et al. 2013). For example, it is known that in humans the developmental decline in SWA begins in posterior brain regions and moves to anterior regions (Kurth et al. 2010b). On the basis of the present results, one would predict that synaptic refinement may progress in a similar posterior-to-anterior manner. Moreover, one would predict that alterations in SWA maturation may reflect changes in synaptic refinement that may underlie some developmental disorders.

GRANTS

This work was funded by National Institutes of Health Grants R01MH099231 and P01NS083514 (to G. Tononi and C. Cirelli). L. Albantakis and E. P. Hoel were funded by Templeton World Charities Foundation Grant TWCF 0067/AB41.

DISCLOSURES

G. Tononi consults for Philips Respironics and is involved in a research study in humans supported by Philips Respironics. This study is not related to the work presented in the current manuscript. The other authors have indicated no financial conflicts of interest.

AUTHOR CONTRIBUTIONS

E.P.H., L.A., C.C., and G.T. conception and design of research; E.P.H. performed experiments; E.P.H. analyzed data; E.P.H., L.A., C.C., and G.T. interpreted results of experiments; E.P.H. prepared figures; E.P.H., C.C., and G.T. drafted manuscript; E.P.H., L.A., C.C., and G.T. edited and revised manuscript; E.P.H., L.A., C.C., and G.T. approved final version of manuscript.