Neural coding of image structure and contrast polarity of Cartesian, hyperbolic, and polar gratings in the primary and secondary visual cortex of the tree shrew

Abstract

We comprehensively characterize spiking and visual evoked potential (VEP) activity in tree shrew V1 and V2 using Cartesian, hyperbolic, and polar gratings. Neural selectivity to structure of Cartesian gratings was higher than other grating classes in both visual areas. From V1 to V2, structure selectivity of spiking activity increased, whereas corresponding VEP values tended to decrease, suggesting that single-neuron coding of Cartesian grating attributes improved while the cortical columnar organization of these neurons became less precise from V1 to V2. We observed that neurons in V2 generally exhibited similar selectivity for polar and Cartesian gratings, suggesting that structure of polar-like stimuli might be encoded as early as in V2. This hypothesis is supported by the preference shift from V1 to V2 toward polar gratings of higher spatial frequency, consistent with the notion that V2 neurons encode visual scene borders and contours. Neural sensitivity to modulations of polarity of hyperbolic gratings was highest among all grating classes and closely related to the visual receptive field (RF) organization of ON- and OFF-dominated subregions. We show that spatial RF reconstructions depend strongly on grating class, suggesting that intracortical contributions to RF structure are strongest for Cartesian and polar gratings. Hyperbolic gratings tend to recruit least cortical elaboration such that the RF maps are similar to those generated by sparse noise, which most closely approximate feedforward inputs. Our findings complement previous literature in primates, rodents, and carnivores and highlight novel aspects of shape representation and coding occurring in mammalian early visual cortex.

tree shrews are small day-active mammals (Emmons 2000) belonging to the order of Scandentia. They are considered to be the closest living relatives of primates (Fan et al. 2013; Petruzziello et al. 2011) and may in fact resemble the ancestor of all placental mammals that lived over 60 million years ago (O'Leary et al. 2013). Recent work has highlighted a close correspondence between tree shrew and macaque primary visual cortex (V1) in the areas of temporal neural entrainment (Veit et al. 2011; Williams et al. 2004), apparent dominance of light decrement responses (Veit et al. 2011; Xing et al. 2010; Yeh et al. 2009a), and subfield overlap and generation of orientation selectivity (Van Hooser et al. 2013; Veit et al. 2013). These functional homologies have been established using conventional stimulus sets, i.e., sparse noise and oriented bars or gratings. However, converging evidence suggests that macaque early visual cortex also encodes information about more complex visual forms, including natural images (Ayzenshtat et al. 2012; Freeman et al. 2013) as well as parametrically generated stimuli such as Hermite functions (Victor et al. 2006) or non-Cartesian gratings (David et al. 2006; Gallant et al. 1993, 1996; Hegde and Van Essen 2000, 2007; Mahon and De Valois 2001). A motivation for the present study was to examine tuning properties to such nonconventional visual stimuli in tree shrew early visual cortex. We chose to use non-Cartesian gratings because they have been previously used in several studies in the macaque and because they collectively approximate some of the rich complexity of natural images while offering the advantage of stimulus orthogonality, allowing the reconstruction of spatial aspects of the receptive field (RF). If visual cortical neurons acted as linear filters, the reconstructed RFs should not depend on grating class and reflect only the characteristics of the feedforward input. Grating-class dependence of RF reconstructions may thus reflect nonlinear cortical signal processing, which is recruited differentially by grating class. To assess the degree of cortical RF elaboration, we compared the reconstructions for each grating class to that obtained with sparse noise. Due to the nature of the sparse noise stimulus, which is composed of spatially isolated light modulations, the corresponding RF maps are thought to primarily reflect feedforward inputs (i.e., from visual thalamus in V1 and from V1 in V2). Sparse noise RF maps can thus serve as a baseline for assessing cortical contributions to RF structure generated by the different grating classes.

Even though tree shrew V1 RFs tend to exhibit a large degree of overlap between white- and black-responsive subfields, the prevalent black dominance renders neurons highly sensitive to the spatial phase of Cartesian gratings (Van Hooser et al. 2013; Veit et al. 2013). Note that the variation of spatial phase has distinct effects depending on grating class, resulting in translation, rotation, and expansion/contraction for Cartesian, radial-polar, and hyperbolic/concentric-polar gratings, respectively. For all grating classes, variations in spatial phase generally result in a spatial shift of boundaries and gradients between white and dark image patches, with the exception of 180° phase modulations. Spatial phase reversals by 180° correspond to polarity inversion of the stimulus and are thus special because they preserve the structure, i.e., local contrast of the grating, while exchanging the location of white and dark patches. In constructing our stimulus set, we generated a number of grating structures for each class with varying spatial frequency, orientation, and 90° spatial phase modulations, each of which was presented at two polarities. Our study thus allows a systematic investigation of how stimulus polarity impacts neural responses in early visual cortex, whereas previous work has used either moving stimuli, which yield averaged responses across spatial phases, or estimates based on a single polarity.

In the tree shrew, V1 is part of a highly developed and differentiated visual system (Fitzpatrick 1996), which also includes secondary visual cortex (V2) as well as a ventral processing stream composed of several higher level visual structures (Sesma et al. 1984; Wong and Kaas 2009). The nature of the transformation of visual information in the mammalian visual hierarchy remains only partly understood, although RF size and optimal stimulus complexity tend to increase as one ascends this hierarchy for most mammalian species (Vermaercke et al. 2014). Our study represents the first investigation of V2 neural responses in the tree shrew, allowing us to delineate both basic RF parameters, responses to the different grating classes, and representational transformation in the visual processing hierarchy in this species. A relevant aspect of our study is that we analyzed both single neurons and the visual evoked potential (VEP) component of the local field potential (LFP). A comparison between neural tuning of these two signal types with respect to visual stimulation parameters can be used to provide insight into the columnar cortical representation of stimulus attributes (Katzner et al. 2009; Liu and Newsome 2006) as well as the locality of neural computations (Liebe et al. 2011; Monosov et al. 2008; Nielsen et al. 2006; Rainer 2008).

MATERIALS AND METHODS

Animal preparation.

All experimental procedures were conducted according to local regulations approved by the veterinary office of the canton of Fribourg and in compliance with European Union directives. Experiments were performed on nine anesthetized tree shrews (Tupaia belangeri), aged 2 to 6 years. Animals were housed in individual cages of 3 cubic meters (123 × 123 × 200 cm) in an environment maintained at 50% humidity and 26°C temperature on a 12:12-h light-dark cycle (light on at 0800). Cages were enriched with wooden sticks, branches, and plastic tubes, and each animal had a nest box (17 × 32 × 16 cm). Food and water were available ad libitum. Animals were anesthetized before the experiments with ketamine (100 mg/kg im; Ketanarkon; Streuli Pharma), followed by atropine (0.02 mg/kg im; Atropinum Sulf Sintetica) to prevent mucus secretion. Analgesics were also administered (1% sc; Scandicain; Astra Zeneca). Vital signs, such as body temperature and heart rate, were constantly monitored. Because our experiments lasted for several hours, all necessary measures were adopted to maintain a stable level of anesthesia as well as minimize metabolic distress. First, animals were tracheotomized to provide artificial respiration at 100 strokes/min (Harvard Instrument Respiratory). A gas mixture of 30% oxygen and 0.5–1.5% isoflurane (Dräger vaporization system; isoflurane IsoFlo; Abbott) maintained stable anesthesia. A muscle relaxant drug was also administered at the beginning of the procedures (0.4 mg/kg ip; Pavulon; Essex Chemie) and every 45 min (0.2 mg/kg ip). Second, we administered a 1-ml subcutaneous injection of 5% glucose in 0.9% NaCl every 2 h to minimize metabolic distress and dehydration. Surgical procedures and experimental recordings were carried out while the animal was lying on a custom-made stereotactic frame (designed at the University of Fribourg), which did not provide any obstacle in the visual field of the animal, thus allowing presentation of large visual stimuli (up to 30° of visual field). Both eyes were treated by local application of atropine (atropine 0.5% collyrium; Pharmacieplus Dr C. Repond) for pupil dilation and installation of hard contact lenses to prevent corneal drying. All visual stimuli were presented monocularly to the right eye by covering the field of view of each animal's left eye with black thick cardboard. Accordingly, neural data were recorded only from the left brain hemisphere.

Primary (V1) and secondary visual cortices (V2) were exposed by craniotomy. First, a small region of the skull was carefully removed over V1 (anteroposterior, −0.5 mm; mediolateral, +4.5 mm relative to the “zero” of the stereotactic device). A larger craniotomy was then performed in the anterolateral direction (toward the animal's earlobe), thus exposing an ∼4-mm-wide window over the brain surface.

Electrophysiology.

Extracellular recordings were performed in V1 and V2 with two tungsten single microelectrodes (1-MΩ impedance; FHC) spaced 500 μm. Electrodes were actioned by a hydraulic microdrive (David Kopf Instruments) controlled by a remote hand wheel. For each electrode penetration, we recorded neural activity at several cortical depths. After we had successfully identified and recorded neural activity from a cortical location (see Experimental procedure), electrodes were advanced in the tissue. Neural activity within the following 100 μm was not further investigated. Regrettably, the two electrodes could not be moved independently, thus reducing the chances of corecording from two well-isolated neurons (see Experimental procedure). In fact, in this study we analyzed neural signals recorded from either electrode but in no case simultaneously from both.

Electrophysiological signals were amplified (RA16PA Medusa preamplifier), filtered, and digitized (RZ5 Biomap processor; Tucker-Davis Technologies, Alachua, FL). The signal was concurrently high-pass filtered at 300 Hz and low-pass filtered at 100 Hz. The high-pass filtered signal, sampled at 24.4 kHz, served as the basis for detection of action potentials. Action potentials were stored as segments of about 1.5 ms (40 samples) centered on the time of threshold crossing and were sorted offline. The low-pass filtered signal, downsampled at 1 kHz, included the LFP.

Histology.

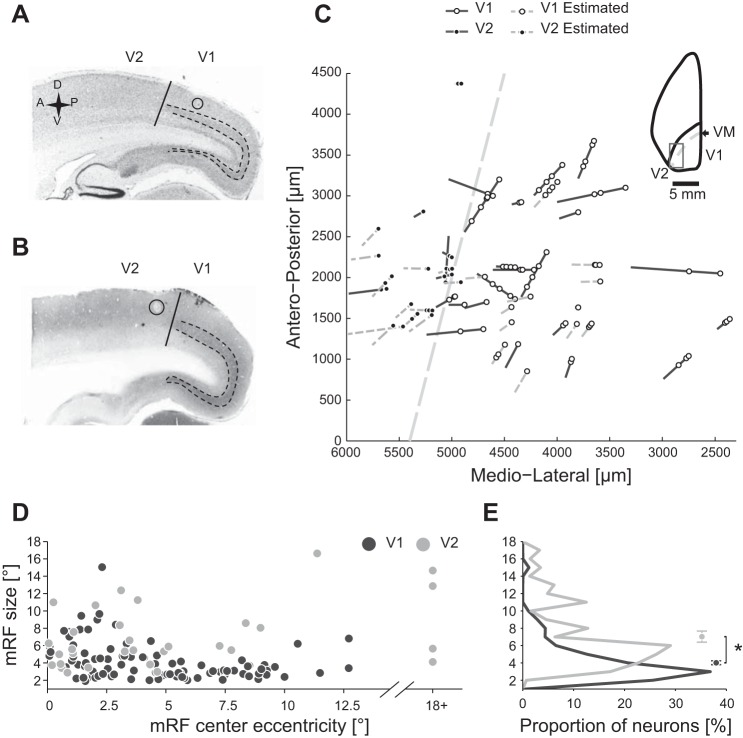
Electrolytic lesions were performed at the end the experiments at several cortical depths of two or three previously visited recording locations. Lesions were performed by stimulating the brain for 10 s with 10 μA of constant current (A360 LA high voltage stimulus isolator; World Precision Instruments). These parameters have been tested in previous studies from our group and were minimum conditions to produce visible lesions in tree shrew V1 without compromising the accuracy of histological localization of the recording electrodes. Next, animals were deeply anesthetized with Esconarkon (600 mg/kg ip) and then perfused transcardially with 0.9% NaCl solution, followed by cold 4% paraformaldehyde in 0.1 M phosphate buffer (pH 7.4). The brain was removed from the skull and postfixed in 4% paraformaldehyde at 4°C overnight. The following day, the brain was transferred in 30% sucrose in the same buffer solution. The brain was cut on the sagittal plane (50 or 30 μm thick) by using a freezing microtome (Microm HM440E), mounted on glass slides, and coverslipped. Recording locations and depth were determined using electrode tracks and lesions observed in Nissl (see Fig. 1A)- or cytochrome oxidase-stained sections (see Fig. 1B). Coordinates of each electrode track were plotted in MATLAB (see Fig. 1C). We were able to assign each recording to either V1 or V2 areas as well as to the cortical subdivisions of supragranular (2 and 3), granular (4), and infragranular (5 and 6) layers. The number of recorded neurons is reported below (see Data analysis).

Fig. 1.

Recordings location and receptive field (RF) size. A and B: sagittal histological sections of a tree shrew's left brain hemisphere. Primary visual cortex (V1) is characterized by a higher density of cells in layer 4 than in secondary cortex (V2), as revealed by Nissl (A) and cytochrome oxidase (B) staining methods (dashed lines mark layer 4 boundaries). Putative border between V1 and V2 is marked by a solid vertical line. Electrolytic lesions are marked by circles. C: recordings were performed in a small region around the V1/V2 border (inset shows a dorsal view of the left hemisphere and the approximate location of all recordings, marked by a rectangle). Electrode tracks were reconstructed from histological landmarks (solid dark gray lines) or estimated from stereotactic coordinates relative to known recording locations (dashed light gray lines). Paths of electrode tracks are projected on a horizontal plane, with open and filled circles marking the recorded locations along the track in V1 and V2, respectively. The position of the border between V1 and V2, that is, the vertical meridian (VM), is shown as a dashed line. D: size of minimum response fields (mRF) plotted as a function of RF eccentricity. E: distribution of mRF sizes of V1 and V2 neurons. Circles and error bars are medians and first and third quartiles of the distribution, respectively.

Visual stimulation.

Visual stimuli were presented using custom-written MATLAB code, running the Psychophysics Toolbox (Brainard 1997; Kleiner et al. 2007) on a Mac Mini. A 21-in. cathode-ray tube computer monitor was placed at 30 cm in front of the animal, subtending ∼60° of visual field. Luminance gamma of the monitor was measured with a Minolta TVCA-II color analyzer and corrected by linearization at software level. The intermediate luminance level (i.e., “gray,” corresponding to 25 cd/m²) served as background color, and it was continuously shown during the entire experimental session (see below). Screen refresh rate was set to the maximal frequency generated by our monitor, namely, 120 Hz, which generates very little entrainment of neuronal activity with the monitor refresh rate in tree shrews (Veit et al. 2011). The stereotactic frame was fixed on a metallic base that could be rotated around a central pivot and locked at each 30° step so that more eccentric RFs could be also stimulated. Distance from the screen was measured at the beginning of each recording to ensure accurate estimation of visual RF size.

Experimental stimuli were static, full-contrast, grayscale sinusoidal gratings, which belonged to three distinct stimulus classes: Cartesian, hyperbolic, and polar (see Fig. 2A). These three stimulus ensembles share the mathematical property of orthogonality, which is defined as lack of linear correlation between stimuli of the ensemble (Papoulis and Pillai 2002). We formally verified this assumption by calculating Pearson's correlation coefficients r between all pairs of images within each grating class, as follows: r = Cov_(x,y)/(Var_xVar_y), where x and y are stimulus images, Cov is covariance, and Var is variance. Orthogonality of stimulus ensembles is a desirable property because it allows us to examine whether the neural response is a linear function of the manipulated stimulus parameters by reverse correlation methods. By convolving the spatiotemporal stimulus with the neural response, reverse correlation can reveal asymmetries of the neural response in favor of either lightness or darkness in the stimulated area that forms the basis for estimation of ON- and OFF-centered subregions of the RF. This RF estimate is equivalent to the minimum response field (mRF) computed from the sparse noise stimulus, which also forms an orthogonal stimulus ensemble. Stimulus sets employed in the present study were computed according to previously published mathematical formulas (Gallant et al. 1996), which describe the grating stimuli as coordinates in a mathematical space whose axes represent stimulus parameters such as orientation, spatial frequency, and spatial phase. Cartesian gratings were generated at four orientations (0, 45, 90, and 135°) and three spatial frequencies (2, 4, and 6 cycles per stimulus; see Fig. 2A, top row), which defined 12 unique stimulus structures. However, the notion of stimulus structure, which depends on orientation and spatial frequency, is not directly comparable between Cartesian and non-Cartesian grating classes. In fact, hyperbolic gratings contain two orthogonal hyperbolas, the unit hyperbola and its conjugate, flanked by orthogonal cross-shaped asymptotes whose intersection lies at the center of the stimulus. Thus the values of orientation for hyperbolic gratings describe the orientation of the asymptotes rather than of the luminous bands. We have generated 12 hyperbolic stimuli by combining 2 orientation values (0 and 45°) and 6 spatial frequencies (ranging from 1 to 3.5 cycles per stimulus; see Fig. 2A, middle row). On the other hand, polar stimuli are characterized by spirals or concentric circles that expand from the center in all directions, thus containing multiple orientation values. Instead, polar gratings are defined solely in terms of radial and concentric spatial frequencies, which specify curvature and density of luminous bands, respectively. We have chosen three concentric and four radial spatial frequencies to generate the concentric pattern and three radial grating samples (see Fig. 2A, bottom row). Each unique grating stimulus structure was then recomputed at four 90° phase-shifted versions. Although the operation of phase shift is mathematically equivalent for each grating class, it produces perceptually different effects depending on the grating type, namely, translation, rotation, and contraction/expansion for Cartesian, radial polar, and hyperbolic and concentric polar, respectively. Moreover, a spatial phase shift results in relocation of boundaries between light and dark patches of the grating image, which in turn alters the relative position of contrast gradients and possibly affects stimulus structure. To minimize this effect on stimulus structure, we restricted our analyses regarding spatial phase to grating stimulus polarity, which considers only a stimulus and its contrast-reversed version (generated by a 180° phase shift). In Fig. 2A, for each grating class, stimuli are sorted on two rows where the second row contains polarity-inverted image versions of the first row. Altogether, the set of experimental stimuli comprised 144 gratings.

Fig. 2.

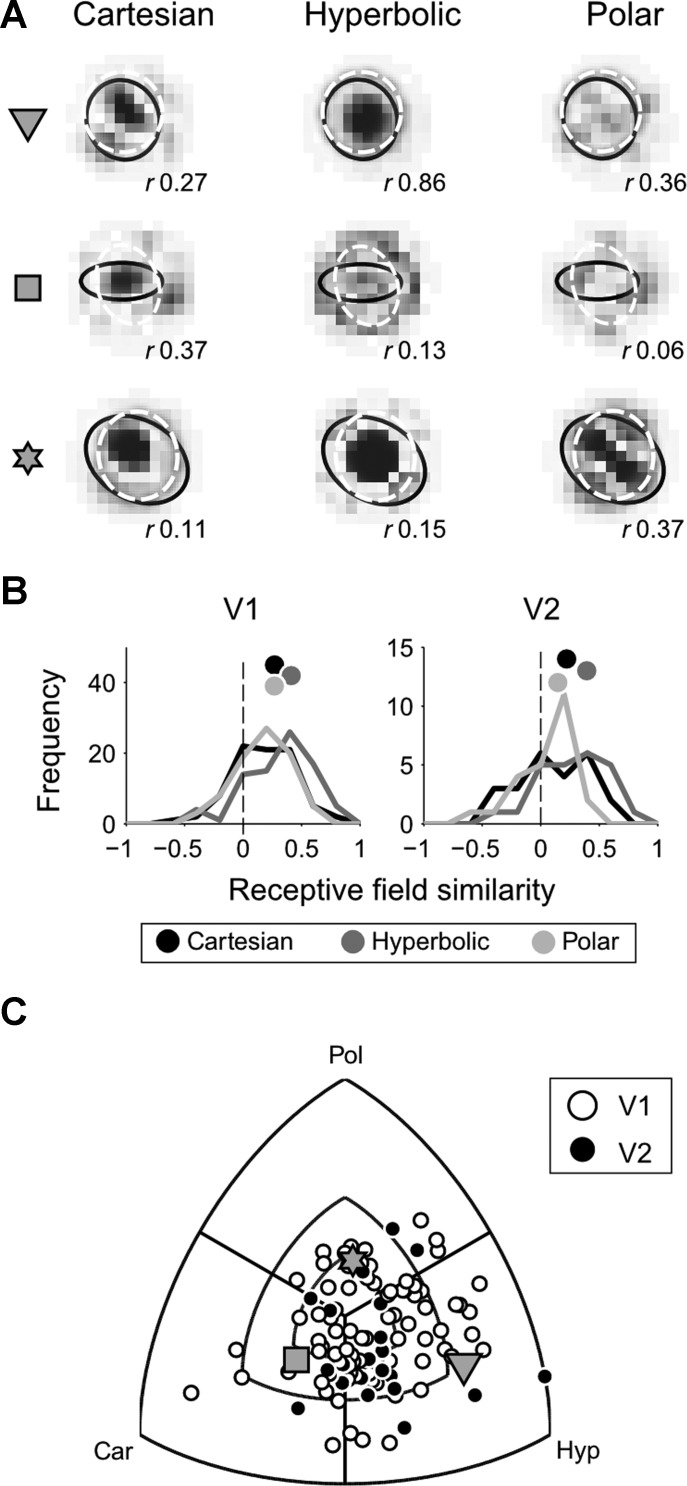
Stimulus set and exemplar neural responses. A: the stimulus set included 144 stimuli sampled from 3 grating classes: Cartesian (Car; top), hyperbolic (Hyp; middle), and polar stimuli (Pol; bottom). Gratings of each class are sorted on 2 rows that show the opposite stimulus polarities, and in groups with the same spatial frequency separated by white vertical lines. B: the responses of 3 exemplar neurons to gratings shown at stimulus size 1 (1× mRF) are displayed as squares whose size is relative to the highest response of this particular neuron across all conditions (grating class and stimulus size), which is the R_max value, displayed at left for each neuron. At right for each neuron, the structure selectivity index (SSI) and polarity sensitivity index (PSI) values are shown for each grating class. Gray symbols for each neuron (triangle, square, and diamond) refer to the same 3 neurons shown in Fig. 3, A and B.

Contextual modulation effects were investigated by systematically varying the stimulus size, ranging from about the estimated RF size (see Experimental procedures) to twice or quadruple that size, which also stimulated surrounding neurons. Importantly, variations in stimulus size were not obtained by scaling the stimulus picture to the desired area; rather, it was the aperture over the stimulus that varied in diameter, thus ensuring that spatial frequency was constant with all stimulus sizes. Stimuli were generated at the screen resolution of 512 × 512 pixels, which corresponded to stimulus size 4, and only one-half or one-quarter of the stimulus was shown for stimulus sizes 2 and 1, respectively. We presented grating stimuli within a circular stimulus aperture to ensure that length of luminance stripes did not depend on stimulus orientation. Also, to minimize responses to sharp edges, the outer 20 pixels of the stimulus aperture were smoothed by convolution with a 2-dimensional half-Gaussian kernel.

Experimental procedure.

Visual RFs were estimated by manually moving a black bar on a white background generated by graphic software across the monitor in different directions while electrodes were slowly advanced into the tissue. Neuronal spikes were visualized on the computer monitor of the recording system and could be heard via a computer speaker. When neuronal activity could be clearly isolated from the background activity, we stimulated with the sparse noise stimulus a large region of visual field around the putative location of the RF (Veit et al. 2013; Yeh et al. 2009b). The sparse noise stimulus consists of black and white small square “dots” that are briefly flashed one at a time on random tiles of an invisible square grid. In this study, we generally employed a 17 × 17-tile-wide grid, which covered 10° of visual field. Each dot covered a surface of 2 × 2 tiles so that each grid pixel was stimulated by 4 unique stimuli of each luminance level, and the entire stimulation was repeated 5 times. When the RF could be stimulated in most grid pixels, we repeated the stimulation with a 20° wide stimulus. Conversely, if there was no grid location that could reliably elicit neuronal spiking activity, we discarded the current recording and moved the electrodes to a new location.

Size and location of the RF were estimated by reverse correlation of the sparse noise stimulus with spike trains occurred from +20 to +100 ms since stimulus onset (Veit et al. 2013). Although we oversampled the grid space by presenting overlapping dots, better approximation of RF size and center was achieved by fitting the time-averaged response map with an oriented two-dimensional Gaussian function (Veit et al. 2013), which resulted in an oriented ellipse. The area within 2 SD from the center of the ellipse, which contains 95% of the responses, was considered as the mRF of the RF. The mRF is thought to represent mostly thalamocortical inputs from the lateral geniculate nucleus (Yeh et al. 2009b). We chose the major ellipse axis as representative of the mRF size. As described above in Visual stimulation, aperture over stimulus diameter was adjusted according to mRF size.

After mRF position and size were estimated, we proceeded with the visual stimulation of the mRF with grating stimuli. Each experimental stimulus was presented for about 83 ms (i.e., 10 frames at 120-Hz monitor refresh rate), with no interstimulus interval, for 12 times in pseudorandom order. The three stimulus sizes were presented in randomized blocks, interleaved by about 30 s of blank period during which gray background color was shown.

Data analysis.

Analyses were performed in MATLAB with custom-written code and built-in functions. Collected data were spiking rates and LFP. Neurons were identified by sorting recorded spikes according to energy, namely, the area below the spike waveform, and interspike intervals. Our data set comprised 126 isolated neurons (95 V1 and 31 V2 neurons) and 122 recordings of the VEPs of the LFP (94 in V1 and 28 in V2). After laminar assignment, we attributed 34, 37, and 19 recordings to layers 2/3, 4, and 5/6 of V1, respectively; 5 recordings were excluded from laminar analysis because of relatively high uncertainty concerning their cortical depth. In V2, we recorded 14 neurons in layers 2/3 and 4, whereas only 3 neurons were located in layer 5/6.

Single-unit activity (SUA) was defined as the spiking rate within a time window from +20 to +100 ms from stimulus onset, averaged across repetitions of the same stimulus. Spiking rate within the 2 s preceding the stimulation protocol, during which neutral gray color was displayed, was subtracted from all spiking responses evoked by visual stimuli presentation. For each recorded neuron, we quantitatively defined two measures of neural tuning, one for image structure and one for stimulus polarity, both of which ranged from 0 to 1. The structure selectivity index (SSI) was defined as SSI = (R^best − R^worst)/R_max, where R^best and R^worst are, respectively, the highest and lowest responses to stimuli of a particular class, and R_max is the maximum response across all conditions of grating class and stimulus size. The polarity sensitivity index (PSI) was computed as the difference between the responses for the two polarities of the preferred stimulus, normalized by dividing by R_max, as follows: PSI = |R_{polarity 1}^{best stimulus} − R_{polarity 2}^{best stimulus}|/R_max.

VEP were obtained by low-pass filtering the LFP signal at 100 Hz with a fourth-order zero-phase digital Butterworth filter. Because VEPs are event-related potentials locked in time to stimulus onset, LFP amplitude segments for each stimulus were averaged in the time domain across stimulus repetitions in a time window from +20 to +100 ms from stimulus onset. VEPs were then converted to a standard score (z score) by using the following formula: VEP_z = (VEP − M_bl)/SD_bl, where M_bl and SD_bl are, respectively, mean and standard deviation of the signal in a 2-s window before the visual stimulation period while the visual RF was stimulated by neutral gray background color. We chose a 40-ms time window centered on the across-trial largest negative peak as the period of maximum activity. SSI and PSI values were then computed as described above for SUA responses after VEP peak responses were multiplied by −1 so that SSI and PSI values assumed only positive values, ranging from 0 to 1.

Statistical analysis.

It is known that RF size increases along the visual information hierarchy from V1 toward higher order visual areas. Under this assumption, we assessed whether histological reconstruction of electrode tracks had reasonably assigned recording locations to V1 and V2 (see Histology) by performing two statistical tests: an unpaired t-test on estimated RF sizes of V1 and V2 neurons and an additional randomization test. For the randomization test, new samples were drawn with replacement from the pool of data while keeping constant the number of V1/V2 labels of the original sample (i.e., 95 V1 and 31 V2 neurons). For each new randomized sample, we calculated a bootstrapped t score (t_bs) of the mean difference between the V1 and V2 groups according to the following formula:

$$t_{\widehat{bs}}=\frac{\langle RFsiz{e}_{\widehat{V1}}\rangle -\langle RFsiz{e}_{\widehat{V2}}\rangle }{\sqrt{\frac{Va{r}_{\widehat{V1}}}{n_{\widehat{V1}}}+\frac{Va{r}_{\widehat{V2}}}{n_{\widehat{V2}}}}},$$

where 〈 ․ ․ ․ 〉 denotes the average RF size in the randomized sample for V1 and V2, Var is the variance within each group, and n is the number of values within the groups. The resampling procedure was repeated 10⁵ times, yielding a normally distributed population of t_bs values centered on 0. This bootstrapped distribution served as basis for a typical two-tailed t-test, by calculating the fraction of t_bs scores that were more extreme (i.e., farther from the mean) than the t score estimated from the empirical data, divided by the total number of randomized samples.

For all V1 and V2 neurons, we have also quantified two functional properties of their RF, namely, overlap of ON and OFF subfields and black dominance. The overlap between ON and OFF regions of the RF was quantified by computing the overlap index OI = (2σ^white + 2σ^black − Δμ)/(2σ^white + 2σ^black + Δμ), where σ is the mean bidimensional spatial spread of the RF size as estimated by sparse noise stimulus with either white or black dots, and Δμ is the Euclidean distance between the two subfields' centers (Kagan et al. 2002; Martinez et al. 2005; Schiller et al. 1976; Veit et al. 2013). Additionally, we have estimated whether RFs were equally selectively to black and white stimulus patches by computing the black-to-white preference ratio as log₂ (A_white/A_black), where A is the peak response in the estimated RF subfield (Veit et al. 2013; Yeh et al. 2009a).

To compare measures of neural selectivity to grating structure and stimulus polarity across different recording sites and neurons, both SSI and PSI include a normalization term, namely, R_max. This procedure, however, has the effect of penalizing highly responsive neurons, which are more frequent in V1 than in V2 as revealed by an unpaired t-test on R_max values of V1 and V2 neurons. Therefore, we have excluded the 47 more responsive V1 neurons from statistical significance tests, either t-tests or post hoc tests, which aimed at comparing V1 to V2. This reduced V1 population included as much as 52 neurons with an average peak response 〈R_max〉 = 51.1 ± 2 spikes/s, which was comparable with that of the V2 population (31 neurons, 〈R_max〉 = 51.3 ± 4 spikes/s; unpaired t-test: P < 0.1). Please note that these V1 neurons were excluded only for the purposes of direct comparisons between V1 and V2. All the remaining analyses were based on the entire V1 data set. We have confirmed that the reduced V1 population closely resembles the entire recorded V1 population in terms of SSI, RF size, and receptive field similarity (RFS) index (ANOVAs with factor reduced vs. remaining V1 population: P = 0.06, P > 0.1, and P > 0.1, respectively, for main effects).

The contribution of grating class and stimulus size to neural tuning to structure and phase was assessed by separate ANOVAs for PSI and SSI values, independently for SUA and VEP. These analyses were performed on all recordings regardless of their cortical laminar position. When significant effects could be demonstrated, we conducted further statistical analyses considering the laminar subdivision as a dependent variable of the ANOVA to examine the layer dependence of these effects. ANOVA on SSI and PSI consisted of a three-way repeated-measures design with one between-subject factor, namely, the assignment to either V1 or V2, and two within-subject factors, grating class and stimulus size, with repeated measures on both factors. We used the open-source statistics software R (R for Windows, version ×64, 3.1.2) to perform the repeated-measures ANOVAs. Where F-tests yielded significant results (P < 0.05), we reported the P value. Additionally, significant F-tests in the ANOVA were followed by appropriate post hoc tests, whose resulting P values were corrected for multiple comparison bias according to the step-down Holm-Šídák method (Holm 1979). The correction was applied as follows: first, P values were sorted in ascending order, and then an iterative process determined whether the null hypotheses of each test could be accepted. For each iteration i, the i-th adjusted P value was estimated as P_i^adj = 1 − (1 − P_i)^{n − i + 1}, where P_i is the unadjusted value, and n is the number of tests to which the correction is applied. Finally, each adjusted P value was compared with a statistical significance threshold α, and the null hypothesis was accepted for P > α, rejected otherwise. A new iteration followed only if the i-th null hypothesis had been rejected; otherwise the procedure stopped and we accepted all subsequent null hypotheses (Holm 1979). We set the threshold value α to 0.05.

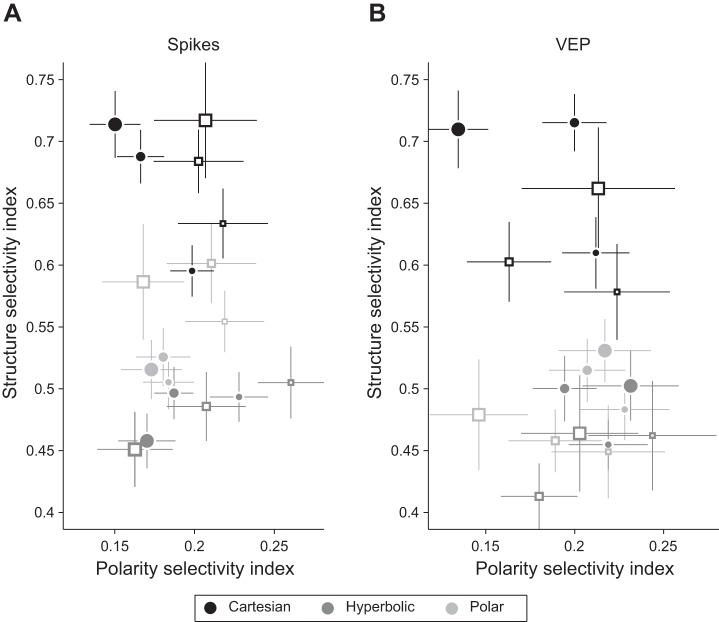
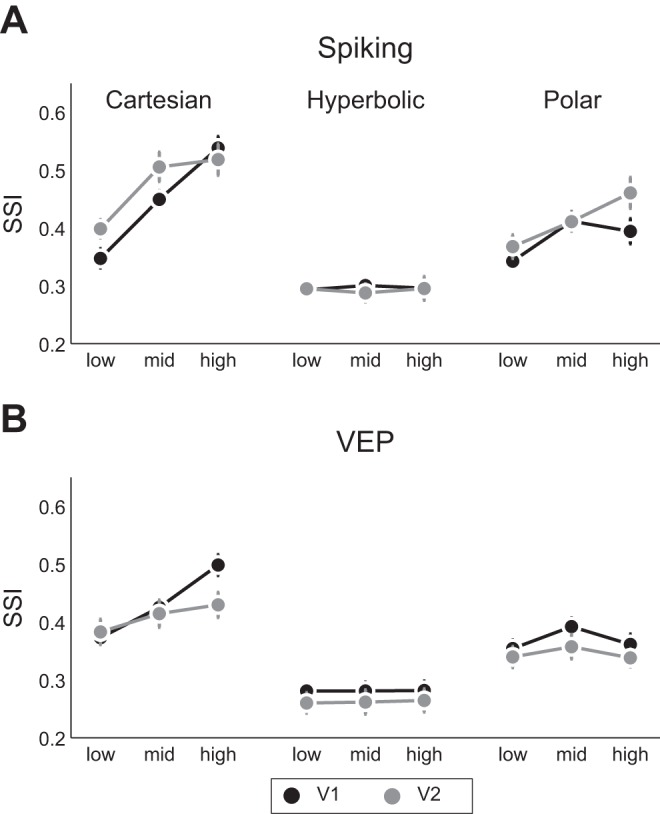
Systematic comparisons between SUA and VEP signals are of increasing relevance in neurophysiological studies, because spiking activity and local potentials originate from two different physiological mechanisms and are generally interpreted as being more closely related to the output and input, respectively, of a cortical region (Katzner et al. 2009). We have investigated the relationship between SUA and VEP following the observation that structure selectivity of polar gratings in V1 was higher than in V2 when estimated on SUA, but it was lower when estimated on VEPs (see Fig. 4). We tested this hypothesis by performing a three-way ANOVA on SSI for polar gratings with V1/V2 and SUA/VEP signal type as between-subject factors and with stimulus size as a between-subject factor with repeated measures.

Fig. 4.

Average SSI and PSI estimated by spiking responses (A) and visually evoked potentials (VEPs; B) are shown for all experimental conditions: grating classes are marked by different shading as indicated at bottom; stimulus sizes 1, 2, and 4 are displayed as symbols of 3 different sizes; V1 and V2 are marked by filled and open symbols, respectively. Vertical and horizontal lines are SEs of mean SSI and PSI values, respectively.

We were also interested in how contextual modulation affected both neural tuning and firing responses. We compared the mean SUA response of each neuron for each grating class with the responses for larger stimuli (i.e., we compared sizes 2× mRF vs. 1×, 4× vs. 1×, and 4× vs. 2×). We assessed statistical significance by using a paired two-sample t-test and reported P values corrected for multiple comparisons. We further tested the relative frequencies of surround suppression and enhancement by performing a χ² test. The comparison of SUA responses for Cartesian gratings presented at stimulus sizes 1 and 4 is shown in Fig. 5.

Fig. 5.

Effect of surround activation. Spiking responses for Cartesian gratings at stimulus sizes 1 and 4 are shown for V1 and V2 neurons. Filled symbols mark neurons that significantly increased (above black line) or decreased (below the line) their firing rate when the surround was concurrently activated (P < 0.05, after correction for multiple comparisons).

We have also investigated the effect of spatial frequency variations on stimulus selectivity. First, we determined for each neuron the preferred spatial frequency among those we have used in our stimulus set. Spatial frequency preference was determined on the basis of mean SUA response for each spatial frequency within a grating class. We constructed histograms of spatial frequency preference in the population of V1 and V2 neurons for each stimulus size. We then tested whether distributions varied for each grating class across stimulus size by performing a χ² test and correcting P values for multiple comparisons. Because we found no significant difference for any of the grating classes (P > 0.5), we averaged the histograms across stimulus size and reported the resulting preference frequencies in Fig. 6. We then compared the preference distributions for V1 and V2 neurons by performing a χ² test between the distribution values. Additionally, we recomputed SSI values, limiting our analysis of SUA and VEP responses to the preferred spatial frequency of each neuron. We then tested the difference between V1 and V2 recordings by performing a three-way ANOVA for SUA and VEP SSI values independently with spatial frequency, V1/V2, and grating class as factors. Significant factors and interactions were further examined by post hoc tests whose resulting P values were corrected for multiple comparison bias.

Fig. 6.

Preferred spatial frequency of each grating class exhibited by V1 (A) and V2 neurons (B), estimated on the basis of spiking responses.

Because RF organization is usually determined from neural responses to sparse noise stimuli, we have estimated the RFS between RFs estimated by sparse noise and the three grating classes examined in this study. RFS is defined as follows: r = Cov_(SN,GR)/(Var_SNVar_GR), where SN and GR are the sparse noise and the grating images, respectively (Yeh et al. 2009b). Computing the RFS is equivalent to calculating the Pearson's correlation coefficient, and it can be interpreted in a similar fashion: RFS equals 1 when the two RFs overlap exactly, and it assumes values close to −1 when RF estimates have the same position and shape but opposite polarity of ON- and OFF-centered subregions; RFS values close to 0 indicate absence of linear correlation between the two maps. Because the sparse noise and the grating stimuli were presented at different sizes and resolutions (15 × 15 pixels for sparse noise and 512 × 512 pixels for the gratings), we resized the sparse noise image by up-sampling it to the grating image resolution, approximating pixels by nearest-neighbor interpolation. Three values of RFS were estimated for each recording, corresponding to the correlation of each grating class to the sparse noise map. RFS values were analyzed with a three-way repeated-measures ANOVA with V1/V2 as a between-subject factor and stimulus size and grating class as within-subject factors. Additionally, we tested whether a particular class had higher RFS values than the others by performing a χ² test and correcting P values for multiple comparisons.

In Figs. 3 and 8C, we show distributions of data points on triple-axis plots, which are the isometric projection of a three-dimensional space whose dimensions are the three grating classes. The advantage of such kind of plot is to show the relative advantage of any grating class over the others; in fact, points that lie close to the origin have similar values for all classes, although not necessarily low values. Additionally, for clarity, we also plot parallel lines of equal distance from the center (which appear similar as inflated triangles) and straight lines departing from the origin that mark meridians of equal distance from pairs of vertices.

Fig. 3.

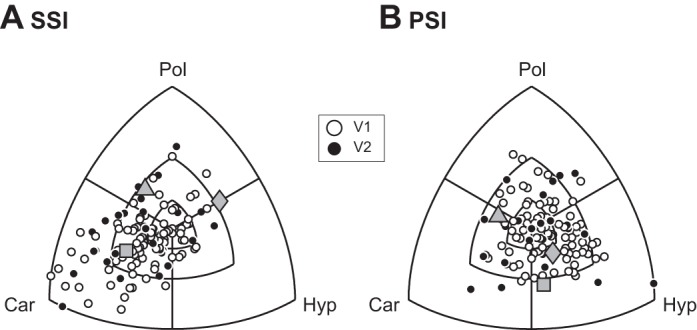
Distribution of SSI (A) and PSI (B) values for both V1 and V2 are shown on a triple-axis plot, which displays the differences in tuning index between grating classes. Concentric parallels mark the 0.1, 0.25, and 0.5 differences in tuning indexes between grating classes. Gray symbols (triangle, square, and diamond) refer to the neurons in Fig. 2B.

Fig. 8.

Receptive field similarity (RFS). A: RFs of 3 exemplar neurons are displayed after reconstruction by reverse correlation with grating stimuli of the Cartesian (left), hyperbolic (center), and polar (right) grating classes. For each new stimulus, white and black pixels are equivalent to light and dark stimulus patches, respectively. Overlaid ellipses show the ON and OFF RF subregions as computed using the sparse noise technique. The correlation between the sparse noise stimulus map and grating stimulus map was computed by 2-dimensional correlation of the 2 maps, and resulting values (r) are shown at bottom right corner of each map. Gray symbols at far left mark the 3 exemplar neurons in C. B: histogram of RFS indexes at stimulus size 1. C: RFS for V1 and V2 neurons is displayed on a triple-axis plot that shows the relative difference between grating classes. Concentric parallels mark the 0.25, 0.50, and 1.0 difference in RFS between grating classes. Gray symbols refer to the 3 neurons marked in A.

RESULTS

Histological reconstruction of recording locations.

Electrophysiological data presented in this report comprise 126 neurons, recorded from the central upper visual field representation at different depths on primary (V1) and secondary (V2) visual cortex of 9 anesthetized tree shrews. Recording locations were reconstructed on the basis of electrolytic lesions and electrode tracks visualized using Nissl and cytochrome oxidase histochemistry. In Nissl staining, lesions were represented by a darker center surrounded by a white halo (Fig. 1A), whereas in the cytochrome oxidase staining, lesions appeared white (Fig. 1B). For both staining methods, a dark band corresponding to the granular layer was visible in V1 but not in V2, allowing a precise localization of the V1/V2 border. With the use of this criterion, 95 and 31 neurons were assigned to V1 and V2, respectively (Fig. 1C).

Receptive field size.

We computed the RF size for SUA using the mRF that we determined by reverse correlation with the sparse noise stimulus (see materials and methods). The RF size for V1 and V2 neurons is shown as a function of the eccentricity of the RF center in Fig. 1D. We note that the smallest RFs were about 2° and 3° in size in V1 and V2, respectively. For neurons with low RF center eccentricities, the RFs often extended into the ipsilateral visual hemifield, consistent with an ipsilateral visual field representation previously reported for tree shrews (Bosking et al. 2000). After histological assignment of each recording to either V1 or V2, we found that RF size was smaller for V1 (4.0 ± 0.2°, mean ± SE) than for V2 neurons (7.0 ± 0.6°), as confirmed by two statistical tests (unpaired samples t-test: P < 0.001; randomization test: P < 0.01). This is consistent with the known increase of RF size along the cortical processing stream from V1 toward temporal areas. The V1 RF sizes reported in this study for the central visual field (eccentricity <10°) and previous findings obtained at higher eccentricities (Veit et al. 2013) are consistent with a linear RF size increase dependent on RF eccentricity in tree shrew V1.

There was less overlap between mRF ON and OFF subfields in V2 than in V1 (V1: 0.83 ± 0.02; V2: 0.66 ± 0.05; unpaired t-test: P < 0.01), whereas the mRF black dominance (i.e., log ratio between peak responses in ON and OFF mRF subfields) was greater in V2 than in V1 (V1: −0.05 ± 0.01; V2: −0.09 ± 0.02; unpaired t-test: P < 0.01).

Spiking activity-based stimulus and polarity selectivity depend on grating class.

We proceeded to record neural activity to three classes of monochrome grating stimuli, including the well-studied Cartesian gratings as well as hyperbolic and both concentric and radial polar gratings. We generated 24 exemplar gratings for each class by varying parameters related to grating structure (orientation, spatial frequency, and spatial phase; Fig. 2A). Each grating was presented at two polarities (original and inverse polarity), allowing estimation of how grating structure and polarity affect visual cortical neuron responses for each of the grating classes. Additionally, three different sizes were tested, ranging from just covering the mRF to two or four times that size, allowing us to examine contextual modulations of neural responses induced by stimulating the RF surround. SUA and VEPs were estimated for each stimulus, taking into account the response latency of visual cortex. Generally, we observed that neurons tended to respond to stimuli from all three grating classes. For clarity, we initially focus on gratings that were restricted to the mRF, corresponding to stimulus size 1, and subsequently expand the analysis to also consider larger stimulus sizes. The activity of three example neurons is illustrated in Fig. 2B. As a first analysis, we estimated the stimulus selectivity across all of the 48 stimuli in each grating class by using the stimulus selectivity index: SSI = (R^best − R^worst)/R_max, where R_max is the maximum response of this neuron across all conditions and sizes. We observed significantly larger R_max values in V1 than in V2 (V1: 64 ± 2 spikes/s; V2: 51 ± 4 spikes/s; unpaired t-test: P < 0.01).

For neuron 1 in Fig. 2B, the SSI is greatest for Cartesian gratings, as a result of robust orientation-selective responses to 45° clockwise-rotated gratings at high spatial frequency. The neuron shows somewhat lower SSI values in response to hyperbolic and polar gratings but clearly tends to respond selectively to certain hyperbolic gratings at mid to high spatial frequencies as well as to concentric polar gratings at mid spatial frequency. Neuron 2 is relatively broadly tuned for spatial frequency and shows intermediate SSI values for all three grating classes with a maximum value for polar gratings. Finally, neuron 3 responds optimally for low spatial frequency gratings with apparent maximum SSI values for polar and hyperbolic gratings. For each neuron, we also computed a polarity sensitivity index: PSI = |R_{polarity 1}^{best stimulus} − R_{polarity 2}^{best stimulus}|/R_max. The PSI quantifies the impact of grating polarity on neural response to the preferred stimulus. For the three example neurons considered in Fig. 2B, PSI tended to vary between near-polarity invariance (e.g., polar gratings, neuron 1) to robust effects of polarity on neural responses (e.g., hyperbolic gratings, neuron 3). To examine the distribution of SSI and PSI systematically for the population of neurons, we constructed triple-axis plots that describe relative preferences of index values between grating classes for stimulus size 1 (see materials and methods). Note that data points near the origin represent similar, but not necessarily low, index values for all three grating classes.

For the SSI (Fig. 3A), a clear preference for Cartesian gratings is apparent. A χ² test for equality of proportions revealed that a larger fraction of neurons preferred Cartesian gratings in both V1 and V2 (P < 0.001). For the PSI, a similar analysis revealed that neurons were most sensitive to stimulus polarity for hyperbolic gratings in V1 but not in V2 (P < 0.05 and P > 0.1, respectively). Whereas many neurons tended to be highly selective for Cartesian gratings, these responses were little modulated by grating polarity. By contrast, although neurons showed little selectivity for hyperbolic gratings, responses to this grating class were highly dependent on stimulus polarity.

Population analysis for spiking and VEP activity as a function of grating class and stimulus size in V1 and V2.

The above-described analyses have illustrated effects of grating class on stimulus and polarity selectivity at size 1. We now present a comprehensive analysis of SSI and PSI values in V1 and V2 as a function of grating class and stimulus size. Because overall neural responsivity can bias modulation indexes, we perform these analyses on V1 and V2 populations that have been matched in terms of R_max firing rate (V1: 52 neurons, 〈R_max〉 = 51.1 ± 2 spikes/s; V2: 31 neurons, 〈R_max〉 = 51.3 ± 4 spikes/s; unpaired t-test: P > 0.1). Potential reasons for reduced neural responsivity in V2 include anesthesia and monocular visual stimulation. The results, shown in Fig. 4A for spiking activity, were analyzed using a repeated-measures three-way ANOVA with grating class and stimulus size as within-subject factors and V1/V2 as a between-subject factor. Confirming the above findings based on neuron counts at size 1 and extending them to larger size stimuli, we found a main effect of grating class (P < 0.001) on SSI, with post hoc tests revealing greater SSI values for Cartesian than hyperbolic or polar gratings in V1 (P < 0.01) at all sizes. In V2, SSI values for Cartesian gratings were higher than those for hyperbolic gratings (P < 0.01) but similar to those for polar gratings (P > 0.1) at all sizes. Thus selectivity for polar gratings emerges in V2, where neurons are equally selective for these stimuli as for Cartesian gratings. We also observed a main effect of stimulus size on SSI, with post hoc tests (P < 0.05) revealing increased SSI for larger stimuli compared with size 1 exclusively for Cartesian gratings. Stimulation of the contextual surround thus tended to enhance stimulus selectivity for Cartesian but not for polar or hyperbolic gratings.

In relation to the polarity sensitivity, we found main effects of grating class and size on PSI (P < 0.05). Because there were no effects of V1/V2 for polarity sensitivity, we focused on V1 polarity sensitivity, basing our results on statistical analysis of the entire population of V1 neurons (n = 95). A two-way ANOVA revealed main effects of size and grating class, with hyperbolic gratings being more sensitive to stimulus polarity than the other two grating classes at size 1, where stimuli are shown within the mRF (post hoc tests: P < 0.01). We consider that this might be related to a correspondence between mRF substructure and hyperbolic gratings, an issue that we address by computing RFS below.

To examine how fluctuations in the VEP reflected stimulus and polarity selectivity for the different grating classes, we performed the analysis described above for the VEP (Fig. 4B). Relating to the SSI, we observed main effects of grating class and V1/V2 (P < 0.05). Cartesian gratings yielded the most pronounced VEPs, and V1 VEPs were generally larger in amplitude than V2 VEPs across grating classes. This is likely due to the less stringent cortical organization (i.e., orientation columns) in V2 compared with V1 or to the lesser degree of direct thalamocortical input to V2. An interesting aspect of these data emerges when differences in neural processing of polar gratings at spike and VEP level between V1 and V2 are considered. A three-way ANOVA for polar gratings with only size, V1/V2, and signal type (spikes/VEP) as factors revealed a main effect of signal type as well as an interaction between V1/V2 and signal type (P < 0.05). This suggests that single neurons in V2 are better tuned for polar gratings but are less consistently organized across the cortical surface.

Contextual surround enhancement specific for Cartesian gratings.

Given the above finding that contextual surround stimulation enhanced stimulus selectivity for Cartesian gratings but not for other grating types, we were interested in relating these neural selectivity modulations to overall firing rate changes associated with stimulation of the extraclassical RF. For each neuron and grating class, we thus compared the activity to each of the 48 stimuli between sizes 1 and 4. We found no difference in average firing rate as a function of surround stimulation for polar or hyperbolic gratings in both V1 and V2 (paired t-tests: P > 0.1). Furthermore, a similar number of V1 neurons showed suppression and enhancement of activity compared with RF center stimulation only (enhancement/suppression: 20/25 and 27/22 for polar and hyperbolic gratings respectively, χ² tests: P > 0.1). For Cartesian gratings, contextual stimulation increased mean firing rate for both size 2 and size 4 stimuli in V1 as well as in V2 (paired t-tests: P < 0.001 I n V1, P < 0.05 in V2). This is illustrated in Fig. 5, which shows the mean firing rate to Cartesian grating stimuli at sizes 1 and 4.

Surround enhancement was also significantly more common than surround suppression in V1 (enhancement: 38; suppression: 14; χ² tests: P < 0.05). Contextual stimulation thus had robust effects on mean activity as well as stimulus selectivity specifically for Cartesian gratings.

Effects of spatial frequency on stimulus selectivity.

We noticed that spatial frequency appeared to have a systematic influence on neural activity. As mentioned above, neuron 1 in Fig. 2B responded with low spiking rates to all Cartesian gratings at the lowest spatial frequency (left group of squares) although exhibiting apparent selectivity for 45°-rotated Cartesian gratings (right group of squares). To systematically analyze the impact of spatial frequency, we first determined the spatial frequency of the optimal stimulus for each grating class, i.e., that stimulus among the 48 exemplars that elicited the maximum response from each neuron, and constructed a histogram of preferred spatial frequencies for each grating class. Because the histograms did not vary significantly with stimulus size (χ² tests: P > 0.1), we show the averaged spatial frequency preferences for the three grating classes (Fig. 6).

For hyperbolic gratings, we observed a broad distribution, suggesting that spatial frequency selectivity tended to vary uniformly across the tested spatial frequency range. On the other hand, the distribution for Cartesian gratings peaked at high spatial frequency for both V1 and V2. Because the stimuli were adapted to the mRF diameter, these values correspond to 3 cycles/RF diameter, i.e., 0.75 cycles/° in V1 and 0.43 cycles/° in V2. For polar gratings, the spatial frequency preference distribution peak shifted significantly from midfrequency in V1 to high frequency in V2 (χ² test: P < 0.01).

To illustrate the impact of spatial frequency on stimulus selectivity, we reanalyzed the data presented in Fig. 4 to estimate SSI separately for each of the spatial frequencies. These index values are shown, averaged across stimulus size, in Fig. 7A for spiking activity and in Fig. 7B for VEP.

Fig. 7.

Effect of spatial frequency variations on SSI. Data are means ± SE for V1 and V2 neurons.

On the basis of a three-way ANOVA with factors of grating class, spatial frequency, and V1/V2, we conclude that for polar gratings, SSI values increased from V1 to V2 for high spatial frequency only (post hoc test: P < 0.01). The overall elevation of stimulus selectivity for polar gratings in V2 described above is thus due to enhanced selectivity of V2 neurons for high spatial frequency polar gratings. For Cartesian gratings, although overall neural selectivity was unchanged in V1 and V2, V2 neurons were more selective for low spatial frequency Cartesian gratings than V1 neurons (post hoc test: P < 0.01). The selectivity enhancements from V1 and V2 for Cartesian and polar gratings thus occurred at opposite ends of the spatial frequency range that we tested. In terms of the VEP (shown in Fig. 7B), a three-way ANOVA with post hoc tests revealed significant differences between V1 and V2 only for high spatial frequency Cartesian gratings (post hoc test: P < 0.01).

Laminar differences in neural tuning characteristics.

Examining how the effects reported above depended on cortical layer, we report two significant observations. The enhanced SSI values for Cartesian gratings were more pronounced in supragranular layers, compared with polar [+31%, t(14) = 4.41, P < 0.01] and hyperbolic gratings [+50%, t(14) = 7.13, P < 0.01], than in the granular layer [polar: +19%, t(21) = 2.58, P < 0.05; hyperbolic: +30%, t(21) = 3.26, P < 0.05]. In relation to contextual modulation observed for Cartesian gratings in V1, we found that for stimulus size 2, which includes stimulation of the near-RF surround, SSI values were higher in both supra- and infragranular layers than in the granular layer (P < 0.01), whereas this was not the case for stimulus size 1, where visual stimulation is restricted to the RF center. Both of these findings are evidence for the importance of the cortical elaboration of pattern selectivity that occurs between granular and supragranular layers in tree shrew V1 (Chisum et al. 2003; Veit et al. 2013).

Hyperbolic gratings yield the best reconstruction of RF subfield structure.

RF reconstructions using the sparse noise stimulus are commonly used to estimate spatial RF characteristics in V1 in reconstructions that 1) recover the linear component of the RF and 2) emphasize thalamocortical inputs to the cortex. Because each of the grating classes in this study also forms orthogonal stimulus ensembles, they also can be used to reconstruct grating class-dependent RFs. If tree shrew V1 were a completely linear system, all of these reconstructions should be identical, and in particular, the same as the sparse noise-based RF. Our results, however, show that RF maps constructed from different grating classes tended to depend strongly on grating class, as shown for three example neurons in Fig. 8A. Reconstructions using Cartesian gratings often contained elongated patches with adjacent regions of opposite polarity (Fig. 8A, left); hyperbolic reconstructions tended to contain circularly symmetric structure (middle), whereas polar reconstructions frequently included radial swirl-like structure with one or more axes of symmetry (right). We employed the RFS index (Yeh et al. 2009b) to quantify how similar the grating class RF maps were to the sparse noise RF map. RFS distributions at 1× mRF (Fig. 8B) demonstrate that RFS depended strongly on grating class in V1 (P < 0.001 for class as main factor; 0.27 ± 0.03, 0.41 ± 0.03, and 0.27 ± 0.03 for Cartesian, hyperbolic, and polar grating classes, respectively) but not in V2 (P > 0.1). Although reconstructions based on hyperbolic gratings provided the closest approximation to the sparse noise mRF maps, reconstructions based on Cartesian and polar gratings exhibited substantial dissimilarities to the sparse noise reconstructions, which is evidence for recruitment of nonlinear RF contributions by these two grating classes in tree shrew V1. A triple-axis plot displaying relative differences of RFS values for the three grating classes (Fig. 8C) suggests that both V1 and V2 populations tend to have higher RFS values for hyperbolic maps (χ² test for equality of proportions: P < 0.01) than for the other two grating classes.

DISCUSSION

Our study provides a detailed investigation of neural responses in the tree shrew early visual cortical areas V1 and V2 to a set of parametrically generated visual patterns including Cartesian (parallel) gratings as well as polar and hyperbolic gratings, two grating classes exhibiting circular and/or radial symmetry. This stimulus set permits us to analyze separately the effects of stimulus selectivity and image polarity on early visual cortical responses within each of the grating classes.

We found that tree shrew early visual cortex is responsive to all of the grating classes, an observation that matches previous findings obtained in the macaque monkey (David et al. 2004, 2006; Gallant et al. 1993, 1996; Hegde and Van Essen 2000, 2007; Mahon and De Valois 2001; Victor et al. 2006). This suggests that in addition to orientation selectivity that is estimated using Cartesian gratings, these cortical areas also encode information about other visual elements such as curved edges or circular structure. In V1, we observed that overall neural selectivity was greater for Cartesian than for both polar and hyperbolic gratings. These findings are consistent with the well-established hallmark of orientation selectivity in V1, as well as with previous results in the macaque, in particular relating to the preference for Cartesian gratings, as well as a weak encoding of hyperbolic gratings (Hegde and Van Essen 2007; Mahon and De Valois 2001; but see Victor et al. 2006). In V2, we found similar levels of stimulus selectivity as in V1 for Cartesian gratings, but a strong enhancement for polar gratings. Indeed, tree shrew V2 was similarly selective for polar and Cartesian gratings, in a manner that was more pronounced than previous findings in macaque (Hegde and Van Essen 2007; Mahon and De Valois 2001). This is consistent with the general notion of refinement and diversification of stimulus representations for higher levels of the visual processing hierarchy. Using RF reconstructions for each grating class, we were able to show that hyperbolic grating RFs closely resembled sparse noise-generated RFs, which was not the case for Cartesian and polar gratings. We suggest that this difference is related to more pronounced nonlinear cortical signal processing for Cartesian and polar than for hyperbolic grating classes. Despite the fact that visual stimuli of the three grating classes spanned the same area of visual space, i.e., 1×, 2×, and 4× mRF, the spatial structure of Cartesian and polar stimuli results in a greater degree of intracortical elaboration of neural activations than is the case for hyperbolic gratings.

Our stimulus set allowed us to examine the impact of spatial frequency on neural selectivity. Whereas the spatial frequency parameter corresponds to a single Fourier decomposition frequency for Cartesian gratings, this is not the case for nonconventional gratings where multiple Fourier components are affected. Nevertheless, stimuli can be usefully grouped by spatial frequency (compare responses at different spatial frequencies in Fig. 2B, notably those of neuron 1 to Cartesian and hyperbolic gratings). For Cartesian gratings, there was no overall increase of neural stimulus selectivity from V1 to V2, since both areas exhibited similar, and high, selectivity for high-frequency gratings. Neural selectivity did, however, significantly increase at low spatial frequency, consistent with cortical refinement of visual representations. This finding is of comparative interest because single neurons in the rodent extrastriate visual cortex also exhibit enhanced selectivity for Cartesian gratings (Vermaercke et al. 2014), whereas in the macaque, higher areas of the ventral stream tend to respond little to Cartesian gratings (Vogels and Orban 1994). For polar gratings, a similar enhancement of selectivity was evident, which was significant at high spatial frequency, suggesting that the overall enhanced stimulus selectivity for polar gratings in V2 mostly stems from neural responses at high spatial frequencies. This is consistent with the observed shift in neural mean firing rate preference from mid to high spatial frequency between V1 and V2. V2 neurons thus extend their selectivity to Cartesian and polar gratings at opposite ends of the spatial frequency spectrum that we tested, suggesting that neural coding enhancement on V2 is not simply a consequence of altered spatial frequency sensitivity. The emergent selectivity in V2 might serve for extraction of linear as well as curved or concentric borders in the visual environment, as well as contributing to figure-ground segregation (Qiu and von der Heydt 2005; von der Heydt et al. 1995).

We found that V1 neurons were particularly sensitive to the polarity of hyperbolic gratings when these were presented within the mRF of the neuron, compared with other stimulus sizes and grating classes. Polarity sensitivity is related to phase sensitivity, which has been extensively studied in response to Cartesian gratings (Chen et al. 2009; Cloherty and Ibbotson 2015; Crowder et al. 2007; Hietanen et al. 2013; Victor and Purpura 1998; Xu et al. 2005) and is thought to arise due to two distinct mechanisms that are evident to different degrees in different mammalian species. In the cat, phase sensitivity results mainly from subfield segregation of bright and dark responsive patches (Martinez et al. 2005). In the tree shrew, phase sensitivity arises mostly due to a pronounced dominance of neural responses to dark patches (Van Hooser et al. 2013; Veit et al. 2011). Both subfield segregation and dark dominance are closely related to the organization of V1 thalamocortical inputs, which may essentially generate the mRF of V1 neurons (but see also Chisum and Fitzpatrick 2004; Mooser et al. 2004). We thus hypothesized that the polarity sensitivity for hyperbolic gratings might result from a close correspondence between the mRF substructure and these grating stimuli. This was indeed the case, such that RF reconstructions using hyperbolic gratings provided the best approximation of ON and OFF subfields estimated using sparse noise. This suggests that hyperbolic gratings, similar to sparse noise, tend to activate mostly thalamocortical inputs to V1, and these signals are not strongly elaborated in the cortex, in contrast to Cartesian and also polar gratings. Consistent with this is our finding that polarity sensitivity is most pronounced when stimuli are confined to the mRF, without substantial stimulation of the contextual surround.

Our study is the first to report the tuning of the VEP to the three grating classes. We observed that VEP tuning was most robust for Cartesian gratings, in general similarity to spiking responses. Because the VEP is generated by pooled synaptic activity of neurons within a few hundred micrometers of the recording site (Katzner et al. 2009; Rainer 2014; Xing et al. 2009), we consider this similar tuning to result from columnar organization for orientation that is present in tree shrew V1, which has a spatial extent of about 300 μm (Bosking et al. 1997; Huang et al. 2014; Mooser et al. 2004). Consistent with the hypothesis is our finding that VEP selectivity decreases from V1 to V2, in line with the fact that orientation columns in V2 tend to be larger and less homogenous than in V1 (McLoughlin and Schiessl 2006). Notably, despite these similarities between spiking and VEP, there are also several differences in tuning properties between these signals in V1 and V2 when grating spatial frequency is considered: at high spatial frequency, Cartesian grating spiking selectivity was similar in V1 and V2, but VEPs were reduced in V2 compared with V1, and similarly, spiking selectivity for polar gratings was enhanced in V2 compared with V1, whereas the VEP was not different. These differences suggest that V2 VEPs less faithfully reflect the activity of the underlying neuronal population than is the case in V1.

Our study is the first to report detailed information on contextual modulation in the tree shrew early visual cortex using a comprehensive set of two-dimensional patterned grating stimuli. Tree shrew V1 displays a high incidence of length summation when studied using elongated bars (Chisum and Fitzpatrick 2004; Chisum et al. 2003) such that these neurons tend to show little end-stopping, but rather firing rates continue to increase with the length of the elongated bar. Our finding that stimulation of the RF surround enhancement outweighed suppression in response to Cartesian gratings is consistent with these previous findings. Importantly, the enhancement in neural activity by surround stimulation was accompanied by an increase in stimulus selectivity, which was not observed in a recent experiment using optogenetic activation of iso-orientation domains in tree shrew V1 (Huang et al. 2014). The restricted activation to supragranular layers or other differences between optogenetic activation and visually evoked neural activity, such as the absence of neural modulation of cortical activity for nonpreferred columns, may explain these divergent results. The absence of activity enhancement for polar and hyperbolic grating conditions certainly emphasizes that the enhanced V1 activity and selectivity are highly specific for elongated bar or grating structures and do not occur for other kinds of surround activation. The dominance of surround enhancement in tree shrew V1 can be directly compared with the findings of studies in other mammalian species in which Cartesian gratings have been employed, where surround suppression dominates contextual effects, particularly in the monkey and cat with prevalence ranges from 65% to 89% (Cavanaugh et al. 2002; Gieselmann and Thiele 2008; Sceniak et al. 2001) and 56% to 77% (Liu et al. 2011; Song and Li 2008; Walker et al. 2000), respectively. With respect to surround suppression, tree shrew V1 may in fact be more similar to mouse V1, where one study has reported only 16% of neurons robustly suppressed (Van den Bergh et al. 2010), similar to the 19% suppression we observed in the present study. However, note that other work in the mouse has reported a higher incidence of surround suppression that is more in line with the species mentioned above, with the discrepancy possibly resulting from effects related to behavioral state or depth of anesthesia (Self et al. 2014; Vaiceliunaite et al. 2013). Although surround suppression has been associated with several functional benefits, including optimization of information transmission and sharpening of neural selectivity (Hallum and Movshon 2014; Okamoto et al. 2009; Osaki et al. 2011; Vinje and Gallant 2002), the benefits of an excitatory surround are less obvious. We speculate that the contextual modulation observed in tree shrew V1 is optimized for the detection of collinear elongated structures, which may be useful for navigation in this particularly fast-moving mammal (Emmons 2000).

GRANTS

This work was supported by Swiss National Science Foundation Grants 31003A_143390/1 and PDFMP3_131786_1.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

J.P., P.D.L., and G.R. conception and design of research; J.P. and P.D.L. performed experiments; J.P., P.D.L., and G.R. analyzed data; J.P., P.D.L., and G.R. interpreted results of experiments; J.P. and P.D.L. prepared figures; J.P., P.D.L., and G.R. drafted manuscript; J.P., P.D.L., and G.R. edited and revised manuscript; J.P., P.D.L., and G.R. approved final version of manuscript.