Primary motor cortex neurons classified in a postural task predict muscle activation patterns in a reaching task

Abstract

Primary motor cortex (M1) activity correlates with many motor variables, making it difficult to demonstrate how it participates in motor control. We developed a two-stage process to separate the process of classifying the motor field of M1 neurons from the process of predicting the spatiotemporal patterns of its motor field during reaching. We tested our approach with a neural network model that controlled a two-joint arm to show the statistical relationship between network connectivity and neural activity across different motor tasks. In rhesus monkeys, M1 neurons classified by this method showed preferred reaching directions similar to their associated muscle groups. Importantly, the neural population signals predicted the spatiotemporal dynamics of their associated muscle groups, although a subgroup of atypical neurons reversed their directional preference, suggesting a selective role in antagonist control. These results highlight that M1 provides important details on the spatiotemporal patterns of muscle activity during motor skills such as reaching.

the motor system precisely controls the activity of muscles to generate smooth and accurate motor actions. For example, goal-directed reaching involves agonist muscle activity to propel the hand toward the goal and antagonistic muscle activity to decelerate and stop at the goal (Flanders et al. 1994; Marsden et al. 1983; Wierzbicka et al. 1986). The selection, onset time, and magnitude of muscle activity during reaching depend on many factors such as target and initial limb position, arm geometry, and external loads (Caminiti et al. 1990; Hong et al. 1994; Karst and Hasan 1991; Scott 1997).

Primary motor cortex (M1) plays an important role in voluntary motor functions such as reaching, but its specific role remains debated. The classic dichotomy is whether its activity reflects muscles or movements (Phillips 1975). The latter suggests that M1's contribution is to define behavioral goals (e.g., direction and extent of movements), leaving subcortical and spinal structures as the primary source for generating spatiotemporal patterns of muscle activity (Georgopoulos 1995; Raphael et al. 2010). Indeed, many studies have shown that M1 activity correlates with many high-level parameters such as direction of hand motion (Georgopoulos et al. 1982; Philip et al. 2013; Toxopeus et al. 2011), hand movement speed (Schwartz 1993), and target direction and speed (Johnson et al. 1999).

The other end of the spectrum is the view that M1 directly generates spatiotemporal patterns of muscle activity for goal-directed movements (Bennett and Lemon 1994; Cherian et al. 2013; Scott 1997, 2003). Although the exact patterns of muscle activity for limb movement are only specified at the spinal level, as spinal afferent feedback will influence motor output, the idea is that basic features such as the selection, timing, and magnitude of muscle activity are specified by neurons in M1. Indeed, several studies have quantified how M1 activity correlates with the activity of hand and wrist muscles (Bennett and Lemon 1996; Evarts 1968; Humphrey 1972; Kakei et al. 1999; Oby et al. 2013) or proximal arm muscles (Cherian et al. 2013; Murphy et al. 1985; Scott 1997; Sergio and Kalaska 2003; Todorov 2000).

The lack of strong causal evidence for one of these options indicates that identifying a simple correlation is not sufficient to identify the role of M1 in voluntary motor control. There are many different patterns of muscle and neural activity, and finding arbitrary correlations is relatively easy (Humphrey 1972). One way to circumvent this problem is to dissociate different movement parameters, such as by making movements with different torques or arm configurations (Cherian et al. 2013; Fromm and Evarts 1977; Kakei et al. 1999; Scott and Kalaska 1997; Sergio and Kalaska 2003). Inevitably, these studies identify that some neuronal activity in M1 can reflect many different features of motor actions. However, the presence of some high-level information in M1 does not preclude its role in specifying spatiotemporal patterns of muscle activity.

Better support for a role in generating patterns of muscle activity is separation of the process for identifying the portion of the motor periphery associated with a given neuron—its motor field—from the process of relating its spatiotemporal activity to muscles in that motor field. A similar concept is the sensory field of a neuron, which is the portion of the periphery to which applying stimuli elicits firing. Identifying a sensory field is relatively straightforward as it requires one to simply apply or present a controlled stimuli. It is less clear how to define motor fields.

The synaptic connectivity of neurons that project to proximal limb motor neuron pools can be roughly identified by spike-triggered averaging (STA) (Cheney and Fetz 1980, 1985; Fetz and Cheney 1978; Kasser and Cheney 1985; McKiernan et al. 1998). However, the variability in STA timing, and the inability to record from all muscles at once, make it very difficult to describe a complete connectivity mapping from STA connectivity. If the scope of investigation is limited to monosynaptically connected corticomotoneurons (CM cells), the proximal limb has reduced CM cell representation compared with the distal limb (Buys et al. 1986; Palmer and Ashby 1992) and CM cell distribution is limited to the caudal (new) section of M1 (Rathelot and Strick 2009). Intracortical microstimulation can be used to identify muscle connectivity by repeated stimulation and stimulus-triggered averaging (Buys et al. 1986; Cheney and Fetz 1985); however, this technique does not guarantee single-neuron activation. Cheney and Fetz (1985) and Lemon et al. (1987) show increased muscle activity for increased stimulation current and conclude that stimulation likely activates multiple neurons in proximity.

The present study used two different behavioral tasks to separate the process for identifying a neuron's motor field from the process of comparing spatiotemporal patterns of activity between neurons and muscles. First, the motor fields of M1 neurons and limb muscles were identified on the basis of their load preference with a posture task consisting of combinations of shoulder and elbow flexion or extension torques (Fig. 1A). A neural network model that we used to drive our predictions (Lillicrap and Scott 2013) highlighted that the torque preference of the model's “cortical” units correlated with the torque preference of their synaptically associated muscle groups. The model predicted that neurons with similar motor fields—defined by the posture task—would show correlated directional preferences in a reaching task. We tested this prediction by examining the directional preferences of monkey M1 neurons during center-out reaching to a range of peripheral targets (Fig. 1B). Consistent with our model, we found that the activity of each neuronal population predicted the spatiotemporal patterns of their respective muscle groups. Interestingly, a small subset of the neurons in each group possessed directional preferences during reaching that were opposite to that observed for its associated muscle group. These atypical neurons may be indicative of selective control when the muscle acts as an antagonist during motor skills.

Fig. 1.

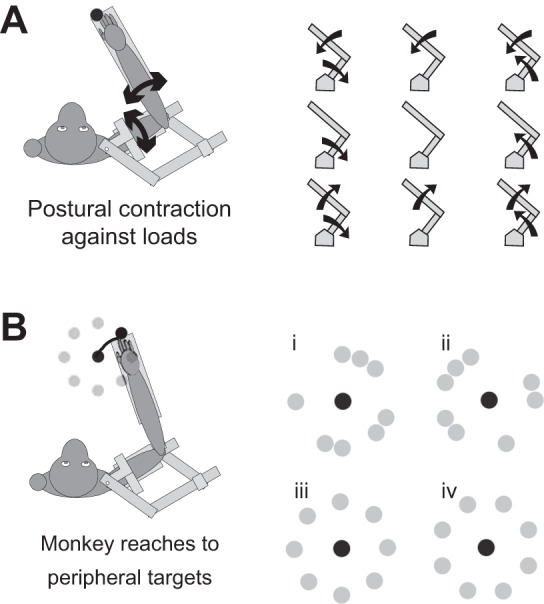
Experimental posture and reaching tasks. A: in the posture task, the monkey was required to maintain its hand at a central target while flexion and/or extension torques were applied at the elbow and shoulder. Right: the 8 combinations of torques and an unloaded condition. B: in the reaching task, relatively fast reaches were made from a central origin to 8 peripheral targets. i–iv: the 4 different combinations of targets used in the data sets.

EXPERIMENTAL PROCEDURES

Subjects and Apparatus

Five male rhesus monkeys (Macaca mulatta, 6–12 kg, monkeys A–E) were trained to perform reaching and posture tasks while attached to a robotic upper limb exoskeleton (KINARM; BKIN Technologies, Kingston, ON, Canada). This exoskeleton maintained the arm in a horizontal plane at shoulder height, permitting motion at the shoulder and elbow and allowing mechanical torques to be applied at either joint (Scott 1999). Targets and a dot representing hand feedback location were presented in the plane of the arm via reflection in semitransparent glass. These experiments were conducted in accordance with protocols reviewed and approved by the Queen's University Animal Care Committee.

Behavioral Tasks

Posture task.

This task has been described previously (Cabel et al. 2001; Herter et al. 2007). In each trial, a constant torque was applied to the elbow and/or shoulder. The monkey then stabilized the hand within a central 0.8-cm-wide stationary target for at least 3 s. Nine constant torques were used, consisting of elbow flexion (EF) or extension (EE), shoulder flexion (SF) or extension (SE), four multijoint torques (SF+EF, SF+EE, SE+EF, SE+EE), and an unloaded condition (Fig. 1A). Torques of magnitude 0.12 Nm were used for monkeys A–C and E and torques of magnitude 0.32 Nm for monkey D. Five blocks were presented, each containing the nine load conditions in random order, for a total of 45 trials.

Reaching task.

This task has been described previously (Kurtzer et al. 2006b). Monkeys began each trial by maintaining their index finger (white dot) within a central start target (8-mm radius). This start target was positioned such that the shoulder and elbow were at approximately 30° and 90°, respectively. After a random time period (1.5–2.0 s), a peripheral target (12-mm radius) then illuminated 6 cm from the central target. The monkey then moved between the start and peripheral targets in 220–350 ms, generating total reach times of ∼500–600 ms when including intratarget acceleration and deceleration. Eight such peripheral targets were located around the start target. For monkeys A and B, these were distributed such that they were roughly distributed uniformly in torque space in two arrangements (Fig. 1B, i and ii). For monkeys C–E, the targets were uniformly distributed in Cartesian space in two arrangements (Fig. 1B, iii and iv). In monkey D, some trials were also performed with 3-cm reaches (target pattern not shown). Five blocks were presented, each containing the eight reach directions in random order, for a total of 40 trials.

Data Collection

Neuronal recordings were obtained from the elbow/shoulder region of M1, contralateral to the arm used to perform the behavioral tasks, with standard recording techniques (Scott et al. 2001; Scott and Kalaska 1997). Activity of these neurons was recorded during both the reaching and posture tasks.

We examined the activity of elbow and shoulder flexor and extensor muscles by electromyography (EMG) during the posture and reaching tasks. In most cases, we recorded through a pair of percutaneous Teflon-coated 50-μm stainless steel wires with standard recording techniques (Scott and Kalaska 1997). In monkeys A and C, we recorded some muscle activity from chronically implanted bipolar multistrand electrodes (Kurtzer et al. 2006b; Scott and Kalaska 1997). Chronic electrode recordings were only selected if they occurred more than a week apart, to minimize redundant data. Recordings were taken from biceps (12 percutaneous, 13 chronic), brachioradialis (7, 11), brachialis (6, 6), long head triceps (5, 19), posterior deltoid (8, 10), lateral triceps (8, 3), middle triceps (2, 0), anterior deltoid (3, 11), and pectoralis major (6, 6). To ensure that the percutaneous recordings were not being skewed by the chronic recordings, we compared the mean preferred torque direction (PTD; described in Data Analysis) between percutaneous and chronic recordings across muscles and found no difference (paired t-test, t₈ = 0.02, P = 0.98), while the average variance in PTD was lower for chronic (3.4°) than percutaneous (7.0°) recordings.

Joint kinematic data and EMG were recorded at 1 kHz (monkeys A–C) or 4 kHz (monkeys D and E). Neuronal firing was binned into 5-ms bins, and EMG and kinematic data were downsampled to 200 Hz for data storage.

Data Analysis

Preferred torque direction.

Combinations of shoulder and elbow torques were described in torque space, where shoulder torque was represented along the x-axis and elbow torque was represented along the y-axis. Positive torque, in each axis, was defined as flexor torque to oppose joint-extending applied torques, so that shoulder flexor torque was at 0°, elbow extensor at 90°, shoulder extensor at 180°, and elbow extensor at 270°. A plane was fit to EMG activity or cell firing rate associated with the elbow/shoulder torque in this space. We used only the EMG activity or cell firing in the last 2 s of hold time to ensure that recordings were from a period of stationary posture. If the plane had a statistically significant slope, the angle of maximal slope was defined as the torque that elicited either a muscle's maximal activation or a neuron's maximal firing rate. This PTD was measured counterclockwise from shoulder flexion.

Preferred reaching direction.

A given reach movement was assigned a reach direction in Cartesian space, increasing counterclockwise from the positive x-axis. It was calculated by the angle from the origin to the hand position at maximal tangential velocity. EMG activity and neuronal firing rate were integrated around (−50 ms to 150 ms) movement onset, which was defined as the time when the hand first attained 5% of maximum hand speed. This activity was fit to a plane based on the angle of each reach and the activity during each reach. If the plane had significant slope, the preferred reaching direction (PRD) was defined as the angle that had maximal slope on the plane. It described the maximum spatial modulation of either a muscle's activation or a neuron's firing rate.

Spatiotemporal dynamics of reaching.

Activities in each trial were aligned temporally on the calculated reach onset time. Baseline activity was removed by calculating the mean activity of each neuron or muscle recording during the initial hold period over all trials and subtracted from all trials for that recording. Activity for each muscle or neuron was then divided by the maximum activity across reaching directions for that recording. Data were smoothed with a Gaussian kernel with a 5-ms standard deviation.

Modeling

To predict the responses of a neural system with defined motor fields, we implemented a static neural network model similar to that developed by Lillicrap and Scott (2013). The model consisted of a vector of “cortical” units, z, which controlled six muscle groups, u, controlling a two-joint arm in the horizontal plane via linear output weights, w (Fig. 2A). Muscle activity was kept positive via the standard sigmoid—that is, u = σ(w·z). Modeled muscle activity generated torques and hand velocities via a function that approximated the biomechanics of a two-joint revolute arm constrained to move in the horizontal plane. This function was computed by linearizing a dynamic model that included limb geometry, intersegmental dynamics, and mono- and biarticular muscles with force generation dependent on length and velocity. Muscle tension forces, t, are obtained by elementwise multiplication of muscle activity with linearized F-L/V scaling factors appropriate for the movement direction, i.e., t = H·u. Joint torques are computed via τ = Mt, and hand velocity is determined by the linear transformation, y = GFτ, where F and G are local linear approximations to limb dynamics and the geometric mapping between joint and hand velocity, respectively. This static model was derived as a simplified version of a dynamic model that executed reaching movements over a sequence of time steps and in which the network model was connected in closed loop with the arm. One of the findings of this previous work was that a static model based on a linearization of the dynamic version captured the most salient features of the population neural activity (Lillicrap and Scott 2013). The static version also has the benefit of being easier to optimize, analyze, and understand. Parameters for the limb biomechanics were derived from published work on monkey limb and muscle characteristics (Cheng and Scott 2000; Graham and Scott 2003; Singh et al. 2002).

Fig. 2.

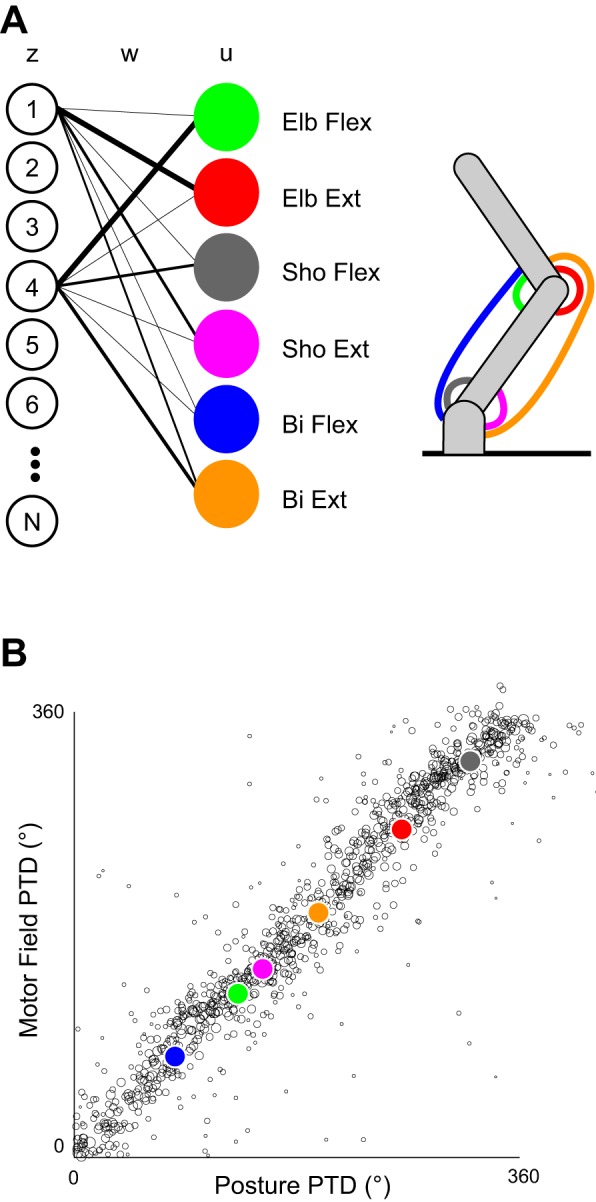
Predictions from the static neural network model. A: representative schematic of 1 of the models. Two network units, z, are shown connected to muscle outputs, u, via random weightings, w, shown by the thickness of the lines. The output variables, u, drove mono- and biarticular muscles on a 2-joint arm, as shown. The values of the units in z were optimized to solve analogs of the reaching and posture tasks. B: the relationship between each unit's preferred torque direction (PTD) in the posture task and the calculated PTD of its motor field (defined by synaptic connectivity) in 1 network of 1,000 units. The size of the circle for each unit corresponds to its strength of tuning. Note that the muscles, plotted here for reference, must lie on the diagonal as they correspond with their own motor field.

We optimized z to solve analogs of the posture and reach tasks while keeping the square of the neural and muscle activities small. For the reaching task, the model captures movement initiation. In this case z* is found by minimizing the difference between target and actual hand velocity for a given movement, e = ẏ_target − ẏ, while keeping unit and muscle activity small, that is, z* = argmin_z = ||ẏ − ẏ_target|| + α||u|| + β||z||. For the posture task, the model captures the steady-state condition during which the joint torques are countered and the arm is at zero velocity. In this case z* is found by minimizing the difference between applied and actual joint torques, e = τ_target − τ, while keeping unit and muscle activity small, that is, z* = argmin_z = ||τ − τ_applied|| + α||u|| + β||z||. In both cases, α and β are set to 1e-6. Importantly, for a given simulation, the elements of the matrix w were drawn randomly from a normal distribution (σ = 0.05) and were unaltered during optimization. This meant that a given unit maintained the same relative contribution to each muscle at the periphery across tasks. Unit activity was optimized to generate 16 target torques (posture task) and 16 target velocities (reach task)—both equally distributed about the unit circle. In practice, we used a preconditioned conjugate gradient descent (PCG) algorithm with back-tracking line searches to find an optimal vector of activity for a given trial. In line with the analysis of biological data, the activity of z and u across all 16 torques and reach directions were plane fit to determine preferred reach and torque directions.

RESULTS

Neural Network Model: Relation of Torque Preference and Motor Field

We used a static neural network model similar to that developed by Lillicrap and Scott (2013) to examine the relationship between neural connectivity, torque preferences during posture, and directional tuning during reaching. The activation of model cortical units, z, were optimized to generate combinations of elbow and shoulder torque for the posture task and different hand velocities for the reaching task. Although we used a PCG algorithm for the results reported here, the same essential results can be obtained with virtually any gradient-based optimization routine. In particular, we find the same results using a limited-memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) algorithm and stochastic gradient descent (SGD), although SGD takes significantly longer to converge. Given that the optimization we perform is nonlinear and high dimensional, we are not able to find a global minimum. Our results are thus based on local minima—but they are robust minima in the following sense: we repeated the simulation 10 times from random initializations of the synaptic weight matrix and found the same characteristic pattern of PTD/PRD distributions in each case. Thus there appears to be a large family of such minima—all of which produce similar behavioral performance and PTD/PRD distributions.

We compared the torque preference of units in the network to its connectivity to evaluate how well its torque preference estimated its motor field. To quantify torque preference, we fit a plane to the activation of each unit across torque combinations in the two-dimensional (2D) elbow/shoulder torque space. The PTD of a unit was the angle in torque space to which the unit was maximally active. Across simulations, we found that 99.4% of units had a significant (P < 0.01) PTD in the posture task. The distribution of the significant PTDs for one training session can be seen in Fig. 3A. The resulting distribution was bimodal (r = 0.31, P < 0.001), aligned in much the same manner as the previously reported distribution of M1 neurons (Herter et al. 2007; Pruszynski et al. 2014), with the majority of units related to whole-limb flexion or extension.

Fig. 3.

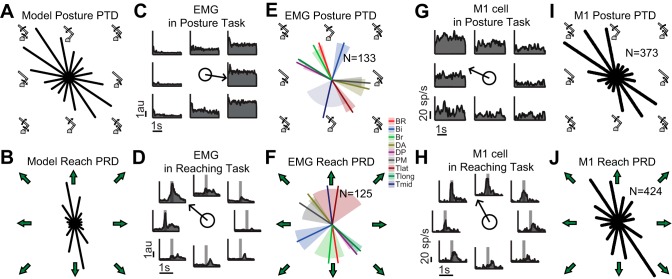
Preferred torque and reaching directions. A: polar histogram of each network unit's PTD in 1 network. Angles are in torque space (shoulder torque x-axis, elbow torque y-axis). B: polar histogram of each network unit's PRD in 1 network. C: exemplar activity of pectoralis major in 8 shoulder/elbow loaded conditions (unloaded condition not shown) during the last 3 s of in the posture task. Arrow in the center denotes the muscle's PTD (351°). au, Arbitrary unit. D: exemplar activity of pectoralis major around reach onset while reaching to the 8 targets (set iii in Fig. 1B). Arrow in the center denotes the muscle's PRD (140°). E and F: averages of the PTD (E) and PRD (F) of all muscle samples are shown with 95% confidence intervals as shaded areas around each line. BR, brachioradialis; Bi, biceps; Br, brachialis; DA, anterior deltoid; DP, posterior deltoid; PM, pectoralis major; Tlat, lateral triceps; Tlong, long head triceps; Tmid, middle triceps. G: activity of an exemplar primary motor cortex (M1) neuron in the 8 shoulder/elbow loaded conditions (unloaded condition not shown) during the last 3 s of in the posture task. Arrow in the center denotes the neuron's PTD (155°). H: activity of an exemplar M1 neuron around reach onset while reaching to the 8 targets (set iii in Fig. 1B). Arrow in the center denotes the neuron's PRD (119°). I and J: polar histograms of all significant PTDs and PRDs across the population of recorded M1 neurons.

In such a straightforward model, one might assume that a given unit would always show an identical relationship between its torque preference and its anatomical connectivity given that the unit can only produce torque in a given direction when activated alone. We calculated the motor field preferred torque direction (MFPTD) of a given unit, z_i, by multiplying its output weights (motor field), w_ij, with the vector of preferred torque direction of each output unit in the posture task, u_j, and then vector summating. It is important to note that the PTD of each output unit is not the simple direction of force production for that unit. Because of the redundant force profiles of the biarticular muscles and the dynamics of the limb the preferred direction of an output unit rotates away from its simple force production direction (Lillicrap and Scott 2013). We found a circular correlation (r = 0.86, P < 0.001) between the unit's MFPTD and its PTD in the posture task (Fig. 2B); however, the relationship was not perfect. To see how different connectivity patterns might be influencing this relationship, we looked at the degree to which a unit coactivated opposite muscle groups together (cocontraction). We normalized each set of weights from a unit to its muscle groups, multiplied these by their respective output unit PTD vectors, and vector averaged them. The length of the resulting vector for each unit was used as an indicator of cocontraction, with a short vector indicating more cocontraction. The average difference between PTD and MFPTD was 22°. Units with low cocontraction (normalized MFPTD vector length > 0.4, 9.1% of units) had an average difference of 7° (r = 0.99), whereas units with high cocontraction (normalized MFPTD vector length < 0.1, 11.7% of units) had an average difference of 62° (r = 0.40). This suggests that the statistical dispersion in the relationship between torque preference and anatomical connectivity is caused by those units with stronger synaptic connections to antagonist muscles.

Neural Network Model: Relation of Torque and Reaching Direction

We used our model to predict the relationship between PTD and reaching activity for units in the neural network model. Reaching activity was described by a PRD—the direction in Cartesian space toward which a reach movement would elicit maximal unit activity. Across all simulations, we found that 98.7% of units had a significant PRD (plane fit P < 0.01). The distribution of significant PRDs for one training session of units can be seen in Fig. 3B. The bimodality (r = 0.52, P < 0.001) toward the top left and bottom right that emerges is stable across simulations. The distribution was consistent for static and dynamic networks (Lillicrap and Scott 2013) and previous observations on M1 neurons (Scott et al. 2001).

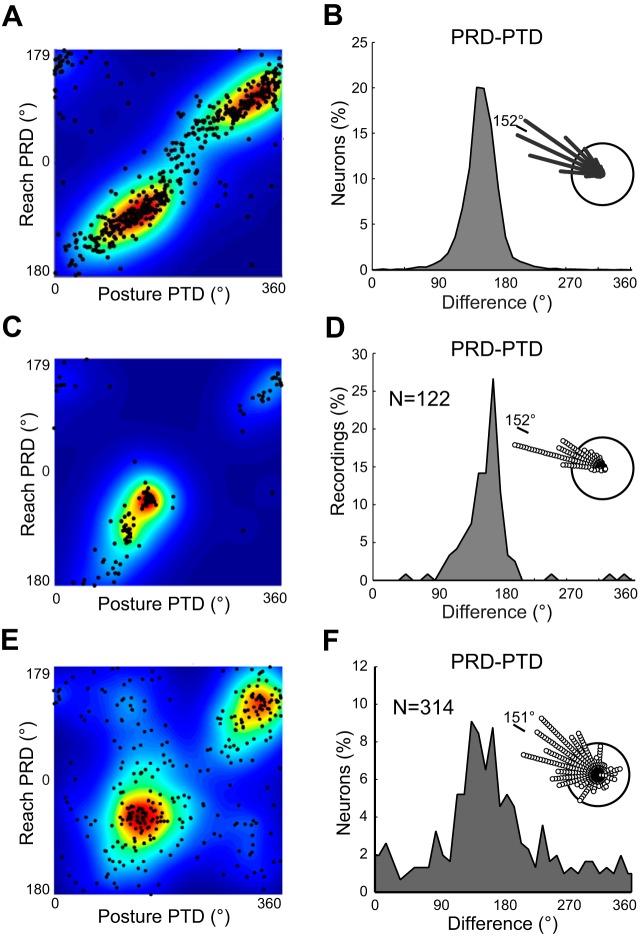
Novel in this study, we compared PTD and PRD for each model unit that had both a significant PTD in the posture task and a significant PRD in the reaching task (98.1%). As can be seen in Fig. 4A, there is a consistent relationship between the PTDs and PRDs, where two clusters emerge because of the interaction of the bimodalities noted in each distribution. Figure 4B displays a histogram of the difference of PTD and PRD angles for all units, with the presence of a mean systematic shift of 152° (circular correlation, r = 0.84, P < 0.001). This angle roughly corresponds to the shift in coordinate frames between torque and hand space, used to define unit responses in the posture and reaching tasks, respectively. This rotational shift was stable across all 10 simulation sets (150–154°, circular SD = 1.2°), indicating that the result is robust. There was some dispersion in the relationship between a unit's PTD and PRD (circular SD = 27°). Even though individual units had different PRD and PTD tuning across simulations, both the population distribution and the relation between a given unit's PTD and PRD remained statistically the same.

Fig. 4.

Relationship between PTD and PRD (directional preferences must be significant in both tasks) for network units, muscles, and M1 neurons. A: scatter relationship for network units. B: histogram of the difference between PTD and PRD for network units. Inset: polar plot. C: scatter relationship for muscle recordings. D: histogram of the difference between PTD and PRD for muscle recordings. E: scatter relationship for M1 neuron recordings. F: histogram of the difference between PTD and PRD for M1 neuron recordings.

Nonhuman Primate Recordings: Muscle Recordings

We recorded and analyzed the EMG activity of nine muscles spanning the shoulder and/or elbow (151 suitable recordings) in five macaque monkeys in posture and reaching tasks. In the posture task, a monkey's arm was maintained in the horizontal plane while combinations of flexor and/or extensor step torques were applied to the shoulder and/or elbow (Fig. 1A). Recordings were made while the monkey held its hand stationary at a central position and countered these torques. Figure 3C shows an example of pectoralis major activity during the posture task. As previously reported (Kurtzer et al. 2006a), this shoulder flexor modulated its activity for torques applied at the elbow in addition to loads at the shoulder, and as a result the PTD for this muscle did not lie at the shoulder flexion (i.e., 0°) line, as one would expect if the muscle activity reflected its anatomical action. Shifts across all muscles (Fig. 3E) showed stereotypical clustering of preferred torque directions—one in the elbow-extension/shoulder-flexion quadrant and the other in the elbow-flexion/shoulder-extension quadrant (Kurtzer et al. 2006a).

In the reaching task, the monkeys made fast center-out reaches to peripheral targets arranged around the starting position (Fig. 1B). Figure 3D shows an example of pectoralis major muscle activity during reaching. Maximal activity in the example was observed toward the top left target, reflecting the need for a large shoulder flexor torque to accelerate the arm toward that target (Graham et al. 2003). In the bottom right direction, an activity peak can be seen ∼200 ms later related to an antagonist burst to decelerate the arm. EMG activity was integrated over a 200-ms period starting 150 ms before movement onset (Fig. 3D, gray bar), to capture the activity associated with initial acceleration. Across all muscles, PRDs (128 significant muscle samples) were skewed toward one of two directions (Fig. 3F), one centered around 110° and one around 280° (Kurtzer et al. 2006a).

As with the novel model analysis, we compared PTD and PRD for each muscle that had both a significant PTD in the posture task and a significant PRD in the reaching task (n = 122). A strong consistent relationship between the PTDs and PRDs can be seen in Fig. 4C, where two clusters emerge: one (bottom left cluster) that includes the shoulder extensors, the elbow flexors, and all biarticulars and the other (top right) that includes the elbow extensors and shoulder flexors. Figure 4D displays a histogram of the difference of PTD and PRD angles for all muscles. There is a systematic shift of 152° (circular r = 0.87, P < 0.001), very similar to that obtained for the network model.

Monkey M1 Recordings

We recorded and analyzed the activity of 540 M1 neurons in five monkeys in the posture and reaching tasks, with the same epochs as for muscle activity. Of these, 373 showed a significant PTD in the posture task (example neuron in Fig. 3G) and 424 M1 neurons showed a significant PRD during the reaching task (example neuron in Fig. 3H). As seen in Fig. 3, I and J, the distributions of PTDs and PRDs for all M1 neurons showed stereotypical bimodalities as have been reported previously (Kurtzer et al. 2006a; Scott et al. 2001).

As with muscles, we compared PTD and PRD for each neuron that had both a significant PTD and a significant PRD (n = 314). Figure 4E shows two distinct clusters when comparing the PTD and PRD of M1 neurons: one cluster with a PRD at 301° and a PTD at 140° (bottom left cluster) and another cluster with a PRD at 123° and a PTD at 325°. The relation between the two preferred directions of M1 neurons is clearly shown in Fig. 4F as a 151° shift (circular r = 0.43, P < 0.001) between PRD and PTD. Cluster locations were maxima of cell preferred directions convolved with a 2D windowed Gaussian distribution (σ = 10°). This shift and clustering is very similar to both the units of the network model and the muscle recordings. Unlike the muscles and network model, a notable portion of M1 neurons show PTD-PRD differences not located near the diagonal of the plot. The result is a relatively low PTD-PRD correlation (r = 0.43 cells, 0.84 model, 0.87 muscles) and large variance in their shift values (circular SD = 61° cells, 27° model, 24° muscles). We estimated whether these variances were significantly different by sampling the PTD-PRD difference values with replacement to create distributions of variances. The distribution of PTD-PRD variance for neurons had no overlap with either muscle or model distributions. The muscle and model distributions of variance shared a 30% overlap.

Prediction of Patterns of Muscle Activity from M1 Population Signals

Our first step to predict muscle activity during reaching was to classify the M1 neurons based on their similarity to muscle groups during a postural load task. Figure 5 highlights the distribution of PTDs of muscle for shoulder and elbow muscles. We defined four ranges in torque space representing flexors and extensors at each joint: elbow flexors (90° to 135°), shoulder extensors (135° to 180°), elbow extensors (270° to 315°), and shoulder flexors (315° to 360°). The four torque groups captured 75% of motor cortical neurons: 55 neurons were classified as elbow flexor neurons, 71 as shoulder extensor neurons, 54 as elbow extensor neurons, and 68 shoulder flexor neurons. When applied to our network model, these groupings captured 60.8% of units, with 14.5–15.6% of units in each group.

Fig. 5.

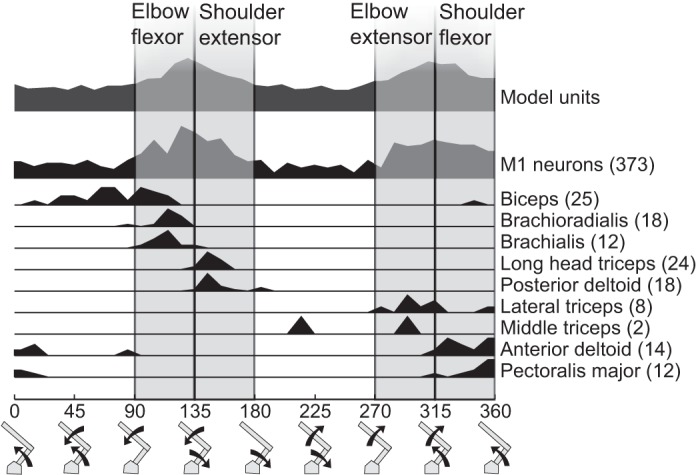
Distribution of load preferences for M1 neurons and individual muscles. The number of recordings for each muscle is indicated in parentheses beside the muscle name. The 4 assigned motor fields are shown as vertical shaded stripes with their titles marked at top.

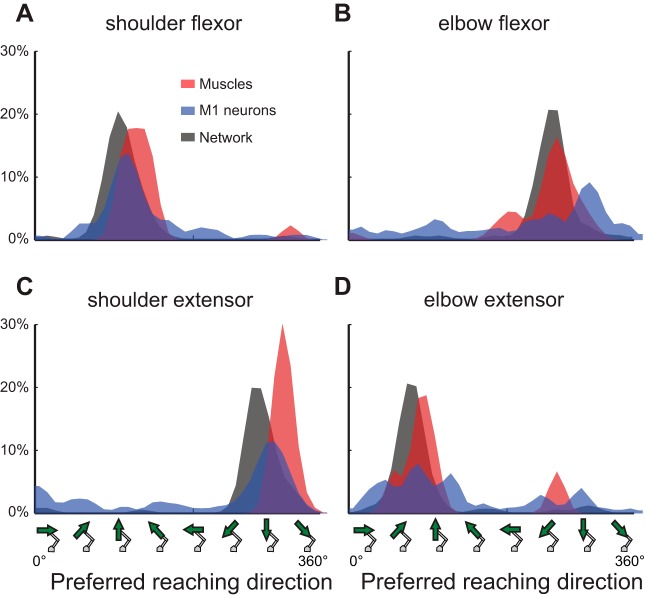
Figure 6 displays the distribution of PRDs for each muscle group, the associated M1 neurons, and associated network units. Note that these distributions represent vertical slices, 45° thick, of the PRD-PTD relationship shown in Fig. 4E. The PRD distributions for each group of muscles were unimodal, with shoulder flexors preferring 134° (r = 0.85, P < 0.001), elbow flexors preferring 261° (r = 0.83, P < 0.001), shoulder extensors preferring 317° (r = 0.99, P < 0.001), and elbow extensors preferring 98° (r = 0.63, P = 0.03). Dispersion was relatively small for each muscle group, illustrating that muscles within a group had similar reaching preferences.

Fig. 6.

Distribution of PRD for each muscle group and assigned M1 neurons and network units. Each distribution is normalized as % of the total number of significant PRDs. x-Axis starts at rightward reach (0°) and increases counterclockwise.

Each group of M1 neurons showed a significant unimodal distribution of PRDs, nearly identical to that of their comparative muscle group (Fig. 6). Shoulder flexor neurons showed a PRD of 128° (r = 0.66, P < 0.001), elbow flexor neurons showed a PRD of 293° (r = 0.32, P < 0.001), shoulder extensor neurons showed a PRD of 313° (r = 0.48, P < 0.001), and elbow extensor neurons showed a PRD of 95° (r = 0.35, P = 0.002). M1 neurons associated with each muscle group showed a much greater range of PRDs. Watson-Williams tests between muscles and cells showed no difference in means, except a small (33.8°) but significant difference for elbow flexors (SF: F_1,72 = 0.02, P = 0.65; EF: F_1,102 = 5.12, P = 0.03; SE: F_1,101 = 0.13, P = 0.71; EE: F_1,55 = 0.01 P = 0.92).

The torque groupings were also used to classify neural network units in a similar fashion (Fig. 6). Shoulder flexor units showed a PRD of 119° (r = 0.92, P < 0.001), elbow flexor units showed a PRD of 269° (r = 0.88, P < 0.001), shoulder extensor units showed a PRD of 298° (r = 0.91, P < 0.001), and elbow extensor units showed a PRD of 89° (r = 0.89, P < 0.001). As the neural network units followed the same pattern as both muscles and M1 neurons in distribution, it was not surprising that each torque-based group also had close overlap with the PRD of both M1 neurons and muscles.

Musclelike Spatiotemporal Dynamics

While predicting the agonist burst activity of the spatiotemporal activity was a first step, we further examined whether M1 neurons could predict the full temporal pattern of shoulder and elbow muscle activity across directions during reaching. We evaluated the population activity of each group of M1 neurons over time and compared this to the activity of each group of muscles.

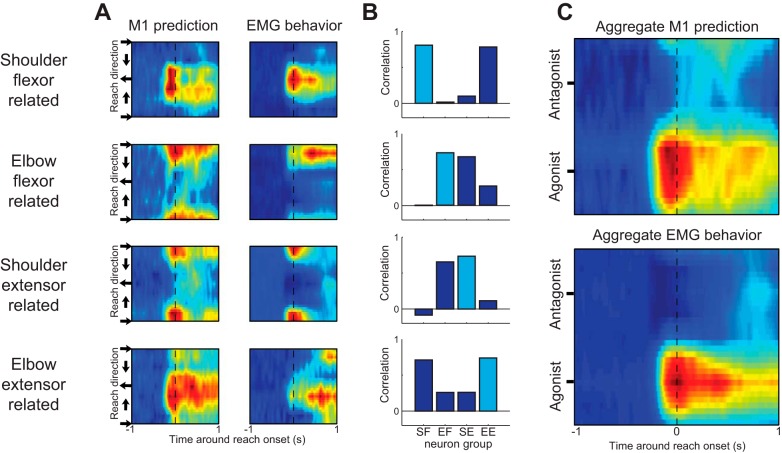
Illustrations of normalized population activity over time and across reach direction for each group of M1 neurons can be seen in Fig. 7A. Clear maxima of activity emerge prior to reach onset in a primary direction for each group. Given that PRD was determined by the epoch of time around reach onset, it is not a surprise that these maxima align with the PRD of each torque-classified group. Qualitatively, the overall patterns of activity are similar between M1 and their corresponding muscle groups. Given that each group seemed to have a similar profile of activity across time but for different reach directions, we computed 2D correlations between each M1 group and all muscle groups (Fig. 7B) and found high degrees of correlation (shoulder flexor r = 0.82, elbow flexor r = 0.74, shoulder extensor r = 0.74, elbow extensor r = 0.75). Each muscle group's spatiotemporal activity was predicted best by its respective M1 neuronal group, with latencies of maximal correlation that show M1 activity precedes muscle activity (shoulder flexor −30 ms, elbow flexor −70 ms, shoulder extensor −30 ms, elbow extensor −65 ms). Figure 7C displays the aggregate of all four groups, highlighting how specific shifts in the timing and magnitude of agonist muscle activity before movement are preceded (average latency −35 ms) by similar spatiotemporal patterns in M1 (Scott 1997).

Fig. 7.

Spatiotemporal dynamics of muscle groups and associated M1 neuron populations during reaching. A: color maps of the aggregate activity over time (x-axis) and across reach direction (y-axis) of each muscle group and associated population of M1 neurons. Data are smoothed in the y-axis for display purposes. B: 2-dimensional correlation coefficients between the spatiotemporal patterns of muscle and neuron groups. Each graph is 1 muscle group, and the bars show the coefficients between that muscle's spatiotemporal pattern and the pattern of the 4 populations of M1 neurons. C: aggregate activity of all neurons and all muscles were generated by rotating the y-axis of each group so that their directions of maximal agonist activity were aligned with the agonist direction and then averaged.

We also investigated the spatiotemporal output of the subset of M1 neurons that appeared to have an atypical, opposing PRD-PTD relationship. We decomposed the aggregate M1 activity by selecting neurons that were within 30° of the expected relationship (around the 151° PRD-PTD) and those that were opposite to these. As can be seen in Fig. 8, A and B, respectively, both sets of neurons seemed to have bursts of activity; however, the atypical M1 neurons had later temporal characteristics for their burst (Fig. 8C), which occurred in the opposite reaching direction. A cross-correlation of the maximum aggregate activity showed that the atypical activity burst occurred 50 ms later than the typical agonist burst. Interestingly, the atypical neurons' agonist-direction activity appeared to be larger with a longer duration than the regular population's antagonist-direction activity, lasting well after the reaching movement was completed. Thus across the population, the preferred direction of these atypical cells was aligned with its motor field after movement when maintaining the hand at the peripheral target.

Fig. 8.

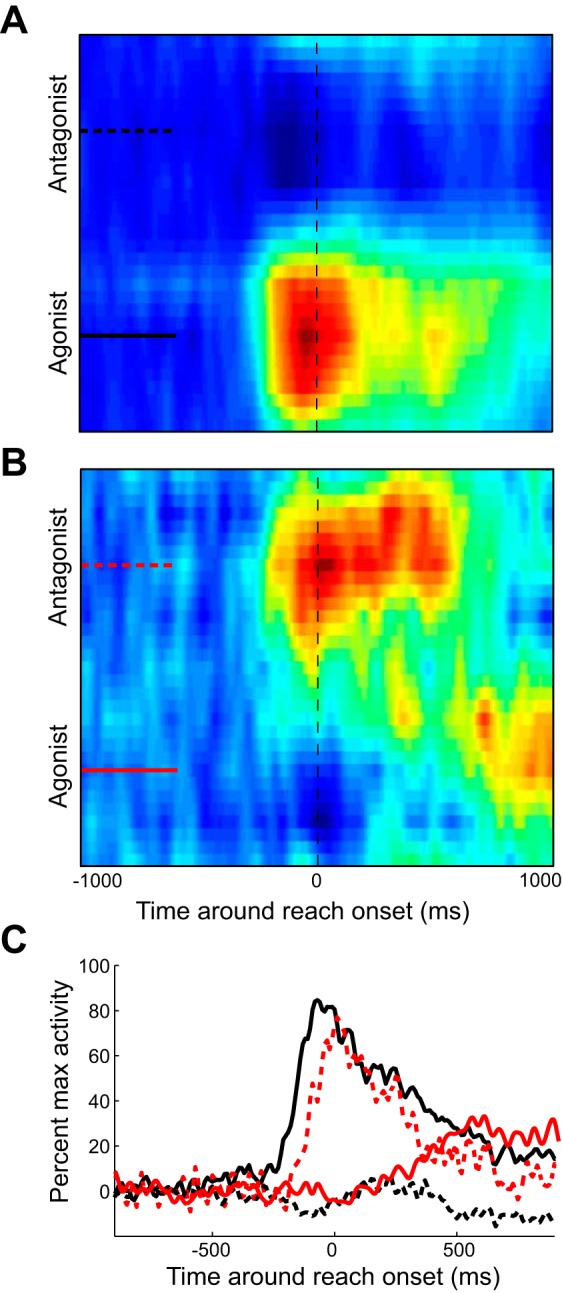
Aggregate spatiotemporal color maps of M1 neurons that have similar and opposing PRDs compared with their associated muscle group. A: color map of population activity of all neurons whose PRD was within 30° of its assigned muscle group (typical neurons). Aggregate of neural activity was rotated as in Fig. 7. B: color map of population activity of all neurons whose PRD was >150° away from that of its assigned muscle group (atypical neurons). C: spatiotemporal pattern of activation for typical (black lines) and atypical (red lines) neurons when the muscle group acts as an agonist (solid lines) or an antagonist (dashed lines).

DISCUSSION

Several studies have shown correlations between M1 activity and EMG in monkeys (Bennett and Lemon 1996; Evarts 1968; Fetz et al. 1989; Humphrey 1972) and cats (Drew 1993; Drew et al. 2002). However, given the diversity of EMG activity across muscles during a motor action, one can likely find that a neuron's activity will correlate with at least one of them. Here we show that these correlations remain when classification and prediction are separated. We classified M1 neurons into one of four distinct motor fields (elbow flexor, elbow extensor, shoulder flexor, and shoulder extensor), using a static load task. We then generated a population signal from each group and predicted the spatiotemporal activity of the corresponding muscle during a dynamic reaching task. The preferred direction of most neurons matched the directional preference of muscles with the same motor field. Interestingly, a small proportion of neurons had preferences in the opposite direction.

A receptive field of a sensory neuron can be defined as the part of the body to which a stimulus elicits activity by this neuron. These can be easily defined by repeated application of stimuli and finding the parts of the body to which firing of a neuron correlates. It is implicitly assumed from this that a neuron that fires in relation to a stimulus is caused by that stimulus. A related concept is a motor field, which can be defined as the portion of the body associated with a given motor-related neuron. While the target innervation, or muscle field, of some neurons, such as CM cells, can be identified by STA of EMG (Cheney and Fetz 1980, 1985), this does not necessarily define the portions of the body to which the neuron fires. Even when limiting to CM cells that have monosynaptic connections to motoneuron pools, Griffin et al. (2015) showed how directional tuning, or motor field, of some CM cells does not necessarily align with the muscle field, or connectivity. As well, CM cells represent only a small fraction of corticospinal neurons that predominantly target the distal musculature in primates (Buys et al. 1986; Palmer and Ashby 1992) and are localized mainly in the caudal portion of M1 or “new M1” (Rathelot and Strick 2009). More directly, a motor field can be defined on the basis of whether a neuron is active when the animal performs a motor action with a given body part, as we have done in the present study. However, unlike sensory fields, it is not necessarily true that there is a causal link between the neuron's activity (motor field) and motor output of that body part.

We examined this relationship using a relatively complex artificial neural network with 1,000 neural units to observe the relationship between a unit's connectivity and activity relative to the motor periphery. The model displayed a strong similarity between the unit's torque preference (PTD) and the activity preference of its motor field (MFPTD) during the postural load task. However, the directional preferences were not identical, as there was a mean difference of 22°. Thus, in general, the activity of the unit during a task was a good indicator of its synaptic connectivity to the motor periphery. This was more accurate for the units that had strong unidirectional connectivity without strong synaptic connections to antagonist muscles.

The presence of PTD-MFPTD variability in the artificial neural network parallels previous experimental work demonstrating a statistical relationship between the muscle field of CM cells (defined by STA; Fetz and Cheney 1978) and the associated patterns of activity of forearm and hand muscles during a precision grip task (Bennett and Lemon 1994). In that study, the observed correlations were relatively modest, the highest of which was 0.69. Some of this variability may be explained by task-dependent variation in the connectivity using STA (Buys et al. 1986). However, our network model showed that a more complex pattern of synaptic connectivity may contribute to a lower overall correlation value. Ultimately, our model suggests that a perfect correlation will not exist between muscle fields and motor fields, as the neuronal activity reflects not only the activity of target muscles but also the activity of the rest of the network (Lillicrap and Scott 2013).

Our model also demonstrated that the preferred pattern of activity relative to the motor periphery remains relatively constant across motor behaviors. In other words, if a unit was maximally active when the elbow flexors were maximally active for postural loads, it will tend to be active when the elbow flexors are maximally active during reaching. A fixed motor field is consistent with the observation that neural responses can be predicted when loads are combined at the shoulder and elbow (Gribble and Scott 2002) and are similar for transient and sustained loads (Herter et al. 2009; Pruszynski et al. 2014). It is also consistent with several studies that highlight how the reaching directional preferences of neurons and muscles both tend to rotate similarly with applied curl fields (Cherian et al. 2013), changes in arm geometry (Scott and Kalaska 1997), or start position (Caminiti et al. 1991; Sergio and Kalaska 1997). Again, there is some dispersion in the directional preference across tasks or conditions, likely reflecting how unit activity is influenced by factors beyond its motor field. Methodology similar to the present study was used by Sergio et al. (2005) to examine M1 activity between isometric force production and a dynamic reaching paradigm. Their results show similar patterns of correlation between isometric force and reaching preferred direction that support the notion of M1 motor fields that persist across tasks. Here we show this specific correlation between the activity of M1 neurons and its motor field.

It is important to recognize that a fixed motor field does not mean that a neuron is always active when its associated muscles are active during voluntary motor actions. It has been shown that neurons strongly active during precision grip were much less active for power grip that required more muscle force (Muir and Lemon 1983). As well, load representations can change between posture and movement, but their directional preference remains relatively constant (Kurtzer et al. 2005) and can be only active when the muscle is used for a specific phase of movement (Griffin et al. 2015). Even when neural activity reflects features such as the direction of the spatial goal, these neurons likely remain associated with a specific body part such as the wrist (Kakei et al. 1999) or elbow/shoulder (Sergio and Kalaska 2003).

While the essential PRD and PTD patterns are quite similar between network model and real neurons, the variability in the difference between the PRDs and PTDs is notably greater in the neurons than in the model. There are many possible sources for this difference in observed variability. First, there is noise in the empirical estimates of the PRDs and PTDs, whereas in the model these quantities can be measured perfectly. As well, the only source of noise in the model, given a fixed and deterministic optimization procedure, is the random initialization of the weights, w. Second, our model assumes that all of the model cortical units directly contributed to driving muscle activity by way of monosynaptic connections. In reality, only a subset of M1 neurons project to the spinal cord, and most of these synapse predominantly on spinal interneurons and can be influenced by spinal processing. As well, we may expect neurons that do not project to the spinal cord—which may connect to other brain areas (Turner and DeLong 2000) or recurrently within M1—to show activity dissociated from the muscles. As well, motor cortical neurons reflect aspects of motor function beyond patterns of motor output, such as correlates of movement kinematics (Kalaska et al. 1989) and behavioral goals (Kakei et al. 1999). Neural activity is also context (Hepp-Reymond et al. 1999), phase (Griffin et al. 2015), and task (Buys et al. 1986; Kurtzer et al. 2005) dependent. These complexities will necessarily influence the relationship between motor cortical activity across postural and movement tasks and likely increase variability in the difference between their PRD and PTD.

At the same time, given the complexity of neural processing in M1 it is surprising that its activity can predict the patterns of muscle activity. The patterns are not exact, however, particularly related to activity patterns when the muscles are antagonists. The general similarity between M1 and muscle activity suggests that spinal processing is not dramatically altering descending commands (Lillicrap and Scott 2013). While adding an additional network layer to our model to simulate the influence of a spinal cord or other systems might have given us a higher network variability, adding complexity was not the aim of this study. We were not interested in exactly modeling the descending stream from M1 but rather in producing testable hypotheses that stem from a system with an unchanging relationship with the periphery.

Our analysis focused on exploring the relationship between M1 neurons and flexor and extensor muscle groups at the shoulder and elbow. However, this does not mean that M1 neurons are associated with all muscles within a given group or that they are only associated with a single muscle group. Most certainly M1 neurons synapse onto many motor neurons (directly or indirectly) including those in different muscle groups and muscles that span multiple joints as demonstrated with STA (Cheney and Fetz 1985; McKiernan et al. 1998; Smith and Fetz 2009). We find several neurons with load preferences related to combined flexor or extensor loads at the shoulder and elbow, a pattern of activity not observed for any muscles (Kurtzer et al. 2006b). These neurons likely have muscle fields that span both joints. Even those neurons with load preferences associated with a single muscle group likely have a motor field beyond that group.

The idea of a motor field is closely related to the idea of muscle synergies. While the basic definition of a muscle synergy is simply the cooperative action of two or more muscles, some theorize that the motor system simplifies control by only varying a small number of muscle synergies (d'Avella et al. 2006). One prediction from this theory is that there would be a fixed number of motor fields represented in a region like M1. In our postural load task, these synergies should appear as clusters of preferred loads in our M1 sample. In fact, the distribution of load preferences does appear to be clustered into two groups: one related to whole-limb flexion and one related to whole-limb extension (Herter et al. 2009; Kurtzer et al. 2006a). However, this bias appears to be due to the presence of biarticular muscles (Lillicrap and Scott 2013)—in a model with no biarticular muscles, the distribution of load preferences is relatively uniform with no obvious clustering. The units spanned all possible combinations of control, rather than showing a reduced set of controls. The spanned distribution was mirrored by the distributions of load and reach preferences observed for neurons in M1. As well, studies using STA also highlight diverse connectivity in their cell samples (Alstermark and Isa 2012; Smith and Fetz 2009). Thus there are likely many more motor fields (and muscle synergies) represented in M1 neurons than muscles in the body.

It was surprising to find atypical cells where the directional preference of the neuron during reaching was opposite to that of its muscle group identified from the postural load task. This subpopulation of neurons could not be identified in Scott (1997). In that study, neurons were first divided into elbow and shoulder groupings by their response to passive movement of the arm. Separation into flexor or extensor subgroups was defined by their preferred direction during reaching, and thus they would have simply been classified with the antagonist muscle group at that joint.

The onset time of this atypical population of neurons was delayed compared with neurons with directional preferences aligned with the directional preference of their motor field. One possible explanation is that these neurons are preferentially involved in controlling muscle activity when it is an antagonist to decelerate the limb. Drew and colleagues (Drew 1993; Drew et al. 2002) found that some M1 neurons in cats during locomotion were only active when a specific modification of the muscle activity was required, suggesting that the activity of some M1 neurons could be task dependent. Task-dependent processing in M1 has also been observed in previous reaching and posture comparisons (Kurtzer et al. 2005). While the latency between atypical and typical activity was much shorter than the latency between the muscular agonist and antagonist, a recent study by Griffin et al. (2015) also showed that cells that were functionally tuned for antagonist activity show activity only shortly after those tuned for agonist activity. The antagonist activity was relatively weak in the present study because of the speed of reaching and the contribution of friction from the exoskeleton assisting the deceleration of the limb. The potential contribution of these atypical neurons to controlling antagonist muscle activity could be examined by modifying the speed of the movement or inertia of the limb.

GRANTS

This work was supported by the Canadian Institutes of Health Research (CIHR). E. A. Heming received a Doctoral Award from National Sciences and Engineering Research Council. M. Omrani received a Vanier Doctoral Award from CIHR. J. A. Pruszynski received salary awards from CIHR and the Human Frontier Science Program. S. H. Scott is supported by a GSK-CIHR Chair in Neuroscience.

DISCLOSURES

S. H. Scott is associated with BKIN Technologies, which commercializes the KINARM device used in this study.

AUTHOR CONTRIBUTIONS

Author contributions: E.A.H. and T.P.L. analyzed data; E.A.H. and S.H.S. interpreted results of experiments; E.A.H. prepared figures; E.A.H. drafted manuscript; E.A.H., M.O., J.A.P., and S.H.S. edited and revised manuscript; T.P.L., M.O., T.M.H., and J.A.P. performed experiments; S.H.S. conception and design of research; S.H.S. approved final version of manuscript.